1 Introduction

The purpose of this paper is to establish a more complete theory of laminar flow in channels with porous walls that is modelled by a fourth order boundary value problem (BVP). We study the existence, uniqueness and approximation of solutions to the following nonlinear, fourth order differential equation

$$\begin{aligned} f^{(iv)} + \mathcal {R}(f'f'' - f f''') = 0, \ \ \ \eta \in [0,1], \end{aligned}$$
(1.1)

where \(f= f(\eta )\), \(\mathcal {R}\) is a Reynolds number and (1.1) is subject to the two-point boundary conditions:

$$\begin{aligned} f(0)=0, \ f''(0) = 0,&f'(1)=0, \ f(1) = 1. \end{aligned}$$
(1.2)

By a solution to the BVP (1.1), (1.2) we mean a function \(f:[0,1] \rightarrow {{\mathbb {R}}}\) such that f is four times differentiable, with a continuous fourth order derivative on [0, 1], which we denote by \(f \in C^4([0,1])\), and our f satisfies both (1.1) and (1.2) for some value of \(\mathcal {R}\).

Laminar flows in channels with porous walls have attracted the attention of applied mathematicians and engineers since the 1940 s. This is partly due to their connection with a diverse range of physical problems that are of significant interest. For example, in aeronautics the method of transpiration cooling has gained attention:

“

In this method, the surfaces to be protected against the influence of a hot fluid stream are manufactured from a porous material and a cold fluid is ejected through the wall to form a protective layer along the surface. Certain areas on the skin of high-velocity aircraft may be provided with these surfaces as protection against the influence of aerodynamic heating. Porous surfaces with suction also are used on airfoils and bodies of aircraft to delay separation or transition to turbulence; in these cases, the flow along the surface is of a boundary-layer type.” [4, pp. 1–2]

In addition, channel flows are seen in plants [6] and animals [9], where vascular systems distribute energy to where it is needed, and enable distal parts of the organism to communicate [8]. Furthermore, channels play a significant role in the transportation of liquids or gases and energy from sites of production to the consumer or industry [8], and the protection of channel walls via transpiration cooling is of primary interest in nuclear applications [4].

There are at least three significant points of distinction between our current work and the existing literature. They include: the mathematical form of the problem under consideration; the types of methods employed; and the nature of the results obtained. We discuss them below.

In much of the literature relating to laminar flow within channels with porous walls (and its variations) [3,4,5, 7, 8, 10,11,12,13,14, 17, 18, 22, 23], the majority of scholars have exclusively considered and analyzed the problem as an equivalent third order BVP

$$\begin{aligned} f''' + \mathcal {R}[(f')^2 - f f''] = K \end{aligned}$$

which was coupled with the three point conditions

$$\begin{aligned} f(0) = f'(1)=f''(0)=0 \end{aligned}$$

where the constant of integration K is to be determined from the remaining boundary condition \(f(1)=1\). There is a minority of authors who have analyzed the problem as equivalent third and fourth order BVPs (and, even fifth order, on occasion), however the attention on the third order problem mostly dominates the scientific discussion therein. Thus we can see that a focus on the equivalent fourth order BVP in the extent literature has not been prevelant. This may have been due to the authors therein favouring lower order problems perhaps due to a perception that its form is more agreeable to work with and seeing its potential to open up interesting avenues. The continued focus on the third order form of the BVP seen in the literature may also be partly due to human nature and the act of conditioning—we tend to see and continue to work with the mathematical forms that we have been conditioned and accustomed to.

In contrast, herein we take the position that the fourth order BVP (1.1), (1.2) presents a natural form to work with. For example, the form enables a complete integration between the differential equation and the boundary conditions, synthesizing the data from the problem as an integral equation. This is in contrast to third order approaches where there are constants of integration in the equation and a fourth “hanging” boundary condition to consider. In addition, the mathematical theory regarding solutions to fourth order BVPs has recently been advanced in directions [1] that potentially can shine new light on (1.1), (1.2) and so we feel that this presents a timely opportunity to directly work with the form of the fourth order BVP (1.1), (1.2).

Extent mathematical methods regarding laminar flow in channels with porous walls can be broadly grouped into: perturbation techniques; asymptotic approaches; numerical and initial value methods; and fixed point techniques with differential inequalities. The above approaches have enabled a deeper understanding of (1.1), (1.2) through: a development of series solutions [3, 11, 17, 18, 23]; fostering the existence and uniqueness of solutions [7, 10, 13, 22]; and furnishing multiple solutions [5, 7, 12] for various values of \(\mathcal {R}\). In particular, the dominant approach for the existence of solutions via fixed point theory has involved topological ideas, such as the Leray-Schauder degree theory. This has been subsequently coupled with uniqueness (or non-multiplicity) concepts involving differential inequalities and then separate approximation methods are drawn on to gain additional insight. In comparison, herein we introduce contraction mapping ideas in what appears to be a first time synthesis and application to the problem of laminar flow in channels with porous walls. There are several advantages in this synthesis. Firstly, a contractive mapping approach forms an integrated strategy towards existence, uniqueness and approximation of solutions by its very nature. Secondly, this synthesis does not depend on whether \(\mathcal {R}\) is positive or negative (unlike some previous approaches that concentrate on either suction or injection). Together, our synthesis offers a more integrated approach than previously developed strategies regarding the existence, uniqueness and numerical aspects of solutions.

Most importantly, our employment of contractive mappings enables an extension of previous results. While the case \(\mathcal {R}<0\) has been shown to possess a unique solution, the case \(\mathcal {R}>0\) is far more open, with the best range for the existence and uniqueness set in [22] at

$$\begin{aligned} 0< \mathcal {R}&< \frac{-(72\sqrt{3}+1) + \sqrt{(72\sqrt{3}+1)^2 + 12\sqrt{3}(72\sqrt{3} -24) }}{48(3\sqrt{3} -1)} \\&\approx 4.005014\times 10^{-2}. \end{aligned}$$

We extend this range herein by at least an order of magnitude.

Our results complement the recent and growing body of knowledge regarding the theory and applications of Navier-Stokes equations [15, 24], laminar flow [2, 19, 21, 27] and swirling flow [26] by establishing a firm mathematical foundation for the problem (1.1), (1.2).

Our paper is organized as follows. In Sect. 2 we briefly derive the problem (1.1), (1.2) with aims of completeness and context for our work, and to enable a comparison between the form of our equations and those that have been previously analyzed. Furthermore, we construct an integral equation that is equivalent to (1.1), (1.2) that forms the basis of our contractive mapping approach. In Sect. 3 we establish new bounds on integrals of various Green’s functions associated with (1.1), (1.2). Some of the estimates therein are sharp and they prove to be useful when developing our main existence, uniqueness and approximation results in Sect. 4. Therein we establish the main results drawing on an approach involving contractive mappings and fixed point theory. We conclude with some open problems for further investigation in Sect. 5.

2 Formulation of the problem

Let us briefly derive the equations of interest, drawing on the ideas and exposition of Berman [3] and Robinson [12]. Further details may be found therein and in [11, 16,17,18, 23].

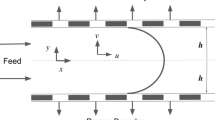
Consider a channel with a rectangular cross section. One side of the cross section that represents the distance between the porous walls is much smaller than the other, and this constraint enables an analysis of the problem as an instance of two-dimensional flow.

Furthermore, consider the steady, incompressible, laminar flow where the fluid is subject to either injection or suction with constant velocity \(\mathcal {V}\) through the walls. We assume that both channel walls have equal permeability.

We choose a coordinate system so that its origin is placed at the centre of the channel. Let x and y denote the co-ordinate axes that are, respectively, parallel and perpendicular to the channel walls, and let \(u=u(x,y)\) and \(v=v(x,y)\) denote the velocity components in the x and y directions, respectively. Let the width of the channel (ie, the distance between the walls) be 2h and let the channel have length L.

Let \(p=p(x,y)\) denote the pressure that we assume is a sufficiently smooth function. Let \(\rho \) denote the density of the fluid and let \(\nu \) denote the constant kinematic viscosity of the fluid. Under the assumed conditions and choice of axes, we introduce the dimensionless variable

$$\begin{aligned} \eta =\frac{y}{h} \end{aligned}$$

and then the Navier–Stokes equations can be expressed as

$$\begin{aligned}&u \frac{\partial u}{\partial x} + \frac{v}{h} \frac{\partial u}{\partial \eta } = - \frac{1}{\rho } \frac{\partial p}{\partial x} + \nu \left( \frac{\partial ^2 u}{\partial x^2} + \frac{1}{h^2} \frac{\partial ^2 u}{\partial \eta ^2}\right) \end{aligned}$$
(2.1)
$$\begin{aligned}&u \frac{\partial v}{\partial x} + \frac{v}{h} \frac{\partial v}{\partial \eta } = - \frac{1}{h \rho } \frac{\partial p}{\partial \eta } + \nu \left( \frac{\partial ^2 v}{\partial x^2} + \frac{1}{h^2} \frac{\partial ^2 v}{\partial \eta ^2}\right) . \end{aligned}$$
(2.2)

The continuity equation takes the form

$$\begin{aligned} \frac{\partial u}{\partial x} + \frac{1}{h} \frac{\partial v}{\partial \eta } = 0 \end{aligned}$$

and the associated boundary conditions are

$$\begin{aligned} u(x,\pm 1) = 0,&v(x,0)=0 \\ v(x,\pm 1) = \pm \mathcal {V},&\frac{\partial u}{\partial \eta }(x,0) = 0. \end{aligned}$$

For a two-dimensional incompressible flow, a stream function \(\psi \) exists such that

$$\begin{aligned} u(x,\eta )= & {} \frac{1}{h} \frac{\partial \psi }{\partial \eta } \end{aligned}$$
(2.3)
$$\begin{aligned} v(x,\eta )= & {} - \frac{\partial \psi }{\partial x} \end{aligned}$$
(2.4)

with the continuity equation being satisfied.

Due to a symmetrical flow about the plane lying midway between the channel walls, we will analyze the solution over half of the channel, i.e., from the midplane to one wall.

For constant wall velocity \(\mathcal {V}\), Berman [3] cleverly observed that the equations of motion and the boundary conditions could be satisfied under an assumption that the velocity component v is independent of x and he skillfully introduced a stream function, \(\psi \), of the form

$$\begin{aligned} \psi (x,\eta ):= [h{{\bar{u}}}(0) - \mathcal {V} x]f(\eta ) \end{aligned}$$

where f is a suitably smooth function of the distance parameter \(\eta \) and f is to be determined later. In addition, \({{\bar{u}}}(0)\) is an arbitrary velocity at \(x = 0\) that will be managed away in due course.

From (2.3) and (2.4) we can derive the velocity components

$$\begin{aligned} u(x,\eta )= & {} \left[ {{\bar{u}}}(0) - \mathcal {V} \frac{x}{h} \right] f'(\eta ) \end{aligned}$$
(2.5)
$$\begin{aligned} v(x,\eta )= & {} v(\eta )= \mathcal {V} f(\eta ). \end{aligned}$$
(2.6)

For constant wall velocity \(\mathcal {V}\), the y component of velocity v becomes a function of \(\eta \) only. If (2.5) and (2.6) are substituted into the equations of motion then we obtain

$$\begin{aligned} -\frac{1}{\rho }\frac{\partial p}{\partial x}= & {} \left[ {{\bar{u}}}(0) - \mathcal {V} \frac{x}{h}\right] \left[ - \frac{\mathcal {V}}{h} [ (f')^2 -ff''] - \frac{\nu }{h^2}f''' \right] \end{aligned}$$
(2.7)
$$\begin{aligned} -\frac{1}{h \rho }\frac{\partial p}{\partial \eta }= & {} \frac{v}{h} \frac{dv}{d\eta } - \frac{\nu }{h^2} \frac{d^2 v}{d \eta ^2}. \end{aligned}$$
(2.8)

The right-hand side of (2.8) is seen to be a function of \(\eta \) only and so differentiation with respect to x yields

$$\begin{aligned} \frac{\partial ^2 p}{\partial x \partial \eta } =0. \end{aligned}$$

If we now differentiate (2.7) with respect to \(\eta \) then we obtain

$$\begin{aligned} \left[ {{\bar{u}}}(0) - \mathcal {V} \frac{x}{h} \right] \frac{d}{d \eta } \left[ \frac{ \mathcal {V}}{h} [(f')^2 - f f''] + \frac{\nu }{h^2} f''' \right] = \frac{\partial ^2 p}{\partial \eta \partial x} \end{aligned}$$

and employing the symmetry of mixed partial derivatives of p we thus obtain

$$\begin{aligned} \left[ {{\bar{u}}}(0) - \mathcal {V} \frac{x}{h} \right] \frac{d}{d \eta } \left[ \frac{ \mathcal {V}}{h} [(f')^2 - f f''] + \frac{\nu }{h^2} f''' \right] = 0. \end{aligned}$$

If the above equation is to hold for all x then we must have

$$\begin{aligned} 0= & {} \frac{d}{d \eta } \left[ \frac{ \mathcal {V}}{h} [(f')^2 - f f''] + \frac{\nu }{h^2} f''' \right] \\= & {} f^{(iv)} + \mathcal {R}[f' f'' - f f''' ] \end{aligned}$$

where

$$\begin{aligned} \mathcal {R}:= \frac{ \mathcal {V} h}{\nu } \end{aligned}$$

is a Reynolds number and we have thus derived (1.1).

The boundary conditions on the function f and its derivatives are obtained from (2.5) and (2.6) to produce (1.2). Note that we have \(\mathcal {R} > 0\) for suction at both walls and \(\mathcal {R} < 0\) for injection at both walls.

Let us establish an equivalency between the BVP (1.1), (1.2) and an integral equation. The integral equation will be critical in Sect. 3 to develop our main results.

Theorem 2.1

The BVP (1.1), (1.2) is equivalent to the integral equation

$$\begin{aligned} f(\eta ) = \int _0^1 G(\eta ,s) \mathcal {R}\left( f'(s)f''(s) - f(s)f'''(s) \right) \ ds + \phi (\eta ), \ \ \ \eta \in [0,1].\nonumber \\ \end{aligned}$$
(2.9)

Above: \(G(\eta ,s)\) is a Green’s function given explicitly by

$$\begin{aligned} G(\eta ,s):= \frac{1}{12} \left\{ \begin{array}{lr} s(1-\eta )^2 [(s^2-3)\eta + 2s^2], &{} \text{ for } \ 0 \le s \le \eta \le 1, \\ \eta (1-s)^2 [(\eta ^2-3)s + 2\eta ^2], &{} \text{ for } \ 0 \le \eta \le s \le 1; \end{array}\right. \end{aligned}$$
(2.10)

and \(\phi \) is given by

$$\begin{aligned} \phi (\eta ) = \frac{1}{2}(3\eta - \eta ^3). \end{aligned}$$
(2.11)

Proof

It is sufficient to construct f from the form

$$\begin{aligned} f(\eta ) = \phi _1(\eta ) + \phi (\eta ) \end{aligned}$$

where \(\phi \) is the solution to

$$\begin{aligned} \phi ^{(iv)} = 0; \ \ \phi (0) = 0, \ \phi ''(0) = 0, \ \phi (1)=1, \ \phi '(1)=0; \end{aligned}$$

and \(\phi _1\) is the solution to

$$\begin{aligned} \phi _1^{(iv)} + \mathcal {R}(\phi _1'\phi _1'' - \phi _1 \phi _1''') = 0; \ \phi _1(0) = 0, \ \phi _1''(0) = 0, \ \phi _1(1)=0, \ \phi _1'(1)=0. \end{aligned}$$

Direct integration and determination of the associated constants shows that

$$\begin{aligned} \phi (\eta ) = \frac{1}{2}(3\eta - \eta ^3). \end{aligned}$$

Integrate both sides of the differential equation for \(\phi _1\) from \(s = 0\) to \(s=\eta \) four times to obtain

$$\begin{aligned} \phi _1(\eta )&= -\frac{1}{6} \int _0^\eta (\eta -s)^3 \mathcal {R}\left( \phi _1'(s)\phi _1''(s) - \phi _1(s)\phi _1'''(s) \right) \ ds \nonumber \\&\quad + A\eta ^3 + B\eta ^2 +C \eta + D \end{aligned}$$
(2.12)

and we determine the constants of integration A, B, C, D from the homogeneous boundary conditions for \(\phi _1\). Our left-hand conditions \(\phi _1(0)=0\) and \(\phi _1''(0)=0\) ensure \(D=0\) and \(B=0\), respectively. In addition, employing the right-hand conditions, we obtain

$$\begin{aligned}&\phi _1(1) =0= -\frac{1}{6} \int _0^1 (1-s)^3 \mathcal {R}\left( \phi _1'(s)\phi _1''(s) - \phi _1(s)\phi _1'''(s) \right) \ ds + A +C\\&\phi _1'(1) = 0= -\frac{1}{2} \int _0^1 (1-s)^2 \mathcal {R}\left( \phi _1'(s)\phi _1''(s) - \phi _1(s)\phi _1'''(s) \right) \ ds + 3 A +C. \end{aligned}$$

Solving the above system of equations for A and C we obtain

$$\begin{aligned} A= & {} \frac{1}{12} \left[ \int _0^1 \left[ 3(1-s)^2 - (1-s)^3\right] \mathcal {R}\left( \phi _1'(s)\phi _1''(s) - \phi _1(s)\phi _1'''(s) \right) \ ds\right] \\= & {} \frac{1}{12}\left[ \int _0^\eta (1-s)^2(s+2) \mathcal {R}\left( \phi _1'(s)\phi _1''(s) - \phi _1(s)\phi _1'''(s) \right) \ ds \right. \\&\left. + \int _\eta ^1 (1-s)^2(s+2) \mathcal {R}\left( \phi _1'(s)\phi _1''(s) - \phi _1(s)\phi _1'''(s) \right) \ ds \right] \\ C= & {} \frac{1}{6}\int _0^1(1-s)^3\mathcal {R}\left( \phi _1'(s)\phi _1''(s) - \phi _1(s)\phi _1'''(s) \right) \ ds - A \\= & {} \frac{1}{12} \left[ \int _0^\eta (1-s)^2(-3s)\mathcal {R}\left( \phi _1'(s)\phi _1''(s) - \phi _1(s)\phi _1'''(s) \right) \ ds \right. \\&+ \left. \int _\eta ^1 (1-s)^2(-3s)\mathcal {R}\left( \phi _1'(s)\phi _1''(s) - \phi _1(s)\phi _1'''(s) \right) \ ds \right] . \end{aligned}$$

Substituting these expressions into (2.12) and applying some algebraic manipulation finally leads us to the form (2.9).

Direct differentiation of our f with the aforementioned values of A and C lead us to the differential equation (1.1). Substitution of appropriate values of \(\eta \) into (2.9) and its derivatives reveals that the boundary conditions (1.2) also hold. \(\square \)

3 Bounds on the Green’s functions

Let us now establish some new bounds involving the integral of the Green’s function in (2.10) and its derivatives. The results will be applied in Sect. 4 to form our main existence, uniqueness and approximation results. In addition, the bounds are of independent mathematical interest as they have the potential to be helpful outside the scope of the present article, for example, in topological approaches to BVPs.

Our first result establishes the non-positivity of G and a new, sharp bound on the integral of |G|.

Theorem 3.1

The Green’s function G in (2.10) satisfies \(G\le 0\) on \([0,1]\times [0,1]\) and

$$\begin{aligned} \int _0^1 |G(\eta ,s) | \ ds \le \frac{39 + 55\sqrt{33}}{65536} < \frac{3}{500}=:\beta _0, \ \text {for all} \ \eta \in [0,1]. \end{aligned}$$
(3.1)

Our estimate is sharp in the sense it is the best result possible.

Proof

For \(0\le s \le \eta \le 1\) we have

$$\begin{aligned} (s^2-3)\eta + 2s^2 = s^2(\eta +2) - 3\eta \le \eta ^2(\eta +2) - 3\eta \le 0 \end{aligned}$$

and so

$$\begin{aligned} s(1-\eta )^2 [(s^2-3)\eta + 2s^2] \le 0 \end{aligned}$$

therein. Similarly, for \(0\le \eta \le s \le 1\) we have

$$\begin{aligned} (\eta ^2-3)s + 2\eta ^2 \le s^2(s+2) - 3s \le 0 \end{aligned}$$

and the non-positivity of G thus also holds on this region.

Combining the above two cases we obtain \(G\le 0\) on \([0,1]\times [0,1]\).

For all \(\eta \in [0,1]\) consider

$$\begin{aligned}&\int _0^1 |G(\eta ,s)| \ ds = -\int _0^1 G(\eta ,s) \ ds \\&=-\frac{1}{12}\left[ \int _0^\eta s(1-\eta )^2 [(s^2-3)\eta + 2s^2] \ ds + \int _\eta ^1 \eta (1-s)^2 [(\eta ^2-3)s + 2\eta ^2] \ ds \right] \\ \\&=\frac{\eta ^4}{24} - \frac{\eta ^3}{16} + \frac{\eta }{48}\\ \\&=\frac{1}{48}\eta (2\eta + 1)(\eta -1)^2. \end{aligned}$$

If we apply calculus to the above quartic function then we see that it achieves its maximum value on [0, 1] at

$$\begin{aligned} \eta ^* = \frac{1 + \sqrt{33}}{16} \end{aligned}$$

which may be substituted into the above quartic function to obtain

$$\begin{aligned} \max _{\eta \in [0,1]} \int _0^1 |G(\eta ,s)| \ ds= & {} \int _0^1 |G(\eta ^*,s)| \ ds \\= & {} \frac{39 + 55\sqrt{33}}{65536} < \frac{3}{500}. \end{aligned}$$

\(\square \)

Our second result complements Theorem 3.1 by generating a new bound on the integral of \(|\partial G/\partial \eta |\).

Theorem 3.2

The Green’s function G in (2.10) satisfies

$$\begin{aligned} \int _0^1 \left| \frac{\partial }{\partial \eta }G(\eta ,s) \right| \ ds < \frac{1}{25} =:\beta _1, \ \text {for all} \ \eta \in [0,1]. \end{aligned}$$
(3.2)

Proof

For all \(\eta \in [0,1]\) consider

$$\begin{aligned}&\int _0^1 \left| \frac{\partial }{\partial \eta } G(\eta ,s) \right| \ ds \\ \\= & {} \int _0^\eta \left| \frac{(\eta -1)s((s^2 - 3)\eta +s^2+ 1)}{4}\right| \ ds + \int _\eta ^1 \left| \frac{(1-s)^2((\eta ^2 -1)s+ 2\eta ^2)}{4} \right| \ ds \\\le & {} \frac{1}{4} \left[ \int _0^\eta (1-\eta )s(-(s^2 - 3)\eta +s^2+ 1)\ ds + \int _\eta ^1 (1 - s)^2(-(\eta ^2 -1)s+ 2\eta ^2) \ ds \right] \\= & {} -\frac{7}{36}\eta ^5 + \frac{1}{3}\eta ^4 - \frac{1}{3} \eta ^3 + \frac{25}{144}\eta ^2 + \frac{1}{48}\\ \\= & {} \frac{1}{144}(1-\eta )(28\eta ^4- 20 \eta ^3 + 28\eta ^2+3\eta + 3). \end{aligned}$$

Now, if we apply calculus to the above quintic function then we see that it achieves its maximum value on [0, 1] at

$$\begin{aligned} \eta ^*=\frac{(13378 + 70\sqrt{94137})^{2/3} + 32(13378 + 70\sqrt{94137})^{1/3} - 656}{70(13378 + 70\sqrt{94137})^{1/3}} \end{aligned}$$

which may be substituted into the above quintic function to obtain

$$\begin{aligned}&\max _{\eta \in [0,1]} \int _0^1 \left| \frac{\partial }{\partial \eta } G(\eta ,s) \right| \ ds \\\le & {} \frac{(-9228485\sqrt{94137} + 14747147607)(13378 + 70\sqrt{94137})^{1/3}}{19373188800000} + \frac{13592477}{360150000} \\&+ \frac{(-2111935 \sqrt{94137} + 317136861) (13378 + 70 \sqrt{94137})^{2/3}}{19373188800000} \\< & {} \frac{1}{25}. \end{aligned}$$

\(\square \)

Our third result constructs a new bound on the integral of \(|\partial ^2 G / \partial \eta ^2|\).

Theorem 3.3

The Green’s function G in (2.10) satisfies

$$\begin{aligned} \int _0^1 \left| \frac{\partial ^2}{\partial \eta ^2} G(\eta ,s) \right| \ ds \le \frac{9}{8} =:\beta _2, \ \text {for all} \ \eta \in [0,1]. \end{aligned}$$
(3.3)

Proof

For all \(\eta \in [0,1]\) consider

$$\begin{aligned}&\int _0^1 \left| \frac{\partial ^2}{\partial \eta ^2} G(\eta ,s) \right| \ ds \\= & {} \int _0^\eta \left| \frac{s((s^2 - 3)\eta + 2)}{2}\right| \ ds + \int _\eta ^1 \left| \frac{\eta (s^3 - 3s + 2)}{2} \right| \ ds \\\le & {} \int _0^\eta \frac{s(-(s^2 - 3)\eta + 2)}{2} \ ds + \int _\eta ^1 \frac{\eta (s^3 - 3s + 2)}{2} \ ds \\= & {} -\frac{1}{4}\left( \eta ^4 - 6\eta ^2 + 2\eta - \frac{3}{2}\right) \eta . \end{aligned}$$

The above quintic function is strictly increasing on [0, 1] and thus must achieve its maximum value on [0, 1] at \(\eta ^*=1\) which gives

$$\begin{aligned} \max _{\eta \in [0,1]} \int _0^1 \left| \frac{\partial ^2}{\partial \eta ^2} G(\eta ,s) \right| \ ds \le \frac{9}{8}. \end{aligned}$$

\(\square \)

Our final result constructs a new, sharp bound on the integral of \(|\partial ^3 G/\partial \eta ^3|\).

Theorem 3.4

The Green’s function G in (2.10) satisfies

$$\begin{aligned} \int _0^1 \left| \frac{\partial ^3}{\partial \eta ^3} G(\eta ,s) \right| \ ds \le \frac{5}{8} =:\beta _3, \ \text {for all} \ \eta \in [0,1]. \end{aligned}$$
(3.4)

Our estimate is sharp in the sense it is the best result possible.

Proof

For all \(\eta \in [0,1]\) consider

$$\begin{aligned}&\int _0^1 \left| \frac{\partial ^3}{\partial \eta ^3} G(\eta ,s) \right| \ ds \\= & {} \int _0^\eta \left| \frac{s(s^2-3)}{2}\right| \ ds + \int _\eta ^1 \left| \frac{(1-s)^2 (s + 2)}{2} \right| \ ds \\= & {} - \frac{1}{2} \int _0^\eta s(s^2-3) \ ds + \frac{1}{2} \int _\eta ^1 (1-s)^2 (s + 2) \ ds \\= & {} -\frac{1}{4} \eta ^4 + \frac{3}{2} \eta ^2 + \frac{3}{8} - \eta . \end{aligned}$$

The above function is increasing on [0, 1] and so must achieve its maximum value on [0, 1] at \(\eta ^*=1\). Thus, we have

$$\begin{aligned} \max _{\eta \in [0,1] }\int _0^1 \left| \frac{\partial ^3}{\partial \eta ^3} G(\eta ,s) \right| \ ds = \left[ \int _0^1 \left| \frac{\partial ^3}{\partial \eta ^3} G(\eta ,s) \right| \ ds \right] _{\eta =1} =\frac{5}{8} \end{aligned}$$

as claimed. \(\square \)

4 Existence, uniqueness and approximation

In this section, we formulate our main results regarding existence, uniqueness and approximation of solutions via fixed point methods under contraction mappings.

4.1 Metrics and spaces

Let us construct a metric in an appropriate metric space. Consider the set of real-valued functions that are defined on [0, 1] and are thrice continuously differentiable therein. Denote this space by \(C^3([0,1])\). For functions \(f,g\in C^3([0,1])\), consider the following metric on \( C^3([0,1])\):

$$\begin{aligned} d(f,g):= \max _{i \in \{0,1,2,3\}}\left\{ W_i \max _{\eta \in [0,1]} |f^{(i)}(\eta )-g^{(i)}(\eta )|\right\} ; \end{aligned}$$
(4.1)

where

$$\begin{aligned} W_0=1, \ W_1 = \frac{\beta _0}{\beta _1} = \frac{3}{20}, \ W_2 = \frac{\beta _0}{\beta _2} = \frac{2}{375}, \ W_3 = \frac{\beta _0}{\beta _3} = \frac{6}{625}. \end{aligned}$$
(4.2)

It is well known that the pair \((C^3([0,1]),d)\) form a complete metric space.

Let \(R>0\) be a constant and let \(\phi \) be defined in (2.11). Our analysis will involve the following set

$$\begin{aligned} B:= & {} \bigg \{ (\eta ,u,v,w, z) \in {{\mathbb {R}}}^5: \eta \in [0,1], \ |u - \phi (\eta )| \le R, \\&\quad |v - \phi '(\eta )| \le \frac{20}{3}R, \ |w - \phi ''(\eta )| \le \frac{375}{2}R, \ |z - \phi '''(\eta )| \le \frac{625}{6}R \bigg \}. \end{aligned}$$

We note that our \(\phi \) in (2.11) satisfies the following inequalities on [0, 1]:

$$\begin{aligned} |\phi | \le 1, \ |\phi '| \le 3/2, \ |\phi ''| \le 3, \ |\phi '''|\le 3. \end{aligned}$$
(4.3)

The following result establishes a critically important bound on parts of (1.1) and will be used in the proof of our main results. In particular, this bound will be of importance in establishing an invariance condition for a mapping between two balls.

Theorem 4.1

Let

$$\begin{aligned} h(u,v,w,z):= \mathcal {R}(vw - uz). \end{aligned}$$
(4.4)

We claim that h is bounded on B by

$$\begin{aligned} M:=|\mathcal {R}|\left[ \frac{8125}{6} R^2 + \frac{4901}{12}R + \frac{15}{2} \right] . \end{aligned}$$
(4.5)

Proof

For \((\eta ,u,v,w,z) \in B\) consider

$$\begin{aligned} |h(u,v,w,z)|= & {} |\mathcal {R}(vw - uz)| \\\le & {} |\mathcal {R}|\left( |v| \ |w| + |u| \ |z| \right) \\= & {} |\mathcal {R}| \left[ |(v - \phi '(\eta )+\phi '(\eta )|)(|w- \phi ''(\eta ) +\phi ''(\eta )|) \right. \\&+ \left. (|u - \phi (\eta ) + \phi (\eta )|) (|z - \phi '''(\eta ) + \phi '''(\eta )|) \right] \\\le & {} |\mathcal {R}| \left[ |(v - \phi '(\eta )| + |\phi '(\eta )|)(|w- \phi ''(\eta )| + |\phi ''(\eta )|) \right. \\&+ \left. (|u - \phi (\eta )| + |\phi (\eta )|) (|z - \phi '''(\eta )| + |\phi '''(\eta )|)\right] \\\le & {} |\mathcal {R}| \left[ \left( \frac{20}{3}R + \frac{3}{2} \right) \left( \frac{375}{2}R + 3 \right) + \left( R + 1 \right) \left( \frac{625}{6}R + 3 \right) \right] \\= & {} |\mathcal {R}|\left[ \frac{8125}{6} R^2 + \frac{4901}{12}R + \frac{15}{2} \right] . \end{aligned}$$

Above, we have repeatedly applied the triangle inequality and used the form of B and (4.3). \(\square \)

Unfortunately, the function h is not globally Lipschitz in the sense of (4.6) on the whole of \([0,1] \times {{\mathbb {R}}}^4\). A global Lipschitz state is a desirable condition in the theory and application of differential equations. However, by strategically restricting our attention to the subset B, the following result ensures that our h will be Lipschitz therein.

Theorem 4.2

Let

$$\begin{aligned} h(u,v,w,z):= \mathcal {R}(vw - uz). \end{aligned}$$

For given \(R>0\) and \({{\mathcal {R}}}\), our h is Lipschitz on B in the sense that there are non-negative constants \(L_i\) (not all zero) such that

$$\begin{aligned} |h(u_0,u_1,u_2,u_3)- & {} h(v_0,v_1,v_2,v_3)| \le \sum _{i=0}^3 L_i |u_i - v_i| \nonumber \\&\text {for all} \ (\eta ,u_0,u_1,u_2,u_3), (\eta ,v_0,v_1,v_2,v_3) \in B. \end{aligned}$$
(4.6)

Proof

It is sufficient to show that h has bounded partial deriatives on B. As we will see, these bounds can then act as the Lipschitz constants \(L_i\).

For all \((\eta ,u,v,w,z) \in B\) consider

$$\begin{aligned} \left| \frac{\partial h}{\partial u} \right|= & {} |- \mathcal {R} z| = |\mathcal {R}| |z - \phi '''(\eta ) + \phi '''(\eta )| \nonumber \\\le & {} |\mathcal {R}| [ |z - \phi '''(\eta )| +|\phi '''(\eta )|] \le |\mathcal {R}| \left[ \frac{625}{6}R + 3 \right] =: L_0. \end{aligned}$$
(4.7)

Also, we can also obtain the following inequalities on B via similar arguments

$$\begin{aligned} \left| \frac{\partial h}{\partial v} \right|\le & {} |\mathcal {R}| \left[ \frac{375}{2}R + 3\right] =: L_1 \end{aligned}$$
(4.8)
$$\begin{aligned} \left| \frac{\partial h}{\partial w} \right|\le & {} |\mathcal {R}| \left[ \frac{20}{3}R + \frac{3}{2}\right] =: L_2 \end{aligned}$$
(4.9)
$$\begin{aligned} \left| \frac{\partial h}{\partial z} \right|\le & {} |\mathcal {R}| \left[ R +1\right] =: L_3. \end{aligned}$$
(4.10)

By the fundamental theorem of calculus we have

$$\begin{aligned}&h(u_0,u_1,u_2,u_3) - h(v_0,v_1,v_2,v_3) \\&= \int _{v_0}^{u_0} \frac{\partial h}{\partial s}{(s,v_1,v_2,v_3)} \ ds + \int _{v_1}^{u_1} \frac{\partial h}{\partial t}{(u_0,t,v_2,v_3)} \ dt \\&\ + \int _{v_2}^{u_2} \frac{\partial h}{\partial q}{(u_0,u_1,q,v_3)} \ dq + \int _{v_3}^{u_3} \frac{\partial h}{\partial p}{(u_0,u_1,u_2,p)} \ dp \end{aligned}$$

and since all partial derivatives are bounded on B we thus have

$$\begin{aligned} |h(u_0,u_1,u_2,u_3) - h(v_0,v_1,v_2,v_3)|\le & {} \sum _{i=0}^3 \left| \int _{v_i}^{u_i} L_i \ dv \right| \\= & {} \sum _{i=0}^3 L_i |u_i - v_i|. \end{aligned}$$

\(\square \)

4.2 Contraction mapping approach

We will draw on the following fixed point theorem credited to Stefan Banach, see [25, Theorem 1.A]. It involves sufficient conditions under which a mapping will admit a unique fixed point, and generates a sequence that converges to this fixed point.

Theorem 4.3

Let X be a nonempty set and let d be a metric on X such that (X, d) forms a complete metric space. If the mapping \(T:X \rightarrow X\) satisfies

$$\begin{aligned} d(Tf,Tg) \le \alpha d(f,g), \ \text {for some} \ 0<\alpha <1 \ \text {and all} \ f,g\in X; \end{aligned}$$
(4.11)

then there is a unique \(z\in X\) such that \(Tz = z\). In addition, for any \(z_0\in X\) we have \(d(z_n,z) \rightarrow 0\) where \(z_n\) is a recursively defined sequence defined via \(z_{n+1}:=Tz_n\).

We are now in a position to synthesize our previous results to form our main results.

Theorem 4.4

If there is a \(R>0\) and \(\mathcal {R}\) such that

$$\begin{aligned} |\mathcal {R}|\left[ \frac{8125}{6} R^2 + \frac{4901}{12}R + \frac{15}{2} \right] \frac{3}{500}\le & {} R \end{aligned}$$
(4.12)
$$\begin{aligned} |\mathcal {R}| \left[ \frac{65}{4}R + \frac{4901}{2000} \right]< & {} 1 \end{aligned}$$
(4.13)

then the BVP (1.1), (1.2) admits a unique solution f with

$$\begin{aligned} (\eta ,f(\eta ),f'(\eta ),f''(\eta ),f'''(\eta )) \in B, \ \ \ \text {for all} \ \eta \in [0,1]. \end{aligned}$$

Proof

To avoid the repeated use of complicated constants and expressions we will draw on the notation defined earlier in this paper. Let the constants \(\beta _i\) be defined in (3.1), (3.2), (3.3), (3.4). Let the function h be defined in (4.4). Let the constants \(L_i\) be defined in (4.7), (4.8), (4.9), (4.10) and let M be defined in (4.5). Choose \(R>0\) to form B where R and \(\mathcal {R}\) satisfy (4.12) and (4.13). Based on the form (2.9), we define the operator \(T:C^3([0,1]) \rightarrow C^3([0,1])\) by

$$\begin{aligned} (Tf)(\eta ):= \int _0^1 G(\eta ,s) \mathcal {R}(f'(s)f''(s) - f(s)f'''(s)) \ ds + \phi (\eta ), \ \ \ \eta \in [0,1]. \end{aligned}$$

Consider the pair \((C^3([0,1]), d)\) where the constants \(W_i\) in our d in (4.1) are defined in (4.2). Our pair forms a complete metric space.

Now, for the constant \(R>0\) and function \(\phi \) in the definition of B, consider the following set \({{\mathcal {B}}}_R \subset C^3([0,1])\)

$$\begin{aligned} {{\mathcal {B}}}_R:= \{ f \in C^3([0,1]): d(f,\phi ) \le R\}. \end{aligned}$$

Since \({{\mathcal {B}}}_R\) is a closed subspace of \(C^3([0,1])\), the pair \(({{\mathcal {B}}}_R,d)\) forms a complete metric space.

Consider the operator \(T:{{\mathcal {B}}}_R \rightarrow C^3([0,1])\) where we have restricted its domain. We wish to show that there exists a unique \(f \in {{\mathcal {B}}}_R\) such that

$$\begin{aligned} Tf = f \end{aligned}$$

which is equivalent to proving the BVP (1.1), (1.2) has a unique solution in \({{\mathcal {B}}}_R\). (Any solutions lying in \(C^3([0,1])\) will also lie in \(C^4([0,1])\) as repeatedly differentiating (2.9) will show.)

To prove that our T has a unique fixed point in \({{\mathcal {B}}}_R\), we show that the assumptions of Theorem 4.3 hold with \(X={{\mathcal {B}}}_R\).

Let us show the invariance condition \(T:{{\mathcal {B}}}_R \rightarrow {{\mathcal {B}}}_R\) holds. For \(f\in {{\mathcal {B}}}_R\) and \(\eta \in [0,1]\), consider

$$\begin{aligned} |(Tf)(\eta ) - \phi (\eta )|\le & {} \int _0^1 |G(\eta ,s)| \ |\mathcal {R}(f'(s)f''(s) - f(s)f'''(s))| \ ds \\\le & {} M \int _0^1 |G(\eta ,s)| \ ds \\\le & {} M \beta _0 \\= & {} |\mathcal {R}|\left[ \frac{8125}{6} R^2 + \frac{4901}{12}R + \frac{15}{2} \right] \frac{3}{500}. \end{aligned}$$

Similarly,

$$\begin{aligned} |(Tf)'(\eta ) - \phi '(\eta )|\le & {} \int _0^1 \left| \frac{\partial }{\partial \eta } G(\eta ,s) \right| \ |\mathcal {R}(f'(s)f''(s) - f(s)f'''(s)))| \ ds \\\le & {} M \int _0^1 \left| \frac{\partial }{\partial \eta } G(\eta ,s) \right| \ ds \\\le & {} M \beta _1 \\= & {} |\mathcal {R}|\left[ \frac{8125}{6} R^2 + \frac{4901}{12}R + \frac{15}{2} \right] \frac{1}{25}. \end{aligned}$$

Thus

$$\begin{aligned} \frac{\beta _0}{\beta _1} |(Tf)'(\eta ) - \phi '(\eta )|\le & {} M \beta _0 \\= & {} |\mathcal {R}|\left[ \frac{8125}{6} R^2 + \frac{4901}{12}R + \frac{15}{2} \right] \frac{3}{500}. \end{aligned}$$

In addition, via similar arguments, we can obtain

$$\begin{aligned} |(Tf)''(\eta ) - \phi ''(\eta )|\le & {} M\beta _2, \\= & {} |\mathcal {R}|\left[ \frac{8125}{6} R^2 + \frac{4901}{12}R + \frac{15}{2} \right] \frac{9}{8};\\ |(Tf)'''(\eta ) - \phi '''(\eta )|\le & {} M\beta _3; \\= & {} |\mathcal {R}|\left[ \frac{8125}{6} R^2 + \frac{4901}{12}R + \frac{15}{2} \right] \frac{5}{8}; \end{aligned}$$

so that

$$\begin{aligned} \frac{\beta _0}{\beta _2} |(Tf)''(\eta ) - \phi ''(\eta )|\le & {} M \beta _0 = |\mathcal {R}|\left[ \frac{8125}{6} R^2 + \frac{4901}{12}R + \frac{15}{2} \right] \frac{3}{500}; \\ \frac{\beta _0}{\beta _3} |(Tf)'''(\eta ) - \phi '''(\eta )|\le & {} M \beta _0 = |\mathcal {R}|\left[ \frac{8125}{6} R^2 + \frac{4901}{12}R + \frac{15}{2} \right] \frac{3}{500}. \end{aligned}$$

Thus, for all \(f\in {{\mathcal {B}}}_R\) we have

$$\begin{aligned} d(Tf,\phi )\le & {} \max \{ M \beta _0, M \beta _0, M \beta _0, M\beta _0\}\\= & {} M\beta _0 \\= & {} |\mathcal {R}|\left[ \frac{8125}{6} R^2 + \frac{4901}{12}R + \frac{15}{2} \right] \frac{3}{500}\\\le & {} R \end{aligned}$$

by assumption (4.12). Hence, for all \(f\in {{\mathcal {B}}}_R\) we have \(Tf \in {{\mathcal {B}}}_R\) so that \(T:{{\mathcal {B}}}_R \rightarrow {{\mathcal {B}}}_R\).

Let us now show that T is contractive on \(\mathcal { B}_R\) with respect to d. For \(f,g \in \mathcal { B}_R\) and \(\eta \in [0,1]\), consider

$$\begin{aligned}&|(Tf)(\eta ) - (Tg)(\eta )| \\\le & {} \int _0^1 |G(\eta ,s)| \ |h(f(s),f'(s),f''(s),f'''(s)) - h(g(s),g'(s),g''(s),g'''(s)) | \ ds \\\le & {} \int _0^1 |G(\eta ,s)| \ \left( \sum _{i=0}^3 L_i\ |f^{(i)}(s) - g^{(i)}(s)| \right) \ ds \\\le & {} \beta _0 \left( L_0 d(f,g) + L_1 \frac{\beta _1}{\beta _0} d(f,g) + L_2 \frac{\beta _2}{\beta _0} d(f,g) + L_3 \frac{\beta _3}{\beta _0} d(f,g) \right) \\= & {} (L_0 \beta _0 + L_1 \beta _1 + L_2\beta _2 + L_3\beta _3)d(f,g)\\= & {} |\mathcal {R}| \left[ \frac{65}{4}R + \frac{4901}{2000} \right] d(f,g) \end{aligned}$$

where we have applied Theorem 4.2.

Similarly, we can show

$$\begin{aligned} |(Tf)'(\eta ) - (Tg)'(\eta )|\le & {} \beta _1\left( L_0 + L_1 \frac{\beta _1}{\beta _0} + L_2 \frac{\beta _2}{\beta _0}+L_3 \frac{\beta _3}{\beta _0} \right) d(f,g); \\ |(Tf)''(\eta ) - (Tg)''(\eta )|\le & {} \beta _2 \left( L_0 + L_1 \frac{\beta _1}{\beta _0} + L_2 \frac{\beta _2}{ \beta _0} + L_3 \frac{\beta _3}{\beta _0}\right) d(f,g);\\ |(Tf)'''(\eta ) - (Tg)'''(\eta )|\le & {} \beta _3\left( L_0 + L_1 \frac{\beta _1}{\beta _0} + L_2 \frac{\beta _2}{ \beta _0} + L_3 \frac{\beta _3}{\beta _0}\right) d(f,g). \end{aligned}$$

Thus, for all \(f,g \in \mathcal { B}_R\) we have

$$\begin{aligned} d(Tf,Tg)= & {} \max _{i \in \{0,1,2,3\}} \left\{ W_i \max _{\eta \in [0,1]} |(Tf)^{(i)}(\eta ) - (Tg)^{(i)}(\eta )) \right\} \\\le & {} (L_0 \beta _0 + L_1 \beta _1 + L_2\beta _2 + L_3\beta _3) d(f,g) \\= & {} |\mathcal {R}| \left[ \frac{65}{4}R + \frac{4901}{2000} \right] d(f,g). \end{aligned}$$

Due to our assumption (4.13) we see that T is a contractive map on \(\mathcal { B}_R\).

Hence all of the conditions of Theorem 4.3 hold with \(X=\mathcal { B}_R\). Theorem 4.3 is applicable and yields the existence of a unique fixed point to T that lies in \(\mathcal {B}_R\subset C^3([0,1])\). This solution is also in \(C^4([0,1])\) as can be verified by differentiating the integral equation (2.9). Thus we have equivalently shown that the BVP (1.1), (1.2) has a unique solution. \(\square \)

The question remains: when do the constraints (4.12) and (4.13) hold? The following result addresses this question by choosing a \(R>0\) that maximizes \(|\mathcal {R}|\).

Theorem 4.5

For all

$$\begin{aligned} |{{\mathcal {R}}}| < \frac{ 2000\sqrt{65}}{19500 + 4901 \sqrt{65}} \approx 0.2732360884 \end{aligned}$$

the BVP (1.1), (1.2) has a unique solution lying in B with

$$\begin{aligned} R = 3 \frac{\sqrt{65}}{325} \approx 0.07442084075. \end{aligned}$$

Proof

Note that (4.12) and (4.13) are equivalent to

$$\begin{aligned} |\mathcal {R}|\le & {} \frac{R}{\left[ \frac{8125}{6} R^2 + \frac{4901}{12}R + \frac{15}{2} \right] \frac{3}{500}} \end{aligned}$$
(4.14)
$$\begin{aligned} |\mathcal {R}|< & {} \frac{1}{\left[ \frac{65}{4}R + \frac{4901}{2000} \right] }. \end{aligned}$$
(4.15)

The two curves of the functions of R that make up the right-hand sides of the inequalities (4.14) and (4.15) intersect at

$$\begin{aligned} R = 3 \frac{\sqrt{65}}{325} \approx 0.07442084075. \end{aligned}$$

The value of these functions at their point of intersection is

$$\begin{aligned} \frac{ 2000\sqrt{65}}{19500 + 4901 \sqrt{65}} \approx 0.2732360884 \end{aligned}$$
(4.16)

and so, for values of \(|\mathcal {R}|\) strictly less than (4.16), both of our inequalities (4.12) and (4.13) will hold. Thus, for these values of R and \(\mathcal {R}\) the conclusion of Theorem 4.4 holds. \(\square \)

Remark 4.1

The range

$$\begin{aligned} |\mathcal {R}| < \frac{ 2000\sqrt{65}}{19500 + 4901 \sqrt{65}} \approx 2.732360884 \times 10^{-1} \end{aligned}$$

in Theorem 4.5 improves the result in [22] for \(\mathcal {R}>0\) who established the existence of a unique solution for

$$\begin{aligned} 0< \mathcal {R}&< \frac{-(72\sqrt{3}+1) + \sqrt{(72\sqrt{3}+1)^2 + 12\sqrt{3}(72\sqrt{3} -24) }}{48(3\sqrt{3} -1)} \\&\approx 4.005014\times 10^{-2}. \end{aligned}$$

We observe that our upper limit for \(\mathcal {R}\) is at least an order of magnitude higher than the result in [22].

Remark 4.2

Due to the rather small value of R in Theorem 4.5, the result can be interpreted as establishing the existence of a solution that uniquely lies within a thin strip, where the graph of function \(\phi \) lies at the centre, and

$$\begin{aligned} \left| f(\eta ) - \phi (\eta ) \right| = \left| f(\eta ) - \frac{1}{2}( 3 \eta - \eta ^3) \right| \le 3 \frac{\sqrt{65}}{325}, \ \ \ \text {for all} \ \eta \in [0,1]. \end{aligned}$$

Part of the significance with the small value of R can be related to the location of our solution. For small R we know that our solution cannot deviate “too much” from the known function \(\phi \).

Remark 4.3

Note that the conclusions of Theorem 4.4 and Theorem 4.5 say nothing about what might happen outside of the set B. Additional solutions may exist whose graphs are not completely contained in B.

Let us now pivot our attention to examine the approximation of solutions to (1.1), (1.2). The following results involve Picard iterants [20, Sec. 2] that will form approximations to the unique solution f of the BVP (1.1), (1.2). The following approximation results are a consequence of Theorem 4.3 holding for the operator T therein, see [25, Theorem 1.A].

Remark 4.4

Let the conditions of Theorem 4.5 hold. If we recursively define a sequence of approximations \(f_n = f_n(\eta )\) on [0, 1] via

$$\begin{aligned} f_0(\eta ):= & {} \phi (\eta ) = \frac{1}{2}(3\eta -\eta ^3) \\ f_{n+1}(\eta ):= & {} \int _0^1 \!\! G(\eta ,s) \mathcal {R}(f_n'(s) f_n''(s) - f_n(s) f_n'''(s))\ ds \!+\! f_0(\eta ), \ \ \ n\!=\!0,1,2,\cdots \end{aligned}$$

then:

  • the sequence \(f_n\) converges to the solution f of (1.1), (1.2) with respect to the d metric and the rate of convergence is given by

    $$\begin{aligned} d(f_{n+1},f)\le & {} (L_0 \beta _0 + L_1 \beta _1 + L_2\beta _2 + L_3 \beta _3) d(f_n,f) \\= & {} |\mathcal {R}| \left[ \frac{65}{4}R + \frac{4901}{2000} \right] d(f_n,f) \end{aligned}$$

  • for each n, an a priori estimate on the error is

    $$\begin{aligned} d(f_n,f)\le & {} \frac{ (L_0 \beta _0 + L_1 \beta _1 + L_2\beta _2 + L_3 \beta _3)^n}{1 - (L_0 \beta _0 + L_1 \beta _1 + L_2 \beta _2 + L_3 \beta _3) }d(f_1,\phi ) \\ \\= & {} \frac{\left[ |\mathcal {R}| \left[ \frac{65}{4}R + \frac{4901}{2000} \right] \right] ^n}{1 - |\mathcal {R}| \left[ \frac{65}{4}R + \frac{4901}{2000} \right] }d(f_1,\phi ) \end{aligned}$$

  • for each n, an a posteriori estimate on the error is

    $$\begin{aligned} d(f_{n+1},f)\le & {} \frac{(L_0 \beta _0 + L_1 \beta _1 + L_2\beta _2 + L_3\beta _3) }{1 - (L_0 \beta _0 + L_1 \beta _1 + L_2\beta _2 + L_3\beta _3) }d(f_{n+1},f_n) \\ \\= & {} \frac{|\mathcal {R}| \left[ \frac{65}{4}R + \frac{4901}{2000} \right] }{1 - |\mathcal {R}| \left[ \frac{65}{4}R + \frac{4901}{2000} \right] }d(f_{n+1},f_n). \end{aligned}$$

Remark 4.5

If we begin with \(f_0\) then we can compute

$$\begin{aligned} f_1(\eta )= & {} -\frac{\eta }{280}\left( \mathcal {R} \eta ^6 + (-3 \mathcal {R} + 140)\eta ^2 + 2\mathcal {R} - 420\right) \\ f_2(\eta )= & {} -\frac{\eta }{8736000} \left[ \left( \eta ^{14} - \frac{300}{77}\eta ^{13} - \frac{78}{11} \eta ^{10} + \frac{390}{7}\eta ^9 + \frac{65}{21}\eta ^8 \right. \right. \\&\left. - \frac{780}{7}\eta ^7 + \frac{1053}{49}\eta ^6 - \frac{234}{7}\eta ^4 + \frac{296027}{1617}\eta ^2 - \frac{58496}{539}) \right) \mathcal {R}^3 \\&+ \left( \frac{3640}{11}\eta ^{10} - 2600 \eta ^9 - 650 \eta ^8 + 23400 \eta ^7 - \frac{14040}{7} \eta ^6 + 8580 \eta ^4 \right. \\&\left. - \frac{6190600}{77} \eta ^2 + \frac{4107350}{77} \right) \mathcal {R}^2 \\&\left. +46800(\eta ^2 - 5)(-1 + \eta )^2 (\eta + 1)^2 \mathcal {R} + 4368000 \eta ^2 - 13104000 \right] \end{aligned}$$

One of the advantages in our method of approximation over that of perturbation techniques (eg, see Terrill’s [16]) is that there we have no constants of integration that need to be calculated and re-calculated with every step of the process. This leads to a much more streamlined and efficient sequence of appproximations than have been available in the previous literature.

5 Opportunities and conclusion

Let us briefly identify some potential open problems for further research.

Two of our estimates in Sect. 2 are sharp, while the remaining two appear to be of a rougher nature. Is it possible to sharpen the bounds in Sect. 2? This would have the potential to further extend the range of \(\mathcal {R}\) under which (1.1), (1.2) would admit a unique solution.

Is it possible to sharpen the conditions (4.12) and (4.13), perhaps via the consideration of alternative metrics or sets? Once again, this would potentially enable an extension of the range of \(\mathcal {R}\) that would ensure uniqueness of solutions.

In this work we have aimed to provide a more complete theory of existence, uniqueness and approximation of solutions to the BVP from laminar flow in channels with porous walls. We advanced the current state of play via a contractive mapping approach and extended the range of Reynolds number under which a unique solution exists.