Global practical stabilization of the double integrator system with an imperfect sensor and subject to a bounded disturbance

Abstract

This paper is concerned with global practical stabilization of the double integrator system with an imperfect sensor and subject to an additive bounded output disturbance. The imperfect sensor nonlinearity possesses the nonlinear characteristics of saturation and dead zone. Because of the presence of output dead zone and the additive disturbance, the states cannot be expected to driven into an arbitrarily small neighborhood of the origin. To solve the global practical stabilization problem, we proposes a low gain-based linear dynamic output feedback law, under which the first state enters and remains in a bounded set whose size is depended on the bound of disturbance and the range of dead zone and the second state enters and remains in a pre-specified arbitrarily small set, both in finite time. Simulation results illustrate the effectiveness of our proposed control method.

1 Introduction

Saturation nonlinearity is ubiquitous in control systems. In particular, sensor saturation, or output saturation, frequently occurs due to physical limitations. In the presence of saturation, the measurement of the sensor is inaccurate when the output enters the saturation region, which may lead to the degradation of system performance. Several results on systems subject to output saturation have been obtained. For example, it is pointed out in Ref. [1] that a single-input single-output linear system subject to output saturation can be globally asymptotically stabilized by a deadbeat controller. Such a control method was then extended to multiple-input multiple-output systems where the output saturation occurs on each component [2] and to the systems with direct feedthrough term [3]. For a neutrally stable linear system subject to output saturation, there exists linear output feedback control laws that achieve global asymptotic stabilization [4]. Furthermore, it is established in Ref. [5] that linear dynamic feedbacks can globally asymptotically stabilize the double integrator system, an unstable linear system, in the presence of output saturation. In Ref. [6], a low gain-based linear dynamic output feedback law is proposed to solve the global practical stabilization problem of the double integrator system subject to output saturation and an additive bounded disturbance. On the other hand, Ref. [7] established that semi-global asymptotic stabilization of a single-input single-output system in the presence of output saturation can be achieved as long as all its invariant zeros are in the closed left-half plane. In the presence of output saturation and output-additive disturbances, an output feedback $\textrm{H}_\infty$ controller was designed in Ref. [8] to solve the local stabilization problem.

Besides saturation, dead-zone nonlinearity is also common in practice. Many efforts have been made in the analysis and design of control systems in the presence of dead-zone nonlinearity. For example, adaptive control designs were proposed in Refs. [9, 10] to deal with unknown dead-zone nonlinearities. Reference [11] considered imperfect actuators that exhibit both saturation and dead-zone nonlinearities, and designed low-and-high gain feedback laws to solve the semi-global stabilization problem for linear systems. Moreover, for a multi-agent system, with an imperfect actuator for each agent, two types of consensus control algorithms, the low-and-high gain feedback and the low gain-based variable structure control, were proposed in Ref. [12] to achieve the semi-global leader-following practical consensus.

In this paper, we focus on the double integrator system with an imperfect sensor and subject to a bounded additive output disturbance, and consider its global practical stabilization. Here, the imperfect sensor is characterized by saturation and dead-zone nonlinearities. Differently from the practical stabilization for systems with input saturation [13] or imperfect actuator [12], in which all the systems states are to be driven into a pre-specified arbitrarily small neighborhood of the origin, practical stabilization with an imperfect sensor we consider in this paper aims for partial states to enter an arbitrarily small neighborhood of the origin. To solve the global practical stabilization problem, we design low gain-based linear dynamic output feedback laws, and propose a set of more relaxed conditions than Ref. [6] to determine the parameters of linear dynamic output feedback laws. Numerical example demonstrates the effectiveness of our proposed design.

The remainder of this paper is organized as follows. In Sect. 2, we present the system description and formulate the global practical stabilization problem. Then we establish three technical lemmas that will be useful in the design of the linear dynamic output feedback laws. In Sect. 3, we construct a family of low gain-based linear dynamic output feedback laws to achieve global practical stabilization of the double integrator system with an imperfect sensor and subject to a bounded disturbance. In Sect. 4, a numerical example demonstrates the effectiveness of our proposed design. Section 5 concludes the paper.

Notation: Throughout the paper, $\mathbb {R}$ denotes the set of real numbers. For a vector x and a matrix M, $x^\textrm{T}$ and $M^\textrm{T}$ denote their transposes. For two integers $l_1$ and $l_2$, $l_2 \geqslant l_1$, $I[l_1,l_2]$ denotes the set of integers $\left\{ l_1,l_1+1,\cdots ,l_2 \right\}$.

2 Preliminaries

Consider the double integrator system with an imperfect sensor and subject to an output-additive disturbance,

$$\begin{aligned} \left\{ \begin{aligned} \dot{x}&= A x + Bu,\\ y&= \sigma (Cx + d), \end{aligned} \right. \end{aligned}$$

(1)

where

$$\begin{aligned} A = \begin{bmatrix} 0 &{} \ 1\\ 0 &{} \ 0 \end{bmatrix},\ B = \begin{bmatrix} 0 \\ 1 \end{bmatrix},\ C = \begin{bmatrix} 1&\ 0 \end{bmatrix}, \end{aligned}$$

$x=[x_1\;x_2]^\textrm{T}\in \mathbb {R}^2$ is the state, $u\in \mathbb {R}$ is the control input, $y\in \mathbb {R}$ is the measured output, $d\in \mathbb {R}$ is a bounded disturbance, that is, $\vert d\vert \leqslant D$, for some positive scalar D, and $\sigma$ represents the input–output characteristic of the imperfect sensor, that is,

$$\begin{aligned} \sigma (s) = \left\{ \begin{array}{l@{~~}l} \varDelta ,&{} s >b+k^{-1}\varDelta ,\\ ks-kb,&{} b< s \le b+k^{-1}\varDelta ,\\ 0, &{} \vert s\vert \le b,\\ ks+kb,&{} -b-k^{-1}\varDelta \le s<-b, \\ -\varDelta ,&{} s < -b-k^{-1}\varDelta ,\\ \end{array} \right. \end{aligned}$$

where $\Delta >0$, $b \geqslant 0$, and $k>0$. The function $\sigma (s)$ exhibits both saturation and dead-zone nonlinearities and is depicted in Fig. 1.

Remark 1

In the definition of function $\sigma$, $\varDelta$ represents the saturation level, b the dead-zone break points, and k the linear slope. Without loss of generality, we can assume that $k = 1$. Otherwise, if $k \ne 1$, we can redefine $\sigma$ as $k^{-1}\sigma$ and add a linear gain k when using y as output feedback. When $b=0$ and $\varDelta =1$, function $\sigma$ simplifies to the standard saturation function.

Note that the linear system represented by (A, B, C) does not have any invariant zeros. It is clear that (A, B) is controllable and (A, C) is observable.

The objective of this paper is to solve the global practical stabilization problem for system (1). To be more specific, we would like to design a dynamic output feedback law such that, for any $x(0) \in \mathbb {R}^2$ and any small interval $s_0 \subset \mathbb {R}$ that contains the zero in its interior, the state $x_1(t)$ will enter and remain in a bounded set and the state $x_2(t)$ will enter and remain in $s_0$, both in finite time.

To deal with the nonlinear function $\sigma (s)$, we establish the following convex hull representation, which will be useful in solving the practical stabilization problem of system (1).

Fig. 1

The input–output characteristic of the imperfect sensor

Lemma 1

Let $v,u\in \mathbb {R}$ with $\vert v\vert \leqslant \varDelta$. Then,

$$\begin{aligned} \sigma (u) \in \textrm{co}\left\{ u-b,\ u+b,\ v\right\} , \end{aligned}$$

where $\textrm{co}$ denotes the convex hull.

Proof

If u resides the positive saturation region, that is, $u > b+\varDelta$, we have

$$\begin{aligned} \sigma (u)=\varDelta =\frac{\varDelta -v}{u-b-v}(u-b)+ \frac{u-b-\varDelta }{u-b-v}v. \end{aligned}$$

Since $\frac{\varDelta -v}{u-b-v}\in [0,1)$, $\frac{u-b-\varDelta }{u-b-v}\in (0,1]$ and $\frac{\varDelta -v}{u-b-v}+\frac{u-b-\varDelta }{u-b-v}=1$, we have $\sigma (u)\in \textrm{co}\left\{ u-b,v\right\}$. Considering that $\textrm{co}\left\{ u-b,v\right\} \subseteq \textrm{co}\left\{ u-b,\ u+b,\ v\right\}$, we have $\sigma (u) \in \textrm{co}\left\{ u-b,\ u+b,\ v\right\}$.

If u resides the positive linear region, that is, $b <u \leqslant b+\varDelta$, we obtain

$$\begin{aligned} \sigma (u)=u-b\in \textrm{co}\left\{ u-b,\ u+b,\ v\right\} . \end{aligned}$$

If u resides the dead-zone region, that is, $\vert u\vert \leqslant b$, we have

$$\begin{aligned} \begin{aligned} \sigma (u)&=0 =\frac{b-u}{2b}(u+b) + \frac{u+b}{2b}(u-b)\\&\in \textrm{co}\left\{ u+b,\ u-b \right\} , \end{aligned} \end{aligned}$$

since $\frac{b-u}{2b}\in [0,1]$, $\frac{u+b}{2b}\in [0,1]$ and $\frac{b-u}{2b}+\frac{u+b}{2b}=1$. Then, we have $\sigma (u) \in \textrm{co}\left\{ u-b,\ u+b,\ v\right\}$.

One can obtain the same convex hull representation of $\sigma (u)$ in the negative saturation and linear regions by a similar analysis. In summary, we finally have

$$\begin{aligned} \sigma (u) \in \textrm{co}\left\{ u-b,\ u+b,\ v\right\} . \end{aligned}$$

This completes the proof. $\square$

Before presenting the main result in this paper, we denote

$$\begin{aligned} \left\{ \begin{aligned}&k_1=h-l_2\not =0,\\&k_2= \frac{h}{h-l_2},\\&k_3=\frac{hl_1+g_1l_1}{h-l_2},\\&k_4=\frac{-g_2l_2h+g_2l_2^2+g_1l_1l_2+hl_1l_2}{(h-l_2)^2},\\&k_5=\frac{g_2h-g_2l_2-l_1l_2-g_1l_1}{h-l_2}.\\ \end{aligned}\right. \end{aligned}$$

(2)

Lemma 2

There exist scalars $g_1$, $g_2$, $l_1$, $l_2$, and h such that the following conditions hold:

$$\begin{aligned} \left\{ \begin{aligned}&k_1< 0,\\&k_2> 1,\\&k_3< 0,\\&k_4> 0,\\&k_5< 0,\\&k_2k_5 + k_4< k_5. \end{aligned} \right. \end{aligned}$$

(3)

Proof

It is easy to find a set of $k_i$’s, $i\in I[1,5]$, that meet all the conditions in (3). Then from the expressions of $k_1$ and $k_2$ in (2), we have

$$\begin{aligned} \left\{ \begin{aligned}&h= k_1k_2<0,\\&l_2= k_1(k_2 - 1)<0.\\ \end{aligned}\right. \end{aligned}$$

(4)

Inspecting the expressions of $k_3$, $k_4$, and $k_5$, we have

$$\begin{aligned} \begin{bmatrix} k_3 \\ k_4 \\ k_5 \end{bmatrix} =S \begin{bmatrix} g_2 \\ l_1 \\ g_1l_1 \end{bmatrix}, \end{aligned}$$

(5)

where

$$\begin{aligned} S=\begin{bmatrix} 0 &{} \dfrac{h}{h-l_2} &{} \dfrac{1}{h-l_2}\\ -\dfrac{l_2}{h-l_2} &{} \dfrac{hl_2}{(h-l_2)^2} &{} \dfrac{l_2}{(h-l_2)^2}\\ 1 &{} -\dfrac{l_2}{h-l_2} &{} -\dfrac{1}{h-l_2} \end{bmatrix}. \end{aligned}$$

Carrying out the elementary operations on S, one can find that matrix S is equivalent to the following matrix:

$$\begin{aligned} \overline{S}=\begin{bmatrix} 0 &{} 0 &{} 1\\ 0 &{} l_2 &{} 0\\ h-l_2 &{} -l_2 &{} -1 \end{bmatrix}. \end{aligned}$$

Note that $h-l_2=k_1<0$ and $l_2<0$. This ensures that matrix $\overline{S}$ is invertible, which implies that matrix S is also invertible. Thus, we can solve (5) for $g_2$, $l_1$, and $g_1$ as follows:

$$\begin{aligned} \left\{ \begin{aligned}&g_2=k_3-l^{-1}_2(h-l_2)k_4,\\&l_1=l^{-1}_2(h-l_2)k_4+k_5 \ne 0,\\&g_1=l^{-1}_1\left( (h-l_2)k_3-(h^2l^{-1}_2-h)k_4-hk_5\right) , \\ \end{aligned}\right. \end{aligned}$$

(6)

in which $l_1 \ne 0$ is ensured by $k_2 \ne 1$ and $k_2k_5 + k_4 \ne k_5$. This completes the proof. $\square$

Lemma 3

Given a set of $k_i$’s, $i\in I[1,5]$, that satisfy the conditions in (3), there exist scalars $p_i$, $i\in I[1,6]$, such that the following conditions hold:

$$\begin{aligned}&p_3k_4+p_5k_5 = 0, \end{aligned}$$

(7)

$$\begin{aligned}&p_2k_2 + p_4 = 0,\end{aligned}$$

(8)

$$\begin{aligned}&p_5k_1 + p_1 = 0, \end{aligned}$$

(9)

$$\begin{aligned}&p_2k_4 + p_4k_5 = -1, \end{aligned}$$

(10)

$$\begin{aligned}&p_1k_2 + p_6k_1 = 1, \end{aligned}$$

(11)

$$\begin{aligned}&p_5k_4 + p_6k_5 = \min \left\{ \frac{b+D}{4p_4k_1 \varDelta },-p_4k_2\right\} -p_4k_2. \end{aligned}$$

(12)

Proof

We will prove this lemma by providing a solution to Eqs. (7)–(12). From (8) and (10), we have

$$\begin{aligned} p_2 = -\frac{1}{k_4-k_2k_5}<0, \end{aligned}$$

and

$$\begin{aligned} p_4 = \frac{k_2}{k_4-k_2k_5}>0. \end{aligned}$$

(13)

From (9) and (11), we obtain

$$\begin{aligned} p_6 = k_1^{-1} + p_5k_2. \end{aligned}$$

(14)

Then substituting (13) and (14) into (12) yields

$$\begin{aligned} \begin{aligned}&2p_5k_4 + 2p_6k_5\\&= 2p_5(k_4+k_2k_5)+2k_5k_1^{-1}\\&=\min \left\{ \frac{(k_4 - k_2k_5)}{2k_1k_2}\frac{b+D}{\varDelta },\frac{-2k_2^2}{k_4 - k_2k_5}\right\} -\frac{2k_2^2}{k_4 - k_2k_5}\\&= \left\{ \begin{aligned}&\frac{-4k_2^2}{k_4 - k_2k_5},\ 0\leqslant \frac{b+D}{\varDelta } < \frac{-4k_1k_2^3}{(k_4-k_2k_5)^2},\\&\frac{(k_4 - k_2k_5)}{2k_1k_2}\frac{b+D}{\varDelta } - \frac{2k_2^2}{k_4 - k_2k_5},\ \text{ otherwise },\\ \end{aligned} \right. \end{aligned}\nonumber \\ \end{aligned}$$

(15)

from which we obtain the expression of $p_5$ as follows:

$$\begin{aligned} p_5 =\left\{ \begin{aligned}&\frac{\frac{-4k_2^2}{k_4 - k_2k_5}-\frac{2k_5}{k_1}}{2(k_4 + k_2k_5)},\ 0\leqslant \frac{b+D}{\varDelta } < \frac{-4k_1k_2^3}{(k_4-k_2k_5)^2},\\&\frac{\frac{(k_4 - k_2k_5)}{2k_1k_2}\frac{b+D}{\varDelta } - \frac{2k_2^2}{k_4 - k_2k_5}-\frac{2k_5}{k_1}}{2(k_4 + k_2k_5)},\ \text{ otherwise }.\\ \end{aligned} \right. \end{aligned}$$

Furthermore, substituting this expression of $p_5$ into (9), (7), and (14), we can obtain the expressions of $p_1$, $p_3$, and $p_6$. This completes the proof. $\square$

Denote

$$\begin{aligned} \overline{A} = \begin{bmatrix} 0 &{} \ 1 &{} \ k_2\\ 0 &{} \ 0 &{} \ k_4\varepsilon \\ k_1\varepsilon ^2 &{} \ 0 &{} \ k_5\varepsilon \end{bmatrix}, \end{aligned}$$

(16)

in which $\varepsilon \in (0,1]$ is a low gain parameter. If scalars $k_i$, $i\in I[1,5]$, have been determined to meet the conditions in (3), one can easily prove that $\overline{A}$ is Hurwitz. In what follows, we denote

$$\begin{aligned} P=\begin{bmatrix} p_1\varepsilon ^2 &{} \ p_2\varepsilon &{} \ p_4\varepsilon \\ p_2\varepsilon &{} \ p_3 &{} \ p_5\\ p_4\varepsilon &{} \ p_5 &{} \ p_6 \end{bmatrix}, \end{aligned}$$

(17)

and

$$\begin{aligned} Q = \begin{bmatrix} q_1\varepsilon ^3 &{} \ 0 &{} \ 0\\ 0 &{} \ q_2\varepsilon &{} \ 0\\ 0 &{} \ 0 &{} \ q_3\varepsilon \end{bmatrix}, \end{aligned}$$

in which

$$\begin{aligned} \begin{aligned} q_1&= -2p_4k_1,\\ q_2&= -2p_2,\\ q_3&= -2(p_4k_2+p_5k_4+p_6k_5). \end{aligned} \end{aligned}$$

(18)

If scalars $k_i$, $i\in I[1,5]$, and $p_i$, $i\in I[1,6]$, are selected to satisfy conditions (3) and (7)–(12), one can easily find that $q_i$, $i\in I[1,3]$, are positive, that is, $Q>0$. Moreover, denote

$$\begin{aligned} \begin{aligned} \xi _1&= p_1+p_5k_1,\\ \xi _2&= p_1k_2+p_2k_4+p_4k_5+p_6k_1,\\ \xi _3&= p_2k_2+p_3k_4+p_5k_5+p_4. \end{aligned} \end{aligned}$$

Then a simple calculation shows that

$$\begin{aligned}&\overline{A}^\textrm{T}P+P\overline{A}\nonumber \\&=\begin{bmatrix} 2p_4k_1\varepsilon ^3 &{} \xi _1\varepsilon ^2 &{} \xi _2\varepsilon ^2\\ \star &{} 2p_2\varepsilon &{} \xi _3\varepsilon \\ \star &{} \star &{} (2p_4k_2+2p_5k_4+2p_6k_5)\varepsilon \end{bmatrix}\nonumber \\&=\begin{bmatrix} 2p_4k_1\varepsilon ^3 &{} 0 &{} 0\\ 0 &{} 2p_2\varepsilon &{} 0\\ 0 &{} 0 &{} (2p_4k_2+2p_5k_4+2p_6k_5)\varepsilon \end{bmatrix}\nonumber \\&= -Q, \end{aligned}$$

(19)

where the second “$=$" holds because of (7)–(11). Since $\overline{A}$ is Hurwitz and $Q>0$, we have $P>0$.

3 Main results

In this section, we propose the following observer-based dynamic output feedback law to achieve global practical stabilization for system (1):

$$\begin{aligned} \left\{ \begin{aligned} \dot{z}&=Az+Bu+L(\varepsilon )(Cz-y), \\ u&=G(\varepsilon )z+H(\varepsilon )y,\\ \end{aligned} \right. \end{aligned}$$

(20)

where $z=[z_1\;z_2]^\textrm{T}\in \mathbb {R}^2$, the feedback gains $G(\varepsilon )$ and $H(\varepsilon )$ and the observer gain $L(\varepsilon )$ are parameterized in a low gain parameter $\varepsilon \in (0,1]$ as follows:

$$\begin{aligned} G(\varepsilon )=\begin{bmatrix} g_1\varepsilon ^2&{}g_2\varepsilon \\ \end{bmatrix},\ L(\varepsilon )=\begin{bmatrix} l_1\varepsilon \\ l_2\varepsilon ^2 \end{bmatrix},\ H(\varepsilon ) = h\varepsilon ^2, \end{aligned}$$

and the scalars $g_1$, $g_2$, $l_1$, $l_2$, and h will be determined later. The resulting closed-loop system can then be written as

$$\begin{aligned} \begin{bmatrix} \dot{x}\\ \dot{z} \end{bmatrix}=&\begin{bmatrix} A &{} BG\\ 0 &{} A+LC+BG \end{bmatrix} \begin{bmatrix} x \\ z \end{bmatrix}\nonumber \\&+ \begin{bmatrix} BH \\ BH-L \end{bmatrix} \sigma (Cx+d). \end{aligned}$$

(21)

Select a set of $k_i$’s, $i\in I[2,5]$, that meets the conditions in (3), and specify

$$\begin{aligned} k_1 = \frac{k_4^2+(k_2-1)k_4k_5}{(k_2-1)^2}. \end{aligned}$$

(22)

It is clear that $k_1<0$, which satisfies (3). Thus, by Lemma 2, we can determine the parameters $g_1$, $g_2$, $l_1$, $l_2$, and h according to (4) and (6). Suppose that the dynamic output feedback law (20) has been designed with these determined parameters $g_1$, $g_2$, $l_1$, $l_2$, and h. The following theorem establishes that the low gain-based dynamic output feedback laws globally practically stabilize system (1).

Theorem 1

Consider the double integrator system (1) under the linear dynamic output feedback law (20). For any given positive scalar D and an arbitrarily small interval $s_0 \subset \mathbb {R}$ that contains the zero in its interior, there exists $\varepsilon ^*\in (0,1]$ such that, for any $\varepsilon \in (0,\varepsilon ^*]$, the state trajectory of system (1) under (20) starting from any initial state in $\mathbb {R}^2$ will enter and remain in a bounded set and $x_2(t)$ will enter and remain in $s_0$, both in a finite time.

Proof

Define two new states $e_2$ and w as

$$\begin{aligned} e_2 =x_2-h(h-l_2)^{-1}z_2, \end{aligned}$$

and

$$\begin{aligned} w = (h-l_2)l^{-1}_1\varepsilon z_1+z_2. \end{aligned}$$

Then we can obtain

$$\begin{aligned} \dot{w} = k_3\varepsilon w+\big ((h-l_2)l^{-1}_1+g_2-k_3\big )\varepsilon z_2. \end{aligned}$$

Noting that $k_1 = (k_2-1)^{-2}\big ( k_4^2 + (k_2-1)k_4k_5 \big )$, we have

$$\begin{aligned} l_2 = k_1(k_2-1) = k_4\big (\frac{k_4}{k_2-1}+k_5 \big ). \end{aligned}$$

On the other hand, according to the expressions of $k_2$ and $l_1$, we have

$$\begin{aligned} l_1 = \frac{k_4}{k_2-1}+k_5, \end{aligned}$$

from which it follows that $l_2 = k_4l_1$. Then we have

$$\begin{aligned} l_2^{-1}(h-l_2)k_4 = l_1^{-1}(h-l_2). \end{aligned}$$

Hence, from the expression of $g_2$ in (6), we obtain

$$\begin{aligned} k_3 = g_2 + l_1^{-1}(h-l_2). \end{aligned}$$

Thus, we have $\dot{w} = k_3\varepsilon w$, and the closed-loop system (21) can be rewritten as

$$\begin{aligned} \begin{bmatrix} \dot{x}_1\\ \dot{e}_2 \\ \dot{z}_2 \\ \dot{w} \end{bmatrix} \!=\! \begin{bmatrix} 0 &{} \ 1 &{} \ k_2 &{} \ 0\\ 0 &{} \ 0 &{} \ k_4\varepsilon &{} \ k_6\varepsilon \\ 0 &{} \ 0 &{} \ k_5\varepsilon &{} \ k_7\varepsilon \\ 0 &{} \ 0 &{} \ 0 &{} \ k_3\varepsilon \end{bmatrix} \begin{bmatrix} x_1\\ e_2 \\ z_2 \\ w \end{bmatrix} \!+\! \begin{bmatrix} 0\\ 0\\ k_1\varepsilon ^2 \\ 0 \end{bmatrix}\sigma (x_1\!+\!d), \end{aligned}$$

(23)

where

$$\begin{aligned} k_6=\frac{-g_1l_1l_2-h l_1l_2}{(h-l_2)^2} \end{aligned}$$

and

$$\begin{aligned} k_7=\frac{l_1l_2+g_1l_1}{h-l_2}. \end{aligned}$$

Note that $\dot{w} = k_3 \varepsilon w$ is asymptotically stable since $k_3<0$. The practical stabilization problem of system (21) is then equivalent to that of the following reduced-order system:

$$\begin{aligned} \begin{bmatrix} \dot{x}_1\\ \dot{e}_2 \\ \dot{z}_2 \end{bmatrix}= & {} \begin{bmatrix} 0 &{} \ 1 &{} \ k_2\\ 0 &{} \ 0 &{} \ k_4\varepsilon \\ 0 &{} \ 0 &{} \ k_5\varepsilon \end{bmatrix} \begin{bmatrix} x_1 \\ e_2 \\ z_2 \end{bmatrix} + \begin{bmatrix} 0 \\ 0 \\ k_1\varepsilon ^2 \end{bmatrix} \sigma (x_1 + d) \nonumber \\= & {} \overline{A} \begin{bmatrix} x_1 \\ e_2 \\ z_2 \end{bmatrix} + \begin{bmatrix} 0 \\ 0 \\ k_1\varepsilon ^2 \end{bmatrix} \left( \sigma (x_1 + d) - x_1\right) , \end{aligned}$$

(24)

where matrix $\overline{A}$ is defined as (16). From (24),

$$\begin{aligned} \begin{aligned} \dot{z}_2&=k_5\varepsilon z_2+k_1\varepsilon ^2\sigma (x_1+d)\\&=k_5\varepsilon (z_2+k_1k^{-1}_5\varepsilon \sigma (x_1+d)). \end{aligned} \end{aligned}$$

Since $k_1<0$ and $k_5<0$, $z_2$ enters and remains in the set $[-k_1k^{-1}_5\varDelta \varepsilon ,\;k_1k^{-1}_5\varDelta \varepsilon ]$ in a finite time. Inside this set, $\vert z_2\vert \le B_z\varepsilon$, where $B_z=\vert k_1k^{-1}_5\varDelta \vert$. Partition the state space of system (1) into the following regions:

$$\begin{aligned} \begin{aligned}&S_{+} =\{ x\in \mathbb {R}^2: x_1>b+\varDelta +D\},\\&S_{0} =\{ x\in \mathbb {R}^2: \vert x_1\vert \leqslant b+\varDelta +D\},\\&S_{-} =\{ x\in \mathbb {R}^2: x_1<-b-\varDelta -D\}. \\ \end{aligned} \end{aligned}$$

Let

$$\begin{aligned} \tilde{x}_1 =\left\{ \begin{array}{ll} b+\varDelta +D,&{}~x \in S_+,\\ x_1,&{}~x \in S_0,\\ -b-\varDelta -D,&{}~x \in S_-, \end{array} \right. \end{aligned}$$

and $\zeta = [x_1\;e_2\;z_2]^\textrm{T}$. Choose the following Lyapunov function:

$$\begin{aligned} V(\zeta )= \begin{bmatrix} \tilde{x}_1\\ e_2\\ z_2 \end{bmatrix}^\textrm{T} P \begin{bmatrix} \tilde{x}_1\\ e_2\\ z_2 \end{bmatrix}+f(x), \end{aligned}$$

where

$$\begin{aligned} f(x)=\left\{ \begin{array}{ll} 2p_1\Delta \varepsilon ^2(x_1-b-\varDelta -D),&{}~x \in S_+,\\ 0,&{}~x \in S_0,\\ -2p_1\Delta \varepsilon ^2(x_1+b+\varDelta +D),&{}~x \in S_-, \end{array} \right. \end{aligned}$$

and matrix P is defined in (17) and its parameters, $p_i$, $i\in I[1,6]$, satisfy all the conditions in Lemma 3. The Lyapunov function $V(\zeta )$ is continuous in the whole state space and is positive for all non-zero states. It is worth mentioning that the Lyapunov function is piecewise and is not differentiable in the intersections $\partial S_+ = \{ x\in \mathbb {R}^2: x_1=b+\varDelta +D\}$ and $\partial S_- = \{ x\in \mathbb {R}^2: x_1=-b-\varDelta -D\}$. In this paper, to analyze the state trajectory of system (1) under the dynamic output feedback control law (20), we utilize the directional derivative of $V(\zeta )$ at $\zeta$ along $\dot{\zeta }$, that is,

$$\begin{aligned} \dot{V}(\zeta ) = \lim \limits _{t\rightarrow 0^+}{\frac{V(\zeta +t\dot{\zeta })-V(\zeta )}{t}}. \end{aligned}$$

Furthermore, we consider the following cases:

Case 1

$x\in S_+$ and $x+t\dot{x}\in S_+ \cup \partial S_+$. In this case, the Lyapunov function can be written as

$$\begin{aligned} \begin{aligned} V(\zeta ) =&p_1(b+\varDelta +D)^2\varepsilon ^2 + 2p_2(b+\varDelta +D)\varepsilon e_2\\&+ 2p_4(b+\varDelta +D)\varepsilon z_2 +p_3e_2^2 + 2p_5e_2z_2 \\&+p_6 z_2^2 +2p_1\varDelta \varepsilon ^2(x_1-b-\varDelta -D), \end{aligned} \end{aligned}$$

and the directional derivative of $V(\zeta )$ is equal to its time derivative, that is,

$$\begin{aligned} \dot{V} =&\ (2p_5k_4+2p_6k_5)\varepsilon z_2^2\\&+ (2p_2k_4+2p_4k_5+2p_6k_1 + 2p_1k_2)\varDelta \varepsilon ^2z_2\\&+ (2p_2k_4 + 2p_4k_5)(b+D)\varepsilon ^2z_2\\&+ 2p_4k_1(b+\varDelta +D)\varDelta \varepsilon ^3 + (2p_3k_4 + 2p_5k_5)\varepsilon e_2z_2 \\&+ (2p_5k_1 + 2p_1)\varDelta \varepsilon ^2 e_2\\ =&\ (2p_5k_4+2p_6k_5)\varepsilon z_2^2-2(b+D)\varepsilon ^2z_2\\&+ 2p_4k_1(b+\varDelta +D)\varDelta \varepsilon ^3, \end{aligned}$$

where the second “$=$" holds due to (7) and (9)–(11). Because of (12), we have

$$\begin{aligned} 2(p_5k_4 + p_6k_5)< \frac{b+D}{2p_4k_1 \varDelta } <0. \end{aligned}$$

Then, for any $z_2 \in \mathbb {R}$, the following inequality holds:

$$\begin{aligned} \frac{2(p_5k_4+p_6k_5)}{b+D}\varepsilon z_2^2-2\varepsilon ^2z_2+ 2p_4k_1\varDelta \varepsilon ^3 <0, \end{aligned}$$

from which, we have

$$\begin{aligned} \dot{V}(\zeta )< 2p_4k_1\varDelta ^2\varepsilon ^3<0. \end{aligned}$$

Case 2

$x\in \partial S_+$ and $x+t\dot{x}\in S_+$. In this case, $x_1 = b+\varDelta +D$. Then the directional derivative of $V(\zeta )$ is given as

$$\begin{aligned} \begin{aligned}&\hspace{-10pt}\dot{V}(\zeta ) \\ =&\lim \limits _{t\rightarrow 0^+}\frac{1}{t}\bigg ( 2p_2(b+\varDelta +D)\varepsilon (e_2+t\dot{e_2})\\&+ 2p_4(b+\varDelta +D)\varepsilon (z_2+t\dot{z_2})+p_3(e_2+t\dot{e_2})^2 \\&+ 2p_5(e_2+t\dot{e_2})(z_2+t\dot{z_2}) +p_6 (z_2+t\dot{z_2})^2\\&+2p_1\varDelta \varepsilon ^2t\dot{x_1}-2p_2(b+\varDelta +D)\varepsilon e_2\\&- 2p_4(b+\varDelta +D)\varepsilon z_2-p_3e_2^2 - 2p_5e_2z_2 -p_6 z_2^2\bigg ) \\ =&2(p_5k_4+p_6k_5)\varepsilon z_2^2-2(b+D)\varepsilon ^2z_2\\&+ 2p_4k_1(b+D)\varDelta \varepsilon ^3+ 2p_4k_1\varDelta ^2\varepsilon ^3\\<&2p_4k_1\varDelta ^2\varepsilon ^3<0. \end{aligned} \end{aligned}$$

From Cases 1 and 2, we can obtain that $\dot{V}(\zeta )<0$ for each $x\in S_+ \cup \partial S_+$. This implies that the state trajectory of the closed-loop system will leave the region $S_+$ in a finite time after it enters $S_+$. Similarly, we calculate the directional derivative $\dot{V}(\zeta )$ in Cases 3 and 4, and then we obtain that $\dot{V}(\zeta )<0$ for each $x\in S_-\cup \partial S_-$, where Case 3 is described as $x\in S_-$ and $x+t\dot{x}\in S_-\cup \partial S_-$ and Case 4 is described as $x\in \partial S_-$ and $x+t\dot{x}\in S_{-}$.

Case 5

$x\in S_{0}$ and $x+t\dot{x}\in S_0$. In this case, $\vert x_1\vert \leqslant b+\varDelta +D$ and the Lyapunov function can be written as

$$\begin{aligned} V(\zeta )= \begin{bmatrix} x_1\\ e_2\\ z_2 \end{bmatrix}^\textrm{T} P \begin{bmatrix} x_1\\ e_2\\ z_2 \end{bmatrix}. \end{aligned}$$

The directional derivative of $V(\zeta )$, which is equal to its time derivative, is given as

$$\begin{aligned} \dot{V} =&\begin{bmatrix} x_1\\ e_2 \\ z_2 \end{bmatrix}^\textrm{T} \left( \overline{A}^\textrm{T}P+P\overline{A}\right) \begin{bmatrix} x_1\\ e_2 \\ z_2 \end{bmatrix}\\&+ 2\begin{bmatrix} x_1\\ e_2 \\ z_2 \end{bmatrix}^\textrm{T} \begin{bmatrix} p_4k_1\varepsilon ^3\\ p_5k_1 \varepsilon ^2\\ p_6k_1\varepsilon ^2 \end{bmatrix} \big (\sigma (x_1+d) - x_1\big )\\ =&-\begin{bmatrix} x_1\\ e_2 \\ z_2 \end{bmatrix}^\textrm{T}Q \begin{bmatrix} x_1\\ e_2 \\ z_2 \end{bmatrix} + 2\left( p_4k_1\varepsilon ^3x_1+ p_5k_1\varepsilon ^2e_2\right. \\&\left. + p_6k_1\varepsilon ^2z_2\right) \big (\sigma (x_1+d) - x_1\big ). \end{aligned}$$

By Lemma 1, $\sigma (x_1+d)$ can be expressed as the following convex hull representation:

$$\begin{aligned} \begin{aligned} \sigma (x_1+d) \in \textrm{co}\Big \{&x_1+d-b,x_1+d+b,\ \frac{\varDelta x_1}{b+\varDelta +D} \Big \}. \end{aligned} \end{aligned}$$

Then, we have

$$\begin{aligned} \dot{V}(\zeta ) \in \textrm{co}\left\{ \varPi _1,\varPi _2,\varPi _3\right\} , \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} \varPi _1 =&-\begin{bmatrix} x_1\\ e_2 \\ z_2 \end{bmatrix}^\textrm{T} Q \begin{bmatrix} x_1\\ e_2 \\ z_2 \end{bmatrix} + 2p_4k_1\varepsilon ^3x_1(d-b)\\&+ 2p_5k_1\varepsilon ^2e_2(d-b) + 2p_6k_1\varepsilon ^2z_2(d-b), \end{aligned} \end{aligned}$$

$$\begin{aligned} \begin{aligned} \varPi _2 =&-\begin{bmatrix} x_1\\ e_2 \\ z_2 \end{bmatrix}^\textrm{T} Q \begin{bmatrix} x_1\\ e_2 \\ z_2 \end{bmatrix} + 2p_4k_1\varepsilon ^3x_1(d+b)\\&+ 2p_5k_1\varepsilon ^2e_2(d+b) + 2p_6k_1\varepsilon ^2z_2(d+b), \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} \varPi _3 =&-\begin{bmatrix} x_1\\ e_2 \\ z_2 \end{bmatrix}^\textrm{T} Q \begin{bmatrix} x_1\\ e_2 \\ z_2 \end{bmatrix} + 2p_4k_1\varepsilon ^3x_1\frac{-b-D}{b+\varDelta +D}x_1\\&+ 2p_5k_1\varepsilon ^2e_2\frac{-b-D}{b+\varDelta +D}x_1\\&+ 2p_6k_1\varepsilon ^2z_2\frac{-b-D}{b+\varDelta +D}x_1. \end{aligned} \end{aligned}$$

Since $\vert d\vert \leqslant D$, we have

$$\begin{aligned}&2p_4k_1\varepsilon ^3x_1(d\pm b)\\&\leqslant 2\vert p_4k_1\varepsilon ^3x_1\vert (D+b)\\&\leqslant 0.5 q_1\varepsilon ^3x_1^2 + 2p_4^2k_1^2(D+b)^2q_1^{-1}\varepsilon ^3,\\&2p_5k_1\varepsilon ^2e_2(d\pm b)\\&\leqslant 2\vert p_5k_1\varepsilon ^2e_2\vert (D+b)\\&\leqslant 0.5 q_2\varepsilon e_2^2 + 2p_5^2k_1^2(D+b)^2q_2^{-1}\varepsilon ^3,\\&2p_6k_1\varepsilon ^2z_2(d\pm b)\\&\leqslant 2\vert p_6k_1\varepsilon ^2z_2\vert (D+b)\\&\leqslant 0.5 q_3\varepsilon z_2^2 + 2p_6^2k_1^2(D+b)^2q_3^{-1}\varepsilon ^3. \end{aligned}$$

On the other hand, since $\vert x_1\vert \leqslant b+ \varDelta +D$, we have

$$\begin{aligned}&2p_4k_1\varepsilon ^3x_1\frac{-b-D}{b+\varDelta +D}x_1\\&\leqslant 2\vert p_4k_1\varepsilon ^3x_1\vert (D+b)\\&\leqslant 0.5 q_1\varepsilon ^3x_1^2 + 2p_4^2k_1^2(D+b)^2q_1^{-1}\varepsilon ^3,\\&2p_5k_1\varepsilon ^2e_2\frac{-b-D}{b+\varDelta +D}x_1\\&\leqslant 2\vert p_5k_1\varepsilon ^2e_2\vert (D+b)\\&\leqslant 0.5 q_2\varepsilon e_2^2 + 2p_5^2k_1^2(D+b)^2q_2^{-1}\varepsilon ^3,\\&2p_6k_1\varepsilon ^2z_2\frac{-b-D}{b+\varDelta +D}x_1\\&\leqslant 2\vert p_6k_1\varepsilon ^2z_2\vert (D+b)\\&\leqslant 0.5 q_3\varepsilon z_2^2 + 2p_6^2k_1^2(D+b)^2q_3^{-1}\varepsilon ^3. \end{aligned}$$

Then $\dot{V}(\zeta )$ in the region $S_0$ satisfies the following inequality:

$$\begin{aligned} \dot{V}(\zeta )\leqslant -0.5\begin{bmatrix} x_1\\ e_2 \\ z_2 \end{bmatrix}^\textrm{T} Q \begin{bmatrix} x_1\\ e_2 \\ z_2 \end{bmatrix} + \varPhi (D,b,\varDelta )\varepsilon ^3, \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} \varPhi (D,b,\varDelta )=&2k_1^2\left( \frac{p_4^2}{q_1} + \frac{p_5^2}{q_2}+ \frac{p_6^2}{q_3}\right) (D+b)^2. \end{aligned} \end{aligned}$$

(25)

Let the positive scalar $\gamma$ satisfy

$$\begin{aligned} \gamma P\varepsilon - 0.5Q<0. \end{aligned}$$

(26)

Such $\gamma$ exists since $P>0$ and $Q>0$. Then,

$$\begin{aligned} \begin{aligned}&\dot{V} + \gamma \varepsilon V\\&\leqslant \begin{bmatrix} x_1\\ e_2 \\ z_2 \end{bmatrix}^\textrm{T} (\gamma P\varepsilon - 0.5Q) \begin{bmatrix} x_1\\ e_2 \\ z_2 \end{bmatrix} + \varPhi (D,b,\varDelta )\varepsilon ^3\\&\leqslant \varPhi (D,b,\varDelta )\varepsilon ^3. \end{aligned} \end{aligned}$$

Furthermore,

$$\begin{aligned} \dot{V} \le -\gamma \varepsilon (V-\gamma ^{-1}\varPhi (D,b,\varDelta )\varepsilon ^2). \end{aligned}$$

Define the following level set of the Lyapunov function $V(\zeta )$:

$$\begin{aligned} \begin{aligned}&\mathcal {E}(D,b,\varDelta ) \\&=\left\{ [x_1\;e_2\;z_2]^\textrm{T} \in \mathbb {R}^3: V\le \gamma ^{-1}\varPhi (D,b,\varDelta )\varepsilon ^2\right\} . \end{aligned} \end{aligned}$$

Then $\dot{V}(\zeta )<0$, $\forall \;[x_1\;e_2\; z_2]^\textrm{T}\in \mathbb {R}^3\setminus (S_0\cap \mathcal {E}(D,b,\varDelta ))$. Considering the fact that in the regions $S_+\cup \partial S_+$ and $S_-\cup \partial S_-$, $\dot{V}(\zeta ) < 0$ and the system trajectory finally leaves $S_+$ and $S_-$, we can see that the system trajectory enters the level set $\mathcal {E}(D,b,\varDelta )$ in a finite time and remains in it. On the other hand, since $P>0$, there exist positive scalars $\alpha$ and $\beta$ such that both the following matrices are positive definite, that is,

$$\begin{aligned} \begin{bmatrix} (p_1-\alpha ^2)\varepsilon ^2 &{} p_2\varepsilon &{} p_4\varepsilon \\ p_2\varepsilon &{} p_3 &{} p_5\\ p_4\varepsilon &{} p_5 &{} p_6 \end{bmatrix}>0 \end{aligned}$$

(27)

and

$$\begin{aligned} \begin{bmatrix} p_1\varepsilon ^2 &{} p_2\varepsilon &{} p_4\varepsilon \\ p_2\varepsilon &{} (p_3-\beta ^2) &{} p_5\\ p_4\varepsilon &{} p_5 &{} p_6 \end{bmatrix}>0. \end{aligned}$$

For any $[x_1\;e_2\; z_2]^\textrm{T}\in \mathcal {E}(D,b,\varDelta )$, we have

$$\begin{aligned} \alpha ^2 \tilde{x}_1^2 \le \gamma ^{-1}\varPhi (D,b,\varDelta ), \end{aligned}$$

and

$$\begin{aligned} \beta ^2 e_2^2 \le \gamma ^{-1}\varPhi (D,b,\varDelta )\varepsilon ^2, \end{aligned}$$

and

$$\begin{aligned} f(x)\le \gamma ^{-1}\Phi (D,b,\Delta )\varepsilon ^2. \end{aligned}$$

Define

$$\begin{aligned} B_{x_1}=\left\{ \begin{aligned}&\alpha ^{-1}\sqrt{\gamma ^{-1}\Phi },\ \alpha ^{-1}\sqrt{\gamma ^{-1}\Phi }\le b+\Delta +D,\\&0.5p_1^{-1}\Delta ^{-1}\gamma ^{-1}\Phi +b+\Delta +D,\ \textrm{otherwise}.\\ \end{aligned} \right. \end{aligned}$$

(28)

Then, we have

$$\begin{aligned} |x_1|\le B_{x_1}. \end{aligned}$$

Furthermore, from $x_2 = e_2+k_2z_2$, we have

$$\begin{aligned} \begin{aligned} \vert x_2\vert&\le \vert e_2\vert +\vert k_2z_2\vert \\&\le \big (\beta ^{-1}\sqrt{\gamma ^{-1}\varPhi (D,b,\varDelta )}+\vert k_2\vert B_z\big )\varepsilon \\&\triangleq B_{x_2}\varepsilon . \end{aligned} \end{aligned}$$

Let

$$\begin{aligned} \mathcal {S}(D,b,\varDelta )=\big \{ x\in \mathbb {R}^2:\vert x_1\vert \le B_{x_1} ,\;\vert x_2\vert \le B_{x_2}\varepsilon \big \}. \end{aligned}$$

Clearly, the set $\mathcal {S}(D,b,\varDelta )$ is bounded. Then the state trajectory of system (1) under (20) that has been determined in Lemma 2 will enter the bounded set $\mathcal {S}(D,b,\varDelta )$, and there exists $\varepsilon ^* \in (0,1]$ such that, for any $\varepsilon \in (0,\varepsilon ^*]$, $x_2$ enters and remains in the given set $s_0$. This completes the proof.

$\square$

Remark 2

Theorem 1 has proven that the dynamic output feedback law (20) with parameters $g_1$, $g_2$, $l_1$, $l_2$, and h determined by a set of $k_i$’s, $i\in I[1,5]$, that satisfies

$$\begin{aligned} \left\{ \begin{aligned}&k_1=\frac{k_4^2+(k_2-1)k_4k_5}{(k_2-1)^2},\\&k_2> 1,\\&k_3< 0,\\&k_4> 0,\\&k_5< 0,\\&k_2k_5 + k_4< k_5, \end{aligned} \right. \end{aligned}$$

(29)

can globally practically stabilize the double integrator system (1). It is clear that such a design of the dynamic output feedback laws applies to the double integrator system subject to standard sensor saturation, which has been studied in Ref. [6]. Note that the scalars $k_i$’s, $i\in I[1,5]$, selected in Ref. [6] are required to satisfy the following conditions:

$$\begin{aligned} \left\{ \begin{aligned}&k_3<0,\ k_4>0,\ k_5<0,\\&4k_5+9k_4\ne 0,\\&\frac{k_4}{k_5^2}<\frac{64}{27},\\&-\frac{5}{12}k_4^2k_5-\frac{1}{3}k_4k_5^2=\Big (\frac{3}{4}k_4+\frac{1}{3}k_5\Big )^2,\\&k_1=\dfrac{k_5}{3}<0,\\&k_2= -\dfrac{9k_4}{4k_5}>0. \end{aligned} \right. \end{aligned}$$

(30)

Comparing conditions (29) and (30), it is obvious that the later is more conservative than the former. This implies that the new design of dynamic output feedback laws proposed in this paper weakens the intricate restriction on the design in Ref. [6], and support a more relaxed selection in the determination of feedback law parameters.

Remark 3

By the definition of $B_{x_1}$ in (28), the values of $\alpha$, $\gamma$, and $\varPhi (D,b,\varDelta )$ determine the value of $B_{x_1}$. We assume that the values of $k_i$’s, $i\in I[1,5]$, have been chosen as in (29). Lemma 3 has established the relationship between $k_i$’s and $p_j$’s, $i\in I[1,5]$, $j\in I[1,6]$. As seen in the proof of Lemma 3, if $\frac{b+D}{\varDelta } \leqslant \frac{-4k_1k_2^3}{(k_4-k_2k_5)^2}$, $p_j$’s are independent of $\frac{b+D}{\varDelta }$. By (26) and (27), $\alpha$ and $\gamma$ are also independent of $\frac{b+D}{\varDelta }$. Furthermore, by its definition, $\varPhi (D,b,\varDelta )$ is not affected by $\varDelta$. This implies that the bound $B_{x_1}$ only depends on the parameters b and D if $\frac{b+D}{\varDelta } \leqslant \frac{-4k_1k_2^3}{(k_4-k_2k_5)^2}$. On the other hand, if $\frac{b+D}{\varDelta } > \frac{-4k_1k_2^3}{(k_4-k_2k_5)^2}$, $p_j$’s, $\alpha$, $\gamma$, and $\varPhi (D,b,\varDelta )$ depend on b, D, and $\varDelta$. Thus, $B_{x_1}$ will be related with all the values of b, D and $\varDelta$.

Remark 4

One can easily observe in the expression of $B_{x_1}$ that $B_{x_1}=0$ if $b=0$ and $D=0$. This implies that in the case of $D=0$ and $b=0$, the state $x_1$ will converge to the zero, which, by the Barbalat lemma, means that the time derivative of $x_1$ will also converge to the zero. Since $\dot{x_1} = x_2$, we have $x_2\rightarrow 0$ as $t\rightarrow \infty$. This implies that the dynamic output feedback law (20) can achieve global asymptotically stabilization of the double integrator system subject to standard output saturation.

4 A numerical example

In this section, we present a numerical example to illustrate that the proposed low gain-based linear dynamic output feedback laws (20) achieve global practical stabilization of system (1). For the input–output characteristic of the sensor, we assume the dead-zone break points $b=1$ and the saturation level $\varDelta = 1$, that is, both the dead zone and the saturation range from $-1$ to 1.

We choose $k_2 = 2$, $k_3 = -1$, $k_4 = 1$, and $k_5 =$ $-2$, which satisfy the conditions in Lemma 2. According to (22), $k_1 = -1$. Then the parameters $g_1$, $g_2$, $l_1$, $l_2$, and h can be determined according to (4) and (6), and we obtain $g_1 = 1$, $g_2= -2$, $l_1 =$ $-1$, $l_2= -1$, and $h= -2$. Let the output-additive disturbance $d = 2\sin (t)+2$. Clearly, $D = 4$.

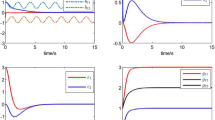
The parameter $\varepsilon$ is chosen as $\varepsilon =0.3$, $\varepsilon =0.2$, and $\varepsilon =0.1$, respectively. Let the initial states be $[x^\textrm{T}(0),\;z^\textrm{T}(0)]=[5,\;-4,\;0,\;0]$. The time trajectories of the states $x_1(t)$ and $x_2(t)$ in the three cases are plotted in Figs. 2 and 3, respectively. For these three values of $\varepsilon$, state $x_1(t)$ enters a bounded set in a finite time and remains in it. On the other hand, a smaller value of $\varepsilon$ drives state $x_2(t)$ to enter and remain in a smaller neighborhood of 0. This implies that the proposed low gain-based linear dynamic output feedback laws indeed achieves global practical stabilization.

Fig. 2

The evolution of the state $x_1$ when $\varepsilon =0.3$, $\varepsilon =0.2$, and $\varepsilon =0.1$

Fig. 3

The evolution of the state $x_2$ when $\varepsilon =0.3$, $\varepsilon =0.2$, and $\varepsilon =0.1$

A phase trajectory of the double integrator system (1) under the proposed low gain-based linear dynamic output feedback is plotted in Fig. 4, which also illustrates global asymptotic behavior of the closed-loop system. On the other hand, we plot in Fig. 5 the evolution of the Lyapunov function $V(\zeta )$ along the trajectory shown in Fig. 4. It is clear that, along this trajectory, the value of the Lyapunov function decreases before the state enters the set $\mathcal {S}(D,b,\varDelta )$. In addition, shown in Fig. 6 is the time trajectory of the output $y=\sigma (x_1+d)$, which continues to oscillate within the saturation region after the system state enters the set $\mathcal {S}(D,b,\varDelta )$.

Fig. 4

The trajectory of $x_1$ and $x_2$ when $\varepsilon =0.1$

Fig. 5

The evolution of the Lyapunov function $V(\zeta )$ when $\varepsilon =0.1$

Fig. 6

The evolution of the output $y=\sigma (x_1+d)$ when $\varepsilon =0.1$

5 Conclusion

This paper considered the global practical stabilization problem for the double integrator system with an imperfect sensor and subject to an additive output disturbance. To solve this problem, we designed a family of low gain-based linear dynamic output feedback laws and presented a set of conditions to determine the parameters of the output feedback. It is proven that under such dynamic output feedback laws, the first state enters a bounded set in finite time and remains in it, and the second state can be driven to an arbitrarily small set that contains the zero in its interior and remains in it. Simulation results illustrate the effectiveness of the proposed design.