1 Introduction

With the rapid development of computer and communication technology, sensor networks are widely applied in engineering systems due to high flexibility, robustness, and ease of placement. One of the important issues is how to design distributed algorithms to estimate unknown parameters in dynamical systems by efficiently using the data from sensor networks. Compared with the centralized algorithms, each sensor in distributed algorithms can exchange information with its neighbors via network structure, and complete the estimation task cooperatively. It is clear that distributed algorithms can greatly reduce the communication and computation burden, and have better robustness to node attacks. Distributed estimation algorithms have a wide range of practical applications such as target tracking, health monitoring, environmental monitoring and pollution prevention [1,2,3,4]. Meanwhile, the theoretical investigation of distributed algorithms has attracted much attention of researchers in various fields, e.g., control theory, system identification, signal processing. (cf., [5,6,7,8]).

For discrete-time dynamical systems, some distributed algorithms were proposed and convergence results of the algorithms were also established for time-invariant parameters (cf., [9, 10]), time-varying parameters (cf., [11, 12]), order estimation (cf., [13]), sparse signals (cf., [8]). However, in many practical scenarios, continuous time signals such as electrical signals, speech signals, attitude control, seismic waves, electromagnetic waves, etc. are widely used, and the dynamical systems are often modeled by (stochastic) differential equations based on specific laws of physics [14,15,16,17,18,19,20]. In recent years, some theoretical results for distributed estimation problems of continuous-time systems are given. For example, Chen and Wen et al. in [21] studied the consensus-type distributed identification algorithm for continuous-time systems where regressors are uniformly bounded and satisfy the cooperative persistent excitation (PE) condition. Nascimento and Sayed in [22] investigated the exponential stability of diffusion-type LMS algorithm with PE regressors. Papusha et al. in [23] investigated the asymptotic parameter convergence of consensus-type distributed gradient algorithm under PE condition. We see that in most of existing results, the regressors are required to be deterministic and satisfy the PE condition, which is hard to be satisfied for the stochastic feedback systems.

The linear regressions are often used to model the engineering systems. Generally speaking, the regression model with higher order and more parameters can fit the data better. However, the model with high order may lead to parameter redundancy as well as computational pressure. How to choose the proper order of a regression model is an important topic in the fields of statistics, machine learning and system identification. For discrete-time linear regression models, some algorithms are constructed by optimizing some information criteria, such as AIC (Akaike Information Criterion) [24], BIC (Bayesian Information Criterion) [25], and CIC (the first letter “C” refers to the information criterion designed for feedback control systems) [26] and their variants, and some theoretical results for the algorithms are obtained. For example, Hannan and Kavalieris in [27] used the AIC criterion to design an algorithm to estimate the system order and unknown parameters, and gave the convergence analysis of the algorithm under stable input signals. Ninness in [28] established the Cramér-Rao lower bound for the order estimation problem of the stable stochastic observation model. Chen and Guo in [29] proposed a least-squares based order estimation algorithm by introducing an information criterion, and the consistent results for the system order and parameters were given under non-persistent excitation condition when the upper bounds of orders are known. Later, Guo and Huang in [30] established the convergence result of the order estimation problem with unknown upper order bounds. Chen and Zhao in [31] proposed a recursive order estimation algorithm with independent and identical distributed input signals. In recent years, some studies have been carried out based on genetic algorithms and neural networks [32, 33]. However, only simulation experiments were conducted to validate the algorithms, no corresponding rigorous theoretical analysis was given. For the order estimation problem of continuous-time models, Victor et al. in [34] designed a two-stage estimation algorithm to estimate the unknown parameters and orders of a noise-free dynamic system and verified the effectiveness of the algorithm by simulation experiments. Belkhatir and Laleg-Kirati in [35] studied local convergence for order estimation and parameter estimation of noisy systems under bounded input–output assumption. Subsequently, Stark et al. in [36] analyzed local convergence results for system order estimation with observation noise. So far, little attention was paid to the design and global convergence of the distributed order estimation problem of continuous-time stochastic systems.

In this paper, we study the distributed estimation problems of continuous-time dynamical systems described by stochastic differential equation with unknown order and parameters over sensor networks. Motivated by the discrete-time distributed order estimation problem (cf., [13]), we introduce a local information criterion based on the \(L_0\) penalty term, and propose a two-step distributed algorithm to simultaneously estimate the unknown orders and parameters of continuous-time stochastic regression models. To be specific, the order estimates are obtained by minimizing the local information criterion at discrete diffusion points. Based on this, the unknown parameters are estimated by using diffusion least square algorithm. Under the cooperative excitation conditions of the regression signals, almost sure global convergence are established for the distributed order estimation as well as the distributed parameter estimation, where some mathematical tools such as stochastic Lyapunov function method, Itô’s theorem, and continuous time martingale estimation theorem are used to deal with the noise effect and the coupling relationship between the estimate of the system order and unknown parameters. Finally, simulation examples are given to verify the effectiveness of the proposed distributed algorithm. Compared with most existing results on distributed adaptive estimation algorithms, the convergence results are established without relying on the commonly used independency, stationarity or ergodicity assumptions on regression signals, which makes it possible to apply our results to the feedback control systems.

The rest of this paper is organized as follows. In Sect. 2, we give the problem formulation. The main results of the proposed algorithm are provided in Sect. 3. A simulation example is given in Sect. 4, and the concluding remarks are made in Sect. 5.

2 Problem formulation

2.1 Some notations and preliminaries

In this section, we will introduce some notation and preliminary results on graph theory and probability theory.

The communication between sensors are modeled as an undirected graph \( \mathcal G = (\mathcal {V, E})\), where \(\mathcal V=\{1,2,\ldots , N\}\) is composed of all sensors and \(\mathcal E\subseteq \mathcal V\times \mathcal V\) is the set of edges. The weighted adjacency matrix \(\mathcal {A}=(a_{ij})_{n\times n}\) is used to describe the interaction weights between sensors, where the weight \(a_{ij}\>0\) if and only if \((i,j)\in \mathcal {E}\). For simplicity of analysis, we assume that the matrix \(\mathcal {A}\) is symmetric and doubly stochastic, i.e., \(a_{ij}=a_{ji}\) and \(\sum _{i=1}^Na_{ij}=\sum _{i=1}^Na_{ji}=1\) for all i and j. A path of length s in the graph \(\mathcal G\) is defined as a sequence of labels \(\{i_1,\ldots ,i_s\}\) satisfying \((i_j,i_{j+1}) \in \mathcal {E}\) for all \(1\le j\le s-1\). The diameter of graph \(\mathcal {G}\), denoted as \(D_{\mathcal {G}}\), is defined as the maximum length of the path between any two sensors. We define \(\mathcal {N}_i=\{j\in \mathcal {V}\vert (j,i)\in \mathcal {E}\}\) as the neighbor set of the graph \(\mathcal {G}\). See [37] for more information about graph theory.

Let \((\varOmega ,\mathcal {F},P)\) be a probability space, and \(\{\mathcal {F}_t,t\ge 0\}\) be a nondecreasing family of sub-\(\sigma \)-algebras of \(\mathcal {F}\). The process \(\{X_t,\mathcal {F}_t;0\le t < \infty \}\) is said to be a martingale if we have \(E(X_t\vert \mathcal {F}_s)=X_s\) almost surely (a.s.) for \(0\le s< t< \infty \) , where \(E[\cdot \vert \cdot ]\) is the conditional mathematical expectation operator. The Wiener process \(\{w(t),\mathcal {F}_t\}\) is an independent incremental process with \(E[w(t)\vert \mathcal {F}_s]=0\) and \(E[w^2(t)]<\infty , t>s\ge 0,\) where \(E[\cdot ]\) is the mathematical expectation operator. For the continuous-time martingale, the following martingale estimation theorem is often used to deal with the continuous-time stochastic noise.

Lemma 1

[38] Let \((M_t, \mathcal {F}_t)\) be a measurable process satisfying \(\int _0^t\Vert M_s\Vert ^2\textrm{d}s<\infty \), a.s. \(\forall t>0\). If \(\{ w_t, \mathcal F_t\}\) is a Wiener process, then as \(t \rightarrow \infty \), \(\int _0^t M_s \textrm{d}w_s=O\big (\sqrt{S(t) \log \log (S(t)+e)}\big ) \ a.s.,\) where S(t) is defined by \(S(t)=\int _0^t\Vert M_s\Vert ^2\textrm{d}s.\)

The Itô formula plays a key role in dealing with continuous-time stochastic processes, which is described as follows:

Lemma 2

[39] Assume that the stochastic process \(\xi (t)\) obeys the equation \(\textrm{d}\xi (t)=a(t,\xi (t)) \textrm{d}t+B(t,\xi (t)) \textrm{d}w(t)\), and {\(a(t,\xi (t)),\mathcal {F}_t\)} is an l-dimensional adaptive process and \(\{B(t,\xi (t)),\mathcal {F}_t\}\) is an \(l\times m\)-dimensional adaptive matrix process satisfying \(\Vert a(\cdot ,\cdot )\Vert ^{\frac{1}{2}}\in \mathcal {P}_t\) and \(\Vert B(\cdot ,\cdot )\Vert \in \mathcal {P}_t\). If the functions \(f_t'(t,x)\), \(f_{x}'(t,x)\) and \(f_{xx}''(t,x)\) are continuous, then

$$\begin{aligned}&\textrm{d}f(t,\xi (t))=f_t'(t,\xi (t))\textrm{d}t+{f'}^\textrm{T}_{\xi (t)}(t,\xi (t)) \textrm{d}\xi (t) \\&+\frac{1}{2}\textrm{tr}\{f_{\xi (t)\xi (t)}''(t,\xi (t))B(t,\xi (t)) (B(t,\xi (t)))^\textrm{T}\}\textrm{d}t. \end{aligned}$$

2.2 Problem formulation

Consider a network consisting of N sensors. The dynamical system of each sensor \(i\in \{1,\ldots ,N\}\) obeys the following continuous-time stochastic differential equation,

$$\begin{aligned} \left\{ \begin{array}{l} \begin{array}{l} y_i(t)=a_1Sy_{i}(t)+\cdots +a_{\bar{p}} S^{\bar{p}}y_{i}(t)+b_1Su_i(t)\\ \quad \quad +\cdots +b_{\bar{q}}S^{\bar{q}}u_i(t)+v_{i}(t), \end{array} \\ u_i(t)=0,\ y_{i}(t)=0,\ t\le 0, \end{array}\right. \end{aligned}$$
(1)

where S is the Itô integral operator (i.e., \(Sy_i(t)=\int _0^ty_i(s)\textrm{d}s\)), \(y_i(t)\) and \(u_i(t)\) are the scalar output and input of the sensor i at time t, \(v_i(t)\) is the system noise and modeled as a standard Wiener process, both the order \((\bar{p}, \bar{q})\) and parameters \(a_1,\ldots ,a_{\bar{p}},b_1,\ldots ,b_{\bar{q}}\) \((a_{\bar{p}}\ne 0,b_{\bar{q}}\ne 0)\) are unknown.

For the convenience of analysis, we assume that the system order has known the upper bounds, i.e., \((\bar{p},\bar{q})\in I,I\triangleq \{(p,q)\ \big \vert \ 0\le p\le U_p,0\le q\le U_q\}\), where \(U_p\) and \(U_q\) are the upper bounds of the order. Denote the vector of regressor and unknown parameters in (1) as follows:

$$\begin{aligned} \begin{aligned}&\phi _i(t;p,q)\\&\quad =[y_i(t), \ldots , S^{p-1}y_i(t), u_i(t), \ldots , S^{q-1}u_i(t)]^\textrm{T},\\&\theta (p,q)=[a_1, \ldots , a_p, b_1, \ldots , b_q]^\textrm{T},\\&a_j=0,\ b_{\tau }=0,\ \bar{p}< j\le p,\ \bar{q}< \tau \le q. \end{aligned} \end{aligned}$$

Then the system (1) can be rewritten into the following regression model,

$$\begin{aligned} \begin{aligned} y_i(t)=\,&S\phi _i^\textrm{T}(t;p,q)\theta (p,q)+v_{i}(t)\ (p\ge \bar{p},q\ge \bar{q})\\ =\,&S\phi _i^\textrm{T}(t;\bar{p},\bar{q})\theta (\bar{p},\bar{q})+v_{i}(t). \end{aligned} \end{aligned}$$
(2)

In this paper, we put forward a two-step distributed algorithm to alternately estimate the system order \((\bar{p},\bar{q})\) and the parameter \(\theta (\bar{p},\bar{q})\) in (2). First, a local information criterion is proposed, by minimizing which the estimate of the system order can be obtained; Then, the diffusion least squares algorithm will be adopted to estimate unknown parameters based on the order estimate due to fast convergence rate of least squares algorithm.

In the following, we first introduce the diffusion least squares algorithm. In this algorithm, the update of unknown parameters only occurs at discrete diffusion time instants which are denoted as \(0=t_0, t_1, t_2, \ldots ,t_k,\ldots \) satisfying \(t_k\rightarrow \infty \) as \(k\rightarrow \infty \). For \( t\in [t_{n},t_{n+1})\), we introduce the following local objective function with fixed order (p, q),

$$\begin{aligned} \begin{aligned}&J_{n,i}(t;p,q,\theta (p,q))\\&\quad =J_{n,i}(t_n;p,q,\theta (p,q))\\&\qquad +\int _{t_n}^{t}\left\{ \frac{\textrm{d}y_i(s)}{\textrm{d}s}-\theta ^\textrm{T}(p,q)\phi _i(s;p,q)\right\} ^2\textrm{d}s,\\&\qquad i=1,2,\ldots ,N, \end{aligned} \end{aligned}$$
(3)

and

$$\begin{aligned}\begin{aligned}&J_{n+1,i}(t_{n+1};p,q,\theta (p,q))\\&\quad =\textstyle \sum \limits _{j\in \mathcal {N}_i}a_{ij}J_{n,j}(t_{n+1};p,q,\theta (p,q)),\ i=1,2,\ldots ,N,\\&J_{0,i}(t_0;p,q,\theta (p,q))=0,~~i=1,2,\ldots ,N, \end{aligned} \end{aligned}$$

where \(0<a_{ij}\le 1\) is the ith row and jth column of the weighted adjacency matrix \(\mathcal A\) of the sensor network, and \(y_i(s), \phi _i(s;p,q)\) are considered as the outcomes, thus, the integral is Riemann integral. By the above recursive form, we have for \(t\in [t_{n},t_{n+1})\)

$$\begin{aligned} \begin{aligned}&J_{n,i}(t;p,q,\theta (p,q))\\&\quad = {\textstyle \sum \limits _{j=1}^N\textstyle \sum \limits _{k=0}^{n-1}}a_{ij}^{(n-k+1)}\int _{t_k}^{t_{k+1}}\left\{ \dfrac{\textrm{d}y_j(s)}{\textrm{d}s}\right. \\&\left. \qquad - \theta ^\textrm{T}(p,q)\phi _j(s;p,q)\right\} ^2\textrm{d}s\\&\qquad +\int _{t_{n+1}}^t\left\{ \frac{\textrm{d}y_i(s)}{\textrm{d}s}-\theta ^\textrm{T}(p,q)\phi _i(s;p,q)\right\} ^2\textrm{d}s, \end{aligned} \end{aligned}$$
(4)

and for \(t=t_{n+1}\)

$$\begin{aligned} \begin{aligned}&J_{n+1,i}(t_{n+1};p,q,\theta (p,q))\\&\quad ={\textstyle \sum \limits _{j=1}^N\textstyle \sum \limits _{k=0}^n} a_{ij}^{(n-k+1)}\int _{t_k}^{t_{k+1}}\left\{ \frac{\textrm{d}y_j(s)}{\textrm{d}s} \right. \\&\left. \qquad -\theta ^\textrm{T}(p,q)\phi _j(s;p,q)\right\} ^2\textrm{d}s. \end{aligned} \end{aligned}$$
(5)

By minimizing the objective functions (4) and (5), we can derive the following diffusion least squares algorithm. The details can be found in [40].

Algorithm 1
figure d

Diffusion least squares algorithm

Full size image

For each sensor \(i\in \{1,\ldots ,N\}\) and any \(t\ge 0\), we introduce the following local information criterion to estimate the order \(\bar{p}\), \(\bar{q}\) of the dynamic system (2),

$$\begin{aligned} \begin{aligned}&F_{n,i}(t;p,q)\\&\quad =J_{n,i}(t;p,q,\theta _{n,i}(t;p,q))\\&\qquad +(p+q)\xi (t),~~t\in [t_n,t_{n+1}),\ n\in \mathbb N, \end{aligned} \end{aligned}$$
(10)

where the definition of \(J_{n,i}(t;p,q,\theta _{n,i}(t;p,q))\) is given in (3), \(\theta _{n,i}(t;p,q)\) is the estimate of \(\theta \) given in Algorithm 1. In (10), the first term is the accumulative error between the system output and the prediction, while the second term \((p+q)\xi (t)\) is the penalty term, and can be regarded as the \(L_0\) regularization of the unknown parameter vector. The function \(\xi (t)\) reflects the balance between the accumulative prediction error and the penalty term, and we will provide a principle to select \(\xi (t)\) in Sect. 3. The distributed order estimation algorithm based on the information criterion (10) is given in the following Algorithm 2.

Algorithm 2
figure e

Distributed order estimation algorithm

Full size image

3 Convergence analysis of Algorithm 2

In this section, we will establish theoretical results for convergence of the distributed order estimation algorithm (Algorithm 2) proposed in Sect. 2.2. For this purpose, we introduce some assumptions on the network topology and regressors.

Assumption 1

The graph \(\mathcal G\) is undirected and connected.

Remark 1

Denote the ith row and jth column element of the matrix \(\mathcal {A}^m\) as \(a_{ij}^{(m)}\). By Lemma 8.1.2 in [37], we know that under Assumption 1, \(a_{ij}^{(m)}\ge a_{\min }>0\) holds for all \(m>D_{\mathcal {G}}\), where \(a_{\min }=\min \nolimits _{i,j\in \mathcal V} a_{ij}^{(D_{\mathcal {G}})}>0\).

In fact, the above assumption for the communication graph can be generalized to the case where \(\mathcal G\) is a strongly connected balanced graph, and the corresponding analysis is similar to the undirected graph case. Thus, we just provide the analysis of Algorithm 2 under Assumption 1.

The properties of regressors are important for the convergence of the identification algorithms. In this paper, we introduce the following cooperative excitation condition on the regressors.

Assumption 2

(Cooperative excitation condition) There exists a real function \(\xi (t)\) that satisfies

(1) \(\xi (t)>0\), for \(t>0\);

(2) \(\xi (t)\rightarrow \infty \), as \(t\rightarrow \infty \);

(3) \(\lim \limits _{t\rightarrow \infty }\frac{\log \left( R(t;U_p,U_q)\right) }{\xi (t)}=0, \) \(\lim \limits _{t\rightarrow \infty }\frac{\xi (t)}{\lambda _{\min }(t;p,q)}=0,\) (p,  q) \(\in I^*,\) a.s. where \(I^* =\left\{ \left( \bar{p}, U_q\right) ,\left( U_p, \bar{q}\right) \right\} \),

$$\begin{aligned}&R(t;U_p,U_q) =\lambda _{\max }\big \{ {P}_0^{-1}(t_0;U_p,U_q)\big \}\\&\qquad +{\textstyle \sum \limits _{i=1}^N}\int _{t_0}^{t}\Vert \phi _i(s;U_p,U_q)\Vert ^2\textrm{d}s,\\&\lambda _{\min }(n;p,q) \\&\quad =\lambda _{\min }\left\{ {\textstyle \sum \limits _{j=1}^N} \int _{t_0}^{t_{n-D_{\mathcal {G}}+1}}\phi _j(s;p,q)\phi _j^\textrm{T}(s;p,q)\textrm{d}s \right. \\&\left. \qquad +{\textstyle \sum \limits _{j=1}^N} P_{0,j}^{-1}(t_0;p,q)\right\} . \end{aligned}$$

Remark 2

The choice of \(\xi (t)\) depends on the regressors, and here we show how to choose it for a special case. Assume that for \(i \in \{1, \ldots , N\}\), the regression vector \(\phi _{i}\left( s;\bar{p}, \bar{q}\right) \) is bounded, and there exists a matrix \(\varUpsilon _i\) such that \(\frac{1}{t} \int _{0}^t \phi _{i}\left( s;\bar{p},\bar{q}\right) \phi _{i}^\textrm{T}\left( s;\bar{p},\bar{q}\right) \textrm{d}s \underset{t \rightarrow \infty }{\longrightarrow }\ \varUpsilon _i\), and \(\sum _{i=1}^N \varUpsilon _i\) is positive definite [41]. Then \(\xi (t)\) can be taken as \(\xi (t)=t^\alpha , 0<\alpha <1\).

Before giving convergence results for the estimation of the system order and parameters in Algorithm 2, we give some preliminary lemmas. We first provide the upper bound on the accumulative noise, which is an important step for the convergence of the algorithm.

Lemma 3

For fixed order (p, q), let

$$\begin{aligned} \begin{aligned}&H_{n+1,i}(t_{n+1};p,q)\\&\quad \triangleq {\textstyle \sum \limits _{j=1}^N \textstyle \sum \limits _{k=0}^{n}} a_{ij}^{(n+1-k)} \int _{t_{k}}^{t_{k+1}}\phi _j(s;p,q)\textrm{d}v_j(s), \\&H_{0,i}(t_{0};p,q)=0. \end{aligned} \end{aligned}$$

Then the following inequality holds:

$$\begin{aligned}&H_{n+1,i}^\textrm{T}(t_{n+1};p,q) P_{n+1,i}(t_{n+1};p,q) H_{n+1,i}(t_{n+1};p,q)\\&\quad = O(\log R(n;p,q)), \end{aligned}$$

where \(P_{n+1,i}(t_{n+1};p,q)\) is defined in (8). \(\square \)

Proof

Denote

$$\begin{aligned} \left\{ \begin{aligned}&\varPsi (t;p,q)\triangleq \mathrm{{diag}}\{\phi _1(t;p,q),\ldots ,\phi _N(t;p,q)\},\\&V(t)\triangleq (v_1(t),\ldots ,v_N(t))^\textrm{T},\\&P_n(t)\triangleq \textrm{diag}\{{P_{n,{1}}(t;p,q),\ldots ,P_{n, N}(t;p,q)}\},\\&H_n(t)\triangleq \mathrm{{col}}\{H_{n,1}(t;p,q),\ldots ,H_{n,N}(t;p,q)\}. \end{aligned}\right. \end{aligned}$$
(12)

For simplicity of expression, we omit (p, q) in the equations without confusion. By the definition of \(H_{n+1,i}(t_{n+1})\) and (12), we have for \(t=t_{n+1}\),

$$\begin{aligned} \begin{aligned} H_{n+1}(t_{n+1}) =\,&{\textstyle \sum \limits _{k=0}^n} \mathscr {A}^{(n+1-k)} \int _{t_k}^{t_{k+1}} \varPsi (s) \textrm{d}V(s)\\ =\,&\mathscr {A}\big ( H_n(t_n) + \int _{t_n}^{t_{n+1}}\varPsi (s) \textrm{d}V(s) \big ), \end{aligned} \end{aligned}$$
(13)

and for \(t\in [t_n,t_{n+1})\), we have

$$\begin{aligned} \begin{aligned} H_n(t) =\,&{\textstyle \sum \limits _{k=0}^{n-1}} \mathscr {A}^{(n-k)}\int _{t_k}^{t_{k+1}}\varPsi (s) \textrm{d}V(s)\\&+ \int _{t_n}^{t}\varPsi (s) \textrm{d}V(s), \end{aligned} \end{aligned}$$
(14)

where \(\mathscr {A}\) is the adjacency matrix of graph \(\mathcal G\). Differentiating both sides of (14), we have \(\textrm{d}H_n(t) = \varPsi (t)\textrm{d}V(t)\). Integrating both sides of this equation over \([t_n,t_{n+1})\) and substituting it into (13), we can derive the following equation:

$$\begin{aligned} \begin{aligned} H_{n+1}(t_{n+1})=\mathscr {A} H_n(t_{n+1}) . \end{aligned} \end{aligned}$$
(15)

Consider the stochastic Lyapunov function \(H_n^\textrm{T}(t)P_n(t)H_n(t)\). By the Itô formula in Lemma 2, we have

$$\begin{aligned}\begin{aligned}&\textrm{d}\big (H_n^\textrm{T}(t)P_n(t)H_n(t)\big ) \\&= H_n^\textrm{T}(t)\textrm{d}P_n(t) H_n(t) + 2H_n^\textrm{T}(t)P_n(t) \textrm{d}H_n(t)\\&\quad +\textrm{tr}(P_n(t)\varPsi (t)\varPsi ^\textrm{T} (t))\textrm{d}t \\&= -H_n^\textrm{T}(t)\big (P_n(t)\varPsi (t)\varPsi ^\textrm{T} (t)P_n(t)\big )H_n(t)\textrm{d}t\\&\quad + 2H_n^\textrm{T}(t)P_n(t)\varPsi (t)\textrm{d}V(t)\\ {}&\quad +\textrm{tr}(P_n(t)\varPsi (t)\varPsi ^\textrm{T} (t))\textrm{d}t. \end{aligned} \end{aligned}$$

Integrating both sides of the equation over \([t_n,t_{n+1})\) yields

$$\begin{aligned} \begin{aligned}&H_n^\textrm{T}(t_{n+1})P_n(t_{n+1})H_n(t_{n+1})\\&\quad =H_n^\textrm{T}(t_{n})P_n(t_{n})H_n(t_{n})\\&\qquad -\int _{t_n}^{t_{n+1}} H_n^\textrm{T}(t)P_n(t)\varPsi (t)\varPsi ^\textrm{T} (t)P_n(t)H_n(t)\textrm{d}t\\&\qquad + 2\int _{t_n}^{t_{n+1}} H_n^\textrm{T}(t)P_n(t)\varPsi (t) \textrm{d}V(t)\\&\qquad + \int _{t_n}^{t_{n+1}} \textrm{tr}\big (P_n(t)\textrm{d}P_n^{-1}(t)\big ). \end{aligned} \end{aligned}$$
(16)

By (15), (16) and lemma A.1 in [10], we have

$$\begin{aligned}\begin{aligned}&H_{n+1}^\textrm{T}(t_{n+1})P_{n+1}(t_{n+1})H_{n+1}(t_{n+1})\\&\quad = H_n^\textrm{T}(t_{n+1})\mathscr {A}P_{n+1}(t_{n+1})\mathscr {A}H_n(t_{n+1})\\&\quad \le H_n^\textrm{T}(t_{n+1})P_n(t_{n+1})H_n(t_{n+1})\\&\quad \le H_n^\textrm{T}(t_{n})P_n(t_{n})H_n(t_{n})\\&\qquad -\int _{t_n}^{t_{n+1}} H_n^\textrm{T}(t)P_n(t)\varPsi (t)\varPsi ^\textrm{T} (t)P_n(t)H_n(t)\textrm{d}t\\&\qquad + 2\int _{t_n}^{t_{n+1}} H_n^\textrm{T}(t)P_n(t)\varPsi (t) \textrm{d}V(t)\\&\qquad + \int _{t_n}^{t_{n+1}} \textrm{tr}\big (P_n(t)\textrm{d}P_n^{-1}(t)\big )\\&\quad \le H_0^\textrm{T}(t_0)P_0(t_0) H_0(t_0)\\&\qquad -{\textstyle \sum \limits _{k=0}^n} \int _{t_k}^{t_{k+1}} H_k^\textrm{T}(t)P_k(t)\varPsi (t)\varPsi ^\textrm{T} (t)P_k(t)H_k(t)\textrm{d}t\\&\qquad + {2\textstyle \sum \limits _{k=0}^n}\int _{t_k}^{t_{k+1}} H_k^\textrm{T}(t)P_k(t)\varPsi (t) \textrm{d}V(t)\\&\qquad + {\textstyle \sum \limits _{k=0}^n}\int _{t_k}^{t_{k+1}} \textrm{tr}\big (P_k(t)\textrm{d}P_k^{-1}(t)\big ). \end{aligned} \end{aligned}$$

This leads to the following equivalent form:

$$\begin{aligned} \begin{aligned}&H_{n+1}^\textrm{T}(t_{n+1})P_{n+1}(t_{n+1})H_{n+1}(t_{n+1})\\&\qquad +\textstyle \sum \limits _{k=0}^n \int _{t_k}^{t_{k+1}} \Vert \varPsi ^\textrm{T} (t)P_k(t)H_k(t)\Vert ^2\textrm{d}t\\&\quad \le {2\textstyle \sum \limits _{k=0}^n}\int _{t_k}^{t_{k+1}} H_k^\textrm{T}(t)P_k(t)\varPsi (t) \textrm{d}V(t)\\&\qquad + {\textstyle \sum \limits _{k=0}^n}\int _{t_k}^{t_{k+1}} \textrm{tr}\big (P_k(t)\textrm{d}P_k^{-1}(t)\big ). \end{aligned} \end{aligned}$$
(17)

By Theorem 1, the first term on the right side of (17) satisfies

$$\begin{aligned} \begin{aligned}&{\textstyle \sum \limits _{k=0}^n}\int _{t_k}^{t_{k+1}} H_k^\textrm{T}(t)P_k(t)\varPsi (t) \textrm{d}V(t)\\&\quad =O(1)+o\left( {\textstyle \sum \limits _{k=0}^n} \int _{t_k}^{t_{k+1}} \Vert \varPsi ^\textrm{T} (t)P_k(t)H_k(t)\Vert ^2\textrm{d}t\right) , \end{aligned} \end{aligned}$$
(18)

and a tedious derivation leads to

$$\begin{aligned} \begin{aligned} {\textstyle \sum \limits _{k=0}^n}\int _{t_k}^{t_{k+1}} \textrm{tr}\big (P_k(t)\textrm{d}P_k^{-1}(t)\big )=O\left( \log R(n)\right) . \end{aligned} \end{aligned}$$
(19)

Substituting (18) and (19) into (17), we have

$$\begin{aligned} H_{n+1}^\textrm{T}(t_{n+1}) P_{n+1}(t_{n+1}) H_{n+1}(t_{n+1}) = O(\log R(n)). \end{aligned}$$

This completes the proof of the lemma. \(\square \)

As we know, in the estimation process of the algorithm, it is possible for the estimated order to be greater than the true order. In the following lemma, we provide an analysis of the parameter estimation error for this case, which is helpful for the subsequent theoretical analysis.

Lemma 4

For any \(p\ge \bar{p}\) and \(q\ge \bar{q}\), the estimation error \(\tilde{\theta }_{k,i}(t;p,q)\) of Algorithm 1 satisfies the following equation,

$$\begin{aligned}\begin{aligned}&P_{k+1,i}^{-1}(t_{k+1};p,q)\tilde{\theta }_{k+1,i}(t_{k+1};p,q)\\&\quad =\textstyle \sum \limits _{j \in \mathcal {N}_i}{a_{ij}}\left[ P_{k,j}^{-1}(t_k;p,q)\tilde{\theta }_{k,j}(t_k;p,q)\right. \\&\left. \qquad - \int _{t_k}^{t_{k+1}}\phi _j(s;p,q)\textrm{d}v_j(s)\right] , \end{aligned} \end{aligned}$$

where \(\tilde{\theta }_{k,i}(t;p,q)=\big [a_1-a_{1,i}(t), \ldots , a_p-a_{p,i}(t), \) \(b_1- b_{1,i}(t), \ldots , b_q-b_{q,i}(t)\big ]^\textrm{T},\) \(\left\{ a_{\tau , i}(t)\right\} _{\tau =1}^p \) and \(\left\{ b_{r, i}(t)\right\} _{r=1}^q\) are components of \(\theta _{k,i}(t;\) p, q) generated by Algorithm 1.

Proof

By (7) we have

$$\begin{aligned} \begin{aligned} \textrm{d}P_{k,i}^{-1}(t;p,q)=\phi _i(t;p,q){\phi _i}^\textrm{T}(t;p,q)\textrm{d}t. \end{aligned} \end{aligned}$$
(20)

By (8) and (20), we have

$$\begin{aligned}\begin{aligned}&\textrm{d}\big (P_{k,i}^{-1}(t;p,q)\tilde{\theta }_{k,i}(t;p,q)\big )\\&\quad =\phi _i(t;p,q){\phi _i}^\textrm{T}(t;p,q)\tilde{\theta }_{k,i}(t;p,q)\textrm{d}t\\&\qquad -\phi _i(t;p,q)\big [{\phi _i}^\textrm{T}(t;p,q)\tilde{\theta }_{k,i}(t;p,q)\textrm{d}t+\textrm{d}v_i(t)\big ]\\&\quad =-\phi _i(t;p,q)\textrm{d}v_i(t). \end{aligned} \end{aligned}$$

Integrating the above equation over \([t_k,t_{k+1})\) leads to

$$\begin{aligned} \begin{aligned}&P_{k,i}^{-1}(t_{k+1};p,q)\tilde{\theta }_{k,i}(t_{k+1};p,q)\\&\quad =P_{k,i}^{-1}(t_k;p,q)\tilde{\theta }_{k,i}(t_k;p,q)-\int _{t_k}^{t_{k+1}}\phi _i(s;p,q)\textrm{d}v_i(s). \end{aligned} \end{aligned}$$
(21)

Thus, we have

$$\begin{aligned}\begin{aligned}&P_{k+1,i}^{-1}(t_{k+1};p,q)\tilde{\theta }_{k+1,i}(t_{k+1};p,q)\\&\quad =P_{k+1,i}^{-1}(t_{k+1};p,q)\theta _{k+1,i}(t_{k+1};p,q)\\&\qquad -P_{k+1,i}^{-1}(t_{k+1};p,q)\theta (p,q)\\&\quad =\textstyle \sum \limits _{j \in \mathcal {N}_i}{a_{ij}}\big [P_{k,j}^{-1}(t_{k+1};p,q)\tilde{\theta }_{k,j}(t_{k+1};p,q)\big ]\\&\quad =\textstyle \sum \limits _{j \in \mathcal {N}_i}{a_{ij}}\big [P_{k,j}^{-1}(t_k;p,q)\tilde{\theta }_{k,j}(t_k;p,q)\\&\qquad -\int _{t_k}^{t_{k+1}}\phi _j(s;p,q)\textrm{d}v_j(s)\big ], \end{aligned} \end{aligned}$$

where the last equation is obtained from (21). We complete the proof. \(\square \)

Now, we give the convergence result for the order estimation of Algorithm 2.

Theorem 5

Under Assumptions 1 and 2, for any \(i \in \{1,\ldots ,n\}\), the order \((p_i(t),q_i(t))\) estimated by Algorithm 2 converges to the true order \((\bar{p},\bar{q})\) almost surely, i.e.,

$$\begin{aligned} \lim _{t\rightarrow \infty }(p_i(t),q_i(t))=(\bar{p},\bar{q}) ~~\text {a.s.},~~i \in \{1,\ldots ,n\}. \end{aligned}$$

Proof

We will show that for any \( i \in \{1,\ldots ,n\}\), \((p_i(t),q_i(t))\) has one and only one limit point \((\bar{p},\bar{q})\) by reduction to absurdity. Suppose \((p_i',q_i')\in I\) is another limit point of \((p_i(t),q_i(t))\) and \((p_i',q_i')\ne (\bar{p},\bar{q})\). Then there exists a subsequence \(\{t_{m_k}\}\) such that

$$\begin{aligned} \begin{aligned} \lim _{k\rightarrow \infty }(p_i(t_{m_k}),q_i(t_{m_k}))= (p_i',q_i'). \end{aligned} \end{aligned}$$
(22)

To prove that \(\lim \limits _{t\rightarrow \infty }(p_i(t),q_i(t))=(\bar{p},\bar{q}),\) we need to show that neither of the following two cases holds,

(1) \(p_i' \ge \bar{p}\), \(q_i' \ge \bar{q}\) and \(p_i'+q_i' > \bar{p}+\bar{q}\);

(2) \(p_i' < \bar{p}\) or \(q_i' < \bar{q}\).

We first consider the case (1). By (1) and (5), we have

$$\begin{aligned}&J_{m_k,i} (t_{m_k};p_i',q_i',\theta _{m_k,i}(t_{m_k};p_i',q_i') \nonumber \\&\quad ={\textstyle \sum \limits _{j=1}^N \textstyle \sum \limits _{\tau =0}^{m_k-1}} a_{ij}^{(m_k-\tau )} \int _{t_{\tau }}^{t_{\tau +1}}\left[ \tilde{\theta }_{m_k,i}^\textrm{T}(t_{m_k};p_i',q_i') \right. \nonumber \\&\left. \qquad \cdot \phi _j(s;p_i',q_i')+\frac{\textrm{d}v_j(s)}{\textrm{d}s}\right] ^2 \textrm{d}s\nonumber \\&\quad =\tilde{\theta }_{m_k,i}^\textrm{T}(t_{m_k};p_i',q_i') \nonumber \\&\qquad \cdot \left[ {\textstyle \sum \limits _{j=1}^N \textstyle \sum \limits _{\tau =0}^{m_k-1}} a_{ij}^{(m_k-\tau )} \int _{t_{\tau }}^{t_{\tau +1}}\phi _j(s;p_i',q_i') \right. \nonumber \\&\left. \qquad \cdot \phi _j^\textrm{T}(s;p_i',q_i') \textrm{d}s \right] \tilde{\theta }_{m_k,i}(t_{m_k};p_i',q_i') \nonumber \\&\qquad +2\tilde{\theta }_{m_k,i}^\textrm{T}(t_{m_k};p_i',q_i') \nonumber \\&\qquad \cdot \left[ {\textstyle \sum \limits _{j=1}^N \textstyle \sum \limits _{\tau =0}^{m_k-1}} a_{ij}^{(m_k-\tau )} \int _{t_{\tau }}^{t_{\tau +1}}\phi _j(s;p_i',q_i')\textrm{d}v_j(s) \right] \nonumber \\&\qquad +{\textstyle \sum \limits _{j=1}^N \textstyle \sum \limits _{\tau =0}^{m_k-1}} a_{ij}^{(m_k-\tau )} \int _{t_{\tau }}^{t_{\tau +1}}\left[ \frac{\textrm{d}v_j(s)}{\textrm{d}s}\right] ^2 \textrm{d}s \nonumber \\&\quad \triangleq \textrm{I} + \textrm{II} + \textrm{III}. \end{aligned}$$
(23)

We first estimate the term \(\textrm{I}\). For any p, q, integrating both sides of the equation (20) over \([t_k,t_{k+1})\), we have

$$\begin{aligned} \begin{array}{l} P_{k,i}^{-1}(t_{k+1};p,q) \\ \quad = P_{k,i}^{-1}(t_k;p,q) +\displaystyle {\int _{t_k}^{t_{k+1}}} \phi _i(s;p,q)\phi _i^\textrm{T}(s;p,q) \textrm{d}s. \end{array} \end{aligned}$$
(24)

Substituting the above equation into (8), we obtain that

$$\begin{aligned} \begin{array}{l} P_{k+1,i}^{-1}(t_{k+1};p,q) = \textstyle \sum \limits _{j\in \mathcal {N}_i} a_{ij} \left\{ P_{k,j}^{-1}(t_k;p,q)\right. \\ \quad \left. +\displaystyle {\int _{t_k}^{t_{k+1}}} \phi _j(s;p,q)\phi _j^\textrm{T}(s;p,q) \textrm{d}s\right\} . \end{array} \end{aligned}$$
(25)

Moreover we have by (24) and (25)

$$\begin{aligned} \begin{aligned}&P_{m_k,i}^{-1}(t_{m_k};p,q) \\&\quad = \textstyle \sum \limits _{j\in \mathcal {N}_i} a_{ij} \left\{ P_{m_k-1,j}^{-1}(t_{m_k};p,q)\right. \\&\left. \qquad +\int _{t_{m_k-1}}^{t_{m_k}} \phi _j(s;p,q)\phi _j^\textrm{T}(s;p,q) \textrm{d}s\right\} \\&\quad = \textstyle \sum \limits _{j=1}^N a_{ij}^{(m_k)} P_{0,j}^{-1}(t_0;p,q)\\&\qquad + {\textstyle \sum \limits _{j=1}^N \textstyle \sum \limits _{\tau =0}^{m_k-1}} a_{ij}^{(m_k-\tau )} \!\!\int _{t_{\tau }}^{t_{\tau +1}}\!\!\phi _j(s;p,q)\phi _j^\textrm{T}(s;p,q) \textrm{d}s. \end{aligned} \end{aligned}$$
(26)

By (26) and Theorem 3.8 in [42] it follows that

$$\begin{aligned} \begin{aligned} \textrm{I}=O\left( \log R(t_{m_k};p_i',q_i')\right) =O\left( \log R(t_{m_k};U_p,U_q)\right) . \end{aligned} \end{aligned}$$
(27)

For the second term \(\textrm{II}\) in (23), it is clear that

$$\begin{aligned} \begin{aligned} \vert \textrm{II}\vert \le \,&2\Big \Vert \tilde{\theta }_{m_k,i}^\textrm{T}(t_{m_k};p_i',q_i')P_{m_k,i}^{-\frac{1}{2}}(t_{m_k};p_i',q_i')\Big \Vert \\&\quad \cdot \left\| P_{m_k,i}^{\frac{1}{2}}(t_{m_k};p_i',q_i')\right. \\&\left. \quad \cdot \left[ {\textstyle \sum \limits _{j=1}^N\textstyle \sum \limits _{\tau =0}^{m_k-1} a_{ij}^{(m_k-\tau )}} \int _{t_{\tau }}^{t_{\tau +1}}\phi _j(s;p_i',q_i')\textrm{d}v_j(s) \right] \right\| . \end{aligned} \end{aligned}$$
(28)

By applying Theorem 3.8 in [42] to the first term in (28), we can get the following equation,

$$\begin{aligned} \begin{aligned}&\big \Vert \tilde{\theta }_{m_k,i}^\textrm{T}(t_{m_k};p_i',q_i')P_{m_k,i}^{-\frac{1}{2}}(t_{m_k};p_i',q_i')\big \Vert \\&\quad =O\big (\log ^{\frac{1}{2}}\big ( R({t_{m_k}};p_i',q_i')\big )\big )\\&\quad =O\big (\log ^{\frac{1}{2}}\big ( R(t_{m_k};U_p,U_q)\big )\big ). \end{aligned} \end{aligned}$$
(29)

From Lemma 3, we see that the second term in (28) satisfies

$$\begin{aligned}{} & {} \left\| P_{m_k,i}^{\frac{1}{2}}(t_{m_k};p_i',q_i')\right. \nonumber \\{} & {} \left. \qquad \cdot \left[ {\textstyle \sum \limits _{j=1}^N \textstyle \sum \limits _{\tau =0}^{m_k-1}} a_{ij}^{(m_k-\tau )} \int _{t_{\tau }}^{t_{\tau +1}}\phi _j(s;p_i',q_i')\textrm{d}v_j(s) \right] \right\| \nonumber \\{} & {} \quad =O\big (\log ^{\frac{1}{2}}\big ( R({t_{m_k}};p_i',q_i')\big )\big )\nonumber \\{} & {} \quad =O\big (\log ^{\frac{1}{2}} \big (R({t_{m_k}};U_p,U_q)\big )\big ). \end{aligned}$$
(30)

By(27)–(29), we see that there exists a constant \(M_1>0\) such that the following inequality holds,

$$\begin{aligned} \begin{aligned}&J_{m_k,i} \big (t_{m_k};p_i',q_i',\theta _{m_k,i}\big (t_{m_k};p_i',q_i'\big )\big )-\textrm{III}\\&\quad \ge -M_1 \log \big ( R(t_{m_k};U_p,U_q)\big ). \end{aligned} \end{aligned}$$
(31)

Next we consider \(J_{m_k,i} (t_{m_k};\bar{p},\bar{q},\theta _{m_k,i}(t_{m_k};\bar{p},\bar{q}))\). By a similar derivation as that of (23), we have

$$\begin{aligned}&J_{m_k,i} \big (t_{m_k};\bar{p},\bar{q},\theta _{m_k,i}(t_{m_k};\bar{p},\bar{q})\big ) \nonumber \\&\quad =\tilde{\theta }_{m_k,i}^\textrm{T}(t_{m_k};\bar{p},\bar{q}) \left[ {\textstyle \sum \limits _{j=1}^N \textstyle \sum \limits _{\tau =0}^{m_k-1}} a_{ij}^{(m_k-\tau )} \!\!\int _{t_{\tau }}^{t_{\tau +1}}\!\!\phi _j(s;\bar{p},\bar{q}) \right. \nonumber \\&\left. \qquad \cdot \phi _j^\textrm{T}(s;\bar{p},\bar{q}) \textrm{d}s \right] \tilde{\theta }_{m_k,i}(t_{m_k};\bar{p},\bar{q})\!+\!2\tilde{\theta }_{m_k,i}^\textrm{T}(t_{m_k};\bar{p},\bar{q}) \nonumber \\&\qquad \cdot \left[ \textstyle \sum \limits _{j=1}^N \textstyle \sum \limits _{\tau =0}^{m_k-1} a_{ij}^{(m_k-\tau )} \int _{t_{\tau }}^{t_{\tau +1}}\phi _j(s;\bar{p},\bar{q})\textrm{d}v_j(s) \right] \nonumber \\&\qquad +{\textstyle \sum \limits _{j=1}^N \textstyle \sum \limits _{\tau =0}^{m_k-1} a_{ij}^{(m_k-\tau )}} \int _{t_{\tau }}^{t_{\tau +1}}\Big [\frac{\textrm{d}v_j(s)}{\textrm{d}s}\Big ]^2 \textrm{d}s \nonumber \\&\quad \triangleq \mathrm {I'} + \mathrm {II'} + \textrm{III}. \end{aligned}$$
(32)

By (26) we have

$$\begin{aligned} \begin{aligned} \mathrm {I'}=\,&\tilde{\theta }_{m_k,i}^\textrm{T}(t_{m_k};\bar{p},\bar{q}) {P}_{m_k,i}^{-1}(t_{m_k};\bar{p},\bar{q}) \tilde{\theta }_{m_k,i}(t_{m_k};\bar{p},\bar{q}) \\&-\tilde{\theta }_{m_k,i}^\textrm{T}(t_{m_k};\bar{p},\bar{q})\Big ( \textstyle \sum \limits _{j=1}^N a_{ij}^{(m_k)} P_{0,j}^{-1}(t_0;\bar{p},\bar{q}) \Big )\\&\cdot \tilde{\theta }_{m_k,i}^\textrm{T}(t_{m_k};\bar{p},\bar{q}). \end{aligned} \end{aligned}$$
(33)

For the second term \(\mathrm {II'}\), we have by Lemma 4,

$$\begin{aligned} \begin{aligned}&P_{m_k,i}^{-1}(t_{m_k};\bar{p},\bar{q})\tilde{\theta }_{m_k,i}(t_{m_k};\bar{p},\bar{q})\\&\quad =\textstyle \sum \limits _{j=1}^N{a_{ij}}P_{m_k-1,j}^{-1}(t_{m_k-1};\bar{p},\bar{q})\tilde{\theta }_{m_k-1,j}(t_{m_k-1};\bar{p},\bar{q})\\&\qquad -\textstyle \sum \limits _{j=1}^N{a_{ij}} \displaystyle {\int _{t_{m_k-1}}^{t_{m_k}}}\phi _j(s;\bar{p},\bar{q})\textrm{d}v_j(s)\\&\quad =\textstyle \sum \limits _{j=1}^Na_{ij}^{(m_k)}P_{0,j}^{-1}(t_0;\bar{p},\bar{q})\tilde{\theta }_{0,j}(t_0;\bar{p},\bar{q})\\&\qquad -\textstyle \sum \limits _{j=1}^N\textstyle \sum \limits _{\tau =0}^{m_k-1}{a_{ij}^{(m_k-\tau )}} \displaystyle {\int _{t_{\tau }}^{t_{\tau +1}}}\phi _j(s;\bar{p},\bar{q})\textrm{d}v_j(s). \end{aligned} \end{aligned}$$
(34)

Substituting (34) into \(\mathrm {II'}\) yields the following equation,

$$\begin{aligned} \begin{aligned} \mathrm {II'}=\,&2\tilde{\theta }_{m_k,i}^\textrm{T}(t_{m_k};\bar{p},\bar{q})\\&\cdot \left[ \textstyle \sum \limits _{j=1}^Na_{ij}^{(m_k)}P_{0,j}^{-1}(t_0;\bar{p},\bar{q})\tilde{\theta }_{0,j}(t_0;\bar{p},\bar{q})\right. \\&\left. -P_{m_k,i}^{-1}(t_{m_k};\bar{p},\bar{q})\tilde{\theta }_{m_k,i}(t_{m_k};\bar{p},\bar{q})\right] . \end{aligned} \end{aligned}$$
(35)

Substituting (33) and (35) into (32) yields

$$\begin{aligned}&J_{m_k,i} \Big (t_{m_k};\bar{p},\bar{q},\theta _{m_k,i}(t_{m_k};\bar{p},\bar{q})\Big )-\textrm{III} \nonumber \\&\quad =\tilde{\theta }_{m_k,i}^\textrm{T}(t_{m_k};\bar{p},\bar{q}) {P}_{m_k,i}^{-1}(t_{m_k};\bar{p},\bar{q}) \tilde{\theta }_{m_k,i}(t_{m_k};\bar{p},\bar{q}) \nonumber \\&\qquad -\tilde{\theta }_{m_k,i}^\textrm{T}(t_{m_k};\bar{p},\bar{q})\Big ( \textstyle \sum \limits _{j=1}^N a_{ij}^{(m_k)} P_{0,j}^{-1}(t_0;\bar{p},\bar{q}) \Big ) \nonumber \\&\qquad \cdot \tilde{\theta }_{m_k,i}^\textrm{T}(t_{m_k};\bar{p},\bar{q})+2\tilde{\theta }_{m_k,i}^\textrm{T}(t_{m_k};\bar{p},\bar{q}) \nonumber \\&\qquad \cdot \left[ \textstyle \sum \limits _{j=1}^Na_{ij}^{(m_k)}P_{0,j}^{-1}(t_0;\bar{p},\bar{q})\tilde{\theta }_{0,j}(t_0;\bar{p},\bar{q}) \right. \nonumber \\&\left. \qquad -P_{m_k,i}^{-1}(t_{m_k};\bar{p},\bar{q})\tilde{\theta }_{m_k,i}(t_{m_k};\bar{p},\bar{q})\right] \nonumber \\&\quad \le -\tilde{\theta }_{m_k,i}^\textrm{T}(t_{m_k};\bar{p},\bar{q})\left( \textstyle \sum \limits _{j=1}^N a_{ij}^{(m_k)} P_{0,j}^{-1}(t_0;\bar{p},\bar{q}) \right) \nonumber \\&\qquad \cdot \tilde{\theta }_{m_k,i}^\textrm{T}(t_{m_k};\bar{p},\bar{q})+2\tilde{\theta }_{m_k,i}^\textrm{T}(t_{m_k};\bar{p},\bar{q}) \nonumber \\&\qquad \cdot \left( \textstyle \sum \limits _{j=1}^Na_{ij}^{(m_k)}P_{0,j}^{-1}(t_0;\bar{p},\bar{q})\tilde{\theta }_{0,j}(t_0;\bar{p},\bar{q})\right) \nonumber \\&\quad \le \textstyle \sum \limits _{j=1}^Na_{ij}^{(m_k)}{\tilde{\theta }_{0,j}}^\textrm{T}(t_0;\bar{p},\bar{q})P_{0,j}^{-1}(t_0;\bar{p},\bar{q})\tilde{\theta }_{0,j}(t_0;\bar{p}, \bar{q}) \nonumber \\&\quad =O(1). \end{aligned}$$
(36)

where the last inequality uses the inequality \( 2 x^\textrm{T} A y\le x^\textrm{T} A x+y^\textrm{T} A y\) for \(A \ge 0 . \) From (31) and (36), there exists a constant \(M_2>0\) such that the following inequality holds,

$$\begin{aligned} \begin{aligned}&J_{m_k,i} (t_{m_k};p_i',q_i',\theta _{m_k,i}(t_{m_k};p_i',q_i'))\\&\qquad -J_{m_k,i}(t_{m_k};\bar{p},\bar{q},\theta _{m_k,i}(t_{m_k};\bar{p},\bar{q}))\\&\quad \ge -M_1 \log \left( R(t_{m_k};U_p,U_q)\right) -M_2. \end{aligned} \end{aligned}$$
(37)

Note that \(p_i(t_{m_k}),q_i(t_{m_k})\) in (22) are positive integers. Then, there exists a \(K\in \mathbb N^+\) such that for \(k>K\), \( (p_i(t_{m_k}),q_i(t_{m_k}))\equiv (p_i',q_i') \). By

$$\begin{aligned} (p_i(t_{m_k}),q_i(t_{m_k}))=\arg \min \limits _{(p,q)\in I}F_{m_k,i}(t_{m_k};p,q), \end{aligned}$$

we know that

$$\begin{aligned} \begin{aligned} F_{m_k, i}\left( t_{m_k};p_i({t_{m_k}}), p_i(t_{m_k})\right) -F_{m_k, i}\left( t_{m_k};\bar{p},\bar{q}\right) \le 0. \end{aligned} \end{aligned}$$
(38)

On the other hand, by (37) and Assumption 2, we have for sufficiently large k,

$$\begin{aligned}\begin{aligned}&F_{m_k, i}\left( t_{m_k};p_i({t_{m_k}}), q_i(t_{m_k})\right) -F_{m_k, i}\left( t_{m_k};\bar{p},\bar{q}\right) \\&\quad =F_{m_k, i}\left( t_{m_k};p_i',q_i'\right) -F_{m_k, i}\left( t_{m_k};\bar{p},\bar{q}\right) \\&\quad =J_{m_k,i} (t_{m_k};p_i',q_i',\theta _{m_k,i}(t_{m_k};p_i',q_i'))\\&\qquad -J_{m_k,i} (t_{m_k};\bar{p},\bar{q},\theta _{m_k,i}(t_{m_k};\bar{p},\bar{q}))\\&\qquad +\left( p_i'+q_i'-\bar{p}-\bar{q}\right) \xi (t_{m_k}) \\&\quad \ge -M_1 \log \left( R(t_{m_k};U_p,U_q)\right) -M_2\\&\qquad +\left( p_i'+q_i'-\bar{p}-\bar{q}\right) \xi (t_{m_k}) \\&\quad =-M_2 +\xi (t_{m_k})\Big (\frac{-M_1 \log \big ( R(t_{m_k};U_p,U_q)\big )}{\xi (t_{m_k})}\\&\qquad +\big (p_i'+q_i'-\bar{p}-\bar{q}\big ) \Big )\rightarrow \infty ,~~k \rightarrow \infty . \end{aligned} \end{aligned}$$

This contradicts (38), so case (1) does not hold.

We next show that the case (2) will not happen. If case (2) holds, i.e., \(p_i'<\bar{p}\) or \(q_i'<\bar{q}\) holds. We construct the following \(\left( \kappa _i+\mu _i\right) \) dimensional vector,

$$\begin{aligned} {\theta }_{m_k, i}\left( t_{m_k};\kappa _i, \mu _i\right) =\big [&a_{1, i}(t_{m_k}), \ldots , a_{\kappa _i, i}(t_{m_k}),\\&b_{1, i}(t_{m_k}), \ldots , b_{\mu _i, i}(t_{m_k})\big ]^\textrm{T}, \end{aligned}$$

where \(\kappa _i=\max \left\{ p_i',\bar{p}\right\} , \mu _i=\max \left\{ q_i',\bar{q}\right\} \), \( a_{m, i}(t_{m_k})\) \( \triangleq \) \( 0\ (p_i'<m \le \bar{p})\) if \(p_i'<\bar{p}\); \(b_{m, i}(t_{m_k}) \triangleq 0\ (q_i'<m \le \bar{q})\) if \(q_i'<\bar{q}\).

Denote \(\tilde{ {\theta }}_{m_k, i}\left( t_{m_k};\kappa _i, \mu _i\right) \triangleq {\theta }\left( \kappa _i, \mu _i\right) - {\theta }_{m_k, i}(t_{m_k};\) \(\kappa _i,\) \( \mu _i)\). Then we have

$$\begin{aligned} \begin{aligned} \big \Vert \tilde{ {\theta }}_{m_k, i}\big (t_{m_k};\kappa _i, \mu _i\big )\big \Vert ^2 \ge \min \left\{ \left| a_{\bar{p}}\big \vert ^2,\big \vert b_{\bar{q}}\right| ^2\right\} \triangleq \gamma _0>0 . \end{aligned} \end{aligned}$$
(39)

Similar to the analysis of (23) and (26), we have

$$\begin{aligned} \begin{aligned}&J_{m_k,i} (t_{m_k};p_i',q_i',\theta _{m_k,i}(t_{m_k};p_i',q_i'))-\textrm{III}\\&\quad ={\textstyle \sum \limits _{j=1}^N \textstyle \sum \limits _{\tau =0}^{m_k-1}} a_{ij}^{(m_k-\tau )} \int _{t_{\tau }}^{t_{\tau +1}} \left[ \frac{\textrm{d}y_j(s)}{\textrm{d}s} \right. \\&\left. \qquad -\theta _{m_k,i}^\textrm{T}(t_{m_k};p_i',q_i')\phi _j(s;p_i',q_i')\right] ^2 \textrm{d}s\\&\quad =\tilde{\theta }_{m_k,i}^\textrm{T}(t_{m_k};\kappa _i,\mu _i) {P}_{m_k,i}^{-1}(t_{m_k};\kappa _i,\mu _i) \\&\qquad \cdot \tilde{\theta }_{m_k,i}(t_{m_k};\kappa _i,\mu _i) -\tilde{\theta }_{m_k,i}^\textrm{T}(t_{m_k};\kappa _i,\mu _i)\\&\qquad \cdot \left( \textstyle \sum \limits _{j=1}^N a_{ij}^{(m_k)} P_{0,j}^{-1}(t_0;\kappa _i,\mu _i) \right) \tilde{\theta }_{m_k,i}^\textrm{T}(t_{m_k};\kappa _i,\mu _i)\\&\qquad +2\tilde{\theta }_{m_k,i}^\textrm{T}(t_{m_k};\kappa _i,\mu _i)\\&\qquad \cdot \left[ { \textstyle \sum \limits _{j=1}^N \textstyle \sum \limits _{\tau =0}^{m_k-1}} a_{ij}^{(m_k-\tau )} \int _{t_{\tau }}^{t_{\tau +1}}\phi _j(s;\kappa _i,\mu _i)\textrm{d}v_j(s) \right] . \end{aligned} \end{aligned}$$
(40)

The following is a term-by-term analysis of the right-hand side of (40). From (26) and Remark 1 it follows that for any p and q the following inequality holds,

$$\begin{aligned} \begin{aligned} \lambda _{\min }\big ( P_{m_k, i}^{-1}(t_{m_k};p, q)\big ) \ge a_{\min } \lambda _{\min }\left( t_{m_k};p,q\right) , \end{aligned} \end{aligned}$$
(41)

where \(a_{\min }=\min \limits _{i, j \in \mathcal {V}} a_{i j}^{\left( D_{\mathcal {G}}\right) }>0\). From (39), (41) and Theorem 2.6 in [13], we obtain the following estimate of the first term at the right-hand side of the equation (40),

$$\begin{aligned} \begin{aligned}&\tilde{\theta }_{m_k,i}^\textrm{T}(t_{m_k};\kappa _i,\mu _i) {P}_{m_k,i}^{-1}(t_{m_k};\kappa _i,\mu _i) \tilde{\theta }_{m_k,i}(t_{m_k};\kappa _i,\mu _i) \\&\quad \ge \gamma _0 a_{\min } \lambda _{\min }\left( t_{m_k};\kappa _i,\mu _i\right) \\&\quad \ge \gamma _0 a_{\min } \min \left\{ \lambda _{\min }\left( t_{m_k};\bar{p},U_q\right) ,\lambda _{\min }\left( t_{m_k};U_p,\bar{q}\right) \right\} . \end{aligned} \end{aligned}$$
(42)

By (41) and Theorem 3.8 in [42], we have for any \(p \ge \bar{p}\) and \(q \ge \bar{q}\),

$$\begin{aligned} \begin{aligned}&\textstyle \sum \limits _{i=1}^n\big \Vert \tilde{ {\theta }}_{n, i}(t;p, q)\big \Vert ^2\\&\quad =O\left( \dfrac{\log R(n;p, q)}{\lambda _{\min }(n;p,q)}\right) , \ t\in [t_n,t_{n+1}). \end{aligned} \end{aligned}$$
(43)

When \(p_i'<\bar{p}\), ( \(q_i'<\bar{q}\) is the same), for the first \(p_i'\) components of \(\tilde{ {\theta }}_{ m_k, i}\left( t_{m_k};\kappa _i,\mu _i\right) \) utilizing (43), then from Theorem 2.6 in [13] and Assumption 2, we have \(\big \Vert \tilde{ {\theta }}_{m_k, i}\left( t_{m_k};\kappa _i,\mu _i\right) \big \Vert =O(1)\). Thus the second term at the right-hand side of (40) satisfies the following relation,

$$\begin{aligned} \begin{aligned}&\tilde{\theta }_{m_k,i}^\textrm{T}(t_{m_k};\kappa _i,\mu _i)\left( \textstyle \sum \limits _{j=1}^N a_{ij}^{(m_k)} P_{0,j}^{-1}(t_0;\kappa _i,\mu _i) \right) \\&\qquad \cdot \tilde{\theta }_{m_k,i}^\textrm{T}(t_{m_k};\kappa _i,\mu _i) \\&\quad \le \lambda _{\max }\left( \textstyle \sum \limits _{j=1}^n a_{i j}^{(t)} {P}_{0, j}^{-1}\left( \kappa _i,\mu _i\right) \right) \left\| \tilde{ {\theta }}_{t_k, i}\left( \kappa _i,\mu _i\right) \right\| ^2\\&\quad =O(1) . \end{aligned} \end{aligned}$$
(44)

Following an analysis similar to that of (28), the following estimate of the third term at the right-hand side of (40) can be obtained by using Lemma 3,

$$\begin{aligned}{} & {} \left| \tilde{\theta }_{m_k,i}^\textrm{T}(t_{m_k};\kappa _i,\mu _i)\right. \nonumber \\{} & {} \left. \quad \left[ {\textstyle \sum \limits _{j=1}^N \textstyle \sum \limits _{\tau =0}^{m_k-1}} a_{ij}^{(m_k-\tau )} \int _{t_{\tau }}^{t_{\tau +1}}\phi _j(s;\kappa _i,\mu _i)\textrm{d}v_j(s) \right] \right| \nonumber \\{} & {} \quad \le \Big \Vert \tilde{\theta }_{m_k,i}^\textrm{T}(t_{m_k};\kappa _i,\mu _i)P_{m_k,i}^{-\frac{1}{2}}(t_{m_k};\kappa _i,\mu _i)\Big \Vert \nonumber \\{} & {} \qquad \cdot \left\| P_{m_k,i}^{\frac{1}{2}}(t_{m_k};\kappa _i,\mu _i)\right. \nonumber \\{} & {} \left. \qquad \cdot \left[ {\textstyle \sum \limits _{j=1}^N \textstyle \sum \limits _{\tau =0}^{m_k-1}} a_{ij}^{(m_k-\tau )} \int _{t_{\tau }}^{t_{\tau +1}}\phi _j(s;\kappa _i,\mu _i)\textrm{d}v_j(s) \right] \right\| \nonumber \\{} & {} \quad =O\left\{ \left\| \tilde{\theta }_{m_k,i}^\textrm{T}(t_{m_k};\kappa _i,\mu _i)P_{m_k,i}^{-\frac{1}{2}}(t_{m_k};\kappa _i,\mu _i)\right\| \right. \nonumber \\{} & {} \left. \qquad \cdot \log ^{\frac{1}{2}}\Big ( R(t_{m_k};U_p,U_q)\Big )\right\} , \end{aligned}$$
(45)

Continuing from (39), (41) and Assumption 2 the final estimate of the third term at the right-hand side of (40) is

$$\begin{aligned} \begin{aligned}&\left| \tilde{\theta }_{m_k,i}^\textrm{T}(t_{m_k};\kappa _i,\mu _i)\right. \\&\left. \qquad \cdot \left[ {\textstyle \sum \limits _{j=1}^N \textstyle \sum \limits _{\tau =0}^{m_k-1}} a_{ij}^{(m_k-\tau )} \int _{t_{\tau }}^{t_{\tau +1}}\phi _j(s;\kappa _i,\mu _i)\textrm{d}v_j(s) \right] \right| \\&\quad =O\left\{ \tilde{\theta }_{m_k,i}^\textrm{T}(t_{m_k};\kappa _i,\mu _i) {P}_{m_k,i}^{-1}(t_{m_k};\kappa _i,\mu _i) \right. \\&\left. \qquad \cdot \tilde{\theta }_{m_k,i}(t_{m_k};\kappa _i,\mu _i)\right\} . \end{aligned} \end{aligned}$$
(46)

Substituting (42), (44) and (46) into (40), it can be shown that there exists a constant \(M_3>0\) such that the following inequality holds,

$$\begin{aligned} \begin{aligned}&J_{m_k,i} (t_{m_k};p_i',q_i',\theta _{m_k,i}(t_{m_k};p_i',q_i'))-\textrm{III}\\&\quad \ge \gamma _0 a_{\min } \min \left\{ \lambda _{\min }\left( t_{m_k};\bar{p},U_q\right) ,\lambda _{\min }\left( t_{m_k};U_p,\bar{q}\right) \right\} \\&\qquad \cdot (1+o(1))-M_3\\&\quad \ge \frac{\gamma _0 a_{\min } \min \left\{ \lambda _{\min }\left( t_{m_k};\bar{p},U_q\right) ,\lambda _{\min }\left( t_{m_k};U_p,\bar{q}\right) \right\} }{2}\\&\qquad -M_3. \end{aligned} \end{aligned}$$
(47)

From (10), (36) and (47) it follows that the following inequality holds for sufficiently large k,

$$\begin{aligned} \begin{aligned} 0\ge \,&F_{m_k, i}\left( t_{m_k};p_i({t_{m_k}}), q_i(t_{m_k})\right) -F_{m_k, i}\left( t_{m_k};\bar{p},\bar{q}\right) \\ =\,&F_{m_k, i}\left( t_{m_k};p_i',q_i'\right) -F_{m_k, i}\left( t_{m_k};\bar{p},\bar{q}\right) \\ =\,&J_{m_k,i} (t_{m_k};p_i',q_i',\theta _{m_k,i}(t_{m_k};p_i',q_i'))\\&-J_{m_k,i} (t_{m_k};\bar{p},\bar{q},\theta _{m_k,i}(t_{m_k};\bar{p},\bar{q})\\&+\left( p_i'+q_i'-\bar{p}-\bar{q}\right) \xi (t_{m_k}) \\ \ge \,&\frac{\gamma _0 a_{\min } \min \left\{ \lambda _{\min }\left( t_{m_k};\bar{p},U_q\right) ,\lambda _{\min }\left( t_{m_k};U_p,\bar{q}\right) \right\} }{2}\\&-M_3+\left( p_i'+q_i'-\bar{p}-\bar{q}\right) \xi (t_{m_k}) \\ \ge \,&-M_3\\&+\frac{\gamma _0 a_{\min } \min \left\{ \lambda _{\min }\left( t_{m_k};\bar{p},U_q\right) ,\lambda _{\min }\left( t_{m_k};U_p,\bar{q}\right) \right\} }{2}\\&\cdot \left\{ 1+\frac{\left( p_i'+q_i'-\bar{p}-\bar{q}\right) \xi (t_{m_k})}{\gamma _0 a_{\min } \min \left\{ \lambda _{\min }\left( t_{m_k};\bar{p},U_q\right) ,\lambda _{\min }\left( t_{m_k};U_p,\bar{q}\right) \right\} }\right\} \\ \ge \,&-M_3\\&+\frac{\gamma _0 a_{\min } \min \left\{ \lambda _{\min }\left( t_{m_k};\bar{p},U_q\right) ,\lambda _{\min }\left( t_{m_k};U_p,\bar{q}\right) \right\} }{4}\\ \rightarrow&\infty ,\ k\rightarrow \infty . \end{aligned} \end{aligned}$$

There is a contradiction, which proves that case (2) is not valid either. \(\square \)

Noting that \(\left( p_i(t),q_i(t)\right) \) and \(\left( \bar{p}, \bar{q}\right) \) are integers, it follows from Theorem 5 that there exists a sufficiently large integer T such that, for any \(t \ge T\), \(p_i(t)=\bar{p}\) and \(q_i(t)=\bar{q}\) hold. Thus by (43) and Assumption 2, the following convergence result on the unknown parameter vector can be obtained.

Theorem 6

Under the condition of Theorem 5, for all \(i \in \{1, \ldots , n\}\) the following equation holds,

$$\begin{aligned} {\theta }_{n, i}\left( t;p_i(t),q_i(t)\right) \underset{t \rightarrow \infty }{\longrightarrow }\ {\theta }\left( \bar{p}, \bar{q}\right) \text {, a.s., } \end{aligned}$$

where \( {\theta }_{n, i}\left( t;p_i(t),q_i(t)\right) \) is given by Algorithm 2.

Theorem 6 provides the almost sure convergence result for Algorithm 2 when both the order and parameters in (2) are unknown. We see that the convergence results are established without assuming the statistical properties of regression vectors, such as independency, stationarity or ergodicity, which makes our results applicable for feedback control systems.

4 Simulation results

In this section, we will verify effectiveness of the proposed distributed order estimation algorithm (Algorithm 2) by a simulation example.

Example 1

Consider a network of ten sensors \((N=10)\). The dynamics of each sensor is described by the following stochastic differential equation

$$\begin{aligned} y_i(t)=S\phi _i^\textrm{T}(t)\theta +v_{i}(t),\ i=1,2,\ldots , 10, \end{aligned}$$

where both the parameter vector \(\theta \in \mathbb R^{\bar{q}}\) and the system order \(\bar{q}\) are to be estimated, \(v_{i}(t)\) is the system noise following the standard Wiener process. For \(q=U_q\), the regressor \(\phi _i(t)\in \mathbb R^{U_q}\ (t\ge 0), i\in \{1,\ldots ,10\}\)) is taken as

$$\begin{aligned} x_i(t)=\,&\left\{ \begin{array}{ll} 0.5t+0.5, &{}\text { if}~~\hbox {mod}(i,3)=0, \\ t+0.5, &{}\text { if}~~\hbox {mod}(i,3)=1,\\ t^2+0.5, &{}\text { if}~~\hbox {mod}(i,3)=2, \end{array}\right. \nonumber \\ \phi _i(t)=\,&[\underbrace{\varvec{e_1},\ldots ,\varvec{0},\varvec{e_\tau },\varvec{0},\ldots ,\varvec{0}}_{U_q} ]^\textrm{T} X_i(t), \end{aligned}$$
(48)

where \(X_i(t)=(\underbrace{x_i(t),\ldots ,x_i(t)}_{U_q})^\textrm{T},\) \(\varvec{0}\) denotes the \(U_q\)-dimensional column vector with all zero elements, \(\tau =2+\hbox {mod}(i,U_q-1)\), the \(\hbox {mod}\) is a remainder operator, and \(\varvec{e_\tau }\) denotes the \(\tau \)th column of the unit matrix \(I_{U_q}\). For \(q<U_q\), the regressor \(\phi _i(t)\) is taken as the first q elements of (48). The network topology \(\mathcal {G}\) is shown in Fig. 1, whose weighted adjacency matrix \(\mathcal {A}=(a_{mi})_{10\times 10}\) is determined by the Metropolis rule (cf. [43]).

Fig. 1
figure 1

Topology of the sensor network

Full size image

All sensors will estimate the true system order of \(\bar{q}=3\) and the unknown parameter vector \(\theta = (0.3,0.4,1.2)^\textrm{T}\). It is clear that the graph \(\mathcal {G}\) is connected and the regressor \(\phi _i(t)\) of all sensors \(i\in \{1,\ldots ,10\}\) satisfies Assumption 2 with \(\xi (t)=t^{\frac{1}{2}}\).

Set the initial estimate \(\theta _i(0)=( \underbrace{ 0,\ldots ,0}_{q})^\textrm{T}\), the fusion time instants \(t_0=0, 0.1, 0.2, 0.3,\ldots \), the upper bound of system order is taken as \(U_q=5\). Algorithm 2 is conducted 100 runs with the same initial setting, and the order estimates \(\{q_i(t)\}, i=1,2,\ldots , 10\) and the average estimation error of parameters can be obtained.

Figure 2 shows the simulation results for the order estimate obtained by Algorithm 2 proposed in this paper and the non-distributed algorithm (namely, \(N=1\) and \(D_{\mathcal G}=1\)). It can be seen that the sequences of order estimates \(\{q_i(t)\}\ (i=1,\ldots ,10)\) by using Algorithm 2 converges to the true order, and not all sequences of order estimates can converge to the true order for the non-distributed order estimation algorithm.

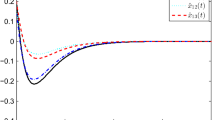
Figure 3 shows the simulation results of the average estimation error of parameters by Algorithm 2 and the non-distributed algorithm. It can be seen that the estimation errors generated by Algorithm 2 for each sensor i converge to zero, while the estimation errors generated by non-distributed algorithm do not tend to zero.

Fig. 2
figure 2

Order estimates generated by (a) Algorithm 2 and (b) non-distributed algorithm

Full size image
Fig. 3
figure 3

Parameter estimation errors by (a) Algorithm 2 and (b) non-distributed order estimation algorithm

Full size image

From this simulation example, we can reveal the cooperative effect of multiple sensors: all sensors can cooperatively estimate unknown system order and parameters, while none of them can do it separately.

5 Concluding remarks

In this paper, we study the distributed order estimation problem of continuous-time stochastic regression models. The distributed order estimation algorithm (Algorithm 2) is designed by minimizing the piecewise continuous local information criterion based on the \(L_0\) penalty term, and utilizing the continuous-time distributed least squares algorithm based on the diffusion strategy. By introducing cooperative excitation condition and dealing with the complex coupling between estimates of system order and parameters, almost surely convergence results of the proposed algorithm are established. The convergence results in this paper is obtained without assuming regression vectors to be bounded or satisfy the persistent excitation conditions, which allows our results to be further used in the related studies of feedback control systems. Finally, the effectiveness of the proposed distributed algorithm for the unknown order and parameters is verified by a simulation example. Some interesting problems such as the distributed order estimation problem with unknown upper bound, the distributed adaptive control problem, deserve to be further studied.