1 Introduction

The theory on the least mean square (LMS) [1, 2] algorithm dates back to the 1960s [3, 4], but comprehensive analyses of the algorithm using the independence assumption seem to have been published in the 1980s [5, 6]. The independence assumption [1, 7] states that the input data vector is statistically independent or that the filter weights are independent of the input data vectors. It has been shown that using this assumption and for moderate step sizes, the theoretical results agree very well with experiments. The convergence of the NLMS was also studied at that time [8]. After this, some results were obtained for non-Gaussian signals [9], and an exact analysis has been published [10]. The exact analysis uses mathematical software to obtain complex expressions for the convergence of the algorithm, resulting in results that agree with experiments also for large step s sizes. One work [11] shows that the LMS and NLMS algorithms are \(H^\infty \) optimum and limit the error signal’s power given the disturbances.

More recently, several efforts have been made to analyze the LMS algorithm without the independence assumption with a less complex theory than the presented in [10], namely using Butterweck iterative procedure [12,13,14,15,16,17]. Moreover, there is ongoing work to generalize the previous analysis to non-stationary and non-Gaussian inputs [7, 18,19,20]. There is also LMS algorithm variants analysis [21, 22]. This work proposes an analysis that allows obtaining some of the known results and new results easily.

2 The LMS and NLMS algorithms

Given a input signal x(n) and a desired response signal d(n), the LMS algorithm can be used to adapt a size N finite impulse response filter \(\textbf{w}(n)=[w_0, w_1, \dots w_{N-1}]^\textrm{T}\) to minimize the error between the filter output, \(y(n)={\textbf{x}^{\textrm{T}}}(n)\textbf{w}(n)\) and d(n), where \(\textbf{x}(n)=[x(n),x(n-1),\dots ,x(n-N+1)]^\textrm{T}\). The LMS algorithm is then described by [1, 2],

$$\begin{aligned} \textbf{w}(n+1) = \textbf{w}(n) + \mu \textbf{x}(n) e(n) \end{aligned}$$
(1)

where \(\mu \) is the step size and e(n) is the error signal

$$\begin{aligned} e(n) = d(n)-\textbf{x}^\textrm{T}(n) \textbf{w}(n). \end{aligned}$$
(2)

Let, \(\textbf{w}_\textrm{o}\) be the filter that minimizes the mean square error (MSE) \({E}[e^2(n)]\) given by the Wiener filter [1], then e(n) can also be written by

$$\begin{aligned} e(n)=\textbf{x}^\textrm{T}(n)(\textbf{w}_o - \textbf{w}(n)) + v(n) \end{aligned}$$
(3)

where v(n) is the background noise and is uncorrelated to \(\textbf{x}(n)\). In the NLMS algorithm [1, 2], \(\mu \) is replaced by \(\mu /(\textbf{x}^\textrm{T}(n) \textbf{x}(n)+q)\) where q is a small regularization factor [23], resulting in:

$$\begin{aligned} \textbf{w}(n+1) = \textbf{w}(n) + \mu \frac{\textbf{x}(n) e(n)}{{\textbf{x}^\textrm{T}(n)\textbf{x}(n)+q}}. \end{aligned}$$
(4)

The NLMS algorithm is stable for \(\mu <2\) [1]. In the following analysis, q is taken to be small or zero.

3 Variation of the misalignment square norm of the LMS

Let the misalignment be the vector formed by the error in the filter weights, \(\Delta (n)=\textbf{w}(n) - \textbf{w}_o\) then for both the LMS and NLMS algorithms

$$\begin{aligned} \Delta (n+1) = \Delta (n) + \mu _\textrm{x}(n) \textbf{x}(n) e(n) \end{aligned}$$
(5)

where \(\mu _\textrm{x}(n)=\mu \) for the LMS and \(\mu _\textrm{x}(n)=\mu /(\textbf{x}^\textrm{T}(n) \textbf{x}(n))\) for the NLMS, and

$$\begin{aligned}{} & {} {\Vert \Delta (n+1)\Vert }^2-{\Vert \Delta (n)\Vert }^2 \nonumber \\{} & {} \quad =2 \mu _\textrm{x}(n) \Delta ^\textrm{T}(n)\textbf{x}(n) e(n) + \mu _\textrm{x}^2(n){\Vert \textbf{x}(n)\Vert }^2 e^2(n) \nonumber \\{} & {} \quad =- 2 \mu _\textrm{x}(n) \{e(n)-v(n)\} e(n) + \mu _\textrm{x}^2(n){\Vert \textbf{x}(n)\Vert }^2 e^2(n)\nonumber \\ \end{aligned}$$
(6)

resulting in

$$\begin{aligned}{} & {} {\Vert \Delta (n+1)\Vert }^2-{\Vert \Delta (n)\Vert }^2 \nonumber \\{} & {} \quad =-\mu _\textrm{x}(n) \{2-\mu _\textrm{x}(n) {\Vert \textbf{x}(n)\Vert }^2\} e^2(n) + 2 \mu _\textrm{x}(n) v(n)e(n).\nonumber \\ \end{aligned}$$
(7)

This equation, although simple, is the main result of this work. It will be useful to get other results. Making \(e(n)=\epsilon (n)+v(n)\) where \(\epsilon (n)=-\textbf{x}^\textrm{T}(n)\Delta (n)\) results in,

$$\begin{aligned}{} & {} {\Vert \Delta (n+1)\Vert }^2-{\Vert \Delta (n)\Vert }^2 \nonumber \\{} & {} \quad = -\mu _\textrm{x}(n) (2-\mu _\textrm{x}(n) {\Vert \textbf{x}(n)\Vert }^2) \epsilon ^2(n) + \nonumber \\{} & {} \quad +\mu _\textrm{x}^2(n) {\Vert \textbf{x}(n)\Vert }^2 v^2(n)\nonumber \\{} & {} \quad -2\mu _\textrm{x}(n)\{1-\mu _\textrm{x}(n){\Vert \textbf{x}(n)\Vert }^2\} v(n)\epsilon (n). \end{aligned}$$
(8)

From this equation, it is possible to obtain one first result. It is not possible to guarantee the stability of the LMS and NLMS algorithm for any input signal. In fact if \(\textbf{x}(n)\) is selected orthogonal to \(\Delta (n)\) so that \(\epsilon (n)=0\), both algorithms diverge since \({\Vert \Delta (n)\Vert }^2\) will in general increase. Of course, this condition is very unlikely to happen in practice since, generally, x(n) is independent of \(\Delta (n)\).

4 LMS with Gaussian signals

The following assumptions are used in this section:

  1. 1.

    all signals will be taken to be Gaussian;

  2. 2.

    x(n) is a stationary process;

  3. 3.

    \(\textbf{x}(n)\) is independent of \(\Delta (n)\) that corresponds to the independence assumption of the LMS [1, 5, 7];

  4. 4.

    v(n) is an independent identically distributed (i.i.d.) process.

Taking expected values on both sides of (8) results in,

$$\begin{aligned}{} & {} \delta (n+1)^2-\delta (n)^2 \nonumber \\{} & {} \quad =-\mu \left\{ 2-\mu \frac{{E}[P_\textrm{T}(n) \epsilon ^2(n)]}{q_{\epsilon }(n)}\right\} q_{\epsilon }(n) + \mu ^2 {\bar{P_\textrm{T}}}q_\textrm{v}. \end{aligned}$$
(9)

where \(\delta (n)^2={E}[{\Vert \Delta (n)\Vert }^2]\), \(q_{\epsilon }(n)={E}[\epsilon ^2(n)]\), \(q_\textrm{v}={E}[v^2(n)]\), \(P_\textrm{T}(n)={\Vert \textbf{x}(n)\Vert }^2\) and \({\bar{P_\textrm{T}}}={E}[P_\textrm{T}(n)]\). Also, let \(q_\textrm{e}(n)={E}[e^2(n)]\) and \(q_\textrm{x}={E}[x^2(n)]\). Now,

$$\begin{aligned}{} & {} {E}[P_\textrm{T}(n) \epsilon ^2(n)] \nonumber \\{} & {} \quad =E[\sum _{i,j,k=1}^N x_i(n) x_i(n) x_j(n) \Delta _j(n) \Delta _k(n) x_k(n)] \end{aligned}$$
(10)

and using the Gaussian moment factoring theorem [1] results in

$$\begin{aligned}{} & {} {E}[P_\textrm{T}(n) \epsilon ^2(n)] \nonumber \\{} & {} \quad =\textrm{tr}\{\textbf{R}\}\textrm{tr}\{\textbf{K}(n)\textbf{R}\} + 2\textrm{tr}\{\textbf{R}\textbf{K}(n)\textbf{R}\}\nonumber \\{} & {} \quad ={\bar{P_\textrm{T}}}q_{\epsilon }(n) + 2\textrm{tr}\{\textbf{R}\textbf{K}(n)\textbf{R}\} \end{aligned}$$
(11)

where \(\textbf{R}={E}[\textbf{x}(n) \textbf{x}^\textrm{T}(n)]\), \(\textbf{K}(n)={E}[\Delta (n) \Delta ^\textrm{T}(n)]\) and noting that \(q_{\epsilon }(n)=\textrm{tr}\{\textbf{K}(n)\textbf{R}\}\) and \({\bar{P_\textrm{T}}}=\textrm{tr}\{\textbf{R}\}\). And, finally,

$$\begin{aligned}{} & {} \delta (n+1)^2-\delta (n)^2 \nonumber \\{} & {} \quad =-\mu \left\{ 2-\mu {\bar{P_\textrm{T}}}\beta (n)\right\} q_{\epsilon }(n) + \mu ^2 {\bar{P_\textrm{T}}}q_\textrm{v}\end{aligned}$$
(12)

where

$$\begin{aligned} \beta (n)=\frac{{E}[P_\textrm{T}(n) \epsilon ^2(n)]}{{\bar{P_\textrm{T}}}q_{\epsilon }(n)}=\left( 1+\frac{2\textrm{tr}\{\textbf{R}\textbf{K}(n)\textbf{R}\}}{{\bar{P_\textrm{T}}}q_{\epsilon }(n)}\right) . \end{aligned}$$
(13)

For the case of white noise \(\textbf{R}=q_\textrm{x}\textbf{I}\) results in \(\beta =1+2/N\). Also, note that \(\beta (n)\) is always less than three.

4.1 Steady-state mean square error and stability

It is known from LMS theory [1] that the convergence of \(\delta (n)\) does not exhibit oscillations. So, at steady state \(\delta (n+1)-\delta (n)=0\) and from (12) results in that,

$$\begin{aligned} q_\textrm{e}(\infty )=q_{\epsilon }(\infty )+ q_\textrm{v}= \frac{\mu {\bar{P_\textrm{T}}}}{\left\{ 2-\mu {\bar{P_\textrm{T}}}\beta (\infty )\right\} } q_\textrm{v}+ q_\textrm{v}\end{aligned}$$
(14)

; this result agrees with the results from [5, 6] for the Gaussian white noise case. Since, for stability, \(\delta (n+1)-\delta (n)\le 0\), the following limit for the step results in,

$$\begin{aligned} \mu < \frac{2}{{\bar{P_\textrm{T}}}\beta (\infty )}. \end{aligned}$$
(15)

4.2 Limit on convergence time

Given a value for the excess noise power \(q_{\epsilon \mathrm{{x}}}\), one can limit the maximum time that \(q_{\epsilon }(n)\ge q_{\epsilon \mathrm{{x}}}\) by the time it would take to \(\delta (n)\) become zero using (12). Namely,

$$\begin{aligned} \delta (n)^2 \le n(-\mu \left\{ 2-\mu {\bar{P_\textrm{T}}}\beta _\textrm{M}\right\} q_{\epsilon \mathrm{{x}}}+ \mu ^2 {\bar{P_\textrm{T}}}q_\textrm{v}) + \delta (0) \end{aligned}$$
(16)

where \(\beta _\textrm{M}\) is the maximal value for \(\beta (n)\), resulting in

$$\begin{aligned} n \le \frac{\delta (0)}{\mu (2-\mu {\bar{P_\textrm{T}}}\beta _\textrm{M}) q_{\epsilon \mathrm{{x}}}- \mu ^2 {\bar{P_\textrm{T}}}q_\textrm{v}}, \end{aligned}$$
(17)

and the maximum excess noise at time n is obtained by merely rewriting the same equation as

$$\begin{aligned} q_{\epsilon }(n) \le \frac{1}{n}\frac{\delta (0)}{\mu (2-\mu {\bar{P_\textrm{T}}}\beta _\textrm{M})} + q_{\epsilon }(\infty ). \end{aligned}$$
(18)

5 NLMS with Gaussian signals

This section analyzes the NLMS using the same assumptions as in the previous section for the LMS. For the NLMS, taking expected values on both sides (8) results in

$$\begin{aligned} \delta (n+1)^2-\delta (n)^2 = -\mu (2-\mu ) \frac{q_{\epsilon }(n)}{{\bar{P_\textrm{T}}}} \gamma _0(n) + \mu ^2 q_\textrm{v}\frac{\gamma _1}{{\bar{P_\textrm{T}}}}\nonumber \\ \end{aligned}$$
(19)

where \(\gamma _0(n)\) is such that

$$\begin{aligned} \frac{q_{\epsilon }}{{\bar{P_\textrm{T}}}} \gamma _0(n) = {E}\left[ \frac{\epsilon ^2(n)}{P_\textrm{T}(n)}\right] \end{aligned}$$
(20)

and \(\gamma _1\) is such that

$$\begin{aligned} \frac{\gamma _1}{{\bar{P_\textrm{T}}}} = {E}\left[ \frac{1}{P_\textrm{T}(n)}\right] . \end{aligned}$$
(21)

Closed-form expressions for \(\gamma _0(n)\) and \(\gamma _1\) were obtained for white input signals. Using the independence assumption,

$$\begin{aligned} {E}\left[ \frac{\epsilon ^2(n)}{P_\textrm{T}(n)}\right] = {E}\left[ \frac{\textbf{x}^\textrm{T}(n)\textbf{K}(n)\textbf{x}(n)}{\textbf{x}^\textrm{T}(n)\textbf{x}(n)}\right] . \end{aligned}$$
(22)

Diagonalizing \(\textbf{K}(n)\) (note that \(\textbf{K}(n)\) is symmetric \(\textbf{K}(n)=\textbf{K}^\textrm{T}(n)\) so the diagonalization matrix \(\textbf{Q}(n)\) is orthogonal \(\textbf{Q}(n)\textbf{Q}^\textrm{T}(n)=\textbf{I}\)) results in

$$\begin{aligned} {E}\left[ \frac{\epsilon ^2(n)}{P_\textrm{T}(n)}\right]= & {} {E}\left[ \frac{\textbf{u}^\textrm{T}(n)\varvec{\Lambda }(n)\textbf{u}(n)}{\textbf{u}^\textrm{T}(n)\textbf{u}(n)}\right] \nonumber \\= & {} \sum _{i=1}^N \lambda _i(n) {E}\left[ \frac{u_i^2(n)}{\sum _{i=1}^N u_i^2(n)}\right] \end{aligned}$$
(23)

where \(\textbf{K}(n)\textbf{Q}(n)=\varvec{\Lambda }(n)\textbf{Q}(n)\) and \(\varvec{\Lambda }(n)\) is a diagonal matrix with entries \(\lambda _i(n)\) and \(\textbf{u}(n)=\textbf{Q}(n)\textbf{x}(n)\). Now, since \(\textbf{x}(n)\) is Gaussian and white, \(\textbf{u}(n)\) is also Gaussian and white, and the expectation does not depend on i. Also,

$$\begin{aligned} {E}\left[ \frac{u_i^2(n)}{\sum _{i=1}^N u_i^2(n)}\right] = \frac{1}{M} {E}\left[ \frac{\sum _{i=1}^N u_i^2(n)}{\sum _{i=1}^N u_i^2(n)}\right] = \frac{1}{M}. \end{aligned}$$
(24)

Finally, this implies \(\gamma _0(n)=1\) since \(q_{\epsilon }(n)=q_\textrm{x}\textrm{tr}\{\textbf{K}(n)\}\) and \({\bar{P_\textrm{T}}}=q_\textrm{x}M\). To calculate \(\gamma _1\), note that (for white noise) \(P_\textrm{T}(n)\) has a chi-square distribution with N degrees of freedom with probability density function (PDF) \(\rho (x)\). Next,

$$\begin{aligned} {E}\left[ \frac{1}{P_\textrm{T}(n)}\right] = \int _0^\infty y \rho (1/y)/y^2 dy = \frac{1}{q_\textrm{x}}\frac{1}{M-2}, \end{aligned}$$
(25)

and \(\gamma _1 = M/(M-2)\). Finally, [9] gets the following approximation for non-Gaussian signals \({E}\left[ 1/P_\textrm{T}(n)\right] = 1/(M+1-\kappa _\textrm{x})/q_\textrm{x}\) where \(\kappa _\textrm{x}\) is the kurtosis of x(n). It is also possible to obtain similar limits using the results in [11], for instance, (65), but these are looser bonds.

5.1 Steady-state mean square error and stability

Proceeding in the same way as for the LMS algorithm, one gets for NLMS,

$$\begin{aligned} q_\textrm{e}(\infty ) = \frac{\mu }{2-\mu } \frac{\gamma _1}{\gamma _0(\infty )} q_\textrm{v}+ q_\textrm{v}. \end{aligned}$$
(26)

Moreover, the algorithm is stable for \(\mu <2\). For the white noise case, \(\gamma _1/\gamma _0=M/(M-2)\). This is the same result as obtained in [8].

5.2 Limit on convergence time

For the NLMS,

$$\begin{aligned} \delta (n)^2 \le n \left( -\mu (2-\mu ) \frac{q_{\epsilon }}{{\bar{P_\textrm{T}}}} \gamma _{0\text {m}} + \mu ^2 q_\textrm{v}\frac{\gamma _1}{{\bar{P_\textrm{T}}}}\right) + \delta (0) \end{aligned}$$
(27)

where \(\gamma _{0\text {m}}\) is minimal value for \(\gamma _0(n)\). This gives the maximal time to reach an excess noise of \(q_{\epsilon \mathrm{{x}}}\),

$$\begin{aligned} n \le \frac{\delta (0) {\bar{P_\textrm{T}}}}{\mu (2-\mu ) q_{\epsilon \mathrm{{x}}}\gamma _{0\text {m}} - \mu ^2 q_\textrm{v}\gamma _1} \end{aligned}$$
(28)

and for the maximum excess noise at time n,

$$\begin{aligned} q_{\epsilon }(n) \le \frac{1}{n}\frac{\delta (0) {\bar{P_\textrm{T}}}}{\mu (2-\mu ) \gamma _{0\text {m}}} + q_{\epsilon }(\infty ). \end{aligned}$$
(29)

Similar but less general results appear in [9].

6 Constant input vector square norm signals

Most of the complications in the previous sections’ calculations come from the dependence between \(e^2(n)\) and \(P_\textrm{T}(n)\). If these signals are independent, then the analysis simplifies considerably. One such case is when \(P_\textrm{T}(n)\) is mostly constant. This can happen if \(x(n)^2\) is constant, for instance, in communications signals, or if the filter size N is large, making the fluctuations in \(P_\textrm{T}(n)\) small. In the previous sections, it was already shown that in the white noise case, the values of \(\beta (n)\), \(\gamma _0(n)\), and \(\gamma _1(n)\) become close to one for large N.

This section presents the same results as the previous sections but for constant \(P_\textrm{T}(n)=P_\textrm{T}\). These results are the same for the LMS and NLMS (with \(\mu =\mu _\textrm{x}=\mu _\text {LMS}=\mu _\text {NLMS}/P_\textrm{T}\)) and correspond in making \(\beta (n)\), \(\gamma _0(n)\) and \(\gamma _1(n)\) equal to one in the previous expressions. The previous results show that this approximation is fair even for moderate N.

Taking expected values on both sides of (7) results simply in

$$\begin{aligned} \delta (n+1)^2-\delta (n)^2 = -\mu (2-\mu P_\textrm{T}) q_\textrm{e}(n) + 2 \mu q_\textrm{v}. \end{aligned}$$
(30)

The steady-state MSE is

$$\begin{aligned} q_\textrm{e}(\infty ) = \frac{2}{(2-\mu P_\textrm{T})} q_\textrm{v}, \end{aligned}$$
(31)

and the maximal MSE at time n is

$$\begin{aligned} q_\textrm{e}(n) \le \frac{\delta (0)^2}{n \mu (2-\mu P_\textrm{T}) } + q_\textrm{e}(\infty ). \end{aligned}$$
(32)

7 LMS with the Cauchy–Schwarz inequality

In the case of the LMS algorithm, obtaining (9) requires v(n) to be i.i.d. However, it does not require the independence assumption, and it is possible to obtain a maximal value for \({E}[P_\textrm{T}(n)\epsilon ^2(n)]\) without using it. Namely, using the Cauchy–Schwarz inequality,

$$\begin{aligned} {E}[P_\textrm{T}(n) \epsilon ^2(n)] \le \sqrt{{E}[P_\textrm{T}^2(n)] {E}[\epsilon ^4(n)]} \end{aligned}$$
(33)

resulting that \(\beta (n)\) in (12) becomes

$$\begin{aligned} \beta ^2(n) \le \kappa _\textrm{x}\kappa _{\epsilon }\end{aligned}$$
(34)

where \(\kappa _\textrm{x}= {E}[P_\textrm{T}^2(n)]/{E}[P_\textrm{T}(n)]^2\) and \(\kappa _{\epsilon }(n) = {E}[\epsilon ^4(n)]/ {E}[\epsilon ^2(n)]^2\) is the kurtosis of \(\epsilon (n)\). When x(n) and \(\epsilon (n)\) are Gaussian signals

$$\begin{aligned} \kappa _\textrm{x}= 1 + 2\frac{\textrm{tr}\{\textbf{R}\textbf{R}\}}{{\bar{P_\textrm{T}}}^2}, \end{aligned}$$
(35)

\(\kappa _\textrm{x}\le 3\), \(\kappa _\textrm{x}= 1+2/N\) for white Gaussian signals and \(\kappa _{\epsilon }= 3\). Note, however, that in general \(\epsilon (n)\) is not Gaussian even with Gaussian input and background noise v(n). It is straightforward to obtain expression for the maximum MSE and other using these values. A value for the step that assures stability is \(\mu \le 2/({\bar{P_\textrm{T}}}\beta ) \le 2/({\bar{P_\textrm{T}}}\sqrt{\kappa _\textrm{x}\kappa _{\epsilon }})\).

8 Simulations

This section presents simulation results to confirm the theoretical findings from the previous sections. Simulations were run for the LMS and NLMS algorithms with a filter size of \(N=10\) and a Gaussian input signal with unit power. The charts result from 100 Monte Carlo runs with different optimal filters and signals during 1000 samples, unless stated otherwise.

The simulation of Fig. 1 shows the variation of the LMS algorithm misalignment square norm ensemble average \(\delta ^2(n) = {E}[{\Vert \Delta (n)\Vert }^2]\) with the squared error signal, more precisely \({E}[e^2(n)(2-\mu P_\textrm{T}(n))]\). The measurement noise signal power was \(q_\textrm{v}=0.1\). It can be seen that both quantities are linear dependent as predicted by (7). The chart shows three lines for three values for the step size \(\mu \).

Fig. 1
figure 1

The variation of the LMS algorithm misalignment square norm expected value with the squared error signal expected value: \({E}[-({\Vert \Delta (n+1)\Vert }^2-{\Vert \Delta (n)\Vert }^2)]\) versus \({E}[(2-\mu P_\textrm{T}(n))e^2(n)]\). The expected value is calculated using the values of 100 simulations. The data are for three values of \(\mu \): 0.01, 0.03, and 0.05

Full size image
Fig. 2
figure 2

Theoretical (red) and experimental (blue) lines of the steady-state MSE of the LMS algorithm as a function of the step size. Lines for three values of \(q_\textrm{v}\) are shown: 0.01, 0.1, and 1. The input signal is colored noise (color figure online)

Full size image
Fig. 3
figure 3

Theoretical (red) and experimental (blue) lines of the steady-state MSE of the LMS algorithm as a function of the step size for a long filter with \(N=100\). Lines for three values of \(q_\textrm{v}\) are shown: 0.01, 0.1, and 1. The input signal is colored noise (color figure online)

Full size image

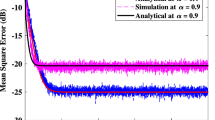
Figures  2 and 4 compare theoretical and experimental curves for the MSE of the LMS and NLMS algorithms as a function of the step size and different values of the measurement noise \(q_\textrm{v}\). Both charts use a colored input signal that results from filtering a white noise signal by a size ten filter with impulse response \(s(n)=\sin (2\pi n/5)\). The theoretical curves were obtained assuming a white noise input signal. The actual input is colored, but the difference in theoretical curves is not high for this power spectrum. They are all close to the long filter case, even for \(N=10\). The curves differ for very small steps because the experiments did not have time to reach a steady state.

Fig. 4
figure 4

Theoretical (red) and experimental (blue) lines of the steady-state MSE of the NLMS algorithm as a function of the step size. Lines for three values of \(q_\textrm{v}\) are shown: 0.01, 0.1, and 1. The input signal is colored noise (color figure online)

Full size image

In the LMS algorithm, the experimental curves agree with theory up to about \(\mu =0.04\), while the theoretical maximum step is 0.2. From this point forward, the independence assumption is no longer valid. It is worth noting that the validity range for the theoretical curves increases and decreases as the signal becomes less or more colored in agreement with [13]. In the NLMS algorithm, the experimental curves are very close to theory for all values of the step size. Figure 3 shows the same plot as in Fig. 2 but for a long filter with \(N=100\). It can be seen that the range of values of the step that the experimental values agree with the theory is much larger. Namely, in Fig. 2 this range is about \(20\% = 0.04/0.2\) of 2/M the theoretical maximum and in Fig. 3, the range is \(40\%\). For \(M=1000\), this range grows to \(70\%\).

Finally, Fig. 5 compares theoretical values for the maximal MSE as a function of the time n, and simulation results with the worst values for the expected value of \(e^2(n)\) using 10,000 Monte Carlo runs. Each run used a random optimal filter and a random input signal coloring filter of size 10. The figure confirms that the theoretical curves limit the MSE at any given time.

Fig. 5
figure 5

Theoretical (red) and experimental (blue) lines for the worst case performance of the NLMS algorithm (color figure online)

Full size image

9 Conclusion

This work shows that the LMS misalignment square norm mean–variation is close to proportional to the error signal power. This allows obtaining formulas for the steady-state MSE of the LMS and NLMS in a simple way. It also allows obtaining formulas for the maximum MSE of the LMS and NLMS at any given time and any input signal. There are still some difficulties in the calculation due to the dependence between the error noise signal and the input signal vector norm. Simulation results confirm the theoretical findings.