1 Introduction

Since 1991, when the well-known Eigenface approach was introduced by Turk and Pentland [1], the method of principal component analysis (PCA) has played a prominent role in face processing. It is especially applicable to face recognition systems. In fact, since then, a wide variety of face recognition algorithms have been proposed where PCA plays a central role [2]. PCA is a powerful mathematical technique for data analysis—the most significant task of it is to remove redundant data and to reduce the dimensionality of the data—which of course is the first step in many image compression applications [3]. Though in its own right PCA is elegant in data reduction to reveal interesting patterns in the data, novel modifications or enhancements are likely to make PCA even more powerful. The existing literature, in fact, points to this direction where PCA-based sub-pattern (Sp-PCA) [4] and modular PCA (mPCA) [5] can be considered as examples or cases in point.

Our aim in this work is very much in the line, in which we want to add a novel modification to the traditional PCA to further enhance its power. To do this, we introduce the elliptic Biharmonic partial differential operator as a preprocessing step into the PCA pipeline. The Biharmonic operator is well known for its “smoothing” properties [6,7,8]. Thus, we postulate that the inherent averaging ability of the discrete Biharmonic operator on images can help reduce the size of images without losing the characteristic features of them. And it is this property of the Biharmonic operator we propose to integrate into the PCA pipeline for creating efficient Eigenfaces which we refer as the BiPCA.

The rest of the paper is organised as follows. First, in Sect. 2, we outline some of the relevant literature related to the topics of discussion of this paper. Then, in Sects. 3 and 4, we discuss the main idea behind the methodology of utilising the Biharmonic function and the ideas we propose to formulate the BiPCA methodology. Section 5 of this paper has been dedicated to discuss our experiments on face recognition and to present the results we obtained. In Sect. 6, we discuss these results further, and finally, in Sect. 7, we conclude the paper.

2 Related work

As highlighted in Introduction, Turk and Pentland [1] introduced the novel concept of Eigenfaces which treats face recognition as a problem in two dimensions where PCA is at the heart of it. An Eigenface essentially can capture important properties relating to the facial features which go beyond the usual visual features such as the eyes, nose and the mouth. A prominent advantage of the Eigenface-based face recognition is its capability to recognise new faces of a given individual in an unsupervised way. Other advantages include the ease of implementation, lower computational complexity and lower sensitivity to minor changes in the faces of a person with the same identity.

In the past, there has been much work in trying to bring about improvements to the Eigenface methodology resulting from the original PCA implementation. For example, a hybrid approach-based sub-pattern technique, within the context of face recognition using PCA, was proposed by Hsieh and Tung [9]. Their idea was inspired by the method of independent component analysis (ICA) [10, 11] and contained the combination two centred principal component analyses which they referred as PCA I and PCA II. They then combined the sub-pattern approach [9] with PCA I and PCA II, which they called Sp-PCA I and Sp-PCA II which they applied for face recognition. This method was tested on three datasets, namely the Yale face database [12], Yale B face database [13] and Weizmann face database [14]. Their experimental results show that this approach outperformed the traditional PCA with recognition reaching up to 98%. One must, however, exercise caution when interpreting their results since they used the leave one out testing approach, and the number of individuals per dataset was comparatively low.

Similar work on improving PCA-based face recognition was carried out by Ghinea et al. [15] whose prime aim was to tackle the problem of illumination variations and pose for face recognition. To do this, they explored gradient orientation based PCA sub-space using the well-known Schur decomposition [16]. They computed Schurvalues and Schurvectors in order to find sub-space projections, which they referred as Schurfaces. For matching, by computing similarities, the Hausdorff distance [17] with the nearest neighbour classifier [18] was used. They tested their approach on two different face datasets, namely the ORL [19] and the Yale [11], and appeared to obtain results with an error rate of 14% for Yale and 15% for ORL compared to the traditional PCA with 25% and 23%, respectively.

While considering research in the use of the PCA, the earlier work of Poon et al. [20] is noteworthy too. They proposed a technique called Gradientfaces to images as a preprocessing step to PCA. Their main idea is to seek the orientation of the gradient of the face at the pixel level. This enables them to re-represent an illumination invariant version of the input face. Their method was tested on the Asian face database, which has 40 subjects with 10 images per subject with various expressions and some illuminations. The results from the Gradientfaces as reported by them indicate there is an improved recognition rate from 6.25% up to 60.75% when compared to the traditional PCA. Again one must note the limitations of this study since they only used one dataset where the images were fairly uniform with distinct lack of noisy images.

In addition to the above, other ideas based on pattern recognition such as linear discriminant analysis (LDA) [21] have also been tried in conjunction with PCA. One notable piece of work in this area is that of Oh et al. [22], who combined PCA with LDA which they refer to as the method of PCA-LDA. For a given set of images, they used PCA to reduce the dimensionality of the feature space and LDA to improve the separation between classes. They tested their approach using two different datasets, namely the ORL [19] and the Yale [12], and the results appear to show 2.5% improvement in accuracy for the ORL dataset and 8.9% for the Yale dataset when compared to the traditional PCA. The main drawback of their methodology is that they have utilised almost 80% of the data for training, while the remaining 20% were used for testing. In addition to this, the datasets they used were somewhat limited; for example, in the Yale database there are only 15 subjects with 11 images per subject.

Thus, there are many proposed methods to improve the Eigenfaces of traditional PCA type. Hence, a question that might spring to the mind of the reader would be, “Why yet another technique to improve the PCA?”. Our motivation for this work is to develop an elegant, computationally less extensive and easy-to-implement method which can improve the traditional PCA. Though the mathematical formulation of the elliptic partial differential operator proposed in this work appears to be complex, we show the discrete Biharmonic operator is intuitive and easy to implement. In addition to this, we also show that our technique of BiPCA is superior in comparison with the existing techniques which can be used to improve the traditional PCA.

3 The Biharmonic function

Given a closed domain \(\varOmega \subset R^{2}\), we seek a “smooth”, differentiable and well-behaved function X such that \(X=(x(u,v), y(u,v)),\) where x(u, v) and y(u, v) are the usual Cartesian forms in \(R^{2}\) spanned by the two parameters u and v. There are various choices for the form of the function X which can be required to take. In this particular case, we require X to be satisfying a boundary value problem whereby X is the solution to the Biharmonic equation,

$$\begin{aligned} \left( \frac{\partial ^{2}}{\partial u^{2}}+\frac{\partial ^{2}}{\partial v^{2}} \right) ^{2}X(u,v)=0, \end{aligned}$$
(1)

such that we prescribe the condition on the boundaries representing the function values and the normals \(\frac{\partial X}{\partial n }\) at the boundary \(\partial \varOmega .\) This particular choice for which X is required to be a function of Biharmonic type is inspired by the many interesting properties of the Biharmonic function of which smoothing is of particular interest in the present context [8].

3.1 The smoothing properties of the discrete Biharmonic operator

To understand the smoothing properties of the Biharmonic operator presented in Eq. 1, let us consider its variational form which can be expressed as

$$\begin{aligned} F=\int L {\text {d}}u{\text {d}}v, \end{aligned}$$
(2)

where the integrand L takes the form

$$\begin{aligned} L=L(X,X_{u},X_{v},X_{uu},X_{vv},X_{uv},\ldots ,X_{uuuu},X_{vvvv}). \end{aligned}$$
(3)

Now, taking the Euler–Lagrange form of Eq. 2 and requiring the first variation of F to tend to zero we can consider

$$\begin{aligned} L= \left| \frac{\partial ^{n}X(u,v)}{\partial u^{n}}\right| +\left| \frac{\partial ^{n}X(u,v)}{\partial v^{n}}\right| , \end{aligned}$$
(4)

where \(n=2\) implies the Biharmonic case.

To consider the smoothing properties associated with the various elliptic operators arising from (4), one can consider \(n=1\) and 2. In the case of \(n=1,\) the resulting operator is simply \(\frac{\partial ^{2}}{\partial u^{2}}+\frac{\partial ^{2}}{\partial v^{2}}\) which is nothing but the Harmonic or the Laplace operator. If we now look at the discrete finite differences associated with this operator, it can be expressed as

$$\begin{aligned} X(i,j)= 1/4[X_{i+1,j}+X_{i-1,j}+X_{i,j+1}+X_{i,j-1}], \end{aligned}$$
(5)

where X(i, j) is the resulting finite difference approximation of the point on (i, j) on a finite difference grid [6, 7].

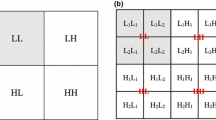
As one can infer from Eq. 5, and from Fig. 1a, applying the Laplace operator to a point results in the arithmetic mean of the immediate neighbouring points corresponding to the north, south, east and west.

Similarly, if we consider the fourth-order operator, \(\frac{\partial ^{4}}{\partial u^{4}}+\frac{\partial ^{4}}{\partial v^{4}}\), the resulting finite difference scheme can be represented as shown in Fig. 1b, where the averaging of the point under consideration is obtained from a more dispersed region, though the averaging still occurs along the parametric directions (north, south, east and west).

On the other hand, if we consider the Biharmonic operator as shown in Eq. 1, the average can be obtained from a more uniform region surrounding a given point, as shown in Fig. 1c. This is due to the fact the Biharmonic operator not only has the fourth-order derivative information but also contains the corresponding mixed derivative information.

Fig. 1
figure 1

Smoothing masks arising from the discrete form of the elliptic operators. a Laplacian, b fourth-order PDE operator and c Biharmonic operator

Full size image

4 Eigenfaces of Biharmonic type

As shown above, the discrete Biharmonic operator provides the very useful averaging processes whose exact form is shown in Eq. 6. We apply this operation to a given set of images as a preprocessing step before the PCA. Within the pixel space, the BiPCA can be considered as a linear pixel operation process and further can be considered as equivalent to a pooling layer within a standard convolutional neural network [23]. Moreover, the BiPCA process can be seen as a form of a downsampling process to reduce an image representation using a filter bank without any complex weights and no associated coefficients. For the purpose of this work, we use a mask of \(3\times 3\) without an overlap between any two regions of the image space for our BiPCA. Thus, the discrete Biharmonic mask B(i, j) can be described as

$$\begin{aligned} B(i,j)= & {} (20X_{i,j}-8(X_{i+1,j}+X_{i-1,j} \nonumber \\&+X_{i,j+1}+X_{i,j-1}) + 2(X_{i+1,j+1} \nonumber \\&+X_{i-1,j+1}+X_{i-1,j-1}+X_{i+1,j-1}) \nonumber \\&+(X_{i+2,j}+X_{i-2,j}+X_{i,j+2}+X_{i,j-2})). \end{aligned}$$
(6)
$$\begin{aligned} K= & {} B(i,j)\oplus I_{\mathrm {resized}}. \end{aligned}$$
(7)

Suppose we have an image I with size \(5\times 6\) pixels as shown in Fig. 2a. The first step, in this case, is to resize it so that the image is equivalent to a square image of \(6\times 6\) (\(I_\mathrm{{resized}}\)) as shown in Fig. 2b. This operation comes especially handy when handling the boundary of the images. Assuming the mask that we use in the convolution is B,  with size \(3\times 3\), the convolution of the Biharmonic operation can be defined using Eq. 7.

Fig. 2
figure 2

Operational procedure to produce a square image. a Original (non-square) image and b resulting (square) image after resizing. Application of the discrete Biharmonic to an image. c Representation of how the Biharmonic mask is applied to the image and d representation of the resulting image

Full size image

Consider the example representation of an image as shown in Fig. 2c. If we now take the Biharmonic mask B of the form in Eq. (6), the resulting image K is the reduced representation as shown in Fig. 2d.

Now, for a given set of images in a dataset, the above procedure can be performed. Further details of this BiPCA procedure are described below.

Let N be the number of images in a training set of some size. The first step is to convert all the images from 2D into 1D. Secondly, in order to take the background of the images in the training set into account, a normalising step is applied. This is done by computing an average and subtracting the mean image from each of the BiPCA image vector \(\varGamma \), where

$$\begin{aligned} \varGamma =\lbrace {I}_{1}, {I}_{2}, {I}_{3}, \ldots , {I}_{N}\rbrace . \end{aligned}$$
(8)

Given that \(\varPsi \) represents the mean image, then we have

$$\begin{aligned} \varPsi = \frac{1}{n} \sum _{i=1}^{n}{\varGamma _{i},\quad i=1,2,3,\ldots ,n.} \end{aligned}$$
(9)

Let \(\phi _{i}\) define a mean centred image as described in Equation 10 such that

$$\begin{aligned} \phi _{i}=\varGamma _{i}-\varPsi ,\quad i=1,2,\ldots ,n. \end{aligned}$$
(10)

Note that Eq. 10 leads to a matrix A of the form such that \( A = [\phi _{1}, \phi _{2}, \ldots , \phi _{n}]\).

To compute the corresponding eigenvectors, the covariance matrix C is calculated whereby

$$\begin{aligned} C=AA^\mathrm{T}. \end{aligned}$$
(11)

If the size of C is large, then the computation of C is

$$\begin{aligned} C=A^\mathrm{T}A. \end{aligned}$$
(12)

To compute the eigenvectors \(v_{i}\) of C, we consider

$$\begin{aligned} A^\mathrm{T}Av_{i}=\lambda _{i}v_{i}, \end{aligned}$$
(13)

where \(\lambda _{i}\) are the corresponding eigenvalues.

Now, multiplying Eq. 13 by A, we obtain

$$\begin{aligned} AA^\mathrm{T}Av_{i}=\lambda _{i}Av_{i}. \end{aligned}$$
(14)

Then, by projecting the eigenvectors \(v_{i}\) on A, we can obtain the Eigenspace \(U_{i}\) such that

$$\begin{aligned} U_{i}=\sum _{i=0}^{m'}{Av_{i}}, \end{aligned}$$
(15)

where \(m'\le n\) is the number of eigenvectors.

Now, for face recognition, given a test image \(\varGamma _{e}\) we apply the Biharmonic mask on the image first, and then, we can project it into the face space. The corresponding BiPCA weights are computed by

$$\begin{aligned} \varOmega _{e}=U^\mathrm{T}(\varGamma _{e}-\varPsi ). \end{aligned}$$
(16)

To compute the similarity between the test images and the training images, one can employ a wide variety of measures. For the sake of demonstration, in this work, the Euclidean distance (ED) is taken as a similarity measure. ED is a measure of similarity between two nonzero vectors of the Minkowski family [24]. To determine a given distance between a test face and the training faces, we then use the following equation,

$$\begin{aligned} \text {ED}(\varOmega _{e}, \varOmega _{i})=\sqrt{( \varOmega _{e}-\varOmega _{i})^{2}}, \end{aligned}$$
(17)

where \(\varOmega _{i}\) are the training weights of \(U_{i}\).

5 Experiments and results

In this section, we outline the various experiments we have undertaken to measure the capacity of the BiPCA approach. In particular, we look at the standard face recognition as an example whereby we compare the BiPCA approach against the traditional PCA approach. Further, we also compare the BiPCA approach with the Schurfaces method discussed in [15].

5.1 Datasets

To carry out our face recognition experiments, we utilise three well-known publicly available datasets, namely the ORL [19], Face95 [25] and Face96 [25].

The ORL dataset contains greyscale images of 40 subjects with 10 distinct images per individual. The images are of resolution \(112\times 92\) pixels. These images are taken at different times of the day, under varying lighting conditions. They contain facial expressions such as smiling and come with and without glasses. All the images in this dataset are predominantly frontal though there are slight tilts of the head in some cases. Figure 3 shows a sample image set from the ORL dataset.

Fig. 3
figure 3

A sample of face images from the ORL dataset

Full size image
Fig. 4
figure 4

A sample of faces from the Face95 database

Full size image

The Face95 dataset consists of colour facial images, represented by 72 individuals with 20 unique images per individual [25]. Thus, a total of 1440 face images are available in this dataset. The resolution of the images in the dataset is \(180\times 200\) pixels. Again, the dataset contains frontal faces with slight facial expressions. Figure 4 shows a sample set of images from Face95. Note, in all case, the images in Face95 have dominant backgrounds. Therefore, in order to further test the accuracy of our methodology, we also created a new dataset where we cropped the faces out—as shown in Fig. 5.

Fig. 5
figure 5

A sample of cropped faces from the Face95 dataset

Full size image
Fig. 6
figure 6

A sample of face images from the Face96 dataset. Note the complex backgrounds in each of the images

Full size image

Similar to Face95 [25], the facial images present in the Face96 dataset is all colour and comprises of 152 individuals with 20 images per individual. Thus, there is a total of 3040 images in this dataset. Also, the resolution of the images in the dataset is \(196 \times 196\) pixels. In contrast to the ORL and Face95, all faces in this dataset have complex backgrounds. Also, the images have been taken under varying lighting conditions, and the faces contain varying degrees of expressions. Figure 6 shows a sample faces from the Face96 dataset. Again, we cropped the faces from all images to remove the complex backgrounds contained to create a new dataset, a sample of which is shown in Fig. 7.

5.2 Results

As discussed, we evaluated the BiPCA approach to face recognition using a series of experiments based on the methodology and the datasets discussed above. To test the reliability of our approach, we ran face matching tests against the traditional PCA and the Schurfaces method discussed in [15]. Our experiments comprised of taking training image samples of individuals, starting from 1 image to 5 images per individual. The rest of the images in each case were used for testing. We compute the ED value using the formulation defined in Eq. 17. For each experiment, we have utilised a tenfold cross-validation whereby the average percentage error rates from the cross-validations are reported. We also note the computational time required in each case. We now present detailed discussions on the experiments along with the results obtained.

Fig. 7
figure 7

A sample of face images from the Face96 dataset with cropped faces to discard the complex backgrounds

Full size image
Table 1 Comparison of the percentage error rates and computational time (in seconds) for face matching between PCA, Schurfaces and BiPCA on faces in the ORL dataset
Full size table

5.2.1 Experiments using the ORL dataset

In this experiment, we applied the BiPCA, Schurfaces and the traditional PCA approach for face recognition on images from the ORL dataset. We ran training routines starting from 1 image to sets of 5 images per subject. The results of this experiment are tabulated in Table 1, where we report the average error rates arising from the tenfold cross-validation for each of the training image sets. As can be observed, the error rates in all cases are much lower for the BiPCA indicating that the BiPCA outperforms the traditional PCA approach.

5.2.2 Experiments using the Face95 dataset

In contrast to the first experiment, in this case, we ran two tests whereby in the first case the PCA, Schurfaces and the BiPCA were applied on the uncropped Face95 images, and in the second case, the same was done on cropped images. Again, in both cases, the training routines were run on images of individuals starting from 1 image to 5 images per subject. The remaining images in each case were used for testing. Results of the tenfold cross-validation are reported. Tables 2 and 3 show the results of these experiments. Again, it can be observed that the BiPCA approach gives us the advantage over the traditional PCA for both cropped and uncropped images.

Table 2 Comparison of the percentage error rates and computational time (in seconds) for face matching between PCA, Schurfaces and BiPCA on the full (uncropped) faces in the Face95 dataset
Full size table
Table 3 Comparison of the percentage error rates and computational time (in seconds) for face matching between PCA, Schurfaces and BiPCA on the cropped faces in the Face95 dataset
Full size table

5.2.3 Experiments using the Face96 dataset

As before, in this experiment, we applied the BiPCA, Shurfaces and PCA to faces from Face96, for cropped and uncropped images. Contrary to the results obtained from the matching experiments on faces from ORL and Face95 datasets, the results show that for the original (uncropped) faces in the Face96 the BiPCA does not provide favourable results as shown in Table 4. However, as the results in Table 5 clearly indicate the BiPCA outperforms the traditional PCA approach when applied to the cropped images.

Table 4 Comparison of the percentage error rates and computational time (in seconds) for face matching between PCA, Schurfaces and BiPCA for full (uncropped) faces in the Face96 dataset
Full size table
Table 5 Comparison of the percentage error rates and computational time (in seconds) for face matching between PCA, Schurfaces and BiPCA for cropped faces in the Face96 dataset
Full size table

6 Discussions

The primary purpose of the study we report in this paper is to see whether the discrete Biharmonic operator applied to images, as a preprocessing step, would lend us any advantage over using the traditional PCA on its own. From the results we have shown above, one can observe in the case of images from the ORL dataset the BiPCA approach gives us lower error rates consistently and in the case of utilising 5 images per individual for training, the percentage error rate comes down to 11 for the BiPCA, while the percentage error rate value is 15 for PCA. In the case of images from Face95, again the error rates were lower for BiPCA for both cropped and uncropped faces, though the error rates are much lower in the case of cropped faces.

Interestingly, for the images from Face96, the results (as shown in Tables 4 and 5) appear to be mixed. In fact, we note for the original (uncropped) images the BiPCA actually performs poorly compared to the traditional PCA. This result along with the results for uncropped images for Face95 (though in this case the BiPCA still outperforms PCA) indicates that the BiPCA approach is very sensitive to background clutter. This is particularly obvious for uncropped images from Face96 since the faces in these images are relatively smaller compared to the background. Hence, the discrete Biharmonic averaging must be dispersing some of the prominent facial features across the images resulting in the loss of sufficient detail which must be available for accurate face matching.

As we mentioned previously, an important advantage of using BiPCA is the ability to reduce image dimensionality with the its inherent ability to preserve features. To demonstrate this further, we conducted a sub-experiment based on face recognition based on the state-of-the-art convolutional neural network-based machine learning. We used the well-established VGGF [26] face model for features extraction and linear support vector machine [27] for classification.

Table 6 Comparison of the CNN-based recognition rates by using three different training mechanisms
Full size table

For this experiment, we used the FEI database [28], which contains 200 subjects with 14 face images per individual. We picked four frontal images per subject and we augmented them in order to obtain four more frontal images. Then, the average Biharmonic face was generated using these 8 images. The resulting Biharmonic average images when used for training gave a recognition rate of 87.2%. To compare these results with, we then picked one original frontal image and augmented it by 20 facial parts. These parts were added along with the average Biharmonic face to the training set. The recognition rate in this case was 85.2% which is lower than the result for one average Biharmonic face. Furthermore, we used the same 20 partial images with one original image in the training and the recognition rate recorded was 81%. Table 6 shows detailed results from this experiment. As it can be clearly inferred, the Biharmonic preprocessing appear to be providing a distinct advantage in terms of reducing the number of images at the image preprocessing stage.

7 Conclusions

In this paper, we introduce a novel modification to the method of PCA to enhance its ability to reduce image dimensionality using the discrete Biharmonic operator as a preprocessing step. The Biharmonic operator is among the family of elliptic operators with intriguing mathematical properties, one of which is the “smoothing” or the averaging. In this work, we have explored this characteristic of the Biharmonic operator which we applied to images to efficiently process them. The resulting images are of lower dimensionality leading to reduced computational complexities while preserving features of interest.

To demonstrate the capacity of the proposed BiPCA approach, we used standard face recognition as an example. For experimentation, we have utilised three publicly available datasets, namely the ORL, Face95 and Face96. The results we have obtained demonstrate that the BiPCA outperforms the traditional PCA. In fact, our experiments do suggest that the BiPCA method has at least 25% average improvement in the error rates when it comes to face recognition.

Though, overall, the BiPCA approach as a preprocessing step in reducing image dimensionality can give good results, there are potential drawbacks of this approach. For example, when we applied the BiPCA approach to face images with very complex backgrounds, it seems to provide poorer results. This is unsurprising as the BiPCA performs complex averaging through the elliptic Biharmonic operator. However, in practical terms, at least in the case of face recognition, this should not pose a major issue since in most cases the faces must be cropped to separate them from any complex backgrounds. And in such cases the BiPCA approach of course outperforms.

To show the capacity of the BiPCA and the potential use of elliptic operators in image processing and enhancement, here we have merely used the Eigenface and face recognition as an example. The application domain of the proposed BiPCA approach is, however, not limited. In fact, it can be used in any image processing pipeline where some form of dimensionality reduction is called for as a preprocessing step. An example which comes to our mind is within the context of machine learning (as discussed in Sect. 6) whereby the BiPCA approach can be of use to reduce the number of images in the training set of a convolutional neural network. Other application areas may include general facial analysis, e.g. [29, 30].

Though we have shown the BiPCA approach has superiority over traditional PCA, it must be stressed that the elliptic operator associated with the Biharmonic function gives rise to a complex averaging processes [31]. Therefore, its use must be carried out with the background knowledge of the problem domain and with an insight into the context of the problem to be solved.

We believe the Biharmonic operator discussed in this paper is elegant, easy to utilise and can be programmed and implemented with little effort. Hence, the application of it can be far broader than the scope of the work discussed in this paper. Thus, we will make the MATLAB code we have developed as part of this research, publicly available to other interested researchers.