Analysis of the selective traveling salesman problem with time-dependent profits

Abstract

We consider a generalization of the selective traveling salesman problem (STSP) in which the benefit of visiting a location changes over time. This new problem, called the selective travelling salesman problem with time-dependent profits (STSP-TDP), is defined on a graph with time-dependent profits associated with the vertices, and consists of determining a circuit of maximal total profit. In the STSP-TDP the tour length must not exceed a maximum value, and its starting and ending times must both lie within a prespecified planning horizon. This problem arises in planning tourist itineraries, mailbox collection, military surveillance, and water sampling, where the traveler accumulates different profits upon visiting the locations throughout the day. We focus on analyzing several variants of the problem depending on the shape of the time-dependent profit function. If this function is not monotonic, it may be worth visiting a site more than once. We propose formulations for the single-visit case and for when multiple visits are allowed, in which case the problem reduces to an STSP, which is adapted to be solved as a longest path problem. These formulations are then solved for piecewise-linear profit functions using a general-purpose solver, and tested on several artificially created instances and on four TSPLib instances involving up to 535 vertices. A detailed analysis of the problem and the solution is performed.

1 Introduction

In several contexts, a traveler holds a list of potential sites of interest, but it may not be possible nor desirable to visit all of them. Some sites will be selected and then visited by means of a single tour. With each solution is associated a profit derived from visiting the sites. One example of this setting occurs in the planning of tourist trips. An interesting application cited in Vansteenwegen et al. (2011) is the Mobile Tourist Guide of Souffriau et al. (2008). Similar tourist trip problems are mentioned by Wang et al. (2008); Schilde et al. (2009) , and da Silva et al. (2018) where the profit is measured in terms of the interest associated with visiting the sites. Another example arises in the collection of letters from mailboxes. Here the benefit can be measured by the mail volume accumulated in the mailbox at each visit. Other applications are encountered in the surveillance activities of submarines or unmanned aircraft (Wang et al. 2008), and in water sampling Zhang et al. (2020). A recent application arises in the context of a parking warden distributing fines for irregularly parked cars (Bruglieri (2020)), where the profit associated with an inspection depends on the time elapsed since the previous inspection.

This problem is known as the selective traveling salesman problem (STSP) Laporte and Martello (1990), sometimes called orienteering problem (Golden et al. 1987; Vansteenwegen et al. 2011), if the profits are time-independent. However, there also exist several settings where the profits are time-dependent. For example, the pleasure associated with a tourist attraction is often related to crowdiness and, therefore, to the time of the day. In postal applications it is clear that mail accumulation is time-dependent. In military applications the profit associated with surveillance activities may vary over time. Hence, we study an extension of the STSP with time-dependent profits (STSP-TDP).

We assume that the problem is defined over a given time horizon and that the sites are to be visited by a single uncapacitated vehicle during a work shift whose length does not exceed that of the planning horizon. Waiting before starting the tour is allowed, i.e., the shift does not necessarily start at the beginning of the planning horizon. Each site has a time window and a service time, and it may be beneficial for the vehicle to wait along its route to let the profit increase at some sites, as is the case of the mail collection application. As we will describe, in some versions of the problem it may be beneficial to visit the same site more than once.

For reviews of the STSP the interested reader is referred to Feillet et al. (2005), Vansteenwegen et al. (2011), Archetti et al. (2014) and Gunawan et al. (2016). Of interest in the context of the STSP-TDP is the survey of Gavalas et al. (2014) which presents a detailed description of the tourist trip design problem. These authors observe that this problem can be viewed as a bicriteria generalization of the TSP, i.e., maximizing the collected profit and minimizing the travel cost. Yu et al. (2019b) investigate the team orienteering problem with time windows and time-dependent scores. In this work, each vertex is associated with a basic score and several recommendation factors that vary depending on the time of visit. The authors propose a mathematical formulation and a hybrid artificial bee colony algorithm to compute optimal solutions for small instances and near-optimal solutions for larger instances.

There also exists a rich literature on several variants of the STSP-TDP studied in this paper, which is summarized in Table 1 but, to the best of our knowledge, our variant is unique and we are the first to provide a formulation solved by means of an exact branch-and-cut algorithm capable of solving instances much larger than was previously achievable. In our version of the STSP-TDP, the starting time of the route is also optimized within the planning horizon and waiting at the sites is allowed in order to arrive at a site when the profit to be collected is optimal. Here we introduce, model, and solve this problem exactly. We perform tests on artificial instances and on TSPLib instances, and we derive insights based on the problem characteristics and on the computational results.

Table 1 Variants of the STSP-TDP

The remainder of this paper is organized as follows. In Sect. 2, we formally describe the problem and a number of its variants, and we propose corresponding mathematical programming models. An analysis of some properties of the problem depending on the shape of the profit functions is presented in Sect. 3. This is followed by computational results in Sect. 4 and by conclusions in Sect. 5.

2 Formal definition and mathematical models

The STSP-TDP is defined on a directed graph ${\mathcal {G}} = ({\mathcal {V}}, {\mathcal {A}})$, where ${\mathcal {V}}$ is the vertex set, $0 \in {\mathcal {V}}$ is the depot and ${\mathcal {V}}' = \{1, \dots , n\}$ is the set of sites. The arc set is defined as ${\mathcal {A}} = \{(i,j): i,j \in {\mathcal {V}}, i \ne j$}. A travel time $\tau _{ij}$ is associated with each arc (i, j). The problem is defined over a planning horizon of length T, and time can be discretized into a set of moments $t \in {\mathcal {T}} = \{1, \dots , T\}$. Each site i has an associated profit $p_i(t)$ that depends on t. A solution is a closed circuit not exceeding L time units ($L \le T$), leaving the depot at time $t_0^d$, returning to the depot at time $t_0^a \le T$ and visiting a subset of the sites, where $t_0^a -t_0^d \le L$. The goal of the problem is to find a solution of maximal total profit for the selective traveling salesman problem with time-dependent profits (STSP-TDP). We assume that there are no vehicle capacity constraints and that one of the following two time-dependent profits is considered:

• 1. Profit is cumulative, i.e., the profit function is monotonically increasing. The later a vertex is visited, the higher is the collected profit. It follows that if a vertex is visited several times, one can achieve the total profit by performing only the last visit. An example of this setting is letter collection in mailboxes.

• 2. Profit depends just on the time the vertex is visited. The profit function is not necessarily monotonically increasing. Then it may be beneficial to visit a vertex more than once. Examples include parking tickets, publicity delivery, or fund collection by humanitarian organizations.

It follows from the second profit function type that a site may be visited more than once, and in both cases imposing a waiting time between successive visits to the same site may be appropriate since the collected profit is the one observed upon arrival.

2.1 At most one visit per site allowed

We first model the case in which at most one visit to each site is allowed. The formulation we propose requires that the profit functions be linear or piecewise linear, with time as a dependent variable. In this case, a time discretization is not required.

We define variables $x_{ij}$ equal to one if and only if arc $(i,j) \in {\mathcal {A}}$ is used in the solution, and variables $t_i$ equal to the time at which vertex $i \in {\mathcal {V}}'$ is visited. In what follows, M is a large positive number. The problem for the continuous single-visit case (SF) is then formulated as follows:

$$\begin{aligned} { (SF) \quad } \text {maximize} \sum \limits _{i \in {\mathcal {V}}'} p_i(t_i) \end{aligned}$$

(1)

subject to

$$\begin{aligned}&\sum \limits _{j \in {\mathcal {V}}, j\ne i} x_{ij} = \sum \limits _{j \in {\mathcal {V}}, j\ne i} x_{ji} \le 1 \quad i \in {\mathcal {V}}' \end{aligned}$$

(2)

$$\begin{aligned}&\sum \limits _{j \in {\mathcal {V}}'} x_{0j} = \sum \limits _{i \in {\mathcal {V}}'} x_{i0} = 1 \end{aligned}$$

(3)

$$\begin{aligned}&t^a_0 - t^d_0 \le L \end{aligned}$$

(4)

$$\begin{aligned}&t_j \ge t_i + { \tau _{ij}} - M(1-x_{ij}) \quad i, j \in {\mathcal {V}}'{ , i \ne j} \end{aligned}$$

(5)

$$\begin{aligned}&t_j \ge t^d_0 + { \tau _{0j}} - M(1-x_{0j}) \quad j \in {\mathcal {V}}' \end{aligned}$$

(6)

$$\begin{aligned}&t^a_0 \ge t_j + { \tau _{j0}} - M(1-x_{j0}) \quad j \in {\mathcal {V}}' \end{aligned}$$

(7)

$$\begin{aligned}&t_{i} \in [0, T] \quad i \in {\mathcal {V}}' \end{aligned}$$

(8)

$$\begin{aligned}&x_{ij} \in \{0,1\} \quad (i,j) \in {\mathcal {A}}. \end{aligned}$$

(9)

The objective function (1) represents the total collected profit to be maximized. Constraints (2) are the flow conservation conditions and ensure that there is at most one incoming and one outgoing arc for each site. Constraint (3) ensures that there is one incoming and one outgoing arc for the depot. Constraint (4) imposes a maximal route duration of L (time units). Constraints (5)–(7) ensure that travel times are respected and eliminate subtours. Finally, constraints (8) and (9) define the domains of the variables.

Note that the case of “exactly one visit” is a particular case arising in the traveling salesman problem with time-dependent profits (TSP-TDP), and hence, its formulation is obtained by just changing “$\le 1$” with “$= 1$” in constraints (2).

We can impose the following bounds on the timing variables, which indicate that one cannot arrive at vertex i earlier than $\tau _{0i}$:

$$\begin{aligned} t_i \ge { \tau _{0i}} \quad i \in {\mathcal {V}}'. \end{aligned}$$

(10)

A similar reasoning can be applied at the end of the planning horizon: one can compute the latest arrival time at vertex i such that one still arrives back at the depot at time T. The following upper bound on $t_i$ can be imposed:

$$\begin{aligned} t_i \le T - \tau _{i0} \quad i \in {\mathcal {V}}'. \end{aligned}$$

(11)

2.2 Multiple visits to sites allowed

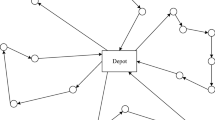
There are two main ways to model problems in which multiple visits to the same site are allowed. Some models do not replicate the sites and allow multiple visits by controlling the number of times a site is visited (see, e.g., Bruck and Iori 2017; Salazar-González and Santos-Hernández 2015; Erdoğan and Laporte 2013, and Munari and Savelsbergh 2022). The other approach is to make several copies of the same site (see, e.g., Gribkovskaia et al. 2007 and Hoff et al. 2009). Here we adopt the second modeling technique. More specifically, we make use of an auxiliary two-dimensional directed graph $\overline{{\mathcal {G}}} = (\overline{{\mathcal {V}}}, \overline{{\mathcal {A}}})$ (see Fig. 1) whose x-axis represents the periods of the planning horizon and whose y-axis represents the sites and the depot. The graph $\overline{{\mathcal {G}}}$ extends the graph ${\mathcal {G}} = ({\mathcal {V}}, {\mathcal {A}})$, so that for every vertex ${ v}\in {\mathcal {V}}$ and every period $t\in {\mathcal {T}}$, there is one vertex ${ {\overline{v}}}\in \overline{{\mathcal {V}}}$ identified with the pair $(t, { v})$, which is labelled as ${ {\overline{v}}}=t\cdot |{\mathcal {V}}| + { v}$. It follows then that, for each given vertex ${ {\overline{v}}}\in \overline{{\mathcal {V}}}$ we can obtain the corresponding period t and site ${ v}$ in graph ${\mathcal {G}}$ as follows: $t({ {\overline{v}}})=\lfloor {{ {\overline{v}}}/|{\mathcal {V}}|\rfloor }$ and ${ v}({ {\overline{v}}})={ {\overline{v}}}/|{\mathcal {V}}| - \lfloor {{ {\overline{v}}}/|{\mathcal {V}}|\rfloor }$. We denote by t(i) and v(i) the time $t\in {\mathcal {T}}$ and the vertex $v \in {\mathcal {V}}$ corresponding to the vertex $i \in \overline{{\mathcal {V}}}$, respectively. Therefore, the profit function at vertex ${ {\overline{v}}}$ is ${\overline{p}}_{{ {\overline{v}}}}={ p_{{ v}}(t)}$. Note that not all arcs are allowed in $\overline{{\mathcal {G}}}$ and that the starting and ending vertices must correspond to the depot. After predefining the set $\overline{{\mathcal {A}}}$, we need to solve a selective TSP with profit on $\overline{{\mathcal {G}}}$, with a maximum route length L no larger than the duration T of the planning horizon. We have then no predefined starting and ending vertices, but these must be selected within a subset $\{ t\cdot |{\mathcal {V}}|: t=0, 1, ..., T \} \subset \overline{{\mathcal {V}}}$ representing the set of depot vertices (T copies of the depot). The set of site vertices is $\overline{{\mathcal {V}}}' = \overline{{\mathcal {V}}} \setminus \{ t\cdot |{\mathcal {V}}|: t=0, 1, ..., T \}$.

Fig. 1

Auxiliary graph $\overline{{\mathcal {G}}} = (\overline{{\mathcal {V}}}, \overline{{\mathcal {A}}})$, where $|{\mathcal {V}}|=N$

The set of available arcs $\overline{{\mathcal {A}}}$ is composed of the set $\overline{{\mathcal {A}}_1}$ of arcs linking vertices from the same site at consecutive periods (for waiting times), and the set $\overline{{\mathcal {A}}_2}$ of arcs linking vertices from different sites and whose difference between their periods equals the travel time between these sites. Therefore,

$$\begin{aligned}&\overline{{\mathcal {A}}_1} = \{(i, j) \,| \,\big (({ v}(i)={ v}(j)) \wedge (t(j){ =t(i)+1})\big ) \},\\&\overline{{\mathcal {A}}_2}= \{(i, j) \,| \, \big (({ v}(i)\ne { v}(j)) \wedge (t(j)-t(i) = { \tau _{ij}})\big ) \}, \end{aligned}$$

and $\overline{{\mathcal {A}}} = \overline{{\mathcal {A}}_1} \cup \overline{{\mathcal {A}}_2}= \{(i, j) \,| \,\big (({ v}(i)={ v}(j)) \wedge (t(j){ =t(i)+1})\big )$$\vee \big (({ v}(i)\ne { v}(j)) \wedge (t(j)-t(i) = { \tau _{ij}})\big ) \}.$

Note that Fig. 1 shows a representation of the horizontal arcs from the set $\overline{{\mathcal {A}}_1}$ and a partial representation of the set $\overline{{\mathcal {A}}_2}$ (dashed arcs). For the sake of clarity, from the latter we only represent arcs departing from the depot.

Note that if $L=T$, the problem over $\overline{{\mathcal {G}}}$ is very similar to the STSP with profits (see Laporte and Martello 1990 and Vansteenwegen et al. 2011). In the extended graph $\overline{{\mathcal {G}}} = (\overline{{\mathcal {V}}}, \overline{{\mathcal {A}}})$, the problem is similar to the STSP, where we have a set of $|\overline{{\mathcal {V}}}| = N\cdot (T+1)-1$ vertices, each with an associated profit.

The difference between our problem in the auxiliary graph and the STSP is that, in our case, the starting and end vertices are not fixed, but belong to the set of depot vertices with zero profit. In order to obtain the STSP, we add two artificial vertices ${ B_1}$ and ${ B_2}$, which will be the starting and ending vertices of the Hamiltonian path, respectively. Accordingly, a set of zero length arcs joining ${ B_1}$ and the depot vertices and the latter with ${ B_2}$ is also added. So, from now on, the problem is defined on ${\hat{G}}=({\hat{V}}, \hat{{\mathcal {A}}})$, where ${\hat{V}}=\overline{{\mathcal {V}}} \cup \{{ B_1}, { B_2}\}$ and $\hat{{\mathcal {A}}}=\overline{{\mathcal {A}}} \cup \{(i,{ B_2})| i\in \overline{{\mathcal {V}}} \setminus \overline{{\mathcal {V}}}' \} \cup \{({ B_1},i)| i\in \overline{{\mathcal {V}}} \setminus \overline{{\mathcal {V}}}' \}$.

We use directed continuous variables $y_{ij}$ representing the flow over arc (i, j) and binary variables $\gamma _i$ equal one if the shift starts at vertex $i \in \{0, ..., T-L\}$. Note that the graph ${\hat{G}}$ is a time-ordered graph, which enables us (for fixed depot departure and arrival times $t_0^d$ and $t_0^a$, being $t^a_0 - t^d_0=L$) to model the problem as a longest path problem. In doing so, we transfer the profit associated with a vertex j to its incoming arcs in $\overline{{\mathcal {A}}_2}$. That is, each arc $(i, j) \in \overline{{\mathcal {A}}_2}$ has an associated profit ${\overline{p}}_{ij}={\overline{p}}_{j}$. The profit associated with the remaining arcs in $\hat{{\mathcal {A}}}$ equals zero. The problem for the discretized multiple-visit case (MF) over ${\hat{G}}$ is formulated as follows:

$$\begin{aligned} { (MF) \quad \text {maximize} \sum \limits _{(i,j)\in \hat{{\mathcal {A}}}} {\overline{p}}_{ij} \cdot y_{ij}} \end{aligned}$$

(12)

subject to

$$\begin{aligned}&\sum \limits _{j \in \delta ^+(i)} y_{ij} - \sum \limits _{j \in \delta ^-(i)} y_{ji}=\left\{ \begin{array}{l} 1 \quad \text { if } i={ B_1}\\ 0 \quad \text { if } i\ne { B_1},{ B_2}\\ -1 \quad \text { if } i={ B_2} \\ \end{array} \right. \end{aligned}$$

(13)

$$\begin{aligned}&y_{Ai} \le \gamma _{t(i)}, \quad i: { v}(i)=0 \text { and } t(i) \in \{0, ..., T-L\} \end{aligned}$$

(14)

$$\begin{aligned}&y_{i+L, B} \le \gamma _{t(i)}, \quad i: { v}(i+L)=0 \text { and } t(i) \in \{0, ..., T-L\} \end{aligned}$$

(15)

$$\begin{aligned}&\sum _{i\in \{0, ..., T-L\}} \gamma _i =1 \end{aligned}$$

(16)

$$\begin{aligned}&\gamma _i \in \{0, 1\} \quad i\in \{0, ..., T-L\} \end{aligned}$$

(17)

$$\begin{aligned}&y_{ij} \ge 0 \quad (i,j)\in \hat{{\mathcal {A}}}. \end{aligned}$$

(18)

The objective function (12) is the total collected profit. Recall that the profit is collected when the vehicle arrives at the vertex. Constraints (13), where $\delta ^+(i)$ and $\delta ^-(i)$ are the sets of successors and predecessors of vertex i in graph ${\hat{G}}$, respectively, ensure that exactly one arc departs from the artificial vertex A to the set of depot vertices, that one unit of flow arrives at B from the same set, and enforce the flow conservation conditions for the remaining vertices, which are the site vertices. Constraints (14) and (15) impose a maximal route duration by means of the $\gamma$ variables. There are as many $\gamma _{y_L}$ variables as $T-L$ time periods. By selecting only one of the $\gamma _{y_L}$ variables, constraints (16) ensure that the route starts at one time instant and ends after exactly L periods. Finally, constraints (17) and (18) impose the binary condition of the $\gamma$ variables and the non-negativity condition of the y variables, respectively.

3 Analysis of the problem and shapes of the profit function

As explained in Sect. 2, depending on the shape of the profit function, the problem possesses certain characteristics. These will not only be influenced by the monotonicity condition of the profit functions, but also by their specific shape.

Observation 1. Let $p_i: {\mathcal {T}}\rightarrow {\mathbb {R}}$ represent the accumulated profit at vertex $i\in {\mathcal {V}}'$ arising from a positive non-cumulative profit function $p^\prime _i: {\mathcal {T}}\rightarrow {\mathbb {R}}^+$, that is, the accumulated profit at vertex i during the time interval [0, t] is calculated as $p_i(t)=\int _0^{t} p^\prime _i (t) dt$. Then, $p_i$ is a monotonically increasing function and the total profit collected visiting vertices i at time $t_1$ and $t_2\in {\mathcal {T}}$ ($t_1<t_2$) equals the profit collected by visiting vertices i only once at time $t_2$.

Proof

If vertex $i\in {\mathcal {V}}'$ is visited at time units $t_1$ and $t_2 \in {\mathcal {T}}$, the total collected profit equals $\int _0^{t_1} p^\prime _i { (t)} dt+\int _{t_1}^{t_2} p^\prime _i { (t)} dt=\int _{0}^{t_2} p^\prime _i { (t)} dt$.

If vertex ${\mathcal {V}}'$ is visited only once at time unit $t_2$, the total collected profit equals $p_i(t_2)=\int _{0}^{t_2} p^\prime _i { (t)} dt$. $\square$

Observation 2. If $p_i(t)=\alpha _i$ for all $i \in {\mathcal {V}}'$, $\alpha { _i} \ge 0$, then the STSP-TDP when at most one visit per site is allowed obviously becomes the STSP. In this case, it does not matter whether $L = T$ or $L < T$ since the collected profit is not time dependent.

Observation 3. Let us assume that L is large enough to visit all vertices in any order and that each site can be visited at most once (following formulation (SF) presented in Sect. 2.1). If all profit functions are linear, i.e., $p_i(t)=\alpha _i t$ for all $i \in {\mathcal {V}}'$, $\alpha _i \ge 0$, $\alpha _i \le \alpha _{i+1}$, and $\tau _{0,i} \ge \tau _{0,i+1}$ for all $i \in {\mathcal {V}}' \setminus \{N\}$, then $x_{i, i+1} =1$ for all $i \in {\mathcal {V}}' \setminus \{N, N-1\}$ and $x_{N0}=1$. $x_{i, j} =0$ for all $j \ne i+1$, $i \in {\mathcal {V}}' \setminus \{N, N-1\}$. That is, under the described conditions, if the vertices are labeled in increasing order with respect to the slope ($\alpha _i \le \alpha _{i+1}$), the visiting order coincides with the labeling order.

Proof

Given two vertices i and $i+1 \in {\mathcal {V}}'$ satisfying the above mentioned conditions, it is always beneficial to first visit the one with the lower slope (in this case i since $\alpha _i\le \alpha _{i+1}$).

Let p(i, j, t) be the profit collected at vertices i and j if vertex i is visited at time t and vertex j at time $t+{ \tau _{ij}}$. Then, starting from vertex 0, the collected profit obtained by visiting first vertex i and then vertex $i+1$ is $p(i, i+1, \tau _{0,i})=\alpha _i \tau _{0,i} + \alpha _{i+1} (\tau _{0,i}+\tau _{i, i+1})$. The collected profit if vertex $i+1$ is visited before vertex i is $p(i+1, i, \tau _{0,i+1})=\alpha _{i+1} \tau _{0,i+1} + \alpha _i (\tau _{0,i+1}+\tau _{i+1, i})$.

Let us demonstrate that the collected profit is larger if vertex i is visited before vertex $i+1$, that is, $p(i, i+1, \tau _{0,i})\ge p(i+1, i, \tau _{0,i+1})$:

$$\begin{aligned}&p(i, i+1, \tau _{0,i})=\alpha _i \tau _{0,i} + \alpha _{i+1} (\tau _{0,i}+\tau _{i, i+1})=\alpha _i \tau _{0,i} + \alpha _{i+1} \tau _{0,i} + \alpha _{i+1} \tau _{i, i+1},\\&p(i+1, i, \tau _{0,i+1})=\alpha _{i+1} \tau _{0,i+1} + \alpha _i (\tau _{0,i+1}+\tau _{i+1, i})= \alpha _{i+1}\tau _{0,i+1}+ \alpha _i \tau _{0,i+1}+ \alpha _i \tau _{i+1, i}. \end{aligned}$$

By reductio ad absurdum, if $p(i, i+1, \tau _{0,i}) < p(i+1, i, \tau _{0,i+1})$, then

$$\begin{aligned} \alpha _i \tau _{0,i} + \alpha _{i+1} \tau _{0,i} + \alpha _{i+1} \tau _{i, i+1} < \alpha _{i+1}\tau _{0,i+1}+ \alpha _i \tau _{0,i+1}+ \alpha _i \tau _{i+1, i}. \end{aligned}$$

Since $\tau _{i+1, i}=\tau _{i, i+1}$, the inequality can be written as follows:

$$\begin{aligned} \tau _{i, i+1}(\alpha _{i+1}-\alpha _i) < (\alpha _{i+1}+\alpha _i)(\tau _{0,i+1}-\tau _{0,i}), \end{aligned}$$

which is not respected given that $\tau _{i, i+1}$, $\alpha _{i+1}-\alpha _i$, and $\alpha _{i+1}+\alpha _i$ are positive values and $\tau _{0,i+1}-\tau _{0,i}\le 0$. Therefore, the left-hand side of the inequality is positive and the right-hand side is negative. $\square$

Observation 4. The STSP-TDP can be viewed as a generalization of the STSP with time windows by setting the profit function as a stepwise function equal to a negative number outside the time window, and equal to a positive constant during the time window interval. That is, if

$$\begin{aligned} p_i(t)=\left\{ \begin{array}{l} -\beta \quad \text { if } t< a_i \\ \alpha _i \quad \text { if } a_i\le t\le b_i\\ -\beta \quad \text { if } b_i <t \\ \end{array} \right. \end{aligned}$$

for all $i \in {\mathcal {V}}'$, $\alpha _i \ge 0$, $\beta \ge 0$, then the STSP-TDP becomes the STSP with time windows $[a_i, b_i]$ for all $i \in {\mathcal {V}}'$. Vertex i would not be visited outside the time window since this yields a negative profit and a corresponding decrease of the objective function (total collected profit).

Observation 5. A new problem called the STSP-TDP with time windows, $[a_i, b_i]$ for all $i \in {\mathcal {V}}'$, can be considered if the profit function has the following shape:

$$\begin{aligned} p_i(t)=\left\{ \begin{array}{l} -\beta \quad \text { if } t< a_i \\ f_i(t) \quad\text{if}\; a_i\le t\le b_i\\ -\beta \quad \text { if } b_i <t \\ \end{array} \right. \end{aligned}$$

for all $i \in {\mathcal {V}}'$, $\beta \ge \alpha _i \ge 0$, with $f_i(t) \ge 0$ being the profit function associated with each vertex $i \in {\mathcal {V}}'$ during the time interval $[a_i, b_i]$ in which the vertex may be visited. Since the objective function is to maximize the total collected profit, negative values of this profit outside its time window $[a_i, b_i]$ ensure that vertex $i \in {\mathcal {V}}'$ will not be visited outside the time window.

Note that Observations 4 and 5 may apply for both the single- and multiple-visit cases.

4 Computational results

When the profit functions are linear or piecewise linear functions of time, the formulation (SF) presented in Sect. 2.1 can be directly applied and there is no need to discretize the time. In the following, we perform two main types of experiments to provide insights into the models: first for artificially created instances defined on a mesh network, and second for benchmark instances from the TSPLib, assigning time-dependent profits to each vertex. These experiments were performed on a machine equipped with an Intel i7-8700 3.20GHz CPU. The model of Sect. 2.1 was implemented in Python 3.8 and solved with Gurobi version 9.1.

4.1 Mesh instances

The first set of experiments is designed to illustrate the behavior of the models when changing the maximum length of routes L and the duration of the planning horizon T, as well as to assess the solver’s performance for different instance sizes. We have considered three instances sizes of 15, 30, and 50 vertices. In all the experiments, the network is constructed following a concentric clockwise labelling procedure, starting from vertex number 1, which acts as the depot and increasing the vertex number consecutively (see Fig. 2 for an illustration of the 15-vertex network). The horizontal and vertical distances between vertices are set to 1 and the arcs travel times have been obtained considering a travel speed equal to a tenth of the total distance needed to visit in order all the vertices, plus the Euclidean distance from the last vertex to the depot, ensuring there is no time to visit all vertices in any of the considered instances.

Fig. 2

Mesh network construction

With respect to the piecewise linear profit functions, for each vertex we consider a non-cumulative one-peak profit function with the following shape (see Fig. 3):

$$\begin{aligned} p_i(t) = \left\{ \begin{matrix} a_i \cdot t &{} \text {if} \ t \le \ t_i^* \\ b_i \cdot t + t_i^* \cdot (a_i - b_i) &{} \text {if} \ t \ge t_i^* \end{matrix} \right. \end{aligned}$$

(19)

where $a_i \ge 0$, $b_i \le 0$, and $t_i^*$ are parameters associated to each vertex $i \in {\mathcal {V}}'$. Regarding the shape of the profit function, we have divided the first set of experiments into two subsets. The first one (experiments 1 to 15) considers values of $t_i^*$ following an increasing vertex label order, i.e. the peak of the profit function of each vertex is proportional to the vertex number. Specifically, $t_i^* = 480/n \times (i-1)$, where n represents the number of vertices of each instance. Moreover, the slopes of the profit function ($a_i$, $b_i$) are also proportional to the vertex index: specifically $a_i=3 \times (i - 1)$ and $b_i= -3 \times (i - 1)$. The second subset of experiments (experiments 16 to 30) considers values of $t_i^*$ following a decreasing order with the index of the vertex, i.e., $t_i^*= 480/n \times (n-(i-1))$.

Fig. 3

Piecewise linear profit function

With these artificially created instances we can test the behavior and performance of the solver on the models. For the first subset of experiments, depending on the values of L and T, since the profit peaks increase with the vertex order it is expected that the optimal routes for the single-visit case will follow a clockwise direction. Alternatively, for the second subset, the optimal routes for the single-visit case should follow a counterclockwise direction. For each subset and for each size (15, 30 and 50 vertices), five experiments were carried out, considering $L=240, \ 480$ and $T=240,\ 480$ and 1440 (which produces the next five combinations $240-240, \ 240-480, \ 240-1440, \ 480-480, \ 480-1440$). The maximum computation time was fixed to $60 \times n$ seconds.

Tables 2 and  3 show the results for the mesh shape instances considering the single-visit (Formulation (SF)) and the multiple-visit (Formulation (MF)) cases, respectively . The table headings are defined as follows:

• Exp. #: experiment number.

• $|{\mathcal {V}}|$: the size of the instance.

• L: maximum length of the route.

• T: planning horizon.

• Profit: total profit obtained, which is the objective function value.

• $t^d_0$: departure time from the depot.

• Gap (%): optimality gap calculated as $\frac{UB - LB}{UB} \cdot 100$, where LB and $UB=\text {(profit)}$ are the best known lower and upper bounds.

• #Vertices visited: number of visited vertices in the solution.

• Time: computation time in seconds.

• Max. time: maximum allowed computation time in seconds.

All instances are solved using the standard truncated branch-and-cut algorithm implemented in Gurobi, truncated after a predefined CPU time limit "Max. time”. As expected, the collected profit is higher for the multiple-visit case and, for both the single- and multiple-visit cases, the collected profit increases with L and T. Moreover, for a given value of L the profit tends to increase with T. Note that all the instances are selective and that, for each instance and fixed values of T, the number of visited vertices in the single-visit case tends to increase with L.

Table 2 Mesh shape instances. Formulation (SF)

Table 3 Mesh shape instances. Formulation (MF)

Figures 4 and 5 depict the resulting selective routes for each of the 30 vertices instances of Table 2. Observe that in Fig. 4, since the profit peak vertices are disposed in increasing order, not all vertices can be visited and the visited ones are those with larger indices, i.e., larger profits. The visiting order follows a clockwise direction, except for some instances for which the optimal solution is not achieved within Max. time. The behavior in experiments 21 to 25, where profit peaks follow a decreasing order, is the opposite. In these experiments, the numbers over the vertices correspond to the profit collected and the visit time. As illustrated, regardless of the instance size, the higher the ratio T/L, the higher is the collected profit. When T is larger than L, the model can move the starting time of the route (column $t_0^d$ in Table 2). Note that for the cases where ${ T} = L$ (240–240, 480–480), the departure from the depot occurs at time $t = 0.00$, thus using the full route length to visit as many vertices as possible, arriving again to the depot at time $t = L$. In general, for a given size of the instance, the number of visited vertices tends to increase with ${ T}$, but this is not always true. See, for instance, experiments 1, 2, and 3, with $L = 240$: although the collected profit increases, the number of visited vertices decreases. Since the model can freely move the route duration interval along the planning horizon, a higher profit can be collected visiting fewer but more profitable vertices. This behavior can also be observed for experiments 4–5, 9–10, and 11–13 in the case of peak profits following an increasing order with time. Similarly, in the opposite order of profit peaks, experiments 19–20, 24–25, and 29–30 exhibit this decrease in the number of visited vertices. Graphical representations of the remaining instances (with 15 and 50 vertices) are provided in the Appendix.

Fig. 4

Mesh instances. Experiments 6 to 10 with 30 vertices, clockwise order

Fig. 5

Mesh instances. Experiments 21 to 25 with 30 vertices, counterclockwise order

As an illustration of the problem with time windows described in Sect. 3, we consider the 15 vertices mesh instances described above but whose vertices have negative profit function values outside predefined time windows. We have considered piecewise linear profit functions similar to those illustrated in Fig. 3, but with time windows around the profit function peaks (see Fig. 6). Table 4 shows the results obtained for the multiple-visit case. It can be observed that, as commented in Observations 4 and 5, the vertices that are visited are indeed visited within their corresponding time window. Recall that, for these experiments, the time windows do not need to be added to the formulation, but they are naturally respected by assigning negative profit function values outside their bounds.

Fig. 6

Piecewise linear profit functions with negative values outside time windows

Table 4 Mesh shape instances with time windows. Formulation (MF)

4.2 TSPLib instances

In this section, we consider different TSTLib instances adapted to the characteristics of our problem, that is, assigning one-peak time-dependent profit functions see Eq. (19) to vertices and considering different space measure scales.

Assuming that the TSPLib coordinates are given in km, we consider constant speed and different scales to study the problem resolution. In this way, e.g., a scale of 1/1000 means that the coordinates are taken in meters. Tables 5 and 6 illustrate the sensitivity of the single- and multiple-visit models, respectively, to different scales for instance eil51 and the following parameter values: $L=480$, $T=1440$, $\text {speed}=35.5$ km/h. The CPU time limit has been set as Max. time=7200 seconds for these experiments. The table headings are defined as follows:

• Scale: different values are considered to rescale the instance eil51. Scale 1 indicates that distance is taken in kilometers and 1/1000 in meters.

• Profit: total profit obtained, which is the objective function value.

• Total distance: total traveled distance in the corresponding scale measure.

• Total distance (km): total traveled distance in km.

• Time: computation time in seconds.

• Gap (%): optimality gap calculated as $\frac{UB - LB}{UB} \cdot 100$.

• $t^d_0$: departure time from the depot.

• #Vertices visited: number of visited vertices in the solution.

Since we consider a constant speed, the smaller the scale, the smaller the distances and, therefore, the more time is available to visit the vertices. It can be observed that this effect influences the resulting solutions, mostly in terms of total collected profit and computation time. Observe that, for the single-visit case (Table 5), the higher the scale, the smaller the total profit obtained and the larger the computing times, being even not possible to obtain a feasible solution within the CPU time limit Max. time=7200 for scale 1/1. The starting time of the shift also changes with the scale, tending to start earlier when the scale is smaller. This is due to the fact that the considered speed is constant and, therefore, the smaller the scale, the larger the freedom to visit the vertices. Table 6, which shows the results obtained for the multiple-visit case, exhibits a similar behavior in terms of the objective function. Although, as expected, much higher values of the objective function are obtained for the multiple-visit case, these values also increase as the scale decreases. However, with respect to the computing times, for the multiple-visit case, the behavior of the computing times is not uniform. In this case, different scales lead to different travel times and, therefore, different arc set $\overline{{\mathcal {A}}_2}$. Since the model allows to wait at the same site, shorter travel times enable to arrive with more flexibility at a site, thus leading to equal or better profits but not necessarily better computing times.

Table 5 Variations to scale for instance eil51

Table 6 Variations to scale for instance eil51

Table 7 presents the results obtained for the single- and multiple-visit cases for TSPLib instances eil51, st70, a280, and ali535. For these experiments, the maximum length of the route $L=480$, the planning horizon $T=1440$, the threshold on the computing time is Max. time = 7200 s and the scale is 1/1000, which is equivalent to considering the original coordinates in meters instead of in kilometers. The table headings are defined as follows:

• TSPLib instance: indicates the name of the benchmark instances.

• Profit: the total profit obtained, which is the objective function value.

• Gap (%): optimality gap calculated as $\frac{UB - LB}{UB} \cdot 100$.

• #Vertices visited: number of visited vertices in the solution.

• Time: computation time in seconds.

• Total distance: total traveled distance in meters (corresponding to scale 1/1000).

• $t^d_0$: departure time from the depot.

As expected, for both cases, the larger the number of vertices, the larger the total collected profit and the computation time. For the multiple-visit case, only instances eil51 and st70 could be solved to optimality within Max. time. For these instances, although the number of visited nodes in the multiple-visit case is considerably lower than for the single-visit case, these nodes are visited several times obtaining more than ten times higher values of the objective function (collected profit). Figure 7 illustrates the resulting routes with Formulation (SF) for the instances presented in Table 7. Since the problem aims at maximizing the total collected profit, the resulting routes differ significantly from those obtained with the usual TSP, where the objective is to minimize the total distance traveled.

Table 7 Results for TSPLib instances for scale 1/1000, $L=480$, $T=1440$

Fig. 7

Representation of the resulting routes for instances of Table 7 with scale 1/1000

As expected, when the objective function is to maximize the total collected profit, the total distance increases with respect to that obtained from a TSP solution. A trade-off analysis between the collected profit and the total distance may shed some light on these differences. To this end, it becomes appropriate to use a multi-objective approach.

4.3 Trade-off between the collected profit and the total distance. Multi-objective approach

Starting from formulation (SF), we consider the $\epsilon$-constraints method proposed by Marglin (1967). That is, we include constraint (20) limiting the total distance of the route to a maximum of $\epsilon$ and the route is then obtained by maximizing the total collected profit and varying parametrically the maximum total distance $\epsilon$:

$$\begin{aligned} \sum _{\begin{array}{c} i,j \in {\mathcal {V}}\\ i\ne j \end{array}}{ \tau _{ij}} x_{ij} \le \epsilon . \end{aligned}$$

(20)

Table 8 represents the results obtained by the $\epsilon$-constraints method for the TSPLib instance eil51 and the following parameter values: $L=480$, $T=1440$, $\text {speed}=35.5 \text {km/h}$, $\text {scale}=1/10$. The table headings are defined as follows:

• Threshold $\epsilon$: threshold on the route total distance.

• Profit: total profit obtained, which is the objective function value.

• Total distance: total traveled distance in hectometers (corresponding to scale 1/10).

• Time: computation time in seconds.

• Gap (%): optimality gap calculated as $\frac{UB - LB}{UB} \cdot 100$.

Table 8 Trade-off between collected profit and total distance for instance eil51 at scale 1/10

Observe that, except for the first four rows, the value of the total distance tends to be similar to that of the upper threshold $\epsilon$. This follows from the fact that the larger the total distance, the less constrained is the problem and, therefore, the larger is the total collected profit, which is the objective function. The first four rows stand for values of $\epsilon$ larger than 131.35, which is the total collected profit when no constraints on the total distance are imposed (see Table 5, third row). This explains the constant values for the first four rows of the third column.

The first and second columns of Table 8 are represented in Figure 8 in the form of a Pareto curve for a trade-off between collected profit and maximum total distance. It can be observed that, as expected, the total collected profit increases as the threshold on the total distance increases. However, the profit stabilizes when the threshold $\epsilon$ reaches 130. In fact, if no threshold is imposed and only the total collected profit is maximized, then the resulting total collected distance equals 131.35. Therefore, for $\epsilon$ values larger than 131.35, the total collected profit remains constant.

Fig. 8

Trade-off between collected profit and total distance for instance eil51 at scale 1/10

The routes associated with some of the solutions of Table 8 are depicted in Figure 9. As $\epsilon$ decreases, the route length decreases and tends to look like a usual TSP solution, in which the total distance is minimized and profit is not considered.

Fig. 9

Representation of the resulting routes for different values of $\epsilon$

5 Conclusions

We have introduced, modeled, and solved the STSP-TDT. The STSP-TDT is a generalization of other well-known variants of the traveling salesman problems such as the TSP itself, the STSP, as well as the TSP and the STSP with time windows. Some interesting properties arise in the context of time-dependent profits. For example, it sometimes makes sense to visit the same vertex multiple times and to optimize the starting time of the tour. We have proposed and tested a formulation of the single-visit problem that can be used if the profit functions are linear or piecewise linear.

We have also proposed and tested an extended formulation for the case when multiple visits to the same vertex are allowed and desirable. In this case, we formulate the problem by means of an extended graph so that this variant reduces to an STSP, adapted to be solved as a longest path problem.

We have analyzed the problem by studying the shape of the time-dependent profit functions. We have also performed several experiments on artificially created instances and on some TSPLib instances considering the single- and multiple-visit cases. Our results on artificially created instances validate the model performance and highlight the importance of allowing a variable starting time of the route. We have considered several scale measures and optimally solved instances containing up to 535 vertices for the single-visit case. We have also compared the results obtained for the single- and multiple-visit cases and analyzed the results of our single-visit case experiments by means of a Pareto frontier representing the trade-off between the collected profit and the total distance traveled. We observe that these objectives are naturally opposed to one another.

Appendix. Results of 15 and 50 vertices mesh instances

See Figs. 10, 11, 12 and 13.

Fig. 10

Mesh instances. Experiments 1 to 5. 15 vertices. Clockwise order

Fig. 11

Mesh instances. Experiments 16 to 20. 15 vertices. Counterclockwise order

Fig. 12

Mesh instances. Experiments 11 to 15. 50 vertices. Clockwise order

Fig. 13

Mesh instances. Experiments 26 to 30. 50 vertices. Counterclockwise order