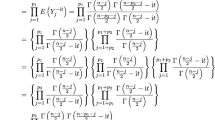Testing hypotheses about correlation matrices in general MANOVA designs

Abstract

Correlation matrices are an essential tool for investigating the dependency structures of random vectors or comparing them. We introduce an approach for testing a variety of null hypotheses that can be formulated based upon the correlation matrix. Examples cover MANOVA-type hypothesis of equal correlation matrices as well as testing for special correlation structures such as sphericity. Apart from existing fourth moments, our approach requires no other assumptions, allowing applications in various settings. To improve the small sample performance, a bootstrap technique is proposed and theoretically justified. Based on this, we also present a procedure to simultaneously test the hypotheses of equal correlation and equal covariance matrices. The performance of all new test statistics is compared with existing procedures through extensive simulations.

1 Motivation and introduction

Covariance matrices contain a multitude of information about a random vector. Therefore, they were the topic of manifold investigations. For testing, an important hypothesis is the equality of covariance matrices from different groups. This was investigated in Bartlett and Rajalakshman (1953) as well as Boos and Brownie (2004). Moreover, Gupta and Xu (2006) proposed tests for a given covariance matrix. Extending on both, Sattler et al. (2022) proposed a unifying framework that allows for investigations of various hypotheses about the covariance. Additional examples cover testing equality of traces or comparing diagonal elements of the covariance matrix.

However, covariance matrices are not scale-invariant. This entails some disadvantages using them in the analysis of random vectors’ dependency structure. For example, a simple change of a measuring unit can completely change the matrix. For this reason alone, it is more useful to consider the correlation matrix instead when inferring dependency structures.

This already starts in the bivariate case, i.e. the investigation of correlations. For ordinal data, rank-based correlation measures are most common. For example, Perreault et al. (2022) provides an approach for general hypotheses testing, while Nowak and Konietschke (2021) focused on simultaneous confidence intervals and multiple contrast tests for Kendall’s $\tau$. Spearman’s rank-correlation coefficient $\rho$ was investigated in Gaißer and Schmid (2010) for the hypothesis of the correlation matrix being an equicorrelation matrix. For metric data, the most common measure of correlation is the Pearson correlation coefficient. Here, tests and confidence intervals for investigating or comparing correlation coefficients have been discussed for the case of one, two or multiple group(s), see (Fisher 1921; Efron 1988; Sakaori 2002; Gupta and Xu 2006; Tian and Wilding 2008; Omelka and Pauly 2012; Welz et al. 2022) and the references cited therein.

For larger dimensions, equality of correlation matrices was investigated, for example, in Jennrich (1970). Moreover, different hypotheses regarding the structure of correlation matrices were treated in Joereskog (1978), Steiger (1980) and Wu et al. (2018). However, the above approaches usually require strong prerequisites on the distribution (such as multivariate normal distribution or particular properties of the moments), the components or the setting (such as bivariate or special structures). Moreover, most can be used only for a few specific hypotheses. Thus, to obtain an approach with fewer assumptions, which is at the same time applicable for a multitude of hypotheses, we expand the approach of Sattler et al. (2022) to the treatment of correlation matrices.

In the following section, the statistical model will be introduced together with examples of different null hypotheses that can be investigated using the proposed approach. Afterwards, the asymptotic distributions of the proposed test statistics are derived (Sect. 3). In Sects. 4 and 5, a resampling strategy and a Taylor-based Monte Carlo approach are used to generate critical values and improve our tests’ small sample behaviour. A combined testing procedure which simultaneously checks the hypothesis of equal correlation matrices and covariance matrices is presented in Sect. 6. The simulation results regarding type-I-error control and power are discussed in Sect. 7, while an illustrative data analysis of EEG data is conducted in Sect. 8. All proofs are deferred to a technical supplement, where also more simulations can be found.

2 Statistical model and hypotheses

To allow for broad applicability, we use a general semiparametric model, given by independent d-dimensional random vectors

$$\begin{aligned}\varvec{X}_{ik}= \varvec{\mu }_i + \varvec{\epsilon }_{ik},\end{aligned}$$

where the index $i=1, \dots , a$ refers to the treatment group and $k=1, \dots ,n_i$ to the individual, on which d-variate observations are measured. As analysing a scalar’s correlation is useless, we assume $d\ge 2$. This model as well as all subsequent results can in principle be expanded for different dimensions of the groups as done in Friedrich et al. (2017). However, as the notation would be a bit cumbersome, we did not follow this approach to increase the readability. The residuals $\varvec{\epsilon }_{i1},\dots ,\varvec{\epsilon }_{in_i}$ are assumed to be centred ${\mathbb {E}}(\varvec{\epsilon }_{i1}) = \textbf{0}_d$ and i.i.d. within each group, with finite fourth moment ${\mathbb {E}}(||\varvec{\epsilon }_{i1}||^4) < \infty$, while across groups, they are only independent. Thus, different distributions per group are possible. For our asymptotic considerations, we additionally assume

• (A1) $\frac{n_i}{N}\rightarrow \kappa _i\in (0,1],~i= 1,...,a$ for $\min (n_1,\dots ,n_a)\rightarrow \infty$

with $N = \sum _{i=1}^a n_i$, to preclude that a single group dominates the setting. In the following, we use ${\mathop {\longrightarrow }\limits ^{\mathcal {P}}}$ to denote convergence in probability and ${\mathop {\longrightarrow }\limits ^{\mathcal {D}}}$ for convergence in distribution as sample sizes increase. It follows from the context whether this means $N\rightarrow \infty$ or $n_i\rightarrow \infty$, respectively.

Moreover, to define correlation matrices, we additionally assume that the covariance matrices ${{\,\textrm{Cov}\,}}(\varvec{\epsilon }_{i1})=\varvec{V}_i=(V_{ijk})_{j,k\le d}$ have positive diagonals $V_{i11},...,V_{idd} > 0$. Throughout, the so-called half-vectorization operation ${{\,\textrm{vech}\,}}$ is used for the covariance matrices, which puts the upper triangular elements of a $d\times d$ matrix into a $p=d(d+1)/2$ dimensional vector. But, for a correlation matrix, the diagonal elements are always one and therefore contain no information, so this is not the best choice here. Hence, a new vectorization operation ${{\,\textrm{vech}\,}}^-$ is defined, which we will call the upper-half-vectorization. With $\varvec{R}_i$ as the correlation matrix for the i-th group, this vectorization operation allows us to define

$$\begin{aligned} \varvec{r}_i={{\,\textrm{vech}\,}}^-(\varvec{R}_i)= (r_{i12},\dots ,r_{i1d},r_{i23},\dots ,r_{i2d},\dots ,r_{i(d-1)d})^\top , \ i=1,\dots ,a, \end{aligned}$$

containing just the upper triangular entries of $\varvec{R}_i$ which are not on the diagonal. The resulting vector has dimension $p_u=d(d-1)/2$, which is substantially smaller than p. We now formulate hypotheses in terms of the pooled correlation vector $\varvec{r}= (\varvec{r}_1^\top ,\dots ,\varvec{r}_a^\top )^\top$ as

$$\begin{aligned} {\mathcal {H}}_0^{\varvec{r}}: \varvec{C}\varvec{r}= \varvec{\zeta }, \end{aligned}$$

(1)

with a proper hypothesis matrix $\varvec{C}\in \mathbb {R}^{m\times a p_{u}}$ and a vector $\varvec{\zeta }\in \mathbb {R}^{m}$. Hereby, we allow m to be much smaller than $ap_u$, which is often useful (e.g. for computational reasons) for hypotheses matrices without full rank. As explained in Sattler et al. (2022) for the case of covariance matrices, $\varvec{C}$ does not have to be a projection matrix as $\varvec{\zeta }$ is allowed to be different from the zero vector, see, for example, hypothesis (c).

Hypotheses which are part of the setting (1) are, among others:

(a) Testing Homogeneity of correlation matrices

$$\begin{aligned} {\mathcal {H}}_0^{\varvec{r}}: \varvec{R}_1 = \dots = \varvec{R}_a, \text { resp. } {{\mathcal {H}}_0^{\varvec{r}}:(\varvec{P}_a\otimes \varvec{I}_{p_u}) \varvec{r}=\textbf{0}_{ap_u}}, \end{aligned}$$

with $\varvec{P}_a:=\textbf{1}_a \textbf{1}_a^\top -\varvec{I}_a/a$ and $\otimes$ denoting the Kronecker product. This hypothesis was, for example, investigated in Jennrich (1970), while for $d=2$, this includes the problem of testing the null hypothesis

$$\begin{aligned} {\mathcal {H}}_0^{\varvec{r}}: \rho _{1} = \rho _2 = \dots = \rho _a \end{aligned}$$

of equal correlations $\rho _i = {{\,\textrm{Corr}\,}}(X_{i11},X_{i12}), i=1,\dots ,a$ within (1). This again contains testing equality of correlations between two groups, see, e.g. Sakaori (2002), Gupta and Xu (2006) or Omelka and Pauly (2012).

(b) Testing a diagonal correlation matrix

$$\begin{aligned} {\mathcal {H}}_0^{\varvec{r}}: \varvec{R}_1 = \varvec{I}_d, \text { resp. } {\mathcal {H}}_0^{\varvec{r}}:{ \varvec{I}_{p_u}\varvec{r}_1=\textbf{0}_{p_u}}. \end{aligned}$$

A test procedure for zero correlations was introduced by Bartlett (1951) for the one-group setting. More hypotheses on the structure of the covariance matrix can be found, for example, in Joereskog (1978), Steiger (1980) and Wu et al. (2018).

(c) Testing for a given correlation Let $\varvec{R}$ be a given correlation matrix, like an autoregressive or compound symmetry matrix. For $a=1$, we then also cover testing the null hypothesis

$$\begin{aligned} {\mathcal {H}}_0^{\varvec{r}}: \varvec{R}_1 = \varvec{R}\text { resp. }{{\mathcal {H}}_0^{\varvec{r}}: \varvec{I}_{p_u}\varvec{r}_1={{\,\textrm{vech}\,}}^-(\varvec{R}) }. \end{aligned}$$

For $d=2$, this also contains the issue of testing the null hypothesis

$$\begin{aligned} {\mathcal {H}}_0^{\varvec{r}}: \rho _{1} = 0 \end{aligned}$$

of uncorrelated random variables with $\rho _1 = {{\,\textrm{Corr}\,}}(X_{111},X_{112})$, see e.g. Aitkin et al. (1968).

(d) Testing for equal correlations For $a=1$, we are interested whether the correlation between all components is the same, i.e.

$$\begin{aligned} {\mathcal {H}}_0^{\varvec{r}}: \varvec{r}_{11}=\varvec{r}_{12}=...=\varvec{r}_{1p_u}{\text { resp. } {\mathcal {H}}_0^{\varvec{r}}: \varvec{P}_{p_u}\varvec{r}_1=\textbf{0}_{p_u}.} \end{aligned}$$

This kind of hypothesis is connected with a compound symmetry matrix and was investigated in Wilks (1946) and Box (1950) for special settings.

3 Asymptotics regarding the vectorized correlation

To infer null hypotheses of the kind ${\mathcal {H}}_0^{\varvec{r}}: \varvec{C}\varvec{r}= \varvec{\zeta },$ it is necessary first to investigate the asymptotic distribution of $\varvec{C}{\widehat{\varvec{r}}}$, while ${\widehat{\varvec{r}}}$ is the pooled vector of upper-half-vectorized empirical correlation matrices. Thereto, Theorem 3.1 from Sattler et al. (2022) is shortly repeated first. Therein, for $\varvec{v}=(\varvec{v}_1^\top ,...,\varvec{v}_a^\top )^\top =({{\,\textrm{vech}\,}}(\varvec{V}_1)^\top ,...,{{\,\textrm{vech}\,}}(\varvec{V}_a)^\top )^\top$ and with empirical covariance matrices ${\widehat{\varvec{V}}}_i$ and $\widehat{\varvec{v}}=({\widehat{\varvec{v}}}_1^\top ,...,{\widehat{\varvec{v}}}_a^\top )^\top =({{\,\textrm{vech}\,}}({\widehat{\varvec{V}}}_1)^\top ,...,{{\,\textrm{vech}\,}}({\widehat{\varvec{V}}}_a)^\top )^\top$, it holds

$$\begin{aligned} \sqrt{N} \varvec{C}({\widehat{\varvec{v}}} -\varvec{v}){\mathop {\longrightarrow }\limits ^{{\mathcal {D}}}} \mathcal {N}_{ap}\left( \textbf{0}_{ap},\varvec{C}\varvec{\Sigma }\varvec{C}^\top \right) . \end{aligned}$$

(2)

Here, the covariance matrix is defined as $\varvec{\Sigma }=\bigoplus _{i=1}^a \frac{1}{k_i} \varvec{\Sigma }_i$, where $\bigoplus$ denotes the direct sum and $\varvec{\Sigma }_i={{\,\textrm{Cov}\,}}({{\,\textrm{vech}\,}}(\varvec{\epsilon }_{i1}\varvec{\epsilon }_{i1}^\top )^\top )$ for $i=1,\dots , a$. First, some additional matrices have to be defined to use this result for correlation matrices. Let $\varvec{e}_{k,p}=(\delta _{k \ell })_{\ell =1}^p$ define the p-dimensional vector, which contains a one in the k-th component and zeros elsewhere.

Moreover, we need a d-dimensional auxiliary vector $\varvec{a}=(a_1,...,a_d)$, given through $a_k=1+\sum _{j=1}^{k-1} (d+1-j)$, $k=1,...,d$. It contains the position of components in the half-vectorized matrix, which are the diagonal elements of the original matrix. In accordance with this, we define the $p_u$-dimensional vector $\varvec{b}$, which contains the numbers from one to p in ascending order without the elements from $\varvec{a}$. This vector $\varvec{b}$ contains the position of components in the half-vectorized matrix, which are non-diagonal elements.

With these vectors, we are able to define a $d\times d$ matrix $\varvec{H}=\varvec{1}_{d}\varvec{a}$ and the vectors $\varvec{h}_1={{\,\textrm{vech}\,}}^-(\varvec{H})$ and $\varvec{h}_2={{\,\textrm{vech}\,}}^-(\varvec{H}^\top )$. Finally, we can define the matrices

$$\begin{aligned} \varvec{M}_1=\sum _{\ell =1}^{p_u} \varvec{e}_{\ell ,p_u}(\varvec{e}_{{\varvec{h}_1}_{\ell },p}+\varvec{e}_{{\varvec{h}_2}_\ell ,p})^\top \quad \text { and } \quad \varvec{L}_p^u=\sum _{\ell =1}^{p_u} \varvec{e}_{\ell ,p_u}\ \varvec{e}_{{\varvec{b}}_{\ell },p}^\top . \end{aligned}$$

This allows us to formulate a connection between the ${{\,\textrm{vech}\,}}$ operator and the ${{\,\textrm{vech}\,}}^-$ operator, since the matrix $\varvec{L}_p^u$ fulfils $\varvec{L}_p^u {{\,\textrm{vech}\,}}(\varvec{A})={{\,\textrm{vech}\,}}^-(\varvec{A})$ for each arbitrary matrix $\varvec{A}\in \mathbb {R}^{d\times d}$. This matrix is comparable to the elimination matrix from Magnus and Neudecker (1980) and adapted to this special kind of half-vectorization.

With all these matrices, a connection can be found between $\sqrt{n_i}({\widehat{\varvec{v}}}_i-\varvec{v}_i)$ and $\sqrt{n_i}({\widehat{\varvec{r}}}_i-\varvec{r}_i)$, which allows getting the requested result by applying (2). The approach to connect vectorized correlation and vectorized covariance is based on Browne and Shapiro (1986) and Nel (1985) and adapted to the current more general setting.

Theorem 3.1

With the previously defined matrices $\varvec{L}_{p}^u$, $\varvec{M}_1$ and

$$\begin{aligned} \varvec{M}(\varvec{v}_i,\varvec{r}_i):=\left[ \varvec{L}_p^u-\frac{1}{2}{\text {diag}}(\varvec{r}_i)\varvec{M}_1 \right] {\text {diag}}({{\,\textrm{vech}\,}}((v_{i11},...,v_{i dd})^\top (v_{i11},...,v_{i dd})))^{-\frac{1}{2}}, \end{aligned}$$

it holds

$$\begin{aligned} \sqrt{n_i}({\widehat{\varvec{r}}}_i-\varvec{r}_i)=\varvec{M}(\varvec{v}_i,\varvec{r}_i)\sqrt{n_i} ({\widehat{\varvec{v}}}_i-\varvec{v}_i)+\scriptstyle \mathcal {O}\textstyle _P(1). \end{aligned}$$

Thus,

$$\begin{aligned} \sqrt{n_i}({\widehat{\varvec{r}}}_i-\varvec{r}_i){\mathop {\longrightarrow }\limits ^{{\mathcal {D}}}}\mathcal {N}_{p_u}(\textbf{0}_{p_u},\underbrace{\varvec{M}(\varvec{v}_i,\varvec{r}_i)\varvec{\Sigma }_i\varvec{M}(\varvec{v}_i,\varvec{r}_i)^\top }_{=:\varvec{\Upsilon }_i}) \end{aligned}$$

and if Assumption (A1) is fulfilled also

$$\begin{aligned} \sqrt{N}({\widehat{\varvec{r}}}-\varvec{r}){\mathop {\longrightarrow }\limits ^{{\mathcal {D}}}}\mathcal {N}_{a p_u}\left( \textbf{0}_{a p_u},\bigoplus \nolimits _{i=1}^a {\kappa _i}^{-1}\varvec{\Upsilon }_i\right) =\mathcal {N}_{a p_u}(\textbf{0}_{ap_u},\varvec{\Upsilon }). \end{aligned}$$

Remark 3.1

The asymptotic normality of $\sqrt{n_i}({\widehat{\varvec{r}}}_i-\varvec{r}_i)$ was also shown for similar statistics in the past. But through the existing relation between $\sqrt{n_i}({\widehat{\varvec{v}}}_i-\varvec{v}_i)$ and $\sqrt{n_i}({\widehat{\varvec{r}}}_i-\varvec{r}_i)$ it is, for example, possible to express $\varvec{\Upsilon }$ as a function of $\varvec{\Sigma }$, which allows to construct an estimator ${\widehat{\varvec{\Upsilon }}}$ using ${\widehat{\varvec{\Sigma }}}$. In Sects. 5 and 6 we show that this relation provides further opportunities.

To use this result, we have to estimate the matrices $\varvec{\Upsilon }_1,...,\varvec{\Upsilon }_a$, which is done with

$$\begin{aligned} {\widehat{\varvec{\Upsilon }}}_i=\varvec{M}({\widehat{\varvec{v}}}_i,{\widehat{\varvec{r}}}_i){\widehat{\varvec{\Sigma }}}_i\varvec{M}({\widehat{\varvec{v}}}_i,{\widehat{\varvec{r}}}_i)^\top , \end{aligned}$$

and ${\widehat{\varvec{\Upsilon }}}:=\bigoplus _{i=1}^a \frac{N}{n_i}{\widehat{\varvec{\Upsilon }}}_i$. To this end, ${\widehat{\varvec{\Sigma }}}_i$ has to be a consistent estimator for $\varvec{\Sigma }_i$. This is fulfilled, e.g. for the estimator from Sattler et al. (2022), given through

$$\begin{aligned} \frac{1}{n_i-1} \sum \limits _{k=1}^{n_i}\left[ {{\,\textrm{vech}\,}}\left( {\widetilde{\varvec{X}}}_{ik}{\widetilde{\varvec{X}}}_{ik}^\top - \sum \limits _{\ell =1}^{n_i}\frac{{\widetilde{\varvec{X}}}_{i\ell }{\widetilde{\varvec{X}}}_{i\ell }^\top }{n_i}\right) \right] \left[ {{\,\textrm{vech}\,}}\left( {\widetilde{\varvec{X}}}_{ik}{\widetilde{\varvec{X}}}_{ik}^\top - \sum \limits _{\ell =1}^{n_i}\frac{{\widetilde{\varvec{X}}}_{i\ell }{\widetilde{\varvec{X}}}_{i\ell }^\top }{n_i}\right) \right] ^\top , \end{aligned}$$

with ${\widetilde{\varvec{X}}}_{ik}:=\varvec{X}_{ik}-{\overline{\varvec{X}}}_i$. As continuous functions of consistent estimators, the estimators ${\widehat{\varvec{\Upsilon }}}_i$ are consistent. With this asymptotic result, test statistics based on quadratic forms can be formulated through:

Theorem 3.2

Let $\varvec{E}_N \in \mathbb {R}^{m\times m}$ fulfilling $\varvec{E}_N {\mathop {\longrightarrow }\limits ^{\mathcal {P}}} \varvec{E}$, where $\varvec{E}\in \mathbb {R}^{m\times m}$ is symmetric. Then, under the null hypothesis $\mathcal {H}_0^r:\varvec{C}\varvec{r}=\varvec{\zeta }$, the quadratic form ${\widehat{Q}}_{\varvec{r}}$, defined by

$$\begin{aligned} {\widehat{Q}}_{\varvec{r}}=N\left[ \varvec{C}{\widehat{\varvec{r}}} - \varvec{\zeta }\right] ^\top \varvec{E}_N\left[ \varvec{C}{\widehat{\varvec{r}}} - \varvec{\zeta }\right] \end{aligned}$$

has asymptotically a “weighted $\chi ^2$-distribution”, i.e. for $N\rightarrow \infty$ it holds that

$$\begin{aligned} {\widehat{Q}}_{\varvec{r}}{\mathop {\longrightarrow }\limits ^{\mathcal {D}}} \sum \limits _{\ell =1}^{ap_u} \lambda _\ell B_\ell , \end{aligned}$$

where $\lambda _\ell , \ell =1,\dots , a p_u,$ are the eigenvalues of $\varvec{\Upsilon }^{1/2}\varvec{C}^\top \varvec{E}\varvec{C}\varvec{\Upsilon }^{1/2}$ and $B_\ell {\mathop { \sim }\limits ^{i.i.d.}} \chi _1^2$.

Thus, quadratic-form-type test statistics can be formulated, similar to Sattler et al. (2022) also for the vectorized correlation matrix. Here, we often consider symmetric matrices $\varvec{E}_N$, which can be written as function of $\varvec{C}$ and ${\widehat{\varvec{\Upsilon }}}$ fullfilling $\varvec{E}_N(\varvec{C},{\widehat{\varvec{\Upsilon }}})=\varvec{E}_N{\mathop {\longrightarrow }\limits ^{\mathcal {P}}}\varvec{E}=\varvec{E}(\varvec{C},\varvec{\Upsilon })$. Examples cover:

$$\begin{aligned} \begin{array}{lrl} &{}\textrm{ATS}_{\varvec{r}}\hspace{-0.1cm}&{}={N}\left[ \varvec{C}({\widehat{\varvec{r}}}-\varvec{r})\right] ^\top \left[ \varvec{C}({\widehat{\varvec{r}}}-\varvec{r})\right] /{\text {tr}}(\varvec{C}\widehat{\varvec{\Upsilon }}\varvec{C}^\top ),\\ &{}\textrm{WTS}_{\varvec{r}}\hspace{-0.1cm}&{}={N}\left[ \varvec{C}({\widehat{\varvec{r}}}-\varvec{r})\right] ^\top (\varvec{C}\widehat{\varvec{\Upsilon }}\varvec{C}^\top )^+\left[ \varvec{C}({\widehat{\varvec{r}}}-\varvec{r})\right] .\end{array} \end{aligned}$$

This leads to an asymptotic valid test $\varphi _{WTS_{\varvec{r}}}=1\hspace{-0.7ex}1\{ {WTS_{\varvec{r}}} \notin (-\infty ,\chi ^2_{{{\,\textrm{rank}\,}}(\varvec{C});1-\alpha }]\}$, in case of $\varvec{\Upsilon }>0$. This is, however, hard to verify due to its complex structure. We therefore do not treat the WTS in the following.

Conversely, the ATS is no asymptotic pivot, but the simulation results from Sattler et al. (2022) suggest to use its Monte Carlo version. Hereto, the according matrices from Theorem 3.2 were estimated, and by this, we also get the estimated eigenvalues. By generating $B_1,...B_{ap_u}$, the weighted sum can be calculated, and by repeating this frequently (e.g. W=10,000 times), the required $\alpha$ quantiles of the weighted $\chi _1^2$ distribution can be estimated, denoted by $q_{\alpha }^{\textrm{MC}}$. For example, this gives us the test $\varphi _{\textrm{ATS}_{\varvec{r}}}:=1\hspace{-0.7ex}1\{ \textrm{ATS}_{\varvec{r}} \notin (-\infty ,q_{1-\alpha }^{\textrm{MC}}]\}$, and a similar approach can be used for all quadratic forms fulfilling Theorem 3.2.

4 Resampling procedures

A resampling procedure may be useful, on the one hand, for a better small sample approximation and, on the other hand, for quadratic forms with critical values that are difficult to calculate. Since the simulations from Sattler et al. (2022) showed clear advantages of the parametric bootstrap, we focus on this approach but also present a wild bootstrap approach in the supplement. For every group $\varvec{X}_{i 1},..., \varvec{X}_{i n_i}$, $i=1,...,a$, we calculate the covariance matrix ${\widehat{\varvec{\Upsilon }}}_i$. With this covariance matrix, we generate i.i.d. random vectors $\varvec{Y}_{i 1}^\dagger ,...,\varvec{Y}_{i n_i}^\dagger$ ${\sim } {\mathcal {N}}_{p_u}(\textbf{0}_{p_u},{\widehat{\varvec{\Upsilon }}}_i)$ which are independent of the realizations and calculate their sample covariances ${\widehat{\varvec{\Upsilon }}}_i^\dagger$, respectively, ${\widehat{\varvec{\Upsilon }}}^\dagger :=\bigoplus _{i=1}^a\frac{N}{n_i} {\widehat{\varvec{\Upsilon }}}_i^\dagger$. For these random vectors, we now consider the asymptotic distribution.

Theorem 4.1

If Assumption (A1) is fulfilled, it holds: Given the data, the conditional distribution of

• (a) $\sqrt{N}\ {\overline{\varvec{Y}}}_i^\dagger$, for $i=1,...,a$, converges weakly to $\mathcal {N}_{p_u}\left( \textbf{0}_{p_u},{\kappa _i}^{-1}\varvec{\Upsilon }_i\right)$ in probability.

• (b) $\sqrt{N}\ {\overline{\varvec{Y}}}^\dagger$ converges weakly to $\mathcal {N}_{ap_u}\left( \textbf{0}_{a p_u}, \varvec{\Upsilon }\right)$ in probability.

Moreover, we have ${\widehat{\varvec{\Upsilon }}}_i^\dagger {\mathop {\rightarrow }\limits ^{\mathcal {P}}} \varvec{\Upsilon }_i$ and ${\widehat{\varvec{\Upsilon }}}^\dagger {\mathop {\rightarrow }\limits ^{\mathcal {P}}} \varvec{\Upsilon }$. Thus, the unknown covariance matrices can be estimated through these estimators.

In consequence of Theorem 4.1, it is reasonable to calculate the bootstrap version of the previous quadratic forms,

$$\begin{aligned} \begin{array}{cl} Q_{\varvec{r}}^\dagger &{}=N[ \varvec{C}{\overline{\varvec{Y}}}^\dagger ]^\top {\varvec{E}}[ \varvec{C}\ {\overline{\varvec{Y}}}^\dagger ]\quad \text { resp. }\quad Q_{\varvec{r}}^\dagger =N[ \varvec{C}{\overline{\varvec{Y}}}^\dagger ]^\top \varvec{E}_N(\varvec{C},{\widehat{\varvec{\Upsilon }}}^\dagger )[ \varvec{C}\ {\overline{\varvec{Y}}}^\dagger ]. \\ \end{array} \end{aligned}$$

The first can be used if the limiting matrix $\varvec{E}=\varvec{E}(\varvec{C},\varvec{\Upsilon })$ of $\varvec{E}_N(\varvec{C},{\widehat{\varvec{\Upsilon }}})$ is known. In the second version $\varvec{E}=\varvec{E}(\varvec{C},\varvec{\Upsilon })$ is estimated via $\varvec{E}_N=\varvec{E}_N(\varvec{C},{\widehat{\varvec{\Upsilon }}}^\dagger )$ which is reasonable if from $\varvec{A}_n{\mathop {\rightarrow }\limits ^{\mathcal {P}}}\varvec{A}$, for random matrices $\varvec{A}_n$ and $\varvec{A}$ it follows $\varvec{E}_N(\varvec{C},\varvec{A}_n) {\mathop {\rightarrow }\limits ^{\mathcal {P}}} \varvec{E}(\varvec{C},\varvec{A})$ [(see e.g. van der Vaart and Wellner (1996)]. This is fulfilled, if the function is continuous in its second component which holds for the trace operator used in the ATS and which we assume in what follows.

The bootstrap versions always approximate the null distribution of ${\widehat{Q}}_{\varvec{r}}$, as established below.

Corollary 4.1

For each parameter vector $\varvec{r}\in \mathbb {R}^{a p_u}$ and $\varvec{r}_0\in \mathbb {R}^{a p_u}$ with $\varvec{C}\varvec{r}_0=\varvec{\zeta }$, under Assumption (A1), we have

$$\begin{aligned} \begin{array}{l} \sup \limits _{x\in \mathbb {R}}\big |P_{\varvec{r}}(Q_{\varvec{r}}^\dagger \le x|\varvec{X})-P_{\varvec{r}_0}({\widehat{Q}}_{\varvec{r}}\le x)\big |{\mathop {\longrightarrow }\limits ^{{\mathcal {P}}}}0,\\ \end{array} \end{aligned}$$

where $P_{\varvec{r}}$ denotes the (un)conditional distribution of the test statistic when $\varvec{r}$ is the true underlying vector.

This motivates the definition of bootstrap tests as $\varphi _{Q_{\varvec{r}}}^\dagger :=1\hspace{-0.7ex}1\{Q_{\varvec{r}}^\dagger \notin (-\infty ,c_{Q_{\varvec{r}}^\dagger ,1-\alpha }]\}$, where $c_{Q_{\varvec{r}}^\dagger , 1-\alpha }$ denotes the conditional quantile of $Q_{\varvec{r}}^\dagger$. The above results ensure that these tests are of asymptotic level $\alpha$, and we will use it for the ATS.

Fisher z-transformed vectors are often used in the analysis of correlation matrices instead of the original vectorized correlation matrices. Although the root of this approach is the distribution of the Fisher z-transformed correlation in the case of normally distributed observations, it is also used for tests without this distributional restriction, see e.g. Steiger (1980). In principle, we could also consider our tests together with the transformed vector. This approach assumes that all components of $\varvec{\zeta }$ differ from one, which is always possible to ensure. We can define tests based on the transformation for each of our quadratic forms, including the tests based on bootstrap or Monte Carlo simulations. Our simulations showed that the tests based on this transformation have more liberal behaviour than the original one, which was also mentioned in Omelka and Pauly (2012) for the case of bivariate permutation tests. Since all of our test statistics were already a bit liberal, it is not useful to consider these versions further. However, some details on this are given in the supplement. Instead, we propose an additional Taylor approximation of higher order as described below.

5 Higher order of Taylor approximation

The main result of Sect. 3 is the connection between the vectorized empirical covariance matrix and the vectorized empirical correlation matrix given through

$$\begin{aligned}\sqrt{n_i}({\widehat{\varvec{r}}}_i-\varvec{r}_i)=\varvec{M}(\varvec{v}_i,\varvec{r}_i)\sqrt{n_i} ({\widehat{\varvec{v}}}_i-\varvec{v}_i)+\scriptstyle \mathcal {O}\textstyle _P(1).\end{aligned}$$

Since this is based on a Taylor approximation, it leads to the question of whether a higher order of approximation could be useful here. In this way, we get

$$\begin{aligned} \sqrt{n_i}({\widehat{\varvec{r}}}_i-\varvec{r}_i)=\varvec{M}({\widehat{\varvec{v}}}_i,{\widehat{\varvec{r}}}_i) \varvec{Y}_i+ f_{{\widehat{\varvec{v}}}_i,{\widehat{\varvec{R}}}_i}(\varvec{Y}_i)/\sqrt{n_i}+\scriptstyle \mathcal {O}\textstyle _P\left( \sqrt{{n_i^{-1}}}\right) \end{aligned}$$

(3)

with $\varvec{Y}_i\sim \mathcal {N}_{p}\left( \textbf{0}_{p},\varvec{\Sigma }_i\right)$ and a function $f_{{\widehat{\varvec{v}}}_i,{\widehat{\varvec{R}}}_i}:\mathbb {R}^p\rightarrow \mathbb {R}^{p_u}$. This equation’s derivation, together with the complex concrete form of the function $f_{{\widehat{\varvec{v}}}_i,{\widehat{\varvec{R}}}_i}$, can be found in the supplementary material. Although the part $f_{{\widehat{\varvec{v}}}_i,{\widehat{\varvec{R}}}_i}(\varvec{Y}_i)/\sqrt{n_i}$ is asymptotically negligible, for small sample sizes, it can affect the performance of the corresponding test. For this purpose, we propose an additional Monte Carlo-based approach with this Taylor approximation. Thereto for each group, we generate $\varvec{Y}_i\sim \mathcal {N}_{p}(\textbf{0}_{p},{\widehat{\varvec{\Sigma }}}_i)$ and transform it to $\varvec{Y}_i^{\textrm{Tay}}:=\varvec{M}({\widehat{\varvec{v}}}_i,{\widehat{\varvec{r}}}_i) \varvec{Y}_i+ f_{{\widehat{\varvec{v}}}_i,{\widehat{\varvec{R}}}_i}(\varvec{Y}_i)/\sqrt{n_i}$. So with the pooled vector $\varvec{Y}^{\textrm{Tay}}=(n_1^{-1/2}{\varvec{Y}_1^{\textrm{Tay}}}^\top ,....,n_a^{-1/2}{\varvec{Y}_a^{\textrm{Tay}}}^\top )^\top$, we get a version of this quadratic form by calculating

$$\begin{aligned} {Q_{\varvec{r}}^{\textrm{Tay}} =N[ \varvec{C}\varvec{Y}^{\textrm{Tay}} ]^\top \varvec{E}_N(\varvec{C},{\widehat{\varvec{\Upsilon }}})[ \varvec{C}\varvec{Y}^{\textrm{Tay}}]}. \end{aligned}$$

If we repeat this frequently enough, an asymptotic correct level $\alpha$ test can be constructed by comparing ${\widehat{Q}}_{\varvec{r}}$ with the empirical $(1-\alpha )$ quantile of $Q_{\varvec{r}}^{\textrm{Tay}}$. Since there it is only necessary to calculate ${\widehat{\varvec{\Upsilon }}}$ one time, this approach is clearly less time-consuming than the corresponding bootstrap approaches.

It would also be possible to use a Taylor approximation of higher order. Since the transformation gets more complex and our simulations suggest that this only affects very small sample sizes, we renounce this here.

6 Combined tests for variances and correlations

The equality of two covariance matrices and the equality of two correlation matrices are interesting null hypotheses that are closely related. In this section, we exemplify how our methodology extends to a simultaneous comparison of variances and correlations. To this end, we combine the above results with those from Sattler et al. (2022) to develop a so-called multiple contrast test. For this, we define the statistic

$$\begin{aligned} \varvec{T}=\begin{pmatrix} T_1\\ \vdots \\ T_p \end{pmatrix}= \sqrt{N}\left( \begin{pmatrix} {\widehat{V}}_{1 11}\\ {\widehat{V}}_{1 22}\\ \vdots \\ {\widehat{V}}_{1 dd}\\ {\widehat{\varvec{r}}}_1 \end{pmatrix}- \begin{pmatrix} {\widehat{V}}_{2 11}\\ {\widehat{V}}_{2 22}\\ \vdots \\ {\widehat{V}}_{2 dd}\\ {\widehat{\varvec{r}}}_2 \end{pmatrix}\right) \end{aligned}$$

which fulfils $\varvec{T}{\mathop {\rightarrow }\limits ^{\mathcal {D}}}\mathcal {N}_p(\textbf{0}_p,\varvec{\Gamma })$ under the null hypothesis $\mathcal {H}_0^{{\varvec{v}}}:\varvec{V}_1=\varvec{V}_2$. The concrete form of the asymptotic covariance matrix $\varvec{\Gamma }$ and its derivation can be found in the online supplement. In case its diagonal elements are positive, i.e. $\Gamma _{11},...,\Gamma _{pp}>0$, we consider the vector of studentized test statistics ${\widetilde{\varvec{T}}}:= {\text {diag}}(\Gamma _{11},...,\Gamma _{pp})^{-1/2} \varvec{T}$. Under the null hypothesis of equal covariances, ${\widetilde{\varvec{T}}}$ is asymptotically normal distributed with expectation vector $\textbf{0}_p$ and covariance/correlation matrix ${\widetilde{\varvec{\Gamma }}}:= {\text {diag}}(\Gamma _{11},...,\Gamma _{pp})^{-1/2}\varvec{\Gamma }{\text {diag}}(\Gamma _{11},...,\Gamma _{pp})^{-1/2}$. Following the concept of multiple contrast tests (see e.g. Bretz et al. 2001 or Konietschke et al. 2013 for more details), we now consider $\max (|{\widetilde{T}}_{1}|,....,|{\widetilde{T}}_{p}|)$ as test statistic and use the two-sided $(1-\alpha )$ equicoordinate quantile of the above limiting distribution $\mathcal {N}_p(\textbf{0}_p,{\widetilde{\varvec{\Gamma }}})$ as the critical value. Denoting this as $z_{1-\alpha ,2,{\widetilde{\varvec{\Gamma }}}}$, we obtain an asymptotic level $\alpha$ multiple contrast test by $\max (|{\widetilde{T}}_{1}|,....,|{\widetilde{T}}_{p}|)\ge z_{1-\alpha ,2,{\widetilde{\varvec{\Gamma }}}}$. This multiple contrast test fulfils the desired properties, i.e. it allows us to simultaneously infer the hypotheses of equal covariances and equal correlations. In fact, if $\max (|{\widetilde{T}}_{d+1 }|,....,|{\widetilde{T}}_{p}|)\ge z_{1-\alpha ,2,{\widetilde{\varvec{\Gamma }}}}$, we can conclude that both groups have significantly different dependence structures and, therefore, neither equal covariance matrices nor equal correlation matrices. However, if $\max (|{\widetilde{T}}_{d+1 }|,....,|{\widetilde{T}}_{p}|)< z_{1-\alpha ,2,{\widetilde{\varvec{\Gamma }}}}$ but $\max (|{\widetilde{T}}_{1}|,....,|{\widetilde{T}}_{d}|)\ge z_{1-\alpha ,2,{\widetilde{\varvec{\Gamma }}}}$, this indicates that both groups have the same dependence structure but different variances, i.e. we can (only) conclude that they have significantly different covariance matrices. Moreover, the information which components of ${\widetilde{\varvec{T}}}$ exceed $z_{1-\alpha ,2,{\widetilde{\varvec{\Gamma }}}}$, in absolute value, helps to clarify where the departures from $\mathcal {H}_0$ might come from. We note that in all of these considerations, we use the same critical value $z_{1-\alpha ,2,{\widetilde{\varvec{\Gamma }}}}$ as common with multiple contrast tests.

Unfortunately, the condition $\Gamma _{11},...,\Gamma _{pp}>0$ is difficult to verify. A bootstrap approach can again resolve this, as was done in Friedrich and Pauly (2017) or Umlauft et al. (2019). However, we introduce an alternative Monte Carlo approach because it is easier to explain and already shows good small sample approximations as will be demonstrated in Sect. 7. To this end, we use that with matrix $\varvec{A}\in \mathbb R^{d\times p}$ given by $\varvec{A}=\sum _{\ell =1}^{d} \varvec{e}_{\ell ,d}\ \varvec{e}_{{\varvec{a}}_{\ell },p}^\top$ it holds that

$$\begin{aligned} \sqrt{n_i}\left( \begin{pmatrix} {\widehat{V}}_{i 11}\\ {\widehat{V}}_{i 22}\\ \vdots \\ {\widehat{V}}_{i dd}\\ {\widehat{\varvec{r}}}_i \end{pmatrix}- \begin{pmatrix} V_{i 11}\\ V_{i 22}\\ \vdots \\ V_{i dd}\\ \varvec{r}_i \end{pmatrix}\right) = \begin{pmatrix} \varvec{A}\\ \varvec{M}(\varvec{v}_i,\varvec{r}_i) \end{pmatrix} \varvec{Y}_i+ \frac{1}{\sqrt{n_i}}\begin{pmatrix}\textbf{0}_d\\ f_{{\widehat{\varvec{v}}}_i,{\widehat{\varvec{R}}}_i}(\varvec{Y}_i) \end{pmatrix}+\scriptstyle \mathcal {O}\textstyle _P(\sqrt{n_i^{-1}}) \end{aligned}$$

with $\varvec{Y}_i\sim \mathcal {N}_{p}(\textbf{0}_p,\varvec{\Sigma }_i)$. Based on the above expansion, we generate $\varvec{Y}_i\sim \mathcal {N}_{p}(\textbf{0}_{p},{\widehat{\varvec{\Sigma }}}_i)$ similarly to Sect. 5 and transform it to

$$\begin{aligned}\varvec{Y}_i^{\textrm{Tay}}:= \begin{pmatrix} \varvec{A}\\ \varvec{M}({\widehat{\varvec{v}}}_i,{\widehat{\varvec{r}}}_i) \end{pmatrix} \varvec{Y}_i+ \frac{1}{\sqrt{n_i}}\begin{pmatrix}\textbf{0}_d\\ f_{{\widehat{\varvec{v}}}_i,{\widehat{\varvec{R}}}_i}(\varvec{Y}_i) \end{pmatrix}.\end{aligned}$$

With this transformed vectors, we calculate $\varvec{T}^{1,\textrm{Tay}}=\sqrt{N}(n_1^{-1/2}\varvec{Y}_1^{\textrm{Tay}}-n_{2}^{-1/2}\varvec{Y}_2^{\textrm{Tay}})$, which has the same asymptotic distribution as $\varvec{T}$, and repeat this B times to get $\varvec{T}^{1,\textrm{Tay}},...,\varvec{T}^{B,\textrm{Tay}}$. To obtain an appropriate multiple contrast test based on these values, we follow Munko et al. (2023b) resp. Munko et al. (2023a), where a corresponding procedure for functional data was developed based on Buhlmann (1998). Thus, for $\ell =1,...,p$, we denote by $q_{\ell ,\beta }$ the empirical $\beta$ quantile of $T_\ell ^{1,\textrm{Tay}},..., T_\ell ^{B,\textrm{Tay}}$. To control the family-wise type-I-error rate by $\alpha$, the appropriate $\beta$ can be found through

$$\begin{aligned} {{\widetilde{\beta }}= \max \left( \beta \in \mathcal {B}\Big |\sum \limits _{b=1}^B \max \limits _{\ell =1,...,p}\frac{\left( 1-1\hspace{-0.7ex}1\left( q_{\ell ,\frac{\beta }{2}}\le T_\ell ^{b,\textrm{Tay}}\le q_{\ell ,1-\frac{\beta }{2}}\right) \right) }{B}\le \alpha \right) } \end{aligned}$$

with $\mathcal {B}=\left\{ 0,\frac{1}{B},..., \frac{B-1}{B}\right\}$. An asymptotic level-$\alpha$ test of the null hypothesis of equal correlation matrices then rejects the null if and only if

$$\begin{aligned} {\max \limits _{\ell =1,...,p}\left( 1-1\hspace{-0.7ex}1\left( q_{\ell , \frac{{\widetilde{\beta }}}{2}}\le T_\ell \le q_{\ell ,1-\frac{{\widetilde{\beta }}}{2}}\right) \right) =1} \end{aligned}$$

or equivalently if

$$\begin{aligned} {\max \limits _{\ell =1,...,p} \left( \max \left( \frac{T_\ell }{q_{\ell ,1-\frac{{\widetilde{\beta }}}{2}}},\frac{q_{\ell ,\frac{{\widetilde{\beta }}}{2}}}{T_\ell }\right) \right) >1.} \end{aligned}$$

Each component of the vector-valued test statistic $\varvec{T}$ is treated in the same way since the same ${\widetilde{\beta }}<\alpha$ is used. This procedure allows for the same conclusions about the reason for the rejection as the above approach based on the equicoordinate quantile.

Of course, this combined test could be generalized to compare more than two groups by using an appropriate Tukey-type contrast matrix, see e.g. Konietschke et al. (2013).

7 Simulations

We analyse the type-I-error rate and power for different hypotheses to investigate the performance. Here, we focus on hypotheses with an implemented algorithm to have an appropriate competitor. In the R-package psych by Revelle (2019) several of these tests are included, like $\varphi _{Jennrich}$ from Jennrich (1970) and $\varphi _{\textrm{Steiger}_{\textrm{Fz}}}$ from Steiger (1980) for equality of correlation matrices. Testing whether the correlation matrix is equal to the identity matrix can be investigated with $\varphi _{\textrm{Bartlett}}$ from Bartlett (1951) and again with $\varphi _{\textrm{Steiger}_{\textrm{Fz}}}$ resp. $\varphi _{\textrm{Steiger}}$. Hereby, $\varphi _{\textrm{Steiger}_{\textrm{Fz}}}$ is the same test statistic as $\varphi _{\textrm{Steiger}}$ but uses a Fisher z-transformation on the vectorized correlation matrices. Therefore, we consider the following hypotheses:

$A_{\varvec{r}}$::

Homogeneity of correlation matrices: ${\mathcal {H}}_0^{\varvec{r}}: \varvec{R}_1 = \varvec{R}_2$,

$B_{\varvec{r}}$::

Diagonal structure of the covariance matrix ${\mathcal {H}}_0^{\varvec{r}}: \varvec{R}_1 = \varvec{I}_p\text { resp. }\varvec{r}_1=\textbf{0}_{p_u}$,

with $\alpha =0.05$. Further hypotheses are investigated in the supplementary material together with other settings and dimensions. The hypothesis matrices are chosen as the projection matrices $\varvec{C}(A_{\varvec{r}})={\varvec{P}_2}\otimes \varvec{I}_{p_u}$ and $\varvec{C}(B_{\varvec{r}})=\varvec{I}_{p_u}$, while $\varvec{\zeta }$ is in both cases a zero vector with appropriate dimension. Based on this the results of Sattler and Zimmermann (2023) can also be simplified to be computational more efficient without affecting the results.

We use 1000 bootstrap steps for our parametric bootstrap, 10,000 simulation steps for the Monte Carlo approach and 10,000 runs for all tests to get reliable results. For $\varphi _{\textrm{Steiger}}$ and $\varphi _{\mathrm{Steiger_{Fz}}}$ from Revelle (2019), the actual test statistic is multiplied with the factor $({N-3})/{N}$. This approach is based on a specific result of the Fisher z-transformation of the correlation vector of normally distributed random vectors for small sample sizes. Asymptotically, this factor has no influence, but it is also used for $\varphi _{\textrm{Steiger}}$, where no Fisher z-transformation was done.

To get a better impression of the impact of such a multiplication, we also include our ATS with parametric bootstrap using such multiplication and denote this with an m for multiplication. This also simplifies the comparison of the tests under equal conditions. At last, we simulated Monte Carlo-based ATS using our Fisher z-transformation. We denote it by ATSFz, while an additional version ATSFz-m is simulated, which is formed by multiplication with the factor $(N-3)/N$.

To have a comparative setting to Sattler et al. (2022), we used d=5 and therefore $p_u=10$, while for one group, we have $n\in \{25,50,125,250\}$, and for two groups, we have $n_1=0.6\cdot N$ and $n_2=0.4\cdot N$ with $N \in \{50, 100, 250, 500\}$. We considered 5-dimensional observations generated independently according to the model $\varvec{X}_{ik} = \vec {\mu }_i + \varvec{V}^{1/2} \varvec{Z}_{ik}, i=1,\dots , a, k=1,\dots ,n_i$ with $(\vec {\mu }_1=(1^2,2^2,...,5^2)/4^\top ), (\vec {\mu }_2={\textbf {0}}_{5})$ and error terms based on

• A standardized centred t-distribution with 9 degrees of freedom.

• A standard normal distribution, i.e. $Z_{ikj} \sim \mathcal {N}(0,1).$

• A standardized centred skewed normal distribution with location parameter $\xi =0$, scale parameter $\omega =1$ and ${\gamma }=4$. The density of a skewed normal distribution is given through $\frac{2}{\omega } \varphi \left( \frac{x-\xi }{\omega }\right) \Phi \left( {\gamma }\left( \frac{x-\xi }{\omega }\right) \right)$, where $\varphi$ denotes the density of a standard normal distribution and $\Phi$ the according distribution function.

For $A_{\varvec{r}}$, we use $(\varvec{V}_{1})_{ij}=1-{|i-j|/2d}$ for the first group, and for the second group, we multiply this covariance matrix with ${\text {diag}}(1,1.2,...,1.8)$. Thus, we have a setting where the covariance matrices are different, but the correlation matrices are equal. To investigate $B_{\varvec{r}}$, we use the matrix, $\varvec{V}={\text {diag}}(1,1.2,...,1.8)$.

7.1 Type-I-error

The results of hypothesis $A_{\varvec{r}}$ can be seen in Table 1 for the Toeplitz covariance matrix. Here, the values in the $95\%$ binomial interval [0.0458, 0.0543] are printed in bold. It is interesting to note that the type-I-error rate of $\varphi _{Steifer_{Fz}}$ and $\varphi _{Jennrich}$ differs more and more from the $5\%$ rate for increasing sample sizes. Therefore, these tests should not be used, at least for our setting. In contrast, all of our tests are too liberal but show a substantially better type-I-error rate. Moreover, these tests fulfil Bradley’s liberal criterion (from Bradley 1978) for N larger than 50. This criterion is often consulted by applied statisticians, for example, in quantitative psychology. It states that a procedure is ‘acceptable’ if the type-I-error rate is between $0.5\alpha$ and $1.5\alpha$.

Similar to the results for covariance matrices, the bootstrap version has slightly better results than Monte Carlo-based tests, while the error rates get closer to the nominal level for larger sample sizes. In each setting, the Monte Carlo-based ATS formulated for Fisher z-transformed vectors has a better performance than the classical one, especially for smaller sample sizes.

Table 1 Simulated type-I-error rates ($\alpha =5\%$) in scenario $A_r$ ($\mathcal {H}_0^{\varvec{r}}:\varvec{R}_{1}=\varvec{R}_{2}$) for ATS and Steiger’s test.

It can be seen that a correction factor, like $(N-3)/N$, which was used for ATS-Par-m, clearly improves the small sample performance. In contrast to the results from Sattler et al. (2022), for testing correlation matrices, the small sample approximation seems a bit worse, making such a correction factor useful. The best performance for smaller sample sizes can be seen for our Taylor-based Monte Carlo approach, which has for $N>50$ an error rate within the $95\%$ interval. Therefore, for this setting, we recommend ATS-Tay, while for larger sample size, ATS-Par-m and ATSFz-m also show good results.

For hypothesis $B_{\varvec{r}}$, the results are included in Table 2. Here, our Taylor-based approach has slightly conservative values, and therefore ATS-Para-m and ATSFz-m have the best results of our test statistics, while the results are slightly better than for hypothesis $A_{\varvec{r}}$. For example, the number of values in the $95\%$ binomial interval [0.0458, 0.0543], printed bold, clearly increases. With the correction factor, these tests have a better type-I-error rate than $\varphi _{\textrm{Steiger}}$ in all settings and are comparable to $\varphi _{\textrm{Steiger}_{\textrm{Fz}}}$.

Table 2 Simulated type-I-error rates ($\alpha =5\%$) in scenario $B_{\varvec{r}}$ ($\mathcal {H}_0^{\varvec{r}}:\varvec{r}_{1}=\textbf{0}_{10}$) for ATS, Steiger’s and Bartlett’s test.

Nevertheless, $\varphi _{\textrm{Bartlett}}$ is a test only developed for this special hypothesis and therefore has an excellent error rate through all distributions. But in addition to the type-I error rate, also other properties are highly relevant.

7.2 Power

Fig. 1

Simulated power curves of different tests for the hypothesis $A_{\varvec{r}}$ (${\mathcal {H}}_0^{\varvec{r}}: \varvec{R}_1 = \varvec{R}_2$) above, and hypothesis $B_{\varvec{r}}$ (${\mathcal {H}}_0^{\varvec{r}}: \varvec{r}_1 = \textbf{0}_{10}$) below, for a five-dimensional skewed normal distribution. For hypothesis $A_{\varvec{r}}$, it holds $n_1=60$, $n_2=40$ and the covariance matrix is $(\varvec{V}_2)_{ij}=1-{|i-j|/2d}$ resp. $\varvec{V}_1=\varvec{V}_2+\delta \varvec{J}_5$. The covariance matrix for hypothesis $B_{\varvec{r}}$ is $\varvec{V}=\varvec{I}_5+\delta \varvec{J}_5$ and $n_1=50$

The ability to detect deviations from the null hypothesis is also an important test criterion. To this aim, we also investigate the power of some of the tests mentioned above. We choose a quite simple kind of alternative suitable for our situation. As covariance matrix, we consider $\varvec{V}_1+\delta \cdot \varvec{J}_d$ for $\delta \in [0,3.5]$ in hypothesis $A_{\varvec{r}}$ and for $\delta \in [0,0.75]$ in hypothesis $B_{\varvec{r}}$. The reason for this considerable difference in the $\delta$ range is that for hypothesis $B_{\varvec{r}}$, the second summand changes the setting from uncorrelated to correlated. For hypothesis $A_{\varvec{r}}$, it just increases the correlations, which is clearly more challenging to detect. Due to computational reasons, we simulate only one sample size, which is $N=100$ resp. $n_1=50$ and consider error terms based on skewed normal distribution, while results for the gamma distribution can be found in the supplementary material. We simulate only the tests with good results for their type-I-error rate, which were for $A_{\varvec{r}}$ $\varphi _{\textrm{ATS}_{\varvec{r}}^\dagger }$ and $\varphi _{\textrm{ATS}_{\varvec{r}}-\textrm{Tay}}$ as well as $\varphi _{\textrm{SteigerFZ}}$ as competitor, despite its performance in Table 1. Because of the similarity of the results from the parametric bootstrap and the more classical Monte Carlo-based approach, we do not consider further test statistics here. For hypothesis $A_{\varvec{r}}$, Fig. 1 shows that the Taylor approximation makes the test slightly less liberal, and therefore reduces the power. This effect can be seen as a shift and does not influence the slope. In general, the power of both approaches is quite good, also $\varphi _{\textrm{SteigerFZ}}$ has even higher power, which furthermore increases faster. But since this test becomes even more liberal for increasing sample size, this is not surprising and makes it for this setting not recommendable. Based on the results from Table 2 for hypothesis $B_{\varvec{r}}$, we consider$\varphi _{\textrm{ATS}_{\varvec{r}}^\dagger }$ and $\varphi _{\textrm{ATS}_{\varvec{r}}-\textrm{Tay}}$ as well as $\varphi _{\textrm{SteigerFz}}$ and $\varphi _{\textrm{Bartlett}}$, while the setting is the same. In Fig. 1 for hypothesis $B_{\varvec{r}}$, it can be seen that $\varphi _{\textrm{ATS}_{\varvec{r}}-\textrm{Tay}}$ has for smaller $\delta$ similar power as $\varphi _{\textrm{Bartlett}}$ which was specially developed for this hypothesis, while for larger deviation, the power of the Monte Carlo approach increases. Here, $\varphi _{\textrm{SteigerFZ}}$ has slightly less power than the parametric bootstrap due to the slightly liberal behaviour of the bootstrap approach.

The type-I error rate and the power for both hypotheses show that our developed tests are useful in many situations, although partially large sample sizes are necessary for good results. This is a known fact for testing hypotheses regarding correlation matrices, which was, for example, mentioned in Steiger (1980). Therefore, the results of ATS-Tay investigating $A_{\varvec{r}}$ for smaller sample sizes are even more convincing.

All in all, the results of this section, together with the additional results from the supplement, allow us to give some general recommendations. Since SteigerFz has a type-I-error rate of more than $9\%$ in Table 1, which also grows for increasing sample sizes, it is not useful apart from single hypotheses like $\mathcal {H}_0^{\varvec{r}}:\varvec{r}_{1}=\textbf{0}_{10}$. This hypothesis can be checked with Bartlett, which had good results but only allows this hypothesis.

On the contrary, for all considered hypotheses, ATS-Par-m and ATS lead to good results for moderate to large sample sizes, while they are liberal for small sample sizes. Such liberality was, for example, also mentioned in Perreault et al. (2022) for tests based on Kendall’s $\tau$. As intended, the bootstrap improves the behaviour for smaller sample sizes, but not enough. In case of small sample sizes, the Taylor-based approach is recommended as it exhibited good small sample performance in all settings. Only for larger sample sizes, it is outperformed by ATS-Par-m.

8 Illustrative data analysis

To illustrate the method, we take a closer look at the EEG data set from the R-package manova.rm by Friedrich et al. (2019). In this study from Staffen et al. (2014), conducted at the University Clinic of Salzburg (Department of Neurology), electroencephalography (EEG) data were measured from 160 patients with different diagnoses of impairments. These are Alzheimer’s disease (AD), mild cognitive impairment (MCI), and subjective cognitive complaints (SCC). Thereby, the last diagnosis can be differentiated between subjective cognitive complaints with minimal cognitive dysfunction (SCC+) and without (SCC−).

MANOVA-based comparisons were already made in Bathke et al. (2018). However, covariance and correlation comparisons were only made in a descriptive way. We now complement their analyses. In Table 3, the number of patients divided by sex and diagnosis can be found. Since in Bathke et al. (2018) and Sattler et al. (2022) no distinction between SCC+ and SCC− was made, we consider both together as diagnosis SCC.

Table 3 Number of observations for the different factor level combinations of sex and diagnosis

The observation vector’s dimension is $d=6$, since there are two kinds of measurements (z-score for brain rate and Hjorth complexity) and three different electrode positions (frontal, temporal, and central), and therefore $p_u=15$. For the evaluation of our results, we should keep in mind that all sample sizes are rather small in relation to this dimension. The considered hypotheses are:

• (a) Homogeneity of correlation matrices between different diagnoses,

• (b) Homogeneity of correlation matrices between different sexes,

while we will denote the corresponding hypothesis regarding the covariance matrix with $\mathcal {H}_0^{\varvec{v}}$.

In Sattler et al. (2022), homogeneity of covariance matrices between different diagnoses as well as different sexes were investigated. Here, we consider the more general hypothesis of equal correlation matrices between the diagnoses and the sexes. Thereby, it is interesting to compare the results from the homogeneity of covariance matrices with those from testing the homogeneity of correlation matrices. We expect higher p values for equality of correlation through the larger hypothesis, but each rejection of equal correlation matrices directly allows us to reject the corresponding equality of covariance matrices. In Table 4 for both hypotheses, the p values for the ATS with parametric bootstrap are displayed, while for equality of correlations, we additionally use our test based on the Taylor-based Monte Carlo approach. For all considered bootstrap tests, 10,000 bootstrap runs are done, as well as 10,000 Monte Carlo steps.

Table 4 P-values of different ATS for testing equality of correlation matrices and equality of covariance matrices

Interestingly, for two hypotheses, the p value ATS-Par for equal correlation matrices is rejected at level $5\%$, while we could not reject the smaller hypothesis of equal covariance matrices. But for both hypotheses, the sample sizes are rather small with $N<40$. Our simulation results for $d=5$ showed that the ATS with parametric bootstrap is too liberal for small sample sizes, which might be the reason why the larger hypotheses can be rejected, and the smaller ones can not. But also ATS-Tay, which had a better small sample performance, rejected $\mathcal {H}_0^{\varvec{r}}$ one time, while $\mathcal {H}_0^{\varvec{v}}$ was not rejected. Moreover, it can be seen that the difference between some hypotheses is relatively small, like for the first three hypotheses, but it can also be quite large as for the comparison of women with AD and with SCC. This shows that from a rejection of $\mathcal {H}_0^{\varvec{v}}$, no conclusion on $\mathcal {H}_0^{\varvec{r}}$ can be drawn.

Due to the small sample size in relation to the dimension of the vectorized correlation matrix $p_u=15$, even the results of ATS-Tay are a bit liberal. But nevertheless, the corresponding rejections allow various ideas for further investigations.

9 Conclusion & Outlook

In the present paper, a series of new test statistics was developed to check general null hypotheses formulated in terms of correlation matrices. The proposed method can be used for many popular quadratic forms, and the low restrictions allow their application for a variety of settings. In fact, existing procedures have more restrictive assumptions or could only be used for special hypotheses or settings. The diversity of possible null hypotheses, these low restrictions and the easy possibility of expansion, like using a Fisher z-transformation, make our approach attractive.

We proved the asymptotic normality of the estimation error of the vectorized empirical correlation matrix under the assumption of finite fourth moments of all components. Based on this, test statistics from a quite general group of quadratic forms were presented, and a bootstrap technique was developed to match their asymptotic distribution. To investigate the properties of the corresponding bootstrap test, an extensive simulation study was done. This also allows checking our test statistic based on a Fisher z-transformation. Here, hypotheses for one and two groups were considered, and the type-I-error control and the power to detect deviations from the null hypothesis were compared to existing test procedures. The developed tests outperform existing procedures for some hypotheses, while they offer good and interesting alternatives for others. Also, it is a known fact that a large sample size is required for testing correlations. Here, for group sample sizes larger than 50, Bradley’s liberal criterion was often fulfilled. Especially our Taylor-based approach was convincing for small sample sizes with multiple groups. An illustrative data analysis completed our investigations.

In future research, we will take a closer look at our newly proposed combined test for simultaneously testing the hypotheses of equal covariance matrices and correlation matrices. Thereto extensive simulations will be done, to, among other things, examine the performance of the corresponding Taylor approach. This relates to studying the large number of possible null hypotheses included in our model. For example, tests for given covariance structures (such as compound symmetry or autoregressive) or structures of correlation matrices with unknown parameters are of great interest. Since there are heterogeneous versions of many popular structures, testing such structures or other patterns can be seen as a combination of testing hypotheses regarding covariance matrices and hypotheses regarding correlation matrices. Moreover, an investigation of Monte Carlo approaches for a higher order of Taylor approximation for real small sample sizes could be interesting.