Probability-enhanced effective dimension reduction for classifying sparse functional data

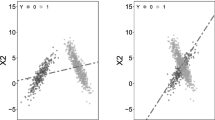
Abstract

We consider the classification of sparse functional data that are often encountered in longitudinal studies and other scientific experiments. To utilize the information from not only the functional trajectories but also the observed class labels, we propose a probability-enhanced method achieved by weighted support vector machine based on its Fisher consistency property to estimate the effective dimension reduction space. Since only a few measurements are available for some, even all, individuals, a cumulative slicing approach is suggested to borrow information across individuals. We provide justification for validity of the probability-based effective dimension reduction space, and a straightforward implementation that yields a low-dimensional projection space ready for applying standard classifiers. The empirical performance is illustrated through simulated and real examples, particularly in contrast to classification results based on the prominent functional principal component analysis.

Appendix: Technical details

Proof of Proposition 1

The proof is similar to that of Lemma 1 in Shin et al. (2014). We first show $S_{p(X)|X}\subseteq S_{Y|X}$, which is equivalent to show that, for any $\{\beta _k\}_{k=1}^K$ such that $X\perp p(X)\,|\,\langle \beta _1, X\rangle , \ldots , \langle \beta _K, X\rangle$, we have $X\perp Y\,|\,\langle \beta _1, X\rangle , \ldots , \langle \beta _K, X\rangle$. Recall $Y\{p(x),\varepsilon ^{*}\}$ is 1 if $\varepsilon ^{*}\le p(x)$ and $-1$ otherwise. As a consequence, $X\perp Y\, |\, p(X)$ and $X\perp Y\,|\,\{p(X), \langle X, \langle \beta _1, X\rangle , \ldots , \langle \beta _K, X\rangle \}$. Since $X\perp p(X)\,|\,\langle \beta _1, X\rangle , \ldots , \langle \beta _K, X\rangle$, we obtain $X\perp Y \,|\, \langle \beta _1, X\rangle , \ldots , \langle \beta _K, X\rangle$ owing to Proposition 4.6 of Cook (1998).

To show $S_{Y|X}\subseteq S_{p(X)|X}$ is equivalent to show $Y\perp X\,|\,\langle \beta _1, X\rangle , \ldots , \langle \beta _K, X\rangle \Rightarrow X\perp p(X)\,|\,\langle \beta _1, X\rangle , \ldots , \langle \beta _K, X\rangle$ for any $\{\beta _k\}_{k=1}^K$. Since $Y\perp X \,|\,\langle \beta _1, X\rangle , \ldots , \langle \beta _K, X\rangle$, we have $E(Y|X)=E(Y|\langle \beta _1, X\rangle , \ldots , \langle \beta _K, X\rangle )$ and $p(X)=E((Y+1)/2|X)=E(Y|\langle X, \beta _k\rangle _{k=1, \ldots , K})/2+1/2$. Hence $X\perp p(X)\,|\,\langle \beta _1, X\rangle , \ldots , \langle \beta _K, X\rangle$. $\square$

Proof of Theorem 1

It suffices to show, if $h\,\bot \, \text{ span }({\varSigma }\beta _1,\cdots , {\varSigma }\beta _K)$, then $\langle h,m(\cdot ,\pi )\rangle =0$. Since $X\perp p(X)\,|\,\langle \beta _1, X\rangle , \ldots , \langle \beta _K, X\rangle$,

$$\begin{aligned} \langle h,m(\cdot ,\pi )\rangle= & {} E\left( E[\langle h,XI\{p(X)\le \pi \}\rangle \,|\,\langle \beta _1, X\rangle , \ldots , \langle \beta _K, X\rangle ]\right) \\= & {} E\left( E[\langle h,X\rangle \,|\,\langle \beta _1, X\rangle , \ldots , \langle \beta _K, X\rangle ]E[I\{p(X)\le \pi \}\,|\,\right. \\&\times \left. \langle \beta _1, X\rangle , \ldots , \langle \beta _K, X\rangle \right) . \end{aligned}$$

Thus, it is enough to show that $E(\langle h, X\rangle |\langle \beta _1,X\rangle ,\cdots ,\langle \beta _K,X\rangle )=0$ with probability 1, which is implied by $E\{E^2(\langle h, X\rangle |\langle \beta _1,X\rangle ,\cdots ,\langle \beta _K,X\rangle )\}=0$. Invoking the linearity condition in Assumption 2 and $E(\langle \beta _k, X\rangle \langle h, X\rangle )=\langle h, {\varSigma }\beta _k\rangle$, for some constants $c_0, \ldots , c_K$,

$$\begin{aligned}&E\{E^2(\langle h,X\rangle |\langle \beta _1,X\rangle ,\ldots ,\langle \beta _K,X\rangle )\} \\&\quad = E\left\{ E\left( \langle h, X\rangle | \langle \beta _1, X\rangle ,\ldots ,\langle \beta _K,X\rangle \right) \left( c_0+\sum _{k=1}^K c_k\langle \beta _k,X\rangle \right) \right\} \\&\quad = E\left\{ E\left( c_0 \langle h, X\rangle +\sum _{k=1}^K c_k \langle \beta _k, X\rangle \langle h, X\rangle \Bigg | \langle \beta _1,X\rangle ,\cdots ,\langle \beta _K,X\rangle \right) \right\} \\&\quad = c_0 E (\langle h, X\rangle ) +\sum _{k=1}^K c_k \langle h, {\varSigma }\beta _k\rangle =0. \end{aligned}$$

$\square$