1 Introduction

Although workpiece clamping and fixturing technology are usually not regarded as the core components of machine tools, they are crucial constituents of the manufacturing system [1, 2]. The position and orientation of workpieces in the work area of machine tools are defined and guaranteed by clamping fixtures during machining, which are located in the accuracy path of the manufacturing system [3]. Therefore, the machining quality is directly related to the precision and dynamic behaviors of the clamping fixtures during machining [4, 5].

In metal-cutting processes, especially of filigree and thin-walled workpieces, static deflections of workpieces usually occur due to cutting forces. They limit the machining accuracy and lead to a great reject rate or rework effort with high unit costs on the one hand. On the other hand, an insufficient dynamic stiffness of the workpiece-fixture system often causes undesirable regenerative vibrations, which result in a poor surface quality and chatter marks and may even damage or destroy parts [6].

However, the design and conception of appropriate clamping fixtures for specific workpieces is a complex and challenging work with respect to the above-mentioned problems. It depends on the selection, configuration and layout of the clamping elements for workpieces with different shapes [7, 8]. Due to the lack of methods for a systematic design and optimization of the clamping fixtures, the expertise on how to design these fixtures is only based on the subjective experience of the designers involved and requires many years of practical experience [9,10,11]. Some earlier research works dealt with the development of software-based configuration and calculation tools, which could enable the automated generation of suitable clamping solutions [12,13,14,15,16,17]. In [18,19,20], the influence of the clamping configuration on resulting machining errors was investigated.

A fundamental approach to identify appropriate clamping configurations was based on the extraction, analysis and classification of workpiece and processing features [21]. Nee et al. combined a method for extracting and grouping machining features from CAD data with an expert system that included machining operations, environmental conditions, tools and workpieces in order to classify and configure clamping fixtures. Bansal et al. presented a STEP-based (data exchanged) extraction of component and processing features as well as a configuration system considering the stability, accessibility and accuracy of the clamping concept [22].

In [23], possible layouts of clamping elements for a workpiece were first determined, taking the principle of the lever into account. Then the optimum was selected by evaluating the accessibility and the position of the instantaneous centre of rotation. To select the suitable configurations, the workpiece deflection, resulting from a clamping configuration under process load, was taken into account in [24, 25]. Zhang et al. presented a method for generating the most form-fitting clamping configurations by means of the Gilbert-Johnson-Keerthi algorithm [26]. Cabadaj et al. developed functional and force-related fixture models. While the functional model was used to find workpiece-specific clamping configurations, the force-related model determined the influence of machining and clamping forces on the workpiece [27]. Methods for automatically evaluating the stability of a clamping configuration and its performance were presented in [28, 29].

In [30], the topology optimization method was employed in the layout of an optimal clamping and supporting of thin-walled parts. Das et al. optimized the design and configuration of assembly fixtures considering a production batch of thin sheet metal parts [31]. In [32,33,34], the correlations between the design of clamping systems, the machine properties and the machining plan were researched. An iterative adjustment of the fixture configuration and process can lead to a holistic optimization. One purpose in fixture planning is, for example, to ensure the machining of a workpiece with as few successive clamping operations as possible [35].

The state of the art regarding computer-aided fixture design systems (CAFD) was summarized in [15, 36,37,38]. The use of artificial intelligence methods, expert systems as well as the development and evaluation of mechanical models represent general solution approaches [39]. A heuristic method for finding optimal clamping points was shown in [40]. In [41, 42], the case-based reasoning procedure for the quick configuration of agile clamping fixtures was surveyed. Kumar et al. implemented genetic algorithms and neural networks for fixture design [43]. In [44], neural networks were applied to optimize the clamping configuration as well. In [45], the solution approach of neural networks was combined with the method of design of experiments (DoE). A linkage to a multi-agent approach can be found in [46].

Chen et al. presented a multi-criteria optimization process based on a genetic algorithm for the reduction of workpiece deformation with respect to the fixture design and clamping force [47]. To calculate the deformation, FEM was employed. Liu et al. used a similar approach [48]. Padmanaban et al. implemented an ant algorithm to optimize the clamping configuration with regard to minimizing the workpiece deformation [49]. The workpiece behavior under mechanical load was also calculated with FEM. In [50], the Cuckoo algorithm was utilized to determine an optimal clamping configuration. The commercial software OptiSLang in combination with ANSYS made it possible to optimize the design parameters for the development machine tools using regression analysis, in order to save time, personnel capacities and the corresponding costs [51]. In [52], Zäh et al. showed the potentials and challenges due to the utilization of ANSYS Mechanical and APDL-macro files and found that the simulation models of additive manufacturing could be coupled with this optimization software.

Most mechanical models for the design and optimization of workpiece clamping systems are based on the application of FEM [53,54,55]. For each individual machining task, this is usually carried out in different simulation steps with different clamping set-ups. Simulation results with regard to deformations, stress, natural frequencies and their modes can provide important information. When the results are inadequate or critical, improvements can be achieved with the trial-and-error approach by changing the positions of fixture elements until an acceptable or good solution is finally found [56, 57]. However, different configurations of fixture elements such as clamping and support elements for various processing steps or positions lead to a large number of calculations, which require a lot of computational effort and time. For this reason, analytical calculation approaches were developed [58], which were limited to relatively simple clamping scenarios. For a more complex scenario, this research work introduces a novel approach based on ML, in order to obtain an optimum from a large amount of fixture configurations, to reduce manufacturing errors and to obtain an increased stiffness of fixtures and machining accuracy.

With a milling test, Möhring and Wiederkehr revealed that the accuracy, performance and reliability of a clamping fixture depend on the number and the configuration of fixture elements [59]. Based on their results, the different positions of the fixture elements were used as input data in this study. The maximum workpiece deflection \({\varDelta }{d}{_{max}}\) and the lowest natural frequency of the fixture system \({f}{_{0}}\) were defined as target variables, which were calculated by FEM simulations for the corresponding configurations of the clamping and support elements.

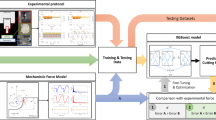
The paper is structured as follows: Section 2 presents the modeling of an exemplary clamping scenario and the generation of the input and output data for ML models based on FEM simulations. Subsequently in Sect. 3, several possible regression algorithms were compared with regard to their suitability for the dataset. By means of a morphological box, the algorithm of XGBoost was selected to train an equivalent model. As described in Sect. 4, XGBoost and other comparable algorithms were implemented in order to analyse how well the regression results can approximate the complex simulations. After training, the XGBoost model could predict the influence of an individual clamping or support element on \({\varDelta }{d}{_{max}}\). As presented in Sect. 5, a quasi-optimal configuration for the selected clamping scenario was suggested by the XGBoost model and validated by FEM simulation in a further loop. Section 6 provides the conclusion of the work as well as an outlook and possibilities for future improvement.

2 Data preparation for ML models

To create FEM models, a comparable clamping situation (Fig. 1), as presented in [59], was selected.

2.1 3D modeling

In this scenario, a thin-walled component with two pockets should be milled out of a plate-shaped semi-finished aluminium alloy part clamped into a fixture. The CAD software Siemens NX was used to carry out the 3D modeling. According to the 3–2–1 rule [7], the workpiece is located and supported from the bottom by three rest pads and two additional supports and clamped from above by three swing clamps (Fig. 2). The workpiece is laterally positioned and orientated by three stoppers.

Fig. 1
figure 1

3D models of the selected clamping situation including a semi-finished workpiece (white), a before and b during machining

Full size image

After modeling, the clamping and supporting elements were numbered as shown in Fig. 2a. Additionally, a two-dimensional Cartesian coordinate system was created so that their positions could be clearly defined. Each clamping point and its corresponding rest pad should be coaxial. Otherwise, undesired turning moments may occur during clamping. Therefore, one clamp and its rest pad have the same position in this coordinate system. It was assumed that the Y-coordinates of clamping points are fixed. Thus, the X-coordinates of the fixture elements (clamps 1–3 and additional supports 1 and 2) and the Y-coordinates of supports 1 and 2 serve as input features to train the ML models later.

Then a random generator program created 100 possible fixture set-ups so that the distribution of all set-ups was homogeneous and unstructured. A top view of this distribution is shown in Fig. 2b. Each of their individual positions was restricted to a certain area in order to avoid collisions between each other. Because of the parametric modeling with NX, 100 corresponding 3D models could be updated quite fast by editing the parameters.

Fig. 2
figure 2

a Exemplary fixture set-up with fixture components, b 100 stochastic fixture set-ups

Full size image

2.2 Finite element analysis

As this work focused on the feasibility of optimizing the clamping concept by the combination of ML methods and FEM simulations, the static structural analysis was performed with the aim of collecting the training data quickly and relatively precisely. Therefore, it was assumed that the constitutive relations of materials are isotropic linear, in other words, the stress-strain behavior follows Hooke’s law. As mentioned above, the material of the workpiece is aluminium with a constant Young’s modulus of 70 GPa, whereas all the fixture parts made of steel have a value of 200 GPa.

Apart from the depth of cut \({a}{_{p}}\) and the feed rate \({v}{_{f}}\), the other process parameters from the milling test by Möhring and Wiederkehr were adopted as shown in Table 1 so that their results are comparable with the simulations in this study. \({a}{_{p}}\) and \({v}{_{f}}\) were calculated with higher values (marked in bold) in order to obtain a greater resultant force, so that the influence of the clamping and supporting elements on the static behavior of the clamping fixture could be interpreted more clearly in Sect. 4.2.

Table 1 Process parameters for FEM simulations
Full size table

The boundary conditions of the FEM simulation are shown in Fig. 3. The internal structures of the hydraulic swing clamps (series B1.849 by Roemheld) are neglected as they are very complex and not the object of this investigation. Furthermore, the unnecessary mesh nodes require much more computing time. Three frictionless supports (A) are fastened to the lateral surface of the three rods, on which the clamping arms are locked, so that they can still move vertically and rotate around the rods. The clamping forces act on the bottom of the rods like a real swing clamp. The predefined clamping force (B) is 2200 N, which corresponds to a working pressure of 230 bar. The resultant cutting force at a certain point in time acting on the workpiece can be decomposed in three components at right angles to each other. In this way, the main cutting force (C), feed force (D) and passive force (E) were respectively calculated and applied to the simulations. The remaining weight of the workpiece (G) at this point in time should be taken into consideration as well. The whole workpiece-fixture system is fixed to the bottom of the base plate (F).

The contacts between the workpiece and the rest pads, between the workpiece and the clamping arms, as well as between the workpiece and the additional supports were defined as frictional. In order to simplify the finite element model, the three stoppers are also neglected. Another reason is that only the clamps and the rest pads should provide the frictional force to guarantee the position against the cutting force. The principle tasks of the stoppers are referencing and orienting the workpiece before clamping and machining, and no external force or torque should act upon them during milling.

Fig. 3
figure 3

FEM model of the workpiece-fixture system and boundary conditions for the FEM simulation

Full size image

The static structural analysis for the previously created 100 fixture set-ups (Fig. 4) shows that the maximum workpiece deflection \({\varDelta }{d}{_{max}}\) caused by the cutting force at a certain moment appeared irregularly at a corner of the workpiece or near the tool. In fact, the position and value of the cutting force are varying in the entire milling process, depending on process parameters such as the feed rate, cut depth and width etc. To simplify this, only the static cutting force with an exemplary position shown in Fig. 2 was taken into consideration. In [59], as the material was removed, the workpiece became more compliant, and the clamping system had a lower fundamental natural frequency than before. Chatter occurred merely in the place, where the fixture possesses the weakest workpiece support. Therefore, the representative position was selected. Predicting the positions of \({\varDelta }{d}{_{max}}\) is a classification task in ML rather than regression. But it is not the object of this study. Only its values are required and considered as the target variables to be predicted.

At the same time, the modal analysis for the clamping system was conducted. As a rule, the greater the natural frequencies of the workpiece-fixture system, the more stable it is. Regarding processing, the lowest natural frequency \({f}{_{0}}\) is important since it is easier to reach than others. Therefore, it is considered as the second target variable, differing tremendously within the range of 377.25–610.34 Hz. This also proves that the dynamic compliance of clamping fixtures depends considerably on the distribution or configuration of the fixture elements.

Fig. 4
figure 4

Max. workpiece deflections \({\varDelta }{d}{_{max}}\) in different positions due to different set-ups

Full size image

3 Selection of the most promising regression algorithm

After the data collection, appropriate algorithms were required for building the equivalent ML model based on the dataset generated in Sect. 2 with respect to the types of input and output values or the data distribution. According to David Wolpert’s “No-Free-Lunch-Theorem” [60], there is no model that always works better than others. The only way to know for sure which model is the best is to implement them all, if absolutely no assumption about the data has been made. Hence, experience is needed to make some reasonable assumptions about the dataset before training.

The problems in which the output data are numerical values are called regression problems. A large number of ML algorithms are available for solving such problems. For evaluating the most suitable regression algorithm, a selection methodology was developed by means of a morphological box. Some ML algorithms employed frequently were considered here.

Table 2 A morphological box for selecting the suitable algorithms
Full size table

The relevant and essential criteria, and attributes of algorithms are listed in the morphological box (Table 2). The ones highlighted in red are an overview of the assumptions made for this work. The independent variables (X-coordinates of clamps 1–3 and supports 1 and 2, and Y-coordinates of supports 1 and 2) are discrete as explained in Sect. 2 (Fig. 2b). Due to the characteristics of all regression methods, the regression model outputs continuous predictive values for dependent variables. In addition, a multicollinearity test carried out by the SPSS statistics software showed that the input data have a very low multicollinearity. Therefore, all seven independent variables are usable and thus can be selected as input features for the ML models [61]. Thus, the number of input features is seven. In this study, a small dataset of 100 samples were collected. Compared with the number of features, it is also large enough to avoid or reduce overfitting by means of regularization, which is crucial for the trained model in order to have a good generalization performance and strong robustness.

Because of the non-linear FEM calculations, non-linear regression methods are desirable as well. As mentioned above, the technique of regularization is necessary due to the risk of overfitting the training set. Another characteristic required for the ML model is a fast learning speed for saving computing time. White-box models can show what regression algorithms have learnt and represented in the model. However, most powerful ML algorithms produce only black boxes, which can make excellent predictions but are incomprehensible though.

Compared with other algorithms, ensemble methods, e.g. the boosted tree algorithm XGBoost, always require less samples to achieve the same good prediction quality [62]. They create only black box models as well. Nevertheless, they enable the interpretation of the significance or meaning of the selected features. This can provide useful information in fixture design. Hence, according to the criteria described in the morphological box (Table 2), XGBoost (its characteristics are highlighted in green) was chosen here to optimize the clamping concept. The decision tree (blue) known as the basic learner of XGBoost is also illustrated in Sect. 4.1.

In order to evaluate the reliability and reproducibility of XGBoost, several comparable models which are applied frequently (yellow) were implemented in this research. Section 4.3 provides a comparison of the following models: XGBoost, decision tree, multilayer perceptron (MLP), polynomial ridge regression, polynomial elastic net, support vector regression (SVR), random forest and k-nearest neighbors (kNN).

4 Implementation of the selected regression methods

It is necessary to know how well the model generalizes to new cases after training. Hence, the data obtained in Sect. 2 were split up into three sets: training, validation and test datasets. In this study, 60 samples (the training set) were used for training different ML models, 20 samples (the validation set) for fine-tuning the model hyperparameters and the remaining 20 ones (the test set) for measuring generalized errors. In addition, by means of cross-validation, this small dataset can be effectively exploited.

Training an ML model means setting its parameters to fit the training data best. For that purpose, a measure of how well the model fits the training data is required. The root mean square error (RMSE) is generally the preferred performance measure for regression tasks. But in practice, it is simpler to minimize the MSE rather than the RMSE. Both have the same results [62].

The MSE and the RMSE are computed as:

$$\begin{aligned} MSE=\frac{1}{n}\sum _{i=1}^{n}\left( y_i-{\widehat{y}}\right) ^{2} \end{aligned}$$
(1)

and

$$\begin{aligned} RMSE=\sqrt{MSE}=\sqrt{\frac{1}{n}\sum _{i=1}^{n}(y_i-{\widehat{y}})^{2}}, \end{aligned}$$
(2)

where n is the sample size, \(y_i\) are the values to be predicted and \({\widehat{y}}\) are the predicted values.

The coefficient of determination \({R{^{2}}}\) measures how well the regression predictions approximate the test dataset. It interprets statistically the proportion of variance in the dependent variable, which can be predicted from the independent variable (Eq. 3). Normally, it ranges from zero to one if the regression models are selected correctly. When \({R{^{2}}}\) equals 1, the regression predictions fit the data perfectly without errors. In contrast, when \({R{^{2}}}\) equals 0, the target variables cannot be predicted.

The most general definition of \({R{^{2}}}\) is:

$$\begin{aligned} R^{2}=1-\frac{{\sum _{i=1}^{n}}\left( y_i-{\widehat{y}}\right) ^{2}}{{\sum _{i=1}^{n}} \left( y_i-{\overline{y}}\right) ^{2}}, \end{aligned}$$
(3)

where \({\overline{y}}\) is the mean value of \(y_i\), \(\sum _{i=1}^{n}\left( y_i-{\widehat{y}}\right) ^{2} \) is the residual sum of squares and \(\sum _{i=1}^{n}\left( y_i-{\overline{y}}\right) ^{2} \) is the total sum of squares.

For training all the ML models mentioned in this paper, the programming language Python and its Scikit-learn application programming interface (API) were employed.

4.1 Regression tree

Decision tree, also called regression tree for regression problems, is an individual element of tree boosting models. To train such ML models, the classification and regression tree algorithm (CART) is used. The idea is quite simple. The algorithm splits up the dataset into two subsets, using a single feature x and a threshold \({t{_{x}}}\). Then it searches for the pair (x, \({t{_{x}}}\)) with which the training data has the greatest reduction of the MSE after splitting [62].

The loss function minimized with the CART algorithm is given by:

$$\begin{aligned} {\mathcal {L}}(j,t_j)=\frac{s_{left}}{s}MSE_{left}+\frac{s_{right}}{s}MSE_{right}, \end{aligned}$$
(4)

where \(s_{left/right} \) is the number of instances in the left or right subset, and \({MSE}_{left/right} \) is the MSE of the left or right subset.

Fig. 5
figure 5

Regression tree represented with Graphviz (units: mm for X, \(\upmu \)m \({^{2}}\) for mse and \(\upmu \)m for value)

Full size image
Table 3 Clarification of the parameters X in Fig. 5
Full size table

Regression trees as white box models are easy to understand and their decision process can be easily interpreted by means of the Graphviz plug-in (Fig. 5) [63]. The parameters X in Graphviz correspond to each feature in the regression tree model (Table 3). “Value” in the leaves (blocks) stands for the value of the predicted \({{\varDelta }d{_{max}}}\). All training data start at the root of the tree from the top and are split downwards to a leaf. At each split, the MSE is reduced as much as possible.

4.2 XGBoost

Most of the time, the summed-up prediction of a group of predictors, e.g. regression trees, is better than the prediction of the best individual model. This technique is known as ensemble learning, which combines several weak learners into a strong learner. XGBoost, developed by T. Chen et al., is one of the most modern algorithms in the ML field. The basic idea of XGBoost and other tree-boosting algorithms is to train the predictors one after the other, so that each tree is aimed at minimizing the MSE of the predecessor until the error can no longer be reduced [64, 65]. Training an XGBoost model is an iteration process. Its mathematical theory is as follows:

For a dataset \(D\!=\!\left\{ \left( X_i,y_i\right) \right\} \!\left( \left| D\right| \!=\!n,X_i\!\in \! {\mathbb {R}}^{m},y_i\!\in \!{\mathbb {R}}\right) \) with n samples and m features, a tree-boosting model with K additive functions can be written as:

$$\begin{aligned} {{\widehat{y}}}_i=\sum \limits _{k=1}^{K}f_k\left( X_i\right) ,\;f_k\in {\mathcal {F}}, \end{aligned}$$
(5)

where \({\mathcal {F}}=\left\{ f\left( X\right) =w_{q(X)}\right\} \;\left( q:\;{\mathbb {R}}^{m}\rightarrow T,\;w\in {\mathbb {R}}\right) \) is the space of regression trees, q represents the structure of each tree, and T is the number of leaves. Each \(f_k \) corresponds to an independent tree structure q and leaf weights\(\;w \). This allows the predictions of each tree to be summed up as the final prediction.

The MSE mentioned above can be selected as loss function:

$$\begin{aligned} l\left( y_i,\widehat{y_i}\right) =\left( y_i-\widehat{y_i}\right) ^{2} \end{aligned}$$
(6)

The objective function contains not only the loss function (Eq. 6) but also a regularization term \(\Omega \) to reduce the complexity of the model:

$$\begin{aligned} {\mathcal {L}}=\sum \limits _{i=1}^{n}l\left( y_i,\widehat{y_i}\right) +\sum \limits _{k=1}^{K}\Omega \left( f_k\right) , \end{aligned}$$
(7)

where \(\Omega (f) = \gamma T+\frac{1}{n} \lambda ||w||^2\), \(\gamma \) and \(\lambda \) are the parameters to be fine-tuned.

To predict the i-th instance at the t-th iteration, the objective function can be rewritten as:

$$\begin{aligned} {\mathcal {L}}^{\left( t\right) }=\sum _{i=1}^{n}l\left( y_i,\widehat{y_i}^ {\left( t-1\right) }+f_t\left( X_i\right) \right) +\Omega \left( f_t\right) +C, \end{aligned}$$
(8)

where the first \((t-1) \) regularization terms can be regarded as the constant C.

Using a second-order Taylor’s expansion with the form:

$$\begin{aligned} f\left( x+\varDelta x\right) \cong f\left( x\right) +f'\left( x\right) \varDelta x+\frac{1}{2}f''\left( x\right) \varDelta x^{2}, \end{aligned}$$
(9)

it is possible to approximate Eq. (8) as:

$$\begin{aligned} \widetilde{{\mathcal {L}}}^{\left( t\right) }=\sum \limits _{i=1}^{n}\left[ g_if_t \left( X_i\right) +\frac{1}{2}h_if_t^{2}\left( X_i\right) \right] +\Omega \left( f_t\right) , \end{aligned}$$
(10)

where \(g_i\!=\!\partial _{{{\widehat{y}}}^{\left( t-1\right) }}l(y_i,{{\widehat{y}}}^{(t-1)})\; \)and \(h_i\!=\!\partial _{{{\widehat{y}}}^{\left( t-1\right) }}^{2}l\!\left( y_i, {{\widehat{y}}}^{\left( t-1\right) }\right) \) are the first- and second-order gradient statistics on the loss function. The constant term C can be neglected here. When the instance set of leaf j is defined as\(\;I_j=\left\{ \left( i\right| q\left( X_i\right) =j\right\} \), then Eq. (10) can be rewritten as follows by expanding \(\Omega \):

$$\begin{aligned} \begin{aligned}\widetilde{{\mathcal {L}}}^{\left( t\right) }=&\sum \limits _{i=1}^{n} \left[ g_if_t\left( X_i\right) +\frac{1}{2}h_if_t^{2}\left( X_i\right) \right] +\gamma T+ \frac{1}{2}\lambda \sum \limits _{j=1}^{T}w_j^{2}\\ =&\sum \limits _{j=1}^{T}\left[ \left( \sum _{i\in I_j}g_i\right) w_j+\frac{1}{2} \left( \sum _{i\in I_j}h_i+\lambda \right) w_j^{2}\right] +\gamma T\\ =&\sum \limits _{j=1}^{T}\left[ G_jw_j+\frac{1}{2}\left( H_j+\lambda \right) w_j^{2}\right] +\gamma T, \end{aligned} \end{aligned}$$
(11)

where \(G_j={\sum \limits _{i\in I_j}{g_i}} \) and \(H_j={\sum \limits _{i\in I_j}{h_i}} \).

The optimal weight for a particular tree structure can be calculated as:

$$\begin{aligned} w_j^*=-\frac{G_j}{H_j+\lambda }, \end{aligned}$$
(12)

and the corresponding optimal objective function is:

$$\begin{aligned} \widetilde{{\mathcal {L}}}^{\left( t\right) }=-\frac{1}{2}\sum _{j=1}^{T}\frac{G_j^{2}}{H_j+ \lambda }+\gamma T \end{aligned}$$
(13)

Hence, the reduction of the objective function after a split can be calculated by:

$$\begin{aligned} \begin{aligned} {{\mathcal {L}}}_{split}& = -\frac{1}{2}\sum _{j=1}^T\frac{\left( G_L+G_R\right) ^2}{H_L+H_R+\lambda }+\gamma T\\ {}& \quad -\left[ -\frac{1}{2}\sum _{j=1}^{T+1}\left( \frac{G_L^2}{H_L+\lambda } +\frac{G_R^2}{H_R+\lambda }\right) +\gamma \left( T+1\right) \right] \\ & = \frac{1}{2}\left[ \frac{G_L^2}{H_L+\lambda }+\frac{G_R^2}{H_R+\lambda } -\frac{\left( G_L+G_R\right) ^2}{H_L+H_R+\lambda }\right] -\gamma \ \end{aligned} \end{aligned}$$
(14)

Because of the small training dataset, the “exact greedy algorithm” was selected to find the best split. The model calculated all possible reductions of \({\mathcal {L}}_{split} \) locally at each split and selected the largest one without taking the global optimum into consideration.

Another important advantage of XGBoost is that it can predict the relative importance of each feature. The XGBoost model shows an importance sequence of all features regarding the prediction of \({\varDelta }{d}{_{max}}\) (Fig. 6). XGBoost estimates the feature importance by default according to the criterion of how often the split of data instances occurs at this feature in the iterative process. To train this model, 1717 regression trees were created. The split at the feature \({X}{_{clamp2}}\) occurred 1673 times. At \({X}{_{clamp1}}\) and \({X}{_{clamp3}}\), the original training instances were split 1101 and 1015 times, respectively. Both influenced the prediction results to a certain extent but less than the \({X}{_{clamp2}}\). The X-coordinate of the additional support 1 (\({X}{_{support1}}\)) was relatively unimportant and had the lowest value of 615.

Fig. 6
figure 6

Importance of each feature for predicting the max. workpiece deflection \({\varDelta }{d}{_{max}}\)

Full size image
Fig. 7
figure 7

Correlation between the features and the max. workpiece deflection \({\varDelta }{d}{_{max}}\)

Full size image

To validate the importance sequence and to reveal the correlation between the features and \({\varDelta }{d}{_{max}}\), the four features marked with red arrows were chosen (Fig. 6) since they have more distance to each other. They correspond to the X-coordinates of the four fixture elements (clamps 1–3 and additional support 1). In Fig 7, they are depicted in blue and arranged in ascending order. The corresponding \({\varDelta }{d}{_{max}}\) values represented by red dots are more discrete and should be fitted by means of a straight regression line. Their slopes a were calculated as well. In this case, the greater the absolute value of the slope a is, the more influence a feature has on the target variable \({\varDelta }{d}{_{max}}\). More influence also means more importance. It was found out that the results of this correlation analysis correspond to the importance sequence given by XGBoost. Hence, XGBoost was validated to predict the feature importance adequately.

4.3 Prediction quality

Before the training, only 100 samples can be split up into \(C_{100}^{80}\) different training and test sets. During the cross-validation, the remaining 80 training samples may once again be split into \(C_{80}^{60}\) different training and validation sets. In reality, it is difficult to perform all the possible datasets. Therefore, the program were run many times to obtain the representative prediction models for each combination of algorithms and target values, thus eliminating around 25% of unstable results.

After training the regression tree (Fig. 8, top left), a value of \({R{^{2}}}\) = 0.82 could be achieved for predicting \({\varDelta }{d}{_{max}}\). To predict \({f{_{0}}}\), a value of \({R{^{2}}}\) = 0.75 was reached (Fig. 8, top right). Compared with this individual regression tree, XGBoost could predict \({\varDelta }{d}{_{max}}\) more precisely with \({R{^{2}}}\) = 0.97 (Fig. 8, bottom left). But for \({f{_{0}}}\), the value of \({R{^{2}}}\) was only 0.79 (Fig. 8, bottom right).

Fig. 8
figure 8

Comparison between the predicted and original test data

Full size image

The question had to be clarified whether a value of \({R{^{2}}}\) = 0.97 is sufficient for a reliable prediction or how high \({R{^{2}}}\) should be in this study. The answer varied for different requirements. Therefore, other regression algorithms were implemented in order to compare their results. These included MLP, polynomial elastic net and SVR, for all of which \({R{^{2}}}\) is above 0.95 (Fig. 9). Hence, a value of 0.95 is considered to be a good criterion. The polynomial ridge regression, random forest, decision tree and kNN have values of \({R{^{2}}}\) below this limit and thus are not usable.

Fig. 9
figure 9

Predictive abilities of the different regression methods

Full size image

None of the regression methods used works perfectly for predicting \({f{_{0}}}\) of the workpiece-fixture system. SVR and polynomial ridge regression show the best \({R{^{2}}}\) value of only 0.86. The modal analysis results of the 100 simulations conducted varied greatly, although the boundary conditions are the same. Fig. 10 depicts the different modes of \({f{_{0}}}\), showing that the lowest natural frequencies are not comparable and can be predicted only to a limited extent.

Fig. 10
figure 10

Four exemplary modes at the lowest natural frequency \({f{_{0}}}\) of different fixture set-ups

Full size image

5 Optimization of the clamping concept

The optimization of the clamping concept is an NP (nondeterministic polynomial)—complete problem that can be solved in nondeterministic polynomial time. Since there are innumerable configuration possibilities, it is impossible to list all possible fixture set-ups and to perform the FEM simulations for them. Nevertheless, the equivalent ML model can suggest a local optimum among the numerous randomly generated set-ups with regard to minimizing unwanted workpiece deflections.

To validate this, 10,000 new possible set-ups were generated using the generation program mentioned above. The XGBoost model predicted the smallest value of \({\varDelta }{d}{_{max}}\) = 125.8 \(\upmu \)m and thus the best set-up. Then the FEM model had to be updated with the new X- and Y-coordinates (Table 4), and the FEM simulation had to be carried out again under the same boundary conditions mentioned above, resulting in a value of \({\varDelta }{d}{_{max}}\) = 126.4 \(\upmu \)m (Fig. 11). The difference is only 0.6 \(\upmu \)m (0.47% of the FE simulation result). Such validations of the XGBoost model were carried out several times, and all the results were similar. Note that the smallest value of \({\varDelta }{d}{_{max}}\) among the 100 training data is 130.4 \(\upmu \)m.

Table 4 X- and Y-coordinates of the best set-up among 10 000 new random configurations
Full size table
Fig. 11
figure 11

Top view of the optimal set-up und comparison of the results from the XGBoost model and the FEM simulation

Full size image

In principle, even more fixture set-ups may be generated to further approximate the global optimal concept. In practice, designers must, however, make quick and correct decisions under time pressure. Due to the modern techniques used, such as out-of-core computing and parallelized tree building, this XGBoost model needed only 8 seconds to output a quasi-optimal concept for positioning the fixture elements.

6 Summary and outlook

This paper presents a new method for optimizing the clamping concept. A morphological box was used to systematically select the most promising regression algorithm based on relevant criteria. The XGBoost model trained with a small training dataset could perfectly predict the maximum workpiece deflection \({\varDelta }{d}{_{max}}\) caused by the cutting force at a certain moment. By generating numerous possible fixture set-ups, the XGBoost model could quickly offer a quasi-optimal concept to increase the static fixture stiffness and to compensate the position and form deviations of workpieces at the design stage. In this way, the XGBoost model may provide a priority of fixture components and support designers, facing trade-off, in making correct decisions. By using XGBoost, engineers may also derive important knowledge for evaluating different design variations.

In addition to \({\varDelta }{d}{_{max}}\) and \({f{_{0}}}\), other target variables can be used as output data as well. In future research, it will be analysed how few samples are necessary to train different ML models and try to reduce their number. An experimental investigation to validate the ML models will be carried out as well. Furthermore, Python script helps to carry out simulations automatically. The effort of data collection will be considered as well. In future work, the tool path based on g-code will be applied in the transient simulation and could optimize the clamping concept with respect to the whole machining process.

Whereas the optimization of the machine hardware requires relatively high development costs, the ML method offers a great potential for improving the machining accuracy, performance and reliability of clamping fixtures effectively and economically.