Abstract
Thermomechanical ring rolling is an evolution of the process where deformation and heat treatment are combined to obtain a product with both the desired geometry and hardness or microstructure in a single step. However, the high sensitivity of the process to the initial condition and to various disturbances limits its repeatability and accuracy. In this paper, the authors implement a concept for hardness control of ring rolling in virtual experiments. A concept based on soft sensors and model predictive control is implemented on a digital twin. The operation of the different models needed for this control loop are detailed and the controller itself is illustrated.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Tangential profile ring rolling (TPRR) is an incremental forming method to produce ring-shaped parts to a near net shape state with little material loss and good productivity. Typical parts includes bearing race. This process is usually carried out at room temperature, and followed by heat treatment to obtain the desired hardness. Recently, a new process called thermomechanical TPRR have been introduced by Brosius et al. [1] with the aim to combine both step into one process to simultaneously obtain the targeted geometry and microstructure. In this process, a semi-hot (800–1000 K) ring is formed while being cooled by a flow of compressed air. Experiments shown that changes occurring in both grain size and dislocation density can lead to significant changes in hardness ranging from 200 HV0.1 for cold rolled parts up to 350 HV0.1 for the thermomechanical process [2].
In this paper, the possibility of the implementation of a control strategy to achieve preset hardness is investigated. First a digital twin representing the real ring rolling machine is introduced. Then a soft sensor, enabling the measurement of the hardness is presented. Finally, a controller concept is implemented and results are discussed.
2 State of the art
Earlier development of TPRR have mainly focused on the cold forming process [3]. The geometrical capability of the process and the influence of the different process parameter, such as tool’s speed and geometry, have been studied [4]. The possibility to produce non-symmetrical rings and complex geometrical shapes have been confirmed [5], and the economical aspect of the process has also been investigated and compared with other roll bearing production methods [6].
A study hot tangential rolling has shown the possibility of influencing microstructural evolution in semi-hot ring rolling [7]. However, despite good geometrical capability [8], the systematic achievement of the desired hardness is more complex. Numerous factors such as initial ring and tool’s temperature, cooling and forming strategies and initial microstructure have a strong influence on the resulting hardness. The link between forming and microstructure in the context of ring rolling has been the subject of several studies. Texture evolution during the process of cold ring rolling has been invetigated by Ryttberg et al. [9]. The simulation of the evolution of the microstructure in ring rolling of steel has been realized by Schwich et al. [10] using FEM-code DEFORM combined with a recrystallization model in post-processing. Good agreement between simulation and experimental results has been observed in this study.
To achieve higher process performance, different control strategies have been applied to ring rolling. The influence of tool displacement control has been studied using FEM-software Abaqus by Jenkouk et al. [11]. Kopp et al. [12] implemented the control of tool displacement following a pre-programmed schedule to improve geometrical reproductability and reduce material loss. Choi et al. [13] proposed the use of a model reference adaptive control in order to improve geometrical accuracy. More recently Cleaver et al. [14] introduce a control method enabling the production of rings with variable wall thicknesses. In a review on the use of closed-loop control schemes for process control of product properties in forming process, Allwood et al. [15] note, that for ring rolling, there have not been any developments in that direction. They state that the implementation of such a strategy could reduce the influence of thermal disturbances.
Brosius et al. [1] proposed a concept based on model predictive control and soft sensors to implement this strategy. In this paper, the capability of such a concept is illustrated using a FEM-based digital twin.
3 Digital twin for TPRR
The implementation of a process control system in the actual rolling machine requires a modification of the machine control system. Moreover, the realization of such tests on a machine in real conditions presents a certain number of challenges (risk of damaging the tools or the machine, etc.). Therefore, first investigations are done as virtual experiments on a digital twin. After successful testing the following methods could be transferred onto an real machine.
3.1 Ring rolling machine
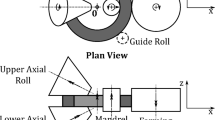
The machine used in this paper is a retrofitted 1986 “UPWS 31,5.2” from VEB Werkzeugmaschinenfabrik Bad Düben, today Profiroll Technologies GmbH. Figure 1 presents the different parts of the TPRR machine.
The mandrel is supported by two fixed supporting rolls and can rotate freely around its axis. The roll, rotating at a constant speed, is driven against the ring at a given speed (roll speed). The round rolls stabilize the ring rotation. Finally, compressed air can be sprayed on the ring to cool it down.
During the process, the ring grows incrementally and the eventual profiles of the tools are impressed on the ring. In this paper, in an effort to reduce the problem complexity, the tools are not profiled, which lead to more homogeneous fields of deformation and temperature. Figure 2 presents the geometries of the tools. The produced rings have a final outside diameter of 90 mm, final thickness of 6 mm and width of 17 mm.
The machine have been equiped with different sensors. Both rolling force and torque are measured using strain gauge, surface temperature is measured using a pyrometer (optris CTlaser 3MH1), and the tool displacement is measured using a linear displacement transducer. The system is completed by an acquisition card (HBM QuantumX). The precision of the temperature measurement using the pyrometer is mainly depending on the precision of the emissivity estimation, which has been estimated by at 8%. Force measurement precision is estimated at 10%, as it is influenced by the linearity of the sensor and friction in the machine. Precision of the tool displacement exceeds 0.01 mm and is therefore not represented in the results.
3.2 FEM model
The main element of the numerical twin is a thermomechanical FE-simulation using LS-DYNA explicit formulation. To quicken the simulation, time scaling with a factor of two is used. The geometry and kinematics of the real machine tools have been faithfully reproduced. The tools are modeled as rigid parts using shells with a constant temperature. The inertia of the tools was determined using CAD and taken into account as well as the damping of the hydraulic system of the round roll. Figure 3 presents the FE-model parts.
The ring is modeled by 6500 brick elements with 8 nodes and one integration point (ELFORM 1 in LS-DYNA). The hourglassing is compensated and it has been verified that the energy dissipated by hourglassing is very low (less than 1% on average) compared to the energy dissipated by the plastic deformation.
The model material in this investigation is 16MnCr5 (1.7131, AISI 5115). Determination of mechanical properties is carried out by performing compression tests on cylindrical samples at strain rates in the range of \(10^{-2}\) to \(1\,\hbox {s}^{-1}\) and in a temperature range from room temperature to 1000 K. Tests were carried out on a servohydraulic testing machine Gleeble 3500.
To model the material, a Johnson-Cook formulation is used. It is found that the unmodified Johnson-Cook equation is not able to fully represent the entire range of temperatures and strains investigated previously. Therefore, only a limited section of the data corresponding to the temperature encountered in the process (450–900 K) is used in fitting, and the parameters in Table 1 were obtained.
LS-DYNA requires the use of an equation of state in combination with the Johnson-Cook formulation. To this purpose, a Grüneisen formulation is used, and parameters are taken from literature [16].
Finally, the thermal model is an isotropic model with value independent of temperature. Heat capacity and thermal conductivity have been taken as standard values for steel: \({480}\,{\hbox {J}\, \hbox {kg}^{-1} \hbox {K}^{-1}}\) and \({52}\, {\hbox {W}\,\hbox {m}^{-1} \hbox {K}^{-1}}\). Thermal conductivity for the contact has been determined by fitting the model with experiments performed on the machine.
The cooling of the ring by compressed air is modeled using an additional part in contact with the ring; the heat transfer coefficient of the contact, named \(h_{c}\), can be changed to reflect the modulation of airflow. This parameter can be estimated by comparison with experiments and FEM simulations.
Depending on the roll speed, and therefore the simulation time, computational cost is between 140 core-hours and 350 core-hours using 24 cores on Intel(R) Xeon(R) CPU E5-2680 v3 of the high performance computing system of the Technical University Dresden.
3.3 Virtual sensors
The output of the simulation can be used to simulate the signal of the “virtual sensors”. Using the python library LS-Reader to read d3plot file produced by LS-DYNA, the following signals are recreated: outside ring radius \(R_{ring}\), temperature measured by the pyrometer \(\theta _{\text {pyro}}\) and roll displacement \(x_{\text {tool}}\).
3.4 Comparison with experiments
Figure 4 shows the results of a ring rolling test and a simulation, without cooling by compressed air, with a roll speed of \({0.19}\,{\hbox {mm}\,\hbox {s}^{-1}}\), and a start temperature of 840 K. The force exerted by the round roll is estimated between 2.0 and 2.5 kN.
A good agreement between simulation and experiment for the temperature measurement is observed.
For the force measurement, the values are in the same range but some differences are noticeable. First of all, the force increase is more progressive in the real test than in the simulation. This may be related to the elasticity of the machine and the tools, which are simulated as rigid parts in the FEM model, and from the hydraulic system. The rapid increase of the force at the end of the test in the experiment is related to the contact between the the mandrel and the roll, this phenomenon is not modeled in the FEM simulation as there is no contact between the tools, but this has no influence on the forming. In the FEM simulation, contacts are only modeled between tools and the ring in order to limit computational cost.
The measurement of the tool displacement shows a strong variation of the speed around 5 s which is correlated with the increase of the rolling force. This change is related to the hydraulic system in the machine.
4 Soft sensor for TPRR
4.1 Concept
The main goal is to control the obtained hardness at the end of the process within the ring. The control of a quantity in any system requires the possibility to measure it. In this case, even if it is possible to measure hardness at the surface using Eddy-Currents [2], it is not possible to do it within the bulk. Therefore, the use of soft sensors is required [17]. By the term soft sensor, it is meant a measuring device with the aim of determining a quantity based on process-dependent model and physical sensors measurements.
Here, the quantity to determine is the hardness inside the ring. The quantities that can be measured are surface temperature (using a pyrometer), tool’s positions and ring size. Using surface temperature the inner temperature can be determined. Plastic deformation can be derived from the tool’s positions, ring size and inner temperature. Finally, knowing plastic deformation and temperature evolution, the hardness can be established using a dynamic recrystallization model. A detailed explanation of the inner working of each model is given in the following sections. Figure 5 presents the link between physical sensors and soft sensors.
The key component of any soft sensor is the measuring function or model that is used to obtain the desired values. It has to be accurate enough to enable measurement but still significantly faster than the actual process to enable control. In this paper, an FE generated dataset is used to design and evaluate these models. The FE model is the one presented in the previous section. 20 simulations are run, with three parameters being changed: initial temperature \(\theta _{\mathrm {start}}\), roll speed \(v_{\mathrm {t}}\), and contact thermal conductivity of the cooling surface \(h_{\mathrm {c}}\). The parameters for each run are determined using a Latin Hypercube sampling using the python library pyDOE2. The range of every parameter is presented Table 2. Simulation results form the database are used in the followings subsections. The computational cost of the simulations represent around 2400 core-hours.
The d3plot results—around 120 GB of raw data—are then processed using python libraries. The following values are computed: ring size, plastic strain in the core of the ring as defined in Fig. 2, temperature in the core of the ring, temperature measured by the pyrometer, ring radius and tool position. 38.826 observation points are established.
4.2 Hardening model
The goal of the soft sensor is the prediction of the hardness change within the ring core. This prediction can be made on the basis of the plastic strain and forming history. In this regard, hardening due to a combination of the Hall-Petch effect as well as due to work hardening was considered, following:
To process the grain size d and dislocation density \(\rho\) during forming, a set of differential equations derived from [18] are used. This empirical formulation is part of a unified set of viscoplastic constitutive equations which will provide a route for further improvement of the FE model by implementing this model directly in LS-DYNA.
The core equation defines the evolution of the normalized dislocation density \({\bar{\rho }}\) (in a range of 0–1) in terms of plastic strain rate \(\dot{\varepsilon _{p}}\) and recrystallization S.
The first term describes the dynamic recovery based on plastic deformation. The second term describes the (usually small) static recovery, with the third term signifying metadynamic recrystallization. The volume fraction of recrystallized material S as well as a time delay to the onset of recrystallization x are modeled by differential equations as well.
Finally, the evolution of the grain size can be obtained by combining grain growth and grain refinement.
Most of these parameters are taken to be material constants, with the recovery parameter \(c_{1}\) and the critical dislocation density \({\bar{\rho }}_{c}\) having a temperature dependence using thermal activation. As the use of these equations in the present work is intended to demonstrate the applicability of a physically-based model in a virtual control setting, values were selected from published data and adjusted to match experimental results for comparable steels. In this way, it is possible to show the general approach and data that can be obtained with only a small number of experiments. Parameter values are presented in the Table 3.
Since the dislocation density \(\rho\) in (1) is used in physical units, the normalized dislocation density \({\bar{\rho }}\) is rescaled assuming a saturated density of \(10^{15}{\mathrm {m}}^{-1}\). In the following part, the relative hardness is presented which is the actual hardness divided by the hardness of the original material.
4.3 Deformation model
The goal of this model is the rapid prediction of plastic deformation in the core of the ring. The modeling of plastic flow in circular rolling is usually done by FEM. This solution can be extremely accurate, but not suitable for this application as the computation time is not compatible with the needs of the soft sensor model. A number of models have been proposed for the rapid simulation of plastic flow in ring rolling with simplified or semi-analytical models: UBET model [19] and pseudo-plain-strain [20] for example. These solutions, although less accurate than FEM simulations, have the advantage of being significantly faster. However, the model used in this sensor must be at least several hundred times faster than the process in order to be used for process control, which is probably not possible with these methods.
In this paper, the use of a Deep Neural Network (DNN) to predict the average plastic strain in the core of the whole ring is proposed. Then a time-strain curve representative of the local plastic strain in the core of the ring is derived.
The DNN ist trained using Tensorflow [21]. The data set is randomly separated in two subsets: a training set with 80% of the data, and a testing set with the remaining data. Four layers are used: a normalization layer, without trainable parameters, two layers with 64 neurons with ReLu (Rectified Linear Unit) as activation function and an output layer without activation function. The model includes 4481 trainable parameters. The initial values of the parameters are determined randomly. Training is undergone using Adam optimizer [22] with a constant value of 0.001 for the learning rate, Mean Average Error (MAE) is used as a cost function. The training takes place over 150 epochs. Tests with less neurons and with more layers have been realised. Increasing the complexity of the network does not provide significant improvements in the network performance (less than 0.5% improvement in MAE). However the use of only 32 neurons for each layers significantly degrade the precision of the model (MAE close to 5% higher). No other activation function or learning algorithm have been tested, as results were already satisfactory. Different values for the learning rates have been tested (0.01, 0.0001) and did not result in any improvement of the DNN.
The final value of MAE is 0.0013 for the training set and 0.000937 for the testing set. The proximity between these two values proves the absence of overfitting. Figure 6 shows the correlation between the real and predicated values by the DNN, as well as the original distribution of the values. This solution shows very good performance. Moreover, once trained, a DNN can be very fast, and therefore be used to predict the average deformation in the ring for use in a servo system.
The use of neural networks allows the determination of the average plastic strain. However, the strain rate is not constant in TPRR. Each element is deformed stepwise as it passes between the tools. The deformation curve as a function of time thus resembles a staircase curve, see Fig. 7. This is very important to determine the evolution of the microstructure, which is dependent on the speed of deformation. It is therefore necessary to determine a local plastic strain curve as a function of time from the evolution of the average strain. It is assumed that the plastic deformation takes place only at regular intervals, when the considered part of the ring passes between the tools. From the FEM simulations it is estimated that the deformation takes place in a zone of about \(\alpha _f= {20}^{\circ }\) at the level of the tools. Given the rotational rate of the roll \(\omega _{r}\), the roll radius \(R_{t}\) and the ring radius \(R_{r}\), the step period T can be calculated following:
And the period in which actual forming occur \(T_{f}\) is given by:
With this solution, it is possible to determine the local plastic strain and plastic strain rate knowing the position of the tool, the radius of the ring and the temperature in the ring. In order to allow the implementation of a controller, it is however necessary to be able to predict the evolution of the forming according to the process parameters. The prediction of the temperature evolution is presented in the next section. The prediction of the tool position, knowing the speed, is done with a simple integration. The determination of the evolution of the ring size is more complex. Studying the data set proposed by FEM, it is clear that the ring size is almost linearly related to the tool position, as shown in Fig. 8. A regression with a second order polynomial on the present data is performed with the python package statsmodels [23] and is very conclusive with an R-square coefficient of 0.964. This curve is used for the prediction of the ring radius values.
It has been shown that it is possible to predict the evolution of the local deformation as a function of the sensor readings and the process schedule. This method is applicable without modification to be performed on a real machine. However, it is necessary to regenerate data for each specific ring geometry and according process parameter window.
4.4 Thermal model
The goal of this model is the precise determination of the temperature in the part along with of the evolution of the temperature depending of the cooling parameter schedule \(h_c\). Due to the small size of the parts studied here, in contrast to the more traditional ring rolling, the temperature difference between the surface and the interior of the part is relatively small (5–30 K). From a physical point of view, two elements influence the temperature of the part: the cooling by the tools and the air flow tend to decrease the temperature, and the dissipation of the plastic deformation energy tends to increase the temperature of the part. From the simulation results, it is shown that the forming energies are about 20 times smaller than the thermal exchange. The temperature is thus only marginally dependent on the plastic strain rate, and thus on the roll speed. Therefore initially, the influence of this parameter on the temperature and its evolution will be neglected.
In the real system, the temperature, as the difference between the internal and surface temperature is very small, the simple delay created by the filtering used allows to model efficiently the temperature. Figure 9 shows the distribution of the absolute error between the predicted and actual temperature obtained from the database. A good correspondence can be observed, and errors are limited to 8 K. The determination of the temperature evolution is more complex. In the virtual system, the parameter influencing the temperature is the cooling rate \(h_c\). In the real system, this value would be the opening of the valve controlling the air flow. The method used for the identification of a behavior law is also transferable to the real system. It is assumed, that the evolution of the temperature follows a curve of exponential decrease such as:
where \(\tau\) and \(\theta _{\infty }\) are two parameters depending on \(h_c\), and \(t_0\) is the beginning of the extrapolation. The two parameters are determined for each simulation using the Differential Evolution algorithm from SciPy [24]. Figure 10 shows the dependency between \(\tau\), \(\theta _{\infty }\) and \(h_c\). Regressions are then performed, with R-square close to 0.90 for both fits. This extrapolation can the be used to predict the influence of the temperature following a scheduled \(h_c\). The predicted values can then be used along the plastic strain to determine the hardness evolution.
5 Model based process control
5.1 Concept: moving horizon predictive control
Nonlinear model predictive control (NMPC) is a method often employed in combination with processes with highly nonlinear models and has been used for more than three decades now [26]. In this framework, a prediction of the process output as a function of the process parameters for a given horizon is computed. The difference to the actual target is then calculated using a cost function. An optimization is then performed to calculate the optimal process parameters. This routine is repeated at a given frequency. The study of the stability of this method or its accuracy is very complex and it is sometimes difficult to obtain an a priori confirmation of the parameters of the controller and of the validity of this strategy [25]. The use of the digital twin allows a first study of the proposed concept.
Three elements are required for the controller. A model for the prediction of the evolution of the target value on the considered prediction horizon, the soft sensor presented above, a cost function and an optimizer. In the following section, cost function and the optimizer used are briefly described.
5.2 Cost function and optimizer
For these first tests the horizon is defined at \(t + {5}\,\hbox {s}\) and the controlling rate is set at 0.5 s.
Figure 11 represents the result in relative hardness obtained for the 20 simulations used in the previous section, obtained with different values of starting temperature, cooling rate and roll speed. It can be seen that depending on the parameters very different values of final hardness can be achieved. One curve is chosen as a virtual target and it is highlighted on the figure. The cost function is as follows:
where \(h_{\text {pred}}\) is the predicted value of the relative hardness, \(h_{\text {targ}}\) the target value, \(t_n\) varies between \(t_0\) the actual time and \(t_n\) the actual time plus 5 seconds, with a prediction frequency of 200 Hz (identical to the soft sensor sampling frequency).
The optimizer enables the finding of an optimal set of process parameters minimizing the cost function in the considered domain. Here, it is a rectangle defined by the boundaries of \(h_\text {c}\) and \(v_\text {t}\). Due to the use of a DNN in the function used, the smoothness is not guaranteed, and the determination of a robust local gradient by a numerical method is not obvious. Therefore, differential evolution, from the python package SciPy, is used. This method has the advantage of offering a good coverage of the whole domain. A similar method has been successfully used for the control of a cutting process by Potočnik et al. [27].
The use of this controller in parallel with the digital twin, presented in the first section, is not without difficulty. Indeed, LS-DYNA does not propose any subroutine allowing an easy implementation of such a complex controller. To counter this problem the simulation is executed piecewise with stops at regular intervals, corresponding to the control frequency. At each stop a memory dump is written to prepare a restart of the simulation. Several scripts, written in Python, enable the simulation of the sensor signals, the operation of the soft sensor and the controller, the writing of a restart file and the restart of the simulation. In this way, it is possible to combine the proposed controller with the finite element simulation. The penalty in terms of calculation time is about 20% and is essentially due to the access time for reading and writing of the d3dump and d3plot files (simulation results). This system is illustrated in Fig. 12.
5.3 Results using the controller
Figure 13 shows the results obtained with the controller for two simulations with two different start temperatures. The parameters at the beginning of the simulation are set to \(v_t\) = 25% of the allowed range, and \(h_c\) = 50% of the range. Here, relative hardness here is calculated directly from the plastic deformation and temperature values from the FEM simulation and can therefore be considered as the “true” value.
Deviation occur between the target and the exact value, but the controller is able to reach the required goal. On average the optimizer reaches a minimum for the cost function within 60 function evaluations. The controller is able to react to variation between predicted value and target and to adapt process parameter to follow the given hardening curve.
These tests confirm that the controller is able to adapt to this first perturbation, is able to find a set of optimal parameters allowing to reach a fixed hardness objective. The controlling period of the controller is high (0.5 s) but is still sufficient to regulate this process. Moreover, it is clear that the soft sensor is able to predict with a sufficient accuracy the evolution of the process over a rather long period (here 5 s of horizon time).
In summary, it is shown that this framework allows the study of the controller in an easier environment compared to its implementation in a real system. Further verification, with other perturbations, but also other parameters for the controller, remain to be investigated.
6 Conclusion
In this paper, a concept for hardness control in a thermomechanical TPRR process using a soft sensor based on a combination of different model types, data-based, physics-based and mixed, has been presented. A framework for testing and evaluating this model with a digital twin has been introduced. A first example of the capabilities of the controller has been demonstrated using virtual experiments.
The following work will focus on the evaluation of the controller and its transferability to a real system: the influence of the control frequency and the horizon time will be studied, as well as the stability and the accuracy against different disturbances.
Moreover, the integration of a sensor allowing the identification of the evolution of the microstructure as proposed by [2] would make it possible to limit the errors due to the hardness model.
Further investigations are needed to fully validate the possibility of ring rolling control, but the results presented here are promising as controller stability could be established for a first disturbance.
References
Brosius A, Tulke M, Guilleaume C (2019) Non-linear model-predictive-control for thermomechanical ring rolling. In: COMPLAS XV: proceedings of the XV international conference on computational plasticity: fundamentals and applications, pp 499–509
Hütter S, Lafarge R, Simonin J, Mook G, Brosius A, Halle T (2021) Determination of microstructure changes by Eddy-current methods for cold and warm forming applications. Adv Ind Manuf Eng 2:100042
Paulig G (1988) Untersuchungen zur Vermeidung von Rissen beim Kaltwalzen von Wälzlageraußenringen, Dissertation TU Dresden
Tauchnitz I (1992) Einflußgrößen zur Verfahrensmodellierung beim Kaltwalzen von Wälzlagerringen, Dissertation TU Dresden
Gebauer G (1985) Ein Beitrag zur Fertigung von Wälzlagerringen mit asymmetrischen Querschnitten, Dissertation TU Dresden
Eberlein L (1994) Lange Lebensdauer—Kaltwalzen von Kugellagerringen ist wirtschaftliche Alternative zum Spanen. Maschinenmarkt, Würzburg, p 28
Zouhar G, Thoms V, Voelkner W, Förster W (2000) Werkstoffentwicklung für das Walzen ring-und rohrförmiger Maschinenelemente. In : Conference on proceedings of Antriebstechnik/Zahnradgetriebe, Dresden, pp 211–226
Ficker T, Hardtmann A, Houska M (2005) Ring rolling research at the Dresden University of Technology—its history from the beginning in the 70s to the present. Steel Res Int 76(2–3):121–124
Ryttberg K, Wedel MK, Recina V, Dahlman P, Nyborg L (2010) The effect of cold ring rolling on the evolution of microstructure and texture in 100Cr6 steel. Mater Sci Eng A 527(9):2431–2436
Schwich G, Henke T, Seitz J, Hirt G (2014) Prediction of microstructure and resulting rolling forces by application of a material model in a hot ring rolling process. Key Eng Mater 622:970–977
Jenkouk V, Hirt G, Franzke M, Zhang T (2012) Finite element analysis of the ring rolling process with integrated closed-loop control. CIRP Ann 61(1):267–270
Kopp R, Koppers U, Wiegels H (1984) New control system for ring rolling. Adv Technol Plast 2:803–807
Choi H, Cho H (1989) An adaptive control approach to the ring geometry control for radial-axial ring rolling processes. Proc Inst Mech Eng Part C Mech Eng Sci 203:243–254
Cleaver CJ, Arthington MR, Mortazavi S, Allwood JM (2016) Ring rolling with variable wall thickness. CIRP Ann 65(1):281–284
Allwood JM, Music O, Raithathna A, Duncan SR (2009) Closed-loop feedback control of product properties in flexible metal forming processes with mobile tools. CIRP Ann 58:287–290
Dulieu-Smith JM, Stanley P (1998) On the interpretation and significance of the Grüneisen parameter in thermoelastic stress analysis. J Mater Process Technol 78:75–83
Fortuna L, Graziani S, Rizzo A, Xibilia MG (2007) Soft sensors for monitoring and control of industrial processes. Advances in industrial control. Springer, Berlin
Lin J, Liu Liu Y, Farrugia DCJ, Zhou M (2005) Development of dislocation-based unified material model for simulating microstructure evolution in multipass hot rolling. Philos Mag 85–18:1967–1987
Hahn YH, Yang DY (1991) UBET analysis of roll torque and profile formation during the profile ring-rolling of rings having rectangular protrusions. J Mater Process Technol 26(3):267–280
Tszeng TC, Altan T (1991) Investigation of ring rolling by pseudo plane-strain FEM analysis. J Mater Process Technol 27(1–3):151–161
Abadi M, Barham P, Chen J, Chen Z, Davis A, Dean J, others (2016) Tensorflow: A system for large-scale machine learning. In: 12th USENIX Symposium on operating systems design and Implementation (OSDI 16), pp 265–283
Kingma DP, Ba J (2015) Adam: a method for Stochastic optimization. In: 3rd International conference for learning representations
Seabold S, Perktold J (2010) statsmodels: Econometric and statistical modeling with python. In: 9th Python in science conference
Virtanen P, Gommers R, Oliphant TE, Haberland M, Reddy T, Cournapeau D, Burovski E, Peterson P et al (2020) SciPy 1.0: fundamental algorithms for scientific computing in python. Nat Methods 17(3):261–272
Allgöwer F, Zheng A (2012) Nonlinear model predictive control, vol 26. Springer, Berlin
Frank PM (ed) (2012) Advances in control: highlights of ECC? 99. Springer, Berlin
Potočnik P, Grabec I (2002) Nonlinear model predictive control of a cutting process. Neurocomputing 43(1–4):107–126
Acknowledgements
The authors would like to thank the Chair for Manufacturing Technology of the FAU Erlangen for performing the mechanical characterization at elevated temperatures. The authors thank the Center for Information Services and High Performance Computing (ZIH) at TU Dresden for generous allocations of computer time. The authors would like to thank the German Research Foundation DFG for the support of the depicted research within the priority program ‘SPP2183’ through project number ‘424337466‘ and under grants number ‘BR 3500/23-1’ and ‘HA5209 /11-1’.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Lafarge, R., Hütter, S., Tulke, M. et al. Data based model predictive control for ring rolling. Prod. Eng. Res. Devel. 15, 821–831 (2021). https://doi.org/10.1007/s11740-021-01063-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11740-021-01063-1