Abstract
Social insects allocate their workforce in a decentralised fashion, addressing multiple tasks and responding effectively to environmental changes. This process is fundamental to their ecological success, but the mechanisms behind it are not well understood. While most models focus on internal and individual factors, empirical evidence highlights the importance of ecology and social interactions. To address this gap, we propose a game theoretical model of task allocation. Our main findings are twofold: Firstly, the specialisation emerging from self-organised task allocation can be largely determined by the ecology. Weakly specialised colonies in which all individuals perform more than one task emerge when foraging is cheap; in contrast, harsher environments with high foraging costs lead to strong specialisation in which each individual fully engages in a single task. Secondly, social interactions lead to important differences in dynamic environments. Colonies whose individuals rely on their own experience are predicted to be more flexible when dealing with change than colonies relying on social information. We also find that, counter to intuition, strongly specialised colonies may perform suboptimally, whereas the group performance of weakly specialised colonies approaches optimality. Our simulation results fully agree with the predictions of the mathematical model for the regions where the latter is analytically tractable. Our results are useful in framing relevant and important empirical questions, where ecology and interactions are key elements of hypotheses and predictions.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Social insects are among the ecologically most successful life forms. They live in elaborately organised colonies, capable of managing a complex network of simultaneous tasks, from scouting and foraging to colony defence, nest building, thermoregulation, and brood care. One of the key factors for their ecological success is the colony’s ability to efficiently allocate its workforce to these different tasks, responding to frequent changes in external conditions and internal requirements (Charbonneau et al. 2013; Grimaldi and Engel 2005; Hölldobler and Wilson 2009; Oster and Wilson 1978; Hölldobler and Wilson 1990; Charbonneau and Dornhaus 2015a; Duarte et al. 2011; Fewell and Harrison 2016; Gordon 1996, 2016; Kang and Theraulaz 2016; Mersch 2016; Robinson 1992). Individual workers select their tasks without any central coordination or control. Deciphering the individual-based rules behind task selection is thus at the heart of understanding how colonies can achieve their collective plasticity in task allocation.
Task allocation in social insects has received a significant amount of attention (Robson and Traniello 2016). The majority of research has focused on the influence of internal factors such as genetics (Oldroyd and Fewell 2007), morphology (Oster and Wilson 1978), and hormones (Robinson 1987). Comparatively, little attention has been given to the underlying mechanisms of social interactions and their role in regulating task allocation. Investigating the mechanistic roles of these factors has recently been proposed as the foundation to a more comprehensive understanding of task allocation (Gordon 2016).
The number of workers performing specific tasks obviously needs to be adjusted to the environment, and this is empirically substantiated in several species (Duarte et al. 2011; Schmickl and Karasai 2019). However, studies have not found that the proportions of morphologically specialised workers change (Gordon 2016; Oster and Wilson 1978; Beshers and Traniello 1996). Thus, it is clear that task allocation must be influenced by dynamic task selection mechanisms at the level of pluripotent individuals. Evidence for this in individual species has been established for quite some time (Gordon 2018; Anderson and Ratnieks 1999; Odonell et al. 2000). In other words, individuals—at least in some species—do adjust their task profiles in reaction to the environment.
Unsurprisingly, a comprehensive survey of research into self-organised task allocation (Duarte et al. 2011) cites environmental conditions alongside genetics, morphology, developmental and nutritional factors, and colony life cycle as a major influence on task choice. Likewise, but on evolutionary time scales, a more recent study of the relation between brain size and task specialisation showed the same influence of environmental conditions (Feinerman and Traniello 2016).
This influence of ecology on task choice at the individual level has not yet been studied widely enough to obtain a clear and complete picture of individual-based mechanisms.
In this context, the purpose of the present paper is twofold: Firstly, we aim to establish a new modelling framework for self-organised task allocation that addresses some of the gaps in current approaches and that allows us to systematically investigate how differences in environment and task characteristics influence individual task choice and collective allocation. Secondly, using this formal framework, we show that the environment can determine whether and to which degree specialisation occurs.
We find that specialisation can emerge from interactions between individuals alone, under a large range of environmental conditions. Our model shows that the ecological conditions are a crucial determinant for the emergence of different forms of specialisation.
More specifically, we investigate whether individual workers focus fully on a single task type or whether they divide their energy between multiple task types. We term the former strong specialisation and the latter weak specialisation. Our model shows that a single fixed set of behavioural rules can result in strong or weak specialisation, depending only on the environmental conditions to which the colony is exposed. While this is almost certainly not a universal feature in all scenarios, our analysis shows that this is a characteristic of biologically plausible scenarios. Contrary to intuition, we also find that strong specialisation can be detrimental to colony efficiency.
Our theoretical results thus point towards promising new directions for empirical work that can bring us a step closer to understanding how social insects achieve their outstanding ecological success.
2 Related work
Mathematical and computational models already play an important role in the analysis of task allocation—see Beshers and Fewell (2001), Duarte et al. (2011) for comprehensive reviews. However, they have limitations when trying to address self-organisation in the context of direct social interaction.
Response threshold models are arguably the most established (Jeanson and Weidenmüller 2014; Jeanne 2016). These models assume that individuals have an internal task-related response threshold and that they are more likely to respond to a task stimulus the more it exceeds this threshold (Bonabeau et al. 1996; Theraulaz et al. 1998; Page and Mitchell 1998; Jeanson et al. 2007; Gove et al. 2009; Graham et al. 2006; Duarte et al. 2012). As an alternative to individual thresholds as causes, the foraging-for-work model shows that differentiation in task allocation can emerge from a colony of identical workers, given non-random distribution of task demands in space (Franks and Tofts 1994; Tofts 1993; Tofts and Franks 1992; Tripet and Nonacs 2004).
How direct interactions modulate task choice has been widely discussed in the empirical literature which suggests that social context is a significant determinant of task engagement (Duarte et al. 2011; Charbonneau and Dornhaus 2015a; Cook and Breed 2013; Gordon and Mehdiabadi 1999; Greene and Gordon 2007). Social interaction has provided an important alternative to the response threshold assumption and other forms of stigmergic communication in modelling task allocation (Beshers and Fewell 2001; Fewell and Bertram 1999; Hogeweg and Hesper 1983; Gordon 1996, 2016; Pereira and Gordon 2001; Kang and Theraulaz 2016; Beshers et al. 2001; Huang and Robinson 1992, 1996; Naug and Gadagkar 1999). However, these models generally do not address self-organisational properties (Beshers and Fewell 2001) and do not typically provide a mechanism of task selection at the individual level. Two interaction-based models that are closer in spirit to our approach are Gordon et al. (1992), Pacala et al. (1996). These are considered in detail in the concluding discussion.
To overcome the limitations outlined above, our proposed new modelling framework is based on game theory and directly incorporates social interactions and environmental conditions as the main factors. Although game theory is a well-established toolbox for the study of interdependent decision-making and has been very successfully applied to many other aspects of sociality in biology (Izquierdo et al. 2012; McGill and Brown 2007; Dugatkin and Reeve 1998; Broom and Rychtář 2013), it has gone virtually unnoticed in the study of task allocation. An exception is Wahl (2002), which investigates co-viruses. However, this study addresses evolutionary time scales rather than behavioural change in an individual’s lifetime.
We use Evolutionary Game Theory (EGT) to investigate how individual task preferences develop in the lifetime of a colony and how specialisation can emerge as a result of these choices (Maynard Smith 1982; Brown 2016). It is important to note that we do not make any reference to evolutionary processes. Rather, our model addresses behavioural change on the scale of colony lifetime. We are not the first to use EGT in this way. EGT has been used before effectively to model behavioural change in ecological time scales (Izquierdo et al. 2012; Traulsen et al. 2009).
We model task allocation as a simple game. Individuals choose how to divide their energy between different tasks. Task performance results in rewards that can be shared between colony members or go directly to the individual. Rewards are modulated by collective levels of investment into the tasks as well as by environmental factors. Groups of individuals repeatedly engage in collective task execution and modify their task selection strategies based on the rewards they receive individually or collectively. This framework provides a large degree of flexibility via simulations, while also allowing for mathematical predictions based on game theory (Hofbauer and Sigmund 1998). Importantly, it is aligned with empirical evidence identifying social interactions and ecology as key factors (Franklin et al. 2012; Ravary et al. 2007; Robinson et al. 2012; Jeanson et al. 2008; Gordon and Mehdiabadi 1999; Greene and Gordon 2007; Cook and Breed 2013).
3 Models and methods
3.1 A task allocation game
Any colony needs to balance its workforce allocation between different tasks in response to the conditions of the environment. As there is no centralised control mechanism, this allocation can only emerge from the task selection decisions that individuals make. From the perspective of the individual, task engagement can be driven by the costs and benefits of the task and by the task choices of other individuals. This suggests game theory as an appropriate framework to investigate task allocation mechanisms. More specifically, shared benefits and individual costs place our scenario squarely into the context of public goods games (Sigmund 2010; Archetti et al. 2011). Consistent with standard game theory terminology, we use the term “benefits to the individual.” However, it is important to note that in social insects this may well be a proxy for colony benefit perceived by an individual rather than a direct benefit to the individual. As an example, individual workers can estimate the level of hunger in the colony by the rate of contact with hungry individuals. A reduction in this rate could constitute a benefit proxy perceived by an individual.
We assume a large group of workers in a colony, who need to balance two prototypical tasks with different characteristics. While in a real colony clearly more than just two tasks need to be balanced, this appears as a natural starting point to achieve a principled understanding, in line with standard binary choice experimental assays.
Different ecological conditions are captured in our model through the payoffs of task execution, which vary across different environments (costs and benefits). Payoffs occur on the group level as well as on the individual level. For example, the benefit of foraging is shared across the whole group. We abbreviate these group-level payoffs, which are typically benefits, as B. However, the cost of task execution, which can be thought of as primarily metabolic or energetic in nature, is incurred on the individual level. We abbreviate this (negative) payoff on the individual level as C. The total payoff \(\varPi _i\) to a single individual i thus equals its share \(B_i\) of the benefits generated by the group minus the cost \(C_i\) of performing its particular tasks.
We use EGT to investigate how individuals modify and adjust their task choice behaviour based on simple rules that take only individual experience and social information into account. Importantly, unlike in classical game theory, there is no underlying assumption of rationality for the individuals and the processes are not driven by striving for collective efficiency or optimality. Only individual behaviour enters explicitly into the model and colony-level task allocation patterns arise solely as an emergent property.
In our model, individuals can choose between two competing tasks, with a regulatory task T (for thermoregulation) and a maximising task F (for foraging) as prototypical examples. T represents a homeostatic task: colonies need to maintain nest and brood temperature within certain bounds, for which a certain amount of collective effort is required. Allocating too little collective effort to this task can lead to regulation failure. Allocating too much effort does not improve the homeostasis and may in fact lead to suboptimal regulation, such as overcooling. Thus, group benefit for T as a function of group effort is a strictly concave function: the maximum benefit is obtained at an intermediate level of group effort. While a sound assumption for our regulation task, concavity does of course not apply to all collective tasks. Collective transport, for example, can exhibit convex benefits in group effort. Similarly, our foraging task F exhibits different characteristics due to the fact that it maximises the net energy intake: the benefit from F is monotonically increasing with the collective effort devoted to foraging. While foraging is not necessarily always a maximising task, this is a commonly used currency in foraging models that is consistent with empirical insights in many scenarios (see Charlton and Houston 2010 for a discussion regarding bumble bees).
What counts is that the specific task types chosen here are biologically plausible; there are clearly many other relevant configurations. As outlined above, our purpose at this point is not to perform an exhaustive evaluation of possible scenarios but to establish that there are plausible scenarios in which the environment conditions determine specialisation patterns. For this, the choice of a single, simple starting point is sound and justified as long as it is plausible and relevant.
Individual task preferences can be determined by an inherent response trait (Duong and Dornhaus 2012; Jeanson et al. 2005; Gordon 2010). The response trait of an individual i is modelled as a continuous value \(0 \le x_i \le 1\), which represents the fraction of effort that individual i invests into task T. Conversely, worker i will invest \(1 - x_i\) effort into task F. This approach is closely related to the familiar concept of a response probability: under the assumption that there is a response probability \(p_i\) for worker i to engage with task T when faced with the choice between F and T, the expected amount of effort invested in T is directly proportional to \(p_i\) (and thus to \(x_i\)).
The state of the colony at any time is given by a vector \((x_i)_{i =1 \ldots N}\). We assume that workers’ interactions are restricted to groups of size n, where \(n < N\). Thus, parameter n accounts for physical and spatial colony constraints. For example, a fanning worker will cool brood only locally, not in every location of the brood chamber. Likewise, social interactions can only take place when workers are in proximity and are thus limited to smaller groups at any point of time.
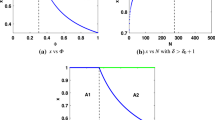
Examples benefit and cost functions. A Individual benefit as a function of collective group effort. The benefit reaches a maximal value only if the proportion of group workforce allocated to both tasks is appropriate. B Individual cost as a function of her own strategy. For \(r < 1\), foraging tends to be more expensive than regulation and the cost is minimised for \(x_i = 1\). For \(r > 1\), regulation tends to be more expensive than foraging and the cost is minimised for \(x_i = 0\). For \(r =1\) both tasks tend to be equally costly
Individual payoffs depend on \(x_i\), as well as on the collective effort invested by all workers in the group \(X=\{x_j | j=1, 2,\ldots , n\}\). More specifically, worker i receives payoff
where B(X) is the total benefit for the group, \(B_i=\frac{1}{n}B(X)\), and \(C_i=C(x_i)\) is the cost for worker i. This reflects that benefits arising from both tasks are shared, whereas costs are borne individually. In the context of our specific scenario, both tasks must be performed to ensure colony fitness: poor maintenance of nest temperature can slow down the development of the brood and some brood may not survive if there is a shortage of food intake. Hence, the total benefit is multiplicative in the benefits of each task.
where \(B_T(X)\) and \(B_F(X)\) are the benefits of task T and F, respectively.
The functions \(B(\cdot )\) and \(C(\cdot )\) thus capture the environmental conditions. Other task compositions would be modelled by a different composition of the individual benefits in the total benefit B(X). For example, two alternative tasks would be represented by additive composition.
Costs, on the other hand, are generally additive:
where \(C_T(x_i)\) and \(C_F(x_i)\) are the costs of task T and F, respectively.
The cost of the regulatory task \(C_T(x_i)\) is linear in the effort \(x_i\). Consider cooling fanning in bees: the amount of energy required depends on physiological factors of the individual, but it is proportionate to the length and intensity of the fanning activity (effort). For the maximising task, we assume marginally decreasing costs, i.e. \(\forall x:\ C_F'(x) >0\) and \(\forall x:\ C_F''(x) <0\). This reflects efficiency improvement through task experience. A foraging bee may become more efficient at finding high value flowers, and thus, the marginal investment for an additional unit of food decreases.
To investigate how colonies perform in different environmental conditions, we introduce two further parameters b and r that link cost and benefit to the characteristics of the environment (Fig. 1). Parameter b captures the ratio between the benefit and cost of task F. Larger values of b represent abundant ecologies where foraging is cheap, whereas small values of b indicate that foraging is more costly. Similarly, r is the cost ratio of T and F, i.e. \(r > 1\) implies thermoregulation is more expensive than foraging per unit effort, for example when the nest temperature is highly above or below the optimum level, and vice versa. Full details are given in the Appendix 1.
We now turn to defining how individuals may use their payoffs to adjust their responses, represented by trait values. We consider and simulate two widespread update rules that are at two opposite ends of the spectrum of individual information processing: individual learning and social learning. In social learning, individuals rely completely on social information to adjust their behavioural choices. In individual learning, individuals rely exclusively on their own experience when altering their behaviour. These two modes are at the two opposing ends of a spectrum and demand different cognitive skills. We hope that carefully studying these two extremes sheds light on the role that different learning assumptions can have in the dynamics. We implement this process in an agent-based model and compare the outcomes to an analytic treatment using adaptive dynamics (Doebeli 2011).
The simulations start from a homogeneous population. At each time step, individuals form random groups of size n and engage in interactions modelled by the game described in Eq. 2, receiving a payoff according to the collective investment in the task and the individual costs. The population then adjusts strategies based on the learning mechanism.
3.2 Individual learning
Individual learning is likely to influence the task performance and responsiveness of colony members in social insects (Jeanson and Weidenmüller 2014; Ravary et al. 2007; Jones et al. 2015; Chittka and Muller 2009). Individuals can adapt their strategies by exploring the current context with previously acquired information (Rendell et al. 2010; Grüter and Leadbeater 2014). Here we use a simple assumption that individuals assess and improve their strategies by making comparisons between their current and previous task performance. More specifically, each individual explores a new strategy with a small probability and switches to it only if the new variant provides a larger payoff in the same environment. This is akin to the ideas of reinforcement learning (Izquierdo et al. 2012; Sandholm 2010) and stochastic hill climbing (Michalewicz and Fogel 2013).
We run an agent-based simulation describing how the population changes across discrete time steps. A heterogenous population is given by a set of \(x_i\) values, for \(i = 1 \ldots N\). In each learning period, each individual will explore a new strategy with probability \(\beta\). If individual i is chosen to explore a new strategy, her new trait is sampled from a normal distribution with mean \(x_i\) and standard deviation \(\gamma\)—the later can be conceived as an exploration parameter. Individual i will adopt her new strategy only if it outperforms the current strategy across k games. The process is described in detail in Algorithm 1.

We note that the exploration loop starting on line 6 of Algorithm 1 can be considered synchronous, i.e. all explorations happen during the same time step t. This is a standard assumption in Evolutionary Game Theory models, whose potential implications have been described elsewhere (Huberman and Glance 1993). Note that the reward associated with a particular strategy is averaged over k groups of co-players, i.e. individuals decide to switch to a new strategy on the basis of its average performance over k different groups.
3.3 Social learning
Although not widely discussed in the context of social insects (Grüter and Leadbeater 2014), social learning is found by empirical studies in bee foraging (Leadbeater and Chittka 2007a; Grüter and Leadbeater 2014; Worden and Papaj 2005; Leadbeater and Chittka 2005, 2007b, 2008; Jones et al. 2015). Social learning has also been established in social spiders (Pruitt et al. 2016, 2018), with the important distinction that these are not eusocial. At the core of our notion of social learning is the concept that an individual copies the behaviour of another individual. This obviously requires a direct interaction or observation. Due to the potential complexity involved, we make no specific assumptions on the proximate mechanisms of social information exchange. We simply assume that individuals are more likely to copy the strategies of others who are successful. Each individual also can explore a new strategy with a small probability. This is similar to the Wright–Fisher process (Imhof and Nowak 2006) or Roulette wheel selection in Evolutionary Computation (Fogel 2000).
We run an agent-based simulation describing how the population changes across discrete time steps. Similar to the case of individual learning, a heterogenous population is given by a set of \(x_i\) values, for \(i = 1 \ldots N\). Likewise, during each learning period each individual will explore a new strategy with probability \(\beta\). If individual i is chosen to explore a new strategy, her new trait is sampled from a normal distribution with mean \(x_i\) and standard deviation \(\gamma\). In contrast to the case of individual learning, here individual i will adopt her new strategy by copying successful strategies in the population with a higher probability. The process is described in detail in Algorithm 2.

Note that individuals that reproduce (Line 9–12 of Algorithm 2) will occupy a random position in the next generation and will therefore face different individuals each time the payoff is evaluated. Thus, similar to Algorithm 1, the performance of a single strategy is evaluated based on its evaluation across different groups. This is a standard assumption in the literature on n-player games (Gokhale and Traulsen 2010).
4 Results
4.1 Long-term dynamics
Our results show that colony-level task specialisation can emerge from the interaction dynamics between individuals and their environments alone (see strong specialisation in Figs. 2 and 3). Under a certain range of environment conditions, the workforce of colonies initially consisting of individuals with identical strategies splits into different groups. In each group, individuals specialise in a single task (strong specialisation), which is driven by social interactions.
Behavioural patterns for individual learning. A The phase space diagram describes the long-term outcomes of task allocation for the model with individual learning over a range of values for parameters b and r. The inset figures B–E are scatter plots of trait values for all individuals against time. They show three typical cases of how individual strategies (x) in a colony develop over time (t). A colony is inviable (B and C) if the average payoff of individuals is not positive, which means that they fail to coordinate and only respond to a single task. Strong specialisation D means that the workforce of a colony splits into two different groups each of which focuses exclusively on a single task. Weak specialisation E means that each individual invests her effort on both tasks. Appendix 3 describes the procedure we follow to classify these results from our simulations
We also find that different environmental conditions (characterised by b and r) can cause variation in task allocation patterns, even in the absence of variation in the underlying individual-based mechanisms. As shown in Figs. 2 and 3, strong specialisation tends to emerge in environments with scarce or poor food resources (when b is small). As the quality of food resources in the environment improves (b increases), individuals are less likely to strongly specialise. Individuals may still prefer one task over the other (\(x_i \ne \frac{1}{2}\)) to balance global demands, but their strategies tend to be consistent across the colony (weak specialisation). Unlike b, the cost ratio r between tasks appears to have a small effect on the behavioural patterns at the colony level.
Behavioural patterns for social learning. A The phase space diagram gives the long-term patterns of task allocation of colonies based on the model with social learning in a range of values for parameters b and r. The inset figures B–E are scatter plots of trait values for all individuals against time. They show three typical cases of how individual strategies (x) in a colony develop over time (t). A colony can be either inviable (B and C), strongly specialised (D) or weakly specialised (E). Being inviable means that the average payoff of individuals in a colony is not positive, and the overall task allocation is out of balance as individuals only respond to a single task. Strong specialisation means that the workforce of a colony splits in two groups each of which specialise in a single task. Weak specialisation means that each individual spends her energy on both tasks. Appendix 3 describes the procedure we use to classify the above results from the simulations
We also fix b and explore how different patterns of task allocation result from changes in group size. These results are shown in Fig. 4. The general prediction is that larger groups are more prone to strongly specialise. This resonates with previous findings addressing similar questions in different models (Karsai and Phillips 2012; Karsai and Wenzel 1998).
The dynamics of our task allocation games are similar to those arising from the continuous Snowdrift game (Doebeli et al. 2004). They can be analysed using a technique known as adaptive dynamics, which is one of the best established methods to analyse EGT models in closed form. It allows us to derive a deterministic approximation of the stochastic dynamics of an EGT model using an infinite population approximation and the assumption of small local variation (Geritz et al. 1997). A full analytical treatment that confirms our simulation results for individual learning and social learning is given in the Appendix. The theoretical prediction, shown in Fig. 5, matches our simulation results presented in Figs. 2A and 3A.
4.2 Efficiency analysis
Although colony optimality is not the driver of the emerging colony organisation, we can use it to quantify group-level efficiency. To do so, we use the notion of relative colony performance, which is the ratio between the average payoff achieved by individuals in a colony and the level of payoff that could be achieved with optimal workforce allocation. This concept is related to the price of anarchy, used in computer science to quantify the cost of decentralised organisation (Koutsoupias and Papadimitriou 2009).
To measure the colony performance, we take parameters b and r and determine if the long-term outcome is a monomorphous or dimorphous population, by computing the equilibrium \(x^*\) and inspecting the higher-order derivatives of the invasion fitness at that point. If the dynamics is monomorphous, the average payoff in equilibrium can be calculated directly using b, r, and \(x^*\), because all the individuals will choose strategy \(x^*\). If the population is dimorphic, we use the replicator equation to determine the frequencies at which specialists choose to fully engage in either task, \(\rho ^*\). With \(\rho ^*\), b, and r, we can compute the average payoff in equilibrium. We divide the average payoff by the optimal payoff, derived from optimising the group payoff. Details for the calculations are given in the Appendix.
As shown in Fig. 6, we find that relative colony performance varies with environmental conditions. Different ecologies result in different forms of specialisation, which in turn leads to different levels of relative colony performance. A relative colony performance of 1 indicates optimality.
Interestingly, weakly specialised colonies turn out to perform close to optimal, while strongly specialised colonies can perform suboptimally. This prediction pertains to both, individual and social learning. Since learning is performed by strategy copying, an individual in a strongly specialised colony can only change strategy by switching tasks completely. Such a task switch can incur significantly higher costs for the individual with only a marginal positive impact on the shared benefit (cf. Fig. 1). Such a switch may be prohibitive from the individual perspective even though it can be beneficial for the colony. In a weakly specialised colony, on the other hand, the individual can adjust her distribution of effort in arbitrarily small steps and thus ensure that a strategy modification represents an improvement from the individual perspective. Such a strategy modification will be performed, nudging the colony in the right direction. Thus, learning can take place more gradually in weakly specialised colonies, accounting for the overall better performance.
Relative colony performance. For a pair of b and r values, the efficiency is the ratio between the mean of individual long-term payoffs and the optimal level that can be theoretically achieved under the environmental condition. Efficiency ranges from 0 to 1. For simplicity, we regard the efficiency of inviable colonies as 0 in which case there does not exist an equilibrium of individual strategies
4.3 Dynamic environments
We find that different learning mechanisms can lead to varying behavioural patterns under environmental fluctuations. Our results suggest that individuals in the colonies based on individual learning tend to flexibly adjust their strategies according to the current environmental conditions. As seen in Fig. 7, the colony based on individual learning changes from weak specialisation to strong specialisation when foraging becomes less profitable (b decreases) and switches back to weak specialisation once the environmental condition has reverted to the original state. This allows the colony to be near optimal efficiency in spite of the environmental fluctuations.
Individual learning and social learning in dynamic environments. We compare the dynamics of learning when the conditions of the environment change between two conditions in which social organisation differs. Panels A and B refer to individual learning, while panels C and D refer to social learning. For individual learning, B—top graph depicts the dynamics of individual strategies (x)—and (B)—bottom graph shows the relative colony performance (\(\varPi ^{'}\)) in a colony over time (t) under environmental fluctuations. The environment is set as three stages: (1) Condition 1 (\(b = 40\)) for \(t \in [0,\,100\,000]\); (2) Condition 2 (b is switched to 10) from \(t = 100\,000\) to \(t = 200\,000\); (3) Condition 1 (b is switched back to 40) until the end of simulation (\(N = 2000\), \(t_{\mathrm{end}} = 300\,000\), \(n = 10\), \(r = 0.7\), \(\beta = 0.001\), \(\gamma = 0.1\), \(k=1000\)). Similarly, for social learning, D—top graph gives the dynamics of individual strategies with the mean—and D—bottom graph illustrates the relative colony performance under environmental fluctuations. The environment is also set as three stages: (1) Condition 1 (\(b = 40\)) for \(t \in [0,\,20\,000]\); (2) Condition 2 (b is switched to 10) from \(t = 20\,000\) to \(t = 40\,000\); (3) Condition 1 (b is switched back to 40) until the end of simulation (\(N = 2000\), \(t_{\mathrm{end}} = 60\,000\), \(n = 10\), \(r = 0.7\), \(\alpha = 2.5\), \(\beta = 0.01\), \(\gamma = 0.005\), \(k=1\)). Here A and C correspond to the region diagrams in Figs. 2 and 3, respectively. The top graphs in (B) and (D) are scatter plots of trait values for all individuals against time with the mean trait value indicated by a red line
Surprisingly, for social learning, our results suggest that the colony-level patterns of task allocation do not only depend on the current condition of the environment, but also on the history of these conditions. As illustrated in Fig. 7, when b decreases, the colony based on social learning changes from weak specialisation to strong specialisation. However, when the environmental conditions return to the original state, the pattern of task allocation at the colony level does not revert to the original pattern of organisation, and the colony cannot regain its original performance. In other words, suboptimal outcomes arise.
In social learning, individuals mainly decide their strategies by directly copying others. Therefore, when the behavioural state of the colony is steady in strong specialisation, individuals can hardly switch to weak specialisation even though the environmental condition changes back to the previous one when weak specialisation arises. In contrast, individuals adjust their strategies gradually based on their interactions with others for individual learning and thus can behave flexibly under fluctuating environmental conditions.
5 Discussion
In order to be able to analyse the function of social interactions, our EGT-based approach explicitly integrates interactions as a fundamental component. The two most commonly used types of models in task allocation, response threshold models (Beshers and Fewell 2001; Jeanson and Weidenmüller 2014) and foraging-for-work models (Tofts and Franks 1992; Tofts 1993), share the characteristics that groups of independent individuals are described as acting in parallel. Interaction between these individuals only takes place indirectly through modification of the environment (stigmergy). There is no genuine place for social interactions in these models. A good example is Theraulaz et al. (2002). It shows how task partitioning can arise based on an empirically validated response threshold model of hunting in Ectatomma ruidim. However, the two tasks analysed (stinging and prey transport) are directly coupled via their stimuli as stinging produces more corpses that require transport. In contrast, our work is concerned with competing tasks that are not directly coupled via stimuli and where task selection is guided by individual and social experience. Two earlier models that incorporate interactions and are close in spirit to our approach are Gordon et al. (1992), Pacala et al. (1996). There are a few important fundamental differences between Gordon et al. (1992) and our work: Firstly, the task selection behaviour (or learning behaviour) in Gordon et al. (1992) is hard-wired into the model, whereas we consider this as a parameter of the model. Indeed, a main use of our model is to analyse the ramifications of different learning behaviours. Secondly, Gordon et al. (1992) use only the relative number of task-specific encounters as input into the individuals’ decision-making process, whereas we use an environmentally modulated task experience. This provides a hook to model the influence of environmental factors more generally. Pacala et al. (1996) present and analyse a very interesting stochastic model of task choice and worker interactions that introduces the notion of “successful” versus “unsuccessful” task execution. Like in our model, task switching behaviour depends on interactions with other workers that have not just executed a task but have done so successfully. However, the notion of success in Pacala et al. (1996) is binary and thus not fine grained enough to capture the environment-related characteristics of a task, for example “diminishing returns.”
The EGT framework allows us to easily exchange the underlying mechanisms of learning and compare the effects of such changes. We have exploited this capability to compare the dynamics of social learning with that of individual learning. Our analysis reveals similar outcomes in behavioural patterns of task allocation by comparing individual learning and social learning. In our simulations, both types lead to different types of specialisation depending on the environment (or, in broader terms, the ecology). The most striking aspect of this is that the ecology alone can determine which type of specialisation arises, without any changes in the underlying proximate mechanisms of task selection.
Our model is based on costs and benefits perceived by the individual. In the context of eusocial insects, it is important to point out that this includes the possibility of a proxy for colony-level benefit that can be perceived by an individual. Such a proxy could be based on direct interactions, such as contact rates with food bearing workers, or stigmergic, such as the level of the honey pots in bumblebee colonies. On the other hand, in animals that are social but not eusocial, such as social spiders, the benefit accrues directly to the individual.
Having tasks costs and benefits as core components of the modelling approach enables us to directly address how characteristics of the environment influence task choice. These are not a normally a core component in the reinforced threshold models (Theraulaz et al. 1998; Duarte et al. 2011), which typically only vary task demands. While this line of work has also found that the amount of specialisation arising can depend on task demands, a direct comparison is difficult since tasks costs are generally not addressed. A recent exception is a two-task response threshold model (Kang and Theraulaz 2016). It considers an “inside” task and an “outside” task and explicitly includes mortality rates and social interactions. A core result of the study states that, in the presence of social interactions, the colony-wide task allocation is determined by the ratio of the mortality demand product of the inside task to the mortality demand product of the outside task. If, on an abstract conceptual level, we equate “demand” with “benefit” and “cost” with “mortality,” this is congruent with our results. However, unlike in our work, individual-level specialisation was not a focus of this study.
It is known that experience-based reinforcement is likely to influence workers’ decision-making in task selection (Jeanson and Weidenmüller 2014). Our model with individual learning predicts that when the resources are less abundant, colonies tend to behave in strong specialisation with different tasks. This is congruent with previous theoretical models of reinforcement of individual experience in task allocation (Theraulaz et al. 1998).
One of the core interests in the study of task allocation is to investigate the primary sources of variation in workers’ task preference and ultimately specialisation (Gordon 2016). Many studies regard inherent inter-individual differentiation as the main cause (Jeanson and Weidenmüller 2014). Some studies have shown that specialisation can arise in colonies of initially identical workers either from reinforcement via individual experience (Theraulaz et al. 1998) or from spatially localised task demands (Tofts and Franks 1992; Johnson 2010). Our results show that social interaction is an alternative driver for specialisation.
There is clear empirical evidence that social learning matters in social insect colonies (Giurfa 2015; Grüter and Leadbeater 2014). However, little is known about the exact mechanisms of social learning in relation to task allocation and there is a clear need for further empirical work in this regard. For our models, we have assumed one of the most basic forms of social learning. Since there is insufficient knowledge about the details of the real biological mechanisms that may be at work, this provides a reasonable starting point. Importantly, the dynamics that these assumptions lead to, so-called replicator dynamics (Hofbauer and Sigmund 1998), are qualitatively stable for a reasonably broad range of changes in the detailed learning mechanisms. Replicator dynamics arises in a surprisingly wide range of different learning scenarios (Sandholm 2010; Izquierdo et al. 2012). It thus provides a good basis for a hypothetical discussion in the absence of more precise empirical insights.
We were able to show that the qualitative behaviour remains unchanged when switching between two extreme ends of the spectrum of learning mechanisms: individual and social. This suggests that the finer details of the social learning mechanisms that may actually be at play will only have a limited impact on this qualitative behaviour.
Our results suggest that individual learning leads to higher colony performance under fluctuating environmental conditions. One may thus expect that social learning is selected against in environment types where it does not achieve high efficiency. However, social learning may arguably provide other benefits to the colony, most importantly a mechanism to spread information through the colony in the absence of local cues. Empirical studies suggest that workers can recognise the tasks that others perform simply by chemical cues or antennal contact (Gordon 1996; Gordon and Mehdiabadi 1999). Spatial movement is widely observed and is likely to influence task allocation in social insects (Gordon 2002; Charbonneau et al. 2013; Seeley 1982; Johnson 2003; Cartar 1992). It is thus conceivable that these benefits outweigh the potential price that is paid in terms of overall performance.
In environment types where both weak and strong specialisation can exist, weak specialisation can be more efficient than strong specialisation. This seems to contradict an often made assumption that strong specialisation is one of the ways how colonies achieve higher efficiency (Oster and Wilson 1978; Charbonneau and Dornhaus 2015a). However, it is established that this is not always the case and that the evidence for this is not consistent (Chittka and Muller 2009; Dornhaus 2008; Jandt et al. 2009; Santoro et al. 2019). Our models show strong specialisation may, in some circumstances, be an emergent by-product of the proximate mechanisms that determine individual task selection rather than a fitness improving outcome (and thus directly selected for).
Our task allocation game is similar to a continuous Snowdrift game (Doebeli et al. 2004), in which the benefit is shared by all individuals at the group level, but the costs are strategy dependent at the individual level and tend to be different across individuals. Both games can be used to explore features of cooperation and illustrate a principle called “Tragedy of the Commune” (Doebeli et al. 2004). This principle describes non-uniform investment across a group that receives uniform benefit: some individuals significantly contribute to generating a common good, while some “free loaders” invest less or nothing and still reap the same benefits. Ultimately, this may give us a new perspective to tackle the puzzle of “lazy” workers in social insect colonies (Charbonneau et al. 2015; Charbonneau and Dornhaus 2015a, b; Hasegawa et al. 2016; Charbonneau et al. 2017).
There are some factors that may influence the outcomes of the modelled process and whose influence remains to be investigated in more detail. One of these is the “interaction range” of individuals. It is well known that individuals in a colony, due to their physical or spatial limitations, typically sample and respond to localised cues as a proxy for the global situation (Gordon 1996). In our model, this is reflected by letting individuals interact in smaller subgroups (the games), to which their information gathering is limited at any point of time. The size of a game then is a proxy for the scale of interaction in the colony. Game size is a factor that can influence the ultimate outcomes of the EGT models (Bonacich et al. 1976), and the impact of games size on our models remains to be investigated. The strength of our modelling approach is that it gives us a principled way to investigate the influence of such factors.
A number of previous studies were specifically concerned with the influence of the distribution of tasks in space, most prominently the foraging-for-work models (Tofts and Franks 1992; Johnson 2010). Recently Richardson et al. (2011) studied how spatial clustering of tasks arises. In contrast to our approach, no learning (i.e. adjustment of task selection behaviour) takes place in their model. In this sense, our approach and the investigation of spatially distributed tasks are almost orthogonal lines of work. There can be no doubt that spatial distributions are a very important factor, and we hope to bring these two lines together by including spatially embedded interactions into our framework next, possibly using compartment-based EGT.
6 Conclusion
We have introduced a new modelling framework for task allocation in social insects, based on evolutionary game theory, and have used this framework to analyse different behavioural patterns in terms of specialisation. This was motivated by the fact that conventional frameworks do not sufficiently address two aspects that are recognised as crucial to the investigation of task allocation: the role of environmental conditions and the role of social interaction (Gordon 2016).
The introduction of our EGT-based framework has allowed us to address two specific questions: (1) what are the factors that can determine whether specialisation arises and (2) how do different behavioural patterns relate to the overall colony efficiency.
While the results discussed above are congruent with existing empirical work, they have also yielded interesting new theoretical insights regarding the influence of environmental conditions on individual task choice and collective task allocation. Most importantly, they directly suggest avenues for new empirical work to address the question whether variations in the “hardness” of tasks in an otherwise unchanged scenario can lead to different patterns of specialisation. Driven by our modelling insights, we have now begun to address this question experimentally.
On the theoretical side, we have only scratched the surface of what the EGT-based framework can afford us. As a starting point, we have modelled the allocation between a homeostatic task and a maximising task. While this addresses some fundamental aspects, the range of possible task types is obviously much larger. Different cost and benefit functions, associated with different task types, must be expected to have a significant influence on the outcomes of the models. Likewise, it may have an important impact on the outcomes if individuals can learn to perform a task more efficiently by practising or social influence (Chittka and Muller 2009). The game-theoretic framework allows us to address these questions by reshaping cost and benefit functions. For example, a task that becomes easier with practice would result in a concave \(C(x_i)\) while an accelerating risk to the individual would result in convex \(C(x_i)\).
Game theory research has shown that a qualitative classification of games by means of their cost and benefit functions can go a long way in determining long-term behaviour (Archetti et al. 2011). This allows us to abstract from the exact quantitative nature of these functions and to switch to a qualitative perspective. This is a powerful concept, since the exact quantitative nature of cost and benefit functions can usually not be ascertained. The hope is that switching to a qualitative view with our framework will allow us to focus the discussion on different fundamental types of tasks that are competing for attention. This should impact both, theoretical work and experiments, and has the potential to open new pathways to central questions in social insect task allocation.
References
Anderson, C., & Ratnieks, F. (1999). Worker allocation in insect societies: Coordination of nectar foragers and nectar receivers in honey bee (Apis mellifera) colonies. Behavioral Ecology and Sociobiology, 46, 73–81.
Archetti, M., Scheuring, I., Hoffman, M., Frederickson, M. E., Pierce, N. E., & Yu, D. W. (2011). Economic game theory for mutualism and cooperation. Ecology Letters, 14(12), 1300–1312.
Beshers, S. N., & Fewell, J. H. (2001). Models of division of labor in social insects. Annual Review of Entomology, 46, 413–440.
Beshers, S. N., Huang, Z.-Y., Oono, Y., & Robinson, G. E. (2001). Social inhibition and the regulation of temporal polyethism in honey bees. Journal of Theoretical Biology, 213(3), 461–479.
Beshers, S. N., & Traniello, J. F. A. (1996). Polyethism and the adaptiveness of worker size variation in the attine ant Trachymyrmex septentrionalis. Journal of Insect Behavior, 9(1), 61–83.
Bonabeau, E., Theraulaz, G., & Deneubourg, J.-L. (1996). Quantitative study of the fixed threshold model for the regulation of division of labour in insect societies. Proceedings of the Royal Society of London. Series B: Biological Sciences, 263(1376), 1565–1569.
Bonacich, P., Shure, G. H., Kahan, J. P., & Meeker, R. J. (1976). Cooperation and group size in the \(n\)-person prisoner’s dilemma. Journal of Conflict Resolution, 20, 687–705.
Broom, M., & Rychtář, J. (2013). Game-theoretical models in biology. Boca Raton, FL: CRC Press.
Brown, J. S. (2016). Why Darwin would have loved evolutionary game theory. Proceedings of the Royal Society B: Biological Sciences, 283(1838), 20160847.
Cartar, R. V. (1992). Adjustment of foraging effort and task switching in energy-manipulated wild bumblebee colonies. Animal Behaviour, 44(1), 75–87.
Charbonneau, D., Blonder, B., & Dornhaus, A. (2013). Social insects: A model system for network dynamics. In P. Holme & J. Saramäki (Eds.), Temporal networks (pp. 217–244). Berlin, Heidelberg: Springer.
Charbonneau, D., & Dornhaus, A. (2015a). When doing nothing is something. How task allocation strategies compromise between flexibility, efficiency, and inactive agents. Journal of Bioeconomics, 17(3), 217–242.
Charbonneau, D., & Dornhaus, A. (2015b). Workers ‘specialized’ on inactivity: Behavioral consistency of inactive workers and their role in task allocation. Behavioral Ecology and Sociobiology, 69(9), 1459–1472.
Charbonneau, D., Hillis, N., & Dornhaus, A. (2015). ‘Lazy’ in nature: Ant colony time budgets show high ‘inactivity’ in the field as well as in the lab. Insectes sociaux, 62(1), 31–35.
Charbonneau, D., Sasaki, T., & Dornhaus, A. (2017). Who needs ‘lazy’ workers? Inactive workers act as a ‘reserve’ labor force replacing active workers, but inactive workers are not replaced when they are removed. PLoS ONE, 12(9), e0184074.
Charlton, N., & Houston, A. (2010). What currency do bumble bees maximize? PLoS ONE, 5(8), e12186.
Chittka, L., & Muller, H. (2009). Learning, specialization, efficiency and task allocation in social insects. Communicative & Integrative Biology, 2(2), 151–154.
Cook, C. N., & Breed, M. D. (2013). Social context influences the initiation and threshold of thermoregulatory behaviour in honeybees. Animal Behaviour, 86(2), 323–329.
Doebeli, M. (2011). Adaptive Diversification. Monographs in Population Biology. Princeton, NJ: Princeton University Press.
Doebeli, M., Hauert, C., & Killingback, T. (2004). The evolutionary origin of cooperators and defectors. Science, 306(5697), 859–862.
Dornhaus, A. (2008). Specialization does not predict individual efficiency in an ant. PLoS Biology, 6(11), e285.
Duarte, A., Pen, I., Keller, L., & Weissing, F. J. (2012). Evolution of self-organized division of labor in a response threshold model. Behavioral Ecology and Sociobiology, 66(6), 947–957.
Duarte, A., Weissing, F. J., Pen, I., & Keller, L. (2011). An evolutionary perspective on self-organized division of labor in social insects. Annual Review of Ecology, Evolution, and Systematics, 42, 91–110.
Dugatkin, L. A., & Reeve, H. K. (1998). Game theory and animal behavior. New York City, NY: Oxford University Press.
Duong, N., & Dornhaus, A. (2012). Ventilation response thresholds do not change with age or self-reinforcement in workers of the bumble bee Bombus impatiens. Insectes sociaux, 59(1), 25–32.
Feinerman, O., & Traniello, J. F. A. (2016). Social complexity, diet, and brain evolution: Modeling the effects of colony size, worker size, brain size, and foraging behavior on colony fitness in ants. Behavioral Ecology and Sociobiology, 70(7), 1063–1074.
Fewell, J. H., & Bertram, S. M. (1999). Division of labor in a dynamic environment: Response by honeybees (Apis mellifera) to graded changes in colony pollen stores. Behavioral Ecology and Sociobiology, 46(3), 171–179.
Fewell, J. H., & Harrison, J. F. (2016). Scaling of work and energy use in social insect colonies. Behavioral Ecology and Sociobiology, 70(7), 1047–1061.
Fogel, D. B. (2000). Introduction to evolutionary computation. Evolutionary Computation, 1, 1–3.
Franklin, E. L., Robinson, E. J. H., Marshall, J. A. R., Sendova-Franks, A. B., & Franks, N. R. (2012). Do ants need to be old and experienced to teach. Journal of Experimental Biology, 215(Pt 8), 1287–1292.
Franks, N. R., & Tofts, C. (1994). Foraging for work: How tasks allocate workers. Animal Behaviour, 48(2), 470–472.
Geritz, S. A. H., Kisdi, E., Meszéna, G., & Metz, H. (1997). Evolutionarily singular strategies and the adaptive growth and branching of the evolutionary tree. Evolutionary Ecology, 12(1), 35–57.
Giurfa, M. (2015). Learning and cognition in insects. Wiley Interdisciplinary Reviews: Cognitive Science, 6(4), 383–395.
Gokhale, C. S., & Traulsen, A. (2010). Evolutionary games in the multiverse. Proceedings of the National Academy of Sciences USA, 107, 5500–5504.
Gordon, D. (2018). The ecology of collective behavior in ants. Annual Review of Entomology, 64, 35–50.
Gordon, D. M. (1996). The organization of work in social insect colonies. Nature, 380(6570), 121–124.
Gordon, D. M. (2002). The organization of work in social insect colonies. Complexity, 8(1), 43–46.
Gordon, D. M. (2010). Ant encounters: Interaction networks and colony behavior. Princeton, NJ: Princeton University Press.
Gordon, D. M. (2016). From division of labor to the collective behavior of social insects. Behavioral Ecology and Sociobiology, 70(7), 1101–1108.
Gordon, D. M., Goodwin, B. C., & Trainor, L. E. H. (1992). A parallel distributed model of the behaviour of ant colonies. Journal of Theoretical Biology, 156(3), 293–307.
Gordon, D. M., & Mehdiabadi, N. J. (1999). Encounter rate and task allocation in harvester ants. Behavioral Ecology and Sociobiology, 45(5), 370–377.
Gove, R., Hayworth, M., Chhetri, M., & Rueppell, O. (2009). Division of labour and social insect colony performance in relation to task and mating number under two alternative response threshold models. Insectes sociaux, 56(3), 319–331.
Graham, S., Oldroyd, B. P., Myerscough, M. R., & Jones, J. C. (2006). Modelling the role of intracolonial genetic diversity on regulation of brood temperature in honey bee (Apis mellifera L.) colonies. Insectes sociaux, 53(2), 226–232.
Greene, M. J., & Gordon, D. M. (2007). Interaction rate informs harvester ant task decisions. Behavioral Ecology, 18(2), 451–455.
Grimaldi, D., & Engel, M. S. (2005). Evolution of the insects. New York City, NY: Combridge University Press.
Grüter, C., & Leadbeater, E. (2014). Insights from insects about adaptive social information use. Trends in Ecology and Evolution, 29(3), 177–184.
Hasegawa, E., Ishii, Y., Tada, K., Kobayashi, K., & Yoshimura, J. (2016). Lazy workers are necessary for long-term sustainability in insect societies. Scientific Reports, 6, 20846.
Hofbauer, J., & Sigmund, K. (1998). Evolutionary games and population dynamics. Cambridge: Cambridge University Press.
Hogeweg, P., & Hesper, B. (1983). The ontogeny of the interaction structure in bumble bee colonies: A MIRROR model. Behavioral Ecology and Sociobiology, 12(4), 271–283.
Hölldobler, B., & Wilson, E. O. (1990). The ants. Cambridge, MA: Belknap Press of Harvard University Press.
Hölldobler, B., & Wilson, E. O. (2009). The superorganism: The beauty, elegance, and strangeness of insect societies. New York City, NY: W. W. Norton & Company.
Huang, Z.-Y., & Robinson, G. E. (1992). Honeybee colony integration: Worker–worker interactions mediate hormonally regulated plasticity in division of labor. Proceedings of the National Academy of Sciences USA, 89(24), 11726–11729.
Huang, Z.-Y., & Robinson, G. E. (1996). Regulation of honey bee division of labor by colony age demography. Behavioral Ecology and Sociobiology, 39(3), 147–158.
Huberman, B. A., & Glance, N. S. (1993). Evolutionary games and computer simulations. Proceedings of the National Academy of Sciences USA, 90, 7716–7718.
Imhof, L. A., & Nowak, M. A. (2006). Evolutionary game dynamics in a Wright–Fisher process. Journal of Mathematical Biology, 52, 667–681.
Izquierdo, L. R., Izquierdo, S. S., & Vega-Redondo, F. (2012). Learning and evolutionary game theory. In N. M. Seel (Ed.), Encyclopedia of the sciences of learning (pp. 1782–1788). Boston, MA: Springer.
Jandt, J. M., Huang, E., & Dornhaus, A. (2009). Weak specialization of workers inside a bumble bee (Bombus impatiens) nest. Behavioral Ecology and Sociobiology, 63(12), 1829–1836.
Jeanne, R. L. (2016). Division of labor is not a process or a misleading concept. Behavioral Ecology and Sociobiology, 70(7), 1109–1112.
Jeanson, R., Clark, R. M., Holbrook, C. T., Bertram, S. M., Fewell, J. H., & Kukuk, P. F. (2008). Division of labour and socially induced changes in response thresholds in associations of solitary halictine bees. Animal Behaviour, 76(3), 593–602.
Jeanson, R., Fewell, J. H., Gorelick, R., & Bertram, S. M. (2007). Emergence of increased division of labor as a function of group size. Behavioral Ecology and Sociobiology, 62(2), 289–298.
Jeanson, R., Kukuk, P. F., & Fewell, J. H. (2005). Emergence of division of labour in halictine bees: Contributions of social interactions and behavioural variance. Animal Behaviour, 70(5), 1183–1193.
Jeanson, R., & Weidenmüller, A. (2014). Interindividual variability in social insects—Proximate causes and ultimate consequences. Biological Reviews, 89(3), 671–687.
Johnson, B. R. (2003). Organization of work in the honeybee: A compromise between division of labour and behavioural flexibility. Proceedings of the Royal Society of London. Series B: Biological Sciences, 270(1511), 147–152.
Johnson, B. R. (2010). Spatial effects, sampling errors, and task specialization in the honey bee. Insectes sociaux, 57(2), 239–248.
Jones, P. L., Ryan, M. J., & Chittka, L. (2015). The influence of past experience with flower reward quality on social learning in bumblebees. Animal Behaviour, 101, 11–18.
Kang, Y., & Theraulaz, G. (2016). Dynamical models of task organization in social insect colonies. Bulletin of Mathematical Biology, 78(5), 879–915.
Karsai, I., & Phillips, M. D. (2012). Regulation of task differentiation in wasp societies: A bottom-up model of the “common stomach”. Journal of Theoretical Biology, 294, 98–113.
Karsai, I., & Wenzel, J. W. (1998). Productivity, individual-level and colony-level flexibility, and organization of work as consequences of colony size. Proceedings of the National Academy of Sciences USA, 95(15), 8665–8669.
Koutsoupias, E., & Papadimitriou, C. (2009). Worst-case equilibria. Computer Science Review, 3(2), 65–69.
Leadbeater, E., & Chittka, L. (2005). A new mode of information transfer in foraging bumblebees? Current Biology, 15(12), R447–R448.
Leadbeater, E., & Chittka, L. (2007a). Social learning in insects—From miniature brains to consensus building. Current Biology, 17(16), R703–R713.
Leadbeater, E., & Chittka, L. (2007b). The dynamics of social learning in an insect model, the bumblebee (Bombus terrestris). Behavioral Ecology and Sociobiology, 61(11), 1789–1796.
Leadbeater, E., & Chittka, L. (2008). Social transmission of nectar-robbing behaviour in bumble-bees. Proceedings of the Royal Society B: Biological Sciences, 275(1643), 1669–1674.
Maynard Smith, J. (1982). Evolution and the theory of games. Cambridge: Cambridge University Press.
McGill, B. J., & Brown, J. S. (2007). Evolutionary game theory and adaptive dynamics of continuous traits. Annual Review of Ecology, Evolution, and Systematics, 38(1), 403–435.
Mersch, D. P. (2016). The social mirror for division of labor: What network topology and dynamics can teach us about organization of work in insect societies. Behavioral Ecology and Sociobiology, 70(7), 1087–1099.
Michalewicz, Z., & Fogel, D. B. (2013). How to solve it: Modern heuristics. Berlin: Springer.
Naug, D., & Gadagkar, R. (1999). Flexible division of labor mediated by social interactions in an insect colony—A simulation model. Journal of Theoretical Biology, 197(1), 123–133.
Odonell, S., Reichardt, M., & Foster, R. (2000). Individual and colony factors in bumble bee division of labor. Insectes Sociaux, 47(2), 164–170.
Oldroyd, B. P., & Fewell, J. H. (2007). Genetic diversity promotes homeostasis in insect colonies. Trends in Ecology & Evolution, 22(8), 408–413.
Oster, G. F., & Wilson, E. O. (1978). Caste and ecology in the social insects. Princeton, NJ: Princeton University Press.
Pacala, S. W., Gordon, D. M., & Godfray, H. C. J. (1996). Effects of social group size on information transfer and task allocation. Evolutionary Ecology, 10(2), 127–165.
Page, R. E, Jr., & Mitchell, S. D. (1998). Self-organization and the evolution of division of labor. Apidologie, 29(1–2), 171–190.
Pereira, H. M., & Gordon, D. M. (2001). A trade-off in task allocation between sensitivity to the environment and response time. Journal of Theoretical Biology, 208(2), 165–184.
Pruitt, J., Wright, C., Keiser, C., DeMarco, A., Grobis, M., & Pinter-Wollman, N. (2016). The Achilles’ heel hypothesis: Misinformed keystone individuals impair collective learning and reduce group success. Proceedings of the Royal Society B: Biological Sciences, 283(1823), 20152888.
Pruitt, J., Wright, C., Lichtenstein, J., Chism, G., McEwen, B., Kamath, A., et al. (2018). Selection for collective aggressiveness favors social susceptibility in social spiders. Current Biology, 28(1), 100–105. e1–e4.
Ravary, F., Lecoutey, E., Kaminski, G., Châline, N., & Jaisson, P. (2007). Individual experience alone can generate lasting division of labor in ants. Current Biology, 17(15), 1308–1312.
Rendell, L., Boyd, R., Cownden, D., Enquist, M., Eriksson, K., Feldman, M. W., et al. (2010). Why copy others? Insights from the social learning strategies tournament. Science, 328(5975), 208–213.
Richardson, T. O., Christensen, K., Franks, N. R., Jensen, H. J., & Sendova-Franks, A. B. (2011). Ants in a labyrinth: A statistical mechanics approach to the division of labour. PLoS ONE, 6(4), e18416.
Robinson, E. J. H., Feinerman, O., & Franks, N. R. (2012). Experience, corpulence and decision making in ant foraging. Journal of Experimental Biology, 215(15), 2653–2659.
Robinson, G. E. (1987). Regulation of honey bee age polyethism by juvenile hormone. Behavioral Ecology and Sociobiology, 20(5), 329–338.
Robinson, G. E. (1992). Regulation of division of labor in insect societies. Annual Review of Entomology, 37(1), 637–665.
Robson, S. K. A., & Traniello, J. F. A. (2016). Division of labor in complex societies: A new age of conceptual expansion and integrative analysis. Behavioral Ecology and Sociobiology, 70(7), 995–998.
Sandholm, W. H. (2010). Population games and evolutionary dynamics. Cambridge, MA: MIT Press.
Santoro, D., Hartley, S., & Lester, P. J. (2019). Behaviourally specialized foragers are less efficient and live shorter lives than generalists in wasp colonies. Scientific Reports, 9, 5366.
Schmickl, T., & Karasai, I. (2019). Integral feedback control is at the core of task allocation and resilience of insect societies. PNAS, 115(52), 13180–13185.
Schuster, P., & Sigmund, K. (1983). Replicator dynamics. Journal of Theoretical Biology, 100, 533–538.
Seeley, T. D. (1982). Adaptive significance of the age polyethism schedule in honeybee colonies. Behavioral Ecology and Sociobiology, 11(4), 287–293.
Sigmund, K. (2010). The calculus of selfishness. Princeton: Princeton University Press.
Storn, R., & Price, K. (1997). Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces. Journal of Global Optimization, 11(4), 341–359.
Taylor, P., & Jonker, L. (1978). Evolutionary stable strategies and game dynamics. Mathematical Biosciences, 40(1–2), 145–156.
Theraulaz, G., Bonabeau, E., & Deneubourg, J.-L. (1998). Response threshold reinforcements and division of labour in insect societies. Proceedings of the Royal Society B: Biological Sciences, 265(1393), 327–332.
Theraulaz, G., Bonabeau, E., Solé, R., Schatz, B., & Deneubourg, J.-L. (2002). Task partitioning in a ponerine ant. Journal of Theoretical Biology, 215(4), 481–489.
Tofts, C. (1993). Algorithms for task allocation in ants. (A study of temporal polyethism: Theory). Bulletin of Mathematical Biology, 55(5), 891–918.
Tofts, C., & Franks, N. R. (1992). Doing the right thing: Ants, honeybees and naked mole-rats. Trends in Ecology & Evolution, 7(10), 346–349.
Traulsen, A., Hauert, C., De Silva, H., Nowak, M. A., & Sigmund, K. (2009). Exploration dynamics in evolutionary games. Proceedings of the National Academy of Sciences USA, 106, 709–712.
Tripet, F., & Nonacs, P. (2004). Foraging for work and age-based polyethism: The roles of age and previous experience on task choice in ants. Ethology, 110(11), 863–877.
Wahl, L. M. (2002). Evolving the division of labour: Generalists, specialists and task allocation. Journal of Theoretical Biology, 219(3), 371–388.
Worden, B. D., & Papaj, D. R. (2005). Flower choice copying in bumblebees. Biology Letters, 1(4), 504–507.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix 1: Details of the payoff function
As task T needs to be controlled at a certain level, under or over performing task T can reduce \(B_T(X)\). We use a simple way to model
Here \(B_T(X)\) is assumed to achieve the maximum value, which is normalised between 0 and 1, when half of the workforce in the game is engaged in task T and to be 0 when none or all of workers in the game are engaged. As task F is a maximising task, which implies, for example, the more food is collected, the more brood can survive, \(B_F(X)\) is simply assumed to be linear
where b is coefficient ratio between the benefit of task F and the cost of task F.
We assume the cost of a homeostatic task to be linear in individual effort and thus define
where r is coefficient ratio of the costs between tasks T and F. We assume that \(C_F(x_i)\) is marginally decreasing with the effort in task F, indicating the scenarios in which foragers initially need to spend more effort exploring their neighbourhood, and once they become familiar with the surrounding areas of food resources, the cost for them tends to be less than the initial stage. As a result, we simply assume
Here the cost of task F for a worker who engage fully in task F per time period is assumed to be 1 unit.
Appendix 2: Theoretical analysis
1.1 Analysis for a monomorphous population: adaptive dynamics
1.1.1 Equilibrium points
We follow the technique used by Doebeli et al. (2004) to study nonlinear public good games in continuous traits. In a game of size n, with \(n-1\) type-I workers of strategy x and 1 type-II worker of strategy y (\(x, y \in [0, 1]\)), the growth rate (invasion fitness) of the type-II worker is
where
and
Thus, the selection gradient is
Then, the singular strategies are given as solutions of
Both strong specialisation and weak specialisation require the condition that there exists such \(x^* \in [0, 1]\) that \(x^*\) is convergence stable
1.1.2 Branching condition (weak or strong specialisation)
In addition to the above condition, strong specialisation emerges if
and weak specialisation requires
In other cases such as when \(x^*\) is convergence unstable, colonies tend to become inviable based on our payoff function, as one task out of the two is abandoned.
1.2 Analysis of dimorphic populations: replicator equation
We provide mathematical analysis of our task allocation game for the case of strong specialisation (only two types of strategies involved) based on the replicator equation (Taylor and Jonker 1978; Schuster and Sigmund 1983).
In a well-mixed colony of large size, the proportion of type-I individuals of strategy x is \(\rho\) and the proportion of type-II individuals of strategy y is \(1 - \rho\) (\(x, y \in [0, 1]\)).
Given that the size of game is n, the dynamics of the fraction of individuals of type I individuals is given by:
where
and
The solutions of \(D(\rho ^*) = 0\) for \(\rho ^* \in (0, 1)\) give the stable equilibrium for the long-term dynamics of individual strategies in a colony. The quantity \(\rho ^*\) is the proportion of strongly specialised individuals who fully engage in foraging.
1.3 Optimal payoff
To evaluate the efficiency achieved by the colony, we also need to know the optimal level associated with different environmental conditions (illustrated in Fig. 8). To find this, for each pair of b and r, we optimise the mean of individual payoffs with potentially different strategies in a game of size n using Differential Evolution (Storn and Price 1997), a stochastic population-based heuristic method for global optimisation (implemented by differential_evolution in the package optimize of Scipy, version 0.19.0).
Appendix 3: Classification of simulation results
For the models with individual learning and social learning, the colonies with the non-positive mean of workers’ payoffs are classified under being inviable (for details of the mean of individual payoffs, see Figs. 9A and 10A). The other colonies are tentatively regarded under strong specialisation if the standard deviation of workers’ strategies exceeds a certain level (set as 0.1) or weak specialisation otherwise (for details of the standard deviation of individual strategies, see Figs. 9B and 10B).
However, a large standard deviation of individual strategies cannot guarantee strong specialisation, as a colony with a wide span of strategies may belong to weak specialisation and correspond to a large standard deviation as well. To capture the span of individual strategies, we verify the above temporary region classification by the Shannon entropy (for details, see Figs. 9C and 10C). For both models, the entropies of individual strategies in colonies with large standard deviation are smaller than those with small standard deviation, which in turn confirms our temporary region classifications. In order to highlight the variation under different environmental conditions, each of the three figures has a unique colour scheme for both individual learning and social learning.
Results of the model with individual learning (\(N = 2000\), \(t_{\mathrm{end}} = 100\,000\), \(n = 10\), \(\beta = 0.001\), \(\gamma = 0.1\), \(k=1000\)). In order to highlight the variation within this model under different environmental conditions, each of the above figures has a unique colour scheme
Results of the model with social learning (\(N = 2000\), \(t_{\mathrm{end}} = 30\,000\), \(n = 10\), \(\alpha = 2.5\), \(\beta = 0.01\), \(\gamma = 0.005\), \(k=1\)). In order to highlight the variation within this model under different environmental conditions, each of the above figures has a unique colour scheme
Appendix 4: Parameters involved in simulation
Notation | Explanation | Values explored |
|---|---|---|
b | Ratio between the benefit and cost of task F | (0, 40) |
r | Ratio of cost between task T and F | (0, 2) |
n | Size of groups that individual interactions are restricted to | [4, 14] |
\(\alpha\) | Selection intensity in social learning | 2.5 |
\(\beta\) | Probability with which an individual explores a new strategy | 0.01 |
\(\gamma\) | Standard deviation of the Gaussian distribution from which new strategies are sampled | 0.005, 0.1 |
k | Number of games in which an individual evaluates her payoff before adopting a new strategy | 1, 1000 |
\(t_{\mathrm{end}}\) | Time period that a simulation program lasts | 30 000, 10 0000 |
\(\theta\) | Threshold used to distinguish colony behaviour between strong and weak specialisation | 0.1 |
Appendix 5: Simulation source code
The source code for our simulations of individual learning and social learning in both static and dynamic environments can be found at https://github.com/rche29/model_task_allocation.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Chen, R., Meyer, B. & Garcia, J. A computational model of task allocation in social insects: ecology and interactions alone can drive specialisation. Swarm Intell 14, 143–170 (2020). https://doi.org/10.1007/s11721-020-00180-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11721-020-00180-4