Introduction

A key aspect of the neutralization process is a chemical reaction, in which an acid and a base react quantitatively with each other. The main aim of this process is to change the pH value by adding the appropriate chemical agent. These reactions are used in titration analysis, and they are one of chemical methods of the quantitative analysis. The neutralization process may be used in the wastewater treatment technology for industrial plants (Sakai et al. 1996; Gitari et al. 2008; Hawkes et al. 2013). This reaction is also applied for various chemical and biological processes (Galán et al. 2004; Barraud et al. 2009).

The neutralization process is carried out in various types of neutralizers in a continuous regime (Adams and Papangelakis 2007; Nam et al. 2013). Following the present results, previous studies have demonstrated that a lot of effort has been put in studying the selection of optimal conditions for the neutralization process, for example, determination of an appropriate neutralization reaction time (Yan et al. 1999). Previous studies have been associated with the selection of appropriate mass streams or process parameters for installations at a laboratory and technical scale (Galán et al. 2004; Barraud et al. 2009). Several authors have reported analyses of trends in pH control applications (Åkesson et al. 2005; Altınten 2007; Barraud et al. 2009). So far, however, there has been little discussion about the solutions of new construction for neutralizers (Watten et al. 2007).

Until recently, there has been little interest in the application of various types of magnetic fields to enhance the efficiency of a chemical process or neutralization reaction. The use of a magnetic field has been under consideration for several years (Hristov 2003, 2009; Lechowska et al. 2019; Rakoczy et al. 2019). Apart from Hausmann et al. (2000), there is a general lack of research upon the intensification of the neutralization process using magnetic field. This work is related to the mass transfer in liquid fluidized beds of magnetic ion-exchange particles (neutralization of the acid form of resin with dilute sodium hydroxide) which was discussed and studied under various conditions.

The static or rotating magnetic fields might be used to intensify the mixing process instead of a stirring (Rakoczy and Masiuk 2011). It is well known that particles with magnetic properties under the action of the rotating magnetic field (RMF) may be applied as micro-stirrers (Rakoczy 2013). These particles could form chains along the field lines and rotate under the action of this kind of MF (Lu and Li 2000; Hristov 2002).

The mixing process increases the homogeneity of a liquid system. The mixing time is a parameter to describe the mixing process, and this quantity contains useful information about the mixing process within a vessel or reactor. The efficiency of this process is defined using the hydrodynamic characteristic such as mixing time (Harnby et al. 2000). Determination of mixing time may be realized using physical methods (e.g., thermal, conductometric) or chemical methods (e.g., decolorization, pH) (Manna 1997). The colorimetric method is mostly applied to ascertain the optimal mixing time. This technique is based on neutralization or redox reactions (Tan et al. 2011).

The purpose of this paper is to investigate the RMF effect on the neutralization process. It was decided that the best reaction to adopt for these investigations was to use weak acid–strong base neutralization. Moreover, the effect of magnetic particles under the action of RMF on the neutralization reaction is tested and discussed. This study has also shown that the information from this reaction might be used to quantitatively characterize the mixing process via mixing time in the magnetically assisted mixer.

Theoretical

The fluid flow under the RMF action may be described using the Navier–Stokes equation (Rakoczy and Masiuk 2011):

$$\frac{{\partial \varvec{w}}}{\partial t} + \left( {\varvec{w}\,{\text{grad}}} \right)\varvec{w} = \nu \Delta \varvec{w} + \frac{{\varvec{F}_{\text{L}} }}{\rho }$$
(1)

where FL—Lorentz magnetic force, N; w—velocity vector, m s−1; t—time, s; ν—kinematic viscosity, m2 s−1; ρ—density, kg m−3.

The governing Eq. (1) may be given as follows:

$$\frac{{\partial \varvec{w}}}{\partial t} + \left( {\varvec{w}\,{\text{grad}}} \right)\varvec{w} = \nu \Delta \varvec{w} + \frac{{\left[ {\sigma_{\text{e}} \;\left( {\varvec{w}\,\varvec{B}} \right)} \right]\varvec{B}}}{\rho }$$
(2)

where B—magnetic field vector, kg A−1 s−2; σe—electrical conductivity, A2 s3 kg−1 m−3.

Equation (2) may be rewritten in the form that is useful for the dimensional analysis:

$$\left( {\frac{{w_{0} }}{{t_{0} }}} \right)\left[ {\frac{{\partial \varvec{w}^{*} }}{{\partial t^{*} }}} \right] + \left( {\frac{{w_{0}^{2} }}{{l_{0} }}} \right)\left[ {\left( {\varvec{w}^{*} \,{\text{grad}}^{*} } \right)\varvec{w}^{*} } \right] = \left( {\frac{{\nu_{0} \;w_{0}^{{}} }}{{l_{0}^{2} }}} \right)\left[ {\nu^{*} \Delta^{*} \varvec{w}^{*} } \right] + \left( {\frac{{\sigma_{{{\text{e}}_{0} }} \;w_{0}^{{}} \;B_{0}^{2} }}{{\rho_{0}^{{}} }}} \right)\left[ {\frac{{\left[ {\sigma_{\text{e}}^{*} \;\left( {\varvec{w}^{*} \,\varvec{B}^{*} } \right)} \right]\varvec{B}^{*} }}{{\rho^{*} }}} \right]$$
(3)

where \(\left\{ \cdot \right\}_{0}\)—reference value of \(\left\{ \cdot \right\}\); \(\left\{ \cdot \right\}^{*}\)—dimensionless value of \(\left\{ \cdot \right\}\).

Equation (3) may be scaled against the term \(\left( {\frac{{\nu_{0} \;w_{0}^{2} }}{{l_{0}^{2} }}} \right)\). Then, the following dimensionless equation is given:

$$\left( {\frac{{l_{0}^{2} }}{{t_{0} \;\nu_{0} \;}}} \right)\left[ {\frac{{\partial \varvec{w}^{*} }}{{\partial t^{*} }}} \right] + \left( {\frac{{w_{0}^{{}} \;l_{0}^{{}} }}{{\nu_{0} \;}}} \right)\left[ {\left( {\varvec{w}^{*} \,{\text{grad}}^{*} } \right)\varvec{w}^{*} } \right] = \left[ {\nu^{*} \Delta^{*} \varvec{w}^{*} } \right] + \left( {\frac{{\sigma_{{{\text{e}}_{0} }} \;B_{0}^{2} \;l_{0}^{2} }}{{\rho_{0}^{{}} \;\nu_{0} }}} \right)\left[ {\frac{{\left[ {\sigma_{\text{e}}^{*} \;\left( {\varvec{w}^{*} \,\varvec{B}^{*} } \right)} \right]\varvec{B}^{*} }}{{\rho^{*} }}} \right]$$
(4)

Equation (4) may be also expressed using the dimensionless groups:

$$\Theta^{ - 1} \left[ {\frac{{\partial \varvec{w}^{*} }}{{\partial t^{*} }}} \right] + \text{Re} \left[ {\left( {\varvec{w}^{*} \,{\text{grad}}^{*} } \right)\varvec{w}^{*} } \right] = \left[ {\nu^{*} \Delta^{*} \varvec{w}^{*} } \right] + {\text{Q}}\left[ {\frac{{\left[ {\sigma_{\text{e}}^{*} \;\left( {\varvec{w}^{*} \,\varvec{B}^{*} } \right)} \right]\varvec{B}^{*} }}{{\rho^{*} }}} \right]$$
(5)

where Re—dimensionless Reynolds number; Q—dimensionless Chandrasekhar number; Θ—dimensionless mixing time number.

From Eq. (5), it follows that:

$$\Theta = f\left( {\text{Re} } \right) \Rightarrow \left( {\frac{{t_{0} \;\nu_{0} }}{{l_{0}^{2} \;}}} \right) = f\left( {\frac{{w_{0}^{{}} \;l_{0}^{{}} }}{{\nu_{0} \;}}} \right)$$
(6)

where D—diameter of glass container, m; t—mixing time, s; w—velocity of fluid, m s−1.

Furthermore, it is meaningful to introduce the dimensionless Reynolds number for the RMF application:

$$\text{Re}_{\text{RMF}} = \frac{{w_{\text{RMF}}^{{}} \;D}}{\nu \;}$$
(7)

where wRMF—velocity of fluid under the action of RMF, m s−1.

The velocity of fluid under the action of RMF, wRMF, may be defined as follows (Spitzer 1999; Story et al. 2014):

$$w_{\text{RMF}} = B_{\max} \;D\sqrt {\frac{{\sigma_{\text{e}} \;\omega_{\text{RMF}} }}{\rho }}$$
(8)

where Bmax—maximal value of magnetic field induction, kg A−1 s−2; ρ—density, kg m−3; ωRMF—angular velocity of RMF (ωRMF is equal to 2π fRMF), rad s−1.

Taking into account the definition of ReRMF, we obtain the following rewritten form of Eq. (6):

$$\Theta = f\left( {\text{Re}_{\text{RMF}} } \right) \Rightarrow \left( {\frac{t\;\nu }{{D^{2} }}} \right) = f\left( {\frac{{w_{\text{RMF}}^{{}} \;D}}{\nu }} \right)$$
(9)

The application of magnetic particles under the RMF action connects to the use of the modified form of Eq. (6) (Rakoczy 2013):

$$\Theta = f\left( {\text{Re}_{\bmod } } \right) \Rightarrow \left( {\frac{t\;\nu }{{D^{2} }}} \right) = f\left( {\frac{{B_{\max}^{2} \;\alpha^{\left( i \right)} }}{{2\;\rho \;\mu_{0} \;\nu }}\frac{{\left( {d_{32} } \right)^{2} }}{\nu }\frac{{\chi^{*} }}{{\left( {1 + \chi^{*} } \right)^{2} }}} \right)$$
(10)

where d32—Sauter mean diameter of magnetic particles, m; Remod—modified dimensionless Reynolds number; μ0—magnetic permeability, kg m A−2 s−2; χ*—volumetric magnetic susceptibility of magnetic particles.

The parameter α(i) in Eq. (11) is defined as follows:

$$\alpha^{\left( i \right)} = 0.0677\left[ {\frac{1}{2}\left( {d_{32} } \right)^{2} \,\mu_{0} \,\sigma_{\text{p}} \,\omega_{\text{RMF}} } \right]$$
(11)

where σp—electrical conductivity of magnetic particles, A2 s3 kg−1 m−3.

Experimental

Experimental setup

All the investigations have been carried out using the experimental setup shown in Fig. 1.

Fig. 1
figure 1

Experimental setup: 1—cooling jacket, 2—RMF generator, 3—glass container, 4—pH electrode, 5—temperature sensor, 6—feeder, 7—AC transistorized inverter, 8—computer, 9—multifunction computer meter CX-701

Full size image

The main part of the experimental setup was RMF generator (2). In the case of this experimental work, this generator was supplied with 50 Hz three-phase alternating current and it allowed to generate the RMF using the three-phase stator of the induction squirrel cage motor. The AC transistorized inverter (7) was used to set the frequency of the power supply and RMF frequency. In this investigation, this frequency varied in the range between 1 and 50 Hz. These elements were connected to a computer (8) equipped with the special software that was used to control the RMF, to record the working parameter of RMF generator as well as various operational parameters. The RMF generator was placed in the cooling jacket (1) to receive the excess heat generated during the operation of the experimental setup. The glass container (3) was placed inside the RMF generator (1). The experimental setup was also equipped with pH electrodes (4), temperature sensor (5), feeder (6) and the multifunctional computer meter CX-701 (9). These instrumentations were applied for the realization of the tested neutralization reaction.

Characterization of the applied magnetic field

The MFs can be divided into two main types: direct current magnetic field (DCMF) and alternating current magnetic field (ACMF). Generally, the DCMF (e.g., static magnetic field—SMF) changes very slowly with time or it does not change with time at all. In contrast to DCMF, ACMF varies with the frequency (e.g., pulsating magnetic field—PMF). The superposition of three 120° out-of-phase PMFs is contributing to a rotating MF (RMF). The rotating magnetic field (RMF) is a special case of the electromagnetic field, which is created due to interaction between the force vectors of the electromagnetic fields, for instance, generated by the coils situated in the circle every 120°. This kind of magnetic field may be generated, e.g., in the stator windings of the induction motor as a result of the supply of windings.

Differences between various types of MFs [static MF (SMF), pulsating MF (PMF) and rotating MF (RMF)] are graphically presented in Fig. 2.

Fig. 2
figure 2

Connection diagram of windings and visualization of the generated magnetic fields: a static magnetic field (SMF); b pulsating magnetic field (PMF); c rotating magnetic field (RMF)

Full size image

The applied RMF is characterized using the maximal values of magnetic induction, Bmax (Rakoczy and Masiuk 2011). Relation between this parameter and the frequency of power supply (it was assumed that this parameter is equal to the RMF frequency) is defined as follows:

$$B_{\max} = 10.39\;\frac{{f_{\text{RMF}} }}{{f_{\max} }} + 23.14$$
(12)

where fRMF—frequency of RMF or power supply, Hz; fmax—maximal value of RMF frequency of RMF or power supply (in the case of this experimental work fmax 50 Hz), Hz.

Neutralization reaction

The analysis of the RMF effect on the neutralization reaction was based on the titration of a weak acid with a strong base. This reaction involves a direct transfer of protons from the weak acid (e.g., CH3COOH) to the hydroxide ion (e.g., NaOH). In the titration of the weak acid with a strong base, the titrant is the strong base and the analyte is the weak acid.

In the case of this work, defined volume of 0.1 M CH3COOH (100 ml) was placed in the glass container (see Fig. 1). In the subsequent step, the base 0.1 M NaOH (100 ml) was introduced into the analyte. The reaction was carried out in the presence of RMF. Time of the base injection was 7 s. The pH was measured as a function of time using the pH electrodes and multifunctional computer meter CX-701 (signals were recorded digitally every 1 s). Localization of the probes and feeder with base is presented in Fig. 1. The neutralization reactions were realized at the temperature solution variation between 20 and 22 °C. Temperature of the working liquid was monitored using the temperature sensor (5 in Fig. 1) cooperating with the multifunction computer meter CX-701 (9 in Fig. 1).

The analysis of neutralization reaction under the action of RMF was performed using visual and instrumental methods for determination of the pH after adding a small amount of base, the pH at the half-neutralization, the pH at the equivalence point and finally the pH after adding the excess base. A few drops of phenolphthalein were added to the acetic acid solution to obtain the change in the solution color due to the change in the acidic environment into the alkaline environment. As it was mentioned above, the titration was also carried out using the pH electrodes to determine the physicochemical changes in the analyzed solutions. The measurement of pH changes was carried out at two extreme points located in the volume of the tested solutions (location of these points is shown in Fig. 1).

Magnetic particle

The magnetic particles (Fe3O4, magnetite) were also introduced into the working solutions and suspended using RMF. These particles may be considered as small agitators, involving the rotational movement and generating eddies or micro-vortices in the tested solution. Thus, the application of magnetic particles may enhance the mixing process during realization of the neutralization reaction. In this work, the influence of the magnetic particles activated by the RMF on the tested process was analyzed. Rakoczy (2013) provided an in-depth analysis of the suspension process of the Fe3O4 particles in a liquid phase. According to this paper, the following relation between the Sauter means diameter and the frequency of power supply (it was assumed that this parameter is equal to the RMF frequency) is used:

$$d_{32} = 0.68\;\frac{{f_{\text{RMF}} }}{{f_{\max} }} + 0.91$$
(13)

Mixing time

The realized neutralization reactions are applied for quantitatively characterizing the mixing time in the tested magnetically assisted mixer. Polusen and Iversen (1997) pointed out that the pH measurements may be adapted to the characterization of mixing in the reactor vessel. According to Tan et al. (2011), the dynamic responses of the pH value of the applied indicator may be used to define the mixing time.

It was assumed that the mixing process was regarded as complete when the average pH of liquid did not change with time. It is difficult to detect precisely the endpoint of the response curve (variation of pH over time) defining the mixing time. In this work, this point relates to the equivalence point of the titration of a weak acid with a strong base.

Results and discussion

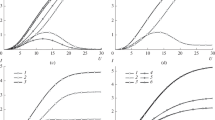
Typical changes in pH during experiments are shown in Fig. 3. Comparison of the obtained pH variation for the neutralization process without and with the action of RMF is presented. Moreover, the effect of the magnetic particle mass, mp, on the neutralization reaction is shown as the function of pH values against time.

Fig. 3
figure 3

Variation of pH values versus time for f = 0 Hz (line 1), f = 10 Hz (line 2), f = 10 Hz and mp = 2 g (line 3), f = 10 Hz and mp = 4 g (line 4)

Full size image

Figure 3 presents that the application of RMF plays an important role in the analyzed neutralization process. The RMF is responsible for the reduction in the duration of the tested reaction. With the use of magnetic particles, a reduction in the duration is more noticeable in comparison with the system without Fe3O4.

Shape of the obtained curves is similar to that of the titration curve (the plot of the pH of the analyte solution versus volume of the titrant added as the titration progresses). The strong base (NaOH) was added as the impulse to the weak acid (CH3COOH). This tracer experiment allowed us to obtain the variation in pH solution versus time for various RMF frequencies as well as for the systems with the application of magnetic particles. Supplementary materials give typical examples of the titration curve obtained for the realized investigations (S.1. The titration curve) and the tracer experiment (S.2. The tracer experiment).

Comparison of the obtained data along with the application of RMF to enhance the neutralization process is given in Fig. 3. The obtained curves can be divided into certain characteristic arras. The initial pH (before the addition of NaOH) is below 3. There is a sharp increase in pH at the beginning of the titration. In this stage of the neutralization reaction, the anion of the weak acid becomes a common ion that reduces the ionization of CH3COOH. After this sharp increase, the curve only changes gradually. This is because the solution is acting as a buffer. In the middle of the obtained curve, the half-neutralization occurs. At this point, the concentration of CH3COOH is equal to the concentration of NaOH (in this point of the process, half of the acid is neutralized). At the equivalence point, the pH is greater than 7, because all CH3COOH is converted into its conjugate base by the addition of NaOH (in this stage of neutralization, the equilibrium moves backward and produces hydroxide). Above the equivalence point, the pH of the solution is dependent only on the excess of added NaOH. Table 1 shows a summary of the characteristic points of the realized neutralization process.

Table 1 Characteristic points of the weak acid (CH3COOH) with the strong base (NaOH) neutralization process
Full size table

The augmentation of the process intensity might be realized by employing the static or rotating magnetic field (SMF or RMF) (Rakoczy and Masiuk 2011; Hajiani and Larachi 2013). It should be noticed that these kinds of MF may be used to enhance the process efficiency instead of mechanical mixing (Hristov 2002). For example, the RMF may be applied as a noninstructive electromagnetic stirrer (Molokov et al. 2007; Moffat 1965). The main feature of this kind of MF is its ability to induce the time-averaged azimuthal force, which drives the flow of the liquid in the azimuthal direction (Rakoczy 2013).

The current study revealed that the RMF may enhance the mixing process of liquid and the RMF acts toward the neutralization process. The tested MF impact on the neutralization process is graphically presented in Fig. 4.

Fig. 4
figure 4

Graphical presentation of the neutralization process without and with the effect of RMF

Full size image

In the case of the RMF application, the liquid (which is weak acid in the case of these investigations) is subjected to the impact of externally applied MF, which induces the force causing movement of the liquid. This phenomenon can be explained based on the “microlevel dynamo concept” (Hristov 2010). The MF interacting with various charged particles, for example, ions, produces eddy currents in the liquid. The eddy currents may generate local MFs around the ions, which, in combination with an externally applied MF, cause induction of their rotation and thus the movement of the liquid following the MF vector. As a consequence of this process, the rotating ions create “dynamos” that cause the effect of micro-mixing. It should be noticed that the mixing process under the RMF action can be enhanced in the liquids, which are highly electrically conductive due to additional ions added, e.g., CH3COO− and H+. The use of RMF caused the enhancement of mixing intensity, which is strongly dependent on the physical parameters of liquid. The obtained result also revealed differences in the duration of the tested process between the neutralization obtained in RMF-exposed conditions versus nonexposed experiment.

The mixing process under the action of the RMF may be strengthened by the application of particles with magnetic properties (e.g., Fe3O4—magnetite). The presence of RMF causes the magnetically assisted fluidization (MAF), which is widely encountered in the manufacturing of drugs, food, chemical products and bioproducts (Saxena et al. 1994; Hristov 1998). In the case of MAF, movement of magnetic particles may be controlled by the field intensity and field orientation and the application of RMF may improve the hydrodynamic conditions in the liquid (Lu et al. 2002).

The idea of the mixing process with the application of magnetic particles under the action of the RMF is graphically presented in Fig. 5.

Fig. 5
figure 5

Graphical presentation of the RMF effect on the applied magnetic particles

Full size image

In the case of the present study, magnetic particles (Fe3O4) were fed into the liquid (weak acid with the addition of strong base) and suspended using the applied RMF. As mentioned in the literature review, the magnetite may be dissolved using the oxalic, sulfuric and nitric acid (Salmimies et al. 2011). This study confirms that the magnetite dissolution process is associated with temperature and acid concentration. It was also shown that the reaction time is very long (about 6 h). The iron oxides dissolution process in oxalic acid was found to be very slow at the range of temperatures between 25 and 60 °C (Lee et al. 2006). These results agree with findings of other studies, in which the rate of process dissolution of iron oxide rapidly increased above 90 °C. It should be noticed that chemical dissolution of iron oxides can be classified into four groups: mineral acids; reductant metal complexes; nonmetallic reductants; and di-, tri- and tetracarboxylic acids (Blesa et al. 1994). The dissolution of magnetite and hematite is possible using oxalic acid, citric acid, malonic acid, EDTA, IDA and HIDA. Low and initial rates of dissolution at room temperature were only observed for EDTA. The dissolution process of magnetite is not observed in the reaction with the application of formic or acetic acids. Supplementary materials give data for quantitative analysis of the neutralization process with and without particles under the RMF action (S.3. Quantitative analysis of the neutralization process with and without particles under the RMF).

Particles with magnetic properties under the action of RMF may generate eddies and micro-vortices in the liquid. Moreover, these particles could form chains along the field lines and rotate with the externally applied RMF. This finding suggests that the magnetic particles may be considered as small agitators that improve the mixing efficiency under the action of RMF. The application of external RMF may lead to a forced, intensive particle movement in the liquid volume. Therefore, the synergistic effect of RMF and magnetic particles is observed for the intensification of the neutralization process. It was found that as the intensity of the MF increases, the time duration of the neutralization process under the action of the applied RMF decreases.

It is decided that the obtained pH curves are described using the following relationship:

$$\left. {\text{pH}} \right|_{{f = \text{var} ;\,m_{\text{p}} = \text{var} }} = p_{1} + \frac{{p_{2} - p_{1} }}{{1 + \left( {p_{3} \,t} \right)^{{p_{4} }} }}$$
(14)

where p1, p2, p3, p4—parameters; t—time, s; \(\left. {pH} \right|_{{f = \text{var} ;\,m_{\text{p}} = \text{var} }}\)—value of pH for the tested operational conditions.

Equation (14) can be converted to the following form:

$$\left. t \right|_{\text{EP}} = \sqrt[{p{}_{4}}]{{\frac{{\left( {p_{2} - p_{1} } \right) - \left( {\left. {pH} \right|_{\text{EP}} - p_{1} } \right)}}{{\left( {\left. {\text{pH}} \right|_{\text{EP}} - p_{1} } \right)\left( {\frac{1}{{p_{3} }}} \right)^{{p_{4} }} }}}}$$
(15)

where \(\left. t \right|_{\text{EP}}\)—time to reach the pH value equal to 8.70, s; \(\left. {\text{pH}} \right|_{\text{EP}}\)—value of pH for the equivalence point (in the case of these experimental results this value is equal to 8.70).

Equation (15) allows to define the time, at which the equivalence point is reached. This point is dependent on the operational conditions, such as the applied RMF and the mass of magnetic particles. Supplementary materials give typical examples of the titration curve obtained for the realized investigations (S.4. The mixing time calculation).

Based on Eq. (9), the relationship for the mixing time for the system without the magnetic particles may be given as follows:

$$\Theta = f\left( {\text{Re}_{\text{RMF}} } \right)\quad \Rightarrow \quad \left( {\frac{{\left. t \right|_{\text{EP}} \;\nu }}{{D^{2} \;}}} \right) = f\left( {\frac{{B_{\max} \;D^{2} }}{\nu }\sqrt {\frac{{\sigma_{\text{e}} \;\omega_{\text{RMF}} }}{\rho }} } \right)$$
(16)

Accordingly, to the proposed relation (16), the plot of data obtained in this work is presented in Fig. 6. The obtained results indicate a great reduction in the dimensionless mixing number with the increase in dimensionless Reynolds number for the RMF application. The results given in this figure suggest that both dimensionless numbers may be analytically connected using the monotonic function:

$$\Theta = a\left( {\text{Re}_{\text{RMF}} } \right)^{b} \quad \Rightarrow \quad \Theta = 7.37\,10^{ - 4} \left( {\text{Re}_{\text{RMF}} } \right)^{ - 0.42}$$
(17)

The influence of magnetic particles on the dimensionless mixing time may be defined in the following form [this relationship is based on Eqs. (10) and (11)]:

$$\begin{aligned} & \Theta = f\left( {\text{Re}_{\bmod } } \right) \\ & \quad \Rightarrow \left( {\frac{{\left. t \right|_{\text{EP}} \nu }}{{D^{2} }}} \right) = f\left( {\frac{{B_{\max}^{2} \,\left( {d_{32} } \right)^{2} }}{{2\;\rho \;\mu_{0} \;\nu^{2} }}\frac{{\chi^{*} }}{{\left( {1 + \chi^{*} } \right)^{2} }}0.0677\left[ {\frac{1}{2}\left( {d_{32} } \right)^{2} \,\mu_{0} \,\sigma_{\text{p}} \,\omega_{\text{RMF}} } \right]} \right) \\ \end{aligned}$$
(18)

The electrical conductivity and averaged magnetic susceptibility of Fe3O4 are about σp = 2.5 × 10−4 Ω−1 m−1 and χ* = 6, respectively (Rakoczy 2013).

Fig. 6
figure 6

Dimensionless mixing characteristics for the system without magnetic particles

Full size image

To establish the effect of modified dimensionless Reynolds number on the dimensionless mixing time, the experimental data are plotted in Fig. 7.

Fig. 7
figure 7

Dimensionless mixing characteristics for the system with magnetic particles

Full size image

The influence of magnetic particle mass on the mixing process can be given as follows:

$$m_{\text{p}} = 2\,{\text{g}} \Rightarrow \Theta = 3.84 \times 10^{ - 5} \left( {\text{Re}_{\text{RMF}} } \right)^{ - 0.18}$$
(19a)
$$m_{\text{p}} = 4\,{\text{g}} \Rightarrow \Theta = 3.79 \times 10^{ - 6} \left( {\text{Re}_{\text{RMF}} } \right)^{ - 0.47}$$
(19b)

The obtained data demonstrate that the dimensionless mixing time decreases with increasing the modified dimensionless Reynolds number. Moreover, the use of the magnetic particles causes reduction in the mixing time. The mixing time is expressed as the time to reach the pH value equal to 8.70 during the neutralization process.

Efficiency of the tested magnetically assisted mixer was determined by evaluating the improvement in mixing time. The RMF effectiveness was defined as a relative improvement of the dimensionless mixing time in the presence of applied magnetic field and magnetic particles, \(\left. \Theta \right|_{{{\text{RMF}} = \text{var} ;\;m_{\text{p}} = \text{var} }}\) compared to this parameter without the action of RMF and the usage of magnetic particles \(\left. \Theta \right|_{{{\text{RMF}} = 0;\;m_{\text{p}} = 0}}\). The factor describing this efficiency is defined as follows:

$$E = \left| {\frac{{\left. \Theta \right|_{{{\text{RMF}} = \text{var} ;\;m_{\text{p}} = \text{var} }} - \left. \Theta \right|_{{{\text{RMF}} = 0;\;m_{\text{p}} = 0}} }}{{\left. \Theta \right|_{{{\text{RMF}} = 0;\;m_{\text{p}} = 0}} }}} \right|100\%$$
(20)

where E—factor describing the efficiency of the mixing process under the action of RMF and the magnetic particle (efficiency factor).

Figure 6 shows the E-factor values for the obtained data in the presence of RMF and the use of various masses of magnetic particles. The E-factor values decrease with the increase in Bmax, which is an expected result. Moreover, the obtained results suggest a strong influence of the mass of the magnetic particle on the dimensionless mixing time. As Fig. 8 shows, there is a significant difference value of E-factor at Bmax > 28 mT and mp = 4 g (the E-factor for this range is equal to about 80%).

Fig. 8
figure 8

E-factor for the mixing process under the RMF action and the use of magnetic particles

Full size image

Conclusions

This paper reports the effect of the RMF and magnetic particles on the neutralization process in the magnetically assisted mixer. The application of RMF caused considerable changes in the duration of the analyzed reactions. The highest improvements were obtained for the application of the Fe3O4 particles. The obtained data from the realized processes were also applied for the analysis of the mixing process under the action of RMF. The effect of this type of magnetic field on the mixing process was discussed using the mixing time. It should be noticed that this time was defined as the time to reach the pH value equal to 8.70 during the neutralization process. One of more significant findings to emerge from this study is that the application of magnetic particles under the action of RMF allows for reducing the mixing time.