1 Introduction

Titanium alloys form an increasingly important class of alloys as lightweight structural engineering materials with the good property-mass ratio.[1] Multiple weight-sensitive high-end applications in aeronautics have benefited from this favorable property-to-weight ratio.[1] However, the high cost of titanium alloys has limited their applications. The high cost is partially due to the raw material cost of alloying elements in current commercial titanium alloys, such as V or Mo.[2] Therefore, it is necessary to design new titanium alloys with low-cost elements, such as Fe, Mn, etc. The properties and processability of engineering alloys depend on the alloy compositions and processing conditions which can be efficiently optimized with the help of computational tools. The CALPHAD (CALculation of PHAse Diagrams) method which employs thermodynamic and kinetic descriptions for the calculation of phase equilibria and phase transformations has been identified as an essential tool for alloy and process design. However, existing titanium thermodynamic and kinetic databases have certain limitations in models and assessments that require improvements.

The binary Ti-Al system is the core binary alloy system for the development of nearly all classes of titanium alloys since Al is the only common metallic α stabilizer and has large solubilities in both the α and β phases. Almost all titanium alloys involve a mass fraction of 3 to 8% of Al as α stabilizer and solid solution strengthener. The most recent and comprehensive assessment of this system was conducted by Witusiewicz et al.[3] and was based on various available experimental data. However, due to the increasing availability of thermodynamic data from density functional theory (DFT) calculations, such as the enthalpy of formation at 0 K for end members in thermodynamic sublattice models, especially the metastable ones, the Ti-Al system should be reassessed based on both experimental and DFT data.

In the 1980 s and 1990 s, Ti-Al-Fe alloys were investigated as a potential substitute of Ti-6Al-4V alloy.[4,5,6]. For example, Ti-5Al-2.5Fe alloy was developed in the early 1980 s as an implant alloy to address the toxicity issue caused by Ti-6Al-4V. The other advantage of Fe compared with V in titanium alloys is its low cost, which makes these titanium alloys cost-acceptable for civil industries, such as automotive industry. Fe is normally not considered as a major alloying element due to the macro-segregation issue in ingot metallurgy.[2] However, due to the recent developments in net-shape and near-net-shape manufacturing technologies, the macro-segregation issue can be avoided in certain manufacturing processes without an ingot/master-alloy making process (e.g., additive manufacturing). Therefore, Fe has become a possible choice as a major alloying element, and a precise Ti-Fe thermodynamic description is essential in applying CALPHAD method for the design of these alloys. Recently, one of the authors presented an attempt in applying the CALPHAD method to design new Ti-Al-Fe alloy for casting process and achieve competitive properties.[7] However, more credible integrated computational materials engineering (ICME) design requires a more robust thermodynamic database. The most recent Ti-Fe assessment was conducted by De Keyzer et al.[8] with good agreement between calculated and experimental phase boundaries. However, as for the Ti-Al system, the enthalpies of formation in this description differ from the results of DFT calculations. Therefore, the same motivation as for Ti-Al system applies for Ti-Fe re-assessment to obtain energy consistency with other binary systems. The Al-Fe binary system was fully investigated by Sundman et al.[9] using a 4 sublattice model to describe the A2-B2-D03 ordering. This assessment used a combination of experimental data and first-principles calculation results and was directly adopted in the present work.

Another important motivation for this investigation was based on the experimental observations in Ti-Al-Fe ternary system. According to the review by Palm and Lacaze,[10] complex body-centered cubic (BCC) order-disorder transformations among A2, B2 and D03/L21 are present in Ti-Al-Fe ternary system. These transformations also affect the equilibria with Laves C14 and several other intermetallic phases. The order sequences of the D03 and L21 phases are ABBB and AABC, respectively. Thus, the commonly used 2-sublattice (2SL) BCC model cannot be used. Therefore, it is necessary to first establish the 4-sublattice (4SL) BCC description in the binary systems. In the 4SL model, the energies of both stable and metastable phases are important since they affect the phase stability in ternary and higher-component systems, which re-emphasizes the importance of the consistency of the descriptions that can be achieved using results from DFT calculation for the binary systems. Therefore, the assessments of the thermodynamic descriptions of Ti-Al, Ti-Fe, and Ti-Al-Fe systems in the present work is based on available experimental and DFT data. Using the 4SL order-disorder model for the BCC description enables modelling of the order-disorder transformations between the A2, B2, and D03/L21 phases. The other issue is the description of the magnetism of the Laves C14 and Heusler phases in both the binary Ti-Fe and ternary Ti-Al-Fe systems. The description of the magnetism of the phases in the Al-Fe binary system has been well established by Sundman et al.[9] while none of the phases in the binary Ti-Al system are magnetic. However, the Laves C14 phase extending from the binary Ti-Fe system as well as the Heusler phase are both magnetic.[11,12] Since the magnetism was not considered in the descriptions of either Ti-Fe or Ti-Al-Fe systems, the magnetism description was included in the present work.

2 Thermodynamic Modeling

The structures of the phases in the Ti-Al, Ti-Fe, Al-Fe and Ti-Al-Fe thermodynamic descriptions are given in Table 1 with the corresponding models.

Table 1 Ti-Al, Ti-Fe, Al-Fe, and Ti-Al-Fe phase information in the present work
Full size table

2.1 Pure Elements

The Gibbs energy of a pure element \(i\) is described as a function of temperature from Scientific Group Thermodata Europe (SGTE) compilation of Dinsdale[13] by:

$$\begin{array}{*{20}c} {^{o} G_{i}^{\phi } -^{o} H_{i}^{{{\text{SER}}}} \left( {298.15\;{\text{K}}} \right) = a + bT + cT\ln \left( T \right) + dT^{2} + eT^{3} + fT^{ - 1} + gT^{7} + hT^{ - 9} + \;^{{{\text{mag}}}} G^{\phi } } \\ \end{array}$$
(1)

where \(^{o} H_{i}^{{{\text{SER}}}} \left( {298.15\;{\text{K}}} \right)\) is the enthalpy of pure element \(i\) at 298.15 K and 1 bar in its standard element reference (SER) state; parameters a to h are coefficients that were adjusted to experimental data. \(^{{{\text{mag}}}} G^{\phi }\) is the contribution to the Gibbs energy from magnetism described by the Hillert–Jarl formalism.[14]

2.2 Disordered Solutions

Disordered solid solution phases, such as liquid, hexagonal close packed (HCP), body centered cubic (BCC), and face centered cubic (FCC), are described by the following equations:

$$\begin{array}{*{20}c} {G_{m}^{\phi } \left( {x_{i} } \right) = \;^{{{\text{ref}}}} G^{\phi } + \;^{{{\text{id}}}} G^{\phi } + \;^{{{\text{ex}}}} G^{\phi } + \;^{{{\text{mag}}}} G^{\phi } } \\ \end{array}$$
(2)
$$\begin{array}{*{20}c} {^{{{\text{id}}}} G^{\phi } = RT\mathop \sum \limits_{i} x_{i}^{\phi } \ln x_{i}^{\phi } } \\ \end{array}$$
(3)
$$^{{{\text{ex}}}} G^{\phi } = \mathop \sum \limits_{v = 0,1,2}^{i,j,i \ne j} x_{i}^{\phi } x_{j}^{\phi } \;^{v} L_{i,j}^{\phi } \left( T \right) + \mathop \sum \limits_{v = 0,1,2}^{i,j,k,i \ne j \ne k} x_{i}^{\phi } x_{j}^{\phi } x_{k}^{\phi } \;^{v} L_{i,j,k}^{\phi } \left( T \right)$$
(4)

where \(\;^{{{\text{ref}}}} G^{\phi }\), \(\;^{{{\text{id}}}} G^{\phi }\), and \(\;^{{{\text{ex}}}} G^{\phi }\) are reference, ideal mixing, and excess Gibbs energies, respectively; \(x_{i}^{\phi }\) is the mole fraction of element \(i\) in phase \(\phi\); \(R\) is the gas constant, 8.314 \(\frac{{\text{J}}}{{{\text{mol}}\;{\text{K}}}}\); T is the absolute temperature, \(\;^{v} L_{i,j}^{\phi } \left( T \right)\) and \(\;^{v} L_{i,j,k}^{\phi } \left( T \right)\) are the temperature dependent interaction parameters that are determined via assessments.

2.3 Intermetallics

Intermetallic compounds, such as Ti5Al11, TiAl2, TiAl3, Ti3Al5, TiAl, D019-Ti3Al, C14-Fe2Ti, τ2 ,τ3 are described by the Compound Energy Formalism (CEF)[15] as \(\left( {X,Ti} \right)_{{n^{\left( 1 \right)} }} \left( {X,Ti} \right)_{{n^{\left( 2 \right)} }} \left( {X,Ti} \right)_{{n^{\left( 3 \right)} }} \left( {X,Ti} \right)_{{n^{\left( 4 \right)} }}\). Their Gibbs energies are described by Eq 2 but with:

$$^{{{\text{ref}}}} G^{\phi } = \mathop \sum \limits_{m} G_{m}^{\phi } \mathop \prod \limits_{s} y_{i}^{\left( s \right)}$$
(5)
$$^{{{\text{id}}}} G^{\phi } = RT\mathop \sum \limits_{s} \mathop \sum \limits_{i} n^{\left( s \right)} y_{i}^{\left( s \right)} \ln y_{i}^{\left( s \right)}$$
(6)
$$^{{{\text{ex}}}} G^{\phi } = \mathop \sum \limits_{s} \mathop \sum \limits_{i} \mathop \sum \limits_{j} y_{i}^{\left( s \right)} y_{j}^{\left( s \right)} \mathop \sum \limits_{r \ne s} \mathop \sum \limits_{j} y_{k}^{\left( r \right)} L_{i:j: \cdots :k}^{\phi } \left( T \right) + \cdots$$
(7)

where \(y_{i}^{\left( s \right)}\) is the mole fraction of element \(i\) in sublattice \(s\); \(n^{\left( s \right)}\) is the stoichiometric factor of the sublattice; \(G_{m}^{\phi }\) is the Gibbs energy of stoichiometric compounds when each sublattices is occupied by only one constituent, aka “end member compounds”; \(L_{i:j: \cdots :k}^{\phi } \left( T \right)\) are the temperature dependent interaction parameters that are determined via assessments.

Different from the description by Witusiewicz et al.[3] the present work adopts the experimental observation of the ordered FCC phase, Ti5Al11, by Braun and Ellner.[16] Instead of the definition as a 2 sublattice model, a 4 sublattice model is used with the end member definitions (enthalpy of formation and specific heat capacity) the same as L10-TiAl and D022-TiAl3, which makes it closer to the ordered FCC, F’ phase, description as illustrated by Braun et al.[17] Ideally, in the Ti-Al binary system, FCC_A1, L10-TiAl, D022-TiAl3, F’-Ti5Al11 phases should be all described by the order-disorder FCC model. However, to describe all of these phases using order-disorder model, 8 sublattices are needed, resulting in serious complications. Therefore, these phases are modeled with independent descriptions, but attention was paid to maintain consistency among their energy definitions.

In the present work, the enthalpies of formation of all end members are based on DFT data from the AFLOW database,[18,19] literature data,[20,21] and the present work. If no specific heat capacity measurements were available, only the contributions from the pure elements are considered. Otherwise, the end members are described using a combination of DFT data and experimentally measured specific heat capacity data.

2.4 Ordered forms of the BCC

In the present work, the ordered BCC phases in Ti-Al, Ti-Fe and Ti-Al-Fe systems are modeled by a 4 sublattice model, \(\left( {{\text{Al}},{\text{Fe}},{\text{Ti}},{\text{Va}}} \right)_{0.25} \left( {{\text{Al}},{\text{Fe}},{\text{Ti}},{\text{Va}}} \right)_{0.25} \left( {{\text{Al}},{\text{Fe}},{\text{Ti}},{\text{Va}}} \right)_{0.25} \left( {{\text{Al}},{\text{Fe}},{\text{Ti}},{\text{Va}}} \right)_{0.25} \left( {{\text{Va}}} \right)_{3}\), where \({\text{Va}}\) is vacancy. In order to represent all possible ordered structures based on the BCC structure, the following end members for the Gibbs energy expression are defined based on the concept of the bond energies:[22]

$$G_{{{\text{B}}_{2} }} = G_{{{\text{Ti}}:{\text{Ti}}:{\text{X}}:{\text{X}}:{\text{Va}}}} = G_{{{\text{X}}:{\text{X}}:{\text{Ti}}:{\text{Ti}}:{\text{Va}}}} = 4u_{{{\text{TiX}}}}$$
$$G_{{{\text{B}}_{32} }} = G_{{{\text{Ti}}:{\text{X}}:{\text{X}}:{\text{Ti}}:{\text{Va}}}} = G_{{{\text{X}}:{\text{Ti}}:{\text{Ti}}:{\text{X}}:{\text{Va}}}} = G_{{{\text{X}}:{\text{Ti}}:{\text{X}}:{\text{Ti}}:{\text{Va}}}} = G_{{{\text{Ti}}:{\text{X}}:{\text{Ti}}:{\text{X}}:{\text{Va}}}} = 2u_{{{\text{TiX}}}} + 3v_{{{\text{TiX}}}}$$
$$G_{{{\text{D}}0_{3} - {\text{Ti}}_{3} {\text{X}}}} = G_{{{\text{Ti}}:{\text{Ti}}:{\text{Ti}}:{\text{X}}:{\text{Va}}}} = G_{{{\text{Ti}}:{\text{Ti}}:{\text{X}}:{\text{Ti}}:{\text{Va}}}} = G_{{{\text{Ti}}:{\text{X}}:{\text{Ti}}:{\text{Ti}}:{\text{Va}}}} = G_{{{\text{X}}:{\text{Ti}}:{\text{Ti}}:{\text{Ti}}:{\text{Va}}}} = 2u_{{{\text{TiX}}}} + 1.5v_{{{\text{TiX}}}} + {\Delta }G_{{{\text{Ti}}_{3} {\text{X}}}}$$
$$G_{{{\text{D}}0_{3} - {\text{TiX}}_{3} }} = G_{{{\text{Ti}}:{\text{X}}:{\text{X}}:{\text{X}}:{\text{Va}}}} = G_{{{\text{X}}:{\text{Ti}}:{\text{X}}:{\text{X}}:{\text{Va}}}} = G_{{{\text{X}}:{\text{X}}:{\text{Ti}}:{\text{X}}:{\text{Va}}}} = G_{{{\text{X}}:{\text{X}}:{\text{X}}:{\text{Ti}}:{\text{Va}}}} = 2u_{{{\text{TiX}}}} + 1.5v_{{{\text{TiX}}}} + {\Delta }G_{{{\text{TiX}}_{3} }}$$
$$G_{{{\text{L}}2_{1} - {\text{A}}_{2} {\text{BC}}}} = G_{{{\text{A}}:{\text{A}}:{\text{B}}:{\text{C}}:{\text{Va}}}} = G_{{{\text{A}}:{\text{A}}:{\text{C}}:{\text{B}}:{\text{Va}}}} = G_{{{\text{B}}:{\text{C}}:{\text{A}}:{\text{A}}:{\text{Va}}}} = G_{{{\text{C}}:{\text{B}}:{\text{A}}:{\text{A}}:{\text{Va}}}} = 2u_{{{\text{AB}}}} + 2u_{{{\text{AC}}}} + 1.5v_{{{\text{BC}}}}$$
$$\begin{aligned} G_{{{\text{Inverse - L}}2_{1} {\text{ - A}}_{2} {\text{BC}}}} & = G_{{{\text{A}}:{\text{B}}:{\text{A}}:{\text{C}}:{\text{Va}}}} = G_{{{\text{A}}:{\text{C}}:{\text{A}}:{\text{B}}:{\text{Va}}}} = G_{{{\text{A}}:{\text{B}}:{\text{C}}:{\text{A}}:{\text{Va}}}} = G_{{{\text{A}}:{\text{C}}:{\text{B}}:{\text{A}}:{\text{Va}}}} = G_{{{\text{B}}:{\text{A}}:{\text{C}}:{\text{A}}:{\text{Va}}}} \\ & = G_{{{\text{C}}:{\text{A}}:{\text{B}}:{\text{A}}:{\text{Va}}}} = G_{{{\text{B}}:{\text{A}}:{\text{A}}:{\text{C}}:{\text{Va}}}} = G_{{{\text{C}}:{\text{A}}:{\text{A}}:{\text{B}}:{\text{Va}}}} \\ & = u_{{{\text{AB}}}} + u_{{{\text{AC}}}} + u_{{{\text{BC}}}} + 1.5v_{{{\text{AB}}}} + 1.5v_{{{\text{AC}}}} \\ \end{aligned}$$
(8)

where \(u_{{{\text{TiAl}}}}\) and \(v_{{{\text{TiAl}}}}\) represent the bond energies between nearest and second-nearest neighbors; \({\Delta }G_{{{\text{Ti}}_{3} {\text{X}}}}\) and \({\Delta }G_{{{\text{TiX}}_{3} }}\) are the parameters for the \({\text{D}}0_{3}\) end members to describe the asymmetry of the system. Not listed above are the Gibbs energies of formation of the end members of pure elements and end members with vacancy occupation in any of the first 4 sublattice sites which are defined as zero.

The Gibbs energy of the ordered BCC phases are given by the following equation:[23]

$$G_{m} = G_{m}^{{{\text{dis}}}} \left( {x_{i} } \right) + G_{m}^{{{\text{ord}}}} \left( {y_{i}^{\prime } ,y_{i}^{\prime \prime } ,y_{i}^{\prime \prime \prime } ,y_{i}^{\prime \prime \prime \prime } } \right) - G_{m}^{{{\text{ord}}}} \left( {x_{i} } \right)$$
(9)

where \(G_{m}^{{{\text{dis}}}} \left( {x_{i} } \right)\) is the Gibbs energy of the disordered BCC phase (Eq 2 and 3); \(G_{m}^{{{\text{ord}}}} \left( {y_{i}^{\prime } ,y_{i}^{\prime \prime } ,y_{i}^{\prime \prime \prime } ,y_{i}^{\prime \prime \prime \prime } } \right)\) is the Gibbs energy of the ordered phase (Eq 2 and 8); \(G_{m}^{{{\text{ord}}}} \left( {x_{i} } \right)\) represents the energy contribution of the disordered state to the ordered phase, in which \(y_{i}^{\prime } = y_{i}^{\prime \prime } = y_{i}^{\prime \prime \prime } = y_{i}^{\prime \prime \prime \prime } = x_{i}\).

2.5 Density-Functional Theory (DFT) Calculation of End Members

In this work, end members not available in existing databases and literature were computed using DFT, including enthalpy of formation and Bohr magneton number. Specifically, all DFT calculations were carried out with Vienna ab initio simulation package (VASP)[24,25]Footnote 1 using projected augmented wave (PAW) formalism. We used vdW-DF-optB88/OptB88vdW (OPT) functional for energetics and structural relaxation. The OPT exchange functional uses the Becke88 (B88) exchange[26] and optimizes the parameters in the B88 enhancement factor. The OPT functional was shown to be very well applicable to solids[27] and, ever since, it has been used to model rare-gas dimers and metallic, ionic, and covalent bonded solids,[27,28] polymers[29] and small molecular systems.[30] When available, we used already relaxed structures from the JARVIS-DFT repository.[31] When not, we obtained the crystal structures from Materials Project,[32] which uses PBE functional, and we re-optimized those structures with OPT for consistency-sake. The k-point and plane-wave cut-off convergence for each material is obtained using the workflow detailed in (Ref 33. Specifically, we performed plane-wave energy cut-off and k-point convergences with 0.001 eV tolerance on energy for each structure in an automated way. The structure relaxation with OPT functional was obtained with 10-8 eV energy tolerance and 0.001 eV/Å force-convergence criteria.

2.6 Treatment of Magnetic Parameters

As mentioned in section 2.4, DFT calculation will produce Bohr magneton number, BM, for end members, which can be directly applied. However, since Curie temperature, TC, value will not be calculated, it was approximated in this assessment under the assumption that in the same phase among different end members, the ratios of Curie temperature and Bohr magnetron are the same:[34]

$$\frac{{T_{{c_{1} }} }}{{T_{{c_{2} }} }} = \frac{{{\text{BM}}_{1} }}{{{\text{BM}}_{2} }}$$
(10)

2.7 Thermodynamic Optimization

In the present work, all thermodynamic parameters are optimized using Thermo-Calc and its PARROT optimization module[35] and trial-and-error based on the available experimental and first-principle calculation results from both literature and this work.

3 Literature Review, Results and Discussion

The assessed descriptions of the Ti-Al, Ti-Fe and Ti-Al-Fe binary systems are given in Table 9 of the “Appendix”. This thermodynamic description was used in the calculation of the phase diagram and related thermodynamic properties described in this section.

3.1 Ti-Al

The most recent thermodynamic assessment of the Ti-Al binary system was conducted by Witusiewicz et al.[3] This description reproduces the experimental data at intermediate temperatures (1300 to 1700 K) well and is focused on the description of the L10-TiAl phase. However, the results from this description show a few discrepancies with the accepted data: enthalpies of formation of solid phases at 298.15 K, D019-Ti3Al and L10-TiAl homogeneity ranges, inverse miscibility gap for liquid at 4000 K, and underestimation of liquidus for the BCC_A2 and HCP_A3 phases. As listed in Table 2, the calculated enthalpies of formation for the solid phases in the Ti-Al binary system from Witusiewicz et al.’s description differ to various degrees from the first-principles calculation results. As shown in Figure 1, the homogeneity ranges of D019-Ti3Al and L10-TiAl have significant discrepancies. The Ti-rich boundary of D019-Ti3Al is not consistent with the experimental literature data and should be reassessed. As for the Al-rich boundary of D019-Ti3Al and Ti-rich boundary of L10-TiAl, it could be caused by the experimental data by Ouchi et al.[36] In the experimental details of Ouchi et al.[36] it was noted that for their diffusion couple experiments, the raw titanium used for fabrication was of low purity (mass fraction of 99.8 %) and might include unknown impurities resulting in inaccurate results. As shown in Fig. 1, at high temperature, an unexpected reverse miscibility gap exists for the liquid phase, which is highly undesirable and might cause problems when developing a database with high melting point phases. Also, the calculated liquidus is too low compared to the data from their own differential thermal analysis (DTA) measurements and those from Schuster and Ipser.[37] Since the liquidus is also critical in high temperature processing design, this discrepancy should be addressed as well.

Table 2 Enthalpies of formation in Ti-Al binary system
Full size table
Fig. 1
figure 1

Calculated Ti-Al phase diagram based on Witusiewicz et al.[3] and comparison with selected experimental data[39]

Full size image

Witusiewicz et al.[3] and Schuster and Ipser[38] presented a comprehensive evaluation of the majority of experimental data from the literature. Therefore, only selected literature data was reviewed for the reassessment. Perepezko et al.,[40] Schuster and Ipser[37] and Witusiewicz et al.[3] used differential thermal analysis (DTA) measurements during heating to determine the liquidus temperatures. Though it is common practice to use the melting peak temperature as the liquidus temperature this could be an underestimation of the liquidus because it is not necessarily the end of melting. Therefore, in the present work, these results were regarded as the lower limit of the liquidus.

In addition, Perepezko et al.[40] used DTA measurements to determine the HCP_A3 → BCC_A2 transformation temperatures. However, it should be noted that the (HCP_A3 + BCC_A2) two-phase region is very narrow. Therefore, the measured temperature can be either the HCP_A3 → (HCP_A3 + BCC_A2) or the (HCP_A3 + BCC_A2) → BCC_A2 transformation temperatures. Therefore, in the present work, these transformation temperatures were given lesser weight in the optimization. The same was applied to the DTA measurement of these transformation temperatures by Mishurda et al.[41]

The comparison with selected experimental data and the calculated phase diagram is shown in Fig. 2. The comparison of the calculated and experimental invariant equilibria is given in Table 3 and shows good agreement. Also, the high temperature inverse miscibility gap was corrected. The enthalpies of formation of the solid phases are given in Table 2 and are compared with DFT and experimental data. The metastable BCC phase diagram (overlaid on the stable phase diagram) is plotted in Fig. 3.

Fig. 2
figure 2

Calculated Ti-Al phase diagram with experimental data[28]

Full size image
Table 3 Invariant reactions in the Ti-Al system
Full size table
Fig. 3
figure 3

Ti-Al phase diagram overlapped with A2-B2 metastable diagram, overlapping with the B2 bubble in the stable phase diagram

Full size image

The D019-Ti3Al phase is critical for determination of Al content in titanium alloy design. The D019-Ti3Al phase usually needs to be avoided because of embrittlement. Therefore, the binary homogeneity range of this phase is critical when evaluating the effects of other elements on it. The same applies to the L10-TiAl phase as well. As show in Fig. 2, the phase boundaries of D019-Ti3Al and L10-TiAl are consistent with the experimental measurements.

As explained in the introduction and literature review, the discrepancies in the enthalpies of formation could lead to unexpected phase stability conflicts with other binary systems when combining them in descriptions of higher-component systems. This is particularly important for the ordered BCC phase since with the order-disorder model incorrect end member contributions will lead to incorrect order-disorder transformations. As given in Table 2, the calculated enthalpies of formation of the solid phases are consistent with the results from DFT calculations.

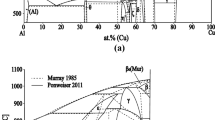
The assessed parameters in this work produce a small area with B2 ordering around 1500 K and xAl = 0.34 mole fraction as shown in Fig. 2. In Fig. 3, the metastable A2-B2 phase diagram is overlayed on top of the stable phase diagram, showing the shape of metastable A2-B2 transformation region. Although the BCC ordering phenomenon was observed experimentally in multiple ternary systems, such as Ti-Al-Nb,[42] Ti-Al-Mn,[43] Ti-Al-Fe,[10] its occurrence in the Ti-Al binary system has not yet been completely verified. Ohnuma et al.[44] presented a possible experimental observation of the BCC ordering in the Ti-Al binary system via differential scanning calorimetry (DSC) experiment, but the observed peak was low in intensity and the reported transformation temperature was close to measurements of regular α → (α + β) or (α + β) → β transformations. Therefore, it should be noted that the BCC ordering phenomenon modeled in the present work is an estimate from this single source.

3.2 Ti-Fe

The most recent thermodynamic assessment of the Ti-Fe binary system was conducted by De Keyzer et al.[8] who applied the 2 sublattice model for BCC_B2 (TiFe) phases to describe their homogeneity ranges. Furthermore, De Keyzer et al.[8] introduced a 3 sublattice model for Laves C14 (Fe2Ti) to describe the shape of the C14 homogeneity range in the Fe-Ni-Ti ternary system. Since a similar homogeneity range of this phase is observed in the Ti-Al-Fe ternary system,[10] this model is adopted in the present work. As for the Ti-Al binary system, the enthalpies of formation for solid phases at 298.15 K, especially for the end members in ordered BCC description, have discrepancies with results from first-principles calculations as given in Table 4.

Table 4 Enthalpies of formation in Ti-Fe binary system
Full size table

The comparison of the calculated Ti-Fe phase diagram with selected experimental data is shown in Fig. 4. The comparison of the calculated and experimental invariant equilibria is given in Table 5 and shows good agreement. The enthalpies of formation of the solid phases are given in Table 4 together with the DFT and experimental data.

Fig. 4
figure 4

Calculated Ti-Fe phase diagram with experimental data[47,48]

Full size image
Table 5 Invariant reactions in the Ti-Fe system
Full size table

As shown in Fig. 4, the 4SL model shows good consistency with the experimental data except for the trend in solubility change for the ordered BCC phase. However, as reported in the original experimental details,[46] the raw materials were not in high purity (atomic fraction of 99.7 %) and the amounts of interstitial elements (C and N) might affect the homogeneity range of the ordered BCC phase. Therefore, in the present work, this experimental work was given less weight in the optimization. According to the experimental work by Booker,[47] the Ti-rich homogeneity limit of C14 at peritectic temperature was estimated (atomic fraction of 63 % of Fe) based on the incipient melting experiments (the maximum was an atomic fraction of 60 %). Therefore, the actual homogeneity limit was re-evaluated based on the extrapolation from results of Murakami et al.[46]

Similar to the argument given for the Ti-Al binary system, Table 4 shows that the calculated enthalpies of formation of solid phases were consistent with DFT calculation results. In contrast to assessment in De Keyzer et al.[8] enthalpy of formation is larger. While De Keyzer at al.'s assessment is based on liquid enthalpy of mixing and phase diagram data only, the current assessment also includes DFT-calculated enthalpies of formation. Considering general database usage, especially regarding compatibility in a multicomponent database, a DFT-based assessment is generally better due to consistent base values of the enthalpy of formation.

3.3 Al-Fe

The most recent thermodynamic assessment of the Al-Fe binary system was conducted by Sundman et al.[9] This assessment applied the 4SL model for BCC to describe the co-existence of disordered A2, ordered B2 and ordered D03 phases. Therefore, this assessment was directly used in this work except for the 4SL model for the FCC because it is not needed for the description of the ternary Ti-Al-Fe system. Additionally, several end members of the C14 Laves phase that do not exist in Al-Fe binary system were entered in the description based on DFT values listed in Table 6.

Table 6 New end members in Al-Fe binary system
Full size table

3.4 Ti-Al-Fe

Palm and Lacaze[10] presented a comprehensive evaluation on the experimental and theoretical information of the ternary Ti-Al-Fe system. Experimental isothermal sections at 800, 900, 1000 and 1200 °C were reported and related experimental data was summarized. The experimental isothermal sections clearly indicate the significant homogeneity ranges of TiFe B2 and TiFe2 C14 phases in the ternary Ti-Al-Fe system and the presence of A2-B2-L21 order-disorder transformation in the Fe-rich corner. Furthermore, two intermetallic compounds were shown: τ2 and τ3. According to Palm and Lacaze,[10] there is no CALPHAD-type description of the whole ternary system at present, which is the motivation in this work.

The comparison of calculated Ti-Al-Fe 800 and 1000 °C isothermal sections with experimental data is shown in Fig. 5. The comparison of the calculated and experimental liquidus data is given in Table 7. It should be noted that when conducting liquidus calculation, τ2 and τ3 phases are excluded from the calculation due to the limitation of simplified sublattice model (further discussed in section 3.5). As shown, the agreement between calculation and experiments is decent, though discrepancies can be observed regarding the first phase formed during solidification. As described by Ducher et al.[51] the first phase formed was determined via microstructural observation and XRD, which can be misleading depending on morphological complexity and order-disorder phase. For example, sample ssm72 was described of forming BCC_A2 first during solidification, but if examining Al-Fe binary system, being close to 55 at.% of Al certainly results in BCC_B2 instead. Therefore, due to uncertainty from original experimental measurements, the first phase formed was given less weight than liquidus temperatures in the assessment. The calculated enthalpies of formation of ternary end members are given and compared with DFT values in Table 8. It should be noted that AlFe2Ti-L21, τ2, and τ3 end members slightly deviate from DFT values in the assessment, which is considered to be within acceptable magnitude. All 3-phase equilibria and 2-phase tie-lines in the Ti and Fe corners are in good agreement with experimental data. Especially, the order-disorder relationship among A2, B2, and L21 phases in both Ti and Fe corners are highly consistent with experimental observations, which was the main goal in this work. However, there were a few limitations in this assessment. These limitations and the discrepancies between experimental and calculated results are discussed in section 3.5.

Fig. 5
figure 5

Calculated isothermal sections of Ti-Al-Fe ternary system at (a and b) 800 °C with and without experimental data, and (c and d) 1000 °C with and without experimental data. Experimental data are from Palm et al.[49] and Kainuma et al.[50]

Full size image
Table 7 Comparison between experimental liquidus and calculated liquidus from this work.
Full size table
Table 8 Enthalpies of formation in Ti-Al-Fe ternary system
Full size table

3.5 Discussion of Limitations and Discrepancies

There were a few limitations in this assessment. The homogeneity ranges from several binary intermetallic phases in Al-rich corner were not included in the assessment to keep the description simple for titanium system applications. In addition, multiple ordered phases which are based on FCC and HCP crystal structure could be treated by the order-disorder model for a complete description of this ternary system. However, these phases were assessed as independent phases for computational efficiency. There are also discrepancies between calculated and experimental 2-phase tie-lines and 3-phase triangles. These discrepancies could be due to both model and experimental errors, which could not be resolved quantitatively in the present work. τ2 and τ3 phases were not fully assessed since it would require a large number of DFT calculations for all of the end members of these two phases. Since these intermetallic phases are not sufficiently described in this ternary system, their liquidus data[41] were not considered in the present work.

As shown in the 800 °C isothermal section in Fig. 5(a), the calculated results do not agree with the experimental tie-lines between BCC_B2 and C14 that are farther away from the Ti-Fe binary and the calculated BCC_B2 (FeTi) homogeneity range is also slightly shifted toward the Ti corner of the system. However, when examining the BCC_B2-C14-τ2 triangle, the equilibria between BCC_B2 and C14 agree well with experiment. Furthermore, when examining BCC_B2-C14 tie-lines in the 1000 °C isothermal section in Fig. 5(b), the calculation agrees better with experimental data. Therefore, these observations indicate that this experimental tie-line should be given less weight during modeling. Similarly, the tie-lines between BCC_L21 and C14 in 1000 °C isothermal section also show discrepancies in compositions, which could be due to either modeling or experimental measurement issues. Issues with the experimental measurements cannot be ruled out since the annealed microstructure was not included in the reference.[40] If phase morphology was lamellar, then compositional measurements may not be reliable. The calculated liquidus temperature of samples ssm58, ssm192, ssm348 and ssm349[41] differs noticeably from the experimental observation, but since the same group of authors showed these samples are potentially outliers in the experimental liquidus projection,[10] these data were given less weight during optimization.

4 Conclusion

This work established a thermodynamic assessment of Ti-Al-Fe ternary system, which is essential for the design of new titanium alloys in this system. The following specific aspects are highlighted:

  1. (1)

    The binary Ti-Al and Ti-Fe systems are reassessed using 4SL BCC model with DFT-calculated end member values, ensuring future compatibility with other DFT-based assessments.

  2. (2)

    The application of 4SL model for BCC phase also enables the successful modeling of the order-disorder transformation of A2-B2-L21 in Ti-Al-Fe system in Fe-rich corners with the majority of calculated phase boundaries agreeing well with experimental data.

  3. (3)

    This description accurately describes phase equilibria among α-Ti, β-Ti, B2-TiFe, and D019-Ti3Al phases, facilitating accurate predictions for intermetallic compound phase stabilities in Ti-rich corner.

  4. (4)

    This description also utilizes the DFT method to construct unstable end members in multiple intermetallic compound phases that having ternary solubility, including ordered BCC (B2, L21), Laves_C14 and τ2 phases.

  5. (5)

    This new thermodynamic description is essential for the determination of Ti-Al-Fe-based higher component thermodynamic systems.