1 Introduction

In-Sn alloys exhibit lower melting temperatures and improved thermal fatigue as compared with Pb-Sn solders;[1,2] they also exhibit superconductivity,[3,4] and they form the basis for the transparent conductor Indium-Tin-Oxide (ITO). In addition to their practical interest, their experimentally determined alloy phase diagram poses several scientific puzzles. This paper applies first principles total energy and band structure calculations, and simple thermodynamic modeling, to address these questions.

The assessed In-Sn binary alloy system[5] exhibits four phases at room temperature and above, all with substantial composition ranges. In order of increasing fraction of Sn, the phases are: α-In, β-In3Sn (both share Pearson type tI2), γ -InSn4 (Pearson type hP1), and β-Sn (Pearson type tI4, “white tin). There exists a different, low temperature, nonmetallic phase α-Sn (Pearson type cF8, “gray tin”) that has low In solubility and is stable below 286 K. α-In and β-In3Sn are separated by a discontinuous transition with a narrow coexistence range around Sn fraction x≈9-11%, despite sharing the same body-centered tetragonal structure and symmetry space group (I4/mmm). This violates the normal Landau-type model of solid-solid phase transformation that supposes group-subgroup relationships between phases. We resolve the puzzle by evaluating the energies along the Bain path of cubic ↔ tetragonal deformation. We also explore the differences in interatomic bonding between the α and β structures.

The experimentally reported solubility range of γ appears nearly temperature-independent and persists towards low temperatures. This suggests a low temperature configurational entropy, in apparent violation of the Third Law of Thermodynamics.[6,7] We propose that γ actually decomposes eutectoidly as temperature drops. β-In3Sn also decomposes eutectoidly. The solubility of Sn in α-In vanishes at low temperature, while the solid solution β-Sn transforms to α-Sn with limited In solubility.

2 Methods

Our calculations follow widely used methods.[8] We utilize the Vienna Ab-Initio Simulation Package VASP[9] to carry out first principles density functional theory (DFT) total energy calculations in the Perdew-Burke-Ernzerhof generalized gradient approximation.[10] We adopt projector augmented wave potentials[11,12] and maintain a fixed energy cutoff of 241.1 eV (the default for Sn). We relax all atomic positions and lattice parameters using the PREC Accurate precision setting, and increase our k-point densities until energies have converged to within 0.1 meV/atom, then carry out a final static calculation using the tetrahedron integration method. Certain other settings are discussed below as needed.

Our structures and phase diagrams are drawn from the ASM phase diagram database[13] and from the Inorganic Crystal Structure Database[14] (ICSD), supplemented with original publications. For solid solution phases we take 16-atom supercells at a variety of compositions and enumerate all possible configurations using enumlib.[15] The supercells of the α and β tI2 structures are 2x2x2. Supercells of γ -InSn4.hP1 are based on an orthorhombic supercell of the hexagonal primitive cell. For β-Sn.tI4, we take a √2x√2x2 supercell. All configurations are fully relaxed, and only the lowest energy configuration is employed in the subsequent analysis.

Given total energies for a variety of structures, we calculate the enthalpy of formation ΔHFor, which is the enthalpy of the structure relative to a tie-line connecting the ground state configurations of the pure elements.[16] Formally, for a compound of stoichiometry In1-xSnx with Sn fraction x we define

$$\Delta H_{{{\text{For}}}} \, = \,H\left( {{\text{In}}_{{{1} - {\text{x}}}} {\text{Sn}}_{{\text{x}}} } \right){-}\left( {{1} - {\text{x}}} \right)H\left( {{\text{In}}} \right){-}{\text{x}}H\left( {{\text{Sn}}} \right)$$

where all enthalpies are per atom. Vertices of the convex hull of ΔHFor constitute the predicted low temperature stable structures. For structures that lie above the convex hull, we calculate the instability energy ΔE as the enthalpy relative to the convex hull.

2.1 T→ 0 K Limit

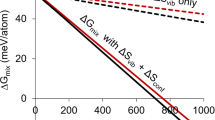
Composition-dependent calculated formation enthalpies are displayed in Fig. 1. Notice that the known stable low temperature phases of pure In and Sn are at ΔHFor = 0, by definition, while all other formation enthalpies are positive. This implies that there are no thermodynamically stable compounds in the T → 0 K limit. In particular, it supports the existence of a lower temperature limit for existence of the intermetallic β-In3Sn phase. It also resolves the apparent third-law violation of the γ -InSn4 phase by showing that it does not extend to 0 K.

Fig. 1
figure 1

Formation enthalpies ΔHFor of In-Sn alloys calculated within density functional theory. Solid lines are linear fits to calculated enthalpies

Full size image

Observe that the composition dependent energy of each phase is nearly linear in the composition, x. Small deviations from linearity reflect specific configurations representative of the solid solutions. Straight lines in Fig. 1 are least-squares fits constrained to pass through the endpoint at x = 0 or x = 1. We obtain

$$\Delta{\text{H}}_{{\text{a}}} = \, 0 \, + \, 0.{1}x \quad \quad \Delta{\text{H}}_{{\text{g}}} = { 4}0 \, + \, 0.{1 }\left( {x - { 1}} \right)$$
$$\Delta{\text{H}}_{{\text{b}}} = \, 0.00{9 } + \, 0.{1}x \quad \quad \Delta{\text{H}}_{{{\text{bSn}}}} = { 41 } + \, 0.000{17 }\left( {x - {1}} \right)$$

Although ΔHα < ΔHβ at x = 0, the lines cross in the vicinity of x = 0.1 (in the middle of the experimental coexistence range), and β is favored over α for larger amounts of Sn. The enthalpy of γ turns up sharply for x < 3/4 (not included in fit) because In-In neighbors cannot be avoided. The energy of β-Sn exceeds the energy of γ -InSn4 for all compositions. As β-Sn.tI4 is known to be a high temperature phase, its stability must be due to some entropic effect, most likely atomic vibrations.[17,18]

2.2 α-β Transition

The assessed In-Sn phase diagrams show a clear discontinuous transition from α to β as the Sn fraction increases. Curiously, the phases have identical Pearson types and space group symmetries; it is unclear why they should be distinct phases. The explanation lies in their c/a ratios, where c/a > √2 for α while c/a < √2 for β. Consider a family of tI2 structures with varying c/a ratios. This is the so-called Bain path.[19] When c/a = 1 the structure is body-centered cubic. At c/a = √2 it is face-centered cubic. For all other c/a the structure is body-centered tetragonal.

As illustrated in Fig. 2, the energy of In.tI2 has a single minimum as a function of atomic volume in the vicinity of 27.5 Å3/atom, but exhibits two minima as a function of c/a. One deep minimum is at c/a ≈ 1.51 > √2, and the other is a shallow minimum at c/a ≈ 1.36 < √2.

Fig. 2
figure 2

Contour plot of In.tI2 energies as a function of atomic volume (horizontal axis, in Å3/atom) and c/a (vertical axis)

Full size image

The valence electron count (VEC) increases with x because Sn lies one column to the right of In in the periodic table. We mimic the effect of alloying by increasing the electron count through the NELECT setting of VASP. Figure 3 shows how the minima evolve as functions of the VEC. For low VEC the high c/a ratio is energetically preferred while high VEC prefers low c/a. The crossover point is around VEC = 13.125, corresponding to composition x = 0.125, close to the experimental α-β coexistence range and to the crossing point in Fig. 1. In all cases the two minima are separated by a barrier, which causes the α-β transition to be discontinuous.

Fig. 3
figure 3

Energy vs. c/a ratio for tI2 structures of volume 27.5 Å3/atom

Full size image

To explore the physical mechanism driving the α-β transition, we investigate the spatial distribution of the excess charge at elevated VEC using the difference in charge density

$$\Delta\rho\left( {\mathbf{r}} \right) \, = \rho_{{{\text{SC}}}} \left( {\mathbf{r}} \right) - \rho_{{{\text{Atomic}}}} \left( {\mathbf{r}} \right)$$

where ρSC is the self-consistent charge density, and ρAtomic is a superposition of atomic charge densities. For VEC ≠ 13 (the VEC of pure In), ρAtomic must be scaled by VEC/13.

Figure 4 plots ρ (r) at low/high c/a with low/high VEC. All figures are at volume 27.5 Å3/atom, and the VASP charge density units are (electrons/Å3) x (cell volume). These figures were created with the assistance of VESTA.[20] Concentrations of charge can be interpreted as covalent bonds between atoms. Evidently, at VEC = 13/atom, there is little charge accumulation at the energetically disfavored low c/a (part (a)) but at the energetically preferred high c/a (part (b)) charge accumulates along nearest neighbor bonds within the horizontal plane. These bonds favor a low value of a. In contrast, at VEC = 13.25/atom (the VEC of In3Sn) and the energetically preferred low c/a (part (c)) a strong charge concentration forms along cell body diagonals. These bonds prefer to reduce the c axis; the minimum bond length for fixed volume would occur at c/a = 1.

Fig. 4
figure 4

Difference charge densities Δρ (r) at various VEC (units e/atom) and c/a. Cut planes and isosurfaces reveal the locus of excess charge density. Color bars range blue-green-red; isosurfaces are at 0.00195 for VEC = 13 and at 0.003 for VEC = 13.25 (Color figure online)

Full size image

2.3 Phase Diagram

To model the composition- and temperature-dependent phase diagram we must model the set of Gibbs free energies {Gi(x,T)} of all phases i\(\in\){α, β, γ, β-Sn, α-Sn}, then find the convex hull of the free energies.[8] We will not concern ourselves with the liquid phase, and hence we restrict our attention to temperatures below ≈ 400 K. Our goal is to gain qualitative understanding that reveals the physical origins of the transitions. We will treat chemical configurational (substitutional) entropy through ideal mixing,

$$S\left( x \right)/k_{{\text{B}}} = \, - x \, ln\left( x \right) \, - \, \left( {1 - x} \right) \, ln\left( {1 - x} \right),$$

and express G(x,T) = ΔHFor (x)-TS(x) for each phase i. As α-Sn.cF8 phase is experimentally known to have low solubility of In, we restrict it to x = 1 with S = 0. We will also discuss, but not directly use, the vibrational free energy

$$F_{v} = k_{B} T\int d v\;\;g\left( v \right)ln\left( {hv/k_{B} T} \right)$$

where g(ν)is the vibrational density of states. The electronic entropy is negligible.

Unfortunately, within this model, neither γ nor the β-Sn phase is predicted to be stable within our temperature range. The difficulty can be traced to the enthalpy difference between those phases and the low temperature phase α-Sn, which DFT predicts to be 40 meV/atom, approximately double the experimentally reported value.[21] Alternate pseudopotentials and exchange-correlation potentials fail to resolve the matter. At x = 1, the α↔β transition of elemental tin is presumably driven by vibrational entropy, and this is supported by the high frequency optical modes in Sn.cF8 that raise the vibrational free energy (see Fig. 5). Our calculated vibrational free energies place the transition at 490 K, far above the experimentally reported 286 K. This overestimate is not adequately resolved in the quasiharmonic approximation.

Fig. 5
figure 5

Vibrational densities of states. A Gaussian smearing of 0.05 THz has been applied for clarity.

Full size image

Given this difficulty we resort to ad-hoc adjustments of the energies and free energies at x = 1. Specifically, we reduce the x = 1 intercepts of γ and β-Sn by 6 and 9 meV, respectively, in order to approximately match their experimental phase boundaries at 400 K. Then we define a temperature-dependent free energy of α-Sn to match the experimental free energy difference of α- and β-Sn.[21] Within these approximations, we identify phase boundaries by solving the equations

$$\frac{{G_{i} }}{{x_{i} }} = \frac{{G_{j} }}{{x_{j} }} = \frac{{G_{j} \left( {x_{j} } \right) - G_{i} \left( {x_{i} } \right)}}{{x_{j} - x_{i} }}$$

Only solutions on the convex hull are retained.

Figure 6 displays the resulting phase diagram. Due to the approximations made we expect only qualitative validity. The key features to observe are the low temperature eutectoid decompositions of the β and γ intermetallic solid solutions. These phases are stabilized by their chemical configurational entropy, and they exist at high temperatures only. Decomposition of β has been previously suggested.[5]

Fig. 6
figure 6

Predicted solid state phase diagram of In-Sn. Dashed lines are boundaries according to[25].

Full size image

The stability of γ has proven problematic. We propose it should decompose below a temperature around 245 K. In contrast, most existing phase diagrams[22,23,24,25] display a broad composition range extending towards low temperature. Two recent investigations,[26,27] however, do indicate a narrowing of the phase with decreasing temperature. Note that the left-hand boundary of γ is frozen at x = 0.75 by the kink in ΔHFor. We have artificially smoothed out the approach of the right-hand boundary to this limit.

3 Conclusion

Our first-principles total energy calculations give insight into otherwise puzzling features of the In-Sn phase diagram. We address two main points. First, we explain the distinction between the tI2 phases, α-In and β-In3Sn on the basis of variation of the energy along the Bain path. At c/a = √2 the otherwise-tetragonal structures become face centered cubic. This symmetric structure occurs at a local maximum of the energy, with the nearby minima corresponding to α- with c/a > √2, and β- with c/a < √2.

Second, we argue that solid solutions β-In3Sn and γ -InSn4 exist only at elevated temperatures, because their formation enthalpies are strictly positive. Eutectoid decomposition of β has been demonstrated experimentally,[23] which is remarkable given the low temperature of the transformation (151 K in our calculation, 140 K experimentally). Eutectoid decomposition of γ has not been conclusively demonstrated experimentally. Early phase diagrams illustrate the composition range extending towards low temperatures, although some recent studies suggest a possible narrowing of the range. We predict a nearly temperature-independent range bounded at low Sn fraction by the kink in energy at x = 3/4, and on the right hand-side by coexistence with β-Sn. However, the range is quickly cut off below 225 K due to competition with α-Sn. γ can transform martensitically to β-Sn,[7,28] but not to α-Sn owing to its distinct crystal structure, cF8 (diamond). Presumably the dynamics of decomposition to α-Sn is too sluggish to readily observe.

Our goal of first-principles phase diagram prediction was not fully met, because of our inability to accurately model the α↔β transformation of pure elemental Sn. The γ-InSn4 and β-Sn phases should not exist at all according to our calculated energies. Correcting this problem may require a post-DFT electronic structure methods such as the random phase approximation.[29] The overestimate of the α↔β energy difference lends support to this possibility. Alternatively, fully anharmonic vibrational free energies[17] may prove to be required as part of the solution.