1 Introduction

Two major metal powder additive manufacturing (AM) processes, laser directed energy deposition (DED) and laser powder bed fusion (PBF), are layer by layer manufacturing techniques that involve melting and subsequent solidification of feedstock powders. Each method has its own distinct process parameters such as laser power and scan velocity that control unique thermal cycles with steep temperature gradients, high cooling rates, and cyclic reheating/remelting of previously deposited layers (Ref 1, 2). In both AM processes, the complex thermal history results in significant residual stress and nonequilibrium microstructures (Ref 3), which are known to influence mechanical performance. Yet, a direct comparison of the microstructure, residual stress, and fatigue performance of different AM manufacturing methods has not been performed, representing one combination of factors impeding this technology from realizing its full potential in cyclic load bearing applications (Ref 4). A deeper understanding of these factors affecting the reliability of AM material fatigue crack growth performance is critical for the widespread adoption of the technology.

The objective of this study is to determine the separate roles of residual stress and microstructure on fatigue crack growth rate (FCGR) in Type 304L stainless steel produced via DED and PBF. The process-induced residual stress of the as-built DED and PBF materials are characterized through slitting measurements and compared. The present experiments are used to evaluate FCGRs in the near-threshold regime (da/dN ≤ 10−8 m/cycle) and their extension into the Paris regime (∆K ≤ 10 MPa m0.5), but well below fracture (which is K > 100 MPa m0.5) for crack growth both perpendicular and parallel to the build directions. The influence of process-induced residual stress on fatigue crack growth behavior is then quantified by the residual stress intensity factor, Kres, determined via the online crack compliance method (Ref 5,6,7,8,9). Values of Kres are used to correct measured fatigue crack growth data for the influence of residual stress (Ref 5, 6, 8) to enable an unbiased evaluation of other influences on FCGR, such as those arising from differences in orientation, microstructure and tensile strength.

2 Material and Methods

2.1 Additively Manufactured Builds

Type 304L stainless steel material built via DED and PBF was evaluated in this study. Previously, the materials produced by both methods have been investigated individually (Ref 10, 11), but the influence of residual stress on their fatigue crack growth properties has not been directly compared. The chemical composition of gas atomized feedstock powders conformed to ASTM requirements for austenitic Type 304L stainless steel material (Ref 12) and has been reported elsewhere for DED and PBF (Ref 10, 11). Small differences in chemical composition were not expected to significantly influence fatigue performance; hence, this study is based on the expectation that the processing method is the primary difference between the two materials under consideration.

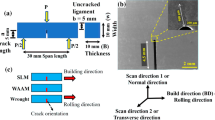
Two replicate DED builds (DED2 and DED3) were fabricated as vertical walls with nominal dimensions of 110 mm (Z-direction, build direction) × 56 mm (Y-direction) × 7.6 mm (X-direction). Both DED builds were produced on the same machine with the same processing parameters over the course of several weeks, which were optimized for 99.9% density and are described in an earlier study of the same material (Ref 13). Two nominally identical PBF builds (PBF-L1 and PBF-L2) were fabricated one year apart on the same machine. The PBF builds were deposited as vertical D-shaped cylinders with processing parameters described in previous work (Ref 11). Nominal dimensions of the wall of interest were 110 mm (Z-direction, build direction) × 36 mm (Y-direction) × 5.1 mm (X-direction). One build from each processing method was used to evaluate FCGRs with a crack propagating parallel to the build direction (vertical, Y-Z) and one build from each method was used to assess FCGRs with a crack propagating perpendicular to the build direction (horizontal, Z-Y). Three crack growth specimens were machined from each of the four builds.

2.2 Microstructure Evaluation

Microstructural heterogeneity was evaluated through electron backscatter diffraction (EBSD) imaging of the DED and PBF materials. Samples for material characterization were extracted via wire electrical discharge machining (EDM), mounted in epoxy and ground to 1200 grit prior to polishing with an alumina suspension of 3 mm, 1 mm, and 0.3 mm. Samples were then vibropolished for 8-9 hours with 0.05 mm colloidal silica prior to examination in the SEM. A Scios Dual-Beam FIB/SEM operating at 15 kV with 3 µm step size was used to examine differences in grain sizes and shapes in the DED and PBF materials in X-Y and X-Z planes. In addition, secondary electron (SE) imaging on a ThermoFisher Quattro ESEM operating at 5 kV and 0.11 nA was used to examine fatigue surfaces and backscatter electron (BSE) imaging at 5 kV and 0.46 nA to examine crack profiles.

2.3 Tensile Testing

Cylindrical specimens for conventional tensile testing were extracted from one replicate DED build and one replicate PBF build. The gauge length of the specimens was 19 mm and the diameter was 2.9 mm. An extensometer with a gauge length of 12.7 mm was used to determine strain during constant crosshead displacement testing at a rate of approximately 0.02 mm/s. The 0.2% offset yield strength, ultimate tensile strength, elongation at failure and reduction of area are reported.

2.4 Residual Stress Measurement

Process-induced residual stress was evaluated in the DED and PBF builds. Plates from each build with similar dimensions in Y and Z were removed via wire EDM as shown by the thin vertical blue lines in Fig. 1. Vishay strain gages were applied on the EDM surface at two equally spaced locations (1 and 2). Build direction residual stress as a function of cut depth was then determined by the slitting method on the two planes of interest (horizontal black lines) (Ref 14). This method is a one-dimensional mechanical relaxation technique that uses strain measured at fixed cut increments (starting from the front face) to determine a through thickness (X-direction) average of residual stress acting in the build direction (Z-direction) as a function of distance from the front face (along the Y-direction). Detailed descriptions of this method are presented elsewhere (Ref 15, 16). Additional slitting measurements were performed during the machining of notches in fatigue crack growth rate test specimens as indicated by the red lines in Fig. 1(c).

Fig. 1
figure 1

Schematic of slitting measurements and specimen extraction of (a) DED and (b) PBF material with (c) C(T) specimen geometry and orientations (Color figure online)

Full size image

To evaluate the contribution of residual stress to the stress intensity factor, values of Kres due to residual stress acting normal to the cut plane were determined from the strain data collected during slitting measurements. The derivative of the strain with respect to cut depth (or crack size), dε/da, was found using a polynomial regression as described in previous work (Ref 10, 11, 17, 18). The strain derivative and a geometry dependent influence function (Z(a)) as described by Schindler (Ref 19) were then used to determine Kres as a function of crack size:

$${K}_{{\text{res}}}\left(a\right)=\frac{{E}^{\prime}}{Z\left(a\right)}\frac{{\text{d}}\varepsilon (a)}{{\text{d}}a}$$
(1)

where E′ is the generalized elastic modulus, taken here as a handbook value of 200 GPa for Type 304L stainless steel under plane stress conditions (Ref 20).

The residual stress intensity factor was also determined in the fatigue test specimens by applying the online crack compliance (OLCC) method to the FCGR test data (Ref 5, 8, 9, 17). In this method, the residual strain (εres) is quantified by extrapolating the linear region of the load versus deformation data (i.e., compliance data) to zero load. The value of eres is nominally equivalent to the strain determined by a slitting measurement and can be used to determine Kres in the same way (Eq 1). Further details on the methodology for determining Kres during FCGR tests are available in recent work (Ref 17).

2.5 Fatigue Crack Growth Rate Testing

The DED and PBF plates were machined into compact (C(T)) specimens in accordance with ASTM E647 (Ref 18) having a specimen width (W) of 26.4 mm and thicknesses of 6.35 mm (DED) and 4.06 mm (PBF). Three specimens were extracted from each build for crack growth testing (Fig. 1). Specimens from the top and bottom (T and B) were used to evaluate near-threshold crack growth rates with decreasing applied stress intensity factor range tests (decreasing ∆Kapp) (Ref 18); specimens from the middle (M) were tested under constant ∆Kapp. Consistent with specimen designations of previous work (Ref 10, 11), FCGRs for a crack propagating perpendicular to the build direction (horizontal (H) crack growth) were determined from specimens extracted from DED2 and PBF-L1; whereas, FCGRs for a crack propagating parallel to the build direction (vertical (V) crack growth) were determined from specimens extracted from builds DED3 and PBF-L2. For reference, the specimen designations and the associated test conditions are presented in Table 1. Two C(T) specimens of each thickness, 6.35 mm and 4.06 mm, were cut from dual-certified, annealed, wrought Type 304/304L stainless steel and were tested under decreasing ∆Kapp conditions to provide reference comparisons for the DED and PBF specimens at their respective thicknesses. Wrought 304L was chosen as the baseline for comparison because it represents the material that would most likely be replaced by additively manufactured 304L and therefore represents an appropriate standard for comparison.

Table 1 Specimen designations for Kres and FCGR measurements
Full size table

An Instron 1331 servo-hydraulic load frame was utilized for fatigue testing in lab air at an applied stress ratio (Rapp) of 0.1 and frequency of 10 Hz. All specimens (AM and wrought) were notched via wire EDM and fatigue precracked to a crack size (a) of 6.6 mm (a/W = 0.25) using the K-decreasing test procedure (tension–tension, R > 0) in accordance with ASTM E647 (Ref 18). Vishay strain gages at the back face of each fatigue specimen were used to monitor back face strain (BFS) (Ref 10, 11). The MTS 790.40 fatigue crack growth software running on a MTS TestStar control system was modified to accept this BFS input to determine compliance and crack size (Ref 13). Constant ∆Kapp fatigue tests were performed at ΔKapp of 6.6 MPa m0.5 by using a load shedding parameter of C = 0 and decreasing ∆Kapp fatigue tests had an initial Kmax of 11.6 MPa m0.5 and C = − 0.08 mm−1 (Ref 18). During the fatigue crack growth tests, load and BFS data (i.e., compliance data) were recorded at crack size increments of 0.05 mm, each with 500 data points averaged over 3 consecutive cycles. Compliance data were then used for post-test data analysis of crack size, FCGRs and Kres via the online crack compliance (OLCC) method based on Eq 1. Post-test examination of fracture surfaces (described in (Ref 11, 13)) demonstrated that the crack sizes determined using specimen compliance and a modulus of 200 GPa agreed well with the physically measured crack sizes for both DED and PBF specimens. Thus, no adjustment of the elastic modulus was needed to correct the compliance-derived crack sizes as specified in ASTM E647 (Ref 18). To account for the separate effects of residual stress and crack closure, values of Kres from each specimen were combined with independent calculations using the adjusted compliance ratio (ACR) method that accounts for crack closure effects (∆Keff = ∆KACR) (Ref 18, 21), resulting in a corrected stress intensity factor range (∆Kcorr) for all FCGR test data that was used to isolate intrinsic material performance (Eq 2) (Ref 5, 6, 8).

$$\Delta {K}_{{\text{corr}}}\left(a\right)=\Delta {K}_{{\text{eff}}}{\left(a\right)}^{1-n}{\left({K}_{{\text{max}},{\text{app}}}\left(a\right)+{K}_{{\text{res}}}(a)\right)}^{n}{\left(1-{R}_{{\text{app}}}\right)}^{n}$$
(2)

where n = 0.25 as determined previously (Ref 13).

3 Results and Discussion

3.1 Microstructure

EBSD images and Inverse Pole Figure (IPF) contour plots for two unique microstructural planes (X-Y and Y-Z) are shown in Fig. 2(a) and (b) for the DED and PBF materials, respectively. Both exhibit similar grain shapes with a distinct elongation of grains in the build direction. Thus, the effective grain sizes are larger in the build direction than in the transverse direction. In the near-threshold regime, preferential grain orientations (crystallographic texture) may influence fatigue crack growth rates as cracks propagate in certain crystallographic directions. The relative lack of texture evident in the IPF contour plots for DED and PBF showing uniform coloration and small values suggests that it is not an important factor in this study.

Fig. 2
figure 2

EBSD orientation images for (a) DED material and (b) PBF material with IPF contour plots

Full size image

The determination of crack size and Kres (Eq 1) both depend on elastic modulus as a material property. In a recent study, Charmi et al. (Ref 22) observed elastic anisotropy in PBF 316L wall builds up to ± 10% for dynamic modulus measurements in the build direction and transverse to it. Therefore, it is important to consider whether elastic anisotropy might influence the present measurements. The tensile tests for this study were not conducted with sufficient extensometer resolution at small strains to determine accurate values of modulus; hence, other evidence must be used.

Two important factors that might influence the elastic modulus of AM materials are porosity and preferred orientations of grains. Charmi, et al. demonstrated that the variations in elastic modulus with specimen orientation within wall builds were entirely explained by the crystallographic texture present in the builds that had limited porosity (Ref 22). The IPF contour plots shown in Fig. 2 reveal that there is no significant texture in the DED or PBF builds examined in this study. Furthermore, all builds were optimized for density and contained only minimal pores; hence, they have negligible porosity. Thus, microstructural evidence indicates that there is no elastic anisotropy in these builds. Furthermore, as described earlier, the physically measured crack sizes agreed with those derived from compliance data obtained during the fatigue crack growth tests, demonstrating that the single modulus value of 200 GPa adequately characterizes the elastic properties of both builds.

The grain morphology of the DED material exhibits a large distribution of shapes and sizes, but with an average grain size that is larger than that of the PBF material. The DED process generally results in thicker layers with average cooling rates ranging from 100 to 10000 K/s (Ref 23,24,25,26). In contrast, the PBF process typically has a smaller layer thickness with significantly higher cooling rates of 106 to 40 × 106 K/s (Ref 27). As such, smaller solidification layers and faster cooling rates in the PBF process limit grain growth as compared to DED. The resulting finer microstructure of the PBF material would commonly be thought to benefit fatigue initiation resistance as characterized by the lifetime of cyclically loaded, smooth-sided specimens (Ref 28). In contrast, the coarser grains observed in DED material are expected to benefit fatigue crack growth resistance (Ref 29, 30).

3.2 Tensile Properties

The averages and standard deviations of the tensile properties are provided in Table 2 for all tested PBF longitudinal and transverse tensile specimens, along with the longitudinal tensile data from the tested DED specimens. Whereas the longitudinal tensile properties of the PBF materials are uniform across all specimens, the strength in the transverse direction is significantly greater than the longitudinal strength, consistent with the finer effective grain size in the former than in the latter. The DED material has a lower strength (with similar ductility), again consistent with its coarser grain size.

Table 2 Tensile properties of AM 304L, comparing PBF in the two principal orientations and DED (L orientation only)
Full size table

3.3 Residual Stress Results

Results from the initial slitting measurements made prior to FCGR specimen extraction are shown in Fig. 3. The overall residual stress profiles of both AM materials show a steep gradient of stress between the center (compression) and the edges of the plates (tension). The tensile residual stress at the edges contributes to positive Kres throughout most of the cut depth. Residual stress and Kres results from the four slitting measurements of the DED plates (two measurements from each of the two plates) demonstrate excellent agreement and indicate repeatability of the measurement as well as reproducibility between builds. The four results of the PBF plates also agree well, indicating that the build direction residual stress is reproducible in the two PBF builds independent of when the deposition was made. The asymmetry in the residual stress profiles of the DED material is attributed to the off-center extraction of the DED plates (vertical blue lines in Fig. 1). The greater residual stress in PBF material, both tensile at the edges and compressive at the center, is attributed to the steeper temperature gradients, which are characteristic of the PBF process (Ref 1).

Fig. 3
figure 3

(a) Residual Stress (RS) and (b) Kres profiles from slitting of DED and PBF plates

Full size image

Figure 4(a) and (b) present the Kres results from notch slitting and OLCC for the DED and PBF specimens, respectively, with Kres in the specimens being smaller than those in the plates (which is consistent with stress release occurring during specimen extraction). The DED specimens have significant tensile Kres in the H orientation (3 to 4 MPa m0.5 for all crack sizes) and smaller Kres in the V orientation (0-2 MPa m0.5 for all crack sizes). The difference in Kres between orientations reflects larger residual stress in the build (Z) direction and smaller residual stress in the transverse (Y) direction. The PBF specimens have larger values of Kres as compared to DED for both orientations (H and V), being 5-7 MPa m0.5 at the notch. Furthermore, Kres decreases more quickly with crack size than in the DED specimens, with values in H specimens dropping to 3 MPa m0.5 at the longest crack size and V specimens to 1 MPa m0.5. While there is a small difference in Kres with orientation for PBF specimens, there is a large difference with orientation for DED specimens, with much lower values in the DED (V) than in the PBF (V).

Fig. 4
figure 4

Full Kres profile for (a) DED and (b) PBF C(T) fatigue specimens with notch slitting to the left of the solid line and OLCC to the right of the dashed line (end of precrack)

Full size image

3.4 Fatigue Crack Growth

Crack growth rates from the constant ΔKapp fatigue tests are shown in Fig. 5. The trends in FCGRs of the DED and PBF specimens follow the trends in the Kres results shown in Fig. 4(a) and (b), respectively. Under constant ∆Kapp, FCGRs decrease with increasing crack size, consistent with the decrease in positive Kres that results from the redistribution of tensile residual stress as the crack extends through the specimen. The PBF (H) specimen has the highest positive Kres for all crack sizes, which contributes to this specimen exhibiting the highest FCGRs. PBF (V) and DED (H) have similar values of Kres, and the similar FCGRs in these specimens are consistent with this measurement. DED (V) has the smallest positive values of Kres, and the lowest FCGR. Because Kres adds to both the minimum (Kmin,app) and maximum (Kmax,app) values of Kapp, positive Kres increases the total stress intensity factor ratio, Rtot (where Rtot = (Kmin,app + Kres)/(Kmax,app + Kres)) compared to the applied stress intensity factor ratio (Rapp = Kmin,app/Kmax,app). Another way of describing this effect is that a positive Kres has the effect of increasing the mean value of K and the FCGRs. Fatigue crack growth data under constant ∆Kapp for these AM materials and orientations are therefore typical of data in other metallic materials that show clear correlation between elevated Rtot and elevated FCGRs in the near-threshold regime (Ref 31). Additionally, both DED and PBF specimens demonstrated transgranular fatigue crack growth as shown in Fig. 6 and in previous work (Ref 10, 11) despite differences in grain size as shown in Fig. 2(a) and (b). This similarity of crack profiles suggests that residual stress has a more significant influence on FCGRs in specimens of these AM materials than does microstructure.

Fig. 5
figure 5

Measured FCGRs for DED and PBF in constant ΔKapp tests

Full size image
Fig. 6
figure 6

Crack profile images of (a) DED2-M (H) (b) PBF-L1-M (H) (c) wrought (B = 6.35 mm) and (d) wrought (B = 4.06 mm)

Full size image

The measured FCGRs for the decreasing ΔKapp tests are presented in Fig. 7(a) for the AM and wrought specimens. At high values of ΔKapp near the beginning of the tests, there are clear differences in rate with the PBF specimens having the highest FCGRs followed by DED, and then wrought. These trends persist over several millimeters of crack growth and are consistent with the values of Kres in the specimens, where prior work (Ref 10, 11) showed wrought specimens to have negligible Kres. Consistent with the trends in Fig. 4(a) and (b) where Kres for both DED and PBF gradually converge to similar values in each orientation at crack sizes approaching 20 mm (~2.5 MPa·m0.5 in (H) and ~ 0.5 MPa m0.5 in (V)), the FCGRs for all AM specimens converge to a nominally common value ΔKapp between 4 and 5 MPa m0.5 at the largest crack sizes in the threshold regime. The somewhat larger spread in FCGR for DED versus PBF, at ΔKapp between 7 and 10 MPa m0.5, is consistent with the greater orientation differences in Kres for specimens of DED material. Both DED and PBF specimens have higher FCGRs at all values of ΔKapp compared to those of annealed wrought material.

Fig. 7
figure 7

(a) Measured FCGRs for DED and PBF compared to wrought and (b) corrected

Full size image

While some differences in FCGR are due to the influence of residual stress, the rates for the wrought specimens are also affected by crack closure. Fig. 8 illustrates compliance data for representative loading cycles for wrought specimens (wrought (B = 6.35 mm) and wrought (B = 4.06 mm)) compared to PBF and DED specimens (DED2-B (H) and PBF-L1-B (H)). In accord with the concepts introduced by Elber (Ref 32), the nonlinearity in the compliance data for the wrought condition indicates that crack closure reduces the effective driving force for fatigue crack growth in those specimens. The linearity of compliance data for the AM specimens suggests a lack of crack closure in those tests. In addition, the amount of crack closure is greater in the thinner wrought specimen (B = 4.06 mm) used for comparison to the PBF material, leading to lower FCGRs compared to the thicker specimen (B = 6.35 mm) used for comparison to the DED material.

Fig. 8
figure 8

Compliance plots for crack growth in the near-threshold region for (a) DED2-B (H) (b) PBF-L1-B (H) (c) wrought (B = 6.35 mm) (d) wrought (B = 4.06 mm) showing linearity in the presence of tensile residual stress (a) and (b) and deviations from linearity from crack closure (c) and (d)

Full size image

To compare FCGR trends among the various specimens, ∆K was adjusted for the effects of residual stress and crack closure. As described in previous work (Ref 11), the influence of crack closure on ΔK was accounted for using the ACR method outlined in the appendix of ASTM E647 (Ref 18, 21). Subsequently, the influence of residual stress was accounted for using a method based on the Walker relationship (Ref 33) in conjunction with measured Kres (Ref 5,6,7,8, 15) to account for changes in Rtot as the crack size increases. These corrections to the data are described by Eq 2. To maintain a consistent approach, the same analysis procedure was applied to data from all specimens. Fig. 7(b) shows the corrected FCGR data for specimens of the AM materials and wrought specimens. When decreasing ΔKapp test data from specimens of the AM materials are corrected—primarily for the contributions of Kres—all data collapse into a single curve independent of processing method and orientation. Furthermore, the corrected AM FCGR data agree with the data for the wrought condition that have been corrected primarily for the influence of crack closure. For example, at ΔK = 6 MPa m0.5, the spread in crack growth rates is 4 × 10-10 to 2 × 10-9 m/cycle in the uncorrected data, but it is reduced to 6 × 10-10 to 1 × 10-9 m/cycle when the data are corrected. The agreement of the corrected data from the DED and PBF fatigue specimens with those from annealed wrought specimens highlights the significant influence of AM process-induced residual stress on fatigue crack growth behavior. The corrected data reflect the intrinsic material condition, independent of crack closure and orientation dependent residual stress fields. Additionally, it appears that any differences in crack growth rates that can be attributed to microstructure are much less significant, which is consistent with the similar, transgranular crack paths for all specimens described previously (Ref 10, 11).

After crack growth testing, specimens from decreasing ΔKapp tests were fractured open by rapid loading for evaluation and comparison of the fatigue surfaces. Fig. 9(a)-(d) illustrates fatigue crack surfaces of select specimens intended to be representative of material from this study. These surfaces reveal relatively smooth crack paths with similar levels of roughness in the near-threshold regime. A few pores are apparent in the DED specimen (arrows) and a small number of secondary cracks can be observed in all specimens (circles). Overall, these images from the interior of the specimens reflect relatively flat, transgranular crack paths observed in these materials. In combination with the transgranular crack profiles reported in this paper (Fig. 6) and in prior studies (Ref 10, 11), these images support the interpretation that the grain morphologies have little impact on fatigue crack growth in this single-phase AM Type 304L stainless steel.

Fig 9
figure 9

Fatigue crack surface images of (a) DED2-T (H) (b) PBF-L1-T (H) (c) wrought (B = 6.35 mm) and (d) wrought (B = 4.06 mm). Build direction is normal to the crack surface for the AM specimens. The arrows identify pores and the circles indicate secondary cracks.

Full size image

4 Conclusions

A comparison of additively manufactured Type 304L stainless steel produced by DED and PBF illustrates the significant influence of residual stress on FCGRs. Slitting measurements verified consistency and reproducibility in residual stress of the two AM processing methods. Tensile residual stress was larger in PBF builds compared to DED builds and this difference is attributed to higher cooling rates in PBF, which are a consequence of the fundamental differences in the processes. Measurements of FCGRs in specimens of DED and PBF materials both parallel and perpendicular to the build directions reveal differences that can be attributed to residual stress. Specifically, specimens from the PBF builds featured comparatively larger tensile residual stress intensity factors for cracks in two different orientations resulting in higher FCGR than observed in specimens of DED material. Electron backscatter diffraction images revealed similar grain shapes for both processing methods, although the grain sizes in the PBF material were smaller than in the DED. Correcting the FCGR data for the influence of the residual stress intensity factor brings the data from specimens from both processing methods and both test orientations into agreement for this as-built austenitic single-phase Type 304L stainless steel. Furthermore, the corrected results agree with those for specimens of an annealed wrought reference material corrected for the influence of fatigue crack closure. After isolating the effects of residual stress in this way, the difference in measured yield strength does not appear to have a measurable influence on FCGRs. Additionally, transgranular crack propagation was observed in all cases (Ref 10, 11), indicating that differences in grain size and grain morphology also have relatively insignificant effects on fatigue crack growth compared to the more significant effect of residual stress.