Introduction

In converter-steelmaking process, gas-blowing technology is commonly used to develop more efficient stirring methods to homogenize liquid steel. The AOD process is a dominant converter process that employs gas injection to enhance the refinement of liquid steel via rapid mixing, thereby accelerating the chemical reaction process. However, due to the harsh environment, it is preferable to study the underlying phenomenon through small-scaled physical models and numerical models prior to industrial-scale trials.[1,2,3,4,5,6,7]

In order to perform detailed numerical modeling of complete metallurgical processes, such as the AOD converter, a substantial number of computational resources are required. As a result, these models are commonly divided into distinct process sections, each of which is modeled with a higher level of detail and utilized as input to integrate the entire process. In the work of Tilliander et al.[2,3] three modeling steps were taken to complete a numerical model of an AOD converter. The authors modeled the heat transfer and fluid flow in an AOD nozzle through CFD calculations to be used as boundary condition input to a fundamental model of the AOD converter. Therefore, essential discoveries were incorporated into their subsequent model such as the gas exiting the nozzle outlet at nearly the speed of sound and its resulting impact on energy distribution around the outlet. This model could capture the gas hold-up in the plume above the nozzle. Continued work[4] further led to a fully developed three-dimensional, three-phase numerical model of an industrial AOD converter which among other achievements was able to predict the fluid flow characteristics and structure. Odenthal et al.[5] and Wupperman et al.[6,7] developed physical and mathematical models to investigate stirring in an AOD. The studies examined oscillation and vibration amplitudes in both models, under various fill levels and gas flow rates, and determined that the CFD simulation was highly effective in providing clarity within the AOD system. In general, when applying side blowing, clockwise circulation is expected with a vortex located closer to the upper part of the vessel.[4,5,6,7]

An extensive amount of research exists in gas-blowing technology of metallurgical converters. Indeed, physical and mathematical models have made it more transparent and possible to understand various phenomena in the process. However, a lot of the work focuses on improving the mixing and kinetic phenomena to achieve a more efficient decarburization process. Nonetheless, the thermodynamics of the process will indeed be of importance. So far, numerical models shallowly report the improvement or alteration of the thermodynamic state and the conditions for chemical reactions.

The AOD converter is a prominent technique employed in the production of stainless steel and primarily relies on the gas stirring via side blowing. A mix of inert and oxygen gas is injected through the side nozzles, enabling stirring and decarburization of the steel. The main reactions taking place during decarburization are shown in Eqs. [1] through [3]:

$$ 2\left[ {\text{C}} \right] + \left\{ {{\text{O}}_{2} } \right\} \leftrightarrow {2}\left\{ {{\text{CO}}} \right\}, $$
(1)
$$ 4\left[ {{\text{Cr}}} \right] + 3\left\{ {{\text{O}}_{2} } \right\} \leftrightarrow 2\left( {{\text{Cr}}_{2} {\text{O}}_{3} } \right), $$
(2)
$$ 3\left[ {\text{C}} \right] + \left( {{\text{Cr}}_{2} {\text{O}}_{3} } \right) \leftrightarrow 2\left[ {{\text{Cr}}} \right]{ + 3}\left\{ {{\text{CO}}} \right\}, $$
(3)

where [] is dissolved in liquid steel, {} is in gas form, and () is in oxide form.

The technical challenge is to oxidize carbon without oxidizing the desired chromium which is well known to be achieved by reducing the partial pressure of CO, hence, driving the reaction above to the right-hand side. This is acknowledged by Wimmer et al.[8] who studied the mass-transfer process in the AOD converter with numerical simulation. The work focuses on the influence of different geometries on metal–slag interface transfer during the reduction process step. With emphasis to the trade-off in lowered partial pressure of CO, the authors observed higher velocities and better mass transfer for a geometry with high bath diameter-to-height ratio. It is important to note that chemical reactions were not considered in the simulations nor were the pressure in the bath monitored or presented in the results.

An extensive amount of work has been devoted to developing mathematical reaction models of the decarburization in the AOD process. The majority of the proposed cost-efficient kinetic models are based on rate expressions for mass transfer and have been reviewed elsewhere.[9,10] Furthermore, a rate expression for mass-transfer-limited reversible reactions was proposed based on the law of mass action, which accounts for the mass-transfer resistances between different phases in the AOD process.[11,12,13,14] The significance of this method is that it assumes that all reactions, oxidation, as well as reduction take place at the reaction interface simultaneously.

More recent models have used commercial thermodynamic software to develop steel-related process model predictions e.g., Thermo-Calc[15] has recently developed a process module which accounts for thermodynamic and kinetic reactions based on the concept of effective equilibrium approach (EERZ).[16,17] In brief, utilizing thermodynamic databases, the kinetic model adopts a local equilibrium calculation methodology at interfaces, which are constrained by mass and heat transfer to and from the interface. In addition, Wei et al.[18] established a time-dependent thermodynamic model of the AOD process using Thermo-Calc software to predict the dissolved nitrogen content throughout the process. Despite producing reasonable outcomes in comparison to genuine industrial heats, the model does not consider any mass transfer of liquid steel and treats the entire domain within a single cell.

To avoid relying on stagnant mathematical descriptions of the reaction interface and one cell thermodynamic calculations, a coupled method between CFD and chemical reactions have been developed to investigate decarburization reactions.[19,20,21] This method integrates fluid dynamics with thermodynamic databases to achieve local cell equilibrium with the present phases and chemical species after each timestep. Andersson et al.[20,21] modeled the decarburization in an AOD converter to predict the early stage in the decarburization process. The model predictions agreed well with an industrial process control model and were able to show local carbon concentration gradients in the converter over time. In addition, the results showed locally decreased decarburization rates at elevated pressures. However, the temperature evolution in this model depends on the regression of precalculated values by another process model called TimeAOD2.

Thus, it is of interest to investigate the possibility of practically altering the pressure conditions to achieve benefits to thermodynamic reactions in the AOD converter. For that it is necessary to have a numerical model which can predict the decarburization in the industrial process. Accordingly, this work aims to develop such a model which in the future could investigate how the pressure around the nozzle will affect decarburization in an AOD converter. The author’s approach is to develop a coupled fluid- and thermodynamic model with the local cell equilibrium method. This model will enable modification of the pressure around the nozzles by elevating the bath height, subsequently altering the partial pressure conditions for CO. The coupling method is similar to the authors’ previous work on a 2D axisymmetric bubble.[22] However, with slight modifications to the coupled model, this study aims to configure a more practical approach for the AOD system with a 3D domain, continuous gas flow, and simulation time periods similar to that of the industrial process.

Methods

The submergence of a high-velocity jet into the liquid imposes significant demands on the global timestep, restricts computational resources, and requires a well-resolved mesh around the nozzle outlet. High-velocity injections in any kind of gas–liquid/liquid–liquid simulation require high computational power and are generally treated with a numerical trick.[5,23,24] Namely, the simulation of jet penetration is conducted in one segment, while the characteristics of the jet flow, located farther away from the nozzle, are imported into another simulation. In this way, it is possible to acquire the flow structure and mixing of the bath imposed by the jet without the need to simulate the extreme velocity at the nozzle outlet. However, to reach a high flow similarity between the model and reality it still requires a lot of computational power as shown in References 25 and 26, where one simulation of a full-scale ladle took 9 months to simulate on a high-performance machine. In anticipation of a dramatically increased simulation time when a combined model is to be used with heat transfer and reactions, it was decided to use a coarse model to transport fluid flow. Previous studies[9,11,12,13] suggest that when the carbon concentration is high, the decarburization is limited by the supply of oxygen. As the carbon concentration is decreased to lower levels, the decarburization starts to depend more on the mass transfer of carbon, e.g., References 12 and 13 predicted that the incoming oxygen is rapidly consumed near the gas nozzle. With this, it is assumed that a coarse-mixing model and a clockwise circulation achieved from side blowing is sufficient at early stages of the decarburization step. This may introduce large uncertainties but comes with a very low computational cost compared to the other approaches. Furthermore, a deficiency with one cell equilibrium model is the forced-acting constant pressure over the whole domain. Even with a coarse model, the pressure would be better represented just by increasing the number of cells in vertical position.

Nozzle Simulation

The gas jet penetration length is affected by the modified Froude number and the density ratio.[27] There are practical ways to increase the penetration depth, either by increasing the gas flow rate or decreasing the nozzle diameter[5,27,28,29,30] which affects the flow behavior and mixing time,[4,5,28,29] e.g., the mixing time decreases as the flow rate increases. However, the effect cannot be attributed to the penetration length alone since an increase in flow rate also increases the kinetic energy to the bath. It was predicted in References 4 and 29 that a high flow rate resulted in a penetration length beyond the center of the bath which in turn changed the flow characteristics. As the jet penetrates closer to the other side of the bath, the rising plume is pushed away from the nozzle wall resulting in a counter-clockwise circulation from the nozzle. On the other hand, if the jet does not penetrate past the center of the bath,[5] the gas plume will rise close to the nozzles and cause clockwise circulation in the bath. Thus, a reasonable jet penetration length in the system is required even in the current coarse model to predict the general flow behavior.

Rather than directly injecting gas into the liquid steel, a simulation of compressible gas flow through a single-industrial nozzle was employed to capture the density and velocity of the gas mixture entering the converter, following exposure to a pressure drop. The values would then serve as input data in the semi-empirical equation for gas jet penetration length derived by Hoefele and Brimacombe,[27] Eq. [4]. This equation has previously[3,4,5] been shown to achieve good agreement with the modeled penetration length and is reasonable to use with the numerical trick discussed above.

$$ {\text{L}} = 10.7{\text{Fr}}^{{\prime 0.46}} d_{{\text{n}}} \left( {\frac{{\rho _{\text{g}} }}{{\rho _{\text{l}} }}} \right)^{{0.35}}, $$
(4)

where \({\text{Fr}}^{\prime}\) is the modified Froude number, \({d}_{\text{n}}\) is the nozzle diameter, and \(\rho \) is the density with the indices \(\text{l}\) and \(\text{g}\) for liquid and gas, respectively. Equation [4] is used to estimate the penetration depth in the AOD model.

Assumptions

  • The cold compressible gas is considered to travel at a very high rate through the nozzle and, therefore, assumed to be unaffected by the temperature difference between the nozzle inlet and outlet. Thus, the temperature is set to 293 K at inlet and outlet.[2,31]

  • Gravity is neglected.

  • The gas is a mix of oxygen and nitrogen.

  • The flow is turbulent.

  • The gas flow in the nozzle is calculated in a steady state.

Boundary conditions and set-up

A two-dimensional axisymmetric model was used to represent the nozzle with nonslip walls and an inlet-outlet pressure as boundary conditions. The governing transport equations solved by the model were conservation of mass, momentum, and thermal energy. Further, the shear stress transport (SST) k-ω model was used to solve the turbulence in the nozzle. The gas was assumed to be ideal, and its density was calculated using Eq. [5].[32]

$$\rho =\frac{{p}_{\text{op}}+{p}_{\text{r}}}{\frac{R}{{M}_{\text{w}}}T},$$
(5)

where \({p}_{\text{op}}\) is the operating pressure, \({p}_{\text{r}}\) is the local relative pressure, \(R\) is the gas constant, \({M}_{\text{w}}\) is the molecular weight of the gas mix, and \(T\) is the temperature.

The Sutherland definition of viscosity as function of temperature was employed, and the inlet pressure was set to 15 bar given from the industry. The outlet pressure was calculated according to Eq. [6]:

$${p}_{\text{outlet}}={p}_{\text{atm}}+\rho gH,$$
(6)

where \({p}_{\text{atm}}\) represents the atmospheric pressure, while the second term on the right-hand side signifies the ferro-static pressure at the nozzle, represented by \(\rho gH\), wherein \(\rho \) represents the density, \(g\) represents gravitational acceleration, and \(H\) the bath height over the nozzle which is assumed to be 1.45 meters. For spatial discretization of the domain, the gradient least-square cell-based method was used with second-order upwind for pressure, momentum, and energy while the turbulence used first-order upwind. The coupled algorithm scheme is used, which is an alternative to the SIMPLE algorithm and allows for coupled instead of segregated solution of the momentum and continuity equations, normally presenting a more efficient option for single-phase steady-state flows.[32] The most important parameters used in the nozzle simulation are presented in Table I and Figure 1.

Table I Parameters and Boundary Conditions Used for the Simple Nozzle Simulation
Full size table
Fig. 1
figure 1

Schematic illustration on the geometry and the boundary conditions employed in the nozzle simulation

Full size image

The simulations were conducted using the Eulerian multiphase model where the average mass flow rate, velocity, density, and pressure were monitored at the outlet. The grid convergence index (GCI)[33] was calculated to estimate numerical uncertainty on a grid containing 58,464 cells. The results of the grid convergence study are presented in Table II. The GCI was determined to be acceptable, and the velocity and density were used in Eq. [4], yielding a penetration length of 37 cm.

Table II Grid Convergence Index on the Nozzle Simulation for a Mesh Containing 58,464 Cells
Full size table

AOD Model

General equations

The Eulerian multiphase model was employed to simulate the liquid steel and process gas phase. The Eulerian[32] model separates yet interact phases by solving a set of equations for each phase. The phases are averaged over each control volume and treated as continuous media where the conservation of mass and momentum are calculated individually. The phases share a single pressure, and the momentum transfer between the gas and liquid is modeled using a drag term, in which a diameter is specified for the secondary phase (in this case, gas), with the diameter of the bubbles set to 10 mm. With the Eulerian multiphase, the conservation of mass for phase \(q\) is calculated from the continuity, Eq. [7]:

$$\frac{\partial }{\partial t}\left({\alpha }_{\text{q}}{\rho }_{\text{q}}\right)+\nabla *({\alpha }_{\text{q}}{\rho }_{\text{q}}{\overrightarrow{v}}_{\text{q}})=\sum_{p=1}^{n}\left({\dot{m}}_{\text{pq}}-{\dot{m}}_{qp}\right)+{S}_{\text{q}},$$
(7)

where \(q\) and \(p\) are phases in the domain, \({\rho }_{\text{q}}\) is the phase density, \(\overrightarrow{{v}_{\text{q}}}\) is the velocity for phase \(q\), \({\dot{m}}_{\text{pq}}\) is the mass transfer from phase \(\text{q}\) to \(\text{p}\) and \({\dot{m}}_{qp}\) is vice versa, \({\alpha }_{\text{q}}\) is the volume fraction of \({q}^{th}\) phase. \({S}_{\text{q}}\) is a source term which by default is set to zero.

The conservation of momentum for the \({q}^{th}\) phase is calculated according to Eq. [8]:

$$ \frac{\partial }{\partial t}\left( {\alpha_{\text{q}} \rho_{\text{q}} \overrightarrow {{v_{\text{q}} }} } \right) + \nabla *\left( {\alpha_{\text{q}} \rho_{\text{q}} \vec{v}_{\text{q}} \vec{v}_{\text{q}} } \right) = - \alpha_{\text{q}} \nabla p + \nabla *\overline{\overline{\tau }}_{\text{q}} + \alpha_{\text{q}} \rho_{\text{q}} \vec{g} + \mathop \sum \limits_{p = 1}^{n} (K_{\text{pq}} \left( {\vec{v}_{\text{p}} - \vec{v}_{\text{q}} } \right) + \dot{m}_{\text{pq}} \vec{v}_{\text{pq}} - \dot{m}_{qp} \vec{v}_{qp} ) + \left( {\vec{F}_{\text{q}} + \vec{F}_{\text{lift,q}} + \vec{F}_{\text{wl,q}} + \vec{F}_{\text{vm,q}} + \vec{F}_{\text{td,q}} } \right), $$
(8)

where \(p\) is the pressure shared by all phases, \(\overrightarrow{g}\) is the gravitational acceleration, \({\overline{\overline{\tau }}}_{\text{q}}\) is the stress–strain tensor for phase \(q\) defined in Eq. [9]:

$$ \overline{\overline{\tau }}_{\text{q}} = \alpha_{\text{q}} \mu_{eff,q} \left( {\nabla \vec{v}_{\text{q}} + \nabla \vec{v}_{\text{q}}^{T} } \right), $$
(9)

where \({\mu }_{\text{eff},q}\) is the effective viscosity for phase \(q\). \({\overrightarrow{F}}_{\text{q}}\),\({\overrightarrow{F}}_{\text{lift,q}}\), \({\overrightarrow{F}}_{\text{wl,q}}\), \({\overrightarrow{F}}_{\text{vm,q}}\), and \({\overrightarrow{F}}_{\text{td,q}}\) are the external body force, lift force, wall lubrication force, virtual mass force, and turbulence dispersion force, respectively, which act between the different phases. Here only the default settings for virtual mass force where used. \({\overrightarrow{v}}_{\text{pq}}\) and \({K}_{\text{pq}}\) are the interphase velocity and momentum exchange coefficients, respectively, where \({K}_{\text{pq}}\) for fluid–fluid exchange is defined as follows, Eq. [10]:

$$ K_{\text{pq}} = \frac{{\rho_{\text{p}} f}}{{6\tau_{\text{p}} }}d_{\text{b,p}} A_{\text{i}}, $$
(10)

where \({\tau }_{\text{p}}\) is the particulate relaxation time, \({d}_{\text{b,p}}\) is the diameter of bubbles of phase \(p\) and \({A}_{\text{i}}\) is interfacial area. \(f\) is the drag function which for the Schiller and Nauman Model is defined as Eq. [11]:

$$ f = \frac{{C_{\text{D}} Re}}{24}, $$
(11)

where \(\text{Re}\) is the Reynolds number, \({C}_{\text{D}}\) is the drag coefficient[32] and has the following expression, Eq. [12]:

$$ C_{\text{D}} = \left\{ {\begin{array}{*{20}l} {\frac{{24\left( {1 + 0.15Re^{0.687} } \right)}}{{{\text{Re}}}}, \;{\text{Re}} \le 1000} \\ {0.44, \;{\text{Re}} \ge 1000} \\ \end{array} } \right. $$
(12)

The relative Reynolds number for the primary and secondary phase is described with Eq. [13]:

$$ {\text{Re}} = \frac{{\rho_{{q\left| {\vec{v}_{\text{p}} - \vec{v}_{\text{q}} } \right|d_{\text{b,p}} }} }}{{\mu_{\text{q}} }}, $$
(13)

where \({\mu }_{\text{q}}\) is the viscosity of the primary phase.

The turbulence in the domain was described with the \(k\)-ε realizable model.[32] This has become the industry standard for many types of engineering problems, especially within the metallurgy industry. The turbulent viscosity is written in terms of kinetic energy (\(k\)) and turbulent dissipation rate (ε) of phase \(q\) in Eq. [14]. The modeled transport equations for \(k\) and ε in are presented in Eqs. [15] and [16] respectively:

$$ \mu_{\text{t}} = \rho_{\text{q}} C_{\mu } \frac{{k^{2} }}{{\varepsilon }}, $$
(14)
$$ \frac{{\partial \left( {\alpha_{\text{q}} \rho_{\text{q}} k_{\text{q}} } \right)}}{\partial t} + \nabla \cdot\left( {\alpha_{\text{q}} \rho_{\text{q}} \vec{v}_{\text{q}} k_{\text{q}} } \right) = \nabla \cdot\left( {\alpha_{\text{q}} \left( {\mu_{\text{q}} + \frac{{\mu_{t,q} }}{{\sigma_{\text{k}} }}} \right)\nabla k_{\text{q}} } \right) + \alpha_{\text{q}} (G_{\text{k,q}} + G_{\text{b}} ) - \alpha_{\text{q}} \rho_{\text{q}} {\varepsilon }_{\text{q}}, $$
(15)
$$ \frac{{\partial \left( {\alpha_{\text{q}} \rho_{\text{q}} \varepsilon_{\text{q}} } \right)}}{\partial t} + \nabla \cdot\left( {\alpha_{\text{q}} \rho_{\text{q}} \vec{v}_{\text{q}} \varepsilon_{\text{q}} } \right) = \nabla \cdot\left( {\alpha_{\text{q}} \left( {\mu_{\text{q}} + \frac{{\mu_{t,q} }}{{\sigma_{\varepsilon } }}} \right)\nabla \varepsilon_{\text{q}} } \right) + \alpha_{\text{q}} \rho_{\text{q}} C_{1} S\varepsilon - \rho_{\text{q}} C_{2} \frac{{\varepsilon^{2} }}{{k + \sqrt {\nu \varepsilon } }} + \alpha_{\text{q}} C_{1\varepsilon } \frac{\varepsilon }{k}C_{3\varepsilon } G_{\text{b}}, $$
(16)

where \({G}_{\text{k}}\) and \({G}_{\text{b}}\) are the production of turbulent kinetic energy due to velocity gradient and buoyancy, respectively. \({\sigma }_{\text{k}}\) and \({\sigma }_{\varepsilon }\) are the turbulent Prandtl numbers for \(k\) and \(\varepsilon, \) respectively, and \(\upnu \) is the kinematic viscosity. \({C}_{1\varepsilon }\), \({C}_{2}\) are constants, \({C}_{3\varepsilon }\) is a coefficient that determines the factor by which \(\varepsilon \) is affected by buoyancy and \({C}_{1}\) is expressed in Eq. [17]:

$$ C_{1} = {\text{max}}\left[ {0.43,\frac{\eta }{\eta + 5}} \right],\;\eta = S\frac{k}{{\varepsilon }}, S = \sqrt {2S_{ij} S_{ij} }. $$
(17)

The energy equation is based on the first law of thermodynamics and is expressed in Eq. [18]:

$$ \frac{\partial }{\partial t}\left( {\alpha_{\text{q}} \rho_{\text{q}} h_{\text{q}} } \right) + \nabla \cdot \left( {\alpha_{\text{q}} \rho_{\text{q}} \vec{v}h_{\text{q}} } \right) = \alpha_{\text{q}} \frac{{\partial p_{\text{q}} }}{\partial t} + \nabla \cdot \left[ {\left( {k_{\text{eff}} \nabla T} \right) - \left( {\overline{\overline{\tau }}_{\text{eff}} \cdot \vec{v}} \right)} \right] + S_{h}, $$
(18)

where \({h}_{\text{q}}\) is the specific enthalpy of the \(q\)th phase treated as Eq. [19], \({k}_{\text{eff}}\) is the effective thermal conductivity, controlled mainly by the turbulence, \({\overline{\overline{\tau }}}_{\text{eff}}\) is the shear energy, and \({S}_{h}\) is a default, zero-source term.

$$ h = e + \frac{p}{\rho }, $$
(19)

where \(e\) is the specific internal energy.

Boundary conditions and set-up

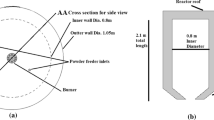
The model geometry and boundary conditions were adjusted to fit an industrial AOD converter of 80 tons. To avoid modeling the demanding high-velocity gas penetration into the steel, a mass flow gas inlet was added to a plateau in the shape of a 90 deg arc. The plateau was estimated to have two thirds the depth of the penetration length (Eq. [4], aided by nozzle simulation described in paragraph 2.1) to cover for the plume spread by the bubbles that ascended before reaching the penetration length. This represented the rising gas plume as the jet penetration depth is reached, and the gas no longer possesses any horizontal momentum which means it is fully controlled by the buoyancy; the details are presented in Figure 2. A degassing outlet was set for the top flat surface exit with a pressure equal to atmospheric pressure. Further, stationary no-slip walls were used.

Fig. 2
figure 2

Schematics of the model geometry based on an 80-ton industrial AOD converter and boundary conditions. The inlet area is within the dashed red line (Color figure online)

Full size image

The phase coupled SIMPLE (Semi-Implicit method for pressure linked equations) algorithm was used for pressure–velocity coupling, which calculates the pressure and velocity fields by an iterative guess and correction method based on the momentum and continuity equations.[34] The spatial discretization was computed with the least-square cell base method with the first-order implicit time integration scheme. In addition, the first-order upwind was used for momentum and turbulent kinetic energy while the second-order upwind was used for pressure. The important parameters of the gas-steel system are presented in Table III.

Table III Important Parameters and Properties Used in Simulations
Full size table

Coupling scheme between Thermo-Calc and Fluent.

The model assumes local cell equilibrium for the chemical reactions. The model is constructed through the integration of two distinct software programs, employing User-Defined Functions (UDF) within ANSYS Fluent and the TQ interface within Thermo-Calc. The UDF allows for dynamical coupling of functions in Fluent and TQ interface implements function in the native language of Thermo-Calc. For this study, Fluent v2022 R2 was used for mass transfer of phases and Thermo-Calc v.2021b with the TCS Metal Oxide Solutions (TCOX10)[37] database was used for chemical reactions. TCOX is a thermodynamic database for slags and oxides which provides the possibility to describe the slag phase as a liquid phase and as solid oxides. If the slag is in a liquid state, then the liquid steel and slag will be treated as the same phase but with different composition, separated by a miscibility gap. The phases are called ionic liquids where for example ionic liquid #1 could represent liquid metal and ionic liquid #2 a liquid slag. This allows the composition of the liquid phase to continuously change from metallic to oxidic when in equilibrium.

The Thermo-Calc software[15] is based on the Calphad approach.[38] In the Calphad approach experimental data is used to fit expressions yielding the molar Gibbs energy of phases as a function of temperature, pressure, and constitution. Since the characteristic state function Gibbs energy is fitted, it is straightforward to switch to other characteristic state functions, for example, Helmholtz energy, using basic thermodynamic relations.[39] This “property” of the Calphad approach is utilized by the Thermo-Calc software in that equilibrium conditions can be set in a quite general manner, e.g., using other variables than those that are natural to Gibbs energy. Computing the equilibrium state is an optimization problem; finding the extrema of the characteristic state function subject to the constraints given by the equilibrium conditions. In this work, the multi-component phase equilibria are calculated in Thermo-Calc with the minimization of the Gibbs free energy method and allows solving for various amounts of phases such as gas, liquid, and slag. The elements considered in this system were C, Cr, Fe, N, Ni, and O.

The model is built to perform the coupling scheme in each finite volume cell within each timestep. Initially, important parameters such as temperature, pressure, and mass for each element are served as input from the CFD solution to Thermo-Calc. In Thermo-Calc, equilibrium is calculated for each phase separately to acquire enthalpy input for a total equilibrium and heat balance. Furthermore, the new temperatures and masses are sent back to the CFD solver which calculates the mass transfer of elements at the next timestep, Figure 3. It is important to note that the physical properties used in the CFD solution are not updated after each equilibrium in Thermo-Calc. Although it is possible to couple the physical properties by updating within each CFD iteration, it is not recommended since it will increase the computational time by orders of magnitude. Also, as will be shown later, the mass transfer in the AOD is very high already, and the macroscopic reactions may not be affected to a sufficient great extent to warrant such a computationally expensive strategy. When dealing with reactive multiphase flows, an essential factor to consider is the mass balance. In this context, i.e., with equilibrium conditions set as outlined above, Thermo-Calc applies a closed system approach, which means that while heat and work can cross the system boundaries, the mass of the system remains constant. This implies that the exact same atoms are conserved, rather than just a constant mass. Fluent employs a control volume approach in which heat, work, and mass can cross the system boundaries, Figure 4.

Fig. 3
figure 3

Flowchart over coupling procedure between CFD and Thermo-Calc

Full size image
Fig. 4
figure 4

The difference between a Control mass (Thermo-Calc) and a Control volume (CFD). The control mass allows energy in form heat and work to be transferred in and out of system boundaries while, unlike a control volume, the mass remains constant

Full size image

In contrast to the closed system approach used by Thermo-Calc, the control volume approach does not permit a change in system volume between states, Figure 5.

Fig. 5
figure 5

Illustration of the system states between non-equilibrium CFD and equilibrium TC

Full size image

If computational time is not a concern, the mismatch between the two approaches can be resolved by iteratively updating fluid properties and transferring mass between phases during each CFD timestep. However, a more efficient solution is to only calculate equilibrium once. This, however, leads to the persisting issue of the mismatch. To minimize the error, mass is conserved over volume by keeping the density of each phase constant and allowing the sum of mass fractions of elements to be less than or even exceed one, Figure 6. It should be noted that density differences between phases do not affect the flow patterns in the system. Instead, the density differences only manifest themselves in the mass fractions. Thus, this can be viewed as a one-way coupling in terms of fluid flow. The fluid flow influences the composition and temperature and redistributes these properties throughout the domain, whereas the high-temperature reactions are influenced by the local properties in the control volumes and can alter the temperature and phase composition.

Fig. 6
figure 6

Mass conservation is enforced while keeping density and volume constant. Mass fractions are scaled to reflect this constraint in order to conserve the mass of elements in each phase. w is the mass fraction of phase with indices denoting number of elements. m is the mass of an element in a phase

Full size image

Numerical procedure

Initially, the simulation was set to develop in transient formulation for 20 seconds with a timestep size of 0.1 s, after which a frozen flow field was employed while tracking the concentration of an inert scalar. A variance in time was introduced by repeating this 5 times with 10 seconds transient simulation increments. Thus, mixing time was extracted in a frozen flow field at 20, 30, 40, 50, and 60 seconds of transient flow. Furthermore, at this stage, no reactions were taken into consideration in the model, and the gas was set to that of the steel temperature.

Mixing time

Mixing time is the critical property that determines the time it takes for a change to take effect in most of the process. The mixing time is defined by a criterion for what constitutes most of the process. In this study, the criterion for mixing time is 95 pct total homogenization, i.e., the time to even out a concentration difference to within ± 5 pct of the mean concentration. Mixing time in the simulation was measured using a User-Defined Scalar model solving equation [20][23,32]:

$$\frac{\partial }{\partial t}\left({\alpha }_{\text{q}}{\rho }_{\text{q}}{\emptyset }_{\text{q}}^{i}\right)+\nabla \cdot \left({\alpha }_{\text{q}}{\rho }_{\text{q}}{\overrightarrow{v}}_{\text{q}}{\emptyset}_{\text{q}}^{i}-{\alpha }_{\text{q}}{\Gamma }_{\text{q}}^{i}\nabla {\emptyset}_{\text{q}}^{i}\right)=0, i=1,\ldots ,N$$
(20)

where \(i\) is the arbitrary scalar in phase \(q\) denoted by \({\emptyset}_{\text{q}}^{i}\), \({\Gamma }_{\text{q}}^{i}\) is the diffusion coefficient in turbulent flows and is computed as follows, Eq. [21]:

$$\Gamma =\rho {D}_{\text{m}}+\frac{{\mu }_{\text{t}}}{S{C}_{\text{t}}},$$
(21)

whereas \({D}_{\text{m}}\) is defined as molecular mass diffusivity and \(S{C}_{\text{t}}\) is the turbulent Schmidt number (0.7) which is more properly formulated as \(\frac{{\mu }_{\text{t}}}{\rho {D}_{\text{t}}}\). Here, \({D}_{\text{t}}\) is the turbulent diffusivity.

For each measured mixing time, a tracer solution was patched in the middle of the domain with a volume of 0.057 m3, which represents approximately 400 kg liquid steel mass. Further, to better capture any dead zones volumetric monitoring was applied where the standard deviation to the mass-averaged tracer concentration was monitored with Eq. [22]. Assuming that the tracer concentration is normal distributed in the domain, then the first standard deviation captures the homogenization in 67 pct of the cells in the domain whereas the second standard deviation captures 95 pct of the cells, which is chosen to represent the mixing time in this case.

$${\sigma }_{std}=\sqrt{\frac{1}{N}\sum_{i=1}^{N}{\left(\frac{{x}_{\text{i}}-{x}_{\infty }}{{x}_{\infty }}\cdot 100\right)}^{2}}$$
(22)

where, \(N\) is the number of cells \({x}_{\text{i}}\) is the concentration of tracer in cell \(i\) and \({x}_{\infty }\) is the fully homogenized tracer concentration (i.e., the mean concentration) in the liquid-steel domain. So roughly speaking, when two standard deviations are below 0.05 then this corresponds to a case where 95 pct of the cells in the domain are within 5 pct of the mean concentration.

Full Model

All the coupled model simulations were solved in the frozen flow field stage after 20 s transient CFD simulation. The elements of each phase were treated with scalar transport locked to its fluid phase in the CFD solution. The liquid slag was transported together with the liquid steel in the CFD solution. The solid-slag phase was allowed to form during the Thermo-Calc equilibrium calculations. However, it was excluded from the CFD solution and instead assumed that it disappears from the system once formed (e.g., it can be assumed to have joined an inert top slag). The equilibrium calculations were performed with a timestep size of 0.6 seconds (after 6 CFD timesteps). This represents the time it takes for the gas to ascend from the nozzle to the outlet, i.e., the gas plume is replaced with new gas. Thus, it was possible to decrease the computational time even more. With this method, a source term was added to the UDF which injected the correct amount of gas based on the mass flow rate into the system for equilibrium calculations. In addition, the gas was injected with a temperature of 300 K. The reactions only took place if the gas volume fraction was between 0.3 and 0.99 in the computational cell.

Both mixing time and reactions were calculated in a domain containing a structured mesh of butterfly type. Four mesh sizes were used to capture the effect of grid difference on mixing time and if that would affect the reactions. The different domains contained 835, 1596, 2672, and 5280 cells. Obviously, these meshes are extremely coarse, but compared to a single-cell approach that is commonly used in process control systems as well as in pure thermodynamics calculations, this is a substantial difference. Emphasis was put on creating a practical model that could capture the entire AOD process within a reasonable simulation time.

Cases 1–3

To ensure the validity of the model, data from two heats containing different steel grades were collected during the process. Further, no additions were added during the investigated period. The heat loss in the system was included as a source term in the UDF which applied a temperature decrease rate of − 1 K min−1 from convection, radiation, and conduction, while keeping the boundaries adiabatic. This temperature decrease rate was an approximate value for the heat losses during periods when there are no reactions, taken from operators of the steel plant. The model allowed both gas, liquid, and solid phases to form during equilibrium calculations. However, the elements present in the solid-slag and gas phases were not tracked in the CFD solver and, therefore, disappeared after formation. The solid-slag formation was assumed to join the top slag and the gas formed, mainly CO and N2, was assumed to escape the domain between each equilibrium calculation. Consequently, only reactions between the liquid and gas phases were considered, and the gas involved in the reactions was assumed to escape from the surface. The simulated cases only modeled the first step of the decarburization which is typically 10–20 minutes depending on the steel grade. The composition of the melt/gas and the starting temperature is defined in Table IV. The initial values from each case have been extracted from the real industrial heats apart from the steel mass pct oxygen, which is an estimated value due to the lack of industrial data. Case1 is based on the first industrial heat, and cases 2 and 3 are based on the second industrial heat. The second industrial heat had a much higher melt mass compared to the first industrial heat. Two approaches were tested to account for the mass increase (Cases 2 and 3). The first being Case 2, where an increase of steel density would represent the mass increase, hence, the added ferro-static pressure of an increased bath height. This case has the correct mass, but the volume is incorrect so there may be some differences in the kinetics. In Case 3, the bath height was altered to represent the actual heat. However, since the age of the converters was slightly different, the grade of erosion of the converter walls were different. This means that the inner diameter was slightly changed, which was compensated for by adjusting the steel density slightly, as can be seen in Table IV.

Table IV Initial Composition and Temperature of Melt and Gas
Full size table

Results and Discussion

The first step of the decarburization in the AOD converter was modeled with CFD and chemical reactions. Since the CFD solution was rather coarse, four meshes were applied to monitor the difference in mixing time and its effect on the reactions in the AOD model. The mixing time is presented in Table V for the different meshes. The evolution of mass pct C, Cr, and temperature are presented in Figure 7, where the initial values from Case 1 were used. Note that the mean and STD of each mixing time value is presented due to the mixing time procedure presented above. I.e., several mixing time calculations have been performed at different times where the flow field has been frozen. While the magnitude of flow field has changed in the finest mesh, thereby impacting the mixing time, the overall direction of the flow remains consistent with previous mesh resolutions. The total simulation times when reactions were started are also presented in Table V. The simulations were executed on a high-performance computing workstation equipped with two AMD EPYC 7301 processors, each featuring 16 cores, and a total of 128 GB of RAM. The computing system was optimized for parallel simulations, but in this research, only serial simulations were conducted. Consequently, there is an opportunity for enhancement by conducting parallel simulations or utilizing more high-performance CPUs. With all this considered, the model is time effective when comparing to other reported work[20,21] using a similar coupling process, simulated 7.5 minutes of blowing time in 1 week. Naturally there are different parameters that contribute to this time such as number of elements included in the thermodynamic description, transport of energy equation, number of computational cores, grid resolution, and equilibrium timestep.

Table V Average Mixing Time Over 5 Measurements for All Mesh Resolutions on the AOD Model
Full size table
Fig. 7
figure 7

The evolution of (a) average mass pct of C, (b) average mass pct of Cr, (c) average temperature, for different grids

Full size image

The mixing phenomena are complex and difficult to measure in the industrial process. Therefore, the actual mixing time is not known in the AOD process and relies on the assumption that it is rather similar to previous water models of the AOD.[6] For that system, a variation of modeling parameters resulted in an interval of 11.3–24.1 s, and the mixing in general of an AOD was considered to be fast due to the efficient stirring characteristics of side blowing. The mixing time on the finest mesh is higher than the other meshes. However, looking at the elements and temperature graphs, it seems to have only a minor effect on the evolution throughout the first decarburization step in Case 1. This observation can be attributed to the small bulk gradients across the domain which arise from the rapid mixing, as illustrated in Figure 8. The circulating motion of the bath can also clearly be seen. Moreover, as the prior studies[9,11,12,13] have proposed, the reactions are governed by the availability of oxygen rather than the mass transfer. Nonetheless, the difference can be neglected since the uncertainties in the industrial measurements are certainly much higher. Thus, the mesh with 835 cells was used which represented a decrease in simulation time by 23 pct over the next mesh level, while the differences in results were minor as can be seen in Figure 7.

Fig. 8
figure 8

The figure exhibits the flow pattern of liquid steel, as indicated by the arrows. The transparent gas plume is positioned on the left side of the figure to enhance visibility. The last three converters depict the local gradients of weight fraction C, Cr, and temperature, respectively, at the end of the simulation

Full size image

Cases 1–3

Figures 9 and 10 show the average temperature and the average mass percentage of element: C, Cr, N, and Ni in steel for Case 1 and Case 3, respectively. The simulation results are compared to measurements from the industrial heats and the data acquired from the online process model (OPM) used to the respective heat. The present study demonstrates a promising degree of similarity between the simulated models and the two industrial heats analyzed. Specifically, the temperature, chromium, and nickel exhibit a very high degree of agreement, while the carbon and nitrogen levels differ from the measured heats. These discrepancies are likely attributed to the distribution of oxygen for the oxidation of different elements. Notably, the industrial heats contain additional elements, such as manganese and silicon, that also undergo oxidation, which are not accounted for in either of the simulated cases (i.e., they are not present in the thermodynamic system at all). Looking at Figure 9(a) it is seen that the temperature is undergoing a rather linear increase, with a slightly higher rate of increase in the beginning and end (0–200, 400–600 seconds) and a slightly lower rate of increase in the middle (200–400 seconds). The temperature is primarily affected by the exothermic reactions of decarburization and chromium oxidation. Figure 9(b) shows the carbon evolution in the melt. It starts immediately with an aggressive rate of decrease (0–400 seconds) after which the rate decreases (400–600 seconds). Compared with the steel plant’s online process model, it is seen that the rate of decarburization is too high in the initial stage. As stated above, this is likely because there are no competing elements, primarily Si and Mn during the 0–200 seconds blowing period. As such the simulation over-predicts the decarburization rate in the beginning. In Figure 9(c) the chromium oxidation can be seen. It does not follow a linear pattern. It is linked to the temperature behavior where it has a higher rate of decrease in the beginning and end (0–200, 400–600 seconds) and a lower rate of decrease in the middle (200–400 seconds). Thus, with the high decarburization and chromium oxidation rate between 0 and 200 seconds, the temperature increases at a higher rate. Between 200 and 400 seconds, the rate of chromium oxidation decreases while the decarburization rate remains linear resulting in a temperature rate decrease. At 400 seconds, the decarburization rate slightly decreases while chromium oxidizes rapidly which is accompanied by a temperature increase. However, it is also seen that there is an initial very high rate of decrease of chromium (0–20 seconds). The simulation perfectly matches the measured chromium value. However, if Si and Mn are added to the model, this may change the behavior. This needs to be examined in more detail in the future. In Figure 9(d), the nitrogen content is plotted against time. It has an initial increase in nitrogen followed by a period of decreasing content until it once again starts to increase. Finally, the nickel content is seen in Figure 9(e). It increases during the blowing period, which is only attributed to the decrease in other elements, which matches the measured data very well. The actual nickel mass is constant during the process. Looking at the industrial online process control system, it is seen that it also gives good predictions in this case. The major difference between the simulation and the online control system is that the former is based on a more fundamental approach whereas the latter is optimized for the current steel plant. The simulation calculates all the transport mechanisms and reactions as part of the solution, based only on the initial and boundary conditions.

Fig. 9
figure 9

The (a) Average temperature, (b) mass pct C, (c) mass pct Cr, (d) mass pct N, (e) mass pct Ni over the first decarburization step in Case 1

Full size image
Fig. 10
figure 10

The (a) Average temperature, (b) mass pct C, (c) mass pct Cr, (d) mass pct N, (e) mass pct Ni over the first decarburization step in Case 3

Full size image

Figure 10(a) shows the temperature evolution in industrial heat 2. It is clear from the graph that the increase is related to the carbon and chromium oxidation in the melt. Figures 10(b) and (c) show that the process starts with a high carbon content (1.33 mass pct), resulting in a low rate of chromium oxidation according to both the simulation and process model, until a significant proportion of the carbon has been decarburized (300–400 seconds). During this time, the rate of the temperature increase is elevating. Subsequently, the rate of chromium oxidation increases extensively, while the decarburization rate decreases slowly (400–800 seconds) leading to the higher rate of temperature increase at (400–800 seconds). This trend aligns well with earlier modeling investigations[12,21,22] of decarburization under analogous AOD conditions. Similar to Case 1, the temperature, chromium, and nickel predictions agree very well with the industrial data and the trends of the OPM. Even the carbon evolution follows the OPM very well but with a slightly higher decarburization rate which is motivated by the same explanation as in Case 1. In Figure 10(d), the nitrogen content is rapidly extracted from the melt during the initial 100 seconds, until the rate of nitrogen removal diminishes, and the introduced nitrogen begins to dissolve into the melt between 200 and 800 seconds.

The mass distribution of oxygen to each element through their respective reactions in both the simulated cases and industrial heats is presented in Table VI. It is noteworthy that the difference in the mass of oxygen distributed to form CO in the model predictions and in the measured heats is of a comparable magnitude to the mass of oxygen distributed to form manganese oxide and silicon oxide. The mass balance in the industrial case has some residual value, but this is easily understood to be coupled to all the other minor elements present in the steel, measurement uncertainty, as well as through the assumptions of which oxides form. Regardless, this further strengthens the explanation that in the absence of a thermodynamic treatment for Si and Mn, there will be an excess decarburization since oxygen will then prefer to react with either C or Cr.

Table VI Distribution of Oxygen for the Oxidation of Different Elements
Full size table

In addition, Figure 11 compares the simulations in Case 2 and Case 3, demonstrating that in a more practical model, a virtual bath height created by increasing the steel density has a negligible effect compared to physically increasing the bath height in the geometry.

Fig. 11
figure 11

(a) The temperature evolution and (b) the carbon evolution of the simulations in Case 2 and Case 3

Full size image

The present study has demonstrated the feasibility of a practical approach to modeling the initial stage of decarburization in the AOD process. The model achieves this by decreasing the requirement for high accuracy in mass transport calculations within the CFD solver. Further work is needed to fully model the AOD process, i.e., by also accounting for the elements Si and Mn into the model to better represent oxygen distribution and element oxidation. In addition, the reaction model would need to account for the liquid steel/slag reactions and the mass transport of solid slag within the CFD solver. However, this would mean greater complexity in the reaction model and an increase in the time required for equilibrium calculations. These issues represent opportunities for future studies.

Conclusion

In this paper, a practical CFD-based approach with chemical reactions for an AOD converter has been presented. It is capable of simulating the entire AOD process within reasonable simulation times on a standard workstation. Local equilibrium is employed, and mass, momentum and energy transfer are handled using a Finite Volume Method CFD approach. Industrial data have been used for validation of the simulations. The results from the simulation and industrial data matches very well for temperature, chromium, and nickel. There is a discrepancy for the carbon content that can easily be explained by the lack of Si and Mn in the thermodynamic description. Specific findings include

At the beginning of the decarburization process, the oxidation of elements is limited to the supply of oxygen rather than the mass transfer of elements. Even with a mixing time increase of 100 pct from approximately 9 to 18 seconds, the model showed small differences in oxidation of elements. This is likely to change at later process stages when the carbon content is lower and as such longer simulation times, including all the steps in the AOD is suggested as future work. The difficult part is how to address additions during the process since these can have large uncertainties associated with them.

Steel grades with low-carbon content initially oxidize both carbon and chromium at a high rate while higher carbon content initially decarburizes the melt before chromium oxidation occurs.

With a coarse mesh, it is possible to capture a high accuracy on the decarburization in the AOD converter within a reasonable amount of simulation time with an average workstation. This can be achieved while maintaining a relevant flow field and mixing time.