Introduction

The use of freeze linings to provide furnace protection against the corrosive nature of molten slags is a widespread technique in industrial pyrometallurgical applications.[1] In particular, it has been adopted to smelting furnace sidewalls to extend their operational lifespan[2,3] and to minimize the refractory relining frequency and corresponding furnace shutdown.[4] With the current trend towards high production rates due to the increase in metal demand,[5] an adequate understanding of freeze lining formation is crucial for optimizing furnace design and operation.

In the past, several laboratory experiments were performed to investigate the fundamentals of freeze-lining formation. Guevara and Irons[6] conducted low-temperature experiments in a Bridgman cell to measure the freeze lining thickness of a slag analog (i.e., 53 wt pct aqueous solution of calcium chloride). The square cavity was differentially heated on each side. Several experiments were conducted under a wide range of superheating conditions. The position of the solid front was tracked using a digital camera and the temperature field was measured using thermocouples. Velocity measurements showed that the motion of the solid crystals was only present near the solidification front, whereas the main freeze-lining core remained virtually motionless.

Verscheure et al.[7] experimentally investigated the solidification microstructure of synthetic slags in laboratory by submerging a water-cooled probe into a liquid slag bath while continuously heating it in a resistance furnace. Freeze linings of two industrial nonferrous slags were produced using this technique, and their growth, microstructure, and compositional profiles were determined as a function of submergence time. The freeze linings formed during the experiments were primarily amorphous in the zones close to water cooling and more crystalline at a higher distance from the probe surface. In the first experiment, no perfect equilibrium was reached because, for long submergence times and low furnace powers, complete solidification of the bath was observed. In subsequent experiments,[8] a steady-state was reached using a less intensive gas-cooled probe.

Fallah-Mehrjardi et al.[9,10,11] performed a series of experiments in which freeze linings in copper-containing slag systems were studied under controlled laboratory conditions using an air-cooled cold finger technique. The authors focused on discussing the effects of melt chemistry on deposit microstructures. Microstructural examinations and temperature measurements of the solid slags formed under steady-state conditions demonstrated that the temperature of the steady-state freeze-lining solidification front could be lower than the equilibrium liquidus temperature of the bulk liquid. The authors also proposed a new mechanism for freeze-lining formation, which assumed that nucleation and growth of the solid phase occurred in a sub-liquidus layer in the fluid phase on the detached crystals ahead of the deposit and that the detached crystalline material was transported to and from the interface by convective flow.

More recently, Nagraj et al.[12] used slag rheology experiments to determine the freeze lining thickness. The bath-freeze lining interface was found to lie below the critical viscosity-temperature (with solid fraction of 41 pct). Furthermore, from the microscopic analysis of the freeze-lining samples, the solid fraction at the hot face of the freeze-lining samples depended on the hydrodynamics of the liquid slag and interactions between the crystals and liquid slag at the interface.

In addition to laboratory experiments and data gathered from metallurgical industries, numerical modeling has also been used to study freeze lining formation. Zietsman and Pistorius[13] proposed a one-dimensional wall model to describe the heat transfer, solidification, and melting in the freeze lining and furnace wall of an ilmenite-smelting DC arc furnace. The main focus of this study was the interactions between the freeze lining and slag bath. The modeling results appeared to yield some insights into the behavior of the freeze lining and slag bath; however, no modeling details or validation against industrial data were provided because of the confidentiality of the ilmenite-smelting operations.

Pan et al.[14] simulated the heat transfer of a six-in-line electric smelting furnace (ESF) for smelting sulfide ores. This model only considered heat transfer by relating the furnace conditions and performances to various control and input parameters. The main feature of the model is its efficiency and portability, with fast execution times for the prediction of the temperature distribution inside the furnace, freeze-lining thickness, and other productivity parameters. The fluid flow was not considered.

Sheng et al.[15,16,17] extended the work of Pan et al.[14] and coupled the solution of Maxwell (for the electromagnetic stirring force), Navier–Stokes, and heat transfer equations. Owing to the large-scale furnaces, the electromagnetic force was found to be negligible compared with the natural convection forces. After incorporating the experimentally obtained data for the electrical potential drop at the electrode surface, accurate predictions of the electrical resistance, temperature distribution, and slag velocity were obtained under various conditions. However, slag solidification was not considered in this case.

Guevara and Irons[18] proposed a two-phase numerical model for the formation of a freeze lining, which included the Navier–Stokes and energy conservation equations and slag solidification. The simulations were compared with the experimental results from the same authors[6] in a Bridgman cell during cooling under natural convection conditions. They concluded that the gradual velocity suppression during slag solidification was more accurately captured when temperature-dependent viscosity was assumed for the slag. The same authors extended their work to model a six-inline ESF electrode.[19] The effects of cooling intensity and temperature-dependent viscosity on the velocity and temperature distributions were studied. The main focus of the authors was the description of global heat transfer through the cooling system rather than the evolution of the freeze lining.

The purpose of the present study is to extend the work of Guevara[19] and establish a numerical framework that considers the global heat fluxes, multiphase transport phenomena, and slag solidification in a smelting furnace so that the freeze lining formation can be captured, as well as its dependency on the operating conditions. The same six-in-line ESF is referred to; however, the boundary conditions and heat transfer terms have been updated. Several aspects of furnace design and operation parameters were systematically studied to achieve a better understanding of the smelting process in the furnace.

Model Description

Mixture Continuum Model for Slag Solidification

An enthalpy-based mixture continuum model, originally proposed for metal alloy solidification,[20] was adapted to describe slag solidification during smelting. The general two-phase description of a binary solidification system was reduced to a single-phase model, where each variable (identified in the Nomenclature section) represents the mixture quantities. The conservation equations for mass, momentum, and energy are listed in Table I.

Table I Governing Equations for Slag Solidification Problem
Full size table

The relationship between the sensible enthalpy and temperature is given by: \(h = \int_{{T_{{{\text{ref}}}} }}^{T} {c_{{\text{p}}} } dT\).

In the present case, the mixture continuum changes from a pure liquid (fℓ = 1) in the bulk molten slag to complete solid (fℓ = 0) in the freeze lining. The as-solidified slag microstructure is approximated with a mushy zone, that is, a liquid and solid mixture (0 < fℓ < 1) in which the solid matrix has a columnar dendritic morphology, as shown schematically in Figure 1. The solid matrix is assumed to be stationary (\(\mathop{u}\limits^{\rightharpoonup} {_{\text{s}}} = 0\)), and the mixture velocity depends only on the liquid phase velocity:

$$ \mathop{u}\limits^{\rightharpoonup} = \frac{1}{\rho }\left( {f_{\ell } \rho_{\ell } \mathop{u}\limits^{\rightharpoonup} {_\ell } } \right). $$
(4)
Fig. 1
figure 1

Schematic of slag solidification with a mushy zone, which represents the zone between fully liquid and fully solid state

Full size image

The release of latent heat due to slag solidification is captured by the second term on the right-hand side of Eq. [3]. The evolution of fs was initially assumed to follow the lever rule.

$$ f_{{\text{s}}} = \frac{1}{{\left( {1 - k} \right)}} \cdot \frac{{\left( {T - T_{{{\text{liq}}}} } \right)}}{{\left( {T - T_{{\text{f}}} } \right)}}. $$
(5)

This relation between fs and T will be analyzed in detail below.

\(\mathop{S}\limits^{\rightharpoonup} {_\text{U}}\) in Eq. [2] is the drag term, which is necessary to guarantee a well-defined one-phase momentum equation and ensures that \(\mathop{u}\limits^{\rightharpoonup} {_\ell } = \mathop{u}\limits^{\rightharpoonup} {{_\text{s}}} = 0\) when the solidification is complete. This is based on the Carman–Kozeny equation for flow in porous media:[20,21]

$$ \overrightarrow {S}_{{\text{U}}} = - K_{0} \frac{{f_{{\text{s}}}^{2} }}{{f_{\ell }^{3} }}\mathop{u}\limits^{\rightharpoonup}, $$
(6)

\(S_{{\text{H}}}\) in Eq. [3] is the energy source term, which represents different phenomena occurring during furnace operation, that is, the electrical energy input from the electrodes, the heat transferred to the slag during matte production, and the heat transfer due to the presence of the feed. Their modeling is discussed later.

Note that this mixture continuum model was used only for the slag phase. As shown in the next section, the matte and refractory were also considered in the simulations of the ESF. The conservation equations were solved separately in each region. For the solid refractory region, only the energy equation (Eq. [3]) is solved, whereas for the liquid-matte region, the Navier–Stokes and energy equations are solved (Eqs. [1] through [3]). In both cases, the variables are not mixture quantities, and the term related to the release of latent heat due to slag solidification (the second term on the right-hand side of Eq. [3]) were not considered. The interaction between the three regions was enforced by the interfacial boundary conditions, which are discussed later.

Modeling Framework for the Smelting Furnace

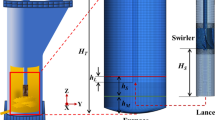
This case study represents an industrial ESF for the smelting of nickel matte. The furnace contained six electrodes. A schematic of the cross-sectional view of the furnace (through one of the electrodes) is shown in Figure 2. During furnace operation, the electrical energy required to smelt the feed is generated by Joule heating created by the passage of an electric current between the carbon electrodes immersed in the molten slag bath. After the furnace was charged with the feed, slag and matte were produced. The denser matte settled through the liquid slag layer at the bottom of the vessel. The cooling system on the smelter sides prompted the formation of a freeze lining. The furnace was tapped periodically to discharge matte and slag through separate tap holes. The total input power (IP) in the furnace was 15 MW, which corresponds to a matte production rate of 35 ton/h.

Fig. 2
figure 2

Schematic of ESF cross-section

Full size image

For the numerical model, owing to symmetry considerations, only 1/12th of the total furnace was considered. This included a section containing half of one electrode. The computational domain consisted of a solid refractory, liquid matte, and liquid slag, as shown in Figure 3. The influence of the feed and gas phases on the general energy balance is considered by assuming an equivalent heat source on the top surface of the computational domain, as discussed later. The fluid flow was assumed to be laminar and the domain size remained unchanged throughout the simulation.

Fig. 3
figure 3

Computational domain and boundary conditions

Full size image

Figure 3 summarizes the momentum and thermal boundary conditions used in the simulations. The outer walls of the furnace were exposed to ambient air, whereas a cooling system was considered at the top of the vertical wall. Convection thermal boundary conditions were assumed for these surfaces. The corresponding heat transfer coefficients (HTC) for each surface, as well as on the top surface, were based on the work of Guevara.[19] Adiabatic boundary conditions were considered on the electrode surface, and symmetry boundary conditions were considered for the remaining surfaces. Coupled boundary conditions are applied to the interfaces between regions (i.e. slag/refractory, slag/matte and matte/refractory), where the solver calculates the heat transfer directly from the solution of the opposite region. For the momentum boundary conditions, a shear stress boundary condition was imposed at the slag-matte interface. This applied the average shear stress between the last layer in the slag region and the first layer in the matte region \(\left( {\overline{\tau } = {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}\left( {\mu \left( {{{{\text{d}}u_{x} } \mathord{\left/ {\vphantom {{{\text{d}}u_{x} } {{\text{d}}y}}} \right. \kern-0pt} {{\text{d}}y}}} \right)_{{{\text{slag,}}\,{\text{bot}}}} + \mu_{mat} \left( {{{{\text{d}}u_{x} } \mathord{\left/ {\vphantom {{{\text{d}}u_{x} } {{\text{d}}y}}} \right. \kern-0pt} {{\text{d}}y}}} \right)_{{{\text{mat,}}\;{\text{top}}}} } \right)} \right),\) to ensure a continuous shear stress profile in the fluid domain. The momentum boundary conditions for the remaining boundaries were no-slip for both the fluid phases.

The Boussinesq approximation was used to account for the natural convection of the slag (with the reference density and temperature being equal to 2801.7 kg/m3 and 1416 K, respectively). The adjusted pressure in Eq. [2] (i.e. \(p^{\prime}\)) from the use of the Boussinesq approximation is accounted for as: \(p^{\prime} = p - \rho (\mathop{g}\limits^{\rightharpoonup} \cdot \mathop{y}\limits^{\rightharpoonup} )\). The magnetohydrodynamic aspects of the flow caused by the presence of an electric current were neglected in the present furnace.[15] The material properties are listed in Table II.

Table II Material Properties
Full size table

The resistance to the motion of the slag during solidification was determined using the drag source term Eq. [6]; thus, the viscosity in the slag phase was treated as a constant. The thermal conductivity in the slag varied linearly in the mushy zone (from the two values given in Table II). Matte solidification is not modeled here, but the viscosity in the matte is assumed to increase rapidly to 3250 Pa·s (i.e., a very large value) once T < Tsol,mat, to ensure that the matte phase behaves as a solid structure in that regime.

The model was implemented using ANSYS FLUENT version 19.2. The number of cells was approximately 3.6 million cells. In the slag region, near the cooling system, the cell size was about 1 cm. Away from the cooling system, the cell size increased gradually until a maximum of 4 cm. A more refined grid was implemented near the cooling system to capture the freeze lining with more detail. In the matte and refractory zones, the cell size was about 4 cm. In each simulation, an approximate solution for the temperature distribution was patched in the refractory region as an initial condition to reduce the total simulation time. The matte and slag regions were always initialized at T0 = 1416 K and zero velocity. A transient simulation was performed until a quasi-steady-state solution was obtained.

Energy Source Terms

One of the critical steps in the modeling of smelting furnaces is to consider a valid global energy balance inside the furnace while still creating a freeze lining. The current model framework considers three main heat transfer mechanisms, as shown in Figure 4.

Fig. 4
figure 4

Energy source terms considered in the simulations

Full size image

Energy Source from the Electrode

As mentioned previously, electrical energy is converted into Joule heat, which is released into the slag. Consequently, the heat distribution is determined by the electrical conductivity of the molten slag and electric potential applied to the electrodes.[15] The former depends on the local temperature, whereas the latter depends on the location in relation to the electrode, and is greatest in the vicinity of the electrodes.[16] Following Guevara,[19] the impact of electrical energy was simplified by assuming that the total heat source was divided into four zones, with different weights assigned to each zone. The locations of these zones are shown in Figure 4. Close to the electrode, a larger weight is considered (\(\gamma_{1} = 60\,{\text{pct}}\)), and with increasing distance from the electrode, the corresponding weight decreases gradually (i.e., \(\gamma_{2} = 25\,{\text{pct}}\), \(\gamma_{3} = 10\,{\text{pct}}\), and \(\gamma_{4} = 5\,{\text{pct}}\)). The energy source term in each zone is then calculated as

$$ S_{{{\text{H}}_{1 - 4} }} = \gamma_{1 - 4} \cdot IP/12/V_{1 - 4}, $$
(7)

where subscripts 1–4 correspond to each of the four zones. The total input power to the furnace was IP = 15 MW. The division by 12 is because the simulation only considers one-twelfth of the entire furnace. The volume integral of \(S_{{{\text{H}}_{1 - 4} }}\) equates to the total IP in the computational section. The corresponding values for \(S_{{{\text{H}}_{1 - 4} }}\) are shown in Figure 4.

Energy Sink from Presence of the Feed

Complex thermal and chemical processes occur during the furnace operation owing to the presence of the feed. Examples of such phenomena are radiative heat transfer between the roof of the furnace and the top of the feed surface through the freeboard, re-melting and possible re-solidification of the feed, and heat dissipation from effluent gases due to chemical reactions. However, modeling of all these phenomena is not yet possible because of the lack of accurate data. Therefore, a constant energy sink term was assumed at the top of the domain to capture the corresponding global heat transfer effect (\(S_{{{\text{H}}_{{5}} }} = - 1.67 \times 10^{6}\) W/m3). The proposed value was derived from an energy balance by Guevara[19] for the current IP. The impact of different \(S_{{{\text{H}}_{5} }}\) on the outcome of the smelting process and freeze-lining formation is discussed later.

Energy Source from Matte Production

The last heat source term necessary for the simulation represents the matte production. The idea behind this mechanism is that, while producing matte from the slag phase, energy is released near the slag-matte interface. This energy source term should be proportional to the mass production rate of the matte (\(\dot{m}\)) and the local enthalpy of the system (\(h\)), and is calculated as

$$ S_{{{\text{H}}_{6} }} = \dot{m} \cdot h/V_{6}. $$
(8)

For the current IP, the furnace produces 35 tons of matte per hour[19] and the average local enthalpy is approximately 0.7 × 106 J/kg, so \(S_{{{\text{H}}_{6} }} = 0.80 \times 10^{6}\) W/m3.

Simulation Results

Temperature

The steady-state temperature distribution is shown in Figure 5. The white line represents the solidification front defined as T = Tliq (i.e., the start of the mushy zone). In addition to the slag and matte regions, the temperature distribution was also observed in the refractory.

Fig. 5
figure 5

Contours of temperature. White line represents the solidification front. Top inset highlights the temperature range inside the slag bath. Bottom inset highlights the temperature gradient near cooling system

Full size image

After reaching a steady-state, the temperature profile remained unchanged over time. In the slag bath, the temperature appeared to be fairly uniform because of the convection flow developed in that region. However, the top inset of Figure 5 provides more details regarding the temperature distribution inside the molten slag bath (as the temperature range of the color scale is reduced). This demonstrates that the local temperature is higher closer to the electrode region and fades with distance. This provided the driving force for natural convection in the molten slag. The temperature in the slag reached 1460 K, which is consistent with the plant data reported by Sheng et al.[16] In contrast, a more stratified temperature distribution was found in the matte phase because of the relatively stagnant flow conditions in this region and the modest heat flux imposed on the outer walls of the furnace. Nevertheless, the temperature in the matte region is always above TSol,mat, implying that (from Table II) the matte always behaves as a liquid, with µmat = 0.004 kg/(m·s).

The main heat removal mechanisms occurred near the furnace wall and near the top of the domain, where steep temperature gradients were established. As discussed later, this has a critical effect on freeze lining formation, as the heat removed from the system creates a thermodynamic driving force for slag solidification (a solidification front appears ahead of the two surfaces). The bottom inset in Figure 5 shows the temperature distribution in a segment of the furnace that encompasses the refractory material (adjacent to the cooling system) and slag. Apart from the temperature gradient, the white line in the inset also suggests the presence of a freeze lining between the refractory and molten slag.

Solid Fraction of the Slag Phase

Figure 6 shows the steady-state solid fraction distribution of the slag phase. The simulation results predicted a solidified slag layer covering the furnace wall and most of the top surface. However, it is important to note that these layers represent two different solid structures. The vertical solid structure near the cooling system corresponds to the freeze-lining layer. However, given the assumptions considered in the current model, the solid structure on the top surface represents the region occupied by the feed. In Figure 6, the freeze lining covers the entire surface of the refractory wall with a relatively uniform thickness. The solid feed completely melted near the electrode owing to the high local heat source; however, its thickness became progressively larger, reaching a maximum near the furnace wall. In the matte region, the solid fraction is zero, indicating that the matte is fully in the molten state.

Fig. 6
figure 6

Contours of solid fraction for slag phase (which includes the freeze-lining layer and feed). White line represents the solidification front. Inset highlights the solid fraction distribution in a section of the furnace, overlaid with arrows representing the mixture slag velocity vector

Full size image

The inset of Figure 6 shows the solid fraction contour in a section of the slag region near the furnace wall, which is overlaid with the direction vectors of the mixture slag velocity. In the present model, it was assumed that the completely solidified freeze lining would be stationary (\(\mathop{u}\limits^{\rightharpoonup} {_{\text{s}}} = 0\)). This can be confirmed in the inset, where the velocity vectors disappear as the solid volume fraction increases in the mushy zone. The solidification front is mostly vertical ahead of the furnace wall; however, it curves in the direction of the slag-matte interface for a small distance before fading away. No extended solid layer separated the molten slag from the matte region. Note that the solid fraction gradient observed on the left side of the freeze-lining layer is due to the node interpolation method employed during post-processing (which interpolate between the nodes on the wall and the nodes on the last cell in the slag region). However, the solid fraction in the cell center adjacent to the wall is one, which means no actual liquid layer separates the wall from the freeze lining.

Velocity

The velocity contours in the matte and slag regions along the three cross-sectional planes are shown in Figure 7. The contours are overlaid with black arrows (with normalized size), which represent the tangential projection of \(\mathop{u}\limits^{\rightharpoonup} {_\ell }\) on the corresponding plane. The color scale represents the velocity magnitude, whereas the arrows represent the flow direction (arrows with velocities under 1 × 10–3 m/s are omitted). The results are shown in the XY plane (with Z = 2.1 m, i.e., through the center of the electrode), YZ plane (with X = 0 m, i.e., symmetry plane), and XZ plane (with Y = 2.5 m, i.e., slightly below the bottom of the electrode).

Fig. 7
figure 7

Mixture velocity shown in: (a) XY plane (with Z = 2.1 m, i.e. through center of electrode), (b) YZ plane (with X = 0 m, i.e. symmetry plane), and (c) XZ plane (with Y = 2.5 m, i.e. slightly under the bottom of the electrode). Black arrows represent the tangential projection of \(\mathop{u}\limits^{\rightharpoonup} {_\ell }\) on the corresponding plane (arrows with velocity under 1 × 10–3 m/s are omitted). White line represents the solidification front. The coordinate system is shown in Fig. 3

Full size image

In Figure 7(a), an anticlockwise flow is observed in the slag region due to natural convection. The maximum velocity is approximately 0.05 m/s in the slag region. This agrees with the values obtained by Sheng et al.[16] for natural convection owing to Joule heating. As a result of the shear stress boundary condition applied at the slag-matte interface, the momentum of the slag phase is partially transferred to the matte phase, which causes the matte near the slag-matte interface to flow towards the electrode. However, deep inside the matte bath, the velocity of the matte was negligible.

In Figure 7(b), the flow field goes up and around the electrode and then circulates along the molten slag-feed interface, creating opposite recirculation patterns in the slag region. The flow distribution was practically symmetric about the XY midplane. Again, in the matte region, the flow field tangential to the YZ plane was negligible. In Figure 7(c), the flow field exhibits a radial pattern in the first section of the XZ plane owing to the cylindrical shape of the electrode. The flow then became approximately perpendicular to the cooled wall.

Heat Fluxes

After reaching a steady-state, the heat fluxes leaving the system through water cooling, refractory lining, and freeze lining should be consistent with each other. Figure 8 schematically illustrates the heat fluxes through each section and plots the corresponding simulation results for the temperature (black line) and solid fraction (black dots).

Fig. 8
figure 8

One-dimensional steady-state heat flux analysis between cooling, refractory and freeze lining. Chart illustrates the simulation results for temperature (black line) and solid fraction (black dots) along the three sections

Full size image

The heat flux Q01 through the cooling system can be calculated directly from a convection heat transfer equation, with the HTC used in the simulations (i.e., 3000 W/m2·K). The temperature of the water introduced into the cooling system was T0 = 307 K (see Figure 3), whereas the temperature of the cooled refractory surface was obtained from the simulation results (T1 = 317 K). The heat fluxes through the refractory and freeze linings (Q12 and Q23) were estimated by conduction heat transfer according to the ratio k/L. In the refractory, kref = 7.7 W/(m·K) and Lref = 0.15 m. In the freeze lining, the thermal conductivity varies during slag solidification between 6.5 W/(m·K) and 8.0 W/(m·K), and so it is approximated with k = 7.6 W/(m·K). The thickness of the freeze lining is estimated from the simulation results, i.e. L = 0.12 m (as demonstrated later). The temperatures required to calculate the heat fluxes were obtained from the simulation results and are shown in Figure 8. In all cases, Q01 ≈ Q12 ≈ Q23 ≈ 30 kW/m2, confirming the integrity of the steady-state heat flux balance. Note that the final global energy balance was reached with a heat input of 1.75 MW from the electrode and matte production, and a heat output of 1.75 MW from the cooling system, the natural cooling at the walls, and the presence of the feed.

Discussion

Analysis of the Energy Balance During Freeze Lining Formation

The computational results illustrated in Figure 6 confirm the presence of freeze lining on the furnace walls adjacent to the cooling system. The formation of a freeze lining is the result of a thermal balance between the total heat input and total heat removal in the ESF system.

The heat input into the system occurs predominantly via the electrical energy from the electrodes to the slag bath (\(S_{{{\text{H}}_{1} }}\) to \(S_{{{\text{H}}_{4} }}\)), which induces the characteristic anticlockwise molten slag flow, as shown in Figure 7(a).[16] However, there is a second major heat source, \(S_{{{\text{H}}_{6} }}\), which plays a decisive role in the final results by ensuring that the slag does not solidify along the slag-matte interface. As shown in Figure 6, the vertical solidification front ahead of the freeze lining reaches the bottom of the slag region. This freeze lining layer extends along the slag-matter interface but quickly fades away because of \(S_{{{\text{H}}_{6} }}\). Guevara[19] did not consider this quantity in their simulations. However, their temperature contours exhibited values under Tliq along the slag-matte interface, which suggests that slag solidification would likely occur in their model. Freeze-lining formation was not discussed by the authors.

As for heat removal, the energy sink associated with the presence of the feed, \(S_{{{\text{H}}_{5} }}\), has a critical effect on the development of the freeze lining. This is demonstrated in Figures 9(a) through (c), where a black volume rendering of the freeze lining layers is shown for the three simulation cases (the white layer represents the solidification front). They have been obtained by varying \(S_{{{\text{H}}_{5} }}\) by ± 10 pct while keeping the remaining parameters unchanged. The colored contours represent the temperature distribution, which varied from 300 K (dark blue) to 1500 K (dark red).

Fig. 9
figure 9

Freeze linings for: (a) \(S_{{{\text{H}}_{5} }} - \,10\,{\text{pct}}\), (b) \(S_{{{\text{H}}_{5} }}\), and (c) \(S_{{{\text{H}}_{5} }} + \,10\,{\text{pct}}\). The contours represent the temperature distribution, which varies from 300 K (dark blue) to 1500 K (dark red) (Color figure online)

Full size image

The change in \(S_{{{\text{H}}_{5} }}\) leads to dynamic adaptation of the system until a new thermal balance is restored. In each case, a new steady-state freeze-lining thickness materializes. In Figure 9(b), the freeze lining thickness reaches an average value of approximately 12 cm, whereas in Figures 9(a) and (c), the average values are 2 and 16 cm, respectively. The reduction of \(S_{{{\text{H}}_{5} }}\) by 10 pct [Figure 9 (a)] leads to a very dangerous condition for the operation of the furnace because the freeze lining layer is too thin, and there are regions where there is no protection at all. However, this scenario is unacceptable for industrial processes. Conversely, increasing \(S_{{{\text{H}}_{5} }}\) by 10 pct [Figure 9(c)], the increase in the freeze lining thickness provides extra protection for the refractory. However, a layer that is too thick is not ideal in terms of the optimal use of resources in the process.[22] These results highlight the importance of accurately determining the total heat loss during furnace operation to correctly capture the freeze-lining mechanism.

Note that the variation in \(S_{{{\text{H}}_{5} }}\) also leads to changes in feed quantity. A larger absolute \(S_{{{\text{H}}_{5} }}\) (i.e., more heat dissipation) was associated with a larger feed quantity at the top of the slag. It was found that the relationship between \(S_{{{\text{H}}_{5} }}\) and feed quantity was not linear. From \(S_{{{\text{H}}_{5} }}\) to \(S_{{{\text{H}}_{5} }} + 10\,{\text{pct}}\), the feed quantity increases by approximately 5 pct, whereas from \(S_{{{\text{H}}_{5} }}\) to \(S_{{{\text{H}}_{5} }} - 10\,{\text{pct}}\), the feed quantity reduces by about 70 pct.

Indication of the freeze Lining Thickness from the Refractory Temperature

Determining the freeze lining thickness is challenging because it cannot be measured directly inside industrial furnaces and depends on various variables that change during the furnace operation. Therefore, it is important for furnace operators to determine whether a safe freeze-lining layer has been formed on the furnace walls based on easily quantifiable variables, such as the refractory temperature. Under real operation conditions, thermocouples can be installed in the refractory to measure the temperature at arbitrary locations.

A parameter study was performed to analyze the change in the freeze-lining thickness and average refractory temperature from the systematic variation of \(S_{{{\text{H}}_{5} }}\). The results are plotted in Figure 10, which displays the relationship between the average freeze-lining thickness and the average temperature along a vertical line located at the center of the refractory wall (in the section adjacent to the cooling system).

Fig. 10
figure 10

Relation between the average temperature in the refractory and the freeze lining thickness

Full size image

From Figure 10, when \(S_{{{\text{H}}_{5} }}\) varies between \(S_{{{\text{H}}_{5} }} \pm 5\,{\text{pct}}\), the average freeze lining thickness keeps a similar value of about 0.12 m and the average refractory temperature is 630 K. This appears to be the optimal operating window, as it provides a safe freeze-lining layer while maintaining a relatively high slag bath temperature (for higher productivity). However, for \(S_{{{\text{H}}_{5} }} + 10\,{\text{pct}}\) or higher, the average refractory temperature is 600 K (with an average freeze lining thickness of 0.16 m), whereas for \(S_{{{\text{H}}_{5} }} - 10\,{\text{pct}}\) or lower, the average temperature in the refractory increases drastically to 810 K (with an average freeze lining thickness of 0.02 m).

All cases have similar slag temperatures near the electrode because they primarily depend on the given energy input (which is the same in all cases in this parameter study). However, the spatial temperature decrease rate from the electrode to the cooled surfaces depends on the magnitude of heat removal (e.g., from \(S_{{{\text{H}}_{5} }}\)). In the cases where the freeze lining is thick enough to guarantee a safe operation, the slag temperature is sufficiently reduced to form a solidification front before reaching the refractory wall (see the top inset in Figure 5), and thus the temperature in the refractory is relatively low. Conversely, in the cases where the freeze lining thickness is not sufficient for safe operation, the temperature isoline in front of the refractory is too high, and only a thin layer is achieved owing to the presence of the cooling system.

From the above-mentioned results, there appears to be a temperature threshold close to Tcrit = 800 K, above which the freeze lining produces a dangerously thin layer. This can be a crucial alert during the furnace operation that the freeze lining protection has disappeared and the process intensity (i.e., production rate and power input) requires to be reduced based on refractory temperature readings. This parameter study can be extended to other variables and different process intensities to obtain a more comprehensive understanding of the furnace operation.

Effect of Bath Chemistry and Slag Solidification Paths

Modern solidification theory has successfully explained the growth and microstructure of metallic alloys during cooling.[23,24] However, slag solidification represents a different class of material transformations (with particular thermodynamic properties, and solidification dynamics and kinetics) that is under-researched.

The aforementioned results were obtained with an assumed solidification path, that is, the lever rule Eq. [5]. In this section, the solidification path is replaced with the Scheil equation and with a linear relation to assess their effect on the freeze lining formation. The equations used are as follows:

$$ f_{{\text{s}}} = 1 - \frac{{\left( {T - T_{{{\text{sol}}}} } \right)}}{{\left( {T_{{{\text{liq}}}} - T_{{{\text{sol}}}} } \right)}}\,\,\,\,{\text{(Linear}}\,{\text{relation)}}. $$
(9)
$$ f_{{\text{s}}} = 1 - \left( {\frac{{\left( {T - T_{{\text{f}}} } \right)}}{{\left( {T_{{{\text{liq}}}} - T_{{\text{f}}} } \right)}}\,} \right)^{{\frac{1}{k - 1}}} \,\,\,{\text{(Scheil equation)}}. $$
(10)

To the best of our knowledge, insufficient information is available in the literature pertaining to the thermodynamic properties of the slag used in the studied ESF. Table III presents the thermodynamic properties of two potential slags with different characteristics. The key difference between the properties of the proposed slags was the liquidus-solidus range of the mushy zone. In slag 1, the values of Tliq and Tsol were those proposed by Guevara,[19] and the nominal composition was based on the slag used by Guevara and Irons.[6] The remaining properties were estimated based on the best knowledge of the authors to obtain a consistent binary FeO-SiO2 phase diagram. In this case, the temperature interval that defines the mushy zone is relatively small, which reduces the chance of visualizing any discrepancy between the three solidification paths. In slag 2, Tsol was set to 1175 K. The main goal was to increase the temperature interval between Tliq and Tsol to obtain a better understanding of the influence of the three solidification paths on freeze lining formation. Slag 1 was used in all previous simulations.

Table III Thermodynamic Properties of Two Potential Slags
Full size table

Figures 11(a1) and (a2) show the relationship between the solid fraction and temperature for the linear (Eq. [9]), lever rule (Eq. [5]), and Scheil (Eq. [10]) equations. The lines represent the theoretical temperature results as a function of the solid fraction for the three considered solidification paths. The symbols represent the simulation results along a line that crosses the entire spectrum of the solid fractions (i.e., from 0 to 1). Figures 11(b1) and (b2) show the simulation results of the solid fraction contours in a section of the freeze-lining layer for the same three solidification paths considered. The top row in Figure 11 represents slag 1 (with k = 0.8), whereas the bottom row represents slag 2 (with k = 0.3).

Fig. 11
figure 11

(a) Solid fraction as function of temperature for Linear, lever and Scheil solidification paths. (b) Slag solid fraction contour (dark blue represents fs = 0.2 and dark red represents fs = 1.0). Top row uses the properties of slag 1, whereas the bottom row uses the properties of slag 2 (Table III) (Color figure online)

Full size image

The consistency between the theoretical (i.e., lines) and simulation results (i.e., symbols) in Figures 11(a1) and (a2) is very good, which validates the implementation of the solidification paths in the numerical model. In slag 1, the linear and lever rule have very similar trends, which is confirmed by Figure 11(b1), where any difference in the freeze lining layer is almot indistinguishable. For the Scheil equation, the solid fraction is typically lower for the same temperature than in the other two cases. This can be observed in the contours of Figure 11(b1), where the mushy zone appears to be slightly larger, particularly at the bottom right corner of the region. In slag 2, the difference between the three solidification paths was more obvious. For the linear relation, owing to the generally smaller solid fractions obtained for the range of temperatures considered, the freeze-lining thickness was reduced significantly. The lever rule and Scheil equation both have a larger freeze lining thickness than the Linear relation, although the Scheil equation exhibits a larger mushy zone. This demonstrates that the accurate consideration of the phase diagram and solidification path has a critical impact on freeze-lining modeling in the ESF process. Nevertheless, experimental results of the freeze lining thickness are still required to validate the above results and determine the appropriate solidification path for slags. Note that, similarly to Figure 6, the blue color on the left of the freeze lining in Figures 11(a2) and (b2) is due to the node interpolation method during post-processing; however, the freeze lining extends completely to the vertical wall.

General Model Considerations

The current model provided a conceptual framework for simulating the ESF process. The accuracy of the results depends on the integrity of the model assumptions. Some of the assumptions are discussed in this section.

Freeze Lining Solidification Front

In the current model, the freeze-lining solidification front begins at T = Tliq. However, according to Fallah–Mehrjardi et al.,[10] the temperature of the slag-freeze lining interface (Tcr) should be lower than Tliq of the slag bath. Similarly, Nagraj et al.[12] determined that freeze-lining started just below the critical viscosity-temperature. The main impact of such a change in the model would be that the freeze-lining layer would be thinner than in the current simulation results. However, the accurate value of Tcr for the current slag is still not well-defined in the literature; therefore, the original T = Tliq was used in the present work. If Tcr was known, this would be an easy change in the model by replacing the initial temperature at which the solidification model starts.

Freeze Lining Microstructure

In the present model framework, the freeze-lining microstructure is approximated as a mushy zone that has a solid matrix with a columnar dendritic morphology. This implies that as the slag solidifies and fs gradually approaches unity through the mushy zone, the solid matrix becomes stationary. In reality, the freeze-lining microstructure has been found to consist of different layers, such as a crystalline layer and additional layers with different-sized interlocked crystals that contain liquid in between.[1] Fallah–Mehrjardi et al.[10] proposed an additional sub-liquidus layer between the above layers and molten slag. It consists of detached crystals that can grow or dissolve owing to convective flow. According to Nagraj et al.,[12] the slag viscosity in this sub-liquidus layer abruptly increases.

Modeling this complex microstructure is beyond the scope of the present work. The consideration of a stationary solid matrix with regions where crystals can move requires the use of a multiphase model, which significantly increases its complexity. This is a common practice in metal alloy solidification models.[25,26,27] However, considering the early stage of model development in the topic of slag solidification, further studies are required to make this improvement possible.

Feed Treatment

Typically, the feed is schematically represented as a solid structure that grows on top of the slag region (see Figure 2). However, in Figures 6 and 9), the results show a solid structure that begins at the top of the computational domain (slag region) and extends downwards into the slag bath. The main reason for this difference is that the domain is assumed to have a fixed geometry, the slag region does not change with furnace operation, and \(S_{{{\text{H}}_{5} }}\) is strictly applied to the top, horizontal surface of the domain (i.e., top of the slag region). In the present model, the sink term \(S_{{{\text{H}}_{5} }}\) is the main reason for formation of the solidified structure representing the feed.

To obtain results comparable to those shown in Figure 2, the geometry could be adapted to include an additional volume above the slag region that would contain only the corresponding feed quantity. However, this solution is not ideal because the additional volume added to the domain would have to be attributed iteratively to perfectly encapsulate the feed quantity and obtain a relatively horizontal slag-feed interface. Alternatively, non-uniform \(S_{{{\text{H}}_{5} }}\) can be imposed on the top of the domain. This possibility was tested and the simulation results indicated significant changes in the final feed structure. In both scenarios, the freeze-lining formation was affected.

In reality, the shape of the feed is far from the simple geometry shown in the diagrams in Figure 2. This implies that any consideration of the feed effect is more complex than that typically considered in numerical models. A more comprehensive description of the feed during furnace operation is essential to determine the most plausible feed structure under steady-state conditions and to assess the impact of these assumptions on the ESF outcome.

Input Power Influence

Increasing the process intensity through an increase in the input power leads to an increase in the slag bath temperature. Consequently, the other energy source terms must be adjusted to achieve an appropriate global thermal balance in the system that produces a freeze-lining layer on the cooled wall. In the simulations, besides increasing \(S_{{{\text{H}}_{1} }}\)–\(S_{{{\text{H}}_{4} }}\) to fit the new input power and increasing \(S_{{{\text{H}}_{6} }}\) to fit the new matte production rate, a new value for \(S_{{{\text{H}}_{5} }}\) must be determined. Guevara[19] proposed values for different process intensities. However, from our current study, these values did not produce acceptable results. More accurate predictions of such heat source terms (as in Reference 28) are necessary for a range of operating conditions.

Conclusions

The current work proposes a new framework for simulating an ESF for nickel smelting. It considers the fluid flow and heat flux in the furnace, as well as the formation of a freeze lining using a slag solidification model. Several energy source terms have been considered to capture the effect of the input power from the electrodes, matte production mechanism, and heat dissipated during furnace operation owing to the presence of the feed. This work extends the original model developed by Guevara,[19] by proposing an extra energy source from the matte production mechanism (which guarantees that no solid layer separates the matte from the slag region) and by providing a detailed description of all the boundary conditions and heat transfer terms necessary for a global energy balance. It also provides a comprehensive analysis on the freeze lining formation, which was still lacking in the literature.

It was found that the formation of a freeze-lining layer depends critically on these heat source terms. In particular, the variation in the energy sink term that represents the presence of the feed was clearly associated with different freeze-lining thicknesses. The heat removal capacity from the energy sink associated with the presence of the feed directly affects the thickness of the freeze lining. An accurate estimation of the thermal effect of the presence of the feed is critical and must be considered in the global energy balance calculations of the furnace.

Two hypothetical simple binary systems (and their corresponding thermodynamic properties) for the slag have also been studied to illustrate the effect of slag bath chemistry and solidification path on freeze lining formation. Although it is generally accepted in the metallurgical community that a linear solidification model is not accurate, it could be an acceptable simplification if the slag properties would combine a relatively large partition coefficient (i.e., close to 1.0) and a relatively small temperature interval between Tliq and Tsol. However, for relatively large mushy zones, solidification paths consisting of the linear, lever rule, or Scheil equation exhibited very different outcomes. The results demonstrated the significant influence of bath chemistry and solidification path on freeze-lining formation. Further studies are necessary to determine the thermodynamic properties of slag and identify an accurate solidification path, as well as to provide suitable data for the validation of the simulation results.

A parameter study was conducted to assess the sensitivity of the temperature in the refractory wall to different freeze-lining thicknesses. A clear relationship was established between the two parameters. In the current work, the temperature was measured at the center of the furnace wall adjacent to the cooling system (other locations would lead to different results). A critical temperature threshold of 800 K was identified, above which the freeze lining was dangerously thin. Below 610 K, the freeze lining became too thick, which affected furnace productivity. The optimal freeze linings (with an average thickness of approximately 0.12 m) were obtained at an average refractory temperature of 630 K. This feature of the model (after certain model refinement and calibration) can be the basis for special tools such as a physics-informed digital twin[29] to provide the real time control of the optimal slag freeze lining thickness during operation.