Abstract
The heat transfer processes and the molten metal bath kinetics of the electric arc furnace are governed by the changes in the arc length and voltage. Thus, information on the electric arc behavior with respect to the voltage is important for accurate computation of the furnace processes and adjustment of the industrial furnace parameters. In this work, the length-voltage characteristics of electric arcs have been studied in a pilot-scale AC electric arc furnace with image analysis, electrical data from the furnace, and slag composition. The arc length was determined with image analysis and the relation between the arc length and voltage from test data. The relation between arc length and voltage was found to be non-linear and dependent on the slag composition. The voltage gradients of the arcs were evaluated as a function of arc length and sum of anode and cathode voltage drops resulting in a reciprocal relation. Furthermore, the electrical conductivity of the arc plasma with respect to arc length was estimated.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
The relation between electrical data and length of the arc has a vital role in electric arc furnace (EAF) heat transfer processes. It can be assumed, with the support of computational models, that convection and radiation dominate for short and long arcs, respectively.[1] Computational studies have shown that, for an AC EAF, operating with long arc lengths decreases the mixing time of the bath.[2] In order to increase heating efficiency and reduce the forming of hot spots on EAF walls in the case of long arcs, foaming of slag is usually required.[3] The foaming slag partially or totally covers the arc and significantly reduces the radiative heat transfer to the furnace walls and roof. A model to study the melting rate of direct reduced iron strongly suggests operating with long arcs, since the thermal homogenization of the molten bath increases with increasing arc length.[4] However, the usage of either maximum or minimum power factor results in arc instability and risk of carbonization of scrap and slag.[5]
The importance of arc length control is evident for industrial furnaces. Decreasing the arc length after the scrap has melted will protect the furnace roof and walls from radiation, and increasing the arc length will raise the mean temperature of the metal bath, e.g., for charging of the direct reduced iron.[6] Since the length of an electric arc in an industrial EAF is difficult to measure experimentally, the arc length is controlled through its dependence on the voltage. A linear dependence between arc length and voltage has been discussed in detail by Montanari et al.[7] The computational modeling of electric arcs frequently utilize a linear dependence between arc length and voltage.[7,8,9,10,11] However, the model described by Bowman et al.[12,13] derives a non-linear relation between voltage and arc length. A description of the Bowman model and its implementation has been provided by Reynolds and Jones.[14] Peng et al.[15] studied a pilot-scale DC arc furnace experimentally and with the Bowman model, reporting a non-linear length-voltage relation for the arcs. They also found out that increasing the current leads to an increase in the voltage.
In this work, the characteristics of the electric arcs with voltage, voltage gradient, and anode-cathode voltage drop have been studied with image analysis in a pilot-scale AC EAF. The slag composition was observed to have a notable effect on these characteristics. The results have been compared to other electric arc studies discussing arc length and voltage, voltage gradient, and voltage drops in the anode and cathode regions. Furthermore, the conductivities of the electric arcs have been estimated by means of image analysis as a function of the arc length.
Methods and Materials
The measurements were carried out at RWTH Aachen University, Germany. The equipment consisted of a pilot-scale AC EAF, a single-lens reflex (SLR) camera, and a data storage computer. The furnace was operated in AC mode with two graphite electrodes. The maximum melting weight of the furnace is 200 kg. The diameter of the electrodes is 0.10 m and the distance between the electrodes 0.30 m. The electrical parameters of the furnace were recorded once per second. The camera was a Baumer SLR camera, which looked into the furnace through three standard green light band-pass filters used for welding and a 0.01 m UV-transparent glass. The frame rate of the camera was 20 pictures/s with an exposure time of 0.05 seconds. The length of the arc was obtained from the electric arc images using a Matlab code. The length was defined to be the distance between the bright glow of the arc on the electrode and the center of the hit spot of the arc on the slag surface. For a more detailed description of the arc length analysis and the measurement set-up, see Reference 16. The slag composition was analyzed with X-ray fluorescence from slag samples after the measurements.
The measurements were performed on three days, which are referred to as heat 1 (H1), heat 2 (H2), and heat 3 (H3). Several measurement periods (Ps) were performed on each heat. The current was changed between the measurement periods, but kept constant during these periods. Due to the reports that the current affects both the voltage[15] and the voltage gradient,[17] the measurement periods have been analyzed separately.
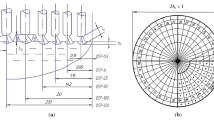
The length of the arc was manually altered during the measurements by changing the electrode position. Plunge tests, during which the electrode was pushed into the slag and then lifted up, were performed several times on each heat. The data from these plunge tests have been used in this work to study the relation between the arc length and voltage, voltage gradient, and the estimated conductivity of the arc. Example arc images from a plunge test are displayed in Figure 1. The arcs that were observed in this study were laminar plasma flows. The electrical input of the furnace is not enough to produce turbulent plasma, which is usually observed in industrial EAFs. The results of this study could, however, be used to estimate the distance between the electrode tip and the slag surface in the case of turbulent plasma flows where the arc path is not a straight line from the electrode to the melt. This estimation could be viable also in the case of foamy slag practice where the foam may cover the arc and affect the arc dynamics.
For thorough investigation of the voltage effects to the electric arc, the sum of anode and cathode voltage drop VAC has been evaluated from the electrical data of the furnace. In arc welding studies, the voltage drop across anode and cathode regions has been found out to be independent of the current.[18,19] The same behavior for anode voltage drop in welding arcs has also been observed for different electrode materials.[20] For this reason, the effect of current to VAC has been approximated to be negligible.
Results and Discussion
The Effect of Slag Composition to Voltage and Resistance
On a single plunge test, the electrode was plunged so deep into the slag that the electrode hit the steel. This contact with the steel produced a voltage of 14.34 V, which is presumed to be very close to the anode-cathode voltage drop VAC. The minimum voltages when the electrode is in contact with the slag, \( U_{\text{min}} \), were observed to be between 55 and 100 V. With the VAC = 14.34 V, the resistance of the slag can be evaluated from
in which I is the current.
The major slag components, \( U_{\text{min}} \), I, and \( R_{\text{slag}} \) have been presented in Table I for each measurement period. From these values, correlations between the slag composition and the \( U_{\text{min}} \) together with the \(R_{\text{slag}}\) can be determined. These correlations have been presented in Figure 2 with linear fits
where a and b are constants. The variables appearing in Eq. [2] have been displayed in Table II. The \( {\text{Slag}}_{\text{sum}} \) in the correlation of Figure 2(a) and Table II is a sum over Al2O3 + CaO + MgO + SiO2 − (FeO + Cr2O3 + MnO); in pct. The \( {\text{Slag}}_{\text{sum}} \) was obtained by summing those slag species that increased with increasing \( U_{\text{min}} \) and subtracting those that decreased with increasing \( U_{\text{min}} \). In this way, all the major slag components were taken into account. The voltage drop, when the electrode is in contact with the steel, can be estimated from Eq. [2] with the variables in Table II for (a) by setting FeO to 100 pct in the \( {\text{Slag}}_{\text{sum}} \). This produces \( U_{\text{min}} \) = 13.98 V, which is very close to the experimental value 14.34 V.
FeO has a key role in the overall correlation with \( U_{\text{min}} \) and \(R_{\text{slag}}\), as can be observed from Figure 2(b). FeO contributes a lot to the electrical conductivity of the slag,[21,22] which supports the result that FeO content of the slag has an effect on the observed voltages. Furthermore, it has been shown by Aula et al.[23] that the optical emissions from the arc in an industrial EAF are dominated by the atomic emissions from the slag components. This suggests that there is a strong interaction between the arc and the slag which also affects the length-voltage characteristics in the industrial practice.
As can be seen from Figure 2(c), there is a distinctive correlation between the \(R_{\text{slag}}\) and the MgO content of the slag. In many studies, the increase of MgO content tends to increase the slag conductivity in varying slag compositions.[24,25,26,27,28] The electrical conductivity of the slag has been reported to increase with decreasing viscosity,[29] to which also MgO contributes.[26,27] Kim et al.[27] argued that the decreasing effect of MgO on the slag viscosity is dampened at high CaO/\(\hbox {SiO}_2\) ratios. Sohn et al.[26] reported that the MgO additions up to 20 pct decrease the viscosity. However, they also pointed out that the MgO has a limited effect if significant amount of strong basic oxides, such as CaO, are present in the slag. Jiang et al.[30] showed that the melting temperature decreases with the increasing MgO content when binary basicity is lower than 1.2 for slags containing also vanadium and titanium. They found out that, with higher basicity, the increase in the MgO content increases the melting temperature.
In our work, the positive correlation between the \(R_{\text{slag}}\) and the MgO could be attributed to the increase of melting temperature due to relatively high MgO content ranging from 9 to 25 pct and binary basicity CaO/\(\hbox {SiO}_2\) higher than 1.1. Since the FeO content of the slag ranges from 7 to 40 pct, it could be that FeO dominates the conductive properties of the slag at this high concentrations. In addition to FeO, also MnO has a positive contribution to the electrical conductivity.[21] The MnO content varies within the range from 1 to 5 pct, which is more subtle than the changes in FeO. Figure 2(d), where the conductive component MnO-pct has been subtracted from the MgO-pct, shows an improved linear correlation with the \(R_{\text{slag}}\) when compared to Figure 2(c).
The Length-Voltage Characteristics of the Arc
Comparison between the lengths derived from the image analysis and Eq. [3] for H3 P2
The image analysis was performed for 8 measurement periods in order to determine the relation between the arc length and voltage. 7 periods were left out of the analysis due to malfunctions in the camera recordings. Arcs shorter than 0.02 m were not analyzable due to the merging glow from the slag and the electrode, which complicates the image analysis. The most reliable arc lengths were determined to be longer than 0.05 m. The arc length and voltage have been plotted in Figure 3 for each measurement period separately. The equation describing the correlation between arc length and voltage is
where a and b are constants. The relation presented in Eq. [3] resemble the non-linear model described by Bowman et al.[12,13]
One measurement period from H3 is presented in Figure 4, in which the voltage, the image analysis arc length, and the arc length derived from Eq. [3] have been displayed. Between 30 and 100 s, the arc is partially behind the electrode and hence the image analysis is not viable, whereas the arc lengths derived with Eq. [3] between 30 and 100 second are close to the actual arc length. On average, the image analysis provides longer arc length than the computed length between 150 and 230 second. This is caused by the arc movement on the slag, which can occur due to changes on the local slag surface composition or the repelling forces between the two arcs. The two electrodes facing each other allow each arc to wander approximately across half of the slag surface area. This can be seen for example in Figures 1(a) and (f) where the arc is closer to the center of the furnace in (a) and further away in (f). The arcs in a three electrode furnace would be more confined due to the repelling forces of the other two arcs.
The computed length has been plotted with respect to the image analysis length in Figure 5. Each image analysis length datapoint is an average over 1 second with standard deviation less than 8 pct. The highest variance between the image analysis length and the computed length was observed in H1, followed by H2 and H3. The higher variance in the H1 and H2 arc lengths can be explained by the higher FeO content of the slag, which depicts the amount of iron in the plasma that contributes a lot to the brightness. A brighter glow of the arc on slag, on the other hand, makes the length analysis more difficult.
It is clear from Figure 5 that the whole measurement data are not suitable for evaluation of the relations between the electrical properties of the arc and the arc length. The image analysis is prone to error due to the glow from the slag, the repelling force between the arcs, and the chance that the arc is only partially visible. Also the slag composition has its effect both on the length analysis and the electrical properties of the arc. Thus, only the periods with the most stable arcs should be used in the evaluation of the voltage gradient. The plunge tests were observed to have the most stable conditions during the measurements, which is supported by the good correlations displayed in Figure 3. Furthermore, the voltage changes the most during the plunge tests with the widest range of voltage values. For this reason, the plunge test values for the arc length and voltage have been used in the voltage gradient analysis.
The equation that is commonly used in the computation of arc length is
where \( l_{\text{arc}} \) is the arc length in m, U is the voltage in V, \( V_{\text{AC}} \) is the sum of anode and cathode voltage drops in V, and Vg is the voltage gradient in V/m. A linear relation between arc length and voltage is usually implemented by fixing the values of \( V_{\text{AC}} \) and Vg as constants. However, a non-linear time-varying model with Vg and \( V_{\text{AC}} \) limits of 500 to 3000 V/m and 10 to 80 V, respectively, has been studied with Eq. [4] showing a good correlation between the model and data from steel plants.[31,32]
The \( V_{\text{AC}} \) in Eq. [4] has been evaluated using a variety of methods in various studies. Haidar[33] studied the anode voltage drop as a function of plasma temperature theoretically in gas tungsten and gas metal arc welding, yielding values of around 4 V. They approximated the voltage drop across the cathode sheath as around 1 V, but neglected it in the model. In modeling fluid flow and heat transfer of a DC EAF, Qian et al.[34] took the anode drop as 4 V and evaluated the cathode region using numerical analysis. Another DC EAF model by Alexis et al.[35] evaluated the cathode voltage drop as a function of electron temperature and the anode voltage drop was assumed to be 4 V according to the work of McKelliget and Szekely[36] on welding arcs. In EAF modeling, several studies have used a constant value of 40 V as the \( V_{\text{AC}} \),[7,8,10] whereas others have studied voltage drop ranges varying from 30 to 80 V.[5,31,32]
Ramírez et al.[37,38] demonstrated, via a mathematical model of a DC electric arc, that the anode drop, current density, and contribution of the heat flux from the arc to the metal bath drop significantly within 0.10 m from the arc center on the melt surface. Ramírez-Argáez et al.[39] studied the effect of different atmospheres with different electrical conductivities to determine the arc properties in a mathematical model, stating that the electrical conductivity determines the voltage drop with constant arc length. The arc power is proportional to the product of the voltage drop and current in the arc,[35] and thus the voltage drop has a key role in the heat transfer and efficiency of the arc. Kiyoumarsi et al.,[40] on the other hand, neglected the anode and cathode voltage drops along with the movement of the arcs in an electromagnetic analysis of a practical three-phase AC EAF.
In studies of electric arc cathode and anode voltage drops, the cathode region in particular has proven difficult to evaluate. Bakken et al.[41] proposed that the cathode problem could be counteracted by including the near-cathode layer and solid cathode tip in the computation or by approximating the cathode layer as a gaseous sub-domain. However, the computation of the whole electric arc system is challenging and time consuming. The usual way to proceed with the computations is to neglect some aspects of the arc or to approximate them with constant values.
The non-linear relation between the voltage and the arc length presented in Figure 3 suggests that the voltage gradient across the arc is not a constant value, but is dependent on the electrical properties of the arc. Thus, the voltage gradient has been derived from Eq. [4] with U from the furnace electrical data and \( l_{\text{arc}} \) from the image analysis together with \( V_{\text{AC}} \) = 14.34 V. The equation describing the correlation between arc length and voltage gradient is
where c and d are constants. These correlations have been plotted in Figure 6.
The constants a, b, c, and d that appear in Eqs. [3] and [5] have been tabulated in Table III for each measurement period with corresponding R2. The relations between a and b together with c and d have been plotted in Figure 7. The constants a and b are connected linearly, whereas the c and d have a reciprocal relation with each other. Both of these correlations take into account the voltage characteristics of the arc as Figure 7(a) is connected the \( U_{\text{min}} \) and (b) to the \( U_{\text{min}} \) − 14.34 V. The constants a, b, c, and d do not correlate with any slag component. The effect of the slag composition to the electrical properties of the arc has been discussed in many occasions, but in order to evaluate the effect of the slag composition to these equations, more tests with emphasis on the slag composition would be required.
Electrical Conductivity
The conductivity of the arc can be determined by the equation
where R is the resistance of the arc in \(\Omega \) and A is the cross-sectional area in \(\hbox {m}^2\). R is obtained from the electrical data of the furnace, whereas the area of the arc can be evaluated from the arc images. The glow from the slag makes it hard to estimate the correct pixel brightness threshold for the arc radius, since the glow from the slag merges with the arc channel. Thus, the values related to conductivity that are presented here should be considered to be proportional to the conductivity of the arc, but not the exact values.
An example arc image for which the conductivity and the area of the arc along the arc axis have been evaluated is presented in Figure 8. The radius of the arc, \( r_{\text{arc}} \) at a given position along the arc axis has been evaluated with the number of pixels exceeding a brightness value 50 of the standard grayscale brightness range from 0 to 255. The resolution of the image is approximately 0.001 m. In Figure 8, an increase in the area is observed around 0.02 m along the arc axis, which is the glow on the electrode surface. The drop between 0.025 and 0.030 m is the beginning of the plasma column, after which the area gradually increases. The conductivity depends reciprocally on the arc area, and thus an opposite behavior can be observed for the conductivity evaluation. As can be seen from Figure 8, the glow from the slag predominates near the slag surface, and the radius of the arc is hard to estimate without a high chance of error. The glow from the slag already starts to merge with the arc column at 0.08 m along the arc axis, after which the radius of the arc is overestimated.
The arc conductivities have been estimated using the arc images near and during the plunge tests performed on H3 for P3, P5, and P6. Due to the low number of measurement periods, the conductivities could not be linked to changes in the slag composition. Since the electrical parameters of the furnace were recorded only once per second and the arc images were taken at a rate of 20 per second, only one arc image per second has been selected for the conductivity evaluation so that the selected arc images were the least affected by the glow from the slag. An example range of images that were used in the analysis is presented in Figure 4 between 100 and 200 second. H3 was chosen for the conductivity analysis due to the lowest amount of FeO in the slag, which means that the glow on the slag was the dimmest for this heat. The conductivity was estimated with an average over the arc section between 0.03 and 0.05 m along the arc axis in Figure 8, for which the glow from the slag has the least effect on the pixel brightness. The estimated conductivity with respect to the arc length is presented in Figure 9 for the section 0.03 to 0.05 m along the arc axis.
The fit between the estimated conductivity and the length of the arc follows
where \(\sigma _{\text{est}}\) is the estimated conductivity in S/m and \(l_{\text{arc}}\) is in m. The increasing conductivity with respect to increasing arc length is related both to the changing radius and resistance of the arc. Despite the high standard deviation, Eq. [7] and Figure 9 give an estimate of how conductivity is affected by the changing arc length. However, since the conductivity of the arc also depends on the temperature of the plasma, that is not considered at all here, Eq. [7] and Figure 9 give only an average trend of the conductivity characteristics of the arcs. For a more detailed relation, the plasma temperature should also be taken into account.
In modeling, the conductivity of the arc is usually assumed to be highly dependent on the plasma temperature. Paik et al.[42] pointed out via numerical modeling that the temperature distribution is more uniform for longer arcs, which increases both the surface temperature and hence the electrical conductivity. In their study, however, they considered only arc lengths of 0.01 and 0.03 m. In another modeling study, Wright et al.[43] modeled 0.20 m arcs with temperature dependence for electrical conductivity. For a plasma temperature range of 6000 K to 8000 K, the electrical conductivity was around 1000 S/m. Additionally, in the work of Bowman and Krüger,[44] the conductivity of arcs containing copper vapor between 5000 K and 8000 K is in the range of 0 to 2000 S/m. Ramirez et al.[45] modeled 0.25 m DC arcs displaying a contour plot for radial and axial electrical conductivity. The conductivity dropped from the cathode value of 12500 S/m to around 2000 S/m for the edge of the plasma and the plasma near the melt surface. In experimental studies, Peng et al.[15] studied DC arc lengths within the range of 0 to 0.24 m assuming that the electrical conductivity depends only on the plasma temperature resulting in conductivities between 0 and 13391 S/m. The temperature dependence of the electrical conductivity is also noted in gas metal arc welding for example,[46] where the arc lengths are usually up to a couple of centimeters.
Our work suggests that the electrical conductivity of the arc also depends on the arc length. However, it should be taken into account that the plasma temperature, which affects conductivity, is not considered in this study. If the values in Figure 9 were assumed to be the exact conductivity values in S/m, the conductivity range would be close to those presented by Bowman and Krüger.[44] Guo et al.[47] simulated a DC plasma torch for less than 0.01 m arcs and found out that the core radius of the arc decreases with increasing arc length. The dependence of the conductivity of the arc on the length of the arc is reasonable under this argument, since the diameter of the arc determines the cross-sectional area of the arc to which the electrical conductivity is reciprocally related.
Conclusions
The electric arcs have been studied with image analysis accompanied with slag composition and electrical data for a pilot-scale AC EAF. The minimum voltages measured for the arc lengths near zero were observed to be affected by the slag composition. In one measurement, the electrode was pushed so deep into the slag that it hit the steel and the observed voltage was 14.34 V, which is close to the estimated value of 13.98 V which is calculated from the correlation between the minimum voltage and the slag composition.
A more detailed analysis was performed for the plunge tests, in which the electrode was manually pushed into the slag and then lifted up. The plunge tests proved to have the most stable arcs with respect to the position of the arc on the slag surface. Only the data from the plunge tests were sufficient for the evaluation of the electrical properties of the arc, since a large variance between the image analysis and the computed arc lengths was observed if all the data were used. The differences between the observed and computed lengths were mainly influenced by momentary poor visibility of the arc.
The relationship between the length of the arc and the voltage was found to follow non-linear characteristics much like the one presented in the Bowman model.[12,13,14] The voltage gradient represents a reciprocal relation with the arc length by assuming a constant anode-cathode voltage drop. In the EAF computation, the voltage gradient is usually assumed to be constant, but the results of this work suggest a more dynamic way of approximating the voltage gradient. Estimation of the electric arc conductivity implies that the conductivity increases with increasing arc length. Even though the arc radius is hard to determine from the images due to the glow from the slag, the evaluated conductivity range is close to the conductivities of the electric arcs presented in the work of Bowman[44] for plasma that contains metal vapors. However, it should be noted that the plasma temperature was not considered when determining the conductivities.
References
A. Fathi, Y. Saboohi, I. Skrjanc, and V. Logar, ISIJ Int., 2015, 55, 7, 1353-60
O. J. P. Gonzalez, M. A. Ramirez-Argaez, and A. N. Conejo, ISIJ Int., 2010, 50, 1, 1-8
J. L. G. Sanchez, A. N. Conejo, and M. A. Ramirez-Argaez, ISIJ Int., 2012, 52, 5, 804-13
M. A. Ramirez-Argaez, A. N. Conejo, and M. S. López-Cornejo, ISIJ Int., 2015, 55, 1, 117-125
V. Logar, D. Dovzan, and I. Skrjanc, ISIJ Int., 2011, 51, 3, 382-91
H.-J. Odenthal, A. Kemminger, F. Krause, L. Sankowski, N. Uebber, and N. Vogl, Steel Res. Int., 2018, 89, 1, 1700098
G. C. Montanari, M. Loggini, A. Cavallini, L. Pitti, and D. Zaninelli, IEEE Trans. Power Deliv., 1994, 9, 4, 2026-2036
R. Garcia-Segura, J. V. Castillo, F. Martell-Chavez, O. Longoria-Gandara, and J. O. Aguilar, Energies, 2017, 10, 9, 1424
R. Horton, T. A. Haskew, and R. F. Burch, IEEE Trans. Power Deliv., 2009, 24, 3, 1450-1457
F. Martell-Chávez, M. Ramírez-Argáez, A. Llamas-Terres, and O. Micheloud-Vernackt, ISIJ Int., 2013, 53, 5, 743-750
H. Samet, T. Ghanbari, and J. Ghaisari, IEEE Trans. Power Deliv., 2015, 30, 2, 764-772
G. R. Jordan, B. Bowman, and D. Wakelam, J. Phys. D: Appl. Phys., 1970, 3, 1089–99
B. Bowman, Electrowarme International, 30 (1972), B2, B87–B93
Q. G. Reynolds and R. T. Jones, J. S. Afr. Inst. Min. Metall., 2004, 104, 6, 345-51
Z. Peng, N. Guo-Hua, M. Yue-Dong, and N. Masaaki, Chin. Phys. B, 2013, 22, 6, 064701
H. Pauna, T. Willms, M. Aula, T. Echterhof, M. Huttula, and T. Fabritius, Plasma Research Express, 2019, 1, 3, 035007
Q. Sun, H. Liu, F. Wang, S. Chen, and Y. Zhai, Phys. Plasmas, 2018, 25, 052117
C. McIntosh and P. F. Mendez, Weld. J., 2017, 96, 4, 121s-32s
C. McIntosh and P. F. Mendez, Weld. J., 2017, 96, 9, 354s-66s
R. Hemmi, Y. Yokomizu, and T. Matsumura, IEEJ Trans. Power Energy, 2004, 124, 1, 143-149
R. Farahat, M. Eissa, G. Megahed, A. Fathy, S. Abdel-Gawad, and M. S. El-Deab, ISIJ Int., 2019, 59, 2, 216-220
C.-Y. Sun, X.-M. Guo, T. Nonferr. Metal. Soc., 2011, 21, 7, 1648-54
M. Aula, A. Leppänen, J. Roininen, E.-P. Heikkinen, K. Vallo, T. Fabritius, and M. Huttula, Metall. Mater. Trans. B., 2014, 45B, 3, 839-49
Y. Wang, L. Wang, and K.-C. Chou, High Temp. Mater. Proc., 2016, 35, 3, 253-259
S. B. Sarkar, ISIJ Int., 1989, 29, 4, 348-51
I. Sohn, and D. J. Min, Steel Res. Int, 2012, 83, 7, 611-30
H. Kim, W. H. Kim, I. Sohn, and D. J. Min, Steel Res. Int., 2010, 81, 4, 261-64
G.-H. Zhang, and K.-C. Chou, Metall. Mater. Trans. B., 2010, 41B, 1, 131-36
W. Li, X. Cao, T. Jiang, H. Yang, and X. Xue, ISIJ Int., 2016, 56, 2, 205-09
T. Jiang, S. Wang, Y. Guo, F. Chen, and F. Zheng, Metals, 2016, 6, 5, 107
S. M. M. Agah, S. H. Hosseinian, H. A. Abyaneh, N. Moaddabi, IEEE Trans. Power Deliv., 2010, 25, 4, 2859-67
F. Illahi, E. El-Amin, and M. U. Mukhtiar, IEEE Trans. Power Deliv., 2018, 33, 4, 1727-34
J. Haidar, J. Appl. Phys., 1998, 84, 7, 3518-3529
F. Qian, B. Faroud, and R. Mutharasan, Metall. Mater. Trans. B, 1995, 26B, 5, 1057-1067
J. Alexis, M. Ramirez, G. Trapaga, and P. Jönsson, ISIJ Int., 2000, 40, 11, 1089-1097
J. W. McKelliget, and J. Szekely, Metall. Trans. A, (1986), 17: 1139–1148
M. Ramírez-Argáez, and G. Trapaga, Metall. Mater. Trans. B, (2004) 35B, 363-72
M. Ramírez-Argáez, G. Trapaga, and J. Garduño-Esquivel, Metall. Mater. Trans. B, 2004, 35B: 373-80
M. A. Ramírez-Argáez, C. González-Rivera, and G. Trápaga, ISIJ Int., 2009, 49, 6, 796-803
A. Kiyoumarsi, A. Nazari, and M. Ataei, in: COMPEL: Int. J. for Computation and Maths in Electrical and Electronic Eng., 2010, vol. 29, pp. 667–85.
J. A. Bakken, L. Gu, H. L. Larsen, and V. G. Sevastyanenko, J. Eng. Phys. Thermophys., 1997, 70, 4, 530-543
S. Paik, and H. D. Nguyen, Int. J. Heat Mass Transf., 1995, 38, 7, 1161-71
D. Wright, P. Delmont, and M. Torrilhon, J. Plasma Phys., (2013), 79: 699-713
B. Bowman and K. Krüger: Arc furnace Physics, Verlag Stahleisen GmbH, Düsseldorf, Germany, 2009
M. Ramírez and G. Trapaga, Metall. Mater. Trans. B, 2004, 35B, 363-72
E. B. F. Dos Santos, L. H. Kuroiwa, A. F. C. Ferreira, R. Pistor, and A. P. Gerlich, Appl. Sci., 2017, 7, 5, 503
Z. Guo, S. Yin, H. Liao, and S. Gu, Int. J. Heat Mass Transf., 2015, 80, 644-652
Acknowledgments
Open access funding provided by University of Oulu including Oulu University Hospital. We wish to acknowledge the support of Research Fund for Coal and Steel under Grant Agreement No. 709923, Academy of Finland for Genome of Steel Grant No. 311934, and Steel and Metal Producers’ Fund for a 2019 postgraduate Grant.
Conflict of interest
The authors declare that they have no conflict of interest.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Manuscript submitted June 19, 2019.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Pauna, H., Willms, T., Aula, M. et al. Electric Arc Length-Voltage and Conductivity Characteristics in a Pilot-Scale AC Electric Arc Furnace. Metall Mater Trans B 51, 1646–1655 (2020). https://doi.org/10.1007/s11663-020-01859-z
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11663-020-01859-z