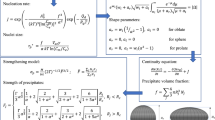
Abstract
A model for vacancy annihilation during aging has been combined with a precipitation model for coupled nucleation, growth, and coarsening in AA 6xxx series aluminum alloys. The simulation results were compared with precipitation parameters from TEM measurements and hardness data obtained for various times during artificial aging. Both simulations and measurements indicated that a combination of an excess concentration of non-equilibrium vacancies at the start of aging and a fast vacancy annihilation rate significantly affected the resulting precipitation and strength evolution. Hence, the model reproduced the short aging time required to reach the maximum strength when direct artificial aging was applied (DAA). In contrast to the fast aging response of DAA, the hardness measurements showed a much slower aging response when artificial aging was performed after prolonged natural aging. This aging behavior was captured in the model simulations by assuming that an equilibrium vacancy concentration is present from the start of the aging.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The mechanical strength of age-hardening Al–Mg–Si AA 6xxx series alloys is obtained through precipitation hardening, solid solution hardening, and strain hardening.[1,2,3] Because precipitation hardening is usually the most important strength contribution, the precipitation sequence and resulting strength evolution occurring during the artificial aging of these alloys have been extensively investigated (e.g., [4,5,6]). In addition, various high-resolution experimental techniques have been used to study the chemical composition and atomic structure of the clusters and hardening precipitate that form.[7,8,9]
Recently, there has been an increased understanding of the important role of vacancies during aging of aluminum alloys.[10,11,12,13,14,15,16,17,18] Following the solution heat treatment, excess vacancies may be "frozen-in" during cooling to room temperature if the cooling rate is sufficiently high. When the alloy is heated to the aging temperature, the excess vacancies are annihilated by diffusion to sinks like grain boundaries and dislocation jogs[19,20] at a rate that depends on the density of such vacancy sinks. Recent studies using positron annihilation lifetime spectroscopy have revealed more details on how long the excess vacancies survive after heating to the artificial aging temperature.[10,17] Even though the lifetime of the excess vacancies is short, they may have an important effect on early-stage precipitation of metastable particles since they increase the diffusion rate significantly.
The annihilation of excess vacancies to sinks during artificial aging occurs simultaneously with a continuous partitioning and repartitioning of vacancies that combine with solute atoms to form different types of solute-vacancy “complexes.” This continuous process is temperature-dependent, and the equilibrium concentration of solute-vacancy complexes and monovacancies can be estimated from the Lomer equation.[10,21] This equation shows that high temperatures promote the dissociation of complexes into monovacancies and solute atoms, while low temperatures promote the formation of solute-vacancy complexes.
Since the effect of vacancies is important for the precipitation during artificial aging, it seems necessary to include vacancy calculations for realistic simulations of the evolution of the precipitation structure. Recently, Yang and Banhart developed a precipitation model that includes vacancy annihilation, trapping, and repartitioning.[10] This model has been successfully used to explain many of the mechanisms related to the effect of excess vacancies versus equilibrium vacancies during the aging of AA 6xxx alloys.[10] The model assumes that once clusters or precipitates form, they do not dissolve, which leads to a continuous increase in the cluster and precipitate volume fraction.
The present article attempts to couple a previously developed precipitation model named NaMo[22,23,24,25] with a vacancy annihilation model developed by Fischer and co-workers.[19,20] The instantaneous vacancy site fraction is calculated from the vacancy annihilation model at each time step and used as input to the nucleation law and the rate law for particle growth and particle dissolution of the precipitation model.
The simulation results are compared with dedicated experiments where a cold rolled Al–Mg–Si alloy sheet was subjected to various aging heat treatment types, including direct artificial aging (DAA) and natural aging followed by artificial aging (NA + AA). The experiments include TEM measurements and hardness measurements at different holding times during artificial aging.
2 Material and Experimental Procedures
2.1 Alloy and Mechanical Tests
Material for the present study was taken from sheets of an Al–Mg–Si alloy with composition 0.85 wt pct Si–0.15 wt pct Fe−0.25 wt pct Mn–0.70 pct Mg. The sheets were produced by conventional direct chill (DC) casting, homogenization, and hot and cold rolling down to a final gauge of 2 mm on commercial production lines at the AluNorf rolling mill in Norf, Germany. Samples were taken from the as-rolled sheets and shipped to SINTEF Industry, Trondheim for further heat treatment. The samples were solution heat treated at 550 °C for 5 minutes in a sand bath, followed by water quenching. Some samples were immediately (i.e., within a few seconds) heated to the artificial aging (AA) temperature of 185 °C in an oil bath and annealed for 10, 20, 30 minutes, 1, 5, 15 hours, and 4 days. Vickers hardness was measured as the mean of five indentations per condition. TEM investigations were performed for the 30 minutes, 5 hours, and 4 days conditions. This route will be referred to as direct artificial aging (DAA). Other samples were kept at room temperature for about 28 days prior to artificial aging at the same temperature and for the same holding times as above. This route has, therefore, natural aging prior to AA and will be referred to as NA + AA. Hardness measurements were performed for each aging time in the same way as for the DAA route. A summary of the measured hardness data is given in Table I.
2.2 Transmission Electron Microscopy (TEM)
TEM specimens were prepared from sheet materials, with the observation direction perpendicular to the rolling direction. The cut slices were thinned down to around 100 μm, punched into 3 mm diameter disks, and electropolished with a TenuPol-5 machine using a mixture of 1/3 HNO3 and 2/3 methanol kept at − 25 °C and a voltage of 20 V.
The samples were characterized with a Jeol JEM-2100 TEM equipped with a LaB6 filament, operated at 200 kV, and used in bright field (BF) and dark field (DF) modes. Parameters of the needle-shaped hardening precipitates (number density, average needle cross-section, length, and volume fraction) have been quantified following the methodology described in Marioara et al.[7] A Gatan imaging filter (GIF), attached to the TEM instrument, was used for specimen thickness measurement by the electron energy loss spectroscopy (EELS) method. For each temper, between eight and fifteen BF and their corresponding DF images were recorded, together with their EELS spectra. The DF images were used to count the needles to determine the volume density, and the BF images were used to measure needle length. In addition, between thirty and fifty BF images at higher magnifications were recorded to measure the needle cross-sections. Between 400 and 800 needle cross-sections were counted from each DF image, and a total of 600 and 700 needle lengths and 200 to 300 cross-section areas were measured from the BF images to ensure good statistical accuracy.
Figure 1 shows TEM images of the precipitate structure after various aging times following solutioning, quenching, and direct artificial aging (DAA). It can be observed that precipitate density is decreasing, and needle size is increasing with increasing AA time. The thickness of the analyzed volume was approximately 50 nm for the 30-minute and 5 h images and 110 nm for the 4-day image. A summary of the results for the measured precipitation data is given in Table II.
Bright field TEM images along the \( \langle {\text{001}}\rangle\) Al zone of samples after various DAA times at 185 °C. (a) 30 minutes. (b) 5 hours. (c) 4 days (96 hours). 1/3 of the needles are observed in cross-sections, and 2/3 are observed perpendicular to their lengths, parallel to \( \langle {\text{100}}\rangle\) Al crystallographic directions
3 Mathematical Modeling
The combined precipitation, yield stress, and work-hardening model of Myhr and Grong, named NaMo,[22,23,24,25] forms the basis for the simulations in the present work. The model consists of a precipitation model for predicting coupled nucleation, growth (and dissolution), and coarsening in dilute alloy systems. Two separate particle size distributions (PSDs) are used in NaMo, where one captures the cluster evolution during natural aging and the other the formation of \(\beta^{\prime\prime}\) and \(\beta^{\prime}\) during artificial aging. The two different PSDs contain separate nucleation and rate laws. They are linked via the continuity equation which records the amount of solute being tied up as precipitates.[25] This allows the mean solute concentration in the aluminum matrix to be computed and shared among the two populations of precipitates. Since the present modeling mainly deals with direct artificial aging (DAA), clusters are assumed not to form. Hence, only the PSD for \(\beta^{\prime\prime}\) and \(\beta^{\prime}\) formation is relevant, except for the last example, which deals with natural aging (NA) prior to artificial aging (AA). For this case study, the PSD for cluster formation is also included in the simulations.
The PSDs calculated by the precipitation model are input to an integrated strength module in NaMo, which uses classic dislocation theory to calculate the room temperature yield stress of the alloy. The PSDs may also be input to a work-hardening module, but since work-hardening is not considered in the present article, this part of the simulation model will not be further discussed.
A detailed description of the assumptions, basic features, and the solution algorithm used to predict the time evolution of the particle size distributions have previously been reported.[22,23,24,25] Hence, only the modifications made to incorporate the effect of excess vacancies are described in the following sections.
The symbols and units used throughout the paper are defined in the Appendix.
3.1 Modeling Excess Vacancy Annihilation
The model by Fischer and co-workers,[19,20] commonly referred to as the FSAK model, has been used to predict vacancy loss to sinks, such as grain boundaries of spherical grains with radius \({r}_{g}\), and dislocation jogs with number density \({n}_{jog}\), during artificial aging. From this model, the annihilation rate, which is the change in the vacancy site fraction \({X}_{v}\) with time \(t\), is given as follows[19,20]:
Here, \({X}_{\text{v}}^{e}\) is the equilibrium vacancy site fraction, \(a\) is the lattice constant for aluminum (equal to 0.4048 nm), \({D}_{\text{eq}}\) is the concentration-weighted diffusion coefficient of solvent, and \({f}_{0}\) is the correlation factor for the fcc lattice, which is equal to 0.7815. In the present modeling, the self-diffusion coefficient of aluminum \({D}_{\text{Al}}\) is used as a reasonable estimate for \({D}_{\text{eq}}\). \({D}_{\text{Al}}\) is given as:
where \({D}_{0}\) is the pre-factor for aluminum self-diffusion, which is set to 1.4 × 10-5 m2/s.[20] \(R\) is the universal gas constant (8.314 J/Kmol), and \({Q}_{\text{m}}\) and \({Q}_{\text{f}}\) are the vacancy migration activation energy and the vacancy formation energy, respectively. There are large variations in the reported values of \({Q}_{\text{m}}\). According to Robson,[26] the values vary from 55.9 kJ/mol to 86.8 kJ/mol (i.e., from 0.58 to 0.90 eV). In the present modeling, we use the average value of \({Q}_{\text{m}}\)=71.4 kJ/mol (0.74 eV).
The equilibrium vacancy site fraction \({X}_{\text{v}}^{e}\) in Eq. [1] is calculated as follows[27]:
where the pre-factor \({X}_{\text{v}0}^{e}\) is related to the entropy of vacancy formation. From Reference 28, the vacancy formation energy is given as \({Q}_{\text{f}}\)=73.3 kJ/mol (0.76 eV). This value is similar to the value that can be extracted from the data in Reference 29, where \({X}_{\text{v}}^{e}\) is given as a function of temperature for pure aluminum. From these data, \({X}_{\text{v}0}^{e}\) was estimated to 17.7, which has been used in the present modeling.
As will be addressed later in more detail, vacancy sinks from dislocation jogs have been ignored in the present modeling since the grain structure consists of recrystallized grains with an approximate radius \({r}_{\text{g}}\) of about 10 μm, and a relatively low dislocation density.
3.2 Precipitation Modeling
Provided that the incubation period can be neglected, the steady-state nucleation rate \(j\) during artificial aging is conveniently expressed as[27]:
Here, \({j}_{0}\) is a pre-exponential term, \({Q}_{\text{d}}\) is the activation energy for diffusion of solute, \({\Delta G}^{*}\) is the energy barrier for heterogeneous nucleation, and \(T\) is the absolute temperature. According to Russel,[30] the nucleation rate scales with the vacancy concentration. If it is assumed that Eq. [4] is valid for nucleation with an equilibrium vacancy site fraction \({X}_{\text{v}}^{e}\) it follows from the statement of Russel that nucleation at a given vacancy site fraction \({X}_{\text{v}}\) can be expressed as follows [24]:
Here, \({A}_{0}\) is a parameter related to the potency of the heterogeneous nucleation sites,[22] \(\overline{C}\) is the mean solute concentration in the matrix, and \({C}_{\text{e}}\) is the equilibrium solute concentration.
Several articles deal with the precipitation of non-spherical particles in aluminum alloys[31,32,33] using non-spherical diffusion fields that represent the shape of the precipitates to give a more accurate description of the diffusion problem. In the present work, the rate law for the dissolution or growth of particles is based on spherical particles, where the equivalent spherical radius \(r\) defines the volume of each particle. Even though this is a simplification, it has been shown in several publications that this approach gives a good estimate of the evolution of the size of the metastable particles in Al–Mg–Si type of alloys.[23,24,25] Hence, the following rate law is used in the simulations[34]:
Here, \({C}_{\text{p}}\) is the solute concentration of the particle, and \({C}_{\text{i}}\) is the particle/matrix interface concentration, which is related to the equilibrium value \({C}_{\text{e}}\) through the Gibbs-Thomson equation,[22] and \(D\) is the equilibrium diffusion coefficient of the solute. If the vacancy concentration deviates from equilibrium, the diffusion coefficient in Eq. [6] must be replaced by the effective diffusion coefficient of the solute \({D}_{\text{eff}}\), which is defined as.[35,36]
By replacing \(D\) in Eq. [6] by \({D}_{\text{eff}}\) from Eq. [7], we get:
It is seen that the rate law, as expressed by Eq. [8], depends on the instantaneous value of the vacancy concentration which is given by \({X}_{\text{v}}/{X}_{\text{v}}^{e}\) as calculated by Eq. [1].
3.3 Strength Modeling
The strength model of NaMo has not been changed in the present work, and only a brief description is given below, while details are given in References 22,23,24,25. The strength contributions are added linearly as follows:
Here, \({\sigma }_{\text{y}}\) is the yield stress, \(M\) and \({M}_{r}\) are the Taylor factor for the relevant alloy and for a reference alloy, respectively. \({\sigma }_{i}\) denotes the intrinsic yield strength of pure aluminum, which is set to 10 MPa.[35] \({\sigma }_{ss}\), \({\sigma }_{p}\), and \({\sigma }_{d}\) represent the strength contributions from elements in solid solution, hardening precipitates, and dislocations, respectively.
In Eq. [9], the strength contribution from elements in solid solution is calculated as follows[1]:
Here, \({C}_{j}\) is the concentration of a specific element in solid solution and \({k}_{j}\) is the corresponding scaling factor for the specific element with values given in Reference 25.
Based on dislocation mechanics and estimated interaction forces between dislocations and obstacles, the strength contribution from hardening precipitates \({\sigma }_{\text{p}}\) is calculated using parameters extracted from the precipitation model described in References 23,24,25. In the present work, the particle size distribution of \(\beta^{\prime\prime}\) and \(\beta^{\prime}\) particles that precipitate during the artificial aging has been used to calculate \({\sigma }_{\text{p}}\). The relationship between the macroscopic yield strength \({\sigma }_{\text{p}}\) and the mean obstacle strength \(\overline{F}\) is then given as follows[35]:
where \(b\) is the magnitude of the Burgers vector, \(l\) is the mean effective particle spacing in the slip plane of the dislocation line, and \(M\) is again the Taylor factor.
Equation [11] is based on a distribution of spherical particles of equal size, whereas the hardening particles shown in Figure 1 are needle-shaped particles aligned along three independent < 100 > directions in the aluminum matrix. The justification for using Eq. [11] for particles that deviate significantly from an idealized spherical particle distribution is discussed in more detail at the end of the article.
The strength contribution from dislocations \({\sigma }_{d}\) in Eq. [9] can be calculated by evolution equations for statistically stored and geometrically necessary dislocations[37] but, as already alluded to earlier, this term is not relevant in the present study since work-hardening is not considered.
In the present work, the measured strength evolution during aging is based on hardness measurements, which means that the predicted yield stress from Eq. [9] is not directly comparable with the measurements. Hence, a simple conversion has been applied based on the following regression formulae[23]:
Here, \(HV\) is the Vickers hardness in VPN, and \({\sigma }_{\text{y}}\) is the yield stress in MPa from Eq. [9].
4 Modeling Results and Validation
In the following, simulation results are shown where the combined vacancy and precipitation model has been used in various case studies related to aging of the present alloy. In this modeling, no attempts have been made to predict annihilation of vacancies during cooling from the solutioning temperature prior to the artificial aging heat treatment. Instead, the vacancy concentration has been introduced as initial values when simulating the aging heat treatment. Furthermore, the simulations do not consider any clusters that may have formed prior to the artificial aging heat treatment. Even though the retention time at room temperature is short, at the same time as the cooling rate from the solutioning temperature and the heating rate to the artificial aging temperature are both fast in direct artificial aging (DAA), some clusters are still expected to form. In the simulations, pre-existing clusters are ignored since it is assumed that nucleation of particles starts from a supersaturated solid solution.
The input data used in the vacancy annihilation model are given in the section above, while input data used in the precipitation and yield stress module of NaMo can be found in Reference 25.
4.1 Precipitation with Constant Vacancy Concentration
The first example is related to precipitation at a specific temperature with constant vacancy concentration, which means that the relative vacancy concentration \({X}_{\text{v}}/{X}_{\text{v}}^{e}\) is constant throughout the simulations. In the precipitation model, this ratio affects the nucleation and the growth/dissolution rates as given by Eqs. [5] and [8], respectively. The results are shown in Figure 2 for the time evolution of the particle number density and the mean particle radius when \({X}_{v}/{X}_{v}^{e}\) was kept constant at 0.01, 1, and 100, respectively. It is evident from Figures 2(a) and (b) that the \({X}_{\text{v}}/{X}_{\text{v}}^{e}\) ratio does not affect the shape of the aging curves, but rather leads to a translation of the curves along the time axis. Hence, by introducing the scaled time \(t\left({X}_{v}/{X}_{v}^{e}\right)\), the three curves for particle number density shown in Figure 2(a) are merged into one curve. The same holds for the three curves for mean particle radius in Figure 2(b). By introducing the scaled time \(t\left({X}_{v}/{X}_{v}^{e}\right)\) in Figure 2(c), the curves in Figures 2(a) and 2(b) are represented by one curve for particle number density, and one curve for the mean particle radius, respectively.
Calculated precipitation parameters during isothermal heat treatment at 185 °C for the present alloy as a function of the relative vacancy concentration \({X}_{\text{v}}/{X}_{\text{v}}^{e}\). (a) Particle number density. (b) Mean particle radius. (c) The curves in (a) and (b) plotted as a function of the scaled time \(t\left({X}_{\text{v}}/{X}_{\text{v}}^{e}\right)\), with particle number density and mean particle radius at the left and right y-axis, respectively
Since the time evolution of the precipitation parameters scales with \(t\left({X}_{\text{v}}/{X}_{\text{v}}^{e}\right)\) for heat treatment at a constant temperature (i.e., isothermal heat treatment), it follows that the time evolution for the yield stress, and likewise for the hardness, also scale with \(t\left({X}_{\text{v}}/{X}_{\text{v}}^{e}\right)\). This is because the yield stress is calculated directly from the particle size distribution (PSD), updated at each time step of the aging heat treatment as described in References 22,23,24,25. Hence, the precipitation model gives the same PSD at two different aging times as long as the scaled time \(t\left({X}_{\text{v}}/{X}_{\text{v}}^{e}\right)\) is identical.
The curves in Figure 3(a) for yield stress and hardness correspond to the curves in Figure 2(a) for the precipitation parameters. A similar scaling as was done in Figure 2(c) gives the combined curve for yield stress and hardness in Figure 3(b) as a function of the scaled time \(t\left({X}_{\text{v}}/{X}_{\text{v}}^{e}\right)\).
Calculated hardness and yield stress evolution curves during isothermal heat treatment at 185 °C for the present alloy. (a) Effect of relative vacancy concentration \({X}_{\text{v}}/{X}_{\text{v}}^{e}\) on the aging response. (b) The same results as shown in (a) plotted against the scaled time parameter \(t\left({X}_{\text{v}}/{X}_{\text{v}}^{e}\right)\)
4.2 Precipitation with Varying Vacancy Concentration
In the aging of aluminum alloys, an excess vacancy concentration may be present at the start of the aging but gradually decrease toward the equilibrium vacancy concentration as the aging proceeds due to loss of vacancies to different type of sinks. When the vacancy concentration changes continuously during aging, it is impossible to scale the time axis, as the previous section did. In such cases, realistic simulations require using the combined vacancy and precipitation model outlined above, where the vacancy model provides the instantaneous vacancy concentration at each time step of the simulation as input to the precipitation model.
In the following case, simulation results using the combined vacancy and precipitation model have been compared with TEM measurements of precipitation parameters and hardness measured during direct artificial aging (DAA). In the first example, the initial vacancy site fraction \({X}_{\text{v}}^{0}\) has been varied while the grain radius \({r}_{\text{g}}\) was kept constant at 10 μm, corresponding to the assumed grain size of the present alloy. The results for the vacancy model simulations are shown in Figure 4(a) where the excess vacancy site fraction has been represented by the relative vacancy site fraction \({X}_{\text{v}}/{X}_{\text{v}}^{e}\), where \({X}_{\text{v}}^{e}\) is the equilibrium site fraction at the aging temperature equal to 7.7 × 10−8 according to Eq. [3]. The figure shows a gradual decrease of \({X}_{\text{v}}/{X}_{\text{v}}^{e}\) for increasing aging time, until the equilibrium vacancy concentration \({X}_{\text{v}}/{X}_{\text{v}}^{e}\) =1 is reached after about 30 minutes independent of the initial vacancy concentration.
Calculated curves for the present alloy during aging at 185 °C for different initial values of the relative vacancy site fraction \({X}_{\text{v}}^{0}/{X}_{\text{v}}^{e}\). (a) Evolution of the relative site fraction \({X}_{\text{v}}/{X}_{\text{v}}^{e}\). (b) Particle number density. (c) Mean particle radius. (d) Particle volume fraction. (e) Resulting hardness and yield stress with error bars representing the estimated standard deviation. The grain radius \({r}_{\text{g}}\) is 10 μm
The corresponding results for the particle number density are shown in Figure 4(b) for the various initial vacancy site fractions \({X}_{\text{v}}^{0}/{X}_{\text{v}}^{e}\). The figure gives measured values from TEM for three different aging times. The simulations underestimate the particle number density for the two shortest aging times and overestimates the particle number density for the longest aging time for all values of \({X}_{\text{v}}^{0}/{X}_{\text{v}}^{e}\) for the given grain radius of 10 μm. This result contradicts the results for the mean particle radius shown in Figure 4(c), where the simulations overestimate the mean particle radius for the two shortest aging times and underestimate the mean particle radius for the longest aging time. Generally, however, these over- and underestimations give a reasonable prediction of the resulting particle volume fraction, as shown in Figure 4(d).
The resulting hardness curves from the present simulations are shown in Figure 4(e). The measurements indicate that there seems to be a kind of plateau where the hardness varies between 127 and 134 HV from 30 to about 1000 minutes. For the simulations, the aging curve for equilibrium vacancy concentration from the start, i.e., \({X}_{\text{v}}^{0}/{X}_{\text{v}}^{e}\) =1, does not show such a plateau, and does not match the measurements very well since the initial hardness increase is too slow compared with the measurements. The hardness seems to reach a peak rather than a plateau. The curve for \({X}_{\text{v}}^{0}/{X}_{\text{v}}^{e}\)=30 on the other hand, shows a pronounced plateau and resembles the measured hardness reasonably, even though the initial hardness increase of the curve is too strong compared to the experiments.
This effect of vacancy concentration on the resulting shape of the aging curves for hardness is further illustrated in Figure 5. Here, two of the curves from Figure 4, i.e., the curves for varying vacancy concentration and a start value \({X}_{\text{v}}^{0}/{X}_{\text{v}}^{e}\) =30, as well as the curve for constant \({X}_{\text{v}}/{X}_{\text{v}}^{e}\)=1, are supplemented with a new curve for a simulation with a constant \({X}_{\text{v}}^{0}/{X}_{\text{v}}^{e}\) ratio of 30. The corresponding relative vacancy site fraction \({X}_{\text{v}}/{X}_{\text{v}}^{e}\) is shown in Figure 5(a), while the simulation results for the coupled vacancy and precipitation model are shown in Figure 5(b). A closer inspection of Figure 5(b) shows that the two curves for constant \({X}_{\text{v}}/{X}_{\text{v}}^{e}\) ratios are similar but shifted along the time axis, since this corresponds to precipitation with constant vacancy concentration as explained in the previous section. These curves display a relatively sharp peak in the hardness, without any indication of a plateau which contrasts the curve for varying \({X}_{v}/{X}_{v}^{e}\) ratio, showing a pronounced hardness plateau. At short aging times, this curve follows the curve for constant \({X}_{\text{v}}/{X}_{\text{v}}^{e}\) =30, but at longer aging times, it starts to deviate from this curve as it gradually approaches the curve for constant \({X}_{\text{v}}/{X}_{\text{v}}^{e}\) =1. Hence, these simulations seem to indicate that the fast aging response of DAA, and the observed hardness plateau can be explained from an initial excess concentration of “frozen-in” vacancies that are gradually annihilated by diffusion to vacancy sinks during aging.
Calculated curves for the present alloy during aging at 185 °C for different values of the relative vacancy site fraction \({X}_{\text{v}}^{0}/{X}_{\text{v}}^{e}\), and measured hardness values during aging. (a) Evolution of the relative site fraction \({X}_{\text{v}}/{X}_{\text{v}}^{e}\). (b) Resulting hardness and yield stress with error bars representing the estimated standard deviation. The grain radius \({r}_{\text{g}}\) is 10 μm
A similar evolution as for the hardness also exists for the evolution of precipitation parameters during aging when an initial excess vacancy concentration is gradually approaching the equilibrium concentration. As for the hardness curves shown in Figure 5(b), the particle number density, the mean particle radius, and the particle volume fraction follow the curve for constant \({X}_{\text{v}}/{X}_{\text{v}}^{e}\) =30 at short aging times, but for long aging times, the curves gradually approach the curve for \({X}_{\text{v}}/{X}_{\text{v}}^{e}\) =1. Due to space limitations, these curves are not shown in the present article.
In the next simulation example, the effect of the density of vacancy sinks on the precipitation is investigated. In the simulations, the initial vacancy concentration \({X}_{\text{v}}^{0}\) is set equal to 2.3 × 10−6 for all simulations, which gives \({X}_{\text{v}}^{0}/{X}_{\text{v}}^{e}\)=30, while the sink density, as represented by the grain radius \({r}_{\text{g}}\), has been varied from 2.5 to 10 μm. Vacancy sinks from dislocation jogs have been ignored in the simulations, but since the effect is similar for grains and dislocation jogs according to Eq. [1], the results are easily transferrable if this type of vacancy sinks dominates.
As can be seen from Eq. [1], \({r}_{\text{g}}\) has a strong effect on the vacancy annihilation rate, which is confirmed by the simulation results in Figure 6. Figure 6(a) shows that the excess vacancies are almost annihilated after only 2 minutes for \({r}_{\text{g}}\) = 2.5 μm, as \({X}_{\text{v}}/{X}_{\text{v}}^{e}\) is close to 1 at this aging time. For the largest \({r}_{\text{g}}\) of 10 μm, the corresponding aging time to reach the equilibrium vacancy concentration is about 30 minutes.
(a) Calculated curves for the present alloy during aging at 185 °C for different values of the grain radius \({r}_{\text{g}}\). (a) Relative vacancy site fraction \({X}_{\text{v}}/{X}_{\text{v}}^{e}\). (b) Particle number density. (c) Mean particle radius. (d) Resulting hardness and yield stress with error bars representing the estimated standard deviation. The initial relative vacancy site fraction \({X}_{\text{v}}^{0}/{X}_{\text{v}}^{e}\)=30
The effect of the grain radius \({r}_{\text{g}}\) on the precipitation is shown in Figures 6(b) and (c) for the particle number density and the mean particle radius, respectively. Since both the nucleation rate, as given by Eq. [5], and the growth/dissolution rate, as given by Eq. [8], are proportional to \({X}_{\text{v}}/{X}_{\text{v}}^{e}\), it is not surprising that the fastest increase in particle number density and mean particle radius is obtained for the largest grain size, i.e., for \({r}_{\text{g}}\)=10 μm, for which a significant excess vacancy concentration is maintained for a relatively long aging time as shown in Figure 6(a). This is in contrast to the smallest grain size \({r}_{\text{g}}\)=2.5 μm where the increase in particle number density and the mean particle radius in Figures 6(b) and (c) show a much slower increase than for \({r}_{\text{g}}\)=10 μm because the excess vacancies are quickly annihilated due to the high density of vacancy sinks caused by this small grain size.
The resulting hardness and yield stress curves are shown in Figure 6(d) together with measured hardness values. All curves coincide at short aging times, but the curve for the smallest \({r}_{\text{g}}\) value of 2.5 μm starts to deviate from the others already after about 0.2 minutes (12 seconds), since the initial excess vacancy concentration for this grain size is reduced to about half the initial value at this aging time as shown in Figure 6(a). For long aging times, all curves are approaching the one for the equilibrium vacancy concentration \({X}_{\text{v}}/{X}_{\text{v}}^{e}\) =1, but the transition is rather complex and depends on the actual value of \({r}_{\text{g}}\).
4.3 Simulations of Natural Aging Prior to Artificial Aging
The simulations and measurements described above are all related to direct artificial aging (DAA), i.e., when the alloy is heated to the artificial aging temperature without any intermediate storing at room temperature after solutioning and quenching. In the rolling industry, DAA is not common since the alloys are usually stored at room temperature for some time before the artificial aging. In the following, this type of heat treatment is referred to as NA + AA.
For NA + AA, the formation of clusters at room temperature must be accounted for in the simulations. Cluster formation in Al–Mg–Si alloys and the interplay between clusters, vacancies, and metastable particles during artificial aging is very complex. A simplified model for cluster formation during natural aging and the effect of the clusters on the subsequent precipitation during artificial aging is implemented in NaMo and is described in Reference 25. The model assumes that clusters that form at low temperatures may survive for a certain period during artificial aging and therefore temporarily tie-up solute that otherwise would have been consumed in precipitation of hardening particles.[25] During artificial aging, the model predicts a gradual dissolution of the clusters, and a simultaneous precipitation of hardening metastable particles promoted by the increase in available solutes as the clusters dissolve.
Figure 7 compares the results from NaMo simulations of NA + AA with hardness measurements. In the figure, simulation results for DAA from Figure 4 for \({X}_{\text{v}}^{0}/{X}_{\text{v}}^{e}\)=30 and \({r}_{\text{g}}\)=10 μm are included together with measured hardness values. The model simulations capture the main trends displayed by the measurements, i.e., a significantly faster aging response for DAA compared with NA + AA, and the development of a plateau in the hardness curve for DAA, compared with a sharper and more pronounced peak for the NA + AA curve. The model simulations for NA + AA underestimates the hardness at short aging times, possibly due to a corresponding underestimation of the strength contribution from clusters or the contribution from solid solution strengthening.
5 Discussion
From Eq. [1], grains and dislocation jogs are assumed to act similarly as sinks for vacancies. Consequently, a certain grain radius can be converted to an equivalent dislocation density with equal vacancy sink density. This means that the present simulations with varying grain radius are equally applicable when vacancy sinks from dislocation jogs are dominating, by simply using the conversion \({n}_{\text{jog}}=15/2\pi a{r}_{\text{g}}^{2}\). From this conversion, the estimated grain radius of the present alloy of 10 μm corresponds to an equivalent jog density of 5.9 × 1019 m−3. By assuming a typical jog fraction of 0.02 (i.e., one jog per 50 atoms),[19,20] this gives a corresponding dislocation density of 1 × 1012 m-2, which is about an order of magnitude higher than the dislocation density expected for undeformed aluminum alloys[38] like the fully recrystallized alloy used in the present work. Hence, this estimate indicates that grains and not dislocation jogs are the dominating vacancy sinks for the present alloy.
In addition to the loss of vacancies to various types of sinks, there is a continuous partitioning between free vacancies and vacancies bound to solute atoms during a heat treatment. The FSAK vacancy model used in the present work only considers the diffusion of monovacancies and ignores formation of vacancy-solute complexes. More sophisticated models for vacancy annihilation[10,17] include the effect of vacancy-solute interactions by updating the partitioning between free vacancies and vacancies bound to solute atoms at each simulation time step by applying the Lomer equation.[21] In such models, positive binding energies between solute atoms and vacancies tend to reduce the annihilation rate of vacancies. Since the FSAK model used in the present work does not consider vacancy-solute interactions, it will overestimate the annihilation rate compared with models that incorporate such interactions.
In Reference 17, the vacancy annihilation rate was calculated following solutioning, quenching, and artificial aging at 180 °C of a 0.39 wt pct Mg and 0.40 wt pct Si ternary Al–Mg–Si alloy. The model used in the study allowed vacancy-solute interactions to be accounted for in simulations of the vacancy annihilation rate. From this study, it is possible to compare simulations where vacancy-solute interactions were accounted for or ignored, respectively. The simulation results showed that the artificial aging time required to reduce the vacancy concentration to a certain level was 55 seconds when vacancy-solute interactions were included, and 40 seconds when vacancy-solute interactions were ignored. Therefore, this study indicates that although the simplified FSAK model overestimates the vacancy annihilation rate, the model may give reasonable estimates compared with more sophisticated models.
In the present model simulations, a certain initial vacancy site fraction \({X}_{\text{v}0}\) at the start of the artificial aging heat treatment has been assumed, and no attempts were made to predict \({X}_{\text{v}0}\) from processes prior to the artificial aging. \({X}_{\text{v}0}\) depends on the cooling rate from the solutioning temperature, the intermediate storing time at room temperature, and the heating rate to the aging temperature. Measurements using positron annihilation lifetime spectroscopy can indicate the \({X}_{\text{v}0}\) fraction. In the above-mentioned study, where Al–Mg–Si alloys were solutionized, quenched, and artificially aged, the vacancy concentration was estimated to be three times the equilibrium concentration after just 1 second aging time. It was found that the measured positron lifetime was significantly increased for alloys with higher alloy composition similar to the one used in the present work, indicating that the initial vacancy concentration was much higher than three times the equilibrium concentration. Hence, the chosen initial vacancy concentration in the present study, up to 30 times the equilibrium value may not be unrealistic.
The present modeling assumes that the nucleation rate scales with the vacancy concentration, which agrees well with the analysis by Russel.[30] In addition, the nucleation barrier \({\Delta G}^{*}\) is supposed to be unaffected by an excess vacancy concentration, which is not necessarily the case since excess vacancies may have several effects on the nucleation barrier.[20,30] One possible effect is a reduction in \({\Delta G}^{*}\) by an increase in the driving force for nucleation provided that vacancies can be incorporated into the crystal lattice of the precipitates.[20,30] In addition, excess vacancies may also relax volumetric misfit strains and compensate for the elastic stress that is present around misfitting precipitates. But these effects of excess vacancies on \({\Delta G}^{*}\) depend on the degree of coherency of the precipitate with the aluminum matrix. According to Russel,[30] the energy barrier would be relatively unaffected by vacancy supersaturation if the precipitates are coherent with the aluminum matrix since vacancies are not created nor annihilated in coherent precipitation.
Hence, the justification for applying the assumption that \({\Delta G}^{*}\) is independent of any excess vacancy concentration depends on whether the precipitates, i.e., the \(\beta^{\prime\prime}\) particles, are fully coherent. In the work by Wenner[39] using scanning transmission electron microscopy (STEM), it was found that the \(\beta^{\prime\prime}\) phase is indeed fully coherent with the aluminum matrix, which supports the assumption in the present modeling.
In addition to \(\beta^{\prime\prime}\) particles, the NaMo model also allows the \(\beta^{\prime}\) phase to nucleate during artificial aging. Contrary to the \(\beta^{\prime\prime}\) phase, \(\beta^{\prime}\) is not fully coherent with the aluminum matrix.[40,41] In the model, this phase is assumed to nucleate on dislocations as described in Reference 25, and which is confirmed by TEM measurements.[40,41] Since the materials were not subjected to any plastic deformation, the simulation model predicted a low dislocation density and no \(\beta^{\prime}\) precipitation. However, in future model simulations with imposed plastic pre-aging deformation, the assumption that \({\Delta G}^{*}\) is independent of any excess vacancies should be applicable since no supersaturation of vacancies is expected to be present close to vacancy sinks like dislocations.[30]
As mentioned previously in the article, Eq. [11] is based on a distribution of spherical particles of equal size, whereas the hardening \(\beta^{\prime\prime}\) and \(\beta^{\prime}\) particles are either needle- or rod-shaped and aligned along different < 100 > directions. The justification for using Eq. [11] for particles that deviate from an idealized spherical particle distribution is due to two mechanisms that tend to cancel each other concerning resulting macroscopic yield strength \({\sigma }_{\text{p}}\). If we consider needle-shaped particles, they intercept more slip planes as their aspect ratio increases, which leads to a decrease in \(l\) in Eq. [11]. But at the same time, the cross-section of the particles decreases as their length increases for a constant particle volume, which, in turn, leads to a decrease in \(\overline{F }\). As a result, the \(\overline{F }/l\)-ratio remains reasonably constant for a wide range of particle aspect ratios, which was first observed in numerical simulations by Bahrami,[42] who concluded that models assuming elongated precipitates of constant aspect ratio do not give significantly better predictions of the strength than models assuming spherical particles, and that the assumption of spherical particles, as a first approximation, is acceptable.
A detailed analysis of the effect of particle strength and aspect ratio on the resulting \(\overline{F }/l\) ratio for rod-shaped particles as well as spherical particles was given in Reference 25 based on the work by Esmaeili.[43] This comparison of obstacle strengths for the two different particle shapes, was based on identical particle volume fractions and particle number densities, an important prerequisite for an unambiguous comparison of the particle shape effect. Using indices \(r\) and \(s\) for rod-shaped and spherical particles, respectively, it was shown that the ratio \(\left({\overline{F} }_{\text{r}}/{l}_{\text{r}}\right)/\left({\overline{F} }_{\text{s}}/{l}_{\text{s}}\right)\) was relatively insensitive to variations in the particle aspect ratio for the typical range observed for \(\beta^{\prime\prime}\) and \(\beta^{\prime}\) particles, which supports the findings in the numerical simulations by Bahrami.[42]
Recently, several articles have dealt in more detail with the effect of the particle shape on the resulting strength contribution from precipitates than has been the scope of the present article. Particularly the model by Holmedal,[44] which has been used in several publications,[44,45,46] gives improved estimates of the resulting strength contribution for non-spherical particles.
6 Summary
The present article combines the FSAK model for vacancy annihilation during aging with the NaMo precipitation model for coupled nucleation, growth, and coarsening in AA 6xxx series aluminum alloys. The combined model was applied in simulations of artificial aging following solutioning and quenching without any intermediate room temperature storing, i.e., direct artificial aging (DAA). The simulation results were compared with precipitation parameters from TEM and hardness data obtained during the DAA heat treatment. The measured hardness curves show a rapid increase at short aging times followed by a plateau where the hardness remains relatively unaffected for a significant time. The model captured this observed time dependence of the hardness during the aging, and predicted a rapid decrease in the excess vacancy concentration at the start of the aging. Model simulations also captured the much slower aging response observed when the artificial aging was performed after 28 days of natural aging (NA).
Abbreviations
- \(a\) :
-
Lattice constant for aluminum (0.4048 nm)
- \({A}_{0}\) :
-
Parameter related to the potency of the heterogeneous nucleation sites (J/mol)
- \(b\) :
-
Magnitude of the Burgers vector (m)
- \(CS\) :
-
Average cross-section of particles (nm2)
- \({C}_{\text{e}}\) :
-
Equilibrium solute concentration (wt pct)
- \({C}_{i}\) :
-
Particle/matrix interface concentration (wt pct)
- \({C}_{j}\) :
-
Concentration of a specific element in solid solution (wt pct)
- \({C}_{\text{p}}\) :
-
Solute concentration of the particle (wt pct)
- \(\overline{C}\) :
-
Mean solute concentration in the matrix (wt pct)
- \(D\) :
-
Equilibrium diffusion coefficient of the solute (m2/s)
- \({D}_{\text{Al}}\) :
-
Self-diffusion coefficient of aluminum (m2/s)
- \({D}_{\text{eff}}\) :
-
Efficient diffusion coefficient of solute (m2/s)
- \({D}_{\text{eq}}\) :
-
Concentration-weighted diffusion coefficient of solvent (m2/s)
- \({D}_{0}\) :
-
Pre-factor for aluminum self-diffusion (m2/s)
- \( \bar{F} \) :
-
Mean obstacle strength (N)
- \(f\) :
-
Particle volume fraction
- \({f}_{0}\) :
-
Fcc correlation factor (0.7815)
- \({\Delta G}^{*}\) :
-
Energy barrier for heterogeneous nucleation (J/mol or J/K)
- \(HV\) :
-
Hardness (VPN)
- \(j\) :
-
Steady-state nucleation rate (#/m3s)
- \({j}_{0}\) :
-
Pre-exponential term in expression for nucleation rate (#/m3s)
- \({k}_{j}\) :
-
Scaling factor for specific element in solid solution expression (MPa/wt pct2/3)
- \(L\) :
-
Average length of particles (nm)
- \(l\) :
-
Mean effective particle spacing in the slip plane of the dislocation line (m)
- \(M\) :
-
Taylor factor
- \({M}_{\text{r}}\) :
-
Taylor factor for a reference alloy
- \(N\) :
-
Particle number density (#/m3)
- \({n}_{\text{jog}}\) :
-
Dislocation jog density (#/m3)
- \({Q}_{\text{d}}\) :
-
Activation energy for diffusion of solute (J/mol or eV)
- \({Q}_{\text{f}}\) :
-
Vacancy formation energy (J/mol or eV)
- \({Q}_{\text{m}}\) :
-
Vacancy migration activation energy (J/mol or eV)
- \(r\) :
-
Particle radius (m)
- \({r}_{\text{eq}}\) :
-
Equivalent spherical radius for the particles (nm)
- \({r}_{\text{g}}\) :
-
Spherical grains radius (m)
- \(R\) :
-
Universal gas constant (8.314 J/Kmol)
- \(t\) :
-
Time (s)
- \(T\) :
-
Temperature (K or oC)
- \({X}_{\text{v}}\) :
-
Vacancy site fraction
- \({X}_{\text{v}}^{e}\) :
-
Equilibrium vacancy site fraction
- \({X}_{\text{v}0}^{e}\) :
-
Pre-factor in vacancy site fraction expression
- \({\sigma }_{\text{d}}\) :
-
Strength contribution from dislocations (MPa)
- \({\sigma }_{i}\) :
-
Intrinsic yield strength of pure aluminum (MPa)
- \({\sigma }_{\text{p}}\) :
-
Strength contribution from hardening precipitates (MPa)
- \({\sigma }_{\text{ss}}\) :
-
Strength contribution from elements in solid solution (MPa)
- \({\sigma }_{\text{y}}\) :
-
Yield stress (MPa)
References
H.R. Shercliff and M.F. Ashby: Acta Metall., 1990, vol. 38, pp. 1789–1802.
J.D. Embury, D.J. Lloyd, and T.R. Ramachandran: Treatise Mater. Sci. Technol., 1989, vol. 31, pp. 579–601.
L.M. Cheng, W.J. Poole, J.D. Embury, and D.J. Lloyd: Metall. Mater. Trans. A, 2003, vol. 34A, pp. 2473–81.
G.A. Edwards, K. Stiller, G.L. Dunlop, and M.J. Couper: Acta Mater., 1998, vol. 46, pp. 3893–3904.
C.D. Marioara, S.J. Andersen, J. Jansen, and H.W. Zandbergen: Acta Mater., 2003, vol. 52, pp. 789–96.
M.A. van Huis, J.H. Chen, M.H.F. Sluiter, and H.W. Zandbergen: Acta Mater., 2007, vol. 55, pp. 2183–99.
C.D. Marioara, S.J. Andersen, H.W. Zandbergen, and R. Holmestad: Metall. Mater. Trans. A, 2005, vol. 36A, pp. 691–702.
O. Engler, C.D. Marioara, Y. Aruga, M. Kozuka, and O.R. Myhr: Mater. Sci. Eng. A, 2019, vol. 759, pp. 520–29.
M.W. Zandbergen, Q. Xu, A. Cerezo, and G.D.W. Smith: Acta Mater., 2015, vol. 101, pp. 136–48.
Z. Yang and J. Banhart: Acta Mater., 2021, vol. 215, p. 117014.
J. Banhart, M.D.H. Lay, C.S.T. Chang, and A.J. Hill: Phys. Rev. B, 2011, vol. 83, p. 014101.
S. Pogatscher, H. Antrekowitsch, M. Werinos, F. Moszner, S.S.A. Gerstl, M.F. Francis, W.A. Curtin, J.F. Löffler, and P.J. Uggowitzer: Phys. Rev. Lett., 2014, vol. 112, pp. 225701–05.
S. Pogatscher, H. Antrekowitsch, H. Leitner, D. Poschmann, Z.L. Zhang, and P.J. Uggowitzer: Acta Mater., 2012, vol. 60, pp. 4496–4505.
S. Pogatscher, H. Antrekowitsch, H. Leitner, T. Ebner, and P. Uggowitzer: Acta Mater., 2011, vol. 59, pp. 3352–63.
J. Banhart, C.S.T. Chang, Z.Q. Liang, N. Wanderka, M.D.H. Lay, and A.J. Hill: Adv. Eng. Mater., 2010, vol. 12, pp. 559–71.
M.D.H. Lay, H.S. Zurob, C.R. Hutchinson, T.J. Bastow, and A.J. Hill: Metall. Mater. Trans. A, 2012, vol. 43A, pp. 4507–13.
M. Madanat, M. Liu, X.-P. Zhang, Q.-N. Guo, J. Cizek, and J. Banhart: Phys. Rev. Mater., 2020, vol. 4, p. 063608.
M. Liu, J. Cížek, C.S.T. Chang, and J. Banhart: Acta Mater., 2015, vol. 91, pp. 355–64.
F.D. Fischer, J. Svoboda, F. Appel, and E. Kozeschnik: Acta Mater., 2011, vol. 59, pp. 3463–72.
E. Kozeschnik, Modelling Solid-State Precipitation, Momentum Press, 2013, pp. 37–349.
H. Mehrer, Diffusion in Solids, Springer, 2007, pp. 95–102.
O.R. Myhr and Ø. Grong: Acta Mater., 2000, vol. 48, pp. 1605–15.
O.R. Myhr, Ø. Grong, and S.J. Andersen: Acta Mater., 2001, vol. 49, pp. 65–75.
O.R. Myhr, Ø. Grong, H.G. Fjær, and C.D. Marioara: Acta Mater., 2004, vol. 52, pp. 4497–4508.
O.R. Myhr, Ø. Grong, and C. Schäfer: Metall. Mater. Trans. A, 2015, vol. 46A, pp. 6018–39.
J.D. Robson: Metall. Mater. Trans. A, 2020, vol. 51A, pp. 5401–13.
D.A. Porter, K.E. Easterling, Phase Transformations in Metals and Alloys, Van Nostrand Reinhold Co. Ltd., 1981, pp. 265–78.
A. Deschamps, G. Fribourg, Y. Brechet, J. Chemin, and C. Hutchinson: Acta Mater., 2012, vol. 60, pp. 1905–16.
D. Altenpohl: Aluminium, 1961, vol. 37, pp. 401–11.
K.C. Russell: Scr. Met., 1969, vol. 3, pp. 313–16.
B. Holmedal, E. Osmundsen, and Q. Du: Metall. Mater. Trans. A, 2016, vol. 47A, pp. 581–88.
D. Bardel, M. Perez, D. Nelias, A. Deschamps, C.R. Hutchinson, D. Maisonnette, T. Chaise, J. Gamier, and F. Bourlier: Acta Mater., 2014, vol. 62, pp. 129–40.
A. Bahrami, A. Miroux, and J. Sietsma: Metall. Mater. Trans. A, 2012, vol. 43A, pp. 4445–53.
H.B. Aaron, D. Fainstain, and G.R. Kotler: J. Appl. Phys., 1970, vol. 41, pp. 4404–10.
A. Deschamps and Y. Brechet: Acta mater., 1999, vol. 47, pp. 293–305.
F. Fazeli, C.W. Sinclair, and T. Bastow: Metall. Mater. Trans. A, 2008, vol. 39A, pp. 2297–2305.
O.R. Myhr, O.S. Hopperstad, and T. Børvik: Metall. Mater. Trans. A, 2018, vol. 49A, pp. 3592–3609.
G.K. Williamson and R.E. Smallman: Philos. Mag., 1956, vol. 1, pp. 34–46.
S. Wenner and R. Holmestad: Scr. Met., 2016, vol. 118, pp. 5–8.
K. Teichmann, C.D. Marioara, S.J. Andersen, K.O. Pedersen, S. Gulbrandsen-Dahl, M. Kolar, R. Holmestad, and K. Marthinsen: Philos. Mag., 2011, vol. 91, pp. 3744–54.
K. Teichmann, C.D. Marioara, S.J. Andersen, and K. Marthinsen: Metall. Mater. Trans. A, 2012, vol. 43A, pp. 4006–14.
A. Bahrami: Doctoral Thesis, Delft University of Technology, Department of Material Science and Engineering, Delft, 2010.
S. Esmaeili, D.J. Lloyd, and W.J. Pool: Acta Mater., 2003, vol. 51, pp. 3467–81.
B. Holmedal: Philos. Mag. Lett., 2015, vol. 95, pp. 594–601.
J.K. Sunde, F. Lu, C.D. Marioara, B. Holmedal, and R. Holmestad: Mater. Sci. Eng. A, 2021, vol. 807, p. 140862.
F. Lu, J.K. Sunde, C.D. Marioara, R. Holmestad, and B. Holmedal: Mater. Sci. Eng. A, 2022, vol. 832, 142500.
Conflict of interest
The authors declare that they have no conflict of interest.
Funding
Open access funding provided by NTNU Norwegian University of Science and Technology (incl St. Olavs Hospital - Trondheim University Hospital).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Myhr, O.R., Marioara, C.D. & Engler, O. Modeling the Effect of Excess Vacancies on Precipitation and Mechanical Properties of Al–Mg–Si Alloys. Metall Mater Trans A 55, 291–302 (2024). https://doi.org/10.1007/s11661-023-07249-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11661-023-07249-9