Reversible Cyclic Softening in HSLA Steels at Low Homologous Temperatures

Abstract

Critical mechanical components employed in energy applications require certification of their mechanical response under monotonic or cyclic loading at various constant temperatures. However, components often experience combined load and temperature changes, which are more complex and time-consuming to evaluate. This work presents previously unreported reversible cyclic softening in low-alloy steel undergoing loading sequences between 293 K and 453 K (0.15 to 0.25 of the homologous temperature). Mechanical cycling at 80 pct of the yield stress results in a similar cyclic response for all temperatures, while cycling at 90 pct of the yield stress doubles the cyclic strain when preceded by cycling at 453 K. The softening can be reversed by maintaining the material at elevated temperatures and cannot be explained by dislocation recovery mechanisms or changes in the microstructure. Instead, serrated deformation at specific deformation levels suggests that Dynamic Strain Aging (DSA) contributes to softening, which is further supported by a theoretical analysis of interstitials and dislocations mean free paths at various temperatures.

1 Introduction

The warranting of the integrity of critical components in energy systems often requires the assessment of material properties at various loading levels coupled with mechanical and thermal cycling. As a result, the number of testing conditions required for certification can rapidly become intractable, unfeasible, or uneconomical. Instead, mechanistic understanding and physic-based modeling can effectively mitigate the experimental needs by ranking the most likely detrimental in-service conditions.

Cyclic deformation in metallic materials is a complex multiscale problem that involves the production, glide, and annihilation of point and line defects. These mechanisms are sensitive to temperature, deformation rate, loading level, and loading history, which results in complex phenomena. An increase in temperature generally leads to softening in metallic materials due to the increase of dislocation recovery mechanisms that are thermally activated (e.g., dislocation climb and annihilation).^[1,2] One notable exception corresponds to Ni-based superalloys, which increase their yield stress above 0.5 homologous temperature. This response is often attributed to the strengthening role of precipitated, which can harden the material depending on the ability of dislocations to cut through precipitates.^[3]

Simple alloys can also result in complex softening and hardening evolution depending on their initial condition. Under isothermal conditions, highly deformed metals tend to soften upon cyclic loading, while well-annealed metals would initially harden followed by softening.^[4,5] Furthermore, the mechanical response depends on the amount of applied deformation, and some materials will exhibit hardening or softening for different applied strains.

A few research efforts have explored the synergetic roles of cyclic deformation and temperature changes in carbon steels. For example, Shin and Lee^[6] studied the effects of temperature on low-cycle fatigue of alloyed carbon steel and showed that strain ranges below 1 pct at 453 K resulted in a higher softening ratio^[7,8] than those at 523 K. Upon applying larger deformation ranges, the softening increases with further temperature changes, which suggests that the mechanism responsible for the anomaly is not present or is subdued at large strains.

Hong et al.^[9] also studied the effect of temperature on the low-cycle fatigue for 316L stainless steel. Their work demonstrated that 316L presents softening ratios that depend on the applied strain amplitude, the strain rate, and temperature. Interestingly, softening increases with temperature up to 453 K, while it peaks for strain amplitudes between 0.4 and 0.5 pct and decreases beyond a 1 pct strain range. Hence, the similarities with the work from Shin and Lee^[6] are evident despite they correspond to different materials with different atomic structures (FCC and BCC). These results suggest that the mechanisms behind the softening cannot depend on recovery mechanisms, which are significantly different among both materials (e.g., different cross-slip likelihood). Instead, Hong et al.^[9] pointed out that dynamic strain aging (DSA) is a potential mechanism to explain the softening mechanism. DSA is a general phenomenon that occurs across metallic systems and is driven by the diffusion of atoms to dislocations at a local scale rather than on the lattice structure or microstructural attributes.

This communication presents novel experimental results that characterize reversible cyclic softening in high-strength low-alloy (HSLA) steels under low cyclic fatigue (LCF) conditions and homologous temperatures below 0.25. We present extensive mechanical testing that supports that the DSA mechanism is responsible for the cyclic evolution observed in HSLA. These results have been further supported by theoretical analyses that identify the deformation and temperature that maximizes the softening based on the diffusion of interstitial atoms.

2 Experimental Work

2.1 Materials and Specimens

This study evaluates the thermomechanical response of carbon manganese HSLA steels with the chemical compositions in weight percentage as presented in Table I. The material was obtained from a hot-rolled seamless pipe for Oil Country Tubular Good (OCTG) applications. Figure 1 presents scanning electron microscopy (SEM) images that depict a microstructure consistent with tempered martensite with an average austenitic grain size of about 12 to 17 μm, typical of HSLA steels. The average grain size was estimated using the mean linear intercept method (ASTM E112) applied on samples etched with picric acid to reveal more clearly prior austenitic grain boundaries.

Table I Chemical Composition in Weight Percentage of the HSLA Steel Evaluated

Fig. 1

SEM characterization of the HSLA steel microstructure, which is consistent with tempered martensite

2.2 Mechanical Testing Procedure

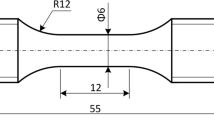
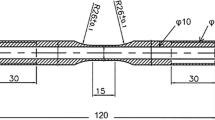
We assessed the mechanical response during thermomechanical cycling with a Gleeble® 3500 thermomechanical simulator. This system applied monotonic or cyclic deformation under stress control while closely controlling the temperature in the range from 293 K to 673 K. Figure 2 presents the specimen dimensions and geometry, which employs a threaded grip to alloys for a smooth transition from tension to compression loading.

Fig. 2

Specimen employed for cyclic testing at Gleeble® thermomechanical simulator. The double thread allows a smooth switch between tension–compression loading

3 Experimental Results

3.1 Baseline Material

First, we evaluated the baseline mechanical response of the material under isothermal conditions following ASTM E08 standards. Figure 3 presents the monotonic response at 293 K and 453 K, which results in yield strengths of 1004 and 900 MPa, respectively. Higher temperatures result in lower yield stresses, but subsequent strain hardening is almost identical, which suggests that forest dislocation hardening relies on similar mechanisms at both temperatures. Multiple tests resulted in almost identical results, the variability being less than the differences between the curves.

Fig. 3

Monotonic strain and stress response at 293 K and 453 K as per standard ASTM E08 testing. The corresponding yield stress are 1004 MPa at 293 K and 892 MPa at 453 K

Figure 4 presents the final stress–strain loop and the peak stress range along 30 cycles at 293 K and 453 K, at a constantly applied deformation range of 6e−3 and frequency of 0.0028 Hz (i.e., 6-minute period). The responses at both temperatures present some limited softening, which rapidly saturates after roughly five cycles at 453 K and 20 cycles at 293 K. The faster saturation at higher temperatures suggests that thermally activated recovery mechanisms (e.g., dislocation annihilation) are responsible for such cyclic softening. This baseline response is in agreement with the general mechanical response previously reported for HSLA steels.^[10,11]

Fig. 4

(a) Strain and stress loop at 293 K and 453 K after 30 cycles and constant strain amplitude of 0.6 pct. (b) Peak stress as a function of the number of cycles at the same constant strain amplitude. Softening is limited and saturates by the end of the experiment

3.2 Cyclic Loading at Various Temperatures

Next, we consider an experiment in which the material underwent 30 fully reversed cyclic at a frequency of 0.0028 Hz (i.e., 6-minute period). The first 10 cycles were applied at 453 K, followed by 10 cycles at 293 K, and finalizing with 10 cycles at 453 K. Temperature transients in between cyclic loading occurred in 10 minutes at zero stress. The testing was done under stress control applying 80 pct of the yield stress for the corresponding temperature (803 MPa at 293 K and 720 MPa at 453 K). Figures 5(a) and (b) present the macroscopic stresses and strains, respectively. These magnitudes were used to compute the cyclic strain in Figure 5(c), which corresponds to the maximum strain difference over a cycle $\left( {\frac{\Delta \varepsilon }{2}} \right)$. In this case, the cyclic strain is about $3.2 \times 10^{ - 3}$ and remains almost unchanged upon accumulation of plastic deformation despite the temperature change.

Fig. 5

Stress (a) and strain (b) responses as a function of time under constant stress amplitude of 80 pct of yield stress starting at 453 K for 10 cycles, followed by 10 cycles at 293 K, and ending with 10 cycles at 453 K. Temperature transitions occurs within 360 s (6 min). (c) The cyclic strain amplitude is almost constant throughout the experiments

Following on, Figure 6(a) presents a similar loading and temperature sequence (10 cycles at 453 K, followed by 10 cycles at 293 K and 10 additional cycles at 453 K), but applying a stress amplitude of 90 pct of the yield stress at the corresponding temperature (903 MPa at 293 K and 803 MPa at 453 K). The results in Figure 6(b) demonstrate that higher loads induce significant cyclic softening at 293 K after cycling the material at 453 K (cycles 1 to 10). Indeed, marginal softening occurs for the first 10 cycles at 453 K, but further cycling at 293 K results in extensive plastic deformation accumulation and doubles the cyclic strain amplitude. Notably, the softening seems to reduce when the material is further cycled at 453 K (cycles 21 to 30).

Fig. 6

Stress (a) and strain (b) responses as a function of time under constant stress amplitude of 90 pct of yield stress starting at 453 K for 10 cycles, followed by 10 cycles at 293 K, and ending with 10 cycles at 453 K. Temperature transitions occurs within 360 s (6 min). (c) Evolution of the cyclic strain amplitude in which some pronounced softening is evident during cycling at room temperature

To further understand the softening process, we evaluated the role of the loading sequence by reverting the temperature order. Figure 7 presents the results after cycling the material for 10 cycles at 293 K, followed by 10 cycles at 453 K, and concluding with 10 cycles at 293 K. Compared to Figure 6, cyclic loading at 90 pct of the corresponding yield stress in a pristine material results in a strain amplitude about 4.5 × 10^–3, both at 293 K and 453 K. Further cycling after reducing the temperature from 453 K to 293 K leads to doubling the cyclic strain amplitude.

Fig. 7

Stress (a) and strain (b) responses as a function of time under constant stress amplitude of 90 pct of yield stress starting at 293 K for 10 cycles, followed by 10 cycles at 453 K, and ending with 10 cycles at 293 K. (c) Evolution of the cyclic strain amplitude in which pronounced softening is evident during the last 10 cycles at room temperature

A final corroboration of the softening evident in Figure 7, but missing in Figure 5, comes from the monotonic tensile test at room temperature after applying both cycling histories. The results in Figure 8 confirm the softening due to cycling at 453 K and 90 pct of the yield stress. Indeed, the monotonic yield stress decreases by about 25 MPa if the material is cycled at 90 pct rather than 80 pct of the yield stress at 453 K. Appendix A complements this analysis with the cyclic stress–strain loops for the tenth cycle in Figures 5 and 7 and demonstrates that only cycling at 90 pct of the yield results in noticeable plastic deformation.

Fig. 8

(a) Monotonic response at 293 K after cycling at 80 or 90 pct of yield stress at various temperatures as shown in Figs. 5 and 7. (b) Detail of the yield point response at 293 K after cycling at 80 or 90 pct of yield stress at various temperatures including the as-produced pristine material response.

Figures 6 and 7 demonstrate that significant softening can occur at 293 K after cyclic for 10 cycles at 453 K. This result is remarkable since 453 K corresponds to 0.25 of the material homologous temperature and recovery mechanisms are not profusely activated at this temperature and low applied strains. Furthermore, Figure 9 presents SEM characterization of the material after cycling at 90 pct of the yield stress (Figure 7). Compared to the as-produced material Figure 1, the softening does not affect the microstructure, which is similar in morphology (i.e., constituents, grain size, and homogeneity).

Fig. 9

Microstructure micrographs after the cyclic loading at × 250

3.3 Cyclic Loading at Various Temperatures with Hold Time

The results in Figure 6 are not only surprising for the softening, but also the apparent recovery of the strength with further cycling at 453 K. Hence, we further consider a cyclic sequence starting at 293 K, but with the addition of a hold time at a higher temperature. Figure 10 presents the cyclic deformation after 10 cycles at 293 K followed by 453 K, a hold time of 14,400 seconds (4 hours) at 673 K, and concluding with 10 cycles at 293 K. The results present no softening after holding the sample and the cyclic strain amplitudes for the first and last 10 cycles at 293 K are identical. A similar deforming sequence but a hold temperature of 523 K resulted also in the reduction of the softening as shown by Figure 11, albeit to a lower degree. Moreover, the comparison of the first 20 cycles from Figures 7, 10, and 11 demonstrates good reproducibility of experiments under identical loading conditions.

Fig. 10

Stress (a) and strain (b) responses as a function of time under constant stress amplitude of 90 pct of yield stress starting at 293 K for 10 cycles, followed by 10 cycles at 453 K, a hold time of 14,400 s (4 h) at 673 K, and ending with 10 cycles at 293 K. (c) Evolution of the cyclic strain amplitude in which no softening occurs during the last 10 cycles at room temperature

Fig. 11

Stress (a) and strain (b) responses as a function of time under constant stress amplitude of 90 pct of yield stress starting at 29 3 K for 10 cycles, followed by 10 cycles at 453 K, a hold time of 14,400 s (4 h) at 523 K, and ending with 10 cycles at 293 K. (c) Evolution of the cyclic strain amplitude in which some softening is evident during the last 10 cycles at room temperature

4 Discussion

4.1 DSA Responsible for Reversible Softening

Our results demonstrate that cycling an HSLA steel at 453 K can induce temporary softening, which can be fully reversed by holding the sample under tension for 4 hours at 673 K. This phenomenon occurs without noticeable microstructural changes, which suggests that nanoscale rather than mesoscale mechanisms is responsible for the softening. Similarly, cycling at 80 pct of the yield strength results in no softening, which becomes evident when cycling at 90 pct of the yield strength. In addition, the softening only occurs if a minimum amount of accumulated cyclic deformation is applied. Hence, the softening is associated with rate- and temperature-dependent plastic deformation mechanisms.

The reversibility of the softening makes it unlikely that the phenomenon is driven by recovery mechanisms linked to dislocation annihilation or microstructural changes, which are normally permanent. Instead, the mechanical response is compatible with DSA, as suggested by Hong et al.^[9] Depinning dislocations from interstitial atoms is a thermally activated process, which determines the number of dislocations that break free. At lower temperatures, Cottrell atmospheres turn most initial dislocations immobile, but higher thermal activation enables dislocations to glide from interstitial atmospheres before new dislocations nucleate. A minimum plastic strain must be applied to allow dislocations to glide far enough—on average—from Cottrell atmospheres.

In HSLA steels, nitrogen and carbon play important roles in strain aging of steel due to their high solubility and diffusivity.^[12] Around 500 K to 1000 K,^[13] these solute atoms can move faster than dislocations and temporarily arrest them, which typically results in DSA-induced serrated flow.^[14,15,16]

Figure 12 presents a detail of the softening response at 453 K and shows evidence of stress serrations that occurred during the loading period (either in tension or compressing) at intermediate strains. Although not conclusive, serrations are a strong indication of active DSA. In addition, Appendix A presents further evidence of serrations under monotonic loading and rules out any spurious error from sampling frequency effects.

Fig. 12

Example of serrations that appears at intermediate strains during loading at 453 K

Hence, we argue that cyclic loading HSLA steel at 453 K progressively displaces dislocations away from their Cottrell atmospheres (e.g., carbon, nitrogen), which facilitates glide and subsequent softening at 293 K. Upon holding the material at a higher temperature, atmospheres can diffuse back to dislocations and reinstate the strengthening. Notably, the cyclic deformation should be limited or additional hardening could compensate for the phenomena by increasing dislocation–dislocation interactions. Similarly, limited deformation or temperature would not allow enough dislocation to glide far enough to significantly break away from Cottrell atmospheres.

4.2 Strength Recovery Prediction

DSA-induced softening requires a minimum displacement from dislocations, along with enough time and temperature to allow interstitial atoms to diffuse to dislocation cores and reinstate strength. Hence, we proceed to demonstrate this rationale with a physics-based engineering model that estimates the time required to recover original the strength. An engineering model capable of predicting the softening requires the estimations of the mean free path of mobile dislocations, the mean diffusion distance, and the strengthening role of interstitials.

4.2.1 The dislocations mean free path

Initial yield in metallic materials is determined by the glide of dislocation segments that can move unobstructed (either existing or newly nucleated dislocations). Following Kocks et al.,^[17] we can relate the slip system shearing ($\gamma$) with the density of mobile dislocations ($\rho$), i.e.,

$$ \gamma = \rho lb, $$

(1)

in which $b$ corresponds to the Burgers vector, $\rho$ is the average mobile dislocation density, and $l$ is the average glide distance. Integrating upon a full loading cycle we can estimate the total plastic strain change per cycle ($\Delta \varepsilon_{{\text{p}}}$), such as

$$ \Delta \varepsilon_{{\text{p}}} = \frac{\rho lb}{M}, $$

(2)

in which $M$ is the Taylor factor and estimates the average slip system shear strain from the total plastic strain and has a value typically between 2 and 3.^[18] Hence, the mean dislocation glide distance can be estimated as follows:

$$ l = \frac{{M\varepsilon_{{\text{p}}} }}{\rho b}. $$

(3)

4.2.2 Strengthening role of interstitials

Carbon content strongly affects the mobility of dislocations and increases the yield strength in the steel. For instance, Calik et al.^[19] provide the bases for a linear correlation between a change in carbon content and the change in yield stress such that

$$ \Delta Y = B\Delta C $$

(4)

in which $\Delta Y$ is the change in yield strength and $\Delta C$ is the change in carbon content in weight. Furthermore, $B$ is a scaling constant that can be approximated as 800 MPa from experiments in Reference 19. Numerous researchers^{[20,21,22,23]} have demonstrated for a wide range of materials that a linear relation exists between yield stress and carbon content. This relation suggests that the saturation of Cottrell atmospheres requires a large content of carbon. Indeed, atomistic simulations have demonstrated that saturation of Cottrell atmospheres occurs at 10 at pct C.^[24] This experimental and theoretical evidence supports the linear relation used for estimating the yield stress.

Even though a linear correlation may not be valid for a large change in carbon concentration, it is likely to be a good approximation for small temporary changes around the equilibrium concentration. In addition, only a fraction of the total carbon atoms will be associated with Cottrell’s atmospheres around mobile dislocations, and the same fraction is associated with the softening by displacing them from mobile dislocations. Hence, the calibration for constant $B$ accounts for this fraction of carbon atoms, which is unknown.

4.2.3 Interstitial diffusion

The diffusion of interstitial can be analyzed with Fick’s second law, which relates the species concentration evolution to the Laplacian of the concentration,

$$ \frac{\partial C}{{\partial t}} = D\frac{{\partial^{2} C}}{{\partial x^{2} }}. $$

(5)

Here, C is the concentration and D is the diffusion coefficient and depends strongly on the temperature following,

$$ D = D_{0} e^{{ - \frac{{E_{{\text{a}}} }}{RT}}}, $$

(6)

where T (K) is the absolute temperature, R is the universal gas constant, $D_{0}$, is the maximal diffusion coefficient, and E_a is the activation energy. The values of E_a and $D_{0}$ for carbon and nitrogen have been extensively studied and reported in the Reference 25.

Considering a 1D problem with a constant boundary concentration of the solute, $C_{0}$, that can diffuse to the dislocation we obtain,

$$ C = C_{0} {\text{erfc}}\left( {\frac{x}{{2\sqrt {Dt} }}} \right), $$

(7)

in which erfc(x) stands for the complementary error function. Then, the change in concentration becomes

$$ \Delta C = C_{0} \left( {1 - {\text{erfc}}\left( {\frac{x}{{2\sqrt {Dt} }}} \right)} \right). $$

(8)

4.2.4 Change in yield strength due to cyclic loading

Finally, by combining Eqs. [3], [4], and [7] we can estimate the change in yield stress as a function of the applied cyclic strain, the temperature, and the hold time,

$$ \Delta Y = BC_{{\text{o}}} \left[ {1 - {\text{erfc}}\left( {\frac{{M\Delta \varepsilon_{{\text{p}}} }}{{2\rho b\sqrt {tD_{0} e^{{ - \frac{Q}{{{\text{RT}}}}}} } }}} \right)} \right]. $$

(9)

To evaluate Eq. [9], we quantify the change in yield stress for our experimental conditions as a function of the hold time and temperature. We consider an applied plastic strain of 4e−3 and 5e−5 that corresponds approximately to 90 and 80 pct yield testing at 453 K, respectively. Furthermore, we consider an initial carbon content of 0.024 for our HSLA steels and a mobile dislocation density of 5e13 m⁻².^[26] All other model parameters are taken directly from the literature and they are summarized in Table II.

Table II Parameters used in Modeling the Recovery from Softening

The results in Figure 13 predict a maximum reduction in yield stress of about 20 MPa due to DSA, which agrees with our experiments and aligns with findings from other researchers.^[27] At 90 pct of the yield stress, most strength can be recovered by holding the sample for 14,400 seconds at 523 K or 360 seconds at 673 K. These results also predict the partial recovery of strength while cycling for 3600 seconds at 453 K (Figure 6). In terms of cycling at 80 pct of the yield stress, the model predicts partial or almost full recovery of the strength after holding at 293 K for 360 seconds or 14,400 seconds, respectively. These results further suggest that softening could occur at 80 pct of the yield, but it would require cryogenic rather than room-temperature cycling.

Fig. 13

Predicted softening after cycling at 80 pct or 905 of the yield stress and waiting for 360 and 14400 s. Room temperature is enough to erase softening history within minutes when cycling at 80 pct of the yield stress, but not for 90 pct of the yield stress

We highlight that the value of Eq. [9] is on representing the nonlinear dependences among plastic strain, temperature, and time. We emphasize that our calculations rely entirely on parameterizations from the literature and the results are surprisingly close to those of the experiments, further supporting DSA as the cause of the softening. Additional experimental results can be pursued to calibrate more accurately constants $B$ and $M$ for the specific material and experimental conditions.

These values correspond to parameters computed from our experiments, standard constants, and parameters estimated independently by the literature.

5 Conclusion

This paper presents multiple experimental results that demonstrate the existence of reversible softening in HSLA steels after being cycled at 453 K. The softening appears under cyclic deformation at 90 pct of the yield stress and not at 80 pct of the yield stress. Similarly, there is no softening while cycling at room temperature.

We discussed different physical mechanisms involved in mechanical softening and presented evidence to support that DSA has a main role. The mechanistic understanding of DSA enabled us to propose a simple model to estimate the time required to recover full strength as a function of the applied cyclic plastic strain and the temperatures. Further work should further expand mechanistic understanding to avoid or make use of temporary softening during service conditions.

Appendix

Figure A1 compares the cyclic stress–strain loop for 80 and 90 pct of yield stress loading at room temperature. The lower stress loading results in an almost elastic response, while the higher loading results in non-negligible plastic deformation. The plastic strain amplitude for 90 pct of yield stress loading was computed to be approximately 3.5e−3.

Figure A1

Stress–strain loop for 80 and 90 pct of yield stress loading at 293 K

Finally, to further explore the existence of DSA, we performed two tensile tests at 255C at different strain rates (2.5 × 10^–4 and 5 × 10^–5) using a sampling frequency of 200 Hz. The results of these experiments in Figure A2 demonstrate that higher deformation rate results in significantly more serrations. A higher deformation rate results in a lower number of data points for equal sampling frequency, which would reduce rather than increase the noise. Hence, these results are also consistent with the existence of underlying DSA.

Figure A2

Monotonic response at 255C and different strain rates with a sampling frequency of 200 Hz