Enhancing the Predictive Capabilities of Microstructure Simulations of PBF-LB/M by an Evaluation of Nucleation Theories

Abstract

Powder Bed Fusion of Metals using a Laser Beam (PBF-LB/M) has proven to be a competitive manufacturing technology to produce customized parts with a high geometric complexity. Due to process-specific characteristics, such as high cooling rates, the microstructural features can be tailored. This offers the possibility to locally control the mechanical properties. Therefore, the grain structure has to be reliably predicted at first. The starting point of the grain formation and the growth process is characterized by the nucleation. Over the course of this study, various nucleation theories were applied to the PBF-LB/M process and their suitability was evaluated. The two Sc-modified aluminum alloys Scalmalloy^® and Scancromal^® were processed with a novel experimental PBF-LB/M setup. By performing melt pool simulations based on the Finite Element Method (FEM), the input data for the nucleation models were obtained. The simulatively predicted nucleation zones based on the different theories were compared to real metallographic images and to literature results. It was found that the phenomenological approach should be used whenever no first-time-right prediction of the simulation is necessary. The physically based models with the heterogeneous nucleation should be applied if a first-time-right prediction is striven for. For applications in PBF-LB/M, the nucleation models should be extended in terms of the influence of precipitates and the high cooling rates during the manufacturing process. The presented approach may be used to further assess grain nucleation models for various additive manufacturing processes.

1 Introduction

In recent years, Additive Manufacturing (AM) has found its way into various industrial domains due to striking advantages over conventional manufacturing processes. In particular, the Powder Bed Fusion of Metals using a Laser Beam (PBF-LB/M) has proven to be a reliable means to manufacture parts with a high geometric complexity¹ and reliable mechanical properties.² The PBF-LB/M enables tailoring the local microstructure by adapting the process parameters during the manufacturing. This allows for the generation of functionally graded materials³ and enables a significant influence on the crack initiation and propagation behavior.^4,5

To exploit this process-specific advantage of the microstructure tailoring, a reliable prediction of the internal grain structure on the part scale is expedient. Cellular Automaton (CA) models are known to be an appropriate means to provide this prediction. This is because they offer the necessary level of detail while having the potential to represent the microstructural evolution on part dimensions.⁶ The validity of the predicted grain structure, however, highly depends on the modeling of nucleation phenomena.⁷ Nucleation describes the formation of aggregates of a new phase and can be seen as the starting point of the grain formation and the growth process.⁸

Since the nucleation phenomena are thermally driven processes,⁹ the temperature distribution within the melt pool needs to be known. The necessary thermal values can be determined by numerical simulations of the PBF-LB/M process and are incorporated into the nucleation models to predict the nucleation locations. In the literature, there are generally two approaches to consider these grain formation processes. These formulations can be stated as the phenomenological approach and the physically based models and are described in the following.

1.1 Phenomenological Approach

This approach is mostly applied to model the nucleation phenomena in microstructure simulations. The model needs to be calibrated by experimentally determined values. It can therefore be categorized as phenomenologically based. The model was first introduced by Rappaz¹⁰ for general solidification processes and was applied to the AM by various researchers. Dezfoli et al.¹¹ set up a coupled FEM-CA model, in which they determined the total nucleation density as a function of the undercooled temperature in the simulated melt pool for the Ti-6Al-4V alloy. They considered nucleation phenomena at the melt pool border as well as within the bulk molten material. They applied calibration constants from the literature and investigated how a secondary heat source influences the nucleation and microstructural evolution. The phenomenological approach was also utilized by Yang et al.¹² for the same material. They also extracted the nucleation calibration values from the literature and investigated how variable thermal cycles influence the microstructure. The approach was then further pursued by Zinoviev et al.¹³ and by Shi et al.¹⁴ for the stainless steel 316L. The former laid their focus on investigating the influence of heat source parameters on the resulting grain structure. The latter studied the effect of nucleation on the microstructure evolution by performing simulations with and without nucleation in the fusion zone. A significant impact of the nucleation modeling on the resulting microstructure could be observed. Mohebbi and Ploshikhin¹⁵ set up a flexible CA simulation tool in terms of nucleation calibration for the aluminum alloy AlSi10Mg. Various criteria were integrated into the nucleation model to first nominate and afterward activate specific CA cells for nucleation. Dezfoli et al.¹⁶ applied this nucleation model to the nickel-based superalloy Inconel 713LC. They focused on modeling and simulating the microsegregation behavior during PBF-LB/M.

1.2 Physically Based Approaches

Based on theoretical considerations and physical relationships, these approaches aim to model the nucleation process without the need for a calibration. They consider generally applicable nucleation models, which take into account the phenomena on the atomic scale. Shi et al.¹⁷ considered the homogeneous and heterogeneous nucleation based on the Classical Nucleation Theory (CNT) to predict the locations of nuclei in a Phase Field and CA model in the PBF-LB/M for Ti-6Al-4V. The authors showed that the nucleation rates as a function of the temperature for both modeling approaches differed strongly from each other. They integrated the heterogeneous nucleation rules at the grain boundaries, while assuming a homogeneous nucleation within the melt pool. As they focused on the effect of the solidification behavior and process parameter variations on the resulting grain structure, no further nucleation modeling approaches were investigated and compared to each other. The CNT was also applied to determine the nucleation sites based on the nucleation rate for Ti-6Al-4V and AlSi10Mg, respectively, and to integrate it into a Phase Field model.^18,19 The authors emphasized the importance of modeling the nucleation behavior for an accurate representation of the resulting grain structure. They, however, only considered heterogeneous nucleation at the melt pool boundary. An evaluation of further promising nucleation models did not take place.

As shown by this literature review, so far only single nucleation models from the literature without a differentiated view are utilized to predict the grain structure evolution during metal-based AM. Also, there is no common consensus of what type of nucleation model to apply, as various approaches are pursued.

The goal of this paper is to enhance the predictive capabilities of microstructure simulations in PBF-LB/M. This was realized by an evaluation of various nucleation theories with respect to their applicability to PBF-LB/M. For this purpose, two aluminum alloys were processed by using a novel research PBF-LB/M setup and the specimens were characterized metallographically. A moving heat source using the FEM was calibrated based on these results, providing the thermal input to the investigated phenomenological and physically based nucleation models. Their predictions concerning the nucleation rate and the locations of nuclei were compared and evaluated.

2 Nucleation Models and Parameters

2.1 Material Characterization

As powder, the Sc-modified aluminum alloys Scalmalloy^® and Scancromal^® (Airbus SE, Germany) were chosen. These alloys exhibit significantly different microstructures. The EN AW-5083 aluminum alloy was selected for the build plate material since it has a similar chemical composition as the utilized powder materials. The chemical composition of the utilized powders^20,21 and the base plate material²² is shown in Table I.

Table I Chemical Composition of the Utilized Alloys

The particle size distribution with the diameters $D_{10}$, $D_{50}$, and $D_{90}$ is stated as 26.6 $\mu$m, 42.5 $\mu$m, and 68.0 $\mu$m for Scalmalloy^®, and 32.8 $\mu$m, 48.0 $\mu$m, and 68.9 $\mu$m for Scancromal^®.

For Scalmalloy^®, the solidus temperature $T_{\text {s}}$ and the liquidus temperature $T_{\text {l}}$ are stated as 853 K and 1053 K, respectively. Scancromal^® is characterized by an $T_{\text {s}} = 913$ K and an $T_{\text {l}} = 1173$ K.

To consider the thermal behavior of the two aluminum alloys in the bulk and the powder form in the simulation, the values for the specific heat capacity, the thermal conductivity, and the density were determined. The material parameters for the bulk 5083 aluminum alloy were also extracted. In accordance with Weirather et al.²³ the material properties were determined by weighting and averaging the data of the chemical elements in the alloys.

For the powder, the value for the thermal conductivity at 298 K was chosen to be 0.15 W/($\text {m}\,\text {K}$), based on Rombouts et al.²⁴ After reaching the $T_{\text {l}}$ of the respective alloys, the bulk parameters were applied. For the specific heat capacity at 298 K, the values from Alkahari et al.²⁵ were used. The densities of Scalmalloy^® and the Scancromal^® powder were taken as 1440 kg/m³²⁰ and 1600 kg/m³,²¹ respectively. Between the $T_{\text {s}}$ and the $T_{\text {l}}$, the thermophysical properties of the powder were increased to the respective bulk characteristics.

The parameters along with their corresponding temperatures are plotted in Figure A1 in the appendix. The discrete values are given in Table A1 in the appendix.

2.2 Phenomenological Approach

This approach, which is based on Oldfield,²⁶ considers the nucleation density N as the relevant parameter to describe the nucleation behavior within a material and is calculated as

$$\begin{aligned} N = \int _0^{\Delta T} \frac{\text {d}N}{\text {d}(\Delta T')} \text {d}(\Delta T') = \frac{N_0}{\Delta T_\sigma \sqrt{2 \pi }} \int _0^{\Delta T} \exp {\left( - \frac{\Delta T' - \Delta T_\text {c}}{\sqrt{2} \Delta T_\sigma } \right) } \; , \end{aligned}$$

(1)

where $\text {d}N/\text {d}(\Delta T')$ describes the increase of the nucleation with an increasing undercooling $\Delta T$, assuming a Gaussian distribution. $N_0$ represents the maximum nucleation density, $\Delta T_{\text {c}}$ the mean nucleation undercooling, and $\Delta T_{\sigma}$ the standard deviation of the distribution.

Using the phenomenological approach, the latter three parameters need to be calibrated. Since the goal of this study is to evaluate the capabilities of the respective models in terms of their ability to predict the correct nucleation locations, no calibration was conducted for these parameters. Instead, the fusion boundary nucleation values for the AlSi10Mg alloy obtained by Mohebbi and Ploshikhin¹⁵ were utilized. The corresponding values are given in Table A2 in the appendix.

$\Delta T$ was calculated as the difference between $T_{\text {l}}$ and the apparent temperature T at a defined location as proposed by Markov.²⁷

2.3 Physically Based Approaches

Different physically based models, which have proven to be consistent with the nucleation of metals, solidifying from their liquid state, were evaluated.

2.3.1 Preliminary calculations

The nucleation rate J of all physically based nucleation models is calculated as

$$\begin{aligned} J = K \cdot \exp {\left( - \frac{\Delta G^*}{k_{\text {B}} \cdot T} \right) } \; . \end{aligned}$$

(2)

$\Delta G^*$ represents the energy barrier at the critical nucleus radius, $k_{\text{B}}$ is the Boltzmann constant, and K represents the kinetic pre-factor. With the frequency of attachment of atoms to the critical nucleus and the Zeldovich factor, the pre-factor K can be calculated by

$$\begin{aligned} K = \frac{2 \sqrt{\gamma } \cdot f \cdot \lambda \cdot \rho_{\text {l}}}{\sqrt{k_{{\text {B}}} \cdot T} \cdot \rho_{\text{s}}} \cdot \exp {\left( - \frac{\Delta U}{k_{{\text{B}}} \cdot T} \right) } \; . \end{aligned}$$

(3)

Here, $\gamma$ describes the specific surface energy, f is the frequency factor, and $\lambda$ is the mean free path of particles in the liquid. The parameters $\rho_{\text{l}}$ and $\rho_{\text{s}}$ describe the number density, describing the number of atoms per unit volume, of the liquid and the solid material, respectively. The $\Delta U$ is the energy of desolvation.

2.3.2 Models

To calculate the nucleation rate J, the model-specific critical nucleation barriers need to be determined, which is discussed in the following.

Homogeneous Nucleation Theory. The energy barrier to be exceeded, until a growable nucleus is built, can be calculated by a limit calculation of the critical nucleus radius. With $\Delta h_{\text{m}}$ as the molar enthalpy of melting, this results for the homogeneous nucleation in Reference 28

$$\begin{aligned} \Delta G_{\text{Hom}}^* = \frac{16 \pi \cdot \gamma ^3 \cdot T_{\text{l}}^2}{3 \cdot \Delta h_{\text{m}}^2 \cdot \Delta T^2 \cdot \rho_{\text{s}}^2} \; . \end{aligned}$$

(4)

Heterogeneous Nucleation Theory. In the heterogeneous nucleation theory, the assumption is made that a nucleus is formed due to the existence of solid objects (seed crystals) in the liquid metal.^27,28 The shape of the nucleus is characterized by a spherical cap with the wetting angle $\theta$, as depicted in Figure 1.

Fig. 1

Definition of the wetting angle $\theta$ (adapted from Porter and Easterling²⁸)

The corresponding energy barrier is calculated as

$$\begin{aligned} \Delta G_{\text{Het}}^* = S(\theta ) \cdot \Delta G_{\text{Hom}}^* \; , \end{aligned}$$

(5)

whereby $S(\theta )$ is the shape factor:

$$\begin{aligned} S(\theta ) = (2+\cos {\theta }) (1-\cos {\theta })^2 / 4 \; . \end{aligned}$$

(6)

Self-consistent Classical Nucleation Theory. The Self-consistent Classical Theory (SCCT) assumes that no energy is necessary to build the first monomer.²⁹ This free energy of the molecule can be determined by

$$\begin{aligned} \Delta G_{1} = \frac{\Delta h_{\text{m}} \cdot \Delta T \cdot \rho_{\text{s}}}{T_{\text{l}} \cdot \rho_{\text{l}}} + 4 \pi \cdot r_{\text{m}}^2 \cdot \gamma \; , \end{aligned}$$

(7)

where

$$\begin{aligned} r_{\text{m}} = \frac{1}{\root 3 \of {\frac{4}{3}\pi \cdot \rho_{\text{l}}}} \end{aligned}$$

(8)

is the radius of the first monomer. For the energy barrier, the following final statement holds:

$$\begin{aligned} \Delta G_{\text{SCCT}}^* = \Delta G_{\text{Hom}}^* - \Delta G_{1} \; . \end{aligned}$$

(9)

Diffuse Interface Theory. The Diffuse Interphase Theory (DIT) was described by various authors.^29,30,31 The density of the nucleus over the radius cannot be assumed to be constant anymore.³² Based on this, the nucleus radius-dependent enthalpy $\Delta h(r)$ and entropy $\Delta s(r)$ of the nucleus were introduced. For the center of the core, the relations $\Delta h(0) = \Delta h_{0}$ and $\Delta s(0) = \Delta s_{0}$ are established.

The energy barrier of the DIT can then be stated as

$$\begin{aligned} \Delta G_{\text{DIT}}^* = - \frac{4 \pi }{3} \cdot \delta ^3 \cdot \Delta g_{0} \cdot \psi (\eta ) \; , \end{aligned}$$

(10)

whereby the thickness $\delta$ of the interface is calculated by

$$\begin{aligned} \delta = \frac{\gamma \cdot v_{\text{c}}}{\Delta h_{\text{m}}} \; , \end{aligned}$$

(11)

with the parameter $v_{\text{c}}$ as the molecule volume. Additionally,

$$\begin{aligned} \psi (\eta ) = 2 \cdot (1+q) \cdot \eta ^{-3} - (3+2q) \cdot \eta ^{-2} + \eta ^{-1} \end{aligned}$$

(12)

holds, with

$$\begin{aligned} q&= \sqrt{1-\eta } \; , \end{aligned}$$

(13)

$$\begin{aligned} \eta&= \Delta g_{0}/\Delta h_{0} \; , \ \text {and} \end{aligned}$$

(14)

$$\begin{aligned} \Delta g_{0}&= \Delta h_{0} - T \cdot \Delta s_{0} \; . \end{aligned}$$

(15)

$\Delta h_{0}$ and $\Delta s_{0}$ are calculated according to

$$\begin{aligned} \Delta h_{0}&= \frac{-\Delta h_{\text{m}} - \int \Delta c_{\text{p}} \text {d} T}{v_{\text{c}}} \ \text {and}\end{aligned}$$

(16)

$$\begin{aligned} \Delta s_{0}&= \frac{- \frac{\Delta h_{\text{m}}}{T_{\text{l}}} - \int \frac{\Delta c_{\text{p}}}{T} {\text {d}}T}{v_{\text{c}}} \; , \end{aligned}$$

(17)

whereby $\Delta c_{\text{p}}$ describes the difference of the specific heat capacity between the solid and the liquid material state, $c_{\text{p,s}}$ and $c_{\text{p,l}}$.

2.3.3 Parameters

To calculate the nucleation rate J based on the proposed physically based nucleation models for the Sc-modified aluminum alloys, the corresponding material parameters were determined. These were calculated by weighting and averaging the data of the respective chemical elements,²³ except for the mean free path and the specific surface energy $\gamma$. For the former, the value for pure aluminum was selected. The latter was estimated for the corresponding elements in the aluminum alloys, based on the relationship from Markov et al.,²⁷ according to which $\gamma_{\text{m}} / \Delta h_{\text{m}} \approx 0.46$ is valid for a high number of metals. The parameter $\gamma_{\text{m}}$ is the molar surface energy. Along with the molar volume of the specific element and the Avogadro constant $N_{\text{A}}$, the specific surface energy can then be calculated by the relationship

$$\gamma = \frac{\gamma_{\text{m}}}{N_{\text{A}} \cdot v_{\text{c}}^{2/3}}.$$

(18)

The wetting angle $\theta$ was tested with different values. The specific heat capacity of the solid $c_{\text{p,s}}$ was calculated according to the relationship from Valencia and Quested³³:

$$c_{\text{p,s}} = e + f \cdot T + g \cdot T^{-2}. $$

(19)

The corresponding parameters e, f, and g are stated in Table A3 in the appendix along with the remaining material-specific values. The general material constants can be found in Table A4 in the appendix.

3 Nucleation Location

3.1 Preparations

To view the nucleation locations in the melt pool more precisely and independently of the finite element mesh size, a sub-mesh, as proposed by Shi et al.¹⁷ and Shi et al.,¹⁴ was created. A schematic illustration is visualized in Figure 2. The sub-mesh had a grid size of 1 $\mu$m. The temperature values at the data points of the finer mesh were determined by linear interpolation based on the nodal values of the finite elements.

Fig. 2

Schematic illustration of the finite elements and the corresponding sub-mesh

The nucleus locations were determined in the mushy zone for the temperature region between $T_{\text{s}}$ and $T_{\text{l}}$. The volume V, in which the nuclei could be built, was calculated by approximating the volume of the half-elliptical shell using the melt pool dimensions from Table III as

$$\begin{aligned} V = \frac{\pi }{3} \cdot (L_{\text{s}} \cdot W_{\text{s}} \cdot D_{\text{s}} - L_{\text{l}} \cdot W_{\text{l}} \cdot D_{\text{l}}) \; . \end{aligned}$$

(20)

3.2 Phenomenological Approach

The nucleation process is primarily a probabilistic phenomenon.³⁴ The final nucleation locations were determined by calculating the probability of forming a critical nucleus during a time period $\Delta t$ in a volume V (see Eq. [20]) as a function of the nucleation density. This was done by using a probabilistic Poisson seeding algorithm¹⁴:

$$\begin{aligned} P_{\text{prob}} = \left( N(t+\Delta t) - N(t) \right) \cdot V \; . \end{aligned}$$

(21)

Subsequently, a field with random values $P_{i}$ between 0 and 1 for each nodal value i of the sub-mesh was created. A nucleation event was assumed to be triggered, if the following inequation is fulfilled:

$$\begin{aligned} P_{\text{prob}} > P_{i} \; . \end{aligned}$$

(22)

3.3 Physically Based Approach

For the physically based approach, the nucleation sites were predicted by applying a probabilistic Poisson seeding method, considering the model-specific nucleation rate J to describe the nucleation process. This method was introduced by Simmons et al.³⁵ and Leonard and Im³⁶ and was applied to PBF-LB/M by multiple authors.^17,19,37 According to this, the following equation holds:

$$\begin{aligned} P_{\text{prob}} = 1 - \exp {(-J \cdot V \cdot \Delta t}) \; . \end{aligned}$$

(23)

In accordance with the phenomenological approach, the location of newly formed nuclei is determined by evaluating in Eq. [22].

4 Experimental and Simulative Setup

4.1 Experiments and Analyses

For the calibration of the moving heat source and the validation of the nucleation simulations, single weld lines and multi-layered cuboids were experimentally generated on a novel PBF-LB/M setup.³⁸ Due to the small dimensions of the build plate of $79 \times 32 \times 4$ mm$^3$, it is highly suited for subsequent metallographic investigations of the fabricated samples. For the two Sc-modified aluminum alloys, the general process parameters can be seen in Table II.

Table II Process Parameters

The cuboids had a cross-sectional area of $10 \times 10$ mm$^2$ and a meander hatching was applied. The hatch spacing was set to 100 $\mu$m. The samples were comprised of ten layers in total. A rotation of the hatching strategy of $90^{\circ }$ after the fifth layer was conducted.

The single and multiple weld lines were cut with a metallographic cut-off machine (Qcut 150 A, QATM, Germany), ground and polished (EcoMet 300 Pro, Buehler, Germany), and etched with the etching agent based on Kroll. The samples were then investigated by means of a digital microscope (VHX-7000, Keyence, Japan).

4.2 Moving Heat Source

The thermal inputs for the nucleation models were generated by a moving volumetric heat source based on the ellipsoid model from Goldak et al.³⁹ It was implemented in the open source FEM solver CalculiX CrunchiX.⁴⁰ The heat source model has already been successfully applied to the PBF-LB/M process for different materials by various researchers.^41,42,43

4.2.1 Governing equations

The heat source is visualized in Figure 3, showing the ellipsoid along with its geometric parameters and its orientation.

Fig. 3

Schematic illustration of the Goldak heat source (adapted from Goldak et al.³⁹)

The parameters a, b, and c represent the geometrical dimensions of the heat source, while $\xi$, y, and z describe the coordinates of a moving coordinate system. The latter has its origin in the center of the heat source and moves with the laser beam scan speed v.

The heat flux distribution of the Goldak heat source, representing the heat input as a result of the interaction of the laser beam with the matter, is calculated as

$$\begin{aligned} q(\xi ,y,z,t) = \frac{6 \sqrt{3} \cdot P \cdot \eta }{a \cdot b \cdot c \cdot \root 3 \of {\pi }} \exp {\left( - \frac{3\xi ^2}{a^2} - \frac{3y^2}{b^2} -\frac{3z^2}{c^2} \right) } \; , \end{aligned}$$

(24)

with

$$\begin{aligned} \xi = x + v \cdot (\tau -t) \; . \end{aligned}$$

(25)

The parameter P describes the power of the laser, $\eta$ represents the efficiency, t is the process time, and $\tau$ describes a lag factor. The latter is needed to define the heat source position at $t = 0$.

4.2.2 Simulation domain

An overview of the different components with their meshes in the simulation area along with their dimensions is given in Figure 4.

Fig. 4

Simulation domain with the different meshes

The simulation area was comprised of a cuboid with the dimension $3 \times 2 \times 0.5$ mm$^3$, representing the substrate plate, and a cuboidal structure with equal x and y dimensions on top of it, describing the powder layer. The height of the powder layer was set to 30 $\mu$m for Scalmalloy^® and 50 $\mu$m for Scancromal^®. In the center of the powder layer, an area with $2.5 \times 0.15$ mm$^2$ with the corresponding layer heights was set up, representing the domain, in which the melt pool was generated later on.

For the melt pool area, a mesh refinement was conducted. Based on this mesh, the remaining powder elements were assigned gradually growing elements with the maximum size of 0.025 mm. The elemental sizes of the base plate were gradually increased to 0.05 mm. The growth factor was set to 1.3.

At the start of each simulation, the nodal temperatures of all components were set to the room temperature of 293.15 K. No convective phenomena due to an inert gas flow were considered, which was in accordance with the experiments. Each element in the substrate plate was assigned the material properties of EN AW-5083. The powder elements and the melt pool elements obtained the material properties of Scalmalloy^® or Scancromal^® powder, respectively, at the start of a simulation. After the elements in the melt pool area were melted, these were assigned the bulk material properties of the respective Sc-modified aluminum alloy.

The time step $\Delta t$ was chosen to be $5 \cdot 10^{-5}$ s for Scalmalloy^® and $3.33 \cdot 10^{-5}$ s for Scancromal^®. This allowed for an overlap of the heat source and therefore for a continuous melt pool from one step to the next. There, the corresponding laser beam scan speed was taken into account.

4.2.3 Mesh convergence study

All elements were chosen to be linear tetrahedrons. For the elements in the melt pool area, a mesh convergence study was conducted with identical heat source parameters. The root-mean-square (RMS) temperature of nine nodes at the topmost z coordinates in the stable melt pool region (see Figure 5) was evaluated. The element sizes were varied and were set to 0.005, 0.01, and 0.015 mm, respectively. The results of this study are illustrated in Figure 6.

Fig. 5

Location of the evaluated nodes for the calibration

Fig. 6

Computation time and root-mean-square temperature for various element sizes

As can be seen in Figure 6, when utilizing 32 central processing units in parallel for each simulation, the computation time increased from 770.38 s to 1825.6 s when lowering the element size from 0.01 mm to 0.005 mm, without changing the RMS value significantly. Using this parameter at the smallest element size as the basis, the relative error of the RMS temperature was calculated to be 1.89  and 0.24 pct for an element size of 0.015 mm and 0.01 mm, respectively. Due to the short simulation time and the small relative error, the element size of 0.01 mm in the melt pool area was chosen for the remaining investigations.

4.2.4 Calibration

For the heat source calibration, the melt pool widths and depths of the single weld line experiments were determined from the microscopic images. In total, four cross sections from two weld lines of each alloy were analyzed and the mean values along with the standard deviations were extracted (see Figure 7).

Fig. 7

Experimental melt pool dimensions

It can be seen that the melt pool dimensions of the two aluminum alloys did not differ significantly from each other. The mean values are at comparable levels and the error bars overlap in wide ranges.

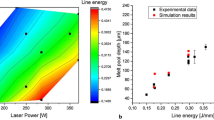
The moving heat source was calibrated by modifying the four parameters a, b, c, and $\eta$. The parameters b and c were calibrated by utilizing the width W and the depth D of the experimentally created melt pools at $T_{\text{s}}$, $W_{\text{s,exp}}$, and $D_{\text {s,exp}}$, respectively. The simulatively predicted width $W_{\text{s,sim}}$ and depth $D_{\text{s,sim}}$ were also evaluated at $T_{\text{s}}$. A comparison between the simulation and the experiment can be seen in Figure 8.

Fig. 8

Comparison of the cross-sectional melt pool dimensions: (a) experimental, (b) simulative

The parameter a, responsible for the melt pool length L, was calibrated based on the determined melt pool lifetime from Liu et al.⁴⁴ There, a melt pool length with a value of 172 $\mu$m could be calculated.

The efficiency parameter $\eta$ was set based on the studies from Liu et al.⁴⁴ They observed a maximum temperature $T_{\text{max}} \approx 2300$ K for the chosen scan speed in the stable area of the melt pool.

The final results of the calibration procedure are shown in Table III. The simulatively determined widths and depths at $T_{\text{s}}$ were within the experimental standard deviations (see Figure 7). The lengths at $T_{\text{s}}$ as well as the $T_{\text{max}}$ corresponded to those from Liu et al.⁴⁴

Table III Calibration Constants of the Goldak Heat Source, the Resulting Melt Pool Dimensions, and the Maximum Melt Pool Temperature $T_{\text{max}}$ for the Two Sc-Modified Aluminum Alloys

5 Results and Discussion

5.1 Nucleation Rates

The nucleation models were implemented and evaluated in MATLAB. To allow for a comparison between the nucleation density and the results of the physically based models, the nucleation density is divided by the respective time step $\Delta t$.

The nucleation rate J at $T_{\text{s}}$ can be stated as $1.990 \cdot 10^{24}$ m$^{-3}$s$^{-1}$ for Scalmalloy^® and $2.990 \cdot 10^{24}$ m$^{-3}$s$^{-1}$ for Scancromal^®. The values of the physically based models at this temperature are given in Table IV.

Table IV Nucleation Rates J Based on the Physically Based Models for Both Sc-Modified Aluminum Alloys at the Solidus Temperature $T_{\text{s}}$

It can be seen that even the lowest nucleation rate J, predicted by the homogeneous nucleation approach, is increased by at least five orders of magnitude and up to 18 orders of magnitude for the heterogeneous nucleation model with $\theta = 0.1 \cdot \pi$ compared to the phenomenological approach. However, the increased nucleation rate J of Scancromal^® compared to Scalmalloy^® is in accordance with the phenomenological approach.

5.2 Nucleation Locations

Based on the calculated nucleation rate J and nucleation densities, the nucleation locations within the mushy zone were determined (see Figure 9).

Fig. 9

Nucleation locations in the melt pool: (a) legend for the nucleation locations, cross-sectional views for the (b) phenomenological approach – Scalmalloy^®, (c) phenomenological approach – Scancromal^®, (d) physically based approaches – Scalmalloy^®, (e) physically based approaches – Scancromal^®, and longitudinal views for the (f) phenomenological approach – Scalmalloy^®, (g) phenomenological approach – Scancromal^®, (h) physically based approaches – Scalmalloy^®, (i) physically based approaches – Scancromal^®

The predicted regions of the nucleation in the melt pool cross sections are illustrated in Figures 9(b) and (c) for the phenomenological approach, and in Figures 9(d) and (e) for the physically based models, each for Scalmalloy^® and Scancromal^®. For reasons of clarity, the heterogeneous nucleation model was only evaluated for $\theta = 0.3 \cdot \pi$.

The depictions showing the physically based results are to be read as follows: the nucleation film of each nucleation model starts at the outer melt pool border. Each further layer to be seen in Figures 9(d) and (e) is therefore an addition to the previous ones.

Based on these results, it can be seen that for both Sc-modified alloys, the phenomenological approach predicted the lowest nucleation rate J from all models. The nucleation spots were determined primarily in the lower part of the mushy zone. Their layer heights did not exceed 1 $\mu$m and they did not spread over about half of the melt pool depth in the z direction. As the same calibrated model constants were used for both alloys, the amount of nuclei of the two materials did not differ significantly.

Concerning the physically based models, the homogeneous nucleation model predicted the thinnest nucleation film, reaching about 1/3 of the mushy zone thickness and spreading along the complete melt pool border. Few additional nucleation spots on top of the homogeneous nucleation layer were predicted by the SCCT and an additional complete layer of about 1 $\mu$m thickness was determined by the DIT. The heterogeneous nucleation predicted the thickest nucleation layer with a thickness of about 85 pct of the total mushy zone thickness. As opposed to the phenomenological approach, the layer thicknesses for Scancromal^® predicted by each physically based model, except for the heterogeneous one, increased by about 10 to 15 pct compared to those of Scalmalloy^®.

The evaluation of the longitudinal section was performed by a cut along the y-z plane through the stable melt pool center. For the phenomenological approach (see Figures 9(f) and (g)), the nucleation location remained at the bottom of the mushy zone and did not expand to the melt pool tail. The results for the physically based approaches (see Figures 9(h) and (i)) are also in compliance with the cross-sectional results. An increase of nucleation phenomena toward the end of the melt pool was predicted. The generally increased layer thicknesses for Scancromal^® compared to Scalmalloy^® persisted.

The fact that the homogeneous approach predicted one of the lowest nucleation layer thicknesses was to be expected. This can be explained by Eqs. [5] and [9], which show that the heterogeneous nucleation and the SCCT are characterized by a reduced energy barrier compared to that for the homogeneous nucleation. Despite the differing derivation and calculation of nucleation for the DIT compared to the SCCT, a comparable nucleation layer thickness was predicted. The slightly increased amount of nucleation for the DIT can be attributed to its consideration of a non-sharp interface between the solid and the liquid, which results in a reduced nucleation barrier. The even further increased number of nuclei for the heterogeneous approach is attributable to the shape factor S, which – depending on the chosen wetting angle $\theta$ – significantly reduces the energy barrier of building a thermodynamically stable nucleus.

5.3 Comparison to the Experimental Results and to the Literature

The respective multi-layer cuboidal specimens were investigated in and perpendicular to the direction of the laser path. The results for both materials are presented in Figure 10.

Fig. 10

Nucleation locations based on the metallographic investigations: cross-sectional views for (a) Scalmalloy^®, (b) Scancromal^®, and longitudinal views for (c) Scalmalloy^®, (d) Scancromal^®

As observed by Kuo et al.,⁴⁵ the Scalmalloy^® specimens exhibited sub-micron-sized grains at the melt pool border (see the bright areas in Figure 10(a). These were generated due to a significantly increased amount of nuclei-building events in this location. The latter are based on Al$_3$Sc and Al$_3$(Sc$_{\text{x}}$, Zr$_{1-\text {x}}$) precipitates, acting as seed crystals during the solidification.⁴⁶ Looking at the longitudinal section (see Figure 10(c)), the sub-micron structures are localized at the bottom of the melt pool. This was also shown by Spierings et al.⁴⁷

Concerning Scancromal^®, the melt pool borders could also be detected after the etching process (see the bright areas in Figures 10(b) and 10(d). However, as opposed to Scalmalloy^®, these shadings along the melt pool border represent the location of Al$_{11}$Cr$_{2}$ and Al$_{13}$Cr$_{2}$/Al$_7$Cr precipitates.^48,49

Additional experimental results showing the nucleation locations along the melt pool borders in Scalmalloy^® and Scancromal^® can be found in Figure A2 in the appendix.

A comparison between the predicted nucleation layers with the microscopic investigations is illustrated in Figure 11 on the left. For the experimental evaluation, a total number of ten melt pools with at least three measuring points for each were selected from the multi-layered specimens.

Fig. 11

Quantitative comparison between the results of the experiment and the simulations with regard to the nucleation layer thicknesses

It can be seen that the simulatively predicted nucleation layer height for Scalmalloy^® was determined to be 11 $\mu$m with the heterogeneous model approach. Each of the remaining models predicted a reduced value. The corresponding experimentally determined mean nucleation layer thickness was 10.5 $\mu$m. Similar thicknesses for Scalmalloy^® were also observed by different authors.^47,48,49 On the one hand, only the heterogeneous approach was able to predict the number of nuclei in the mushy zone. The remaining physically based models did not correctly describe the nucleation behavior, as the layer thicknesses were too thin. Only the results based on the DIT were within the standard deviation. On the other hand, the phenomenological approach is the only approach being capable of predicting the correct nucleation locations in the longitudinal section. This approach, however, did not predict the correct number of nuclei, as these spread almost across the whole mushy zone thickness. Additionally, the phenomenological approach needs a calibration for this specific material, not allowing for an actual prediction of the nucleation process.

A quantitative comparison between the experimental and simulative results can be also seen for Scancromal^® in Figure 11 on the right. As in the case of Scalmalloy^®, the closest matching results were obtained by the heterogeneous approach. The created precipitates have a strong mismatch in their crystal structure compared to the surrounding aluminum matrix. These precipitates can therefore not act as effective nuclei,⁴⁹ which results in a strong columnar grain structure with a <100> texture. At the same time, the elements Sc and Zr, which ensured the grain refining effects at the melt pool border in Scalmalloy^®, are believed to be incorporated into the Cr phases. This strongly reduces the creation of grain refining precipitates in Scancromal^®.⁴⁹ Therefore, the predicted grains must not act as a starting point for growing grains.

The heterogeneous nucleation modeling is the only approach resulting in a nucleation layer thickness in close accordance with the experimental results for both materials. This can be attributed to the fact that it considers a reduction of the energy barrier due to external factors to build a thermodynamically stable nucleus. These external factors can be exemplarily described by precipitates or non-molten particles in the previously solidified layers.¹⁵ Neither the homogeneous nucleation model nor the DIT takes into account such effects. The reduction of the energy barrier by the energy to build the first monomer $\Delta G_1$ in the SCCT was found to be not sufficient.

The comparison between the presented models and the experimental results and the literature for the two Sc-modified aluminum alloys emphasized the need for an extension of the different modeling approaches. So far, these essentially predict the nucleation events based on $\Delta T$. The extension of the models has to be twofold: first, the models need to be extended in terms of precipitations as a function of the chemical composition and their coherency. A basis for this might be provided by the CALPHAD method.⁵⁰ However, this method is not suited for domains with high solidification rates, leading to metastable equilibria and undiscovered phases.⁵¹ This is the case for the PBF-LB/M process, where cooling rates of about $10^6$ K/s⁵² are present. Therefore, the models secondly need to be extended in a way to incorporate the respective time scale during the process.

6 Conclusions and Outlook

For PBF-LB/M, it is necessary to model the nucleation phenomena that take place during the building process to correctly predict the resulting microstructure. In this paper, a phenomenological model and physically based nucleation approaches were discussed. The models were implemented and fed with simulatively determined thermal values. Their results were compared to each other as well as to experimental results and to observations in the literature.

The phenomenological approach does not allow for an actual prediction of the nucleation process, as a calibration is needed in advance. However, it offers the highest flexibility of all investigated models because of a reduced amount of material parameters. It also has the capability of describing the nucleation behavior correctly at the melt pool tail, which is why this approach should be used whenever no first-time-right prediction of the simulation is necessary.

The physically based models considering the heterogeneous nucleation should be applied if a first-time-right prediction is striven for. The further evaluated models based on the homogeneous nucleation, the SCCT and the DIT, did not provide satisfactory results. Applying the heterogeneous approach is only valid if it can be made sure that there are no elements in the considered alloy, which reduces the amount of grain refining precipitates. Specifically for Scancromal^®, the Cr reduced the precipitates created by Sc and Zr. Therefore, the effect of chemical elements on the nucleation behavior during the manufacturing process needs to be taken into account.

The scope of future work is an automated first-time-right prediction of the nucleation location. To achieve this goal, the nucleation models have to be extended in terms of the formation of precipitates and their coherency, and with regard to the high cooling rates during the manufacturing process.

The different approaches were only applied to two specific aluminum alloys. How far the investigated models are applicable to widely used materials in PBF-LB/M, such as the Nickel-based superalloy Inconel 718 and the titanium alloy Ti-6Al-4V, also needs to be investigated.

Appendix A Material properties

See Figures A1, A2, and Tables A1, A2, A3, and A4.

Fig. A1

Thermophysical properties of the utilized materials: (a) thermal conductivity, (b) specific heat capacity, (c) density

Table A1 Calculated Thermophysical Properties of the Utilized Alloys

Table A2 Nucleation Values for the Phenomenological Approach

Table A3 Material-Specific Values for the Physically Based Nucleation Models

Table A4 Material Constants for the Physically Based Nucleation Models

Fig. A2

Further metallographic investigations on the nucleation locations: cross-sectional views for (a) Scalmalloy^®, (b) Scancromal^®, and longitudinal views for (c) Scalmalloy^®, (d) Scancromal^®