Explaining Deviatoric Residual Stresses in Aluminum Matrix Composites with Complex Microstructure

Abstract

The residual stresses in multiphase metal matrix composites with both random planar-oriented short fibers and particles were studied by neutron diffraction and by a model based on the reformulation of classic Maxwell’s homogenization method. Contrary to common understanding and state-of-the-art models, we experimentally observed that randomly oriented phases possess non-hydrostatic residual stress. The recently developed modeling approach allows calculating the residual stress in all phases of the composites. It rationalizes the presence of deviatoric stresses accounting for the interaction of random oriented phases with fibers having preferential orientation.

1 Introduction

Metal matrix composites (MMC) are advanced materials for various applications in automotive and aerospace industries.[1,2] Due to the combination of metallic matrix and ceramic reinforcement phases, it is possible to achieve improved mechanical properties, such as strength and creep resistance with no significant increase in weight of the component.[3,4,5,6]

During production (i.e., cooling from casting or heat treatment temperatures) of such multiphase materials, the mismatch of thermal expansion coefficients (CTE) of the different phases leads to the formation of residual stresses.[7,8,9,10,11] The effect of these microscopic internal residual stresses on the macroscopic material behavior can be detrimental.[8,12] In Al composites reinforced with SiC particles, it can lead to the asymmetry of yielding in tension and compression, so-called strength differential effect.[8] It was shown that matrix residual stress in MMC with ceramic reinforcement can have strong influence on the creep behavior of the composite.[12] Therefore, it is important to account for residual stresses by the assessment of the mechanical properties of the composites and evaluation of damage scenarios.

The advances of composite materials with high-performance mechanical properties go together with a complex microstructure, leading to unknown residual stress state after fabrication. In our previous investigations,[13,14,15] we have followed the evolution of internal stresses as a function of applied load for the same materials investigated in this work. A model to predict such stresses has been developed, which successfully rationalize the experimental observations. However, the determination of residual stress is far more complicated: from an experimental point of view, challenging metrological problems appear (e.g., the stress-free reference d₀); from a theoretical point of view, on the one hand, the detailed knowledge of the materials history and of the variation of its properties would be required, and on the other hand, analytical models would anyway require drastic simplifications to tackle the problem. While for composites Eshelby theory-based models have proven to be successful,[8,16,17] only recently a model has appeared rationalizing residual stress in multiphase materials.[18] It is, however, undiscussed that the measurement of residual stresses is a crucial point in the investigation of new materials. Several techniques are available to experimentally determine macro-residual stress (see Reference 19 for their definition) by both destructive and non-destructive methods. Among the most used destructive techniques are the hole drilling method[20] and the contour method.[21] In spite of the fact that those techniques can provide accurate information about the RS state of the component, they are not able to measure phase-specific stresses in composite materials (the so-called micro-stresses, see also Reference 19).

The non-destructive determination of RS has greatly advanced with the development of dedicated neutron and synchrotron X-ray diffraction instruments. These techniques are of paramount importance for composites, since they provide the possibility to determine stresses in each constituent within the same specimen. Moreover, energy dispersive methods (Time-of-Flight Neutron Diffraction or Energy Dispersive Synchrotron Radiation Diffraction) can even measure the full diffraction pattern without the use of any angular scan. This allows fast determination of stresses in different crystal families of the same phase. These techniques therefore are frequently used to determine the so-called intergranular stresses.[22,23]

In the present work, we evaluate residual stresses in mechanically anisotropic four- and five-phase metal matrix composites by neutron diffraction. In the investigated materials, the anisotropy of mechanical properties (at a macro level) is caused by the preferential orientation (random planar) of short fibers. The other phases possess isotropic properties and random spatial orientation. According to literature, a random spatial orientation of a phase would lead to hydrostatic residual stresses in this phase.[1] This, however, contradicts the results of neutron diffraction experiments, which show that randomly oriented phases may have non-hydrostatic residual stress. To explain this phenomenon, we apply a recently developed modeling approach[18] to calculate principal phase-specific residual stresses. We show that by taking into account the interaction among the different phases, the deviatoric stress state in random oriented phases can also be theoretically predicted.

2 Materials and Methods

2.1 Materials

Two types of composites produced by squeeze casting[24] were investigated. Type I is an AlSi12CuMgNi alloy (for alloy composition see Table I) reinforced with 15 pct vol. of Al₂O₃—Saffil short fibers and Type II is the AlSi12CuMgNi alloy reinforced with 7 pct vol. of Al₂O₃—Saffil short fibers and 15 pct vol. of SiC particles. Saffil fibers, which consist of 96 to 97 pct Al₂O₃ and 3 to 4 pct SiO₂ binder, in both composites have planar random orientation while SiC particles are randomly distributed within the volume. Prior to the Al alloy infiltration, the preforms (130 × 130 × 20 mm³) with ceramic reinforcements were preheated up to 1000 °C for 12 hours. Then, hot preforms were inserted to the squeeze casting machine and the molten Al alloy (at temperature 800 °C) was poured in. To squeeze the molten Al alloy to the preform some pressure was applied: first 72 MPa for 15 seconds and then 144 MPa for 90 seconds. The magnitude and the duration of the applied pressure are the most important parameters in squeeze casting process. The pressure leads to rapid solidification and hence affects the microstructure and the mechanical properties of squeeze-cast components. In particular, the rapid solidification of near eutectic Al-Si matrix alloy from the eutectic temperature (577 °C) results in the formation of a eutectic Si phase in the form of lamellae between the initially solidified α-Al dendrites. Also, stable intermetallic phases are formed because of the presence of transition elements in the matrix alloy. These intermetallics, together with the eutectic Si and the ceramic reinforcements, improve the mechanical properties of the material. The cooling was performed at room temperature. As a result, casting plates with a diameter of 205 mm and height of 50 mm were obtained, where the composite is sorrounded by some excess matrix (see also References 13,14,15 for further details).

Table I AlSi12CuMgNi Alloy Composition

2.2 Microstructural Characterization

The microstructure of the composites was characterized by scanning electron microscopy (SEM). The samples were embedded in Bakelite, first ground with silica paper and finally polished with 1µm diamond paste.

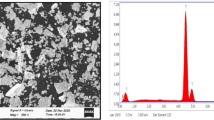
The resulting SEM microphotographs disclose the microstructure of Type I and Type II composites, both in-plane (Figures 1(a) and (c)) and out-of-plane (Figures 1(b) and (d)) of fibers. Images show the Al solid solution in gray (background, for the remainder referred to as Al phase), Al₂O₃ fibers and SiC particles in dark gray, the eutectic Si in light gray, and intermetallics (IM) in white. It can be seen that different IM particles are interconnected with the eutectic Si and the ceramic reinforcements. The eutectic Si appears between SiC particles that are agglomerated between fibers, thereby creating clusters (Figures 1(c) and (d)). Moreover, the Si phase connects all phases building the interconnected network. For both composites, the preferential orientation of Saffil fibers within the 1–2 plane (from preform condition) could be clearly observed (see inset in Figure 2).

Fig. 1

SEM microphotographs of Al matrix composites: (a) Type I composite cross-section parallel to the fibers plane; (b) Type I composite cross-section orthogonal to the fibers plane; (c) Type II composite cross-section parallel to the fibers plane; (d) Type II composite cross-section orthogonal to the fibers plane

Fig. 2

Schematic setup for the neutron diffraction measurements. The sample orientation for the radial (a) and axial components (b). The fiber plane is within 1–2 plane

2.3 Neutron Diffraction Stress Analysis

Residual stresses in Al, Si, and SiC phases of the investigated composites were determined by neutron diffraction. (As for the micrographs, the Al solid solution is called Al phase). The neutron diffraction experiments were carried out at the neutron instrument STRESS-SPEC (FRM II, Munich, Germany[25]). Cylindrical samples with a diameter of 6 mm and length of 12 mm were machined out of the casting blocks (see above) by electrical discharge machining (EDM). For both composites, the fiber plane was perpendicular to the axial direction of the sample and, therefore, all stress components are assumed to be equal in such plane.

The wavelength of the monochromatic neutron beam was set to λ = 1.672 Å to have maximum intensity for the Si phase. A gauge volume of 4 × 4 × 5 mm³ (positioned in the center of the specimen) was defined by primary (horizontal and vertical) slits and a radial collimator. A position sensitive detector was used to acquire the Al-311, Si-422, and SiC-116 peaks at Bragg angles 2θ = 86, 98, and 79 deg, respectively. The Al-311 peak was chosen since these grains are elastically and plastically isotropic,[26] and showed high diffracted intensity at all sample orientations.

The RS were determined by using the sin²ψ method. ψ is the tilt angle between the axial direction of the sample and the scattering vector $\vec{q}$, defined as $\vec{q} = \vec{K} - \vec {{K_{0} }}$, where wave vectors $\vec {{K_{0} }}$ and $\vec{K}$ describe the direction of incoming and outgoing beam (Figure 2). The sample was tilted in the scattering plane from the axial direction ψ = 0 deg (out-of-plane of the fiber mat) to the radial direction ψ = 90 deg (in-plane of the fiber mat) in 7 steps. For each tilt angle ψ the counting time was 3 minutes for the Al and SiC phases and 15 minutes for the Si phase. A diffraction peak of the Saffil alumina short fibers was observed; however, it suffered a strong broadening effect due to the nanocrystalline (and partially amorphous) nature of the fibers. Therefore, a reliable peak position could not be obtained. It was also not possible to observe diffraction peaks of any of the IM phases, most probably because of their low individual volume fraction. The diffraction peaks were fitted with a Gaussian function using the StressTex software.[27]

The calculation of the phase absolute stresses requires the measurement of lattice spacing d₀ of the stress-free reference samples in every phase. In the case of the investigated materials, the stress-free samples were unavailable due to the following reasons: the powders of the alloy contained the percolating network of eutectic Si and IMs; dissolution of the Al matrix and aluminides did not result in pure eutectic Si, most probably because of a chemical reaction among phases during the deep etching process; finally, the raw SiC particles were not available.

Assuming as usual quasi-isotropic materials behavior,[26] the principal stresses are related to the principal strains as following:

$$ \begin{aligned} \sigma_{1} = \frac{E}{1 + \nu }\varepsilon_{1} - \frac{E\nu }{{\left( {1 + \nu } \right)\left( {1 - 2\nu } \right)}}\left( {\varepsilon_{1} + \varepsilon_{2} + \varepsilon_{3} } \right) \hfill \\ \sigma_{2} = \frac{E}{1 + \nu }\varepsilon_{2} - \frac{E\nu }{{\left( {1 + \nu } \right)\left( {1 - 2\nu } \right)}}\left( {\varepsilon_{1} + \varepsilon_{2} + \varepsilon_{3} } \right) \hfill \\ \sigma_{3} = \frac{E}{1 + \nu }\varepsilon_{3} - \frac{E\nu }{{\left( {1 + \nu } \right)\left( {1 - 2\nu } \right)}}\left( {\varepsilon_{1} + \varepsilon_{2} + \varepsilon_{3} } \right) \hfill \\ \end{aligned} $$

(1)

where E and ν are plane-specific Young’s modulus and Poisson’s ratio.

The elastic strain in a direction i can be calculated based on the shift of the diffraction angle:

$$ \varepsilon_{i} = - \left( {\theta_{i} - \theta_{0} } \right)\cot \left( {\theta_{0} } \right) $$

(2)

where θ₀ is the diffraction angle of the stress-free sample and θ_i is the diffraction angle in the direction of scattering vector $\vec{q}$. Since stress-free samples were unavailable, we calculated the absolute stress differences to eliminate the dependence on the θ₀,[17,28] assuming that the small changes in diffraction angle θ are irrelevant in the cotangent term in Eq. [2]. As a result, the stress differences were calculated using the following equations:

$$ \begin{aligned} \sigma_{1} - \sigma_{3} = - \frac{E}{1 + \nu }(\theta_{1} - \theta_{3} )\cot \theta \hfill \\ \sigma_{2} - \sigma_{3} = - \frac{E}{1 + \nu }(\theta_{2} - \theta_{3} )\cot \theta \hfill \\ \sigma_{1} - \sigma_{2} = - \frac{E}{1 + \nu }(\theta_{1} - \theta_{2} )\cot \theta \hfill \\ \end{aligned} $$

(3)

where angle θ was taken equal to the theoretical (i.e., tabulated for the pure materials, see ICSD) diffraction angle for every measured phase.

For the calculation of stress, we used the plane-specific diffraction elastic constants, which were calculated using XEC software,[29] adopting a Kröner model,[30] and are listed in Table II.

Table II Phase-Specific Isotropic Elastic and Thermal Properties

2.4 Micromechanical Modeling

To model residual stresses in anisotropic multiphase composites, we use the approach recently developed by Sevostianov and Bruno[18] who suggested to use Maxwell’s homogenization technique for this goal (as interpreted by Sevostianov and Giraud[31] and Sevostianov[32]). In this study, we follow the terminology introduced by Mura[33]; an inclusion is a part of a body subjected to a known eigenstrain and with the same thermal and mechanical properties as the surrounding material; an inhomogeneity, instead, is a part of the body characterized by thermal and mechanical properties different from the surrounding material; an inhomogeneous inclusion means an inhomogeneity subjected to eigenstrain. All details of the model can be found in Reference 18.

Sevostianov and Bruno[18] considered a piece of (matrix) material, characterized by the tensor of elastic stiffness ${\mathbf{C}}_{ 0}$, containing multiple inhomogeneous inclusions, characterized by an elastic stiffness tensor ${\mathbf{C}}_{i}$ and an eigenstrain ${\varvec{\upvarepsilon}}^{{{\mathbf{*}}(i)}}$, from two points of view: as a large representative domain $\varOmega$ of volume $V_{\varOmega }$ with unknown stiffness ${\mathbf{C}}_{eff}$ subjected to unknown eigenstrain ${\varvec{\upvarepsilon}}^{*\varOmega }$ and as a piece of a material (of the same shape and size) containing multiple small inhomogeneous inclusions of (individual) volumes $V_{m}$ and stiffnesses ${\mathbf{C}}_{m}$, subjected to eigenstrains ${\varvec{\upvarepsilon}}^{*\left( m \right)}$. Following Maxwell’s idea, they equated the far fields produced by these two systems (note that J is the fourth-rank unit tensor):

$$ V_{\varOmega } \left[ {{\mathbf{J}} + \left( {{\mathbf{C}}_{eff} - {\mathbf{C}}_{{\mathbf{0}}} } \right):{\mathbf{P}}_{\varOmega } } \right]^{ - 1} :{\mathbf{C}}_{eff} :{\varvec{\upvarepsilon}}^{*\varOmega } = \sum\nolimits_{m} {V_{m} \left[ {{\mathbf{J}} + \left( {{\mathbf{C}}_{m} - {\mathbf{C}}_{{\mathbf{0}}} } \right):{\mathbf{P}}_{m} } \right]^{ - 1} :{\mathbf{C}}_{m} :{\varvec{\upvarepsilon}}^{*\left( m \right)} } $$

(4)

It gives an explicit expression for ${\varvec{\upvarepsilon}}^{*\varOmega }$

$$ {\varvec{\upvarepsilon}}^{*\varOmega } = {\mathbf{S}}_{eff} :\left[ {{\mathbf{J}} + \left( {{\mathbf{C}}_{eff} - {\mathbf{C}}_{{\mathbf{0}}} } \right):{\mathbf{P}}_{\varOmega } } \right]:\sum\nolimits_{m} {\frac{{V_{m} }}{{V_{\varOmega } }}\left[ {{\mathbf{J}} + \left( {{\mathbf{C}}_{m} - {\mathbf{C}}_{{\mathbf{0}}} } \right):{\mathbf{P}}_{m} } \right]^{ - 1} :{\mathbf{C}}_{m} :{\varvec{\upvarepsilon}}^{*\left( m \right)} } $$

(5)

where P_Ω is Hill’s tensor of the equivalent inclusion of volume V_Ω. Then, the constrained strain in $\varOmega$ is given by the following expression:

$$ {\varvec{\upvarepsilon}}^{\varOmega } = {\mathbf{P}}_{\varOmega } :\sum\nolimits_{m} {\varphi_{m} \left[ {{\mathbf{J}} + \left( {{\mathbf{C}}_{m} - {\mathbf{C}}_{{\mathbf{0}}} } \right):{\mathbf{P}}_{m} } \right]^{ - 1} :{\mathbf{C}}_{m} :{\varvec{\upvarepsilon}}^{*\left( m \right)} } $$

(6)

where $\varphi_{m} = {{V_{m} } \mathord{\left/ {\vphantom {{V_{m} } {V_{\varOmega } }}} \right. \kern-0pt} {V_{\varOmega } }}$ is the volume fraction of m-th inhomogeneity, and it holds $\mathop \sum \limits_{m} \varphi_{m} + \varphi_{0} = 1$, where φ₀ is the volume fraction of the matrix. This is the effective field acting on the inhomogeneities inside $\varOmega$. Superposing this expression with Eshelby solution, they obtained an explicit expression for the constrained strain inside i-th inhomogeneity

$$ \begin{aligned} {\varvec{\upvarepsilon}}^{\left( i \right)} = \left( {{\mathbf{J}} + {\mathbf{P}}:\left( {{\mathbf{C}}_{i} - {\mathbf{C}}_{{\mathbf{0}}} } \right)} \right)^{ - 1} :{\mathbf{P}}_{i} :{\mathbf{C}}_{i} :{\varvec{\upvarepsilon}}^{{{\mathbf{*}}(i)}} \hfill \\ \quad \quad - {\mathbf{P}}_{\varOmega } :\sum\nolimits_{m} {\varphi_{m} \left[ {{\mathbf{J}} + \left( {{\mathbf{C}}_{m} - {\mathbf{C}}_{{\mathbf{0}}} } \right):{\mathbf{P}}_{m} } \right]^{ - 1} :{\mathbf{C}}_{m} :{\varvec{\upvarepsilon}}^{*\left( m \right)} } \hfill \\ \end{aligned} $$

(7)

and the residual stresses in i-th inhomogeneity:

$$ {\varvec{\upsigma}}^{\left( i \right)} = {\mathbf{C}}_{i} :\left( {{\varvec{\upvarepsilon}}^{\left( i \right)} - {\varvec{\upvarepsilon}}^{{{\mathbf{*}}\left( i \right)}} } \right) $$

(8)

To the best of our knowledge, this is the only approach suitable for the calculation of the residual stresses in anisotropic multiphase composites.

Based on the analysis of the X-ray computed tomography (XCT) images,[13] materials were modeled as a multiphase transversely isotropic composite consisting of a continuous aluminum alloy matrix and three or four families of inhomogeneities (Type I and II, respectively):

• (1) Saffil Al₂O₃ fibers of average aspect ratio of 40. They were assumed to be randomly oriented in the plane 1-2 and have volume fraction of 15 pct in Type I composite and 7 pct in Type II composite;

• (2) Eutectic Si phase. This was modeled by strongly oblate spheroidal platelets of aspect ratio 0.3 with random orientation (in 3D). Their volume fraction was set to 7 pct in both composites.

• (3) Intermetallic particles. The shape analysis of the IM particles based on the computed tomography data[34] showed a concave geometry of most of them. Therefore, the IM phases (all confounded) were modeled as concave particles with aspect ratio of 1. The total volume fraction of all types of IMs was set to 5 pct.

• (4) SiC particles (Type II composite). They were modeled as randomly oriented (in 3D) slightly prolate spheroids of aspect ratio 4, and volume fraction of 15 pct.

The volume fractions of eutectic Si and IM phases were taken based on the analysis of XCT reconstructed volumes and previously reported by Cabeza et al.[13]

The thermal and mechanical properties of the constituents are summarized in Table II (which includes macroscopic and peak-specific properties). In case of IMs, the global (averaged) values of the elastic constants (E and ν) were calculated based on nanoindentation results,[35] while the global value of the CTE was calculated based on literature results of high temperature X-ray diffraction experiments.[36] The components of tensor ${\mathbf{P}}$ for a spheroidal inhomogeneity[45] are given in the Appendix. Eigenstrains in inhomogeneities of i-th phase were calculated as the product of an effective temperature change and the difference in thermal expansion coefficients between the inhomogeneities and the matrix. The effective temperature change has been taken as ∆T = − 200 K.[7,16]

In the micromechanical model, we used the values of the room temperature elastic constants. The temperature dependence of the mechanical properties was not taken into account since the effective temperature change (ΔT = − 200 K) is small.

3 Results and Discussion

Commonly, the random orientation of particles of any shape would lead to hydrostatic residual stress after manufacturing or heat treatments. However, it was shown in the literature that the addition of random planar-oriented fibers or the presence of texture in anisotropic matrix polycrystals (i.e., with symmetry lower than the hexagonal one) result in anisotropic stresses.[9,37] This is because the whole composite becomes transverse isotropic.[9,17,38] As previously reported, after cooling from the processing or heat treatment temperature, the matrix residual stress must be equal in any direction within the fiber plane, and larger than those in the direction normal to the fiber plane.[9,13,37]

The evolution of the lattice spacings d as a function of sin²ψ for Al, Si, and SiC phases are shown in Figure 3. A linear fit for each data set was carried out and is also shown in Figure 3. Note that sin²ψ = 0 corresponds to the axial component (out-of-plane of fibers) and sin²ψ = 1 to the radial (in-plane of fibers), see Figure 2.

Fig. 3

Phase-specific lattice spacing d vs sin²ψ plots for Type I and Type II composites: (a) Type I Al-311; (b) Type I Si-422; (c) Type II Al-311; (d) Type II Si-422; (e) Type II SiC-208; and (f) Type II SiC-116. Note that the scale for all plots is the same. The measured peak integral intensities normalized by the maximum intensities are indicated below each plot

The Al phase also possesses deviatoric stresses in both composites (Figure 3). The axial-to-radial lattice spacing gradient in the Type I composite is larger than in Type II. This is an effect of the larger volume fraction of the random planar-oriented fibers. Remarkably, both the eutectic Si and the SiC particles, which have aspect ratios of about 0.3 and 4, respectively, also show non-hydrostatic behavior, in spite of the fact that they are randomly oriented. This behavior cannot be rationalized by an Eshelby–Withers model.

The slight deviation from linearity of the d vs sin²ψ plots for Al phase (Figures 3(a) and (b)) can classically be related to the effect of coarse grain or texture. The presence of texture essentially introduces a variation of the diffraction elastic constants as a function of the tilt angle because different grains are sampled. Since the investigated materials were produced by casting, one can expect a minor effect of the crystallographic texture. However, it was observed that the diffracted intensity shows some variation as a function of sin²ψ (Figures 3(a) and (b)). This indicates that both coarse grain effect and crystallographic texture contribute to the wavy shape of the curves in Figure 3.

The experimental stress differences in Al, Si, and SiC phases for both types of investigated composites were calculated according to Eq. [3] (see Table III). The Sevostianov–Bruno model [18] results (stress differences) are also listed in Table III (including all phases).

Table III Experimentally Obtained and Modeled σ₃− σ₁ Stress Difference (in MPa) for Type I and Type II Composites

In general, the model results are in good agreement with the experimental ones. They show that the residual stress in all phases possesses hydrostatic and deviatoric terms, also in the randomly oriented Si and SiC particles. We also notice that the model overestimates the deviatoric stress in the Al phase, but clearly reproduces the decrease of stress differences as a function of the decreasing volume fraction of Al₂O₃ fibers (larger stress difference in Type I composite). One of the reasons for the overestimation of the Al phase stresses can be the fact that in the model stresses in the Al matrix were calculated as balance of the other phases. Therefore, they are affected by an error magnified by the error propagation. Additionally, we will see below that a slight variation (few vol pct) of the fraction of the reinforcing phases has a large impact on the matrix stress. Finally, the properties of pure Al were taken as properties of the matrix, but the matrix alloy consists of dissolved alloying elements as well as around 1.6 wt pct of Si. The different thermal and mechanical properties of the matrix lead to the increase of error in stress calculation.

The model allows going beyond the results as shown in Table III. First, the principal stresses for each phase can be calculated for both composites. They are presented in Figure 4 as functions of the volume fraction of Al₂O₃ fibers and SiC particles (in the case of Type II). Stresses in both directions (in-plane and out-of-plane) for the Al matrix are tensile, while for all reinforcing phases they are compressive. Corroborating the experimental data shown above, the stress state in all the phases is not hydrostatic. While it is expected for Al₂O₃ fibers, which have a transverse isotropic distribution as a function of orientations (in-plane random), other phases have three-dimensional random distribution, so that deviatoric stresses are caused by the interaction with the fibers. The plots in Figure 4 indicate that deviatoric tensile stresses in matrix increase with increasing volume fraction of fibers and may reach the yield limit of aluminum (although our model does not take plasticity into account). Moreover, debonding (formation of cracks at matrix/inhomogeneity interfaces) seems to be the most realistic mechanism for energy release during damage, since the ultimate strength of the interfaces is usually lower than the yield limit.

Fig. 4

Calculated principal residual stresses in all phases as a function of volume fraction of Al₂O₃ fibers in Type I (a, b), Type II (c, d) composites and as a function of volume fraction of SiC particles in Type II composite (e, f). The gray vertical line indicates the volume fractions of Al₂O₃ fibers and SiC particles in the investigated materials

Our model involves several assumptions and simplifications that may yield additional errors but cannot be avoided. Namely we assumed that the residual stresses are completely associated with thermal misfit, so that the eigenstrain in Eqs. [7] and [8] were taken as follows:

$$ \left[ {{\varvec{\upvarepsilon}}^{{{\mathbf{*}}\left( i \right)}} } \right]_{kl} = \left( {\alpha_{i} - \alpha_{0} } \right)\Delta T\delta_{kl} $$

(9)

where $\alpha_{0}$ and $\alpha_{i}$ are bulk thermal expansion coefficient of the matrix and inhomogeneities of i-th phase, respectively (assumed isotropic); $\Delta T$ is the temperature change. The variation of temperature was assumed to change from annealing[1] to room temperature, i.e., $\Delta T \approx - \,200K$. It is difficult, however, to estimate the accuracy of this approximation, since some stress relaxation takes always place during cooling. In fact, while Withers et al.[16] and Arsenault[7] used $\Delta T \approx - \,200\,K$, other authors used different values (Maeda used ΔT ~ − 550 K,[39] Fernandez used ΔT ~ − 70 K[8]). Many other improvements to the model can be made, for instance related to the shapes of the inhomogeneities. Indeed, approximating the complicated shapes observed by computed tomography[34,40,41,42] by ellipsoids of revolution may produce errors in the determination of stresses.[43,44] The real shapes of the inhomogeneities are quite irregular, may be concave and form clusters.[13,34] Modeling the elastic properties of these objects has recently advanced,[43] but it would represent a formidable task in the present context.

In conclusion, however, in spite of the necessary approximations to render the model analytically closed, we could show that the introduction of an interaction term among reinforcement phases does predict the observed deviatoric residual stresses in multiphase composites.

4 Conclusion

Experimental evidence shows that micro-residual stress in multiphase composites can be deviatoric, a fact that has remained unexplained to date. We have applied (for the first time) a recently developed analytical model (based on Maxwell’s homogenization scheme) to rationalize our observations (captured by neutron diffraction). We found that in our composites, containing Si and intermetallic inclusions as well as planar random oriented Saffil fibers and SiC particle reinforcements, residual stresses in all phases possess a deviatoric character. This was matched well by the model predictions, thereby proving that some interaction occurs among secondary phases (while Eshelby–Withers models assume the stress is transferred solely from the matrix to the secondary phases). We therefore proved the validity of the model to rationalize the complicated stress state in multiphase materials with complicated microstructures.

Future work will concentrate on studies to mimic the behavior of realistic particle shapes (observable, for example, by high resolution computed tomography) or to determine the temperature jump during production more precisely.

Appendix

1.1 Cartesian Components of Hill’s Tensor for Ellipsoidal and Spheroidal Inhomogeneities

For an ellipsoidal inclusion or inhomogeneity with semi-axes $a_{1} \ge a_{2} \ge a_{3}$, the components $P_{ijkl}$ of Hill’s tensor are expressed in terms of elliptical integrals (see Reference 45):

$$ \begin{aligned} P_{1111} = \frac{1}{{16\pi G\,\left( {1 - \nu^{2} } \right)^{{}} }}\left[ {\left( {1 - 4\nu^{2} } \right)\;I_{1} + 3a_{1}^{2} I_{11} - \nu a_{2}^{2} I_{12} - \nu a_{3}^{2} I_{13} } \right] \hfill \\ P_{1122} = \frac{1}{{16\pi G\,\left( {1 - \nu^{2} } \right)^{{}} }}\left[ { - \left( {1 - 2\nu } \right)\;I_{1} - 3\nu a_{1}^{2} I_{11} + a_{2}^{2} I_{12} - \nu a_{3}^{2} I_{13} } \right] \hfill \\ P_{1212} = \frac{1}{{32G\pi \left( {1 - \nu } \right)}}\left[ {\left( {1 - 2\nu } \right)\left( {I_{1} + I_{2} } \right) + \left( {a_{1}^{2} + a_{2}^{2} } \right)I_{12} } \right] \hfill \\ \end{aligned} $$

(A1)

where

$$ \begin{aligned} I_{1} = \frac{{4\pi a_{1} a_{2} a_{3} }}{{\left( {a_{1}^{2} - a_{2}^{2} } \right)^{{}} \sqrt {a_{1}^{2} - a_{3}^{2} } }}\left[ {F\left( {\theta ,k} \right) - E\left( {\theta ,k} \right)} \right] \hfill \\ I_{3} = \frac{{4\pi a_{1} a_{2} a_{3} }}{{\left( {a_{2}^{2} - a_{3}^{2} } \right)^{{}} \sqrt {a_{1}^{2} - a_{3}^{2} } }}\left[ {\frac{{a_{2} \sqrt {a_{1}^{2} - a_{3}^{2} } }}{{a_{1} a_{3} }} - E\left( {\theta ,k} \right)} \right] \hfill \\ \end{aligned} $$

(A2)

$F\left( {\theta ,k} \right)$ and $E\left( {\theta ,k} \right)$ are incomplete elliptic integrals of the first and second kinds,

$$ F\left( {\theta ,k} \right) = \int_{\;0}^{\;\theta } {\frac{{{\text{d}}w}}{{\sqrt {1 - k^{2} \sin^{2} w} }}} \;,\quad \quad E\left( {\theta ,k} \right) = \int_{\;0}^{\;\theta } {\sqrt {1 - k^{2} \sin^{2} w} \,\,{\text{d}}w} $$

(A3)

and $\theta = arcsin\sqrt {1 - \left( {{{a_{3} } \mathord{\left/ {\vphantom {{a_{3} } {a_{1} }}} \right. \kern-0pt} {a_{1} }}} \right)^{2} } ,\,k = \sqrt {{{\left( {a_{1}^{2} - a_{2}^{2} } \right)} \mathord{\left/ {\vphantom {{\left( {a_{1}^{2} - a_{2}^{2} } \right)} {\left( {a_{1}^{2} - a_{3}^{2} } \right)}}} \right. \kern-0pt} {\left( {a_{1}^{2} - a_{3}^{2} } \right)}}^{{}} }$.

Other $P_{ijkl}$ are obtained by cyclic rearrangements of (1,2,3)-indices applied to all quantities $P_{ijkl}$, $a_{i} ,\;\;I_{i} \,$and $I_{ij}$. The components that cannot be obtained by such rearrangements are zeros. The following relations between integrals hold ($1 \to 2 \to 3 \to 1$) (see Reference 33):

$$ \begin{aligned} I_{1} + I_{3} + I_{2} = 4\pi \hfill \\ I_{12} = \frac{{I_{2} - I_{1} }}{{a_{1}^{2} - a_{2}^{2} }} \hfill \\ 3I_{11} + I_{12} + I_{13} = \frac{4\pi }{{a_{1}^{2} }} \hfill \\ 3a_{1}^{2} I_{11} + a_{2}^{2} I_{12} + a_{3}^{2} I_{13} = 3I_{1} \hfill \\ \end{aligned} $$

(A4)

In the case of a spheroidal inhomogeneity/inclusion with $a_{1} = a_{2} = a$, all integrals $I_{i} {\text{ and }}I_{ij}$, as well as tensor $\varvec{P}$ are elementary functions of the aspect ratio $\gamma = {{a_{3} } \mathord{\left/ {\vphantom {{a_{3} } a}} \right. \kern-0pt} a}$. Equation (A2) for $I_{1}$ in this case yields

$$ I_{1} = \frac{{2\pi \left( {1 - g\left( \gamma \right)} \right)}}{{1 - \gamma^{2} }} $$

(A5)

where

$$ g = \left\{ {\begin{array}{*{20}l} {\frac{1}{{\gamma \sqrt {1 - \gamma^{2} } }}\arctan \frac{{\sqrt {1 - \gamma^{2} } }}{\gamma },\quad {\text{oblate shape}}\;\left( {\gamma \le 1} \right)} \hfill \\ {\frac{1}{{\gamma \sqrt {\gamma^{2} - 1} }}\ln \left( {\gamma + \sqrt {\gamma^{2} - 1} } \right),\quad {\text{prolate shape}}\;\left( {\gamma \ge 1} \right)} \hfill \\ \end{array} } \right. $$

(A6)

and other integrals $I_{i}$, $I_{ij}$ are expressed in terms of $I_{1}$ as follows:

$$ \begin{aligned} I_{2} = I_{1} ;I_{3} = 4\pi - 2I_{1} ; \hfill \\ I_{12} = I_{11} = I_{22} = \frac{{\pi - {{3I_{1} \gamma^{2} } \mathord{\left/ {\vphantom {{3I_{1} \gamma^{2} } 4}} \right. \kern-0pt} 4}}}{{a^{2} \left( {1 - \gamma^{2} } \right)}} \hfill \\ I_{13} = I_{23} = \frac{{\gamma^{2} \left( {3I_{1} - 4\pi } \right)}}{{a^{2} \left( {1 - \gamma^{2} } \right)}};\,I_{33} = \frac{{\gamma^{2} \left( { - 2I_{1} + {{4\pi \left( {1 + \gamma^{2} } \right)} \mathord{\left/ {\vphantom {{4\pi \left( {1 + \gamma^{2} } \right)} 3}} \right. \kern-0pt} 3}} \right)}}{{a^{2} \left( {1 - \gamma^{2} } \right)}} \hfill \\ \end{aligned} $$

(A7)

Introducing two functions, expressed in terms of $g\left( \gamma \right)$:

$$ f_{0} = \frac{1 - g}{{2\left( {1 - \gamma^{2} } \right)}},\,f_{1} = \frac{1}{{4\left( {1 - \gamma^{2} } \right)^{2} }}\left[ {\left( {2 + \gamma^{2} } \right)g - 3\gamma^{2} } \right] $$

(A8)

the components of Hill’s tensor are given by

$$ \begin{aligned} P_{1111} = P_{2222} = \frac{1}{4G}\left[ {\left( {4 - 3\kappa } \right)f_{0} + 3\kappa f_{1} } \right],\,P_{3333} = \frac{1}{G}\left[ {\left( {1 - \kappa } \right)\left( {1 - 2f_{0} } \right) + 2\kappa f_{1} } \right] \hfill \\ P_{1122} = P_{2211} = \frac{\kappa }{4G}\left( { - f_{0} + f_{1} } \right),\,P_{1133} = P_{2233} = P_{3311} = P_{3322} = - \frac{\kappa }{G}f_{1} \hfill \\ P_{1212} = \frac{1}{4G}\left[ {\left( {2 - \kappa } \right)f_{0} + \kappa f_{1} } \right],\,P_{1313} = P_{2323} = \frac{1}{4G}\left( {1 - f_{0} - 4\kappa f_{1} } \right) \hfill \\ \end{aligned} $$

(A9)

where $\kappa = {1 \mathord{\left/ {\vphantom {1 {\left[ {2\left( {1 - \nu } \right)} \right]}}} \right. \kern-0pt} {\left[ {2\left( {1 - \nu } \right)} \right]}}$.

For a spherical inhomogeneity

$$ I_{1} = {{4\pi } \mathord{\left/ {\vphantom {{4\pi } 3}} \right. \kern-0pt} 3},\,g\left( 1 \right) = 1,\,f_{0} = {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0pt} 3},\,f_{1} = {1 \mathord{\left/ {\vphantom {1 {15}}} \right. \kern-0pt} {15}} $$

(A10)

and

$$ \begin{aligned} P_{1111} = P_{2222} = P_{3333} = \frac{5 - 3\kappa }{15G} \hfill \\ P_{1122} = P_{2211} = P_{1133} = P_{2233} = P_{3311} = P_{3322} = \frac{ - \kappa }{15G} \hfill \\ P_{1212} = P_{1313} = P_{2323} = \frac{5 - 2\kappa }{30G} \hfill \\ \end{aligned} $$

(A11)