Abstract
Boron steel, classed as an ultra high-strength steel (UHSS), has been utilized in anti-intrusion systems in automobiles, providing high strength and weight-saving potential through gage reduction. UHSS spot welds exhibit unique hardness distributions, with a hard nugget and outlying base material, but with a soft heat-affected zone in-between these regions. This soft zone reduces the strength of the weld and makes it susceptible to failure. Due to the interaction of various weld zones that occurs during loading, there is a need to characterize the loading response of the weld for accurate failure predictions. The loading response of certain weld zones, as well as failure loci, was obtained through physical simulation of the welding process. The results showed a significant difference in mechanical behavior through the weld length. An important result is that instrumented indentation was shown to be a valid, quantitative method for verifying the accuracy with which weld microstructure has been recreated with regard to the target weld microstructure.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Due to environmental considerations, there has been a need to improve fuel economy and reduce emissions in the automotive industry. A factor which contributes to this aim is reducing vehicle weight. High-strength boron steel exhibits desirable characteristics and has been utilized to reduce vehicle weight and maintain passenger safety through gage reduction of load-bearing parts. The high strength is achieved by hot-forming, whereby the steel is rapidly quenched from above 900 °C to achieve a strong martensitic microstructure.[1]
Resistance spot welding (RSW) is one of the most widely used joining techniques of steel vehicle parts, with several thousand welds made on a single car. By its very nature, the weld and surrounding material have been exposed to a wide range of temperatures. These range from above 1300 °C at the center of the nugget, to ambient temperature at distances far away from the weld. As a consequence, the material is non-homogeneous and anisotropic.
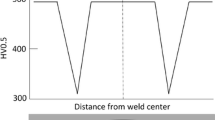
Predicting failure of welds made on martensitic boron steels presents a unique challenge. Whereas welds in non-martensitic materials show a gradual decline in hardness from the nugget to the base material (BM), martensitic steel welds show a sudden softening in the heat-affected zone (HAZ) and a sharp increase in hardness back into the BM. The cause for this sudden drop has been established to be due to tempering of the parent martensitic microstructure.[2,3,4] It is this microstructural mismatch between the hard nugget/BM and soft HAZ which causes the HAZ to be a critical area, with reduced mechanical properties.[5]
The varying material properties have a profound influence on the load-bearing capacity and failure strength of the weld as a whole. It may be tempting to focus on, and characterize, the weakest section of the weld to predict failure, but significant stress redistributions result during mechanical loading. Specifically, the stress concentration at the notch tip may be modified due to the difference in mechanical properties between the nugget/BM and HAZ.[6] As a result, all the varying material properties must be taken into account in predicting the load-bearing capacity of the weld.
1.1 Microstructure Evolution
Hot-stamped boron steel consists of a significant proportion of martensite, which is the base microstructure from which welding commences. Martensite is a product of diffusionless transformation, where it is formed in a sudden shear process in the austenite lattice by rapid quenching. The addition of boron decreases the cooling rate necessary for martensitic transformations by suppressing the high-temperature diffusion controlled ferrite and pearlite reactions. This means that a martensitic transformation is more likely to occur further away from the nugget in boron steel than in DP600, given sufficient austenitization.
It has been reported that a rapid softening occurs in martensitic steels in the early stages of tempering.[7] This is due to martensite being a supersaturated solid solution of carbon in iron and is readily decomposed upon heating. In the initial stages of tempering, martensite precipitates carbon in the form of carbide phases while reducing its tetragonal crystal structure. In the later stages of tempering, martensite has lost all tetragonality and transformed to ferrite and cementite. As stated, it is this tempering which causes the sudden drop in hardness in the HAZ.
1.2 Phase Transformation Behavior and Weld Properties
During spot welding, the steel experiences a gradient of decreasing temperature, and hence a microstructure gradient, extending radially out from the weld center.
When temperature exceeds Ac3, martensite is austenitized, with the degree of austenitization depending on the time and temperature above Ac3. In the weld center, austenite is transformed back into martensite, due to temperatures far exceeding Ac3 and rapid quenching provided by water-cooled electrodes. This results in a hard, brittle nugget.
In close proximity to the nugget, known as the Coarse Grained HAZ (CGHAZ), austenite grains can grow to a few hundred microns[8] and become more fine as distance is increased from the weld center. Due to high cooling rates, martensite forms within the austenite grains, giving high strength and brittle properties.
Extending further out, in the Intercritical HAZ (IHAZ), partial phase transformations occur, with the martensite undergoing an incomplete transformation to austenite. The cooling rate in this region is sufficiently low that a proportion of the austenite transforms into ferrite,[9] giving reduced hardness and strength. Moving further out into the subcritical HAZ (SCHAZ), the BM has not undergone phase transformation; however, the temperature is sufficient for tempering to occur. Tempering reduces brittleness in this region, leaving it more ductile.
DP600 steel has been used in this work as a reference material. DP600 is composed of 15 to 20 pct martensite and the remainder being ferrite.[10] Due to austenitization/partial-austenitization occurring near the fusion zone, the martensite volume fraction is increased in the CGHAZ and IHAZ,[11] leading to a hard, brittle region. The SCHAZ is a softer, more ductile zone, due to tempering of the pre-existing martensite phase.[12]
1.3 Literature Review
O’Keeffe et al.[13] conducted cross-tension tests to examine failure of welds fabricated on fully hardened and tempered boron steel base materials. The tempered steel BM exhibited approximately 39 pct decrease in hardness compared to the fully hardened variant. It was observed that the tempered steel exhibited greater deflection before failure; however, there was only a 5 and 3 pct difference in peak load and energy absorption, respectively, between the tempered and fully hardened test specimens. The authors stated that the similar results may be due to tempered martensite in the HAZ. This highlights that, even if boron steels with tailored properties are utilized, the weld HAZ still has an important effect on the failure.
The stress–strain response of a material is traditionally obtained from tensile specimens. However, due to the small dimensions of the HAZ, extracting tensile specimens directly from the weld is impractical. A solution is to create standard tensile specimens exposed to identical thermal histories as certain points along the length of the weld. For such physical simulations, a Gleeble thermo-mechanical simulator[14] is often employed.
Sommer[5] obtained weld constitutive behavior and failure criteria through tensile testing of weld material physically simulated through a Gleeble simulator. Data points for the failure locus were extracted through inverse simulation of tensile tests. The study assumed that the simulations were accurate from force–displacement curves; however, the presented data showed deviations between the simulated and measured curves. An improvement may be to directly measure failure data through Digital Image Correlation (DIC). The study also focused on 3 weld areas (BM, HAZ, and nugget). Given the sharp gradient of hardness through the HAZ, a potential improvement may be to discretize the HAZ into separate areas for finer resolution of characterization.
Abspoel et al.[15] also employed a Gleeble simulator; however, the application was to investigate boron steel constitutive behavior under hot stamping conditions. A novel sample geometry, consisting of 4 lateral “legs” for current shunting, was used to ensure homogeneous heating. Samples were austenized, cooled to a lower temperature (between 500 °C and 900 °C), and tensile tested at the constant target temperature. The sample geometry exhibited excellent homogeneous heating through the sample length.
Eller et al.[16] undertook a novel approach, in which large tensile specimens with physical RSWs in the gage area were tested. The measured force–displacement curves were used in inverse FE modeling to optimize the parameters for a strain hardening model. The author focused on characterizing the “critical HAZ,” which was defined as the point of lowest hardness in the HAZ.
In terms of fracture characterization, a central-hole tensile test and bending test were performed. In all test specimens, the HAZ was located such that strain localization and fracture initiation occurred in the HAZ. In this author’s opinion, the tests were well thought out; however, the influence of the surrounding BM was not considered. Additionally, for the bending tests, data scatter was evident due to misalignment of the punch over the HAZ. In terms of modeling, Eller linked different HAZ areas through linear interpolation. Such a method is valid and allows for a reduced number of experiments. However, as stated for Sommer, an increased number of data extraction areas in the HAZ could potentially result in more accurate data, rather than interpolated data.
Due to the small dimensions of the HAZ, instrumented indentation has proven to be a popular characterization method for welds.[17,18,19] The 3 most common techniques to extract material properties from instrumented indentation data are the representative strain method,[20,21] iterative FEA,[19,22] and artificial neural networks (ANN).[23] The ANN technique is beyond the scope of this paper and will not be discussed.
Kim et al.[22] extracted mechanical properties of steel butt welds. Yield strengths were calculated from a polynomial equation utilizing a coefficient (α), defined as the ratio of the strain at the starting point of strain hardening to the initial yield strain. In other words, α is obtained from tensile stress–strain curves.
Due to the difficulty of extracting tensile curves from the weld material, the authors performed FE analyses of indentations to obtain representative α values for the HAZ and nugget. The authors stated that the sharp microstructural changes in the HAZ could have a significant effect on the value of α, with a potential variation as the position is moved through the HAZ.
In terms of verification of the extracted yield strengths, the BM showed a 1.3 pct difference between the tensile and instrumented indentation values. No similar comparison was given for the yield strengths of the HAZ. Verification of the extracted HAZ properties was shown through an FE simulation of a tensile test with a butt weld in the gage length. The authors stated that the difference between simulated and measured load–strain curves may be due to the averaged properties of the HAZ.
Pham et al.[24] extracted yield strengths of weld microstructural phases and bulk weld material through nano- and micro-indentations, respectively. Two different reverse analyses were performed depending on the indentation size scale. The stress–strain behavior of the microstructural phases was assumed to follow a power law, and thus the authors used Dao’s algorithm[20] which was developed based on the same constitutive behavior. Due to the different microstructural phases, the authors employed a statistical convolution technique, whereby microstructural properties were approximated by a Gaussian distribution. This technique would lead to approximated yield strength values, although, by comparing results to literature values, the authors stated that the obtained mechanical properties were “acceptable.” The bulk material analysis was performed using the same method as previously described for Kim,[22] due to the bulk material exhibiting a plastic plateau due to Luders band formation.
Dao et al.[20] developed closed-form analytical functions, based on large deformation theory, to estimate material properties from experimental load–displacement curves. The authors verified the developed algorithm by comparing material properties calculated through the reverse analyses with uniaxial compression test data of 2 aluminum grades. It was found that the calculated yield strengths displayed strong sensitivity to the measured loading and unloading curve parameters. The authors concluded that the accuracy with which material parameters are calculated depends strongly on the accuracy with which the load–depth curves were measured. It was recommended to reduce this sensitivity by analyzing multiple indents for a given material.
There are several issues regarding the use of instrumented indentation to extract material properties. One issue is uniqueness, where it is assumed that only one set of elastic-plastic parameters exists that can reproduce a simulated indentation load–displacement curve with respect to an experimental one.[25] Equivalently, there is the assumption that a unique set of material parameters can be extracted from a single experimental load–displacement curve.
Cheng and Cheng[26] investigated the uniqueness problem by using dimensionless functions to calculate material properties from measured load–displacement curves.
It was found that, in certain instances, multiple values of strain hardening coefficient and yield strengths were obtained for a single curve. Dao et al.[20] stated that, even if 2 measured load curves were identical, small variations in the unloading slope and residual impression were sufficient to calculate unique values of strain hardening and yield strength. No indication of the level of variation needed to calculate unique values was given; therefore, it would be advisable to use additional references to calculate the properties from indentation experiments.
Another issue facing instrumented indentation is taking pile-up and sink-in of the indented material into account. Without independent knowledge of the strain hardening behavior, it is difficult to know what correction to apply.[27] Dao[20] attempted to take pile-up/sink-in into account by incorporating a geometric constant related to the true contact area. No direct comparison between physical and calculated contact areas was given. However, by comparing their work to Oliver and Pharr,[28] Young’s moduli were calculated with greater accuracy, which was associated with the introduced geometrical constant.
As discussed, previous authors have used Gleeble physical simulation or instrumented indentation for weld characterization studies. The discussed Gleeble studies[5,16] characterized a single HAZ area, which may lead to an averaging of mechanical properties. Boron steel HAZ exhibits sharp property changes; therefore, the studies may be improved by discretizing the HAZ into smaller sections and characterizing the individual sections. Eller[16] obtained failure criteria by directly tensile testing RSWs; however, the influence of the BM was not taken into account. An improvement would be to test a tensile geometry consisting of a homogeneous microstructure in the gage length.
Sommer[5] did test homogeneous gage length samples, although a dog-bone sample was used to obtain uniaxial failure strain and triaxiality. An improvement would be to use a central-hole tensile specimen.[29]
In terms of instrumented indentation tests, only representative values of the α coefficient could be obtained by Kim,[22] due to difficulties in directly tensile testing the HAZ. The author stated that sharp microstructural changes in the HAZ could have a significant effect on the value of α. The closed-form analytical functions developed by Dao[20] allow the use of measured load–displacement curves to be directly used from the HAZ. The analytical functions do exhibit significant sensitivity to the measured loading and unloading parameters, and thus it is recommended to use data from multiple indented points.
In summary, both Gleeble and instrumented indentation techniques have inherent difficulties. However, the final characterized results may be improved if a combination of both techniques is used. The Gleeble method allows physical testing of recreated weld material and instrumented indentation may be used as a tool to verify the extracted properties are correct.
For the work presented in this paper, weld material is physically simulated on tensile specimens. Failure locus data and constitutive behavior of the Gleeble samples are extracted from tensile tests. Physical welds are subjected to instrumented indentation tests, from which yield strengths are calculated. These yield strengths serve as a verification tool to gauge how accurately the Gleeble simulations have recreated weld material with respect to the physical weld.
DP600 steel is used as a reference material. DP600 is a dual-phase steel, consisting of ferrite and 15 to 20 pct martensite.[10,30] The steel is well documented and provides a ready source from which to verify experimental results. For example, the known BM yield strength formed one of the validation parameters from which to gauge the accuracy of the instrumented indentation tests. This mixed ferrite-martensite steel was also compared to the results from the soft boron steel HAZ.
2 Experimental Method
2.1 Producing the Spot Weld
1.5-mm-thick unhardened 22MnB5 steel sheets, supplied by Tata Steel, were hot formed in accordance with Mohr,[31] on a 500 t Enefco press. Spot welding was performed with a Matuschek welding control system and ARO servo-controlled spot welding gun. The weld schedule, obtained from an automotive OEM, consisted of 2 pulses. DP600 steel, also supplied by Tata Steel in 1.5 mm gage thickness, was welded with the same fixed weld schedule.
Peel testing was performed according to the ISO 10447:2007[32] specification to ensure button pull-out failure occurred consistently. It was also checked that the nugget diameters conformed to the automotive standard of 4√t to 5√t,[33] where t is the sheet thickness.
2.2 Hardness Measurements and Defining Points of Interest
A physical weld was sectioned in half, through thickness, using a Buehler IsoMet 4000 linear precision saw. The sectioned sample was then mounted in a thermosetting resin using a Buehler SimpliMet hot mounting press and subsequently polished, using a final stage 3 μm diamond suspension polishing liquid. The polished sample was then etched with 2 pct Nital.
Hardness measurements were performed on a Wilson Hardness Tukon 1202 hardness tester with a motorized stage. Hardness tests were performed in accordance with BS EN ISO 6507-1:1998.[34] The measured hardness distribution was used to determine the locations from which the temperature histories were obtained, as shown in Figure 1. The BM is conservatively defined to start at 6.6 mm from the weld center and is referred to as point D.
2.3 SORPAS Simulation and Extraction of Thermal Histories
To obtain thermal histories to drive the Gleeble physical simulations, the weld schedule was input into SORPAS welding simulation software.[35] The final simulated nugget size compared favorably to the measured physical nugget size, giving validation to the simulation. Figure 2 shows the peak temperature distribution of the weld obtained through SORPAS. Points A to C are shown in the figure. Point D is the base material, and hence does not need to be physically simulated.
The extracted thermal histories are shown in Figure 3. The figure shows that three peak temperature regimes were used, namely 575 °C, 725 °C, and 1100 °C. It was attempted to characterize an additional point halfway between points A and B; however, due to experimental error, this point is omitted from the current work.
Sayles[36] performed dilatometry tests on a similar steel composition as used in this work. It was found that the Ac1 temperature is 733 °C and the Ac3 temperature is 858 °C. Considering this information, it is reasonable to expect that the samples produced by the heating regimes of 575 °C and 725 °C will produce tempered martensite, as they are below the transformation temperatures.
2.4 Gleeble Physical Simulation
2.4.1 Material preparation
The as-delivered sheets of 1.5-mm-thick boron steel were guillotined into specimens of 20 × 130 mm. These specimens were then hot formed in accordance with Mohr.[31] Hardness tests confirmed a fully developed martensitic microstructure through the thickness of the specimens.
2.4.2 Gleeble grip selection
Due to the Gleeble utilizing water-cooled grips, a temperature gradient develops along the sample length, with the center experiencing the highest temperature. To obtain a temperature gradient that was as homogeneous as possible, stainless steel half-contact grips were recommended by a Gleeble representative. The low thermal conductivity of these grips results in a relatively flat thermal profile by drawing a reduced amount of heat from the sample ends.
A drawback of the half-contact grips is that electrical arcing and localized hot spots occur when using very fast heating rates. Other grips types, such as full-contact copper grips allow for fast heating rates to be applied; however, a highly parabolic heating profile occurs along the sample length and preliminary tests showed that unsatisfactory hardness distributions occurred along the gage length.
Taking the advantages and disadvantages of each grip type into account, it was decided that the focus of the Gleeble trials was to obtain tensile specimens with microstructurally homogeneous gage lengths, thus ensuring consistent tensile results without the effect of microstructural gradients along the gage length. This meant that half-contact stainless steel grips would be used; however, this limits the experiment to slower heating rates to avoid arcing and hot spots. The effect of slower heating rates on phase transformation kinetics will be discussed later in the paper.
2.4.3 Establishing heating times
With the heating rate limitations placed by the half-contact stainless steel grips, the challenge was to obtain the fastest heating rate possible as well as to consistently reach the correct peak temperature. A preliminary investigation, where heating rates approximating those given by the SOPRAS simulation were used, resulted in uneven heating and localized hot spots. Hardness results indicated unsatisfactory results. Thus, the heating rates were reduced to accommodate the limitations imposed by the chosen grips.
The investigation into finding the fastest heating time is illustrated in Figure 4, which shows 3 heating times applied to each of the 3 peak temperatures. As the target temperature increases, the fastest heating time (5 seconds) results in the greatest undershoot. The 7 seconds heating time reached the target temperatures in all regimes except the 1100 °C regime, with an undershoot of approximately 30 °C. Given that 1100 °C is far above the Ac3 transformation temperature, such a small undershoot would have a minimal effect on the final microstructure.
It was decided, as a compromise between heating time and peak temperature accuracy, to scale the target heating regime to achieve peak temperature within 7 seconds. In this sense, the “target heating regime” is defined as the collection of temperatures, shown in Figure 3, obtained through the SORPAS simulation.
2.4.4 Physical simulation trials
The fully hardened boron steel samples were placed in the Gleeble test chamber, shown in Figure 5 and heated to the three peak temperature regimes. After reaching peak temperature, an air quench system was activated to approximate the cooling rates achieved during physical spot welding. The quench system was set to the maximum pressure of 8.5 MPa to achieve optimum cooling. A total of 36 samples were produced, consisting of 3 repeats for each tensile geometry at each temperature regime.
A comparison of achieved vs target cooling rates is given in Figure 6. It can be seen that, as the peak temperature decreases, the achieved and target cooling rates converge. It is interesting to note the latent heat release from martensite formation, evidenced through the inflections of the cooling curves in Figure 6(a).
2.4.5 Thermal gradients and hardness distributions
The thermal gradients across the samples were investigated by attaching thermocouples in the center of the sample and at 10, 15, and 20 mm from the central thermocouple. A final thermocouple was attached at the edge of the sample, midway along the length, as indicated in Figure 7. Three repeats of each peak temperature regime were performed.
Figure 8 shows the difference in measured peak temperature between the central thermocouple and other indicated distances. The difference in temperature increases with distance from the center, with the 1100 °C regime exhibiting the largest difference in temperature.
As stated previously, the Ac1 temperature has been established to be 733 °C; hence, the temperature difference along the length of the 725 °C heating regime samples is not expected to lead to significant microstructural gradients. The 1100 °C heating regime is far above the Ac3 temperature, and hence minimal microstructural effects are expected from the temperature difference along the length of the sample. From these measurements, it may be assumed that a relatively flat thermal profile has developed along the sample length, which will be confirmed through hardness measurements.
Hardness tests were performed in accordance with BS EN ISO 6507-1:1998.[37] Measurement lines were made along the longitudinal direction at 3 equidistant depths in the sheet thickness direction. Indents were performed at 1-mm intervals along the sample length.
Figure 9 shows the average hardness distribution from the three measurement lines taken on the Gleeble simulated samples. For each peak temperature regime, the samples exhibit a homogeneous hardness distribution approximately 60 mm in length. The hardness variation beyond 20 mm was due to slight misalignment of the air quench system. This hardness distribution will not affect the tensile test results significantly, as they fall well within the grip length of the tensile destructive samples. These results have given confidence that microstructural gradients will not affect material property extraction though tensile destructive testing. An in-depth microstructural discussion of the hardness results will be presented later in this work.
2.4.6 Obtaining tensile destructive geometries from Gleeble samples
Four different tensile geometries were machined out of the rectangular Gleeble samples using Electrical Discharge Machining (EDM). Such a machining method results in minimal heat input,[38] thus not introducing unforeseen heat treatments onto the samples. The four geometries are shown in Figure 10. The dog-bone geometry is used to extract material properties such as tensile and yield strength. The other 3 geometries are used in the creation of the failure loci.
Lanzerath[29] reported that standard dog-bone specimens cannot be used in the development of a failure locus. This is due to the need to keep the stress state constant during deformation until failure occurs. As suggested by Lanzerath, a central-hole uniaxial tensile sample is employed to extract uniaxial failure locus data.
2.5 Extraction of Stress–Strain Curves Through Tensile Testing
All tensile tests were performed on a screw-driven Instron 5800R tensile test machine with a 100-kN load cell, accurate to ± 25 N. All dog-bone specimens were placed under uniaxial tension with a displacement rate of 1 mm/min. A high-speed camera was used to capture digital image correlation (DIC) images for post-test strain measurements and samples were sprayed with a speckle pattern before testing, to enable DIC image capture.[39]
2.6 Extracting Fracture Strain and Triaxiality Values for Failure Loci
A failure locus is typically represented as strain at failure (εf) against a variable denoting the stress state, being either the stress triaxiality (η) or ratio of principal strains (α).
In a failure locus plot, the shear and plane-strain α values are local minima and uniaxial tension is a local maximum. Bao and Wierzbicki[40] reported that simple parabolic curves in the ranges of \( - 1 \le \alpha \le - 1/2 \) and \( - 1/2 \le \alpha \le 0 \) were found to be in good agreement with experimental data. Therefore, to construct a fracture locus, only the minimum and maximum points need to be measured and parabolic curves fitted between them. Such a method was successfully employed by Beaumont[39] and is adopted in this work.
The tensile geometries were tested under uniaxial loading with a displacement rate of 1 mm/min. The failure strain and triaxiality values were extracted from the point of fracture on the measured DIC grid, as indicated by the black crosshairs in Figure 11. High-speed photography was used to establish the fracture locations on the 3 destructive samples. Fracture was found to occur in the sample center of the plane-strain geometry. For the uniaxial sample, fracture occurred at the free edge of the hole. For the shear geometry, previous work by Beaumont[39] determined the failure mode to be a shear in-plane mode II crack. It was therefore recommended to extract strain from the broad central region of even strain in the gage area.
As stated previously, the locus can be approximated by a second-order polynomial fitted through the measured data points.[40] The reader is referred to Raath[41] for the methodology of constructing the locus. This procedure was performed for all samples.
2.7 Extracting Yield Strength Through Instrumented Indentation
An example of a typical load–depth (P–h) curve is shown in Figure 12, where load is designated as P and depth of penetration as h. The load is applied from zero up to a prescribed maximum value and then back to zero. When the indenter is withdrawn, a residual impression is left due to plastic deformation, with some elastic recovery occurring due to relaxation of elastic strains in the material. By analyzing the initial portion of the unloading curve, the elastic modulus may be calculated from the following equation:
where dP/dh is the unloading slope, A is the projected contact area, and E* is known as the reduced modulus, which takes into account the material properties of the indenter and specimen material being indented, through the equation:
where the subscript in refers to the indenter and ν is Poisson’s ratio. The projected contact area (A) is calculated from the known indenter geometry and depth of penetration at the area of contact (hc). For example, the projected contact area of a Vickers indenter is given by A = 24.504h 2c .[42]
Dao[20] developed a set of dimensionless functions with their closed-form relationships between the load–depth response and elasto-plastic material properties. The algorithm will be employed in this work and a brief outline of the method will be given. The indented material is modeled as elastic-plastic, with true stress–strain behavior as follows:
If the total strain is defined as consisting of elastic and plastic parts, then beyond the elastic stress, Eq. [3] can be written as
where the subscripts y and p refer to elastic and plastic parts, respectively. Dao stated that, with the previously defined constitutive law, the material’s elasto-plastic behavior can be fully described by the representative stress (σr) and strain hardening exponent. It was found that εr = 0.033 best normalized the dimensionless functions with respect to strain hardening, where εr is the representative strain.
A short description of Dao’s method will be given. Firstly, the maximum and residual penetration depths are read from the measured P–h curve. In the next step, the unloading slope and fourth dimensionless function (being a function of residual and maximum penetration depths) are used to obtain the true contact area and reduced modulus. Next, the first dimensionless function (being a function of reduced modulus and representative stress) is used to calculate the representative stress at a strain of 0.033. Then, the second dimensionless function (being a function of reduced modulus, representative stress, and strain hardening exponent) and unloading slope are used to calculate the strain hardening exponent. If the calculated strain hardening exponent is greater than zero, then the yield stress is solved for from the following equation:
Indentations were performed in accordance with ISO 14577-1:2002 on an MTS Nano Indenter XP at the Open University on both boron steel and DP600 spot welds using a Berkovich tip. A loading rate of 100 nm/s was used with a prescribed maximum load of 500 mN.
Indents in the HAZ were made at 0.25-mm intervals. Due to time constraints on the indenter machine, indents in the nugget were performed in steps of 1 mm. Previous Vickers hardness tests indicated minimal variation through the nugget length, and hence larger steps were deemed acceptable.
Three line scans were performed, spanning from the BM, through the weld and back into the BM, with the line scans being equidistant through the sheet thickness.
In accordance with ISO 14577-1:2002, the force was held constant for two periods during the test, at maximum load (to ensure creep is completed) and at the end of the unloading stage (to compensate for thermal drift). After these corrections have been applied, the measured load–depth curves were processed via Dao’s algorithm.
3 Results and Discussion
3.1 Validating Instrumented Indentation Results
The purpose of this section is to establish the correlation between the yield strengths extracted through tensile testing and instrumented indentation. These two independent results are therefore used to quantify how accurately the HAZ microstructure has been recreated onto the tensile destructive specimens and therefore the confidence that can be placed in the material constitutive behavior to be presented later in this work.
The three measured P–h curves for each point are shown Figure 13. Figures 13(a) and (d) show the smallest penetration depths, as would be expected for hard martensitic material. The P–h curves for point B shows the largest indenter penetration, correlating well with soft material. The maximum penetration depth for point D decreases as the indenter is driven into harder material.
Figure 14 shows the calculated yield strength distribution of the boron steel spot weld, taken as the average of the 3 line scans. Although individual data points show scatter, the average in the nugget shows a consistent level of high yield values, with an average of 1040 MPa. The BM (right-most data point at 6.6 mm from the weld center) exhibits a yield strength of approximately 1011 MPa. Such values are typically associated with fully hardened boron steel.[43]
Next, a direct comparison is made between the yield strengths extracted from instrumented indentation and uniaxial tensile tests for the boron steel BM. Figure 15 shows the stress–strain curve of the boron steel BM, taken from the uniaxial dog-bone tests, with the instrumented indentation calculated BM yield stress overlaid. The 0.2 pct offset yield from the experimental stress–strain curve is 1047 MPa and the calculated yield is 1011 MPa, showing a close correlation.
Due to limited allocated experimental time, indents were not made into the far-field BM; therefore, the instrumented indentation yield value presented for the BM is from the average of three data points at 6.6 mm in Figure 14. Hardness tests indicated that the BM and nugget exhibit similar hardness levels. Taking the thermal histories into account, where both the BM and nugget were austenitized and rapidly quenched, both parts are composed of significant amounts of martensite. The high level of consistent yield strengths in the nugget is therefore used as verification that the data point at 6.6 mm is calculated to be at an acceptable value.
Figure 16 shows the calculated yield strength distribution of the DP600 spot weld. The yield strength in the nugget shows an average value of 925 MPa. Figure 17 shows the average stress–strain curve of 5 tensile tests of DP600 BM. It is clear that the instrumented indentation calculated yield strength gives a closer correlation to the 0 pct offset yield from tensile dog-bone tests.
So far, it has been shown that the instrumented indentation calculated yield strengths of the boron steel and DP600 BM compare well with the experimentally measured yield strengths from the corresponding steel BM tensile tests. The results from the DP600 BM are used as verification that the algorithm works for softer materials. An assumption is made that, since close correspondence has been achieved between tensile and instrumented indentation tests for the softer DP600 BM, a similar correspondence is expected of the soft boron steel HAZ.
It is interesting to note that the calculated yields of the hard boron steel BM correlate well with the 0.2 pct offset yield values, but the softer DP600 BM calculations correlate better with the 0 pct offset yield results. A possible explanation for the different yield percentage correlations is due to the material behavior under indentation.
For hard materials, an increase in stress has relatively little impact on strain. For softer materials, a large change in strain is expected for a relatively small increase in pressure. Considering that all indents were performed under the same pressure, the difference between harder and softer behavior under the same pressure could be a possible reason for the different yield strength correspondence.
3.2 Hardness, Yield, and Microstructure Comparisons
3.2.1 Point A (1100 °C peak temperature)
Figure 18(a) compares the hardness of point A on the physical weld HAZ with that of the Gleeble sample heated to a peak temperature of 1100 °C. The hardness values of the Gleeble sample are taken from an average of 3 line measurements in the range of − 5 to 5 mm from the sample centers, with indents spaced 1 mm apart. The target weld hardness is the average of 3 measurements taken at point A’s location.
The Gleeble hardness corresponds closely to the target hardness value, with a value approximately 4 pct below the target value, within the uncertainty. This close correspondence is due to both materials experiencing temperatures far beyond the Ac3 temperature. Due to the slower heating rate of the Gleeble runs compared to the target weld heating rates, the Gleeble samples have been austenitized for longer than the physical weld.
The physical weld reached peak temperature within 1 second, whereas the Gleeble samples reached peak temperature within 7 seconds. The hardness results indicate that cooling rates in both physical welding and Gleeble trials were sufficient for martensitic transformations to occur, evidenced by high hardness values.
Figure 18(b) compares the yield strengths calculated from instrumented indentation tests with the 0 and 0.2 pct offset yield strength taken from the uniaxial tensile tests of the Gleeble samples corresponding to point A. It was previously shown that there was a different correspondence between hard and soft materials with either 0 or 0.2 pct offset yield strengths, and hence both definitions are presented.
The yield extracted through instrumented indentation shows a closer correlation to the 0.2 pct offset yield of the Gleeble uniaxial tensile tests, with a 0.8 pct difference. The difference between the instrumented indentation and 0 pct yield values is 26 pct. As stated previously, the difference in yield correspondence may be due to materials behavior under indentation.
Figure 19 compares the microstructure of point A on the physical weld with that of the Gleeble sample. Figure (a) shows the hardness indent at 3.8 mm from the weld center. It appears that the indent is at the border of two different microstructural zones. The lower left hand corner of Figure 19(a) shows what appears to be a very fine martensitic microstructure. Martensite is inferred due to the lath-like structure and high hardness value.
The physically simulated microstructure in Figure 19(b) shows a much coarser martensitic microstructure. Due to the longer time spent being austenitized, austenite grain enlargement may have occurred in the Gleeble sample, which led to a coarser structure. Although the microstructures appear visually different, they correspond well in terms of mechanical properties (hardness and yield strength).
3.2.2 Point B (725 °C peak temperature)
Figure 20(a) shows a close correspondence in hardness values between the weld and Gleeble, with a 10 pct difference between the two. Figure 20(b) compares the instrumented indentation yield with the two yield definitions taken from Gleeble tensile tests. The instrumented indentation yield value corresponds more closely to the 0 pct yield value. This is consistent with the observation that the softer DP600 BM instrumented indentation yield showed closer correlation to the 0 pct yield than the 0.2 pct yield.
The microstructural comparison between the physical HAZ point B and corresponding Gleeble sample is shown in Figure 21. The Gleeble sample displays a more finely dispersed microstructure than the corresponding weld microstructure, with the weld exhibiting larger ferrite grains (shown in white). Ferrite is inferred due to the low hardness of this region. It is clear that a large portion of martensite has been transformed into ferrite, with the cementite at the grain boundaries shown in black. The weld does exhibit a finer microstructure than the Gleeble sample. This could be due to the Gleeble sample spending a longer time at elevated temperatures, leading to more carbon being precipitated out and a coarser microstructure being formed.
3.2.3 Point C (575 °C peak temperature)
Figure 22(a) shows an 18 pct difference in hardness between the physical point C HAZ hardness and Gleeble sample. Again, this difference may be attributed to the Gleeble sample spending longer times at elevated temperatures and thus experiencing a greater degree of tempering.
Figure 22(b) shows a closer correlation of the instrumented indentation yield with the 0 pct offset yield than the 0.2 pct offset yield. This is consistent with observations so far that harder materials correspond closer to 0.2 pct offset yield and softer materials correspond closer to 0 pct offset yield. There is a 1 and 35 pct difference between the instrumented indentation yield and 0 and 0.2 pct offset yields, respectively.
The difference in microstructure between the HAZ at point C and corresponding Gleeble sample is shown in Figure 23. The white microstructure in Figures 23(a) and (b) is inferred to be ferrite, due to the reduced hardness. The ferrite islands appear to be of comparable size in both images. The Gleeble sample does appear to exhibit a more distinguishable lath microstructure.
3.2.4 General discussion of HAZ material reproduction
The previous analyses have shown that the physical weld and Gleeble samples correlate well in terms of hardness and yield strengths. The most likely cause of deviations in material properties between the physical weld and Gleeble samples is due to the slower heating rate used in Gleeble experiments. This is further evidenced by differences in microstructure. For samples heated to austenitization, the increased time at elevated temperatures has caused increased austenite growth and grain enlargement. For the samples heated to lower temperatures, excessive tempering has occurred.
In the preceding analyses, yield strength calculated through instrumented indentation was used as one of the verification parameters to gauge correspondence between the physical weld and Gleeble samples. It is important to note that the method is highly sensitive to the accuracy with which P–h curves were measured. Multiple indents were performed per location, to increase the accuracy of calculated yield strengths.
Additionally, indenter loading rate has an influence on the measured P–h curve, due to strain-rate effects.[44] Aggag[45] performed a loading rate study on steel hardness standard blocks and found that loading rates of 100 to 10,000 nm/s gave similar P–h curves. Significant variations were seen for loading rates of 100,000 nm/s and above.
For the work presented in this paper, a parametric study was not performed to establish the optimum loading rate; however, the utilized loading rate of 100 nm/s would suggest that strain-rate effects are kept to a minimum. As previously stated, the method is highly sensitive to the accuracy with which P–h curves are measured, and it is likely that different yield values would be obtained if the loading rate was varied.
3.3 Stress–Strain Curves and Failure Loci
The preceding analyses have given confidence that the presented stress–strain curves are representative of the mechanical properties distributed through the boron steel HAZ.
Figure 24 shows the stress–strain curves for each peak temperature regime, along with the BM results. Points A and D lie in hard martensitic regions, with the corresponding stress–strain curves exhibiting a UTS of approximately 1450 MPa. This value is typically associated with fully hardened boron steel.[43]
The softer HAZ regions (curves B and C) exhibit ductile behavior, with larger elongations, as would be expected from tempered steel. There is a significant difference in mechanical strength and ductility between the martensitic regions of points A and D and the tempered zone represented by points B and C. As stated previously, these lower strength areas are due to tempering of martensite.
Figure 25 shows the failure loci for all Gleeble temperature ranges. The softer HAZ areas (curves B and C) exhibit higher failure strains across shear (α = − 1), uniaxial tension (α = − 0.5), and plane-strain (α = 0) stress states, compared to the higher strength materials (curves A and D). The lower failure strains across all stress states for the martensitic points of A and D indicate brittle material. Again, the preceding comparisons of instrumented indentation and Gleeble yields have given confidence that the presented failure loci are representative of the mechanical property distribution of the HAZ.
4 Conclusions
A study was presented to extract boron steel HAZ material properties through tensile destructive testing, where tensile samples where physically simulated through a Gleeble machine by exposing the samples to similar temperature histories experienced by certain points in the weld.
Due to limitations of the chosen Gleeble grips, deviations from the target weld microstructures were expected. To validate the correspondence between the target weld microstructures and the physically simulated Gleeble samples, a new validation methodology was presented.
This method consisted of comparing the physical weld region hardness to that of the corresponding physically simulated samples. The second verification tool was comparing the calculated yield strengths of the physical weld regions, obtained through instrumented indentation, to the yield strengths taken from stress–strain curves of destructively tested Gleeble samples. To the author’s knowledge, instrumented indentation has not previously been used to verify the accuracy of heat-treated samples with respect to their target microstructures. Therefore, this work explores a new application of instrumented indentation.
Microstructural analysis indicated that the Gleeble microstructures deviated from their targets. Considering that all samples reached the correct target temperatures, the deviation can be attributed to the extended times spent at elevated temperatures. The use of calculated yield strengths provided an additional parameter from which to gauge the accuracy of material recreation and gave more confidence in utilizing the physically simulated samples.
Once confidence has been established that the calculated yield strengths are accurate, instrumented indentation can be a valuable tool for gaging the accuracy of recreated microstructures.
An interesting observation was made that the calculated yield strengths of the hard boron steel BM correlated well with the 0.2 pct offset yield strength of the tensile curve. However, the calculated yield strengths of the relatively soft DP600 BM corresponded well with the 0 pct offset yield strength of the tensile curve. This difference in yield offset correspondence may be attributed to the difference in behavior of hard and soft materials under indentation.
References
R. Mohan Iyengar, B. Fedewa, Y.W. Wang, D.F. Maatz Jr., and R.L. Hughes: SAE Int., 2008, pp 1–14.
2. Yu, Y., C. Wang, S. Chen and Z. Lu, Adv. Mater. Res., 2011. 339: pp 375-78.
3. Choi, H.S., G.H. Park, W.S. Lim and B.M. Kim, J. Mech. Sci. Technol., 2011. 25: pp 1543-50.
4. Kong, J.P., T.K. Han, K.G. Chin, B.G. Park and C.Y. Kang, Mater. Des., 2013. 54(1): pp 598-609.
5. Sommer, S., IOP Conf. Series: Materials Science and Engineering, 2010. 10(1): pp 1-10.
T. Lienert, T. Siewert, S. Babu, and V. Acoff: ASM Handbook Volume 6A Welding Fundamentals and Processes, ASM International, 2011.
7. Furuhara, T., K. Kobayashi and T. Maki, ISIJ Int., 2004. 44(11): pp 1937 - 44.
R. Blondeau: Metallurgy and Mechanics of Welding. Wiley: London (2013).
9. Liang, X., X. Yuan, H. Wang, X. Li, C. Li and X. Pan, Int. J. Precis. Eng. Manuf., 2016. 17(12): pp 1659 - 64.
10. Matya, M. and X.Q. Gayden, Weld. J., 2005. 84(11): pp 172-82.
11. Ma, C., D.L. Chen, S.D. Bhole, G. Boudreau, A. Lee and E. Biro, Mater. Sci. Eng. A, 2008. 485(1): pp 334 - 46.
12. Farabi, N., D.L. Chen, J. Li, Y. Zhou and S.J. Dong, Mater. Sci. Eng. A, 2010. 527(4): pp 1215 - 22.
13. O’Keeffe, C., J. Imbert-Boyd, M. Worswick, C. Butcher, S. Malcolm, J. Dykeman, P. Penner, C. Yau, R. Soldaat, and W. Bernert, Procedia Eng., 2017. 197(1): pp 294 - 303.
Dynamic Systems Inc. Gleeble. 2015 [cited 2015 23/10/2015]; www.gleeble.com.
15. Abspoel, M., B.M. Neelis and P. van Liempt, J. Mater. Process. Technol., 2016. 228(1): pp 34 - 42.
16. Eller, T.K., L. Greve, M.T. Andres, M. Medricky, H.J.M. Geijselaers, V.T. Meinders and A.H. van den Boogaard, J. Mater. Process. Technol., 2016. 234(1): pp 309-22.
17. Ye, D., F. Mi, J. Liu, Y. Xu, Y. Chen and L. Xiao, J. Mater. Sci. Eng. A, 2013. 564(1): pp 76 - 84.
18. Chung, K.H., W. Lee, J.H. Kim, C. Kim, S.H. Park, D. Kwon and K. Chung, Int. J. Solids Struct., 2009. 46(2): pp 344 - 63.
19. Sun, G., F. Xu, G. Li, X. Huang and Q. Li, Comput. Mater. Sci., 2014. 85(1): pp 347 - 62.
20. Dao, M., N. Chollacoop, K.J. van Vliet, T.A. Venkatesh and S. Suresh, Acta Mater., 2001. 49(19): pp 3899-918.
21. Lee, J., C. Lee and B. Kim, Mater. Des., 2009. 30(9): pp 3395 - 404.
22. Kim, J.J., T.H. Pham and S.E. Kim, Int. J. Mech. Sci., 2015. 1(103): pp 265 - 74.
23. Atrian, A., G.H. Majzoobi, S.H. Nourbakhsh, S.A. Galehdari and R.M. Nejad, Adv. Powder Technol., 2016. 27(4): pp 1821 - 27.
24. Pham, T.H. and S.E. Kim, Constr. Build. Mater., 2017. 155(1): pp 176 - 86.
25. De Bono, D.M., T. London, M. Baker and M.J. Whiting, Int J Mech Sci, 2017. 123(1): pp 162 - 76.
26. Cheng, Y.T. and C.M. Cheng, J. Mater. Res., 1999. 14(9): pp 3493 - 96.
27. Oliver, W.C. and G.M. Pharr, J Mater Res, 2004. 19(1): pp 3 - 20.
28. Oliver, W.C. and G.M. Pharr, J Mater Res, 1992. 7(6): pp 1564 - 83.
H. Lanzerath, A. Bach, G. Oberhofer, and H. Gese: SAE Int., 2007, pp 1–10.
30. Avramovic-Cingara, G., Y. Ososkov, M.K. Jain and D.S. Wilkinson, Mater. Sci. Eng., 2009. 516(1): pp 7-16.
31. Mohr, D. and F. Ebnoether, Int. J. Solids Struct., 2009. 46: pp 3535-47.
Institute, B.S., BS EN ISO 10447:2007. British Standards, 2007.
33. den Uijl, N., T. Okada, T. Moolevliet, A. Mennes, E. van den Aa, M. Uchihara, S. Smith, H. Nishibata, T. van der Veldt, and K. Fukui, Weld. World, 2012. 56(8): pp 51-63.
Institute, B.S., BS EN ISO 6507-1:1998 Metallic materials - Vickers hardness test British Standards, 1998.
SORPAS User Manual 7.0. 2007: SWANTEC Software and Engineering ApS.
A. Sayles: Tata Steel Test Report Number 11KT1037. 2011, Tata Steel.
Institute, B.S., BS EN ISO 6507-1:1998. British Standards, 1998.
38. Prime, M.B., T. Gnaupel-Herold, J.A. Baumann, R.J. Lederich, D.M. Bowden and R.J. Sebring, Acta Mater., 2006. 54(15): pp 4013-21.
R.A. Beaumont: Determining the Effect of Strain Rate on the Fracture of Sheet Steel. Ph.D. Thesis, University of Warwick, 2012.
40. Bao, Y. and T. Wierzbicki, Int J Mech Sci, 2004. 46(1): pp 81 - 98.
N.D. Raath: Ph.D. Thesis, University of Warwick, 2014.
A.C. Fischer-Cripps: Nanoindentation. Springer, Berlin, 2011.
43. Barcellona, A. and D. Palmeri, Metall. Mater. Trans. A, 2009. 40(5): pp 1160-74.
44. Lucas, B.N. and W.C. Oliver, Metall. Mater. Trans. A, 1999. 30(3): pp 601 - 10.
G. Aggag and A. Abu-Elezz: in XVIII IMEKO Worl Congress, Rio de Janeiro, 2006.
Acknowledgments
The authors would like to thank Tata Steel, WMG, and the EPSRC for funding this work. Thank you to the Open University for providing instrumented indentation support. Thank you to Swansea University for providing Gleeble support. Thank you to Ellen van den Aa, Guido Hensen, Martin Thornton, Darren Stewardson, Martyn Wilkinson, David Cooper, Darren Grant, Stefan Kousoulas, Carl Lobjoit, and Zachary Parkinson.
Author information
Authors and Affiliations
Corresponding author
Additional information
Manuscript submitted July 21, 2017.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Raath, N.D., Norman, D., McGregor, I. et al. Characterization of Loading Responses and Failure Loci of a Boron Steel Spot Weld. Metall Mater Trans A 49, 1536–1551 (2018). https://doi.org/10.1007/s11661-018-4502-x
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11661-018-4502-x