1 Introduction

The conventional approach for producing steel plate involves thick slab casting, reheating, and hot rolling. A recent alternative is the process of Thin Slab Casting Direct Rolling (TSCDR). The advent of TSCDR offers several advantages including reduced capital, energy, labor, and inventory costs.[1,2] However, the elimination of slab reheating and roughing deformation leaves fewer opportunities for grain refinement due to the small number of deformation passes available in the TSCDR process (5 to 7 passes). Studies of TSCDR show that thermomechanical processing can reduce the average grain size, but cannot eliminate the large grains present at the center of the slab, especially for heavy gage products.[3,4] This makes it extremely important to control the as-cast microstructure and the grain size evolution at high temperatures in order to achieve acceptable final mechanical properties. Second phase particles have been used extensively to control the kinetics of grain growth at high temperature during TSCDR. In microalloyed steels, for example, dispersions of nano-scale Ti, V, and/or Nb carbonitrides are employed to limit grain growth.[5–7] When the steel is held at high temperature for an extended period of time, however, these precipitates become ineffective at pinning grain growth for two reasons: First, these nano-scale particles coarsen rapidly because of their small size and as a consequence the pinning force drops very rapidly. Secondly, most of these fine particles will dissolve at very high temperatures. In some cases, it is possible to use more stable precipitates, such as TiN. The problem then is that these particles form in the liquid and coarsen quickly to a large size which limits their effectiveness at pinning grain growth. Some authors proposed the use of oxide dispersions to pin grain growth at high temperatures.[8,9] While promising results have been obtained using this approach, the main challenges are how to produce fine dispersions of these particles in the caster. In the absence of particle pinning, austenite grains in excess of 2 mm may form prior to the onset of thermomechanical processing.[10,11]

This work proposes a novel alternative, in which, a two-phase mixture of austenite and delta-ferrite is utilized to control the grain size evolution at high temperature. The basic concept is to design steels in which austenite and delta-ferrite co-exist over a wide temperature range. The particles of the minor phase would then pin grains of the major phase. The pinning effect is very stable due to the fact that the second phase particles are large and as a result, there is a small driving force for them to coarsen. This contribution has the modest aim of illustrating this new concept using a model Fe-Al alloy in which the two-phase (austenite/ferrite) region extends from 1123 K to 1578 K (850 °C to 1305 °C). The austenite particle coarsening kinetics and the delta-ferrite grain growth kinetics were carefully measured over the above temperature range. The interaction between the coarsening of the austenite particles and the growth of the delta-ferrite grains was analyzed as a function of the particle volume fraction, heating temperature, and holding time.

2 Materials and Experimental Procedure

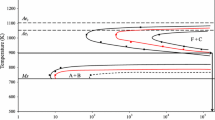
In order to investigate the Austenite particle coarsening behavior and pinning of the austenite/delta-ferrite two-phase microstructure at high temperature, 1.5 pct Al was added to a Ti- and Nb-free version of APIX60 steel (Table I). The addition of Al has the effect of stabilizing the body centered cubic (BCC) phase as shown in Figure 1. In alloys, similar to the one considered here, one could not distinguish between alpha-ferrite and delta-ferrite because the BCC phase is present at all temperatures. For this reason, the terms ferrite and delta-ferrite will be used interchangeably. The model Fe-1.5Al alloy steel was prepared by induction melting at Canmet MATERIALS Technology Laboratories (Hamilton, Canada); a heat of 40 kg was cast and hot rolled to a plate of 10-mm thickness. The as-received microstructure was ferritic with a grain size of approximately 85 μm.

Table I Composition of the Model Alloy Used in This Investigation (Weight Percent). The Composition of APIX60 Steel is Included for Comparison
Full size table
Fig. 1
figure 1

Phase diagram of Fe-1.5 pctAl-0.051 pctC-1.0 pctMn-0.36 pct Si model alloy predicted by ThermoCalc using the TCFE2 database[12]

Full size image

The coarsening of the austenite particles (minor phase) and the evolution of the ferrite grain size were studied using a high-temperature tube furnace. Samples were cut to 10 mm × 10 mm × 15 mm and sealed individually in vitreous silica under a back pressure of helium which varied so as to produce a pressure of 1 atm at the holding temperature. In order to determine the coarsening kinetics at the various temperatures and in the presence of various particle volume fractions, the samples were heated to 1123 K, 1333 K, 1473 K, 1533 K, 1553 K, 1568 K, 1572 K, 1578 K, and 1583 K (850 °C, 1060 °C, 1200 °C, 1260 °C, 1280 °C, 1295 °C, 1299 °C, 1305 °C, and 1310 °C) for different holding times. After each heat treatment, the samples were quenched into icy water and the capsules were broken in order to increase the cooling rate. All samples were sectioned and prepared using standard metallographic techniques. The ferrite grain boundaries were revealed using either 2 pct Nital or supersaturated picric acid with sodium dodecylbenzene sulfonate as a wetting agent. The microstructure was studied using optical microscopy and Scanning Electron Microscopy. Image analysis was performed using Clemex PE5.0 software. In order to obtain reliable statistics, six micrographs were analyzed for each sample, thus ensuring that at least 2000 austenite particles and 200 ferrite grains were analyzed. The average particle and grain sizes were measured based on the equivalent circular diameter. The austenite particle size distribution and the area fraction were also determined.

3 Results

Selected microstructures are shown in Figure 2 for various holding times at 1123 K, 1473 K, 1553 K, 1572 K, 1578 K, and 1583 K (850 °C, 1200 °C, 1280 °C, 1299 °C, 1305 °C, and 1310 °C). The dark regions are the austenite particles which transformed to martensite on quenching. The matrix is ferrite. The austenite area fraction was measured for each reheating condition. It was found that the austenite area fraction did not change with holding time for the conditions investigated. The measured austenite area fractions are compared to the equilibrium volume fractions calculated using the TCFE2 database of ThermoCalc[12] (Table II). While the measured and predicted volume fractions are in good qualitative agreement, their absolute values are significantly different between 1333 K and 1553 K (1060 °C and 1280 °C). This discrepancy will be further discussed in Section IV–A which deals with the effect of particle volume fraction on the coarsening kinetics.

Fig. 2
figure 2

Fe-Al model alloy microstructure obtained after (a) 6 h at 1123 K (850 °C), (b) 288 h at 1123 K (850 °C), (c) 15 min at 1473 K (1200 °C), (d) 180 min at 1473 K (1200 °C), (e) 5 min at 1553 K (1280 °C), (f) 60 min at 1553 K (1280 °C), (g) 15 min at 1572 K (1299 °C), (h) 15 min at 1578 K (1305 °C), and (i) 3 min at 1583 K (1310 °C). The dark particles are the austenite phase which transformed to martensite when quenched to room temperature and the gray matrix is delta-ferrite

Full size image
Table II Comparison of the Measured Austenite Area Fractions and Calculated Equilibrium Volume Fraction Using the TCFE2 Database of ThermoCalc (Percent)[12]
Full size table

The measured austenite particle size and the ferrite grain size, as a function of reheating temperature and holding time, are summarized in Figures 3(a) and (b), respectively. As expected, the austenite coarsening rate increases with increasing temperature. The evolution of ferrite grain size is more complicated due to the strong pinning effect exerted by the austenite particles. There is no grain growth at 1123 K (850 °C). At 1333 K and 1473 K (1060 °C and 1200 °C), the grain size evolution shows two regions; at shorter holding times, the grain size is almost constant, while at longer times, grain growth is observed. When the reheating temperature is increased to 1553 K and 1568 K (1280 °C and 1295 °C), grain growth occurs for all of the times investigated. A dramatic increase in the rate of grain growth is observed when the material is reheated to 1583 K (1310 °C) (Figure 2(i)) because the austenite particle volume fraction approaches zero.

Fig. 3
figure 3

(a) The measured austenite particle size as a function of temperature and holding time, (b) The measured delta grain size as a function of temperature and holding time. Solid diamond represents 1123 K (850 °C), solid square refers 1333 K (1060 °C), solid triangle means 1473 K (1200 °C), solid circle represents 1553 K (1280 °C), and hollow triangle refers 1568 K (1295 °C)

Full size image

4 Discussion

Austenite particles pin ferrite grain growth over a wide temperature range in the present Al-containing model steel. Experimental results suggest that ferrite grain growth is strongly retarded up to 1578 K (1305 °C). To start, the austenite particle coarsening kinetics are analyzed, followed by a discussion of the grain growth kinetics of ferrite and the pinning effect exerted by the austenite particles.

4.1 Austenite Particle Coarsening

The classical theory for particle coarsening was developed by Greenwood,[13] Lifshitz and Slyozov,[14] and Wagner,[15] and is often referred to as the LSW theory. The classical treatment relies on a diffusion analysis in which the rate of change of the diameter of each particle is independent of the position of other particles. The principal predictions of the LSW theory are a linear increase of the cube of average particle size with time and the self-similarity of the particle size distribution. For the present model alloy, the functional form of the variation of average austenite particle radius, \( \bar{r} \), with time, t, was deduced by plotting the data in terms of \( \left( {\bar{r}^{n} - \bar{r}_{0}^{n} } \right) \) vs (t − t 0) for various values of the coarsening exponent, n, where \( \bar{r}_{0} \) and t 0 are the initial values of the average austenite particle radius and time. An example for a reheating temperature of 1473 K (1200 °C) is shown in Figure 4. In order to identify the value of the growth exponent, n, which best describes the experimental data, the average particle radius was assumed to evolve as \( r = \sqrt[n]{{r_{0}^{n} + k(t - t_{0} )}} \), where k is the coarsening coefficient. The goalseek function within Microsoft Excel was then utilized to identify the values of n and k which result in the best fit of the experimental data. The analysis was limited to coarsening exponents of 1, 2, 3, and 4. For the above example [1473 K (1200 °C)], the best fit is obtained using an exponent of 3, as shown in Table III. Similar calculations revealed that an exponent of 3 also provides the best fit of the experimental data at 1553 K and 1568 K (1280 °C and 1295 °C), as shown in Figure 5(a). A coarsening exponent of 3 is expected under conditions of volume diffusion control. As expected, the coarsening coefficient, k, which is given by the slope in Figure 5(a), increased with increasing temperature. On the other hand, an exponent of 4 resulted in the best fit of the experimental data at 1123 K (850 °C) and 1333 K (1060 °C) which is attributed to grain boundary diffusion control, as shown in Figure 5(b). The transition from grain boundary control, at low temperatures, to bulk diffusion control, at high temperatures, is consistent with theoretical predictions based on the higher activation energy for bulk diffusion compared to grain boundary diffusion.

Fig. 4
figure 4

Plots of \( \left( {\bar{r}^{n} - \bar{r}_{0}^{n} } \right) \) vs (t − t 0) for various values of the coarsening exponent n at 1473 K (1200 °C) (a) n = 1, (b) n = 2, (c) n = 3, and (d) n = 4

Full size image
Table III Calculation of \( r = \sqrt[n]{{r_{0}^{n} + k(t - t_{0} )}} \) with n = 1, 2, 3, 4 at a Reheating Temperature 1473 K (1200 °C)
Full size table
Fig. 5
figure 5

Plots of (r n− r n0 ) vs (t − t 0) for (a) 1473 K, 1553 K, and 1568 K (1200 °C, 1280 °C, and 1295 °C, n = 3 (b) 1123 K and 1333 K (850 °C and 1060 °C), n = 4 (the value (r n − r n0 ) at 1123 K (850 °C) is shown on the secondary axis). \( \bar{r}_{0} \) is the initial average austenite particle radius at time t 0

Full size image

4.1.1 Bulk diffusion control

Thermodynamic calculations using the TCFE2 database of ThermoCalc[12] indicate that Mn and C partition to the austenite phase while Al partitions to the ferritic matrix. The concentration of Si is essentially the same in austenite and ferrite over the temperature range of interest. When the heat treatment temperature is above 1273 K (1200 °C), the observed coarsening exponent, n = 3, suggests that austenite particle coarsening is controlled by bulk diffusion through the delta-ferrite matrix. According to LSW theory[14,15]

$$ \bar{r}^{3} - \bar{r}_{0}^{3} = \frac{{8D\sigma_{\delta \gamma } N_{\delta } V_{\text{m}} t}}{{9{\mathcal{R}}T}}, $$
(1)

where D is the bulk diffusivity of the rate limiting solute in the ferrite matrix, \( \sigma_{\delta \gamma } \) is the austenite/ferrite interfacial energy, N δ is the solute molar fraction in ferrite, V m is the molar volume, and \( {\mathcal{R}} \) is the gas constant. The assumptions of the LSW theory, however, correspond to the approximation of a zero particle volume fraction, which obviously is not valid for large volume fractions of second phase particles. Asimow[16] and Ardell[17] were the first to incorporate the particle volume fraction into the framework of the LSW theory leading to the so-called Modified LSW theory (MLSW). Ardell[17] assumed that the diffusion of solute to a growing particle will depend on a distance characteristic of the spatial distribution of particles in the matrix. Asimow[16] modified the coarsening theory by modifying the diffusion geometry, but failed to perform the statistical averaging of the diffusion interactions between particles that is necessary for a satisfactory solution to this problem. Other models were later developed including models by Brailsford and Wynblatt,[18] Voorhees and Glicksman,[19] Marqusee and Ross[20] and Davies et al.[21] While the quantitative predictions of the models differ significantly, they all demonstrate that the coarsening rate should be larger than that predicted by the classical LSW model when the volume fraction of particles is large.

In order to quantify our observations, the following expression is used, as suggested by Martin et al.[22 23]:

$$ \bar{r}^{3} - \bar{r}_{0}^{3} = Kt, $$
(2)

where the austenite particle coarsening rate constant is given by

$$ K = \frac{{8f(F_{\text{v}} )D\sigma_{\delta \gamma } N_{\delta } (1 - N_{\delta } )V_{\text{m}} }}{{9{\mathcal{R}}T(N_{\gamma } - N_{\delta } )^{2} [1 + \partial \ln \gamma /\partial \ln N_{\delta } ]}}, $$
(3)

where N γ is the molar solute fraction in austenite, \( \varepsilon = 1 + \left( {\partial \ln \gamma /\partial \ln N_{\delta } } \right) \) is referred to as the Darken correction factor for non-ideality, in which γ is the activity coefficient.[24] In Eq. [3], f(F v) is an unknown function of the particle volume fraction, F v. Since the ferrite/austenite interface is incoherent, a reasonable value for \( \sigma_{\delta \gamma } \) is 0.56 Jm−2.[22] The molar volume, V m, is 7.11 cm3. The values of the equilibrium compositions of the substitutional elements in austenite (γ) and ferrite (δ) were extracted from the TCFE2 database[12] and summarized in Table IV. The Darken factor was also calculated[12,24] using the same database.[12] Finally, the diffusion coefficients of aluminum and manganese in the ferrite matrix were obtained from the MOB2 database of DICTRA[12] and are listed in Table IV.

Table IV Equilibrium Compositions of Austenite and Ferrite at Different Temperatures: 1578 K, 1568 K, 1553 K and 1473 K (1305 °C, 1295 °C, 1280 °C and 1200 °C)
Full size table

As shown in Table IV, Mn and Al have comparable diffusivities in ferrite and one cannot assume that one of the two solutes will dominate the coarsening kinetics. It is therefore necessary to treat the multi-component diffusion problem. Following Morral and Purdy[25] the generalized LSW treatment for multi-component systems is written as

$$ K = \frac{{f(F_{\text{v}} )8\sigma_{\delta \gamma } V_{\text{m}} }}{{9\left( {N_{\gamma } - N_{\delta } } \right]\left[ M \right]^{ - 1} [N_{\gamma } - N_{\delta } )}}. $$
(4)

In this equation square brackets refer to a square (n − 1) × (n − 1) matrix, e.g., [A], while the use of a round bracket followed by a square one, e.g., (A], represents a 1 × (n − 1) row matrix. Using the same notation, an (n − 1) × 1 column matrix is represented by a square bracket followed by a round one, e.g., [A). Thus, [M]−1 represents the inverse of the diffusion mobility matrix, (N γ  − N δ ] is a 1 × (n − 1) row concentration matrix, and [N γ  − N δ ) is an (n − 1) × 1 concentration matrix. It can be shown that when the cross-diffusion effects are negligible, the coarsening coefficient predicted by Eq. [4] simplifies to

$$ \frac{1}{{K_{\text{Total}} }} = \sum\limits_{i} {\frac{1}{{K_{i} }}} $$
(5)

and

$$ K_{i} = \frac{{f(F_{\text{v}} )8\sigma_{\delta \gamma } D_{i} N_{i}^{\delta } \left( {1 - N_{i}^{\delta } } \right)}}{{9{\mathcal{R}}T\left( {N_{i}^{\gamma } - N_{i}^{\delta } } \right)^{2} \left[ {1 + \partial \ln r/\partial \ln N_{i}^{\delta } } \right]}}, $$
(6)

where i refers to the various solutes present (e.g., Mn, Al, Si, C).

The same expression was applied by Martin et al.[22] and Lee et al.[26,27] In order to assess the applicability of this simplification to the present alloy system, the coarsening constant K, was evaluated from Eq. [4] using the full diffusion matrix and using Eq. [5], which only includes the diagonal diffusion coefficient. The results were found to be within 1.2 pct of each other. As a result, the simplified equation is used subsequently as it offers a more transparent picture of what is controlling the coarsening kinetics.

To start, the volume correction function, f(F v), is assumed to be 1 which is strictly true only for an infinitely small particle volume fraction. The predicted austenite particle coarsening rate constant based on Eq. [5] and that measured experimentally are compared in Table V. The ratio of the measured to the predicted coarsening rate shows a strong dependence on the austenite particles fraction. This ratio varies from 1.5 at low volume fraction (F v = 1.2 pct) to a value of 4.7 at a volume fraction of F v = 34.4 pct. The discrepancy between the calculations Eq. [5] and the experiments is likely due to the volume fraction correction factor. These measured ratios could be used to back-calculate the volume fraction correction factor, f(F v). The result of this calculation is compared with the predictions of the various models for the effect of volume fraction on coarsening kinetics[22,28] in Figure 6. The models of Asimow[16] and Voorhees and Glicksman[19] are in reasonable agreement with the experimental data for volume fractions up to 15 pct. None of the models, however, appears to offer a satisfactory fit of the experimental data at the highest volume fraction. It is difficult to comment on the origin of the poor agreement at the highest volume fraction because, as pointed out earlier, the thermodynamically predicted, equilibrium, volume fraction of 34.4 pct is much higher than the experimentally measured value of 21 pct at 1473 K (1200 °C). This could reflect an inaccuracy in the thermodynamic assessment of the system, or it may point to the fact that full (equilibrium) partitioning of the alloying elements is not achieved under the present experimental conditions. As such, it is not possible to make a critical comparison between the models and experimental data at the highest volume fraction. If attention is limited, however, to the high temperature data [>1473 K (1200 °C)], where the measured and predicted volume fractions are in good agreement, one concludes that the Asimow model[16] and that of Voorhees and Glicksman[19] offer a reasonable description of the experimental results. The model of Ardell,[17] on the other hand, appears to overestimate the volume fraction effect. This is probably due to the assumption that the diffusion of the solute to a growing particle will depend on a distance characteristic of the spatial distribution of particles in the matrix; this localized interaction of the diffusion fields around particles will exaggerate the effect of volume fraction on the coarsening rate. The Brailsford–Wynblatt Model[18] and that of Voorhees and Glicksman[19] approach the problem by accounting for the short- and long-range diffusion fields of a collection of particles. This approach appears to offer a more reasonable description of the experimental data. Interestingly, the Asimow model offers reasonable agreement with the experimental data in spite of the fact that it does not account for the statistical averaging of the diffusion interactions between particles.

Table V Comparison of Model Predicted Austenite Particle Coarsening Rate Constant and Measured Data
Full size table
Fig. 6
figure 6

Comparison of the predicted correction factors, ƒ(F v). The experimental data is presented using triangles, the solid lines represent the predictions of existing coarsening models[22,28]

Full size image

An additional comparison between the experimental data and the various coarsening models could be performed based on the particle size distribution. All coarsening models predict a self-similar particle size distribution. This is confirmed experimentally as shown in Figure 7, which shows the austenite particle size distributions at 1553 K (1280 °C) for holding times of 15, 30, 60, and 90 minutes. The particle size distributions at other temperatures are summarized as a function of the particle volume fraction in Figure 8(a). The predicted particle size distributions are shown in Figure 8(b) for the Voorhees and Glicksman model, Figure 8(c) for the Brailsford and Wynblatt model, and Figure 8(d) for the Ardell model.

Fig. 7
figure 7

Austenite particle size distribution at a heating temperature 1553 K (1280 °C) for holding time (a) 15 min, (b) 30 min, (c) 60 min, and (d) 90 min

Full size image
Fig. 8
figure 8

Comparison of measured and model predicted particle size distributions for different particle volume fractions (a) the measured austenite particle size distribution with different volume fractions: solid diamond, 1578 K (1305 °C), F v = 1.3 pct; solid square, 1572 K (1299 °C), F v = 2.6 pct; solid triangle, 1568 K (1295 °C), F v = 6.7 pct; hollow circle, 1553 K (1280 °C), F v = 9.6 pct; hollow triangle, 1533 K (1260 °C), F v = 12.1 pct; and solid circle, 1473 K (1200 °C), F v = 21.0 pct, (b) Voorhees & Glicksman model predicted particle size distribution,[19] (c) Brailsford & Wynblatt model predicted particle size distribution,[18] and (d) Ardell model predicted particle size distribution[17]

Full size image

The most meaningful comparison is obtained at temperatures above 1473 K (1200 °C) where the morphology of the austenite particles approaches the ideal spherical geometry assumed in the models. When the particle volume faction is <10 pct, the measured size distributions are in good agreement with the Voorhees and Glicksman model (Figure 8(b)).[19] For example, a maximum frequency of 1.95 is observed at r/r* = 1.1 when the particle volume fraction is 1.3 pct, which is very close to the position of the peak in the model. Once the volume fraction is above 10.0 pct, the experimental data appears to be in better agreement with the Brailsford–Wynblatt distribution.[18,23] A maximum frequency 1.55 is observed at r/r* = 1.0 when the volume fraction is 9.6 pct. With increasing volume fraction, the determination of the particle size distribution became more difficult due to the increasing aspect ratio of the particles. However, the general trend is that the distribution is broader and more symmetrical as the volume fraction increases.

4.1.2 Grain boundary control

It is well known that grain boundary diffusion becomes dominant when the reheating temperature is below 0.75 to 0.8T m.[22,23] The apparent diffusion coefficient, D, is related to the grain boundary and bulk diffusivities by the following equation:

$$ D = \left( {1 + \frac{{D_{\text{gb}} \times h}}{{D_{\text{Bulk}} \times \bar{R}}}} \right) \times D_{\text{Bulk}} , $$
(7)

where D Bulk is the bulk diffusion coefficient, D gb is the grain boundary diffusion coefficient, \( \bar{R} \) is the mean grain size, and h is the grain boundary thickness. When D gb × h is greater than \( D_{\text{Bulk}} \times \bar{R} \), grain boundary diffusion becomes the dominant diffusion mechanism. This seems to be the case at temperatures below 1473 K (1200 °C), where the particle coarsening exponent was 4 as expected from grain boundary controlled coarsening.[29,30] It is also worth pointing out that most particles were located on the grain boundaries at low temperatures (e.g., Figure 2(b)).

According to Kirchner,[30] the rate of coarsening under grain boundary control is

$$ \bar{r}^{4} - \bar{r}_{0}^{4} = \frac{{9hD_{\text{gb}} \sigma_{\sigma \gamma } N_{{\alpha ({\text{gb}})}} V_{\text{m}} t}}{32ABRt}, $$
(8)

where \( N_{{\alpha ({\text{gb}})}} \) is the molar fraction of solute at a grain boundary in equilibrium with an infinitely large particle, \( \sigma_{\delta \gamma } \) is the austenite/ferrite interfacial energy, while A and B are define as \( A = 2/3 + (\gamma_{\text{gb}} /2\sigma_{\delta \gamma } ) + (1/3)(\gamma /2\sigma_{\delta \gamma } ) + (1/3)(\gamma_{\text{gb}} /2\sigma_{\delta \gamma } )^{3} \) and \( B = (1/2)\ln (1/f_{\text{b}} ) \), γ gb is the grain boundary energy, and f b is the fraction of the grain boundary covered by the precipitates. It is very difficult to determine the values of the grain boundary diffusivities, and therefore, Eq. [8] was not directly used to model the coarsening kinetics. It suffices to point out that, as expected, the coarsening rate (the slope in Figure 5(b)) increased as the heating temperature increased from 1123 K to 1333 K (850 °C to 1060 °C).

4.2 Austenite Particle Pinning Effects

Second phase particles have been used extensively to control the kinetics of grain growth. For the case in which the particles are randomly distributed in the matrix and the grain size is much larger than the interparticle spacing, the pinning pressure is well described by the classical Zener pressure, P Z:[31]

$$ P_{\text{Z}} = \frac{{3F_{\text{v}} \gamma_{\text{gb}} }}{{2\bar{r}}}. $$
(9)

In this equation, γ gb denotes the grain boundary interfacial energy. In the present two-phase alloy, ferrite grain growth will be retarded by austenite particle pinning. When the volume fraction of second phase particles is large, the interparticle spacing may have the same value or smaller value than the grain size and Eq. [9] would no longer be applicable. Considering the effects of boundary-particle correlation, the following equation is used to estimate the maximum pinning pressure P ZC, when all the particles are located at the grain corners:[32–35]

$$ P_{\text{ZC}} = \frac{{1.2F_{\text{v}}^{2/3} \gamma_{\text{gb}} }}{{\bar{r}}}. $$
(10)

The ferrite grain growth rate is related to the effective driving pressure ∆P:[32,33]

$$ \frac{{{\text{d}}\overline{{R_{\delta } }} }}{{{\text{d}}t}} = M\Delta P = M(P - P_{\text{ZC}} ) = M\left( {\frac{{\alpha \gamma_{\text{gb}} }}{{\overline{{R_{\delta } }} }} - \frac{{1,2F_{\text{v}}^{2/3} }}{{\bar{r}}}} \right), $$
(11)

where α is a geometric constant near unity, \( \overline{{R_{\delta } }} \) is the mean radius of an individual grain, and M is the grain boundary mobility. When the driving force P is less than the particle drag pressure P ZC shown in Eq. [11], ferrite grain growth will stagnate due to the complete pinning of grain growth by the austenite particles. If the driving force for grain growth is comparable to the pinning pressure, then some growth can take place due to the coarsening of the pinning particles at high temperature. The relationship between ferrite grain size and austenite particle radius at different temperatures is shown in Figure 9. The particle pinning effects can be divided into three categories depending on the austenite/ferrite two-phase microstructure:[36]

Fig. 9
figure 9

The relationship between delta grain size and austenite particle radius at different temperatures. Solid circle represents 1123 K (850 °C), solid square represents 1333 K (1060 °C), solid triangle means 1473 K (1200 °C), hollow circle represents 1553 K (1280 °C), and solid diamond means 1568 K (1295 °C)

Full size image
  1. (a)

    When the particle pinning pressure is much larger than the driving force, the ferrite grain boundaries will be totally pinned and no grain growth is observed. An example of this is observed when the model alloy is reheated to 1123 K (850 °C). As shown Figures 2(a) and (b), no grain growth is observed over the experimental times which ranged from 1 to 288 hours. The driving pressure due to grain boundary curvature and the particle pinning pressure were calculated for different holding times at 1123 K (850 °C) as shown in Table VI. A grain boundary energy, γ gb, of 0.5 Jm−2 was used for these calculations. The effective driving pressures for ferrite grain growth are negative which is in agreement with experimental observation of negligible grain growth.

    Table VI Effective Driving Pressure for Delta-Ferrite Grain Growth at 1123 K (850 °C): P Represents Driving Force for Grain Growth, P zc Refers to the Maximum Particle Pinning as per Eq. [10], and ∆P is Effective Driving Force as per Eq. [11]
    Full size table
  2. (b)

    When the austenite particle pinning pressure is only slightly larger than the driving force for grain growth, grain growth will be pinned initially, but it can later start to occur due to the coarsening of the austenite particles. The growth of the ferrite grains would then occur at a rate which is controlled by the rate of change of the austenite particle size:[32,37]

    $$ \frac{{{\text{d}}\overline{{R_{\delta } }} }}{{{\text{d}}t}} = k\frac{{{\text{d}}\bar{r}}}{{{\text{d}}t}}. $$
    (12)

    The rate of particle coarsening was discussed in Section IV–A. When the reheating temperature was 1333 K (1060 °C), the ferrite grain size remained constant at about 90 μm for holding times of <4 hours. For longer holding times, ferrite grain growth started to take place as shown in Figures 3(b) and 9. The calculation of the effective driving pressure for ferrite grain growth is shown in Table VII. The effective driving pressure for ferrite grain growth becomes positive when the holding time is longer than 4 hours, and this appears to be in good agreement with the experimental observations. The coarsening process will decrease the particle pinning pressure according to Eq. [11]. Similar results are seen at 1473 K (1200 °C) (Table VIII). Figures 2(c), (d), 3(b), and 9 show that when the heat treatment temperature was increased to 1473 K (1200 °C), the delta-ferrite grain growth was pinned for the first 15 minutes. The onset of grain growth could be estimated by equating the driving force and the pinning force. Once again, good agreement is observed for the onset of grain growth which is predicted to occur between 15 and 180 minutes in agreement with the experiments.

  3. (c)

    In the case when the austenite particle pinning pressure is smaller than the driving pressure, delta grain growth would occur under a net driving force of P − P ZC. The calculations of the effective particle pinning pressure at 1553 K (1280 °C) are shown in Table IX, similar results are obtained at 1568 K (1295 °C) (Table X). In both cases, the effective driving force is positive at all times. The net driving force, however, is only 2 to 5 kN/m2 compared to 9 to 16 kN/m2 which is the driving force for grain growth in the absence of pinning. As such, grain growth will occur at these two temperatures but it will occur at a rate which is significantly smaller than what would be expected in the absence of pinning.

    Table VII Effective Driving Pressure for Delta-Ferrite Grain Growth at 1333 K (1060 °C): P Represents Driving Force for Grain Growth and P zc Refers to the Maximum Particle Pinning as per Eq. [10], and ∆P is Effective Driving Force as per Eq. [11]
    Full size table
    Table VIII Effective Driving Pressure for Delta-Ferrite Grain Growth at 1473 K (1200 °C): P Represents Driving Force for Grain Growth and P zc Refers to the Maximum Particle Pinning as per Eq. [10], and ∆P is Effective Driving Force as per Eq. [11]
    Full size table
Table IX Effective Driving Pressure for Delta-Ferrite Grain Growth at 1553 K (1280 °C): P Represents Driving Force for Grain Growth and P zc Refers to the Maximum Particle Pinning as per Eq. [10], and ∆P is Effective Driving Force as per Eq. [11]
Full size table
Table X Effective Driving Pressure for Delta-Ferrite Grain Growth at 1568 K (1295 °C): P Represents Driving Force for Grain Growth and P zc Refers to the Maximum Particle Pinning as per Eq. [10], and ∆P is Effective Driving Force as per Eq. [11]
Full size table

When the reheating temperature was increased to 1583 K (1310 °C), the austenite particle volume fraction approached zero, as shown in Figure 1(i). As a consequence of the elimination of particle pinning, the ferrite grain size increases at a rate which is much larger than that reported in the presence of particle pinning at a slight lower temperature, 1568 K (1295 °C). This confirmed the concept of using a small volume fraction of austenite to pin ferrite grain growth over a wide temperature range.

All of the experiments performed in this contribution involved reheating samples with a very homogenous microstructure that was obtained by rolling and homogenization. Under industrial conditions, such as TSCDR conditions and welding, the ferrite and austenite grain growth both occur in a heterogeneous (segregated) microstructure produced by solidification. In order to verify the effectiveness of the model alloy in inhibiting high temperature grain growth under realistic starting conditions, some work was performed to reproduce the as-cast microstructures. The results are presented in the companion paper. Part II: Experimental Validation and Applications.

5 Conclusions

  1. 1.

    When the reheating temperature is higher than 1473 K (1200 °C), the coarsening of the austenite particles was bulk diffusion controlled. When the reheating temperature is lower than 1473 K (1200 °C), the coarsening of austenite particles is controlled by grain boundary diffusion. The austenite particle coarsening rate constant was predicted from modified LSW theory by taking account of multi-components diffusion, particle volume fraction, and the thermodynamics of a non-ideal solution. The austenite particle size distribution was invariant with time during coarsening. When the particle volume faction is <10 pct, the measured size distributions are in good agreement with Voorhees and Glicksman model.

  2. 2.

    The relationship between the austenite particle coarsening kinetics and ferrite grain growth kinetics was examined. When the austenite particle pinning pressure is much larger than the driving force for ferrite grain growth, grain growth is completely arrested. Once the pinning pressure is equal to the driving force for grain growth, grain growth proceeds at a rate controlled by the coarsening kinetics of the austenite particles. For the condition in which the pinning pressure is smaller than the driving force, grain growth occurs at a reduced rate which is much lower than that without pinning. In this Fe-1.5Al model alloy steel, austenite particles can retard ferrite grain growth up to 1578 K (1305 °C). The results confirm the possibility of using this austenite/ferrite two-phase microstructure to control the microstructure evolution at high temperature.