Entropy-based fuzzy clustering of interval-valued time series

Abstract

This paper proposes a fuzzy C-medoids-based clustering method with entropy regularization to solve the issue of grouping complex data as interval-valued time series. The dual nature of the data, that are both time-varying and interval-valued, needs to be considered and embedded into clustering techniques. In this work, a new dissimilarity measure, based on Dynamic Time Warping, is proposed. The performance of the new clustering procedure is evaluated through a simulation study and an application to financial time series.

1 Introduction

In this paper, we propose a fuzzy C-medoids-based clustering method with entropy regularization to group data objects characterized by two sources of complexity: they are both time-varying and interval-valued data, i.e. interval-valued time series (ITS). Specifically, ITS are time series for which an interval covering the observed values rather than a single value is associated with each time point: they are thus characterized by lower and upper boundaries, as well as by centres and radii.

The proposed clustering procedure is based on a new dissimilarity measure suitable for ITS which builds on the Dynamic Time Warping (DTW) and accounts for within-series variability rather than intrinsic imprecision.

It is worth noting that there has been a growing interest in these complex data in recent years, as they have become much more widely available and are being used in a variety of contexts. However, as the next section will detail, research about ITS clustering is still relatively limited. The main reason for deeply investigating this area of research is motivated by the importance of clustering these complex data objects taking into account intra-series variability, without losing this source of information by considering a summary of it as the corresponding mean or median values. Developing effective methods for handling and clustering ITS is proved to be highly valuable, especially when studying the range of variation of a particular variable over time. For instance, ITS can be used for analyzing wind speed levels, daily asset prices, electricity demand in regions, or a person’s blood pressure fluctuations over time, among others. In general, there is a growing need for methodologies that deal with this type of symbolic data. According to the above considerations, we propose a new clustering technique for ITS based on a fuzzy approach, whose main advantage is that it produces a blurred partition of the objects to the clusters; in this way, there is no crisp assignment of units to clusters, allowing the identification of the second-best cluster too (Everitt and Leese 2001). Moreover, fuzzy clustering is distribution-free (Hwang et al. 2007). The fuzziness is introduced in the objective function through a regularization term based on the Shannon entropy (Li and Mukaidono 1995, 1999; Miyamoto and Mukaidono 1997). We consider a medoids-based clustering technique (Fcmd, Krishnapuram et al. 1999, 2001), given that the identification of the “virtual” prototype, i.e. the time series centroid, in this context may be meaningless, unlike the time series medoid, which is instead an observed time series.

The paper is structured as follows. Section 2 contains a review of the literature on time series clustering while Sect. 3 provides a formal definition of the ITS and then focuses on the new proposed dissimilarity measure. Section 4 introduces the fuzzy clustering method with entropy regularization based on the proposed dissimilarity while Sect. 5 contains the simulation plan. Section 6 shows the results of applying the clustering method to the components of the FTSE-MIB by considering the monthly minimum and maximum prices, ranging from October 2018 to October 2022 while Sect. 7 contains conclusions and some general remarks.

2 Literature review

Regarding the general approach to time series clustering, we argue that it has been widely used and applied in various fields including economics, finance, environmental and social sciences. As stated in Caiado et al. (2015), we can distinguish among the following three main approaches: observation-based, features-based, and model-based. Clustering techniques belonging to the first group compute the dissimilarity based on the observed values of the time series (D’Urso 2005; D’Urso et al. 2018, 2021a) while those belonging to the second group are based on several features like quantile cross-spectral densities (López-Oriona et al. 2022a, b, c), quantile autocovariance (Vilar et al. 2018; Lafuente-Rego et al. 2020), autocorrelation function (Alonso and Maharaj 2006; D’Urso and Maharaj 2009) and generalized cross-correlation (Alonso et al. 2021), cepstral coefficients (Maharaj and D’Urso 2011), periodogram (Caiado et al. 2006, 2009), wavelets decomposition (Maharaj et al. 2010; D’Urso and Maharaj 2012; D’Urso et al. 2023). Finally, techniques belonging to the third group compute the dissimilarity among the parameter estimates arising from suitable fitted time series models like ARIMA models (Piccolo 1990; Xiong and Yeung 2004; D’Urso et al. 2015a), GARCH and INGARCH models (Otranto 2008, 2010; Caiado and Crato 2010; D’Urso et al. 2013, 2016; Otranto and Mucciardi 2019; Cerqueti et al. 2022), extreme value analysis (D’Urso et al. 2017a), splines coefficients (Garcia-Escudero and Gordaliza 2005; D’Urso et al. 2021b) and copulas (De Luca and Zuccolotto 2011; Durante et al. 2014, 2015; De Luca and Zuccolotto 2017; Disegna et al. 2017).

Regarding clustering techniques for interval-valued data, in the literature (see Noirhomme-Fraiture and Brito 2011 for an extensive review), many works have been devoted to this scope (De Carvalho et al. 2006a, b; De Carvalho and Tenório 2010; D’Urso et al. 2015b, 2017b; Montanari and Calò 2013; de Carvalho and Simões 2017; Kejžar et al. 2021; Umbleja et al. 2021), while clustering techniques for interval-valued time series are almost unexplored; indeed, few papers deal with imprecise time series such as Coppi and D’urso (2002) and Coppi and D’Urso (2003) that introduce three types of dissimilarity: the instantaneous, the velocity and the simultaneous dissimilarity measures, respectively; Maharaj et al. (2019) and D’Urso et al. (2023) that follow a features-based approach.

In this work, we follow an observation-based approach within the fuzzy framework, exploiting all the advantages of dynamic time-warping, as discussed in the next section.

3 A dissimilarity measure for interval-valued time series

3.1 Interval-valued time series

An interval time-series (ITS) can be seen as an interval variable observed over T times; formally, we can define a interval data time matrix as follows:

$$\begin{aligned} \varvec{X}\equiv \lbrace x_{it}=(l_{it}, h_{it}),\;i=1,\ldots ,N, \; t=1,\ldots ,T \rbrace \end{aligned}$$

where i and t denote the units and the times, respectively; then $x_{it}=(l_{it},h_{it})$ is the interval variable observed on the i-th unit at time t: in particular, $l_{it}$ is the minimum value observed on the i-th unit, at time t, while $h_{it}$ is the maximum value observed on the same i-th unit at the same time t.

We can also consider the corresponding following matrices:

$$\begin{aligned} \varvec{L}&\equiv \lbrace l_{it};\;i=1,\ldots ,N, \; t=1,\ldots ,T \rbrace \\ \varvec{H}&\equiv \lbrace h_{it};\; i=1,\ldots ,N, \; t=1,\ldots ,T \rbrace \end{aligned}$$

where $\varvec{L}$ is the matrix of time series of minima and $\varvec{H}$ that of the maxima.

In the following section, the Dynamic Time Warping is presented, being used, then, to define the new dissimilarity for ITS.

3.2 Dynamic time warping

Let $\textbf{x}_{i}$ and $\textbf{x}_{j}$ be two time series of length T and $T^{\prime }$ respectively, where we do not restrict $T=T^{\prime }$. The Dynamic Time Warping (DTW, Velichko and Zagoruyko 1970; Berndt 1994) between these two time series works finding the optimal match between them under certain restrictions. Therefore, the sequences are warped nonlinearly to match each other.

The so-called “warping path” that “realigns” the time indices of the multivariate time series so that each data point in $\textbf{x}_{i}$ is compared to the “closest” data point in $\textbf{x}_{j}$ is defined as

$$\begin{aligned} \Phi _{l} = (\varphi _{l},\psi _{l}), \quad l = 1,\ldots , L \end{aligned}$$

where $\varphi _{l}$ and $\psi _{l}$, for $l = 1,\ldots , L$, are the set of realigned indices of $1,\ldots , T$ and $1,\ldots , T^{\prime }$ respectively, subject to the following constraints:

• 1. boundary condition: $\Phi _{1}=(1, 1), \Phi _{L}=(T, T^{\prime })$;

• 2. monotonicity condition: $\varphi _{1}\le \cdots \le \varphi _{l}\le \cdots \le \varphi _{L} \, {\textit{and}} \, \psi _{1}\le \cdots \le \psi _{l} \le \cdots \le \psi _{L}.$

Among the possible wrapping curves, the DTW is the one that minimizes the total dissimilarity between $\textbf{x}_{i}$ and $\textbf{x}_{j}$ computed as:

$$\begin{aligned} d_{{\textit{DTW}}}(\textbf{x}_{i},\textbf{x}_{j})=\sum _{l=1}^{L}d (\textbf{x}_{i,\varphi _{l}},\textbf{x}_{j,\psi _{l}})m_{l,\Phi } \end{aligned}$$

(1)

where $m_{l,\Phi }$ is a local weighting coefficient and $d(\cdot ,\cdot )$ is, usually, the Euclidean distance for multivariate time series.

Even if the DTW algorithm could be problematic with long time series, when used in the Partitioning around Medoids (PAM) method, its computational burden is reduced since the distance matrix is computed only once in the iterative process.

Based on DTW, we define a new dissimilarity measure suitable when dealing with interval-valued time series, as follows.

3.3 A dissimilarity measure for ITS

Given two interval-valued time-series $\varvec{x}_{i}$ and $\varvec{x}_{j}$ of length T and $T^{\prime }$ (with $T\geqslant T^{\prime }$ or $T\leqslant T^{\prime }$), respectively, we define a new dissimilarity measure based on the Dynamic Time Warping. Therefore, we propose:

$$\begin{aligned} _{{\textit{ITS}}}d (\varvec{x}_{i},\varvec{x}_{j})= d^{*}_{{\textit{DTW}}}(\varvec{l}_{i},\varvec{l}_{j})+d^{*}_{{\textit{DTW}}}(\varvec{h}_{i},\varvec{h}_{j})+\vert d^{*}_{{\textit{DTW}}}(\varvec{l}_{i},\varvec{h}_{i})- d^{*}_{{\textit{DTW}}}(\varvec{l}_{j},\varvec{h}_{j})\vert \end{aligned}$$

(2)

where $\varvec{l}_{i}=(l_{i1},\ldots ,l_{it},\ldots ,l_{iT})^{\prime }$, $\varvec{l}_{j}=(l_{j1},\ldots ,l_{jt},\ldots ,l_{jT^{\prime}})^{\prime }$, $\varvec{h}_{i}=(h_{i1},\ldots ,h_{it},\ldots ,h_{iT})^{\prime }$ and $\varvec{h}_{j}=(h_{j1},\ldots ,h_{jt},\ldots ,h_{jT^{\prime}})^{\prime }$ are the vectors of the minima and maxima pertaining to the time series of the i-th and j-th unit, respectively. $d^{*}_{{\textit{DTW}}}(\cdot \,; \cdot )$ denotes the normalized $d_{{\textit{DTW}}}( \cdot \,; \cdot )$, i.e. the latter is divided by its maximum so that it varies in [0, 1]. Specifically:

• $d^{*}_{{\textit{DTW}}}(\varvec{l}_{i},\varvec{l}_{j})$ is the normalized DTW among the time series of the minima of units i and j;

• $d^{*}_{{\textit{DTW}}}(\varvec{h}_{i},\varvec{h}_{j})$ is the normalized DTW among the time series of the maxima of units i and j;

• $d^{*}_{{\textit{DTW}}}(\varvec{l}_{i},\varvec{h}_{i})$ is the normalized DTW among the time series of the minima and the maxima of the unit i;

• $d^{*}_{{\textit{DTW}}}(\varvec{l}_{j},\varvec{h}_{j})$ is the normalized DTW among the time series of the minima and the maxima of the unit j;

We finally remark that $_{ITS}d_{ij}$ thus can take values in the interval [0, 3].

In the next Section, we introduce the Entropy-based fuzzy clustering method ($Fcmd_{ITS}$) for interval-valued time series based on the above dissimilarity measure.

4 Entropy-based fuzzy clustering of interval-valued time series

A fuzzy C-medoids clustering method with entropy regularization is defined to group N interval-valued time series into C homogeneous clusters based on the new dissimilarity measure (2), henceforth named $Fcmd_{ITS}$. The aim is to identify the matrix of fuzzy membership degrees $\textbf{U}_{N \times C}$ whose generic element $u_{ic}$ is the membership degree of the i-th time series to the c-th cluster, with $i=1,\ldots N$, $c=1,\ldots ,C$ and the corresponding C prototypes, i.e. the C time series medoids; both are the solutions of the following constraint optimization problem:

$$\begin{aligned} \left\{ \begin{aligned} {\textit{min}}:J_{p,C}\left( \varvec{U}, \varvec{\tilde{X}}\right)&=\sum _{i=1}^{N} \sum _{c=1}^{C} u_{ic} \, _{{\textit{ITS}}}d (\varvec{x}_{i},\varvec{\tilde{x}}_{c})+p \sum _{i=1}^{N} \sum _{c=1}^{C} u_{ic} ln \left( u_{ic}\right) \\&= \sum _{i=1}^{N} \sum _{c=1}^{C} u_{ic} \bigg [ d^{*}_{{\textit{DTW}}}(\varvec{l}_{i},\varvec{\tilde{l}}_{c})+d^{*}_{{\textit{DTW}}}(\varvec{h}_{i},\varvec{\tilde{h}}_{c})\\&\quad +\vert d^{*}_{{\textit{DTW}}}(\varvec{l}_{i},\varvec{h}_{i})- d^{*}_{{\textit{DTW}}}(\varvec{\tilde{l}}_{c},\varvec{\tilde{h}}_{c})\vert \bigg ] +p \sum _{i=1}^{N} \sum _{c=1}^{C} u_{ic} ln \left( u_{ic}\right) \\&s.t. \sum _{c=1}^{C} u_{ic}=1, \, u_{ic}\ge 0.\\ \end{aligned} \right. \end{aligned}$$

(3)

where $_{ITS}d (\varvec{x}_{i},\varvec{\tilde{x}}_{c})$ is the dissimilarity (2) between the i-th ITS and the ITS medoid of the c-th cluster.

In this objective function, the fuzziness is due to the entropy regularization term; its extent is controlled through the weight factor $p>0$, which is called degree of fuzzy entropy since the higher p the higher the degree of fuzziness. In particular, the second term is $-p$ $\times$ the Shannon entropy, so that the optimization problem aims at maximizing both the entropy measure and the internal cohesion.

The iterative solutions of (3) are:

$$\begin{aligned} u_{ic} = \dfrac{1}{\sum _{c^{\prime }=1}^{C} \left[ \dfrac{{\textit{exp}} \left( \dfrac{1}{p}{\left[ d^{*}_{{\textit{DTW}}}(\varvec{l}_{i},\varvec{\tilde{l}}_{c})+d^{*}_{{\textit{DTW}}}(\varvec{h}_{i},\varvec{\tilde{h}}_{c})+\vert d^{*}_{{\textit{DTW}}}(\varvec{l}_{i},\varvec{h}_{i})- d^{*}_{{\textit{DTW}}}(\varvec{\tilde{l}}_{c},\varvec{\tilde{h}}_{c})\vert \right] }\right) }{{\textit{exp}}\left( \dfrac{1}{p}{\left[ d^{*}_{{\textit{DTW}}}(\varvec{l}_{i},\varvec{\tilde{l}}_{c^{\prime }})+d^{*}_{{\textit{DTW}}}(\varvec{h}_{i},\varvec{\tilde{h}}_{c^{\prime }})+\vert d^{*}_{{\textit{DTW}}}(\varvec{l}_{i},\varvec{h}_{i})- d^{*}_{{\textit{DTW}}}(\varvec{\tilde{l}}_{c^{\prime }},\varvec{\tilde{h}}_{c^{\prime }})\vert \right] }\right) }\right] } \end{aligned}$$

(4)

The proof of the iterative solutions (4) is given below, while the computational steps of the proposed clustering method are given in Algorithm 1.

Starting from the vector of the degrees of membership $\textbf{u}_i$ and using the Lagrangian mutiplier, we get:

$$\begin{aligned} L_p(\textbf{u}_i,\lambda )&=\sum _{i=1}^{N}\sum _{c=1}^{C} u_{ic} \big [ d^{*}_{{\textit{DTW}}}(\varvec{l}_{i},\varvec{\tilde{l}}_{c}) +d^{*}_{{\textit{DTW}}}(\varvec{h}_{i},\varvec{\tilde{h}}_{c})\nonumber \\&\quad +\vert d^{*}_{{\textit{DTW}}} (\varvec{l}_{i},\varvec{h}_{i})- d^{*}_{{\textit{DTW}}}(\varvec{\tilde{l}}_{c}, \varvec{\tilde{h}}_{c})\vert \big ]\nonumber \\&\quad +p\sum _{i=1}^{n}\sum _{c=1}^{C} u_{ic} ln(u_{ic}) -\lambda \left( \sum _{c=1}^{C}u_{ic}-1\right) , \end{aligned}$$

(5)

where $\textbf{u}_i=(u_{i1},\ldots ,u_{ic},\ldots ,u_{iC})^{\prime }$ and $\lambda$ is the Lagrange multiplier. Therefore, we set the first derivatives of (5) with respect to $u_{ic}$ and $\lambda$ equal to zero, yielding:

$$\begin{aligned} \frac{\partial L_p(\textbf{u}_i,\lambda )}{\partial u_{ic}}&=0 \, \Leftrightarrow \, \big [ d^{*}_{{\textit{DTW}}}(\varvec{l}_{i},\varvec{\tilde{l}}_{c}) +d^{*}_{{\textit{DTW}}}(\varvec{h}_{i},\varvec{\tilde{h}}_{c})\nonumber \\&\quad +\vert d^{*}_{{\textit{DTW}}} (\varvec{l}_{i},\varvec{h}_{i})- d^{*}_{{\textit{DTW}}}(\varvec{\tilde{l}}_{c}, \varvec{\tilde{h}}_{c})\vert \big ]\nonumber \\&\quad +p \left[ ln(u_{ic})+1\right] -\lambda =0, \end{aligned}$$

(6)

$$\begin{aligned} \frac{\partial L_p(\textbf{u}_i,\lambda )}{\partial \lambda }&=0 \, \Leftrightarrow \, \sum _{c=1}^{C}u_{ic}-1=0. \end{aligned}$$

(7)

From (6) we obtain:

$$\begin{aligned} ln(u_{ic})=\dfrac{1}{p}\left( \lambda -\left[ d^{*}_{{\textit{DTW}}}(\varvec{l}_{i},\varvec{\tilde{l}}_{c}) +d^{*}_{{\textit{DTW}}}(\varvec{h}_{i},\varvec{\tilde{h}}_{c})+\vert d^{*}_{{\textit{DTW}}}(\varvec{l}_{i},\varvec{h}_{i})- d^{*}_{{\textit{DTW}}}(\varvec{\tilde{l}}_{c},\varvec{\tilde{h}}_{c})\vert \right] \right) -1 \end{aligned}$$

(8)

and, then:

$$\begin{aligned} u_{ic}={\textit{exp}} \left\{ \dfrac{\lambda }{p}-\dfrac{1}{p}\left( \left[ d^{*}_{{\textit{DTW}}}(\varvec{l}_{i},\varvec{\tilde{l}}_{c})+ d^{*}_{{\textit{DTW}}}(\varvec{h}_{i},\varvec{\tilde{h}}_{c})+\vert d^{*}_{{\textit{DTW}}}(\varvec{l}_{i},\varvec{h}_{i})- d^{*}_{{\textit{DTW}}}(\varvec{\tilde{l}}_{c},\varvec{\tilde{h}}_{c})\vert \right] \right) -1 \right\} \end{aligned}$$

(9)

By considering (7):

$$\begin{aligned} {\textit{exp}} \left( \dfrac{\lambda }{p}-1\right) =\dfrac{1}{\sum _{c^{\prime }=1}^{C} \dfrac{1}{{\textit{exp}} \left( \dfrac{1}{p}\left[ d^{*}_{{\textit{DTW}}}(\varvec{l}_{i},\varvec{\tilde{l}}_{c^{\prime }})+d^{*}_{{\textit{DTW}}}(\varvec{h}_{i},\varvec{\tilde{h}}_{c^{\prime }})+\vert d^{*}_{{\textit{DTW}}}(\varvec{l}_{i},\varvec{h}_{i})- d^{*}_{{\textit{DTW}}}(\varvec{\tilde{l}}_{c^{\prime }},\varvec{\tilde{h}}_{c^{\prime }})\vert \right] \right) }}. \end{aligned}$$

(10)

and by replacing Eq. (10) in (9), we have the solution as in (4).

Algorithm 1

Fcmd_ITS algorithm

5 A simulation study

A simulation plan has been considered to assess the proposed fuzzy clustering method’s performance. Three different scenarios have been simulated as described in the next section.

5.1 Simulated scenarios

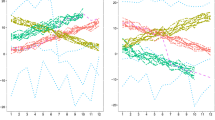
First scenario The first scenario considered 45 simulated interval-valued time series clustered in 3 equally sized groups with length $T=100$; they are shown in Fig. 1a while in (b) a sample of three ITS, one per group, is represented.

In detail, the time series of minima belonging to the first group (C1) have been simulated by a random walk with drift so that:

$$\begin{aligned} l_t=\delta _0+l_{t-1}+w_t, \end{aligned}$$

with $\delta _0=-1$ and $w_t \sim N(0,4);$ then, we shifted it by 50 so that $l_t=l_t+50$.

The time series of minima belonging to the second group (C2) have been simulated by a random walk with drift so that:

• for $t \in [1,T/2],$

  $$\begin{aligned} l_t=\delta _0+l_{t-1}+w_t, \end{aligned}$$

  with $\delta _0=1.5$ and $w_t \sim N(0,4)$;

• for $t \in [(T/2)+1, T],$

  $$\begin{aligned} l_t=\delta _0+l_{t-1}+w_t, \end{aligned}$$

  with $\delta _0=2$ and $w_t \sim N(0,4).$

The time series of minima belonging to the third group (C3) have been simulated by a Moving Average (MA) model so that:

• for $t \in [1,(T/2)+10],$

  $$\begin{aligned} l_t=\mu +w_t+\phi w_{t-1}, \end{aligned}$$

  with $\mu =0$ $\phi =-0.5$ and $w_t \sim N(0,0.25)$;

• for $t \in [(T/2)+11, T],$

  $$\begin{aligned} l_t=\mu +w_t+\phi w_{t-1}, \end{aligned}$$

  with $\mu =-5$ $\phi =-0.5$ and $w_t \sim N(0,0.25)$.

The time series of maxima have been simulated as follows:

$$\begin{aligned} h_{t}=l_{t}+U(1,10)+10 \end{aligned}$$

Fig. 1

First scenario: a all simulated time series b a sample of three simulated ITS, one per group

Second scenario The second scenario, plotted in Fig. 2, considered 45 simulated interval-valued time series clustered in 3 equally sized groups with length $T=100$ too. The time series of minima have been simulated as in the first scenario while the time series of maxima as follows:

• $h_{t}=l_{t}+U(1,10)+70$, for $h_t \in C1$,

• $h_{t}=l_{t}+U(1,10)+20$, for $h_t \in C2$,

• $h_{t}=l_{t}+U(1,10)+80$, for $h_t \in C3$.

Fig. 2

Second scenario: a all simulated time series b a sample of three simulated ITS, one per group

Third scenario In the third scenario, plotted in Fig. 3, we considered 30 time series clustered in 3 equally sized groups, with length $T=200$. The time series of minima belonging to the first group (C1) have been simulated by an Autoregressive (AR) model so that:

$$\begin{aligned} l_t=\alpha +\psi l_{t-1}+ w_t, \end{aligned}$$

with $\psi =0.7$, $\alpha =10(1-\psi )$ and $w_t \sim N(0,1)$.

The time series of minima belonging to the second group (C2) have been simulated by an ARMA model so that:

$$\begin{aligned} l_t= \mu + \psi l_{t-1}+ w_t+ \phi w_{t-1}, \end{aligned}$$

with $\mu =20$, $\psi =-0.3$, $\phi =0.5$ and $w_t \sim N(0,1)$.

The time series of minima belonging to the third group (C3) have been simulated by an MA model so that:

• for $t \in [1,(T/2)],$

  $$\begin{aligned} l_t=\mu +w_t+\phi w_{t-1}, \end{aligned}$$

  with $\mu =40$ $\phi =-0.5$ and $w_t \sim N(0,1)$;

• for $t \in [(T/2)+1, T],$

  $$\begin{aligned} l_t=\mu +w_t+\phi w_{t-1}, \end{aligned}$$

  with $\mu =50$, $\phi =-0.5$ and $w_t \sim N(0,1)$.

The time series of maxima have been simulated as follows:

• $h_{t}=l_{t}+U(1,6)+10$, for $h_t \in C1$,

• $h_{t}=l_{t}+U(1,6)+20$, for $h_t \in C2$,

• $h_{t}=l_{t}+U(1,6)+30$, for $h_t \in C3$.

Fig. 3

Third scenario: a all simulated time series b a sample of three simulated ITS, one per group

Remark 1

A suitable pre-processing of the data may be required, such as normalization/standardization. Here, we propose the following normalization procedure:

$$\begin{aligned} {l^{\prime }}_{it}=\frac{{l}_{it}-{\textit{min}}({l}_{i1},\ldots , {l}_{iT})}{{\textit{max}}({h}_{i1},\ldots ,{h}_{iT})- {\textit{min}}({l}_{i1},\ldots ,{l}_{iT})}, \end{aligned}$$

and

$$\begin{aligned} {h^{\prime }}_{it}=\frac{{h}_{it}-{\textit{min}}({l}_{i1},\ldots , {l}_{iT})}{{\textit{max}}({h}_{i1},\ldots ,{h}_{iT}) -{\textit{min}}({l}_{i1},\ldots ,{l}_{iT})}, \end{aligned}$$

$\forall \, t=1,\ldots ,T$ and $i=1,\ldots ,N$.

This normalization implies that the values are in the interval [0, 1] also ensuring that the order among minima and maxima of each time series is always preserved. It has been used for all clustering methods in the simulation.

5.2 Benchmark methods

To compare our clustering method with some possible competitors, we consider the following dissimilarity measures:

• 1.
  $$\begin{aligned} d^{2}(\varvec{x}_{i},\varvec{\tilde{x}}_{c})=\sum _{t=1}^{T} \left( \Vert l_{it}- l_{ct}\Vert ^{2}+ \Vert h_{it}- h_{ct}\Vert ^{2} \right) . \end{aligned}$$

  (11)

  The above dissimilarity (11) between the i-th time series and the c-th medoid can be obtained from the dissimilarity measure (4.1) proposed in Coppi and D’Urso (2003) for LR fuzzy time trajectories by simply setting the centres $c_{it}=0$ and by considering the left and right spreads, $l_{it}$ and $r_{it}$, as the minimum ($l_{it}$) and maximum ($h_{it}$) of the interval time series at time t, $\forall \, t=1,\ldots ,T$ and $i=1,\ldots ,N$.

  The iterative solutions $u_{ic}$, for $i=1,\ldots ,N$ and $c=1,\ldots ,C$, of the entropic Fcmd based on (11) are:

  $$\begin{aligned} u_{ic} = \dfrac{1}{\sum _{c^{\prime }=1}^{C} \left[ \dfrac{{\textit{exp}} \left( \dfrac{1}{p}{\left[ \sum _{t=1}^{T} \left( \Vert l_{it}- \tilde{l}_{ct}\Vert ^{2}+ \Vert h_{it}- \tilde{h}_{ct}\Vert ^{2} \right) \right] }\right) }{exp\left( \dfrac{1}{p}{\left[ \sum _{t=1}^{T} \left( \Vert l_{it}- \tilde{l}_{c^{\prime }t}\Vert ^{2}+ \Vert h_{it}- \tilde{h}_{c^{\prime }t}\Vert ^{2} \right) \right] }\right) }\right] }. \end{aligned}$$

  (12)

  We name, henceforth, in the simulation study, this clustering method as $Fcmd_{EU}$.

• 2. We extend the unweighted generalized Minkowski distance of order q (Billard and Diday 2006) to the case of time series as:

  $$\begin{aligned} d(\varvec{x}_{i},\varvec{\tilde{x}}_{c})= \left( \sum _{t=1}^{T} \phi (x_{it},\tilde{x}_{ct})^q \right) ^{1/q}, \end{aligned}$$

  (13)

  where $\phi (x_{it},\tilde{x}_{ct})$ is the Ichino and Yaguchi dissimilarity¹ (Ichino and Yaguchi 1994) between the i-th time series and the c-th medoid at time t.

  The iterative solutions $u_{ic}$, for $i=1,\ldots ,N$ and $c=1,\ldots ,C$, of the entropic Fcmd based on the square of (13) and $q=2$ are:

  $$\begin{aligned} u_{ic} = \dfrac{1}{\sum _{c^{\prime }=1}^{C} \left[ \dfrac{{\textit{exp}} \left( \dfrac{1}{p}{\left[ \sum _{t=1}^{T} \phi (x_{it},\tilde{x}_{ct})^2 \right] }\right) }{{\textit{exp}}\left( \dfrac{1}{p}{\left[ \sum _{t=1}^{T} \phi (x_{it},\tilde{x}_{c^{\prime }t})^2 \right] }\right) }\right] }. \end{aligned}$$

  (14)

  We name, henceforth, in the simulation study, this clustering method as $Fcmd_{IY2}$.

  The iterative solutions $u_{ic}$, for $i=1,\ldots ,N$ and $c=1,\ldots ,C$, of the entropic Fcmd based on (13) and $q=1$ are:

  $$\begin{aligned} u_{ic} = \dfrac{1}{\sum _{c^{\prime }=1}^{C} \left[ \dfrac{{\textit{exp}} \left( \dfrac{1}{p}{\left[ \sum _{t=1}^{T} \phi (x_{it},\tilde{x}_{ct}) \right] }\right) }{{\textit{exp}}\left( \dfrac{1}{p}{\left[ \sum _{t=1}^{T} \phi (x_{it},\tilde{x}_{c^{\prime }t}) \right] }\right) }\right] }. \end{aligned}$$

  (15)

  We name, henceforth, in the simulation study, this clustering method as $Fcmd_{IY1}$.

• 3. We extend the Euclidean Hausdorff distance (Billard and Diday 2006) to the case of time series as:

  $$\begin{aligned} d(\varvec{x}_{i},\varvec{\tilde{x}}_{c})= \left( \sum _{t=1}^{T} \upsilon (x_{it},\tilde{x}_{ct})^2 \right) ^{1/2}, \end{aligned}$$

  (16)

  where $\upsilon (\varvec{x}_{it},\varvec{\tilde{x}}_{ct})$ is the Hausdorff distance between the i-th time series and the c-th medoid at time t.

  The iterative solutions $u_{ic}$, for $i=1,\ldots ,N$ and $c=1,\ldots ,C$, of the entropic Fcmd based on the square of (16) are:

  $$\begin{aligned} u_{ic} = \dfrac{1}{\sum _{c^{\prime }=1}^{C} \left[ \dfrac{{\textit{exp}} \left( \dfrac{1}{p}{\left[ \sum _{t=1}^{T} \upsilon (x_{it},\tilde{x}_{ct})^2 \right] }\right) }{{\textit{exp}}\left( \dfrac{1}{p}{\left[ \sum _{t=1}^{T} \upsilon (x_{it},\tilde{x}_{c^{\prime }t})^2 \right] }\right) }\right] }. \end{aligned}$$

  (17)

  We name, henceforth, in the simulation study, this clustering method as $Fcmd_{H2}$.

  Then, we also consider:

  $$\begin{aligned} d(\varvec{x}_{i},\varvec{\tilde{x}}_{c})= \sum _{t=1}^{T} \upsilon (x_{it},\tilde{x}_{ct}). \end{aligned}$$

  (18)

  The iterative solutions $u_{ic}$, for $i=1,\ldots ,N$ and $c=1,\ldots ,C$, of the entropic Fcmd based on (18) are:

  $$\begin{aligned} u_{ic} = \dfrac{1}{\sum _{c^{\prime }=1}^{C} \left[ \dfrac{{\textit{exp}} \left( \dfrac{1}{p}{\left[ \sum _{t=1}^{T} \upsilon (x_{it},\tilde{x}_{ct}) \right] }\right) }{{\textit{exp}}\left( \dfrac{1}{p}{\left[ \sum _{t=1}^{T} \upsilon (x_{it},\tilde{x}_{c^{\prime }t}) \right] }\right) }\right] }. \end{aligned}$$

  (19)

  We name, henceforth, in the simulation study, this clustering method as $Fcmd_{H1}$.

We argue that, to the best of our knowledge, these benchmark methods are, however, a novelty in the state of the art of fuzzy clustering.

5.3 Simulation results

All the clustering methods, i.e. $Fcmd_{ITS}$, $Fcmd_{IY2}$, $Fcmd_{IY1}$, $Fcmd_{IH2}$, $Fcmd_{IH1}$ and $Fcmd_{EU}$ respectively, for each scenario, have been applied to 100 simulated datasets by setting $C \in \lbrace 2,3 \rbrace$ choosing the best $C^*$ according to the Fuzzy silhouette Index (FS, Campello and Hruschka 2006), a well-known internal validity criterion that lies in $[-1,1]$, so that the higher is the value of the Fuzzy Silhouette index, the better is the assignment of the units to the C clusters. For each setting, we considered 100 random restarts and set the maximum number of iterations to 1000.

To assess the impact of the fuzziness parameter, we ran $Fcmd_{ITS}$ by varying $p \in \lbrace 0.05,0.10,0.15,0.40 \rbrace$. It is worth noting that the effect of p in terms of degree of fuzziness of the partition also depends on the scaling of the dissimilarity matrix. In these simulations, the benchmark methods are somewhat favoured because they have a larger scale thus leading to a less blurred partition while keeping the same value of p.

To take this into account and to provide comparable results as far as possible, we consider $p \in \lbrace 0.10,0.20,0.30,0.80 \rbrace$ for all the benchmark methods whose ratio between its mean distance and that of the proposed clustering method, over 100 simulations, was above 10 (see Table 1 for the details).

Table 1 Ratio between the mean distance of benchmark method and that of $Fcmd_{ITS}$ over 100 simulations

To evaluate the performance, we compared the 100 obtained partitions with the true one by means of the Fuzzy Adjusted Rand Index (ARI, Campello 2007), an external validation criterion that lies in $[-1,1]$: the higher is its value, the higher is the agreement between the compared partitions.

The simulation results for all clustering methods are summarised in Table 2: for each scenario and for increasing values of p, the table reports the mean and standard error of the Fuzzy ARI index as well as the number of times, based on the FS value, the method leads to choose $C^*=3$ over 100 simulated data set (the column named Rate). Then, in Figs. 4, 5 and 6 the Fuzzy ARI distribution associated with each clustering method and setting is also shown by means of the violin plots.

Table 2 Simulation results: mean, standard error of the Fuzzy ARI index and the number of times, based on the FS value, the method leads to choose $C^*=3$ over 100 simulations for all clustering methods and all scenarios

Notice that $Fcmd_{ITS}$ performs very well in all scenarios, including the second and the third, where the minima and maxima time series have different widths, sometimes overlapping. This positive evidence comes from considering that it shows a very good performance both in terms of ARI and the choice of the right C. In fact, a correct assessment of the quality of performance has to be based on the combination of both measures.

Moreover, in the third scenario, the role of p is more evident: the higher its value, the lower the performance, since we have compared a crisp partition with a fuzzy one (the low value of the Fuzzy ARI in the third scenario is only due to the huge effect that $p=0.40$ has on the membership degree).

The comparison with the other benchmarks leads to the following considerations. For the first scenario, based on the results in Table 2 and also looking at the distribution of the fuzzy ARI in Fig. 4, $Fcmd_{H1}$ can be considered as a valid competitor, although it is favoured by the scaling of its dissimilarity matrix (see Table 1), which reduces the influence of p with respect to $Fcmd_{ITS}$.

For the second scenario, looking at the Table 2 and Fig. 5, the performance of $Fcmd_{ITS}$ is fairly comparable in particular with that of $Fcmd_{Y1}$ and $Fcmd_{H1}$ respectively, although both favoured again by the scaling of the dissimilarity.

The third scenario is the one for which the best performance of our proposal is evident (see Table 2 and Fig. 6). The only slightly comparable clustering method is again the one based on the Hausdorff distance, i.e. $Fcmd_{H1}$, because it is the only one that achieves good results both in terms of Fuzzy ARI and identification of the true number of clusters.²

Furthermore, we point out that, unlike point-to-point dissimilarity measures, our clustering method is the only one able to deal with time series of different lengths, thus broadening its applicability. Based on these very good results, in the next section, we apply the proposed clustering method to a real data set and we highlight that the choice of the best value of the fuzziness parameter p strictly depends on the scaling of the dissimilarity used and the degree of separation among groups; thus in practical applications, we recommend taking into account all these issues and selecting the best combinations of C and p based on some internal validity criterion.

Fig. 4

First scenario: violin plots of the Fuzzy ARI for all the clustering methods according to the different values of the p parameter

Fig. 5

Second scenario: violin plots of the Fuzzy ARI for all the clustering methods according to the different values of the p parameter

Fig. 6

Third scenario: violin plots of the Fuzzy ARI for all the clustering methods according to the different values of the p parameter

6 An application to FTSE-MIB components

The proposed clustering approach has been applied to study the performance over time of the stocks that currently compose the FTSE-MIB index, which is listed on the Italian Stock Exchange owned by the London Stock Exchange.

The stocks composing the index can vary over time, based on their market capitalization and liquidity; moreover any stock may never account for more than 15% of the index.

We argue that, in the case of financial time series, the analysis of point-valued prices does not allow capturing the dynamics of prices’ volatility, which is proxied by price range (Parkinson 1980; Chou et al. 2010). In this study, hence, we considered the monthly minimum and maximum prices of the FTSE-MIB components, spanning from October 2018 to October 2022, shown in Fig. 7.

Fig. 7

Monthly minimum and maximum prices of the FTSE-MIB components, spanning from October 2018 to October 2022. Each plot header is the stock’s acronym whose corresponding name can be found in Table 3—second column

In this regard, we can highlight that almost all the stocks experimented large reduction in the prices around the first pandemic period. However, not all the stocks’ prices reverted to their pre-shock values, with some that incremented their values (e.g. AMP.MI) and others that observed huge losses (e.g. BPE.MI). Some heterogeneity can be also observed considering the magnitude of the prices’ changes due to the COVID-19 shock. Therefore, we use cluster analysis to deeply insight about common patterns in these stocks.

The ITS have been normalized using the proposed procedure in the remark 2. The best solution, i.e. the optimal number of clusters $C^*$, has been chosen based on the combination of C and the p that maximizes the Fuzzy Silhouette index. Considering $C \in \lbrace 2,\ldots , 10 \rbrace$ and $p \in \lbrace 0.05,0.08,0.10,0.12 \rbrace$, we computed the Fuzzy Silhouette index accordingly.

Fig. 8

Fuzzy silhouette index according to $C \in \lbrace 2,\ldots , 10 \rbrace$ and $p \in \lbrace 0.05,0.08,0.10,0.12 \rbrace$

As can be seen from Fig. 8, regardless of the value of p, the best partition is for $C^*=2$. Moreover, both the partition and the medoid units are stable as the value of p increases. Therefore, we focus only on the first “less fuzzy” partition, i.e. that based on $p=0.05$, reported in Table 3.

Table 3 Fuzzy partition with $C=2$ and $p=0.05$

The last column shows the corresponding crisp partition obtained by fixing a cut-off value for the $u_{ic}$ equal to 0.7. The medoid units are those with the $u_{ic}$ in bold, therefore Snam (SRG.MI) and Generali (GI.MI) whose corresponding time series are plotted in Fig. 9.

Fig. 9

The medoids units

Snam is Europe’s leading operator in natural gas transport and storage, with an infrastructure enabling the energy transition. It ranks among the top ten Italian listed companies by market capitalization and has been a public company, since 2001, while Generali is one of the largest global insurance and asset management providers, active in 50 countries in the world.

The medoid of the first group is characterized by a rapid increase in both minimum and maximum prices after the slump in March 2020, thus quickly reverted to the pre-shock values. Conversely, the medoid of the second group took many months to recover pre-shock values. This suggests that this medoid is characterized by a stronger persistency than the one of the first group for the months after the shock. Another interesting difference between the two cluster medoids is the magnitude of the price changes in March 2020, as the price reduction is larger for the second cluster medoid than for the first one.

The same differences between the two medoids can be retrieved in the two groups as we can see by looking at Fig. 10 that shows the crisp partition of all ITS with cut-off value 0.7, $C=2$ and $p=0.05$.

Fig. 10

Crisp partition with cut-off value 0.7, $C=2$ and $p=0.05$

Overall, we find in the Cluster 2 stocks characterized by a slower prices’ recovery rate after the shock and stocks that did not recover completely. In the Cluster 1, differently, we find stocks whose shock impact has been lower than those placed in Cluster 2 and/or with very quick recovery rates. Moreover, in terms of trend, Cluster 1 includes stocks with positive trends pre-shock that were not affected negatively by the COVID-19 pandemic (e.g. PRY.MI, REC.MI ot TRN.MI). Another interesting features of clusters’ composition, is that stocks in Cluster 1 show larger average price range compared with those in Cluster 2. In particular, the former have an average price range equal to 4.81 while the latter to 1.08. This means that, on average, Cluster 1 groups together more volatile stocks.

7 Concluding remarks

The interest in clustering complex data, such as Interval-valued time series, is today a need rather than only an opportunity.

The increasing availability of this type of data must be seen as a resource that may lead research towards more advanced statistical challenges. The use of summaries as the mean or median can produce a loss of information in terms of intra-series variability. The evolution of the range of variation of a variable over time is particularly relevant and could not be assumed to be ignored unless in some specific cases. Handling such symbolic data in the clustering process has not yet been thoroughly studied, indeed few works deal with it.

We propose a new fuzzy clustering method suitable for ITS that not only fills a gap in the literature but also, as shown by simulations, overcomes some well-known dissimilarity measures for interval-valued data. Furthermore, unlike point-to-point dissimilarity measures, our clustering method can be used for time series of different lengths, broadening its applicability. Therefore, we propose a new fuzzy clustering method suitable for ITS to enrich the existing literature. Simulation results have been very promising and the application has revealed the goodness of our proposed clustering technique even with real data.

As a further development of this work, we will extend our methodological proposal by considering new dissimilarity measures as well as the possibility to define a metric robust against outliers or noisy data. Another interesting research perspective to be explored is the extension of the proposed fuzzy methods to other types of complex structures of data such as count (de Nailly et al. 2023; Roick et al. 2021) and categorical (López-Oriona et al. 2023) time series.