Introduction

In the last two decades, there have been many space missions dedicated to researching various geophysical aspects related both exterior and interior of the Earth. For example, the following missions were connected with the recovery of the gravity field: the Challenging Mini-Satellite Payload (CHAMP) (Reigber et al. 2005), the Gravity Recovery and Climate Experiment (GRACE) (Tapley et al. 2004) and the Gravity Field and Steady-State Ocean Circulation Explorer (GOCE) (Rummel et al. 2011). Currently (January 2021), the Earth’s gravity field is monitored by the successor of the GRACE mission—the Gravity Recovery and Climate Experiment Follow-On mission (GRACE-FO) (Kornfeld et al. 2019). The main products of these missions are gravity field models, estimated based on sets of obtained measurements. For the proper scaling of these models, the measurements taken should be positioned as accurately as possible in the reference frame related to the Earth, which requires the orbit determination for the satellites operating in the space missions. Usually, this is performed using code-phase Global Positioning System (GPS) observations, obtained using an on-board GPS receiver (Bock et al. 2011). There are basically two approaches to the orbit determination problem. In the dynamic approach, besides GPS observations, the models of gravitational and non-gravitational perturbing forces are also taken into account and a number of parameters (for example scaling factors) relating to these models are determined (Casotto et al. 2013). In the kinematic approach, an orbit determined is solely based on the GPS measurements, and it is therefore particularly sensitive to the quality of these measurements (Jäggi et al. 2006). One may also speak about an intermediate approach in which the process of determining the orbit also includes the estimation of an additional set of orbital parameters. These parameters are also called pseudo-stochastic parameters, because we can talk about the determined orbit as a special case of the solution of the equation of motion, although it is possible to assign to these parameters statistical properties such as the expected value or a priori variance (Jäggi et al. 2006; Jäggi 2007). Orbits based on the geometric strength of GPS observations with the use of dynamic models together with the estimation of initial conditions and a set of pseudo-stochastic parameters are referred to as reduced-dynamic orbits (Jäggi et al. 2006). This term is related to the weakening of the impact of dynamic models on the satellite motion caused by the estimated pseudo-stochastic parameters, which may include, for example, satellite accelerations at specific time intervals (Jäggi 2007). Pseudo-stochastic parameters have an important property of partial error absorption of the dynamic models used in the orbit determination process (Bock et al. 2011). The dynamic models include mathematical models of gravitational and non-gravitational forces acting on a satellite.

The one-dimensional accuracy of the aforementioned reduced-dynamic orbits, after the validation with the Satellite Laser Ranging (SLR) technique, achieved a few centimeters, ranging from 1.6 cm (in 2010) for the GOCE satellite (Bock et al. 2014), through 2.5 cm for the GRACE mission satellites (Jäggi 2007), up to 3.2 cm for the CHAMP satellite (Jäggi et al. 2006). The SLR technique is routinely used to validate orbits determined using GPS measurements. SLR residuals resulting from the differences in the distance to satellites obtained from SLR measurements and determined based on the validated orbits are a measure of the external accuracy of these orbits (Bock et al. 2011).

In addition to pseudo-stochastic parameters in the form of piece-wise accelerations, which are used in this work, for the sake of completeness, one can also mention an alternative type of pseudo-stochastic parameters sometimes used to determine satellite orbits. These are instantaneous velocity pulses, i.e., changes in the instantaneous satellite velocity in discrete equidistant epochs (Jäggi 2007). For example, instantaneous velocity pulses were estimated every 12 h in the process of determining the orbits of Galileo satellites (Sidorov et al. 2020).

However, simultaneously with the determination of the orbits of the satellites of aforementioned missions, studies on the pseudo-stochastic orbit modeling were carried out. The results of these studies, presented especially in the two works: (Jäggi et al. 2006) and (Jäggi 2007), concern the question of interpretability of piecewise constant accelerations and piecewise linear accelerations and their correlation with measured real accelerations by an accelerometer of the CHAMP satellite. Another aspect of the pseudo-stochastic orbit modeling presented in these works is connected with the comparison of the accuracy of the orbits determined with the use of different types of parameterization, i.e., piecewise constant accelerations, piecewise linear accelerations and velocity pulses. An important issue raised in the first of the discussed works was that if the number of estimated parameters is large enough, the determined reduced-dynamic orbits may be used to recover (in certain degree) parameters of the force field, for example spherical harmonic coefficients of the gravity field model (Jäggi et al. 2006). The best results in this regard were obtained based on orbits parameterized by piecewise accelerations. However, an important question is that the orbital parameters, in this case piecewise accelerations, should be estimated at 30 s subintervals. Such orbits are referred to as highly reduced-dynamic orbits (Jäggi 2007). For reduced-dynamic orbits, spectral analyses were also performed in the second work, indicating the effect of the suppression of high-frequency noise in the orbit positions due to pseudo-stochastic modeling (Jäggi 2007). An interesting remark given in this work concerned the dependence of the obtained satellite positions on the dynamic models used in the orbit determination process. This dependence cannot be avoided without introducing pseudo-stochastic parameters for each observation epoch (Jäggi 2007).

The presented work is based on the data from the GOCE mission, which operated in the years 2009–2013. For the first time, on-board the satellite, in addition to the GPS receiver, a three-axis electrostatic gradiometer was installed for observing the gravity gradient tensor. The collected observational data made it possible to determine several generations of Earth gravity field models, which were the main products of the mission (Rummel et al. 2011). Another important product of this mission is the Precise Science Orbit (PSO) (Bock et al. 2011) of the GOCE satellite. The availability of the PSO orbit of the extremely low GOCE satellite was an opportunity for further study relating to pseudo-stochastic orbit modeling. Such an orbit, with an average height of about 255 km, is particularly sensitive to gravitational perturbations, which is associated with the possibility of determining a set of orbital parameters compensating for deficiencies of the used dynamic models (Eshagh and Najafi-Alamdari 2007). Using positions on this centimeter-accuracy orbit (Bock et al. 2014) as pseudo-observations in an a priori orbit improvement process, the study of limitations and efficiency of various variants of the piecewise pseudo-stochastic modeling was carried out. In this study, results for different orbital arcs with different lengths were obtained. This enabled the identification of the best variants of orbital modeling depending on the arc length and, thus, the required number of estimated orbital parameters. In turn, the number of estimated parameters for a given direction determines, for a given arc length, the temporal resolution of these parameters, dividing orbital arcs into time intervals of equal lengths. For selected lengths of orbital arcs, the obtained results allowed to indicate the best solutions in the set of tested variants and the corresponding models generating satellite accelerations, which are functions of estimated parameters. These best solutions, especially for shorter arc lengths, are promising for possible use in improving longer orbital arcs.

In the next section, the theoretical aspects of piecewise acceleration modeling and research methodology are presented. The last two sections contain the obtained results of numerical tests and closing remarks.

Piecewise acceleration modeling and research methodology

The motion of a satellite around the Earth is governed primarily by the gravitational attraction, as described by the main Newtonian term, and to a much lesser extent by perturbing forces, which can be divided into perturbing forces of a gravitational and non-gravitational nature. This can be expressed in the inertial frame by the following equation (Jäggi 2007):

$$\ddot{\varvec{r}} = - GM\frac{\varvec{r}}{{r^{3} }} + \varvec{f}_{p} \left( {t,\varvec{r},\dot{\varvec{r}},\varvec{p}} \right) = f,$$
(1)

where:

\(\mathrm{GM}\) – the gravitational parameter of the Earth,

\({{r}},\dot{{{r}}}\) – the geocentric satellite position and velocity vectors, respectively,

\({{\varvec{f}}}_{\mathrm{p}},{\varvec{f}}\) – the perturbing acceleration vector depending on time \(t\) and the total acceleration vector acting on the satellite, respectively,

\({\varvec{p}}\) – the parameter vector containing additional empirical parameters.

Empirical parameters, that make up the vector \({\varvec{p}}\), improve the modeling of perturbing acceleration vector \({{\varvec{f}}}_{p}.\) They can be divided into two groups differing in relation to a specific part of the modeled perturbing acceleration. Parameters belonging to the first group may be scaling factors of background models describing the gravitational and non-gravity perturbing accelerations. On the other hand, parameters of the second group may be the aforementioned pseudo-stochastic parameters, introducing additional perturbing accelerations, which can partially compensate for deficiencies of the background models (Bock et al. 2014). These additional accelerations operate at specific constant time intervals or, in other words, have a specific temporal resolution. This means that an orbital arc is divided into the integer number of such intervals in which the aforementioned additional accelerations are active.

In this work, apart from the corrections to the initial conditions of the satellite’s orbit, only the parameters from the second group were estimated, i.e., unconstrained pseudo-stochastic parameters, which are related to the need to emphasize their ability to improve the orbit. It is also connected with the possibility of examining the sensitivity of the determined orbit to the changing number of estimated parameters and their temporal resolution in terms of changing the accuracy of fit to observations.

The core tool in orbital processing software was called the Toruń Orbit Processor (TOP). This package is described in (Drożyner 1995). The TOP package enables performing the process of dynamic orbit determination in an a priori force field, including the gravity field and remaining perturbing forces. In the TOP package, a satellite orbit is numerically integrated making use of the Cowell 8-th-order predictor–corrector procedure. Moreover, thanks to the ability of incorporation of observations, it is possible to improve an orbit by the estimation of the above-mentioned corrections to initial conditions, i.e., corrections to the initial satellite position and velocity components at the given initial epoch. This is realized in the least squares sense by successive iterations until convergence is achieved.

For the purposes of this work, the TOP package has been extended with procedures written in the Fortran language (Intel Corp. 2020), which enabled the implementation of the piecewise acceleration approach (Jäggi 2007) for satellite orbit modeling, which significantly increased the set of determined orbital parameters. As already mentioned in the previous section, the GOCE satellite positions in the centimeter-accuracy reduced-dynamic PSO orbit were taken as the pseudo-observations. Strictly speaking, the estimation of all orbital parameters was based on fitting to the time series of rectangular coordinates of the GOCE satellite. The comparison of estimated orbits with the reference PSO orbit was performed in the inertial reference frame (IRF) of the standard epoch J2000.0 (ESA 2010). Therefore, these rectangular coordinates as the pseudo-observations were recomputed from the ITRF2005 reference frame into the IRF frame. For this purpose, the time series of quaternions delivered by the European Space Agency (ESA), defining the instantaneous transformation matrix between both of the reference frames, mentioned above, was used. Ten 1-day arcs of the reduced-dynamic PSO orbit of the GOCE satellite have been arbitrarily selected as reference orbits. These arcs were taken from the range between Nov 6, 2009 and Jan 25, 2010. According to the information obtained on the ESA website, these days were typical “orbital days” without any poor GPS tracking conditions. The a priori values of being corrected initial conditions, i.e., the components of the satellite’s position and velocity, were taken from the reference PSO orbits in the initial epochs \(.\) In the orbit determination process, the a priori force field was described by the ITG-GRACE2010s (Mayer-Gürr et. al. 2010) gravity model up to degree and order of 180 of the spherical harmonic coefficients, the Monitoring Earth Rotation and the Intercomparison of Techniques (MERIT) standards model (Melbourne et al. 1983) – ocean and solid Earth tides, the planetary ephemerides DE200/LE200 (Standish et al. 1992) – third body effects, the solar radiation pressure model – both direct and albedo effects and the Painleve formulation with the Schwarzschild metric – relativity effects as implemented in the TOP package (Drożyner 1995). Due to the drag-free mode flight of the GOCE satellite (Bock et al. 2011), the influence of air drag pressure was neglected.

In the presented research, the estimation of the orbital parameters is based on the observation equation at the given epoch \(t\) in the following form:

$$x_{i}^{{\text{o}}} \left( t \right) + v_{i} \left( t \right) = x_{i}^{{\text{c}}} \left( t \right) + \mathop \sum \limits_{j = 1}^{n} \frac{{\partial x_{i}^{{\text{c}}} \left( t \right)}}{{\partial p_{j} }}\left( {p_{j} - p_{j0} } \right),$$
(2)

where: \({x}_{i}^{\mathrm{o}}\left(t\right)\) – is the pseudo-observation being the \(i\)-th Cartesian coordinate of the GOCE PSO reduced- dynamic orbit, \({x}_{i}^{\mathrm{c}}\left(t\right)\) – is the \(i\)-th Cartesian coordinate of the satellite in the a priori orbit (computed orbit), \({v}_{i}(t)\)– is the residual of \(i\)-th Cartesian coordinate; \(i=1, 2, 3; {x}_{1}=x, {x}_{2}=y, {x}_{3}=z,\) \(\frac{\partial {x}_{i}^{\mathrm{c}}\left(t\right)}{\partial {p}_{j}}\) – is the partial derivative of \(i\)-th Cartesian coordinate of a priori orbit w.r.t. the parameter \({p}_{j},\) \({p}_{j},{p}_{j0}\)– is the actual orbital parameter and the a priori orbital parameter, respectively, \(n=6+{n}_{p}\)– it is the total number of parameters, which consists of six corrections to the initial. conditions, i.e., to the position and velocity components in the initial epoch and the number of estimated pseudo-stochastic piece-wise parameters.

The process of orbit determination according to Eq. (2) can be treated as improving this orbit in subsequent iterations, where the actual parameters estimated in the previous iteration become the a priori ones in the next iteration. An important part of the orbit improvement process is the propagation of the partial derivatives of the a priori orbit with respect to the parameters, i.e., \(\partial {x}_{i}^{\mathrm{c}}\left(t\right)/\partial {p}_{j}\). The mentioned above propagation is connected with the system of variational equations, which is obtained as the partial derivative of Eq. (1) for the a priori orbit with respect to the given parameter \({p}_{j}\) in the form (Jäggi et al. 2006):

$$\frac{{\partial \ddot{\varvec{r}}^{c} \left( t \right)}}{{\partial p_{j} }} = \frac{{\partial \varvec{f}}}{{\partial \varvec{r}^{{\text{c}}} \left( t \right)}}\frac{{\partial \varvec{r}^{{\text{c}}} \left( t \right)}}{{\partial p_{j} }} + \frac{{\partial \varvec{f}}}{{\partial \dot{\varvec{r}}^{c} \left( t \right)}}\frac{{\partial \dot{\varvec{r}}^{c} \left( t \right)}}{{\partial p_{j} }} + \frac{{\partial \varvec{f}_{{\text{p}}} }}{{\partial p_{j} }}.$$
(3)

In this expression, \(\partial {\varvec{f}}/\partial {{\varvec{r}}}^{\mathrm{c}}\left(t\right)\) and \(\partial {\varvec{f}}/\partial {\dot{{\varvec{r}}}}^{\mathrm{c}}\left(t\right)\) are the partial derivatives of the total acceleration vector \({\varvec{f}}\) with respect to the position and velocity vectors in the a priori orbit, respectively. Because of the orbital parameters do not depend explicitly on the velocity (Jäggi 2007), the second term in the right-hand side of Eq. (3) can be omitted. In turn, the form of the partial derivative of the perturbing acceleration vector \({{\varvec{f}}}_{\mathrm{p}}\) with respect to the parameter \({p}_{j}\) is related to the given model of the piecewise accelerations. This model describes these accelerations using polynomials, which are functions of a normalized time \(T\) of orbital arc. Thus, the given piecewise acceleration can be expressed by the following formula:

$$~a_{{id}} \left( {T\left( t \right)} \right)~ = \left\{ \begin{gathered} \mathop \sum \limits_{{k = 1}}^{{n_{{\text{int} }} }}\,\, p_{{kd}} T^{{k - 1}} ;~~~~~~~t_{{i - 1}} \le t < ~t_{i} ~,~ \hfill \\ 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,;\,\,\,\,\,\,\,\,otherwise, \hfill \\ \end{gathered} \right.$$
(4)

where: \({a}_{id}\left(T(t)\right)\) – the time-dependent piecewise acceleration acting in the \(i\)-th time interval describing by the condition \({t}_{i-1}\le t\le {t}_{i}\) along the d- th direction, \(d=1, 2, 3 -\) this corresponds. to the radial-track, along-track and cross-track direction, respectively, pkd- the \(k\)-th estimated piecewise orbital parameter in the \(i\)-th time interval for the \(d\)-th direction, \(n_{{\text{int}}}\)\({-}\)the number of estimated parameters in each time interval, i.e., in each piece of orbital arc, if \({n}_{int}=1\), then the piecewise constant acceleration case is obtained. The normalized time \(T\) of the orbital arc is calculated using the formulae:

$$T = \frac{{t - t_{0} }}{{t_{{\text{E}}} - t_{0} }} .$$
(5)

In the above expression, \(t,{t}_{0},{t}_{\mathrm{E}}\) denote the current, initial and last epoch time, respectively. The estimation of piecewise parameters generates an additional acceleration vector \({{\varvec{a}}}_{e}(t)\), which, together with other acceleration vectors, also makes up the perturbing acceleration vector \({{\varvec{f}}}_{\mathrm{p}}\), which occurs in Eq. (1). This additional vector \({{\varvec{a}}}_{e}(t)\) can be treated as the sum of the three acceleration vectors for the radial-track, along-track and cross-track direction, respectively:

$${\varvec{a}}_{e} \left( t \right) = {\varvec{a}}_{1} \left( t \right) + {\varvec{a}}_{2} \left( t \right) + {\varvec{a}}_{3} \left( t \right).$$
(6)

Each of these three acceleration vectors \({{\varvec{a}}}_{d}(t)\) (\(d\) = 1, 2, 3) in the direction \(d\) can be presented in the following form (Jäggi 2007):

$${\varvec{a}}_{d} \left( t \right) = \mathop \sum \limits_{i = 1}^{m} \left[ {\varepsilon \left( {t,t_{i - 1} ,t_{i} } \right) \cdot a_{id} \left( {T\left( t \right)} \right)} \right]{\varvec{e}}_{d} \left( t \right),$$
(7)

where \({\varvec{e}}_{d} \left( t \right)\) denotes the unit vector defining the given direction \(d\) and \(m\) is the number of pieces into which a given orbital arc is divided. The factor \(\varepsilon \left( {t,t_{i - 1} ,t_{i} } \right)\) enables the acceleration \(a_{id} \left( {T\left( t \right)} \right)\) at the appropriate interval \(< t_{i - 1} ,t_{i} )\) and therefore:

$$\varepsilon \left( {t,t_{i - 1} ,t_{i} } \right) = \left\{ {\begin{array}{*{20}c} {1;\,\,\, if\,\ t_{i - 1} \le t < t_{i,} } \\ {0; \,\,\,otherwise.} \\ \end{array} } \right.$$
(8)

Taking into account Eq. (3) with omitting the second term on the right-hand side and Eq. (4) and knowing that the contribution of piecewise acceleration \({a}_{id}\) in the perturbing acceleration vector \({{\varvec{f}}}_{\mathrm{p}}\) is of the form \({a}_{id}{{\varvec{e}}}_{d}\), the system of variational equations used in this work can be presented by the following equation:

$$\frac{{\partial \ddot{\varvec{r}}^{c} \left( t \right)}}{{\partial p_{j} }}~ = ~\frac{{\partial \user2{f}}}{{\partial \user2{r}^{{\text{c}}} \left( t \right)}}~~\frac{{\partial \user2{r}^{{\text{c}}} \left( t \right)}}{{\partial p_{j} }}~~ + \left\{ \begin{gathered} \frac{{\partial \user2{f}_{{\text{p}}} }}{{\partial p_{j} }} = \user2{e}_{d} \cdot \frac{{\partial a_{{id}} }}{{\partial p_{{kd}} }};~~~~~~~~~~t_{{i - 1}} \le t < t_{i} ,~ \hfill \\ \frac{{\partial \user2{f}_{{\text{p}}} }}{{\partial p_{j} }} = 0;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,otherwise,~ \hfill \\ \end{gathered} \right.$$
(9)

It should be noted that the piecewise parameter \({p}_{j}\) from Eq. (3) corresponds to the piecewise parameter \({p}_{kd}\) from Eq. (4) and therefore:

$$\frac{{\partial {\varvec{f}}_{{\text{p}}} }}{{\partial p_{j} }} \equiv \frac{{\partial {\varvec{f}}_{{\text{p}}} }}{{\partial p_{kd} }} .$$
(10)

The partial derivatives of the a priori orbit for the parameter \({p}_{j}\) in the given epoch \(t\), i. e.,

$$\frac{{\partial {\varvec{r}}^{{\text{c}}} \left( t \right)}}{{\partial p_{j} }} = \left[ {\frac{{\partial x^{c} \left( t \right)}}{{\partial p_{j} }},\frac{{\partial y^{c} \left( t \right)}}{{\partial p_{j} }},\frac{{\partial z^{c} \left( t \right)}}{{\partial p_{j} }}} \right]^{{\text{T}}} ,$$
(11)

were determined by the numerical integration of Eq. (9), almost simultaneously with the numerical integration of equations of motion (1) in the TOP orbital package. However, the partial derivatives \(\frac{\partial {\varvec{f}}}{\partial {{\varvec{r}}}^{\mathrm{c}}\left(t\right)}\) were obtained analytically by the determination of gravity gradient tensor components using the a priori gravity field model, in this case, the ITG-GRACE2010s model. Similarly, the partial derivatives \(\frac{\partial {{\varvec{f}}}_{\mathrm{p}}}{\partial {p}_{j}}\) were calculated analytically using the expression on the right-side hand of Eq. (9).

To obtain the best possible results of the orbit improvement, the extended TOP (eTOP) package was launched in a closed-loop environment, which made it possible to determine the optimal number of pieces \(m\) for different lengths of the orbital arc, with a different form of parameterization according to the formula (4). The main indicator characterizing the accuracy of the obtained solutions is the three-dimensional root-mean-square (3-D RMS) difference between the estimated orbit using the eTOP package and the “observed” orbit, i.e., the PSO reference orbit. By increasing the number of pieces \(m\) for the predefined directions, the accuracy of fit of the closed-loop estimated orbit to the “observed” orbit increases until the lowest possible RMS value is obtained. The increase in the number of pieces \(m\) is associated with an increase in the total number of estimated parameters \({n}_{T}\) which, in the given case, can be determined by the formula:

$$n_{T} = 6 + 3n_{int} m,$$
(12)

where 6 is the parameter number for improving the initial conditions (IC) and \({n}_{int}\) is the number of estimated parameters in each piece of arc. The expression (12) shows that the parameters are estimated in \(m\) pieces of the arc for each direction separately, i.e., in the radial-, along- and cross-track directions.

Results of numerical experiments

Using the eTOP software package, several variants of the GOCE orbit improvement were obtained to illustrate capabilities of piecewise acceleration orbit modeling in terms of efficiency and accuracy depending on particular estimated arcs and their lengths. Different parameterizations established according to the formula (4), including the piecewise acceleration modeling by the polynomials up to degree 9 in the radial-track, along-track and cross-track directions, were numerically tested. For the given computational variant, the piecewise accelerations along the aforementioned directions were calculated using the polynomials with the same degree but with the different coefficients, which were estimated as the set of piecewise orbital parameters. The results presented below apply to the maximum of fourth-order polynomials, because when using higher-order polynomials, the obtained numerical accuracy was significantly lower. In some cases, for example, for the degree of polynomial great than 9, the solutions were not stable, which was related to the ill-conditioned normal matrix of the orbit determination process. The obtained solutions for selected ten 1-day arcs from the closed-loop orbit improvement process, with corresponding the optimal numbers \(m\) of pieces into which the given orbital arc was divided, will be presented below (Sect. 3.2). Additionally, selected five 1-day arcs were divided into shorter and longer sub-arcs to investigate how the regarded orbit parameterization works depending on a changing length of orbital arc. In all five cases, the obtained solutions were on the similar level of numerical accuracy ranging from sub-millimeters up to a few millimeters. Moreover, the obtained solutions for all five considered cases (related to the division of the appropriate five 1-day arcs) contain a similar pattern concerning the preferred polynomial degrees for different lengths of the arcs. Generally speaking, the second-order to fourth-order polynomials give better results for shorter arcs, whereas the zero-order and first-order polynomials are preferred for longer arcs. Therefore, detailed results for different orbital arc lengths are given below for the division of a one selected representative 1-day arc. The solutions will be shown separately for shorter and longer arcs (Sect. 3.3 and 3.4). The arc lengths were selected arbitrarily. The basic arc was the 90-min arc, which corresponds to approximately one orbital revolution of the GOCE satellite. Set of the integration steps of the orbit determination process was tested. In the set of values: 1, 5, 10, 20 and 30 s, the best solutions were obtained for the 5 s integration step, which was taken for all computational variants. This step is exactly half the pseudo-observation sampling interval.

Introductory remarks concerning numerical accuracy

All presented below RMS values of fit of estimated arcs into the reference orbit for various solution variants are at the level of a few millimeters or even sub-millimeters. On the other hand, it is known that the accuracy of the reference orbit is at the level of 1–2 cm. Therefore, the obtained results can be considered from the two perspectives. Firstly, taking into account the accuracy level of the reference orbit, all the obtained solution variants are equivalent, i.e., they are all close enough to this orbit. This is because the obtained RMS values are within the accuracy of the reference orbit. However, it is also possible to assume that the reference orbit can be treated as the error-free orbit in a numerical sense, as in the simulation environment, and to compare different variants of solutions in terms of the numerical accuracy achieved. In other words, this approach makes it possible to compare different variants of piecewise acceleration modeling in terms of the ability of absorption of differences between the a priori orbit and the reference orbit in a strictly numerical sense. Therefore, the sub-millimeter and millimeter RMS values shown in the following chapters are a measure of the numerical accuracy of the obtained solutions, in contrast to their real accuracy, which is close to the real accuracy of the reference orbit (1–2 cm). Basically, RMS values are given to the one decimal place. However, in the case of testing the option with unequal numbers of estimated parameters in the three predefined directions, in order to show subtle differences in the obtained solutions, the results are given to the two decimal places. In the series of RMS values generated in the closed loop with changing numbers of estimated parameters, no numerical noise was noticed at the first and second decimal place.

Solutions for different 1-day arcs

As mentioned above, ten 1-day arcs of the reference orbit were used in the computations. Their initial epochs correspond to the following dates: Nov 6, Nov 12, Nov 19, Nov 24, Nov 29, Dec 18, 2009 and Jan 08, Jan 13, Jan 19, Jan 24, 2010. In all cases, the same hours, minutes, and seconds are assigned to the initial epoch, i.e., 23 h 59 m 45.00 s UTC. The estimation results of the corresponding ten 1-day arcs, in terms of the RMS values, are given in Table 1. Starting RMS values, obtained before using piecewise parameters and denoted as RMS IC, range from 1.72 to 2.92 m. The estimation of piecewise parameters improves the numerical accuracy of the solutions by a factor from about 480 to 1460. This means that all presented solutions have the numerical accuracy between about 2 and 4 mm. Numerically, the best solutions were obtained for the zero-degree-order polynomial acceleration modeling, denoted as \({a}_{0} (\) piecewise constant acceleration modeling), and for the first-degree-order polynomial acceleration modeling (not shown here). Table 1 shows that the obtained RMS values for the \({a}_{0}\) option are between 2.0 and 3.3 mm. However, to achieve such level of RMS values, this option requires the estimation of many parameters, up to 9,000, and therefore is the most time-consuming—typically several dozen hours for the Intel Core i9-9900 K CPU (3.60 GHz) and 64 GB RAM. Such significant estimation times of the above solutions are related to the fact that their RMS values are close to the limit values that can be achieved in the given numerical conditions. As additional research (not shown here) has been revealed, alternative solutions with the numerical accuracy decrease from 0.2 to 0.8 mm can be considered. These are the variants of the same option (piecewise constant acceleration modeling \({a}_{0}\)) with the number of estimated parameters equal to 1800. The estimation times for such variants with different 1-day arcs ranged from 7 to 12 min (with the integration step of 5 s at the pseudo-observation sampling interval of 10 s). In addition, another option related to the second-order degree polynomial acceleration modeling is given in Table 1. In this case, the total number of estimated parameters is only 309, 606 and 612, which dramatically lowers the estimation time to a few minutes. In this case, the numerical accuracy decreases by 0.6 to 1.3 mm.

Table 1 RMS values of the fit of estimated 1-day arcs into the reference orbits for the piecewise acceleration modeling by the zero- and second-order polynomials
Full size table

Comparing the results for several arcs in Table 1, especially for \({a}_{0}\) acceleration modeling, is seen that the two arcs of date Nov 07, 2009 and Dec 18, 2009 are fitted clearly better than the remaining eight ones. For these 1-day arcs, the numerical accuracy of 2.00 mm was achieved. The next four arcs have the RMS of fit at the level of about 3 mm, whereas the RMS values for the four remaining ones are slightly larger—about 3.3 mm. The obtained RMS differences may reflect the differences in the accuracy of the individual orbital arcs. More accurate arcs can be “smoother” and therefore easier to fit.

As previously mentioned, the numerical tests were also carried out for the estimation of orbital arcs of various lengths based on the division of five selected 1-day arcs. In the next two sections, the representative example of solutions for shorter and longer arcs resulting from the division of 1-day arc on Nov 19, 2009 will be presented.

Solutions for short arcs: 1-day arc on Nov 19, 2009 division case

In the first group of estimated arcs, the lengths between 1.0 and 45.0 min were taken. Similarly to Table 1, to show the efficiency of the piecewise acceleration modeling, the estimation variants including only an improvement of IC were computed. The RMS values for these variants determine the starting thresholds as a reference for the further orbit improvement by incorporating the piecewise parameters. In Table 2, the RMS values of the fit of estimated orbital arcs into the reference PSO orbit, depending on the form of piecewise acceleration modeling, are given. For particular arcs, the three cases of the estimation are given. For the first case, the piecewise constant acceleration modeling is realized by the estimation of parameter \({a}_{0}\) in each piece of arc, i.e., this is the zero-degree polynomial case. The remaining cases include the piecewise nonzero-degree polynomial acceleration modeling. For these cases, the coefficients of polynomials are estimated in each piece of the arc as the orbital parameters. As shown in Table 2, these polynomials are the first to fourth-degree ones, each of which has the first constant term \({a}_{0}\) equal to zero. To emphasize the efficiency of given computational variants, the efficiency factor (EF) was calculated by dividing the RMS values of the fit for the IC correction by the corresponding RMS values of the fit for the full set parameter estimation. As one can see in Table 2, the RMS values obtained generally remain at the level of a few millimeters. As the length of the orbital arc increases, the RMS values increase but remain below 3 mm. The EF factors also increase, which is caused by faster growth of the RMS values for the IC improvement variants. Of course, to maintain the millimeter level of the fit of the estimated orbit, with increasing arc length, the number of estimated piecewise parameters also increases, reaching the value of 522 for the third variant for the 45-min arc. It can also be seen that a twofold increase in the arc length causes an approximately twofold increase in the number of piecewise parameters determined. Generally, the solutions based on the non-zero-degree polynomial are better than the solutions for the zero-degree polynomial, i.e., the piecewise constant acceleration case. The differences between the corresponding RMS values reach up to about 1 mm, for example, in the case of an arc length of 5.0 min. The results obtained for the shortest arc of 1-min length are exceptional in this respect. There is a large disproportion between the RMS value for the first case – solution for the zero-degree polynomial with the RMS of 2.7 mm and the RMS values for the other two cases, including the solutions for the second- and fourth-degree polynomials – only 0.1 mm. For these two variants, the REF factor equals 28.0, which is the greatest value for the variants considered. This proves the particularly high sensitivity of the 1-min arc of the orbit, under given numerical conditions, to the modeling using piecewise acceleration by the second- and fourth-order polynomials. In the latter case, the number of pieces \(m\) is equal to 1, which means modeling the entire arc in the given direction by the same polynomial. Table 2 also shows that the temporal resolutions of estimated piecewise parameters, i.e., the time interval corresponding to each piece of the orbit, range from about 20 s to 60 s. These values are several times greater than the pseudo-observation sampling interval, which is equal to 10 s.

Table 2 Results of the fit of the estimated GOCE orbits into the PSO reference orbit using the different degree polynomials in the piecewise acceleration modeling for the short arcs
Full size table

For the shortest arc, the RMS values were additionally calculated in the radial-track, along-track and cross-track directions in the case of modeling with the zero- and second-order polynomial. As shown in Table 3, the distribution of RMS values is very different for both variants. Characteristic distribution of RMS values can be observed in the first case—\({a}_{0}\) modeling. The RMS values for the radial- and cross-track directions remain the same at the level of 0.1 mm, whereas the RMS value for the along-track direction is more than an order of magnitude larger and amounts to 2.7 mm. A similar pattern also repeats for other arc lengths in all variants with \({a}_{0}\) modeling. On the other hand, in the second case (polynomial \({a}_{1}T+{a}_{2}{T}^{2}\)), the RMS value of 0.1 mm in the radial-track and along-track direction can be noted, however, for the cross-track direction, the RMS value is 0.0 mm (in the sense of the first decimal place).

Table 3 RMS values of the fit of estimated 1-min arc along taken directions for the piecewise acceleration modeling using the zero- and second-order polynomial
Full size table

Solutions for longer arcs: 1-day arc on Nov 19, 2009 division case

As mentioned previously, the division of the estimated orbital arcs into two groups according to their lengths was performed arbitrarily. However, it was assumed that in the case of arcs belonging to the second group, the best-obtained solutions concern the modeling of piecewise accelerations using zero- and first-order polynomials. In other words, modeling using second- and higher-order polynomials loses its importance due to the higher RMS values with respect to the solutions with the zero- and first-order polynomials. This is especially true for the longest tested arcs. In the case of solutions presented in Table 4 for the longer arcs between 90 and 1440 min, the smallest RMS values were achieved for the zero- and first-order polynomial acceleration modeling. For the longest tested arc, i.e., 1,440 min. (1-day), it is clearly seen that the zero-order polynomial modeling (the piecewise constant acceleration modeling) and the first-order polynomial modeling give the best RMS results practically at the same level close to 3 mm. Similarly to the shorter arcs, the increasing number of estimated piecewise parameters allows maintaining the millimeter numerical accuracy of solutions and the effect of an approximate doubling of the number of estimated piecewise parameters is visible when doubling the length of the orbit arc (only for \({a}_{0}\) and \({a}_{1}T\)). The exception is the case of transition from a 12-h arc to a 24-h arc, where the number of estimated piecewise parameters reaches 9,000 (Table 4). With a higher number of piecewise parameters at the given numerical conditions, the solution was not achievable because of an ill-conditioning of the normal matrix. The increasing RMS of the fit for the solutions with only the IC correcting from 0.14 m (90-min arc) to 2.12 m (1440-min arc) at the almost constant millimeter RMS level of solutions for the full set of parameters (IC parameters plus piecewise acceleration parameters) is responsible for a significant increase in the efficiency of solutions compared to shorter arcs. This is expressed by the EF factors in the range between 50.4 and 706.5 (Table 4—longer arcs) with respect to the corresponding range from 1.0 to 28.0 (Table 2—shorter arcs). It is also clearly seen that acceleration modeling using the second-order polynomial, otherwise than in the case of shorter arcs, provides a noticeable lower numerical accuracy of solutions, especially for arc lengths greater than 90.0 min. However, as also noted previously, for the second-order polynomial modeling, a considerable lower number of piecewise parameters (612) is estimated. Comparing the zero-order polynomial modeling variant with the second-order polynomial modeling one for the 1-day arc, it is clearly seen that the obtained numerical accuracy decreases from 3.0 mm to 3.9 mm. The question of whether such a decrease is acceptable could be raised. On the one hand, it is acceptable, taking into account the accuracy of the PSO reference orbit at the level of about 1–2 cm, however, on the other hand, in the numerical aspect, when the estimated orbit approaches a few millimeters on average from the reference orbit, the decrease in accuracy by almost 1 mm is significant. The lower achieved numerical accuracy for the second-order polynomial is related to the significantly smaller amount of estimated piecewise parameters, e.g., 612 compared to 9,000 (zero-degree polynomial) in the case of the 1-day arc (Table 4). This is also connected with the substantially increased time interval of each orbital piece for the second-order polynomial modeling. The length of this interval increases with the length of the orbital arc from 42.5 s (90-min arc) to 847.1 s (1440-min arc). Such values are too large to achieve results similar to the first two variants (zero- and first-order polynomial modeling). Shortening these quantities, resulted in an increase in the number of estimated piecewise parameters and modeling with the second-order polynomial turned out to be impossible under the given numerical conditions. With the larger numbers of parameters in this variant, the solution is unstable because the normal matrix became ill-conditioned (or insufficiently conditioned).

Table 4 RMS of the fit of the estimated orbits into the PSO reference orbit depending on the piecewise acceleration modeling for the longer orbital arcs
Full size table

Similar to the previous section, the distribution of RMS values for the two similar variants, i.e., with the zero-order and the second-order polynomial modeling of the piecewise accelerations, is given in Table 5. This time, the obtained RMS values are presented for the longest 1-day arc. It is clearly seen that other than for the shortest 1-min arc (Table 3), there is no substantial difference between the two presented RMS distributions for the zero- and second-order polynomial modeling. In both cases, the RMS values for the radial- and cross-track direction are the same, whereas the RMS value for the along-track is clearly dominant, being greater by about one order of magnitude and about factor 3 for the zero-order and second-order polynomial modeling, respectively (Table 5). Thus, both variants of modeling show the similar behavior in terms of the “directional” RMS values with the “central peak” of RMS value for the along-track direction and the much smaller “symmetrically located” and equal RMS values for the remaining directions (Table 5). Comparing this behavior with the shortest 1-min arc, it can clearly be seen that in the case of piecewise constant acceleration modeling (zero-order polynomial), the RMS distribution is very similar. However, all RMS values have lower values for the shortest arc (Table 3). For the RMS values in the case of the radial- and cross-track directions, the decrease w.r.t. the longest arc is almost two times (from 0.2 mm to 0.1 mm), whereas for the along-track direction, the RMS value for the shortest arc is only slightly smaller than for the longest arc (2.7 mm against 3.0 mm). In the case of second-order polynomial modeling, the along-track dominating RMS value is evident for the longest 1-day arc (Table 5). However, for the shortest arc, this value is approximately at the same level as the RMS values for the two remaining directions (Table 3). This means there was a systematic increase in the RMS value for the along-track direction regarding the remaining directions for the second-order polynomial modeling with the increased arc length of the orbit. Thus, unlike in the case of the short 1-min arc, this type of modeling loses the ability to similarly fit in the three taken directions for the long 1-day arc.

Table 5 RMS values of the fit of estimated 1-day arc along in the three predefined directions for the piecewise acceleration modeling using zero- and second-order polynomial
Full size table

It seems that the significantly higher RMS values for the along-track direction, especially for the solutions based on zero- order and first-order polynomial modeling, may be related to a special distinction of this direction in the case of the GOCE satellite. The motion of the satellite was strongly perturbed in this direction, at an average altitude of about 255 km, especially by the atmospheric drag force. To compensate for the influence of this force, the Attitude and Orbit Control System/Drag-Free Attitude Control System (AOCS/DFACS) and an Ion Thruster Assembly (ITA) were installed on-board the satellite (Drinkwater et al. 2003). Despite the operation of the AOCS/DFACS and ITA systems, some residual perturbating acceleration could modify the satellite’s motion in the along-track direction. Therefore, modeling the satellite motion in this direction becomes particularly difficult, which is reflected in the much higher RMS value than for the two remaining directions. At this point, it is worth mentioning again two solution variants for the shortest 1-min arc, which are an exception to this scheme. In this case, the distribution of the RMS value is not dominated by the RMS value in the along-track direction. These solutions result from the piecewise acceleration modeling using the second- and fourth-order polynomials. The results achieved in these variants indicate the particular usefulness of the incomplete (with the free term equal to zero) second- and fourth-degree polynomials for modeling short orbital arcs of the GOCE satellite.

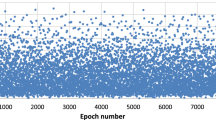
Looking at Tables 2 and 4, it can be seen that the RMS values for the solutions obtained using the second-order polynomial are present for almost all given arc lengths. In Fig. 1, RMS values of the solutions for different arc lengths using this second-order polynomial are given. This figure shows that with the increase in the arc length, the RMS values increase, which means a gradual deterioration of the fit of the given estimated arc to the reference orbit. This deterioration may be due to some accumulation of numerical errors in the orbit fitting process with the increasing amount of processed data. Furthermore, the changes in the obtained RMS values when doubling the length of the orbital arc follow a logartymic curve. It proves a certain regularity of the series of obtained solutions and may indicate the presence of systematic effects in the estimation of arcs of various lengths.

Fig. 1
figure 1

RMS of the fit of estimated arcs to the reference orbit depending on the different arc lengths in the case of the use of second-order polynomial. The initial epoch for all estimated arcs: Nov 19, 2009 23 h 59 m 45.00 s UTC

Full size image

At the end of this section, the orbit modeling will be characterized depending on the number of estimated piecewise parameters for selected numerical accuracy thresholds in the case of the longest 1-day arc with the use of the piecewise constant accelerations. Table 6 shows a relatively small increase in the number of estimated piecewise parameters from the 10 mm threshold to the 6 mm numerical accuracy threshold. This increment is 60. An increase in the accuracy to 4 mm entails an increase in the number of estimated piecewise parameters by 273. In the case of a transition from the 4 mm threshold to the 3 mm boundary threshold, there is a rapid increase in the number of estimated parameters, amounting to 8409. This proves that the used modeling variant is approaching an numerical accuracy limit in the adopted numerical conditions, including the 1-day arc, the 5 s integration step and the 10 s observation sampling interval. The aforementioned accuracy limit is at the level of 3 mm in the case of regarded 1-day arc. Such a significant increase in the number of estimated parameters at the transition to the threshold of 3 mm is associated with a huge increase in the CPU time consumed from 2.05 min (accuracy threshold 4 mm, 591 parameters) to 2769.65 min (~ 46 h, accuracy threshold 3 mm, 9,000 parameters). Therefore, it would be reasonable, from the point of view of computation time, to stay with a numerical accuracy threshold of 4 mm.

Table 6 Numbers of estimated piecewise parameters depending on the assumed accuracy thresholds for the zero-order polynomial modeling of the 1-day arc
Full size table

Selected solutions in terms of residuals: 1-day arc on Nov 19, 2009 case

Apart from taking into account and comparing only the RMS values, it is also worth looking at the distribution of the “O-C” residuals, i.e., the observed minus computed coordinate values in the three predefined directions, along the 1-day arc on Nov 19, 2009. The two solution variants for the given 1-day arc with the piecewise zero-order polynomial (piecewise constant accelerations) modeling and with the piecewise second-order polynomial modeling have a very different residual distribution. Figure 2 presents the residuals for the first solution, i.e., the piecewise constant acceleration modeling. It is clearly seen, that the residual distribution in all three directions is regular and similar. The residuals oscillate around zero. However, in the case of the along-track direction, there is about an order of magnitude greater spread of values than for the remaining directions (Fig. 2b). For the along-track direction, the values of residuals are between -9.4 and 9.8 mm but for the radial-track and cross-track direction, these values range from only about -0.8 to 0.8 mm (Table 7). This effect is also reflected in terms of RMS values in Table 5. Different behavior of residuals can be noted for the second-order polynomial piecewise acceleration solution. In the radial-track and cross-track direction, most of the residuals are concentrated in the range from -3 to 3 mm, in some places exceeding this range (e.g., in the epoch number 3000, Fig. 3a and c), which results in an increase in the range boundaries in both cases (about -6 to 6 mm). Such local increases in the values of the residuals may be caused by the boundary effects related to changes in the second-order polynomials in particular orbital intervals (pieces). As previously noted, these changing second-order polynomials describe the additional satellite accele-

Fig. 2
figure 2

Residuals of the piecewise constant acceleration solution along the 1-day orbital arc in the three predefined directions

Full size image
Table 7 Residual statistics for the two selected 1-day arc solutions – boundary values of residual ranges and mean values of residuals in the radial-track, along-track and cross-track directions
Full size table
Fig. 3
figure 3

Residuals of the second-order polynomial piecewise acceleration solution along the 1-day orbital arc in the three predefined directions

Full size image

rations along the predefined directions. However, the residuals in the along-track direction show the different behavior (Fig. 3a). They are distributed in a range from -11.4 to 11.0 mm (Table 7). As can be seen, this time, unlike the previous case, the width of residual range in the along-track direction is greater only by a factor of two than the width of residual ranges for the other two directions (Table 7). The residuals in the along-track direction, although distributed throughout the whole range, form characteristic diagonal parallel stripes (Fig. 3b). Such different distribution of the residuals for the along-track direction may be related to the aforementioned occurrence of perturbations in this direction related to the impact of non-gravitational forces on the satellite motion, especially the atmospheric drag. Comparing the widths of residual ranges for both considered solutions, a certain disproportion between the differences of these widths for the along-track direction and the remaining directions can be seen. Firstly, the range width for the radial- and cross-track directions in the case of piecewise constant acceleration solution is about seven times smaller than for the piecewise second-order polynomial acceleration solution. Secondly, the width of the residual ranges for the along-track direction remains practically at the same level for both solutions. The residuals are in a range of approximately form -10 to 10 mm (Table 7). Therefore, despite a significantly smaller number of estimated parameters (612 vs 9,000), the piecewise second-order polynomial acceleration solution almost maintained the numerical accuracy level of the piecewise constant acceleration solution in the along-track direction. Table 7 also shows that there are no significant systematic effects in both solutions since the mean values of the residuals in the taken directions are either equal or close to zero.

Solution variants with the non-equal numbers of pieces in the predefined directions

To increase the research capabilities, the eTOP package was expanded by adding the possibility of determining the optimal numbers of orbital pieces in the radial- along- and cross-track directions, provided that the RMS value of the fit of the estimated orbit to the reference orbit is minimized. This process was realized using procedures including closed loops with the possibility of determining the area of searching for the optimal set of numbers of orbital pieces. Basically, this option finds equal numbers of pieces in given three directions. However, this software was also designed for searching non-equal numbers of pieces starting from the obtained equal numbers of pieces in all directions. The equal numbers of pieces for the optimal solution are additionally modified to find a better value of RMS in the defined area of search. This obviously leads to a change in the number of estimated parameters. Table 8 presents sample solutions for non-equal numbers of pieces compared to corresponding solutions with equal numbers of pieces. It is seen that in presented cases, the modification of numbers of pieces gives only slightly better solutions. The resulting RMS decreases from 0.02 mm (second-order polynomial accelerations for 90-min arc) to 0.04 mm (piecewise constant accelerations for 90-min arc). The similar values were obtained for other (not shown here) solutions. It shows that the estimated orbits are not too sensitive for the introduction of different numbers of pieces in the particular directions.

Table 8 Solutions with the non-equal numbers of pieces in the radial- along- and cross-track direction w.r.t. solutions with equal numbers of pieces in the aforementioned directions
Full size table

Summary, conclusions and perspectives

Various variants of the piecewise acceleration modeling of the GOCE satellite orbit were numerically tested. Using the dedicated extended TOP software, the initial conditions and the piecewise orbital parameters were estimated in the least squares sense for the best fit of the estimated orbit to the reduced-dynamic PSO orbit of the GOCE satellite, which the Cartesian coordinates served as the pseudo-observations. The parameters were estimated in successive intervals (pieces) into which the orbital arcs were divided. The optimal numbers of pieces for the modeling variants were obtained by the sequence of adjustments with a changing number of pieces until the minimization of the resulting RMS of fit value in a closed-loop environment. In the orbit modeling process, the piecewise accelerations were described by polynomials with respect to the normalized time of arc. The coefficients of these polynomials were estimated as the orbital parameters. In particular, for the zero-order polynomial, the estimated parameters were also pseudo-stochastic piecewise constant accelerations. The solutions were basically determined for equal numbers of orbital pieces in the radial- along- and cross-track directions. In some cases, the numbers of pieces in the given directions were changing, leading to obtaining the solutions with non-equal numbers of pieces. In all such cases, however, a slight increase in the numerical accuracy from 0.02 to 0.04 mm was observed.

Due to the centimeter-accuracy of the reference orbit, all obtained solution variants, characterized by the millimeter-level of the RMS of the fit, can be treated as equivalent. Therefore, taking into account the presented variants of solutions, e.g., for the 1-day arcs, the preferred solutions would be the solutions with the smaller number of estimated parameters, based on the estimation of piecewise accelerations using the second-order polynomials.

However, comparing the individual solution variants can be performed strictly numerically. Thus, it is possible to identify variants with the best numerical efficiency with, for example, the option of use for the orbit modeling of low satellites at a height close to the height of the GOCE satellite (at the level of 250 km). Such option is possible assuming that a better numerical efficiency of absorption of the differences between the a priori orbit and the reference orbit corresponds also to a better efficiency of absorption of deficiencies of the background models. This is possible because the background models were included in the estimation process of the aforementioned variants of solutions. The numerical efficiency of the adopted piecewise acceleration modeling can be presented on the example of the solutions for the ten 1-day arcs, after its application, the RMS of fit decreased from 1.72 to 2.92 m (only IC estimation) to 2.0–4.0 mm (estimation of IC and the parameters for the piecewise acceleration modeling).

The obtained results in terms of numerical accuracy indicate that the preferred solutions for the one-day arcs are associated with the use of zero- and first-order polynomials for the computation of piecewise accelerations.

Additionally, the numerical tests were also performed for the arcs with the lengths less than one day. In all five groups of tested arcs with different lengths, resulting from the division of the five aforementioned 1-day arcs, similar patterns concerning the numerical efficiency of solutions have been obtained. For the case of arcs with the lengths of 90.0, 180.0, 360.0 and 720.0 min, the best numerical accuracy was obtained when piecewise accelerations were determined using zero- and first-order polynomials. For arcs with the lengths of 1.0, 5.0, 10.0, 22.5 and 45.0 min, the better numerical accuracy was obtained for variants of solutions based on determining piecewise accelerations with the second- third- and fourth-order polynomials, which means that these degrees of the polynomial are preferred in the group of tested arcs with the shortest lengths.

The mentioned differences in the preferences of polynomial degrees depending on the length of the arcs are related to a numerical determinability of the coefficients of these polynomials. In the case of shorter arcs, the limitation of determinability of the coefficients of the zero- and first-order polynomials is greater (in the sense of obtained numerical accuracy) than in the case of the coefficients of the second- third- and fourth-order polynomials. The situation is reversed for the longer arcs—the limitation of determinability is greater for the second- and higher-order polynomials. The limitation of determinability occurs when there is a numerical instability of a given solution variant, related to the insufficient conditioning of the normal matrix.

In some cases, a certain asymmetry of the solutions was observed, namely the RMS value for the along-track direction is clearly greater than the RMS values for the other two directions, which remain at the level from tenths of millimeter to about one millimeter. The difference is even one order of magnitude. This indicates a difficulty and some challenge when it comes to modeling the orbit for the along-track direction. Moreover, it is known that the perturbations of the GOCE orbit in this direction were associated in particular with the compensation of the atmospheric drag force, which was significant in such a low orbit. It is possible that some residual drag force is manifested by higher RMS values in the along-track direction.

At this point, a question can be asked whether the presented results can to some extent correspond to the results obtained in the case of using real observations in the process of determining the orbit, and not pseudo-observations? It seems that to some extent, yes, because the pseudo-observations used in this work are also determined on the basis of real GPS code-phase measurements, the errors of which are in some way present in the aforementioned pseudo-observations.

In order to further improve the efficiency of piecewise accelerations of fitting the estimated 1-day orbits to the pseudo-observations, taking into account the results obtained for short arcs, especially when using the fourth-order polynomial, it might be reasonable to perform the aforementioned fitting as a sequence of piecewise adjustments of short arcs of an appropriate length.