Terrestrial water storage variations and their effect on polar motion

Abstract

The role of continental water in polar motion excitation can be illustrated by determining Hydrological Angular Momentum calculated from terrestrial water storage (TWS). In this paper we compare global and regional changes in TWS computed using Coupled Model Intercomparison Project Phase 5 climate models, Global Land Data Assimilation System (GLDAS) land hydrology models and observations from the Gravity Recovery and Climate Experiment (GRACE) satellite mission. We also compare hydrological excitation functions derived from models with those obtained from the GRACE mission and the hydrological signal in observed polar motion excitation (the so-called geodetic residuals). The results confirm that GLDAS models of seasonal and non-seasonal TWS change are more consistent with GRACE data than climate models; on the other hand, none of the considered models are fully consistent with GRACE data or geodetic residuals. In turn, GRACE observations are most consistent with the non-seasonal hydrological signal in observed excitation. A detailed study of the contribution of different TWS components to the hydrological excitation function shows that soil moisture dominates.

Introduction

Earth’s rotation parameters, including polar motion and length of day variation, have been investigated for several decades (Munk and MacDonald 1960). Its rotation axis is represented by x, y coordinates that are referred to the terrestrial reference frame. These coordinates are characterized by two components: The Chandler wobble—a free oscillation with a period of about 435 days—and seasonal changes created by continuous angular momentum exchange between the solid Earth and geophysical fluids, including the atmosphere, ocean and land hydrosphere (Lambeck 1980).

Variation in polar motion observed by geodetic techniques can be described by equatorial components χ₁ and χ₂ of Geodetic Angular Momentum (GAM), which can be determined using x, y measurements (Eubanks 1993). Geophysical excitation functions describe external transfers of angular momentum from geophysical fluids to the solid Earth. The ΔC₂₁ and ΔS₂₁ coefficients of Earth’s gravity field are proportional to χ₁ and χ₂ components of the polar motion excitation function (Chen and Wilson 2008).

Variability in the Earth’s rotation is caused by the external, gravitational influence of the Moon, the Sun and the planets together with variation in the distribution of the masses of Earth’s surficial fluids. The inner and outer cores are also important contributors to polar motion. Recent work (e.g. Kuang et al. 2017) has shown that strong polar motion on decadal timescales, including the ~ 30-year Markowitz wobble, may be excited by the fluid outer core through electromagnetic core–mantle coupling. Additionally, the rotation of the inner core, which is flattened and tilted with respect to the outer core and mantle, could also have an impact on the direction of Earth’s rotation on these timescales (Dumberry and Bloxham 2002; Greiner-Mai and Barthelmes 2001).

Geophysical polar motion excitation functions describe the impact of non-tidal changes in Earth’s surficial fluids on polar motion variation. However, despite the numerous geophysical models that describe these fluid layers, the agreement between geophysical and geodetic excitation is still not satisfactory, and the results vary from one model to another. Current models differ in terms of the number of parameters, detail in the process representation, meteorological model forcing data, algorithms, and temporal and spatial resolution (Güntner 2008). They are also characterized by different numbers and depths of soil layers, as well as different numbers and heights of pressure levels. Sources of uncertainties include, among others, the lack of adequate observations at large spatial scales, unrealistic simulations of some variables and the lack of some water storage components.

The major contributor to non-tidal rotation is variation in the global balance of Earth’s angular momentum due to mass redistribution of geophysical fluids. These changes are described as Atmospheric Angular Momentum (AAM), Oceanic Angular Momentum (OAM) and Hydrological Angular Momentum (HAM). The impact of AAM and OAM is well established following extensive research in recent years (Brzeziński et al. 2005, 2009; Gross et al. 2003; Nastula and Ponte 1999; Nastula et al. 2007). Many papers have confirmed that the principal drivers of polar motion, over periods of up to several years, are changes in AAM and OAM. A number of regional analyses have further improved our understanding (Nastula 1997; Nastula et al. 2000, 2009).

However, despite numerous studies, variation in polar motion observed by geodetic techniques has not been fully explained (Brzeziński et al. 2005; Nastula and Ponte 1999; Ponte et al. 1998). At seasonal scales, HAM is thought to be a main contributor and the land hydrosphere is known to play a far more significant role than OAM. At interannual and shorter timescales, several studies have shown that both atmosphere and land hydrosphere have a major impact (Chen et al. 2012; Gross et al. 2003). At decadal and longer scales, the situation is less clear (Gross et al. 2005; Nastula et al. 2011). Despite many studies of the impact of HAM, its role is still not fully understood (Chen et al. 2000; Jin et al. 2010, 2012; Meyrath and van Dam 2016; Nastula et al. 2008, 2011; Seoane et al. 2011; Winska et al. 2016, 2017). An assessment of the contribution of continental water to polar motion is difficult due to the lack of precise, global water measurements. Land hydrology models used in earlier work have resulted in different amplitudes and phases (Chen and Wilson 2005; Nastula et al. 2011). This is unsurprising, as terrestrial water storage (TWS) has not been adequately measured at the continental scale (Lettenmaier and Famiglietti 2006). In recent years, HAM estimates have been based on observations of the time-varying gravity field provided by the GRACE (Gravity Recovery and Climate Experiment) mission (Brzeziński et al. 2009; Chen and Wilson 2005), while other studies have used different land hydrosphere models (Jin et al. 2012).

In this context, there is a need for an in-depth analysis of TWS distribution over land. TWS is defined as all forms of water stored on the Earth’s surface, including surface water, soil moisture, groundwater, vegetation, snow, ice and permafrost. It is not only a component of the global water cycle and an issue in climate change (Famiglietti 2004), but also affects polar motion (Chao and O’Connor 1988). Changes in TWS can be estimated from observations of Earth’s gravity field provided by the GRACE mission’s twin satellites. This mission offered an unprecedented view of global variation in TWS and was a new opportunity to study hydrological excitation. From 2002 to 2017, GRACE provided temporal observations of change in Earth’s gravity field related to mass redistribution.

As noted above, ΔC₂₁ and ΔS₂₁ coefficients are proportional to χ₁ and χ₂ components of the polar motion excitation function. After removing mass effects of the atmosphere and ocean, together with postglacial rebound, the remaining signal (on monthly to interannual timescales) is an indication of TWS variation. This estimation can then be compared with the mass term of geophysical excitation. With a spatial resolution of a few hundred kilometres and monthly temporal resolution, GRACE is thought to be able to monitor TWS changes to an accuracy of 1 cm (Dahle et al. 2014). The extension of the mission—GRACE Follow-On—was launched in May 2018 and will provide new observations with similar or even better accuracy.

Another TWS estimation method is the use of state and flux parameters that determine water content on land. These parameters are available as individual variables in climate or land hydrosphere models. The Global Land Data Assimilation System (GLDAS) provides several examples (Fang et al. 2008). GLDAS land surface variables are the result of integrating satellite and ground-based observations using various data assimilation techniques and advanced land surface modelling (Rodell et al. 2004). An alternative to the GLDAS data set are models provided by the World Climate Research Programme’s Coupled Model Intercomparison Project Phase 5 (CMIP5). The project studies global warming and assesses past, present and future climate change (Taylor et al. 2012). The project’s models provide numerous parameters that describe processes in the atmosphere, oceans and land hydrosphere. CMIP5 simulations may be helpful in understanding variations in Earth’s rotation under climate change. Contemporary climate change, accompanied by accelerated ice loss and associated sea level rise, as well as changes in the amount of water held within continents influence polar motion. A recent paper (Adhikari and Ivins 2016) has shown that the visible deviation in polar motion drift observed since 2000 is probably caused by climate-induced mass redistribution. The Greenland and Antarctic Ice Sheet mass losses were the predominant cause of the last shift of Earth’s pole. Nevertheless, changes in global water cycle intensity, resulting from droughts and heavy rains in certain parts of the globe, are other important contributors.

In recent years there have been many attempts to assess change in TWS and its impact on polar excitation. Global and regional analyses have been derived from GRACE observations (Humphrey et al. 2016; Hassan and Jin 2016; Landerer and Swenson 2012). Other papers have validated land hydrosphere models based on GRACE data (Zhang et al. 2016, 2017). Although the influence of the land hydrosphere on polar motion excitation has been repeatedly investigated, most studies have focused on HAM functions derived from GRACE observations (Meyrath and van Dam 2016; Seoane et al. 2011). This paper addresses this gap; the hydrological contribution to polar motion excitation is computed from data from multiple sources: climate (CMIP5) and hydrological (GLDAS) models, and GRACE observations.

The determination of the impact of land hydrology on polar motion excitation is an important application of GRACE observations in the present-day geodesy (Nastula et al. 2011; Winska et al. 2016, 2017). However, quantifying the contribution of continental water to polar motion remains a challenge due to a lack of precise TWS measurements. Current hydrological models contain significant uncertainties due to a lack of in situ data. At the same time, although GRACE satellites can measure TWS variation, spatial resolution is low. Nevertheless, GRACE measurements are more consistent with observed geodetic excitation than either land hydrosphere or climate models. While the latter models can optimize parameters describing processes affecting the global water cycle, not all of them are useful in determining hydrological excitation.

Here, we compare TWS estimations from various data sources and examine the impact on polar motion excitation functions. Specifically, we present the results of a comparison of TWS estimates based on GRACE observations, four GLDAS models (NOAH, MOSAIC, VIC and CLM) and two CMIP5 climate models (MPI-ESM-LR and MIROC5) at seasonal and non-seasonal timescales. It should be noted that these models differ from each other in terms of assimilation algorithms and input data. Moreover, they have been developed for different purposes and specific regions. This comparison of TWS and HAM estimations attempts to answer the following questions: (i) Which GLDAS and CMIP5 models correlate best with GRACE data, both in terms of TWS and polar motion excitation; (ii) which model correlates best with observed polar motion; and (iii) which TWS components contribute the most to hydrological excitation functions. Analyses are divided into a comparison of TWS time series based on data from multiple sources and a comparison of hydrological excitation functions (determined from climate and hydrological models, and GRACE observations) with observed geodetic excitation. “Data” section presents a detailed description of the data. “Analysis and results” section describes the results. Finally, a summary and some conclusions are given in “Conclusions” section.

Data

Methodology

TWS variation was determined by summing regional changes. Data sources are presented in Table 6 (Appendix 1), and they include both GRACE observations and climate and hydrosphere models. The calculation of changes in TWS (Δq) from GRACE observations uses spherical harmonics coefficients of Earth’s gravity field (Wahr et al. 1998) as shown below:

$$\Delta q\left( {\lambda ,\phi } \right) = \frac{{\Delta \bar{\sigma }\left( {\lambda ,\phi } \right)}}{{\rho_{w} }}$$

(1)

$$\Delta \bar{\sigma }\left( {\lambda ,\phi } \right) = \frac{{2\pi a\rho_{\text{ave}} }}{3}\mathop \sum \limits_{l = 0}^{L} \frac{2l + 1}{{1 + k_{l} }}W_{l} \mathop \sum \limits_{m = 0}^{l} \bar{P}_{\text{lm}} \left( {\sin \phi } \right) \cdot \left( {\Delta \bar{c}_{\text{lm}} \cos \left( {m\lambda } \right) + \Delta \bar{s}_{\text{lm}} \sin \left( {m\lambda } \right)} \right)$$

(2)

where a is the mean radius of Earth, ρ_ave and ρ_w are the average density of the Earth and the water, respectively, W_l is a Gaussian averaging kernel (Wahr et al. 1998), $\bar{P}_{\text{lm}}$ is a normalized associated Legendre function, and $\bar{c}_{\text{lm}}$ and $\bar{s}_{\text{lm}}$ are normalized and dimensionless Stokes coefficients.

It should be noted here that there is a significant difference between TWS designated from GRACE observations and TWS based on variables from numerical models (Yang et al. 2013; Chen et al. 2016). While all land surface models provide changes of water storage in layers with specific thickness and depth, GRACE measures total changes in terrestrial water in all its components. Nevertheless, the GRACE satellites are not able to reconcile these individual parameters (Famiglietti and Rodell 2007).

TWS both for GLDAS hydrological models and for CMIP5 climate models was computed as follows:

$$\left( {\text{TWS}} \right)_{n} = \left( {{\text{SM}}_{n} + {\text{AS}}_{n} } \right)$$

(3)

where n is the number of epochs (months), SM is soil moisture (summed for all layers), and AS is snow water equivalent. However, TWS also includes water in biomass, surface water, groundwater and glaciers that are not simulated either in CMIP5 or in GLDAS models.

The GLDAS-2 documentation recommends that users include SM, AS and plant canopy surface water (Rui and Beaudoing 2018). Although GLDAS models provide all three components, CMIP5 only provides the first two; consequently, our estimation only included SM and AS. We introduced the variable mrso, which represents monthly averaged SM in all phases summed over all soil layers of the model and averaged over each grid cell. For AS, we used the variable snw, which is also summed over all snow layers and averaged over grids.

Another issue is groundwater, which is not taken into account here. Typically, groundwater variation is determined by subtracting SM and AS from GRACE-based TWS (Chen et al. 2016; Jin and Feng 2013; Rzepecka et al. 2017). However, Lawrence et al. (2011) report that global seasonal variation is relatively low compared to SM and AS. In addition, it has been found to affect interannual rather than seasonal TWS variability (Güntner et al. 2007).

Monthly change in TWS (ΔTWS_n) can either be obtained as the difference between current and previous TWS values or from flux variables (precipitation P; evaporation E; and total surface runoff R) as follows:

$$\Delta {\text{TWS}}_{n} = \, P_{n} - E_{n} - R_{n}$$

(4)

Winska et al. (2017) examined differences between hydrological excitation functions (HAM) computed from TWS state (Eq. 3) and flux (Eq. 4) parameters. This study showed that the use of SM and AS agrees better with both GRACE and hydrological signals in observed polar motion excitation than applying Eq. 4.

GRACE observations

Observations of change in water content over land areas by GRACE satellites are provided in the form of monthly grids of mass anomalies based on time-variable gravity data relative to a time-mean baseline. Three major data centres have computed Stokes coefficients as well as adequate water storage layer: the Centre for Space Research (CSR), the Jet Propulsion Laboratory (JPL) and GeoForschungsZentrum (GFZ). In addition, there are many other scientific institutes, including Tongji University, Wuhan University and others, that developed time series of Earth’s gravity field coefficients known as GRACE Level-2 data. However, this research draws upon GRACE Level-3 products in the form of monthly land mass grids provided by the NASA MEaSUREs Program (Swenson and Wahr 2006) and available from the Jet Propulsion Laboratory website (GRACE Tellus, http://grace.jpl.nasa.gov). These solutions (CSR RL05, JPL RL05 and GFZ RL05) have grid resolution of 1° and time resolution of one month and contain current surface mass change in equivalent water height units (centimetres) processed by Swenson (Landerer and Swenson 2012; Swenson and Wahr 2006). Two filters are applied: a destriping filter to minimize the effect of North–South stripes in monthly maps and a 300-km-wide Gaussian filter for signal noise reduction. A glacial isostatic adjustment was also applied. The GRACE data set records TWS anomalies relative to the 2004.0–2009.9 time-mean baseline.

Because the uncertainty in C₂₀ (degree 2 order 0) is higher for values obtained from GRACE data compared to satellite laser ranging (SLR) observations, C₂₀ coefficients are replaced with SLR solutions. GRACE satellites are unable to measure degree-1 terms that are proportional to the position of the geocentre in relation to the Earth-fixed reference frame. The distance between the centre of the Earth’s mass and the centre of the Earth’s figure can be obtained either from SLR observations, or through a combination of GRACE data and the output of ocean models. In the GRACE Level-3 data products that are used in this study, degree-1 coefficients were estimated on the basis of the second method. A detailed description of the algorithm can be found in Swenson et al. (2008). GRACE coefficients for degrees 2 and higher from the CSR Release-05 solution, together with two oceanic models, JPL ECCO (Gross et al. 2003; Stammer et al. 2002) and OMCT (Thomas 2002), were used. The set of degree-1 coefficients computed in this manner can be obtained from ftp://podaac.jpl.nasa.gov/allData/tellus/L2/degree_1/. It should be noted here that all oceanic models are relative to the centre-of-figure (CF) frame, while GRACE satellites use the centre-of-mass (CM) frame. The CM and CF frames are related to one another by translation, and they are characterized by different values of the Love number k₁ (Swenson et al. 2008). It is therefore essential when comparing GRACE measurements and models to ensure that each type of data is related to the same reference frame. Swenson et al. (2008) discussed this issue when presenting their procedure to determine degree-1 coefficients.

TWS variation is attenuated by postprocessing, filtering and truncation of spherical harmonics up to d/o 60. It was therefore necessary to apply appropriate scale factors (Landerer and Swenson 2012). Scaling coefficients, organized in the form of a grid, are available from http://grace.jpl.nasa.gov. The scaling grid is the same size as TWS land mass grids and, in our study, every TWS time series was multiplied by the scaling coefficient at the same position. Finally, recent work (e.g. Sakumura et al. 2014) has found that the mean of CSR, JPL and GFZ solutions is an effective noise reduction method for GRACE observations, and this was also used in our research.

GLDAS models

GLDAS was developed by the National Aeronautics and Space Administration’s (NASA) Goddard Space Flight Centre. The United States National Oceanic and Atmospheric Administration’s National Centre for Environmental Prediction (NCEP) provides optimized land surface and flux variables. These products are essential for modelling the water cycle, atmospheric circulation, weather forecasting and studying climate change (Fang et al. 2008).

The integration of ground-based and satellite observations, and the development of advanced land surface modelling and data assimilation techniques have resulted in global models with a time resolution of one month, 1° × 1° latitude–longitude grid and data from January 1979 to the present (Rui and Beaudoing 2018; Rodell et al. 2004).

GLDAS land hydrology models contain state (SM, AS and canopy surface water) and flux variables (rainfall rate, evaporation and runoff) that can be used to calculate (change in) TWS. These models have been a valuable source of information for a number of global-scale GRACE investigations (Chen et al. 2005; Syed et al. 2008). Four GLDAS models have been developed: NOAH (Ek et al. 2003; Rodell and Beaudoing 2013), Variable Infiltration Capacity (VIC) (Rodell and Beaudoing 2007a), MOSAIC (Suarez et al. 2005; Rodell and Beaudoing 2007b) and the Community Land Model (CLM) (Dai et al. 2003; Oleson et al. 2010; Rodell and Beaudoing 2007c). This paper uses data from these four models covering the period from January 2003 to December 2015. Each has a spatial resolution of 1° and time resolution of 1 month. Data are available at https://mirador.gsfc.nasa.gov.

CMIP5 models

The aim of the CMIP5 project was to study the climate in the context of global warming, assess past climate evolution and predict future weather changes (Taylor et al. 2012). Among more than 50 models developed by about 20 scientific institutions, some have analysed long-term or decadal climate change. Others simulate future changes or analyse historical ones. They contain a series of variables that describe the processes taking place in the atmosphere, oceans and land hydrosphere and differ in terms of their spatial and temporal resolution, the number and type of variables, and methods.

Geodetic residuals computation

Geodetic residuals (GAOs) are the difference between observed GAM and the sum of AAM and OAM, as follows:

$${\text{GAO}} = {\text{GAM}}{-}{\text{AAM}}{-}{\text{OAM}}$$

(5)

GAM functions are available from the International Earth Rotation and Reference Systems Service (IERS) website. These time series include equatorial components of observed polar motion excitation χ₁ and χ₂ that are calculated from daily combined C04 series of Earth orientation parameters derived from GNSS, SLR and VLBI, fully consistent with the International Terrestrial Reference Frame 2014 and updated on a regular basis (Bizouard and Gambis 2017). In this study, observed polar motion excitations were computed from C04 series using IERS online tool (http://hpiers.obspm.fr/eop-pc/index.php?index=excitactive&lang=en).

HAM and GAO comparisons have been the subject of other studies (Jin et al. 2010, 2012; Nastula et al. 2011; Winska et al. 2016, 2017). In contrast to these earlier papers, in this study we use several atmospheric and oceanic models to determine GAO. Various combinations of AAM and OAM models led to four GAO determinations, presented in Table 1. In subsequent analyses we used mean GAOs. Consequently, the resulting hydrological signal, taken as our reference for HAM functions, differs from the work cited above.

Table 1 Geodetic residuals used for the analyses

AAM and OAM have been computed from various models. Here, we use three AAM models: (i) the National Centre for Environmental Prospect/National Centre for Atmospheric Research (NCEP/NCAR) reanalysis model, which is provided by the Sub-bureau for Atmosphere of the Global Geophysical Fluid Centre (GGFC) (Salstein et al. 1993); (ii) effective AAM time series obtained from GFZ and calculated from 6-hourly ECMWF (European Centre for Medium-range Weather Forecasts) operational atmospheric forcing data (Dobslaw et al. 2010); and (iii) AAM obtained from the operational analysis of the ECMWF provided by Technische Universität Wien (TU Wien). These time series are official products of the IERS, and here they are referred to as ECMWF TU Wien.

We also used three OAM models: (i) effective OAM functions calculated from the 6-hourly Max Planck Institute Ocean Model (MPIOM) (Thomas 2002) provided by the GFZ—here called MPIOM GFZ; and (ii) two ECCO models (ECCO kf079 and ECCO kf080) obtained from the IERS Special Bureau for the Oceans and developed by JPL researchers during their participation in the Estimating the Circulation and Climate of the Ocean (ECCO) consortium (Gross et al. 2003; Stammer et al. 2002). The ECCO kf80 model includes altimetry observations of sea surface heights, while ECCO kf079 was computed without data assimilation.

It should be noted that when different AAM and OAM models are combined, consistency must be maintained between oceanic and atmospheric excitations. Therefore, only OAM forced by the same atmosphere model that was used to compute the AAM should be added to the AAM. ECCO_kf079 and ECCO_kf080 models from the JPL are forced by surface wind stress, surface heat flux and surface freshwater flux from the NCEP/NCAR reanalysis (Gross et al. 2003). Consequently, to maintain the mass balance, OAM models from the JPL can only be combined with AAM derived from NCEP/NCAR. As far as the MPIOM ocean model is concerned, it is forced with atmospheric surface pressure, wind stress, temperature, incoming solar radiation and precipitation from the ECMWF model (Thomas 2002). OAM from the MPIOM should be therefore added only to the ECMWF AAM. As shown in Table 1, GAO1, GAO2 and GAO3 are consistent, while GAO4 does not maintain the mass balance. However, differences remain between all geodetic residuals, and finally, we decided to use the mean of GAO1–GAO4 in subsequent analyses.

It should be mentioned here that AAM from the ECMWF TU Wien and ECMWF GFZ are based on the same atmospheric model. They differ in that excitations provided by the GFZ are in the form of χ₁ and χ₂ components of mass and motion terms of atmospheric excitation, while AAM functions based on the solution from TU Wien are available in the form of Earth’s inertia tensor (c₁₃, c₂₃ and c₃₃) components and relative angular momentum. Other differences concern the temporal resolution: three hours for ECMWF GFZ and six hours for ECMWF TU Wien.

Another issue concerns whether or not the atmospheric model includes the inverted barometer (IB) assumption and whether or not the oceanic model is forced by atmospheric pressure. It is important to ensure that the effect of atmospheric pressure variations is not included twice. The NCEP/NCAR reanalysis includes the IB response of the ocean to the overlying atmospheric pressure. For the ECMWF GFZ model, the IB correction was applied over ocean regions (Dobslaw and Dill 2017). For ECMWF TU Wien data, we adopted mass terms with IB assumptions. As far as oceanic models are concerned, ECCO kf079 and kf080 ocean models are not forced by surface pressure. To ensure consistency between the MPIOM ocean model and the Atmospheric Angular Momentum function, the inverse IB correction was applied over oceans.

GAO (computed using (3)) should give the impact of the land hydrosphere on polar motion excitation. However, it should be noted that they contain unmodelled signals from change in the mass of ice sheets or the effects of earthquakes (Naito et al. 2000; Zhou et al. 2005). As a result, they do not describe hydrological signals exactly. Further studies should focus on improving AAM and OAM estimations of these functions, especially motion terms. Nevertheless, comparing hydrological excitation with GAO is commonly used to assess the influence of the land hydrosphere on polar motion.

Analysis and results

In “CMIP models” section we compare TWS series from ten CMIP5 models with GRACE observations in order to determine the best ones to use in further analyses. “Comparisons of TWS time series” section presents the results of the analysis of TWS time series computed from all data sources (GRACE, GLDAS and the selected CMIP5 models). “Comparison of HAM and GAO” section outlines the results of comparing hydrological excitation (HAM) functions with GAO. “Contribution of TWS components to HAM” section compares HAM functions based on TWS computed from different components (SM, AS and sum of these two parameters).

CMIP models

Several papers have compared CMIP climate models and GRACE observations (e.g. Freedman et al. 2014; Wu et al. 2015; Zhang et al. 2015, 2017). These studies have shown that SM determinations are very different, both in terms of the number and depth of soil layers and in terms of the complexity of the model. Some have resulted in unrealistic TWS variations that are out of phase with the real water cycle. It is therefore necessary to select carefully climate models. We addressed this problem by determining correlation coefficients and explained variance for TWS series computed from CMIP and those based on GRACE observations (Table 2). The critical value of the correlation coefficient was 0.75 for a significance level α equal to 0.05. Variance in GRACE TWS series explained by CMIP5 models was computed using the following formula:

Table 2 Correlation coefficients between TWS series obtained from CMIP5 models and GRACE and percentage of relative variance in GRACE TWS series explained by CMIP5

$${\text{Var exp}} = \left( {\frac{{{\text{Var}}^{\text{TWS GRACE}} - {\text{Var}}^{{\left( {{\text{TWS GRACE}} - {\text{TWS model}}} \right)}} }}{{{\text{Var}}^{\text{TWS GRACE}} }}} \right) \cdot 100{\text{\% }}$$

(6)

Relative explained variance describes the amplitude agreement between TWS series obtained from GRACE observations and TWS data computed from models. The best compatibility between series (explained variance is equal to 100%) occurs when differences between GRACE-based and modelled TWS are the same for all time series points. (The variance of the difference is equal to zero.) Relative explained variance can be negative if the variance of differences (Var^{(TWS GRACE˗TWS model)}) between TWS from GRACE observations and from the model is higher than TWS GRACE variance. This can occur in two situations: (1) when Var^{(TWS model)} is much higher than Var^{(TWS GRACE)}; or when (2) Var^{(TWS model)} is much lower than Var^{(TWS GRACE)}. However, it should be noted that despite the poor amplitude agreement (low relative explained variance) between series, the correlation may be high, indicating good phase agreement between series.

Table 2 shows that the best agreement was obtained from CNRM-CM5, GISS-E2-H, MIROC5 and MPI-ESM-LR, with correlations above 0.80. Similar results were obtained by Wu et al. (2015). Two models were chosen for further analyses: MPI-ESM-LR and MIROC5. These were distinguished by their agreement with GRACE time series (correlation coefficients above 0.84 and relative explained variance above 63%).

Comparisons of TWS time series

While many attempts have been made to validate global and regional seasonal changes in TWS based on models and GRACE observations (e.g. Chen et al. 2009; Freedman et al. 2014; Hassan and Jin 2016; Syed et al. 2008; Tangdamrongsub et al. 2016; Zhang et al. 2015, 2016), non-seasonal time bands have not been taken into account. Here, we present seasonal and non-seasonal analyses. Seasonal oscillations are calculated using the least squares method. The fitted model included the second-order polynomial and sum of sinusoids with periods of 365.25, 182.625 and 121.75 days. Non-seasonal changes were obtained after removing annual, semiannual and terannual signals.

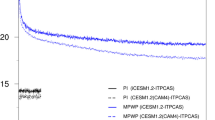
Figure 1 presents a comparison of seasonal TWS variation for GRACE data, and GLDAS and CMIP5 models. The values of amplitudes, and phases of annual, semiannual and terannual TWS oscillations are also included in Table 7 (Appendix 3). All time series are dominated by annual oscillations (note that the scale in the top-left diagram is different to the others). Here, there is good agreement in amplitude between all models. These results are consistent with regional patterns (Appendix 2). However, phase correspondence is poor. With respect to semiannual and terannual changes, all climatic and hydrological models have bigger amplitudes than GRACE observations. Surprisingly, annual CLM oscillations are smallest, while terannual oscillations are biggest. Furthermore, oscillations in this model have the highest phase difference and lowest amplitude compared to GRACE observations.

Fig. 1

Phasor diagrams of seasonal (annual, semiannual and terannual) TWS change derived from GRACE data (mean of CSR, JPL and GFZ), GLDAS models (NOAH, MOSAIC, VIC and CLM) and CMIP5 climate models (MPI-ESM-LR and MIROC5). The analysis concerns the period 2003.0–2016.0. The reference epoch is January 1, 2003

Non-seasonal change is compared in Fig. 2. The results suggest that there is no clear agreement between these models and satellite gravimetry observations. In terms of amplitude, CLM is lower than GRACE and other models, but VIC and MOSAIC are higher. The latter two models agree closely in terms of amplitude and phase. Although the remaining models (NOAH, MIROC5 and MPI-ESM-LR) are more consistent with GRACE, phase compatibility is poor. Among them, the NOAH model is most consistent with GRACE data.

Fig. 2

Comparison of non-seasonal TWS time series based on GRACE data (mean of CSR, JPL and GFZ) with GLDAS (top panel) and CMIP5 models (bottom panel). Units are given in centimetres per one land grid

It should be noted that GLDAS models also contain, apart from terrestrial data, a number of satellite observations. Satellite-based hydrological products that were integrated with ground-based models and observations include: snow cover, water equivalent, surface temperature, soil moisture and leaf area index (Rodell et al. 2004). This may be the main reason for the fact that the CMIP5 simulation, which does not contain satellite data, is less consistent with GRACE observations. Moreover, TWS anomalies provided by GLDAS models are commonly used to determine the scaling factors that have to be applied in GRACE Level-3 products. For this reason, there is a relationship between GLDAS and GRACE. Scaling coefficients are needed in order to reduce signal attenuation and leakage errors that arise from the application of GRACE postprocessing filters. A detailed description of the gain factor determination from the NOAH model can be found in Landerer and Swenson (2012). Since the output of the GLDAS-NOAH model has been used in the determination of gain factors in GRACE Tellus data (https://grace.jpl.nasa.gov/), other hydrological models (MOSAIC, VIC and CLM) may be less consistent with GRACE observations.

It is clear that seasonal agreement between GRACE observations and individual models is much better than non-seasonal agreement because the former is sinusoid; consequently, this type of analysis may seem meaningless. However, differences remain and lower correlation coefficients may be caused by a phase shift of one series relative to another. For an objective assessment of the correlation, we determined the critical value of correlation coefficients for both seasonal and non-seasonal oscillations using the autocorrelation function (which describes how a time series correlates with itself over different timescales). The number of independent points is a function of the degree of filtering. We estimated the number of independent points required for the autocorrelation function to drop to 1/e. Then, on the basis of the Student’s T test and an assumed significance level α equal to 0.05, we determined the critical value of the correlation coefficient. For non-seasonal oscillations, the analysis found that 15 independent points corresponded to a critical correlation value of 0.48. In comparison, the number of independent points and the correlation coefficient for seasonal variation were 5 and 0.75, respectively.

Seasonal correlation coefficients are high for all GLDAS models: MOSAIC is highest (0.99) and CLM is lowest (0.81). Values are slightly lower for CMIP5 climate models, but still significant (0.83 and 0.93 for MPI-ESM-LR and MIROC5, respectively). With respect to non-seasonal change, only GLDAS-NOAH provides meaningful correlations with GRACE observations (0.69), while coefficients are close to zero for GLDAS-CLM and CMIP5-MPI-ESM-LR models.

In practice, analysis of variance is a more appropriate method than correlation coefficients, as it reflects amplitude correspondence between series. Therefore, we computed the percentage of relative explained variance for both seasonal and non-seasonal variations using (6) (Table 3).

Table 3 Correlation coefficients between TWS series obtained from models (GLDAS and CMIP5) and GRACE and percentage of variance in GRACE TWS series explained by GLDAS and CMIP5

The results for seasonal change indicate that MOSAIC and VIC models explain the biggest percentage of TWS variability derived from GRACE observations (88.93% and 76.85%, respectively). The worst results are obtained for both climate models (below 60%). On the other hand, only NOAH agrees significantly with GRACE observations for non-seasonal change (almost 34%). Values are negative for all other models, and they are particularly high for MOSAIC and VIC. Negative numbers indicate smaller TWS variation in GRACE observations than variance of differences between model and GRACE. These conclusions are confirmed by Fig. 10 (Appendix 2) that presents differences in variance between GRACE observations and all models. These analyses lead us to conclude that MOSAIC and VIC successfully model seasonal change, but none of the models accurately simulate non-seasonal oscillations. As noted above, a visual inspection of non-seasonal TWS time series (Fig. 2) confirms that MOSAIC and VIC are characterized by very high mutual correlation.

Climate models (MPI-ESM-LR and MIROC5) proved to be the least correlated with GRACE observations, especially for non-seasonal change. They also explain the smallest percentage of seasonal variance obtained from the mission’s observations. We therefore conclude that, generally, GLDAS performs better than CMIP5. For non-seasonal change, the most appropriate model is GLDAS-NOAH. However, any GLDAS model is better than MPI-ESM-LR or MIROC5.

Comparison of HAM and GAO

This section addresses the correspondence between TWS time series and the hydrological polar motion excitation function. Specifically, we examine all GLDAS models in order to determine whether the apparently better performance in terms of correlation and variance also extends to the HAM function. Given the poor performance of CMIP5, MPI-ESM-LR and MIROC5 were excluded from further analyses.

HAM functions were validated using a reference GAO data set computed from observations of polar motion (see “Geodetic residuals computation”). Here, we compare HAM time series based on TWS estimations with GAO obtained using the formula given in (5). The analysis examines variability, phasor diagrams, correlation coefficients and relative explained variance. Equatorial components of HAM functions are computed using TWS grids according to the formulas given below:

$$\chi_{1} = - \frac{{1.098R_{e}^{2} }}{C - A}{\iint }\Delta q\left( {\phi ,\lambda ,t} \right)\sin \phi \cos \phi \cos \lambda dS$$

(7)

$$\chi_{2} = - \frac{{1.098R_{e}^{2} }}{C - A}{\iint }\Delta q\left( {\phi ,\lambda ,t} \right)\sin \phi \cos \phi \sin \lambda dS,$$

(8)

where Δq(ϕ,λ,t) are changes in water storage (kg/m²), R_e is Earth’s mean radius, dS is the surface area, and C and A are Earth’s principal moments of inertia. The factor 1.098 accounts for the yielding of the solid Earth to surface load, rotational deformation and core–mantle decoupling (Eubanks 1993).

It is well known that GRACE data agree best with observed (GAO) hydrological excitation. Here, we investigate which land hydrology model is best correlated with both GRACE and GAO results. Specifically, we considered HAM functions based on GRACE observations (mean of CSR, JPL and GFZ solutions) and the four GLDAS models (NOAH, MOSAIC, VIC and CLM). The reference for this time series is mean GAO (Table 1). All time series were interpolated in 30 days steps from 2003.0 to 2016.0, and Gaussian smoothing was applied. Before separating seasonal and non-seasonal oscillations in all time series the linear trends were removed.

For seasonal HAM change, we analysed prograde and retrograde annual and semiannual oscillations using phasor diagrams (Fig. 3). Complex-valued components were computed using the least squares method (Brzeziński et al. 2009). The fitted model includes the second-order polynomial and the sum of complex sinusoids with periods of 365.25, 182.625 and 121.75 days. Phase φ of the oscillation is defined by the annual or semiannual term as sin(2π(t − t₀) + φ), where t₀ is a reference epoch (2003.0). The values of amplitudes and phases of prograde and retrograde annual and semiannual oscillations are also included in Tables 8 and 9 (Appendix 3). It was unsurprising to find that annual oscillations were stronger than semiannual ones. (Note that the scales of the top graphs and bottom graphs in Fig. 3 are different.) Figure 3 shows that, in general, GAO amplitudes are higher than those of HAM. GLDAS models are more comparable with GAO for semiannual changes. Here again, the CLM model is distinguished by the smallest amplitudes (except for the retrograde annual term) and the least phase agreement with both GRACE and GAO.

Fig. 3

Phasor diagrams of prograde and retrograde seasonal (annual and semiannual) variation in χ₁ + iχ₂ for geodetic residuals (GAOs) and HAM functions calculated from GRACE data (mean of CSR, JPL and GFZ solutions) and GLDAS (NOAH, MOSAIC, VIC and CLM) models. The analysis was performed over the period 2003.0–2016.0. The reference epoch is 2003.0

Figure 4 shows non-seasonal change in χ₁ and χ₂ computed using TWS from GRACE observations and GLDAS models (Eqs. 7, 8). To facilitate comparison, these plots also show GAO. Non-seasonal changes are estimated by extracting trends and seasonal (sum of annual, semiannual and terannual) oscillations from global time series.

Fig. 4

Comparison of equatorial components (χ₁ and χ₂) of non-seasonal change in geodetic residuals (GAOs) with HAM functions derived from GRACE data (mean of CSR, JPL and GFZ solutions) and GLDAS models (NOAH, MOSAIC, VIC and CLM)

The results indicate that for all considered time series, non-seasonal oscillations are stronger for the χ₂ component. Earlier work has confirmed the apparently poorer results for χ₁ (Winska et al. 2016; Meyrath and van Dam 2016). This finding can be explained by the fact that χ₂ plays a more significant role in polar motion than χ₁. The former is more sensitive to changes in mass over land as it is the result of land and ocean distribution on Earth (Eubanks 1993; Chen et al. 2012). While the y coordinate is more sensitive to mass change over continents, x is more responsive to mass change over oceans.

A visual inspection of Fig. 4 confirms that GRACE observations agree best with GAO. Similar conclusions have been drawn by other authors for seasonal plus non-seasonal (Nastula et al. 2011; Winska et al. 2016, 2017), non-seasonal (Winska et al. 2017), seasonal (Winska et al. 2017) and interannual (Meyrath and van Dam 2016) hydrological polar motion excitations. However, none of the HAM functions derived from GLDAS models fully explain GAO. Our analysis suggests that the GLDAS-NOAH model is most consistent, in terms of correlation and amplitude, with both GRACE observations and GAO. The CLM model has the smallest χ₁ and χ₂ amplitude, which corresponds to the lowest non-seasonal TWS variation (Fig. 1 and Appendix 2). The close agreement between MOSAIC and VIC models can be seen again here.

A comparison of Fig. 4 with Fig. 2 highlights a visible, quasi-5-8-year oscillation in non-seasonal TWS and polar motion excitation time series. These variations are stronger for the χ₂ component. This can be related to the greater sensitivity of χ₂ to mass change over continents. It is well known that at interannual and shorter timescales, the major contributors to polar motion are the atmosphere and the hydrosphere. However, the longer oscillations visible in Fig. 4 are the result of other geophysical causes. The main drivers of long-term, non-seasonal polar motion variation are ice mass loss and groundwater effects. This topic has been investigated in recent papers (e.g. Youm et al. 2017). Indeed, since the beginning of the twentieth century, we have observed significant mass loss in both the Greenland and Antarctic Ice Sheets and glaciers, mainly as a result of a warmer climate (Adhikari and Ivins 2016; Velicogna et al. 2014). Ice mass loss in polar regions is acknowledged to be a main contributor to recent long-period polar motion changes. Groundwater depletion has also an impact on longer than interannual polar motion oscillations. Long-term groundwater loss, caused by, among other reasons, intensive extraction for drinking water, irrigation and industry, is a current problem in many major aquifers (Wada et al. 2010). On the other hand, some authors have suggested that the outer core may also affect the excitation of Earth’s pole in terms of decadal variations. Specifically, Kuang et al. (2017) developed numerical electromagnetic simulations to demonstrate that the liquid outer core can excite polar motion through core–mantle coupling. However, these effects may be a contributor at timescales longer than those observed in this study.

Turning to non-seasonal change, we computed correlation coefficients and percentage of relative explained variance (Table 4). Correlations between GRACE and GAO were also estimated. The estimated number of independent points required for the autocorrelation function of non-seasonal χ₁ and χ₂ change to drop to 1/e is 30 and 20, respectively. For a significance level α equal to 0.05, the critical correlation coefficients are 0.35 for χ₁ and 0.40 for χ₂. As Table 4 shows, correlations with GAO are generally higher for χ₂. However, if we examine agreement with GRACE observations, χ₁ correlations are higher for all GLDAS models. This analysis suggests that the best agreement with the non-seasonal hydrological signal in observed polar motion excitation is achieved for GRACE data (correlation coefficients 0.35 and 0.65 for χ₁ and χ₂, respectively). Among the GLDAS models, NOAH is best correlated with both GRACE (0.65 and 0.49 for χ₁ and χ₂, respectively) and GAO (0.18 and 0.52).

Table 4 Correlation coefficients and percentage of relative explained variance for non-seasonal χ₁ and χ₂ components of HAM functions: GLDAS and GRACE vs GAO; GLDAS vs GRACE

The largest percentage of variance of observed hydrological signal in polar motion excitation is explained by GRACE data (32.52% and 54.60 for χ₁ and χ₂, respectively) and the GLDAS-NOAH model (16.16% and 62.34%). Relative explained variances for χ₁ are negative for MOSAIC and VIC models. As it is detected in Fig. 4, the amplitudes of non-seasonal HAM oscillations for these two models are higher than for all other models and GRACE. As a result, the difference in variance between GRACE observations and these two models is higher than the variance of the HAM function derived from the mission.

Winska et al. (2017) examined differences between HAM functions computed from TWS state and flux parameters. This study showed that, especially for χ₂, the use of SM and AS (as in Eq. 3) agrees better with both GRACE and GAO than applying Eq. 4.

Contribution of TWS components to HAM

The previous section showed that GRACE data are most consistent with the hydrological signal in observed polar motion excitation. We also concluded that the GLDAS-NOAH model is most consistent with both GAO and GRACE observations. Similar conclusions were drawn for the global TWS analysis (“Comparisons of TWS time series”).

TWS used in HAM determination is calculated from models with two parameters, SM and AS (Eq. 3). Here, we examine which of these two components has the bigger impact on the HAM function. We therefore computed HAM in three ways: (i) with SM, (ii) with AS and (iii) with the sum of these two parameters. The analysis was carried out for the GLDAS-NOAH model, as it proved to be most consistent with GRACE data and GAO. Here again, our analyses were conducted for non-seasonal and seasonal oscillations.

Figure 5 shows non-seasonal χ₁ and χ₂ time series for the three HAM estimations. To facilitate comparison, GAO and HAM time series based on GRACE observations are also included. The results indicate that the HAM function computed with SM alone has almost the same amplitude and phase as the function based on the sum of the two components. On the other hand, AS alone resulted in significantly less powerful oscillations, which are often in opposite phases compared to SM and SM + AS time series.

Fig. 5

Comparison of equatorial components (χ₁ and χ₂) of non-seasonal time series based on GAO, GRACE data (mean of CSR, JPL and GFZ solutions) and the GLDAS-NOAH model. The NOAH HAM function was calculated from soil moisture (SM), snow water equivalent (AS) and their sum

The agreement between NOAH HAM and GRACE and GAO was computed as correlation coefficients and relative explained variance (Table 5). For a significance level α equal to 0.05, the critical value of correlation coefficients is 0.35 for χ₁ and 0.40 for χ₂. As Table 5 shows, correlation coefficients and relative explained variance are significantly better for HAM computed from SM than from AS, while best results are obtained with the sum of the two. However, including AS does not improve the correlation significantly; moreover, for non-seasonal χ₁, adding it can result in slightly worse agreement with GAO. SM clearly dominates as it explains a higher percentage of the hydrological signal than AS.

Table 5 Correlation coefficients and percentage of relative explained variance for non-seasonal χ₁ and χ₂ components of the HAM function calculated with soil moisture (SM), snow water equivalent (AS) and their sum. GLDAS vs GAO and GLDAS vs GRACE

Seasonal agreement was investigated using phasor diagrams of prograde and retrograde annual and semiannual oscillations (Fig. 6). Here, we compared GAO with HAM based on GRACE data, together with HAM computed with the use of SM and AS individually and their sum. The analysis found that phase agreement was better for HAM computed using SM than using AS. For annual oscillations, HAM based on SM and HAM based on AS have opposite phases, which results in a very small complex χ₁ + iχ₂ component computed from SM + AS both for prograde and retrograde oscillations. On the other hand, amplitudes are similar. For annual change, the best agreement was found for SM alone, while for semiannual amplitudes the sum of SM and AS performed best. This suggests that while the inclusion of AS degrades annual results, it improves agreement on a semiannual basis.

Fig. 6

Phasor diagrams of prograde and retrograde seasonal (annual and semiannual) variation in the complex-valued component χ₁ + iχ₂ of geodetic residuals (GAO) and HAM functions based on GRACE observations (mean of CSR, JPL and GFZ solutions) and the GLDAS-NOAH model. HAM from GLDAS-NOAH was calculated with the use of soil moisture (SM), snow water equivalent (AS) and their sum. The reference epoch is 2003.0

Our results are consistent with earlier work. An analysis of seasonal change based on different TWS components was presented in Freedman et al. (2014) for the Mississippi River Basin. The authors investigated annual cycles of SM, AS, groundwater and surface water from the CCSM4 model. This found that AS was distinguished by smaller amplitudes than SM and overall TWS (defined as the sum of all TWS components). Additionally, the AS component was shifted in phase with respect to SM and total TWS. It was also demonstrated that the sum of SM + AS corresponded closely with the annual TWS cycle observed by GRACE, while including groundwater and surface water did not improve this agreement significantly. The Freedman study focused on changes in TWS, while our analysis concerns the hydrological excitation function. However, the close correspondence of the sum of SM and AS with the GRACE TWS estimation, and the poor agreement between AS and the same observations may have an impact on the agreement of HAM functions. Our study found a clear correspondence with TWS (notably for GRACE and the GLDAS-NOAH model) and HAM (notably for GRACE, GAO and GLDAS-NOAH).

Our results confirm the findings of Winska et al. (2017). In particular, in the case of χ₂, the use of SM and AS (as in Eq. 3) improves agreement with both GRACE and GAO.

Conclusions

In this paper, we presented the results of a comparison of TWS series determined from different data sources. The aim was to estimate the impact of variability in TWS on hydrological polar motion excitation. Hydrological excitation functions computed from GRACE observations were compared with hydrology and climate models, and we demonstrated the impact of two TWS components (SM and AS) on excitation.

The results found a significant correlation between seasonal TWS change based on GRACE data and GLDAS and climate models. However, only the GLDAS-NOAH model was satisfactory in terms of correlation and variance agreement for non-seasonal change. Significantly smaller amplitudes were found for both seasonal and non-seasonal TWS changes for the GLDAS-CLM model compared to both the other models and GRACE data. MOSAIC and VIC were closely correlated with each other and were very consistent with GRACE observations for seasonal change; however, the amplitude of non-seasonal oscillations was much higher than for satellite gravimetry observations and the other models.

In general, GLDAS models are more consistent with GRACE observations than climate models, especially at non-seasonal scales. However, it should be noted that, unlike CMIP5, GLDAS models integrate both ground-based and satellite observations. Moreover, we only examined two of the over 50 climate models that are available, although this decision was guided by the fact that not all CMIP5 simulations include the variables that are needed to determine TWS. Future research should focus on a detailed analysis of other CMIP5 models.

Our comparison of polar motion excitation functions χ₁ and χ₂ found that GRACE observations are most consistent with the non-seasonal hydrological signal. Among the various GLDAS models, GLDAS-NOAH was most consistent (highest correlation coefficients and relative explained variance) with the hydrological signal in observed polar motion excitation and GRACE observations in terms of both TWS and HAM. However, this model still does not represent TWS without surface water components.

The analysis of different water storage components shows that the soil moisture layer has a dominant impact on hydrological polar motion excitation. Amplitudes are higher for HAM computed with SM for non-seasonal χ₁ and χ₂ changes, and correlations and variance provide better agreement with respect to GRACE observations and GAO. Our results showed that the HAM function determined from the sum of SM and AS was better correlated with both GRACE data and GAO than HAM obtained from individual parameters. However, this agreement is still unsatisfactory.

In fact, our results underlined that none of the model-based HAM functions fully explain global geophysical polar motion excitation. This study supports earlier work showing that GRACE observations are most consistent with the hydrological signal in observed polar motion excitation for both seasonal and non-seasonal oscillations. However, similarly for hydrosphere models, gravimetric excitation functions based on GRACE solutions also do not explain this signal entirely.

There is a need for further studies on this topic. At present, there is no consensus regarding which hydrological model performs best in terms of improving agreement between geophysical (AAM + OAM + HAM) and geodetic (GAM) functions. Since geodetic residuals are affected by uncertainties associated with different oceanic and atmospheric models, research should focus on improving AAM and OAM estimations, given the apparent discrepancies between models and the resulting GAO. Further improvement in the agreement between geophysical and geodetic estimates of polar excitation also needs to take into account the global sea-level mass balance.

Additional improvements in GRACE data processing methods may improve the agreement between gravimetric and geodetic excitation functions. Additionally, a new laser ranging system installed on board the GRACE Follow-On twin satellites is expected to result in higher-quality determinations of Earth’s gravity field, which also could improve gravimetric excitation functions determinations.

Appendices

Appendix 1

Table 6 presents a summary of the data sources used to determine TWS and the corresponding hydrological excitation (HAM) functions. All models and data cover the time period from January 2003 to December 2015. Variables from MPI-ESM-LR and MIROC5 were interpolated into regular 1° × 1° grids for further analyses. GRACE data represent the mean of CSR RL05, JPL RL05 and GFZ RL05 solutions.

Table 6 GRACE data and models used for TWS determination

Appendix 2

Regional TWS patterns were used to calculate global time series. TWS distribution has been the subject of many earlier studies (e.g. Chen et al. 2009; Freedman et al. 2014; Hassan and Jin 2016; Tangdamrongsub et al. 2016), which have focused on a comparison of TWS based on satellite observations and land surface models for specific regions such as continents or river basins. Other works such as Syed et al. (2008) and Zhang et al. (2015, 2016) have considered global TWS.

GRACE data have been used in many hydrological applications at both regional and global scales: regional drought event identification (Chen et al. 2009; Thomas et al. 2014), change in groundwater level (Chen et al. 2016; Jin and Feng 2013; Rodell et al. 2009), large-scale hydrological extremes assessment (Sun et al. 2017) or flood prediction (Reager et al. 2014). Other studies have aimed to validate land surface or climate models (Freedman et al. 2014; Scanlon et al. 2018; Zhang et al. 2015, 2017). Another way to assess the accuracy of hydrological models is to use ground-based observations from gauge stations (Chen et al. 2009), data from terrestrial reflectance (Tangdamrongsub et al. 2016) or global satellite precipitation data (Tangdamrongsub et al. 2016; Hassan and Jin 2016). Although many papers have analysed and validated TWS based on models and GRACE observations, most focus on seasonal change (Hassan and Jin 2016; Syed et al. 2008) or trends (Hassan and Jin 2016; Scanlon et al. 2018). Here, we compare regional and global TWS time series at seasonal and non-seasonal timescales.

Specifically, we compared regional TWS change derived from GRACE observations and GLDAS and CMIP5 models. To do this, we prepared maps of variance in TWS for each model and for GRACE data. Maps were prepared separately for seasonal and non-seasonal change.

Figure 7 shows variance in seasonal TWS for GRACE data (mean of CSR, JPL and GFZ solutions), for the four GLDAS models (NOAH, MOSAIC, VIC and CLM) and for the two CMIP5 climate models (MPI-ESM-LR and MIROC5). This figure shows that the areas where variability is highest are similar for GRACE observations and for almost all models. These places are mostly located in the tropical zone: the Amazon Basin, the Congo Basin and South-east Asia. GLDAS models also highlight significant variability in Eastern Europe. Variability is smallest in desert areas: the Sahara in Africa, the Gobi in Asia and many parts of Australia. The GLDAS-CLM model is distinguished by the smallest seasonal variance, and high amplitudes are only observed for northern parts of Europe, Asia and North America. Tropical areas, where variability should be highest, are not detected by this model.

Fig. 7

Maps of variance in seasonal TWS computed for GRACE data (mean of CSR, JPL and GFZ solutions), GLDAS land hydrology models (NOAH, MOSAIC, VIC and CLM) and CMIP5 climate models (MPI-ESM-LR and MIROC5). Units are cm², and the analysis concerns the period 2003.0–2016.0

Figure 8 replicates Fig. 7, but for non-seasonal change. Here, geographical patterns differ as a function of the model or data. For GRACE observations variance is highest in South Africa and the basins of major rivers such as the Amazon, the Ganges and Brahmaputra, the Euphrates and the Tigris. Only the GLDAS-NOAH model is similar. Values for the GLDAS-MOSAIC and VIC models are much higher, while variability is smallest for the GLDAS-CLM model.

Fig. 8

Maps of variance in non-seasonal TWS computed for GRACE data (mean of CSR, JPL and GFZ solutions), GLDAS land hydrology models (NOAH, MOSAIC, VIC and CLM) and CMIP5 climate models (MPI-ESM-LR and MIROC5). Units are cm², and the analysis concerns the period 2003.0–2016.0

We also compared GRACE TWS patterns with those from each model in detail. To do this, we prepared maps of the variance difference between the model and the GRACE solution. Figure 9 shows the results for all models. In areas shown in warm colours (yellow to red) GRACE observations have higher variance than the model. Cold tones correspond to the opposite situation: Variance is higher for the model. The figure shows that in high-variance areas (the Amazonian Basin, the Congo Basin and South-east Asia) variance is lower for land hydrosphere models (NOAH, MOSAIC, VIC and CLM), but higher in Northern Europe, western Siberia and north-east regions of North America. The CLM model is notable as variance is lower than GRACE data almost for the whole Earth with the exception of Northern Europe and north-east parts of North America. Although variability is higher in tropical Africa in CMIP5 models compared to GLDAS, the former fail to detect strong oscillations in the Amazon Basin and South-east Asia (the Indian subcontinent and the Indochinese Peninsula). Unlike GLDAS, climate models give lower TWS variance than GRACE data in Europe. The smallest differences for all considered models are observed in dry regions such as the Sahara, Kalahari and Gobi deserts, central Australia and the Arabian Peninsula.

Fig. 9

Comparison of variance differences in seasonal TWS between GRACE data and GLDAS (NOAH, MOSAIC, VIC and CLM) and CMIP5 climate models (MPI-ESM-LR and MIROC5). Units are cm², and the analysis concerns the period 2003.0–2016.0

Figure 10 replicates Fig. 9 at the non-seasonal level. This shows that the GLDAS-NOAH model is most consistent with GRACE data. The highest positive differences concern the tropics and the Labrador Peninsula, while the highest negative differences relate to Northern Asia and Southern Africa. Variation is much higher for MOSAIC and VIC models than GRACE data. This discrepancy mainly concerns South America, central Africa, South-east Asia, Europe and Siberia. The CLM model does not detect big changes as almost all differences are positive. With respect to climate models, MIROC5 variance is much higher than both MPI-ESM-LR and GRACE. The smallest absolute differences are observed for MPI-ESM-LR.

Fig. 10

Comparison of variance differences in non-seasonal TWS between GRACE data and GLDAS (NOAH, MOSAIC, VIC and CLM) and CMIP5 climate models (MPI-ESM-LR and MIROC5). Units are cm², and the analysis concerns the period 2003.0–2016.0

The results of our regional, seasonal comparison are similar to those obtained by other authors. Hassan and Jin (2016), for example, investigated annual TWS variations in Africa observed based on GRACE data and GLDAS hydrological models. This study showed that land hydrology models significantly underestimated annual TWS amplitudes and trends compared to GRACE data. It also suggested that the GLDAS-CLM model appears to be characterized by small variations. Similarly, Chen et al. (2009) found that the GLDAS-NOAH model underestimated TWS changes in the Amazon Basin in relation to GRACE observations.

Our research underlines that neither GLDAS nor CMIP5 models can fully explain the TWS seasonal signal that is observed by GRACE satellites. However, it should be emphasized that land surface models do not account for groundwater variation. In their study of TWS in the Mississippi River Basin based on CMIP5 models and GRACE data, Freedman et al. (2014) showed that MIROC5 annual TWS cycles corresponded well to GRACE observations. They also found that the mean of multiple models fitted GRACE data better than most individual CMIP5 models. Nevertheless, as our research demonstrates, climate models still cannot fully represent the non-seasonal TWS variation and further work is needed. Our paper presented the results of such an investigation and showed that most hydrological models overestimate non-seasonal TWS change, notably GLDAS-MOSAIC and VIC.

Appendix 3

See Tables 7, 8 and 9.

Table 7 Amplitudes and phases of annual, semiannual and terannual TWS oscillations derived from GRACE observations (mean of CSR, JPL and GFZ solutions) and GLDAS models (NOAH, MOSAIC, VIC and CLM)

Table 8 Amplitudes and phases of prograde and retrograde annual oscillations of geodetic residuals (GAOs) and HAM functions based on GRACE observations (mean of CSR, JPL and GFZ solutions) and GLDAS models (NOAH, MOSAIC, VIC and CLM)

Table 9 Amplitudes and phases of prograde and retrograde semiannual oscillations of geodetic residuals (GAOs) and HAM functions based on GRACE observations (mean of CSR, JPL and GFZ solutions) and GLDAS models (NOAH, MOSAIC, VIC and CLM)