High-dimensional Bayesian optimization with projections using quantile Gaussian processes

Abstract

Key challenges of Bayesian optimization in high dimensions are both learning the response surface and optimizing an acquisition function. The acquisition function selects a new point to evaluate the black-box function. Both challenges can be addressed by making simplifying assumptions, such as additivity or intrinsic lower dimensionality of the expensive objective. In this article, we exploit the effective lower dimensionality with axis-aligned projections and optimize on a partitioning of the input space. Axis-aligned projections introduce a multiplicity of outputs for a single input that we refer to as inconsistency. We model inconsistencies with a Gaussian process (GP) derived from quantile regression. We show that the quantile GP and the partitioning of the input space increases data-efficiency. In particular, by modeling only a quantile function, we overcome issues of GP hyper-parameter learning in the presence of inconsistencies.

1 Introduction

Studies in robotics, machine learning, software development, recommendation systems and medicine are governed by design and parameter choices. For instance, changing gait properties of legged robots leads to different robustness and walking speed performances [5]. Adjusting controller configurations in drones results in reduced feedback-error of closed loop systems [2]. Clever tuning of hyper-parameters settings in multi-layer convolutional neural networks speeds up learning and lowers generalization error [19]. Since the process of evaluating the performance of each parameter configuration can be time consuming, automatically finding configurations that yield optimal performance is notoriously hard and demands data-efficient approaches.¹ In an ideal setting, we are interested in a globally optimal solution.

A promising algorithm for data-efficient optimization is Bayesian optimization (BayesOpt) [7, 12, 14, 16] where a surrogate function is built for predicting the performance of a set of parameters. The exploration/exploitation trade-off to obtain a globally optimal solution is taken care of by an acquisition function. This approach has proven successful in various fields such as movie recommendation systems [21], parameter estimation of biological models [23] and automatic algorithm configuration [10].

The key to the success of BayesOpt relies on two steps: (i) using previous experiments to train statistical surrogate models and then (ii) using this model within an acquisition function to find input locations that yield the best added value for the optimization. These steps, however, come at a computational cost that remains often small in low dimensions. However, in high dimensions, we typically need a significantly larger number of experiments to find a good statistical model of the true objective function. Optimizing the acquisition function requires many evaluations of the surrogate model and constitutes a computational bottleneck in BayesOpt.

To reduce the negative effects of the high dimensionality on BayesOpt, Wang et al. [24] assume that the objective lives only on a linear subspace of the input domain that is d-dimensional with $d\ll D$, where D is the original dimensionality. Strong theoretical results show that performing BayesOpt under these assumptions is equivalent to learning and optimizing the true objective on a random embedding. However, robust implementation requires further deftness to account for box-constraints and non-injectivity of the mapping from the embedding to the original domain. Kandasamy et al. [13] decompose the objective f as a sum of z-independent lower-dimensional function components $f_{1},\ldots ,f_{z}$ defined on orthogonal domains ${\varvec{\Theta }}^{(1)},\ldots ,{\varvec{\Theta }}^{(z)}$ of dimensionality at most d. Each subproblem is optimized independently using the Upper Confidence Bound (UCB) acquisition function [20]. This approach scales the optimization of the acquisition linearly in the number of components by including specific structural assumptions about f. Ulmasov et al. [23] propose a different decomposition of the input by randomly selecting subsets of the input parameters and assigning a different model for each subset. Each model is then trained with a separate dataset to address the problem of inconsistencies introduced by axis-aligned projections.

Fig. 1

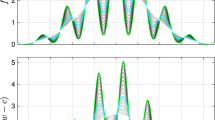
a Vanilla GP hyper-parameter learning can result in unrealistic estimates and largely useless generalization capabilities. This is a clear sign of underfitting where the data with inconsistency is modeled as noise. The resulting acquisition function from this model will favor pure exploitation leading to pre-mature convergence of the algorithm. b The Quantile GP overcomes the issue of inconsistencies by explicitly modeling only a quantile function

Optimization in these lower-dimensional spaces suffers from observation ambiguity, e.g., $(\theta ^*_1, f(\theta ^*_1, \theta _2)), (\theta ^*_1, f(\theta ^*_1, \tilde{\theta }_2))$ are two observations collected for a single lower-dimensional input $\theta ^*_1$. We refer to this as inconsistency or ambiguity and show their effect in Fig. 1. To amend this issue Ulmasov et al. [23] adopts multiple separate subsets of experiments resulting in a data-costly strategy.

In this article, we propose a scalable method based on projections that overcomes issues inherent in axis-aligned projections. We formulate an optimization approach based on independent sub-problems for each subset of $d\ll D$ parameters. We address the issue of inconsistencies with a sensible choice of the model by using a quantile GP (QGP). The key idea behind the QGP is that we only model a lower $\tau$-quantile of function values, which also allows us to retain a simpler explanation of the data. The QGP maintains well-calibrated confidence bounds in posterior predictions in the presence of noisy multiplicity of outputs see Fig. 1.

2 Problem setting

We consider the problem of finding a minimizer

$$\begin{aligned} \varvec{\theta }^{*} = \underset{\varvec{\theta }\in {\varvec{\Theta }}}{\text {argmin }}f(\varvec{\theta }) \end{aligned}$$

(1)

of an unknown function $f:\varvec{\varTheta }\subset \mathbb {R}^{D}\rightarrow \mathbb {R}$ defined on a D-dimensional parameter space $\varvec{\varTheta }$ that we will assume to be a bounded hypercube $\varvec{\varTheta }=\left[ 0, 1\right] ^{D}$. We further assume that observations y of f are corrupted by i.i.d. Gaussian noise, i.e., $y_{i}=f(\varvec{\theta }_{i}) + \varepsilon$, where $\varepsilon \sim \mathcal {N}(0, \sigma _{n}^{2})$ with unknown variance $\sigma _n^2$. Gradient information of the black-box function f with respect to the inputs $\varvec{\theta }\in \varvec{\varTheta }$ are not available, and we cannot make any convexity assumptions.

2.1 Gaussian processes

In this article, we consider a Gaussian process (GP) as the probabilistic surrogate for the black-box objective function we seek to optimize. GPs allow for deriving a posterior of f in a fully Bayesian framework and expressing the uncertainty in its estimation through well calibrated error bars. GPs are commonly used in machine learning to express prior assumptions in nonlinear regression problems and have proven successful in Bayesian optimization [18], learning control [6], probabilistic numerics [9], and time series-predictions [8]. When a function $f:{\varvec{\Theta }}\rightarrow \mathbb {R}$ is distributed as a GP we write $f\sim \mathcal {GP}(m(\cdot ), k(\cdot , \cdot ))$. A GP is fully determined by a mean function$m:{\varvec{\Theta }}\rightarrow \mathbb {R}$ and a covariance function or kernel$k:{\varvec{\Theta }}\times {\varvec{\Theta }}\rightarrow \mathbb {R}$, which encodes high-level properties and characteristics of the function as mean and covariance structure between function values. Common choices of covariance functions for BayesOpt include the squared exponential and Matern$_{52}$ kernels  [7, 17] given by

$$\begin{aligned}&k_{exp}(r) = \exp \left( -\tfrac{r^2}{2l^2}\right) ,\quad k_{m5/2}(r) = \left( 1 + \tfrac{r\sqrt{5}}{l} + \tfrac{5r^{2}}{3l^{2}}\right) \exp \left( -\tfrac{r\sqrt{5}}{l}\right) \end{aligned}$$

(2)

respectively, where $l>0$ is a lengthscale parameter. These are stationary kernels, i.e., they only depend on the distance $r=\Vert \varvec{\theta }-\varvec{\theta }'\Vert$ between two inputs $\varvec{\theta }$ and $\varvec{\theta }'$. With a Gaussian likelihood we obtain a closed-form posterior distribution $p(f(\varvec{\theta }_{\star })|\mathcal {D}_N) = \mathcal N(\mu (\varvec{\theta }_{\star }), \sigma ^{2}(\varvec{\theta }_{\star }))$, where

$$\begin{aligned} \mu (\varvec{\theta }_{\star })&= m_{\star } + \mathbf {k}_{\star }^{T}\left( \mathbf {K} + \sigma _{n}^{2}\mathbf {I}\right) ^{-1}(\mathbf {y}-\mathbf {m})\,, \end{aligned}$$

(3)

$$\begin{aligned} \sigma ^{2}(\varvec{\theta }_{\star })&= k_{\star \star }-\mathbf {k}_{\star }^{T}\left( \mathbf {K} + \sigma _{n}^{2}\mathbf {I}\right) ^{-1}\mathbf {k}_{\star }\,, \end{aligned}$$

(4)

where $k_{\star \star } = k(\varvec{\theta }_{\star }, \varvec{\theta }_{\star })$, $\mathbf {k}_{\star }=\left[ k(\varvec{\theta }_{i}, \varvec{\theta }_{\star })\right] _{i=1}^{N}$, $\mathbf {K}=\left[ k(\varvec{\theta }_{i}, \varvec{\theta }_{j})\right] _{i,j}$, $m_{\star }=m(\varvec{\theta }_{\star })$ is the mean function evaluated at the test input, $\mathbf {m} = [m(\varvec{\theta }_{1}),\ldots , m(\varvec{\theta }_{N})]^{T}$ contains the mean function values at the training inputs and $\mathbf {y}=[y_{1},\ldots ,y_{N}]^{T}$ contains all observations.

2.2 Bayesian optimization

Bayesian optimization is performed in two steps: (i) we train a statistical model $p(f|\mathcal {D}_{t})$, usually a GP, of the latent function f based on observations collected up to iteration t; (ii) we select inputs $\varvec{\theta }_{t+1}^{*}$ by maximizing an acquisition function, $\alpha :\varvec{\varTheta }\rightarrow \mathbb {R}$ that trades off exploration and exploitation, such that

$$\begin{aligned} \varvec{\theta }_{t+1}^{*} = \underset{\varvec{\theta }\in \varvec{\varTheta }}{\text {argmax }}\alpha (\varvec{\theta }\,|\,p(f| \mathcal {D}_t))\,. \end{aligned}$$

(5)

The acquisition function formalizes the notion of how useful each input parameter $\varvec{\theta }$ is for optimization of f. Given a probabilistic model for f, the acquisition function automatically trades off low expected function values (exploitation) with regions where the latent f has high estimated uncertainty (exploration). Different acquisition functions have been defined that characterize different exploration-exploitation trade-offs for global optimization. Examples are

$$\begin{aligned}&\text {Probability of improvement (PI):}\quad \varPhi (Z) \end{aligned}$$

(6)

$$\begin{aligned}&\text {Expected improvement (EI):}\qquad \quad \sigma (\varvec{\theta })Z\varPhi (Z) + \sigma (\varvec{\theta })\phi (Z)\end{aligned}$$

(7)

$$\begin{aligned}&\text {Upper confidence bound (UCB):}\quad -\mu (\varvec{\theta }) + \beta _{t}\sigma (\varvec{\theta }) \end{aligned}$$

(8)

where $f(\varvec{\theta }^{-})=\min f(\varvec{\theta }_{1:t})$ is the current minimum observed in the exploration history, and $Z = (f(\varvec{\theta }^{-})-\mu (\varvec{\theta }))/\sigma (\varvec{\theta })$. Moreover, $\varPhi$ and $\phi$ are the standard cumulative and normal density, respectively. $\beta _{t}$ in UCB accounts for the trade off between exploration and exploitation.

We refer to  [18] for a more detailed overview on acquisition functions. Increasing the dimensionality D of the input space ${\varvec{\Theta }}$ raises a series of challenges. The number of evaluations required to cover the search space increases exponentially in D. This makes GP learning a computationally demanding task. GPs, as common choices for probabilistic modeling of the response surface, scale cubically in the number of data points for training and quadratically for predicting [17]. Computational demands of acquisition function optimizers also become significant. Heuristic strategies based on multi-start methods [4], and dividing rectangle searches (DiRect) [11] require an exponential number of evaluations of the response surface with respect to D.

3 High-dimensional Bayesian optimization with projections

We propose a novel Bayesian optimization algorithm based on axis-aligned projections that uses quantile regression models for learning a low-dimensional projection of the response surface. Under the assumption that the black-box function is effectively lower-dimensional, projections onto d-dimensional features tackle the curse of dimensionality for both the learning of the response surface and the maximization of the acquisition function.

We select z possible projections that partition the D-dimensional input space, such that $\cup _{i}{\varvec{\Theta }}^{(i)}={\varvec{\Theta }}$, and $\cap _{i}{\varvec{\Theta }}^{(i)}=\emptyset$. This convention allows us to partition the dimensions into a maximum of z projections, or components. We then define the projection as a set of d coordinates, $proj(i)=\{ p_{i, 1}, \ldots , p_{i, d}\}$, to select from the original input space for $i=1,\ldots ,z$. Given an input $\varvec{\theta }=[\theta _{1},\ldots ,\theta _{D}]\in \mathbb {R}^{D}$, we identify its i-th projection as $\varvec{\theta }^{(i)}=[\theta _{p_{i,1}}, \ldots , \theta _{p_{i,d}}]\in \mathbb {R}^{d}$, that is from the high-dimensional vector of parameters we select the components with indices $p_{i,1}, .., p_{i,d}$. The projected vector is defined in the low-dimensional space ${\varvec{\Theta }}^{d}$ and we say that this d-dimensional space is defined by the projection proj(i). When performing optimization from projected data we consider the data set $\{{\varvec{\Theta }}^{(i)}, \mathcal {Y}\}$ with lower-dimensional inputs $\varvec{\theta }^{(i)}$.

Projections along the axes cause inconsistencies, i.e., multiple values $y_{1}, \ldots , y_{m}$ for the same input location. For instance, if we observe $y_{1}, y_{2}$ from a function with two-dimensional inputs, i.e., $\hat{f}(\theta _{1}, \theta _{2}), \hat{f}(\theta _{1}, \tilde{\theta }_{2})$, and we plot them w.r.t. the first coordinate we obtain multiple output values in correspondence to $\theta _{1}$, i.e., $(\theta _{1}\,,\,\hat{f}(\theta _{1}, \theta _{2}))$ and $(\theta _{1}\,,\,\hat{f}(\theta _{1}, \tilde{\theta }_{2}))$. The effect of these inconsistencies/ambiguities is illustrated in Fig. 1. A standard GP would model this multiplicity of outputs as additive Gaussian noise. This modeling may result in a mis-interpretation of data as unstructured noise. Figure 1 shows an example of this shortcoming.

For our purpose of obtaining reliable posterior predictions after training, we are interested in removing such inconsistencies, e.g., by automatically selecting only the best (lowest) observations for each parameter sub-configuration. Selecting extreme (small) observations is intuitive in our minimization context, and we validate this choice with empirical results. Quantile regression provides a method for function estimation that effectively embodies this notion of automatic selection. We detail the steps of our method with quantile GP models for each projection in Algorithm 1.

4 Quantile GP regression

We are interested in modeling a proportion of the data with a GP. This proportion is referred to as quantile, $\tau$, and defines the probability $P(y\le \mu _{\tau })=\tau$ of observations y to be below the functional estimate $\mu _{\tau }$ [22]. The basic intuition behind quantile regression is that minimizing the l1-loss function, $\sum ^{N}_{i=1}{|y_{i}-\mu _{\tau }(\varvec{\theta }_{i})|}$ yields a functional estimator of the median, which corresponds to quantile $\tau =0.5$. For an arbitrary $\tau$, direct estimation of the quantile functions is obtained by minimizing a tilted loss function (pinball loss)

$$\begin{aligned}&l_{\tau }(\xi ) = {\left\{ \begin{array}{ll} \tau \xi &{} \text {if }\xi \ge 0\\ (\tau -1)\xi &{} \text {if }\xi <0, \end{array}\right. } \end{aligned}$$

(9)

where $\xi = y_{i}-\mu _{\tau }(\varvec{\theta }_{i})$. The regression problem that optimizes the cumulative loss $\sum ^{N}_{i=1}{l_{\tau }(y_{i}-\mu _{\tau }(\varvec{\theta }_{i}))}$ consistently produces $\tau$-th quantile function estimates [22].

Fig. 2

Two different approaches to quantile regression. Red dots show inconsistencies, i.e. different observations $y_{1},\ldots ,y_{m}$ for the same input $\varvec{\theta }$. Left (direct estimation): the blue line shows the tilted loss for $\tau =0.1$, ys above the functional estimates generate a loss 10-times smaller than those that appear at the same distance below $\mu _{\tau }$. Right (Bayesian formulation): the blue line represents how likely data points are given the quantile model $\mu _{\tau }$ (colour figure online)

In our predictions, we model the uncertainty of our estimate $\mu _{\tau }$ as a posterior probability over function values derived in a Bayesian framework. The quantile-GP model (QGP) [3] allows for such a formulation and computation of posterior predictions through approximate inference via Expectation Propagation (EP) [15]. We introduce a standard GP prior over quantile functions, i.e., $\mu _{\tau }\sim \mathcal {GP}(m, k)$, and reformulate the tilted loss (9) in terms of a renormalized reward $\mathbf {R}(y_{i}, \mu _{\tau }) = Z_{i}\exp \left( l_{\tau }(\mu _{\tau }, y_{i})\right)$, where $Z_{i}$ is a normalizing constant, and $\mathbf {R}(y_{i}, \mu _{\tau })$ evaluates the Asymmetric Laplace Distribution (ALD). The basic intuition behind this definition is also displayed in Fig. 2 for a quantile $\tau =0.1$. The reward represents the likelihood $p(y_{i}|\mu _{\tau }, \varvec{\theta }_{i}, \varvec{\theta }_{GP})$ of each input $\varvec{\theta }_{i}$ and model hyper-parameters $\varvec{\theta }_{GP}$, which includes the lengthscales of the kernel. We perform training of QGP hyper-parameters via a type-II maximum likelihood approach [17], that is we select the lengthscale parameters of the kernel by maximizing the marginal likelihood at each BayesOpt iteration, i.e.

$$\begin{aligned} \underset{\varvec{\theta }_{GP}}{\text {argmax }}\int p(\mathbf {y}|\mu _{\tau }, {\varvec{\Theta }}_{N}, \varvec{\theta }_{GP})p(\mu _{\tau }| \varvec{\theta }_{GP}) d\mu _{\tau }. \end{aligned}$$

(10)

The integral (10) is intractable and we approximate it via EP. Expectation Propagation [15] is an approximate inference method that expresses the likelihood, $p(\mathbf {y}|\mu _{\tau }, {\varvec{\Theta }}_{N}, \varvec{\theta }_{GP})$, with a product of unnormalized Gaussian distributions in the latent variable, $\mu _{\tau }$, called local likelihood approximations$\tilde{\pi }_{i}=\tilde{Z}_{i}\mathcal {N}(\mu _{\tau }; \tilde{\mu }_{i}, \tilde{\sigma }^{2}_{i})$. In our setting, the rewards are independent for each $y_{i}$ so that the model likelihood $p(\mathbf {y}|\mu _{\tau }, {\varvec{\Theta }}_{N}, \varvec{\theta }_{GP})$ factorizes as $\prod _{i=1}^{N}\mathbf {R}(\mu _{\tau }, y_{i})$. The EP approximates each of these N-likelihood factors with a local Gaussian approximation, we therefore apply an approximation with N local likelihoods. Each local approximation is characterized by the site parameters:$\tilde{\mu }_{i}, \tilde{\sigma }^{2}_{i}$, for $i=1,\ldots ,N$, where the effect of the normailzation constants, $\tilde{Z}_{i}$, on the marginal likelihood can be expressed as a function of the site parameters [17]. These are are the targets of the EP algorithm and are updated in an iterative process until convergence. The convergence guarantee for the EP procedure has not been proven but rather conjectured [17] for log-concave likelihoods such as ALD and has been reported that EP works relatively well for GP models. After convergence, each local approximation $\tilde{\pi }_{i}$ will contribute to the posterior as the original likelihood in $p(\mathbf {y}|\mu _{\tau }, {\varvec{\Theta }}_{N}, \varvec{\theta }_{GP})$, still retaining nice properties of analytical integration against Gaussian distributions. Algorithm 2 shows the main steps involved in the approximate inference procedure.² For a further explanation of the EP steps the reader could refer to [15, 17].

The approximate Gaussian posterior predictive distribution resembles the posterior mean and variance equations in (3) and (4) and is

$$\begin{aligned} \mu (\varvec{\theta }_{\star })&= \mathbf {k}_{\star }^{T}(\mathbf {K} + {\varvec{\tilde{\Sigma }}})^{-1}\tilde{\varvec{\mu }} \end{aligned}$$

(11)

$$\begin{aligned} \sigma ^{2}(\varvec{\theta }_{\star })&= k_{\star \star }-\mathbf {k}_{\star }^{T}(\mathbf {K} + {\varvec{\tilde{\Sigma }}})^{-1}\mathbf {k}_{\star } \end{aligned}$$

(12)

where $\tilde{\varvec{\mu }}=\left[ \tilde{\mu }_{i}\right] _{i}$ and ${\varvec{\tilde{\Sigma }}}=\text {diag}(\tilde{\sigma }^{2}_{1},\ldots ,\tilde{\sigma }^{2}_{N})$ are obtained from parameters of local Gaussian approximations.

5 Experiments

In this section, we assess the quantile GP model for Bayesian optimization on axis-aligned projections. In our analysis, we dedicate a set of experiments to validate our choice of the quantile $\tau$ with empirical evidence. In high-dimensional settings, we test our approach on the commonly assumed additivity property by imposing and violating this assumption. In addition, we include an empirical analysis of performances when the axis-aligned assumption is violated, that is under an arbitrary rotation of the original domain.

Performing BayesOpt on subsets of dimensions, we define fixed groups and update each partition component in parallel during one optimization step. We avoid over-fitting to a single acquisition function comparing performances across a set of acquisitions: expected improvement (EI), [16], upper confidence bound (UCB) [20], and probability of improvement (PI) [14]. For the Gaussian process model in each baseline, we select the Matern$_{52}$ kernel.

5.1 Sensitivity analysis

The use of a QGP introduces $\tau$ as an additional hyper-parameter. This value models the proportion of observations that are modeled by the QGP and, consequently, the shape of the response surface from posterior predictions. Here, we evaluate the sensitivity of BayesOpt to different choices of the quantile parameter $\tau$. We restrict our selection of quantiles to a maximum of $\tau =0.5$ since we require our model to be sensible with respect to low observations. Intuitively, in a minimization setting, proportions of the data below the median represent good indicators of the location of a minimum and we therefore expect performances to deteriorate for $\tau >0.5$.³

We use the Hartmann benchmark function, which has total of six effective dimensions, and lift it into a high-dimensional input space of dimensionality $D=60$. Relevant dimensions are distributed uniformly at random over the 60 dimensions, and care is taken to ensure that all relevant dimensions are not contained in the same group.

Fig. 3

We show results on a set of quantile choices, $\tau =[0.01, 0.1, 0.2, 0.3, 0.4, 0.5]$, and compare performances across different acquisition functions: aEI, bUCB, cPI. Performances for small values, $\tau =[0.1, 0.2, 0.3]$, lead to similar convergence results both in terms of data efficiency and in final optimal guess. Error bars show the standard error over a set of 20 independent restarts

Figure 3 shows the progression of the best (lowest) observations collected during the independent optimization runs. Error bars represent twice the standard error over runs from different initializations. We evaluate performances in terms of best observed value at termination of the algorithm and data efficiency of each baseline which denotes the steepness of the descent in the succession towards the optimum. The collected results show good performances for moderate values of the quantile such as 0.1, 0.2, 0.3 while extreme values such as 0.5 and 0.01 retain a much slower descent. We observe that the extremely small quantile tends to overfit to lowest observations and reduces generalization capabilities. This renders exploration of the BayesOpt algorithm expensive in the number of function evaluations and increases the number of local optima of the optimization landscape. Large quantiles also correspond to poor performances. Selecting $\tau =0.5$, the QGP models the median which is sensible with respect to mid-range outputs. The lowest observations are treated as outliers and the resulting response surface landscape fails to capture downhill slopes relevant for global minimization. In our set of experiments, modeling the 0.1 proportion of observations proves effective, and we identify the choice of $\tau =0.1$ as our best configuration for the remaining experiments on synthetic data. In the subsequent we also introduce a Gamma hyper-prior for the lengthscales $\textit{Ga}(\textit{shape}=1, \textit{scale}=1)$ in each baseline to enforce exploration during optimization.

5.2 Additive high-dimensional objectives

In our second experiment, we assess the scalability of BayesOpt with Quantile GPs (QGP) by comparing to a set of baselines for high-dimensional optimization. We include random embeddings (REMBO) [24], random search (RS) [1], additive models (Add-GP) [13] and Lipschitz continuous optimization with GP (GP-Lip).

The algorithm REMBO: Random EMbeddings Bayesian Optimization [24] performs standard Bayesian optimization in a low-dimensional box constraint (embedding), i.e. $\mathbf {z}\in [z_{\text {min}},z_{\text {max}}]^{d}$ and then projects the selected location to the original input space via a linear mapping $\varvec{\theta } = \mathbf {A}\mathbf {z}$. The matrix $\mathbf {A}$ has entries sampled from standard Gaussian, i.e. $[\mathbf {A}]_{i,j}\sim \mathcal {N}(0, 1)$ and the values $z_{\text {min}},z_{\text {max}}$ are provided such that the optimum is contained in the embedded space with arbitrarily high probability.

Random Search [1] simply selects a set of T locations $\{\varvec{\theta }\}_{0:T-1}$ uniformly at random in the high-dimensional input space and evaluates the objective functions on these locations without any adaptive search strategy.

Add-GP [13] learns a d-dimensional Gaussian process for each addend of the sum $f_{1},\ldots ,f_{z}$. Each component then independently optimizes an acquisition function and updates the corresponding set of d-coordinates.

The last baseline GP-Lip manually applies axis-aligned projections in a partition of the input space and resolves the inconsistencies by selecting lowest observations in pairs of points that violate Lipschitz continuity assumption. It then learns plain GP response surface (instead of QGP) in each axis-aligned projection. This baseline compares with the automatic selection applied implicitly by the QGP in the presence of inconsistencies. The Lipschitz constant is the maximum element of a set of $5\cdot 10^{6}$ gradients evaluated on a random selection of input locations for each benchmark function. We choose the Michalewicz function as a benchmark, which has effective dimensionality $d_{ef}=10$ and satisfies the additivity assumption. It is a sum of one-dimensional components $f_{i}$, each of which is defined as $f_{i}(\theta _{i}) = -\sin (\theta _{i})\sin ^{2m}\left( \frac{i{\theta }_{i}^{2}}{\pi }\right)$ with parameter $m=0.5$ for $i=1,\ldots ,10$. To assess scalability to high dimensions, we test the optimization in a $D=100$-dimensional input space and optimize components of dimensionality $d=10$, where the relevant dimensions are distributed uniformly randomly (with replacement) across the 10 components of the partition by enforcing that all the relevant dimensions are not contained in a single component. In this experiment we emphasize that Add-GP conforms to the properties of the objective function and is therefore a reference baseline for good performances. Figure 4 shows the progression of all optimization algorithms. Overall, we see that optimization with axis-aligned projections with the QGP model is an effective and competitive method for Bayesian optimization when f is decomposable as sum of low-dimensional components. We also note that both QGP and Lip-GP show consistent gap in data efficiency and optimization, which motivates the QGP as a model in the presence of inconsistencies for effective optimization along projections.

Fig. 4

Results with Michalewicz benchmark function showing convergence results under additivity assumption with error bars showing twice standard error. The figures show comparison across different acquisition functions: aEI, bUCB, cPI. Convergence results of QGP recover best results after Add-GP which complies with Michalewicz additive properties

5.3 Non-additive high-dimensional objective

This experiment analyzes the performance of the QGP BayesOpt in a high-dimensional search space, when we no longer make any assumptions on additive decomposability of the objective. More specifically, we define the objective, $f(\varvec{\theta })=10\sin {\theta _{1}}\prod \nolimits _{i=1}^{10}\sin (\theta _{i})$, with effective dimensionality of 10. We optimize 10-dimensional components in a fixed partition of a 100-dimensional input space avoiding condensing all relevant dimensions in a single group.

Figure 5 shows that QGP model attains the best observation at termination with respect to other baselines in both EI and UCB acquisition functions. For PI the QGP model shows a slower progression than Add-GP and GP-Lip during the early stages of optimization. Other baselines, such as REMBO, flatten out quite early. We explain poor performances of the REMBO baseline by noting that it performs exploration only on a d-dimensional space. Using a linear mapping it can only span at most d directions in the D-dimensional space, and this heavily restricts exploration. We observe that even relaxing assumptions on additivity, the additive model still maintains similar performances both in terms of progress and value at termination for most acquisition functions considered remaining however suboptimal on exploration with expected improvement and upper confidence bound. Overall the QGP results are competitive for different properties of the black-box function and prove robust with respect to model hyper-parameter $\tau$. These results highlight the QGP as a good model for optimization with projected data.

Fig. 5

We compare results on a 10-dimensional, non-additive, objective with all acquisition functions: aEI, bUCB, cPI. We assess performances with functions that are effectively lower-dimensional and non additive and assess performances of the QGP model

Fig. 6

Results with Michalewicz benchmark function showing convergence results under arbitrary rotation of the high-dimensional space. We report a comparison across different acquisition functions: aEI, bUCB, cPI. Convergence results of QGP recover best steepest descent and better optimum at termination on all acquisitions

5.4 Rotated high-dimensional objective

Our last experiment analyses the performances of the QGP-BayesOpt approach under arbitrary rotation of the high-dimensional domain. In particular, we consider the rotated additive Michalewicz benchmark function, $g(\varvec{\theta })=f(\mathbf {U}\varvec{\theta })$, where $\mathbf {U}\in \mathbb {R}^{D\times D}$ is an arbitrary orthogonal matrix, obtained by applying orthonormalization of a random matrix $\mathbf {B}$, where $[\mathbf {B}]_{i,j}\sim \mathcal {N}(0, 1)$, and f is defined as in Sect. 5.2. We maintain the same model selection procedure for the GP models in each baseline i.e. with Gamma hyper-prior Ga(shape=1, scale=1) on the kernel lengthscales and the marginal likelihood defined as in Eq. (10). Figure 6 shows the results obtained with each baseline. Performances of both axis-aligned projections-based baselines, namely QGP model and Add-GP, clearly deteriorate w.r.t. the original experiment in Sect. 5.2. The random projection-based baseline REMBO, instead, shows steeper descent and better optimum at termination of optimization. Moreover, lengthscale kernel-parameters for the QGP model become shorter. In fact, by averaging over the 20 random initializations and the 250 iterations, we observe that at least⁴$95\%$ of lengthscales have decreased from the axis-aligned experiment. The variance (over random initializations and iterations) of the lengthscale parameters also becomes smaller. In particular, the average variance (averaging over all lengthscales) for the rotated objective experiment decreases by a factor⁵ of 0.014. This is a sign of a more highly nonlinear response surface, characterized by many local minima and therefore harder to optimize. The QGP model, however, still retains best performances also w.r.t. random projection-based methods on all acquisitions.

6 Conclusion

We proposed a framework for scaling Bayesian optimization to high dimensions by using axis-aligned projections. We considered a quantile regression approach that allows for generalizations from projected data and we empirically showed low sensitivity of QGP-BayesOpt w.r.t. to the choice of the quantile parameter $\tau$. Based on experimental results, we argue that modeling extreme functions from projected data maintains good indicators of the optimum location.

One observation is that QGP BayesOpt features sensible modeling of the response surface from unstructured data and has an effective update strategy on all. We acknowledge that careful modeling and corresponding complexity of the learning is also an important trade-off to consider. The QGP approximates the GP posterior with EP, which becomes computationally involved for a large number of data points.

To address this downside, future work will tackle computational efficiency with sparse GP methods and extend applicability to a large number of data points in short time. Future work will also investigate whether to concentrate BayesOpt updates on projections that matter and neglect those that leave f unchanged. Analysis of the GP hyper-parameters could allow for introducing an on-line selection strategy based on the optimization history.