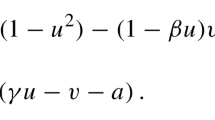1 Introduction

In this paper, we shall consider the following FithzHugh-Nagumo system with linear cross-diffusion terms:

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \frac{\partial u}{\partial t}=u(1-u^2)-(1-\beta u)v+\nabla ^2u+d_v\nabla ^2v\,, &{}\qquad \text {on}\, \Omega \times {\mathbb {R}}_+ ,\\ \\ \displaystyle \frac{\partial v}{\partial t}=\varepsilon \left( \gamma u- v-a\right) +d_u\nabla ^2u+d\nabla ^2v, &{}\qquad \text {on}\,\Omega \times {\mathbb {R}}_+ ,\\ \\ \displaystyle \frac{\partial u}{\partial n}= \frac{\partial v}{\partial n}=0, &{}\qquad \text {on}\, \Omega \times {\mathbb {R}}_+ ,\\ \,\\ \displaystyle u({\textbf{x}},0)= u^{in} ({\textbf{x}}), \quad v({\textbf{x}},0)= v^{in}({\textbf{x}}), &{}\qquad \hbox { on}\,\ \Omega . \end{array} \right. \end{aligned}$$
(1.1)

In particular, we shall study the stationary patterns emerging from the instabilities exhibited by the above system in the excitable regime, see [8] for the proof of the existence, and under what conditions, of these instabilities. We refer the reader to [6, 8] for a thorough explanation of the meaning of the terms appearing in the above system and for their biological motivation. Here, we mention that \(u({\textbf{x}},t)\) and \(v({\textbf{x}},t)\) are the activator and the inhibitor species, respectively; that \(\Omega \) will be a finite interval for \(m=1\) and a rectangular domain for \(m=2\); and that, throughout the paper, we shall assume the following conditions on the coefficients of the system (1.1):

$$\begin{aligned}&\varepsilon>0, \quad \gamma >0, \quad 0\le \beta \ll 1, \quad a\in {\mathbb {R}}, \end{aligned}$$
(1.2a)
$$\begin{aligned}&\qquad d>0, \quad d_u\ge 0, \quad d_v\ge 0. \end{aligned}$$
(1.2b)

In the parameter region where the FHN model exhibits excitability, and in the presence of only ordinary diffusion terms, the system (1.1) does not admit any Turing instability [8, 15]. Therefore, small-amplitude stationary patterns close to equilibrium do not exist. However, excitability coupled to a strong lateral inhibition, namely with d sufficiently large, leads to forming far-from-equilibrium structures: they have large amplitude and do not emerge from a Turing bifurcation, see [5]. In [8], we proved that when the local behavior of the system (1.1) is excitable, a sufficiently large value of the cross-diffusion coefficient \(d_u\) is able to induce the formation of small-amplitude periodic patterns. We have called these structures cross-Turing patterns: cross-diffusion is responsible for their formation through a mechanism opposite to the classical Turing one, where the inhibitor must diffuse much faster than the activator. In fact, one obtains them for a sufficiently small value of the inhibitor/activator diffusivity ratio [8].

In this paper, we shall continue the analysis of the cross-Turing patterns initiated in [8]. First, we shall show that, as one can see in the monostable regime [6], the cross-Turing patterns are always out-of-phase, i.e., the concentration of the activator (or prey) is higher in regions of low inhibitor (or predator) concentration. This is a typical feature of the patterns observed within a cell [11, 13], which have been generally modeled by an activator-depleted substrate reaction coupled with simple diffusion [10]. We shall therefore prove that even if in the system (1.1), the reaction kinetics is not of activator-depleted substrate-type, a sufficiently high value of the inhibitor cross-diffusion may excite a stationary instability, leading to spatial segregation of the species.

Second, using the formalism of the amplitude equations, we shall perform a weakly nonlinear (WNL) analysis to construct the cross-Turing patterns. The WNL theory leads to amplitude equations, and provides a direct and exhaustive framework for classifying the different pattern outcomes supported by the model system (1.1). Adopting a multiple scales expansion, we shall derive the normal form of the bifurcation, so giving a reduced description of the pattern in terms of its amplitude [1, 4, 12].

On 1D or rectangular 2D domains, the Stuart-Landau equation is the normal form arising at a regular bifurcation via a simple eigenvalue. The analysis of the Stuart-Landau equation allows us to distinguish between super- and sub-critical instabilities; they correspond to the onset of qualitatively different spatial structures. The supercritical pattern grows from zero amplitude with the increasing distance from the bifurcation threshold; it is spatially extended, and it is usually subject to secondary instabilities in large domains, where different unstable modes can interact; the subcritical pattern, instead, has a large amplitude with hysteretic behavior; it is robust against small variations in the bifurcation parameter and, on large domains, sets the conditions for the birth of localized solutions through a mechanism known as homoclinic snaking [3].

On 2D domains, if the bifurcation occurs through a degenerate eigenvalue, the emerging pattern is characterized by different amplitudes, whose temporal evolution is governed by a coupled Stuart-Landau equation system. We shall show that the analysis of these coupled amplitude equations reveals a broad scenario of supported patterns, such as mixed-mode and hexagonal patterns.

Finally, we shall numerically address the effect of the cross-diffusion terms on the occurrence of far-from-equilibrium stationary patterns determined by the combination of lateral inhibition and excitability. In the absence of cross-diffusion terms, in [5], the authors prove the existence of large amplitude stationary peak solutions to the excitable FHN model on 1-D spatial domains with Neumann boundary conditions. These structures are not Turing patterns, as the FHN reaction kinetics does not support any diffusion-driven instability. In [5], the authors noted that the formation of the pattern requires a very large value of the diffusivity ratio. Here we show that the presence of small cross-diffusion terms enlarges the parameter region where the pattern occurs, allowing for the formation of the large amplitude pulses in the case of lateral activation. In fact, on 1-D and 2-D spatial domains, we show that small positive values of the cross-diffusion coefficients determine the settlement of large stationary patterns also when the activator diffuses faster than the inhibitor, making the pattern mechanism more robust and extending the class of initial conditions from which the structures develop.

The plan of the paper is the following. In Sect. 2, we shall address the pattern selection problem through a weakly nonlinear analysis. The first-order solution will show that the activator and the inhibitor spatially segregate past the bifurcation, forming out-of-phase spatial configurations. Moreover, we shall derive the system of amplitude equations and classify the stability of the corresponding steady states related to different spatial configurations. In Sect. 3, we shall consider far-from-equilibrium pulse-like solutions outside the Turing regime and numerically show how the presence of the cross-diffusion terms broadens the parameter region that allows for pattern formation.

2 Cross-turing patterns and amplitude equations

In this section, we shall construct the cross-Turing patterns in the excitable regime on 1D and 2D rectangular domains through the formalism of the amplitude equations. In [6], one can find the analysis of the monostable regime.

2.1 Notation and assumptions

In what follows, we shall fix the notation and recall the assumptions necessary for the system (1.1) to have a Turing bifurcation in the excitable regime.

For the system (1.1) to be excitable, it has to admit a single stable equilibrium \(E_0\equiv (u^*, v^*)\), located in the outer branch of the u-nullcline, see Fig. 1.

Fig. 1
figure 1

Nullclines of the local FHN system (1.1). The parameters are \(\varepsilon =0.1\), \(\beta =0.2\), \(\gamma =1.12\). a The excitable case, with \(a=-0.35\). b The excitable case, with \(a=0.5\). The labels m and M indicate the minimum and the maximum of the u-nullcline

Full size image

In terms of the system parameters, this implies that the following conditions hold:

$$\begin{aligned}&4p+3\left( {u}^*-\frac{\beta \gamma }{3}\right) ^2>0,&\qquad&\text { with }p=a\beta +\gamma -1-\frac{\beta ^2\gamma ^2}{3}, \end{aligned}$$
(2.1a)
$$\begin{aligned}&\varepsilon _H<0,&\qquad&\mathrm{with\ \ }\varepsilon _H=1+\beta v^*-3u^{*2}. \end{aligned}$$
(2.1b)

Specifically, condition (2.1a) ensures that the system admits a unique equilibrium \(E_0\), while condition (2.1b) guarantees that the equilibrium is stable, and located on the outer branch of the u-nullcline. The details on how to obtain the conditions (2.1a) and (2.1b) are in the Propositions 2.1 and 2.3 of [8].

The linearized dynamics of (1.1) in the neighborhood of \(E_0\) is:

$$\begin{aligned} \displaystyle \frac{\partial {\textbf{w}}}{\partial t}= & {} {\mathcal {L}}{\textbf{w}},\qquad \textrm{where}\quad {\mathcal {L}}=K+D\nabla ^2,\quad {\textbf{w}}^T=\left( \begin{array}{c} u-u^*\\ v-v^* \end{array}\right) \end{aligned}$$
(2.2)
$$\begin{aligned} K= & {} \left( \begin{array}{ccc} \varepsilon _H &{} -(1-\beta u^*)\\ \varepsilon \gamma &{} -\varepsilon \end{array}\right) \quad \text {and}\quad D=\left( \begin{array}{cc}1&{}d_v\\ d_u &{}d \end{array}\right) . \end{aligned}$$
(2.3)

For the well-posedness of the system (1.1), we will henceforth impose that the following condition is satisfied:

$$\begin{aligned} \det (D) =d-d_ud_v>0. \end{aligned}$$
(2.4)

The steady-state solution \(E_0\) undergoes a Turing bifurcation if it is stable against spatially uniform perturbations and loses stability due to spatially non-homogeneous perturbations. Looking for instability to perturbation proportional to \(\cos ({\textbf{k}}\cdot {\textbf{x}})\) leads to the following dispersion relation, which gives the eigenvalue \(\lambda \) as a function of the wavenumber k:

$$\begin{aligned} \lambda ^2+g\left( k^2\right) \lambda + h\left( k^2\right) =0, \end{aligned}$$
(2.5)

with:

$$\begin{aligned} h\left( k^2\right)= & {} \det (D)k^4+qk^2+\det (K),\nonumber \\ g\left( k^2\right)= & {} k^2\textrm{tr}(D)-\textrm{tr}(K),\nonumber \\ \text {and }q= & {} -(K_{11}D_{22}+K_{22}D_{11})+K_{12}D_{21}+K_{21}D_{12}, \end{aligned}$$
(2.6)

where \(K_{ij},\ D_{ij}\) are the entries of the matrices K and D, respectively.

Turing instability arises if \({\mathfrak {R}}(\lambda (k)) > 0\) for some \(k \ne 0\). The local stability of \(E_0\) implies that \(g(k^2)>0\), therefore instability can occur if, thanks to diffusion terms, one of the solutions of (2.5) crosses zero for some \(k \ne 0\), or equivalently if \(h(k^2)\) is negative for some \(k \ne 0\). Since the minimum of \(h(k^2)\) is attained at:

$$\begin{aligned} k_c^2=-\frac{q}{2\det (D)}, \end{aligned}$$
(2.7)

then the conditions necessary for Turing instability to develop are as follows [14]:

figure a

The bifurcation value \(d_c\) is determined by solving (2.8b) when the equality holds. Details on the above discussion can be found in Theorem 5.2 in [8], where also the expression of the above given conditions (2.8a)–(2.8b) in terms of the parameters of the original system (1.1) are given.

2.2 One dimensional domain

Fig. 2
figure 2

Cross-diffusion-driven small-amplitude patterns: the pattern amplitude scales as \(\mu \), where \(\mu ^2= (d_c-d) /d_c\). The solid (dotted) curve indicates the profile of the u- (v-) species. The red horizontal line corresponds to the excitability threshold for u. The parameters are chosen as \(\beta =0.2, a=-0.35, \gamma =1.12 ,\varepsilon =0.1 \) so that \(E_0=(-0.6163, -0.3403)\) with \(d_v=0.1\), \(d_c=0.01117193\) and \({{\bar{u}}}=-0.4962\) is the excitability threshold (color figure online)

Full size image

In this section, we shall address the construction of the cross-Turing pattern on a one-dimensional spatial domain. Let \(\mu \), defined by \(\mu ^2= (d_c-d) /d_c\), be the control parameter that measures the distance from the bifurcation threshold. We shall consider the following asymptotic expansions for \({\textbf{w}}, t\) and d:

$$\begin{aligned} {\textbf{w}}= & {} \mu {\textbf{w}}_1+\mu ^2 {\textbf{w}}_2+\mu ^3 {\textbf{w}}_3+\dots , \end{aligned}$$
(2.9)
$$\begin{aligned} t= & {} t+\mu T_1+\mu ^2 T_2+\dots , \end{aligned}$$
(2.10)
$$\begin{aligned} d= & {} d_c+\mu d^{(1)}+\mu ^2 d^{(2)}+\mu ^3 d^{(3)}\dots \ , \end{aligned}$$
(2.11)

where \(d^{(i)} <0, \ i=1, 2, \dots \). The procedure to construct the \({\textbf{w}}_i\) is given in [6]. Here we report the expression for the first order perturbation \({\textbf{w}}_1\), namely:

$$\begin{aligned} \begin{array}{ll} {\textbf{w}}_1=A(T_1,T_2,\dots ){\varvec{\varrho }}\cos (k_cx),\quad {\textrm{with}}\\ {\varvec{\varrho }}=\left( \begin{array}{c}1\\ M\end{array}\right) \in Ker(K-k_c^2 D^c)\quad \text {and}\quad M=\displaystyle \frac{\varepsilon _H-k_c^2}{1-\beta u^*+k_c^2d_v}, \end{array} \end{aligned}$$
(2.12)

where \(k_c\) is defined in (2.7), \(D_c\) is the matrix D given in (2.2) computed at \(d=d_c\), and A is the stable stationary solution of the following Stuart-Landau equation:

$$\begin{aligned} \frac{d A}{dT_2}=\sigma A-LA^3. \end{aligned}$$
(2.13)

In (2.13), the constants \(\sigma >0\) and the Landau coefficient L are computed in terms of the parameters in (1.1).

The explicit expression of the first order solution given in (2.12) shows that, in the emerging structures formed by presence of the cross-diffusion, the u- and v-species are out-of-phase. This can be proved as follows: the pattern grows along the unstable manifold associated to the positive eigenvalue of the linearized dynamics. Recalling that in the excitable regime \(\varepsilon _H<0\), the explicit form of the eigenvector \({\varvec{\varrho }}\), given by formula (2.12), shows that the components of the eigenvector \({\varvec{\varrho }}\) have opposite signs, corresponding to out-of-phase spatial distribution of the species. In fact, the numerical simulations performed on 1D and 2D spatial domains, when the nonlinear terms come into play, validate the results supplied by the linear analysis, as shown in Fig. 3e–f.

In the above amplitude equation (2.13), the sign of L characterizes the bifurcation, discerning between a supercritical (\(L>0\)) and a subcritical (\(L<0\)) transition. In the supercritical case, the emerging solution of the system (1.1) on a one-dimensional domain can be predicted by the following

Theorem 1.1

(Asymptotic solution in the supercritical case).

Given the system (1.1), let \(E_0=(u^*, v^*)\) be the unique homogeneous steady state, satisfying the hypotheses of Theorem 5.2 in [8] for the onset of a cross-diffusion driven instability in the excitable regime.

If:

  1. (i)

    the distance from the bifurcation value is small enough such that \(k_c\) is the only unstable mode admitted by the boundary conditions;

  2. (ii)

    the coefficient L of the Stuart-Landau equation (2.13) is positive, i.e. the bifurcation is supercritical;

then the asymptotic solution of the system (1.1) on a one dimensional domain [0, L] is:

$$\begin{aligned} {\textbf{w}}=\mu A_{\infty }{\varvec{\varrho }}\cos (k_cx)+O(\mu ^2), \end{aligned}$$
(2.14)

where \(A_{\infty }\) is the stable steady state of the equation (2.13) and \({\varvec{\varrho }}\) is defined in (2.12).

We remark that under the hypotheses of Theorem 2.1, the inhibitor’s cross-diffusion term stabilizes the close-to-equilibrium patterns (2.14), whose amplitude scales with \(\mu \). Such small-amplitude structures do not arise in the excitable FHN system with classical diffusion terms, where excitability coupled with diffusion generates only large amplitude patterns. In Fig. 2, we show that if one chooses the value of the bifurcation parameter d sufficiently close to the bifurcation value \(d_c\), a stationary structure emerges whose amplitude, for the u-species, remains below the excitability threshold (see Fig. 2a–e). For larger d values, the pattern grows as predicted by WNL; some portions of the pattern may overcome the excitability threshold, see Fig. 2f, still remaining in the WNL predicted regime, which shows significant robustness of the Turing structures. The excitability effect seems to show in the fast-growing amplitude of the inhibitor pattern.

In the subcritical case (\(L<0\)), below the threshold Eq.(2.13) does not admit any stable solution, and, therefore, it is not able to capture the amplitude of the resulting pattern. In this case, the analytical approximation of the emerging solution requires the computation of higher orders of the asymptotic expansion, see [7].

The explicit analysis of the sign of L in Eq.(2.13) as a function of all the system parameters is complicated. We have, therefore, numerically computed L and shown the corresponding results in Fig. 3.

Fig. 3
figure 3

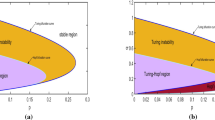
a In the \((d_u, d)\)-plane, we represent the regions of the parameter where Turing patterns form. The black and gray regions correspond to cross-Turing subcritical and cross-Turing supercritical bifurcation. The parameters are as in Fig. 2. We discern subcritical from supercritical behavior through the Landau constant L sign. b–c Numerically computed bifurcation diagrams as the parameter d is varied, showing super/sub transitions at the onset for different values of \(d_u\). The red (black) branches indicate stable (unstable) stationary solutions. The parameter values are as in (a) with \(d_u=0.11\), in (b), is in the supercritical region, while, in (c), \(d_u=0.3\) is in the subcritical region. d Cross-Turing instability for \(d\le d_c\): graph of the coefficient L of the amplitude equation (2.13) versus \(d_u\) for different choices of \(d_v\). The kinetic parameters are as in (a). e Cross-Turing supercritical pattern. The solid (dotted) curve indicates the profile of the u- (v-) species. The parameters are as in (b) with \(d=0.01116<d_c=0.01117193\). f Cross-Turing subcritical pattern. The solid (dotted) curve indicates the profile of the u- (v-) species. The parameters are as in (c) and \(d=0.10046<d_c=0.10148\) (color figure online)

Full size image

In Fig. 3a we have reported the classification of the bifurcation for a fixed set of kinetic parameters and for \(d_v=0.1\): the black (gray) region corresponds to cross-Turing subcritical (supercritical) bifurcation. We observe that high values of the inhibitor cross-diffusion \(d_u\) favour the insurgence of subcritical phenomena. The numerically computed bifurcation diagrams reported in Fig. 3b, c confirm the predictions of the weakly nonlinear analysis given in Fig. 3a, as they show the occurrence of a supercritical and a subcritical transition, respectively, when the parameters are chosen in the corresponding region of Fig. 3a. In Fig. 3d we have reported the sign of L as a function of \(d_u\) for the same values of the kinetic parameters chosen in Fig. 3a and for different values of \(d_v\): the graph shows that increasing \(d_v\) enlarges the areas of the instability region where one has subcriticality. A supercritical cross-Turing pattern is shown in Fig. 3e and a subcritical one in Fig. 3f.

2.3 Two-dimensional domain

On a two-dimensional rectangular domain \(\Omega \equiv [0, L_x]\times [0, L_y]\), the solution to the linearized system (2.2) subject to the no-flux boundary conditions is:

$$\begin{aligned} {\textbf{w}}=\sum _{m,n\in {\mathbb {N}}}{\textbf{f}}_{mn}e^{\lambda (k^2_{mn})t} \cos (\phi x)\cos (\psi y), \end{aligned}$$
(2.15)

with:

$$\begin{aligned} \phi =\frac{m\pi }{L_x}, \quad \psi =\frac{n\pi }{L_y},\qquad m,n\in {\mathbb {N}}, \end{aligned}$$
(2.16)

where \({\textbf{f}}_{mn}\) are the Fourier coefficients of the initial perturbation, \(\lambda \) are the eigenvalues provided by the dispersion relation (2.5). The integers m and n appearing in (2.16) are such that

$$\begin{aligned} k_c^2=\phi ^2+\psi ^2, \end{aligned}$$
(2.17)

where \(k_c\) is critical wavenumber, computed as in (2.7). In what follows, we shall assume that there exists only one unstable wavenumber \(k_c\) admitted by the boundary conditions imposed on the spatial domain \(\Omega \). The bifurcation is regular or degenerate, depending on the existence of one or two mode pairs of integers (m, n) satisfying conditions (2.16) and (2.17). Therefore, the WNL analysis will predict the emerging solution of the original system (1.1). The following Theorem holds:

Theorem 1.2

(Asymptotic solution at a regular bifurcation in the supercritical case).

In the rectangular domain \(\Omega \equiv [0,L_x]\times [0,L_y]\), consider the system (1.1); let \(E_0=(u^*, v^*)\) be the unique homogeneous steady state, satisfying the hypotheses of Theorem 5.2 in [8] for the onset of a cross-diffusion driven instability in the excitable regime. Suppose that

  1. (i)

    the distance \(\mu \) from the bifurcation value \(d_c\) is small enough so that \(k_c\) is the only unstable wavenumber admitted by the boundary conditions;

  2. (ii)

    there exists only one mode pair of integers (m, n), defined as in (2.16), and satisfying condition (2.17);

  3. (iii)

    the bifurcation is supercritical, i.e., the coefficient L of the Stuart-Landau equation (2.13) is positive.

Then, the asymptotic solution of the system (1.1) is:

$$\begin{aligned} {\textbf{w}}=\mu A_\infty {\varvec{\varrho }}\cos (\phi x)\cos (\psi y)+O(\mu ^2), \end{aligned}$$
(2.18)

where \(A_\infty \) is the stable steady state of the equation (2.13), \({\varvec{\varrho }}\) is given in (2.12), \(\phi \) and \(\psi \) are defined as in (2.16)–(2.17).

Below we provide a numerical simulation that illustrates the cross-Turing pattern arising at a regular bifurcation, as predicted by (2.18). All the numerical simulations of system (1.1) reported in this section are obtained using a second-order Runge-Kutta time-stepping scheme with \(dt = 10^{-2}\) and a Fourier spectral solver with \(256 \times 256\) spatial modes.

In Fig. 4 we show a square cross-Turing pattern, emerging as solution of the FHN system (1.1) when the hypotheses of Theorem 5.2 in [8] hold and the conditions \(i)-iii)\) of Theorem 2.2 are satisfied. In the square domain \(\left[ 0,2\pi \right] \times \left[ 0,2\pi \right] \), choosing the parameters as in Fig. 4, the most unstable mode \(k_c\approx 4.25065\) corresponds to the unique pair of integers \((m,n)=(6,6)\) satisfying the condition (2.17). The emerging cross-Turing pattern is well approximated by (2.18) with \(A_\infty \approx 1.63094\), where \(A_\infty \) is the unique stable equilibrium of the Stuart-Landau equation (2.13). The spectra of the numerical solution of the system (1.1), reported in Fig. 4b–d, show the agreement with the expected form of the solution, as (6, 6) is the pair of modes of the numerical solution with higher amplitude. The mode pairs (12, 0) and (0, 12) are sub-harmonics which can be predicted at order \(\varepsilon ^2\). We notice that, as discussed in [8] and in Sect. 2.2, in the excitable case the diffusive-instability is determined solely by the presence of a sufficiently strong cross-diffusion term of the inhibitor species: therefore, since the inhibitor avoids high concentration areas of activator, the arising patterns are out-of-phase spatially distributed, as shown in Fig. 4a–c.

Fig. 4
figure 4

Cross-Turing supercritical pattern supported by the system (1.1) in the excitable case at a regular bifurcation. The kinetics parameters are chosen as \(\beta =0.1\), \(a=0.3\), \(\gamma =1.02\) and \(\varepsilon =2\) with \(d_v=0\), \(d_u=2.16375, d=0.0082<d_c=0.008312\), that gives \(k_c^2=18\). In the square domain \(\left[ 0,2\pi \right] \times \left[ 0,2\pi \right] \) the most unstable mode \(k_c\approx 4.25065\) corresponds to the unique couple of integers \((m,n)=(6,6)\) satisfying the condition (2.17). a–c Numerical solutions of the system (1.1) computed using a spectral algorithm. b–d Spectrum of the solutions

Full size image

In Fig. 5 we have chosen the parameters in such a way that a subcritical regular cross-Turing bifurcation is expected on the basis of the theoretical analysis. The numerically computed solution is reported in Figs. 5a–c. We recall that the subcritical patterns cannot be predicted by the asymptotic procedure developed here, as one should push the analysis up to higher orders, see details in [7]. In fact, the inspection of the numerical spectrum, reported in Figs. 5b–d, reveals that several pair modes, other than the critical one, result excited with comparable intensity.

Fig. 5
figure 5

Cross-Turing subcritical pattern supported by the system (1.1) in the excitable case at a regular bifurcation. The parameters are chosen as \(\beta =0.2\), \(\gamma =1.1\), \(a=-0.4\), \(\varepsilon =2\), \(d_u=3\) and \(d_v=0.2\), \(d=0.62<d_c^-\approx 0.6392\). In the square domain \(\left[ 0,\frac{4\sqrt{2}\pi }{k_c}\right] \times \left[ 0,\frac{4\sqrt{2}\pi }{k_c}\right] \) the most unstable mode \(k_c\approx 3.0192\) corresponds to the unique couple of integers \((m,n)=(4,4)\) satisfying the condition (2.17). a–c Numerical solutions of the system (1.1) computed using a spectral algorithm. b–d Spectrum of the solutions

Full size image

Suppose, now, that the bifurcation is degenerate with multiplicity 2, i.e. there are two pairs of integers \((m_i, n_i), i=1,2\) satisfying the conditions (2.16) and (2.17). Moreover, the following non-resonance conditions hold:

$$\begin{aligned} \begin{array}{ccc} \phi _i+\phi _j\ne \phi _j &{} \text { or }&{} \psi _i-\psi _j\ne \psi _j\\ &{}\text {and}&{}\\ \phi _i-\phi _j\ne \phi _j &{} \text { or }&{} \psi _i+\psi _j\ne \psi _j, \end{array},\quad \text {where}~~ \phi _i=\frac{m_i \pi }{L_x},\ \psi _i=\frac{n_i \pi }{L_y}. \end{aligned}$$
(2.19)

Performing the WNL analysis up to \(O(\varepsilon ^3)\), we find that the amplitudes \(A_1\) and \(A_2\) of the expected emerging pattern should obey to the following two coupled Landau equations:

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle \frac{dA_1}{dT_2}=\sigma _1 A_1-L_1A_1^3+\Omega _1 A_1A_2^2\,,\\ \\ \displaystyle \frac{dA_2}{dT_2}=\sigma _2 A_2-L_2A_2^3+\Omega _2 A_1^2A_2\,. \end{array} \right. \end{aligned}$$
(2.20)

The details of the analysis to find the system (2.20) and to determine the conditions for the existence and stability of its equilibria are given in [6, 9] and are not reported here. The following Theorem holds:

Theorem 1.3

(Asymptotic solution at a degenerate non-resonant bifurcation).

Given the system (1.1), let \(E_0=(u^*, v^*)\) be the unique homogeneous steady state, satisfying the hypotheses of Theorem 5.2 in [8] for the onset of a cross-diffusion driven instability in the excitable regime. If:

  1. (i)

    the distance \(\mu \) from the bifurcation value \(d_c\) is small enough such that \(k_c\) is the only unstable wavenumber admitted by the boundary conditions;

  2. (ii)

    in the rectangular domain \(\Omega \equiv [0,L_x]\times [0,L_y]\) there exist two mode pairs of integers \((m_i,n_i), i=1,2\) defined as in (2.16) and satisfying condition (2.17);

  3. (iii)

    the non-resonance conditions (2.19) hold;

  4. (iv)

    the amplitudes system (2.20) admits at least one stable equilibrium;

then the asymptotic solution of the system (1.1) on a two-dimensional rectangular domain \(\Omega \) approximated at the leading order is:

$$\begin{aligned} {\textbf{w}}=\mu {\varvec{\varrho }}\left( A_{1\infty } \cos (\phi _1 x)\cos (\psi _1 y)+A_{2\infty } \cos (\phi _2 x)\cos (\psi _2 y)\right) +O(\mu ^2), \end{aligned}$$
(2.21)

where \(\left( A_{1\infty }, A_{2\infty }\right) \) is a stable steady state of the system (2.20), \({\varvec{\varrho }}\) is given in (2.12), \(\phi _i\) and \(\psi _i,\, i=1,2\) are defined as in (2.16)–(2.17).

In Fig. 6 we show the mixed mode cross-Turing pattern emerging when the system parameters are fixed so that the hypotheses of Theorem 5.2 in [8] hold and the conditions \(i)-iv)\) of Theorem 2.3 are satisfied. For the chosen parameter set, there exist the two mode pairs (8, 16) and (16, 8) satisfying the conditions (2.17) in the square domain \([0, 2\pi ]\times [0, 2\pi ]\). Then the emerging solution at the leading order is well approximated by:

$$\begin{aligned} {\textbf{w}}=\mu {\varvec{\varrho }}\left( A_{1\infty } \cos (4 x)\cos (8 y)+A_{2\infty } \cos (8 x)\cos (4 y)\right) +O(\mu ^2), \end{aligned}$$
(2.22)

computed as in (2.21), with \((A_{1\infty } , A_{2\infty }) \approx (0.6573, 0.6573)\) unique stable equilibrium of the amplitude system (2.20). The other modes appearing in the spectrum of the numerical solutions given in Fig. 6 are subharmonics that could be predicted at higher \(\mu \)-order.

Fig. 6
figure 6

Cross-Turing mixed-mode pattern supported by the system (1.1) when the excitable equilibrium loses stability via a degerate bifurcation and non-resonance conditions (2.19) hold. The parameters are chosen as \(\beta =0.1\), \(a=0.3\), \(\gamma =1.02\), \(\varepsilon =2\) and \(d_u=2.0654\), \(d_v=0.05\), \(d=0.1036<d_c^-\approx 0.1037\). In the square domain \(\left[ 0,2\pi \right] \times \left[ 0,2\pi \right] \) the most unstable mode \(k_c\approx 8.9443\) corresponds to the two couples of integers \((m_1,n_1)=(8,16)\) and \((m_2,n_2)=(16,8)\) satisfying the condition (2.17). a–c Numerical solutions of the system (1.1) computed using a spectral method. b–d Spectrum of the solutions

Full size image

In the latter case, we assume that the bifurcation is still degenerate with multiplicity 2, but the mode pairs satisfy the following resonant conditions:

$$\begin{aligned} \begin{array}{ccc} \phi _i+\phi _j=\phi _j &{} \text { or }&{} \psi _i-\psi _j=\psi _j\\ &{}\text {and}&{}\\ \phi _i-\phi _j=\phi _j &{} \text { or }&{} \psi _i+\psi _j=\psi _j, \end{array}, \quad {where }~~ \phi _i=\frac{m_i \pi }{L_x},\ \psi _i=\frac{n_i \pi }{L_y},\ i=1,2 \,.\nonumber \\ \end{aligned}$$
(2.23)

The WNL analysis at \(O(\varepsilon ^3\)) predicts that the amplitudes \(A_1\) and \(A_2\) of the pattern must satisfy the following equations, see details in [6, 9]:

$$\begin{aligned} \left\{ \begin{array}{lll} \displaystyle \frac{dA_1}{dT}=\sigma _1 A_1-L_1A_1A_2+\Omega _1 A_1^3+\Phi _1 A_1A_2^2\,,\\ \,\\ \displaystyle \frac{dA_2}{dT}=\sigma _2 A_2-L_2A_1^2+\Omega _2 A_2^3+\Phi _2A_1^2A_2\,, \end{array} \right. \end{aligned}$$
(2.24)

and the following Theorem hold:

Theorem 1.4

(Asymptotic solution at a degenerate resonant bifurcation).

Given the system (1.1), let \(E_0=(u^*, v^*)\) be the unique homogeneous steady state, satisfying the hypotheses of Theorem 5.2 in [8] for the onset of a cross-diffusion driven instability in the excitable regime. If:

  1. (i)

    the distance \(\mu \) from the bifurcation value \(d_c\) is small enough such that \(k_c\) is the only unstable wavenumber admitted by the boundary conditions;

  2. (ii)

    in the rectangular domain \(\Omega \equiv [0,L_x]\times [0,L_y]\) there exists two mode pairs of integers \((m_i,n_i), i=1,2\) defined as in (2.16) and satisfying condition (2.17);

  3. (iii)

    the resonance conditions (2.23) hold;

  4. (iv)

    the amplitudes system (2.24) admits at least a stable equilibrium.

Then the emerging solution of the system (1.1) in a two-dimensional rectangular domain \(\Omega \) approximated at the leading order is:

$$\begin{aligned} {\textbf{w}}=\mu {\varvec{\varrho }}\left( A_{1\infty } \cos (\phi _1 x)\cos (\psi _1 y)+A_{2\infty } \cos (\phi _2 x)\cos (\psi _2 y)\right) +O(\mu ^2), \end{aligned}$$
(2.25)

where \(\left( A_{1\infty }, A_{2\infty }\right) \) is the stable state of the system (2.24), \({\varvec{\varrho }}\) is given in (2.12), \(\phi _i\) and \(\psi _i\) are defined as in (2.16)–(2.17).

The solutions in (2.25), satisfying the resonant conditions (2.23) describes rolls (if \(A_{1\infty }=0\)) or hexagons, see [9] for details. The hexagons are subcritical structures, and the WNL analysis perfectly predicts the dominant modes. The overall quantitative accuracy is relatively low, which is typical for subcritical transitions. In Fig. 7, we show the cross-Turing hexagonal pattern supported by the system (1.1) when the parameters are such that the hypotheses of the Theorem 5.2 in [8] hold and the conditions \(i)-iv)\) of Theorem 2.4 are satisfied.

Fig. 7
figure 7

Cross-Turing hexagonal pattern supported by the system (1.1) when the excitable equilibrium loses stability via a degerate bifurcation and resonance conditions (2.23) hold. The parameters are chosen as \(\beta =0.2\), \(a=-0.35\), \(\gamma =1.12\), \(\varepsilon =0.1\) with \(d_u=0.562\), \(d_v=2\) and \(d=1.1317<d_c^-\approx 1.1329\). In the rectangular domain \(\left[ 0,2\pi \right] \times \left[ 0,2\sqrt{3}\pi \right] \) the most unstable mode \(k_c\approx 2\) corresponds to the two couples of integers \((m_1,n_1)=(2,6)\) and \((m_2,n_2)=(4,0)\) satisfying the condition (2.17). a–c Numerical solutions of the system (1.1) computed via spectral methods. b–d Spectrum of the solutions

Full size image

3 Far-from-equilibrium solutions

In this section, we shall perform a numerical investigation of the stationary large-amplitude patterns to (1.1). Without cross-diffusion terms, the FHN system does not support any Turing pattern. However, assuming Neumann boundary conditions, far-from-equilibrium solutions appear: the proof of their existence is in [5]. Using a shooting method, the authors show that the coupling of excitability and lateral inhibition produces the insurgence of symmetric solitary and periodic stationary pulses on an infinite one-dimensional domain. In [5], the stability of such solutions is also studied using numerical simulations: to reflect lateral inhibition and excitability, the authors select a large value of the ratio of diffusivities d and a small value of \(\varepsilon \), respectively. Under this assumption, the numerical experiments show that an initial condition consisting of a square small-width centered impulse, whose height exceeds the excitability threshold, evolves into a symmetric large amplitude solitary peak solution. Moreover, starting from a datum consisting of a symmetric wavetrain of square impulses, symmetric multipeak stationary solutions arise, whose amplitude remains constant as d is varied.

In what follows, we shall numerically study the impact of the cross-diffusion terms on such solutions, extending the analysis to rectangular plane domains. In all the subsequent numerical experiments, we shall choose the parameters outside the cross-diffusion-driven instability region to investigate the structures whose formation is not due to the cross-Turing mechanism.

In Fig. 8, on the spatial interval \(\Omega =[0,16 \pi ]\), we set the initial condition as follows:

$$\begin{aligned} u(x,0)= \left\{ \begin{array}{ll} u^*&{}\qquad \text {for} ~x \in \Omega \setminus S,\\ u_0&{} \qquad \text {for} ~x \in S, \end{array} \right. \qquad \qquad v(x,0)= v^*, \end{aligned}$$
(3.1)

where \((u^*,v^*) \) are the coordinates of the equilibrium point \(E_0\), \(S\equiv [22\pi /3, 26\pi /3]\) and \(u_0=-0.2\), higher than the excitation threshold \({{\bar{u}}}=-0.4962\). (see Fig. 8a). In the absence of diffusion, the effect of excitability on the initial datum \((u_0, v^*)\) would be a large excursion of the species before settling to \((u^*, v^*)\). Our numerical tests reveal that, without cross-diffusion (\(d_u=d_v=0\)), there exists a threshold value \(d^t\approx 4.9936\) of the diffusion coefficient d for the formation of a peak solution. At \(d=d^t\), the solution monotonously evolves towards the single peak pulse shown in Fig. 8b. When \(0<d<d^t\), the solution evolves towards the homogeneous state (not shown here). We then select a value of d less than one, namely \(d=0.99\), together with \(d_v=0\). We numerically obtain that at \(d_u=d_u^t\approx 0.5505\), the single peak solution shown in Fig. 8c emerges. On the other hand, with \(d_u<d_u^t\), no nonconstant solution forms. The chosen parameter regime does not support cross-Turing instability, given that \(d=0.99>d_c=0.3415\). Therefore, a sufficiently high value of \(d_u\) allows the forming of a localized solution also in the presence of lateral activation, namely a fast diffusing activator and a slowly diffusing inhibitor. Notice that if the cross-diffusion term is present in the model, the spatial distribution of the two species displays peaks of one species corresponding to troughs of the other (see Fig. 8c).

Fig. 8
figure 8

The parameters are chosen as \(\beta =0.2\), \(\gamma =1.12\), \(a=-0.35\), \(\varepsilon =0.1\). a Initial condition for u, consisting of a square perturbation of the equilibrium \(u^*\), centered at \(x=8\pi \) and having width \(\Delta x=4\pi /3\), where \(u_0=-0.2\). The initial condition for v is chosen as \(v=v^*\) for \(x \in [0,16 \pi ]\). b Stationary single peak pulse solution when \(d_u=d_v=0\) and \(d=d^t\approx 4.9936\) (d) Stationary single peak pulse solution when \(d_u=d_u^t\approx 0.5505\), \(d_v=0\) and \(d=0.99 >d_c\approx 0.3415\)

Full size image
Fig. 9
figure 9

The width of the initial perturbation is half of that in Fig. 8a. In this case, in absence of cross-diffusion terms, the solution evolves towards the homogeneous equilibrium (not shown here). The parameters are chosen as in Fig. 8c. a Initial condition for u, consisting of a square perturbation of the equilibrium \(u^*\), centered at \(x=8\pi \) and having width \(\Delta x=2\pi /3\), where \(u_0=-0.2\). The initial condition for v is chosen as \(v=v^*\) for \(x \in [0,16 \pi ]\). b Stationary single peak pulse solution

Full size image

The numerical simulations indicate that the presence of cross-diffusion terms makes the pattern more robust: with the same parameter set as in Fig. 8, in Fig. 9a we impose the initial condition as in (3.1), with \(S\equiv [23\pi /3, 25\pi /3]\), i.e., the width of the initial perturbation of u is half of that in Fig. 8a. Choosing \(d, d_u\), and \(d_v\) as in Fig. 8c, no spatially non-constant solutions form. However, one can still get the formation of spatially non-homogeneous solutions, provided that a value of \(d_u\ge d_u^t\approx 0.7299\) is selected. In Fig. 9b, we show the pulse obtained at \(d_u= d_u^t\approx 0.7299\). Thus, halving the width of the initial perturbation for u, the peak solution still emerges, although at a slightly larger value of the cross-diffusion coefficient. Conversely, in the absence of cross-diffusion, the simulations show that even increasing the value of d up to \(d\simeq 1000\), the stationary pulse does not form, and the solution evolves towards the spatially homogeneous steady state (not shown here).

In Fig. 10, we show another numerical test that illustrates how the threshold values \(d^t\) and \(d_u^t\) depend on the choice of the initial condition. We choose the same parameter set as in Fig. 8, and impose the initial condition as in (3.1), with \(S\equiv [16 \pi /3, 20\pi /3] \cup [28 \pi /3, 32\pi /3]\), see Fig. 10a. In Fig. 10b, we show the two-peak stationary pulse solution that emerges without cross-diffusion terms when the diffusion coefficient \(d=d^t\approx 6.3196\). With d and \(d_v\) as in Fig. 8c, the two-peak stationary pulse solution reported in Fig. 10c emerges at \(d_u=d_u^t\approx 0.555\).

Fig. 10
figure 10

The parameters are chosen as in Fig. 8. a Initial condition for u, consisting of two square perturbations of the equilibrium \(u^*\), centered at \(x=15 \pi /2\) and \(x=17 \pi /2\), respectively, and having width \(\Delta x=4\pi /3\), where \(u_0=-0.2\). The initial condition for v is chosen as \(v=v^*\) for \(x \in [0,16 \pi ]\). b Stationary two-peak pulse solution for \(d_u=d_v=0\) and \(d=d^t\approx 6.3196\). c Stationary two-peak pulse solution for \(d=0.99\), \(d_v=0\) and \(d_u=d_u^t\approx 0.555\)

Full size image

We now present some numerical simulations performed on 2D domains. In analogy to the 1D case, we assign as an initial condition a centered square homogeneous perturbation of the equilibrium for u and the equilibrium value for v, i.e.:

$$\begin{aligned} u(x,0)= \left\{ \begin{array}{ll} u^*&{}\qquad \text {for}~ (x,y) \in \Omega \setminus S,\\ u_0&{} \qquad \text {for} ~(x,y) \in S, \end{array} \right. \qquad \qquad v(x,0)= v^*, \end{aligned}$$
(3.2)

where \(\Omega \equiv [0, 24\pi ]\times [0, 24\pi ]\), \(S\equiv [8\pi , 16\pi ]\times [8\pi , 16\pi ]\) and \(u_0=-0.2\), as shown in Fig. 11a. Under these conditions and without cross-diffusion terms, a high value of the diffusivity ratio is necessary to generate a stationary solution. In Fig. 11, we show the stationary solution emerging at \(d=d^t\approx 16.5501\). Instead, including small cross-diffusion terms allows for the formation of stationary structures for small values of d and even in the presence of a fast diffusing activator. In Fig. 12, we show the stationary pattern which emerges by choosing \(d=0.99\), \(d_v=0\) and \(d_u=d_u^t\approx 0.6991\), starting from the same initial condition as in Fig. 11.

Fig. 11
figure 11

The parameters are chosen as in Fig. 8 with \(d_u=d_v=0\) and \(d=d^t\approx 16.5501\). a Initial condition for u, consisting of one square perturbation of the equilibrium \(u^*\), centered at \((x,y)=(12 \pi , 12 \pi )\) and having width \((\Delta x, \Delta y)= (8\pi , 8\pi )\), where \(u_0=-0.2\). The initial condition for v is chosen as \(v=v^*\) for \((x,y) \in \Omega \). b Stationary patterned solution for u. c Stationary patterned solution for v

Full size image
Fig. 12
figure 12

The parameters are chosen as in Fig. 8 with \(d=0.99\), \(d_v=0\) and \(d_u=d_u^t\approx 0.6991\). a Initial condition for u. The initial condition is assigned as in Fig. 11a. b Stationary pattern obtained for u. c Stationary pattern obtained for v

Full size image

To conclude this section, we show that, as already observed in the 1-D case, the cross-diffusion terms make the 2-D patterns more robust: in Fig. 13, we select the parameter set as in Fig. 12, and we impose the initial condition for u as a centered square perturbation of the equilibrium \(u^*\) of smaller extent than in Fig. 12. Namely, the initial datum is as in (3.2) with \(S\equiv [10\pi , 14\pi ]\times [10\pi , 14\pi ]\), as shown in Fig. 13a. Without cross-diffusion, the solutions settle to the homogeneous equilibrium (not shown here), even increasing the diffusion coefficient up to \(d\approx 1000\). In contrast, the presence of cross-diffusion determines the insurgence of far-from-equilibrium patterns. In Fig. 13b, c, we show the stationary pattern which emerges choosing \(d=0.99\), \(d_v=0\) and \(d_u=d_u^t\approx 0.8119\) (no nonconstant solution emerges for \(d_u<d_u^t\)).

Fig. 13
figure 13

The parameters are chosen as in Fig. 12 with \(d_u=0.8119\). a Initial condition for u, consisting of one square perturbation of the equilibrium \(u^*\), centered at \((x,y)=(12 \pi , 12 \pi )\) and having width \((\Delta x, \Delta y)= (4\pi , 4\pi )\), where \(u_0=-0.2\). The initial condition for v is chosen as \(v=v^*\) for \((x,y) \in \Omega \). b Stationary pattern obtained for u. c Stationary pattern obtained for v

Full size image

4 Conclusions

In this paper, we have analyzed the stationary patterns supported by a FHN-type model in its excitable regime with linear cross-diffusion terms. We have first investigated close-to-equilibrium structures, the cross-Turing patterns, which emerge due to a Turing instability driven by cross-diffusion. Through the WNL analysis, we have derived the equations for the amplitude of the cross-Turing patterns. The amplitude equation has provided qualitative and quantitative information close to the Turing bifurcation threshold: we have distinguished between supercritical and subcritical bifurcation. Moreover, several patterns, such as rolls, mixed-mode, and hexagons patterns, have appeared, all predicted by the WNL. Secondly, we have numerically investigated the existence of stationary pulse solutions that occur far from equilibrium. We have observed that cross-diffusion allows the formation of large amplitude structures also with short-range inhibition and lateral activation (differently from the classical theory [5]). Moreover, these solitary stationary structures obtained in the presence of cross-diffusion are more robust than their analog ones obtained in the presence of large values of the diffusivity ratio.

An issue that deserves investigation is the formation of cross-diffusion-driven patterns when the reaction term displays bistability. In this regime, one observes the formation of large amplitude structures that engulf both homogeneous equilibria, and that can be predicted through normal form reduction near the codimension-2 Turing-pitchfork bifurcation point [2].

Moreover, since the FHN system also supports Hopf instability, we believe that a further issue to explore is the spatiotemporal structures arising close to the codimension-2 Turing-Hopf bifurcation point.