Excitable FitzHugh-Nagumo model with cross-diffusion: long-range activation instabilities

Abstract

In this paper, we shall study a spatially extended version of the FitzHugh-Nagumo model, where one describes the motion of the species through cross-diffusion. The motivation comes from modeling biological species where reciprocal interaction influences spatial movement. We shall focus our analysis on the excitable regime of the system. In this case, we shall see how cross-diffusion terms can destabilize uniform equilibrium, allowing for the formation of close-to-equilibrium patterns; the species are out-of-phase spatially distributed, namely high concentration areas of one species correspond to a low density of the other (cross-Turing patterns). Moreover, depending on the magnitude of the inhibitor’s cross-diffusion, the pattern’s development can proceed in either case of the inhibitor/activator diffusivity ratio being higher or smaller than unity. This allows for spatial segregation of the species in both cases of short-range activation/long-range inhibition or long-range activation/short-range inhibition.

1 Introduction

The FitzHugh-Nagumo (FHN) system, initially introduced as a simplification of the Hodgkin–Huxley model to describe the conduction of electric impulses along a nerve axon [8, 22], has become a prototype of reaction-diffusion models of excitable media. FitzHugh-Nagumo-type equations are used to describe excitable behavior in many biological, chemical, and physical systems ranging from tissue muscles, intestine, and cardiac cells, to reaction kinetics, to deposition phenomena on metal surfaces [29]. In addition to excitability, the reaction kinetics of the FHN system can reproduce other qualitatively different dynamics, such as oscillations and bistability, by simply tuning the values of the parameters (see the classification of the local dynamics given in Sect. 2). Therefore, given its mathematical simplicity, the FHN model is widely adopted to mimic the mechanisms responsible for the formation of a variety of coherent structures such as stationary patterns, traveling waves, dissipative solitons, and complex spatiotemporal dynamics [6, 7, 19, 24, 26, 28, 33].

In this paper, we are interested in the formation of stationary patterns for the following FithzHugh-Nagumo-type model with cross-diffusion terms:

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \frac{\partial u}{\partial t}=u(1-u^2)-(1-\beta u)v+\nabla ^2u+d_v\nabla ^2v, &{}\quad \hbox {on } \Omega \times {\mathbb {R}}_+,\\ \displaystyle \frac{\partial v}{\partial t}=\varepsilon \left( \gamma u- v-a\right) +d_u\nabla ^2u+d\nabla ^2v, &{}\quad \hbox {on } \Omega \times {\mathbb {R}}_+,\\ \displaystyle \frac{\partial u}{\partial n}= \frac{\partial v}{\partial n}=0, &{}\quad \hbox {on }\Omega \times {\mathbb {R}}_+,\\ \,\\ \displaystyle u({\textbf{x}},0)= u^{in} ({\textbf{x}}), \quad v({\textbf{x}},0)= v^{in}({\textbf{x}}), &{}\quad \hbox {on } \Omega , \end{array} \right. \end{aligned}$$

(1.1)

where $u({\textbf{x}},t)$ and $v({\textbf{x}},t)$ are the activator and the inhibitor species, respectively; ${\textbf{x}}\in \Omega \subset {\mathbb {R}}^m$, where $\Omega$ is a spatial domain; here and in the companion paper [10], $\Omega$ will be either a finite interval (for $m=1$), or a square domain (for $m=2$); ${\partial }/{\partial n}$ is the derivative along the unit normal vector to the boundary $\partial \Omega$. The parameter d is the ratio between the diffusivities of v and u, respectively, and the parameters $d_u$ and $d_v$ are the cross-diffusion coefficients. The parameters $\varepsilon , \beta , \gamma$, and a characterize the local reaction dynamics: $\varepsilon$ is the ratio between the typical timescales of the two species, $\gamma$ and a control the number of intersections and the relative position of the nullclines, $0 \le \beta <1$ is a small parameter which breaks the symmetry $(u\rightarrow -u, v\rightarrow -v, a\rightarrow -a)$. All parameters are nonnegative, except a, which can be positive and negative. Throughout the paper, the coefficients of the above system will therefore satisfy the following conditions:

$$\begin{aligned}&\varepsilon>0, \quad \gamma >0, \quad 0\le \beta \ll 1, \quad a\in {\mathbb {R}}, \end{aligned}$$

(1.2a)

$$\begin{aligned}&\qquad d>0, \quad d_u\ge 0, \quad d_v\ge 0. \end{aligned}$$

(1.2b)

Throughout the paper, we shall consider the region of the parameter space where the system (1.1) admits a unique stable homogeneous equilibrium $E_0\equiv \left( u^*,v^*\right)$. For this reason, we shall impose the following conditions on the parameters: $\varepsilon >\varepsilon _H$ and $\gamma > \varepsilon _H/\left( 1-\beta u^*\right)$, where $\varepsilon _H=1+\beta v^*-3u^{*2}$ (for more details, see Sect. 2).

A typical mechanism leading to stationary patterns in reaction–diffusion systems is the Turing mechanism [31], where a small perturbation of the homogeneous equilibrium grows until saturation. The formation of this kind of structure for system (1.1) is the subject of the present paper. In the companion paper [10], we shall consider a different class of patterns arising from finite-amplitude localized perturbations of stable equilibrium. Such far-from-equilibrium structures occur in excitable or bistable systems, provided the inhibitor species diffuses sufficiently fast [4, 7, 28]. System (1.1) displays both bistability and excitability. In [10], we shall focus on the excitable regime.

The occurrence of Turing patterns is well-studied for the FitzHugh-Nagumo system in the monostable regime, where the reaction kinetics satisfies the requirements imposed by the diffusion-driven instability, namely, the self-activating species u promotes the growth of v while the self-inhibitor v suppresses the increase of u [11, 37]. In [9], the authors studied the effects of introducing linear cross-diffusion terms on forming stationary patterns in the monostable regime. Generalizing reaction–diffusion systems by introducing off-diagonal terms in the diffusion matrix accounts for the fact that the gradient of one species determines the dispersal of another species, a phenomenon frequently observed in real systems [23, 27, 32, 34]. In [9], the introduction of the cross-diffusion term was motivated in the context of population dynamics, as one can see that the FHN model rules the evolution of a perturbation of the homogeneous equilibrium in a predator–prey system describing plankton dynamics. The presence of cross-diffusion or nonlinear diffusion terms alters the pattern-forming properties of the models, enlarging the parameter region where the instability occurs or introducing otherwise unexpected solutions (see also [1, 13, 15,16,17, 20, 25]). In [9], the authors prove that a positive value of the inhibitor cross-diffusion $d_u$ broadens the region of the Turing instability and relaxes the requirement of a rapidly diffusing inhibitor, allowing for pattern formation also for comparable values of the diffusion coefficients or when the activator diffuses faster than the inhibitor. For a fixed and sufficiently large value of $d_u$, the homogeneous steady-state undergoes a double bifurcation as the ratio of diffusivities is varied: as prescribed by the classical Turing theory, the first bifurcation occurs for values of the diffusivity ratio above a critical threshold, $d_c^+$, and determines the birth of stationary periodic patterns where the species are in-phase spatially distributed. The second bifurcation is due to the presence of the cross-diffusion terms, taking place for values of the diffusivity ratio below a second critical threshold, $d_c^-$, where $d_c^- \le d_c^+$. In the latter case, the instability is driven by the inhibitor cross-diffusion $d_u$. The emerging stationary structures, named cross-Turing patterns, present spatial segregation of the species that distribute on the domain with opposite phasing. Moreover, for increasingly large values of the inhibitor cross-diffusion, the two thresholds, $d_c^+$ and $d_c^-$ coalesce and disappear so that the instability sets in independently of the value of the diffusivities ratio, whose magnitude only selects the relative phasing of the pattern.

In this work, we shall analyze the impact of the linear cross-diffusion terms on the onset of small-amplitude stationary nonhomogeneous solutions to the FHN system in the excitable regime. Roughly, an excitable system possesses the capability to amplify a superthreshold perturbation for a transient time before the response amplitude decreases. In a dynamical system, this property results in the existence of a unique equilibrium and of a threshold. In the presence of a perturbation whose size is below the threshold, the system quickly settles to equilibrium; if the perturbation is above the threshold, the system undergoes a large excursion before returning to the fixed point. The effect of cross-diffusion terms on wave-like solutions to excitable systems has been studied over the last decades in diverse contexts [2, 3, 18, 33, 35, 36]. However, the impact of non-diagonal diffusion terms on the formation of stationary patterns in excitable models has received less attention. In this paper we shall assume $d, d_u$ and $d_v>0$ to describe the following type of dispersal: both species diffuse and move away from high-density areas of the other species. In predator–prey systems, this type of cross-diffusion models a hunting strategy of the predator, consisting of heading to low-density areas of the prey to maximize its hunting success [12, 30]. In plankton models, the cross-diffusion term describes the tendency of the grazing zooplankton to avoid high concentrations of the toxin-producing phytoplankton [5, 15].

In the excitable regime, the linearized kinetics of the FHN system in the neighborhood of the homogeneous steady state does not satisfy the requirements of the classical Turing theory, so, in the presence of only ordinary diffusion terms, small amplitude patterns close to equilibrium do not develop [28]. However, if one assumes lateral inhibition, namely a rapid diffusion of the inhibitor relative to that of the activator, one can prove [7] the existence of large amplitude solitary and periodic stationary structures, which do not arise due to a Turing mechanism. In this work, we shall prove that when the local FHN dynamics is excitable, the presence of cross-diffusion terms may drive the appearance of small amplitude periodic structures of the same type observed in the monostable regime below the threshold $d_c^-$. Such cross-Turing patterns, in fact, occur for sufficiently high values of the inhibitor cross-diffusion $d_u$ and for values of the ratio of the diffusivities d below a given threshold. Moreover, depending on the value of the cross-diffusion coefficient $d_u$, the pattern may form for values of d less than unity, namely when the inhibitor species diffuses slower than the activator. In this case, the pattern-forming mechanism is opposite to what is prescribed by the classical Turing theory, which requires the inhibitor to diffuse much faster than the activator. In a companion paper [10], adopting an asymptotic procedure based on a multiple scales expansion, we shall construct the cross-Turing patterns and derive the corresponding amplitude equations.

The plan of the paper is the following. In Sect. 2, we shall classify the different dynamical regimes of the local FHN system and state the conditions for the existence and stability of a unique equilibrium; this leads to identifying two regions in the parameter space, where two different regimes, the monostable and the excitable one, occur. In Sect. 3, we shall perform the Turing instability analysis to determine the conditions under which Turing patterns generated by the cross-diffusion can emerge. In Sects. 4–5, we shall express such conditions in terms of the parameters of the original system (1.1), for the two cases of the monostable and excitable regime, respectively. Such analysis will provide the critical values of the bifurcation parameter and the wavenumber of the resulting solution. A thorough analysis of the monostable case is in [9], and we shall summarize the main results here for the reader’s convenience. In the concluding section, we discuss our results and the possible focus of future research.

2 Local dynamics of the FitzHugh-Nagumo system

In this Section we shall focus on the reaction term of (1.1), namely we shall consider the following dynamical system:

2.1 Classification of the equilibria

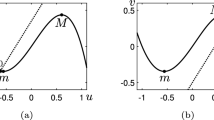
Depending on the values of the parameters $\beta$, $\gamma$ and a, one can have different relative positions of the u- and v-nullclines of the system (2.1a)–(2.1b). Following [9], we shall denote by m and M the points of the (u, v)-plane corresponding to the local minimum and maximum of the nullcline $f(u,v)=0$, respectively (see Fig. 1). The dynamics of the system (2.1a)–(2.1b) can be classified, according to the possible intersections of the u- and v-nullclines, as follows ([9, 14]):

• (i) monostable or oscillatory case, when the system (2.1a)–(2.1b) admits a unique stable equilibrium that lies on the inner branch of the u-nullcline, namely that portion of the curve that lies between m and M, see Fig. 1a. In this case, we shall say that the system (1.1) admits a unique inner equilibrium;

• (ii) excitable case, when the system (2.1a)–(2.1b) has a unique stable equilibrium that lies on one of the outer branches of the u-nullcline, namely those portions of the curve that lie on the left of m or on the right of M, see Fig. 1b or c. In this case, we shall say that the system (1.1) admits a unique outer equilibrium;

• (iii) bistable case, when the system (2.1a)–(2.1b) admits three equilibria, two stable and one unstable.

Fig. 1

Nullclines of the local FHN system (2.1a)–(2.1b). The parameters are $\varepsilon =0.1$, $\beta =0.2$, $\gamma =1.12$. a The monostable or oscillatory case, with $a=0.05$. b The excitable case, with $a=-0.35$. c The excitable case, with $a=0.5$. The labels m and M indicate the minimum and the maximum of the u-nullcline. The matrices give the signs of the derivatives $f_u, f_v, g_u, g_v$ evaluated at the equilibrium point

In this paper, we shall restrict the analysis to the region of the parameter space where the system (2.1a)–(2.1b) admits only one stable equilibrium, which corresponds to the two cases of the monostable and the excitable regime. According to the signs of the partial derivatives $f_u, f_v, g_u, g_v$ evaluated at the stable equilibrium point $E_0$ (see Fig. 1), one can classify the local interaction between u and v as of the activator-inhibitor type [21]. In fact, in all cases, at the stable equilibrium $E_0$, one has $g_u>0$ so that the activator u promotes the growth of v, and $f_v<0$, so that the inhibitor v dampens the increase of u. However, while in the monostable case the u-species is self-activating (since $f_u >0$), in the excitable case u is self-inhibiting (since $f_u <0$). As a consequence of the form of the nullclines, in the excitable regime, the dynamics of (2.1a)–(2.1b) exhibits a threshold behavior, namely, a sufficiently large perturbation from the equilibrium causes the species to undergo a large excursion before returning to the steady state.

2.2 Conditions for the existence of a unique equilibrium and its stability

Given the system (2.1a)–(2.1b), let $E_0\equiv \left( u^*,v^*\right)$ be an equilibrium point. First, we recall the conditions for $E_0$ to be a unique equilibrium of (2.1a)–(2.1b).

Proposition 2.1

(Conditions for the existence of a unique equilibrium) Given the system (2.1a)–(2.1b), where the parameters satisfy the conditions (1.2a), let $u^*$ be a real root of $u^3-\beta \gamma u^2+(a\beta +\gamma -1)u-a=0$. If:

$$\begin{aligned} 4 p+3\left( {u}^{*}-\frac{\beta \gamma }{3}\right) ^{2}>0, \qquad \hbox {with}\qquad p=a\beta +\gamma -1-\beta ^{2}\gamma ^{2}/3, \end{aligned}$$

(2.2)

then $E_0\equiv \left( u^*,v^*\right)$, where $v^*=\gamma u^*-a$, is the unique equilibrium point of (2.1a)–(2.1b).

The proof of the above Proposition is in the appendix of [9].

Remark 1

In the symmetrical case, when $\beta =0$, the condition (2.2) simplifies to $\gamma >1-3u^{*2}/4$. In the non-symmetrical case, $0<\beta \ll 1$, the condition (2.2) is equivalent to $\gamma _{-}<\gamma <\gamma _+$, where

$$\begin{aligned} \gamma \pm -=\left[ (2-\beta u^*)\pm {\sqrt{(2-\beta u^*)^2+4a\beta ^3+\beta ^2(3u^{*2}-4)}}\right] /\beta ^2, \end{aligned}$$

with $\lim _{\beta \rightarrow 0} \gamma _-=1-3u^{*2}/4$ and $\lim _{\beta \rightarrow 0} \gamma _+=+\infty$. Hence, by choosing a sufficiently small value of $\beta$, there is an arbitrarily large interval of $\gamma$-values such that the system admits a unique equilibrium.

Proposition 2.2

(Monostable or oscillatory case) Given the system (2.1a)–(2.1b), suppose the hypotheses of Proposition 2.1 are satisfied. If

$$\begin{aligned} \varepsilon _H>0, \qquad \hbox {with}\qquad \varepsilon _H=1+\beta v^*-3u^{*2}, \end{aligned}$$

(2.3)

then $E_0\equiv \left( u^*,v^*\right)$ is the unique inner equilibrium point of (2.1a)–(2.1b).

Proposition 2.3

(Excitable case) Given the system (2.1a)–(2.1b), suppose the hypotheses of Proposition 2.1 are satisfied. If

$$\begin{aligned} \varepsilon _H<0, \qquad \hbox {with}\qquad \varepsilon _H=1+\beta v^*-3u^{*2}, \end{aligned}$$

(2.4)

then $E_0\equiv \left( u^*,v^*\right)$ is the unique outer equilibrium point of (2.1a)–(2.1b).

The proof of Propositions 2.2 and 2.3 relies on the following observation: along the u-nullcline $v(u)= {u(1-u^2)}/({1-\beta u})\,$, one has:

$$\begin{aligned} v'(u^*)=\frac{\varepsilon _H}{1-\beta u^*}, \end{aligned}$$

(2.5)

so that, given that $1-\beta u^*>0$, the sign of $\varepsilon _H$ coincides with the sign of $v'\left( u^*\right)$. Hence, $\varepsilon _H>0$ on the inner branch of the u-nullcline, while $\varepsilon _H<0$ on the outer branches of the u-nullcline.

We now pass to analyze the stability of $E_0$. By setting ${\textbf{w}}=(u-u^*,v-v^*)^T$, we get the following linearized dynamics of (2.1a)–(2.1b) in the neighborhood of $E_0$:

$$\begin{aligned} \begin{array}{ccccc} {\textbf{w}}_t=K{\textbf{w}}, &{} \qquad &{}\hbox { with }&{}\quad &{} K=\left( \begin{array}{ccc} \varepsilon _H &{} -(1-\beta u^*)\\ \varepsilon \gamma &{} -\varepsilon \end{array}\right) , \end{array} \end{aligned}$$

(2.6)

and where $\varepsilon _H=1+\beta v^*-3u^{*2}$.

The following Proposition holds:

Proposition 2.4

(Stability of the unique equilibrium point) Given the system (2.1a)–(2.1b), suppose the hypotheses of Proposition 2.1 are satisfied. If

$$\begin{aligned} \textrm{tr}(K)= & {} -\varepsilon +\varepsilon _H<0, \end{aligned}$$

(2.7)

$$\begin{aligned} \det (K)= & {} \varepsilon \left[ -\varepsilon _H+\left( 1-\beta u^*\right) \gamma \right] >0. \end{aligned}$$

(2.8)

then $E_0\equiv \left( u^*,v^*\right)$ is a stable equilibrium point of (2.1a)–(2.1b).

Remark 2

In the excitable case, where $\varepsilon _H<0$, the conditions (2.7) and (2.8) are always satisfied and the equilibrium is stable. In the monostable regime, where $\varepsilon _H>0$, the equilibrium can undergo either a Hopf bifurcation, when $\varepsilon _H=\varepsilon$, or a pitchfork bifurcation, when $\varepsilon _H=\left( 1-\beta u^*\right) \gamma$.

3 Turing instability analysis

In this Section, we shall perform the Turing bifurcation analysis of the reaction–diffusion system (1.1) on the assumption of the existence of a unique stable equilibrium, i.e., under the hypotheses of Proposition 2.1 and of Proposition 2.4. The linearized dynamics of (1.1) in the neighborhood of $E_0$ is:

$$\begin{aligned} \frac{\partial {\textbf{w}}}{\partial t}={\mathcal {L}}{\textbf{w}}, \end{aligned}$$

(3.1)

where:

$$\begin{aligned} {\mathcal {L}}=K+D\nabla ^2,\qquad D=\left( \begin{array}{cc}1&{}\quad d_v\\ d_u &{}\quad d \end{array}\right) , \end{aligned}$$

(3.2)

and K is given in (2.6). Hereafter, we shall assume that the following necessary condition for the well-posedness of the system (1.1) is satisfied:

$$\begin{aligned} \det (D) =d-d_ud_v>0. \end{aligned}$$

(3.3)

The condition for steady state solution $E_0$ to undergo a Turing bifurcation is that it is stable against spatially uniform perturbations while it loses stability due to spatially non-homogeneous perturbations. Namely, if we look for instability to perturbations of the form $\cos {({\textbf{k}} \cdot {\textbf{x}})}$, the linear stability analysis leads to the following eigenvalue problem:

$$\begin{aligned} \lambda \, {\textbf{w}}= {\mathcal {M}}(k^2) \,{\textbf{w}}, \end{aligned}$$

(3.4)

where

$$\begin{aligned} {\mathcal {M}}(k^2) = K- k^2 D, \end{aligned}$$

(3.5)

and $k^2={\textbf{k}} \cdot {\textbf{k}}$. Instability sets in if ${\mathfrak {R}}(\lambda (k)) > 0$ for some $k \ne 0$, where $\lambda (k)$ is an eigenvalue of ${\mathcal {M}}(k^2)$, namely a solution of the following dispersion relation:

$$\begin{aligned} \lambda ^2+g\left( k^2\right) \lambda + h\left( k^2\right) =0, \end{aligned}$$

(3.6)

where the coefficients of the above dispersion relation are:

$$\begin{aligned} h\left( k^2\right)= & {} \det ({\mathcal {M}}(k^2))=\det (D)k^4+qk^2+\det (K),\nonumber \\ g\left( k^2\right)= & {} -\textrm{tr}({\mathcal {M}}(k^2))=k^2\textrm{tr}(D)-\textrm{tr}(K),\nonumber \\ q= & {} -(K_{11}D_{22}+K_{22}D_{11})+K_{12}D_{21}+K_{21}D_{12}, \end{aligned}$$

(3.7)

and $K_{ij},\ D_{ij}$ are the elements of the matrices K and D, respectively.

Since by Proposition 2.4 the equilibrium $E_0$ is stable for the kinetics, condition (2.7) holds so that the trace of ${\mathcal {M}}(k^2)$ is negative, i.e. $g\left( k^2\right) >0$ for all k. Therefore, Turing instability can occur only if, due to the presence of the diffusion terms, one of the eigenvalues of the matrix ${\mathcal {M}}(k^2)$ crosses zero, namely if the curve $h(k^2)=\det ({\mathcal {M}}(k^2))$ assumes negative values for some k. Since $h(k^2)$ attains its minimum at:

$$\begin{aligned} k_c^2=-\frac{q}{2\det (D)}, \end{aligned}$$

(3.8)

the necessary conditions for yielding the Turing instability are the following [21]:

Condition (3.9a) ensures that the minimum of $h(k^2)$ is attained at a positive value of $k^2$. Condition (3.9b) ensures that, past the bifurcation, the minimum value of $h(k^2)$ is negative, so to have a finite bandwidth of unstable wavenumbers $k^2$. Equality in (3.9b) holds at the bifurcation and, for fixed values of the other parameters, defines the critical value $d_c$ of the bifurcation parameter d.

In the next two Sections, we shall express the above-given conditions (3.9a)–(3.9b) together with the necessary condition for well-posedness, condition (3.3), in terms of the parameters of the original system (1.1). We shall consider separately the two cases of the monostable and excitable regimes.

In Sect. 4, we shall briefly treat the case of the monostable regime, already extensively analyzed in [9]. In Sect. 5, we shall treat the case of the excitable regime, the present paper’s main topic.

4 Diffusive instability: the monostable regime

In the absence of the cross-diffusion terms, the local behavior of the nullclines in the proximity of a monostable equilibrium satisfies the necessary conditions for the classical diffusion-driven instability and, therefore, allows for the onset of Turing patterns (see Fig. 1a). The presence of cross-diffusion terms, although non-necessary for the appearance of stationary patterns, enlarges the parameter region where instability may occur and introduces a new type of pattern.

For any nonnegative fixed value of $d_v$, conditions (3.3) and (3.9a) are both satisfied if:

$$\begin{aligned} \left\{ \begin{array}{ll} d> {\bar{d}}&{} \quad \hbox {for } d_u<\delta _u^{(1)},\\ d> d_v d_u &{} \quad \hbox {for } d_u \ge \delta _u^{(1)}, \end{array}\right. \end{aligned}$$

(4.1)

where

$$\begin{aligned} {\bar{d}}: =\frac{1}{\varepsilon _H}(\varepsilon (1+\gamma d_v)+(\beta u^*-1)d_u) \quad \hbox {and} \quad \delta _u^{(1)}: =\frac{\varepsilon (1+\gamma d_v)}{1-\beta u^*+\varepsilon _H d_v}. \end{aligned}$$

(4.2)

${\bar{d}}$ is the threshold value of the bifurcation parameter d above which one gets $q<0$ (i.e. a positive value of $k^2_c$) and $\delta _u^{(1)}$ defines in the $(d_u,d)$-plane the abscissa of the intersection point between the two straight lines $d={\bar{d}}$ and $d=d_u d_v$, see Fig. 2.

Fig. 2

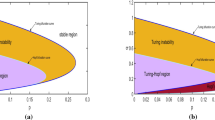
a–b Monostable case: geometrical representation of the conditions for the diffusive instability for two different choices of $d_v$. The regions in the $(d_u,d)$-plane above the two straight lines $d=d_u\, d_v$ (dashed line) and $d={\bar{d}}$ (dotted line) correspond to the fulfillment of conditions (3.3)–(3.9a). The gray shaded areas represent the diffusive instability regions in the $(d_u,d)$-plane, corresponding to the fulfillment of both (3.3)–(3.9a) and (3.9b). The boundaries of the Turing region are $d=d_c$, or $P(d)=0$, (solid line) and $d=d_v d_u$ (dashed line). The other parameters are chosen as $\beta =0.1, a=0.0001, \gamma =1.02,\varepsilon =2$, so that $E^*=(0.0051, 0.0051)$. (a) $d_v=0.1$, which gives $\delta _u^{(2)}=2.2051, \delta _u^{(1)}=2.0045$. b $d_v=1$, which gives $\delta _u^{(2)}=4.0421, \delta _u^{(1)}=2.0201$. c Turing pattern obtained by the numerical simulation of the system (1.1) in the competition regime, with $d_v=0.1$, $d_u=2.0194$ and $d=0.32> d_c^{+}=0.3191$ (so that $k_c^{+}=0.75$). The other parameters are chosen as in (a). The profile of the activator (inhibitor) is represented by a solid (dotted) line. d Cross-Turing pattern obtained by the numerical simulation of the system (1.1) in the competition regime, with $d_v=0.1$, $d_u=2.0194$ and $d=0.20423<d_c^{-}=0.20432$ (so that $k_c^{-}=2$). The other parameters are chosen as in (a). The profile of the activator u (inhibitor v) is represented by a solid (dotted) line

We now enforce condition (3.9b), where equality gives the threshold values for d. Written in terms of the system parameters, (3.9b) is expressed by the following second degree inequality:

$$\begin{aligned} P(d):=\varepsilon _H^2 \, d^2 - 2 d \, \left( \varepsilon _H^2 {\bar{d}}\ + 2 \det (K) \right) + \varepsilon _H^2 {\bar{d}}^2 + 4 \det (K) d_u d_v \ge 0. \end{aligned}$$

(4.3)

It is not difficult to prove that, in the $(d_u,d)$-plane, the locus where $P(d)=0$ is a parabola, see Fig. 2a, b. A detailed study of the solutions to (4.3), gives the conditions under which (3.9b) is verified, see [9] for details. Here we briefly report the results: Upon defining

$$\begin{aligned} \delta _u^{(2)}=\frac{\varepsilon (1+\gamma d_v)}{1-\beta u^*}, \quad \mathrm{}\quad \delta _u^{(3)}=\frac{\varepsilon _H\, \varepsilon (1+\gamma d_v)+\det (K)}{\varepsilon _H(1-\beta u^*+\varepsilon _Hd_v)}, \end{aligned}$$

(4.4)

we distinguish the following three different cases, depending on the value of the parameter $d_u$:

• (i) $d_u<\delta _u^{(1)} \qquad$ (Diffusion-dominated regime)

  For $d_u<\delta _u^{(1)}$, one has $d\ge {\bar{d}}>d_v\, d_u$. The quadratic polynomial P(d) given by (4.3) admits two real roots, of whom only one, $d_c$, is greater than ${\bar{d}}$. It follows that conditions (3.3) and (3.9a)–(3.9b) will be verified for $d \ge d_c$ (see Fig. 2a, b).

• (ii) $\delta _u^{(1)}\le d_u\le \delta _u^{(3)}\qquad$ (Competition regime)

  In this case ${\bar{d}}<d_v\, d_u$, so that, to satisfy (3.9a) and (3.3), we have to take $d> d_v\ d_u$ (see (4.1)). The quadratic polynomial P(d) given by (4.3) still admits two real roots, say $d_c^-$ and $d_c^+$, which both lie above the straight line $d=d_v d_u$ (see Fig. 2a, b).

• iii) $d_u>\delta _u^{(3)}\qquad$ (Cross-diffusion-dominated regime) In this region, being $\delta _u^{(1)}<\delta _u^{(3)}<d_u$, to satisfy (3.9a) and (3.3), we take $d> d_vd_u$. The polynomial P(d) never vanishes and (3.9b) is always satisfied. Therefore, the diffusion-driven instability occurs for all $d>d_v d_u$ that guarantee the well-posedness of the system (see Fig. 2a, b).

Hence, we have the following:

Theorem 4.1

(Diffusive instability—monostable case) Given the system (1.1) under the conditions (1.2a)–(1.2b). Suppose:

• 1. The hypotheses of Proposition 2.1 are satisfied;

• 2. The hypotheses of Proposition 2.2 are satisfied;

• 3. The hypotheses of Proposition 2.4 are satisfied.

Let ${\bar{d}}$, $\delta _u^{(1)}$, $\delta _u^{(2)}$ and $\delta _u^{(3)}$ be given by (5.3), (5.6) and (4.4), respectively.

Then:

• (i) if $d_u<\delta _u^{(1)}$, then the equilibrium $E_0$ loses stability through a Turing bifurcation whenever $d \ge d_c ={\bar{d}}+\xi ^+$, where $\xi ^+$ is the positive root of the following quadratic polynomial:

  $$\begin{aligned} P_1(\xi )=\varepsilon _H^2\xi ^2+4\det (K)\xi -4\det (K)({\bar{d}}-d_ud_v). \end{aligned}$$

  (4.5)

  At $d=d_c$ the critical wavenumber is given by:

  $$\begin{aligned} k_c= {\sqrt{-\frac{q_c}{2 \det (D_c)}}}, \end{aligned}$$

  (4.6)

  where:

  $$\begin{aligned} q_c= -\varepsilon _H d_c-(1-\beta u^*)d_u+\varepsilon (1+\gamma d_v), {\quad } \text {and} {\quad } \det (D_c)= d_c - d_u d_v . \end{aligned}$$

  (4.7)

• (ii) if $\delta _u^{(1)}\le d_u \le \delta _u^{(3)}$, then the equilibrium $E_0$ loses stability through a Turing bifurcation for

  $$\begin{aligned} d_v d_u<d\le d_c^-=d_v d_u+\xi _1 \qquad \hbox { or for }\qquad d\ge d_c^+=d_v d_u+\xi _2, \end{aligned}$$

  where $0<\xi _1<\xi _2$ are the roots of the following polynomial:

  $$\begin{aligned} \varepsilon _H^2\xi ^2-2 \xi \left\{ \left[ \varepsilon _H^2d_v+ \varepsilon _H (1-\beta u^*)\right] (\delta _u^{(3)}- d_u) +\det (K)\right\} +\varepsilon _H^2 \left( {\bar{d}}- d_u d_v\right) ^2. \end{aligned}$$

  (4.8)

  At $d=d_c^\pm$ the critical wavenumber is given by:

  $$\begin{aligned} k_c^\pm = {\sqrt{-\frac{q_c^\pm }{2 \det (D_c^{\pm })}}}, \end{aligned}$$

  (4.9)

  where:

  $$\begin{aligned} q_c^\pm = {-}\varepsilon _H d_c^\pm -(1-\beta u^*)d_u+\varepsilon (1+\gamma d_v) {\qquad } \text {and} {\qquad } \det (D_c^\pm )= d_c^\pm -d_ud_v. \end{aligned}$$

  (4.10)

• (iii) if $d_u>\delta _u^{(3)}$, then the equilibrium $E_0$ loses stability through a Turing bifurcation for all $d>d_v d_u$. For every fixed value of $d_u$ and d, the most unstable wavenumber is given by:

  $$\begin{aligned} k= {\sqrt{-\frac{q}{2 \det (D)}}}, \end{aligned}$$

  (4.11)

  where D and q are given in (3.3) and (5.2), respectively.

Theorem 4.1 states, for the monostable case, the existence of three different regimes, characterized, for any fixed value of $d_v$, by different values of the inhibitor cross-diffusion $d_u$. For small values of $d_u$, the pattern-forming instability is driven by the classical mechanism; the effect of the cross-diffusion term is to lower the bifurcation value of the diffusivity ratio $d_c$. The reason is easily understood: the classical Turing mechanism requires high mobility of the inhibitor, to which, here, also cross-diffusion contributes. Increasing values of $d_u$ reduce further the bifurcation threshold $d_c$ and may drive it below unity, allowing the pattern formation for a slowly diffusing inhibitor. As predicted by the classical theory, one can show that the species spatially distribute in phase, with values of the activator peaks higher than the inhibitor maxima. We have named this regime diffusion-dominated.

For increasing values of $d_u$, according to Theorem 4.1 one has the competition regime: for the same parameter set, the homogeneous equilibrium of (1.1) undergoes a double bifurcation as d is varied so that two qualitatively different patterns form for $d\le d_c^-$ and for $d \ge d_c^+$, respectively. The latter is just the continuation of the branch observed in the diffusion-dominated regime, with in-phase spatially distributed species. On the other hand, the pattern arising for $d\le d_c^-$ is a new phenomenon, determined by the presence of the cross-diffusion $d_u$, where the spatial concentration of the activator is out-of-phase with respect to the density of the inhibitor, see Fig. 2. As the cross-term drives it, we have called this structure a cross-Turing pattern.

Finally, for increasingly large values of $d_u$, the two bifurcation values $d_c^+$ and $d_c^-$ approach and collide at $d_u= \delta _u^{(3)}$. The cross-diffusion dominated regime is obtained for values of $d_u$ larger than $\delta _u^{(3)}$: the mechanism of pattern formation is now driven solely by the cross-diffusion and the instability sets in independently on d, whose value only determines the relative phasing of the species.

5 Diffusive instability: the excitable regime

In this Section, we shall derive the conditions for the onset of diffusive instabilities in the excitable regime, i.e., when the kinetics of the system (1.1) admits a single outer equilibrium. Therefore, throughout this Section, we shall assume to hold the conditions of Proposition 2.1 (ensuring uniqueness of the equilibrium), and of Propositions 2.3 and 2.4 (ensuring excitability and stability, respectively). namely:

$$\begin{aligned} 1-\beta u^*>0 \quad \hbox {and} \quad \varepsilon _H <0. \end{aligned}$$

(5.1)

We shall express the condition for the reality of the critical wavenumber, i.e., (3.9a), the bifurcation condition, i.e., (3.9b), and the necessary condition for well-posedness, i.e., (3.3), in terms of the system parameters, considering d as the bifurcation parameter.

The plan of the Section is the following. First, in Sect. 5.1, we shall show how, without cross-diffusion, no pattern would arise. Second, in Sect. 5.2, we shall impose the reality of the critical wavenumber, condition (3.9a), deriving the conditions (5.3) and (5.4). In Sect. 5.3, we shall impose the well-posedness condition, deriving the condition (5.7), that includes the conditions (5.3) and (5.4). In Sect. 5.4, we shall impose the bifurcation condition (3.9b), proving Proposition 5.1. In Sect. 5.5 we shall state the Theorem 5.2, that summarizes the analysis, and discuss the obtained results.

5.1 Classical diffusion coupled with excitable kinetics does not allow Turing instability

In the absence of the cross-diffusion terms, the linearized dynamics in the neighborhood of a single outer equilibrium (see Fig. 1b, c) prohibits the onset of Turing instability. Although the interaction between the two species is of activator-inhibitor type (being $f_v <0,\, g_u>0$), the requirement $f_u\, g_v<0$ is not satisfied: namely, the inhibitor v, is not self-activating. In fact, when the inhibitor species is autocatalytic, a smaller value of the activator diffusivity may allow for the onset of a stationary instability resulting in out-of-phase patterns of the two species [21]. The excitable kinetics, instead, when the model includes the classical diffusion only, forbids the instability of the equilibrium point. In what follows, we shall show that the presence of the cross-diffusion terms can destabilize the equilibrium, so determining a finite-size Turing region in the parameter space. We shall also highlight the role of varying $d_u$ and $d_v$ separately, showing that they have opposite influences on the width of the Turing region.

5.2 The first necessary condition for the cross-diffusion-driven instability: Eq. (3.9a) $q<0$

Expliciting q as defined in (3.7) in terms of the system parameters, yields:

$$\begin{aligned} q=-\varepsilon _H d-(1-\beta u^*)d_u+\varepsilon (1+\gamma d_v). \end{aligned}$$

(5.2)

When the equilibrium point $E_0$ of the reaction terms (2.1a)–(2.1b) lies on either one of outer branches of the u-nullcline, one has that $\varepsilon _H<0$. So that it is easily seen that condition (3.9a), $q<0$, is verified for:

$$\begin{aligned} d<{\bar{d}}, \quad \hbox {where} \ {\bar{d}}: =\frac{1}{\varepsilon _H}(\varepsilon (1+\gamma d_v)+(\beta u^*-1)d_u). \end{aligned}$$

(5.3)

Therefore, ${\bar{d}}$ is the threshold value of the bifurcation parameter d below which $q<0$ and one gets a positive value of $k^2_c$.

However, ${{\bar{d}}}$ could be negative, which would make the condition (5.3) impossible to verify. Therefore, we now investigate the conditions under which ${{\bar{d}}}\ge 0$. In the $(d_u,d)$-plane, for fixed $d_v$, the condition $d < {{\bar{d}}}$ corresponds to the region below the straight line $d={\bar{d}}$, see Fig. 3a and b. Since $1-\beta u^* >0$ and $\varepsilon _H <0$, the slope of the line $d={\bar{d}}$ is positive, while the intercept with the d-axis $I_c=\varepsilon (1+\gamma d_v)/\varepsilon _H$ is negative. An equivalent condition to have a non-negative value of ${{\bar{d}}}$ is therefore that:

$$\begin{aligned} d_u >\delta _u^{(2)}, \quad \hbox {where} \quad \delta _u^{(2)}: =\frac{\varepsilon (1+\gamma d_v)}{1-\beta u^*}. \end{aligned}$$

(5.4)

The conditions (5.3) and (5.4), both necessary conditions for the onset of a cross-diffusion-driven instability, are the main results of the present Subsection.

Fig. 3

Geometrical representation of the conditions for the Turing instability in the excitable case. a–b For two different choices of $d_v$, the dark gray regions in the $(d_u,d)$-plane delimited by the two straight lines $d=d_u\, d_v$ (dashed line) and $d={\bar{d}}$ (dotted line) correspond to the fulfillment of conditions (3.3)–(3.9a). The other parameters are chosen as $\beta =0.2, a=-0.35, \gamma =1.12,\varepsilon =0.1$, so that $E_0=(-0.6163, -0.3403)$. a $d_v=0.1$, which gives $\delta _u^{(2)}=0.099, \delta _u^{(1)}=0.1009, I_c=-0.5357$. b $d_v=1$, which gives $\delta _u^{(2)}=0.1887, \delta _u^{(1)}=0.2315, I_c=-1.0213$. c–d Depicted in gray the Turing instability region in the $(d_u,d)$-plane, corresponding to the fulfillment of both (3.3)–(3.9a) and (3.9b) for two different values of $d_v$.The boundaries of the Turing region are $d=d_c$, or $P(d)=0$, (solid line) and $d=d_v d_u$ (dashed line). c The parameters are chosen as in (a). d The parameters are chosen as in (b)

5.3 Intersection of the well-posedness condition $d>d_u d_v$ with $d<{{\bar{d}}}$

In addition to condition (3.9a), which is equivalent to (5.3), we have to satisfy the well-posedness condition (3.3). Therefore, we must have

$$\begin{aligned} d_ud_v<d<{{\bar{d}}}. \end{aligned}$$

In the $(d_u,d)$-plane, the above conditions are satisfied in the intersection of two half-planes, see also Fig. 3a and b. In the $(d_u,d)$-plane, this intersection is nonempty if and only if the slope $d_v$ of the line $d=d_v\, d_u$ is smaller than the slope of the line $d={\bar{d}}$. Such requirement imposes a condition on $d_v$, namely:

$$\begin{aligned} d_v<\delta _v: =\displaystyle \frac{\beta u^*-1}{\varepsilon _H}. \end{aligned}$$

(5.5)

When (5.5) is verified, the two lines meet at the value $d_u= \delta _u^{(1)}$ where:

$$\begin{aligned} \delta _u^{(1)}: =\frac{\varepsilon (1+\gamma d_v)}{1-\beta u^*+\varepsilon _H d_v}, \end{aligned}$$

(5.6)

that defines the abscissa of the leftmost point of the region in the $(d_u,d)$-plane where both conditions (3.3) and (3.9a) are verified (see Fig. 3a, b). On the other hand, one has to take into account the condition (5.4): however, by inspection, $\delta _u^{(1)} \ge \delta _u^{(2)}$ for any non-negative $d_v$; therefore, condition (5.4) can be dropped. One finally gets the following requirement for $d_u$:

$$\begin{aligned} d_u\ge \delta _u^{(1)}, \quad \hbox {where} \ \delta _u^{(1)}: =\frac{\varepsilon (1+\gamma d_v)}{1-\beta u^*+\varepsilon _H d_v}. \end{aligned}$$

In conclusion, the main result of the present subsection are the following conditions:

$$\begin{aligned} d_v<\delta _v, \qquad d_u\ge \delta _u^{(1)} \qquad d_ud_v< d < {{\bar{d}}} \end{aligned}$$

(5.7)

which is an improved version of the condition (5.3).

We finally notice that the quantity $\delta _u^{(1)}$ is an increasing function of $d_v$, so that increasing the cross-diffusion of the activator $d_v$ reduces the width of the Turing region. This is also apparent from the comparison of Fig. 3a and b.

5.4 The second necessary condition for the cross-diffusion-driven instability: Eq.(3.9b)

Supposing that (5.7) is satisfied, let us now consider the last condition (3.9b), where equality gives the threshold values for d. We shall prove the following

Proposition 5.1

Given the system (1.1) under the conditions (1.2a)–(1.2b), suppose that the hypotheses of Propositions 2.1 and of Proposition 2.3 are satisfied. Let $d_v<\delta _v$ and $d_u\ge \delta _u^{(1)}$, with $\delta _v$ and $\delta _u^{(1)}$ given by (5.5) and (5.6), respectively. Then, there exists $d_c\in ({{\bar{d}}}, d_ud_v)$, such that $P(d_c)=0$, with

$$\begin{aligned} P(d):=\varepsilon _H^2 \, d^2 - 2 d \, \left( \varepsilon _H^2 {\bar{d}}\ + 2 \det (K) \right) + \varepsilon _H^2 {\bar{d}}^2 + 4 \det (K) d_u d_v. \end{aligned}$$

(5.8)

Moreover, for any $d\in (d_c, d_ud_v)$, one has that $P(d)>0$.

Proof

Making it explicit in (3.9b) the dependence on the system parameters, one gets a second degree inequality for d, namely:

$$\begin{aligned} P(d):=\varepsilon _H^2 \, d^2 - 2 d \, \left( \varepsilon _H^2 {\bar{d}}\ + 2 \det (K) \right) + \varepsilon _H^2 {\bar{d}}^2 + 4 \det (K) d_u d_v \ge 0. \end{aligned}$$

(5.9)

The condition for criticality in (5.9) is given by $P(d)=0$, that represents in the $(d_u,d)$-plane a parabola (see Fig. 3c, d). It is easy to prove that the symmetry axis that the symmetry axis of the parabola has the same slope of the line $d={\bar{d}}$. The discriminant of P(d) reads:

$$\begin{aligned} \Delta =4\det (K)(\det (K)+\varepsilon _H^2({\bar{d}}-d_ud_v)). \end{aligned}$$

(5.10)

The discriminant $\Delta$ is positive: in fact, $\det (K) >0$ since, by Propositions 2.3 and 2.4, $E_0$ is stable for the kinetics. Moreover, by (5.7), ${\bar{d}}>d_ud_v$ (see also Fig. 3a, b). From the positivity of $\Delta$, it follows that the polynomial P(d) admits two real roots. By the Descartes’ rule of signs, such roots are both positive. We now prove that only one of the two roots of P(d) belongs to the interval $(d_u d_v, \, {\bar{d}} )$, as required by (5.7). To find the roots $d_c$ that lie below the threshold ${\bar{d}}$, we substitute $d= {\bar{d}}-\xi$ in P(d) defined by (5.9). By inspection, one sees that the resulting quadratic polinomial in $\xi$, namely:

$$\begin{aligned} \varepsilon _H^2\xi ^2+4\det (K)\xi -4\det (K)({\bar{d}}-d_ud_v), \end{aligned}$$

(5.11)

admits only one real positive root $\xi ^+$. Similarly, it is easy to prove that such root

$$\begin{aligned} d_c\equiv {{\bar{d}}} -\xi ^+ \end{aligned}$$

(5.12)

is such that $d_c>d_ud_v$. We have therefore proved that there exists a unique value of the parameter $d=d_c$, given by (5.12), with $d_c \in (d_u d_v, \, {\bar{d}} )$ such that $P(d_c)=0$ and $P(d)>0$ for $d \in (d_u d_v, \, d_c )$. $\square$

5.5 Main result and discussion

The analysis of the Sects. 5.2, 5.3 and 5.4 can be summarized as follows:

Theorem 5.2

(Diffusive instability—excitable case) Given the system (1.1) under the conditions (1.2a)–(1.2b). Suppose:

• 1. The hypotheses of Proposition 2.1 are satisfied;

• 2. The hypotheses of Proposition 2.3 are satisfied;

• 3.
  $$\begin{aligned} \begin{array}{ll} d_v < \delta _v, &{} \quad \hbox { with } \quad \delta _v ={(\beta u^*-1)}/{\varepsilon _H},\\ d_u>\delta _u^{(1)}, &{} \quad \hbox { where } \quad \delta _u^{(1)}={\varepsilon (1+\gamma d_v)}/{(1-\beta u^*+\varepsilon _H d_v)}. \end{array} \end{aligned}$$

  (5.13)

Let $\xi ^+$ be the positive root of the polynomial (5.11), then the equilibrium $E_0$ loses stability through a Turing bifurcation whenever $d_ud_v<d \le d_c$, where $d_c={\bar{d}}-\xi ^+$. The critical wavenumber is given by:

$$\begin{aligned} k_c={\sqrt{ -\frac{q_c}{2 \det (D_c)}}}, \end{aligned}$$

(5.14)

where:

$$\begin{aligned} q_c= -\varepsilon _H d_c-(1-\beta u^*)d_u+\varepsilon (1+\gamma d_v) \quad \hbox {and} \quad \det (D_c)= d_c-d_ud_v. \end{aligned}$$

(5.15)

Proof

Given that the hypotheses of Proposition 2.1 are satisfied, the equilibrium $E_0$ is unique. Moreover, by the hypotheses of Proposition 2.3 and by Proposition 2.4, $E_0$ is stable with excitable dynamics. By the hypotheses given in (5.13), one has that $d_u d_v <{{\bar{d}}}$, where ${{\bar{d}}}$ is given by (5.3), see Sect. 5.2. Therefore, choosing $d_v <\delta _v$ and $d_u\ge \delta _u^{(1)}$, one has that for any d such that $d_u d_v<d<{{\bar{d}}}$, the necessary condition for well-posedness is satisfied and the critical wavenumber is real-valued, see Sect. 5.3. Finally, Proposition 5.1 guarantees that there exists a unique value $d_c={\bar{d}}-\xi ^+$ such that:

• (i) for $d=d_c$:

  • $\lambda (k_c)=0$, i.e. the growth rate $\lambda (k_c)$ of the critical wavenumber $k_c$ is zero;

  • $\lambda (k)<0,\ \forall k\ne k_c$, i.e. the growth rate of all the wavvembers except $k_c$ is negative;

• (ii) for $d<d_c$ there exists a band of wavenumbers $k\in (k_1,k_2)$ such that:

  • $\lambda (k)>0$ for $k \in (k_1,k_2)$, $\lambda (k)<0$ for $k <k_1 \cup k >k_2$ and $\lambda (k_1)=\lambda (k_2)=0$; i.e. only the wavenumbers belonging to the interval $(k_1,k_2)$, have positive growth rate.

$\square$

5.5.1 Discussion

Theorem 5.2 reveals that including in the model the cross-diffusion terms relaxes the requirements on the reaction kinetics imposed by the classical Turing mechanism for the formation of patterns. Classically, diffusion-driven instability not only requires the reaction kinetics to be of activator-inhibitor-type, but it is also necessary that either: (a) the activator species is self-activating, and the inhibitor is self-inhibiting (so that the linearized kinetics matrix is of the form shown in Fig. 1a); or (b) that the activator is self-inhibiting, and the inhibitor is self-activating (so that in the linearized kinetics, one has $f_u<0, f_v<0, g_u>0, g_v>0$). Neither of the two conditions, (a) or (b), is valid for the FitzHugh-Nagumo model (1.1) in the excitable regime: By the linearized kinetics close to the equilibrium, one easily derives that the u-species (activator) is self-inhibiting but, contrarily to what the Turing mechanism requires, the v-species (inhibitor) is self-inhibiting too. In the absence of autocatalytic effects of the inhibitor and if only classical diffusion terms are present, any small perturbation of the equilibrium decays, inhibiting pattern formation.

More precisely, Theorem 5.2 explains that, with excitable dynamics, the cross-diffusion causes instability when present in the inhibitor equation. To understand this, take both the cross-diffusion coefficients equal to zero: from the expression (5.3), one can see that the threshold ${\bar{d}}$ below which condition (3.9a) is satisfied assumes the negative value $\varepsilon /\varepsilon _H$, so that no positive value of d would make it possible a bifurcation at $E_0$. An increase of $d_v$ maintaining $d_u=0$, further lowers the threshold ${\bar{d}}$ to the value $I_c={\varepsilon (1+\gamma d_v)}/\varepsilon _H$ (see Fig. 3a, b), preventing even more the occurrence of the instability. On the other hand, if one chooses $d_v=0$, (3.9a) is satisfied for all values of $d_u$ greater than $\delta _u^{(1)}=\delta _u^{(2)}$, i.e., in the region of the $(d_u, d)$-plane delimited by the $d_u$-axes and the straight line $d={\bar{d}}$. Therefore, one can enforce condition (3.9b), giving rise to the instability region. The cross-diffusion coefficient of the inhibitor $d_u$ is the key parameter to initiate the pattern formation.

The existence of a threshold on the cross-diffusion coefficient $d_u$ to set in the instability means that the inhibitor has to diffuse sufficiently fast away from increasing concentrations of the activator. In addition, one has to require a small value of the self-diffusivities ratio; namely, the activator has to disperse faster than the inhibitor. To stabilize the pattern, in fact, a sufficiently high value of the activator self-diffusion coefficient is necessary to guarantee a net flux of activator species from regions with low inhibitor/high activator concentration towards zone with a small activator/high inhibitor density. Therefore, the emerging structures formed by the u- and v-species are out-of-phase. We postpone the classification of the pattern-phasing to [10]. The effect of varying separately $d_u$ and $d_v$ also confirms the opposite roles played by the two cross-diffusion terms on the width of the instability region. As one can see from the comparison of Fig. 3a, b, the shaded area is reduced upon increasing $d_v$, while, for fixed $d_v$, increasing $d_u$ makes it larger the interval of values of d where (3.9a) is verified. A similar effect has varying $d_u$ and $d_v$ on the condition (3.9b) (see Fig. 3c, d): for fixed $d_v$, increasing $d_u$ moves the threshold $d_c$ upwards, so enlarging the instability region. Conversely, from the comparison of Fig. 3c and d, it is apparent that an increase in $d_v$ determines a downward shift of the threshold $d_c$, so reducing the width of the instability region. Therefore, while the presence of an increasingly strong cross-diffusion in the inhibitor dynamics helps the onset of the instability, the cross-diffusion of the activator hampers the formation of stationary patterns.

6 Conclusions

This paper investigates the pattern formation process driven by linear cross-diffusion in a FHN-type model. For completeness, we have included some results concerning the monostable regime; more details on this regime are in [9]. However, most of our analysis has focused on the excitable regime.

We have proved that, although the qualitative form of the kinetics in the neighborhood of the homogeneous equilibrium does not satisfy the conditions required by the classical Turing theory, cross-diffusion terms can promote the formation of small-amplitude patterns. In fact, cross-diffusion-driven patterns also arise in the presence of long range activation and short range inhibition, contrarily to what happens when only classical diffusion is present.

In a companion paper [10] we shall construct the cross-Turing pattern on 1D and 2D spatial domain and study far-from-equilibrium stationary solutions.