Abstract
We consider a SIR-like reaction-diffusion epidemic model which embeds opinion-driven human behavioural changes. We assume that the contagion rate is theoretically saturated with respect to the density of the disease prevalence. The model extends the general reaction-diffusion epidemic model proposed in 1993 by Capasso and Di Liddo. We study the nonlinear attractivity of the endemic steady state solution by employing a special Lyapunov function introduced in 2006 by S. Rionero. Sufficient conditions for the conditional nonlinear stability of the endemic equilibrium are derived.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The stability analysis of equilibria of dynamical systems modelling biological phenomena is always mapped in a major issue: the assessment of the robustness of the biological equilibrium. The semantic of such stability sometime is positive (e.g., Is the pest eradication stable w.r.t. possible pest importation?) other times it is negative (e.g., Is the invasion equilibrium robust?). An important biological application of dynamical systems is the area of modelling the spread and the control of infectious diseases, i.e. the Mathematical Epidemiology (ME) [7, 15]. Although the vast majority of mathematical studies in the area of ME focuses on purely temporal models, a number of significant studies have been devoted to spatio-temporal models [1,2,3, 7, 14, 15, 20, 23, 30]. A relevant example is the general reaction–diffusion epidemic model proposed in 1993 by Capasso and Di Liddo to study the role of cross–diffusion [8]. They primarily focused on global attractivity of the uniform steady state solutions and indicated several specific diseases whose transmission may be described in such general settings, including host–vector diseases (as malaria and schistosomiasis) and carrier-borne diseases (as typhoid fever). The work [8] is of interest because later studies showed that in other important contexts in theoretical population dynamics the presence of cross-diffusion induces instability and patterning [16, 19]. This makes the results of [8] even more important, since the global stability of the endemic equilibrium was shown there. Moreover, and more closely related to the present work, the study by Capasso and Di Liddo stimulated some interesting works on the application of nonlinear Lyapunov Stability to Mathematical Biology [17, 22].
However, classical models of ME suffer of a major drawback: they are based on the analogy between contagion and chemical reactions, thus modelling the infections by means of the mass action law and the recovery as chemical degradation. In other words, classical models of ME essentially see human beings as molecules and therefore neglect the human behavioural changes. This approximation is not always adequate to represent real scenarios since the two major determinants of the epidemic spread, i.e. the degree of enacted social distancing and the degree of adherence to vaccination programs, fully depend on human decisions. The same could be said for the adoption of antiviral drugs, when available. This consideration has led to the birth of a new field, the Behavioural Epidemiology of Infectious Diseases (BEID) [21, 29]. Remarkably, the first pioneering example of BEID has probably been the paper on modelling social distancing published in 1978 by Capasso and Serio [9]. In such a paper, the contact rate was considered as a dynamical parameter that ‘adapts’ to the current state of the disease spread during an epidemic outbreak. Inexplicably, the paper [9] had a limited impact for more than a quarter of century but the basic concepts contained therein are nowadays fundamental in contemporary BEID and are at the basis of many works [21]. For example, in the paper [13] the adaptation depends on the state of the present and past information on the spread of epidemic and endemic diseases. As far as spatio–temporal effects in the framework of BEID are concerned, the body of research on this important aspect remained limited so far [4, 12, 18].
Our aim in this paper is twofold. From one hand, starting from the Capasso and Di Liddo general setting, we aim at providing a further relevant case, i.e. we propose a SIR-like reaction-diffusion epidemic model which embeds opinion-driven human behavioural changes. The model extends along the line of d’Onofrio et al. [12] the above-mentioned model by Capasso and Serio. On the other hand, we intend to give a new application of a special Lyapunov function introduced in 2006 by S. Rionero to study the nonlinear stability of equilibria of both spatially homogeneous and spatially non-homogeneous systems of differential equations [24,25,26,27]. Such a function has been successfully employed in a number of problems in theoretical population biology. For example, it has been applied to diffusive population models like predator–prey interactions [10], pioneer and climax species [5], Lotka–Volterra with special functional response [11]. It has been also used to study ODE systems like SIR and SEIR classical epidemic models [6, 27]. In our case, we aim at using this approach to investigate the degree of the robustness of the endemic equilibrium induced by the human behaviour. At the best of our knowledge, this is its first application of the approach due to S.Rionero to models of BEID.
The rest of the paper is organized as follows: in Sect. 2 we introduce the general family of epidemic models and we discuss the existence of equilibria; in Sect. 3, we derive the perturbation system and rewrite it in an sort of ‘optimized form’ amenable to its analysis by means of the Rionero’s function. The problem of the nonlinear \(L^2\)-stability of the endemic equilibrium is discussed in Sect. 4. Some conclusions end this work.
2 The model
Capasso and Di Liddo [8] considered the following general system of reaction–diffusion equations:
with boundary conditions
where \(\partial w/\partial \nu \) is the outward normal derivative and \(w^*\) is a constant vector in \(\textbf{R}^m\).
The following assumptions are also considered:
- (i):
-
The function \(f:G\subseteq \textbf{R}^m \rightarrow \textbf{R}^m\), \(m\in \textbf{N}\backslash \left\{ 0 \right\} \), is a locally Lipschitz function;
- (ii):
-
The constant vector \(w^*\) is a spatially uniform steady state of (1–2), i.e. \(f(w^*)=0\);
- (iii):
-
The domain \(\varOmega \) is a bounded open connected set of \(\textbf{R}^n\), \(n\in \textbf{N}\backslash \left\{ 0 \right\} \). If \(n>1\), then \(\varOmega \) is assumed to be uniformly of class \(C^{1+\alpha }\), with boundary \(\partial \varOmega \) uniformly of class \(C^{2+\alpha }\), for some \(\alpha >0\);
- (iv):
-
The constants \(\alpha \) and \(\beta \) in (2) are nonnegative and such that \(\alpha +\beta >0\);
- (v):
-
The term D is a linear operator on \(\textbf{R}^m\) such that:
where \(d_{ij}\) are the coefficients of the matrix D. In other words, the matrix D is positive definite.
d’Onofrio et al. [12] consider the following spatially structured SIR model with opinion-driven human behavioural changes in \(\varOmega \times (0,T)\):
where S is the spatial density of Susceptible subjects and I is the spatial density of infectious subjects; \(D_S\) and \(D_I\) are the diffusion rates of, respectively, susceptible and Infectious subjects; \(\hat{\mu }\) is the death rate due to natural causes (for the sake of the simplicity, the recruitment rate is assumed to be equal to the death rate).
The function \(\varPsi (S,I)\) models the contagion rate. The dependence by S and I mimics the opinion-driven human behavioural changes in contact rate (in other words, the opinion-driven adoption of social distancing). In particular, it is assumed that \(\varPsi (S,I)\) can be decomposed as follows
where C(S, I) is the contagion rate in absence of human behavioural response and \(\varPhi (I)\) models the impact of social distancing on the contagion rate. These assumptions implies that:
(i) \(0\le \varPhi (I) \le 1\), \(\varPhi (0)=1\), \(\varPhi ^{\prime }(I)<0\);
(ii) \(C(S,0)=C(0,I)=0\), \(\partial _IC(S,I)>0\), \(\partial _SC(S,I)>0\).
According to the general setting proposed by Capasso and Di Liddo [8] we append boundary conditions (2). Note that \(\alpha =0\) means Neumann homogeneous boundary conditions and \(\beta =0\) means Dirichlet boundary conditions. However, in order to apply the Lyapunov function proposed by S. Rionero, we will assume that both \(\alpha \) and \(\beta \) are strictly positive constants.
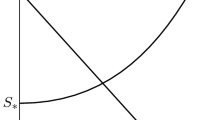
Model (3) admits the Disease–Free equilibrium \(DFE=(1,0)\). Denote by \(E=(\tilde{S},\tilde{I})\) a spatially homogeneous equilibrium with \(,\tilde{I}>0\) (Endemic equilibrium). Then:
and
Therefore,
where
and
Now, we first assume that the behavioural reaction of individuals influences the contact rate by making it no more constant. Namely, we assume that the effective contact rate is a decreasing function of the information on the disease prevalence: \(\beta _{eff}(I)\), with \(\beta _{eff}^{\prime }(I)<0\). Second, we also assume that the contagion rate \(\beta _{eff}(I)I S\) remains an increasing function of the disease prevalence. This biologically realistic constraint can be fulfilled by many functions. However, following [9, 13], we choose:
In other words, the contagion rate is theoretically saturated with respect to the density of the disease prevalence:
Under such assumption, there exists an unique endemic equilibrium
where \(\tilde{S}\) is given by (4) and:
where
3 Perturbation system
3.1 Preliminaries
Consider the perturbations u, v such that:
where \(k_1\) and \(k_2\) are two positive quantities. We get:
In the next subsection we will manipulate the kinetics terms of this system to write them a form that can be convenient for the application of the Rionero’s approach to stability.
3.2 Reformulation of the first equation
From the first equation, set:
We have:
Introduce some unknown quantities, \(a_{11}\), \(a_{12}\), A, and impose that F(u, v) takes the form:
One has:
and
The first equation of (9) becomes
3.3 Reformulation of the second equation
Set
that is
Introduce the quantities \(a_{21}\), \(a_{22}\), B, C, and impose that G(u, v) takes the form:
It follows:
and
where we have used the equilibrium condition \((\hat{\mu }+\hat{\nu })\left( 1+\hat{\alpha }\tilde{I} \right) =\hat{\beta } \tilde{S}\). Furthermore,
The second equation of (9) becomes
In conclusion, the perturbation system is:
which must be studied with the following boundary conditions in \(\partial \varOmega \times \mathbf{R_+}\):
4 Nonlinear \(L^2\)-stability
In this section, we will apply the method developed in a series of papers by Rionero [24,25,26] to get the nonlinear \(L^2\) stability of the equilibrium E given in (7). The method is based on the analysis of a suitable linear planar system of ordinary differential equations. The stability will be studied with respect to the perturbations (u, v) belonging, for all \(t\in \textbf{R}_+\), to \([W^{1,2}(\varOmega ,\alpha ,\beta ,D)]\), where \(W^{1,2}(\varOmega )\) is the functional space such that
In the space \(W^{1,2}(\varOmega ,\alpha ,\beta ,D)\) the following inequality holdsFootnote 1
where \(||\cdot ||\) denotes the \(L^2\)-norm, \(||\cdot ||_{\partial \varOmega }\) denotes the \(L^2(\partial \varOmega )\)-norm and the positive constant \(\hat{\lambda }(\varOmega ,\alpha ,\beta ,D)\) is the lowest eigenvalue of the problem
in \(W^{1,2}(\varOmega ,\alpha ,\beta ,D)\), that is the principal eigenvalue of \(-\varDelta \).
Now, take
add and subtract the quantities
where \(\overline{\epsilon }\) is a constant to be chosen later, in the first and the second equation of (14), respectively. Take also into account of (18). System (14) now reads
where,
and
and
Now take the constant \(\overline{\epsilon }\) in (19) such that:
In this way, it follows that \(b_{22}<0\) (since \(a_{22}<0\)) and \(I<0\), \(\hat{A}>0\) where
are the principal invariants of the matrix J associated to the linear terms in (20).
Now, consider the Rionero’s special type of Lyapunov functions [24,25,26]:
It immediately follows that the time derivative along the solution of (20) is given by
where
and
where \(\left\langle \cdot \right\rangle \) denotes the scalar product in \(L^2(\varOmega )\), and
Our aim now is to estimate the terms \(\hat{\varPsi }\) and \(\varPsi ^*\) in (27). Let us begin by observing that from (10), (11), (12), (13), (21) it follows that \(a_{12}b_{22}>0\) and \(a_{21}b_{11}<0\). Therefore it can be taken
to get: \(\overline{\alpha }_3=0\). As a consequence, taking into account the estimate (17) we obtain
From (22) first term may be written
Rearranging and using the divergence theorem we have
Therefore, taking into account the boundary conditions (15), we can write
Using the inequality (17) and \(- \overline{\alpha }_1\overline{\epsilon } \left\| u \right\| ^2_{\partial \varOmega } < 0\), it follows
Reasoning in the same way when managing the term \(\left\langle \overline{\alpha }_2\,v\,,G^* \right\rangle \) in (31), one gets:
where \(\overline{\alpha }=\min \left\{ \overline{\alpha }_1,\;\overline{\alpha }_2 \right\} > 0\).
Now we need to estimate the term \(\varPsi ^*\) in (27) where \(\overline{\alpha }_3=0\),i.e.:
By considering perturbations such that \(k_2\,v>-\tilde{I}\), from (23) one gets:
and
where \(c_i\), \(i=1,\dots ,4\) are suitable positive constants. Therefore we get:
Using the Hölder inequality it follows
where \(\hat{h} = \min \left\{ k_1^{-1}\left| \overline{\alpha }_1\right| ,\;k_2^{-1}\left| \overline{\alpha }_2\right| \right\} \). Using the inequality [28]:
where \(\kappa =\kappa (\varOmega )\) is a positive constant, we have
where \(M=\max \left\{ c_1, c_2+c_3+c_4 \right\} \). Now, from the (26), being \(\hat{A}>0\), it follows that W is positive definite and equivalent to the \(L^2(\varOmega )\)-norm. In particular, there exist two constants \(\tilde{\kappa }_1\) and \(\tilde{\kappa }_2\), such that
Recalling that \(I<0\), from (27), (31) and (36), (37) one gets
Now take the initial value of W, say \(W_0\), such that:
Then, \(\dot{W}(0)<0\), and \(\dot{W}(\tilde{t})<0\) when
Therefore
We conclude that:
so that:
This estimates indicates that the endemic equilibrium is nonlinearly stable in the W-norm, and therefore in the \(L^2\)-norm, although the restriction (38) on the initial data makes the stability not verified for all initial data, i.e. it is only conditional stability [28].
5 Conclusions
In this work, we focus on the problem of nonlinear stability of an uniform endemic equilibrium induced by human behaviour in a spatio-temporal SIR epidemic model. The impact of human behaviour on the contact rate is assumed to be of inverse linear affine type, which means that as result of opinion-driven adoption of social distancing the contagion rate is theoretically saturated with respect to the density of the disease prevalence. We use the Rionero’s special type of Lyapunov function, which has been previously fruitfully employed in a number of problems in theoretical population biology. The task has been non-trivial despite of the simple form that we use to represent the human behavioural response. For the proposed model, we obtain a stability result which is subject to a restriction on the initial perturbation. Assessing the global stability of the endemic equilibrium remains an open problem.
Data availability statement
Data sharing not applicable to this article as no datasets were generated or analysed during the current study.
Notes
To obtain the inequality (17) starts from (18) to get \(\varphi \varDelta \varphi + \lambda \varphi ^2 = 0\). Then integrating over \(\varOmega \) and applying the divergence theorem one gets \(\int _{\partial \varOmega } \varphi \nabla \varphi \cdot {\textbf{n}} d\sigma -\int _{\varOmega } (\nabla \varphi )^2 d\varOmega + \lambda \int _{\varOmega }\varphi ^2 d\varOmega = 0\). Taking into account of (15) one has \( -\frac{\alpha }{D\beta }\int _{\partial \varOmega } \varphi ^2 d\sigma -\int _{\varOmega } (\nabla \varphi )^2 d\varOmega + \lambda \int _{\varOmega }\varphi ^2 d\varOmega =0 \), and therefore (17), where \(\hat{\lambda }\le \lambda \).
References
Aronson, D.G.: The asymptotic speed of propagation of a simple epidemic. Nonlin. Diff. 14, 1–23 (1977)
Bailey, N.T.J.: The simulation of stochastic epidemics in two dimensions. Proc. Fifth Berkeley Symp. Math. Statist. Prob. 4, 237–257 (1967)
Bailey, N. T. J.: The mathematical theory of infectious diseases and its applications, 2nd edition, Charles Griffin and Company Ltd, (1975)
Banerjee M., Ghosh, S., Manfredi P., d’Onofrio, A.: Spatio-temporal chaos and clustering induced by nonlocal information and vaccine hesitancy in the SIR epidemic model, Chaos Solit. Fract., 170, Art n. 113339 (2023)
Buonomo, B., Rionero, S.: Linear and nonlinear stability thresholds for a diffusive model of pioneer and climax species interaction. Math. Methods Appl. Sci. 32(7), 811–824 (2009)
Buonomo, B., Rionero, S.: On the Lyapunov stability for SIRS epidemic models with general nonlinear incidence rate. Appl. Math. Comput. 217(8), 4010–4016 (2010)
Capasso, V.: Mathematical structures of epidemic systems. Corrected reprint of the 1993 original. Lecture Notes in Biomathematics, 97. Springer, Berlin, (2008)
Capasso, V., Di Liddo, A.: Global attractivity for reaction-diffusion systems. The case of nondiagonal diffusion matrices. J. Math. Anal. Appl. 177(2), 510–529 (1993)
Capasso, V., Serio, G.: A generalization of the Kermack-McKendrick deterministic epidemic model. Math. Biosci. 42(1–2), 43–61 (1978)
Capone, F.: On the dynamics of predator-prey models with the Beddington-De Angelis functional response, under Robin boundary conditions. Ric. Mat. 57(1), 137–157 (2008)
Capone, F., Piedisacco, M., Rionero, S.: Nonlinear stability for reaction-diffusion Lotka-Volterra model with Beddington-DeAngelis functional response. Rend. Accad. Sci. Fis. Mat. Napoli 4(73), 85–97 (2006)
d’Onofrio, A., Banerjee, M., Manfredi, P.: Spatial behavioural responses to the spread of an infectious disease can suppress Turing and Turing-Hopf patterning of the disease. Physica A 545, 123773 (2020)
d’Onofrio, A., Manfredi, P.: Information-related changes in contact patterns may trigger oscillations in the endemic prevalence of infectious diseases. J. Theor. Biol. 256, 473–478 (2009)
Ducrot, A., Giletti, T.: Convergence to a pulsating travelling wave for an epidemic reaction-diffusion system with non-diffusive susceptible population. J. Math. Biol. 69, 533–552 (2014)
Keeling, M.J., Rohani, P.: Modeling Infectious Diseases in Humans and Animals. Princeton University Press, NJ (2008)
Kumar, N. , Horsthemke, W.: Effects of cross diffusion on Turing bifurcations in two-species reaction-transport systems. Physical Review E, 83, Art no. 036105 (2011)
Lombardo, S., Mulone, G., Trovato, M.: Nonlinear stability in reaction-diffusion systems via optimal Lyapunov functions. J. Math. Anal. Appl. 342, 461–476 (2008)
Lupica, A., Manfredi, P., Volpert, V., Palumbo, A., d’Onofrio, A.: Spatio-temporal games of voluntary vaccination in the absence of the infection: the interplay of local versus non-local information about vaccine adverse events. Math. Biosci. Eng. 17, 1090–1131 (2020)
Madzvamuse, A., Ndakwo, H.S., Barreira, R.: Cross-diffusion-driven instability for reaction-diffusion systems: analysis and simulations. J. Math. Biol. 70, 709–743 (2015)
Malchow, H., Petrovskii, S. V., Venturino, E.: Spatiotemporal patterns in ecology and epidemiology: theory, models, and simulation, Chapman and Hall/CRC, (2007)
Manfredi, P., d’Onofrio, A. (eds.): Modeling the interplay between human behavior and the spread of infectious diseases. Springer, New York (2013)
Mulone, G., Straughan, B.: Nonlinear stability for diffusion models in biology. SIAM J. Appl. Math. 69, 1739–1758 (2009)
Murray, J.D.: Mathematical biology II. Springer Verlag, New York, Spatial models and biomedical applications (2001)
Rionero, S.: \(L^2\)–stability of the solutions to a nonlinear binary reaction–diffusion system of P.D.E.s., Atti Accad. Naz. Lincei Cl. Sci. Fis. Mat. Natur. Rend. Lincei (9) Mat. Appl. 16 (2005), no. 4, 227-238 (2006)
Rionero, S.: A rigorous reduction of the \(L^2\)-stability of the solutions to a nonlinear binary reaction-diffusion system of PDE’s to the stability of the solutions to a linear binary system of ODE’s. J. Math. Anal. Appl. 319(2), 377–397 (2006)
Rionero, S.: A nonlinear \(L^2\)-stability analysis for two-species population dynamics with dispersal. Math. Biosci. Eng. 3(1), 189–204 (2006)
Rionero, S.: On the nonlinear stability of the critical points of an epidemic SEIR model via a novel Liapunov function. Rend. Accad. Sci. Fis. Mat. Napoli 4(75), 115–129 (2008)
Straughan, B.: The energy method, stability, and nonlinear convection. Vol. 91. Springer Science and Business Media, (2013)
Wang, Z., Bauch, C.T., Bhattacharyya, S., d’Onofrio, A., Manfredi, P., Perc, M., Perra, N., Salathé, M., Zhao, D.: Statistical physics of vaccination. Phys. Rep. 664, 1–113 (2016)
Zhao, L., Wang, Z.C., Ruan, S.: Traveling wave solutions in a two-group SIR epidemic model with constant recruitment. J. Math. Biol. 77, 1871–1915 (2018)
Acknowledgements
The authors thank Florinda Capone (University of Naples Federico II) for her valuable suggestions and discussions. This work has been performed under the auspices of the Italian National Group for Mathematical Physics (GNFM) of the National Institute for Advanced Mathematics (INdAM). B.B. acknowledges EU funding within the NextGenerationEU—MUR PNRR Extended Partnership initiative on Emerging Infectious Diseases (Project no. PE00000007, INF-ACT) and PRIN 2020 project (No. 2020JLWP23) “Integrated Mathematical Approaches to Socio–Epidemiological Dynamics”.
Funding
Open access funding provided by Università degli Studi di Napoli Federico II within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The author states that there is no conflict of interest.
Additional information
This paper is dedicated to the memory of professor Salvatore Rionero, Scientist and Master of great passion and humanity.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Buonomo, B., d’Onofrio, A. The Rionero’s special type of Lyapunov function and its application to a diffusive epidemic model with information. Ricerche mat 73 (Suppl 1), 51–65 (2024). https://doi.org/10.1007/s11587-023-00807-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11587-023-00807-8