The non-linear energy stability of Brinkman thermosolutal convection with reaction

Abstract

We use the energy method to obtain the non-linear stability threshold for thermosolutal convection porous media of Brinkman type with reaction. The obtained non-linear boundaries for different values of the reaction terms are compared with the relevant linear instability boundaries obtained by Wang and Tan (Phys Lett A 373:776–780, 2009). Using the energy theory we obtain the non-linear stability threshold below which the solution is globally stable. The compound matrix numerical technique is implemented to solve the associated system of equations with the corresponding boundary conditions. Two systems are investigated, the heated below salted above case and the heated below salted below case. The effect of the reaction terms and Brinkman term on the Rayleigh number is discussed and presented graphically.

1 Introduction

Convection in porous media has attracted the attention of many researchers and has been an area of great interest in addition to its wide range of applications. Thermal convection in porous media and stability analysis returns back to Horton and Rogers [2], Lapwood [3] and Nield and Barletta [4]. The problem of double-diffusive convection in porous media is well investigated by Nield [5], Rudraiah et al. [6], Wollkind and Frisch [7, 8], Nield and Bejan [9], Ingham and Pop [10, 11], Vafai [12, 13] and Vadasz [14]. Bdzil and Frisch [15] performed a linear stability analysis where the fluid catalysed at the lower boundary of the layer and they developed their work in Bdzil and Frisch [16] and a similar work carried by Gutkowicz-Krusin and Ross [17]. Many recent studies in double and multi-component convection are accomplished by Rionero [18–21]. The first study on the reactive convection in porous media was due to Steinberg and Brand [22, 23]. More studies were carried out by Gatica et al. [24, 25], Viljoen et al. [26] and Malashetty and Gaikwad [27]. Pritchard and Richardson [28] figured out a model similar to that of Steinberg and Brand [22, 23]. They considered the Darcy model to study the onset of thermosolutal convection using linear instability technique. Wang and Tan [1] extended the previous work of Pritchard and Richardson [28] in which Wang and Tan [1] considered Darcy-Brinkman model and used normal mode analysis to carry out a linear instability analysis.

We are studying nonlinear stability using an energy stability method. This method is being used extensively by many leading mathematicians, see for example, Straughan [29, 30], Rionero [31], Capone et al. [32], Straughan [33], Capone and De Luca [34], Rionero and Torcicollo [35], Capone et al. [36], Lombardo and Mulone [37], Rionero [38], De Luca [39] and De Luca and Rionero [40]. The work in this paper may be considered as an extension of Wang and Tan [1] and Pritchard and Richardson [28]. Al-Sulaimi [41] used the energy method to carry out a nonlinear stability analysis of Darcy thermosolutal convection with reaction. In this article, the energy stability of Brinkman thermosolutal convection with reaction is considered. The compound matrix numerical technique is used to solve the associated system of equations with the corresponding boundary conditions. Two systems are investigated separately, the heated below-salted above system and the heated below-salted below system. The energy stability boundaries obtained for different values of the reaction rates are compared with the relevant linear instability boundaries. Some linear instability boundaries are obtained by Wang and Tan [1], but they do not correspond directly to what we require and hence we recompute also the linear values using the $D^{2}$ Chebyshev tau method.

The aim of the study is to obtain the nonlinear stability boundaries below which the solution is globally stable by using the energy method and compare the nonlinear boundaries with the relevant linear instability boundaries obtained by Wang and Tan [1]. Considering a porous medium of Brinkman type occupying a bounded three-dimensional domain, the variation of the onset of thermosolutal convection with the reaction rate and Brinkman coefficient is discussed.

2 Basic equations

Our model consists of the Brinkman equation with the density in the buoyancy term depends linearly on the temperature T and salt concentration C, the continuity equation, the advection–diffusion equation for the transport of heat and the equation for the transport of solute with reaction terms,

$$\begin{aligned}&\displaystyle p_{,i}=-\frac{\mu }{K}v_{i}-\rho _{0}[1-\alpha _{T} (T-T_{0})+\alpha _{C}(C-C_{0})]gk_{i}+\lambda \Delta v_{i},&\nonumber \\&\displaystyle v_{i,i}=0,&\nonumber \\&\displaystyle \frac{1}{M}T_{,t}+v_{i}T_{,i}=k_{T}\Delta T,&\nonumber \\&\displaystyle \hat{\phi } C_{,t}+v_{i}C_{,i}=\hat{\phi } k_{C}\Delta C+\hat{k}[f_{1}(T-T_{0})+f_{0}-C].&\end{aligned}$$

(1)

Here $v_{i}, p, T, C$ are the velocity, pressure, temperature and salt concentration. K is the matrix permeability, $\mu$ is the fluid viscosity, $\rho _{0}$ is the fluid density. $k_{C}, k_{T}$ are the molecular diffusivity of the solute through the fluid and the effective diffusivity of the heat through the saturated medium. M is the ratio of the heat capacity of the fluid to the heat capacity of the medium, $\hat{\phi }$ is the matrix porosity, $\hat{k}$ is the reaction coefficient and $f_{0}+f_{1}(T-T_{0})=C_{eq}(T)$ in Pritchard and Richardson [28], where $f_{0}$, $f_{1}$ and $T_{0}$ are constants. Moreover, g is the gravity, $\mathbf k =(0,0,1)$ and $\alpha _{T}$ and $\alpha _{C}$ are the thermal and solutal expansion coefficients respectively. The symbol $\Delta$ is the Laplace operator. The Eq. (1) are taken in the domain ${\mathbb {R}}^{2}\times (0,d)\times \{t>0\}$. The boundary conditions are

$$\begin{aligned} v_{i}= & {} 0 \ on \ z=0,d,\nonumber \\ T= & {} T_{L} \ on \ z=0,\ \ T=T_{U} \ on \ z=d,\nonumber \\ C= & {} C_{L} \ on \ z=0,\ \ C=C_{U} \ on \ z=d, \end{aligned}$$

(2)

where $T_{L}, T_{U}, C_{L}, C_{U}$ all constants, with $T_{L}>T_{U}$ since our systems are heated below. For the salted above porous medium $C_{U}>C_{L}$ while for the salted below case $C_{L}>C_{U}$. In the steady state, we look for

$$\begin{aligned} \bar{v}_{i}= & {} 0,\nonumber \\ \bar{T}= & {} \bar{T}(z),\nonumber \\ \bar{C}= & {} \bar{C}(z). \end{aligned}$$

(3)

Assuming $C_{eq}(\bar{T}(z))=\bar{C}(z)$ (see Pritchard and Richardson [28] and Al-Sulaimi [41]), we find the steady solution or the basic state to (1) which we are interested in studying its stability and which satisfies (2) as

$$\begin{aligned} \bar{v}_{i}= & {} 0,\nonumber \\ \bar{T}(z)= & {} -\beta _{T}z + T_{L},\nonumber \\ \bar{C}(z)= & {} -\beta _{C}z + C_{L}, \end{aligned}$$

(4)

where $\beta _{T}=(T_{L}-T_{U})/d$ and $\beta _{C}=(C_{L}-C_{U})/d$ are the temperature and salt gradients respectively.

To analyze the stability of the solutions (4) we define perturbations $(u_{i}, \pi , \theta , \phi )$ such that

$$\begin{aligned} v_{i}= & {} {\bar{v}}_{i}+u_{i},\nonumber \\ p= & {} {\bar{p}}+\pi ,\nonumber \\ T= & {} {\bar{T}}+\theta ,\nonumber \\ C= & {} {\bar{C}}+\phi \end{aligned}$$

(5)

Using these perturbations in Eq. (1) we derive the equations governing $(u_{i}, \pi , \theta , \phi )$ as

$$\begin{aligned} \pi _{,i}= & {} -\frac{\mu }{K}u_{i}+\rho _{0}gk_{i}\alpha _{T}\theta -\rho _{0}gk_{i}\alpha _{C}\phi +\lambda \Delta u_{i},\nonumber \\ u_{i,i}= & {} 0,\nonumber \\ \frac{1}{M}\theta _{t}+u_{i}\theta _{,i}= & {} \beta _{T}w+k_{T}\Delta \theta ,\nonumber \\ \hat{\phi }\phi _{t}+u_{i}\phi _{,i}= & {} \beta _{C}w+\hat{\phi }k_{C}\Delta \phi +\hat{k}f_{1}\theta -\hat{k}\phi , \end{aligned}$$

(6)

where $w=u_{3}$. To non-dimensionalize the system (6), we define the length, time and velocity scales, L, $\tau$ and U, by $L=d$, $\tau =d/MU$ and $U=k_{T}/d$. We introduce pressure, temperature and salt scales as

$$\begin{aligned} P=\frac{Ud\mu }{K}, \quad T^{\sharp ^{2}}=\frac{\mu \beta _{T}k_{T}}{\alpha _{T}\rho _{0}gK}, \quad C^{\sharp ^{2}}=\frac{\mu \beta _{C}k_{T}Le}{\alpha _{C}\rho _{0}gK\hat{\phi }}, \end{aligned}$$

where $Le=k_{T}{/}k_{C}$ is the Lewis number. The temperature and salt Rayleigh numbers are defined as

$$\begin{aligned} R= & {} \sqrt{\frac{\beta _{T}d^{2}K\alpha _{T}\rho _{0}g}{k_{T}\mu }} \ ,\\ R_{s}= & {} \sqrt{\frac{\beta _{C}d^{2}K\alpha _{C}\rho _{0}gLe}{\hat{\phi }k_{T}\mu }} \ \ \ when \ \ C_{L}>C_{U} \ \ or \ \ R_{s}=\sqrt{\frac{\vert \beta _{C}\vert d^{2}K\alpha _{C}\rho _{0}gLe}{\hat{\phi }k_{T}\mu }} \ \ \ when \\&\quad C_{L}<C_{U}. \end{aligned}$$

Then, the fully nonlinear, perturbed dimensionless form of (6) is

$$\begin{aligned} \pi _{,i}= & {} -u_{i}+Rk_{i}\theta -R_{s}k_{i}\phi + \tilde{\gamma }\Delta u_{i},\nonumber \\ u_{i,i}= & {} 0,\nonumber \\ \theta _{,t}+u_{i}\theta _{,i}= & {} Rw+\Delta \theta ,\nonumber \\ \varepsilon \phi _{,t}+\frac{Le}{\hat{\phi }}u_{i}\phi _{,i}= & {} \mp R_{s}w+\Delta \phi +h\theta -\eta \phi , \end{aligned}$$

(7)

where $\varepsilon =MLe$, $\tilde{\gamma }=\lambda K/\mu d^{2}$ the Brinkman coefficient and h and $\eta$ are the reaction terms

$$\begin{aligned} h=\frac{\hat{k}f_{1}d^{2}T^{\sharp }}{\hat{\phi }k_{C}C^{\sharp }} \ \ and \ \ \eta =\frac{\hat{k}d^{2}}{\hat{\phi }k_{C}}. \end{aligned}$$

Moreover, $+R_{s}$ is taken for the salted below system and $-R_{s}$ is taken for the salted above system. The corresponding boundary conditions are

$$\begin{aligned} Dw=w=\theta =\phi =0 \, \mathrm{on} \, z=0 \quad \mathrm{and} \quad z=1. \end{aligned}$$

(8)

3 Linear instability theory

To study the linear instability, we drop the nonlinear terms of (7) and take the double curl of equation (7)$_{1}$ and retaining only the third component of the resulting equation to reduce (7) to studying the system

$$\begin{aligned} \begin{aligned}&\Delta w -R\Delta ^{*}\theta + R_{s}\Delta ^{*}\phi - \tilde{\gamma }\Delta ^{2}w = 0,\\&\theta _{,t}=Rw + \Delta \theta ,\\&\varepsilon \phi _{,t}=\mp R_{s}w + \Delta \phi + h\theta - \eta \phi , \end{aligned} \end{aligned}$$

(9)

where $\Delta ^{*}$ is the horizontal Laplacian. Assuming a normal mode representation for w, $\theta$ and $\phi$ of the form $w=W(z)f(x,y)\ ,\ \theta =\varTheta (z)f(x,y)$ and $\phi =\varPhi (z)f(x,y)$ where f(x, y) is a plan tiling function satisfying

$$\begin{aligned} \Delta ^{*}f=-a^{2}f ; \end{aligned}$$

(10)

(see Straughan [29]) and a is a wave number. Using (10) and applying the normal mode representations to (9), we find

$$\begin{aligned} \begin{aligned}&(D^{2}-a^{2})W + Ra^{2}\varTheta - R_{s}a^{2}\varPhi -\tilde{\gamma }(D^{2}-a^{2})^{2}W =0 ,\\&\sigma \varTheta = RW + (D^{2}-a^{2})\varTheta ,\\&\varepsilon \sigma \varPhi = \mp R_{s}W + (D^{2}-a^{2})\varPhi + h\varTheta - \eta \varPhi , \end{aligned} \end{aligned}$$

(11)

where $D=d{/}dz$. This is an eigenvalue problem for $\sigma$ to be solved subject to the boundary conditions

$$\begin{aligned} DW=W=\varTheta =\varPhi =0 \ ,\ on \ z=0,1. \end{aligned}$$

(12)

System (11) with the corresponding boundary conditions (12) is solved using the $D^{2}$ Clebyshev tau method. Detailed numerical results for the heated below-salted above and heated below-salted below are reported separately in the subsections (6.1) and (6.2). We determine the critical Rayleigh number given by $Ra^{2}_{L}=min_{a^{2}}R^{2}(a^{2})$ where for all $R^{2}>Ra^{2}_{L}$ the system is unstable.

4 Nonlinear energy stability theory

In order to study the nonlinear stability of the Brinkman model for the double diffusive convection, we consider the nonlinear system of equations in the dimensionless form (7) and the corresponding boundary conditions (8). Taking into consideration the periodicity of the system and the smoothness of the boundary to allow the application of the Divergence Theorem. Multiply Eq. (7)$_{1}$ by $u_{i}$ and integrate over V using integration by parts. Similarly, multiply Eq. (7)$_{3}$ by $\theta$ and Eq. (7)$_{4}$ by $\phi$ and integrate. The following system of energy equations is obtained

$$\begin{aligned} 0= & {} -\Vert \mathbf u \Vert ^{2}+R(\theta , w)-R_{s}(\phi ,w) - \tilde{\gamma }\Vert \nabla \mathbf u \Vert ^{2}, \nonumber \\ \frac{d}{dt}\frac{1}{2}\Vert \theta \Vert ^{2}= & {} R(\theta , w)-\Vert \nabla \theta \Vert ^{2}, \nonumber \\ \frac{d}{dt}\frac{\varepsilon }{2}\Vert \phi \Vert ^{2}= & {} \mp R_{s}(\phi , w)-\Vert \nabla \phi \Vert ^{2}+h(\theta ,\phi )-\eta \Vert \phi \Vert ^{2}. \end{aligned}$$

(13)

Then we form the combination of the equations in system (13) as

$$\begin{aligned} (13)_{1} + (13)_{2} + \lambda (13)_{3}, \end{aligned}$$

where $\lambda$ a coupling parameter. This leads to the energy identity

$$\begin{aligned} \frac{dE}{dt}=I-D=-D\left( 1-\frac{I}{D}\right) , \end{aligned}$$

(14)

where

$$\begin{aligned} E= & {} \frac{1}{2}\Vert \theta \Vert ^{2}+\frac{\varepsilon \lambda }{2}\Vert \phi \Vert ^{2}, \nonumber \\ I= & {} 2R(\theta , w)+\lambda h(\theta , \phi )-(1 \pm \lambda )R_{s}(\phi , w), \nonumber \\ D= & {} \Vert \mathbf u \Vert ^{2} + \Vert \nabla \theta \Vert ^{2} + \lambda \Vert \nabla \phi \Vert ^{2} + \lambda \eta \Vert \phi \Vert ^{2} + \tilde{\gamma }\Vert \nabla \mathbf u \Vert ^{2}. \end{aligned}$$

(15)

Then

$$\begin{aligned} \frac{dE}{dt}\le -D\left( 1-\max _{H}\frac{I}{D}\right) =-D\left( 1-\frac{1}{R_{E}}\right) \end{aligned}$$

(16)

is an energy inequality which follows from the energy identity, where H is the space of admissible solutions. Namely

$$\begin{aligned} H=\left\{ u_{i}, \theta , \phi \in H^{1}(V): u_{i}=\theta =\phi =0\ on\ z=0,1\right\} , \end{aligned}$$

and

$$\begin{aligned} \frac{1}{R_{E}}=\max _{H}\frac{I}{D}. \end{aligned}$$

(17)

The nonlinear stability ensues when $R_{E}>1$ which implies that $1-1/R_{E}>0$.

By using the Poincaré inequality we can show

$$\begin{aligned} D \ge 2k\pi ^2\left( \frac{\Vert \theta \Vert ^{2}+\lambda \varepsilon \Vert \phi \Vert ^{2}}{2}\right) =2k\pi ^{2}E , \end{aligned}$$

(18)

where $k=min\left\{ \frac{1}{MLe} , 1\right\}$. Then from (16) we may derive the inequality

$$\begin{aligned} \frac{dE}{dt}\le -2a_{1}k\pi ^{2}E(t), \end{aligned}$$

where the coefficient $a_{1}$ is defined by

$$\begin{aligned} a_{1}=\frac{R_{E}-1}{R_{E}}. \end{aligned}$$

Upon integration we obtain

$$\begin{aligned} E(t)\le E(0)e^{-2a_{1}k\pi ^{2}t}. \end{aligned}$$

(19)

Inequality (19) shows that under the condition $R_{E}>1$, $E(t) \rightarrow 0$ as $t\rightarrow \infty$. This result according to Eq. (15)$_{1}$, proves that $\Vert \theta \Vert ^{2}\rightarrow 0$ and $\Vert \phi \Vert ^{2}\rightarrow 0$ as $t\rightarrow \infty$. To show the decay of $\Vert \mathbf u \Vert$, we have to use the Poincaré inequality, the Arithmetic–Geometric Mean inequality and the fact $\Vert w\Vert ^{2} \le \Vert \mathbf u \Vert ^{2}$ in the energy equation (13)$_{1}$ to obtain

$$\begin{aligned} (1+\tilde{\gamma }\pi ^{2})\Vert \mathbf u \Vert ^{2}\le \left( \frac{R\alpha }{2}+\frac{R_{s}\beta }{2}\right) \Vert \mathbf u \Vert ^{2}+\frac{R}{2\alpha }\Vert \theta \Vert ^{2}+\frac{R_{s}}{2\beta }\Vert \phi \Vert ^{2}, \end{aligned}$$

(20)

where $\alpha$ and $\beta$ are constants to be chosen such that $R\alpha +R_{s}\beta =1$, which gives $\alpha =1/2R$ and $\beta =1/2R_{s}$. This leads to

$$\begin{aligned} \left( \frac{1}{2}+\tilde{\gamma }\pi ^{2}\right) \Vert \mathbf u \Vert ^{2}\le R^{2}\Vert \theta \Vert ^{2}+R^{2}_{s}\Vert \phi \Vert ^{2}. \end{aligned}$$

(21)

Inequality (21) shows that $R^{-1}_{E}$ guarantees in addition to the decay of $\Vert \theta \Vert$ and $\Vert \phi \Vert$, also decay of $\Vert \mathbf u \Vert$.

Turning our attention to the maximization problem (17). We have to solve it by deriving the Euler–Lagrange equations. The maximum problem is

$$\begin{aligned} \frac{1}{R_{E}}=\max _{H}\frac{2R(\theta , w) + \lambda h(\theta , \phi ) - R_{s}(1\pm \lambda )(\phi , w)}{\Vert \mathbf u \Vert ^{2} + \Vert \nabla \theta \Vert ^{2} + \lambda \Vert \nabla \phi \Vert ^{2} + \lambda \eta \Vert \phi \Vert ^{2} + \tilde{\gamma }\Vert \nabla \mathbf u \Vert ^{2}}. \end{aligned}$$

(22)

Rescaling $\phi$ by putting $\tilde{\phi }=\sqrt{\lambda }\phi$. Equation (22) will be

$$\begin{aligned} \frac{1}{R_{E}}=\max _{H}\frac{2R(\theta , w) + \sqrt{\lambda }h(\theta , \tilde{\phi }) - R_{s}f(\lambda )(\tilde{\phi } , w)}{\Vert \mathbf u \Vert ^{2} + \Vert \nabla \theta \Vert ^{2} + \Vert \nabla \tilde{\phi }\Vert ^{2} + \eta \Vert \tilde{\phi }\Vert ^{2} + \tilde{\gamma }\Vert \nabla \mathbf u \Vert ^{2}}\ , \end{aligned}$$

(23)

where

$$\begin{aligned} f(\lambda )=\frac{1\pm \lambda }{\sqrt{\lambda }}. \end{aligned}$$

The Euler–Lagrange equations for this maximum are

$$\begin{aligned} \begin{aligned}&2u_{i}-2RR_{E}k_{i}\theta + R_{s}R_{E}fk_{i}\tilde{\phi } - 2\tilde{\gamma }\Delta u_{i} = -R_{E}P_{,i}\\&\quad - 2\Delta \theta - 2R_{E}Rw - \sqrt{\lambda }R_{E}h\tilde{\phi } =0\\&\quad - 2\Delta \tilde{\phi } + 2\eta \tilde{\phi } + R_{E}R_{s}fw - \sqrt{\lambda }R_{E}h\theta =0, \end{aligned} \end{aligned}$$

(24)

where P is a Lagrange multiplier. To remove the Lagrange multiplier, we take the double Curl of equation (24)$_{1}$ and retaining only the third component of the resulting equation to reduce (24) to

$$\begin{aligned} \begin{aligned}&\Delta w - RR_{E}\Delta ^{*}\theta + \left( \frac{1\pm \lambda }{2}\right) R_{s}R_{E}\Delta ^{*}\phi - \tilde{\gamma }\Delta ^{2}w =0 \ ,\\&\Delta \theta + R_{E}Rw + R_{E}\frac{\lambda h}{2}\phi =0 \ ,\\&(\Delta - \eta )\phi - R_{E}R_{s}\left( \frac{1\pm \lambda }{2\lambda }\right) w + R_{E}\frac{h}{2}\theta =0 , \end{aligned} \end{aligned}$$

(25)

where $\Delta ^{*}=\partial ^{2}/\partial x^{2}+\partial ^{2}/\partial y^{2}$ is the horizontal Laplacian. Introducing the normal mode representation as presented in Sect. 3, system (25) becomes

$$\begin{aligned} \begin{aligned}&(D^{2}-a^{2})W - \tilde{\gamma }(D^{2}-a^{2})^{2}W + a^{2}R_{E}R\varTheta - a^{2}R_{E}R_{s}\left( \frac{1\pm \lambda }{2}\right) \varPhi =0,\\&R_{E}RW +(D^{2}-a^{2})\varTheta + \left( \frac{h\lambda }{2}\right) R_{E}\varPhi =0,\\&R_{E}R_{s}\left( \frac{1\pm \lambda }{2\lambda }\right) W - \frac{h}{2}R_{E}\varTheta + \eta \varPhi - (D^{2}-a^{2})\varPhi =0. \end{aligned} \end{aligned}$$

(26)

The Laplace operator is equivalent to $\Delta =D^{2}-a^{2}$, where $D=\partial /\partial z$. The corresponding boundary conditions are

$$\begin{aligned} DW=W=\varTheta =\varPhi =0\ ,\ on \ z=0,1. \end{aligned}$$

(27)

We can determine the critical Rayleigh number given by $Ra^{2}_{E}\!=\!\max _{\lambda }\min _{a^{2}}R^{2}(a^{2},\lambda )$, where for all $R^{2}<Ra^{2}_{E}$ the system is stable.

5 Numerical method

We have used the $D^{2}$ Chebyshev tau method (Dongarra et al. [42]) to find the bound for the linear instability theory, system (11) and the corresponding boundary conditions (12). For the energy theory we have used the compound matrix technique (Lindsay and Straughan [43]).

5.1 The $D^{2}$ Chebyshev tau method for the linear theory

Using the $D^{2}$ Chebyshev to solve (11) subject to (12), we have to introduce a variable $\chi$ such that $\chi =\Delta w$. Then, Eq. (11) will be

$$\begin{aligned} \begin{aligned}&(D^{2}-a^{2})W - \chi = 0,\\&\tilde{\gamma }(D^{2}-a^{2})\chi - \chi - a^{2}R\varTheta + a^{2}R_{s}\varPhi = 0,\\&(D^{2}-a^{2})\varTheta + RW = \sigma \varTheta ,\\&(D^{2}-a^{2})\varPhi - \eta \varPhi + h\varTheta \mp R_{s}W = \varepsilon \sigma \varPhi . \end{aligned} \end{aligned}$$

(28)

The functions $W,\chi , \varTheta$ and $\varPhi$ are expanded in terms of Chebyshev polynomials

$$\begin{aligned} W(z)= & {} \varSigma _{n=1}^{N}w_{n}T_{n}(z),\ \chi (z)=\varSigma _{n=1}^{N}\chi _{n}T_{n}(z),\ \varTheta (z)=\varSigma _{n=1}^{N}\theta _{n}T_{n}(z),\\ \varPhi (z)= & {} \varSigma _{n=1}^{N}\phi _{n}T_{n}(z). \end{aligned}$$

Since $T_{n}(\pm 1)=(\pm 1)^{n}$ and $T^{\prime }_{n}(\pm 1)=(\pm 1)^{n-1}n^{2}\$, implies that the boundary conditions (12) become

$$\begin{aligned} \begin{aligned}&w_{2}+w_{4}+w_{6}+\cdots +w_{N}=0,\\&w_{1}+w_{3}+w_{5}+\cdots +w_{N-1}=0 \end{aligned} \end{aligned}$$

(29)

with similar representations for $\theta _{n}$ and $\phi _{n}$

$$\begin{aligned} \begin{aligned}&\theta _{2}+\theta _{4}+\theta _{6}+\cdots +\theta _{N}=0,\\&\theta _{1}+\theta _{3}+\theta _{5}+\cdots +\theta _{N-1}=0, \end{aligned} \end{aligned}$$

(30)

$$\begin{aligned} \begin{aligned}&\phi _{2}+\phi _{4}+\phi _{6}+\cdots +\phi _{N}=0,\\&\phi _{1}+\phi _{3}+\phi _{5}+\cdots +\phi _{N-1}=0, \end{aligned} \end{aligned}$$

(31)

while the boundary condition $Dw=0$ becomes

$$\begin{aligned} \begin{aligned}&2^{2}w_{2}+4^{2}w_{4}+6^{2}w_{6}+\cdots +N^{2}w_{N}=0,\\&w_{1}+3^{2}w_{3}+5^{2}w_{5}+\cdots +(N-1)^{2}w_{N-1}=0 \end{aligned} \end{aligned}$$

(32)

Therefore, the Chebyshev tau method reduces to solving the matrix system $A\mathbf x =\sigma B\mathbf x$, where $\mathbf x =(w_{1},w_{2},\ldots ,w_{N}, \chi _{1},\chi _{2},\ldots ,\chi _{N}, \theta _{1},\ldots ,\theta _{N},\phi _{1},\ldots ,\phi _{N})$ and the matrices A and B are given by

$$\begin{aligned} A= & {} \begin{pmatrix} 4D^{2}-a^{2}I &{}\quad -I &{}\quad 0 &{}\quad 0 \\ BC1 &{}\quad 0\cdots 0 &{}\quad 0\cdots 0 &{}\quad 0\cdots 0 \\ BC2 &{}\quad 0\cdots 0 &{}\quad 0\cdots 0 &{}\quad 0\cdots 0 \\ 0 &{}\quad 4D^{2}-a^{2}I-\frac{I}{\tilde{\gamma }} &{}\quad -a^{2}R\frac{I}{\tilde{\gamma }} &{}\quad a^{2}R_{s}\frac{I}{\tilde{\gamma }}\\ BC7 &{}\quad 0\cdots 0 &{}\quad 0\cdots 0 &{}\quad 0\cdots 0 \\ BC8 &{}\quad 0\cdots 0 &{}\quad 0\cdots 0 &{}\quad 0\cdots 0 \\ RI &{}\quad 0 &{}\quad 4D^{2}-a^{2}I &{}\quad 0 \\ 0\cdots 0 &{}\quad 0\cdots 0 &{}\quad BC3 &{}\quad 0\cdots 0 \\ 0\cdots 0 &{}\quad 0\cdots 0 &{}\quad BC4 &{}\quad 0\cdots 0 \\ \mp R_{s}I &{}\quad 0 &{}\quad hI &{}\quad 4D^{2}-(a^{2}+\eta )I \\ 0\cdots 0 &{}\quad 0\cdots 0 &{}\quad 0\cdots 0 &{}\quad BC5 \\ 0\cdots 0 &{}\quad 0\cdots 0 &{}\quad 0\cdots 0 &{}\quad BC6 \end{pmatrix} \end{aligned}$$

$$\begin{aligned} B= & {} \begin{pmatrix} 0 &{} 0 &{} 0 &{} 0 \\ 0\cdots 0 &{} 0\cdots 0 &{} 0\cdots 0 &{} 0\cdots 0 \\ 0\cdots 0 &{} 0\cdots 0 &{} 0\cdots 0 &{} 0\cdots 0 \\ 0 &{} 0 &{} 0 &{} 0 \\ 0\cdots 0 &{} 0\cdots 0 &{} 0\cdots 0 &{} 0\cdots 0 \\ 0\cdots 0 &{} 0\cdots 0 &{} 0\cdots 0 &{} 0\cdots 0 \\ 0 &{} 0 &{} I &{} 0 \\ 0\cdots 0 &{} 0\cdots 0 &{} 0\cdots 0 &{} 0\cdots 0 \\ 0\cdots 0 &{} 0\cdots 0 &{} 0\cdots 0 &{} 0\cdots 0 \\ 0 &{} 0 &{} 0 &{} \varepsilon I \\ 0\cdots 0 &{} 0\cdots 0 &{} 0\cdots 0 &{} 0\cdots 0 \\ 0\cdots 0 &{} 0\cdots 0 &{} 0\cdots 0 &{} 0\cdots 0 \end{pmatrix} \end{aligned}$$

where in the matrix A the notations BC1, BC2 refer to the boundary conditions (29), BC3, BC4 refer to (30) , BC5, BC6 refer to (31) and BC7, BC8 refer to the boundary conditions (32). We solved the matrix system by the QZ algorithm (Dongarra et al. [42]).

5.2 The compound matrix technique for the energy theory

To employ the compound matrix method (Lindsay and Straughan [43]), we have to write system (26) as

$$\begin{aligned} D^{4}W= & {} -a^{4}W+2a^{2}D^{2}W-\frac{a^{2}}{\tilde{\gamma }}W+\frac{1}{\tilde{\gamma }}D^{2}W+R_{E}R\frac{a^{2}}{\tilde{\gamma }}\varTheta -\frac{a^{2}}{\tilde{\gamma }}\left( \frac{1\pm \lambda }{2}\right) R_{E}R_{s}\varPhi ,\nonumber \\ D^{2}\varTheta= & {} a^{2}\varTheta - R_{E}RW - \left( \frac{h\lambda }{2}\right) R_{E}\varPhi ,\nonumber \\ D^{2}\varPhi= & {} \left( a^{2}+\eta \right) \varPhi - \frac{h}{2}R_{E}\varTheta + \left( \frac{1\pm \lambda }{2\lambda }\right) R_{E}R_{s}W. \end{aligned}$$

(33)

The compound matrix for (33) works with the $4\times 4$ minors of the $8\times 4$ solution matrix formed from

$$\begin{aligned} \begin{aligned}&U_{1}=\left( W_{1},W_{1}^{\prime },W_{1}^{\prime \prime },W_{1}^{\prime \prime \prime },\varTheta _{1} ,\varTheta _{1}^{\prime },\varPhi _{1},\varPhi _{1}^{\prime } \right) ,\\&U_{2}=\left( W_{2},W_{2}^{\prime },W_{2}^{\prime \prime },W_{2}^{\prime \prime \prime },\varTheta _{2} ,\varTheta _{2}^{\prime },\varPhi _{2},\varPhi _{2}^{\prime } \right) ,\\&U_{3}=\left( W_{3},W_{3}^{\prime },W_{3}^{\prime \prime },W_{3}^{\prime \prime \prime },\varTheta _{3} ,\varTheta _{3}^{\prime },\varPhi _{3},\varPhi _{3}^{\prime } \right) ,\\&U_{4}=\left( W_{4},W_{4}^{\prime },W_{4}^{\prime \prime },W_{4}^{\prime \prime \prime },\varTheta _{4} ,\varTheta _{4}^{\prime },\varPhi _{4},\varPhi _{4}^{\prime } \right) . \end{aligned} \end{aligned}$$

(34)

The solutions $U_{i}$ for $i=1,2,3,4$ are independent solutions to (33) for different initial values, $U_{i}$’s correspond to solutions for starting values

$$\begin{aligned}&(0,0,1,0,0,0,0,0)^{T}\ ,\ (0,0,0,1,0,0,0,0)^{T},\\&(0,0,0,0,0,1,0,0)^{T}\ ,\ (0,0,0,0,0,0,0,1)^{T}, \end{aligned}$$

respectively. We define $C^{8}_{4}=70$ new variables $y_{1}, \ldots , y_{70}$ as the $4\times 4$ minors. For example

$$\begin{aligned} y_{1}= \begin{vmatrix} W_{1}&\quad W_{2}&\quad W_{3}&\quad W_{4} \\ W_{1}^{\prime }&\quad W_{2}^{\prime }&\quad W_{3}^{\prime }&\quad W_{4}^{\prime } \\ W_{1}^{\prime \prime }&\quad W_{2}^{\prime \prime }&\quad W_{3}^{\prime \prime }&\quad W_{4}^{\prime \prime } \\ W_{1}^{\prime \prime \prime }&\quad W_{2}^{\prime \prime \prime }&\quad W_{3}^{\prime \prime \prime }&\quad W_{4}^{\prime \prime \prime } \\ \end{vmatrix} \end{aligned}$$

implies that $y_{1}= W_{1}W_{2}^{\prime }W_{3}^{\prime \prime }W_{4}^{\prime \prime \prime }+\cdots$, which gives 24 terms for $y_{1}$. So, the idea is to derive $y_{2}, \ldots , y_{70}$ similarly and then obtain differential equations for the $y_{i}$’s by differentiation. There is no need to write out the whole determinant each time. The first term, $y_{1}$, suffices. By differentiating each $y_{i}$ and substituting from Eq. (33) we obtain differential equations for the $y_{i}$, cf. Lindsay and Straughan [43] and chapter 19 of Straughan [29]. These equations are integrated numerically from $0\ to\ 1$. We keep the boundary conditions (27) at $z=0$ and replace the ones at $z=1$ by

$$\begin{aligned} W_{1}^{\prime \prime }(0)=W_{2}^{\prime \prime \prime }(0) =\varTheta _{3}^{\prime }(0)=\varPhi _{4}^{\prime }(0)=1, \end{aligned}$$

(35)

which using the $y_{i}$’s yields the initial condition for the $y_{i}^{\prime }$’s as

$$\begin{aligned} y_{60}(0)=1. \end{aligned}$$

(36)

Using $y_{i}$’s, the final condition which satisfies (27) is seen to be

$$\begin{aligned} y_{11}(1)=0. \end{aligned}$$

(37)

The eigenvalue R is varied until (37) is satisfied to some pre-assigned tolerance.

6 Numerical results and conclusion

6.1 Heated below salted above system

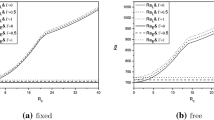
The numerical integration is carried out for different values of the reaction rates, $h\ and\ \eta$ and different values of the Brinkman coefficient $\tilde{\gamma }$. We found that when the layer is heated below and salted above in the case of no reaction i.e.$\ h=\eta =0$ and when Brinkman coefficient $\tilde{\gamma }=1$ that the numerical methods used give exactly the same values for $Ra_{L}$ and $Ra_{E}$. The graphical representation of these values shows that the linear instability threshold coincide with the energy stability threshold as it is clear in Fig. 1a and that there is no region of subcritical instability. As we increase the values of the reaction rates h and $\eta$, the linear instability boundary starts to diverge from the energy stability boundary. Figure 1 shows the effect of increasing the values of the reaction rates, as we increase the values of h and $\eta$, the gap between the boundaries increases. Any point $(Rs^{2},Ra^{2})$ in the space above the linear instability boundary, the solid line $Ra_{L}^{2}$, represents a region where the system is unstable because the linear instability boundary guarantees instability. On the other hand, if $(Rs^{2},Ra^{2})$ lies below the energy stability boundary, the dashed line $Ra_{E}^{2}$, represents the space where the system is definitely stable. Note that as the reaction rates increase, the peak of the linear instability curve moves to a higher position resulting in a wider region of possible subcritical instability between the energy stability threshold and the linear instability threshold. Moreover, there is a slight noticeable decrease in the energy stability threshold as the values of $R_{s} \rightarrow +\infty$. Table 1 represents some numerical values obtained.

Fig. 1

Linear instability and energy stability boundaries for the salted above Brinkman convection problem for different values of the reaction rates h and $\eta$. a $h=\eta =0$. b $h = 5, \eta = 3$

Table 1 Some numerical values obtained for the linear boundary $Ra_{L}$ and energy boundary $Ra_{E}$ temperature Rayleigh number with corresponding salt Rayleigh number $R_{s}$ and the the corresponding critical wave numbers $a_{L}$ and $a_{E}$ when $\tilde{\gamma }=1$, $h=9$ and $\eta =6$ in the case of heated below salted above system

To study the effect of each one of h and $\eta$ on the stability of the system, a bigger difference between their values is considered. It has been noticed that when h is bigger compared to $\eta$, the region of possible subcritical instability is wider and increasing the value of h implies more divergence of the linear instability boundary from the energy stability boundary and a movement of the peak value of the linear instability threshold to a higher position, as Fig. 2a shows. Compared to the case when $\eta$ has a bigger value than h, the linear and energy boundaries coincide as shown in Fig. 2b and the linear boundary covers the content of stability. This is expected, as system (7) shows that $h\varTheta$ is a destabilizing term while $-\eta \varPhi$ is a stabilizing term.

Fig. 2

Linear instability and energy stability boundaries for the salted above Brinkman convection problem. The difference between the values of the reaction rates h and $\eta$ is large. a $h=10$, $\eta =0$. b $h=0$, $\eta =10$

Examining the effect of different values of the Brinkman coefficient (effective viscosity term) on the stability boundaries, reveals that increasing the value of $\tilde{\gamma }$ results in a wider space of global stability below the energy stability threshold and a wider region of potential subcritical instability. The effect of different values of $\tilde{\gamma }(= 0.5, 2)$ are presented graphically in Fig. 3.

Fig. 3

Linear instability and energy stability boundaries for the salted above Brinkman convection problem for different values of the Brinkman constant when $h=9$ and $\eta =6$. a $\tilde{\gamma }=0.5$. b $\tilde{\gamma }=2$

6.2 Heated and salted Below system

It is instructive to write system (7) and the boundary conditions (8) for the salted below case as an abstract equation of form

$$\begin{aligned} A\mathbf u _{t}=L(\mathbf u )+N(\mathbf u ), \end{aligned}$$

where $\mathbf u =(u_{1}, u_{2}, u_{3}, \theta , \phi )$, $N(\mathbf u )$ represents the nonlinear terms in (7) so

$$\begin{aligned} N(\mathbf u )= \begin{pmatrix} 0 \\ 0 \\ 0 \\ -u_{i}\theta _{,i}\\ -\frac{Le}{\hat{\phi }}u_{i}\phi _{,i} \end{pmatrix}, \end{aligned}$$

and L is the linear operator. In fact, the linear operator for (7) is

$$\begin{aligned} L=\begin{pmatrix} -1+\tilde{\gamma }\Delta &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad -1+\tilde{\gamma }\Delta &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad -1+\tilde{\gamma }\Delta &{}\quad R &{}\quad -R_{s} \\ 0 &{}\quad 0 &{}\quad R &{}\quad \Delta &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad R_{s} &{}\quad h &{}\quad \Delta -\eta I \end{pmatrix}. \end{aligned}$$

We may split L into a symmetric plus skew-symmetric part as follows

$$\begin{aligned} L=L_{s}+L_{A}\ , \end{aligned}$$

where

$$\begin{aligned} L_{s}= \begin{pmatrix} -1+\tilde{\gamma }\Delta &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad -1+\tilde{\gamma }\Delta &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad -1+\tilde{\gamma }\Delta &{}\quad R &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad R &{}\quad \Delta &{}\quad \frac{h}{2} \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad \frac{h}{2} &{}\quad \Delta -\eta I \end{pmatrix}, \end{aligned}$$

and

$$\begin{aligned} L_{A}= \begin{pmatrix} 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad -R_{s} \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad -\frac{h}{2} \\ 0 &{}\quad 0 &{}\quad R_{s} &{}\quad \frac{h}{2} &{}\quad 0 \end{pmatrix}. \end{aligned}$$

For the salted above case, the previous subsection, $L_{A}$ would be zero and the analogous linear operator L would be symmetric. Even when $h=0$ in the salted below case, we expect some problem with nonlinear energy stability theory since

$$\begin{aligned} (\mathbf u , L(\mathbf u ))\ne (\mathbf u , L_{s}(\mathbf u )) \end{aligned}$$

where $(\cdot , \cdot )$ is the inner product on $(H^{1}(V))^{5}$ with V being a period cell for the solution. For the problem of this subsection, governed by Eqs. (7) and (8) for the salted below case, we have two sources of anti-symmetry, the $R_{s}$ term and the h term.

The numerical values are presented graphically for different values of the reaction rates h and $\eta$ in Fig. 4. It has been noticed that as the reaction rate increases, the gap between the linear instability and energy stability boundaries increases due to the divergence of the linear threshold yielding a wider region of potential subcritical instability. Whereas, the energy stability threshold is approximately constant or more precisely it is decreasing unnoticeably as shown in Figs. 4 and 5. As expected from system (7) one sees that $h\varTheta$ will destabilize the system while $-\eta \varPhi$ will stabilize the system which is clear and shown in Fig. 5 i.e, when the value of h is smaller compared to $\eta$ the space of possible subcritical instability is less compared to the case when h is larger than $\eta$. The effect of changing the value of $\tilde{\gamma }$ can be noticed in Fig. 6 for $\tilde{\gamma }=0.5,\ 2$. The gap between the boundaries increases and the space of global stability is wider as $\tilde{\gamma }$ increases.

Fig. 4

Linear instability and energy stability boundaries for the salted below Brinkman convection problem for different values of the reaction rates h and $\eta$. a $h=\eta =0$. b $h=9, \eta =6$

Fig. 5

Linear instability and energy stability boundaries for the salted below Brinkman convection problem. The difference between the values of the reaction rates h and $\eta$ is large. a $h=20, \eta =1$. b $h=1, \eta =20$

Fig. 6

Linear instability and energy stability boundaries for the salted below Brinkman convection problem for different values of the Brinkman coefficient when $h=10$ and $\eta =0$. a $\tilde{\gamma }=0.5$. b $\tilde{\gamma }=2$

The numerical values and their graphical representations show that the linear instability theory does not necessarily represent accurately the onset of convection and we may explain that this is due to the two sources of anti-symmetry the $R_{s}$ term and the h term. By this we mean that the linear instability boundary is definitely a threshold for instability, but in this case, it may be possible for instability to arise with a Rayleigh number below the linear instability boundary.