Abstract
We propose a novel concept of a Systemic Optimal Risk Transfer Equilibrium (SORTE), which is inspired by the Bühlmann’s classical notion of an Equilibrium Risk Exchange. We provide sufficient general assumptions that guarantee existence, uniqueness, and Pareto optimality of such a SORTE. In both the Bühlmann and the SORTE definition, each agent is behaving rationally by maximizing his/her expected utility given a budget constraint. The two approaches differ by the budget constraints. In Bühlmann’s definition the vector that assigns the budget constraint is given a priori. On the contrary, in the SORTE approach, the vector that assigns the budget constraint is endogenously determined by solving a systemic utility maximization. SORTE gives priority to the systemic aspects of the problem, in order to optimize the overall systemic performance, rather than to individual rationality.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
We introduce the concept of Systemic Optimal Risk Transfer Equilibrium, denoted by SORTE, that conjugates the classical Bühlmann’s notion of an equilibrium risk exchange with capital allocation based on systemic expected utility optimization.
The capital allocation and risk sharing equilibrium that we consider can be applied to many contexts, such as: equilibrium among financial institutions, agents, or countries; insurance and reinsurance markets; capital allocation among business units of a single firm; wealth allocation among investors.
In this paper we will refer to a participant in these problems (financial institution or firms or countries) as an agent; the class consisting of these N agents as the system; the individual risk of the agents (or the random endowment or future profit and loss) as the risk vector \(\mathbf {X}:=[X^{1},\ldots ,X^{N}]\); the amount \(\mathbf {Y} :=[Y^{1},\ldots ,Y^{N}]\) that can be exchanged among the agents as random allocation. We will generically refer to a central regulator authority, or CCP, or executive manager as a central bank (CB).
We now present the main concepts of our approach and leave the details and the mathematical rigorous presentation to the next sections. In a one period framework, we consider N agents, each one characterized by a concave, strictly monotone utility function \(u_{n}:\mathbb {R\rightarrow R}\) and by the original risk \(X^{n}\in L^{0}(\Omega ,{\mathcal {F}},P),\) for \(n=1,\ldots ,N\). Here, \((\Omega ,{\mathcal {F}},P\mathbf {)}\) is a probability space and \( L^{0}(\Omega ,{\mathcal {F}},P)\) is the vector space of real valued \({\mathcal {F}} \)-measurable random variables. The sigma-algebra \({\mathcal {F}}\) represents all possible measurable events at the final time T. \({\mathbb {E}}\left[ \cdot \right] \) denotes the expectation under P. Given another probability measure Q, \(E_{Q}\left[ \cdot \right] \) denotes the expectation under Q. For the sake of simplicity and w.l.o.g., we are assuming zero interest rate. We will use the bold notation to denote vectors.
-
1.
Bühlmann’s risk exchange equilibrium
We recall Bühlmann’s definition of a risk exchange equilibrium in a pure exchange economy (or in a reinsurance market). The initial wealth of agent n is denoted by \(x^{n}\in {\mathbb {R}}\) and the variable \(X^{n}\) represents the original risk of this agent. In this economy each agent is allowed to exchange risk with the other agents. Each agent has to agree to receive (if positive) or to provide (if negative) the amount \({\widetilde{Y}}^{n}(\omega )\) at the final time in exchange of the amount \(E_{Q}[{\widetilde{Y}}^{n}]\) paid (if positive) or received (if negative) at the initial time, where Q is some pricing probability measure. Hence \({\widetilde{Y}}^{n}\) is a time T measurable random variable. In order that at the final time this risk sharing procedure is indeed possible, the exchange variables \({\widetilde{Y}} ^{n}\) have to satisfy the clearing condition
$$\begin{aligned} \sum _{n=1}^{N}{\widetilde{Y}}^{n}=0 \ P{\text {-}}a.s.\,\,\,. \end{aligned}$$As in Bühlmann [12, 13], we say that a pair (\(\widetilde{\mathbf {Y}}_{\mathbf {X}},Q_{\mathbf {X}})\) is an risk exchange equilibrium if:
-
(a)
for each n, \({\widetilde{Y}}_{\mathbf {X}}^{n}\) maximizes: \({\mathbb {E}} \left[ u_{n}(x^{n}+X^{n}+{\widetilde{Y}}^{n}-E_{Q_{\mathbf {X}}}[{\widetilde{Y}} ^{n}])\right] \) among all variables \({\widetilde{Y}}^{n}\);
-
(b)
\(\sum _{n=1}^{N}{\widetilde{Y}}_{\mathbf {X}}^{n}=0\) P-a.s. .
It is clear that only for some particular choice of the equilibrium pricing measure \(Q_{\mathbf {X}}\), the optimal solutions \({\widetilde{Y}}_{\mathbf {X} }^{n}\) to the problems in (a) will also satisfy the condition in (b).
In addition it is evident that the clearing condition in (b) requires that all agents accept to exchange the amount \({\widetilde{Y}}_{ \mathbf {X}}^{n}(\omega )\) at the final time T.
Define
$$\begin{aligned} {\mathcal {C}}_{{\mathbb {R}}}:=\left\{ \mathbf {Y}\in (L^{0}(\Omega ,{\mathcal {F}} ,P))^{N}\mid \sum _{n=1}^{N}Y^{n}\in {\mathbb {R}}\right\} \end{aligned}$$(1)that is, \({\mathcal {C}}_{{\mathbb {R}}}\) is the set of random vectors such that the sum of the components is P-a.s. a deterministic number.
Observe that with the change of notations \(Y^{n}:=x^{n}+{\widetilde{Y}} ^{n}-E_{Q_{\mathbf {X}}}[{\widetilde{Y}}^{n}]\), we obtain variables with \(E_{Q_{ \mathbf {X}}}[Y^{n}]=x^{n}\) for each n, and an optimal solution \(Y_{\mathbf { X}}^{n}\) still belonging to \({\mathcal {C}}_{{\mathbb {R}}}\) and satisfying
$$\begin{aligned} \sum _{n=1}^{N}Y_{\mathbf {X}}^{n}=\sum _{n=1}^{N}x^{n}\quad P{\text {-}}a.s.\,\,. \end{aligned}$$(2)As can be easily checked
$$\begin{aligned} \sup _{{\widetilde{Y}}^{n}}{\mathbb {E}}\left[ u_{n}(x^{n}+X^{n}+{\widetilde{Y}} ^{n}-E_{Q_{\mathbf {X}}}[{\widetilde{Y}}^{n}])\right] =\sup _{Y^{n}}\left\{ {\mathbb {E}}\left[ u_{n}(X^{n}+Y^{n})\right] \mid E_{Q_{\mathbf {X} }}[Y^{n}]\le x^{n}\right\} . \end{aligned}$$Hence the two above conditions in the definition of a risk exchange equilibrium may be equivalently reformulated as
-
(a’)
for each n, \(Y_{\mathbf {X}}^{n}\) maximizes: \({\mathbb {E}}\left[ u_{n}(X^{n}+Y^{n})\right] \) among all variables satisfying \(E_{Q_{\mathbf {X} }}[Y^{n}]\le x^{n}\);
-
(b’)
\(\mathbf {Y}_{\mathbf {X}}\in {\mathcal {C}}_{{\mathbb {R}}}\) and \( \sum _{n=1}^{N}Y_{\mathbf {X}}^{n}=\sum _{n=1}^{N}x^{n}\) P-a.s.
We remark that here the quantity \(x^{n}\in {\mathbb {R}}\) is preassigned to each agent.
-
2.
Systemic optimal (deterministic) allocation
To simplify the presentation, we now suppose that the initial wealth of each agent is already absorbed in the notation \(X^{n}\), so that \(X^{n}\) represents the initial wealth plus the original risk of agent n. We assume that the system has at disposal a total amount of capital \(A\in {\mathbb {R}}\) to be used at a later time in case of necessity. This amount could have been assigned by the Central Bank, or could have been the result of the previous trading in the system, or could have been collected ad hoc by the agents. The amount A could represent an insurance pot or a fund collected (as guarantee for future investments) in a community of homeowners. For further interpretation of A, see also the related discussion in Sect. 5.2 of Biagini et al. [7]. In any case, we consider the quantity A as exogenously determined. This amount is allocated among the agents in order to optimize the overall systemic satisfaction. If we denote with \(a^{n}\in {\mathbb {R}}\) the cash received (if positive) or provided (if negative) by agent n, then the time T wealth at disposal of agent n will be \((X^{n}+a^{n})\). The optimal vector \(\mathbf {a_{\mathbf {X}}\in } {\mathbb {R}}^{N}\) could be determined according to the following aggregate time-T criterion
$$\begin{aligned} \sup \left\{ \sum _{n=1}^{N}{\mathbb {E}}\left[ u_{n}(X^{n}+a^{n})\right] \mid \mathbf {a\in }{\mathbb {R}}^{N}\text { s.t. }\sum _{n=1}^{N}a^{n}=A\right\} . \end{aligned}$$(3)Note that each agent is not optimizing his own utility function. As the vector \( \mathbf {a\in }{\mathbb {R}}^{N}\) is deterministic, it is known at time \(t=0\) and therefore the agents have to agree to provide or receive money only at such initial time.
However, under the assumption that also at the final time the agents have confidence in the overall reliability of the other agents, one can combine the two approaches outlined in Items 1 and 2 above to further increase the optimal total expected systemic utility and simultaneously guarantee that each agent will optimize his/her own single expected utility, taking into consideration an aggregated budget constraint assigned by the system. Of course an alternative assumption to trustworthiness could be that the rules are enforced by the CB.
We denote with \({\mathcal {L}}^{n}\subseteq L^{0}(\Omega ,{\mathcal {F}},P)\) a space of admissible random variables and assume that \({\mathcal {L}}^{n}+ \mathbb {R=}{\mathcal {L}}^{n}\). We will consider maps \(p^{n}:{\mathcal {L}} ^{n}\rightarrow {\mathbb {R}}\) that represent the pricing or cost functionals, one for each agent n. As we shall see, in some relevant cases, all agents will adopt the same functional \(p^{1}=\cdots =p^{N}\), which will then be interpreted as the equilibrium pricing functional, as in Bühlmann’s setting above, where \(p^{n}(\cdot ):=E_{Q}[\cdot ]\) for all n. However, we do not have to assume this a priori. Instead we require that the maps \(p^n\) satisfy for all \(n=1,\ldots ,N\):
-
(i)
\(p^{n}\) is monotone increasing;
-
(ii)
\(p^{n}(0)=0;\)
-
(iii)
\(p^{n}(Y+c)=p^{n}(Y)+c\) for all \(c\in {\mathbb {R}}\) and \(Y\in {\mathcal {L}} ^{n}\).
Such assumptions in particular imply \(p^{n}(c)=c\) for all constants \(c\in {\mathbb {R}}\). A relevant example of such functionals are
where \(Q^n\) are probability measures for \(n=1,\ldots ,N\). Another example could be \(p^{n}=-\rho ^{n}\), for convex risk measures \(\rho ^{n}\).
Now we will apply both approaches, outlined in Items 1 and 2 above, to describe the concept of a Systemic Optimal Risk Transfer Equilibrium.
-
3.
Systemic optimal risk transfer equilibrium
As explained in Item 1, given some amount \(a^{n}\) assigned to agent n, this agent may buy \({\widetilde{Y}}^{n}\) at the price \(p^{n}({\widetilde{Y}} ^{n}) \) in order to optimize
$$\begin{aligned} {\mathbb {E}}\left[ u_{n}(a^{n}+X^{n}+{\widetilde{Y}}^{n}-p^{n}({\widetilde{Y}} ^{n}))\right] . \end{aligned}$$The pricing functionals \(p^{n}\), \(n=1,\ldots ,N\) have to be selected so that the optimal solution verifies the clearing condition
$$\begin{aligned} \sum _{n=1}^{N}{\widetilde{Y}}^{n}=0\quad P-\text {a.s.} . \end{aligned}$$However, as in Item 2, \(a^{n}\) is not exogenously assigned to each agent, but only the total amount A is at disposal of the whole system. Thus the optimal way to allocate A among the agents is given by the solution \(( {\widetilde{Y}}_{\mathbf {X}}^{n},p_{\mathbf {X}}^{n},a_{\mathbf {X}}^{n})\) of the following problem:
 (5)
(5) (6)
(6)From (5) and (6) it easily follows that an optimal solution \(({\widetilde{Y}}_{ \mathbf {X}}^{n},p_{\mathbf {X}}^{n},a_{\mathbf {X}}^{n})\) fulfills
$$\begin{aligned} \sum _{n=1}^{N}p_{\mathbf {X}}^{n}({\widetilde{Y}}_{\mathbf {X}}^{n})=0. \end{aligned}$$(7)Further, letting \(Y^{n}:=a^{n}+{\widetilde{Y}}^{n}-p_{\mathbf {X}}^{n}( {\widetilde{Y}}^{n})\), from the cash additivity of \(p_{\mathbf {X}}^{n}\) we deduce \(p_{\mathbf {X}}^{n}(Y^{n})=a^{n}+p_{\mathbf {X}}^{n}({\widetilde{Y}} ^{n})-p_{\mathbf {X}}^{n}({\widetilde{Y}}^{n})=a^{n}\) and \(\sum _{n=1}^{N}Y_{ \mathbf {X}}^{n}=\sum _{n=1}^{N}a^{n}+\sum _{n=1}^{N}{\widetilde{Y}}_{\mathbf {X} }^{n}-\sum _{n=1}^{N}p_{\mathbf {X}}^{n}({\widetilde{Y}}_{\mathbf {X} }^{n})=\sum _{n=1}^{N}a^{n}\) and, as before, the above optimization problem can be reformulated as
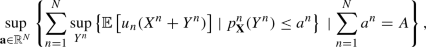 (8)
(8) (9)
(9)where analogously to (7) we have that a solution \((Y_{\mathbf {X }}^{n},p_{\mathbf {X}}^{n},a_{\mathbf {X}}^{n})\) satisfies \(\sum _{n=1}^{N}p_{ \mathbf {X}}^{n}(Y_{\mathbf {X}}^{n})=A\), by (8) and (9).
The two optimal values in (5) and (8) coincide. We see that while each agent is behaving optimally according to his preferences, the budget constraint \(p_{\mathbf {X}}^{n}(Y^{n})\le a^{n}\) are not a priori assigned, but are endogenously determined through an aggregate optimization problem. The optimal value \(a_{\mathbf {X}}^{n}\) determines the optimal risk allocation of each agent. It will turn out that \(a_{\mathbf {X} }^{n}=p_{\mathbf {X}}^{n}(Y_{\mathbf {X}}^{n})\). Obviously, the optimal value in (5) is greater than (or equal to) the optimal value in (3), which can be economically translated into the statement that allowing for exchanges also at terminal time increases the systemic performance.
In addition to the condition in (9), we introduce further possible constraints on the optimal solution, by requiring that
$$\begin{aligned} \mathbf {Y}_{\mathbf {X}}\in {\mathcal {B}}, \end{aligned}$$(10)where \({\mathcal {B}}\subseteq {\mathcal {C}}_{{\mathbb {R}}}\).
In the paper, see Sect. 3.4, we formalize the above discussion and show the existence of the solution \((Y_{\mathbf {X}}^{n}\), \(p_{\mathbf {X} }^{n},a_{\mathbf {X}}^{n})\) to (8), (9) and (10), which we call Systemic Optimal Risk Transfer Equilibrium (SORTE). We show that \(p_{\mathbf {X}}^{n}\) can be chosen to be of the particular form \(p_{ \mathbf {X}}^{n}(\cdot ):=E_{Q_{\mathbf {X}}^{n}}[\cdot ]\), for a probability vector \(\mathbf {Q}_{\mathbf {X}}=[Q_{\mathbf {X}}^{1},\ldots ,Q_{\mathbf {X}}^{N}]\) . The crucial step, Theorem 4.5, is the proof of the dual representation and the existence of the optimizer of the associated problem (29). The optimizer of the dual formulation provides the optimal probability vector \(\mathbf {Q}_{\mathbf {X}}\) that determines the functional \( p_{\mathbf {X}}^{n}(\cdot ):=E_{Q_{\mathbf {X}}^{n}}[\cdot ]\). The characteristics of the optimal \(\mathbf {Q}_{\mathbf {X}}\) depend on the feasible allocation set \({\mathcal {B}}\). When no constraints are enforced, i.e., when \({\mathcal {B}}={\mathcal {C}}_{{\mathbb {R}}}\), then all the components of \(\mathbf {Q}_{\mathbf {X}}\) turn out to be equal. Hence we find that the implicit assumption of one single equilibrium pricing measure, made in the Bühlmann’s framework, is in our theory a consequence of the particular selection \({\mathcal {B}}={\mathcal {C}}_{{\mathbb {R}}}\), but for general \(\mathcal {B }\) this in not always the case. At this point it might be convenient for the reader to have at hand the example of the exponential utility function that is described in Sects. 3.5, and 5, where we obtain an explicit formulation of the optimal solution \(\mathbf {Y}_{\mathbf {X}}\), of the equilibrium pricing measure \(\mathbf {Q}_{\mathbf {X}}\) and of the optimal vector \(\mathbf {a}_{\mathbf {X}}\).
Remark 1.1
We emphasize that the existence of multiple equilibrium pricing measures \( \mathbf {Q}_{\mathbf {X}}=(Q_{\mathbf {X}}^{1},\ldots ,Q_{\mathbf {X}}^{N})\) is a natural consequence of the presence of the - non trivial - constraints set \( {\mathcal {B}}\). Indeed, even in the Bühlmann setting, if we add constraints, of a very simple nature, a single equilibrium pricing measure might not exists any more. Consider the following extension of a Bühlmann risk exchange equilibrium.
Let \({\mathcal {B}}\subseteq {\mathcal {C}}_{{{\mathbb {R}}}}\) be fixed. We say that a pair (\(\widetilde{\mathbf {Y}}_{\mathbf {X}},Q_{\mathbf {X}})\) is a constrained risk exchange equilibrium if:
(a2) for each n, \({\widetilde{Y}}_{\mathbf {X}}^{n}\) maximizes: \({\mathbb {E}} \left[ u_{n}(x^{n}+X^{n}+{\widetilde{Y}}^{n}-E_{Q_{\mathbf {X}}}[{\widetilde{Y}} ^{n}])\right] \) among all variables \({\widetilde{Y}}^{n}\);
(b2) \(\widetilde{\mathbf {Y}}_{\mathbf {X}}\in {\mathcal {B}}\) and \(\sum _{n=1}^{N} {\widetilde{Y}}_{\mathbf {X}}^{n}=0\) P-a.s. .
We show with the next example that such an equilibrium (with one single probability \(Q_{\mathbf {X}})\) does not exist in general. The example we present is rather simple, yet instructive, since it shows that the absence of the equilibrium arises not from technical assumptions, like integrability conditions, but is rather a structural problem caused by the presence of additional constraints. Here we provide the intuition for it. Suppose that two isolated systems of agents have, under suitable assumptions, their own (unconstrained) equilibria, and that such two equilibria do not coincide. As shown in the next example, we might then consider the two systems as one single larger system consisting of two isolated clusters, expressing this latter property with the addition of constraints. Then it is evident that an equilibrium (with a unique pricing measure) cannot exist for such unified system.
Example 1.2
In order to ignore all integrability issues, in this example we assume that \( \Omega \) is a finite set, endowed with the sigma algebra of all its subsets and the uniform probability measure. Consider \(N=4,\) \(u_{n}(x):=(1-e^{- \alpha _{n}x}),\) \(\alpha _{n}>0,\) \(\,n=1,\dots ,4\), and some vectors \( \mathbf {x}\in {{\mathbb {R}}}^{4}\), and \(\mathbf {X}\in (L^{\infty })^{4}\). Moreover take
Thus \(\mathbf {X}\) and \({\mathcal {B}}\) model a single system of 4 agents which can exchange the risk only in a restricted way (agent 1 with agent 2, and agent 3 with agent 4), so that in effect the system consists of two isolated clusters of agents. Then a constrained risk exchange equilibrium in general does not exists. By contradiction, suppose that (\( \widetilde{\mathbf {Y}}_{\mathbf {X}},Q_{\mathbf {X}})\) is a constrained risk exchange equilibrium. It is easy to verify that \(([\widetilde{{Y}}_{\mathbf {X }}^{1},\widetilde{{Y}}_{\mathbf {X}}^{2}],Q_{\mathbf {X}})\) is a (unconstrained) risk exchange equilibrium with respect to \([X^{1},X^{2}]\) and \([x^{1},x^{2}]\) (i.e. it satisfies (a) and (b) for \(N=2\)). Similarly, \(([ \widetilde{{Y}}_{\mathbf {X}}^{3},\widetilde{{Y}}_{\mathbf {X}}^{4}],Q_{ \mathbf {X}})\) is a (unconstrained) risk exchange equilibrium with respect to \([X^{3},X^{4}]\) and \([x^{3},x^{4}]\). This implies using Eq. (2) in Bühlmann [13] that
which clearly gives a contradiction, since \(\mathbf {X}\) is arbitrary.
Observe, however, that in this example a constrained equilibrium exists if we allow for possibly different pricing measures, namely if we may replace the measure \(Q_{\mathbf {X}}\) with a vector \(\mathbf {Q}_{\mathbf {X }}\). This would amount to replacing (a2) with (a3) below, namely to require that:
(a3) for each n, \({\widetilde{Y}}_{\mathbf {X}}^{n}\) maximizes: \({\mathbb {E}} \left[ u_{n}(x^{n}+X^{n}+{\widetilde{Y}}^{n}-E_{Q_{\mathbf {X}}^{n}}[\widetilde{ Y}^{n}])\right] \) among all variables \({\widetilde{Y}}^{n}\);
(b2) \(\widetilde{\mathbf {Y}}_{\mathbf {X}}\in {\mathcal {B}}\) and \(\sum _{n=1}^{N} {\widetilde{Y}}_{\mathbf {X}}^{n}=0\) P-a.s. .
Then such an equilibrium exists. Indeed, by the results in Bühlmann [13], we can guarantee the existence of the risk exchange equilibrium \( ([\widetilde{{Y}}_{\mathbf {X}}^{1},\widetilde{{Y}}_{\mathbf {X}}^{2}],Q_{ \mathbf {X}}^{12})\) with respect to \([X^{1},X^{2}]\) and \([x^{1},x^{2}]\), and the risk exchange equilibrium \(([\widetilde{{Y}}_{\mathbf {X}}^{3},\widetilde{ {Y}}_{\mathbf {X}}^{4}],Q_{\mathbf {X}}^{34})\) with respect to \([X^{3},X^{4}]\) and \([x^{3},x^{4}]\). Then \(([\widetilde{{Y}}_{\mathbf {X}}^{1},\widetilde{{Y}}_{\mathbf {X}}^{2}, \widetilde{{Y}}_{\mathbf {X}}^{3},\widetilde{{Y}}_{\mathbf {X}}^{4}],[Q_{ \mathbf {X}}^{12},Q_{\mathbf {X}}^{12},Q_{\mathbf {X}}^{34},Q_{\mathbf {X} }^{34}])\) satisfies (a3) and (b2). The conclusion is that, even in the Bühlmann case, the presence of constraints implies multiple equilibrium pricing measures.
From the mathematical point of view, this fact is very easy to understand in our setup, described in Assumption 3.10. More constraints implies a smaller set \({\mathcal {B}}_{0}\) of feasible vectors \(\widetilde{\mathbf {Y}} \in {\mathcal {B}}\) such that \(\sum _{n=1}^{N}{\widetilde{Y}}_{\mathbf {X}}^{n}=0\) and this in turn implies a larger polar set of \({\mathcal {B}}_{0}\) (which we will denote with \({\mathcal {Q}}\), see the definition in Sect. item 4). The equilibrium exists only if we are allowed to pick the pricing vector \(\mathbf {Q}_{\mathbf {X}}\) in this larger set \({\mathcal {Q}}\) , but the elements in \({\mathcal {Q}}\) don’t need to have all equal components. Economically, multiple pricing measures may arise because the risk exchange mechanism may be restricted to clusters of agents, as in this example, and agents from different clusters may well adopt a different equilibrium pricing measure. For further details on clustering, see the Examples 3.17 and 4.20.
Bühlmann’s equilibrium (\(\mathbf {Y}_{\mathbf {X}}\)) satisfies two relevant properties: Pareto optimality (there are no feasible allocation \(\mathbf {Y}\) such that all agents are equal or better off - compared with \(\mathbf {Y}_{\mathbf {X}}\) - and at least one of them is better off) and Individual Rationality (each agent is better off with \(Y_{ \mathbf {X}}^{n}\) than without it). Any feasible allocation satisfying these two properties is called an optimal risk sharing rule, see Barrieu and El Karoui [4] or Jouini et al. [30].
We show that a SORTE is unique (once the class of pricing functionals is restricted to those in the form \(p^{n}(\cdot )=E_{Q^{n}}[\cdot ]\)). We also prove Pareto optimality, see the Definition 3.1 and the exact formulation in Theorem 4.17.
However, a SORTE lacks Individual Rationality. This is shown in the toy example of Sect. 5.2, but it is also evident from the expression in Eq. (8). As already mentioned, each agent is performing rationally, maximizing her expected utility, but under a budget constraint \( p_{\mathbf {X}}^{n}(Y^{n})\le a_{\mathbf {X}}^{n}\) that is determined globally via an additional systemic maximization problem (\(\sup _{\mathbf { a\in }{\mathbb {R}}^{N}}\{\ldots \mid \sum _{n=1}^{N}a^{n}=A\}\)) that assigns priority to the systemic performance, rather than to each individual agent. In the SORTE we replace individual rationality with such a systemic induced individual rationality, which also shows the difference between the concepts of SORTE and of an optimal risk sharing rule. We also point out that the participation in the risk sharing mechanism may be appropriately mitigated or enforced by the use of adequate sets \({\mathcal {B}}\), see e.g. Example 4.20 for risk sharing restricted to subsystems. From the technical point of view, we will not rely on any of the methods and results related to the notion of inf-convolution, which is a common tool to prove existence of optimal risk sharing rules (see for example [4] or [30]) in the case of monetary utility functions, as we do not require the utility functions to be cash additive. Our proofs are based on the dual approach to (systemic) utility maximization. This is summarized in Sect. 4.1. Furthermore, the exponential case is treated in detail in Sect. 5.
Remark 1.3
As customary in the literature on general equilibrium and risk sharing, we could have considered, in place of (8) and (9), the more general problem


where the positive weights \(\gamma =(\gamma _{1},\ldots ,\gamma _{N})\in {\mathbb {R}}^{N}\) could have been selected exogenously, say by a social planner. In such more general problems, equilibria will generally depend on the selected weights. However, in this paper we are focused on existence, uniqueness and Pareto optimality of the equilibrium and for this analysis we may restrict, without loss of generality, our attention to the utilitarian choice \(\gamma _{1}=\cdots =\gamma _{N}=1\), as we now explain. It is easy to check that given \( u_{1},\dots ,u_{N}\) satisfying our assumptions (namely Assumption 3.10 .(a)), the associated functions \(x\mapsto u_{n}^{\gamma }(x):=\gamma _{n}u_{n}(x),\,n=1,\dots ,N\) will satisfy the same Assumption 3.10.(a) and so (11) can be written as

Thus, technically speaking, the study of the existence, uniqueness and Pareto optimality of the equilibrium in a non-utilitarian setup (\(\gamma \ne 1\)) boils down to the one in (8) and (9). Of course it could be of interest to study the dependence of the optimal solution from the vector \(\gamma \) and to analyze the stability properties of the equilibrium with respect to the utility functions. In Sect. 5.3 we address this problem for exponential utility functions, but the general case is left for future investigation.
Review of literature This paper originates from the systemic risk approach developed in Biagini et al. [6, 7]. In [7] the main focus was the analysis of the systemic risk measure
which computes systemic risk as the minimal capital \(\sum _{n=1}^{N}Y^{n}\in {\mathbb {R}}\) that secures the aggregated system \(({\mathbb {E}}\left[ \sum _{n=1}^{N}u_{n}(X^{n}+Y^{n})\right] \ge B)\) by injecting the random allocation \(Y^{n}\) into the single institution \(X^{n}\).
The notion of a SORTE is inspired by the following utility maximization problem, associated to the risk minimization problem (14),
that was also introduced in [7]. Related papers on systemic risk measures are Feinstein et al. [23], Acharya et al. [2], Armenti et al. [3], Chen et al. [17], Kromer et al. [32]. For an exhaustive overview on the literature on systemic risk, see Hurd [29] and Fouque and Langsam [27].
For a review on Arrow–Debreu Equilibrium (see Debreu [20]; Mas Colell and Zame [34] for the infinite dimensional case) we refer to Sect. 3.6 of Föllmer and Schied [26], which is close to our setup. In the spirit of the Arrow–Debreu Equilibrium, Bühlmann [12, 13] proved the existence of risk exchange equilibria in a pure exchange economy. Such risk sharing equilibria had been studied in different forms starting from the seminal papers of Borch [11], where Pareto-optimal allocations were proved to be comonotonic for concave utility functions, and Bühlmann and Jewell [14]. The differences with Bühlmann’s setup and our approach have been highlighted before in detail.
In Barrieu and El Karoui [4] inf-convolution of convex risk measures has been introduced as a fundamental tool for studying risk sharing. Existence of optimal risk sharing for law-determined monetary utility functions is obtained in Jouini et al. [30] and then generalized to the case of non-monotone risk measures by Acciaio [1] and Filipovi ć and Svindland [25], to multivariate risks by Carlier and Dana [15] and Carlier et al. [16], to cash-subadditive and quasi-convex measures by Mastrogiacomo and Rosazza Gianin [35]. Further works on risk sharing are also Dana and Le Van [19], Heath and Ku [28], Tsanakas [39], Weber [40]. Risk sharing problems with quantile-based risk measures are studied in Embrechts et al. [22] by explicit construction, and in [21] for heterogeneous beliefs. In Filipovi ć and Kupper [24] Capital and Risk Transfer is modelled as (deterministically determined) redistribution of capital and risk by means of a finite set of non deterministic financial instruments. Existence issues are studied and related concepts of equilibrium are introduced. Recent further extensions have been obtained in Liebrich and Svindland [33].
2 Notations
Let \((\Omega ,{\mathcal {F}},P\mathbf {)}\) be a probability space and consider the following set of probability vectors on \((\Omega ,{\mathcal {F}})\)
For a vector of probability measures \(\mathbf {Q}\) we write \(\mathbf {Q}\ll P\) to denote \(Q^{1}{\ll P},\dots ,Q^{N}\ll P\). Similarly for \(\mathbf {Q}\sim P \) . Set \(L^{0}(\Omega ,{\mathcal {F}},P;{\mathbb {R}}^{N}\mathbf {)}=(L^{0}(P))^{N}\). For \(Q\in {\mathcal {P}}^{1}\) let \(L^{1}(Q\mathbf {):=}L^{1}(\Omega ,{\mathcal {F}} ,Q;{\mathbb {R}}\mathbf {)}\) be the vector space of \(Q-\) integrable random variables and \(L^\infty (Q):=L^{\infty }(\Omega ,{\mathcal {F}},Q;{\mathbb {R}} \mathbf {)}\) be the space of \(Q-\) essentially bounded random variables. Set  and
and  . For \(\mathbf {Q}\in {\mathcal {P}}^{N}\) let
. For \(\mathbf {Q}\in {\mathcal {P}}^{N}\) let
We also set \(\mathbb {R}_{+}=[0,+\infty )\) and \(\mathbb {R}_{++}=(0,+\infty )\).
For each \(j=1,\ldots ,N\) consider a vector subspace \({\mathcal {L}}^{j}\) with \({ {\mathbb {R}}}\subseteq {\mathcal {L}}^{j}\subseteq L^{0}(\Omega ,{\mathcal {F}},P; {\mathbb {R}}\mathbf {)}\) and set
Consider now a subset \(\mathscr {Q}\subseteq {\mathcal {P}}^{N}\) and assume that the pair \(({\mathcal {L}},\mathscr {Q})\) satisfies that for every \(\mathbf {Q }\in \mathscr {Q}\)
One could take as \({\mathcal {L}}^{j}\), for example, \(L^{\infty }\) or some Orlicz space. Our optimization problems will be defined on the vector space \( {\mathcal {L}}\) to be specified later.
For each \(n=1,\ldots ,N\), let \(u_{n}:\mathbb {R\rightarrow R}\) be concave and strictly increasing. Fix \(\mathbf {X=[}X^{1},\ldots ,X^{N}\mathbf {]\in }{\mathcal {L}}\).
For \((\mathbf {Q},\,\mathbf {a,}\,A)\in \mathscr {Q}\mathbf {\times }{\mathbb {R}} ^{N}\mathbf {\times }{\mathbb {R}}\) define
Obviously, such quantities depend also on \(\mathbf {X}\), but as \(\mathbf {X}\) will be kept fixed throughout most of the analysis, we may avoid to explicitly specify this dependence in the notations. As \(u_{n}\) is increasing we can replace, in the definitions of \(U_{n}^{Q^{n}}(a^{n}),\) \(S^{ \mathbf {Q}}(A)\) and \(\Pi ^{\mathbf {Q}}(A)\) the inequality in the budget constraint with an equality.
When a vector \(\mathbf {Q}\in \mathscr {Q}\) is assigned, we can consider two problems. First, for each n, \(U_{n}^{Q^{n}}(a^{n})\) is the optimal value of the classical one dimensional expected utility maximization problem with random endowment \(X^{n}\) under the budget constraint \(E_{Q^{n}}[Y]\le a^{n}\) , determined by the real number \(a^{n}\) and the valuation operator \( E_{Q^{n}}[\cdot ]\) associated to \(Q^{n}\). Second, if we interpret the quantity \(\sum _{n=1}^{N}u_{n}(\cdot )\) as the aggregated utility of the system, then \(\Pi ^{\mathbf {Q}}(A)\) is the maximal expected utility of the whole system \(\mathbf {X,}\) among all \(\mathbf {Y}\in {{\mathcal {L}}}\) satisfying the overall budget constraint \(\sum _{n=1}^{N}E_{Q^{n}}\left[ Y^{n} \right] \le A\). Notice that in these problems the vector \(\mathbf {Y}\) is not required to belong to \({\mathcal {C}}_{{\mathbb {R}}}\), but only to the vector space \({\mathcal {L}}\). We will show in Lemma 4.11 the quite obvious equality \(S^{\mathbf {Q}}(A)=\Pi ^{\mathbf {Q}}(A).\)
3 On several notions of equilibrium
3.1 Pareto allocation
Definition 3.1
Given a set of feasible allocations \(\mathscr {V}\subseteq {\mathcal {L}}\) and a vector \(\mathbf {X}\in {\mathcal {L}}\), \(\widehat{\mathbf {Y}} \in \mathscr {V}\) is a Pareto allocation for \(\mathscr {V}\) if
imply \({\mathbb {E}}\left[ u_{n}(X^{n}+Y^{n})\right] ={\mathbb {E}}\left[ u_{n}(X^{n}+{\widehat{Y}}^{n})\right] \) for all n.
In general Pareto allocations are not unique and, not surprisingly, the following version of the First Welfare Theorem holds true. Define the optimization problem
Proposition 3.2
Whenever \(\widehat{\mathbf {Y}}\in \mathscr {V}\) is the unique optimal solution of \(\Pi (\mathscr {V})\), then it is a Pareto allocation for \( \mathscr {V}\).
Proof
Let \(\widehat{\mathbf {Y}}\) be optimal for \(\Pi (\mathscr {V})\), so that \( {\mathbb {E}}\left[ \sum _{n=1}^{N}u_{n}(X^{n}+{\widehat{Y}}^{n})\right] =\Pi ( \mathscr {V}).\) Suppose that there exists \(\mathbf {Y}\) such that (19) holds true. As \(\mathbf {Y}\in \mathscr {V}\) we have:
by (19). Hence also \(\mathbf {Y}\) is an optimal solution to \(\Pi ( \mathscr {V})\). Uniqueness of the optimal solution implies \(\mathbf {Y}= \widehat{\mathbf {Y}}\). \(\square \)
3.2 Systemic utility maximization
The next definition is the utility maximization problem, in the case of a system of N agents.
Definition 3.3
Fix \(\mathbf {Q}\in \mathscr {Q}\). The pair \((\mathbf {Y}_{\mathbf {X} },\mathbf {a}_{\mathbf {X}})\in {\mathcal {L}}\mathbf {\times }{\mathbb {R}}^{N}\) is a \(\mathbf {Q}-\)Optimal Allocation with budget \(A\in {\mathbb {R}}\) if:
-
1)
for each n, \(Y_{\mathbf {X}}^{n}\) is optimal for \(U_{n}^{Q^{n}}(a_{ \mathbf {X}}^{n}),\)
-
2)
\(\mathbf {a}_{\mathbf {X}}\) is optimal for \(S^{\mathbf {Q}}(A),\)
-
3)
\(\mathbf {Y}_{\mathbf {X}}\in {\mathcal {L}}\).
Note that in the above definition the vector \(\mathbf {Q}\in \mathscr {Q}\) is exogenously assigned. Given a total budget \(A\in {\mathbb {R}}\), the vector \( \mathbf {a}_{\mathbf {X}}\in {\mathbb {R}}^{N}\) maximizes the systemic utility \( \sum _{n=1}^{N}U_{n}^{Q^{n}}(a^{n})\) among all feasible \(\mathbf {a\in } {\mathbb {R}}^{N}\) ( \(\sum _{n=1}^{N}a^{n}\le A\)) and \(Y_{\mathbf {X}}^{n}\) maximizes the single agent expected utility \({\mathbb {E}}\left[ u_{n}(X^{n}+Y) \right] \) among all feasible allocations \(Y\in {\mathcal {L}}^{n}\) s.t. \( E_{Q^{n}}[Y]\le a_{\mathbf {X}}^{n}\). Since \(\mathbf {Q}\in \mathscr {Q}\) is given, the budget constraint \(E_{Q^{n}}[Y]\le a_{\mathbf {X}}^{n}\) is well defined for all \(\mathbf {Y}\in {\mathcal {L}}\) and we do not need additional conditions of the form \(\mathbf {Y}\in {\mathcal {C}}_{{\mathbb {R}}}\). A generalization of the classical single agent utility maximization yields the following existence result.
Proposition 3.4
Under Assumption 3.10 (a) select \(\mathscr {Q}=\{ \mathbf {Q}\}\) for some \(\mathbf {Q}\in {\mathcal {Q}}_{v}\) (see (26)) with \(\mathbf {Q}\sim P\). Set \({\mathcal {L}}=L^{1}(Q^{1})\times \dots \times L^{1}(Q^{N})\) and let \(\mathbf {X} \in M^{\Phi }\) (see (79)). Then a \(\mathbf {Q}-\)Optimal Allocation exists.
Proof
The proof can be obtained with the same arguments employed in Sect. 4.2 [7]. \(\square \)
Let \((\mathbf {Y}_{\mathbf {X}},\mathbf {a}_{\mathbf {X}})\in {\mathcal {L}}\mathbf { \times }{\mathbb {R}}^{N}\) be a \(\mathbf {Q}-\)Optimal Allocation. Due to Lemma 4.11, \(\Pi ^{\mathbf {Q}}(A)=S^{\mathbf {Q}}(A)\) and
where we replaced the inequalities with equalities in the budget constraints, as \(u_{n}\) are monotone. Hence the systemic utility maximization problem \(\Pi ^{\mathbf {Q}}(A)\) with overall budget constraint A reduces to the sum of n single agent maximization problems, where, however, the budget constraint of each agents is assigned by \(a_{\mathbf {X}}^{n}=E_{Q^{n}}[Y_{\mathbf {X}}^{n}]\) and the vector \(\mathbf {a}_{\mathbf {X}}\) maximizes the overall performance of the system. We will also recover this feature in the notion of a SORTE, where the probability vector \(\mathbf {Q}\) will be endogenously determined, instead of being a priori assigned, as in this case.
3.3 Risk exchange equilibrium
We here formalize Bühlmann’s risk exchange equilibrium in a pure exchange economy, [12, 13], already mentioned in conditions (a’) and (b’), Item 1 of the Introduction. Let \({\mathcal {Q}}^{1}\) be the set of vectors of probability measures having all components equal:
To be consistent with Definition 3.3 we keep the same numbering for the corresponding conditions.
Definition 3.5
Fix \(A\in {{\mathbb {R}}},\,\mathbf {a}\in {\mathbb {R}}^{N}\) such that \(\sum _{n=1}^{N}a^{n}=A\). The pair \((\mathbf {Y}_{\mathbf {X}},\mathbf {Q}_{ \mathbf {X}})\in {\mathcal {L}}\mathbf {\times }{\mathcal {Q}}^{1}\) is a risk exchange equilibrium (with budget A and allocation \(\mathbf {a}\in {\mathbb {R}}^{N}\)) if:
-
1)
for each n, \(Y_{\mathbf {X}}^{n}\) is optimal for \(U_{n}^{Q_{\mathbf {X} }^{n}}(a^{n})\),
-
3)
\(\mathbf {Y}_{\mathbf {X}}\in {\mathcal {C}}_{{\mathbb {R}}}\), \(\sum _{n=1}^{N}Y_{ \mathbf {X}}^{n}=A\) \(P-{\text {a.s.}}\).
Theorem 3.6
(Bühlmann [13]) For twice differentiable, concave, strictly increasing utilities \(u_{1},\dots ,u_{n}:{{\mathbb {R}}}\rightarrow {{\mathbb {R}}}\) such that their risk aversions are positive Lipschitz and for \({\mathcal {L}} =(L^{\infty }(P))^{N},\) \(\mathscr {Q}={\mathcal {Q}}^{1}\) and \(\mathbf {X} \in {\mathcal {L}}\), there exists a unique risk exchange equilibrium that is Pareto optimal.
Proof
See [13]. \(\square \)
In a risk exchange equilibrium with budget A, the vector \(\mathbf {a}\in {\mathbb {R}}^{N}\) such that \(\sum _{n=1}^{N}a^{n}=A\) is exogenously assigned, while both the optimal exchange variable \(\mathbf {Y}_{\mathbf {X}}\) and the equilibrium price measure \(Q_{\mathbf {X}}\) are endogenously determined. On the contrary, in a \(\mathbf {Q}-\)Optimal Allocation the pricing measure is assigned a priori, while the optimal allocation \(\mathbf {Y}_{\mathbf {X }}\) and optimal budget \(\mathbf {a}_{\mathbf {X}}\) are endogenously determined. We shall now introduce a notion which requires to endogenously recover the triple \((\mathbf {Y}_{\mathbf {X}},\mathbf {Q}_{\mathbf {X}},\mathbf { a}_{\mathbf {X}})\) from the systemic budget A.
3.4 Systemic optimal risk transfer equilibrium (SORTE)
The novel equilibrium concept presented in Eqs. (8), (9) and (10) can now be formalized as follows. To this end, recall from (1) the definition of \({\mathcal {C}}_{{\mathbb {R}}}\) and fix a convex cone
of admissible allocations such that \({{\mathbb {R}}}^{N}+{\mathcal {B}}={\mathcal {B}} \).
Definition 3.7
(SORTE) The triple \((\mathbf {Y}_{\mathbf {X}},\mathbf {Q}_{\mathbf {X}}, \mathbf {a}_{\mathbf {X}})\in {\mathcal {L}}\mathbf {\times }\mathscr {Q}\mathbf { \times }{\mathbb {R}}^{N}\) is a Systemic Optimal Risk Transfer Equilibrium with budget \(A\in {\mathbb {R}}\) if:
-
1)
for each n, \(Y_{\mathbf {X}}^{n}\) is optimal for \(U_{n}^{Q_{\mathbf {X} }^{n}}(a_{\mathbf {X}}^{n}),\)
-
2)
\(\mathbf {a}_{\mathbf {X}}\) is optimal for \(S^{\mathbf {Q}_{\mathbf {X}}}(A),\)
-
3)
\(\mathbf {Y}_{\mathbf {X}}\in {\mathcal {B}}\subseteq {\mathcal {C}}_{{\mathbb {R}}}\) and \(\sum _{n=1}^{N}Y_{\mathbf {X}}^{n}=A\) \(P-{\text {a.s.}}\).
Remark 3.8
It follows from the monotonicity of each \(u_{n}\) that \( \sum _{n=1}^{N}a_{\mathbf {X}}^{n}=A\) and \(E_{Q_{\mathbf {X}}^{n}}[Y_{\mathbf {X} }^{n}]=a_{\mathbf {X}}^{n}.\) Hence
and
The main aim of the paper is to provide sufficient general assumptions that guarantee existence and uniqueness as well as good properties of a SORTE.
Remark 3.9
We will show the existence of a triple \((\mathbf {Y}_{\mathbf {X}},\mathbf {Q}_{ \mathbf {X}},\mathbf {a}_{\mathbf {X}})\in {\mathcal {L}}\mathbf {\times } \mathscr {Q}\mathbf {\times }{\mathbb {R}}^{N}\) verifying the three conditions in Definition 3.7. Hence, we also obtain the existence of the SORTE in the formulations given in (5), (6), (10) or in (8), (9), (10), for generic functional \( p^{n}\) verifying the conditions (i), (ii) and (iii) stated in the Introduction (see also Remark 4.3).
In the sequel we will work under the following Assumption 3.10.
Assumption 3.10
-
(a)
Utilities \(u_{1},\dots ,u_{N}:{{\mathbb {R}}}\rightarrow { {\mathbb {R}}}\) are strictly concave, strictly increasing differentiable functions with
$$\begin{aligned} \lim _{x\rightarrow -\infty }\frac{u_{n}(x)}{x}=+\infty \,\,\,\,\,\lim _{x\rightarrow +\infty }\frac{u_{n}(x)}{x}=0, \text { for any } n\in \{1,\dots ,N\}. \end{aligned}$$Moreover we assume that the following property holds: for any \(n\in \{1,\dots ,N\}\) and \(Q^{n}\ll P\)
$$\begin{aligned}&{\mathbb {E}}\left[ v_{n}\left( \lambda \frac{\mathrm {d}Q^{n}}{\mathrm {d}P} \right) \right]<+\infty \text { for some }\lambda>0\,\,\Longleftrightarrow \,\,{\mathbb {E}}\left[ v_{n}\left( \lambda \frac{ \mathrm {d}Q^{n}}{\mathrm {d}P}\right) \right] < +\infty \text { for all } \lambda >0, \nonumber \\ \end{aligned}$$(22)where \(v_{n}(y):=\sup _{x\in {\mathbb {R}}}\left\{ u_{n}(x)-xy\right\} \) denotes the convex conjugate of \(u_{n}\).
-
(b)
Constraints \({\mathcal {B}}\subseteq {\mathcal {C}}_{\mathbb { R}}\) is a convex cone, closed in probability, such that \({{\mathbb {R}}}^{N}+ {\mathcal {B}}={\mathcal {B}}\).
Remark 3.11
In particular, Assumptions 3.10 (b) implies that all constant vectors belong to \({\mathcal {B}}\). The condition (22) is related to the Reasonable Asymptotic Elasticity condition on utility functions, which was introduced in [38]. This assumption, even though quite weak (see [8] Sect. 2.2), is fundamental to guarantee the existence of the optimal solution to classical utility maximization problems (see [8, 38]).
Theorem 3.12
A Systemic Optimal Risk Transfer Equilibrium \((\mathbf {Y}_{\mathbf {X}},\mathbf {Q}_{ \mathbf {X}}, \mathbf {a}_{\mathbf {X}})\) exists, with \({Q}^1_{\mathbf {X} },\dots ,{Q}^N_{\mathbf {X}}\) equivalent to P.
Theorem 3.13
Under the additional Assumption that \({\mathcal {B}}\) is closed under truncation (Definition 4.13) the Systemic Optimal Risk Transfer Equilibrium is unique and is a Pareto optimal allocation.
The formal statements and proofs are postponed to Sect. 4, Theorems 4.12 and 4.17.
Remark 3.14
A priori there are no reasons why a \(\mathbf {Q}\)-optimal allocation \(\mathbf { Y}_{\mathbf {X}}\) in Definition 3.3 would also satisfy the constraint \( \sum _{n=1}^{N}Y_{\mathbf {X}}^{n}\in {\mathbb {R}}\). The existence of a SORTE is indeed the consequence of the existence of a probability measure \(\mathbf {Q} _{\mathbf {X}}\) such that the \(\mathbf {Q}_{\mathbf {X}}\)-optimal allocation \( \mathbf {Y}_{\mathbf {X}}\) in Definition 3.3 satisfies also the additional risk transfer constraint \(\sum _{n=1}^{N}Y_{\mathbf {X}}^{n}=A\) \(P-a.s. .\)
Remark 3.15
Without the additional feature expressed by 2) in the Definition 3.7 , for all choices of \(\mathbf {a}_{\mathbf {X}}\) satisfying \(\sum _{n=1}^{N}a_{ \mathbf {X}}^{n}=A\) there exists an equilibrium \((\mathbf {Y}_{\mathbf {X}}, \mathbf {Q}_{\mathbf {X}})\) in the sense of Definition 3.5 (see Theorem 3.6). The uniqueness of a SORTE is then a consequence of the uniqueness of the optimal solution in condition 2).
Remark 3.16
Depending on which one of the three objects \((\mathbf {Y},\mathbf {Q},\mathbf {a })\in {\mathcal {L}}\mathbf {\times }\mathscr {Q}\times {\mathbb {R}}^{N}\) we keep a priori fixed, we get a different notion of equilibrium (see the various definitions above). The characteristic features of the risk exchange equilibriums and of a SORTE, compared with the more classical utility optimization problem in the systemic framework of Sect. 3.2, are the condition \(\sum _{n=1}^{N}Y_{\mathbf {X}}^{n}=A\) \(P{\text {-}}a.s.\) and the existence of the equilibrium pricing vector \(\mathbf {Q}_{\mathbf {X}}\).
For both concepts of equilibrium (Definitions 3.5 and SORTE), each agent is behaving rationally by maximizing his expected utility given a budget constraint. The two approaches differ by the budget constraints. In Bühlmann’s definition the vector \(\mathbf {a}\in {\mathbb {R}}^{N}\) that assigns the budget constraint (\(E_{Q_{\mathbf {X}}^{n}}[Y^{n}]\le a_{n})\) is prescribed a priori\(\mathbf {.}\) On the contrary, in the SORTE approach, the vector \(\mathbf {a}\in {\mathbb {R}}^{N}\), with \(\sum _{n=1}^{N}a_{n}=A,\) that assigns the budget constraint \(E_{Q_{\mathbf {X}}^{n}}[Y^{n}]\le a_{n}\) is determined by optimizing the problem in condition 2), hence by taking into account the optimal systemic utility \(S^{\mathbf {Q}_{\mathbf {X}}}(A)\), which is (by definition) larger than the systemic utility \( \sum _{n=1}^{N}U_{n}^{Q_{X}^{n}}(a^{n})\) in Bühlmann’s equilibrium. The SORTE gives priority to the systemic aspects of the problem in order to optimize the overall systemic performance. A toy example showing the difference between a Bühlmann’s equilibrium and a SORTE is provided in Sect. 5.2.
Example 3.17
We now consider the example of a cluster of agents, already introduced in [7]. For \(h\in \left\{ 1,\cdots ,N\right\} ,\) let \( \mathbf {I}:=(I_{m})_{m=1,\ldots ,h}\) be some partition of \(\{1,\cdots ,N\}\). We introduce the following family
For a given \(\mathbf {I}\), the values \((d_{1},\cdots ,d_{h})\) may change, but the elements in each of the h groups \(I_{m}\) is fixed by the partition \(\mathbf {I}\). It is then easily seen that \({\mathcal {B}}^{(\mathbf {I})}\) is a linear space containing \({\mathbb {R}}^{N}\) and closed with respect to convergence in probability. We point out that the family \({\mathcal {B}}^{( \mathbf {I})}\) admits two extreme cases:
-
(i)
the strongest restriction occurs when \(h=N,\) i.e., we consider exactly N groups, and in this case \({\mathcal {B}}^{(\mathbf {I})}={\mathbb {R}} ^{N}\) corresponds to no risk sharing;
-
(ii)
on the opposite side, we have only one group \(h=1\) and \(\mathcal { B}^{(\mathbf {I})}={\mathcal {C}}_{{\mathbb {R}}}\) is the largest possible class, corresponding to risk sharing among all agents in the system. This is the only case considered in Bühlmann’s definition of equilibrium.
Remark 3.18
As already mentioned in the Introduction, one additional feature of a SORTE, compared with the Bühlmann’s notion, is the possibility to require, in addition to \(\sum _{n=1}^{N}Y^{n}=A\) that the optimal solution belongs to a pre-assigned set \({\mathcal {B}}\) of admissible allocations, satisfying Assumption 3.10 (b). In particular, we allow for the selection of the sets \({\mathcal {B}}={\mathbb {R}}^{N}\) or \({\mathcal {B}}={\mathcal {C}}_{{\mathbb {R}}}\). The characteristics of the optimal probability \(\mathbf {Q}_{\mathbf {X}}\) depend on the admissible set \({\mathcal {B}}\). For \({\mathcal {B}}={\mathcal {C}}_{ {\mathbb {R}}}\), all the components of \(\mathbf {Q}_{\mathbf {X}}\) turn out to be equal. We also know (see Lemma 4.21) that for \({\mathcal {B}}= {\mathcal {B}}^{(\mathbf {I})}\) all the components \(Q_{\mathbf {X}}^{i}\) of \( \mathbf {Q}_{\mathbf {X}}\) are equal for all \(i\in I_{m}\), for each group \( I_{m}\). Additional examples of sets \({\mathcal {B}}\) are provided in Sect. 4.5.
3.5 Explicit formulas in the exponential case
We believe it is now instructive to anticipate the explicit solution to the SORTE problem in the exponential case for \({\mathcal {B}}={\mathcal {C}}_{{\mathbb {R}}}\). This is a particular case of a more general situation treated in detail in Sect. 5.
Theorem 3.19
Take exponential utilities
Then the SORTE for \({\mathcal {B}}={\mathcal {C}}_{{\mathbb {R}}}\) is given by
where \(\beta :=\sum _{n=1}^N\frac{1}{\alpha _{n}}\), \({\overline{X}} :=\sum _{n=1}^NX^{n}\), \(R(n):=\frac{\frac{1}{\alpha _{n}}}{\sum _{k=1}^{N}\frac{1}{\alpha _{k}}}\) for \(n=1,\ldots N\), \(\alpha :=[\alpha _{1},\ldots ,\alpha _{N}]\), \(E_{R}\left[ \ln (\alpha )\right] =\sum _{n=1}^{N}R(n)\ln (\alpha _{n})\).
4 Proof of Theorems 3.12 and 3.13
We need to introduce the following concepts and notations:
-
1.
The utility functions in Assumption 3.10 induce an Orlicz Space structure: see “Appendix A.1” for the details and the definitions of the functions \(\Phi \) and \(\Phi ^{*}\), the Orlicz space \( L^{\Phi }\) and the Orlicz Heart \(M^{\Phi }\). Here we just recall the following inclusions among the Banach Spaces \((L^{\infty }(\mathbf {P} ))^{N}\subseteq M^{\Phi }\subseteq L^{\Phi }\subseteq (L^{1}(\mathbf {P}))^{N}\) and that \(\frac{\mathrm {d}\mathbf {Q}}{\mathrm {d}{\mathbb {P}}}\in L^{\Phi ^{*}}\) implies \(L^{\Phi }\subseteq L^{1}(\mathbf {Q})\). From now on we assume that \(\mathbf {X} \in M^{\Phi }\).
-
2.
For any \(A\in {{\mathbb {R}}}\) we set
$$\begin{aligned} {{\mathcal {B}}_{A}:={\mathcal {B}}\cap \{\mathbf {Y}\in (L^{0}(P))^{N}\mid \sum _{n=1}^{N}Y^{n}\le A\,P\text {-}a.s.\}.} \end{aligned}$$Observe that \({\mathcal {B}}_{0}\cap M^{\Phi }\) is a convex cone.
-
3.
We introduce the following problem for \(\mathbf {X}\in M^{\Phi }\) and for a vector of probability measures \(\mathbf {Q}\ll P,\) with \(\frac{\mathrm {d }\mathbf {Q}}{\mathrm {d}P}\in L^{\Phi ^{*}}\),
 (25)
(25)Notice that in (25) the vector \(\mathbf {Y}\) is not required to belong to \({\mathcal {C}}_{{\mathbb {R}}}\), but only to the vector space \(M^{\Phi } \). In order to show the existence of the optimal solution to the problem \( \pi ^{\mathbf {Q}}(A)\), it is necessary to enlarge the domain in (25).
-
4.
\({\mathcal {Q}}\) is the set of vectors of probability measures defined by

Identifying Radon-Nikodym derivatives and measures in the natural way, \( {\mathcal {Q}}\) turns out to be the set of normalized (i.e. with componentwise expectations equal to 1), non negative vectors in the polar of \( {\mathcal {B}}_{0}\cap M^{\Phi }\) in the dual system \((M^{\Phi },L^{\Phi ^{*}})\). In our N-dimensional systemic one-period setting, the set \( {\mathcal {Q}}\) plays the same crucial role as the set of martingale measures in multiperiod stochastic securities markets.
-
5.
We introduce the following convex subset of \({\mathcal {Q}}\):
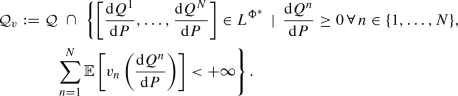 (26)
(26) -
6.
Set
$$\begin{aligned} {\mathcal {L}}:=\bigcap _{\mathbf {Q}\in {\mathcal {Q}}_{v}}L^{1}(Q^{1})\times \dots \times L^{1}(Q^{N}),\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\mathscr {Q}:={\mathcal {Q}} _{v}. \end{aligned}$$(27)
Note that \(M^{\Phi }\subseteq {\mathcal {L}}\) and that \({\mathcal {L}}\) has the product structure \({\mathcal {L}}={\mathcal {L}}^1\times \dots \times {\mathcal {L}}^N\): let \(\text {Proj}_n\) denote the projection on the \(n-\)th component, defined on \({\mathcal {Q}}_v\), and take the corresponding image \({\mathcal {Q}}_n:=\text {Proj}_n({\mathcal {Q}}_v)\) (consisting of a family of probability measures, all absolutely continuous with respect to \(P\)). Set \({\mathcal {L}}^n:=\bigcap _{Q\in {\mathcal {Q}}_n}L^1(Q)\). Then \({\mathcal {L}}={\mathcal {L}}^1\times \dots \times {\mathcal {L}}^N\).
We will consider the optimization problems (16), (17) and (18) with the particular choice of \(({\mathcal {L}},\mathscr {Q})\) in (27) and will show that, with such choice, \(\pi ^{\mathbf {Q}}(A)=\Pi ^{\mathbf {Q} }(A). \) Observe that if all utilities are bounded from above, the requirement \(\sum _{n=1}^{N}{\mathbb {E}}\left[ v_{n}\left( \frac{\mathrm {d}Q^{n} }{\mathrm {d}P}\right) \right] <+\infty \) is redundant, but it becomes important if we allow utilities to be unbounded.
We also require some additional definitions and notations:
-
(a)
\(\overline{{\mathcal {B}}_{0}}\) is the polar of the cone \(co( {\mathcal {Q}}_{v})\) in the dual pair
$$\begin{aligned} \left( L^{\Phi _{1}^{*}}\times \dots \times L^{\Phi _{N}^{*}}\,,\,\bigcap _{\mathbf {Q}\in {\mathcal {Q}}_{v}}L^{1}(Q^{1})\times \dots \times L^{1}(Q^{N})\right) , \end{aligned}$$that is

It is easy to verify that
$$\begin{aligned} {\mathcal {B}}_{0}\cap M^{\Phi }\subseteq \overline{{\mathcal {B}}_{0}}. \end{aligned}$$ -
(b)
For any \(A\in {{\mathbb {R}}}\) we define \(\overline{{\mathcal {B}}_{A}}\) as the set

We will prove that \(\overline{{\mathcal {B}}_{A}}\) is the correct enlargement of the domain \({\mathcal {B}}_{A}\cap M^{\Phi }\) in order to obtain the existence of the optimal solution of the primal problem.
-
(c)
\(\left\{ \mathbf {e_{i}}\right\} _{i=1,\ldots ,N}\) is the canonical base of \({{\mathbb {R}}}^{N}\).
Lemma 4.1
In the dual pair \((M^{\Phi },L^{\Phi ^{*}}),\) consider the polar \(({\mathcal {B}}_{0}\cap M^{\Phi })^{0}\) of \({\mathcal {B}} _{0}\cap M^{\Phi }\). Then \(({\mathcal {B}}_{0}\cap M^{\Phi })^{0}\cap (L_{+}^{0})^{N}\) is the cone generated by \({\mathcal {Q}}\).
Proof
From the definition of \({\mathcal {B}}_{0}\) and the fact that \({\mathcal {B}}\) contains all constant vectors, we may conclude that all vectors in \({{\mathbb {R}}}^{N}\) of the form \(\mathbf {e_{i}}-\mathbf {e_{j}}\) belong to \({\mathcal {B}} _{0}\cap M^{\Phi }\). Then for all \(\mathbf {Z}\in ({\mathcal {B}}_{0}\cap M^{\Phi })^{0}\) and for all \(i,j\in \{1,\dots ,N\}\) we must have: \({\mathbb {E}} \left[ Z^{i}\right] -{\mathbb {E}}\left[ Z^{j}\right] \le 0\). As a consequence, \(\mathbf {Z}\in ({\mathcal {B}}_{0}\cap M^{\Phi })^{0}\) implies \( {\mathbb {E}}\left[ Z^{1}\right] =\dots ={\mathbb {E}}\left[ Z^{N}\right] \) and so
where \({{\mathbb {R}}}_{+}:=\{b\in {{\mathbb {R}}},b\ge 0\}\). \(\square \)
Lemma 4.2
\({\mathcal {Q}}_{v}^{e}:=\{\mathbf {Q}\in {\mathcal {Q}}_{v}\text { s.t. }\mathbf {Q}\sim P\}\ne \varnothing .\)
Proof
The condition \({\mathcal {B}}\subseteq {\mathcal {C}}_{{\mathbb {R}}}\) implies \( {\mathcal {B}}_{0}\cap M^{\Phi }\subseteq ({\mathcal {C}}_{{\mathbb {R}}}\cap M^{\Phi }\cap \{\sum _{n=1}^{N}Y^{n}\le 0\})\), so that the polars satisfy the opposite inclusion: \(({\mathcal {C}}_{{\mathbb {R}}}\cap M^{\Phi }\cap \{\sum _{n=1}^{N}Y^{n}\le 0\})^{0}\subseteq ({\mathcal {B}}_{0}\cap M^{\Phi })^{0}\). Observe now that any vector \((Z,\dots ,Z)\), for \(Z\in L_{+}^{\infty }\), belongs to \(({\mathcal {C}}_{{\mathbb {R}}}\cap M^{\Phi }\cap \{\sum _{n=1}^{N}Y^{n}\le 0\})^{0}\). In particular, \(({\mathcal {B}}_{0}\cap M^{\Phi })^{0}\) contains vectors in the form \(\left( \frac{\varepsilon +Z}{ 1+\varepsilon },\dots ,\frac{\varepsilon +Z}{1+\varepsilon }\right) \) with \( \varepsilon >0\) and \(Z\in L_{+}^{\infty }\), \({\mathbb {E}}\left[ Z\right] =1\). Each component of such a vector has expectation equal to 1, belongs to \( L_{+}^{\infty }\) and satisfies \(\frac{\varepsilon +Z}{1+\varepsilon }\ge \frac{\varepsilon }{1+\varepsilon }\). All these conditions imply that there exists a probability vector \(\mathbf {Q\in }{\mathcal {Q}}\) such that \(\frac{ \mathrm {d}\mathbf {Q}}{\mathrm {d}P}>0\) \(P-a.s.\) with \(\sum _{n=1}^{N}{\mathbb {E}} \left[ v_{n}\left( \frac{\mathrm {d}Q^{n}}{\mathrm {d}P}\right) \right] <\infty \), hence \({\mathcal {Q}}_{v}^{e}\ne \varnothing \). \(\square \)
4.1 Scheme of the proof
The proof of Theorem 3.12 is inspired by the classical duality theory in utility maximization, see for example [18, 31] and by the minimax approach developed in [5]. More precisely, our road map will be the following:
-
1.
First we show, in Remark 4.4, how we may reduce the problem to the case \(A=0.\)
-
2.
We consider
 (29)
(29)In Theorem 4.5 we specialize the duality, obtained in Theorem A.3 for a generic convex cone \({\mathcal {C}}\), for the maximization problem \(\pi (0)\) over the convex cone \({\mathcal {C}}=\) \({\mathcal {B}}_{0}\cap \)\(M^{\Phi }\) and prove: (i) the existence of the optimizer \( \widehat{\mathbf {Y}}\) of \(\pi (0)\), which belongs to \({\mathcal {B}}_{0}\); (ii) the existence of the optimizer \(\widehat{\mathbf {Q}}\) to the dual problem of \(\pi (0)\). Here we need all the assumptions on the utility functions and on the set \({\mathcal {B}}\) and an auxiliary result stated in Theorem A.4 in “Appendix”.
-
3.
Proposition 4.7 will show that also the elements in the closure of \({\mathcal {B}}\cap \)\(M^{\Phi }\) satisfy the key condition \( \sum _{n=1}^{N}E_{{Q}^{n}}\left[ Y^{n}\right] \le \sum _{n=1}^{N}Y^{n}\in {\mathbb {R}}\) for all \(Q\in \mathscr {Q}\).
-
4.
Theorem A.3 is then again applied, to a different set \( \mathcal {C=}\left\{ \mathbf {Y}\in M^{\Phi }\!\mid \! \sum _{n=1}^{N}E_{{Q}^{n}} \left[ Y^{n}\!\right] \! \le \! 0\!\right\} \), to derive Proposition 4.9, which establishes the duality for \(\pi ^{\mathbf {Q}}(0)\) and \(\pi ^{\mathbf {Q }}(A)\) in case a fixed probability vector \(\mathbf {Q}\) is assigned.
-
5.
The minimax duality:
$$\begin{aligned} \pi (A)=\min _{\mathbf {Q}\in {\mathcal {Q}}_{v}}\pi ^{\mathbf {Q}}(A)=\pi ^{ \widehat{\mathbf {Q}}}(A), \end{aligned}$$is then a simple consequence of the above results (see Corollary 4.10). This duality is the key tool to prove the existence of a SORTE (see Theorem 4.12).
-
6.
Uniqueness and Pareto optimality are then proved in Theorem .
Remark 4.3
Notice that in the definition of \(\pi (A)\) there is no reference to a probability vector \(\mathbf {Q}\). However, the optimizer of the dual formulation of \(\pi (A)\) is a probability vector \(\widehat{\mathbf {Q}}\) (that will be the equilibrium pricing vector in the SORTE). Even if in the Eqs. (8), (9), (10) we do not a priori require pricing functional of the form \(p^{n}(\cdot )=E_{Q^{n}}[\cdot ]\), this particular linear expression naturally appears from the dual formulation.
4.2 Minimax approach
Remark 4.4
Only in this Remark, we need to change the notation a bit: we make the dependence of our maximization problems on the initial point explicit. To this end we will write

It is possible to reduce the maximization problem expressed by \(\pi _{ \mathbf {X}}(A)\) (and similarly by \(\pi _{\mathbf {X}}^{Q}(A)\)) to the problem related to \(\pi _{\cdot }(0)\) (respectively, \(\pi _{\cdot }^{Q}(0))\) by using the following simple observation: for any \(\mathbf {a_{0}}\in {{\mathbb {R}}}^{N} \) with \(\sum _{j=1}^{N}a_{0}^{j}=A\) consider

where last equality holds as we are assuming that \({{\mathbb {R}}}^{N}+{\mathcal {B}}={\mathcal {B}}\). The last line represents the original problem, but with \( A=0 \) and a different initial point. This fact will be used in the conclusion of the proof of Theorem 4.5.
In the following Theorem we follow a minimax procedure inspired by the technique adopted in [8].
Theorem 4.5
Under Assumption 3.10 we have
The minimization problem in (31) admits a unique optimum \(({\widehat{\lambda }},\widehat{\mathbf {Q}})\in {{\mathbb {R}}} _{++}\times {\mathcal {Q}}\) with \(\widehat{\mathbf {Q}}\sim P\). The maximization problem in (30) admits a unique optimum \(\widehat{ \mathbf {Y}}\in \overline{{\mathcal {B}}_{A}}\), given by
which belongs to \({\mathcal {B}}_{A}\). In addition,
Proof
We first prove the result for the case \(A=0\).
Step 1
We first show that
so that we will be able to apply Theorem A.3 with the choice \( {\mathcal {C}}:={\mathcal {B}}_{0}\cap M^{\Phi }\). We distinguish two possible cases: \(\sum _{j=1}^Nu_j(+\infty )=+\infty \) or \(\sum _{j=1}^Nu_j(+\infty )<+ \infty \).
For \(\sum _{j=1}^Nu_j(+\infty )=+\infty \): observe that for any \(\mathbf {Q}\in {\mathcal {Q}}_{v}\) (which is nonempty by Lemma 4.2) and \(\lambda >0\) we have
We exploited above Fenchel’s Inequality and the definition of \({\mathcal {Q}} _{v}\). Observing that the last line does not depend on \(\mathbf {Y}\) and is finite, and using the well known relation \(v_j(0)=u_j(+\infty ),j=1,\dots ,N\), we conclude that
For \(\sum _{j=1}^Nu_j(+\infty )<+\infty \): if the inequality in (34) were not strict, for any maximizing sequence \((\mathbf { Y}_{m})_{m}\) we would have, by monotone convergence, that
Up to taking a subsequence we can assume the convergence is also almost sure. Since all the terms in \(\sum _{j=1}^{N}\left( u_{j}(+\infty )-u_{j}(X^{j}+Y_{m}^{j})\right) \) are non negative, we also see that \( u_{j}(X^{j}+Y_{m}^{j})\rightarrow _{m}u_{j}(+\infty )\) almost surely for every \(j=1,\dots ,N\). By strict monotonicity of the utilities, this would imply that, for each j, \(Y_{m}^{j}\rightarrow _{m}+\infty \). This clearly contradicts the constraint \(\mathbf {Y}_{m}\in {\mathcal {B}}_{0}\).
Step 2
We will prove Eqs. (30) and (31), with a supremum over \(\overline{{\mathcal {B}}_A}\) in place of a maximum, since we will show in later steps (STEP 4) that this supremum is in fact a maximum.
We observe that since \({\mathcal {B}}_{0}\cap M^{\Phi }\subseteq \overline{ {\mathcal {B}}_{0}}\)
Moreover, by the Fenchel inequality
Equations (30) and (31) follow from Theorem A.3 replacing there the convex cone \({\mathcal {C}}\) with \({\mathcal {B}}_{0}\cap M^{\Phi }\) and using Eq. (28), which shows that \(({\mathcal {C}}_{1}^{0})^{+}={\mathcal {Q}}\).
Step 3
We prove that if \({\widehat{\lambda }}\) and \(\widehat{\mathbf {Q}}\) are optima in Eq. (31), then \({\widehat{Y}}^{j}:=-X^{j}-v_{j}^{ \prime }\left( \widehat{\lambda }\frac{\mathrm {d}{\widehat{Q}}^{j}}{\mathrm {d}P }\right) \) defines an element in \(\overline{{\mathcal {B}}_{0}}\). Observe that \( {\widehat{\lambda }}\) minimizes the function
which is real valued and convex. Also we have by Monotone Convergence Theorem and Lemma A.2.1. that the right and left derivatives, which exist by convexity, satisfy
hence the function is differentiable. Since \({\widehat{\lambda }}\) is a minimum for \(\psi \), this implies \(\psi ^{\prime }({\widehat{\lambda }})=0\), which can be rephrased as
i.e.,
Now consider minimizing
for fixed \({\widehat{\lambda }}\) and \(\mathbf {Q}\) varying in \({\mathcal {Q}}_{v}\) . Let again \(\widehat{\mathbf {Q}}\), with \(\hat{\eta }:=\frac{ \mathrm {d}\widehat{\mathbf {Q}}}{\mathrm {d}P}\), be an optimum and consider another \(\mathbf {Q}\in {\mathcal {Q}}_{v}\), with \({\eta }:=\frac{ \mathrm {d}\mathbf {Q}}{\mathrm {d}P}\). By Assumption 3.10, the expression \(\sum _{j=1}^{N}{\mathbb {E}}\left[ v_{j}\left( \lambda \frac{\mathrm {d}Q^{j}}{ \mathrm {d}P}\right) \right] \) is finite for all choices of \(\lambda \). Observe that by convexity and differentiability of \(v_{j}\) we have
Hence by Lemma A.2.1. and \(\widehat{\mathbf {Q}},\mathbf {Q} \in {\mathcal {Q}}_{v}\) we conclude that
To prove that also the negative part is integrable, we take a convex combination of \(\widehat{\mathbf {Q}},\mathbf {Q}\in {\mathcal {Q}}_{v}\), which still belongs to \({\mathcal {Q}}_{v}\). By optimality of \({\widehat{\eta }}\) the function
has a minimum at 0, thus the right derivative of \(\varphi \) at 0 must be non negative, so that:
Define \(H_{j}(x):=v_{j}\left( (1-x){\widehat{\lambda }}\widehat{\eta }^{j}+x {\widehat{\lambda }}\eta ^{j}\right) \) and observe that as \(x\downarrow 0\) by convexity
Write now explicitly Eq. (38) in terms of incremental ratios and add and subtract the real number \({\mathbb {E}}\left[ \sum _{j=1}^{N}\left( H_{j}(1)-H_{j}(0)\right) \right] \) to get
The first limit is trivial. Observe that by (39) and Monotone Convergence Theorem we also may compute the second limit and then deduce:
and therefore
Since \(\sum _{j=1}^{N}v_{j}^{\prime }\left( \widehat{\lambda }{\widehat{\eta }} ^{j}\right) {\widehat{\eta }}^{j}\in L^{1}(P) \) by Lemma A.2.1, and \(\sum _{j=1}^{N}\left( v_{j}^{\prime }\left( {\widehat{\lambda }} {\widehat{\eta }}^{j}\right) \eta ^{j}\right) ^{+}\in L^{1}(P)\) by Eq. (37), we deduce that \(\sum _{j=1}^{N}\left( v_{j}^{\prime }\left( {\widehat{\lambda }}{\widehat{\eta }}^{j}\right) \eta ^{j}\right) ^{-}\in L^{1}(P)\) so that
We conclude that \(v_{j}^{\prime }\left( \widehat{\lambda }{\widehat{\eta }} ^{j}\right) \eta ^{j}\) defines a vector in \(L^{1}(P)\times \dots \times L^1(P)\) , hence
Moreover Eq. (38) can be rewritten as:
Now rearrange the terms in (43)
and use (35):
This proves that
and then \(\widehat{\mathbf {Y}}\in \overline{{\mathcal {B}}_{0}}\).
Step 4 (Optimality of \(\widehat{\mathbf {Y}}\) )
Under our standing Assumption 3.10 it is well known that \(u(-v^{\prime }(y))=v(y)-yv^{\prime }(y),\,\forall y\ge 0\). As a consequence we get by direct substitution
and
Use now the expression in (35) to substitute in the first RHS term:
The optimality of \(\widehat{\mathbf {Y}}\) follows then by optimality of \(( {\widehat{\lambda }},\widehat{\mathbf {Q}})\) in (31).
Using now our findings in STEP 2 together with optimality of \(\widehat{ \mathbf {Y}}\), the proof of Eq. (30) is complete.
Step 5 ( \(\widehat{\mathbf {Y}}\in {\mathcal {B}}_{0}\) )
By Lemma 4.2 there exists a \(\mathbf {Q}\in {\mathcal {Q}}_{v}^{e}:=\{ \mathbf {Q}\in {\mathcal {Q}}_{v}\) s.t. \(\mathbf {Q}\sim P\}\) and from (42) we know that \(v_{j}^{\prime }\left( \lambda \frac{\mathrm {d}{\widehat{Q}}^{j} }{\mathrm {d}P}\right) \in L^{1}(Q^{j})\), \(\lambda >0\). Also, for every \( j=1,\dots ,N,\) \(v_{j}^{\prime }(0+)=-\infty ,\) so that \(Q^{j}\left( \frac{ \mathrm {d}{\widehat{Q}}^{j}}{\mathrm {d}P}=0\right) =0\). As \(\mathbf {Q}\sim P\), this in turn implies \(P\left( \frac{\mathrm {d}{\widehat{Q}}^{j}}{\mathrm {d}P} =0\right) =0\), for every \(j=1,\dots ,N\). Hence \(\widehat{\mathbf {Q}}\sim P\). Theorem A.4 now can be applied to \(K:=({\mathcal {B}}_{0}\cap M^{\Phi })\) and \({\mathcal {Q}}_{v}^{e}\) to get
As \(\widehat{\mathbf {Y}}\in \overline{{\mathcal {B}}_{0}}\) and \(\overline{ {\mathcal {B}}_{0}}\) is included in the RHS of (45), we deduce that \(\widehat{\mathbf {Y}}\) belongs to the LHS of (45). Now by Eq. (36) we see that \(\widehat{\mathbf { Y}}\) satisfies \(\sum _{j=1}^{N}{\mathbb {E}}\left[ {\widehat{Y}}^{j}\frac{\mathrm {d }{\widehat{Q}}^{j}}{\mathrm {d}P}\right] =0\), and this implies that:
the \(L^{1}({\widehat{Q}}^{1})\times \dots \times L^{1}({\widehat{Q}}^{1}) \)-(norm) closure of \({\mathcal {B}}_{0}\cap M^{\Phi }\). In particular \(\widehat{\mathbf {Y }}\) is a \(\widehat{\mathbf {Q}}\) (hence P)- a.s. limit of elements in \( {\mathcal {B}}_{0}\) which is closed in probability P, so that \(\widehat{ \mathbf {Y}}\in {\mathcal {B}}_{0}\).
Step 6
The conditions in (33) are proved in (36) and (44). We conclude with uniqueness. By the strict concavity of the utilities and the convexity of \(\overline{{\mathcal {B}}_{0}}\), it is evident that the maximization problem given by \(\sup _{\overline{{\mathcal {B}}_{0}} }\sum _{j=1}^{N}{\mathbb {E}}\left[ u_{j}\left( X^{j}+Y^{j}\right) \right] \) admits at most one optimum. Now clearly if \(({\widehat{\lambda }},\widehat{ \mathbf {Q}})\) and \(({\widetilde{\lambda }},\widetilde{\mathbf {Q}})\) are optima for the minimax expression (31), they both give rise to two optima \(\widehat{\mathbf {Y}},\,\widetilde{\mathbf {Y}}\) as in the previous steps. Uniqueness of the solution for the primal problem implies \(\widehat{ \mathbf {Y}}=\widetilde{\mathbf {Y}}\). Under Assumption 3.10.(a) the functions \(v_{1}^{\prime },\dots ,v_{N}^{\prime }\) are injective and therefore we conclude that \({\widehat{\lambda }}\frac{\mathrm {d}\widehat{ \mathbf {Q}}}{\mathrm {d}P}=\widetilde{\lambda }\frac{\mathrm {d}\widetilde{ \mathbf {Q}}}{\mathrm {d}P}\). Taking expectations we get \({\widehat{\lambda }}= {\widetilde{\lambda }}\) and then \(({\widehat{\lambda }},\widehat{\mathbf {Q}})=( \widetilde{\lambda },\widetilde{\mathbf {Q}})\).
Conclusion
The more general case \(A\ne 0\) can be obtained using Remark . We just sketch one step of the proof, as the other steps follows similarly. Using \(\mathbf {a_{0}}\) as in Remark 4.4, in STEP 3 we see that
which yields that \(\widehat{\mathbf {Y}}\in \overline{{\mathcal {B}}_{A}}\). \(\square \)
Remark 4.6
Notice that \(\mathbf {Y}\in {\mathcal {B}}\cap M^{\Phi }\) implies that \(\mathbf {Z}\in {\mathcal {B}}_{0}\), where \(\mathbf {Z}\) is defined by \(Z^{j}:=Y^{j}-x^{j}\sum _{k=1}^{N}Y^{k}\) for any \(\mathbf {x}\in {{\mathbb {R}} }^{N}\) such that \(\sum _{j=1}^{N}x^{j}=1\). To see this, recall that we are assuming that \({{\mathbb {R}}}^{N}+{\mathcal {B}}={\mathcal {B}}\). As \( \sum _{j=1}^{N}Y^{j}\in {{\mathbb {R}}}\), then \(\mathbf {Z}\in {\mathcal {B}}\) and, since also trivially integrability is preserved and \(\sum _{j=1}^{N}Z^{j}=0\), we conclude that \(\mathbf {Z}\in {\mathcal {B}}_{0}\).
Proposition 4.7
For all \(\mathbf {Y}\in {\mathcal {B}}\cap M^{\Phi }\) and \(\,\mathbf {Q}\in {\mathcal {Q}}\)
Moreover, denoting by \(cl_{\mathbf {Q}}\left( {\mathcal {B}}\cap M^{\Phi }\right) \) the \(L^{1}(Q^{1})\times \dots \times L^{1}(Q^{N})\)-norm closure of \( {\mathcal {B}}\cap M^{\Phi }\), inequality (47) holds for all \(\,\mathbf { Y}\in cl_{\mathbf {Q}}\left( {\mathcal {B}}\cap M^{\Phi }\right) \) and \(\mathbf {Q}\in {\mathcal {Q}},\) \(\mathbf {Q}\sim P.\) In particular, (47) holds for \(\widehat{\mathbf {Q}}\sim P\) and \(\widehat{\mathbf {Y}}\in cl_{ \widehat{\mathbf {Q}}}\left( {\mathcal {B}}_{0}\cap M^{\Phi }\right) \) defined in Theorem 4.5.
Proof
Take \(\mathbf {Y}\in {\mathcal {B}}\cap M^{\Phi }\) and argue as in Remark 4.6, with the notation introduced there. By the definition of the polar, \(\sum _{j=1}^{N}{\mathbb {E}}\left[ Z^{j}\varphi ^{j}\right] \le 0\) for all \(\mathbf {\varphi }\in ({\mathcal {B}}\cap M^{\Phi })^{0}\), and in particular for all \(\mathbf {Q}\in {\mathcal {Q}}\)
As to the second claim, take a sequence \((\mathbf {k}_{n})_{n}\) in \({\mathcal {B}}\cap M^{\Phi }\) converging both \(\mathbf {Q}\)-almost surely (hence P-a.s.) and in norm to \(\mathbf {Y}\) and apply (47) to \(\mathbf {k}_{n}\) to get
\(\square \)
Remark 4.8
In particular (47) shows that \(\forall \,\mathbf {Q}\in {\mathcal {Q}}\)
and therefore \(\pi (A)\le \pi ^{\mathbf {Q}}(A).\)
4.3 Utility maximization with a fixed probability measure
The following represents a counterpart to Theorem 4.5, once a measure is fixed a priori.
Proposition 4.9
Fix \(\mathbf {Q}\in {\mathcal {Q}}_{v}\). If \(\pi ^{\mathbf {Q} }(A)<+\infty \), then

If additionally any of the two expressions is strictly less than \( \sum _{j=1}^{N}u_{j}(+\infty )\), then
Proof
Again, we prove the case \(A=0\) since Remark 4.4 can be used to obtain the general case \(A\ne 0\). From \(M^{\Phi }\subseteq {\mathcal {L}} \subseteq L^{1}(\mathbf {Q})\) we obtain:

by the Fenchel inequality. Define the convex cone
The hypotheses on \({\mathcal {C}}\) of Theorem A.3 hold true and inequality (51) shows that \(\pi ^{\mathbf {Q}}(0)<+\infty \) for all \(\mathbf {X}\in M^{\Phi }\). The finite dimensional cone \(\left\{ \lambda \left[ \frac{\mathrm {d}Q^{1}}{\mathrm {d}P},\dots ,\frac{\mathrm {d}Q^{N}}{ \mathrm {d}P}\right] ,\,\,\lambda \ge 0\right\} \subseteq L^{\Phi ^{*}}\) is closed, and then by the Bipolar Theorem \({\mathcal {C}}^{0}=\left\{ \lambda \left[ \frac{\mathrm {d}Q^{1}}{\mathrm {d}P},\dots ,\frac{\mathrm {d}Q^{N}}{ \mathrm {d}P}\right] ,\,\,\lambda \ge 0\right\} \). Hence the set \(({\mathcal {C}}_{1}^{0})^{+}\) in the statement of Theorem A.3 is exactly \( \left\{ \left[ \frac{\mathrm {d}Q^{1}}{\mathrm {d}P},\dots ,\frac{\mathrm {d} Q^{N}}{\mathrm {d}P}\right] \right\} \) and Theorem A.3 proves that \(\pi ^{\mathbf {Q}}(0)\) is equal to the RHS of (51). We can similarly argue to prove (50). \(\square \)
To conclude, we provide the minimax duality between the maximization problems with and without a fixed measure
Corollary 4.10
The following holds:
where \(\mathbf {{\widehat{Q}}}\) is the minimax measure from Theorem 4.5.
Proof
It is an immediate consequence of Theorem 4.5 and Proposition 4.9. \(\square \)
Lemma 4.11
For all \(\mathbf {Q}\in \mathscr {Q}\) we have \(\Pi ^{ \mathbf {Q}}(A)=S^{\mathbf {Q}}(A)\) and, if \(\mathbf {{\widehat{Q}}}\) is the minimax measure from Theorem 4.5, then
Proof
Let \(\mathbf {Y}\in {\mathcal {L}}\), \(\mathbf {Q}\in \mathscr {Q}\), \( a^{n}:=E_{Q^{n}}[Y^{n}]\) and \(Z^{n}:=Y^{n}-a^{n}\). As \({\mathcal {L}}+{\mathbb {R}} ^{N}={\mathcal {L}}\), \(Z^{n}\in {\mathcal {L}}^{n}\) and
The first equality in (52) follows from Corollary and the second one from (49). \(\square \)
4.4 Main results
Theorem 4.12
Take \(\mathscr {Q}={\mathcal {Q}}_{v}\) and set \({\mathcal {L}}=\bigcap _{\mathbf {Q}\in {\mathcal {Q}}_{v}}L^{1}(\mathbf {Q})\). Under Assumption 3.10, for any \(\mathbf {X}\in M^{\Phi }\) and any \(A\in { {\mathbb {R}}}\) a SORTE exists, namely \((\widehat{\mathbf {Y}},\widehat{\mathbf {Q }})\in \) \({\mathcal {B}}_{A}\times \)\({\mathcal {Q}}_{v}\) defined in Theorem and
satisfy:
-
1.
\({\widehat{Y}}^{n}\) is an optimum for \(U_{n}^{{\widehat{Q}}^{n}}(\widehat{ a}^{n})\), for each \(n\in \{1,\dots ,N\}\),
-
2.
\(\widehat{{\mathbf {a}}}\) is an optimum for \(S^{\widehat{\mathbf {Q}} }(A),\)
-
3.
\(\widehat{\mathbf {Y}}\in {\mathcal {B}}\) and \(\sum _{n=1}^{N}{\widehat{Y}} ^{n}=A\) P-a.s.
Proof
- (1)::
-
We prove that \(U_{n}^{{\widehat{Q}}^{n}}({\widehat{a}}^{n})={\mathbb {E}}\left[ u_{n}\left( X^{n}+{\widehat{Y}}^{n}\right) \right] <u_{n}(+\infty )\), for all \(n=1,\dots ,N\), thus showing that \({\widehat{Y}}^{n}\) is an optimum for \(U_{n}^{{\widehat{Q}}^{n}}({\widehat{a}}^{n}).\) As \({\widehat{Y}}^{n}\in {\mathcal {L}}^{n}\) for all \(n=1,\dots ,N\), then by definition of \(U_{n}^{ {\widehat{Q}}^{n}}({\widehat{a}}^{n})\) we obtain:

If, for some index, the last inequality were strict we would obtain the contradiction
$$\begin{aligned} \pi ^{\widehat{\mathbf {Q}}}(A)=\pi (A)\overset{\text {Thm. } {4.5}}{=}\sum _{n=1}^{N}{\mathbb {E}}\left[ u_{n}\left( X^{n}+ {\widehat{Y}}^{n}\right) \right] <\sum _{n=1}^{N}U_{n}^{{\widehat{Q}}^{n}}( {\widehat{a}}^{n})\le S^{\widehat{\mathbf {Q}}}(A)=\pi ^{\widehat{\mathbf {Q}} }(A)\,, \nonumber \\ \end{aligned}$$(54)where we used (52) in the first and last equality. In particular then \({\mathbb {E}}\left[ u_{n}\left( X^{n}+{\widehat{Y}} ^{n}\right) \right] <u_{n}(+\infty )\), for all \(n=1,\dots ,N\) . Indeed, if the latter were equal to \(u_{n}(+\infty )\), then \(u_{n}\) would attain its maximum over a compact subset of \({{\mathbb {R}}}\), which is not the case.
- (2)::
-
From (33) we know that
 . From (52) we have
. From (52) we have 
- (3)::
-
We already know that \(\widehat{\mathbf {Y}}\in \) \({\mathcal {B}}_{A} {:={\mathcal {B}}\cap \{\mathbf {Y}\in (L^{0}(P))^{N}\mid \sum _{n=1}^{N}Y^{n}\le A\}}\). From Proposition 4.7 we deduce
$$\begin{aligned} A={\sum _{n=1}^{N}}E_{{\widehat{Q}}^{n}}[{\widehat{Y}}^{n}]\le {\sum _{n=1}^{N} {\widehat{Y}}^{n}\le A.} \end{aligned}$$
\(\square \)
We now turn our attention to uniqueness and Pareto optimality, but we will need an additional property and an auxiliary result.
Definition 4.13
(Def. 4.18 in [7]) We say that \({\mathcal {B}}\subseteq (L^{0}(P))^{N}\) is closed under truncation if for each \(\mathbf {Y}\in {\mathcal {B}}\) there exists \(m_{Y}\in {\mathbb {N}}\) and \(\mathbf {c}_{Y}=(c_{Y}^{1},\ldots ,c_{Y}^{N}) \in {\mathbb {R}}^{N}\) such that \(\sum _{n=1}^{N}c_{Y}^{n}= \sum _{n=1}^{N}Y^{n}:=c_{Y}\in {\mathbb {R}}\) and for all \(m\ge m_{Y}\)
Remark 4.14
We stress the fact that all the sets introduced in Example 3.17 satisfy closedness under truncation.
Lemma 4.15
Let \({\mathcal {B}}\) be closed under truncation. Then for every \(A\in {{\mathbb {R}}}\)
Proof
Fix any \(\mathbf {Q}\in {\mathcal {Q}}_v\) and argue as in Proposition 4.20 in [7]: let \(\mathbf {Y}\in {\mathcal {B}}_A\cap {\mathcal {L}}\subseteq L^1( \mathbf {Q})\) and consider \(\mathbf {Y}_{m}\) for \(m\in {\mathbb {N}}\) as defined in (55), where w.l.o.g. we assume \(m_{Y}=1\). Note that \( \sum _{n=1}^{N}Y_{m}^{n}=c_{Y}(=\sum _{n=1}^{N}Y^{n}\le A)\) for all \(m\in {\mathbb {N}} \). By boundedness of \(\mathbf {Y}_{m}\) and (55), we have \(\mathbf {Y}_{m}\in {\mathcal {B}}\cap M^{\Phi }\) for all \(m\in {\mathbb {N}}\) . Further, \(\mathbf {Y}_{m}\rightarrow \mathbf {Y}\) P-a.s. for \( m\rightarrow \infty \) , and thus, since \(|\mathbf {Y}_{m}|\le \max \{| \mathbf {Y}|,|\mathbf {c}_{Y}|\}\in L^{1}(\mathbf {Q})\) for all \(m\in {\mathbb {N}} \), also \(\mathbf {Y}_{m}\rightarrow \mathbf {Y}\) in \(L^{1}(\mathbf {Q})\) for \( m\rightarrow \infty \) by dominated convergence.
Now, if \(\mathbf {Q}\sim P\) we can directly apply Proposition to get that \(\sum _{n=1}^N E_{Q^n}[Y^n]\le \sum _{n=1}^NY^n\le A\). If we only have \(\mathbf {Q}\ll P\) we can see that (48) still holds, with the particular choice of \((\mathbf {Y} _{m})_m\) in place of \((\mathbf {k_n})_n\), because the construction of \( \mathbf {Y}_{m}\) is made P-almost surely. \(\square \)
Define
Lemma 4.16
Let \({\mathcal {B}}\) be closed under truncation. If \( \mathbf {{\widehat{Q}}}\) is the minimax measure from Theorem , then
Proof
It is clear that since \({\mathcal {B}}_{A}\cap M^{\Phi }\subseteq {\mathcal {B}} _{A}\cap {\mathcal {L}}\) we have \(\pi (A)\le \Pi (A)\) just by definitions (29) and (56). Now observe that by Lemma 4.15 we have \({\mathcal {B}}_{A}\cap {\mathcal {L}}\subseteq \overline{{\mathcal {B}}_{A}}\), so that \(\Pi (A)\le \Pi ^{\widehat{\mathbf {Q}}}(A)\). The chain of equalities then follows by Lemma 4.11. \(\square \)
Theorem 4.17
Let \({\mathcal {B}}\) be closed under truncation. Under the same assumptions of Theorem 4.12, for any \(\mathbf {X} \in M^{\Phi }\) and \(A\in {\mathbb {R}}\) the SORTE is unique and is a Pareto optimal allocation for both the sets

Proof
Use Proposition 4.9 and Corollary 4.10 to get that for any \(\mathbf {Q}\in {\mathcal {Q}}_{v}\)
Let \((\widetilde{\mathbf {Y}},\widetilde{\mathbf {Q}},\widetilde{\mathbf {a}})\) be a SORTE and \((\widehat{\mathbf {Y}},\widehat{\mathbf {Q}},\widehat{\mathbf {a }})\) be the one from Theorem 4.12.
By 1) and 2) in the definition of SORTE, together with Lemma , we see that \(\widetilde{\mathbf {Y}}\) is an optimum for \(\Pi ^{\widetilde{\mathbf {Q}}}(A)=S^{\widetilde{\mathbf {Q}}}(A)\). Also, \( \widetilde{\mathbf {Y}}\in {\mathcal {B}}_{A}\cap \overline{{\mathcal {B}}_{A}}\) by Lemma 4.15. We can conclude by Eq. (30) that
which tells us that \(\pi (A)=\pi ^{\widetilde{\mathbf {Q}}}(A)=\sum _{n=1}^{N} {\mathbb {E}}\left[ u_{n}\left( X^{n}+{\widetilde{Y}}^{n}\right) \right] .\)
By Theorem 4.5, we also have \(\pi (A)=\sum _{n=1}^{N} {\mathbb {E}}\left[ u_{n}\left( X^{n}+{\widehat{Y}}^{n}\right) \right] \). Then \( \widehat{\mathbf {Y}},\widetilde{\mathbf {Y}}\in \overline{{\mathcal {B}}_{A}}\) (Lemma 4.15) and \(\Pi (A)=\pi (A)\) (Lemma 4.16 ) imply that both \(\widehat{\mathbf {Y}},\widetilde{\mathbf {Y}}\) are optima for \(\Pi (A)\). By strict concavity of the utilities \(u_{1},\dots ,u_{N}\), \( \Pi (A)\) has at most one optimum. From this, together with uniqueness of the minimax measure (see Theorem 4.5), we get \((\widetilde{ \mathbf {Y}},\widetilde{\mathbf {Q}})=(\widehat{\mathbf {Y}},\widehat{\mathbf {Q} })\). We infer from Eq. (53) and Remark 3.8 that also \(\widetilde{\mathbf {a}}=\widehat{\mathbf {a}}\).
To prove the Pareto optimality observe that Theorem 4.5 proves that \(\widehat{\mathbf {Y}}\in \overline{{\mathcal {B}}_{A}}\mathcal { \subseteq L}\) is the unique optimum for \(\Pi (A)\) (see Lemma 4.16) and so it is also the unique optimum for \(\Pi ^{\widehat{ \mathbf {Q}}}(A)\). Pareto optimality then follows from Proposition 3.2, noticing that \(\Pi (\mathscr {V})\) for the two sets in (58) are \( \Pi (A) \) and \(\Pi ^{\widehat{\mathbf {Q}}}(A)\) respectively. \(\square \)
4.5 Dependence of the SORTE on \(\mathbf {X}\) and on \({\mathcal {B}}\)
We see from the proof of Theorem 4.12 that the triple defining the SORTE (obviously) depends on the choice of A. We now focus on the study of how such triple depends on \(\mathbf {X}\). To this end, we first specialize to the case \({\mathcal {B}}={\mathcal {C}}_{{\mathbb {R}}}\).
Proposition 4.18
Under the hypotheses of Theorem 4.12 and for \({\mathcal {B}}={\mathcal {C}}_{{\mathbb {R}}}\), the variables \(\frac{\mathrm {d} \widehat{\mathbf {Q}}}{\mathrm {d}P}\) and \(\mathbf {X}+\widehat{\mathbf {Y}}\) are \(\sigma (X^1+\dots +X^N)\) (essentially) measurable.
Proof
By Theorems 4.12 and 4.17 we have that \(({\widehat{\lambda }},\widehat{\mathbf {Q}})\) is an optimum of the RHS of Eq. (31). Notice that in this specific case \( \mathbf {Y}:=\mathbf {e_{i}}1_{A}-\mathbf {e_{j}}1_{A}\in {\mathcal {B}}\cap M^{\Phi }\) for all i, j and all measurable sets \(A\in {\mathcal {F}}\). Let \( \mathbf {Q}\in {\mathcal {Q}}\). Then from (47) \( \sum _{n=1}^{N}(E_{Q^{n}}[Y^{n}]-Y^{n})\le 0\) and so \( Q^{i}(A)-1_{A}-Q^{j}(A)+1_{A}\le 0,\) i.e., \(Q^{i}(A)-Q^{j}(A)\le 0\). Similarly taking \(\mathbf {Y}:=-\mathbf {e_{i}}1_{A}+\mathbf {e_{j}}1_{A}\in {\mathcal {B}}\), we get \(Q^{j}(A)-Q^{i}(A)\le 0\). Hence all the components of vectors in \({\mathcal {Q}}\) are equal. Let \({\mathcal {G}}:=\sigma (X^{1}+\dots +X^{N})\). Then for any \(\lambda \in {{\mathbb {R}}}_{++}\) and any \(\mathbf {Q} =[Q,\dots ,Q]\in {\mathcal {Q}}\) we have:

where in the last inequality we exploited the tower property and Jensen inequality, as \(v_{1},\dots ,v_{N}\) are convex. Notice now that  defines again a probability measure (on the whole \({\mathcal {F}}\), the initial sigma algebra) and that this measure still belongs to \({\mathcal {Q}}\) since all its components are equal. As a consequence, the minimum in Eq. (31) can be equivalently taken over \(\lambda \in {{\mathbb {R}}} _{++}\) (as before) and \(\mathbf {Q}\in {\mathcal {Q}}\cap \left( L^{0}(\Omega , {\mathcal {G}},P)\right) ^{N}\). The claim for \(\widehat{\mathbf {Y}}\) follows from (32). \(\square \)
defines again a probability measure (on the whole \({\mathcal {F}}\), the initial sigma algebra) and that this measure still belongs to \({\mathcal {Q}}\) since all its components are equal. As a consequence, the minimum in Eq. (31) can be equivalently taken over \(\lambda \in {{\mathbb {R}}} _{++}\) (as before) and \(\mathbf {Q}\in {\mathcal {Q}}\cap \left( L^{0}(\Omega , {\mathcal {G}},P)\right) ^{N}\). The claim for \(\widehat{\mathbf {Y}}\) follows from (32). \(\square \)
It is interesting to notice that this dependence on the componentwise sum of \(\mathbf {X}\) also holds in the case of Bühlmann’s equilibrium (see [13] page 16 and [11]).
Remark 4.19
In the case a cluster of agents, see the Example 3.17, the above result can be clearly generalized: the i-th component of the vector \( \widehat{\mathbf {Q}}\), for i belonging to the m-th group, only depends on the sum of those components of \(\mathbf {X}\) whose corresponding indexes belong to the m-th group itself. It is also worth mentioning that if we took \({\mathcal {B}}^{(\mathbf {I})}={\mathbb {R}}^{N}\), we would see that each component of \(\widehat{\mathbf {Q}}\) and of \(\widehat{\mathbf {Y}}\) is a measurable function of the corresponding component of \(\mathbf {X}\). This is reasonable since, in this case, at the final time each agent would be only allowed to share and exchange risk with herself/himself and the systemic features of the model we are considering would be lost.
We provide now some additional examples, to the ones in Example 3.17, of possible feasible sets \({\mathcal {B}}\) and study the dependence of the probability measures from \({\mathcal {B}}\).
Example 4.20
Consider a measurable partition \(A_{1},\dots ,A_{K}\) of \( \Omega \) and a collection of partitions \(\mathbf {I}^{1},\dots ,\mathbf {I} ^{K} \) of \(\{1,\dots ,N\}\) as in Example 3.17. Take the associated clusterings \({\mathcal {B}}^{(\mathbf {I}^{1})},\dots ,{\mathcal {B}}^{(\mathbf {I} ^{K})}\) defined as in (23). Then the set
satisfies Assumptions 3.10 and is closed under truncation, as it can be checked directly.
The set in (60) can be seen as a scenario-dependent clustering. A particular simple case of (60) is the following. For a measurable set \(A_1\in {\mathcal {F}}\) take \( A_2=\Omega \setminus A_1\). Then the set \({\mathcal {C}}_{{\mathbb {R}}} 1_{A_1}+{ {\mathbb {R}}}^N 1_{A_2}\) is of the form (60) and consists of all the \(\mathbf {Y}\in (L^{0})^N\) such that (i) there exists a real number \( \sigma \in {{\mathbb {R}}}\) with \(\sum _{n=1}^NY^n=\sigma \) \(P-\)a.s. on \(A_1\), (ii) there exists a vector \(\mathbf {b}\in {{\mathbb {R}}}^N\) such that \(\mathbf {Y}= \mathbf {b}\) \(P-\)a.s. on \(A_2\) and (iii) \(\sigma =\sum _{n=1}^Nb^n\) (recall that \(\mathbf {Y}\in {\mathcal {C}}_{{\mathbb {R}}}\) by (60)).
Let us motivate Example 4.20 with the following practical example. Suppose for each bank i a regulator establishes an excessive exposure threshold \(D^i\). If the position of bank i falls below such threshold, we can think that it is too dangerous for the system to let that bank take part to the risk exchange. As a consequence, in the clustering example, on the event \(\{X^i\le D^i\}\) we can require the bank to be left alone. Also the symmetric situation can be considered: a bank j whose position is too good, say exceeding a value \(A^j\), will not be willing to share risk with all others, thus entering the game only as isolated individual or as a member of the groups of “safer”banks. Both these requirements, and many others (say considering random thresholds) can be modelled with the constraints introduced in Example 4.20.
It is interesting to notice that, as in Example 3.17, assuming a constraint set of the form given in Example 4.20 forces a particular behavior on the probability vectors in \({\mathcal {Q}}_{v}\).
Lemma 4.21
Let \({\mathcal {B}}\) be as in Example 4.20 and let \(\mathbf {Q\in }{\mathcal {Q}}_{v}\). Fix any \(i\in \left\{ 1,\ldots ,K\right\} \) and any group \(\mathbf {I}_{m}^{i}\) of the partition \(\mathbf {I}^{i}=(\mathbf { I}_{m}^{i})_{m}\). Then all the components \(Q^{j}\), \(j\in \mathbf {I}_{m}^{i}\) , agree on \({\mathcal {F}}|_{A_{i}}:=\{F\cap A_{i},\,F\in {\mathcal {F}}\}\).
Proof
We think it is more illuminating to prove the statement in a simplified case, rather than providing a fully formal proof (which would require unnecessairly complicated notation). This is “without loss of generality” in the sense that it is clear how to generalize the method. To this end, let us consider the case \(K=2\) (i.e. \(A_2=A_1^c\)) and \({\mathcal {B}}^{(\mathbf {I^1})} :={\mathcal {C}}_{{\mathbb {R}}}\), \({\mathcal {B}}^{(\mathbf {I^2})}:={{\mathbb {R}}}^N\). For any \(F\in {\mathcal {F}}\) and \(i,j\in \{1,\dots ,N\}\) we can take \(\mathbf {Y} :=\left( 1_{F}(\mathbf {e_i}-\mathbf {e_j})\right) 1_{A_1}+\mathbf {0}1_{A_2}\) to obtain \(\mathbf {Y}\in {\mathcal {C}}_{{\mathbb {R}}} 1_{A_1}+{{\mathbb {R}}}^N1_{A_2}\) , \(\sum _{j=1}^NY^j=0\). By definition of \({\mathcal {Q}}_v\) we get for any \( \mathbf {Q}\in {\mathcal {Q}}_v\) that \(Q^i(A\cap F)-Q^j(A\cap F)\le 0\), and interchanging i, j yields \(Q^i(A\cap F)=Q^j(A\cap F)\) for any \(i,j=1\dots ,N\) , \(F\in {\mathcal {F}}\). \(\square \)
5 Exponential case
We now specialize our analysis to the exponential setup, where
This allows us to provide explicit formulas for a wide range of constraint sets \({\mathcal {B}}\) (namely, all those introduced in Example 3.17) and so the stability properties of SORTE, with respect to a different weighting of utilities, will be evident.
5.1 Explicit formulas
We consider a set of constraints of the form \({\mathcal {B}}={\mathcal {B}}^{( \mathbf {I})}\) as given in Example 3.17. Given \(\mathbf {X}\in M^{\Phi }\) and \(m\in \{1,\dots ,h\}\), we set:
Theorem 5.1
Take \(u_{1},\dots ,u_{N}\) as given by (61) and \({\mathcal {B}}={\mathcal {B}}^{\mathbf {(I)}}\) as in Example 3.17. For \( {\mathcal {L}}\) and \(\mathscr {Q}\) defined in Theorem 4.12, the SORTE is given by
where
Proof
The utilities in (61) satisfy Assumption 3.10 (a) and \( {\mathcal {B}}\) satisfies Asssumption 3.10 (b) and closedness under truncation, hence Theorems 4.12 and 4.17 guarantee existence and uniqueness. Recall that from this choice of \( {\mathcal {B}}\) we have that for each \(\mathbf {Q}\in {\mathcal {Q}}_{v}\), all the components of \(\mathbf {Q}\) are equal in each index subset \(I_{m}\).
It is easy to check that
Substitute now \(y=\frac{\mathrm {d}Q^{n}}{\mathrm {d}P}\in {\mathcal {Q}}_{v}\) in the above expressions and take expectations to get
Let \(K\left( \lambda ,\frac{\mathrm {d}\mathbf {Q}}{\mathrm {d}P}\right) \) be the functional to be optimized in (31). Set
Then from (64) we deduce
Set
The associated first order condition obtained differentiating in \(\lambda \) yields the unique solution
which can be substituted in \(K\left( \cdot ,\frac{\mathrm {d}\widehat{\mathbf { Q}}}{\mathrm {d}P}\right) \) yielding
We now guess that the vector of measures \(\widehat{\mathbf {Q}}\) defined via (62) is optimal and compute the associated \(\mu \):
Hence
and substituting (67) in the explicit formula for \( {\widehat{\lambda }}\) we get
Using Eq. (32) we define, for the measure given in (62),
By (63) (with \(\lambda =1\)) we obtain, for \(k\in I_{m},\) \( v_{k}^{\prime }(y)=\frac{1}{\alpha _{k}}\ln \left( \frac{y}{\alpha _{k}} \right) \) and
Hence for \(k\in I_{m}\) we have
A simple computation yields \(\widehat{\mathbf {Y}}\in M^{\Phi }\), \(\sum _{k\in I_{m}}Y^{k}\in {{\mathbb {R}}}\) and \(\sum _{n=1}^{N}{\widehat{Y}}^{n}=A\), so that \( \widehat{\mathbf {Y}}\in {\mathcal {B}}_{A}\cap M^{\Phi }\).
Moreover
As a consequence
which implies
To sum up we have
Consequently \(\widehat{\mathbf {Y}}\) is the (unique) optimum for the optimization problem in LHS of (30), and \(({\widehat{\lambda }},\widehat{\mathbf {Q}})\) is the (unique) optimum to the minimization problem in (31).
Moreover, setting \({\widehat{a}}^{n}:=E_{{\widehat{Q}}^{n}}[{\widehat{Y}} ^{n}],\quad n=1,\dots ,N,\) the SORTE (which, as already argued, exists and is unique) is given by \(\left( \widehat{\mathbf {Y}},\widehat{\mathbf {Q}}, \widehat{\mathbf {a}}\right) \). \(\square \)
Remark 5.2
We observe that in the terminal part of the proof above we also got an explicit formula for the maximum systemic utility:
where \(K\left( \widehat{\lambda },\frac{\mathrm {d}\widehat{\mathbf {Q}}}{ \mathrm {d}P}\right) \) is given in (70).
5.2 A toy example
In the following two examples we compare a Bühlmann’s Equilibrium with a SORTE in the simplest case where \(\mathbf {X}=\mathbf {0}:=[0,\ldots ,0]\) and \( A=0. \) In the formula below we use the well known fact:
where \(H(Q,P)=E[\frac{\mathrm {d}Q}{\mathrm {d}P}\ln (\frac{\mathrm {d}Q}{\mathrm {d}P})]\) is the relative entropy, for \(Q\ll P\).
Example 5.3
(Bühlmann’s equilibrium solution) As \(\mathbf {X}:=\mathbf {0}\) then \({\overline{X}}_{N}=\sum _{k=1}^{N}X^{k}=0\) and therefore the optimal probability measure \(Q_{\mathbf {X}}\) defined in Bühlmann is:
i.e. \(Q_{\mathbf {X}}=P.\) Take \(\mathbf {a=0}=[0,\ldots ,0]\). We compute
as \(H(P,P)=0\), so that
As a consequence, and as \(u_{n}(0)=0\), the optimal solution for each single n is obviously \(Y_{\mathbf {X}}^{n}=0.\)
Conclusion The Bühlmann’s equilibrium solution associated to \( \mathbf {X}:=\mathbf {0}\) (and \(A=0)\) is the couple \((\mathbf {Y}_{\mathbf {X}}, \mathbf {Q}_{\mathbf {X}})=(\mathbf {0},P)\). Here the vector \(\mathbf {a}\) is taken a priori to be equal to \([0,\ldots ,0].\)
Example 5.4
(SORTE) From Theorem 5.1 with \(\mathbf {X}:=\mathbf {0}\) and \(A=0\) we obtain for the SORTE that: the optimal probability measure \( \widehat{\mathbf {Q}}\) coincides again with P; the optimal \({\widehat{Y}}\) is:
Recalling that \(\widehat{\mathbf {Q}}\) is in fact a minimax measure for the optimization problem \(\pi _{0}(\mathbf {0})\) (see the proof of Theorem 4.12), we can say that
Notice that if the \(\alpha _{n}\) are equal for all n, then \(S^{P}(0)=0,\) but in general
Indeed, by Jensen inequality:
From (74) we deduce that the \(\alpha _{n}\) are equal for all n if and only if \({\widehat{a}}^{n}=0\) for all n, but in general \({\widehat{a}}^{n}\) may differ from 0. As \({\widehat{Y}}^{n}={\widehat{a}}^{n}\), the same holds also for the optimal solution \({\widehat{Y}}\). When \({\widehat{a}}^{n}<0\) a violation of Individual Rationality occurs.
Conclusion The SORTE solution associated to \(\mathbf {X}:=\mathbf {0} \) (and \(A=0)\) is the triplet \((\widehat{\mathbf {Y}},P,\widehat{\mathbf {a}})\) where \(\widehat{\mathbf {Y}}=\widehat{\mathbf {a}}\) is assigned in Eq. ( 74).
The above comparison shows that a SORTE is not a Bühlmann equilibrium, even when \(\mathbf {X}:=\mathbf {0}\) and \(A=0\). When the \(\alpha _{n}\) are all equal, then the Bühlmann and the SORTE solution coincide, as all agents are assumed to have the same risk aversion.
Remark 5.5
In this example, notice that we may control the risk sharing components \( Y^{n}\) of agent n in the SORTE by:
Suppose that \(\alpha _{\min }<\alpha _{\max }\) and consider the expression for \({\widehat{Y}}^{n}={\widehat{a}}^{n}\) in (74). If \(\alpha _{j}=\alpha _{\min }\) then the corresponding \({\widehat{Y}}^{j}<0\) is in absolute value relatively large (divide by \(\alpha _{\min }\)), while if \(\alpha _{k}=\alpha _{\max }\) the corresponding \({\widehat{Y}}^{k}>0\) is in absolute value relatively small (divide by \(\alpha _{\max }\)).
5.3 Dependence on weights and stability
We now provide a detailed study of the dependence on weights, as introduced in Remark 1.3, in the exponential case. Given \(\gamma _{n}\in (0,+\infty ),\,n=1,\dots ,N\) and \(u_{1},\dots ,u_{N}\) satisfying Assumption 3.10 (a), we recall that \(u_{n}^{\gamma }(x):=\gamma _{n}u_{n}(x),\,n=1,\dots ,N\) and we denote by \(v_{n}^{\gamma }(\cdot )\) their convex conjugates. These functions \(u_{n}^{\gamma }\) satisfy Assumption 3.10 (a).
In our exponential setup and under closedness under truncation, a different weighting only results in a translation of both allocations at initial and terminal time of a SORTE, without affecting the optimal measure:
Proposition 5.6
Consider \(u_{1},\dots ,u_{N}\) as given in (61) and take the associated \(u_{1}^{\gamma },\dots ,u_{N}^{\gamma }\) as above. Suppose \({\mathcal {B}}\) satisfies Assumption 3.10 (b) and is closed under truncation. Call \(\left( \widehat{\mathbf {Y}},\widehat{\mathbf {Q}},\widehat{ \mathbf {a}}\right) \) the unique SORTE associated to \(u_{1},\dots ,u_{N}\), and similarly define \(\left( \widehat{\mathbf {Y}}_{\gamma },\widehat{\mathbf { Q}}_{\gamma },\widehat{\mathbf {a}}_{\gamma }\right) \) as the unique SORTE associated to \(u_{1}^{\gamma },\dots ,u_{N}^{\gamma }\). Then
where
Proof
For a general set \({\mathcal {B}}\), we here provide only a sketch of the proof. Using the formulas for \(v_{1},\dots ,v_{N}\), after some computations one can write explicitly the minimax expression (31). Then use the gradient formula (32) to deduce (76). A more direct proof, that works only for sets \({\mathcal {B}}\) in the form described in Example 3.17, is based on the observation that
Hence, \(\left( \widehat{\mathbf {Y}}_{\gamma },\widehat{\mathbf {Q}}_{\gamma }, \widehat{\mathbf {a}}_{\gamma }\right) \) can be obtained by a straightforward computation from the solution \(\left( \widehat{\mathbf {Y}},\widehat{\mathbf {Q }},\widehat{\mathbf {a}}\right) \), which is explicitly given in Theorem 5.1, using \(X^{n}-\frac{1}{\alpha _{n}}\ln (\gamma _{n}),\,n=1,\dots ,N\) in place of \(\mathbf {X}\). \(\square \)
References
Acciaio, B.: Optimal risk sharing with non-monotone monetary functionals. Finance Stoch. 11(2), 267–289 (2007)
Acharia, V.V., Pedersen, L.H., Philippon, T., Richardson, M.: Measuring systemic risk. Rev. Financ. Stud. 30(1), 2–47 (2017)
Armenti, Y., Crepey, S., Drapeau, S., Papapantoleon, A.: Multivariate shortfall risk allocation and systemic risk. SIAM J. Financ. Math. 9(1), 90–126 (2018)
Barrieu, P., El Karoui, N.: Inf-convolution of risk measures and optimal risk transfer. Finance Stoch. 9(2), 269–298 (2005)
Bellini, F., Frittelli, M.: On the existence of minimax martingale measures. Math. Finance 12(1), 1–21 (2002)
Biagini, F., Fouque, J.-P., Frittelli, M., Meyer-Brandis, T.: A unified approach to systemic risk measures via acceptance sets. Math. Finance 29(1), 329–367 (2019)
Biagini, F., Fouque, J.-P., Frittelli, M., Meyer-Brandis, T.: On fairness of systemic risk measures. Finance Stoch. 24(2), 513–564 (2020)
Biagini, S., Frittelli, M.: Utility maximization in incomplete markets for unbounded processes. Finance Stoch. 9(4), 493–517 (2005)
Biagini, S., Frittelli, M.: A unified framework for utility maximization problems: an orlicz space approach. Ann. Appl. Probab. 18(3), 929–966 (2008)
Biagini, S., Frittelli, M.: On the extension of the Namioka–Klee theorem and on the Fatou property for risk measures. In: Optimality and Risk—Modern Trends in Mathematical Finance, pp. 1–28. Springer, Berlin (2009)
Borch, K.: Equilibrium in a reinsurance market. Econometrica 30(3), 424–444 (1962)
Bühlmann, H.: An economic premium principle. Astin Bull. 11(1), 52–60 (1980)
Bühlmann, H.: The general economic premium principle. Astin Bull. 14(1), 13–21 (1984)
Bühlmann, H., Jewell, W.S.: Optimal risk exchange. Astin Bull. 10(3), 243–262 (1979)
Carlier, G., Dana, R.-A.: Pareto optima and equilibria when preferences are incompletely known. J. Econ. Theory 148(4), 1606–1623 (2013)
Carlier, G., Dana, R.-A., Galichon, A.: Pareto efficiency for the concave order and multivariate comonotonicity. J. Econ. Theory 147(1), 207–229 (2012)
Chen, C., Iyengar, G., Moallemi, C.: An axiomatic approach to systemic risk. Manag. Sci. 56(6), 1373–1388 (2013)
Cvitanic, J., Karatzas, I.: Convex duality in constrained portfolio optimization. Ann. Appl. Probab. 2(4), 718–767 (1992)
Dana, R.A., Le Van, C.: Overlapping sets of priors and the existence of efficient allocations and equilibria for risk measures. Math. Finance 20(3), 327–339 (2010)
Debreu, G.: Theory of Value: An Axiomatic Analysis of Economic Equilibrium. Cowles Foundation for Research in Economics at Yale University, Monograph 17. Wiley, Hoboken (1959)
Embrechts, P., Liu, H., Mao, T., Wang, R.: Quantile-based risk sharing with heterogeneous beliefs. Math. Program. 181(2), 319–347(2020)
Embrechts, P., Liu, H., Wang, R.: Quantile-based risk sharing. Oper. Res. 66(4), 936–949 (2018)
Feinstein, Z., Rudloff, B., Weber, S.: Measures of systemic risk. SIAM J. Financ. Math. 8(1), 672–708 (2017)
Filipović, D., Kupper, M.: Optimal capital and risk transfers for group diversification. Math. Finance 18(1), 55–76 (2008)
Filipović, D., Svindland, G.: Optimal capital and risk allocations for law- and cash-invariant convex functions. Finance Stoch. 12(3), 423–439 (2008)
Föllmer, H., Schied, A.: Stochastic Finance: An Introduction In Discrete Time, 4th edn. De Gruyter, Berlin (2016)
Fouque, J.-P., Langsam, J.A.: Handbook on Systemic Risk. Cambridge University Press, Cambridge (2013)
Heath, D., Ku, H.: Pareto equilibria with coherent measures of risk. Math. Finance 14(2), 163–172 (2004)
Hurd, T.R.: Contagion! Systemic Risk in Financial Networks. Springer, Berlin (2016)
Jouini, E., Schachermayer, W., Touzi, N.: Optimal risk sharing for law invariant monetary utility functions. Math. Finance 18(2), 269–292 (2008)
Karatzas, I., Lehoczky, J., Shreve, S., Xu, G.: Martingale and duality methods for utility maximization in an incomplete market. SIAM J. Control Optim. 29(3), 702–730 (1991)
Kromer, E., Overbeck, L., Zilch, K.: Systemic risk measures on general measurable spaces. Math. Methods Oper. Res. 84(4), 323–357 (2016)
Liebrich, F.B., Svindland, G.: Risk sharing for capital requirements with multidimensional security markets. Finance Stoch. 23(4), 925–973 (2019)
Mas Colell, A., Zame, W.: Equilibrium theory in infinite dimensional spaces. In: Handbook of Mathematical Economics IV. Elsevir Science Publisher, Amsterdam (1991)
Mastrogiacomo, E., Rosazza Gianin, E.: Pareto optimal allocations and optimal risk sharing for quasiconvex risk measures. Math. Financ. Econ. 9, 149–167 (2015)
Rao, M.M., Ren, Z.D.: Theory of Orlicz Spaces. Marcel Dekker Inc, New York (1991)
Rockafeller, R.T.: Integrals which are convex functionals. Pac. J. Math. 24(3), 525–540 (1968)
Schachermayer, W.: Optimal investment in incomplete markets when wealth may become negative. Ann. Appl. Probab. 11(3), 694–734 (2001)
Tsanakas, A.: To split or not to split: capital allocation with convex risk measures. Insur. Math. Econ. 44(2), 268–277 (2009)
Weber, S.: Solvency II, or how to sweep the downside risk under the carpet. Insur. Math. Econ. 82, 191–200 (2018)
Acknowledgements
Open access funding provided by Università degli Studi di Milano within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
J-P. Fouque: Work supported by NSF Grant DMS-1814091.
A Appendix
A Appendix
1.1 A.1 Orlicz spaces and utility functions
We consider the utility maximization problem defined on Orlicz spaces, see [36] for further details on Orlicz spaces. This presents several advantages. From a mathematical point of view, it is a more general setting than \(L^{\infty }\), but at the same time it simplifies the analysis, since the topology is order continuous and there are no singular elements in the dual space. Furthermore, it has been shown in [9] that the Orlicz setting is the natural one to embed utility maximization problems, as the natural integrability condition \(\mathbb {E}[u(X)]>-\infty \) is implied by \( \mathbb {E}[\phi (X)]<+\infty \).
Let \(u:\mathbb {R}\rightarrow \mathbb {R}\) be a concave and increasing function satisfying \(\lim _{x\rightarrow -\infty }\frac{u(x)}{x}=+\infty .\) Consider \(\phi (x):=-u(-|x|)+u(0).\) Then \(\phi :\mathbb {R}\rightarrow [0,+\infty )\) is a strict Young function, i.e., it is finite valued, even and convex on \(\mathbb {R}\) with \(\phi (0)=0\) and \(\lim _{x\rightarrow +\infty }\frac{\phi (x)}{x}=+\infty \). The Orlicz space \(L^{\phi }\) and Orlicz Heart \(M^{\phi }\) are respectively defined by
and they are Banach spaces when endowed with the Luxemburg norm. The topological dual of \(M^{\phi }\) is the Orlicz space \(L^{\phi ^{*}},\) where the convex conjugate \(\phi ^{*}\) of \(\phi \), defined by
is also a strict Young function. Note that
Remark A.1
It is well known that \(L^{\infty }(P;\mathbb {R} )\subseteq M^{\phi }\subseteq L^{\phi }\subseteq L^{1}(P;\mathbb {R} ) \). In addition, from the Fenchel inequality \(xy\le \phi (x)+\phi ^{*}(y) \) we obtain
for some probability measure \(Q\ll P\), and we immediately deduce that \(\frac{dQ}{dP}\in L^{\phi ^{*}}\) implies \(L^{\phi }\subseteq L^{1}(Q;\mathbb {R})\).
Given the utility functions \(u_{1},\cdots ,u_{N}:\mathbb {R}\rightarrow \mathbb {R}\), satisfying the above conditions, with associated Young functions \(\Phi _{1},\cdots ,\Phi _{N}\), we define
1.2 A.2 Auxiliary results
Lemma A.2
Let \(v:[0,+\infty )\rightarrow {\mathbb {R}}\cup \{+\infty \}\) be a convex function, and suppose that its restriction to \( (0,+\infty )\) is real valued and differentiable. Let \(Q\ll P\) be a given probability measure with \(v\left( \lambda \frac{\mathrm {d}Q}{\mathrm {d}P} \right) \in L^1(P)\) for all \(\lambda >0\). Then
-
1.
\(v^{\prime }\) is defined on \((0,+\infty )\) and real valued there and extendable to \([0,+\infty )\) by taking \(\lim _{x\rightarrow 0}v^{\prime }(x)\in {\mathbb {R}}\cup \{-\infty \}\). Also, \(\frac{\mathrm {d}Q}{\mathrm {d}P} v^{\prime }\left( \lambda \frac{\mathrm {d}Q}{\mathrm {d}P}\right) \in L^1(P)\) for all \(\lambda >0\).
-
2.
If g is such that \(g+\frac{1}{g}\in L^\infty _+(P)\), then \(v\left( g \frac{ \mathrm {d}Q}{\mathrm {d}P}\right) \in L^1(P)\).
-
3.
If \(v^{\prime }(0+)=-\infty \), \(v^{\prime }(+\infty )=+\infty \) and v is strictly convex \(F(\gamma ):=\mathbb {E} \left[ \frac{\mathrm {d}Q}{\mathrm {d} P}v^{\prime }\left( \gamma \frac{\mathrm {d}Q}{\mathrm {d}P}\right) \right] \) is a well defined bijection between \((0,+\infty )\) and \({\mathbb {R}}\).
Proof
Lemma 2 of [8]. \(\square \)
The following dual representation holds:
Theorem A.3
Let \(u_{1}\dots ,u_{n}:{\mathbb {R}}\rightarrow {\mathbb {R} }\) be strictly increasing and concave functions. Let \(\mathcal {C}\subseteq M^{\Phi }\) be a convex cone such that for every \(i,j=1,\dots ,N,\) \(\mathbf { e_{i}}-\mathbf {e_{j}}\in \mathcal {C}\). Denote by \(\mathcal {C}^{0}\) the polar of the cone \(\mathcal {C}\) in the dual pair \((M^{\Phi },L^{\Phi ^{*}})\)
Set
and suppose that
Then
If any of the two expressions above is strictly smaller than \( \sum _{j=1}^{N}u_{j}(+\infty )\), then
Proof
Observe first that \(\mathbf {X}\mapsto \rho (\mathbf {X}):=-\sup _{\mathbf {Y} \in \mathcal {C}}\left( \sum _{j=1}^{N}\mathbb {E}\left[ u_{j}\left( X^{j}+Y^{j}\right) \right] \right) \) is a non increasing, finite valued, convex functional on the Fréchet lattice \(M^{\Phi }\). Only convexity is non-evident: to show it, consider \(\mathbf {X},\mathbf {Z}\in M^{\Phi }\) and \( \mathbf {Y},\mathbf {W}\in \mathcal {C}\). For any \(0\le \lambda \le 1,\) we have by concavity
as \(\lambda \mathbf {Y}+(1-\lambda )\mathbf {W}\in \mathcal {C}\). Thus taking suprema over \(\mathbf {Y},\mathbf {W}\in \mathcal {C}\) we get
Now the Extended Namioka-Klee Theorem (see [10] Theorem A.3) can be applied and we obtain
where
Observe now that \(-U(\mathbf {z}):=\sum _{j=1}^{N}-u_{j}(z^{j})\) for \(\mathbf {z }\in {\mathbb {R}}^{N}\) defines a continuous, convex, proper function whose Fenchel transform is
Now we apply Corollary on page 534 of [37] with \(L=M^{\Phi }\), \(L^{*}=L^{\Phi ^{*}}\), \(F(\mathbf {x})=-U(\mathbf {x})\) to see that
and replacing this in (80) we get:
Now observe that there are two possibilities:
-
either \(\mathbf {Z}\in \mathcal {C}^0\), and in this case \(\alpha (\mathbf {Z })=E_\mathbb {P} \left[ \sum _{j=1}^Nv_j(Z^j)\right] \) since \(\mathbf {0}\in \mathcal {C}\)
-
or \(\alpha (\mathbf {Z})=+\infty \), since \(v_{1},\dots ,v_{N}\) are bounded from below.
Hence
Moreover, since for every \(i,j=1,\dots ,N\) \(\mathbf {e_{i}}-\mathbf {e_{j}}\in \mathcal {C}\) we can argue as in Lemma 4.1 to deduce that \( \mathcal {C}^{0}\cap (L_{+}^{0})^{N}={\mathbb {R}_{+}}\cdot (\mathcal {C} _{1}^{0})^{+}\). Replacing this in the expression (81) we get
To prove the last claim, observe that if the optimum \(\lambda \) in the right hand side was 0, we would have
which contradicts our hypotheses. \(\square \)
Theorem A.4
Let \(u_{1},\dots ,u_{N}\) satisfy Assumption 3.10 . Let \(K\subseteq M^{\Phi }\) be a convex cone such that for all \(i,j\in \{1,\dots ,N\}\) \(\mathbf {e_{i}}-\mathbf {e_{j}}\in K\) and suppose that \( \mathcal {Q}_{v}^{e}\ne \emptyset \), where
Then denoting by \(cl_{\mathbf {Q}}(\dots )\) the closure in \(L^{1}\left( Q^{1}\right) \times \dots \times L^{1}\left( Q^{N}\right) \) with respect to the norm \(\left\| \mathbf {X}\right\| _{\mathbf {Q}}:=\sum _{j=1}^{N}\left\| X^{j}\right\| _{L^{1}(Q^{j})}\) we have
Proof
We modify the procedure in [8] Theorem 4. The inclusion (\(LHS\subseteq RHS\)) can be checked directly. As to the opposite one (\(RHS\subseteq LHS\)), suppose we had a \(\mathbf {k}\in RHS\) and a \(\mathbf {Q}\in \mathcal {Q} _{v}^{e} \) with \(\mathbf {k}\notin cl_{\mathbf {Q}}\left( K-L_{+}^{1}\left( \mathbf {Q}\right) \right) \), that is \(\mathbf {k}\notin LHS\). We stress that by construction
In the dual system
the set \(cl_{\mathbf {Q}}\left( K-L_{+}^{1}\left( \mathbf {Q}\right) \right) \) is convex and \(\sigma \left( L^{1}(\mathbf {Q}),L^{\infty }(\mathbf {Q})\right) \) -closed by compatibility of the latter topology with the norm topology. Thus we can use Hahn-Banach Separation Theorem to get a class \(\widehat{{\xi }}\in L^{\infty }(\mathbf {Q})\) with
We now work componentwise. First observe that
so that \({\widehat{\xi }}^{j}\ge 0\) \(Q^{j}\)-a.s. for every \(j=1,\dots ,N\). Hence \(\widehat{\xi }^{j}\frac{\mathrm {d}Q^{j}}{\mathrm {d}P}\ge 0\) P-a.s. for every \(j=1,\dots ,N\).
Moreover, since for all \(i,j\in \{1,\dots ,N\}\) \(\mathbf {e_{i}}-\mathbf {e_{j} }\in K\), we have
It follows that for every \(j=1,\dots ,N\)
since if this were not the case all the terms in Eq. (84) would be null, which would yield \({\widehat{\xi }} ^{1}\frac{\mathrm {d}Q^{1}}{\mathrm {d}P}=\dots ={\widehat{\xi }}^{N}\frac{ \mathrm {d}Q^{N}}{\mathrm {d}P}=0\), a contradiction with (83).
Hence the vector
is well defined and identifies a vector of probability measures \( [Q_{1}^{1},\dots ,Q_{1}^{N}]\). We trivially have that
and by Eq. (83), together with (84)
We observe that if we could prove \(\mathbf {Q}_{1}\in \mathcal {Q}_{v}^{e}\), we would get a contradiction with (82). However this needs not to be true, since we cannot guarantee \(Q_{1}^{1},\dots ,Q_{1}^{N}\sim P\).
As \(\mathbf {Q}\in \mathcal {Q}_{v}^{e}\), we have \(\mathbf {Q}\sim P\), and for \( \mathbf {Q}_{1}\) above we have \(\mathbf {Q}_{1}\ll \mathbf {Q}\), \(\frac{\mathrm { d}Q_{1}^{k}}{\mathrm {d}Q^{k}}\in L^{\infty }(Q^{k})=L^{\infty }(P)\). Take \( \lambda \in (0,1]\) and define \(\mathbf {Q}_{\lambda }\) via
We now prove that \(\mathbf {Q_{\lambda }}\in \mathcal {Q}_{v}^{e}\). It is easy to check that
so that Lemma A.2.2. with \(g=g^{k}:=\frac{\mathrm {d} Q_{\lambda }^{k}}{\mathrm {d}Q^{k}}\), together with \(\mathbb {E}\left[ v_{k}\left( \frac{\mathrm {d}Q^{k}}{\mathrm {d}P}\right) \right] <+\infty \,\forall \,k=1,\dots ,N\) (\(\mathbf {Q}\in \mathcal {Q}_{v}^{e}\) by construction), yields
Moreover \(\mathbf {Q}\in \mathcal {Q}_{v}^{e}\) and \(\lambda >0\) imply \(\mathbf { Q}_{\lambda }^{k}\sim P\) for all \(k=1,\dots ,N\). This, together with Eq. (85), yields
We can conclude that \(\mathbf {Q}_{\lambda }\in \mathcal {Q}_{v}^{e},\,\forall \lambda \in (0,1]\). At the same time
which gives a contradiction with Eq. (82). We conclude that \(RHS\subseteq LHS\). \(\square \)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Biagini, F., Doldi, A., Fouque, JP. et al. Systemic optimal risk transfer equilibrium. Math Finan Econ 15, 233–274 (2021). https://doi.org/10.1007/s11579-020-00277-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11579-020-00277-8






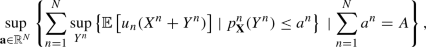



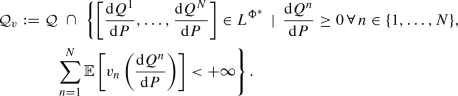




 . From (
. From (