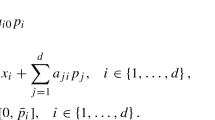Abstract
A Systemic Optimal Risk Transfer Equilibrium (SORTE) was introduced in: “Systemic optimal risk transfer equilibrium”, Mathematics and Financial Economics (2021), for the analysis of the equilibrium among financial institutions or in insurance-reinsurance markets. A SORTE conjugates the classical Bühlmann’s notion of a risk exchange equilibrium with a capital allocation principle based on systemic expected utility optimization. In this paper we extend such a notion to the case when the value function to be optimized is multivariate in a general sense, and it is not simply given by the sum of univariate utility functions. This takes into account the fact that preferences of single agents might depend on the actions of other participants in the game. Technically, the extension of SORTE to the new setup requires developing a theory for multivariate utility functions and selecting at the same time a suitable framework for the duality theory. Conceptually, this more general framework allows us to introduce and study a Nash Equilibrium property of the optimizer. We prove existence, uniqueness, and the Nash Equilibrium property of the newly defined Multivariate Systemic Optimal Risk Transfer Equilibrium.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
A Systemic Optimal Risk Transfer Equilibrium, denoted with SORTE, was introduced and analyzed in Biagini et al. (2021). The SORTE concept was inspired by Bühlmann’s notion of a Risk Transfer Equilibrium in insurance-reinsurance markets. However, in Bühlmann’s definition the vector assigning the budget constraints was given a priori. On the contrary, in the SORTE, such a vector is endogenously determined by solving a systemic utility maximization problem. As remarked in Biagini et al. (2021), “SORTE gives priority to the systemic aspects of the problem, in order to optimize the overall systemic performance, rather than to individual rationality”. For the precise definition of a SORTE, its existence, uniqueness and Pareto optimality we refer to Biagini et al. (2021). In Sect. 1.1 we will only very briefly recall its motivation and heuristic definition in order to compare it with the results of the present paper. We will not address any integrability issues in this Introduction.
The capital allocation and risk sharing equilibrium that we consider in this new work, similarly to the one introduced in Biagini et al. (2021), can be applied to many contexts, such as: equilibrium among financial institutions, agents, or countries; insurance and reinsurance markets; capital allocation among business units of a single firm; wealth allocation among investors.
The key novelty in this work is that we consider preferences of agents which depend on other agents’ choices. This is modeled using multivariate utility functions.
Let \((\Omega ,{\mathcal {F}},{\mathbb {P}}\mathbf {)}\) be a probability space and \(L^{0}(\Omega ,{\mathcal {F}},{\mathbb {P}})\) be the vector space of (equivalence classes of) real valued \({\mathcal {F}}\)-measurable random variables. The sigma algebra \({\mathcal {F}}\) represents all possible measurable events at the terminal time. \(\mathbb {E}_{\mathbb {Q}}\left[ \cdot \right] \) denotes the expectation under a probability \(\mathbb {Q}\). For the sake of simplicity, we are assuming zero interest rate.
In a one period setup we consider N agents. The individual risk (or the random endowment or the future profit and loss) plus the initial wealth of each agent is represented by the random variable \(X^{j}\in L^{0}(\Omega , {\mathcal {F}},{\mathbb {P}})\). Thus the risk vector \(X=[X^{1},\ldots ,X^{N}]\in (L^{0}(\Omega ,{\mathcal {F}},{\mathbb {P}}))^{N}\) denotes the original configuration of the system.
We assume that the system has at disposal a total amount of capital \(A\in \mathbb {R}\) to be used in case of necessity. This amount could have been assigned by the Central Bank, or could have been the result of the previous trading in the system, or could have been collected ad hoc by the agents. The amount A could represent an insurance pot or a fund collected (as guarantee for future investments) in a community of homeowners. For further interpretation of A, see also the related discussion in Section 5.2 of Biagini et al. (2020). In any case, we consider the quantity A as exogenously determined and our aim is to allocate this amount among the agents in order to optimize the overall systemic satisfaction.
In this paper we work with a multivariate utility function \(U:{\mathbb {R}} ^{N}\rightarrow {\mathbb {R}}\) that is strictly concave and strictly increasing with respect to the partial componentwise order. However, some results (see Corollary 6.2) hold also without the strict concavity or the strict monotonicity. We develop a condition on the multivariate utility U, see Definition 3.4, that will play the same role as the Inada conditions in the one dimensional case. Details and precise assumptions are deferred to Sects. 1.2 and 3. Examples of utility functions U satisfying our assumptions are collected in Sect. 7.
Systemic optimal (deterministic) initial-time allocation If we denote with \(a^{j}\in \mathbb {R}\) the cash received (if positive) or provided (if negative) by agent j at initial time, then the time T wealth at disposal of agent j will be \(X^{j}+a^{j}\). The optimal allocation \({a_{{X}}\in }\mathbb {R}^{N}\) could then be determined as the solution to the following aggregate criterion
As the vector \({a_{{X}}\in }\mathbb {R}^{N}\) is deterministic, it is known at the initial time and therefore the allocation is distributed (only) at such initial time and this is to the advantage of each agent. Indeed, if the agent j receives the fund \({a_{{X}}^{j}}\) at initial time, the agent may use this amount to prevent financial ruin of future default.
By the monotonicity of U, we may formalize the budget constraints set in the utility maximization problem (here and below) using equivalently the equality \(\sum _{j=1}^{N}a^{j}=A\) or the inequality \(\sum _{j=1}^{N}a^{j}\le A \).
Systemic optimal (random) final-time allocation We are now going to replace in \(\Pi _{A}^{\det }\) the constant vectors \({ a\in }\mathbb {R}^{N}\) with random vectors \(Y=[Y^{1},\ldots ,Y^{N}]\in (L^{0}(\Omega ,{\mathcal {F}},{\mathbb {P}}))^{N}\) representing final-time random allocations. Set
and note that each component \(Y^{j}\) of the vector \(Y\in {\mathcal {C}}_{ \mathbb {R}}\) is a random variable (measurable with respect to the sigma algebra at the terminal time), but the sum of the components is \(\,{\mathbb {P }}\)-a.s. equal to some constant in \(\mathbb {R}\). We may impose additional constraints on the vectors Y of random allocations by requiring that they belong further to a prescribed set \( {\mathcal {B}}\) of feasible allocations. It will be assumed that
and that \({\mathcal {B}}\) is translation invariant: \({\mathcal {B}}+{\mathbb {R}}^{N}= {\mathcal {B}}\). We consider a family of probability vectors \(\mathbb {Q}:=[\mathbb {Q}^{1},\ldots ,\mathbb {Q}^{N}]\in {\mathcal {Q}}_{{\mathcal {B}} ,V}\) (see (23)) associated to \({\mathcal {B}}\) and to the convex conjugate V of U, and we take \({\mathcal {L}}:=\bigcap _{{\mathbb {Q}}\in {\mathcal {Q}}_{{\mathcal {B}} ,V}}L^{1}({\mathbb {Q}})\) for \(L^{1}({{\mathbb {Q}}):=}L^{1}(\Omega ,{\mathcal {F}},{\mathbb {Q}}^{1}{ )\times \cdots \times }L^{1}(\Omega ,{\mathcal {F}},{\mathbb {Q}}^{N})\).
With these notations, a different possibility to allocate the amount A among the agents is to consider the following criterion
It is clear that \(\Pi _{A}^{\det }(X)\le \Pi _{A}^{\text {ran}}(X)\), thus random allocations realizes, as obvious, a greater systemic expected utility, as the dependence among the components \(X^{j}\) of the original risk can be taken into account by the terms \(X^{j}+Y^{j}\). The condition \( \sum _{j=1}^{N}Y^{j}=A\) is instrumental for the allocation of the amount A.
The optimization problem in (2) can be seen as the maximization of systemic utility for the allocation of the amount A over feasible allocations \(Y\in {\mathcal {B}}\), in a regulatory approach. Indeed, only the utility of the whole system is taken into account in (2), while optimality for single agents is not required. The problem (2) is similar in spirit to classical risk sharing problems (see Barrieu & Karoui, (2005)). Unlike in the classical risk sharing problems, we have a multivariate value function in place of the classical sum of univariate ones.
We observe that the “budget” constraints in \(\Pi _{A}^{\text {ran}}\) are not expressed in the classical way using expectation under some (or many) probability measures, but are instead formalized as \(\mathbb {P}-{a.s.}\) equality. Only in case \(N=1\) the problem becomes trivial, as \(\Pi _{A}^{\text {ran}}(X)=\mathbb {E}\left[ U(X+A)\right] .\)
On a technical level our first main result of this paper in the detailed study of the problem \(\Pi _{A}^{\text {ran}}.\) We first show in Theorem that \(\Pi _{A}^{\text {ran}}(X)\) can be rewritten with the budget contraint assigned by the family of probability vectors \({\mathcal {Q}}_{{\mathcal {B}} ,V}\), namely
We prove (Theorem and Corollary 4.7): (i) the existence of the optimizer \({\widehat{Y}}\in {\mathcal {L}}\) of the problem in (3); (ii) its dual formulation as a minimization problem over \({\mathcal {Q}}_{{\mathcal {B}},V}\); (iii) the existence of the optimizer \(\widehat{{\mathbb {Q}}}\in {\mathcal {Q}}_{{\mathcal {B}},V}\) of such dual formulation; (iv) that (2) and (3) have the same optimizer. Additionally, in (35) we prove that for such an optimizer \(\widehat{{\mathbb {Q}}}\) we have
We now present some more conceptual motivation for the analysis of this problem.
As stated above, \(\Pi _{A}^{\text {ran}}(X)\) is greater than \(\Pi _{A}^{\det }(X)\) and the random variables \(Y=[Y^{1},\ldots ,Y^{N}]\) in \(\Pi _{A}^{\text {ran} }(X)\) are terminal time allocations, as they are \({\mathcal {F}}\)-measurable. However, obviously one may split Y in two components
for some \(a\in \mathbb {R}^{N}\) such that \(\sum _{j=1}^{N}a^{j}=A\), which then represents an initial capital allocation \(a=(a^1,\ldots ,a^N)\) of A and a terminal time risk exchange \({\widetilde{Y}}\) satisfying \(\sum _{j=1}^{N}{\widetilde{Y}} ^{j}=0,\) as \(A=\sum _{j=1}^{N}Y^{j}=\sum _{j=1}^{N}a^{j}+\sum _{j=1}^{N} {\widetilde{Y}}^{j}=A+\sum _{j=1}^{N}{\widetilde{Y}}^{j}.\) We pose two natural questions:
-
1.
Is there an “optimal” way to select such initial capital \(a\in \mathbb {R}^{N}\) ?
-
2.
Could we discover a risk exchange equilibrium among the agents that is embedded in the problem \(\Pi _{A}^{\text {ran}}?\)
From the formulation in (4), one could conjecture that the amount \({\widehat{a}} ^{j}\) assigned as the expectation of the optimizer of \(\Pi _{A}^{\text {ran} }(X)\) under the probability \(\widehat{{\mathbb {Q}}}^{j},\) namely \({\widehat{a}} ^{j}:=\mathbb {E}_{\widehat{{\mathbb {Q}}}^{j}}[{\widehat{Y}}^{j}]\), could have a special relevance. We will show indeed that the optimal solution to the above problem \(\Pi _{A}^{\text {ran}}(X)\) coincides with a multivariate version of the Systemic Optimal Risk Transfer Equilibrium (SORTE) introduced in Biagini et al. (2021).
In order to answer these questions more precisely we need to recall the notion of a risk exchange equilibrium, as proposed by Bühlmann (1980, 1984).
1.1 Risk exchange equilibrium and systemic optimal risk transfer equilibrium
We recall that in this paper we work with a multivariate utility function but, in order to illustrate the risk exchange equilibrium and the SORTE concepts, in this subsection we assume that the preferences of each agent j are given via expected utility, by a strictly concave, increasing utility function \(u_{j}:\mathbb { R\rightarrow R}\), \(j=1,\ldots ,N.\) In this case the corresponding multivariate utility function would be \(U(x):=\sum _{j=1}^{N}u_{j}(x^j),\quad x\in {\mathbb {R}} ^{N}\). The vector \(X=(X^{1},\ldots ,X^{N})\in (L^{0}(\Omega ,{\mathcal {F}},{\mathbb {P}}))^{N}\) denotes the original risk configuration of the system (the individual risk plus the initial wealth) and each agent is an expected utility maximizer. At terminal time a reinsurance mechanism is allowed to happen, in that each agent j agrees to receive (if positive) or to provide (if negative) the amount \({\widetilde{Y}} ^{j}(\omega )\) at the final time in exchange of the amount \(\mathbb {E}_{ \mathbb {Q}^{j}}\left[ {\widetilde{Y}}^{j}\right] \) paid (if positive) or received (if negative) at the initial time, where \(\mathbb {Q}:=[\mathbb {Q} ^{1},\ldots ,\mathbb {Q}^{N}]\) is some pricing probability vector (the equilibrium price system). The reinsurance nature of this reallocation comes from the fact that the clearing condition
is required to hold, which models a terminal-time risk transfer mechanism. Integrability or boundedness conditions on \({\widetilde{Y}}^{j}\) will be added later when we rigorously formalize the setting. We use the \(\sim \) in the notation \({\widetilde{Y}}\) for the sake of consistency with the previous work (Biagini et al. 2021).
As defined in Bühlmann (1980, 1984) , a pair (\({\widetilde{Y}}_{{X}},{\mathbb {Q}}_{{X}})\) is a risk exchange equilibrium w.r.to the vector X if:
(\(\alpha \)) for each j, \({\widetilde{Y}}_{{X}}^{j}\) maximizes: \(\mathbb {E}_{{ \mathbb {P}}}\left[ u_{j}(X^{j}+{\widetilde{Y}}^{j}-\mathbb {E}_{{\mathbb {Q}}_{{X }}^{j}}[{\widetilde{Y}}^{j}])\right] \) among all r.v. \({\widetilde{Y}}^{j}\);
(\(\beta \)) \(\sum _{j=1}^{N}{\widetilde{Y}}_{{X}}^{j}=0\) \(\mathbb {P}\)-a.s.;
(\(\gamma \)) \(\mathbb {Q}_{{X}}^{1}=\cdots =\mathbb {Q}_{{X}}^{N}.\)
The optimal value in (\(\alpha \)) is denoted by
Remark 1.1
A key point of Bühlmann’s risk exchange equilibrium, which carries over to SORTE and mSORTE, is that in (\( \alpha \)) the single agent j is optimizing over all possible random variables \({\widetilde{Y}}^{j}\) and not over only those that satisfies the clearing condition (\(\beta \)). Indeed for the single myopic agent the clearing condition is irrelevant. Observe that if in (\(\alpha \)) we consider a generic probability vector \(\mathbb {Q}\), the solutions \({\widetilde{Y}}_{{X} }^{j}\) of the single N problems in (\(\alpha \)) will typically not satisfy the clearing condition (\(\beta \)). It is only the selection of the equilibrium pricing vector \({\mathbb {Q}}_{{X}}\) in (\(\alpha \)) that permits to comply with the clearing condition (\(\beta \)).
Remark 1.2
Differently from Bühlmann’s notion we will also impose that the exchange vector \({\widetilde{Y}}\) belongs to a prescribed set \({\mathcal {B}}\) of feasible allocations, as already mentioned. If there are no further constraints, i.e. \({\mathcal {B}}={\mathcal {C}}_{\mathbb {R}}\), then \(\mathbb {Q}_{{ X}}^{1}=\cdots =\mathbb {Q}_{{X}}^{N}\) holds in Bühlmann’s risk exchange equilibrium. But the presence of the constraints on \({\widetilde{Y}},\) represented by \({\mathcal {B}}\) , forces to abandon the condition (\(\gamma \)) in Bühlmann’s risk exchange equilibrium and to allow for a generic vector \(\mathbb {Q}_{X}:=[\mathbb {Q}_{X}^{1},\ldots ,\mathbb {Q }_{X}^{N}]\). Indeed, it was shown in Biagini et al. (2021) Example 1.2 that the equilibrium exists only if the components of the pricing vector \({{\mathbb {Q}}}_X\) are not all equal. Economically, multiple pricing measures may arise because the risk exchange mechanism may be restricted to clusters of agents and agents from different clusters may well adopt a different equilibrium pricing measure. This feature appears also in SORTE and mSORTE for analogous reasons.
This prompt us to define a \({\mathcal {B}}\)-risk exchange equilibrium w.r.to the vector X as a pair (\({\widetilde{Y}}_{{X}},{\mathbb {Q}}_{ {X}})\) satisfying:
(\(\alpha \)) for each j, \({\widetilde{Y}}_{{X}}^{j}\) maximizes: \(\mathbb {E}_{{ \mathbb {P}}}\left[ u_{j}(X^{j}+{\widetilde{Y}}^{j}-\mathbb {E}_{{\mathbb {Q}}_{{X }}^{j}}[{\widetilde{Y}}^{j}])\right] \) among all r.v. \({\widetilde{Y}}^{j}\);
(\(\beta \)) \(\sum _{j=1}^{N}{\widetilde{Y}}_{{X}}^{j}=0\) \(\mathbb {P}\)-a.s. and \( {\widetilde{Y}}\in {\mathcal {B}}\).
After this review of the concept of risk exchange equilibrium, we now return to our problem of allocating the amount \(A\in {\mathbb {R}}\). Observe that if \(a\mathbf {\in }\mathbb {R}^{N}\) is allocated at initial time among the agents and \(\sum _{j=1}^{N}a^{j}=A\) then the initial risk configuration of each agent becomes \((a^{j}+X^{j})\) and they may enter in a risk exchange equilibrium w.r. to such modified vector \((a+X).\)
According to Biagini et al. (2021), a triple \(({\widetilde{Y}}_{{X}},{\mathbb {Q}}_{{X} },a_{{X}})\) is a Systemic Optimal Risk Transfer Equilibrium (SORTE) with budget \(A\in {\mathbb {R}}\) if:
-
(a)
the pair (\({\widetilde{Y}}_{{X}},{\mathbb {Q}}_{{X}})\) is a \({\mathcal {B}}\) -risk exchange equilibrium w.r.to the vector \((a_X+X)\),
-
(b)
\(a_{{X}}\mathbf {\in }\mathbb {R}^{N}\) maximizes \( \sum _{j=1}^{N}V^{{\mathbb {Q}}_{{X}}^{j}}(a^{j}+X^{j})\) among all \(a\mathbf {\in }\mathbb {R}^{N}\) s.t. \( \sum _{j=1}^{N}a^{j}=A\).
Thus the optimal value in (b) equals
Observe that SORTE explains how optima can be realized conjugating optimality for the system as a whole (optimization over \(a\in {\mathbb {R}}^{N}\) in (8)) and convenience for single agents (the inner supremum in (8)). Under fairly general assumptions, existence, uniqueness and Pareto Optimality of a SORTE were proven in Biagini et al. (2021).
In this paper we propose a multivariate version of this concept, which we label with mSORTE, and prove that the optimizer \({\widehat{Y}}\) of \(\Pi _{A}^{ \text {ran}}(X)\), the optimizer \(\widehat{{\mathbb {Q}}}\) of the dual formulation of \(\Pi _{A}^{\text {ran}}(X)\), the selection \({\widehat{a}}^{j}:= \mathbb {E}_{^{\widehat{{\mathbb {Q}}}^{j}}}[{\widehat{Y}}^{j}]\) in the splitting (5) determine the (unique) mSORTE.
1.2 Multivariate systemic optimal risk transfer equilibrium
Essentially, in this paper we answer to the following question: what can we say about a concept of equilibrium similar to SORTE, with the same underlying exchange dynamics, when preferences of each agent depend on the actions of the other agents in the system? In our analysis, we consider a multivariate utility function \(U:{\mathbb {R}}^{N}\rightarrow {\mathbb {R}}\) for the system. Mildly speaking, U is a utility associated to the system as a whole. U determines the preferences of single agents in the system, who take into account the actions and choices of the others: if the random vector \(Z^{[-j]}=[Z^{1},\dots ,Z^{j-1},Z^{j+1},\dots ,Z_{N}]\) models the positions of agents \(1,\dots ,j-1,j+1,\dots ,N\), we suppose that each agent j is an expected utility maximizer, in the sense that he/she seeks \( W\mapsto \max \mathbb {E}_{\mathbb {P}}\left[ U([Z^{[-j]};W])\right] \) where \( [Z^{[-j]};W]:=\left[ Z^{1},\dots ,Z^{j-1},W,Z^{j+1},\dots ,Z^{N}\right] \). U can be thought as nontrivial aggregation of preferences of single agents: if each agent has preferences given by univariate utility functions \( u_{1},\dots ,u_{N}:{\mathbb {R}}\rightarrow {\mathbb {R}}\), then given an aggregation function \(\Gamma :{\mathbb {R}}^{N}\rightarrow {\mathbb {R}}\) which is concave and nondecreasing we can consider \(U(x)=\Gamma (u_{1}(x^{1}),\dots ,u_{N}(x^{N}))\), in the spirit of Liebrich and Svindland (2019a) Definition 4, as a natural candidate for U. Alternatively, U is a counterpart to the multivariate loss function \( \ell \) considered e.g. in Armenti et al. (2018) in the framework of Systemic Risk Measures. Just setting \(U(x)=-\ell (-x),\) \(x\in {\mathbb {R}}^{N},\) produces a natural candidate for our U starting from a loss function \(\ell \). The difference between loss functions and utility is not conceptual here, being instead just an effect of considering as positive amounts losses (as in the case of \(\ell \)) or gains (as in the case of standard utility functions). Multivariate utility functions could be employed also to describe the case of a single firm having investments in N units, where the interconnections among the N desks are relevant.
We will impose on our multivariate utility function U conditions which play the same role of Inada conditions in the univariate case. Examples of utility functions satisfying our assumptions are collected in Sect. 7. Notice that the setup and results in Biagini et al. (2021) can be recovered from the ones in this paper by setting \(U(x)=\sum _{j=1}^Nu_j(x^j),x\in {\mathbb {R}}^N\) , as described in Sect. 7.1.
In this paper we introduce and analyze the following concept. A mSORTE is a triple \(( {\widetilde{Y}}_{X},a_{X},{\mathbb {Q}}_{X})\) where:
-
\(({\widetilde{Y}}_{X},a_{X})\) solve the double optimization problem
$$\begin{aligned} \sup \left\{ \sup _{{\widetilde{Y}}}\mathbb {E}_{\mathbb {P}}\left[ U\left( a+X+ {\widetilde{Y}}-{\mathbb {E}_{{{\mathbb {Q}}}_{X}}[{\widetilde{Y}}]}\right) \right] \mid a\in {\mathbb {R}}^{N},\,\sum _{j=1}^{N}a^{j}=A\right\} ; \end{aligned}$$(9) -
the pricing vector \({\mathbb {Q}}_{X}\) is selected in such a way that the optimal solution \({\widetilde{Y}}_{X}\) belongs to the set of feasible allocations \({\mathcal {B}}\) and verifies the clearing condition (6).
We provide an example that describes one possible situation underlying the concept of mSORTE, as detailed in (9). Suppose a conglomerate runs several corporations and that one of these is in financial distress. The conglomerate may provide some capital A to support the corporation in distress. Then, the corporation has to allocate this resource among the N interconnected business lines or subsidiary companies that constitute the corporation. In this example, U is thus the objective function of the corporation, and A is the total amount that the corporation has to allocate to each company.
We are particularly interested in mSORTE since, differently from the case of SORTE (compare with (8)), here agents are taking into account other agents’ choices. Indeed, a Nash Equilibrium property (see (30)) shows how also in this more complex setup, each agent is still maximizing his/her expected utility, although other agents’ actions now appear explicitly in such utility maximization problems. As illustrated by Theorem 4.5 and its proof, the problem in (9) is intimately related to the ones already motivated and introduced (2), (3) and (4). We prove existence and uniqueness of a mSORTE. Quite remarkably, this generalization of a SORTE allows us to introduce and to study a Nash Equilibrium property for a mSORTE, as shown in Section (see Theorem 4.5). In Sect. 4.3 we provide an example of a class of exponential multivariate utility functions with the explicit computations of the mSORTE.
From a technical perspective, our results can be considered as consequences of Theorem 4.2 and Theorem 4.3. The proof of Theorem 4.2, which is the most lengthy and complex, is split in several steps and collected in Sect. 6. We use a Komlós- type argument, in contrast with the gradient approach in Biagini et al. (2021). This allows us to obtain existence of optimizers for both the primal and the dual problems without requiring differentiability of \(U(\cdot )\), which is a rather unusual result in the literature. We also remark that, differently from Biagini et al. (2021), we need to construct the dual system \((M^{\Phi },K_{\Phi })\), where \(M^{\Phi }\) is a multivariate Orlicz Heart having as topological dual space the Köthe dual \(K_{\Phi }\). Here, we denote with \(\Phi :({ \mathbb {R}}_{+})^{N}\rightarrow {\mathbb {R}}\) the multivariate Orlicz function \(\Phi (x):=U(0)-U(-x)\) associated to the multivariate utility function U. Details of this construction are provided in Sect. 2.1.
As already mentioned, this paper is a somehow natural prosecution of Biagini et al. (2021). Thus, as far as the conceptual aspects are concerned, we refer to the literature review in Biagini et al. (2021) for extended comments. Here, we limit ourselves to mentioning that Biagini et al. (2021), and so indirectly this work, originated from the systemic risk approach developed in Biagini et al. (2019), Biagini et al. (2020). For an exhaustive overview on the literature on systemic risk, see Fouque and Langsam (2013) and Hurd (2016).
Risk sharing equilibria have been studied in Borch (1962), Bühlmann (1980, 1984), Bühlmann and Jewell (1979). In Barrieu and El Karoui (2005) inf-convolution of convex risk measures has been introduced as a fundamental tool for studying risk sharing. Further developments in this direction have been obtained in Acciaio (2007), Filipović and Svindland (2008), Jouini et al. (2008), Mastrogiacomo and Rosazza Gianin (2015). Among other works on risk sharing are also Dana and Le Van (2010), Embrechts et al. (2020), Embrechts et al. (2018), Filipović and Kupper (2008), Heath and Ku (2004), Tsanakas (2009), Weber (2018). Recent further extensions have been obtained in Liebrich and Svindland (2019b). We refer to Carlier and Dana (2013), Carlier et al. (2012), for Risk sharing procedures under multivariate risks. Regarding multivariate utility functions, which have been widely exploited in the study of optimal investment under transaction costs, we cite Campi and Owen (2011), Deelstra et al. (2001), Kamizono (2004), Bouchard and Pham (2005) and references therein.
The paper is organized as follows. Section 2.1 is a short account on multivariate Orlicz spaces and on the relevant properties needed in the sequel of the paper. The multivariate utility functions used in this paper are introduced is Sect. 3, together with our setup and assumptions. The core of the paper is Section , where we formally present the key concepts and provide our main results. Section 5 collects some preliminary results on duality and utility maximization. Most of the proofs are deferred to Sect. 6. The Appendix collects some additional technical results and some of the proofs related to Sect. 2.1.
2 Preliminary notations and multivariate Orlicz spaces
Let \((\Omega ,{\mathcal {F}},{\mathbb {P}}{)}\) be a probability space and consider the following set of probability vectors on \( (\Omega ,{\mathcal {F}})\)
For a vector of probability measures \({{\mathbb {Q}}}\) we write \({{\mathbb {Q}} }\ll {\mathbb {P}}\) to denote \({\mathbb {Q}}^{1}{\ll {\mathbb {P}}},\dots ,{ \mathbb {Q}}^{N}\ll {\mathbb {P}}\). Similarly for \({{\mathbb {Q}}}\sim {\mathbb { P}}\). For \({\mathbb {Q}}\in {\mathcal {P}}^{1}\) let
be the vector spaces of (equivalence classes of) \({\mathbb {Q}}\)-a.s. finite, \({\mathbb {Q}}\)-integrable and \({\mathbb {Q}}\)-essentially bounded random variables respectively, and set \(L_{+}^{p}({\mathbb {Q}})=\left\{ Z\in L^{p}({ \mathbb {Q}})\vert Z\ge 0\,{\mathbb {Q}}-\text {a.s.}\right\} \) and \( L^{p}(\Omega ,{\mathcal {F}},{\mathbb {Q}};\mathbb {R}^{N}{)}=(L^{p}({\mathbb {Q}} ))^{N}\), for \(p\in \{0,1,\infty \}\). For \({{\mathbb {Q}}}=[{\mathbb {Q}} ^{1},\dots ,{\mathbb {Q}}^{N}]\in {\mathcal {P}}^{N}\) and \(p\in \{0,1,\infty \}\) define
and write \(\mathbb {E}_{{\mathbb {Q}}}[Z]=\left[ \mathbb {E}_{{{\mathbb {Q}}}^1}[Z^1],\dots ,\mathbb {E}_{{{\mathbb {Q}}}^N}[Z^N]\right] \) for \(Z\in L^1({{\mathbb {Q}}})\). Given a vector \(y\in {\mathbb {R}}^{N}\) and \(n\in \{1,\dots ,N\}\) we will denote by \(y^{[-n]}\) the vector in \(\mathbb {R}^{N-1}\) obtained suppressing the n-th component of y for \(N\ge 2\) (and \(y^{[-n]}=\emptyset \) if \(N=1\) ) and we set
We will write \({\mathbb {R}}_{+}:=[0,+\infty )\) and \({\mathbb {R}} _{++}:=(0,+\infty )\), \(\langle x,y\rangle =\sum _{j=1}^Nx^jy^j\) for the usual inner product of vectors \(x,y\in {\mathbb {R}}^N\). For a vector \(x\in {\mathbb { R}}^N\), \((x)^\pm \) denote the vectors of positive, negative parts respectively of the components of x. Same applies to \(\left| x\right| \).
2.1 Multivariate Orlicz spaces
Given a univariate Young function \(\phi :{\mathbb {R}}_{+}\rightarrow { \mathbb {R}}\) we can associate its conjugate function \(\phi ^{*}(y):=\sup _{x\in {\mathbb {R}_{+}}}\left( xy-\phi (x)\right) \) for \(y\in { \mathbb {R}}_{+}\). As in Rao and Ren (1991), we can associate to both \(\phi \) and \( \phi ^{*}\) the Orlicz spaces and Hearts \(L^{\phi },M^{\phi },L^{\phi ^{*}},M^{\phi ^{*}}\). For univariate utility functions, the economic motivation and the mathematical convenience of using Orlicz spaces theory in utility maximization problems were shown in Biagini and Frittelli (2008). We now introduce multivariate Orlicz functions and spaces induced by multivariate utility functions. The following definition is a slight modification of the one in Appendix B of Armenti et al. (2018).
Definition 2.1
A function \(\Phi :({\mathbb {R}} _{+})^{N}\rightarrow {\mathbb {R}}\) is said to be a multivariate Orlicz function if it is null in 0, convex, continuous, increasing in the usual partial order and satisfies: there exist \(A>0,B\) constants such that \(\Phi (x)\ge A\sum _{j=1}^{N}x^{j}-B\,\,\forall x\in ({\mathbb {R}}_{+})^{N}\).
For a given multivariate Orlicz function \(\Phi \) we define, as in Armenti et al. (2018), the Orlicz space and the Orlicz Heart respectively:
where \(\left| X\right| :=\left[ \left| X^{j}\right| \right] _{j=1}^{N}\) is the componentwise absolute value, and \(L^{0}\left( \Omega , {\mathcal {F}},{\mathbb {P}}\right) \) is the set of equivalence classes of \({{\mathbb {R}}}\)-valued \({\mathcal {F}}\)-measurable functions. We introduce the Luxemburg norm as the functional
defined on \(\left( L^{0}\left( \Omega ,{\mathcal {F}},{\mathbb {P}}\right) \right) ^{N}\) and taking values in \([0,+\infty ]\).
Lemma 2.2
Let \(\Phi \) be a multivariate Orlicz function. Then:
-
1.
the Luxemburg norm is finite on X if and only if \(X\in L^\Phi \);
-
2.
the Luxemburg norm is in fact a norm on \(L^\Phi \), which makes it a Banach space;
-
3.
\(M^\Phi \) is a vector subspace of \(L^\Phi \), closed under Luxemburg norm, and is a Banach space itself if endowed with the Luxemburg norm;
-
4.
\(L^\Phi \) is continuously embedded in \((L^1({\mathbb {P}}))^N\);
-
5.
convergence in Luxemburg norm implies convergence in probability;
-
6.
\(X\in L^\Phi \), \(\left| Y^j\right| \le \left| X^j\right| \,\forall j=1,\dots , N\) implies \(Y\in L^\Phi \), and the same holds for the Orlicz Heart. In particular \(X\in L^\Phi \) implies \(X^\pm \in L^\Phi \) and the same holds for the Orlicz Heart;
-
7.
the topology of \(\left\| \cdot \right\| _{\Phi }\) on \(M^{\Phi }\) is order continuous (see Edgar & Sucheston, (1992)) Definition 2.1.13 for the definition) with respect to the componentwise \({\mathbb {P}}\)-a.s. order and \(M^{\Phi }\) is the closure of \((L^{\infty }({\mathbb {P}}))^{N}\) in Luxemburg norm;
-
8.
\(M^{\Phi }\) and \(L^{\Phi }\) are Banach lattices if endowed with the topology induced by \(\left\| \cdot \right\| _{\Phi }\) and with the componentwise \({\mathbb {P}}\)-a.s. order.
Proof
Claims (1)–(5) follow as in Armenti et al. (2018). (6) is trivial from the definitions. As to (7), sequential order continuity is an application of Dominated Convergence Theorem, and order continuity follows from Theorem 1.1.3 in Edgar and Sucheston (1992). (8) is evident from the previous items. \(\square \)
Now we need to work a bit on duality.
Definition 2.3
The Köthe dual \(K_{\Phi }\) of the space \(L^{\Phi }\) is defined as
Proposition 2.4
\(K_{\Phi }\) can be identified with a subspace of the topological dual of \(L^{\Phi }\) and is a subset of \((L^{1}({\mathbb {P}} ))^{N} \).
Proof
See Sect. A.3. \(\square \)
By Proposition 2.4\(K_{\Phi }\) is a normed space which can be naturally endowed with the dual norm of continuous linear functionals, which we will denote by
This norm will play here the role of the Orlicz norm, and the relation between the two norms \(\left\| \cdot \right\| _\Phi \) and \(\left\| \cdot \right\| _\Phi ^*\) is well understood in the univariate case (see Theorem 2.2.9 in Edgar and Sucheston (1992)). The following Proposition summarizes useful properties which show how the Köthe dual can play the role of the Orlicz space \(L^{\Phi ^{*}}\) for \(M^{\Phi }\) in univariate theory, and are the counterparts to Corollary 2.2.10 in Edgar and Sucheston (1992).
Proposition 2.5
The following hold:
-
1.
\(K_{\Phi }=\left\{ Z\in \left( L^{0}\left( \Omega ,{\mathcal {F}},{\mathbb {P}}\right) \right) ^{N} \mid \sum _{j=1}^{N}X^{j}Z^{j}\in L^{1}({\mathbb {P}}),\,\forall \,X\in M^{\Phi }\right\} \,;\)
-
2.
the topological dual of \((M^{\Phi },\left\| \cdot \right\| _{\Phi })\) is \((K_{\Phi },\left\| \cdot \right\| _{\Phi }^{*})\);
-
3.
suppose \(L^{\Phi }=L^{\Phi _{1}}\times \dots \times L^{\Phi _{N}}\) for univariate Young functions \({\Phi _{1}},\dots ,{\Phi _{N}}\). Then we have that \(K_{\Phi }=L^{\Phi _{1}^{*}}\times \dots \times L^{\Phi _{N}^{*}}\) .
Proof
See Sect. A.3. \(\square \)
We now provide an example connecting the multivariate theory to the univariate classical one.
Remark 2.6
Even thought we will not make this assumption in the rest of the paper, suppose in this Remark that \(\Phi (x)=\sum _{j=1}^{N}\Phi _{j}(x^{j})\) for univariate Orlicz functions, that is each separately satisfying Definition 2.1 for \(N=1\). Then we could consider the multivariate spaces \(L^{\Phi }\) and \(M^{\Phi }\) as above or we could take \(L^{\Phi _{1}}\times \dots \times L^{\Phi _{N}}\) and \(M^{\Phi _{1}}\times \dots \times M^{\Phi _{N}}\).
As shown in Sect. A.3, the following identity between sets holds:
and furthermore
Observe that in the setup of this Remark, from Proposition 2.5 Item 3, we have
3 Setup and assumptions
Definition 3.1
We say that \(U:{\mathbb {R}}^{N}\rightarrow { \mathbb {R}}\) is a multivariate utility function if it is strictly concave and strictly increasing with respect to the partial componentwise order. When \(N=1\) we will use the term univariate utility function instead. For a multivariate utility function U we define the convex conjugate in the usual way by
Observe that by definition \(U(x)\le \left\langle x,y\right\rangle +V(y)\) for every \(x,y\in {\mathbb {R}}^{N}\), and \(V(\cdot )\ge U(0)\) that is V is lower bounded.
Definition 3.2
For a multivariate utility function U, we define the function \(\Phi \) on \(( {\mathbb {R}}_{+})^{N}\) by
Remark 3.3
The well known Inada conditions, for (one-dimensional) concave increasing utility functions \(u:{\mathbb {R}} \rightarrow {\mathbb {R}}\), have an evident economic significance and are very often assumed to hold true in order to solve utility maximization problems.
As it is easy to check, they can be equivalently rewritten as:
Consider now the condition weaker than Inada\((-\infty )\):
One can again easily check that the two conditions (14) and (15) are equivalent to the following single statement: there exists an Orlicz function \({\widehat{\Phi }}:{\mathbb {R}}_{+}\rightarrow {\mathbb {R}}\) and a function \(f:{\mathbb {R}}_{+}\rightarrow {\mathbb {R}}\) such that
Motivated by the above remark, we now introduce a condition that will replace (16) in the multivariate case and will play the same role as the Inada in the one dimensional case.
Definition 3.4
We say that a multivariate utility function \(U:{ \mathbb {R}}^{N}\rightarrow {\mathbb {R}}\) is well controlled if there exist a multivariate Orlicz function \({\widehat{\Phi }}:{\mathbb {R}} _{+}^{N}\rightarrow {\mathbb {R}}\) and a function \(f:{\mathbb {R}} _{+}\rightarrow {\mathbb {R}}\) such that
Lemma 3.5
Suppose that the multivariate utility function U is well controlled. Then:
-
(i)
the function \(\Phi (x)=U(0)-U(-x),\) \(x\in {\mathbb {R}}_{+}^{N},\) defines a multivariate Orlicz function;
-
(ii)
\(L^{\Phi }\subseteq L^{{\widehat{\Phi }}}\);
-
(iii)
for every \(\varepsilon >0\) small enough there exist a constant \( b_{\varepsilon }\) such that
$$\begin{aligned} U(x)\le \varepsilon \sum _{j=1}^{N}(x^{j})^{+}+b_{\varepsilon }\,\,\,\,\,\forall x\in {\mathbb {R}}^{N}; \end{aligned}$$(18) -
(iv)
there exist \(a>0\), \(b\in {\mathbb {R}}\) such that
$$\begin{aligned} U(x)\le a\sum _{j=1}^{N}(x^{j})^{+}-2a\sum _{j=1}^{N}(x^{j})^{-}+b\,\,\,\,\,\forall \,x\in {\mathbb {R}}^{N}. \end{aligned}$$(19)
Proof
Recall that by Definition 2.1 there exist \(A>0,B\in { \mathbb {R}}\) such that \({\widehat{\Phi }}((x)^{-})\ge A\sum _{j=1}^{N}(x^{j})^{-}-B\). Therefore, if U is well controlled then
-
(i)
: It is enough to show the existence of \(A_{\Phi }>0\), \(B_{\Phi }\in { \mathbb {R}}\) such that \(\Phi (x)\ge A_{\Phi }\sum _{j=1}^{N}x^{j}-B_{\Phi }\,\forall x\in {\mathbb {R}}_{+}^{N}\). For any \(x\in {\mathbb {R}}_{+}^{N}\), using (20) with \(\varepsilon =\frac{A}{2},\) we obtain
$$\begin{aligned} U(-x)\le -A\sum _{j=1}^{N}x^{j}+B+\frac{A}{2}\sum _{j=1}^{N}x^{j}+f\left( \frac{A}{2}\right) =-\frac{A}{2}\sum _{j=1}^{N}x^{j}+\left( B+f\left( \frac{A }{2}\right) \right) , \end{aligned}$$and the desired inequality follows letting \(A_{\Phi }:=\frac{A}{2}\) and \( B_{\Phi }:=-\left( U(0)-f\left( \frac{A}{2}\right) -B\right) .\)
-
(ii)
: From (17) one can easily see that \( \Phi (x)\ge {\widehat{\Phi }}(x)-\varepsilon \sum _{j=1}^Nx^j+\text {constant}\) for all \(x\in ({\mathbb {R}}_+)^N\). The claim then follows recalling that \( X\in L^\Phi \Rightarrow X\in (L^1({\mathbb {P}}))^N\) by Lemma 2.2 Item 4.
-
(iii)
: Follows from (20) if \(\varepsilon <A\) and \( b_{\varepsilon }:=B+f(\varepsilon ).\)
-
(iv)
: Follows with \(a=\frac{A}{3},\) \(b=B+f(\frac{A}{3})\) choosing \( \varepsilon =\frac{A}{3}\) in (20).
\(\square \)
Remark 3.6
In the proofs in multivariate setting, the inequalities (18) and (19) will play the same role that respectively (14) and (15) have in the unidimensional case. In Proposition we use the aforementioned univariate Inada conditions to make sure that (17) holds when U has a particular form.
We observe that the inclusion \(L^{{\widehat{\Phi }}}\subseteq L^{\Phi }\), opposite of (ii), is a simple integrability requirement, which can be rephrased as: if for \(X\in (L^{0}\left( (\Omega ,{\mathcal {F}},{\mathbb {P}} );[-\infty ,+\infty ]\right) )^{N}\) there exist \(\lambda >0\) such that \( \mathbb {E}_{\mathbb {P}}\left[ {\widehat{\Phi }}(-\lambda \left| X\right| ) \right] >-\infty \), then there exists \(\alpha >0\) such that \( \mathbb {E}_{\mathbb {P}}\left[ U(-\alpha \left| X\right| )\right] >-\infty \). This request is rather weak and there are many examples of choices of U that guarantee this condition is met (see Section 7). Without further mention, the following two standing assumptions hold true throughout the paper.
StandingAssumptionI
The function \(U:{\mathbb {R}}^{N}\rightarrow {\mathbb {R}}\) is a multivariate utility function which is well controlled (Definition ) and such that for \({\widehat{\Phi }}\) in (17)
StandingAssumptionII
\({\mathcal {B}}\subseteq {\mathcal {C}}_{{\mathbb {R}}}\) is a convex cone, closed in probability, \(0\in {\mathcal {B}}\), \({\mathbb {R}}^{N}+{\mathcal {B}}={\mathcal {B}} \). The vector X belongs to the Orlicz Heart \(M^{\Phi }.\)
Observe that the Standing Assumption II implies that all constant vectors belong to \({\mathcal {B}}\), so that all (deterministic) vector in the form \( e^{i}-e^{j}\) (differences of elements in the canonical base of \({\mathbb {R}} ^{N}\)) belong to \({\mathcal {B}}\cap M^{\Phi }\). We recall the following concept, introduced in Biagini et al. (2020) Definition 5.15, that was already used in Biagini et al. (2021).
Definition 3.7
\({\mathcal {B}}\) is closed under truncation if for each \(Y\in {\mathcal {B}}\) there exists \(m_{Y}\in \mathbb {N}\) and \( c_{Y}\in {\mathbb {R}}^{N}\) such that \(\sum _{j=1}^{N}Y^{j}= \sum _{j=1}^{N}c_{Y}^{j}\) and for all \(m\ge m_{Y}\)
Assumption 3.8
\({\mathcal {B}}\) is closed under truncation.
As pointed out in Biagini et al. (2020), \({\mathcal {B}}={\mathcal {C}}_{\mathbb {R}}\) is closed under truncation. Closedness under truncation property holds true for a rather wide class of constraints. For a more detailed explanation and examples, see also Biagini et al. (2021) Example 3.17 and Example 4.20. We will also need the following additional notation.
-
1.
For any \(A\in {\mathbb {R}}\) we consider the set of feasible random allocations
$$\begin{aligned} {\mathcal {B}}_{A}:={\mathcal {B}}\cap \left\{ Y\in (L^{0}({\mathbb {P}}))^{N}\mid \sum _{j=1}^{N}Y^{j}\le A\right\} \subseteq {\mathcal {C}}_{\mathbb {R}}\,. \end{aligned}$$ -
2.
\({\mathcal {Q}}\) is the set of vectors of probability measures \({\mathbb { Q}}=[{\mathbb {Q}}^{1},\dots ,{\mathbb {Q}}^{N}]\), with \({\mathbb {Q}}^{j}\ll { \mathbb {P}}\,\) \(\forall \,j=1,\dots ,N\), defined by
$$\begin{aligned} {\mathcal {Q}}:=\left\{ {\mathbb {Q}}\mid \left[ \frac{\mathrm {d}{\mathbb {Q}}^{1} }{\mathrm {d}{\mathbb {P}}},\dots ,\frac{\mathrm {d}{\mathbb {Q}}^{N}}{\mathrm {d}{ \mathbb {P}}}\right] \in K_{\Phi },\,\sum _{j=1}^{N}\mathbb {E}_{\mathbb {Q}^{j}} \left[ Y^{j}\right] \le 0\,\text {\ }\forall \,Y\in {\mathcal {B}}_{0}\cap M^{\Phi }\right\} \,. \end{aligned}$$(22)Identifying Radon–Nikodym derivatives and measures in the natural way, this can be rephrased as: \({\mathcal {Q}}\) is the set of normalized (i.e. with componentwise expectations equal to 1), non negative vectors in the polar of \({\mathcal {B}}_{0}\cap M^{\Phi }\), in the dual system \((M^{\Phi },K_{\Phi }) \). Observe that \(M^{\Phi }\subseteq L^{1}({\mathbb {Q}})\) for all \({ \mathbb {Q\in }}{\mathcal {Q}}\) and that \({\mathcal {Q}}\) depends on the set \( {\mathcal {B}}\).
-
3.
In the definition of mSORTE we will adopt the subset \({\mathcal {Q}}_{{\mathcal {B}},V}\subseteq {\mathcal {Q}}\) of vectors of probability measures having “finite entropy”
$$\begin{aligned} {\mathcal {Q}}_{{\mathcal {B}},V}:=\left\{ {\mathbb {Q}}\in {\mathcal {Q}}\mid \mathbb { E}_{\mathbb {P}}\left[ V\left( \lambda \frac{\mathrm {d}{\mathbb {Q}}}{\mathrm {d }{\mathbb {P}}}\right) \right] <+\infty \text { for some }\lambda >0\right\} \end{aligned}$$(23)and the set \({\mathcal {L}}\) of the random allocations satisfying the integrability requirements defined by
$$\begin{aligned} {\mathcal {L}}:=\bigcap _{{\mathbb {Q}}\in {\mathcal {Q}}_{{\mathcal {B}},V}}L^{1}({ \mathbb {Q}})={\mathcal {L}}^{1}\times \dots \times {\mathcal {L}}^{N}\,. \end{aligned}$$(24)Here \({\mathcal {L}}^{j}:=\left\{ Y^{j}\in L^{1}({\mathbb {Q}}^{j})\,\forall { \mathbb {Q=[{\mathbb {Q}}}}^{1},\ldots ,{\mathbb {{\mathbb {Q}}}}^{N}{\mathbb {]\in }} {\mathcal {Q}}_{{\mathcal {B}},V}\right\} .\)
4 Multivariate systemic optimal risk transfer equilibrium
4.1 Main concept
We now provide the formal definition of the concept already illustrated in the Introduction (see Eq. 9). It is the natural generalization of SORTE as introduced in Biagini et al. (2021) Definition 3.7.
Definition 4.1
The triple \(({\widetilde{Y}}_{X},{\mathbb {Q}}_{X},a_X)\in {\mathcal {L}}\mathbf {\times }{\mathcal {Q}}_{{\mathcal {B}},V}\mathbf {\times }\mathbb {R}^{N}\) is a Multivariate Systemic Optimal Risk Transfer Equilibrium (mSORTE) with budget \(A\in {\mathbb {R}}\) if
-
1.
\(({\widetilde{Y}}_{X},a_{X})\) is an optimum for
$$\begin{aligned} \sup \left\{ \sup \left\{ \mathbb {E}_{\mathbb {P}}\left[ U(a+X+{\widetilde{Y}}-\mathbb {E}_{{{\mathbb {Q}}}_X}[{\widetilde{Y}}])\right] \mid {\widetilde{Y}}\in \mathcal {L }\right\} \mid a\in {\mathbb {R}}^{N} \sum _{j=1}^{N}a_{j}=A\right\} \,; \end{aligned}$$ -
2.
\({\widetilde{Y}}_{X}\in {\mathcal {B}}\) and \(\sum _{j=1}^{N}{\widetilde{Y}}_{X}^{j}=0\,\, {\mathbb {P}}\) -a.s..
4.2 Main results
We provide sufficient conditions for existence, uniqueness and the Nash Equilibrium property of a mSORTE, see Theorems 4.5 and 4.6 . Such results are relatively simple consequences of the following key duality Theorem , whose proof in Sect. 6 will involve several steps. As demonstrated in Sect. 6.1, Theorems 4.2, 4.5 and 6.1 below also hold true if Assumption 3.8 is replaced with an assumption on the utility function U.
Theorem 4.2
Under Assumption 3.8 the following holds:
Moreover
-
1.
there exists an optimum \({\widehat{Y}}\in {\mathcal {L}}\) to the problem in (25). Such an optimum satisfies \({\widehat{Y}} \in {\mathcal {B}}_{A}\cap {\mathcal {L}}\) and for any optimum \(({\widehat{\lambda }} ,\widehat{{\mathbb {Q}}})\) of (26) the following holds:
$$\begin{aligned} \sum _{j=1}^{N}\mathbb {E}_{\widehat{{\mathbb {Q}}}^{j}}[{\widehat{Y}} ^{j}]=A=\sum _{j=1}^{N}{\widehat{Y}}^{j},\quad {\mathbb {P}}-{a.s.}; \end{aligned}$$(27) -
2.
any optimum \(({\widehat{\lambda }},\widehat{{\mathbb {Q}}})\) of (26) satisfies \({\widehat{\lambda }}>0\) and \( \widehat{{\mathbb {Q}}}\sim {\mathbb {P}}\);
-
3.
there exists a unique optimum to (25). If U is additionally differentiable, there exists a unique optimum \(( {\widehat{\lambda }},\widehat{{\mathbb {Q}}})\) of (26).
Proof
The case \(A=0\) is covered in Theorem 6.1 and Corollary 6.8, the latter only proving the equality following (26). In Section we then explain how we can apply also to \(A\ne 0\) the same arguments used for \(A=0\). \(\square \)
The following result is the counterpart to Theorem 4.2, once a vector \({\mathbb {Q}}\in {\mathcal {Q}}_{{\mathcal {B}},V}\) is fixed, and will be applied in Theorem 4.6.
Theorem 4.3
Under Assumption 3.8, for every \({ \mathbb {Q}}\in {\mathcal {Q}}_{{\mathcal {B}},V}\) and \(A\in {\mathbb {R}}\) the following holds:
Proof
Consider first \(A=0\). By Eqs. (61) and (62)
Observing that \(M^{\Phi }\subseteq {\mathcal {L}}\subseteq L^{1}({\mathbb {Q}})\) , we have
by Remark 4.4 below. The case \(A=0\) is then proved. The case \( A\ne 0\), instead, follows from Sect. 6.3. \(\square \)
Remark 4.4
From the definition of V we obtain the Fenchel inequality
Recall that \(M^{\Phi }\subseteq L^{1}({\mathbb {Q}})\) for all \({\mathbb {Q\in } }{\mathcal {Q}}.\) For all \(X\in M^{\Phi }\), for all \({\mathbb {Q\in }}{\mathcal {Q}} \) and Y such that \(\sum _{j=1}^{N}\mathbb {E}_{\mathbb {Q}^{j}}\left[ Y^{j} \right] \le A\) we then have:
and the last expression is finite if \({\mathbb {Q\in }}{\mathcal {Q}}_{{\mathcal {B}},V}.\)
On the existence of a mSORTE and Nash Equilibrium
Theorem 4.5
Under Assumption 3.8 a Multivariate Systemic Optimal Risk Transfer Equilibrium \(({\widetilde{Y}}_X,{\mathbb {Q}_X}, a_X)\in {\mathcal {L}}\times {\mathcal {Q}}_{{\mathcal {B}},V}\times {\mathbb {R}}^{N}\) exists, with \(\mathbb {E}_{{{\mathbb {Q}}}^j_X}[{\widetilde{Y}}^j_X]=0\) for every \(j=1,\dots ,N\). Furthermore, the following Nash Equilibrium property holds for any mSORTE \(({\widetilde{Y}}_X,{\mathbb {Q}_X}, a_X)\): for every \(j=1,\dots ,N\)
where \({\mathcal {L}}^j=\bigcap _{{{\mathbb {Q}}}\in {\mathcal {Q}}_{{\mathcal {B}},V}}L^1({{\mathbb {Q}}}^j)\), and
Proof
Take \({\widehat{Y}}\) as in Theorem 4.2 Item 1, \(\widehat{{\mathbb {Q}}}\) an optimizer of (26), and set \({\widehat{a}}^{j}:=\mathbb {E}_{ \widehat{{\mathbb {Q}}}^{j}}[{\widehat{Y}}^{j}]\), \(j=1,\dots ,N,\). Then, from (25) and (26),
where the second last equation is a simple reformulation of (31). By Item 1 of Theorem 4.2, the optimizer \({\widehat{Y}} \in {\mathcal {L}}\) satisfies the constraints of the problem in (31), and by (27) \(({\widehat{Y}},{\widehat{a}})\) yields an optimum for the problem in (32). By Lemma A.2, setting \(a_X:={\widehat{a}}\in {{\mathbb {R}}}^N\), \({\widetilde{Y}}_X={\widehat{Y}}-a_X\in {\mathcal {L}}\), \({{\mathbb {Q}}}_X={\widehat{{{\mathbb {Q}}}}}\) we have that \(({\widetilde{Y}}_X,{\widehat{a}})\) satisfies Item 1 in Definition 4.1. Observe also that \({\widehat{Y}}\in {\mathcal {B}}\Rightarrow {\widetilde{Y}}_X\in {\mathcal {B}}\) since \({\mathcal {B}}+\mathbb {R}^N={\mathcal {B}}\), and that \(\sum _{j=1}^N{\widetilde{Y}}_X^j=\sum _{j=1}^N{\widehat{Y}}^j-\sum _{j=1}^Na^j=A-A=0\), so that also Item 2 in Definition 4.1 is satisfied. Also, by its very definition \(\mathbb {E}_{{{\mathbb {Q}}}^j_X}[{\widetilde{Y}}^j_X]=\mathbb {E}_{{\widehat{{{\mathbb {Q}}}}}^j}[{\widehat{Y}}^j]-\mathbb {E}_{{\widehat{{{\mathbb {Q}}}}}^j}[{\widehat{Y}}^j]=0\).
Let finally \((Y_{X},{\mathbb {Q}}_{X},a_X)\in {\mathcal {L}}\mathbf {\times }{\mathcal {Q}}_{{\mathcal {B}},V} \mathbf {\times }\mathbb {R}^{N}\) be a mSORTE as in Definition 4.1. We prove the Nash Equilibrium property (30). For any \(Z\in {\mathcal {L}}^{j}\), using Item 1 of Definition 4.1
\(\square \)
On uniqueness of a mSORTE
Theorem 4.6
Under Assumption 3.8, suppose additionally that U is differentiable. Then there exists a unique mSORTE \(({\widetilde{Y}}_X,{\mathbb {Q}_X}, a_X)\) with \(\mathbb {E}_{{{\mathbb {Q}}}^j_X}[{\widetilde{Y}}^j_X]=0\) for every \(j=1,\dots ,N\).
Proof
Take a mSORTE \(({\widetilde{Y}}_X,{\mathbb {Q}_X}, a_X)\) with \(\mathbb {E}_{{{\mathbb {Q}}}^j_X}[{\widetilde{Y}}^j_X]=0\) for every \(j=1,\dots ,N\). Set \({\widehat{Y}}:={\widetilde{Y}}_X+a_X-\mathbb {E}_{{{\mathbb {Q}}}_X}[{\widetilde{Y}}_X]={\widetilde{Y}}_X+a_X\). We claim that \({\widehat{Y}}\) is an optimizer of (25) and \({{\mathbb {Q}}}_X\) is an optimizer of (26). Observe that \({\widehat{Y}}\in {\mathcal {B}} _{A}\cap {\mathcal {L}}\) (using \({\mathcal {B}}+{{\mathbb {R}}}^N={\mathcal {B}}\) and \(\sum _{j=1}^N{\widehat{Y}}^j=\sum _{j=1}^N{\widetilde{Y}}^j_X+\sum _{j=1}^Na^j_X-\sum _{j=1}^N\mathbb {E}_{{{\mathbb {Q}}}^j_X}[{\widetilde{Y}}^j_X]=0+A-0\)) and \({{\mathbb {Q}_X}}\in {\mathcal {Q}}_{{\mathcal {B}},V}.\) Since \({\widehat{Y}}\in {\mathcal {B}} _{A}\cap {\mathcal {L}}\) and we are assuming that the set \({\mathcal {B}}\) is closed under truncation, by Lemma A.1 we have that \(\sum _{j=1}^N\mathbb {E}_{\mathbb {Q} ^j} \left[ {\widehat{Y}}^j\right] \le A\) for all \({\mathbb {Q}}\in {\mathcal {Q}}_{{\mathcal {B}},V}\). As \({{\mathbb {Q}_X}}\in {\mathcal {Q}}_{{\mathcal {B}},V}\), we then obtain
where (34) is a consequence of Fenchel inequality (29), the expression in (35) is a reformulation of the one in the previous line, (36) follows from Lemma A.2 and (37) holds true because\(({\widetilde{Y}}_X,{\mathbb {Q}_X}, a_X)\) is a mSORTE and therefore \(({\widetilde{Y}}_X, a_X)\) is an optimizer of the problem in (36). Notice that Theorem 4.3 guarantees that the \(\inf \) in (34) is a \(\min \). We then deduce that all above inequalities are equalities and \( {\widehat{Y}}\) is an optimizer of (25) and \( {{\mathbb {Q}}_X}\) is an optimizer of (26). Now, take another mSORTE \(({\widetilde{Z}}_X,\mathbb {D}_X,b_X)\) with \(\mathbb {E}_{\mathbb {D}^j_X}[{\widetilde{Z}}^j_X]=0\) for every \(j=0,\dots ,N\). Arguing exactly as above for \({\widehat{Z}}:={\widetilde{Z}}_X+b_X\) we get that \( {\widehat{Z}}\) is an optimizer of (25) and \(\mathbb {D}_X\) is an optimizer of (26). Theorem 4.2 Item 3 yields \({\widehat{Z}}={\widehat{Y}}\) and \({{\mathbb {Q}}}_X=\mathbb {D}_X\). Taking expectations componentwise we get that \(b_X^j=\mathbb {E}_{\mathbb {D}^j_X}[{\widehat{Z}}^j]=\mathbb {E}_{{{\mathbb {Q}}}^j_X}[{\widehat{Y}}^j]=a^j_X\) for every \(j=1,\dots ,N\), which yields \(a_X=b_X\). Finally, from the definitions of \({\widehat{Z}},{\widehat{Y}}\) we get \({\widetilde{Z}}_X={\widetilde{Y}}_X\).
\(\square \)
Corollary 4.7
Under Assumption 3.8 and if U is differentiable there exists a unique optimum \({\widehat{Y}}\) for the problem \(\Pi _{A}^{\mathrm {ran}}(X)\) in (2). Such an optimum is given by \({\widehat{Y}}={\widetilde{Y}}_X+a_X\), where \(({\widetilde{Y}}_X,{\mathbb {Q}_X}, a_X)\) is the unique mSORTE with \(\mathbb {E}_{{{\mathbb {Q}}}^j_X}[{\widetilde{Y}}^j_X]=0\) for every \(j=1,\dots ,N\) and budget A.
Proof
Take \({\widehat{Y}}={\widetilde{Y}}_X+a_X\) for \(({\widetilde{Y}}_X,{\mathbb {Q}_X}, a_X)\) as described in the statement (Theorems 4.2 and 4.6 ). By Lemma A.1, \(\Pi _{A}^{\mathrm {ran}}(X)\le \) (25). Since \({\widehat{Y}}\in {\mathcal {L}}\cap \mathcal { B}_A\) is an optimum for (25) (see the proof of Theorem 4.6), existence follows. Uniqueness is a consequence of strict concavity of U, by standard arguments. The arguments above also show automatically the link between the unique optimum for \(\Pi _{A}^{\mathrm {ran}}(X)\) and the unique mSORTE for the budget A. \(\square \)
4.3 Explicit computation in an exponential framework
With a particular choice of the utility function U (see (38) below) we can explicitly compute primal (\({\widehat{Y}}\)) and dual (\({\widehat{{{\mathbb {Q}}}}}\)) optima in Theorem 4.2. Consequently, the (unique) mSORTE can be explicitly computed. Recall from the proof of Theorem 4.5 that the mSORTE is produced by setting \({a}_X^{j}:=\mathbb {E}_{ \widehat{{\mathbb {Q}}}^{j}}[{\widehat{Y}}^{j}]\), \({\widetilde{Y}}_X={\widehat{Y}}-a_X\), \({{\mathbb {Q}}}_X={\widehat{{{\mathbb {Q}}}}}\). As we are able to find explicit formulas, we prefer to anticipate this example even if the proof of Proposition 4.8 relies on two propositions in Sect. 7.
Proposition 4.8
Take \(\alpha _1,\dots ,\alpha _N>0\) and consider for \(x=[x^1,\dots ,x^N]\in {{\mathbb {R}}}^N\)
Select \({\mathcal {B}}={\mathcal {C}}_{{\mathbb {R}}}\) and define
Then the dual optimum in (26) is given by
and the primal optimum \({\widehat{Y}}\) in \(\sup \limits _{Y\in {\mathcal {B}}_{A}\cap M^{\Phi }}\mathbb {E}_{\mathbb {P}}\left[ U(X+Y) \right] \) is given by
Proof
To begin with, one can easily check that the assumptions of Propositions 7.1 and 7.3 are satisfied, and so is then Standing Assumption I. Standing Assumption II is trivially satisfied, once we take \(X\in M^\Phi \). Also, \(U(x)=\frac{N^2}{2}-\frac{1}{2}\left( \sum _{j=1}^N e^{-\alpha _j x^j}\right) ^2\). The conjugate V, as well as its gradient, are computed explicitly in Lemma A.4.
Our aim is to show that primal and dual optima, whose existence and uniqueness are stated in Theorem 4.2 Item 2 and 3, are given by \({\widehat{Y}}^j:=-X^j-\frac{\partial V}{\partial w^j}\left( {\widehat{\lambda }}_X\frac{\mathrm {d}{\widehat{{{\mathbb {Q}}}}}}{\mathrm {d}{{\mathbb {P}}}},\dots ,{\widehat{\lambda }}_X\frac{\mathrm {d}{\widehat{{{\mathbb {Q}}}}}}{\mathrm {d}{{\mathbb {P}}}}\right) \) and \(\left( {\widehat{\lambda }}_X,\left[ \frac{\mathrm {d}{\widehat{{{\mathbb {Q}}}}}}{\mathrm {d}{{\mathbb {P}}}},\dots ,\frac{\mathrm {d}{\widehat{{{\mathbb {Q}}}}}}{\mathrm {d}{{\mathbb {P}}}}\right] \right) \in (0,+\infty )\times {\mathcal {Q}}_{{\mathcal {B}},V}\), for \({\widehat{\lambda }}_X\) and \({\widehat{{{\mathbb {Q}}}}}\) given in (41) and (39) respectively. By direct computation one can then check that \({{\mathbb {P}}}\sim [{\widehat{{{\mathbb {Q}}}}},\dots ,{\widehat{{{\mathbb {Q}}}}}]\in {\mathcal {Q}}_{{\mathcal {B}},V}\) and \({\widehat{Y}}\in M^\Phi \) whenever \(X\in M^\Phi \), where in view of Propositions 7.1 and 7.3 we have \(M^\Phi =M^{\exp }\times \dots \times M^{\exp }\) for
Recall now that \(U(-\nabla V (w))=V(w)-\sum _{j=1}^Nw^j\frac{\partial V}{\partial w^j}(w)\) for every \(w\in (0,+\infty )^N\) (see Rockafellar (1970) Chapter V). Then, given (81), we can write
for \(\frac{\mathrm {d}{\widehat{{{\mathbb {Q}}}}}}{\mathrm {d}{{\mathbb {P}}}}\) and \({\widehat{\lambda }}_X\) given in (39) and (41) respectively. In view of Theorem 4.2 primal and dual optimality then follow, once we check that \({\widehat{Y}}\in {\mathcal {B}}_A\cap M^\Phi \). Given \({\widehat{{{\mathbb {Q}}}}}\) and \({\widehat{\lambda }}_X\), \({\widehat{Y}}\) can be directly computed as (40) and we can check that \(\sum _{j=1}^N {\widehat{Y}}^j=A\), which completes the proof. \(\square \)
Remark 4.9
The key point in the proof of Proposition 4.8 above was guessing the particular form of \({\widehat{{{\mathbb {Q}}}}}\). Such a guess is a consequence of imposing \(\sum _{j=1}^N{\widehat{Y}}^j=A\) for the candidate optimum \({\widehat{Y}}\). Indeed, imposing that \(\sum _{j=1}^N{\widehat{Y}}^j=A\) for \({\widehat{Y}}^j:=-X^j-\frac{\partial V}{\partial w^j}\left( {\widehat{\lambda }}\frac{\mathrm {d}{\widehat{{{\mathbb {Q}}}}}}{\mathrm {d}{{\mathbb {P}}}},\dots ,{\widehat{\lambda }}\frac{\mathrm {d}{\widehat{{{\mathbb {Q}}}}}}{\mathrm {d}{{\mathbb {P}}}}\right) \) (\({\widehat{\lambda }}>0\) is a constant, yet to be found precisely at this initial stage), we get that for some \(\eta \in {{\mathbb {R}}}\)
Here, we also used the explicit formula (80) for the gradient of V. This computation implies that \({\widehat{{{\mathbb {Q}}}}}\) needs to satisfy (39).
4.4 Dependence on X of mSORTE
We study here the dependence of mSORTE on the initial data X. We recall that both existence and uniqueness are guaranteed (see Theorems 4.5 and 4.6).
Proposition 4.10
Under the same assumptions of Theorem 4.6 and for \({\mathcal {B}}={\mathcal {C}}_{\mathbb {R}}\), given the unique mSORTE \(({\widetilde{Y}}_X,{\mathbb {Q}_X}, a_X)\) with \(\mathbb {E}_{{{\mathbb {Q}}}^j_X}[{\widetilde{Y}}^j_X]=0\) for every \(j=1,\dots ,N\), the variables \(\frac{\mathrm {d}{{{\mathbb {Q}}}_X}}{\mathrm {d}{\mathbb {P}}}\) and \(X+a_X+{\widetilde{Y}}_X\) are \(\sigma (X^{1}+\dots +X^{N})\) (essentially) measurable.
Proof
By Theorem 4.6 there exists a unique mSORTE. Recall the proof of Theorem 4.5, where we showed that the optimizers \(({\widehat{Y}},\widehat{{\mathbb {Q}}})\) in Theorem 4.2, together with \({\widehat{a}}^{j}:=\mathbb {E}_{ \widehat{{\mathbb {Q}}}^{j}}[{\widehat{Y}}^{j}]\), \(j=1,\dots ,N,\) yield the mSORTE via \(a_X={\widehat{a}}\), \({{\mathbb {Q}}}_X={\widehat{{{\mathbb {Q}}}}}\), \({\widetilde{Y}}_X={\widehat{Y}}-{\widehat{a}}\). Notice that in this specific case \(Y:={e_{i}}1_{A}-{e_{j}}1_{A}\in {\mathcal {B}}\cap M^{\Phi }\) for all i, j. The same argument used in the proof of Biagini et al. (2021) Proposition 4.18 can be then applied with obvious minor modifications (i.e. using \(V(\cdot )\) in place of \(\sum _{j=1}^Nv_j( \cdot )\) and taking any \({\mathbb {Q}}\in {\mathcal {Q}}_{{\mathcal {B}},V}\)) to show that \(\frac{ \mathrm {d}\widehat{{\mathbb {Q}}}}{\mathrm {d}{\mathbb {P}}}\) is \({\mathcal {G}} :=\sigma (X^1+\dots +X^N)\)-(essentially) measurable. We stress the fact that, similarly to Biagini et al. (2021) Proposition 4.18, all the components of any \({ \mathbb {Q}}\in {\mathcal {Q}}_{{\mathcal {B}},V}\) are equal.
We now focus on \(X+{\widehat{Y}}\): consider \({\widehat{Z}}:=\mathbb {E}_\mathbb {P} \left[ X+{\widehat{Y}}\mid {\mathcal {G}}\right] -X\) (the conditional expectation is taken componentwise). Then it is easy to check that \(\sum _{j=1}^N{\widehat{Z}} ^j=\sum _{j=1}^N {\widehat{Y}}^j=A\) which yields \({\widehat{Z}}\in {\mathcal {B}}_A\). We now prove that \({\widehat{Z}}\in {\mathcal {L}}=\bigcap _{{\mathbb {Q}}\in {\mathcal {Q}} _{{\mathcal {B}},V}}L^1({\mathbb {Q}})\). This will imply that \(\sum _{j=1}^N\mathbb {E}_{\mathbb { Q}^j} \left[ {\widehat{Z}}^j\right] \le A\) for all \({\mathbb {Q}}\in {\mathcal {Q}} _{{\mathcal {B}},V} \), by Lemma A.1. Since \(X\in M^\Phi \), it is clearly enough to prove that \(\mathbb {E}_\mathbb {P} \left[ X+ {\widehat{Y}}\vert {\mathcal {G}}\right] \in {\mathcal {L}}\). Observe first that for any given \({\mathbb {Q}}\ll {\mathbb {P}}\), the measure \({\mathbb {Q}}_ {\mathcal {G}}\) defined by \(\frac{\mathrm {d}{\mathbb {Q}}^j_{\mathcal {G}}}{\mathrm {d} {\mathbb {P}}}:=\mathbb {E}_\mathbb {P} \left[ \frac{\mathrm {d}{\mathbb {Q}}^j}{ \mathrm {d}{\mathbb {P}}}\vert {\mathcal {G}}\right] \), \(j=1,\dots ,N\), satisfies
To see this, recall that all the components of \({\mathbb {Q}}\) are equal, hence so are those of \({\mathbb {Q}}_{\mathcal {G}}\). Moreover
and \(\mathbb {E}_\mathbb {P} \left[ V\left( \lambda \frac{\mathrm {d}{\mathbb {Q}} _{\mathcal {G}}}{\mathrm {d}{\mathbb {P}}}\right) \right] \le \mathbb {E}_\mathbb { P} \left[ V\left( \lambda \frac{\mathrm {d}{\mathbb {Q}}}{\mathrm {d}{\mathbb {P}}} \right) \right] \) by conditional Jensen inequality.
Now, for any \(j=1,\dots ,N\) and \({\mathbb {Q}}\in {\mathcal {Q}}_{{\mathcal {B}},V}\)
As a consequence, since by (42) \({\mathcal {L}} \subseteq L^1({ \mathbb {Q}}_{\mathcal {G}})\) and \({\widehat{Y}}\in {\mathcal {L}}\), we get \(X+ {\widehat{Y}}\in L^1({\mathbb {Q}})\), and the fact that \({\widehat{Z}}\in {\mathcal {L}}\) follows.
Finally, observe that \(\mathbb {E}_\mathbb {P} \left[ U\left( X+{\widehat{Z}} \right) \right] = \mathbb {E}_\mathbb {P} \left[ U\left( \mathbb {E}_\mathbb {P} \left[ X+{\widehat{Y}}\vert {\mathcal {G}}\right] \right) \right] \ge \mathbb {E}_ \mathbb {P} \left[ U(X+{\widehat{Y}})\right] \) by conditional Jensen inequality. Hence \({\widehat{Z}}\) is another optimum for the optimization problem in (25). By strict concavity of U then we get \( {\widehat{Y}}={\widehat{Z}}\). Since \(X+{\widehat{Z}}\) is \({\mathcal {G}}\) -(essentially) measurable, so is clearly \(X+{\widehat{Y}}\). \(\square \)
It is interesting to notice that this dependence on the componentwise sum of X also holds in the case of SORTE (Biagini et al., 2021, Section 4.5) and of Bühlmann’s equilibrium (see Bühlmann, 1984 page 16, which partly inspired the proof above, and Borch, 1962).
Remark 4.11
In the case of clusters of agents, the above result can be clearly generalized (see Biagini et al., (2021) Remark 4.19).
5 Systemic utility maximization and duality
In this Section we collect some remarks and properties of the polar cone of \( {\mathcal {B}}_0\cap M^\Phi \), which will play an important role in the following.
Remark 5.1
If \(X\in M^{\Phi }\), then for any fixed \(k=1,\dots ,N\) we have \([0,\dots ,0,X^{k},0,\dots ,0]\in M^{\Phi } \). This in turns implies that for any \(Z\in K_{\Phi }\) and \(X\in M^{\Phi }\) , \(X^{j}Z^{j}\in L^{1}({\mathbb {P}})\) for any \(j=1,\dots ,N\).
Remark 5.2
In the dual pair \((M^{\Phi },K_{\Phi })\) take the polar \(({\mathcal {B}}_{0}\cap M^{\Phi })^{0}\) of \({\mathcal {B}}_{0}\cap M^{\Phi } \). Since all (deterministic) vector in the form \(e^{i}-e^{j}\) belong to \({\mathcal {B}}_{0}\cap M^{\Phi }\), we have that for all \(Z\in ( {\mathcal {B}}_{0}\cap M^{\Phi })^{0}\) and for all \(i,j\in \{1,\dots ,N\}\) \( \mathbb {E}_{\mathbb {P}}\left[ Z^{i}\right] -\mathbb {E}_{\mathbb {P}}\left[ Z^{j}\right] \le 0\). It is clear that, as a consequence, \(Z\in ({\mathcal {B}} _{0}\cap M^{\Phi })^{0}\Rightarrow \mathbb {E}_{\mathbb {P}}\left[ Z^{1}\right] =\dots =\mathbb {E}_{\mathbb {P}}\left[ Z^{N}\right] \). Recall that \({\mathbb {R }}_{+}:=\{b\in {\mathbb {R}},b\ge 0\}\) and the definition of \({\mathcal {Q}}\) provided in (22). We then see:
that is, \(({\mathcal {B}}_{0}\cap M^{\Phi })^{0}\) is the cone generated by \( {\mathcal {Q}}\).
Remark 5.3
The condition \({\mathcal {B}}\subseteq {\mathcal {C}}_{{\mathbb {R}}}\) implies \({\mathcal {B}}_{0}\cap M^{\Phi }\subseteq ( {\mathcal {C}}_{{\mathbb {R}}}\cap M^{\Phi }\cap \{\sum _{j=1}^{N}Y^{j}\le 0\})\) , so that the polars satisfy the opposite inclusion: \(({\mathcal {C}}_{{\mathbb { R}}}\cap M^{\Phi }\cap \{\sum _{j=1}^{N}Y^{j}\le 0\})^{0}\subseteq (\mathcal { B}_{0}\cap M^{\Phi })^{0}\). Observe now that any vector \([Z,\dots ,Z]\), for \( Z\in L_{+}^{\infty }\), belongs to \(({\mathcal {C}}_{{\mathbb {R}}}\cap M^{\Phi }\cap \{\sum _{j=1}^{N}Y^{j}\le 0\})^{0}\). In particular, take \(a>0\) for which (19) is satisfied. Then
It follows that \([{\mathbb {P}},\dots ,{\mathbb {P}}]\in {\mathcal {Q}}_{{\mathcal {B}},V}\ne \emptyset \) since \(\mathbb {E}_\mathbb {P} \left[ V\left( a\left[ \frac{ \mathrm {d}{\mathbb {P}}}{\mathrm {d}{\mathbb {P}}},\dots ,\frac{\mathrm {d}{ \mathbb {P}}}{\mathrm {d}{\mathbb {P}}}\right] \right) \right] <+\infty \).
Proposition 5.4
(Fairness) For all \({\mathbb {Q}}\in {\mathcal {Q}}\)
Proof
Let \(Y\in {\mathcal {B}}\cap M^{\Phi }\). Notice that the hypothesis \({\mathbb {R} }^{N}+{\mathcal {B}}={\mathcal {B}}\) implies that the vector \(Y_{0}\), defined by \( Y_{0}^{j}:=Y^{j}-\frac{1}{N}\sum _{k=1}^{N}Y^{k}\), belongs to \({\mathcal {B}} _{0} \). Indeed, \(\sum _{k=1}^{N}Y^{k}\in {\mathbb {R}}\) and so \(Y_{0}\in {\mathcal {B}} \) and \(\sum _{j=1}^{N}Y_{0}^{j}=0\). By definition of polar, \( \sum _{j=1}^{N}\mathbb {E}_{\mathbb {P}}\left[ Y_{0}^{j}Z^{j}\right] \le 0\) for all \(Z\in ({\mathcal {B}}\cap M^{\Phi })^{0}\), and in particular for all \({ \mathbb {Q}}\in {\mathcal {Q}}\)
and we recognize \(\sum _{j=1}^{N}\mathbb {E}_{\mathbb {Q}^{j}}\left[ Y^{j} \right] -\sum _{j=1}^{N}Y^{j}\) in RHS. \(\square \)
Theorem 5.5
Let \({\mathcal {C}}\subseteq M^\Phi \) be a convex cone with \(0\in {\mathcal {C}}\) and \(e_i-e_j\in {\mathcal {C}}\) for every \( i,j\in \{1,\dots ,N\}\). Denote by \({\mathcal {C}}^0\) the polar of the cone \( {\mathcal {C}}\) in the dual pair \((M^\Phi ,K_\Phi )\):
and set
Suppose that for every \(X\in M^\Phi \)
Then the following holds:
If any of the two expressions is strictly smaller than \(V(0)=\sup _{{\mathbb {R }}^{N}}U\), then the condition \(\lambda \ge 0\) in (44) can be replaced with the condition \(\lambda >0\).
Proof
The proof can be obtained with minor and obvious modifications of the one in Biagini et al. (2021) Theorem A.3 by replacing \(\sum _{j=1}^N u_j(\cdot ),\,\sum _{j=1}^N v_j(\cdot ), L^{\Phi ^*}\) there with \( U(\cdot ),\,V(\cdot ),\,K_\Phi \) respectively. \(\square \)
We also provide an analogous result when working with the pair \(((L^\infty ({ \mathbb {P}}))^N,(L^1({\mathbb {P}}))^N)\) in place of \((M^\Phi , K_\Phi )\), which will be used in Sect. 6.2.
Theorem 5.6
Replacing \(M^\Phi \) with \((L^\infty ({\mathbb {P} }))^N\) and \(K_\Phi \) with \((L^1({\mathbb {P}}))^N\) in the statement of Theorem 5.5, all the claims in it remain valid.
Proof
As in Theorem 5.5, the proof can be obtained with minor and obvious modifications of the one in Biagini et al. (2021) Theorem A.3, using Theorem 4 of Rockafellar (1968) in place of Corollary on page 534 of Rockafellar (1968). \(\square \)
6 Proof of Theorem 4.2
We now take care of the proof of Theorem 4.2 for the case \(A=0\). For the reader’s convenience, we first provide a more detailed statement for all the results we prove, which also provides a road map for the proof. It is easy to reconstruct the content of Theorem 4.2 from the statement below.
Theorem 6.1
Under Assumption 3.8 the following hold:
-
1.
for every \(X\in M^\Phi \)
$$\begin{aligned}&\sup _{Y\in {\mathcal {B}}_{0}\cap M^{\Phi }}\mathbb {E}_{\mathbb {P}}\left[ U(X+Y)\right] =\sup \left\{ \mathbb {E}_{\mathbb {P}}\left[ U(X+Y)\right] \mid { Y\in {\mathcal {L}}},\,\sum _{j=1}^N\mathbb {E}_{\mathbb {Q}^j} \left[ Y^j\right] \le 0\,\,\forall {\mathbb {Q}}\in {\mathcal {Q}}_{{\mathcal {B}},V}\right\} \end{aligned}$$(45)$$\begin{aligned}&\quad =\min _{\mathbb {Q}\in {\mathcal {Q}}_{{\mathcal {B}},V}}\min _{\lambda \ge 0}\left( \lambda \sum _{j=1}^{N}\mathbb {E}_{\mathbb {Q}^{j}}\left[ X^{j}\right] +\mathbb {E}_{ \mathbb {P}}\left[ V\left( \lambda \frac{\mathrm {d}{\mathbb {Q}}}{\mathrm {d}{ \mathbb {P}}}\right) \right] \right) \,. \end{aligned}$$(46)Every optimum \(({\widehat{\lambda }},\widehat{{\mathbb {Q}}})\) of (46) satisfies \({\widehat{\lambda }}>0\) and \( \widehat{{\mathbb {Q}}}\sim {\mathbb {P}}\). Moreover, if U is differentiable, (46) admits a unique optimum \(( {\widehat{\lambda }},\widehat{{\mathbb {Q}}})\), with \(\widehat{{\mathbb {Q}}} \sim {\mathbb {P}}\).
Furthermore, there exists a random vector \({\widehat{Y}}\in (L^1({\mathbb {P}} ))^N\) such that:
-
2.
\({\widehat{Y}}\) satisfies:
$$\begin{aligned} {\widehat{Y}}^{j}\frac{\mathrm {d}{\mathbb {Q}}^{j}}{\mathrm {d}{\mathbb {P}}}\in L^{1}({\mathbb {P}})\,\,\,\forall {\mathbb {Q}}\in {\mathcal {Q}}_{{\mathcal {B}},V},\forall \,j=1,\dots ,N\,\text { and }\sum _{j=1}^{N}\mathbb {E}_{\mathbb {Q}^{j}}\left[ {\widehat{Y}}^{j}\right] \le 0\,\,\,\forall {\mathbb {Q}}\in {\mathcal {Q}}_{{\mathcal {B}},V}\,.\nonumber \\ \end{aligned}$$(47)and for any optimizer \(({\widehat{\lambda }},\widehat{{\mathbb {Q}}})\in {\mathbb { R}}_+\times {\mathcal {Q}}_{{\mathcal {B}},V}\) of (46)
$$\begin{aligned} \sum _{j=1}^{N}\mathbb {E}_{\widehat{\mathbb {Q}}^{j}}\left[ {\widehat{Y}}^{j} \right] =0=\sum _{j=1}^{N}{\widehat{Y}}^{j}\,. \end{aligned}$$(48) -
3.
\({\widehat{Y}}\) is the unique optimum to the following extended maximization problem:
$$\begin{aligned} \sup \left\{ \mathbb {E}_{\mathbb {P}}\left[ U(X+Y)\right] \mid {Y\in {\mathcal {L}}} ,\,\sum _{j=1}^N\mathbb {E}_{\mathbb {Q}^j} \left[ Y^j\right] \le 0\,\,\forall { \mathbb {Q}}\in {\mathcal {Q}}_{{\mathcal {B}},V}\right\} =\mathbb {E}_\mathbb {P} \left[ U(X+ {\widehat{Y}})\right] \,.\nonumber \\ \end{aligned}$$(49)
Proof
STEP 1: we show the equality chain in (45) and (46).
We introduce for \(A\in {{\mathbb {R}}}\)
We start recognizing \(\pi _0(X)\) as the LHS of (45) and observing that \( -\infty <\pi _0(X)\) since \({\mathcal {B}}_A\cap M^\Phi \ne \emptyset \) and by Fenchel inequality \(\pi _0(X)<+\infty \) (combining Remark 5.3 to guarantee \({\mathcal {Q}}_{{\mathcal {B}},V}\ne \emptyset \), Proposition 5.4 and the inequality chain in Remark 4.4). Again by Proposition 5.4 and Remark 4.4, it is enough to show that
This equality follows by Theorem 5.5, taking \({\mathcal {C}} :={\mathcal {B}}_{0}\cap M^{\Phi }\) and noticing that minima over \({\mathcal {Q}}\) can be substituted with minima over \({\mathcal {Q}}_{{\mathcal {B}},V}\) since the expression in LHS of (45) is finite. Observe at this point that, if any of the three expressions in (45) and (46) were strictly smaller than \(V(0)=\sup _{x\in {\mathbb {R}}^N}U(x)\), direct substitution of \(\lambda =0\) in the expression would give a contradiction, no matter what the optimal probability measure is.
STEP 2: we show the existence of a vector \({\widehat{Y}}\) as described in Items 2 and 3 of the statement, made exception for the first equality in (48). More precisely, we first (\({\underline{{Step 2a}}}\)) identify a natural candidate \({\widehat{Y}}\) using a maximizing sequence, and we show that it satisfies \(\sum _{j=1}^N{\widehat{Y}} ^j=0\). Then (\({\underline{{Step 2b}}}\)) we show that such candidate satisfies the integrability conditions and inequalities in (47) . Finally (\({\underline{{Step 2c}}}\)) we show optimality stated in Item 3. The proof of the first equality in (48) is postponed to STEP 5.
\({\underline{\mathrm{Step\,2a}}}\). First observe that \(X+Y\ge -\left( \left| X\right| +\left| Y\right| \right) \) in the componentwise order, hence for \(Z\in {\mathcal {B}}_0\cap M^{\Phi }\ne \emptyset \), as \(X,Z\in M^{\Phi }\), we get
Take now a maximizing sequence \((Y_{n})_{n}\) in \({\mathcal {B}}_0\cap M^{\Phi }\) . W.l.o.g. we can assume that
since if this were not the case (i.e. if the inequality were strict) we could add a \(\varepsilon >0\) small enough to each component without decreasing the utility of the system or violating the constraint \(Y_n\in {\mathcal {B}}_0\).
Observe that
and \(\mathbb {E}_{\mathbb {P}}\left[ U(X+Y_{n})\right] \ge \mathbb {E}_{ \mathbb {P}}\left[ U(X+Y_{1})\right] =:B\in {\mathbb {R}}\). Then Lemma Item 1 applies with \(Z_{n}:=X+Y_{n}\). Using also \( \left| X^{j}\right| +\left| Y_{n}^{j}\right| \le \left| X^{j}+Y_{n}^{j}\right| +2\left| X^{j}\right| ,\,j=1,\dots ,N\) we get
Now we apply Corollary A.7 with \({\mathbb {P}} _{1}=\dots ={\mathbb {P}}_{N}={\mathbb {P}}\) and extract the subsequence \( (Y_{n_{h}})_{h}\) such that for some \({\widehat{Y}}\in (L^{1}({\mathbb {P}} ))^{N} \)
We notice that by convexity the random vectors \(W_{H}\) still belong to \( {\mathcal {B}}_0\cap M^{\Phi }\), and \({\widehat{Y}}\in {\mathcal {B}}_0\) as \( {\mathcal {B}}_0\) is closed in probability (since so is \({\mathcal {B}}\)). Moreover, we have that
so that the second equality in (48) holds.
\({\underline{\mathrm{Step\,2b}}}\). We first work on integrability. We proceed as follows: we show that for any \({\mathbb {Q}}\in {\mathcal {Q}}_{{\mathcal {B}},V}\) we have \(\sum _{j=1}^N {\widehat{Y}}^j\frac{\mathrm {d}{\mathbb {Q}}^j}{\mathrm {d}{\mathbb {P}}}\in L^1({ \mathbb {P}})\). Then we show that \(({\widehat{Y}})^-\in L^{{\widehat{\Phi }}}\), and conclude the integrability conditions in (47).
Let us begin with showing \(\sum _{j=1}^N {\widehat{Y}}^j\frac{\mathrm {d}{ \mathbb {Q}}^j}{\mathrm {d}{\mathbb {P}}}\in L^1({\mathbb {P}})\). By definition of \(V(\cdot )\), we have
This implies
so that \(\left( V(\lambda Z)+\left\langle X+{\widehat{Y}}, \lambda Z\right\rangle \right) ^-\in L^1({\mathbb {P}})\).
We prove integrability also for the positive part, assuming now \(Z=\frac{ \mathrm {d}{\mathbb {Q}}}{\mathrm {d}{\mathbb {P}}},\,{\mathbb {Q}}\in {\mathcal {Q}}_{{\mathcal {B}},V}\) and taking \(\lambda >0\) such that \(\mathbb {E}_\mathbb {P} \left[ V(\lambda Z)\right] <+\infty \). By (51) \(W_H\rightarrow _H{\widehat{Y}}\,{ \mathbb {P}}\)-a.s. so that
Now since \(\mathbb {E}_\mathbb {P} \left[ \left\langle W_H, \lambda Z\right\rangle \right] \le 0\)
Also by (52)
Now use (18):
We also have, \(Y_1\) being the first element in the maximizing sequence, that \(\inf _H\left( \mathbb {E}_\mathbb {P} \left[ U(X+W_H)\right] \right) \ge \mathbb {E} _\mathbb {P} \left[ U(X+Y_1)\right] \) by construction. Thus, continuing from (55), we get
since the sequence \(W_H\) is bounded in \((L^1({\mathbb {P}}))^N\) (see (51)) and \(\mathbb {E}_\mathbb {P} \left[ U(X+Y_1)\right] >-\infty \).
From (53), (54), (56) we conclude that
To sum up, for \(Z\in {\mathcal {Q}}_{{\mathcal {B}},V}\) and \(\lambda \) s.t. \(\mathbb {E}_{ \mathbb {P}}\left[ V(\lambda Z)\right] <+\infty \)
which gives \(\left\langle {\widehat{Y}},Z\right\rangle \in L^{1}({\mathbb {P}}),\forall Z\in {\mathcal {Q}}_{{\mathcal {B}},V}\). Hence we have
Next, we prove that \(({\widehat{Y}})^-\in L^{{\widehat{\Phi }}}\). To see this, we observe from (17) that for \(\varepsilon >0\) sufficiently small
which readily gives
By Fatou Lemma we than conclude
From this we infer \((X+{\widehat{Y}})^-\in L^{{\widehat{\Phi }}}\).
We are now almost done showing integrability. Since by (21) \(L^{{\widehat{\Phi }}}=L^\Phi \), we conclude that \((X+{\widehat{Y}})^-\in L^{\Phi }\). By the very definition of \(K_\Phi \) and \({\mathcal {Q}}_{{\mathcal {B}},V}\subseteq K_\Phi \), we have \(\sum _{j=1}^N(X^j+{\widehat{Y}}^j)^- \frac{\mathrm {d}{\mathbb {Q}}^j}{\mathrm {d}{\mathbb {P}}}\in L^1({\mathbb {P}})\) , which clearly implies \((X^j+{\widehat{Y}}^j)^-\frac{\mathrm {d}{\mathbb {Q}}^j }{\mathrm {d}{\mathbb {P}}}\in L^1({\mathbb {P}})\) for every \(j=1,\dots ,N\). At the same time we observe that
and all the terms in RHS are in \(L^1({\mathbb {P}})\) (recall (57)). Thus, \(\sum _{j=1}^N(X^j+{\widehat{Y}}^j)^+\frac{ \mathrm {d}{\mathbb {Q}}^j}{\mathrm {d}{\mathbb {P}}}\in L^1({\mathbb {P}})\) and \( (X^j+{\widehat{Y}}^j)^+\frac{\mathrm {d}{\mathbb {Q}}^j}{\mathrm {d}{\mathbb {P}}} \in L^1({\mathbb {P}})\) for every \(j=1,\dots ,N\). We finally get that \( {\widehat{Y}}\in \bigcap _{{\mathbb {Q}}\in {\mathcal {Q}}_{{\mathcal {B}},V}}L^1({\mathbb {Q}})\) and our integrability conditions in (47) are now proved.
To conclude Step 2b, we need to show that \(\sum _{j=1}^{N}\mathbb {E}_{\mathbb { Q}^{j}}\left[ {\widehat{Y}}^{j}\right] \le 0\,\forall {\mathbb {Q}}\in {\mathcal {Q}}_{{\mathcal {B}},V}\,.\) This is a consequence of Lemma A.1 with \(A=0\), since \({\widehat{Y}}\in {\mathcal {B}}_0\cap {\mathcal {L}}\).
\({\underline{\mathrm{Step\,2c.}}}\) Observe now that
by concavity of U and the fact that \((Y_{n_{h}})_{h}\) is again a maximizing sequence. From the expression in (59) we get that for every \(\varepsilon >0\), definitely (in H)
Apply now Lemma A.3 Item 2 for \( B=\sup _{Y\in {\mathcal {B}}_0\cap M^{\Phi }}\mathbb {E}_{\mathbb {P}}\left[ U(X+Y) \right] -\varepsilon \) to the sequence \((X+W_{H})_{H}\) for H big enough (this sequence is bounded in \((L^{1}({\mathbb {P}}))^{N}\) by (51)) to get that for every \(\varepsilon >0\)
Clearly then \({\widehat{Y}}\) satisfies
Now recall that by (19) for some \(a>0, b\in { \mathbb {R}}\)
and since RHS is in \(L^{1}({\mathbb {P}})\) we conclude that \(\mathbb {E}_{ \mathbb {P}}\left[ U(X+{\widehat{Y}})\right] <+\infty \). Hence:
It is now enough to recall that by (47), which we proved in Step 2b, \({\widehat{Y}}\) satisfies the constraints in LHS of (49): \({Y\in {\mathcal {L}}},\,\sum _{j=1}^N \mathbb {E}_{\mathbb {Q}^j} \left[ Y^j\right] \le 0\,\,\forall {\mathbb {Q}}\in {\mathcal {Q}}_{{\mathcal {B}},V}\). Optimality claimed in Item 3 then follows.
STEP 3: we prove uniqueness of the optimum for the maximization problem in Item 3 and condition \({\widehat{\lambda }}>0\) for every optimum \(({\widehat{\lambda }},\widehat{{\mathbb {Q}}})\) of (46).
The uniqueness for the optimum follows from strict concavity of U (see Standing Assumption I): if two distinct optima existed, any strict convex combination of the two would still satisfy the constraint and would produce a value for \(\mathbb {E}_{\mathbb {P}}\left[ U(X+\bullet )\right] \) strictly greater than the supremum.
Recall now from STEP 1 that to prove the claimed \({\widehat{\lambda }}>0\) it is enough to show that any of the three expressions in (45) and (46) is strictly smaller than \(\sup _{x\in {\mathbb {R}}^N}U(x)\). Property \(\widehat{ \lambda }>0\) is easily obtained if \(\sup _{z\in {\mathbb {R}}^{N}}U(z)=+\infty \) , since we proved that \(\mathbb {E}_\mathbb {P} \left[ U(X+{\widehat{Y}})\right] <+\infty \) in Step 2c. Suppose that instead \(\sup _{z\in {\mathbb {R}} ^{N}}U(z)<+\infty \) and notice that, setting \({\mathcal {K}}:=\{Y\in {\mathcal {L}} ,\,\sum _{j=1}^N\mathbb {E}_{\mathbb {Q}^j} \left[ Y^j\right] \le 0\,\,\forall { \mathbb {Q}}\in {\mathcal {Q}}_{{\mathcal {B}},V}\}\)
If we had \(\sup _{Y\in {\mathcal {K}}}\mathbb {E}_{\mathbb {P}}\left[ U(X+Y)\right] =\sup _{z\in {\mathbb {R}}^{N}}U(z)\), then we would also have
so that:
which implies \(\sup _{z\in {\mathbb {R}}^{N}}U(z)=U(X+{\widehat{Y}})\) \({\mathbb {P }}\)-a.s.. In particular, from the fact that \(X+{\widehat{Y}}\) is finite almost surely, it would follow that U almost surely attains its supremum on some compact subset of \({\mathbb {R}}^{N}\), which is clearly a contradiction given that U is strictly increasing.
STEP 4: we study a related optimization problem when a \({ \mathbb {Q}}\in {\mathcal {Q}}_{{\mathcal {B}},V}\) is fixed.
We show that for any fixed \(X\in M^\Phi \) and \({\mathbb {Q}}\in {\mathcal {Q}}_{{\mathcal {B}},V}\) it holds that
\(\pi _{0}^{\mathbb {Q}}(X)<+\infty \) follows from Remark 4.4. The equality between (61) and (62) follows from Theorem 5.5, and the fact that
We stress the fact that (61) and (62) hold also dropping Assumption 3.8.
We observe that if (61) is strictly smaller than V(0) then the minimum in (62) can be taken over \( (0,+\infty )\) in place of \([0,+\infty )\).
Let now \(X\in M^\Phi \) be fixed and \(\pi _0(\cdot ),\, \pi _0^{\mathbb {Q} }(\cdot ) \) be as in (50), (61) respectively. Then from STEP 1 together with (61) and (62)
and whenever \((\widehat{\lambda ,}\widehat{{\mathbb {Q}}})\) is an optimum for (46), then \(\widehat{{\mathbb {Q}}}\) is an optimum for (63).
STEP 5: we show that for any optimum \(({\widehat{\lambda }}, \widehat{{\mathbb {Q}}})\in {\mathbb {R}}_+\times {\mathcal {Q}}_{{\mathcal {B}},V}\) of (46) we have \(\widehat{{\mathbb {Q}}}\sim {\mathbb {P}}\) and the first equality in (48) holds.
We start observing that for any optimal \(\widehat{{\mathbb {Q}}}\) as in the claim we have that by STEP 4
The last equality in particular follows observing that by trivial set inclusions and Fenchel inequality
We now prove that \(\widehat{{\mathbb {Q}}}\sim {\mathbb {P}}\), using an argument inspired by Föllmer and Schied (2016) Remark 3.32: if this were not the case then \({\mathbb {P}}(A_{k})>0,\) where \(A_{k}:=\{\frac{\mathrm {d}\widehat{{ \mathbb {Q}}}^{k}}{\mathrm {d}{\mathbb {P}}}=0\},\) for some component \(k\in \{1,\dots ,N\}\). Then the vector \({\widetilde{Y}}\) defined by \({\widetilde{Y}} ^{k}:={\widehat{Y}}^{k}+1_{A_{k}}\), \({\widetilde{Y}}^{j}:={\widehat{Y}}^{j},j\ne k \) would still satisfy \(\sum _{j=1}^{N}\mathbb {E}_{\widehat{{\mathbb {Q}}}^j}[ {\widetilde{Y}}^{j}] \le 0\)
and by monotonicity \(\mathbb {E}_{\mathbb {P}}\left[ U(X+{\widetilde{Y}})\right] \ge \mathbb {E}_{\mathbb {P}}\left[ U(X+{\widehat{Y}})\right] \). Thus \( {\widetilde{Y}}\) would be another optimum, different from \({\widehat{Y}}\). Since now U is strictly concave and \(\{ Y\in {\mathcal {L}}, \sum _{j=1}^N\mathbb {E} _{\widehat{{\mathbb {Q}}}^j}[Y^j]\le 0\}\) is convex, we would get a contradiction arguing in the same way as in STEP 3.
We move to \(\sum _{j=1}^{N}\mathbb {E}_{\widehat{\mathbb {Q}}^{j}}\left[ {\widehat{Y}}^{j}\right] =0\): if this were not the case, by (47) we would have \(\sum _{j=1}^{N}\mathbb {E}_{ \widehat{\mathbb {Q}}^{j}}\left[ {\widehat{Y}}^{j}\right] <0\) so that adding \( 0<\varepsilon \) sufficiently small to each component of \({\widehat{Y}}\) would give a vector still satisfying the constraints of RHS of (64), but having a corresponding expected utility strictly grater that the supremum (U is strictly increasing, and \(\widehat{ Y}\) is an optimum as showed by (64)), which is a contradiction.
STEP 6: we prove uniqueness of the optimum for (46) under the additional differentiability assumption.
Take \({\mathcal {C}}:={\mathcal {B}}_{0}\cap M^{\Phi }\), and observe that (46) can be rewritten, by (43), as
which from strict convexity of \(V(\cdot )\) (Rockafellar (1970) Theorem 26.5) admits a unique optimum \(0\le {\widehat{Z}}\ne 0\). We then get that, since \( {\widehat{\lambda }}=\mathbb {E}_{\mathbb {P}}\left[ {\widehat{Z}}\right] ,\,\frac{ \mathrm {d}\widehat{{\mathbb {Q}}}}{\mathrm {d}{\mathbb {P}}}=\frac{{\widehat{Z}}}{ \mathbb {E}_{\mathbb {P}}\left[ {\widehat{Z}}\right] }\) (again by (43)), uniqueness for optima in (46) follows. \(\square \)
We now consider the possibility of weakening the requirements of strict monotonicity and concavity of U. To do so, we introduce the additional condition \({\mathcal {B}}=-{\mathcal {B}}\). We stress that, for \({\mathcal {B}}= {\mathcal {C}}_{\mathbb {R}}\) both Assumption 3.8 and \(-{\mathcal {B}}= {\mathcal {B}}\) hold true.
Corollary 6.2
Suppose that the function \(U:{\mathbb {R}}^{N}\rightarrow {\mathbb {R}}\) is (not necessarily strictly) concave and (not necessarily strictly) increasing with respect to the partial componentwise order. Suppose that there exist a multivariate Orlicz function \({\widehat{\Phi }}:{\mathbb {R}} _{+}^{N}\rightarrow {\mathbb {R}}\) and a function \(f:{\mathbb {R}} _{+}\rightarrow {\mathbb {R}}\) such that (17) holds and \(L^{{\widehat{\Phi }}}=L^{\Phi }\). Suppose that Assumption 3.8 holds and that \(-{\mathcal {B}}={\mathcal {B}}\). Then the following statements in Theorem 6.1 still hold: the equalities in (45) = (46), the fact that any optimum \(\widehat{ \lambda }\) for (46) is strictly positive, all the claims in Item 2 and optimality (not uniqueness) in Item 3. Moreover, existence (not uniqueness) for a mSORTE holds.
Proof
Observe first that all the statements in Lemma 3.5 still hold, since we did not need strictness of concavity and monotonicity in their proof. Looking back at the proof of Theorem 6.1 we observe that we used strict convexity and strict monotonicity only from STEP 5 on and for the following reasons: on the one hand, to prove uniqueness for \({\widehat{Y}},\widehat{ \lambda },\widehat{{\mathbb {Q}}}\) and that \(\widehat{{\mathbb {Q}}}\sim { \mathbb {P}}\), on the other hand to prove that \(\sum _{j=1}^{N}\mathbb {E}_{ \widehat{{\mathbb {Q}}}^{j}}[{\widehat{Y}}^{j}]=0\). We now show that under the hypotheses of the Corollary it is indeed possible to show the latter equality also when U is just increasing and concave, neither of the two being necessarily strict. More precisely, we show that for any optimum \(( {\widehat{\lambda }},\widehat{{\mathbb {Q}}})\) of (46) we have \(\sum _{j=1}^{N}\mathbb {E}_{ \widehat{{\mathbb {Q}}}^{j}}[{\widehat{Y}}^{j}]=0\) for the vector \({\widehat{Y}}\) obtained in STEP 2.
To see this, it is indeed enough to observe that \(Y\in {\mathcal {B}}_0 \Leftrightarrow -Y\in {\mathcal {B}}_0\), thus the sequence \(Y_m\) we used in (76) satisfies \(\mathbb {E}_{\mathbb {P}}\left[ \sum _{j=1}^{N}Y_{m}^{j}\frac{\mathrm {d}{\mathbb {Q}}^{j}}{\mathrm {d}{\mathbb {P }}}\right] =0\) for any \({\mathbb {Q}}\in {\mathcal {Q}}_{{\mathcal {B}},V}\) (recall the definition of \({\mathcal {Q}}_{{\mathcal {B}},V}\) in (23)). Then, the inequality in (77) is an equality, and our claim follows. To conclude, observe that from this point on literally the same arguments of the proof of Theorem 6.1 yield the equalities in (45)\(=\)(46), the fact that any optimum \({\widehat{\lambda }}\) for (46) is strictly positive, all the claims in Item 2 and optimality (not uniqueness) in Item 3. Also, Theorem does not in practice require strict concavity or monotonicity in its proof, so it still holds if these assumption is dropped. Finally, a counterpart to the existence in Theorem 4.5 can be obtained with the same argument. Take indeed \(({\widehat{Y}},{\widehat{{{\mathbb {Q}}}}})\) as in Theorem 4.2 and adopt the notation from Lemma A.2. Then one can check that \(S^{{\widehat{{{\mathbb {Q}}}}}}(A)=H^{{\widehat{{{\mathbb {Q}}}}}}(A)\), and that \(({\widehat{a}}:=\mathbb {E}_{{\widehat{{{\mathbb {Q}}}}}}[{\widehat{Y}}], {\widetilde{Y}}_X:={\widehat{Y}}-{\widehat{a}})\) is an optimum for \(H^{{\widehat{{{\mathbb {Q}}}}}}(A)\). To see this, it is enough to observe that the inequality \(S^{{\widehat{{{\mathbb {Q}}}}}}(A)\ge H^{{\widehat{{{\mathbb {Q}}}}}}(A)\) can be obtained as in Lemma A.2, and that
since \(\mathbb {E}_{{\widehat{{{\mathbb {Q}}}}}}[{\widehat{Y}}]={\widehat{a}}\) with \(\sum _{j=1}^N{\widehat{a}}^j=A\) and \(({\widehat{Y}},{\widehat{a}})\) is optimal for \(S^{{\widehat{{{\mathbb {Q}}}}}}(A)\) as in the proof of Theorem 4.5. \(\square \)
6.1 Replacing Assumption 3.8
In this Section we present a counterpart to some of our findings, with Assumption 3.8 replaced by the following one.
Assumption 6.3
The function \({\widehat{\Phi }}(\cdot )\) in (17) satisfies \({\widehat{\Phi }}(x)=\sum _{j=1}^{N} {\widehat{\Phi }}_{j}(x)\,\,\forall x\in {\mathbb {R}}_{+}^{N}\), with \(\, {\widehat{\Phi }}_{j}:{\mathbb {R}}\rightarrow {\mathbb {R}}\) differentiable on \( {\mathbb {R}_{++}}\) and
Notice in particular that the condition \(\lim _{z\rightarrow +\infty }\frac{ {\widehat{\Phi }}_{j}(z)}{z}=+\infty \) guarantees that \({{\widehat{\Phi }}} _{j}^{*}(z)<+\infty \) for every \(z\ge 0\).
We now present two preliminary propositions before stating the main result of the section. In Orlicz space theory the well known \(\Delta _{2}\) condition on a Young function \(\Phi :{\mathbb {R}}\rightarrow {\mathbb {R}}\) guarantees that \(L^{\Phi }=M^{\Phi }\). We say that \(\Phi \in \Delta _{2}\) if:
First, we show how Assumption 6.3 is linked to the \(\Delta _2\) condition for the conjugate of \({{{\widehat{\Phi }}}}_j\) :
Proposition 6.4
Let \(\Phi :{\mathbb {R}}\rightarrow {\mathbb {R}}\) be a Young function differentiable on \({\mathbb {R}}\setminus \{0\}\) and let \( \Phi ^{*}:{\mathbb {R}}\rightarrow {\mathbb {R}}\) be its conjugate function. Then
In particular, under Assumption 6.3 we have \({{{\widehat{\Phi }}}} _{1}^{*},\dots ,{{{\widehat{\Phi }}}}_{N}^{*}\in \Delta _{2}\) which implies
Proof
The equivalence of the two conditions in (65) can be checked along the lines of Theorem 2.3.3 in Rao and Ren (1991), observing that the argument still works in our slightly more general setup (use Proposition 2.2 (Rao & Ren, 1991) in place of Theorem 2.2.(a) (Rao & Ren, 1991)). We now prove the final claim. By Standing Assumption I and Remark , \(L^\Phi =L^{{\widehat{\Phi }}}=L^{{{{\widehat{\Phi }}}}_{1}}\times \dots \times L^{{{{\widehat{\Phi }}}}_{N}}\). Since \(L^\Phi =L^{{\widehat{\Phi }}}\), by definition \(K_\Phi =K_{{{\widehat{\Phi }}}}\). Furthermore, by Proposition 2.5 Item (3), \(K_{{{\widehat{\Phi }}}}=L^{{{{\widehat{\Phi }}}} _{1}^{*}}\times \dots \times L^{{{{\widehat{\Phi }}}}_{N}^{*}}\). To conclude, under Assumption 6.3\({{{\widehat{\Phi }}}}_{j}^{*}\in \Delta _{2}\) by the previous part of this proof, which in turns implies \(L^{{ {{\widehat{\Phi }}}} _{j}^{*}}=M^{{{{\widehat{\Phi }}}}_{j}^{*}},\,j=1,\dots ,N.\) \(\square \)
We also need a sequential w\(^{*}\)-compactness result, see Doldi (2021) Proposition 2.6.10, partly inspired by Dellacherie and Meyer (1978) Chap. II, proof of Theorem 24. A similar result is stated in Orihuela and Ruiz Galán (2012), proof of Theorem 1, with a more technical (even though shorter) proof. For these reasons we omit the proof.
Proposition 6.5
Assume that \(\Phi \), \(\Phi ^{*}:{\mathbb {R}} _+\rightarrow {\mathbb {R}}\) are (univariate) conjugate Young functions, both everywhere finite valued. Then the balls in \(L^{\Phi }\), endowed with Orlicz norm, are \(\sigma \left( L^{\Phi },M^{\Phi ^{*}}\right) \) sequentially compact.
We are now ready for stating and proving the main result of this Section.
Theorem 6.6
Theorems 4.2, 4.3, 4.5 and 6.1 hold true by replacing Assumption 3.8 with Assumption 6.3
Proof
We do not need to start from scratch. In fact, most of the proof of Theorem 6.1 carries over with no modifications. The only point which needed closedness under truncation was proving that \( \sum _{j=1}^{N}\mathbb {E}_{\mathbb {Q}^{j}}\left[ {\widehat{Y}}^{j}\right] \le 0\,\forall {\mathbb {Q}}\in {\mathcal {Q}}_{{\mathcal {B}},V}\,\) using Lemma A.1. If we show this in an alternative way, all the rest can be done exactly in the same way. We observe that by (58) we have for each \(j=1,\dots ,N\)
If \(\gamma <1\) we immediately conclude that \(\sup _H\left\| (X^j+W^j_H)^-\right\| _{{\widehat{\Phi }}_j}\le 1\). If conversely \(\gamma >1\) using convexity of \({\widehat{\Phi }}_j\) we have
thus \(\sup _H\left\| (X^j+W^j_H)^-\right\| _{{\widehat{\Phi }}_j}\le \gamma \). In conclusion, \(\sup _H\left\| (X^j+W^j_H)^-\right\| _{{\widehat{\Phi }}_j}\le \max (\gamma ,1)\). Now we apply Propositions 6.4 and Proposition 6.5. Given the sequences \( (X^{j}+W_{H}^{j})^{-}\), \(j=1,\dots ,N\), a diagonalization argument yields a common subsequence such that \(((X^{j}+W_{H}^{j})^{-})_{H}\) converges in \( \sigma \left( L^{{\widehat{\Phi }}_{j}},M^{{\widehat{\Phi }}_{j}^{*}}\right) \) on \(L^{{\widehat{\Phi }}_{j}}\) for every j. Call such limit \(Z_{j}\). Almost sure convergence
implies \(Z=(X+Y)^{-}\). Indeed, if this were not the case assume without loss of generality \({\mathbb {P}}(Z^{j}>(X^{j}+Y^{j})^{-})>0\) for some j. On a measurable subset D of the event \(\{Z^{j}>(X^{j}+Y^{j})^{-}\}\), \({\mathbb {P }}(D)>0\), the convergence is uniform (by Egoroff Theorem, Theorem 10.38 in Aliprantis and Border (2006)). Consequently, by Dominated Convergence Theorem plus \( \sigma \left( L^{{\widehat{\Phi }}_j }({\mathcal {F}}),M^{{\widehat{\Phi }}_j ^{*}}({\mathcal {F}})\right) \) convergence and the fact that \(L^{\infty }\subseteq M^{{\widehat{\Phi }}_{j}^{*}},\,j=1,\dots ,N\) we get \(\mathbb {E}_{\mathbb {P} }\left[ Z^{j}1_{D}\right] =\mathbb {E}_{\mathbb {P}}\left[ (X^{j}+Y^{j})^{-}1_{D}\right] \), which is a contradiction. Since by Proposition 6.4
we get for any \({\mathbb {Q}}\in {\mathcal {Q}}_{{\mathcal {B}},V}\)
By Fatou Lemma and \(x^{+}=x+x^{-}\)
where we used (66) and the fact that \( \sum _{j=1}^{N}W_{H}^{j}\) is a numeric sequence converging (\({\mathbb {P}}\) -a.s.) to \(\sum _{j=1}^{N}{\widehat{Y}}^{j}\) to move from \(\liminf \) to the sum of limits. As a consequence
We get \((X+{\widehat{Y}})^\pm \in L^{1}({\mathbb {Q}})\), hence \({\widehat{Y}}\in L^{1}({\mathbb {Q}})\) and rearranging terms in (67)
In particular, since \({\widehat{Y}}\in {\mathcal {B}}_{0}\), we conclude that \( \sum _{j=1}^{N}\mathbb {E}_{\mathbb {Q}^{j}}\left[ {\widehat{Y}}^{j}\right] \le 0\,\forall {\mathbb {Q}}\in {\mathcal {Q}}_{{\mathcal {B}},V}\,\). As mentioned before, all the remaining parts of the proof are identical to the ones for Assumption . Hence Theorem 6.1 holds true. Now we get counterparts to Theorems 4.2 and 4.3 with the exact same arguments, recalling for the latter that (61) and (62) still hold dropping Assumption 3.8 (see the proof of Theorem 6.1). Again using the same arguments of Theorem we then get its counterpart under the alternative Assumption 6.3. \(\square \)
6.2 Working on \((L^\infty ({\mathbb {P}}))^N\)
The following result is a counterpart to Theorem 6.1 Item 1 when working with the dual system
in place of \((M^{\Phi },K_{\Phi })\).
Theorem 6.7
Under Assumption 3.8 the following holds:
Proof
To check (68) we can apply the same argument used in STEP 1 of the proof of Theorem 6.1 , by replacing Theorem 5.5 with Theorem 5.6. What is left to prove then is that for \({\mathcal {C}} ={\mathcal {B}}_{0}\cap (L^{\infty }({\mathbb {P}}))^{N}\), the set
is in fact \({\mathcal {Q}}_{{\mathcal {B}},V}\). To see this, observe that as consequence of Lemma A.5 we have \({\mathcal {N}}\subseteq K_\Phi \). From this, by closedness under truncation we have for any \(Y\in {\mathcal {B}} _0\cap M^\Phi \) a sequence \((Y_n)_n\subseteq {\mathcal {B}}_0\cap (L^\infty ({ \mathbb {P}}))^N\) such that for each \({\mathbb {Q}}\in {\mathcal {N}}\), for each \( j=1,\dots ,N\) \(Y^j_n\rightarrow _n Y^j\) \({\mathbb {Q}}^j\)-a.s. and the convergence is dominated: argue as in Lemma A.1. Thus for any \(Y\in {\mathcal {B}}_0\cap M^\Phi \) we have by Dominated Convergence Theorem that \( \sum _{j=1}^{N}\mathbb {E}_{\mathbb {Q}^{j}}\left[ Y^{j}\right] \le 0\). This completes the proof that \({\mathcal {N}}={\mathcal {Q}}_{{\mathcal {B}},V}\). \(\square \)
Corollary 6.8
Under Assumption 3.8 we have
Proof
By Theorem 6.1 Item 1 and Theorem 6.7, both LHS and RHS of (69) are equal to the minimax expression
\(\square \)
6.3 General case: total wealth \(A\in {\mathbb {R}}\)
In this section we extend previous results to cover the case in which the total wealth A might not be equal to 0. For \( A\in {\mathbb {R}}\) and \({\mathbb {Q}}\in {\mathcal {Q}}_{{\mathcal {B}},V}\) recall the definitions of \(\pi _A(X)\) in (50) and introduce, coherently with (61),
It is possible to reduce the maximization problem expressed by \(\pi _A(X)\) (and similarly \(\pi _A^{\mathbb {Q}}(X)\)) to the problem related to \( \pi _0(\cdot )\) (respectively, \(\pi _0^{\mathbb {Q}}(\cdot )\)).
Take any \(a=[a^1,\dots ,a^N]\in {\mathbb {R}}^N\) with \(\sum _{j=1}^Na^j=A\). Then
where last line holds since \({\mathbb {R}}^{N}+{\mathcal {B}}={\mathcal {B}}\) under Standing Assumption II. We recognize then that \(\pi _A(X)\) is just \(\pi _{0}(\cdot )\), with different initial point \((X+a)\) in place of X.
The same technique adopted above can be exploited to show that for any \(a\in { \mathbb {R}}^N\) with \(\sum _{j=1}^Na^j=A\)
The argument above shows how to generalize Theorem 6.1, Theorem 6.7, Corollary 6.8 to cover the case \(A\ne 0\), exploiting the same results with \(X+a\) in place of X.
Thus the statements of Theorem 6.1, Theorem 6.7, Corollary 6.8 remain true replacing \(0,\,{\mathcal {B}}_{0}\) with \(A,\,{\mathcal {B}}_{A}\) respectively, and Equation (62) (similarly for (46), (68)) with
7 On the assumptions and examples
We here present a technique to produce a wide variety of multivariate utility functions fulfilling our requirement. First, we show how to produce multivariate utility functions satisfying (17).
Proposition 7.1
Let \(u_{1},\dots ,u_{N}\) be univariate utility functions such that \(u_{1}(0)=\dots =u_{N}(0)=0\) and that the Inada conditions hold (see Remark 3.3). Let \(\Lambda :{\mathbb {R}} ^{N}\rightarrow {\mathbb {R}}\) be concave and increasing, both not necessarily strictly, and bounded from above. Set
where \({\widehat{\Phi }}_{j}(z):=-u_{j}(-z)\) for \(z\ge 0\). Then \(\,\widehat{ \Phi }\) is a multivariate Orlicz function and it ensures that U is well controlled (see Definition 3.4). If additionally, for every \(j=1,\dots ,N,\) \(u_{j}\) satisfies asymptotic elasticity at \(-\infty \), that is \(u_{j}\) is differentiable on \({\mathbb {R}}\) and
then also Assumption 6.3 holds true.
Proof
First we motivate why U in (70) is a multivariate utility function: this follows from the fact that U inherits strict concavity and strict monotonicity from \(u_1,\dots ,u_N\) which are univariate utility functions.
Now we show that the control from above in (17) holds true. To this end, notice that using the fact that \( u_j(x)=u_j((x)^+)+u_j(-(x)^-)\) we have for any \(z\ge 0\)
where \(\frac{\mathrm {d}^+u_j}{\mathrm {d}x^j}(z)\) are the usual right derivatives at z.
The Inada conditions imply that: for any \(\varepsilon >0\) there exists \(z\ge 0\) such that \(\max _{j=1}^N\frac{\mathrm {d}^+u_j}{\mathrm {d}x^j}(z)\le \varepsilon \), and there exist \(A>0,B\in {\mathbb {R}}\) such that \( u_j(-(x^j)^-)\ge -A(x^j)^-+B\). From the latter we conclude that \(\widehat{ \Phi }(\cdot )\) is a multivariate Orlicz function according to Definition 2.1. From the former, continuing from (71) once \(\varepsilon >0\) had been fixed,
which clearly implies the existence of \({\widehat{\Phi }},f\) satisfying (17).
To conclude, we prove the claim concerning Assumption 6.3. Differentiability of \({\widehat{\Phi }}_1,\dots ,{\widehat{\Phi }}_N\) on \( (0,+\infty )\) follows from differentiability of \(u_1,\dots ,u_N\). It is finally easy to verify that asymptotic elasticity at \(-\infty \) implies \( \liminf _{z\rightarrow +\infty }\frac{z{\widehat{\Phi }}_j ^{\prime }(z)}{ {\widehat{\Phi }}_j (z)}>1\,\,\,\forall \,j=1,\dots ,N\,.\) \(\square \)
It remains now to elaborate on how to guarantee the integrability condition \( L^{{\widehat{\Phi }}}=L^\Phi \) to obtain examples in which Standing Assumption I holds. At this point we introduce a definition, inspired by Definition 2.2.1 (Rao & Ren, 1991), which will serve precisely for the scope (see Proposition 7.3).
Definition 7.2
Let \(u:\mathbb {R\rightarrow R}\) and \({\widetilde{u}}: \mathbb {R\rightarrow R}\). We say that \(u\preceq {\widetilde{u}}\) if there exist \(k\in {\mathbb {R}}\), \(c\in {\mathbb {R}}_{+},\) \(C\in {\mathbb {R}}_{+}\) such that \({\widetilde{u}}(x)\ge Cu(cx)+k\) for each \(x\le 0\).
Note that such control is required to hold only for negative values.
Proposition 7.3
Under the same assumptions and notation of Proposition 7.1 suppose additionally that
for bounded from above, (not necessarily strictly) concave increasing \(\Lambda ^1,\dots ,\Lambda ^K:{{\mathbb {R}}}\rightarrow {{\mathbb {R}}}\). Suppose that for every \(k=1,\dots ,K\) it holds that \(u_{j}\preceq \Lambda ^k\), for each \(j=1,\dots ,N\). Then Standing Assumption I holds true.
Proof
By Proposition 7.1 we only need to prove that \(L^\Phi =L^{ {\widehat{\Phi }}}\), which will conclude the proof of the fact that Standing Assumption I holds. For the sake of notational simplicity, we take \(K=1\). It will become clear at the end of the proof that the generalization to \(K\ge 2\) is immediate. By the concavity of \(\Lambda ^1\) we have, for every \(x\in { \mathbb {R}}^{N},\)
By \(u_{j}\preceq \Lambda ^1,\) and boundedness from above of \(\Lambda ^1\) we have for each \( x\in ((-\infty ,0])^{N}\) and from (72)
If \(X\in L^{{\widehat{\Phi }}}\), then by definition there exists a \(\lambda _{0}>0\) such that the inequality \(\mathbb {E}_{\mathbb {P}}\left[ u_{j}(\lambda (-\left| X^{j}\right| )\right] >-\infty \) holds for every \(\lambda \le \lambda _{0}\) and \(j=1,\dots ,N\). This and (73) then imply the existence of some \(\lambda _0>\lambda _{1}>0\) such that \(\mathbb {E}_{\mathbb {P}}\left[ \Lambda (-\lambda \left| X\right| ) \right] >-\infty \) for every \(\lambda \le \lambda _{1},\) that is \(X\in L^{\Phi }.\) \(\square \)
Just to mention a few explicit examples, any of the following multivariate utility functions satisfy the Standing Assumption I and Assumption 6.3:
where \(u:\mathbb {R\rightarrow R}\), for some \(p>1,\) is any one of the following functions:
and \(u_{1},\dots ,u_{N}\) are exponential utility functions (\( u_{j}(x^{j})=1-\exp {(-\alpha _{j}x^{j})},\,\alpha >0\)) for any choice of u as above.
The function \(\Lambda \) in (70) could also be constructed as follows. Let \(G:\mathbb {R}^{N}\mathbb {\rightarrow R}\) be convex, monotone decreasing and bounded from below, and \(F:\mathbb { R\rightarrow R}\) be concave and monotone decreasing on range(G). Then \( \Lambda :\mathbb {R}^{N}\mathbb {\rightarrow R}\) defined by
is concave, monotone increasing and bounded above by \(F(\inf G).\) Notice that we require differentiability only in few circumstances, mainly concerning uniqueness. We here provide an example in which our assumptions are met, covering the non differentiable case. Take \(\gamma _{j}\ge 0,\,j=1,\dots ,N\), \(G(x):=\sum _{j=1}^{N}\gamma _{j}(x^{j}-k^{j})^{-}\) and take \(F:\mathbb {R\rightarrow R}\) defined by \(F(x):=-x^{\alpha }\) , \(\alpha \ge 1\), which is concave and monotone decreasing on \(range(G)=[0,\infty ).\) Then
is concave, monotone increasing and bounded above by 0, and \( U(x):=\sum _{j=1}^{N}u_{j}(x^{j})+\Lambda (x)\), with \(u_{1},\dots ,u_{N}\) exponential utility functions and \(\Lambda \) assigned in (75), satisfies Standing Assumption I.
We conclude this Section providing a method to identify suitable candidates for Standing Assumption I.
Remark 7.4
Let U be a multivariate utility function, bounded from above. Define for each \(j=1,\dots ,N\)
Then \(u_1^\infty ,\dots ,u_N^\infty \) are real valued, concave and nondecreasing, and satisfy
With the same notation for \({\widehat{\Phi }}\) and \({\widehat{\Phi }}_{j}\) in Proposition 7.1 (with \(u_j^\infty \) in place of \(u_j\)), we see that \(U(x)\le -{\widehat{\Phi }}((x)^{-})+\sup _{z\in {\mathbb {R}} ^{N}}U(z)\). Thus, if one can guarantee, say by explicit computation, that (a) \(u_{1}^{\infty },\dots ,u_{N}^{\infty }\) are strictly concave and strictly increasing, (b) that \(L^{{\widehat{\Phi }}}=L^{\Phi }\), then Standing Assumption I is satisfied.
7.1 Comparison with (univariate) SORTE
We suppose now that U has the form (74) for \(u\equiv 0\) (which is allowed, since u needs not be strictly concave nor strictly increasing by Propositions 7.1 and 7.3). Assumption 3.8 and Assumption 6.3 are left untouched, and Standing Assumption I is satisfied automatically provided that \( u_1,\dots ,u_N\) satisfy the assumptions in Proposition 7.1. Theorems 4.5 and 4.6 show that both existence and uniqueness can be obtained assuming closedness under truncation for far less strong assumptions than the ones in Biagini et al. (2021) (that is, without requesting the validity of Equation (22) in Biagini et al. (2021)). In particular then the following holds true.
Corollary 7.5
Let let \(u_{1},\ldots ,u_{j}:{\mathbb {R}} \rightarrow {\mathbb {R}}\) be strictly increasing, strictly concave and satisfying the Inada conditions. Then under either Assumptions 3.8 or 6.3 a SORTE, as defined in Biagini et al. (2021), exists.
References
Acciaio, B. (2007). Optimal risk sharing with non-monotone monetary functionals. Finance and Stochastics, 11(2), 267–289.
Aliprantis, C. D., & Border, K. C. (2006). Infinite dimensional analysis (3rd ed.). Berlin: Springer.
Armenti, Y., Crépey, S., Drapeau, S., & Papapantoleon, A. (2018). Multivariate shortfall risk allocation and systemic risk. SIAM Journal on Financial Mathematics, 9(1), 90–126.
Barrieu, P., & El Karoui, N. (2005). Inf-convolution of risk measures and optimal risk transfer. Finance and Stochastics, 9(2), 269–298.
Barrieu, P., & Karoui, N. E. (2005). Pricing, hedging and optimally designing derivatives via minimization of risk measures. In Volume on indifference pricing (pp. 144–172). Princeton University Press.
Biagini, F., Doldi, A., Fouque, J.-P., Frittelli, M., & Meyer-Brandis, T. (2021). Systemic optimal risk transfer equilibrium. Mathematics and Financial Economics, 15(2), 233–274.
Biagini, F., Fouque, J.-P., Frittelli, M., & Meyer-Brandis, T. (2019). A unified approach to systemic risk measures via acceptance sets. Mathematical Finance, 29(1), 329–367.
Biagini, F., Fouque, J.-P., Frittelli, M., & Meyer-Brandis, T. (2020). On fairness of systemic risk measures. Finance and Stochastics, 24(2), 513–564.
Biagini, S., & Frittelli, M. (2008). A unified framework for utility maximization problems: An Orlicz space approach. Annals of Applied Probability, 18(3), 929–966.
Borch, K. (1962). Equilibrium in a reinsurance market. Econometrica, 30(3), 424–444.
Bouchard, B., & Pham, H. (2005). Optimal consumption in discrete-time financial models with industrial investment opportunities and nonlinear returns. Annals of Applied Probability, 15(4), 2393–2421.
Bühlmann, H. (1980). An economic premium principle. Astin Bulletin, 11(1), 52–60.
Bühlmann, H. (1984). The general economic premium principle. Astin Bulletin, 14(1), 13–21.
Bühlmann, H., & Jewell, W. S. (1979). Optimal risk exchanges. Astin Bulletin, 10(3), 243–262.
Campi, L., & Owen, M. P. (2011). Multivariate utility maximization with proportional transaction costs. Finance and Stochastics, 15(3), 461–499.
Carlier, G., & Dana, R.-A. (2013). Pareto optima and equilibria when preferences are incompletely known. Journal of Economic Theory, 148(4), 1606–1623.
Carlier, G., Dana, R.-A., & Galichon, A. (2012). Pareto efficiency for the concave order and multivariate comonotonicity. Journal of Economic Theory, 147(1), 207–229.
Dana, R. A., & Le Van, C. (2010). Overlapping sets of priors and the existence of efficient allocations and equilibria for risk measures. Mathematical Finance, 20(3), 327–339.
Deelstra, G., Pham, H., & Touzi, N. (2001). Dual formulation of the utility maximization problem under transaction costs. Annals of Applied Probability, 11(4), 1353–1383.
Dellacherie, C., & Meyer, P.-A. (1978). Probabilities and potential North-Holland Mathematics Studies (Vol. 29). Amsterdam-New York: North-Holland Publishing Co.
Doldi, A. (2021). Equilibrium, systemic risk measures and optimal transport: A convex duality approach. Doctoral Thesis, available at https://air.unimi.it/.
Edgar, G. A., & Sucheston, L. (1992). Stopping times and directed processes, Volume of 47 Encyclopedia of Mathematics and its Applications. Cambridge: Cambridge University Press.
Embrechts, P., Liu, H., Mao, T., & Wang, R. (2020). Quantile-based risk sharing with heterogeneous beliefs. Mathematical Programming, 181(2, Ser. B), 319–347.
Embrechts, P., Liu, H., & Wang, R. (2018). Quantile-based risk sharing. Operation Research, 66(4), 936–949.
Filipović, D., & Kupper, M. (2008). Optimal capital and risk transfers for group diversification. Mathematical Finance, 18(1), 55–76.
Filipović, D., & Svindland, G. (2008). Optimal capital and risk allocations for law- and cash-invariant convex functions. Finance and Stochastics, 12(3), 423–439.
Föllmer, H., & Schied, A. (2016). Stochastic Finance (fourth revised and extended). Berlin: An introduction in discrete time. De Gruyter Graduate. De Gruyter.
Fouque, J.-P., & Langsam, J. A. (Eds.). (2013). Handbook on systemic risk. Cambridge: Cambridge University Press.
Heath, D., & Ku, H. (2004). Pareto equilibria with coherent measures of risk. Mathematical Finance, 14(2), 163–172.
Hurd, T. R. (2016). Contagion! Systemic risk in financial networks. SpringerBriefs in Quantitative Finance. Springer.
Jouini, E., Schachermayer, W., & Touzi, N. (2008). Optimal risk sharing for law invariant monetary utility functions. Mathematical Finance, 18(2), 269–292.
Kamizono, K. (2004). Multivariate utility maximization under transaction costs. In Stochastic processes and applications to mathematical finance (pp. 133–149). River Edge, NJ: World Scientific Publishing.
Komlós, J. (1967). A generalization of a problem of Steinhaus. Acta Mathematica Academiae Scientiarum Hungaricae, 18, 217–229.
Liebrich, F.-B., & Svindland, G. (2019a). Efficient allocations under law-invariance: A unifying approach. Journal of Mathematical Economics, 84, 28–45.
Liebrich, F.-B., & Svindland, G. (2019b). Risk sharing for capital requirements with multidimensional security markets. Finance and Stochastics, 23(4), 925–973.
Liero, M., Mielke, A., & Savaré, G. (2018). Optimal entropy-transport problems and a new Hellinger-Kantorovich distance between positive measures. Inventiones Mathematicae, 211(3), 969–1117.
Mastrogiacomo, E., & Rosazza Gianin, E. (2015). Pareto optimal allocations and optimal risk sharing for quasiconvex risk measures. Mathematics and Financial Economics, 9(2), 149–167.
Orihuela, J., & Ruiz Galán, M. (2012). Lebesgue property for convex risk measures on Orlicz spaces. Mathematics and Financial Economics, 6(1), 15–35.
Rao, M. M., & Ren, Z. D. (1991). Theory of Orlicz spaces, volume 146 of Monographs and Textbooks in Pure and Applied Mathematics (Vol. 146). New York: Marcel Dekker Inc.
Rockafellar, R. T. (1968). Integrals which are convex functionals. Pacific Journal of Mathematics, 24, 525–539.
Rockafellar, R.T. (1970). Convex analysis. Princeton Mathematical Series, No. 28. Princeton, NJ: Princeton University Press.
Tsanakas, A. (2009). To split or not to split: Capital allocation with convex risk measures. Insurance: Mathematics and Economics, 44(2), 268–277.
Weber, S. (2018). Solvency II, or how to sweep the downside risk under the carpet. Insurance: Mathematics and Economics, 82, 191–200.
Acknowledgements
the authors would like to thank Achraf Tamtalini for pointing out the necessity of closedness under truncation for the arguments in Sect. 6.2.
Funding
Open access funding provided by Università degli Studi di Milano within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
Lemma A.1
Suppose Assumption 3.8 is satisfied. Then for any \(Y\in {\mathcal {L}}\cap {\mathcal {B}}_A\) and any \({{\mathbb {Q}}}\in {\mathcal {Q}}_{{\mathcal {B}},V}\) it holds that
Proof
Taking \(Y_{m}\) as in Definition 3.7, we have
and
hence by Dominated Convergence Theorem
where the inequality for LHS comes from the fact that \(Y_{m}\in {\mathcal {B}} _{A}\cap (L^{\infty })^{N}\subseteq {\mathcal {B}}_{A}\cap M^{\Phi }\) and \({ \mathbb {Q}}\in {\mathcal {Q}}_{{\mathcal {B}},V}\), so that by Proposition 5.4\(\mathbb {E}_{\mathbb {P}} \left[ \sum _{j=1}^{N}Y^{j}_m\frac{\mathrm {d}{\mathbb {Q}} ^{j}}{\mathrm {d}{ \mathbb {P}}}\right] =\sum _{j=1}^{N}\mathbb {E}_{\mathbb {Q}^{j}}\left[ Y^{j}_m \right] \le \sum _{j=1}^N Y_m^j\le A.\) \(\square \)
Lemma A.2
For every \({{\mathbb {Q}}}\in {\mathcal {Q}}_{{\mathcal {B}},V}\)
Furthermore, any optimum \(({\widehat{Y}},{\widehat{a}})\) for \(S^{{{\mathbb {Q}}}}(A)\) produces an optimum \(({\widetilde{Y}},{\widehat{a}})\) for \(H^{{{\mathbb {Q}}}}(A)\) by setting \({\widetilde{Y}}={\widehat{Y}}-{\widehat{a}}\), and any optimum \(({\widetilde{Y}},{\widehat{a}})\) for \(H^{{{\mathbb {Q}}}}(A)\) produces an optimum \(({\widehat{Y}},{\widehat{a}})\) for \(S^{{{\mathbb {Q}}}}(A)\) by setting \({\widehat{Y}}={\widetilde{Y}}+{\widehat{a}}-\mathbb {E}_{{\mathbb {Q}}}[{\widetilde{Y}}]\).
Proof
We fist show \(S^{{{\mathbb {Q}}}}(A)\ge H^{{{\mathbb {Q}}}}(A)\). Take \(a\in {{\mathbb {R}}}^N\) with \(\sum _{j=1}^Na^j=A\) and \({\widetilde{Y}}\in {\mathcal {L}}\). Define \(Y:=a+{\widetilde{Y}}-\mathbb {E}_{{{{\mathbb {Q}}}}}[{\widetilde{Y}}]\). Then \(Y\in {\mathcal {L}}\) and \(\mathbb {E}_{{{{\mathbb {Q}}}}^j}[Y^j]=a^j\), therefore \(S^{{{\mathbb {Q}}}}(A)\ge {\mathbb {E}}_{\mathbb {P}} \left[ U(X+Y)\right] ={\mathbb {E}}_{\mathbb {P}} \left[ U(X+a+{\widetilde{Y}}-\mathbb {E}_{{{{\mathbb {Q}}}}}[{\widetilde{Y}}])\right] \). Taking now a supremum over \(\{{\widetilde{Y}}\in {\mathcal {L}},a\in {{\mathbb {R}}}^N\text { s.t. }\sum _{j=1}^Na^j=A\}\) the claim follows.
Now we show \(S^{{{\mathbb {Q}}}}(A)\le H^{{{\mathbb {Q}}}}(A)\). Observe first that since U is strictly increasing the budget constraints are tight, so that all the inequalities in the definition of \(S^{{{\mathbb {Q}}}}(A)\) can be turned into equalities without affecting the value of the supremum.
Take \(Y\in {\mathcal {L}},a\in {{\mathbb {R}}}^N\) with \(\sum _{j=1}^Na^j=A\) and \(\mathbb {E}_{{{{\mathbb {Q}}}}}[Y]=a^j,j=1,\dots ,N\). Define \({\widetilde{Y}}:=Y-a\) and observe that \({\widetilde{Y}}\in {\mathcal {L}}\) and \(\mathbb {E}_{{{{\mathbb {Q}}}}}[{\widetilde{Y}}]=0\) . Then \(H^{{{\mathbb {Q}}}}(A)\ge {\mathbb {E}}_{\mathbb {P}} \left[ U(X+a+{\widetilde{Y}}-\mathbb {E}_{{{{\mathbb {Q}}}}}[{\widetilde{Y}}])\right] = {\mathbb {E}}_{\mathbb {P}} \left[ U(X+Y)\right] \). The claim follows taking a supremum over \(\{Y\in {\mathcal {L}},a\in {{\mathbb {R}}}^N \text { s.t. }\mathbb {E}_{{{{\mathbb {Q}}}}}[Y]=a^j,\sum _{j=1}^Na^j=A\}\). This argument also shows how optima for one of these problems produce optima for the other in the way descried in the statement (just observe that in this case all the inequalities above become equalities). \(\square \)
1.1 Additional properties of multivariate utility functions
We work under Standing Assumption I and II without further mention.
Lemma A.3
Let \((Z_n)_n\) be a sequence of random variables taking values in \({\mathbb {R}}^N\) such that \(\mathbb {E}_\mathbb {P} \left[ U(Z_n)\right] \ge B\) for all n, for some \(B\in {\mathbb {R}}\).
-
1.
If \(\sup _n\left| \sum _{j=1}^N\mathbb {E}_ \mathbb {P} \left[ Z^j_n\right] \right| <+\infty \) then \(\sup _n\sum _{j=1}^N \mathbb {E}_\mathbb {P} \left[ \left| Z^j_n\right| \right] <\infty \).
-
2.
If \(Z_n\rightarrow Z\) \({\mathbb {P}}\)-a.s. and \(\sup _n\sum _{j=1}^N\mathbb {E}_\mathbb {P} \left[ (Z^j_n)^+\right] <+\infty \) then \(\mathbb {E}_\mathbb {P} \left[ U(Z)\right] \ge B\).
Proof
Item 1. Suppose that
From the boundedness of
we conclude that \(\sup _{n}\sum _{j=1}^{N}\mathbb {E}_{\mathbb {P}}\left[ (Z_{n}^{j})^{-}\right] =+\infty \). Select a, b as in (19) . Then we have
which is clearly a contradiction.
Item 2. For \(\varepsilon >0\) define the function \(\Gamma _{\varepsilon }\) as
where the coefficient \(b_{\varepsilon }\) is the one in (18). Then \(\Gamma _{\varepsilon }\ge 0\) and by Fatou Lemma we have
As a consequence
Since the term multiplying \(\varepsilon \) is finite by hypothesis and the inequality holds for all \(\varepsilon >0\) we conclude that \(\mathbb {E}_{ \mathbb {P}}\left[ U(Z)\right] \ge B\). \(\square \)
1.2 Explicit computation of the convex conjugate in an exponential setup
Lemma A.4
Take \(\alpha _1,\dots ,\alpha _N>0\) and consider for \(x=[x^1,\dots ,x^N]\in {{\mathbb {R}}}^N\)
Define
Then the conjugate \(V(w)=\sup _{x\in {{\mathbb {R}}}^N}\left( U(x)-\sum _{j=1}^Nx^jw^j\right) \) satisfies: for any \(w\in (0,+\infty )^N\cap \mathrm {dom}(V)\)
and for any \(w=[z,\dots ,z]\in (0,+\infty )^N\cap \mathrm {dom}(V)\)
Proof
Take \(w=[w^1,\dots ,w^N],w^j>0\,\forall j=1,\dots ,N\) with \(w\in \mathrm {dom}(V)\). Then
where in \((\star )\) we exploited the minimax Theorem 2.4 in Liero et al. (2018). Now observe that since \(w\ne 0\), if the infimum over h were attained at \(h=0\) we would get \(V(w)=+\infty \). Hence, recalling that \(w\in \mathrm {dom}(V)\),
where in the last equality we set \(2\log (h)=-x\). Now, recalling that \(\sup _{x\in {{\mathbb {R}}}}\left( -e^{-\gamma x}-xw\right) =\frac{w}{\gamma }+\frac{w}{\gamma }\log \left( \frac{w}{\gamma }\right) \) we get from the equation above that (79) holds. Expressions (80) and (81) can then be obtained by direct computation. \(\square \)
1.3 Results on multivariate Orlicz spaces
Proof of Proposition 2.4
We show that \(K_{\Phi }\) is a subspace of the topological dual of \(L^{\Phi }\) and is a subset of \((L^{1}({\mathbb {P}}))^{N}\).
For \(Z\in K_{\Phi }\) consider the well defined linear map \(\phi :L^{\Phi }\rightarrow L^{1}({\mathbb {P}})\), \(X\mapsto \sum _{j=1}^{N}X^{j}Z^{j}\). Suppose \(X_{n}\rightarrow X\) in \(L^{\Phi }\) and \(\phi (X_{n})\rightarrow W\), then we can extract a subsequence \((X_{n_{k}})\) converging almost surely to X, since convergence in Luxemburg norm implies convergence in probability (Lemma 2.2 Item 5). It is then clear that \(\phi (X_{n_{k}})=\sum _{j=1}^{N}X_{n_{k}}^{j}Z^{j}\rightarrow _{k}\sum _{j=1}^{N}X^{j}Z^{j}=W\,{\mathbb {P}}\)-a.s., thus the graph of \(\phi \) is closed in \(L^{\Phi }\times L^{1}({\mathbb {P}})\) (endowed with product topology). By Closed Graph Theorem (Aliprantis & Border, 2006 theorem 5.20) the map is then continuous, thus any vector in \(K_{\Phi }\) identifies a continuous linear functional on \(L^{\Phi }\). Finally since \([sign(Z^{j})]_{j=1}^{N}\in L^{\infty }({\mathbb {P}})\subseteq M^{\Phi }\subseteq L^{\Phi }\), \( \sum _{j=1}^{N}\left| Z^{j}\right| \in L^{1}({\mathbb {P}}) \) yielding \(K_{\Phi }\subseteq L^{1}({\mathbb {P}}).\) \(\square \)
Proof of Proposition 2.5 Item 1
We show that for any extended real valued vector
we have
and that, moreover
Argue as in Proposition 2.2.8 of Edgar and Sucheston (1992): take any \(X\in L^\Phi \) and \( Z\in (L^0({\mathbb {P}}))^N\) and assume w.l.o.g. both are componentwise nonnegative (multiplying by signum functions will not affect Luxemburg norms by definition). Take sequences of simple functions \((Y_{n}^{j})_{n}\), \( j=1,\dots ,n\) each converging to \(X^{j}\) monotonically from below. Clearly \( \left\| Y_{n}\right\| _{\Phi }\le \left\| X\right\| _{\Phi }\) for each n and by Monotone Convergence Theorem
This implies that
since \(L^{\infty }\subseteq M^{\Phi }\). The converse inequality is evident, so that (82) follows. Now suppose
Observe (by using \(\left| X^{j}\right| sgn(Z^{j})\) in place of \( X^{j} \) in RHS below) that
where we used a Closed Graph Theorem argument similar to the one in the proof of Proposition 2.4, with \(M^\Phi \) in place of \( L^\Phi \), to show finiteness of RHS: since \(X\mapsto \sum _{j=1}^NX^jZ^j\) is well defined and continuous on \(M^\Phi \) it must have finite operator norm, i.e. RHS. Now it follows that
which in turns provides \(Z\in K_{\Phi }\). \(\square \)
Proof of Proposition 2.5 Item 2
We prove that the topological dual of \((M^{\Phi },\left\| \cdot \right\| _{\Phi })\) is \((K_{\Phi },\left\| \cdot \right\| _{\Phi }^{*})\). By order continuity, for a given linear functional \(\phi \) in the topological dual of \(M^{\Phi }\) we have that \(A\mapsto \phi ([0,\dots ,0,1_{A},0,\dots ,0])\) defines a (finite) absolutely continuous measure with respect to \({\mathbb {P}}\). This gives by Radon–Nikodym Theorem a vector \( Z\in (L^{1})^{N} \) satisfying: for every vector of simple functions \(s\in (L^{\infty }({\mathbb {P}}))^{N}\) \(\phi (s)=\sum _{j=1}^{N}\mathbb {E}_{\mathbb { P}}\left[ s^{j}Z^{j}\right] \) We now prove that Z belongs to \(K_{\Phi }\): take \(X\ge 0\) and a sequence \((Y_{n})_{n}\) of non negative simple functions (vectors of simple functions more precisely) converging to X from below.
By order continuity of the topology on \(M^{\Phi }\) we have
Thus by Monotone Convergence Theorem
This proves that \(Z\in K_{\phi }\), since the argument above can be applied to any \(0\le X\in M^{\Phi }\) and subsequently to any \(X\in M^{\Phi }\). Finally, the norm we use on \(K_{\Phi }\) is exactly the usual one for continuous linear functionals, so \((K_{\Phi },\left\| \cdot \right\| _{\Phi }^{*})\) is isometric to the topological dual of \((M^{\Phi },\left\| \cdot \right\| _{\Phi })\). \(\square \)
Proof of Proposition 2.5 Item 3
We show that if we suppose
then we have that \(K_{\Phi }=L^{\Phi _{1}^{*}}\times \dots \times L^{\Phi _{N}^{*}}\). To see this, observe that
Now apply Corollary 2.2.10 in Edgar and Sucheston (1992) componentwise. \(\square \)
Proof of Remark 2.6
To prove the claims, observe that \(M^{\Phi }\subseteq M^{\Phi _{1}}\times \dots \times M^{\Phi _{N}}\) follows from the fact that \(\mathbb {E}_{\mathbb {P }}\left[ \Phi _{j}(\lambda \left| X^{j}\right| )\right] \le \mathbb { E}_{\mathbb {P}}\left[ \Phi (\lambda \left| X\right| )\right] \), while the converse \((\supseteq )\) is trivial.
We now prove inequalities (12). First observe that for \( X\in M^{\Phi }\) and for every \(j=1,\dots ,N\) the functions \(\gamma \mapsto \mathbb {E}_{\mathbb {P}}\left[ \Phi (\frac{1}{\gamma }\left| X\right| )\right] \) and \(\gamma \mapsto \mathbb {E}_{\mathbb {P}}\left[ \Phi _{j}(\frac{ 1}{\gamma }\left| X^{j}\right| )\right] \) are continuous by Dominated Convergence Theorem, hence for \(\left\| X\right\| _{\Phi }\ne 0\) and every \(j=1,\dots ,N\)
Since also for \(\left\| X\right\| _{\Phi }=0\) we have \(X=0\) and as a consequence \(\left\| X^{j}\right\| _{\Phi _{j}}=0,\,j=1,\dots ,N\), we have
Moreover for \(X\ne 0\) set \(\lambda :=\max _{j}\left( \left\| X^{j}\right\| _{\Phi _{j}}\right) \). Then
Hence for \(X\ne 0\)
and the same trivially holds for \(X=0\). In general then
Now inequalities (12) follow from inequalities (84) and (85) and the claims are proved. \(\square \)
Lemma A.5
Let \(Z\in (L^1({\mathbb {P}}))^N\) be such that for some \(\lambda >0\) \(\mathbb {E}_\mathbb {P} \left[ V(\lambda Z)\right] <+\infty \). Then \(Z\in K_\Phi \).
Proof
By definition of V we have for any \(x,z\in {\mathbb {R}}^{N}\) \( -\left\langle x,z\right\rangle \le V(z)-U(X)\). Take Z with \(\mathbb {E}_{ \mathbb {P}}\left[ V(\lambda Z)\right] <+\infty \) for some \(\lambda >0\). For any \(X\in M^{\Phi }\) consider \({\widehat{X}}\) defined as
and observe that \({\widehat{X}}\in M^{\Phi }\). Moreover we have \(\lambda \left\langle \left| X\right| ,\left| Z\right| \right\rangle =-\left\langle {\widehat{X}},\lambda Z\right\rangle \le V(\lambda Z)-U( {\widehat{X}})\). If \({\widehat{X}}\in M^{\Phi }\) then, by (13), \(\mathbb {E}_\mathbb {P} \left[ U({\widehat{X}})\right] >-\infty .\) Since \(V(\lambda Z)\in L^{1}({\mathbb {P}})\) by hypothesis, we conclude that \(\left\langle X,Z\right\rangle \in L^{1}({\mathbb {P}})\) for every \(X\in M^{\Phi }\), which in turns yields \(Z\in K_{\Phi }\) by Proposition 2.5 Item 1. \(\square \)
1.4 On Komlós Theorem
We now recall the original Komlós Theorem:
Theorem A.6
(Komlós) Let \((f_{n})_{n}\subseteq L^{1}((\Omega , {\mathcal {F}},{\mathbb {P}},);{\mathbb {R}})\) be a sequence with bounded \(L^{1}\) norms. Then there exists a subsequence \((f_{n_{k}})_{k}\) and a g again in \( L^{1}\) such that for any further subsequence the Césaro means satisfy:
Proof
See Komlós (1967) Theorem 1a. \(\square \)
Corollary A.7
Let a sequence \((Y_n)_n\) be given in \(L^1({ \mathbb {P}}_1)\times \dots \times L^1({\mathbb {P}}_N)\) such that for probabilities \({\mathbb {P}}_1,\dots ,{\mathbb {P}}_N\ll {\mathbb {P}}\)
Then there exists a subsequence \((Y_{n_h})_h\) and an \({\widehat{Y}}\in L^1({ \mathbb {P}}_1)\times \dots \times L^1({\mathbb {P}}_N)\) such that every further subsequence \((Y_{n_{h_k}})_k\) satisfies
Proof
We suppose \(N=2\), the argument can be iterated. The result follows from a diagonal argument: take the first component, we have a subsequence and an \( {\widehat{Y}}^1\) s.t. each further subsequence has \({\mathbb {P}}_1\)-a.s. converging Césaro means as in Theorem A.6. Now take this sequence in place of the one we began with, and do the same for the second component. Notice that in the end we get a subsequence for the second component too, and the corresponding indices yield a subsequence of the one we extracted for the first component. The claim follows. \(\square \)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Doldi, A., Frittelli, M. Multivariate systemic optimal risk transfer equilibrium. Ann Oper Res 336, 435–480 (2024). https://doi.org/10.1007/s10479-022-04652-0
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10479-022-04652-0