On the influence of collection cost on reverse channel configuration

Abstract

This paper revisits the impact of collection cost on a manufacturer’s optimal reverse channel choice. A manufacturer who remanufactures his own products has the choice between managing collection of used products himself, let the retailer manage collection or involve a third party company to manage collection. In particular, we consider a convex collection cost function depending on the collection rate. Contrary to previous literature, we show that the manufacturer always prefers retailer-managed collection, independent of collection cost. The retailer will always choose a positive collection rate. If collection cost is above a certain threshold, not all used products will be collected and the manufacturer (almost) collects all channel profits. Third party-managed collection is always dominated. In extensions, we also consider a restriction to equilibria and a minimum collection rate, which may be imposed by regulation. Both extensions may change the reverse channel choice to manufacturer-managed. Moreover, we see that it may be impossible for regulation to increase collection because the profit-maximizing collection rate may already be the highest economically viable one.

1 Introduction

Today, the importance of the environmental performance of products and processes for sustainable manufacturing is widely recognized. Legislation in economic areas like Europe, North America, and Japan encourages this awareness, and many companies also take proactive measures. Accordingly, remanufacturing has become increasingly popular. The remanufacturing process starts with the reclamation of used products. Mostly, they are then disassembled, cleaned and inspected. Depending on the quality of the used products, some spare parts may be added and, finally, they are reassembled to “like-new” products (see, e.g., Lund and Hauser 2010). In doing so, manufacturers are establishing economically viable production and distribution/collection systems that enable remanufacturing of used products in parallel with the manufacturing of new products. In this paper, we consider products with no distinction between new and remanufactured products, and we refer to the combination of (re-)manufacturing and distribution/collection system as closed-loop supply chain.

In practice, three major reverse channel configurations are observed (see, e.g., Savaskan et al. 2004). First, some manufacturers like Canon, Hewlett-Packard, and Xerox collect their used products directly from customers. Second, companies like (no longer existing) Eastman Kodak collect their single-use cameras through retailers. Other examples include Haier and Changhong who not only set up their own subsidiaries that primarily engage in collecting and handling used products but also established a coalition with large retailers (e.g., Suning, Gome) in China (see, e.g. Li et al. 2002; Swami and Shah 2011). Third, the “big three” US auto makers use dedicated companies for managing used-product collection. Third parties like GENCO are also used by some consumer goods manufacturers. The most prominent example is Apple, who uses several third party companies for collection (e.g. Brightstar in Germany and Phobio in the US).

In this paper, we investigate how reverse channel choice affects forward channel decisions, used-product return rate, and profits in a two-echelon supply chain. We model a single manufacturer-retailer dyad with product remanufacturing.¹ Based on observations from practice and the existing literature, we consider three reverse channel structures: (1) The manufacturer directly collects used products from the customers (model M). (2) The manufacturer contracts the collection of used products to the retailer (model R). Finally, (3) he may contract collection to a third party (model 3P). All supply chain members seek to maximize their profits. However, the manufacturer has sufficient channel power over the retailer and the third party collector to act as a Stackelberg leader. Compared to the extant literature (i.e. Atasu et al. 2013), we consider a wider range of cost parameters that only excludes trivial solutions like no remanufacturing or no activity at all. By contrast, the parameter range is usually restricted to improve tractability and only equilibria are analyzed.

In this context, we address the following research questions:

• (1) Given that no party has an operational advantage, which reverse channel configuration is chosen by the manufacturer?

• (2) How does this choice depend on his restriction to equilibria? After all, as the Stackelberg leader, he is free to choose his decision.

• (3) How do wholesale price, retail price, and profits depend on demand and cost parameters for each configuration? And how do these parameters influence the incentives to invest in used-product collection and the product return rates?

• (4) Finally, how does an exogenously given collection rate, which may be imposed by regulation, influence the manufacturer’s choice?

Some of the paper’s key results demonstrate that without the restriction to equilibria, the manufacturer always prefers retailer-managed collection because this allows the manufacturer interesting strategies to nudge the retailer towards the desired collection effort. This contrasts Atasu et al. (2013), whose manufacturer is constrained to equilibria and sometimes prefers to manage collection himself. If collection costs are high, not all used products are collected and the manufacturer collects almost all channel profits, whereas he leaves an arbitrarily small share to the retailer to ensure his participation. Interestingly, for some ranges of collection cost, the reverse channel choice does not influence total channel profit, but only who pays for collection. If, however, the manufacturer is constrained to equilibria, he sometimes prefers retailer-managed collection and sometimes collects himself. Regarding the minimum collection rate, we demonstrate that this may change the reverse channel choice. Sometimes, it is even impossible for the manufacturer to profitably ensure a higher collection rate.

The remainder of this paper is organized as follows: Sect. 2 briefly reviews related literature. The model and notation are given in Sect. 3 while Sect. 4 contains the analysis and comparison of the different reverse channel structures. Section 5 restricts the manufacturer—analogous to Atasu et al. (2013)—to equilibria. Moreover, the case of a given minimum collection rate is presented in Sect. 6. The final Sect. 7 summarizes main findings and presents conclusions.

2 Literature

Research on remanufacturing and closed-loop supply chains has mushroomed during the last two decades and consists of a plethora of areas. For example, empirical work has tried to estimate the size of the remanufacturing industry (e.g. Lund and Hauser 2010; Giuntini and Gaudette 2003) or customer behavior, for example whether remanufactured products cannibalize new product sales (Guide and Li 2010). Lots of analytical papers focus a supply chain perspective. Among them, Ferguson and Toktay (2006) as well as Oraiopoulos et al. (2012) focus on whether to remanufacture at all as well as pricing and quantity decisions of a manufacturer and a competing remanufacturer. Other research focuses the acquisition (Guide et al. 2003; Gönsch 2014, 2015), sorting and usage (as spare parts, for remanufacturing, or waste, e.g. Galbreth and Blackburn 2006; Ferguson et al. 2011) of used products. Related is also research on material flows in recycling networks (e.g. Walther et al. 2009) or on closed-loop supply chain design with a rather spatial focus (e.g. Altmann and Bogaschewsky 2014). Krapp and Kraus (2019) review coordination contracts for reverse supply chains and Pishchulov et al. (2014) as well as Zhang et al. (2014) are recent examples of this research. The literature has been reviewed by Guide and van Wassenhove (2009) as well as Govindan et al. (2015).

In this paper, we add to a literature stream that analyzes the reverse channel configuration of a closed-loop supply chain. It goes back to the seminal paper of Savaskan et al. (2004), who are the first to analyze the three reverse channel configurations considered here. They set the modelling framework for a stream of follow-up papers that analyze a variety of supply chain structures (see Table 1). As we also use this framework, we briefly describe and discuss their main assumptions.

Table 1 Overview of Savaskan et al. (2004) literature stream (n.a.: not applicable, M: manufacturer, R: retailer, 3P: third party collector)

In the basic closed-loop supply chain, a manufacturer produces new products and remanufactures used ones; new and remanufactured products are indistinguishable. Remanufacturing is cheaper, but requires used products. The products are sold to a retailer, who sells to customers. All contracts simply consist of per-unit payments. Used products are collected by the retailer or a third party company, which then sells them to the manufacturer. All used products collected are identical and can (and will) be remanufactured. In more detail, Savaskan et al. (2004) use the following assumptions:

• A static one-period model assumes the previous existence of the product in the market. The focus of the analysis is on average values per period when the product’s life cycle is much longer than its useful life with a customer. For example, a specific type of single-use camera is produced for several month or years, but used by the customer for weeks at most.

• Linear, mix-dependent production cost with per unit costs depending on the mix of new and remanufactured products. In particular, unit cost linearly decreases in the share of remanufactured products, which, in the static model, is equal to the collection rate. This assumption states that remanufacturing is cheaper than manufacturing and, ceteris paribus, the manufacturer strictly prefers a higher return rate. Savaskan et al. (2004) note that different quality levels of used products would not structurally change the results as they obviously only decrease remanufacturing’s per unit cost savings.

• Rate-dependent collection cost imply collection costs are convex and increase in the collection rate. In most papers, collection cost are a quadratic function of the rate. This is motivated as costs associated with securing a supply of used products to be collected, for example, advertisement or investment costs. The idea is to increase the “response of consumers who have an incentive/enthusiasm for the remanufacturing of their used products as a result of the promotional/advertising activities of the agent in the reverse channel” (Savaskan et al. 2004, Sect. 3). Please note that this assumption does not exclude collection cost that depend linearly on quantity; in fact, Savaskan et al. (2004) include such a parameter as well. However, it is important to realize that the latter cost represent, for example, per unit mailing costs and not a direct payment to customers. Although dubbed so by some authors (e.g., Qiaolun et al. 2008; Jena and Sarmah 2014), this would suggest that the resulting residual value might influence customers’ firsthand buying decisions. Moreover, in the models of Savaskan et al. (2004) and most of the follow up papers, this parameter is structurally irrelevant as only the difference of per-unit collection cost and per-unit cost savings from remanufacturing matters.

• Linear demand functions result from a uniform willingness-to-pay distribution. Although the generalizability of the results in this regard is an open question, it seems to be shared for tractability with large parts of the supply chain literature.

• No operational advantages are enjoyed by any supply chain configuration. This assumption is not explicitly stated by most of the literature and implies that, for example, securing the same collection rate implies identical costs, no matter which party manages collection.

• The manufacturer acts as a Stackelberg leader because of sufficient channel power. Industry provides ample examples of this traditional power structure, for example supply chains with giant OEMs with a strong brand such as GM, Toyota, or Apple. However, during the last decades, retailing giants like Wal-Mart, Tesco, or Hudson’s Bay have developed, and it is widely observed that the respective supply chains are led by them. Related is also that all information is public and the leader thus knows the followers’ reaction functions.

• Only interior solutions and equilibria are considered, that is, solutions resulting from first order conditions. This assumption is shared by almost all the literature and usually interior solutions are ensured by restricting the parameter space accordingly. Some models apparently possess exactly one interior solution without further restrictions.

Table 1 gives an overview of the literature stream that follows Savaskan et al. (2004). The last seven columns represent the above assumptions. The symbol ✔ signals that the paper shares an assumption, whereas ✖ symbolizes a deviation. In the following, we give a brief overview of the papers’ focus. Savaskan and van Wassenhove (2006) do not consider a third party, but competing retailers. Qiaolun et al. (2008) compare the three reverse channel configurations with customers who are paid per unit to return their used products and the return rate increases in this acquisition price. Although this is the motivation given by the authors, given the discussion above, an interpretation as some sort of variable collection effort may be more appropriate. Wei and Zhao (2011) consider manufacturer-managed collection with two competing retailers and fuzzy demand and costs. Hong and Yeh (2012) consider a special setting with recycling instead of remanufacturing and a non-profit collection firm. Atasu et al. (2013) is the basis for this paper and discussed in depth below. Choi et al. (2013) investigate Stackelberg leadership by each of the three agents in the chain. Huang et al. (2013) consider competition in collection. De Giovanni and Zaccour (2014) analyze a dynamic version of Savaskan et al. (2004) and consider operational advantages. They find that the manufacturer outsources collection only when the retailer or third-party is more efficient in terms of collection cost or return rate. Jena and Sarmah (2014) consider a system with two manufacturers and a retailer to investigate different coalitions. Zhang et al. (2014) study the problem of designing contracts when collection cost is the retailer’s private information. Maiti and Giri (2015) compare four different power structures to the coordinated supply chain with endogenous product quality. Wei et al. (2015) compare the manufacturer and retailer with symmetric and asymmetric information. Gao et al. (2016) consider channel power structures if collection effort influences demand. Zu-Jun et al. (2016) compare various coalitions in a closed-loop supply chain with a retailer and two competing third parties who manage collection. Han et al. (2016) consider remanufacturing cost risks in a setting with the retailer as Stackelberg leader. Wu and Zhou (2017) compare the configurations chosen in competing supply chains, each consisting of a manufacturer and a retailer. Apparently independently from each other, Zhao et al. (2017) and Liu et al. (2017) investigate simultaneous collection by two agents.

In addition, there is ample literature that only shares some or none of the assumptions. For example, Chuang et al. (2014) use a newsvendor model to compare the three classic channel structures for a short-life high-tech product with uncertain demand and an exogenously given collection rate.

Savaskan et al. (2004) focus on interior solutions (i.e. not all products are collected) and conclude that retailer-managed collection is optimal for the manufacturer under certain assumptions. Later, Atasu et al. (2013) extend this work by relaxing bounds which Savaskan et al. (2004) apparently introduced to ensure interior equilibria or reduce the number of cases. In particular, they consider a wider parameter range for investment cost and relax an artificial bound on the transfer price for used products, one of the manufacturer’s decision variables. However, although a Stackelberg setting is considered where the manufacturer decides first, they still focus on equilibria in the sense that no one can improve his profit by marginally deviating from the solution and find that the manufacturer prefers to manage collection himself for extremely low and high collection costs. The latter is surprising as this investment cost range is also considered in Savaskan et al. (2004) and the relaxation regarding transfer price, at first glance, should incline the results more towards channel configurations with this variable, i.e. third party- and retailer-managed collection. Although the relaxation of the bound also removes a possible equilibrium, there are still solutions at the border where the retailer earns zero profit and is indifferent between participating and not. Atasu et al. (2013) do not consider this border where one agent is indifferent due to their restriction to equilibria. Most other papers avoid this situation by restricting the parameter space.

This paper directly extends Atasu et al. (2013). In line with the above research, we use a static one-period model with linear, mix-dependent production cost. Likewise, we share the standard assumption that customers’ willingness-to-pay is uniformly distributed. Collection is operationally the same no matter who controls it. That is, all parties share the same efficiency regarding collection cost and return rate. In line with most of the literature, the manufacturer is the Stackelberg leader, which ensures comparability.

Our main deviation from the previous literature is that we do not restrict the manufacturer to equilibria, but also allow him to choose a solution that is not stable in the sense that he would be better off with a marginal deviation. In the literature, this issue is often not explicitly stated but it is simply assumed that for a continuous problem an agents’ discrete behavior is still the same at the border where he is indifferent. For example, in an extension, Savaskan et al. (2004, Sect. 6) assume that the retailer still agrees to some coordination contract if her profit equals profit from a linear contract. In other streams of literature, it is widely assumed that indifferent customers buy. By contrast, we do not frame this situation as a (maybe misleading) equilibrium but require the Stackelberg leader to choose a solution not at, but arbitrarily close to the border. We transparently report that our results are valid in the limit, but not at the border. While we feel that the above is largely a matter of presentation, we also apply this reasoning to the case where the structure of the solution changes in the limit, i.e. the retailer’s profit function loses concavity. From an industry perspective, we motivate this as the leader deliberately choosing a solution that yields less profit for him but improves a partner’s situation, which is widely observed in reality where companies seek to build long-term relationship and increase supply-chain stability.

In an extension, we consider an exogenously given minimum collection rate, that is imposed, for example, by regulation or company policy. Mirroring reality, this is a minimum collection rate; such that the collection rate is still a decision variable. This allows us to identify, for example, when the minimum rate changes the configuration chosen or it is impossible to increase collection profitably.

3 The model

To analyze the effect of collection cost on the reverse channel choice, we consider the same model as Atasu et al. (2013). The key difference is that we allow the manufacturer as the Stackelberg leader to freely make his decision and do not constrain him to equilibria. Besides that, the model is almost identical to Savaskan et al. (2004), who give a detailed discussion of the model and its assumptions.

In the following, a brief summary of the model is given. In this regard, Table 2 provides an overview of the notation used. To improve readability, we stick to the notation used by Savaskan et al. (2004) and Atasu et al. (2013), which is shared almost entirely by all papers in this stream of literature. Lowercase letters refer to (re)manufacturing cost parameters, while uppercase letters refer to collection cost parameters.

Table 2 List of notation

3.1 Forward channel

A decentralized, uncoordinated two-echelon (one manufacturer and one retailer) supply chain sells undifferentiated new and remanufactured products through the same retailer. The classic example is Kodak’s (deceased) single-use camera, where the customer is aware that the product may generally contain used parts but does not know whether his specific camera contains some. The manufacturer is a Stackelberg leader and sells both new and remanufactured products at the same wholesale price $w$ to the retailer, who in turn sells both products at price $p$ to customers. Demand is given by $q\left( p \right) = \left( {1 - p} \right)\phi$, where $\phi$ is a constant that may be interpreted as market size. Thus, customers’ willingness-to-pay (WTP) is uniformly distributed and normalized to the interval $\left[ {0,1} \right]$. Note that this is where the model in Atasu et al. (2013) is slightly less general than Savaskan et al. (2004), who also consider uniform WTP but do not normalize the maximum WTP to 1. The cost of producing a new product is denoted $c_{m}$ whereas the cost of producing a remanufactured product is $c_{rm}$. To avoid trivial solutions, we assume $0 \le c_{rm} < c_{m} < 1$. Let $\tau$ denote the fraction of demand satisfied by remanufactured products. Then, the manufacturer’s profit from selling $q$ units to the retailer is $wq - c_{m} \left( {1 - \tau } \right)q - c_{rm} \tau q$. Define ${{\Delta }} = c_{m} - c_{rm}$ as the cost saving from remanufacturing one unit, then the average cost of manufacturing one unit becomes $c_{m} - \tau {{\Delta }}$ and we can rewrite the manufacturer’s profit as $q\left( {w - c_{m} + \tau {{\Delta }}} \right)$. Note that $\tau$ is the collection rate as well as the share of remanufactured products, because with undifferentiated products, it is optimal to remanufacture and sell all used products collected (under the assumption that all products can be remanufactured). As a static one period model is considered, the collection volume equals $q\tau$. We assume the feasible range of the collection rate is $0 \le \tau \le 1$, although the maximum range may be limited in practice.

3.2 Reverse channel and collection cost

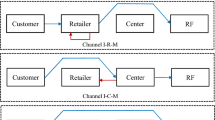
Regardless of who handles the actual collection operation, the party who determines the collection rate and incurs the collection cost is regarded as the one who manages collection. This can be the manufacturer, the retailer, or a third-party firm (see Fig. 1) and incurs a cost $A \le {{\Delta }}$ (e.g. for shipping) for each unit collected as well as an investment cost. Savaskan et al. (2004) argue that this investment may cover promotional/advertising activities to nudge customers to return their used products. Such activities typically have diminishing returns on investment. Thus, they assume that the investment cost increases quadratic in the collection rate and use $\tau^{2} C_{L}$, where $C_{L} > 0$ is a scaling factor.

Fig. 1

Decentralized reverse channel configurations (Atasu et al. 2013)

4 Analysis

In this section, we first determine the optimal solutions for retailer-, manufacturer, and third-party-managed collection. Then, we compare the solutions and show which reverse channel choice is preferred by the manufacturer. Let ${{\varPi }}_{x}^{y}$ denote the profit of company $x$ when company $y$ manages collection, where $x,y \in \left\{ {M,R,3P} \right\}$. Here, $M$ denotes the manufacturer, $R$ the retailer, and $3P$ the third party.

4.1 Retailer-managed collection

When the retailer manages collection, she chooses the sales price $p$ and the collection rate $\tau$ to maximize her profit

$${{\varPi }}_{R}^{R} \left( {p,\tau } \right) = \left( {p - w} \right)q\left( p \right) + \left( {b - A} \right)\tau q\left( p \right) - \tau^{2} C_{L}$$

(1)

where $b$ is the transfer price the retailer receives from the manufacturer for each collected unit. The first term is the profit from the forward chain, the second term is the profit from operating the collection, and the third term is the investment cost for collection. After the manufacturer decides $b$ and $w$, the retailer determines her best response $p\left( {b,w} \right)$ and $\tau \left( {b, w} \right)$ such that her profit ${{\varPi }}_{R}^{R} \left( {p,\tau } \right)$ is maximized. The manufacturer anticipates her decision and chooses $b$ and $w$ such that his profit

$${{\varPi }}_{M}^{R} \left( {b,w} \right) = \left[ {w - c_{m} + \tau \left( {b,w} \right){{\Delta }}} \right]q\left( {p\left( {b,w} \right)} \right) - b\tau \left( {b,w} \right)q\left( {p\left( {b,w} \right)} \right)$$

(2)

is maximized. Here, the first term is the profit from production and sales to the retailer and the second term is the cost for buying used products from the retailer. Depending on the value of the collection cost parameter $C_{L}$, the manufacturer can choose from up to two out of the following four options (see “Appendix A.1” for details and proofs).

Option 1: If and only if $C_{L} < \frac{\phi }{4}\left( {{{\Delta }} - A + \frac{{1 - c_{m} }}{2}} \right)^{2}$, the manufacturer can choose $b^{*}$ and $w^{*}$ such that the retailer’s profit function ${{\varPi }}_{R}^{R}$ is concave. Then, it is best for the manufacturer to choose $b^{*}$ such that the retailer’s stationary best response is pushed to the boundary, i.e. $\tau \left( {b^{*} ,w^{*} } \right) = 1$. The profits are ${{\varPi }}_{M}^{R} = \frac{1}{8}\phi \left( {1 - c_{m} } \right)\left( {2\left( {{{\Delta }} - A} \right) + 1 - c_{m} } \right)$ and ${{\varPi }}_{R}^{R} = \frac{1}{16}\phi \left( {2\left( {{{\Delta }} - A} \right) + 1 - c_{m} } \right)^{2} - C_{L}$. Both are positive and the retailer participates.

Option 2: If and only if $C_{L} \ge \frac{\phi }{4}\left( {{{\Delta }} - A + \frac{{1 - c_{m} }}{2}} \right)^{2}$, the manufacturer can no longer push the retailer’s stationary best response to the boundary because ${{\varPi }}_{R}^{R}$ is no longer even locally concave at the corresponding values for $b$ and $w$. However, his profit is increasing in $b$, and there is a threshold $\overline{b} = A + 2\sqrt {\frac{{C_{L} }}{\phi }}$, below which ${{\varPi }}_{R}^{R}$ is concave. If the manufacturer now chooses $b^{*}$ close to but below $\overline{b}$, he can preserve concavity of ${{\varPi }}_{R}^{R}$ and the retailer’s best response is an interior solution with $\tau \left( {b^{*} ,w^{*} } \right) < 1$. More formally, we have ${{\varPi }}_{M}^{R} \nearrow \frac{{\left( {1 - c_{m} } \right)^{2} \phi }}{{8 - 4\sqrt {\frac{\phi }{{C_{L} }}} \left( {{{\Delta }} - A} \right)}}$ and ${{\varPi }}_{R}^{R} \searrow 0$ for $b \nearrow \overline{b} = A + 2\sqrt {\frac{{C_{L} }}{\phi }}$. Again, both profits are positive and the retailer participates. Although in this case optimal values in the classical sense do not exist for $b$ and $w$, we believe that the manufacturer as the Stackelberg leader is free to choose “good” values close to the threshold if this is better than his other options. Moreover, it is intuitive that with convex collection cost, a large cost parameter $C_{L}$ implies that only a fraction of the used products is collected.

Option 3: If and only if $C_{L} < \frac{\phi }{16}\left( {1 - c_{m} + {{\Delta }} - A} \right)^{2}$, the manufacturer has another option. By choosing $b > \overline{b} = A + 2\sqrt {\frac{{C_{L} }}{\phi }}$, he deprives the retailer of any interior solutions and forces him to a boundary. In principle, the retailer has four boundaries to choose from: $p_{R}^{*} = 0$, $p_{R}^{*} = 1$, $\tau_{R}^{ *} = 0$, and $\tau_{R}^{ *} = 1$. Obviously, at $p_{R}^{*} = 1$ the retailer sells nothing and obtains zero profit. At $p_{R}^{*} = 0$, total supply chain profit is nonpositive. So either the retailer or the manufacturer does not participate. The manufacturer can prevent the retailer from choosing this boundary by setting $b < w + A$. At $\tau_{R}^{ *} = 0$, the supply chain operates without collection and we have the strictly positive profits ${{\varPi }}_{M}^{R} = \frac{1}{8}\phi \left( {1 - c_{m} } \right)^{2}$ and ${{\varPi }}_{R}^{R} = \frac{1}{16}\phi \left( {1 - c_{m} } \right)^{2}$, respectively. Finally, the manufacturer can force the retailer to collect everything ($\tau_{R}^{ *} = 1$) by setting $b^{*}$ high enough. As for each unit sold one unit is returned, only the difference $w^{*} - b^{*}$ matters to the retailer and the manufacturer. The manufacturers’ maximal profit is ${{\varPi }}_{M}^{R} = \frac{1}{8}\phi \left( {1 - c_{m} + {{\Delta }} - A} \right)^{2}$, which is obviously better than without remanufacturing and the retailer obtains ${{\varPi }}_{R}^{R} = \frac{1}{16}\phi \left( {1 - c_{m} + {{\Delta }} - A} \right)^{2} - C_{L}$, which is positive for $C_{L} < \frac{\phi }{16}\left( {1 - c_{m} + {{\Delta }} - A} \right)^{2}$.

Option 4: If and only if $\frac{\phi }{16}\left( {1 - c_{m} + {{\Delta }} - A} \right)^{2} \le C_{L} < \frac{\phi }{4}\left( {1 - c_{m} + {{\Delta }} - A} \right)^{2}$, the manufacturer has an option that is similar to option 3. However, if he was to choose his optimal difference $w^{*} - b^{*}$ from option 3 to enforce $\tau_{R}^{ *} = 1$, we had ${{\varPi }}_{R}^{R} \le 0$ and the retailer would not participate. He can avoid this by sacrificing part of his profit and decrease $w^{*} - b^{*}$ to allow the retailer a positive profit and ensure his participation. In particular, for $\left( {w^{*} - b^{*} } \right) \nearrow \left( {1 - A - 2\sqrt {\frac{{C_{L} }}{\phi }} } \right)$, we have ${{\varPi }}_{R}^{R} \searrow 0$ and ${{\varPi }}_{M}^{R} \nearrow \sqrt {C_{L} \phi } \cdot \left( {1 - c_{m} + {{\Delta }} - A} \right) - 2C_{L}$, which is positive if and only if $C_{L} < \frac{\phi }{4}\left( {1 - c_{m} + {{\Delta }} - A} \right)^{2}$.

Figure 2 compares the options and states the manufacturer’s choice. The upper part with the first three rows is a graph where the collection cost $\tau$ increases from left to right. In the first row, three values partition the domain of $\tau$ into four intervals. The next two rows visualize for each interval, which of the options are possible and chosen by the manufacturer to maximize his profit. The lower part of the figure is a table where each column refers to an interval and shows key values for the option that is preferred by the manufacturer in that interval. As option 1 is not preferred in any interval, we share the corresponding values in the lower right corner.

Fig. 2

Options possible and preferred by the manufacturer for retailer-managed collection (R)

Please note that only option 2 implies $\tau < 1$. Where the manufacturer chooses between option 2 and option 4, he may force the retailer to collect everything, but at the expense of his own profit. Please note that the solution is continuous, although we distinguish three cases regarding $C_{L}$.

It is easy to see that $\tau_{R}$ and $w_{R}$ are nonincreasing in $C_{L}$, whereas $b_{R}$ is nondecreasing. Interestingly, $q_{R}$ is first constant, then increases and finally decreases in $C_{L}$. Obviously, $p_{R}$ displays exactly the opposite behavior. All profits are nonincreasing in $C_{L}$. For low $C_{L}$, when the manufacturer induces $\tau_{R}^{*} = 1$ independent of $C_{L}$, all decisions are independent of $C_{L}$ and only the retailer’s profit is affected by $C_{L}$. For bigger collection costs, the retailer’s profit is arbitrary close to zero and the manufacturer’s decreases in $C_{L}$. The influence of the other parameters on profits is as expected. Moreover, the collection rate $\tau_{M}$ and quantity $q_{m}$ are nonincreasing in $c_{m}$ and $A$ and nondecreasing in ${{\Delta }}$ and $\phi$, whereas the influence is opposite for the price $p_{R}$. Interestingly, the wholesale price $w_{R}$ is nondecreasing in $c_{m}$ and $\phi$ and nonincreasing in ${{\Delta }}$ and $A$. The transfer price $b$ is nondecreasing in $A$ and $C_{L}$ and nonincreasing in $\phi$. For a numerical example with $\phi = 5$, ${{\Delta }} = 0.3$, $c_{m} = 0.5$, and $A = 0.1$, these results are illustrated in Fig. 3 (profits) and Fig. 4 (collection rate, prices, quantity). As option 1 is never preferred by the manufacturer, it is not shown in the figures.

Fig. 3

Profits with retailer-managed collection ($\phi = 5$, ${{\Delta }} = 0.3$, $c_{m} = 0.5$, $A = 0.1$)

Fig. 4

Collection rate, prices, quantity with retailer-managed collection ($\phi = 5$, ${{\Delta }} = 0.3$, $c_{m} = 0.5$, $A = 0.1$)

4.2 Manufacturer-managed collection

When the manufacturer manages collection, he offers the retailer a wholesale price $w$ and the retailer concentrates on the forward channel. Thus, she chooses the sales price $p$ to maximize her profit

$${{\varPi }}_{R}^{M} \left( p \right) = \left( {p - w} \right)q\left( p \right)$$

(3)

Her profit function is concave in $p$ and the manufacturer anticipates the retailer’s best response $p\left( w \right)$. Besides $w$, the manufacturer now also decides on the collection rate $\tau$ and his profit is given by

$${{\varPi }}_{M}^{M} \left( {\tau ,w} \right) = \left[ {w - c_{m} + \tau {{\Delta }}} \right]q\left( {p\left( w \right)} \right) - A\tau q\left( {p\left( w \right)} \right) - \tau^{2} C_{L}$$

(4)

The first term is the profit from production and sales to the retailer, the second term is the cost for the acquisition of used products and the third term is the investment to ensure a collection rate of $\tau$. Again, the solution’s structure depends on the collection cost $C_{L}$. We distinguish two (mutually exclusive) options (see “Appendix A.2” for detailed proofs).

Option 1: If and only if $C_{L} \ge \frac{\phi }{8}\left( {{{\Delta }} - {\text{A}}} \right)\left( {{{\Delta }} - A + 1 - c_{m} } \right)$, the manufacturer’s profit function ${{\varPi }}_{M}^{M}$ is jointly concave in $\tau$ and $w$ and the unique stationary point $\left( {\tau_{M}^{*} , w^{*} } \right)$ is feasible, i.e. $\tau_{M}^{*} \le 1$. We have ${{\varPi }}_{M}^{M} = \frac{{C_{L} \left( {1 - c_{m} } \right)^{2} \phi }}{{8C_{L} - \phi \left( {{{\Delta }} - A} \right)^{2} }}$ and ${{\varPi }}_{R}^{M} = \frac{{4C_{L}^{2} \left( {1 - c_{m} } \right)^{2} \phi }}{{\left( {8C_{L} - \phi \left( {{{\Delta }} - {\text{A}}} \right)^{2} } \right)^{2} }}$. Both are positive if the condition holds.

Option 2: If and only if $C_{L} \le \frac{\phi }{8}\left( {{{\Delta }} - {\text{A}}} \right)\left( {{{\Delta }} - A + 1 - c_{m} } \right)$, there is no interior stationary point. If the condition is only slightly violated, the stationary point is infeasible. If $C_{L}$ is even lower, ${{\varPi }}_{M}^{M}$ is not even locally jointly concave and no stationary points exist, but it is always concave in $w$. Thus, we check the boundaries $\tau_{M}^{*} = 0$ and $\tau_{M}^{*} = 1$. For $\tau_{M}^{*} = 0$, the manufacturer obtains again ${{\varPi }}_{M}^{M} = \frac{1}{8}\phi \left( {1 - c_{m} } \right)^{2}$. For $\tau_{M}^{*} = 1$, we have $\varPi_{M}^{M} = \frac{1}{8}\phi \left( {{{\Delta }} - A + 1 - c_{m} } \right)^{2} - C_{L}$, which is higher if the condition holds. The manufacturer chooses $\tau_{M}^{*} = 1$ and the retailer obtains ${{\varPi }}_{R}^{M} = \frac{1}{16}\phi \left( {{{\Delta }} - A + 1 - c_{m} } \right)^{2}$. Both are strictly positive if the condition holds.

Figure 5 summarizes the results for manufacturer-managed collection in detail. It is easy to see that $\tau_{M}$ is nonincreasing in $C_{L}$, whereas both $w_{M}$ and $p_{M}$ are nondecreasing. Thus, $q_{M}$ is nonincreasing in $C_{L}$. All profits are nonincreasing in $C_{L}$. It is interesting to note that for low $C_{L}$, when the manufacturer sets $\tau_{M}^{*} = 1$ independent of $C_{L}$, all decisions are independent of $C_{L}$ and only the manufacturer’s profit is affected by $C_{L}$. The influence of the other parameters on profits is as expected. Moreover, the collection rate $\tau_{M}$ and the quantity $q_{m}$ decrease in $c_{m}$ and $A$ and increase in ${{\Delta }}$, whereas the influence is opposite for the prices $w_{M}$ and $p_{M}$. Again, we illustrate this with our example ($\phi = 5$, ${{\Delta }} = 0.3$, $c_{m} = 0.5$, and $A = 0.1$) in Fig. 6 (profits) and Fig. 7 (collection rate, prices, quantity).

Fig. 5

Options for manufacturer-managed collection (M)

Fig. 6

Profits with manufacturer-managed collection ($\phi = 5$, ${{\Delta }} = 0.3$, $c_{m} = 0.5$, $A = 0.1$)

Fig. 7

Coll. rate, prices, quantity with manufacturer-managed collection ($\phi = 5$, ${{\Delta }} = 0.3$, $c_{m} = 0.5$, $A = 0.1$)

4.3 Third-party-managed collection

When a third company manages collection, the retailer operates as in manufacturer-managed collection. The manufacturer offers her a wholesale price $w$ and the retailer concentrates on the forward channel. Analogous to (3), she chooses the sales price $p$ to maximize her profit

$${{\varPi }}_{R}^{3P} \left( p \right) = \left( {p - w} \right)q\left( p \right)$$

(5)

The third-party company is offered a transfer price $b$ for each unit collected by the manufacturer. Thus, the third-party company chooses $\tau \left( {b,w} \right)$ to maximize

$${{\varPi }}_{3P}^{3P} \left( \tau \right) = \left( {b - A} \right)\tau q\left( {p\left( w \right)} \right) - \tau^{2} C_{L}$$

(6)

Both profit functions are concave and the manufacturer chooses $b$ and $\tau$ to maximize his profit function given the retailer’s and the third party’s best responses

$${{\varPi }}_{M}^{3P} \left( {\tau ,w} \right) = \left[ {w - c_{m} + {{\Delta }}\tau \left( {b,w} \right)} \right]q\left( {p\left( w \right)} \right)$$

(7)

Again, we distinguish two (mutually exclusive) options:

Option 1: If $C_{L} \ge \frac{\phi }{16}\left( {{{\Delta }} - {\text{A}}} \right)\left( {{{\Delta }} - A + 1 - c_{m} } \right)$ holds, ${{\varPi }}_{M}^{3P}$ has an interior maximizer with $\tau_{3P}^{*} > 0$. If and only if the condition holds, we have $\tau_{M}^{*} \le 1$. However, ${{\varPi }}_{M}^{3P}$ is not necessarily globally concave and we have to check the boundaries $\tau_{3P}^{*} = 0$ and $\tau_{3P}^{*} = 1$. For $\tau_{3P}^{*} = 0$, the manufacturer obtains again ${{\varPi }}_{M}^{3P} = \frac{1}{8}\phi \left( {1 - c_{m} } \right)^{2}$. For $\tau_{3P}^{*} = 1$, we have $\varPi_{M}^{3P} = \frac{1}{8}\phi \left( {{{\Delta }} - A + 1 - c_{m} } \right)^{2} - 2C_{L}$. If the condition holds, the manufacturer’s profit is highest at the interior maximizer and the profits are given by ${{\varPi }}_{M}^{3P} = \frac{{2C_{L} \left( {1 - c_{m} } \right)^{2} \phi }}{{16C_{L} - \phi \left( {{{\Delta }} - {\text{A}}} \right)^{2} }}$, ${{\varPi }}_{R}^{3P} = \frac{{16C_{L}^{2} \left( {1 - c_{m} } \right)^{2} \phi }}{{\left( {16C_{L} - \phi \left( {{{\Delta }} - {\text{A}}} \right)^{2} } \right)^{2} }}$, and ${{\varPi }}_{3P}^{3P} = \frac{{C_{L}^{{}} \left( {{{\Delta }} - A} \right)^{2} \left( {1 - c_{m} } \right)^{2} \phi^{2} }}{{\left( {16C_{L} - \phi \left( {{{\Delta }} - {\text{A}}} \right)^{2} } \right)^{2} }}$. All are strictly positive if the condition holds.

Option 2: If and only if $C_{L} \le \frac{\phi }{16}\left( {{{\Delta }} - {\text{A}}} \right)\left( {{{\Delta }} - A + 1 - c_{m} } \right)$, there is no interior stationary point. If the condition is only slightly violated, the stationary point is infeasible. If $C_{L}$ is even lower, ${{\varPi }}_{M}^{3P}$ is not even locally jointly concave and no stationary points exist, but it is always concave in $w$. Thus, we check the boundaries $\tau_{3P}^{*} = 0$ and $\tau_{3P}^{*} = 1$. For $\tau_{3P}^{*} = 0$, the manufacturer obtains again ${{\varPi }}_{M}^{3P} = \frac{1}{8}\phi \left( {1 - c_{m} } \right)^{2}$. For $\tau_{3P}^{*} = 1$, we have $\varPi_{M}^{3P} = \frac{1}{8}\phi \left( {{{\Delta }} - A + 1 - c_{m} } \right)^{2} - 2C_{L}$, which is higher if the condition holds. The manufacturer chooses $\tau_{3P}^{*} = 1$ and the retailer obtains ${{\varPi }}_{R}^{3P} = \frac{1}{16}\phi \left( {{{\Delta }} - A + 1 - c_{m} } \right)^{2}$; the third party obtains ${{\varPi }}_{R}^{3P} = C_{L}$. All are strictly positive if the condition holds.

Figure 8 summarizes the results for third-party-managed collection in detail. It is easy to see that $\tau_{M}$ is nonincreasing in $C_{L}$, whereas $w_{3P}^{*}$ and $b_{3P}^{*}$ are nondecreasing in $C_{L}$. Thus, $q_{M}$ is nonincreasing in $C_{L}$. All profits are nonincreasing in $C_{L}$ for high $C_{L}$. It is interesting to note that for low $C_{L}$, when the manufacturer sets $\tau_{M}^{*} = 1$ independent of $C_{L}$, all decisions are again independent of $C_{L}$ and only the manufacturer’s and the third-party’s profits are affected by $C_{L}$. Whereas the manufacturer’s profit declines, the third party’s increases in $C_{L}$ as long as the manufacturer seeks to ensure that all products are collected. Then it also declines. The influence of the other parameters on profits is as expected. Moreover, collection rate $\tau_{3P}$ and quantity $q_{3P}$ decrease in $c_{m}$ and $A$ and increase in ${{\Delta }}$ and $\phi$, whereas the influence is opposite for the prices $b_{3P}$, $w_{3P}$ and $p_{3P}$. Again, we illustrate this with our example in Fig. 9 (profits) and Fig. 10 (collection rate, prices, quantity).

Fig. 8

Options for third-party-managed collection (3P)

Fig. 9

Profits with third-party-managed collection ($\phi = 5$, ${{\Delta }} = 0.3$, $c_{m} = 0.5$, $A = 0.1$)

Fig. 10

Collection rate, prices, quantity with third-party-managed collection ($\phi = 5$, ${{\Delta }} = 0.3$, $c_{m} = 0.5$, $A = 0.1$)

4.4 Comparison of the reverse channel structures

We compare the manufacturer’s profits to determine his choice of the collection channel. All proofs are given in “Appendix A.4”. First, we compare manufacturer- and third-party-managed collection. Here, manufacturer-managed collection obviously dominates. Assume there is a setting where the third-party has positive profit. Then, the manufacturer could simply choose the same decisions and collect himself to additionally accrue the third-party’s profit. To compare manufacturer- and retailer-managed collection, we compare the manufacturer’s profit from both configurations for every cost value $C_{L}$. To do so, we have to distinguish two intervals for manufacturer-managed collection and only three intervals for retailer-managed, because option 2 is chosen in the last two intervals there. Next, we observe that the border between the two intervals of manufacturer-managed collection is anywhere in the first two intervals of retailer-managed collection. Now, if it is in the first interval, we have to compare manufacturer’s profit with both configurations in the resulting four intervals. Likewise, when the border falls into the second interval, again four intervals have to be considered. Thus, in total, we distinguish 8 cases, where the comparisons are done with sometimes tedious, but basic rearrangements. It shows that the manufacturer always prefers retailer-managed collection. Figure 11 compares the profits obtained by the parties with the different collection channel structures for our example.

Fig. 11

Comparison of profits ($\phi = 5$, ${{\Delta }} = 0.3$, $c_{m} = 0.5$, $A = 0.1$)

5 Restriction to equilibria

In this section, we restrict ourselves to the consideration of equilibria, that is, solutions where no party can improve its profit by marginally deviating.

Obviously, the solutions considered in Sect. 4 for manufacturer-managed collection and third-party-managed collection are all equilibria. Both options 1 are interior solutions at stationary points for all parties. Both options 2 are at a border ($\tau = 1$). With manufacturer-managed collection, there is no feasible stationary point in option 2. As all profit functions are continuous, the best solution at a border is an equilibrium. Likewise, option 2 for third-party-managed collection is also an equilibrium.

Retailer-managed collection is a bit more involved. Option 1 is an interior solution and, thus, an equilibrium. With option 3, the third party is at the $\tau = 1$ boundary, which is an equilibrium and the manufacturer is at an interior stationary point. Thus, option 3 is also an equilibrium. Options 2 and 4 are not equilibria as the manufacturer can always improve his profit at the cost of the retailer by slightly increasing the wholesale price $w$. Accordingly, retailer-managed collection is only stable for $C_{L} < \frac{\phi }{4}\left( {\frac{{1 - c_{m} }}{2} + {{\Delta }} - A} \right)^{2}$.

To determine whether the manufacturer still always prefers retailer managed collection (if possible), we compare the remaining options (see “Appendix A.5” for details). As the collection cost $C_{L}$ increases, areas where the manufacturer prefers retailer-managed collection and where he collects himself may alternate (see Fig. 12). If $\frac{\phi }{16}\left( {1 - c_{m} + \Delta - A} \right)^{2} < \frac{\phi }{8}\left( {{{\Delta }} - A} \right)^{2}$ does not hold, the corresponding area simply vanishes and manufacturer-managed collection is only preferred for high collection cost, where there is no equilibrium for retailer-managed collection.

Fig. 12

Options possible and preferred with restriction to equilibria (If not $\frac{\phi }{16}\left( {1 - c_{m} + \Delta - A} \right)^{2} < \frac{\phi }{8}\left( {{{\Delta }} - A} \right)^{2}$, the corresponding area vanishes.)

Again, we illustrate the results with our example. It is now slightly changed such that the area where the manufacturer collects at intermediate collection costs appears ($\phi = 5$, ${{\Delta }} = 0.6$, $c_{m} = 0.9$, and $A = 0.1$). Figure 13 shows the profits and Fig. 14 shows the corresponding collection rate, prices, and quantity. Contrary to the analysis without the restriction to equilibria in the preceding section (Figs. 3, 6 and 9 for profits as well as Figs. 4, 7, and 10 for rate, price, and quantity), all optimal values are no longer continuous with regard to changes in the collection cost, but jumps occur whenever the party who collects changes. In particular, for very low collection cost ($C_{L} \le 0.11$), the manufacturer chooses retailer-managed collection with option 3. As collection cost increases, he collects himself with option 2, which suddenly halves his profit ($0.11 \le C_{L} \le 0.16$). Next, he chooses retailer-managed collection again, this time with option 1 ($0.16 \le C_{L} \le 0.38$). This change is associated only with a small reduction in profit. Finally, for $0.38 \le C_{L}$, he collects himself again with option 1. As he switches, his profits suddenly vanish almost completely.

Fig. 13

Profits with equilibria only ($\phi = 5$, ${{\Delta }} = 0.6$, $c_{m} = 0.9$, $A = 0.1$)

Fig. 14

Collection rate, prices, quantity for equilibria only ($\phi = 5$, ${{\Delta }} = 0.6$, $c_{m} = 0.9$, $A = 0.1$)

6 Exogenously given minimum collection rate

In this section, we consider a minimum collection rate $\tau^{min}$, that is imposed, for example, by regulation or company policy. Figure 15 shows how and how far the manufacturer can increase the collection rate and still participates (see “Appendix A.6” for the proofs). Remember that a collection rate of $\tau_{R}^{*} = 1$ is chosen even without a minimum collection rate for $C_{L} \le \frac{\phi }{4}\left( {\frac{{1 - c_{m} }}{2} + \Delta - A} \right)^{2}$. For $\frac{\phi }{4}\left( {\frac{{1 - c_{m} }}{2} + \Delta - A} \right)^{2} < C_{L} < \frac{\phi }{4}\left( {1 - c_{m} + {{\Delta }} - A} \right)^{2}$, the collection rate is increased to $\tau_{R} = 1$ by choosing retailer managed collection with option 4 if $\tau^{min} > \tau_{R}$. If the area of $\frac{\phi }{4}\left( {1 - c_{m} + {{\Delta }} - A} \right)^{2} \le C_{L} < \frac{{\phi \left( {\Delta - A} \right)^{2} }}{{\left( {4 - \sqrt 8 } \right)^{2} }}$ exists, it is not possible to increase the collection rate there. It is not possible for the manufacturer to nudge the retailer to a higher collection rate with option 2 in the framework considered, i.e. through setting $b$ and $w$. To obtain a higher collection rate, the manufacturer needs to collect himself, which is not profitable for rates above the retailer’s collection rate. If $C_{L}$ is even higher, the manufacturer can increase the collection rate by collecting himself for $\tau^{min} \le \frac{{\sqrt \phi \left( {1 - c_{m} } \right)}}{{\sqrt {8C_{L} } - \sqrt \phi \left( {{{\Delta }} - A} \right)}}$ and still has a positive profit. This solution is a generalization of manufacturer-managed collection (option 1) with the collection rate $\tau^{min}$. If $C_{L}$ is below the threshold, this maximal collection rate with manufacturer-managed collection is below the collection rate of option 2 from retailer-managed collection.

Fig. 15

Options possible and preferred with minimum collection rate (If not $\left( {1 - c_{m} + \Delta - A} \right)^{2} < \frac{1}{{4\left( {2 - \sqrt 2 } \right)^{2} }}\left( {{{\Delta }} - A} \right)^{2}$, the corresponding area vanishes.)

Overall, it is interesting to see that the impact of a minimum collection rate strongly depends on collection costs. For low collection cost, always all products are collected ($\tau = 1$). For intermediate values, not all products are collected ($\tau < 1$), but no increase is possible in the framework considered. For high collection cost, an increase is possible, but the manufacturer has to collect himself.

7 Conclusion

Overall, we have seen that the optimal reverse channel configuration crucially depends on the context. If the manufacturer can credibly choose non-equilibrium solutions, it is always best for him to let the retailer manage collection, as this attenuates double marginalization. If collection costs are high, not all used products are collected and the manufacturer collects almost all channel profits, whereas he leaves an arbitrarily small share to the retailer to ensure his participation. Interestingly, for low collection costs, the reverse channel choice does not influence total channel profit, but only who pays for collection.

If, however, the manufacturer is constrained to equilibria, he prefers retailer-managed collection for low and rather high collection costs. He collects himself for rather low and high collection costs.

Furthermore, we show that a minimum collection rate that is exogenously imposed on the manufacturer may change his reverse channel choice. For high collection costs, he chooses to collect himself at the minimum rate. For slightly lower collection costs, he cannot profitably operate at a collection rate exceeding the equilibrium one. If collection costs are rather low, the manufacturer chooses another equilibrium where all used products are collected. For low collection costs, nothing changes as everything is collected anyways.

Albeit we followed a popular modelling approach from literature, it is important to note that the results depend on our assumptions. Some are less critical, we conjecture that other demand functions and probably also production costs would not structurally change our results. Others are more critical, for example the assumption that the manufacturer is restricted to contracts that are linear in quantities. That is, he can only choose a wholesale price for new products and a transfer price for used products. However, it is well-known that other contract forms, for example two-part nonlinear contracts consisting of fixed and linear components, prevent double marginalization. Thus, the incentive for retailer-managed collection—given the retailer has no structural advantage (i.e. lower collection cost because of being closer to the customer, see, e.g. De Giovanni and Zaccour 2014)—would vanish. Contract design in the context of the model of Savaskan et al. (2004) has already been investigated (see, e.g. Zhang et al. 2014), but is still far behind work on forward supply chains (Govindan et al. 2013). Here, we conjecture that for every closed-loop supply chain configuration there exists a contract that perfectly coordinates it and, thus, all configurations become equal to the centrally coordinated chain. Moreover, previous work has shown the influence of different power structures (e.g. Choi et al. 2013, Maiti and Giri 2015) and we believe that our results would also be affected by such a change. As especially retailer-led supply chains increasingly arise, this is also an interesting topic to cover. To sum up, we must leave the generalizability of the results with other assumptions to future work, but think this direction constitutes an interesting and valuable avenue.

Appendix

1.1 A.1 Retailer-managed collection

Our derivations first largely follow Savaskan et al. (2004) and Atasu et al. (2013). When the retailer manages collection, she chooses the sales price $p$ and the collection rate $\tau$ to maximize her profit ${{\varPi }}_{R}^{R} \left( {p,\tau } \right) = \left( {p - w} \right)q\left( p \right) + \left( {b - A} \right)\tau q\left( p \right) - \tau^{2} C_{L}$. We have $\frac{{\partial^{2} {{\varPi }}_{R}^{R} }}{{\partial p^{2} }} = - 2\phi < 0$ and the determinant of the Hessian is ${ \det }\left( {H\left( {{{\varPi }}_{R}^{R} } \right)} \right) = \phi \left( {4C_{L} - \phi \left( {b - A} \right)^{2} } \right)$. Thus, ${{\varPi }}_{R}^{R}$ is not necessarily concave. For now, we assume it is, i.e. $4C_{L} - \phi \left( {b - A} \right)^{2} > 0$. From f.o.c., we obtain $p\left( {w,b} \right) = \frac{{2C_{L} \left( {w + 1} \right) - \phi \left( {b - A} \right)^{2} }}{{4C_{L} - \phi \left( {b - A} \right)^{2} }}$ and $\tau \left( {w,b} \right) = \frac{{\phi \left( {1 - w} \right)\left( {b - A} \right)}}{{4C_{L} - \phi \left( {b - A} \right)^{2} }}$. Substituting this into the manufacturer’s profit function, we obtain ${{\varPi }}_{M}^{R} \left( {b,w} \right) = \frac{{2C_{L} \phi \left( {1 - w} \right)\left( {\phi \left( {A\left( {c_{m} - w} \right) + b - {{\Delta }}\left( {1 - w} \right)} \right) + 4C_{L} \left( {w - c_{m} } \right)} \right)}}{{\left( {4C_{L} - \phi \left( {b - A} \right)^{2} } \right)^{2} }}$ with $\frac{{\partial^{2} {{\varPi }}_{M}^{R} }}{{\partial w^{2} }} = - \frac{{4C_{L} \phi \left( {4C_{L} - \phi \left( {{{\Delta }} - A} \right)\left( {b - A} \right)} \right)}}{{\left( {4C_{L} - \phi \left( {b - A} \right)^{2} } \right)^{2} }}$. For now, assume $4C_{L} - \phi \left( {{{\Delta }} - A} \right)\left( {b - A} \right) > 0$ such that $\frac{{\partial^{2} {{\varPi }}_{M}^{R} }}{{\partial w^{2} }} < 0$ and ${{\varPi }}_{M}^{R} \left( {b,w} \right)$ is concave in $w$. Then, a maximizer must satisfy $\frac{{\partial {{\varPi }}_{M}^{R} }}{\partial w} = 0$. We solve this for $w\left( b \right)$ and substitute it into ${{\varPi }}_{M}^{R} \left( {b,w} \right)$ to obtain ${{\varPi }}_{M}^{R} \left( b \right) = \frac{{C_{L} \left( {1 - c_{m} } \right)^{2} \phi }}{{8C_{L} - 2\phi \left( {b - A} \right)\left( {{{\Delta }} - A} \right)}}$. If $4C_{L} - \phi \left( {{{\Delta }} - A} \right)\left( {b - A} \right) > 0$ as assumed above, this is positive and increasing in $b$. Thus, at the retailer’s stationary best response, the manufacturer chooses $b$ as big as possible. However, we see that the retailer's response $\tau \left( {w\left( b \right),b} \right) = \frac{{\phi \left( {b - A} \right)\left( {1 - c_{m} } \right)}}{{2\left( {4C_{L} - \phi \left( {{{\Delta }} - A} \right)\left( {b - A} \right)} \right)}}$ also increases in $b$ if $4C_{L} - \phi \left( {{{\Delta }} - A} \right)\left( {b - A} \right) > 0$. Thus, the manufacturer can only increase $b$ until $\tau \left( {w\left( b \right),b} \right) = 1$, i.e. to $b^{*} = A + \frac{{8C_{L} }}{{\phi \left( {2\left( {{{\Delta }} - A} \right) + 1 - c_{m} } \right)}}$. Analyzing higher $b$ is not necessary, as it is equivalent to a corresponding reduction in $w$. From $\frac{{\partial {{\varPi }}_{M}^{R} }}{\partial w} = 0$, we obtain $w^{*} = b^{*} - {{\Delta }} + \frac{{1 + c_{m} }}{2}$. Thus, the condition for the monotonicity of ${{\varPi }}_{M}^{R} \left( b \right)$ in $b$ and the concavity of ${{\varPi }}_{M}^{R} \left( {b,w} \right)$ in $w$ is satisfied, because $4C_{L} > \phi \left( {A + \frac{{8C_{L} }}{{\phi \left( {2\left( {{{\Delta }} - A} \right) + 1 - c_{m} } \right)}} - A} \right)\left( {{{\Delta }} - A} \right) \Leftrightarrow 2\left( {{{\Delta }} - A} \right) + 1 - c_{m} > 2\left( {{{\Delta }} - A} \right)$.

Now, if and only if $4C_{L} < \phi \left( {{{\Delta }} - A + \frac{{1 - c_{m} }}{2}} \right)^{2}$ (option 1), we have $4C_{L} - \phi \left( {b - A} \right)^{2} > 0$ because $4C_{L} > \phi \left( {A + \frac{{8C_{L} }}{{\phi \left( {2\left( {{{\Delta }} - A} \right) + 1 - c_{m} } \right)}} - A} \right)^{2} \Leftrightarrow \phi \left( {{{\Delta }} - A + \frac{{1 - c_{m} }}{2}} \right)^{2} > 4C_{L}$ and, thus ${{\varPi }}_{R}^{R}$ is concave. In this case, we have the positive profits ${{\varPi }}_{M}^{R} = \frac{1}{8}\phi \left( {1 - c_{m} } \right)\left( {2\left( {{{\Delta }} - A} \right) + 1 - c_{m} } \right)$ and ${{\varPi }}_{R}^{R} = \frac{1}{16}\phi \left( {2\left( {{{\Delta }} - A} \right) + 1 - c_{m} } \right)^{2} - C_{L}$. The latter’s positivity follows from the condition and ensures participation of the retailer. It is also obvious from the fact that we consider a global maximizer and the retailer obtains zero profit if she does nothing.

Until now, our elaborations closely mirror Atasu et al. (2013). However, for $4C_{L} > \phi \left( {{{\Delta }} - A + \frac{{1 - c_{m} }}{2}} \right)^{2}$, they conclude that no interior equilibrium exists and simply check the retailer’s boundaries ($\tau_{R} = 0$ and $\tau_{R} = 1$). We honor the fact that the manufacturer acts as a Stackelberg leader and, by contrast, let him freely choose $b$ and $w$, which leads to additional solutions.

If and only if the condition $C_{L} \ge \frac{\phi }{4}\left( {{{\Delta }} - A + \frac{{1 - c_{m} }}{2}} \right)^{2}$ holds, the manufacturer can no longer push the retailer’s stationary best response to the boundary because ${{\varPi }}_{R}^{R}$ is no longer even locally concave because, at the corresponding values for $b$ and $w$, we have ${ \det }\left( {H\left( {{{\varPi }}_{R}^{R} } \right)} \right) = \phi \left( {4C_{L} - \phi \left( {b - A} \right)^{2} } \right) < 0$. However, if the manufacturer chooses $b$ below the threshold $\overline{b} = A + 2\sqrt {\frac{{C_{L} }}{\phi }}$, the retailers profit ${{\varPi }}_{R}^{R}$ is concave. We evaluate this option in the following (option 2). As described before, we obtain $p\left( {w,b} \right)$ and $\tau \left( {w,b} \right)$ from f.o.c. and substitute them into the manufacturer’s profit function to obtain ${{\varPi }}_{M}^{R} \left( {b,w} \right)$. We have $\frac{{\partial^{2} {{\varPi }}_{M}^{R} }}{{\partial w^{2} }}< {0 \Leftrightarrow 4C_{L} - \phi \left( {{{\Delta }} - A} \right)\left( {b - A} \right)} > 0$ which follows from the condition and the selection of $b$. Thus, if the manufacturer chooses $b$ below the threshold, his profit is concave in $w$. Again, we solve $\frac{{\partial {{\varPi }}_{M}^{R} }}{\partial w} = 0$ for $w\left( b \right)$ and substitute this into ${{\varPi }}_{M}^{R} \left( {b,w} \right)$ to obtain ${{\varPi }}_{M}^{R} \left( b \right)$. This still increases in $b$ because $4C_{L} - \phi \left( {{{\Delta }} - A} \right)\left( {b - A} \right) > 0$. Thus, the manufactuerer chooses $b$ as high as possible, i.e. slightly below the threshold. For $b \nearrow \overline{b} = A + 2\sqrt {\frac{{C_{L} }}{\phi }}$, we have ${{\varPi }}_{M}^{R} \nearrow \frac{{\left( {1 - c_{m} } \right)^{2} \phi }}{{8 - 4\sqrt {\frac{\phi }{{C_{L} }}} \left( {{{\Delta }} - A} \right)}}$ and ${{\varPi }}_{R}^{R} \searrow 0$. The solution is interior as $0 < \tau \left( {b^{*} ,w^{*} } \right) < 1$.

On the other hand, the manufacturer may choose $b > \overline{b} = A + 2\sqrt {\frac{{C_{L} }}{\phi }}$ to deprive the retailer of any interior maximizers and forces him to a boundary (option 3). In principle, the retailer then has four boundaries to choose from: $p_{R}^{*} = 0$, $p_{R}^{*} = 1$, $\tau_{R}^{ *} = 0$, and $\tau_{R}^{ *} = 1$. Obviously, the first two imply nonpositive total supply chain profits and, thus, are unacceptable to at least the retailer or the manufacturer. The retailer will not choose $p_{R}^{*} = 0$ as this implies zero profit for him, and the manufacturer can prevent him from choosing $p_{R}^{*} = 1$ by setting $b < w + A$. At $\tau_{R}^{ *} = 0$, the supply chain operates without collection and we have the strictly positive profits ${{\varPi }}_{M}^{R} = \frac{1}{8}\phi \left( {1 - c_{m} } \right)^{2}$ and ${{\varPi }}_{R}^{R} = \frac{1}{16}\phi \left( {1 - c_{m} } \right)^{2}$, respectively. Finally, the manufacturer can force the retailer to collect everything ($\tau_{R}^{ *} = 1$) by setting $b^{*}$ high enough. In this case, the retailer’s profit is given by ${{\varPi }}_{R}^{R} \left( {p,\tau_{R} = 1} \right) = \left( {p - w + b - A} \right)\phi \left( {1 - p} \right) - C_{L}$. We have $\frac{{\partial^{2} {{\varPi }}_{R}^{R} }}{{\partial p^{2} }} = - 2\phi < 0$ and from f.o.c. obtain $p_{{}}^{*} = \frac{A - b + w + 1}{2}$. Substituting this into the manufacturer’s profit function, we obtain ${{\varPi }}_{M}^{R} \left( {b,w} \right) = \left[ {w - c_{m} + {{\Delta }} - b} \right]\phi \frac{1 - A + b - w}{2}$ which obviously is a function of only the difference $w - b$. We have $\frac{{\partial^{2} {{\varPi }}_{M}^{R} \left( {w - b} \right)}}{{\partial \left( {w - b} \right)^{2} }} = - \phi < 0$. From $\frac{{\partial {{\varPi }}_{M}^{R} \left( {w - b} \right)}}{{\partial \left( {w - b} \right)}} = 0$ we obtain $w - b = \frac{{c_{m} + 1 - {{\Delta }} - A}}{2}$ and the manufacturer’s profit is $\varPi_{M}^{R} \left( {\tau_{R}^{ *} = 1} \right) = \frac{1}{8}\phi \left( {1 - c_{m} + \Delta - A} \right)^{2} > {{\varPi }}_{M}^{R} \left( {\tau_{R}^{ *} = 0} \right) = \frac{1}{8}\phi \left( {1 - c_{m} } \right)^{2}$. The retailer obtains ${{\varPi }}_{R}^{R} = \frac{1}{16}\phi \left( {1 - c_{m} + {{\Delta }} - A} \right)^{2} - C_{L}$, which is positive for $C_{L} < \frac{\phi }{16}\left( {1 - c_{m} + {{\Delta }} - A} \right)^{2}$.

Finally (option 4), if the retailer does not participate at the solution described above because $C_{L} > \frac{\phi }{16}\left( {1 - c_{m} + {{\Delta }} - A} \right)^{2}$ and ${{\varPi }}_{R}^{R} \le 0$, the manufacturer can sacrifice part of his profit and decrease $w^{*} - b^{*}$ to allow the retailer a positive profit and ensure his participation (option 4). To guarantee ${{\varPi }}_{R}^{R} \left( {p^{*} ,\tau_{R} = 1} \right) = \left( {\frac{ - A + b - w + 1}{2}} \right)\phi \frac{ - A + b - w + 1}{2} - C_{L} > 0$, we need $\left( {w^{*} - b^{*} } \right) < \left( {1 - A - 2\sqrt {\frac{{C_{L} }}{\phi }} } \right)$. For $\left( {w^{*} - b^{*} } \right) \nearrow \left( {1 - A - 2\sqrt {\frac{{C_{L} }}{\phi }} } \right)$, we have ${{\varPi }}_{R}^{R} \searrow 0$ and ${{\varPi }}_{M}^{R} \nearrow \sqrt {C_{L} \phi } \cdot \left( {1 - c_{m} + {{\Delta }} - A} \right) - 2C_{L}$, which is positive if and only if $C_{L} < \frac{\phi }{4}\left( {1 - c_{m} + {{\Delta }} - A} \right)^{2}$.

1.2 A.2 Manufacturer-managed collection

Given $w$, the retailer maximizes ${{\varPi }}_{R}^{M} \left( p \right) = \left( {p - w} \right)q\left( p \right)$. It is easy to see that $\frac{{\partial^{2} {{\varPi }}_{R}^{M} }}{{\partial p^{2} }} = - 2\phi < 0$ and, thus, the retailers best response is $p\left( w \right) = \frac{1 + w}{2}$. Then, the manufacturer’s profit function is given by ${{\varPi }}_{M}^{M} \left( {\tau ,w} \right) = \left[ {w - c_{m} + \tau {{\Delta }}} \right]\phi \left( {1 - \frac{1 + w}{2}} \right) - A\tau \phi \left( {1 - \frac{1 + w}{2}} \right) - \tau^{2} C_{L}$.

First consider the condition $C_{L} \ge \frac{\phi }{8}\left( {{{\Delta }} - {\text{A}}} \right)\left( {{{\Delta }} - A + 1 - c_{m} } \right)$ (option 1). ${{\varPi }}_{M}^{M} \left( {\tau ,w} \right)$ is globally concave because $\frac{{\partial^{2} {{\varPi }}_{M}^{M} }}{{\partial w^{2} }} = - \phi < 0$ and the determinant of the Hessian is $2C_{L} - \frac{1}{4}\phi^{2} \left( {{{\Delta }} - A} \right)^{2} > 0$. Thus, there is only one stationary point which maximizes ${{\varPi }}_{M}^{M}$: $\tau_{M}^{*} = \frac{{\left( {1 - c_{m} } \right)\phi \left( {{{\Delta }} - {\text{A}}} \right)}}{{8C_{L} - \phi \left( {A - {{\Delta }}} \right)^{2} }}$ and $w^{*} = \frac{{4C_{L} \left( {c_{m} + 1} \right) - \phi \left( {{{\Delta }} - {\text{A}}} \right)^{2} }}{{8C_{L} - \phi \left( {{{\Delta }} - {\text{A}}} \right)^{2} }}$. From the condition and $c_{m} < 1$, $0 < w^{*} \le 1$ and $0 < \tau_{M}^{*}$ follow. Moreover, the condition is equivalent to $\tau_{M}^{*} \le 1$. Thus, we have ${{\varPi }}_{M}^{M} = \frac{{C_{L} \left( {1 - c_{m} } \right)^{2} \phi }}{{8C_{L} - \phi \left( {{{\Delta }} - A} \right)^{2} }}$ and ${{\varPi }}_{R}^{M} = \frac{{4C_{L}^{2} \left( {1 - c_{m} } \right)^{2} \phi }}{{\left( {8C_{L} - \phi \left( {{{\Delta }} - {\text{A}}} \right)^{2} } \right)^{2} }}$. It is easy to see that both are strictly positive.

Next, consider the condition $C_{L} \le \frac{\phi }{8}\left( {{{\Delta }} - {\text{A}}} \right)\left( {{{\Delta }} - A + 1 - c_{m} } \right)$ (option 2). Now, for $\frac{\phi }{8}\left( {{{\Delta }} - {\text{A}}} \right)^{2} < C_{L} \le \frac{\phi }{8}\left( {{{\Delta }} - {\text{A}}} \right)\left( {{{\Delta }} - A + 1 - c_{m} } \right)$, the unique stationary point from option 1 still exists, but we would have $\tau_{M}^{*} > 1$. For $C_{L} < \frac{\phi }{8}\left( {{{\Delta }} - {\text{A}}} \right)^{2}$, the determinant of the Hessian is negative and ${{\varPi }}_{M}^{M}$ is not even locally concave. Thus, in option 2, there is no feasible stationary point and we have to check the boundaries $\tau_{M}^{*} = 0$ and $\tau_{M}^{*} = 1$. For $\tau_{M}^{*} = 0$, the manufacturer again obtains ${{\varPi }}_{M}^{M} = \frac{1}{8}\phi \left( {1 - c_{m} } \right)^{2}$ as in the decentralized-forward-only configuration. For $\tau_{M}^{*} = 1$, we have ${{\varPi }}_{M}^{M} \left( w \right) = \left[ {w - c_{m} + {{\Delta }}} \right]\phi \left( {1 - \frac{1 + w}{2}} \right) - A\phi \left( {1 - \frac{1 + w}{2}} \right) - C_{L}$. From $\frac{{\partial {{\varPi }}_{M}^{M} }}{\partial w} = 0$ we obtain $w^{*} = \frac{1}{2}\left( {1 + c_{m} - \left( {\Delta - A} \right)} \right)$. Thus, we have ${{\varPi }}_{M}^{M} \left( {\tau_{M}^{*} = 1} \right) = \frac{1}{8}\phi \left( {{{\Delta }} - A + 1 - c_{m} } \right)^{2} - C_{L} > \frac{1}{8}\phi \left( {1 - c_{m} } \right)^{2} = {{\varPi }}_{M}^{M} \left( {\tau_{M}^{*} = 0} \right)$ if the condition holds.

1.3 A.3 Third-party-managed collection

The retailer operates as in manufacturer-managed collection and his best response is again $p\left( w \right) = \frac{1 + w}{2}$. The third party maximizes ${{\varPi }}_{3P}^{3P} \left( \tau \right) = \left( {b - A} \right)\tau q\left( {p\left( w \right)} \right) - \tau^{2} C_{L}$. We have $\frac{{\partial^{2} {{\varPi }}_{3P}^{3P} }}{{\partial \tau^{2} }} = - 2C_{L} < 0$ and his best response is $\tau_{3P}^{*} = \frac{{\phi \left( {1 - w} \right)\left( {b - A} \right)}}{{4C_{L} }}$. Substituting both into the manufacturer’s profit function yields ${{\varPi }}_{M}^{3P} \left( {b,w} \right) = \frac{{\phi \left( {1 - w} \right)}}{2}\left( {w - c_{m} + \frac{{\phi \left( {b - A} \right)\left( {1 - w} \right)\left( {{{\Delta }} - b} \right)}}{{4C_{L} }}} \right)$. We have $\frac{{\partial^{2} {{\varPi }}_{M}^{3P} }}{{\partial w^{2} }} = - \frac{{\phi^{2} \left( {1 - w} \right)^{2} }}{{4C_{L} }} < 0$ for $w \ne 1$ and the determinant of the Hessian is $\det \left( {H\left( {\varPi_{M}^{3P} \left( {b,w} \right)} \right)} \right) = \frac{{\phi^{3} \left( {1 - w} \right)^{2} \left( {4C_{L} - \phi \left( {A^{2} + A{{\Delta }} - 3Ab + 3b^{2} - 3b{{\Delta }} + {{\Delta }}^{2} } \right)} \right)}}{{16C_{L}^{2} }}$. From f.o.c, we obtain $b^{*} = \frac{{A + {{\Delta }}}}{2}$ and $w^{*} = \frac{{8C_{L} \left( {c_{m} + 1} \right) - \phi \left( {{{\Delta }} - {\text{A}}} \right)^{2} }}{{16C_{L} - \phi \left( {{{\Delta }} - A} \right)^{2} }}$ and the determinant there is $\det \left( {H\left( {\varPi_{M}^{3P} \left( {b^{*} ,w^{*} } \right)} \right)} \right) = \frac{{\phi^{3} \left( {1 - c_{m} } \right)^{2} }}{{16C_{L} - \phi \left( {{{\Delta }} - A} \right)^{2} }}$.

Now, if $C_{L} \ge \frac{\phi }{16}\left( {{{\Delta }} - {\text{A}}} \right)\left( {{{\Delta }} - A + 1 - c_{m} } \right)$ holds, the unique stationary point $\left( {b^{*} ,w^{*} } \right)$ is a local maximizer as $\det \left( {H\left( {\varPi_{M}^{3P} \left( {b^{*} ,w^{*} } \right)} \right)} \right) > 0$. Moreover, we have $\tau_{3P}^{*} \left( {b^{*} ,w^{*} } \right) = \frac{{\phi \left( {1 - c_{m} } \right)\left( {{{\Delta }} - A} \right)}}{{16C_{L} - \phi \left( {{{\Delta }} - A} \right)^{2} }}$ with $0 < \tau_{3P}^{*} \le 1$. The profits are given by ${{\varPi }}_{M}^{3P} = \frac{{2C_{L} \left( {1 - c_{m} } \right)^{2} \phi }}{{16C_{L} - \phi \left( {{{\Delta }} - {\text{A}}} \right)^{2} }}$, ${{\varPi }}_{R}^{3P} = \frac{{16C_{L}^{2} \left( {1 - c_{m} } \right)^{2} \phi }}{{\left( {16C_{L} - \phi \left( {{{\Delta }} - {\text{A}}} \right)^{2} } \right)^{2} }}$, and ${{\varPi }}_{3P}^{3P} = \frac{{C_{L}^{{}} \left( {{{\Delta }} - A} \right)^{2} \left( {1 - c_{m} } \right)^{2} \phi^{2} }}{{\left( {16C_{L} - \phi \left( {{{\Delta }} - {\text{A}}} \right)^{2} } \right)^{2} }}$. All are strictly positive if the condition holds. However, ${{\varPi }}_{M}^{3P}$ may be only locally concave and we have to check the boundaries. Independent of $C_{L}$, we have the following boundaries:

• $\tau_{3P}^{*} = 0$ when $b = A$ and, again, the manufacturer again obtains ${{\varPi }}_{M}^{3P} = \frac{1}{8}\phi \left( {1 - c_{m} } \right)^{2}$ as in the decentralized-forward-only configuration.

• $\tau_{3P}^{*} = 1$ when $b = A + \frac{{4C_{L} }}{{\phi \left( {1 - w} \right)}}$. Now, ${{\varPi }}_{M}^{3P} \left( {A + \frac{{4C_{L} }}{{\phi \left( {1 - w} \right)}},w} \right)$ maximizes at $w^{*} = \frac{{A - {{\Delta }} + c_{m} + 1}}{2}$ with $b^{*} = A + \frac{{8C_{L} }}{{\phi \left( {\Delta - A + 1 - c_{m} } \right)}}$. There, the manufacturer obtains ${{\varPi }}_{M}^{3P} = \frac{1}{8}\phi \left( {{{\Delta }} - A + 1 - c_{m} } \right)^{2} - 2C_{L}$.

Now, if the condition $C_{L} \ge \frac{\phi }{16}\left( {{{\Delta }} - {\text{A}}} \right)\left( {{{\Delta }} - A + 1 - c_{m} } \right)$ holds, the unique stationary point $\left( {b^{ *} ,w^{ *} } \right)$ is an interior local maximizer with $0 < \tau_{3P}^{ *} \le 1$ (option 1). Moreover, from the condition follows that ${{\varPi }}_{M}^{3P}$ is maximal at the stationary point because ${{\varPi }}_{M}^{M} \left( {\tau_{M}^{*} = 0} \right) = \frac{1}{8}\phi \left( {1 - c_{m} } \right)^{2} < \frac{{2C_{L} \left( {1 - c_{m} } \right)^{2} \phi }}{{16C_{L} - \phi \left( {{{\Delta }} - {\text{A}}} \right)^{2} }} = {{\varPi }}_{M}^{3P} \left( {b^{*} ,w^{*} } \right)$ and ${{\varPi }}_{M}^{M} \left( {\tau_{M}^{*} = 1} \right) = \frac{1}{8}\phi \left( {{{\Delta }} - A + 1 - c_{m} } \right)^{2} - 2C_{L} \le \frac{{2C_{L} \left( {1 - c_{m} } \right)^{2} \phi }}{{16C_{L} - \phi \left( {{{\Delta }} - {\text{A}}} \right)^{2} }} = {{\varPi }}_{M}^{3P} \left( {b^{*} ,w^{*} } \right)$.

If and only if $C_{L} \le \frac{\phi }{16}\left( {{{\Delta }} - {\text{A}}} \right)\left( {{{\Delta }} - A + 1 - c_{m} } \right)$, there is no interior stationary point (option 2) and we just check the above boundaries: ${{\varPi }}_{M}^{M} \left( {\tau_{M}^{*} = 0} \right) = \frac{1}{8}\phi \left( {1 - c_{m} } \right)^{2} < \frac{1}{8}\phi \left( {{{\Delta }} - A + 1 - c_{m} } \right)^{2} - 2C_{L} = {{\varPi }}_{M}^{M} \left( {\tau_{M}^{*} = 1} \right)$. The manufacturer chooses $\tau_{3P}^{*} = 1$ and the retailer obtains ${{\varPi }}_{R}^{3P} = \frac{1}{16}\phi \left( {{{\Delta }} - A + 1 - c_{m} } \right)^{2} > 0$; the third party obtains ${{\varPi }}_{R}^{3P} = C_{L} > 0$ and both participate.

1.4 A.4 Comparison

It is easy to show that third-party-managed collection is always dominated by manufacturer-managed collection. For $C_{L} < \frac{\phi }{16}\left( {1 - c_{m} + {{\Delta }} - A} \right)^{2}$, we have ${{\varPi }}_{M}^{3P} = \frac{1}{8}\phi \left( {{{\Delta }} - A + 1 - c_{m} } \right)^{2} - 2C_{L} < \frac{1}{8}\phi \left( {\Delta - A + 1 - c_{m} } \right)^{2} - C_{L} = \varPi_{M}^{M}$. For $\frac{\phi }{16}\left( {1 - c_{m} + {{\Delta }} - A} \right)^{2} < C_{L} < \frac{\phi }{8}\left( {1 - c_{m} + {{\Delta }} - A} \right)^{2}$, we have ${{\varPi }}_{M}^{3P} = \frac{{2C_{L} \left( {1 - c_{m} } \right)^{2} \phi }}{{16C_{L} - \phi \left( {{{\Delta }} - {\text{A}}} \right)^{2} }} < \frac{1}{8}\phi \left( {\Delta - A + 1 - c_{m} } \right)^{2} - C_{L} = \varPi_{M}^{M}$ and for $C_{L} > \frac{\phi }{8}\left( {1 - c_{m} + {{\Delta }} - A} \right)^{2}$, we have ${{\varPi }}_{M}^{3P} = \frac{{2C_{L} \left( {1 - c_{m} } \right)^{2} \phi }}{{16C_{L} - \phi \left( {{{\Delta }} - {\text{A}}} \right)^{2} }} < \frac{{C_{L} \left( {1 - c_{m} } \right)^{2} \phi }}{{8C_{L} - \phi \left( {\Delta - A} \right)^{2} }} = \varPi_{M}^{M}$. This is also intuitive as the third-party must have a positive profit and the manufacturer can take the same operational decisions when collecting himself and simply accrue the third-party’s profit.

Thus, we compare retailer-managed and manufacturer-managed collection in the following. As $\frac{\phi }{8}\left( {{{\Delta }} - {\text{A}}} \right)\left( {{{\Delta }} - A + 1 - c_{m} } \right) < \frac{\phi }{4}\left( {\frac{{1 - c_{m} }}{2} + \Delta - A} \right)^{2}$, we have to distinguish the following 8 cases:

• $\frac{\phi }{8}\left( {\Delta - A} \right)\left( {\Delta - A + 1 - c_{m} } \right) < \frac{\phi }{16}\left( {1 - c_{m} + \Delta - A} \right)^{2} \Leftrightarrow {{\Delta }} - A < 1 - c_{m}$:

• (a) $C_{L} < \frac{\phi }{8}\left( {\Delta - A} \right)\left( {\Delta - A + 1 - c_{m} } \right)$

  We compare option 2 from manufacturer-managed collection and option 3 from retailer managed collection. Obviously, we have ${{\varPi }}_{M}^{M} = \frac{1}{8}\phi \left( {{{\Delta }} - A + 1 - c_{m} } \right)^{2} - C_{L} < \frac{1}{8}\phi \left( {1 - c_{m} + \Delta - A} \right)^{2} = {{\varPi }}_{M}^{R}$ and the manufacturer prefers retailer managed collection with option 3.

• (b) $\frac{\phi }{8}\left( {\Delta - A} \right)\left( {\Delta - A + 1 - c_{m} } \right) < C_{L} < \frac{\phi }{16}\left( {1 - c_{m} + \Delta - A} \right)^{2}$

  We compare option 1 from manufacturer-managed collection and option 3 from retailer managed collection. We have ${{\varPi }}_{M}^{M} = \frac{{C_{L} \left( {1 - c_{m} } \right)^{2} \phi }}{{8C_{L} - \phi \left( {{{\Delta }} - A} \right)^{2} }} < \frac{1}{8}\phi \left( {1 - c_{m} + \Delta - A} \right)^{2} = {{\varPi }}_{M}^{R}$, using $\frac{\phi }{8}\left( {\Delta - A} \right)\left( {\Delta - A + 1 - c_{m} } \right) < C_{L}$.

• (c) $\frac{\phi }{16}\left( {1 - c_{m} + \Delta - A} \right)^{2} < C_{L} < \frac{\phi }{4}\left( {\frac{{1 - c_{m} }}{2} + \Delta - A} \right)^{2}$

  We compare option 1 from manufacturer-managed collection and option 4 from retailer managed collection. We have ${{\varPi }}_{M}^{M} = \frac{{C_{L} \left( {1 - c_{m} } \right)^{2} \phi }}{{8C_{L} - \phi \left( {{{\Delta }} - A} \right)^{2} }} < \sqrt {C_{L} \phi } \left( {1 - c_{m} + \Delta - A} \right) - 2C_{L} = {{\varPi }}_{M}^{R}$. We already know that for retailer-managed collection, option 4 is better than option 1. Thus, we show the above by showing that the manufacturer prefers retailer-managed collection with option 1 over manufacturer-managed collection with option 1, that is ${{\varPi }}_{M}^{M} = \frac{{C_{L} \left( {1 - c_{m} } \right)^{2} \phi }}{{8C_{L} - \phi \left( {{{\Delta }} - A} \right)^{2} }} < \left( {1 - c_{m} } \right)\left( {\frac{\Delta - A}{4} + \frac{{1 - c_{m} }}{8}} \right) = {{\varPi }}_{M}^{R}$, which holds because $\frac{\phi }{16}\left( {1 - c_{m} + \Delta - A} \right)^{2} < C_{L}$.

• (d) $\frac{\phi }{4}\left( {\frac{{1 - c_{m} }}{2} + {{\Delta }} - A} \right)^{2} < C_{L}$

  We compare option 1 from manufacturer-managed collection and option 2 from retailer managed collection. We have ${{\varPi }}_{M}^{M} = \frac{{C_{L} \left( {1 - c_{m} } \right)^{2} \phi }}{{8C_{L} - \phi \left( {{{\Delta }} - A} \right)^{2} }} < \frac{{\left( {1 - c_{m} } \right)^{2} \phi \sqrt {C_{L} } }}{{8\sqrt {C_{L} } - 4\sqrt \phi \left( {\Delta - A} \right)}} = {{\varPi }}_{M}^{R}$.

• $\frac{\phi }{8}\left( {\Delta - A} \right)\left( {\Delta - A + 1 - c_{m} } \right) > \frac{\phi }{16}\left( {1 - c_{m} + {{\Delta }} - A} \right)^{2} \Leftrightarrow {{\Delta }} - A > 1 - c_{m}$:

• (e) $C_{L} < \frac{\phi }{16}\left( {1 - c_{m} + {{\Delta }} - A} \right)^{2}$, see above (a)

• (f) $\frac{\phi }{16}\left( {1 - c_{m} + {{\Delta }} - A} \right)^{2} < C_{L} < \frac{\phi }{8}\left( {\Delta - A} \right)\left( {\Delta - A + 1 - c_{m} } \right)$

  We compare option 2 from manufacturer-managed collection and option 4 from retailer managed collection. We have

  ${{\varPi }}_{M}^{M} = \frac{1}{8}\phi \left( {\Delta - A + 1 - c_{m} } \right)^{2} - C_{L} < \sqrt {C_{L} \phi } \left( {1 - c_{m} + \Delta - A} \right) - 2C_{L} = {{\varPi }}_{M}^{R}$

  $\Leftrightarrow 0 > \left[ {\sqrt {C_{L} } - \left( {1 - c_{m} + {{\Delta }} - A} \right)\frac{\sqrt \phi }{2}\left( {1 - \sqrt {\frac{1}{2}} } \right)} \right] \cdot \left[ {\sqrt {C_{L} } - \left( {1 - c_{m} + {{\Delta }} - A} \right)\frac{\sqrt \phi }{2}\left( {1 + \sqrt {\frac{1}{2}} } \right)} \right]$ $\Leftrightarrow \left( {1 - c_{m} + {{\Delta }} - A} \right)^{2} \frac{\phi }{4}\left( {1 - \sqrt {\frac{1}{2}} } \right)^{2} < C_{L} < \left( {1 - c_{m} + {{\Delta }} - A} \right)^{2} \frac{\phi }{4}\left( {1 + \sqrt {\frac{1}{2}} } \right)^{2}$

  with $\left( {1 - c_{m} + {{\Delta }} - A} \right)^{2} \frac{\phi }{4}\left( {1 - \sqrt {\frac{1}{2}} } \right)^{2} < \frac{\phi }{16}\left( {1 - c_{m} + {{\Delta }} - A} \right)^{2}$ and

  $\frac{\phi }{8}\left( {\Delta - A} \right)\left( {\Delta - A + 1 - c_{m} } \right) < \left( {1 - c_{m} + {{\Delta }} - A} \right)^{2} \frac{\phi }{4}\left( {1 + \sqrt {\frac{1}{2}} } \right)^{2}$

  Thus, the product is negative for the entire range regarding $C_{L}$ covered by case (f) and the manufacturer always prefers retailer managed collection.

• (g) $\frac{\phi }{8}\left( {\Delta - A} \right)\left( {\Delta - A + 1 - c_{m} } \right) < C_{L} < \frac{\phi }{4}\left( {\frac{{1 - c_{m} }}{2} + \Delta - A} \right)^{2}$

  We compare option 1 from manufacturer-managed collection and option 4 from retailer managed collection. We have ${{\varPi }}_{M}^{M} = \frac{{C_{L} \left( {1 - c_{m} } \right)^{2} \phi }}{{8C_{L} - \phi \left( {\Delta - A} \right)^{2} }} < \sqrt {C_{L} \phi } \left( {1 - c_{m} + \Delta - A} \right) - 2C_{L} = {{\varPi }}_{M}^{R}$, which has already been shown in (c) for a bigger interval regarding $C_{L}$.

• (h) $C_{L} > \frac{\phi }{4}\left( {\frac{{1 - c_{m} }}{2} + {{\Delta }} - A} \right)^{2}$, see above (d)

1.5 A.5 Comparison with equilibria only

Where retailer managed collection is stable with options 1 and 3 ($C_{L} < \frac{\phi }{4}\left( {\frac{{1 - c_{m} }}{2} + {{\Delta }} - A} \right)^{2}$), we compare it to manufacturer-managed collection in the following. As $\frac{\phi }{8}\left( {{{\Delta }} - {\text{A}}} \right)\left( {{{\Delta }} - A + 1 - c_{m} } \right) < \frac{\phi }{4}\left( {\frac{{1 - c_{m} }}{2} + \Delta - A} \right)^{2}$, we have to distinguish the following 7 cases:

• $\frac{\phi }{8}\left( {\Delta - A} \right)\left( {\Delta - A + 1 - c_{m} } \right) < \frac{\phi }{16}\left( {1 - c_{m} + \Delta - A} \right)^{2} \Leftrightarrow {{\Delta }} - A < 1 - c_{m}$:

• (a) $C_{L} < \frac{\phi }{8}\left( {\Delta - A} \right)\left( {\Delta - A + 1 - c_{m} } \right)$

  We compare option 2 from manufacturer-managed collection and option 3 from retailer managed collection. As before, the manufacturer prefers retailer managed collection with option 3.

• (b) $\frac{\phi }{8}\left( {\Delta - A} \right)\left( {\Delta - A + 1 - c_{m} } \right) < C_{L} < \frac{\phi }{16}\left( {1 - c_{m} + \Delta - A} \right)^{2}$

  We compare option 1 from manufacturer-managed collection and option 3 from retailer managed collection. Again, as before, the manufacturer prefers retailer managed collection.

• (c) $\frac{\phi }{16}\left( {1 - c_{m} + \Delta - A} \right)^{2} < C_{L} < \frac{\phi }{4}\left( {\frac{{1 - c_{m} }}{2} + \Delta - A} \right)^{2}$

  We already showed that the manufacturer prefers retailer-managed collection with option 1 over manufacturer-managed collection with option 1.

• $\frac{\phi }{8}\left( {\Delta - A} \right)\left( {\Delta - A + 1 - c_{m} } \right) > \frac{\phi }{16}\left( {1 - c_{m} + {{\Delta }} - A} \right)^{2} \Leftrightarrow {{\Delta }} - A > 1 - c_{m}$:

• (d) $C_{L} < \frac{\phi }{16}\left( {1 - c_{m} + {{\Delta }} - A} \right)^{2}$, see above (a)

• (e) $\frac{\phi }{16}\left( {1 - c_{m} + {{\Delta }} - A} \right)^{2} < C_{L} < \frac{\phi }{8}\left( {\Delta - A} \right)\left( {\Delta - A + 1 - c_{m} } \right)$

  We compare option 2 from manufacturer-managed collection and option 1 from retailer managed collection. We have

  ${{\varPi }}_{M}^{M} = \frac{1}{8}\phi \left( {\Delta - A + 1 - c_{m} } \right)^{2} - C_{L} < \phi \left( {1 - c_{m} } \right)\left( {\frac{{1 - c_{m} }}{8} + \frac{\Delta - A}{4}} \right) = {{\varPi }}_{M}^{R}$

  $\Leftrightarrow \frac{\phi }{8}\left( {{{\Delta }} - A} \right)^{2} < C_{L}$

  Thus, we now distinguish two subcases

  • (e1) $\frac{\phi }{8}\left( {\Delta - A} \right)^{2} \le \frac{\phi }{16}\left( {1 - c_{m} + {{\Delta }} - A} \right)^{2}$

    Then, retailer-managed collection with option 1 is optimal for $\frac{\phi }{16}\left( {1 - c_{m} + {{\Delta }} - A} \right)^{2} < C_{L} < \frac{\phi }{8}\left( {\Delta - A} \right)\left( {\Delta - A + 1 - c_{m} } \right)$

  • (e2) $\frac{\phi }{8}\left( {{{\Delta }} - A} \right)^{2} > \frac{\phi }{16}\left( {1 - c_{m} + {{\Delta }} - A} \right)^{2}$

    Then, manufacturer-managed collection with option 2 is optimal for $\frac{\phi }{16}\left( {1 - c_{m} + {{\Delta }} - A} \right)^{2} < C_{L} \le \frac{\phi }{8}\left( {{{\Delta }} - A} \right)^{2}$ and retailer-managed collection with option 1 is optimal for $\frac{\phi }{8}\left( {{{\Delta }} - A} \right)^{2} < C_{L} < \frac{\phi }{8}\left( {\Delta - A} \right)\left( {\Delta - A + 1 - c_{m} } \right)$

• (f) $\frac{\phi }{8}\left( {\Delta - A} \right)\left( {\Delta - A + 1 - c_{m} } \right) < C_{L} < \frac{\phi }{4}\left( {\frac{{1 - c_{m} }}{2} + \Delta - A} \right)^{2}$

  We already showed that the manufacturer prefers retailer-managed collection with option 1 over manufacturer-managed collection with option 1.

1.6 A.6 Minimum collection rate

We consider the following cases for $\tau^{min} > \tau_{R}^{*}$:

• $\frac{\phi }{4}\left( {\frac{{1 - c_{m} }}{2} + \Delta - A} \right)^{2} < C_{L} < \frac{\phi }{4}\left( {1 - c_{m} + {{\Delta }} - A} \right)^{2}$: Retailer-managed collection with option 4 provides a rate of $\tau_{R}^{*} = 1$. At the same time, it provides a higher revenue than manufacturer-managed collection with option 1 (see Appendix A.4). Retailer-managed collection with option 2 provides $\tau_{R}^{*} \nearrow \frac{{\sqrt \phi \left( {1 - c_{m} } \right)}}{{4\sqrt {C_{L} } - 2\sqrt \phi \left( {{{\Delta }} - A} \right)}}$. This cannot be increased while preserving the structure of option 2 as the retailer’s objective already loses its interior stationary point at the limit. Thus, if $\tau^{min} > \tau_{R}^{*}$, the manufacturer choses retailer-managed collection with option 4 and $\tau_{R} = 1$.

• Next, we consider $\frac{\phi }{4}\left( {1 - c_{m} + {{\Delta }} - A} \right)^{2} \le C_{L}$: Here, we compare retailer-managed collection with option 2 and manufacturer-managed collection. With the optimal collection rate from option 1 we have $\tau_{M}^{*} = \frac{{\left( {1 - c_{m} } \right)\phi \left( {\Delta - A} \right)}}{{8C_{L} - \phi \left( {A - \Delta } \right)^{2} }} < \sqrt {C_{L} \phi } \left( {1 - c_{m} + \Delta - A} \right) - 2C_{L} = \tau_{R}^{*}$. Thus, the only possibility to attain a $\tau^{min} > \tau_{R}^{*}$ is for the manufacturer to collect himself. As his profit in option 1 is jointly concave in $\tau$ and $w$, he chooses $\tau_{M} = \tau^{min}$. From f.o.c., we obtain $w\left( {\tau^{min} } \right) = \frac{1}{2}\left[ {1 + c_{m} - \tau^{min} \left( {{{\Delta }} - A} \right)} \right]$. Substituting this into the profit function yields ${{\varPi }}_{M}^{M} \left( {\tau^{min} ,w\left( {\tau^{min} } \right)} \right) = \frac{\phi }{8}\left[ {1 - c_{m} + \tau^{min} \left( {{{\Delta }} - A} \right)} \right]^{2} - \tau^{{{min}}^{{2}}} C_{L}$. Moreover, we have ${{\varPi }}_{M}^{M} \left( {\tau^{min} ,w\left( {\tau^{min} } \right)} \right) \ge 0 \Leftrightarrow \tau^{min} \le \frac{{\sqrt \phi \left( {1 - c_{m} } \right)}}{{\sqrt {8C_{L} } - \sqrt \phi \left( {{{\Delta }} - A} \right)}}$. As we only consider $\tau^{min} > \tau_{R}^{*}$, we have to check whether such $\tau^{min}$ exists: $\frac{{\sqrt \phi \left( {1 - c_{m} } \right)}}{{4\sqrt {C_{L} } - 2\sqrt \phi \left( {\Delta - A} \right)}} \le \frac{{\sqrt \phi \left( {1 - c_{m} } \right)}}{{\sqrt {8C_{L} } - \sqrt \phi \left( {{{\Delta }} - A} \right)}} \Leftrightarrow C_{L} \ge \frac{{\phi \left( {{{\Delta }} - A} \right)^{2} }}{{\left( {4 - \sqrt 8 } \right)^{2} }}$