Collective action and geoengineering

Abstract

This paper investigates some of the myriad collective action implications of geoengineering. Its two major components – carbon dioxide reduction and albedo modification – present diverse collective action and strategic aspects. Carbon dioxide reduction may be characterized by Prisoners’ Dilemma, threshold, or harmony games, depending on capture and sequestration procedures. In contrast, albedo modification may abide by chicken, coordination, or threshold games. Once deployed, albedo modification presents an addiction problem that makes current efforts difficult to alter, even by countries originally opposed to such modification. With its many procedures, geoengineering is tied to a host of collective action problems that may ensue prior, during, or after geoengineering deployment. For carbon dioxide reduction, governance concerns encouraging action, while for albedo modification, governance concerns inhibiting unilateral action. The latter may be a more difficult governance issue.

It [geoengineering] might increasingly simplify greenhouse policy transforming an exceedingly complicated regulatory regime to a problem in international cost sharing, a problem that we are familiar with. (Schelling 1996, p. 303).

1 Introduction

Geoengineering involves large-scale deliberate manipulation of the environment to counter some manifestations of anthropogenic climate change (Barrett 2008; Bodansky 1996; Keith 2000; National Research Council 2015a; Schneider 2001; Shepherd et al. 2009). This environmental manipulation may take the form of carbon dioxide reduction (CDR) strategies or albedo modification (AM) actions. CDR influences Earth’s carbon cycle by affecting the carbon storage capacity of the oceans, soil, and forests. By augmenting the storage or sequestration of carbon on Earth, CDR curtails the greenhouse effect associated with the burning of fossil fuels (National Research Council 2015b). This can be achieved by limiting greenhouse gas (GHG) concentration in the atmosphere through actions to capture and sequester carbon. By contrast, AM primarily affects how much solar energy is reflected back into space (Keith 2000; Govindasamy and Caldeira 2000; National Research Council 2015b). This enhanced reflection can occur on Earth by increasing the albedo of land areas (e.g., the deserts), in the atmosphere by increasing the albedo of clouds, or beyond the Earth’s atmosphere by orbiting mirrors or diffraction gratings.

This paper serves to highlight, gather, and extend collective action insights from the environmental economic literature in a form that may stimulate further research on geoengineering by international political economists. Contrary to the current investigation, earlier contributions generally treat geoengineering as a generic collective action problem; they do not distinguish different collective action concerns for alternative forms of geoengineering. The key message of the current paper is that alternative procedures of geoengineering present a vast array of collective action problems, none of which are easy to address.¹ My characterization of the collective action difficulties of, say, AM geoengineering differs markedly from that of Schelling (1996), because cost sharing is not an easy problem to address as countries prefer others to do the sharing.

Many forms of CDR concern collective action difficulties akin to those of carbon mitigation owing to an embedded Prisoners’ Dilemma (Keohane and Victor 2011; Sandler 1997, 2004). In other instances, CDR may require threshold effort to make the method economically feasible, thus raising coordination concerns. For low-cost AM methods, a single country’s action may be sufficient to reduce temperature. However, some countries may oppose unilateral action because they prefer a warmer climate or do not want the risks of potential negative side effects from AM. Stopping action by one or a few countries may be extremely challenging, similar to the global community’s attempts to halt nuclear weapon proliferation. Once AM is deployed, addiction issues arise as temperatures would return rapidly to some equilibrium state if modification is ended (Crutzen 2006; Govindasamy and Caldeira 2000). Other forms of AM may imply coordination dilemmas, where a coalition is needed to surpass a research and development (R & D) and deployment threshold. For select AM methods, this coalition may be large, given the technical complexity of some actions.

A key consideration is the moral hazard problem that AM poses by masking some of the harmful consequences of GHG accumulation in the atmosphere (National Research Council 2015a, 2015b). If countries come to view AM as a substitute for GHG cutbacks, then countries will expend even less efforts to control their GHG emissions.² Under the best of circumstances, AM is a very imperfect substitute for cutting GHGs. For example, AM’s ability to reduce temperatures does not curb the rising acidity of the oceans, which harms aquatic life. CDR is a more general fix by addressing the underlying problem of climate change, namely, atmospheric accumulation of carbon. Another related concern of geoengineering is uncertainty with respect to its harmful side effects (see, e.g., Heutel et al. 2016; Millard-Ball 2012: National Research Council 2015a).

The global implications of some forms of AM necessitate a governance structure that internalizes negative externalities imposed on countries that are harmed from a cooler planet (e.g., Russia, Canada, and parts of Northern Europe) or are risk averse to unknown side effects. The form of this governance is an open question, although alternatives have been offered that borrow features of the United States as a hegemon, the Montreal Protocol on ozone depletion, and the Nuclear Nonproliferation Treaty (Barrett et al. 2014; Bodansky 1996; Keohane and Victor 2011; Lloyd and Oppenheimer 2014). For CDR, governance is concerned with encouraging action, while for AM, governance is primarily concerned with inhibiting action. Weitzman (2015) likens CDR to a free-rider problem and casts AM as a “free-driver” problem. For the latter, one or more countries act on their preferences to cool the atmosphere by deploying a technology to the detriment of some countries.³ This gives rise to an initiation problem that poses a difficult governance issue. Once initiated, AM maintenance is an easier governance issue because curbing ongoing AM has dire consequences.

The remainder of the paper contains six sections. Alternative geoengineering methods are briefly presented in Section 2. In Section 3, the standard carbon mitigation game is indicated in its classic Prisoners’ Dilemma form, followed by a game-theoretic discussion of CDR in Section 4. Section 5 depicts game forms for AM. Section 6 contains remarks on governance, while Section 7 presents concluding remarks.

2 Alternative geoengineering methods

2.1 CDR

All CDR methods work with the environment to capture and/or to sequester carbon, thereby limiting atmospheric accumulation.⁴ Reforestation and afforestation involve planting fast-growing trees to sequester carbon. The former includes lands deforested within the last 50 years, while the latter includes lands not deforested within the last 50 years. Table 1 indicates that the potential rate of CO₂ capture is 2 to 5 gigatons of CO₂ (GtCO₂) per year. The uptake of CO₂ is limited over time, because mature forests balance sequestration with the decay of dead organic matter (National Research Council 2015a, 2015b). As indicated in Table 2, the cost in $/tCO₂ ranges from $1 to $100, with any risk to the environment being low. There are, however, some biodiversity worries from single-species plantations, but these and other concerns (reduced albedo or evaporation) are not viewed as great (National Research Council 2015a). Reforestation cost is lower for faster-growing trees planted in places with soil and weather ideally suited to forests.

Table 1 Description of alternative geoengineering methods

Table 2 Geoengineering methods: costs and risks

Intensive cultivation tied to agricultural production results in carbon emissions from the soil. Low-till planting practices minimize soil disturbance, resulting in augmented retention of organic matter in the soil (National Research Council 2015a). As a consequence, there is less atmospheric emission of carbon. As indicated in Table 1, such practices could result in the capture of 0.35 to 1.2 GtCO₂ per year for about two decades at a cost of $1 to $100 per tCO₂. The environmental risk of such procedures is very low.

Land-based weathering brings CO₂ in contact with calcium carbonate, which, in turn, neutralizes soil acidity. The potential rate of capture is 2 GtCO₂ per year in just the United States at a cost of between $10 and $1000 per tCO₂ (National Research Council 2015a). In a similar fashion, ocean-based weathering brings CO₂ in contact with silicate minerals, which augment the alkalinity of seawater. The potential rate of capture is just 1 GtCO₂ per year at a cost between $50 and $1000 per tCO₂. Neither process poses much of an environmental risk, but their cost is currently prohibitive owing to energy requirements associated with the mining of silicate minerals, such as olivine. The required scale of mining, coupled with the cost, makes weathering impractical at this time. In a best case scenario, countries must pool their efforts to achieve the necessary mining scale economies to make weathering competitive to abatement, especially for the high-end weathering cost estimates. This pooling effort may correspond to surpassing a threshold effort.

A more feasible CDR method is bioenergy with capture and sequestration. This procedure first converts biomass into heat, electricity, or fuels. During the combustion process, the released carbon is captured and then sequestered underground. With this procedure, the potential rate of capture is 15 to 18 GtCO₂ per year at a cost of approximately $100 per tCO₂. Any risk to the environment is in the moderate range, based on sequestration method (National Research Council 2015a).

Another CDR procedure is that of ocean fertilization with iron being added to iron-poor regions of the oceans as a way to increase the growth of plankton. Such growth will capture and sequester carbon. The potential rate of capture is 1 to 4 GtCO₂ per year at a cost of $500 per tCO₂. This expensive procedure presents medium risk to the environment as there are downstream consequences on nutrient supply and ecosystems in other ocean regions (National Research Council 2015a, p. 61). Moreover, this method may run afoul of the London Convention on the Prevention of Marine Pollution by Dumping.

Direct air capture and sequestration refers to chemical scrubbing of CO₂ directly out of the atmosphere via absorption and absorption separation using an alkaline sorbent. Not only must the CO₂ be trapped, but it must also be stored. Moreover, the sorbent must be recycled. Huge and costly trapping structures are required, leading to cost estimates in the $400 to $1000 per tCO₂ range. This is four to ten times the expense of CO₂ capture from scrubbing coal-fired power plants’ emissions (National Research Council 2015a, pp. 65–72).⁵ Even though environmental risk is deemed low and capture could be upward of 10 GtCO₂ per year, this method is currently not feasible. Feasibility may require countries pooling efforts to surpass some threshold to bring down cost through R & D and design breakthroughs.

In summary, most CDR processes are currently too expensive to be practical. The feasible ones – reforestation, afforestation, low-till agriculture, and bioenergy with capture and sequestration – can capture rather modest amounts of carbon at low environmental risk – see Table 2. Consequently, a lot of countries would have to contribute to these efforts.

2.2 AM

Stratospheric sulfur dioxide release involves the injection of sulfur particles to an altitude of 20 to 30 km by guns, planes, or balloons (Barrett 2014; Crutzen 2006; Keith 2000; MacCracken 2006; McClellan et al. 2012). At this altitude, these reflective particles would remain aloft for upward of two years before falling disproportionately in the Polar Region. Such particles would cool the planet by reflecting sunlight back to outer space, not unlike the release of sulfur during the 1991 eruption of Mt. Pinatubo in the Philippines. This eruption reduced the Earth’s surface temperature by about 0.5 °C for two years (National Research Council 2015b). By injecting sufficient sulfur (i.e., 5 million metric tons (Mt)), this procedure could offset anthropogenic increases in CO₂ emissions (Crutzen 2006). McClellan et al. (2012) provide cost estimates of alternative delivery systems for placing 1–5 million metric tons of sulfur dioxide to an altitude of 18 to 30 km. Annual cost of putting 5 Mt. aloft ranges from $2 to $8 billion per year. For these estimates, delivery vehicles involve Boeing 747 aircraft, modified Gulfstream planes, and newly designed planes. This cost does not account for potential environmental harm and development uncertainties. For these delivery scenarios, the “cost may be less than 1% of the climate damage or the cost of mitigation” (McClellan et al. 2012, p. 3). Other delivery systems – Mark 7, 16″ Guns or Rockets – may result in cost of $137 billion and $390 billion per 1 Mt./yr., respectively, which is not currently viable without significant cost reduction through R & D. The latter may require two or more countries pooling R & D and deployment efforts. Environmental risks are potentially high owing to concomitant side effects including some destruction of the ozone layer (Tilmes et al. 2008), acid deposition in the Polar Regions, and unknown effects from increased sulfur dioxide loads in the stratosphere. This sulfur release reduces temperature but does not balance these temperature reductions globally, nor does it counter some harmful effects of atmospheric carbon accumulation, such as acidification of oceans. In addition, once applied, the world would be dependent or addicted to continuing the process since sudden secession would cause rapid temperature rises with potentially dire consequences (National Research Council 2015b; Victor 2008).

Another feasible AM option is to brighten marine clouds with sprayed seawater, thereby augmenting these clouds’ reflectivity. The sea spray can be produced by ocean fleets of unmanned boats, propelled by spinning cylinders. Such fleets would operate continuously. Unlike other albedo-modifying schemes, environmental risks would be small; however, an addiction problem is still a concern. To counter the anticipated CO₂ accumulation during this century, the cost of cloud brightening is very modest at just $5 billion a year, not counting R & D cost (National Research Council 2015b). As such, the procedure is feasible for a single country or a small coalition of countries to institute (Moreno-Cruz et al. 2012).

A more fanciful AM scheme comes from placing large mirrors (2000 km in surface area) or diffraction grating at a stable gravitation point between the Earth and the Sun. Such a mirror or gratings (henceforth, mirror) can reduce incoming solar radiation by about 1%, sufficient to offset anticipated increases in CO₂ during the twenty-first century. This mirror would be manufactured on the moon, rather on Earth, to save cost, and then launched in pieces and reassembled or else launched in one piece and unfurled at the Lagrange point, thereby necessitating the building of a moon manufacturing base. This particular AM scheme would require multiple countries to join efforts in order to surpass feasibility and expense thresholds. “There is no known way to modify albedo to yield a pattern of top-of-atmosphere solar radiative forcing that is similar (seasonally and geographically) but of opposite sign and amplitude to the radiative forcing pattern due to an increase of CO₂” (National Research Council 2015b, 47). Thus, AM offsets part of the climate change problem, which may limit such things as melting ice shelves.

Tables 1 and 2 summarize these CDR and AM methods. There are other methods – e.g., painting roof tops white – that are not discussed because their aggregate effect on climate change is very limited.

Table 3 presents contrasting considerations concerning CDR and AM. Many of these contrasts are captured in the earlier discussion. The differences in underlying game structures are made clear in Sections 4 and 5. Once developed, AM is very seductive as a backup to failed efforts to mitigate and abate carbon emission, because such modification is inexpensive (except for a space mirror) and its effect on temperature is immediate. Unlike most CDR methods, unilateral action is possible for AM.

Table 3 Contrasting considerations concerning carbon dioxide reduction and albedo modification

3 Standard carbon-mitigation game

I now turn to a game-theoretic representation of carbon mitigation (or carbon abatement) that captures essential collective action considerations. This representation is provided for comparison purposes with games later shown to characterize various forms of geoengineering.

Figure 1 depicts a symmetric six-country, carbon-mitigation game matrix that could be extended to any number of countries. Each country has two strategies: not to mitigate its carbon emissions, or to mitigate its carbon emissions by some set percentage (say 20%). The second strategic choice is a greater commitment than abiding by an existing GHG-reducing treaty, such as the Kyoto Protocol on Climate Change. For illustrative purposes, each country that cuts its emissions by 20% confers a benefit, b _i , of 6 on itself and on each of the other five countries in this example,⁶ at a cost, c _i , of 9 to just itself. To generate, the Prisoners’ Dilemma, it is essential that Nb _i  > c _i  > b _i , because not mitigating then dominates mitigating regardless of the number of other mitigators (Sandler 1997).

Fig. 1

Stylized six-country carbon-mitigation game

The payoffs in the game matrix of Fig. 1 are computed as follows: If country i does not mitigate its emissions and no other country mitigates its emissions, then there is no cost or benefit, so that i nets 0. If, however, country i does not mitigate and one other country mitigates emissions, then i receives 6 as a free rider. The remaining entries in the top row of Fig. 1 equal 6 times the number of other countries that engages in emission reduction. In the bottom row, country i receives −3 if it mitigates emissions alone as 6 in benefits are reduced by 9 in cost. If, say, country i mitigates and is joined by two other countries, then i nets 9 as total benefits of 18 (= 3 × 6) are reduced by i’s cost of 9. The other payoffs in the bottom row are computed in an analogous fashion. Country i has a dominant strategy not to mitigate since each payoff in the top row is larger than the corresponding payoff in the bottom row. The Nash equilibrium for this game is where no country mitigates since 0 > −3, so that neither country i nor any other country would unilaterally alter its inaction if given the chance. The social optimum occurs where every country mitigates, thereby giving an aggregate net benefit of 162 (= 27 × 6). For this six-country example, the Nash equilibrium is suboptimal by this amount, since aggregate gains at the Nash equilibrium is 0. In general, suboptimality increases as the number of countries increases in this stylized symmetric mitigation game, consistent with one of Olson’s (1965) maxims of collective action. Compared to the social optimum, the shortfall of the Nash equilibrium is N × (Nb _i  − c _i ) for N countries. Even for asymmetric countries, similar concerns arise provided that c _i  > b _i . If, however, there are some countries where b _i  > c _i , then these countries will mitigate, while those where c _i  > b _i will free ride. This scenario is reminiscent of how countries behaved for the Kyoto Protocol before its recent Paris Agreement reformulation.

Next, I extend the symmetric game graphically to the case of an arbitrary number of countries, denoted by N. In Fig. 2, payoffs are measured on the vertical axes, while the number of contributing countries other than i, denoted by n, is measured on the horizontal axis. At the far right of the horizontal axis, N – 1 denotes the maximum value of n. Two linear functions, based on the previous mitigation game, are displayed. The shirking payoff function is captured by s(n), and the participation payoff function is denoted by p(n + 1). For the shirking payoff, the representative country receives 6 times the number of contributors or s(n) = 6n, which attains a maximum of 6N − 6 on the right-hand vertical axis. The participation payoff reflects being a participant when n other countries reduce CO₂ emissions by the required percentage. For p(1), n = 0, and the representative country acts alone for a net gain of b _i  − c _i  =  − 3. For N − 1 other abating countries, country i nets (N − 1)b _i  + b _i  − c _i  = 6N − 9 when mitigating, as displayed on the right-hand vertical axis. In-between payoffs for the participating relationship are calculated in a similar fashion for different values of n. Country i shirks because s(n) > p(n + 1) for all values of n, leading to a Nash equilibrium at E, where no collective action is undertaken. The extent of the suboptimality equals N × (6N − 9), which increases with group size.

Fig. 2

N-country mitigation game

4 Alternative games for CDR

Reforestation or low-till agriculture possesses cost of $1–$100 per tCO₂ that is either cheaper or about the same as that of abatement efforts (see Table 2). When these two methods are cheaper than abatement, the difference between the benefit and cost per unit (i.e., b _i  − c _i ) may be positive, resulting in a harmony game where the net gain from participation exceeds that of shirking so that acting is the dominant strategy for countries with favorable geoclimatic conditions for growing forests. In terms of reforestation, country-specific gains – e.g., reduced erosion, enhanced watersheds, improved micro climates, and increased beauty – can also foster the harmony outcome by lifting the value of b _i above per unit cost. Analogously, carbon credits can also raise per unit reforestation benefits so that a harmony game results. Such credits act like selective incentives that promote collective action (Olson 1965). Even when a harmony scenario applies for reforestation and low-till agriculture, there is a concern that the long-run capture possibilities are limited for these CDR procedures as previously indicated in Table 1. If, however, these procedures have cost nearer to or above that of abatement, then we are back to the Prisoners’ Dilemma game, previously displayed in Figs. 1 and 2. As such, some, but not all, CDR methods confront the same collective action difficulties as those of carbon emission reduction. This Prisoners’ Dilemma scenario also applies to bioenergy with capture and sequestration, whose cost of about $100 per tCO₂ is about that of abatement, resulting in per unit cost exceeding provider-derived benefits. Associated publicly derived benefits from captured carbon are not anticipated to be internalized by the provider as in the case of abatement.

Next consider the game structure associated with land-based and ocean-based weathering, where cost per tCO₂ can be easily many hundreds of dollars, which is far greater than the usual cost per tCO₂ of abatement. For these weathering methods to become feasible, a group of countries must pool their efforts to surpass the necessary large-scale mining efforts to realize measurable benefits. As such, a threshold assurance game with cost-sharing may apply.⁷ This game scenario may also hold for costly direct air capture and sequestration, whose cost may be between $400 and $1000 tCO₂ removed from the air. In fact, the American Physical Society Report Committee (2011) puts this cost as far greater for some capture technologies. Massive investments are necessary for the structure to capture carbon from the air (National Research Council 2015a). To achieve feasibility for direct air capture, a coalition of countries may again need to pool their efforts to realize net benefits beyond some threshold provision level. I therefore view either weathering methods or direct air capture and sequestration as being a threshold game with cost sharing, whose analysis I now consider.

Initially, there are six symmetric countries, of which three are needed to pool their effort to surpass the threshold effort necessary to reap benefits from, say, direct air capture and sequestration. Three countries confer an aggregate benefit of 18 (or 6 per contributor) on each of the six countries; each additional contributor (beyond three) confers another 6 in benefits on each of the six countries. This follows because enhanced direct air capture benefits increase with effort expended. Given the need to surpass a threshold of effort before benefits are realized, b _i  = 6 for n = 3, while b _i  = 0 for n < 3 as the threshold is not attained. If n > 3, then each country receives 6n prior to its assigned cost. There is cost sharing in which each country, contributor or otherwise, pays cost of C _i  = c _i n/N, where unit cost, c _i , is 12, n is the number of contributors, and N = 6 is the number of countries.⁸

With N = 6, cost to each country is 2 times the number of contributors. Payoffs are computed as follows in Fig. 3: In the top row, a nonprovider’s net payoffs equal 0 when no one contributes; they equal −2 when one other country contributes; and they equal −4 when two other countries contribute. These payoffs follow from cost sharing prior to the threshold of three contributors being attained. Once three or more countries contribute to the project, a nonprovider receives 6 times the number of providers in benefits, from which shared cost of 2n must be subtracted, so that payoffs are 6n − 2n = 4n. In the bottom row, net payoffs are −2 when country i contributes alone with its cost being shared, and net payoffs equal −4 when country i and one other country contributes with their cost of 24 being shared. If, say, country i and two other countries jointly contribute to the project, then country i nets 12 (=3 × 6 − 2 × 3). The other payoffs are computed similarly in the bottom row. As shown in Fig. 3, there is no strictly dominant strategy. Past the threshold, contributing provides a larger payoff than not contributing. There are two Nash equilibriums – no country contributes and every country contributes – where the latter is the social optimum.

Fig. 3

Stylized six-country CDR threshold game with cost sharing

The associated cost-sharing problem still implies a collective action concern, because there is still a strong tendency to remain at the do-not-contribute Nash equilibrium. The problem becomes even more difficult when a subset of potential contributors share costs, since countries favor being designated a nonsharer of costs in the hopes of achieving a free ride. Cost sharing may assist collective action, but only after a cost-sharing agreement is enacted, wherein countries accept this responsibility (Sandler 2004, 2015). Consummating such an agreement may pose significant collective action difficulties of its own.

Figure 4 translates this game into an N-country analogue, where n on the horizontal axis is the number of other contributors. The participation path, p(n + 1), equals −12(n + 1)/N for n < 2, and it equals

$$ \left( n+1\right)\left(6-\frac{12}{N}\right) $$

Fig. 4

N-country CDR (threshold) game

for b _i  = 6 and n ≥ 3. Hence, the participation path is discontinuous at n = 2. In Fig. 4, the shirking function equals −12n/N for n < 3 and it equals

$$ n\left(6-\frac{12}{N}\right) $$

for n ≥ 3 since b _i  = 6. The discontinuity for the shirking path is at n = 3. In Fig. 4, there are two Nash equilibriums: at E ₂, where n = 0, and at E = 6N − 12, where everyone contributes. Prior to the threshold of three contributors, s(n) > p(n + 1) and the equilibrium involves no contributions. Once the threshold is surpassed at three contributors, every country has an incentive to partake in the activity given that p(n + 1) > s(n). Collective action is more hopeful for small thresholds and asymmetric countries.⁹ With a smaller threshold, fewer countries need to pool their efforts to achieve the action. With asymmetries, countries’ taste and endowment differences can foster some countries with a stronger taste for carbon reduction and/or greater means for action to privilege others with the reduction (Sandler 2015). If only a subset of countries agrees to share costs, then the participation equilibrium includes an N equal to those countries that agreed to participate. As the N decreases, the prognosis for collective action improves as fewer countries must then commit to cost sharing, which is always a difficult decision with intricate negotiations.

5 Albedo-modification games

I begin my collective action analysis of AM with stratospheric sulfur dioxide release, which is extremely cheap according to some of the simulations performed by McClellan et al. (2012). This estimated cost ranges from $2 to $8 billion a year to deliver 5 Mt. of sulfur dioxide to 18–30 km by Boeing 747s. Given this very modest cost, one capable country can achieve what is needed to offset temperature consequences of projected GHG accumulation. In so doing, derived benefit exceeds provision cost. These derived benefits come from not heating the atmosphere. In Fig. 5, we display a stylized chicken game scenario for six countries,¹⁰ where if no country acts to address rising temperatures, each country suffers a cost of 20 – any large cost will do. Suppose that this geoengineering action offers a constant benefit of 14 to all countries. Consequently, in the top row of Fig. 5, free-rider countries gain 14 once one country provides the required action. For this stylized game, any positive benefit that is greater than provision cost works. The albedo-modifying country nets 4 as it covers its cost of, say, 10. The important thing is that the sole provider gains a net benefit. Action beyond the injection to maintain 5 Mt. of sulfur dioxide aloft does not increase free-rider benefit and may reduce the benefit owing to side effects. There are six Nash equilibriums, each involving a single provider. If all countries come to view this type of geoengineering positively, the necessary coordination is for some country to step forward. If we allowed for N countries, the resulting chicken game would have N equilibriums each with a single provider if all countries are capable. With fewer capable countries, the number of equilibriums consists of the number of such countries.

Fig. 5

Chicken albedo modification game for inexpensive stratospheric sulfur dioxide

For symmetric countries, there is uncertainty as to whether some country will address the problem. This is analogous to bystanders coming to the aid of a rape victim, who cries for help (Dixit et al. 2015, pp. 454–458). For the matrix in Fig. 5, acting alone yields B − C = 4, while not acting, when no other country acts, gives −20. If the country does not act when one other country acts, then the non-acting country gains 4. For independent probabilities, the probability of no other country acting is f ^N − 1, and the probability of at least one other country acting is 1 − f ^N − 1 . To find a country’s mixed-strategy equilibrium from acting or not, we equate the country’s expected payoff, −20f ^N − 1 + B(1 − f ^N − 1), from not acting to its payoff from acting, B − C . This gives

$$ f={\left(\frac{C}{B+20}\right)}^{1/ N-1} $$

as the equilibrium probability of not acting by any one country. It is then easy to show that the probability of action by some other country, 1 − f ^N − 1, falls to 0 as N goes to infinity. Moreover, the probability that at least one of N countries takes action, 1 − f ^N, decreases and approaches

$$ 1-\left(\frac{C}{B+20}\right) $$

as N increases. Ceteris paribus, the possibility of action falls with group size in the symmetric case. Action is more likely by some country as the cost of inaction, i.e., −20, rises in absolute value or the cost of action falls in value.

This example could be extended to two sets of countries—those that gain from AM and those that lose from AM. The first set faces a chicken game as displayed in Fig. 5. The second set opposes this modification because these countries either gain from the warmer atmosphere or are opposed to potential albedo-modifying risks. Forestalling action by the second set is likely a threshold game, for which some coalition must accumulate sufficient might or persuasion to stop action.

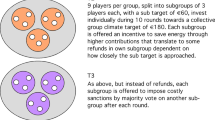
Next, I consider the case where multiple countries must act in unison to modify the Earth’s albedo sufficiently to offset some dire consequence stemming from a warmer climate. Consider McClellan et al.’s (2012) cost estimates for using either naval guns ($137 billion) or rockets ($390 billion) for delivering one Mt. per year to the stratosphere. These costs may be sufficiently great for injecting 5 Mt. per year that multiple countries must join forces to accomplish the necessary effort in terms of R & D and sulfur deployment cost.¹¹ This AM game is displayed in Fig. 6a for six symmetric countries.

Fig. 6

Stylized six-country chicken, albedo modification games

As in the single-country chicken game, the dire consequence is −20 before the required action is achieved by three countries acting together. This AM game is displayed in Fig. 6a as a chicken game requiring precisely three participating countries. The chicken representation is particularly appropriate for symmetric countries that view AM as averting disaster once carbon accumulation has reached an advanced level. In this first three-country chicken example, more participating countries beyond the required threshold do not improve or worsen environmental benefits as the minimal action averts disaster, so that the free riders always gain 20 even if more were to join the action. In the bottom row of Fig. 6a, country i nets −30 =  − 20 − c _i when it participates alone or is joined by one other country so that the minimal effort is not attained. When two or more countries participate along with country i, the latter receives 10 = 20 − c _i , which is greater than the previous example where positive benefits were smaller. The Nash equilibriums correspond to no country participating and precisely three countries participating,¹² thereby giving 10 to participants and 20 to nonparticipants. There are in total 21 Nash equilibriums. Once again, there is a coordination problem to achieve exactly the required number of participating countries, no more and no less. There is a clear incentive to be a free rider so as to escape provision cost. Thus, AM in this case implies coordination problems that may be difficult to address, unlike Schelling (1996) optimistic characterization. Some asymmetry where some countries gain more from stemming the rising temperature may foster the required coordination problem by identifying those most likely to come forward (Buchholz and Sandler 2017).

The game captured by Fig. 6b is a variation on a theme, for which efforts beyond the threshold reduces country i’s total benefit, B _i , by, say, 5 per additional participating country owing to negative side effects of AM. This alternative is in keeping with the notion that AM can have side effects, so that doing more than averting a disaster may be ill-advised. Thus, B _i  = 20 − 5(n − 3) for n > 3, prior to cost of 10 being subtracted for contributors. The configuration of Nash equilibriums remains as in Fig. 6a; however, there is a strong incentive not to surpass the threshold.

Figures 7 and 8 provide the N-country analogues to the chicken games in Fig. 6. In Fig. 7, the participation and shirking paths are made up of two discontinuous horizontal segments, with equilibriums at no one contributing (E ₂) or exactly three countries contributing (E). When penalties for exceeding the threshold are introduced in Fig. 8, the line segments at and rightward of E are downward sloping with slope − 5, equal to the marginal cost of exceeding the threshold. Other variants can be displayed depending on whether pre-threshold cost is refundable.

Fig. 7

N-country chicken, albedo modification game

Fig. 8

N-country albedo modification with penalty for more than 3 contributors

Finally, I consider the situation of placing a mirror or diffraction gratings at the Lagrange point, which would be exceedingly expensive, requiring a moon mining base and other infrastructure. This is again a chicken game with no effort being expended until there are a sufficient number of committing countries for the large-scale project to be realized. As such, the threshold number of countries will likely be large, making it difficult to achieve the necessary collective action. If the consequences of not addressing the warming problem is sufficiently dire and if cheaper methods imply too much harm to the environment (e.g., reductions to the ozone layer), then this threshold action may be surpassed. Moreover, penalties for exceeding the threshold are germane because reflecting too much sunlight from Earth will surely have negative consequences. Thus, the chicken game (not displayed) is like that of Fig. 8, but with equilibriums at a larger n and a more pronounced penalty for surpassing the threshold number of contributors.

5.1 AM addiction game

For AM, a serious concern is addiction – the inability to give up such modification once deployed. Ending such efforts can result in rapid rises in temperature with ensuing dire consequences (Lloyd and Oppenheimer 2014; National Research Council 2015b; Ricke et al. 2013; Victor 2006, 2008). Countries, once opposed to AM, may have no choice but to support its continued use.

To address addiction, I return to a symmetric representation. A possible addiction representation is captured by the game matrix in Fig. 9 for six countries, where provision cost per participating (continuing) country is 10. As in Fig. 6, three countries must coordinate efforts for an expensive sulfur-dioxide AM to be successful.¹³ For nonparticipants, each loses 80 if no country continues AM. If there are only one or two continuing countries, then a free rider loses −80 + 30n or −50 and −20, respectively, compared to the status quo of continued AM. If a fourth country adds to AM, then a free rider loses 10 − 20(n − 3), reflecting a penalty of −20 for surpassing the three-participant threshold. Next, consider the three albedo-modifying countries that must decide whether or not to continue their efforts.¹⁴ When less than three countries continue their efforts, contributing countries receive −c _i  − 80 + 30n, where 30 is gained for every participant up to the threshold. At the threshold, a participant makes no additional gain over the status quo. Beyond the threshold, a participant loses 20 times the number of surplus countries owing to the penalty of too much modification.

Fig. 9

Albedo modification addiction game, once modification is in place

The payoffs for country i as it continues AM follow accordingly. As shown in Fig. 9, the original three modifying countries receive 0 when they maintain their efforts. Country i loses 30 or 60 when one or more of the original modifiers drop out, respectively. Beyond the threshold, country i loses 20 for each new modifier. For the boldfaced matrix in Fig. 9, this is a harmony game for the original three modifiers, with the Nash equilibrium of maintaining the status quo. There is an incentive for the nonmodifiers to do anything different. As such, addiction is maintained. If, however, one of the original modifiers were no longer capable of doing so, then a different game would follow, analogous to those in Fig. 6, in which a new coalition of three is apt to form.

This information is translated into an N-country version in Fig. 10, where the participation and shirking functions are displayed. The sole stable Nash equilibrium is at point E, at which country i and two others (n = 2) maintain their AM action. Prior to point E, the participation payoff exceeds the shirking payoff, while beyond E, the opposite is true, so that the status quo is maintained with three contributors.

Fig. 10

Albedo modification addiction

6 Governance

Both forms of geoengineering are in need of some kind of transnational governance structure, because collective action concerns are pervasive. By sharing the same game structure as carbon mitigation, the governance for CDR is analogous to that of the latter. For CDR, too little action is often anticipated, similar to carbon mitigation. The logical institution to embrace this reduction is the Paris Agreement, so that mitigation efforts can be coordinated along with CDR. Transnational governance is necessary to stimulate low-risk actions to bolster CDR from the atmosphere. In some cases, this governance can coordinate financing for expensive procedures such as direct air capture and sequestration. If cost sharing is appropriate, then an agreed cost-sharing arrangement similar to the one used to share UN peacekeeping cost can be instituted for participants. Each country would be assigned a cost share that may change over time as circumstances change (e.g., relative wealth of participants).

A different kind of governance is needed for AM, in which one or two countries take actions to reduce global temperatures, thereby having adverse consequences on some countries. Harnish et al. (2015) show that countries view AM differently; e.g., the United States and the United Kingdom see the need for research, while Germany takes a much slower and more cautious approach. Such philosophical differences among countries may make a global approach exceedingly difficult to formulate and follow.

Three alternative institutional arrangements are mentioned for governance in regards to AM: through the United Nations, by a single state, or through a consortium of states (Virgoe 2009). The United Nations is considered because AM has global implications, so that the United Nations has the potential to internalize all externalities. Unfortunately, enacting treaties or agreements through the United Nations can be very time consuming and the treaties’ stipulation can be diluted as a consensus is sought (Victor 2006). In some instances, a small number of countries can block action or at least hold it up. If climate change poses imminent concerns, time would be short to institute action to curb rising temperatures.

A second institutional arrangement involves a single country soliciting input from other affected countries and then taking action. Obviously, the country for such a role would be the United States, or another with the means to engage in AM. For nuclear weapon nonproliferation, the United States assumed this single-country role with mixed success. The United States had more success in its pivotal role with the Internet and the INTELSAT communication network. With a single country in charge of AM, action is rapid, but the interests of the pivotal country and its friends are favored, with significant distributional consequences.

A third structure – coalition governance – involves a small number of countries that include those capable of AM and those most affected by such modification. Major economic powers should also be included if they do not fall into the other two categories of countries. Lloyd and Oppenheimer (2014, p. 53) put forward an institutional design, in which membership is small, rules are flexible, votes are counted equally, and legalization is weak. Such a structure allows the main stake-holding countries the ability to coordinate actions, share research, and consult on technical development. This coalition can coordinate efforts to meet thresholds for both kinds of geoengineering projects. Having such a coalition in place might inhibit a single country from unilateral action. A sufficiently small coalition can act rather swiftly when the need for action arises. Structural flexibility allows for institutional change as knowledge of geoengineering progresses over time.

An alternative governance structure for AM can be inferred from a recent game theory article. Moreno-Cruz (2015) puts forward a two-stage game wherein countries decide carbon mitigation in stage 1 and capable countries determine AM in stage 2. He shows that, with sufficient asymmetry among countries, the potential introduction of geoengineering in stage 2 can induce countries to mitigate to a much greater extent in stage 1. That is, the threat of geoengineering can serve as a “governance” structure to reduce the subsequent need for geoengineering. This governance is virtually transaction-cost free.

Thus far, the governance structures above address the initiation or free-driving problem of AM. There is also maintenance governance once AM is initiated because stopping AM has dire consequences. This maintenance governance is easier to address than forestalling initiation because of the underlying harmony game associated with addiction. Countries, not part of the original effort, are apt to willingly support the free drivers if their efforts need bolstering.

7 Concluding remarks

There are some clear messages that derive from the conceptual analysis of this paper. First, geoengineering presents myriad collective action concerns. Many strategic forms apply because geoengineering may assume a plethora of procedures, some simple and some complex, with different interactions among countries. Second, unlike Schelling’s (1996) optimistic characterization, albedo-modifying geoengineering is more than a simple cost-sharing problem that the international community can readily address by drawing on its past experiences, because of widespread negative externalities and the need for the proper size coalition to come forward. Third, CDR is sometimes represented by Prisoners’ Dilemma, analogous to the strategic concerns plaguing carbon mitigation. In other instances, however, this reduction is best characterized as a threshold assurance game that differs from carbon abatement. Fourth, AM presents more difficult collective action issues than CDR. In some instances, collective action involves keeping a country or coalition from acting unilaterally, thus harming some high-latitude countries’ well-being and closing up future options owing to addiction. Once developed, AM is tempting because it can be so cheap in some forms (e.g., stratospheric sulfur dioxide injection) compared to carbon mitigation. Generally speaking, there is an interesting contrast between CDR and AM; namely, the former is expensive but usually presents low risk, while the latter is cheap but usually presents high risk. Given its high risk, governance is more essential for AM than for CDR. Fifth, perhaps the most difficult collective action problem is to find the proper mix of carbon mitigation, CDR, and AM. This is particularly true because strategic aspects may at times work in unison and at other times work at cross-purposes among these three efforts. Moreover, the timing of these efforts can present interesting strategic issues as Moreno-Cruz (2015) and others show.

Future studies need to meld strategic considerations of geoengineering with the design of governance structures for both classes of geoengineering. Any such structure must be multifaceted to account for the various types of geoengineering.