1 Introduction

Histogram Equalization (HE) is a classical method for improving the global contrast of an image. It linearizes the gray value histogram, such that the result image uses the full range of the possible gray values. A drawback of this method is, however, that local variations are not taken into account. Adaptive Histogram Equalization (AHE) [4, 5, 11] solves this issue by considering only the gray values within a rectangular filter window around each pixel to compute an individual HE transfer function for the respective pixel. Because AHE can lead to over-amplification of noise, Pizer et al. [12] proposed Contrast-Limited Adaptive Histogram Equalization (CLAHE), which allows to limit the maximum desired contrast in homogeneous regions. Due to its efficacy, CLAHE is still a popular image preprocessing method [9, 14] and has successfully been used to improve the performance of Deep Learning models [2, 13]. The computational complexity of AHE and CLAHE is very high, because they require computing the histogram of each filter window. Using a naive implementation in which the histogram is recomputed explicitly for each window, the runtime can easily become multiple seconds, minutes, or even hours, depending on the size of the filter window. To circumvent this problem, most publicly available implementations of AHE and CLAHE are based on an approximative algorithm that is fast, but can lead to visible artifacts in the resulting image. This severely impacts the applicability of AHE in many real-world scenarios, where runtimes of just a few milliseconds are required and visual artifacts are not acceptable. Because of this restriction, we only consider methods that implement an exact variant of AHE and CLAHE and thus do not lead to such artifacts.

In this work, we propose a fast constant-time algorithm for AHE and CLAHE that is free of visual artifacts and thus suitable for practical applications. Section 2 discusses related work. In Sect. 3, we describe the \(\mathcal {O}(1)\) algorithm for sliding-window histograms as well as efficient implementations of the AHE and CLAHE transfer functions. In Sect. 4, we benchmark our method against previous algorithms and discuss the results. Finally, Sect. 5 presents our conclusions.

2 Related work

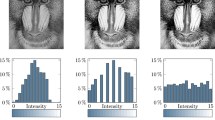
In the past, many improvements for AHE and CLAHE have been proposed. Pizer et al. [12] suggest an approximative approach in which the HE transfer function is computed only for a subset of all pixels and interpolated between these points. This method is also referred to as Interpolated Adaptive Histogram Equalization (IAHE). It is a popular choice in many computer vision libraries due to its low execution time. However, the interpolation can lead to artifacts, as shown in Fig. 1. In practice, filtering an image translated by several pixels can lead to a significantly different result than filtering the original image, meaning that the interpolation-based approach is not shift-equivariant. This poses a problem, e.g., in industrial inspection, where the artifacts might be interpreted as defects, leading to falsely rejected parts. Our work differs fundamentally from IAHE in that we compute the exact transfer function for each pixel and thus avoid the interpolation artifacts shown in Fig. 1b. Kim et al. [7] propose Block-Overlapped Histogram Equalization (BOHE), which applies Huang’s \(\mathcal {O}(n)\) sliding-window histogram method [3] to AHE. The core idea in [3] is that when the window slides one pixel to the right, one can simply update the histogram computed for the previous pixel instead of fully recomputing it. Sund et al. [15, 16] propose Sliding-Window Adaptive Histogram Equalization (SWAHE), which applies the \(\mathcal {O}(n)\) algorithm from [3] to CLAHE. Wang and Tao [17] also apply [3] to AHE and propose several small improvements to speed up the computation of the HE transfer function. Kong and Ibrahim [8] propose Multiple Layers Block-Overlapped Histogram Equalization (MLBOHE), which also applies Huang’s \(\mathcal {O}(n)\) algorithm [3] to AHE. Furthermore, they employ an optimized zig-zag sliding order to avoid recomputation of the window histogram at the beginning of each row. Kim et al. [6] propose Partially Overlapped Sub-Block Histogram Equalization (POSHE), where HE is applied to overlapping sub-blocks of the image and the results are accumulated. Due to the large stride of half the window size, the result must be filtered to reduce blocking artifacts. Fu et al. [1] propose POSHE-based Optimum Clip-Limit Contrast Enhancement (POSHEOC), which combines POSHE [6] with CLAHE.

Our work mainly follows [7] and [15,16,17] in that we improve the computational complexity of the AHE and CLAHE algorithms. In contrast to the existing linear-time methods, our proposed method has a constant per-pixel runtime that is independent of the filter window size. Contrary to [1, 6, 12], we do not use approximative algorithms. This means that our method reproduces the exact same results as the original algorithms for AHE and CLAHE and does not introduce visual artifacts.

Fig. 1
figure 1

Interpolation artifacts of IAHE. (a) shows the original input image with a linear gray value ramp. (b) shows the result of IAHE, with banding artifacts due to the interpolation. (c) shows the smooth result of exact CLAHE. The artifacts on the left and right are due to border treatment and thus inevitable

Full size image

3 Efficient adaptive histogram equalization

In this section, we describe the main building blocks for efficient AHE: First, we show how the gray value histogram of a sliding window can be maintained with \(\mathcal {O}(1)\) complexity. Second, given the histogram for a window, we compute the HE transfer function for the center pixel of the window in an efficient manner. Third, we describe how the CLAHE transfer function can be implemented efficiently. Fourth, we describe how multilevel histograms can be applied to AHE and CLAHE, respectively. A high-level overview on the complete AHE and CLAHE process is given in Algorithm 1.

Algorithm 1
figure a

High-level overview on AHE and CLAHE

Full size image

3.1 Notation

We consider an image \(\mathcal {I} \in \{0,\dots ,255\}^{M \times N}\) with rows \(i \in \{0,\dots ,M-1\}\) and columns \(j \in \{0,\dots ,N-1\}\). Note that we use 8-bit images in this description, but the underlying methods are not restricted to this case. Without loss of generality, we consider a square filter window with radius \(r \in \mathbb {N}\), hence the window size is \((2r+1) \times (2r+1)\). We denote the gray value histogram of the window centered at pixel (i, j) as the kernel histogram \(H_{i,j} \in \mathbb {N}^L\), where the number of bins \(L \in \mathbb {N}\) is typically 256 for 8-bit images. The histogram bin \(H_{i,j}(g)\) counts how often a gray value g occurs in the filter window

$$\begin{aligned} H_{i,j}(g) = \sum _{x=i-r}^{i+r}\sum _{y=j-r}^{j+r} \left[ \mathcal {I}_{x,y} = g\right] , \end{aligned}$$
(1)

where \(\left[ \mathcal {I}_{i,j} = g\right]\) is the indicator function that evaluates to 1 if \(\mathcal {I}_{i,j} = g\) and 0 otherwise. The cumulative histogram is defined as

$$\begin{aligned} C_{i,j}(g) = \sum _{k=0}^{g} H_{i,j}(k). \end{aligned}$$
(2)

It counts the number of pixels that have a gray value less than or equal to g.

3.2 Sliding-window histogram computation

For each pixel position (i, j) in the image, AHE requires the computation of a histogram \(H_{i,j}\) for the filter window centered at the pixel (i, j). This is implemented using a sliding window approach where the filter window moves pixel-wise from left to right for each row. Histograms of sliding windows have been used for a long time in the filtering literature, e.g., to compute the median filter [3]. Thus, there exist efficient algorithms that avoid redundant computations in the overlap regions of neighboring windows. The choice of a suitable sliding window histogram method is crucial, because the runtime of existing AHE and CLAHE implementations is dominated by the computation of histograms. In the following, we describe the sliding-window histogram algorithms commonly used in the literature.

A naive but straightforward implementation of a sliding window histogram algorithm simply computes the full histogram at each spatial position in the image. To compute the histogram for a window, all \((2r+1)^2\) pixels within the window need to be assessed and the corresponding histogram bins are increased. This operation requires \((2r+1)^2\) bin increments; hence, its computational complexity is \(\mathcal {O}(r^2)\).

Huang et al. [3] noticed that most of the computation in the naive algorithm is redundant and can be avoided by only updating the parts of the histogram that actually changed. Their improved algorithm starts with initializing a full histogram of the window centered at the first pixel (i, 0) in row i. When the window moves one column to the right, the histogram is updated by removing the values of the leftmost column \(j-r\) from the histogram and adding the new rightmost column \(j+r+1\). Although the initialization of the first window of each row still requires \((2r+1)^2\) bin increments, each further update only requires \(2r+1\) subtractions and \(2r+1\) additions. Thus, for large image sizes, the amortized computational complexity becomes \(\mathcal {O}(r)\). A slight modification of Huang’s algorithm was proposed by Kong and Ibrahim [8]. They propose a “zig-zag” sliding order where the window first slides from left to right, then down by one row, and then slides backwards from right to left. Using this sliding order, the full histogram needs to be initialized only once instead of at the beginning of each row. However, since each update of the sliding-window histogram still requires \(2r+1\) bin decrements and \(2r+1\) bin increments, the overall computational complexity remains \(\mathcal {O}(r)\).

Perreault and Hébert [10] noticed that in Huang’s algorithm, each pixel is still added to and removed from \(2r+1\) histograms, since no information is retained when the window slides down by one row. Their improved algorithm makes use of the distributivity of histograms, i.e., the property that the kernel histogram can be expressed as the sum of the histograms of the filter window’s columns. For the current row i, column histograms \(h_c \in \mathbb {N}^L\) are defined as

$$\begin{aligned} h_c(g) = \sum _{x=i-r}^{i+r} \left[ \mathcal {I}_{x,c} = g\right] . \end{aligned}$$
(3)

Using this to rearrange Eq. (1), the kernel histogram can be expressed as

$$\begin{aligned} H_{i,j}(g) = \sum _{c=j-r}^{j+r} h_c(g). \end{aligned}$$
(4)

Note that this implies that, in addition to the kernel histogram, N additional column histograms \(h_c\) are maintained, where \(c \in \{0,\dots ,N-1\}\). Starting at the top-left pixel of the image, the kernel histogram is initialized by summing over its column histograms as in Eq. (4). Moving the window one column to the right, the kernel histogram is updated by subtracting the leftmost column histogram \(h_{j-r}\) and adding the new rightmost column histogram \(h_{j+r+1}\). When moving the window down to the next row, the column histograms are updated by subtracting the gray values of the top row \(i-r\) and adding the gray values of the new bottom row \(i+r+1\). For a single window, each update consists of one addition and one subtraction for updating the new rightmost column histogram, as well as L additions and L subtractions for updating the kernel histogram. Since the update step for the kernel histogram is now independent of the filter mask radius r, the amortized per-pixel complexity becomes \(\mathcal {O}(1)\). In practice, the addition of histograms with \(L=256\) bins is naturally vectorizable using SIMD instructions, which leads to a relatively low constant cost of the update step. Furthermore, when moving to the next row, all column histograms can be updated at once, which leads to a more advantageous memory access pattern.

AHE and CLAHE can be implemented based on the sliding window histogram methods described above. The histogram obtained for each window is then used to compute the output gray value in the center of the window. This mapping, called histogram equalization, is described in detail in the next section.

3.3 Histogram equalization

HE improves the contrast of an image by mapping the gray values proportional to their rank. As a consequence, the histogram of the resulting image has a uniform distribution over the whole gray value range. The HE transfer function f(g) for the gray value g is given by the cumulative histogram

$$\begin{aligned} f(g) = \frac{L-1}{n} C(g) = \frac{L-1}{n} \sum _{k=0}^{g} H(k), \end{aligned}$$
(5)

where n is the number of pixels under consideration, i.e., all pixels in the image for classical HE or \(n=(2r+1)^2\) for window-based approaches.

AHE computes the transfer function for pixel (i, j) using the histogram of the filter window centered at pixel (i, j). Thus, the transfer function is not the same for the whole image, but depends on the local neighborhood of each pixel. This has the advantage that local variations in the image can be considered for the mapping, but it comes with increased computational cost. In the following, we describe how the per-pixel cost can be reduced.

The HE transfer function f(g) given in Eq. (5) requires the computation of the cumulative histogram C(g). In a straightforward implementation, one could simply compute \(\sum _{k=0}^{g} H(k)\), which requires \(g+1\) additions. In the worst case, when the window contains only the gray value \(g=L-1\), this leads to L additions. As Wang and Tao [17] point out, the amount of computation required for C(g) can be reduced by utilizing the fact that the number of values n within a window is constant

$$\begin{aligned} n = \sum _{k=0}^{L-1} H(k) = \sum _{k=0}^{g} H(k) + \sum _{k=g+1}^{L-1} H(k). \end{aligned}$$
(6)

Using this, the summation can be split such that at most half of the bins need to be added

$$\begin{aligned} C(g) = \left\{ \begin{array}{ll} \sum _{k=0}^{g} H(k) &{} \quad \text {if } g < \frac{L}{2} \\ n - \sum _{k=g+1}^{L-1} H(k) &{} \quad \text {otherwise.} \\ \end{array} \right. \end{aligned}$$
(7)

Using Eq. (7), the computation of f(g) requires at most \(\frac{L}{2}\) additions and one subtraction, as well as one multiplication with a constant factor \(\frac{L-1}{n}\). Note that the number of operations depends only on the number of histogram bins L and is therefore in \(\mathcal {O}(1)\) with respect to the filter window size.

3.4 Histogram clipping

In homogeneous image regions, the dominant gray values typically produce high peaks in the respective histogram bins. After the equalization, an originally narrow range of input values will be mapped to a wide range of output values, which can lead to an undesired over-amplification of noise. CLAHE [12] reduces the amount of contrast enhancement by limiting the histogram bins to a clip limit \(\mathcal {C} \in \mathbb {N}\) before computing the HE transfer function f(g). The clipped values \(n_\mathcal {C} \in \mathbb {N}\) are redistributed evenly over all histogram bins. Algorithm 2 shows how the clipped and redistributed histogram \(\hat{H}\) is computed.

Algorithm 2
figure b

Compute clipped histogram \(\hat{H}\), based on the description in [12]

Full size image

Analogous to Eq. (5), the CLAHE transfer function is defined as

$$\begin{aligned} \hat{f}(g) = \frac{L-1}{n} \sum _{k=0}^{g} \hat{H}(k), \end{aligned}$$
(8)

where \(\hat{H}\) is the clipped and redistributed histogram as described in Algorithm 2. Note that, for a sliding-window implementation of CLAHE, we need to evaluate the transfer function only for the gray value in the center of the window. Hence, it is unnecessary to compute the entire clipped histogram explicitly. Instead, we introduce a more efficient algorithm to compute the clipped cumulative histogram \(\hat{C}(g)\) as follows. We split the sum in Eq. (8) into the sum of the clipped histogram up to g and the sum of redistributed values up to g

$$\begin{aligned} \sum_{k=0}^{g} \hat{H}(k) &= \sum_{k=0}^{g} \left( \min\{H(k), \mathcal{C}\} + \frac{n_\mathcal{C}}{L} \right) \\ &= (g+1)\frac{n_\mathcal{C}}{L} + \sum_{k=0}^{g} \min\{H(k), \mathcal{C}\}\end{aligned}$$
(9)

Using a similar approach as in Eq. (6), we can express \(n_\mathcal {C}\) as the difference between the total number of gray values and the sum of the clipped, but not yet redistributed histogram bins

$$\begin{aligned} n_\mathcal{C} &= \sum_{k=0}^{L-1} \max\{0, H(k)-\mathcal{C}\} \\ &= n - \sum_{k=0}^{L-1} \min\{H(k), \mathcal{C}\}.\end{aligned}$$
(10)

Combining the rearrangements made in Eqs. (9) and (10), we end up with Algorithm 3, where we compute \(\hat{C}(g)\) in a single pass over the histogram. Note that the number of operations depends only on the number of histogram bins L and is therefore in \(\mathcal {O}(1)\) with respect to the filter window size.

Algorithm 3
figure c

Efficient evaluation of \(\hat{C}(g)\)

Full size image

3.5 Multilevel histograms

Perreault and Hébert [10] propose using multilevel histograms and conditional updating of the kernel for the median filter. In the following, we investigate how these optimizations can be applied to AHE and CLAHE.

The idea of multilevel histograms is as follows: Instead of a single histogram, two histograms with different granularity are maintained. The “fine” histogram counts the frequency of each gray value, whereas a bin in the “coarse” histogram accumulates a segment of multiple gray values. Typically, the fine histogram consists of 256 bins, while the coarse histogram only consists of 16 bins, each containing the sum of 16 corresponding fine bins. In our experiments, we also evaluate a configuration with 8 coarse bins, where each bin contains the sum of 32 corresponding fine bins.

Keeping two histograms in parallel introduces a slight computational overhead, but allows two interesting optimizations. First, the cumulative sum up to a certain bin can be computed with fewer additions by summing over the coarse histogram. Second, segments of the fine histogram can be computed on demand, as the sum of the segments is already stored in the corresponding bins of the coarse histogram. This is particularly beneficial when the image is smooth, such that the histograms of neighboring filter windows differ only slightly. Then, most bins of the histogram stay unchanged and only a few fine segments need to be updated. On the contrary, high-frequency images can lead to significantly slower processing times due to the increased overhead. Note that the coarse and fine column histograms as well as the coarse kernel histogram are always updated. The segments of the fine kernel histogram are updated only on demand.

Extending AHE with multilevel histograms is straightforward. We compute the HE transfer function Eq. (5) by first summing over the coarse histogram, followed a single fine histogram segment up to the gray value g. The extension of CLAHE with multilevel histograms is more complicated, because the naive implementation described in Algorithm 2 requires computing the full histogram on the fine level. This would render multilevel histograms useless, as the increased overhead of computing them is not compensated. Using our method proposed in Algorithm 3, however, we can skip segments of the fine histogram conditionally based on the value of the corresponding coarse bin. In our experiments, we only update the fine segment when the value of the coarse bin is above the clip limit. This simple criterion ensures that none of the corresponding fine histogram bins exceeds the clip limit. Thus, there is no need to clip them.

4 Experiments

In this section, we benchmark our method against previous algorithms and discuss the results. To measure the effect of the proposed improvements independently from each other, we separately evaluate the sliding-window methods and the transfer function implementations for AHE and CLAHE, respectively.

We measure the runtimes of the algorithms using a dataset of 25 grayscale images taken from the MVTec HALCON machine vision library.Footnote 1 The images cover different scenes with varying contrast and are scaled to a size of \(1000\times 1000\) pixels. Figure 2 shows an overview of the dataset. For each image, we first perform 3 warm-up runs and then measure the average time over 10 runs. The reported values are the mean over the average times of all 25 images. Timing was conducted on an Intel Core i9-10900X CPU using a single thread. Note that, in general, all described methods can be further accelerated using parallelization with multiple threads. We implemented all algorithms in C for the best performance. Furthermore, we ensure that all analyzed implementations of AHE and CLAHE produce the exact same result images by computing the sum of absolute differences (SAD) with respect to the results of a baseline implementation. The SAD is 0 for all analyzed variants of AHE and CLAHE, respectively.

Fig. 2
figure 2

The dataset of 25 images used for our experiments

Full size image

4.1 Sliding-window methods

We compare the runtime of our \(\mathcal {O}(1)\) algorithm for AHE against the sliding-window methods described in Sect. 3.2. For this, we implemented AHE using the naive \(\mathcal {O}(r^2)\) method, the \(\mathcal {O}(r)\) method based on Huang’s algorithm [3, 7, 15,16,17], and the \(\mathcal {O}(r)\) method with zig-zag sliding order proposed in [8]. Figure 3 shows the timings as a function of the filter radius \(r \in \{1,\dots ,300\}\). The naive \(\mathcal {O}(r^2)\) method exhibits very high execution times, even for small filter sizes. It already takes about 1 s for a filter radius of \(r=22\), which makes the method impracticable for real-world applications. The runtimes of the \(\mathcal {O}(r)\) methods grow linearly with the filter size. It can be observed that the zig-zag sliding order [8] has a slight runtime advantage, particularly for large filter sizes. For instance, at \(r=300\), it is about 8% faster than Huang’s algorithm. Our proposed \(\mathcal {O}(1)\) method achieves constant processing times of around \(45\,\hbox {ms}\) for arbitrary filter sizes. Note that the \(\mathcal {O}(r)\) methods are slightly faster for very small filter sizes due to the higher constant cost of our method. For \(r=9\), our \(\mathcal {O}(1)\) method is on par with the \(\mathcal {O}(r)\) methods, and for larger filter sizes, it is significantly faster. For instance, at \(r=300\), it is about 94% faster than the \(\mathcal {O}(r)\) methods.

Note that we do not provide extensive benchmark data for sliding window implementations of CLAHE, since the results for AHE are transferable. The only difference is a slightly higher constant cost. See Sect. 4.2 for details.

Fig. 3
figure 3

Runtime comparison of AHE implementations using different sliding-window methods on images of size \(1000\times 1000\) pixels

Full size image

4.2 Transfer function computation

We provide benchmarks for the efficient implementations of the AHE and CLAHE transfer functions described in Sect. 3.3 and Sect. 3.4, as well as the multilevel histogram approach described in Sect. 3.5. Tables 1 and 2 show the runtimes of AHE and CLAHE, respectively, with different implementations of the transfer functions. Although the runtime of our sliding-window approach is basically independent of the filter mask size, we report the runtimes for \(r=25\), \(r=150\), and \(r=300\). Our experiments show that the runtime increases slightly with increasing filter radius due to the increased overhead for managing large filter windows.

The AHE baseline achieves runtimes between \({40.4}\,\hbox {ms}\) and \({47.8}\,\hbox {ms}\), depending on the filter radius. Splitting the histogram range as described in Eq. (7) improves the runtime only slightly by \(0.6-1.5\%\). Even though one might theoretically expect a higher speedup based on Eq. (7), the additional branching and the diverse gray value distributions of real images diminish the advantage of this optimization. Using multilevel histograms with 16 coarse bins, the runtime improves significantly by \(16.7-30.2\%\). Using multilevel histograms with only 8 coarse bins improves the runtime further by \({26.4}-{32.2}\%\) compared to the baseline. Note that the histogram splitting optimization does not decrease the runtime any further when using multilevel histograms. Furthermore, note that both optimizations make assumptions on the gray value distributions in the image and thus make the runtime dependent on the image content.

The CLAHE baseline described in Algorithm 2 achieves runtimes of 68.5 ms to 75.4 ms for \(\mathcal {C}=0.1n\) and 71.5 ms to 81.8 ms for \(\mathcal {C}=0.01n\). Note that a lower clip threshold \(\mathcal {C}\) leads to clipping more bins and thus to an increased computation time. Computing the transfer function implicitly, as described in Algorithm 3, improves the runtime significantly by 8.6–14.5%. It can be observed that the optimization is particularly beneficial for low clip thresholds as well as small mask radii. The benefits of multilevel histograms for CLAHE are mixed. For a high clip limit of \(\mathcal {C}=0.1n\), the runtime improves by 7.8–19.7% using 16 coarse bins and by 26.1–35.6% using 8 coarse bins. For a low clip limit of \(\mathcal {C}=0.01n\), the runtime worsens by 8.7–46.9% using 16 coarse bins. Using 8 coarse bins, the runtime improves by 16.1% for \(r=25\), but worsens by 4.3–12.2% for larger mask radii.

In general, multilevel histograms turn out to be more beneficial for small mask sizes and for high clip thresholds, where AHE can be seen as a special case of CLAHE with \(\mathcal {C}=1\), i.e., no clipping occurs. Small mask sizes lead to sparse changes in the histogram, meaning that many fine segments of the histogram do not need to be updated. High clip thresholds lead to a high probability that the values in a segment do not need to be clipped, which allows skipping whole segments when computing the CLAHE transfer function. Low clip thresholds lead to a high probability that a segment of the histogram must be clipped. Then, it becomes necessary to compute the respective fine histogram segment for the evaluation of the transfer function. Unfortunately, our decision criterion causes too many fine histogram updates for low clip thresholds and thus diminishes the advantages of the multilevel histogram optimization.

Table 1 Timing of the proposed AHE algorithm using different implementations for computing the transfer function. ‘Multilevel’ refers to the usage of multilevel histograms and the number of coarse bins. ‘Split’ denotes whether the transfer function is computed using Eq. (7)
Full size table
Table 2 Timing of the proposed CLAHE algorithm using different implementations for computing the transfer function. ‘Multilevel’ refers to the usage of multilevel histograms and the number of coarse bins. ‘Implicit’ denotes whether the transfer function is computed using Algorithm 3
Full size table

5 Conclusion

In this work, we presented an efficient \(\mathcal {O}(1)\) algorithm for AHE and CLAHE. Our method reduces the processing time by at least an order of magnitude to just a few milliseconds, even when using very large filter sizes. This allows using contrast enhancement methods, such as AHE and CLAHE, to be used in practical applications. Contrary to commonly used approximative approaches like IAHE, our method computes the exact HE transfer function for each pixel without interpolation artifacts. Future work might address the constant cost of computing the HE transfer function for each window. If f(g) could be computed incrementally [18], it could be updated in the next window instead of being recomputed from scratch. Furthermore, multilevel histograms have proven very effective for AHE, but not for CLAHE. We encourage researchers to find a better suiting implementation of multilevel histograms for CLAHE, because the potential speedup is promising.