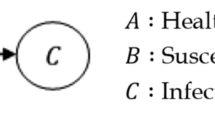The Role of Mobility in the Dynamics of the COVID-19 Epidemic in Andalusia

Abstract

Metapopulation models have been a popular tool for the study of epidemic spread over a network of highly populated nodes (cities, provinces, countries) and have been extensively used in the context of the ongoing COVID-19 pandemic. In the present work, we revisit such a model, bearing a particular case example in mind, namely that of the region of Andalusia in Spain during the period of the summer-fall of 2020 (i.e., between the first and second pandemic waves). Our aim is to consider the possibility of incorporation of mobility across the province nodes focusing on mobile-phone time-dependent data, but also discussing the comparison for our case example with a gravity model, as well as with the dynamics in the absence of mobility. Our main finding is that mobility is key toward a quantitative understanding of the emergence of the second wave of the pandemic and that the most accurate way to capture it involves dynamic (rather than static) inclusion of time-dependent mobility matrices based on cell-phone data. Alternatives bearing no mobility are unable to capture the trends revealed by the data in the context of the metapopulation model considered herein.

1 Introduction

Human mobility has played an indisputable role in COVID-19 dynamics (Chinazzi et al. 2020; Kraemer et al. 2020) with as many as $86\%$ of global cases having been imported from Wuhan, the original location of the pandemic. Studies of the epidemic in China have shown that in the early stages thereof, the probability of an outbreak was correlated with the frequency of imported cases from Wuhan (Kraemer et al. 2020). The trajectory of the epidemic over a similar time period was also studied in Li et al. (2020) using an SEIR (Susceptible-Exposed-Infected-Recovered) stochastic metapopulation model, where it was determined that undocumented infections played a crucial role in the rapid spread of the epidemic. These early and high-profile studies render it clear that a systematic consideration of such mobility aspects of the pandemic and of theoretical models thereof is a key ingredient toward appreciating its potential for spreading across countries and regions.

Continuing along this vein, in a subsequent study (Wells et al. 2020), the probability of case importations to countries having airports with direct flights to and from mainland China was estimated. It was assumed that the probability of importation is proportional to the number of airports in the country with direct connections to mainland China. With the implementation of Wuhan’s travel ban and the subsequent international travel restrictions, Chinazzi et al. (2020) analyzed the effect of quarantine measures on local, national, and international pandemic spread. Even though the spread of the virus could only be delayed in the Chinese mainland, the mitigation of the transmission would be notable around the world. Modeling the course of the epidemic in other countries such as England and Wales, Danon et al. (2021) also incorporated daily commuting as an important factor in the spread of the disease. It was assumed that infectious hosts may infect others both at home during the night and away during the day in the span of a day’s cycle. A study evaluating confinement and other mitigation measures in Spain (Arenas et al. 2020) used workforce mobility as a proxy for confinement. For Brazil, commuter and airline data were used to calibrate a stochastic epidemic model (Costa et al. 2020). The model was used to investigate the spatial spread of the disease at various geographical scales (ranging from municipalities to states). It should be clear that these are only some select studies within a continuously expanding large volume of literature, which has now also been reviewed, e.g., in Calvetti et al. (2020) (see also earlier reviews such as Chen 2014; McCallum et al. 2001).

Of course, such models have a time-honored history in earlier instances of disease-spread modeling. For example, the Global Epidemic and Mobility (GLEAM) team integrates real-world pandemic transmission models with mobility data, including airline transportation network flows, ground mobility flows, and sociodemographic features, to capture spatiotemporal connections between mobility and an epidemic’s spread (Chinazzi et al. 2020; Balcan et al. 2009). A model for influenza in the USA (Pei et al. 2018) accounted for both daily commuting and random travels between states. One of the main findings there was that the metapopulation model more accurately predicts the onset, peak timing and intensity than models only accounting for specific locations. A study of long-term influenza patterns in the US (Viboud et al. 2006) used mortality data and the gravity model, whereby population flows between nodes of the metapopulation network are determined by considerations akin to Newton’s law of gravity, to study the spreading of influenza across states. References (Balcan et al. 2009; Zipf 1946) also showed correlation between infection spread and human movements. Theoretical metapopulation studies, where the travel rates are given by the gravity model, also exist (Belik et al. 2011). Other works use the rates at which hosts leave and return to their permanent locations to infer the coupling strengths in their ODE model (Kelling and Rohani 2002). In earlier work, the bubonic plague epidemic was modeled using a similar approach (Keeling and Gilligan 2000), with adjacent metapopulations on a lattice coupled to rates chosen to fit historical data.

Studies looking at human mobility under lenses that go beyond gravity models also exist. One such example is the radiation model (Simini et al. 2012), which is based on the assumption that population density dictates employment opportunities, so when density is low, commuters need to travel longer distances. Hence, the predicted flux depends on the origin and destination populations and on the population of the region surrounding the origin location. More recently, a new mobility law (Schlapfer et al. 2021) has been proposed showing that the number of visitors to any location is proportional to the inverse square of the product of the frequency of visits and distance traveled. This law has been applied in the context of urban mobility (within-city mobility), where it has shown a remarkable agreement with data.

When traffic data are available, they may be leveraged using entropy maximization techniques (Gomez et al. 2019; Van Zuylen and Willumsen 1980) aiming to reconstruct origin–destination matrices (Willumsen 1981) describing human mobility among various locations. However, in more recent considerations where mobile-phone data are available, these have been found to more accurately represent the actual movements of people (Tizzoni et al. 2014; Wesolowski et al. 2016). During the first and second COVID-19 pandemic waves, in the US (Badr et al. 2020; Glaeser et al. 2022), Japan (Yabe et al. 2020), and in China (Chinazzi et al. 2020), among others, mobile-phone location data were utilized to explore the effects of mobility on the reported cases reduction.

We should also note in passing that other approaches to examining the spatial spread of COVID-19 have also been deployed, including, e.g., models based on partial differential equations (Kevrekidis et al. 2021; Mammeri 2020; Viguerie et al. 2021). These modeling efforts take into account local population density by modifying the transmission coefficients accordingly (Kevrekidis et al. 2021) (compared to an ordinary differential equations model), emphasize the importance of inflows from neighboring regions (Viguerie et al. 2021), and utilize time-varying diffusion coefficients to account for the effect of mitigation measures (Kevrekidis et al. 2021; Mammeri 2020).

In the present work, we wish to explore some of the practical challenges of applying a metapopulation model to a concrete region during the COVID-19 pandemic, and also when attempting to systematically compare model results with existing data. In line with our earlier studies (Cuevas-Maraver et al. 2021), we bring to bear an epidemic model that accounts for both symptomatic and asymptomatic infections and includes appropriate recovered compartments, as well as a compartment for the fatalities, since the latter appears to be the most accurate dataset (Holmdahl and Buckee 2020). However, since we have examined already aspects of the identifiability of such models, as well as their usefulness in the context of age-structured populations (Cuevas-Maraver et al. 2021), we do not focus on such aspects herein. Instead, our emphasis is on the availability of different approaches to couple the nodes of such a model into a network pattern for a metapopulation description of a region of interest. In that vein, we compare and contrast the findings of an implementation neglecting the mobility between provinces, with one incorporating it. When incorporating such mobility traits, we comment on our attempts to do so, based on “standard” techniques such as those stemming from gravity models or transportation-based origin–destination matrices.

Our case example of interest is the region of Andalusia in Spain for numerous reasons, including the familiarity of our group with the region (aiding an understanding of the observed mobility patterns and, e.g., their seasonal variation). A significant feature facilitating and enabling our study is a large-scale data analysis of the Transportation Ministry of the Spanish Government (https://www.mitma.gob.es/ministerio/covid-19/evolucion-movilidad-big-data) that provides time-resolved mobility data across the provinces within this region and hence a dynamic incorporation of the relevant patterns based on an “as accurate as possible” characterization of the mobility within the area of interest. We calibrate the model using fatality data from Andalusia (https://cnecovid.isciii.es/covid19/), focusing on the summer and early fall period of 2020 (i.e., from around the end of the first and the beginning of the second pandemic wave). During this period, mitigation measures were relatively relaxed and mobility among provinces was high due to summer vacations and later due to higher education-related relocation. We find that we are unable to obtain a quantitative match with the observed data in each province (and hence Andalusia as whole) without mobility —or with static patterns of mobility produced by some of the above mentioned “standard” techniques—. Instead, our most accurate quantitative description of the observations stems from the incorporation of the above described “dynamic mobility” as obtained from the time-dependent mobile-phone provided by MITMA (https://www.mitma.gob.es/ministerio/covid-19/evolucion-movilidad-big-data).

Our presentation is structured as follows. In Sect. 2, we present the model, including the relevant metapopulation network considerations. We also show how mobility matrices, an input to the metapopulation model, that are obtained from different data sets compare. In Sect. 3, we present our results, including the parameter fitting approach used and the comparison with the existing data for COVID-19 fatalities in each Andalusian province. Finally, in Sect. 4, we present our conclusions and a discussion toward future steps within these classes of models. The Appendix contains information on the determination of the origin–destination matrix using either the gravity method or mobile-phone data.

2 Modeling Framework

2.1 Epidemic Model for Each Node

In the ordinary differential equation (ODE) model that we put forth (a slight variant of the ones previously considered, e.g., in Cuevas-Maraver et al. 2021; Kevrekidis et al. 2021), there are seven compartments for each node. Susceptible individuals, S, become exposed (latently infected, not infectious yet), E, after contact with either asymptomatically infectious hosts, A, or symptomatically infectious hosts, I. Recall that the importance of asymptomatically induced transmission, especially in the context of COVID-19 has been argued in numerous studies (Peirlinck et al. 2020; Calvetti et al. 2020). We assume standard incidence $\beta _{AS, IS}/(N-D)$, where $N-D = S +E +A +I +U +R$ is the total living population. However, as the number of individuals in the deceased class D is quite small in most cases, from now on it will be ignored compared to N, namely we will set the incidence to $\beta _{AS, IS}/N$, where the transmission coefficient $\beta _{AS, IS}$ can be assumed constant over the considered periods of time. We have selected the time interval under consideration as one involving high mobility without changes in mitigation measures, so as to reflect more clearly the genuine role of transportation effects in the model results.

Fig. 1

Schematic diagram of the Susceptible-Exposed-Asymptomatic-Infected-Recovered (SEAIR) model for each metapopulation node (Color figure online)

Once in the exposed class E, a fraction of hosts $\varphi$ never develop symptoms and moves into the asymptomatically infectious class A at a rate $\sigma _A$. Asymptomatic hosts are assumed to recover at an average rate $\gamma _A$ and move into the recovered compartment U. The remaining exposed host fraction $1-\varphi$ develops symptoms at a rate $\sigma _I$ and these individuals move into the symptomatically infectious class I. A fraction $\omega$ of symptomatic hosts die at an average rate $\chi$ (moving into the compartment D) and the remaining fraction $1-\omega$ recovers at a rate $\gamma _I$ and moves into the recovered class R. A schematic diagram of the above description is shown in Fig. 1. The relevant equations governing the spreading of the epidemic read:

$$\begin{aligned} S'&= - \beta _{AS} S \frac{A}{N} - \beta _{IS} S \frac{I}{N}, \end{aligned}$$

(1)

$$\begin{aligned} E'&= \beta _{AS} S \frac{A}{N}+ \beta _{IS} S \frac{I}{N} - (\kappa _A + \kappa _I) E, \end{aligned}$$

(2)

$$\begin{aligned} A'&= \kappa _A E - \gamma _A A, \end{aligned}$$

(3)

$$\begin{aligned} I'&= \kappa _I E - (\kappa _R + \kappa _D)I, \end{aligned}$$

(4)

$$\begin{aligned} U'&= \gamma _A A, \end{aligned}$$

(5)

$$\begin{aligned} R'&= \kappa _R I, \end{aligned}$$

(6)

$$\begin{aligned} D'&= \kappa _D I, \end{aligned}$$

(7)

where we set

$$\begin{aligned} \kappa _A = \varphi \sigma _A, ~~~ \kappa _I = (1-\varphi ) \sigma _I, ~~~\kappa _R= (1-\omega ) \gamma _I, ~~~\kappa _D = \omega \chi . \end{aligned}$$

(8)

In what follows, in order to reduce parameter redundancy in the model, we fit the following seven parameters and parameter combinations

$$\begin{aligned} \beta _{AS},~\beta _{IS},~\kappa _A = \gamma _A . \end{aligned}$$

(9)

This version of the model will be used when considering the fatalities within Andalusia’s provinces but without any (mobility-induced) coupling between them and when considering the entire Andalusia (no metapopulation). It is straightforward to observe that for system (1–7), the total population $N =S +E +A +I +R+U+D$ is conserved. Moreover, the subset $\{S \ge 0, E \ge 0, A \ge 0, I \ge , U \ge 0, R \ge 0, D \ge 0 \}$ of ${\mathbb {R}}^7$ is positively invariant for the system. Hence, the system is well-posed for any initial condition.

All variables and model parameters are defined in Table 1.

Table 1 Variables and parameters

2.2 Metapopulation Model

We are implementing a coupling between the different provinces in line with (Belik et al. 2011). Namely, we assume that individuals are indistinguishable and travel from node i to node j at some rate given by human mobility data, without assigning any base location to them. Hence, individuals in node i are instantaneously assigned to node j upon arrival, regardless of their prior node (no memory). The same individual may change multiple nodes, in principle, within the model. Connections between the nodes depend on the mobility flow of susceptible S, exposed E, and infectious hosts, A and I. To avoid a highly complicated model, we do not incorporate terms such as $S_i A_j$, $S_i I_j$ in the equations., i.e., we assume that the primary source of infection is through interactions of susceptible with infectious individuals within each node (no direct long-range transmission).

The metapopulation model assumes the following form (with $i = 1, \ldots i_{\text {max}}$ where $i_{\text {max}} =8$ since Andalusia has eight provinces):

$$\begin{aligned}&S_i' = - \beta _{AS} S_i \frac{A_i}{N_i} - \beta _{IS} S_i \frac{I_i}{N_i} +\theta \left( \sum _j M_{ij} \frac{S_j}{N_j} - \sum _j M_{ji} \frac{S_i}{N_i} \right) , \end{aligned}$$

(10)

$$\begin{aligned}&E_i' = \beta _{AS} S_i \frac{A_i}{N_i} + \beta _{IS} S_i \frac{I_i}{N_i} - (\kappa _A +\kappa _I) E_i + \theta \left( \sum _j M_{ij} \frac{E_j}{N_j} - \sum _j M_{ji} \frac{E_i}{N_i} \right) , \end{aligned}$$

(11)

$$\begin{aligned}&A_i' = \kappa _A E_i - \gamma _A A_i + \theta \left( \sum _j M_{ij} \frac{A_j}{N_j} - \sum _j M_{ji} \frac{A_i}{N_i} \right) , \end{aligned}$$

(12)

$$\begin{aligned}&I_i' = \kappa _I E_i - (\kappa _R + \kappa _D) I_i + \theta \left( \sum _j M_{ij} \frac{I_j}{N_j} - \sum _j M_{ji} \frac{I_i}{N_i} \right) , \end{aligned}$$

(13)

$$\begin{aligned}&U_i' = \gamma _A A_i, \end{aligned}$$

(14)

$$\begin{aligned}&R_i' = \kappa _R I_i \end{aligned}$$

(15)

$$\begin{aligned}&D_i' = \kappa _D I_i, \end{aligned}$$

(16)

$$\begin{aligned}&N_i' = \theta \left( \sum _j M_{ij} - \sum _j M_{ji} \right) , \end{aligned}$$

(17)

The last equation shows how the population of node i is updated over time. Our model is along the lines of Li et al. (2020) and Pei et al. (2018). If mobility is ignored by setting $\theta =0$, the total population within each node $N_i$ is conserved. Otherwise, when $\theta =1$, solely the total population over all provinces is conserved. We note that $\theta$ is a binary parameter, assuming the value 1 (0) when human mobility is considered (not considered). $M_{ij}$ is the daily rate of people traveling from j to i. Then, one multiplies this rate with the proportion of S, E, A, I in the total node population $N_j$. This can be interpreted as the probability of an individual from these four classes traveling if we choose randomly from $N_j$. Symptomatically infectious individuals I are assumed to be able to move, but not U or R. In any event, the latter two do not affect further the dynamics in the network as they are terminal classes of the model. Allowing U and R to move (since no re-infection is considered on the time-scales used in the present work) only has the effect of redistributing the recovered population among the network nodes: the infection dynamics are not expected to be directly affected. However, movement of individuals in these compartments may still change the population size of a given location, which could slightly affect incidence (frequency-dependent transmission with $1/N_i, 1/N_j$ terms). It is relevant to also note that, over the time scale considered, these individuals are assumed to have immunity (upon recovery) and, hence, it is not considered to be a possibility for the population in U or R to re-enter the susceptible population, over the time frame of interest. Therefore, we only allow the susceptible class, S, which consists the majority of the population, and the exposed, E, and infectious, A and I, classes to move among the network nodes. Furthermore, since there were no mobility restrictions at the time, we assume that the movement of exposed, asymptomatic, and infected individuals is the same as the movement of susceptible individuals. While quarantine and isolation were required at the time for infectious and exposed individuals, we consider that they all travel and at the same rate since it is not straightforward to estimate compliance. Should, however, such compliance data become available, it would be an easy fix to multiply $M_{ij}$ with the appropriate compliance rate.

One may easily observe that as long as $N_i>0$, $i=1, \ldots , 8$ the metapopulation model is well-posed for any initial condition. This follows since the region

$$\begin{aligned} \{S_i \ge 0, E_i \ge 0, A_i \ge 0, I_i \ge , U_i \ge 0, R_i \ge 0, D_i \ge 0 \} \subset {\mathbb {R}}^{56} \end{aligned}$$

is positively invariant and for the time period studied, while $N_i$ fluctuate, they stay positive for all $i=1, \ldots , 8$.

We note that based on the mobility data (https://www.mitma.gob.es/ministerio/covid-19/evolucion-movilidad-big-data), the network of the eight Andalusian provinces is a complete graph and the population flows $M_{ij}$ are time-dependent. In the following subsection we discuss how we determined the daily movement rates, i.e., the population flows, between two network nodes, and alternative ways to determine them if mobile-phone records are not available.

2.3 Human Mobility Estimation

Mobility flows are commonly estimated from mobile-phone records. In this work the flows we analyzed are based on a study performed by the Spanish government (Ministerio de Transportes, Movilidad y Agenda Urbana-MITMA) https://www.mitma.gob.es/ministerio/covid-19/evolucion-movilidad-big-data) that included all of Spain for the period beginning on March 14, 2020. The main data source was anonymized mobile-phone data for more than 13 million mobile lines as well as locations of communication towers and antenna orientations. Population data as well as information about the transportation network (airport locations, railways) were leveraged. Figure 2 shows the time-dependent population flows for each province, i.e., each network node, of Andalusia as determined by the mobile-phone data. They are shown for the time duration of our study, starting on July 10, 2020 till October 29, 2020 (112 days). Note the significant time dependence of the inter-province population flows.

Fig. 2

Time-varying daily population flows (the daily rate of individuals traveling $M_{ij}$) for each Andalusian province as determined from mobile-phone data (https://www.mitma.gob.es/ministerio/covid-19/evolucion-movilidad-big-data). The destinations are shown on the vertical axis. The code name for the eight provinces in Andalusia is: Alm: Almeria, Cad: Cadiz, Cor: Cordoba, Gra: Granada, Hue: Huelva, Jae: Jaen, Mal: Malaga, Sev: Seville (Color figure online)

Daily mobility data among locations, such as those provided by mobile phones, may not be always readily and publicly available. When this is the case, other types of data and alternative models are used to determine the population flows. One avenue is to rely on census surveys and base the coupling of the epidemiological model on daily commuting data (Danon et al. 2009, 2021). In this approach, workdays and weekend, as well as commuters and non-commuters, should be distinguished using additional travel surveys. Failure to consider non-work related trips may lead to an erroneous slowing down of the epidemic (Danon et al. 2009). This fine tuning is not required when using time-varying mobility matrices as in the present work.

Another avenue is to utilize commonly used trip-distribution modeling techniques, like the gravity model to construct the origin–destination (O–D) matrix for the metapopulation network. The gravity law is used extensively in the literature to model travel demand between O–D pairs (e.g., Erlander and Stewart 1990; Ortúzar and Willumsen 2011). We assume a region where n denotes the nodes (or centroids ) of the cities in the regional transportation network and m their highway links. A trip matrix element (number of trips per day) is denoted by $w_{ij}$, where i and j are the origin and destination nodes of the considered trip, respectively. Given the population of these cities and their distances, the O–D matrix elements are computed by

$$\begin{aligned}&w_{ij} = C\frac{N_i^\alpha N_j^\gamma }{e^{\beta _G {\text {dis}}_{ij}}}, \end{aligned}$$

(18)

where C is a constant, $\text {dis}_{ij}$ is the distance between the O–D pair (ij), $\alpha$ and $\gamma$ are parameters associated with the populations $N_i$ and $N_j$ of the pair (ij), and $\beta _G$ is a constant parameter whose value —measured in units of inverse distance, indeed in our case of 1/km— depends on the distance between the network nodes, as explained in Appendix A. Once the elements of the O–D matrix have been estimated, the force of infection on susceptible hosts $S_j$ in location j in the metapopulation model, which reads $\beta _{AS} A_j/N_j, ~ \beta _{IS} I_j/N_j$ in Eqs. (10, 11) is modified as Xia et al. (2004)

$$\begin{aligned} \beta _{AS} \frac{1}{N_j} \Big (A_j + C N_j^{\gamma } \sum _{i \ne j} \frac{A_i^{\alpha }}{e^{\beta _G {\text {dis}}_{ij}}} \Big ), ~~ \beta _{IS}\frac{1}{N_j} \Big ( I_j + C N_j^{\gamma } \sum _{i \ne j} \frac{I_i^{\alpha }}{e^{\beta _G {dis}_{ij}}} \Big ). \end{aligned}$$

(19)

A notable difference between models implementing (19) and the metapopulation model (10–17) is the following. Whereas the model defined by (10–17) introduces mobility via changes directly in the rates of change of the S, E, A, and I populations (for $\theta =1$), models using (19) implement mobility through modification of the transmission terms.

It is relevant to note that the accuracy of gravity-like models has received considerable recent criticism (Schlapfer et al. 2021; Simini et al. 2012). In the present work, we will not embark on a detailed comparison of a metapopulation model based on the gravity law and our own approach (based on time-dependent mobile-phone records). Nevertheless, for completeness, we would like to illustrate that in the absence of alternative and possibly quite superior data sets, the method can be used to capture some principal features of mobility flows in workdays (Friday and Tuesday; no mobility restrictions in place); see, in particular, Fig. 3. More concretely, due to the scarcity of reported traffic count data—they are averaged over a year— only a static O–D matrix can be obtained. Also, the traffic count data available to us were from 2019-2020, namely prior to the pandemic. The O–D matrices in Fig. 3 show that the gravity-law method roughly captures the main mobility trends. For instance, there is substantial support within the matrix between the rows 2–4 and columns 6–8 (and vice-versa), as well as, e.g., between Seville and Huelva or Malaga etc. Therefore, in the absence of more detailed and accurate mobility information, it can be used as an alternative. The O–D matrix presented in Fig. 3 , left panel, reproduces the gravity-law data shown in Table 6 in the “Appendix”. It should be noted however, that the gravity-law O–D is in terms of vehicle trips per day, whereas the mobility flows from the Spanish government reported in Movilidad y Agenda Urbana Ministerio de Transportes (https://www.mitma.gob.es/ministerio/covid-19/evolucion-movilidad-big-data) are expressed in terms of people traveling per day. To convert one into the other one would need to know on average the number of people traveling in vehicles: as the comparison is qualitative we opted not to convert population flows to trips per day.

Fig. 3

Origin–destination matrices based on the gravity-law method (vehicle trips per day) for a pre-pandemic day left panel and from the mobility data based on mobile-phone records (people traveling per day) for Friday, July 10, 2020 (middle panel) and Tuesday, October 27, 2020 (right panel) (Color figure online)

3 Results

3.1 Period of Study and Rationale

The time period considered begins on July 10, 2020, and ends on October 29, 2020 (112 days). We use the first 84 days from July 10 till October 1, 2020, as the fitting period, and the remaining 28 days from October 2 to October 29, 2020, as the prediction interval. Since the goal of the present study is to investigate of the role of mobility on the spread of an epidemic, the period of study was chosen to satisfy the following two conditions. First, that there would be no imposed mobility restrictions except at the end. In fact, on October 29, the regional government imposed a curfew at nights and closed the border with the rest of Spain and limited mobility between the provinces. That is the reason we chose to perform our analysis up to the end of October 2020, and not longer, as afterward the mobility patterns were modified due to the imposed restrictions on travel. Second, the period should include the initial exponential growth of the epidemic peak.

3.2 Parameter Fitting and Model Predictions

We first use the model of Eqs. (1)–(7) for the entire region of Andalusia. We use the norm

$$\begin{aligned} {\mathcal {N}} = \sum _{i=1}^{84} \left( \frac{D_{\textrm{num}}(t_i)}{D_{\textrm{obs}}(t_i)}-1 \right) ^2, \end{aligned}$$

(20)

as the objective function. We minimized it to fit the fatality data $D_{\textrm{obs}}(t_i)$, where $t_i$ stands for day i, from our start point of July 10, 2020, and $D_{\textrm{num}}(t_i)$, denotes the fatality estimate for the same day, obtained from the model. It is worth noting again that we are not attempting to fit to case data, since these are believed to be significantly less reliable than fatality data, due to under-reporting as has been the case in other countries as well (Cuevas-Maraver et al. 2021; Kevrekidis et al. 2022). Indeed, when trying to fit both case and fatality data, we obtained results that are considerably less satisfactory than the ones presented below.

In addition to the seven parameters shown in (9), we also obtain estimates for the initial parameters $I_0, A_0, E_0$ when the entire autonomous community of Andalusia is considered. We performed 500 optimizations with an initial guess for each parameter uniformly sampled within a pre-specified range. The upper and lower limits of the variation ranges were used as boundaries in the constrained minimization algorithm (implemented in MATLAB via the fmincon function). The outcome of the fitting, for values taken from July 10 to October 1, 2020 (84 days), allowed us to retrieve an approximation for the initial values for the I, E and A compartments. Their median (they had a very small dispersion) was used as initial condition for the metapopulation model (10–17), weighted by $\omega _j=C_j/C$, with $C_j$ being the number of cases in the j-th province in the period from July 4 to July 10 and C the total number of cases in Andalusia in the whole period. We minimized the norm

$$\begin{aligned} {{\mathcal {N}}}=\sum _{j=1}^{8} {{\mathcal {N}}_j}, \end{aligned}$$

(21)

with

$$\begin{aligned} {{\mathcal {N}}_j}=\sum _i^{84} \Big ( \frac{D_{j,\text {num}}(t_i)}{D_{j,\text {obs}}(t_i)}-1\Big )^2, \end{aligned}$$

(22)

and $D_{j,\textrm{num}}(t_i)$ and $D_{j,\textrm{obs}}(t_i)$ being, respectively, the fatality estimate and data for the day $t_i$ at province j. In the metapopulation model, we focused on two values of $\theta$, $\theta =1$ and $\theta =0$, which will be denoted as the metapopulation model with and without mobility, respectively. As mentioned previously, the coupling matrices $M_{ij}$ were obtained from mobile-phone data (https://www.mitma.gob.es/ministerio/covid-19/evolucion-movilidad-big-data).

Fig. 4

Model fit and prediction of the fatalities time series for the entire region of Andalusia. Data points are shown as black dots, the output of the metapopulation model with mobility ($\theta =1$) is shown as a red curve, the output of the metapopulation model with mobility turned off ($\theta =0$) is shown as a blue curve, and the fit to the ODE model (Eqs. 1–7) is shown as a green curve. The light blue vertical line corresponds to the date when fitting stops (day 84) and prediction begins. The interquartile range is highlighted in red (Color figure online)

Figure 4 shows the fit of the SEAIR model of Eqs. (1)–(7), no metapopulation, together with the metapopulation model (10–17) with ($\theta =1$) and without ($\theta =0$) mobility for the case of the whole region of Andalusia. Part of the data (the first 84 days, from July 10 to October 1) is used for parameter fitting, and the remaining is used for prediction (till day 112, from October 2 to October 29). We observe that while all three curves are close to each other and trail the data points with a satisfactory level of accuracy during the fitting period (since we are fitting them to the data), they diverge afterward. Only the metapopulation model with mobility follows the same trend as the data in the prediction interval. One possible reason is that during summer the fatality curves in all provinces behave similarly, i.e., they are quite homogeneous, but later on they follow different trends, and they become heterogeneous. Hence, the overall fatality curve (black dots in the figure), the one corresponding to the entire autonomous community of Andalusia, diverges from the homogeneous curve.

Another explanation is that it is possible to fit different models to the same data set, but not all models will be able to make accurate predictions. This is especially true when fitting to epidemic data in the period before the inflection point of the epidemic peak has been reached (Prasse et al. 2022).

Further insight on the dynamical evolution of the fatalities in each of the provinces is provided in Fig. 5. During the months considered in the present study, due to relaxation or complete absence of mitigation measures, different nodes of the network exhibit different characteristics. This can be attributed to some nodes being touristic destinations (Malaga, Huelva), others being close to country borders (Cadiz with Gibraltar and Huelva with Portugal), while yet others undergoing annual exodus over the summer months (Seville). This is evident in Figs. 2 and 6, where we show the variation in mobility flows and population, respectively, for the eight provinces forming our network.

Fig. 5

Fatality data (black dots) and model fit for each province of Andalusia. The output of the metapopulation model, Eqs. (10)–(17), with mobility ($\theta =1$) is shown as a red curve and the output of the metapopulation model with mobility turned off ($\theta =0$) is shown as a blue curve. The light blue vertical line corresponds to the date when fitting stops (day 84) and prediction begins. The interquartile range is highlighted in light-red for red curve, while for the blue curve, the interquartile range is so narrow that it is not visible in the plot. Note the different y-axis scales (Color figure online)

Fig. 6

The ratio of the population of each province $N_i(t)$ to the initial population $N_0$, the latter based on data from Instituto Nacional de Estadística. The light blue vertical line corresponds to the day when fitting stops (day 84) and validation begins. Note the different y-axis scales (Color figure online)

It is relevant to make the following observations in connection with the results. With the exception of Cordoba (featuring a systematic underestimation within the prediction interval for which we do not have a definitive explanation) and Huelva (with a corresponding overestimation in the prediction interval), data points typically follow qualitative trends consonant with the interquartile range. Huelva is a major vacation hub, both in the summer period and during weekends, mainly from residents in Seville (who also commonly spend their holidays in the province of Cadiz). If people return to their permanent residence to receive treatment and quarantine (or are anyway logged as cases within these regions), this may explain the disparity between the observed and predicted fatalities. It is worthwhile to note an apparently similar overestimation trend within the prediction interval for Cadiz; however, in this case, the situation is somewhat less clear, due to an opposite trend within the fitting interval. Also, high population density over the summer could partially explain the overestimation: the model is trained with more people residing there, who subsequently depart to return to their regular residence. Also, compared to other provinces, fatalities are relatively small in number, which makes it prone to stochastic effects (Calleri et al. 2021; Ando et al. 2021), as is also evident in the trends of the data.

Figure 6 shows the population in each province during the period of our study. Two major trends emerge. First, there is a weekly oscillation, due to increased mobility during the weekends. This is due to residents traveling from their primary residence to vacation destinations, such as the ones we described before between Seville and Huelva or Cadiz; similar patterns are found between other pairwise transitions: e.g., in the case of Cordoba, such movements happen to and from Malaga, Seville and Jaen. In any event, the real-time data used in this work provide a clear picture of the dynamics across the network and the key interactions across its nodes. Second, there is a significant variation in the population of most provinces, ranging from mild (0.99$-$1.06 in Jaen, 0.93–1 in Cordoba) to extreme (0.75$-$1.2 in Huelva). Others, experience a peak in late summer (Almeria, Cadiz, Malaga) before their population drops again in October. Granada and Seville exhibit a reverse behavior, where their population increases in the fall, when people resume living in their permanent residence. This is the seasonal trend that is superposed to the weekly trend. A similar observation may be made by considering Fig. 2 where the time-dependent population flows between any two provinces are shown. In line with our above observations, some clear signatures are obvious, such as weekly periodicity, overall increased mobility in the summer months and other trends, such as the consistent mobility between specific pairs of provinces, as discussed above.

Fig. 7

Snapshots of the evolution of the number of fatalities occurring from (and including) July 10 at each province at different days from September to October. Top and middle row maps correspond to the numerical fit/prediction of the metapopulation model with and without mobility, whereas bottom row maps represent the observed number of fatalities. Bottom map in the first snapshot includes the code for the name of each province (AL: Almeria, CA: Cadiz, CO: Cordoba, GR: Granada, H: Huelva, J: Jaen, MA: Malaga, SE: Seville) (Color figure online)

Figure 7 depicts the time evolution of the fatalities in the form of a heat map. We can observe how the model predicts the spreading of the epidemic from Almeria to neighboring provinces. Note, however, that in the reported data there was a spot in Malaga, probably caused by people traveling from other places in the world (a process which is not included in the current work). We also observe that Seville and Malaga are the provinces that eventually exhibit the highest number of fatalities, an observation correlated to their higher population. The maps also show that the model without mobility predicts a very much smaller number of fatalities than the model with mobility. Although at an early stage of the prediction both models are fairly comparable, later on, within the prediction interval, the model with mobility is significantly more accurate toward predicting the spread of the epidemic within the metapopulation network than the model without it. Both the detailed (individual province, cf. Figure 5) quantitative findings, and this overarching figure are convincing, in our view, of the relevance at such regional levels of the consideration of metapopulation approaches. Additionally, the concrete trends that our mobility data reveal illustrate the relevance of the dynamic consideration of the coupling matrices $M_{ij}$.

The best-fit parameters are shown in Table 2, whereas Table 3 presents the initial conditions for each province in the metapopulation model. For the initial condition of the population ($N_0$) we took the census data for January 1, 2020 (https://www.ine.es/en/). We must note that the data we compared with correspond to the day when events (such as deaths) actually occurred, and were extracted from the data available in the National Epidemiological Center of Spain (https://cnecovid.isciii.es/covid19/), as well as that each fatality is assigned to the residence province. It is worth mentioning that the initial value for the infections in Almeria is about 12 times the value in Seville, despite Almeria having a third of the province of Seville’s population. This is attributed to an outbreak that occurred in July which originated at a settlement of temporary workers in the province of Almeria, that also expanded to the neighboring province of Granada (https://www.diariosur.es/andalucia/junta-andalucia-califica-20200717141402-nt.html) .

Table 4 shows the residuals for the fitting and predictions. The former is found by computing (20) at each simulation and taking the median and quartiles of all these values; for getting the latter, the same procedure is followed but extending the summation in (20) to 114.

Table 2 Best fit parameter values

Table 3 Initial conditions

Table 4 Residuals

3.3 Effective Reproduction Number

Given the importance of the reproduction number during the initial stages of an epidemic wave, we use the Next Generation Matrix approach (Diekmann et al. 1990) to evaluate the effective reproductive number $R_t$. In doing so, we treat this epidemic wave as a “new epidemic" assuming that most of the population is still susceptible. This assumption practically renders $R_t=R_0$, namely the effective reproduction number, is equal to the basic reproduction number $R_0$. For $t>0$ it holds $R_{t} = R_0 S(t)/N$, Cintron-Arias et al. (2009). Hence, the calculated effective reproduction number refers to the first day of our simulations, July 10th, 2020. The reproduction number for the one-node model (1–7) (with either $N-D$ in the denominator or the simplified version $N-D \approx N$) is

$$\begin{aligned} R_t = \frac{\kappa _A}{\kappa _A+\kappa _I} \frac{\beta _{{ AS}}}{\gamma _A} + \frac{\kappa _I}{\kappa _A+\kappa _I} \frac{\beta _{{ IS}}}{\kappa _D+\kappa _R}. \end{aligned}$$

(23)

The first term is the contribution to $R_t$ from asymptomatic hosts A while the second is the contribution from the symptomatically infectious hosts I. Each term represents the fraction of asymptomatic $\kappa _A/(\kappa _A+\kappa _I)$ or symptomatically infected $\kappa _I/(\kappa _A+\kappa _I)$ hosts generated in the lifespan of an exposed host E, or equivalently the fraction of individuals reaching A or I after going through state E, multiplied by the number of new infected hosts generated in the lifespan of the corresponding infectious host, $\beta _{{ AS}}/\gamma _A$, $\beta _{{ IS}}/(\kappa _D+\kappa _R)$, respectively.

Using the estimated parameters shown in the first column of Table 2, the value of $R_t$ is (the interquartile range in parenthesis)

$$\begin{aligned}R_t = 1.4848~ (1.4798-1.4903). \end{aligned}$$

We calculated $R_t$ based on the 500 sets of parameter values, see the discussion following Eq. (20). The interquartile range was calculated as follows. First, using the 500 accepted sets of the model parameters, we calculate $R_t$. From those values, we then obtain the lower and upper quartiles and the median. When the metapopulation model is used without mobility ($\theta =0$), then the same expression, Eq. (23), applies with the parameters of the second column yielding

$$\begin{aligned}R_t = 1.5972~ (1.5945-1.5983).\end{aligned}$$

Finally, for the entire metapopulation network, $R_t$ is calculated as follows. We define the relevant vectors, focusing on the infectious/infected compartments ($E_i$, $A_i$, $I_i$) and ignoring the rest ($S_i$, $U_i$, $R_i$, $D_i$):

$$\begin{aligned} {\mathcal {F}}&=\left( \begin{array}{c} \frac{\beta _{AS}}{N_1} S_1 A_1 + \frac{\beta _{IS}}{N_1} S_1 I_1 \\ 0 \\ 0\\ \vdots \\ \frac{\beta _{AS}}{N_8} S_8 A_8 + \frac{\beta _{IS}}{N_8} S_8 I_8 \\ 0 \\ 0\\ \end{array} \right) , {\mathcal {V}} = \left( \begin{array}{c} (\kappa _A +\kappa _I) E_1 - \theta \left( \sum _j M_{1j} \frac{E_j}{N_j} - \sum _j M_{j1} \frac{E_1}{N_1} \right) \\ -\kappa _A E_1 +\gamma _A A_1 - \theta \left( \sum _j M_{1j} \frac{A_j}{N_j} - \sum _j M_{j1} \frac{A_1}{N_1} \right) \\ -\kappa _I E_1 + (\kappa _R +\kappa _D) I_1 - \theta \left( \sum _j M_{1j} \frac{I_j}{N_j} - \sum _j M_{j1} \frac{I_1}{N_1} \right) \\ \vdots \\ (\kappa _A +\kappa _I) E_8 - \theta \left( \sum _j M_{8j} \frac{E_j}{N_j} - \sum _j M_{j8} \frac{E_8}{N_8} \right) \\ -\kappa _A E_8 +\gamma _A A_8 - \theta \left( \sum _j M_{8j} \frac{A_j}{N_j} - \sum _j M_{j8} \frac{A_8}{N_8} \right) \\ -\kappa _I E_8 + (\kappa _R +\kappa _D) I_8 - \theta \left( \sum _j M_{8j} \frac{I_j}{N_j} - \sum _j M_{j8} \frac{I_8}{N_8} \right) \end{array} \right) \end{aligned}$$

We then find the Jacobian matrices of ${\mathcal {F}}, {\mathcal {V}}$ with respect to $E_i, A_i, I_i$ in the order in which they appear. This yields two $24 \times 24$ matrices of the form:

$$\begin{aligned}&F= \left( \begin{array}{ccccc} F_{11} &{} O_{3 \times 3} &{} O_{3 \times 3} &{} \dots &{} O_{3 \times 3}\\ O_{3 \times 3} &{} F_{22} &{} O_{3 \times 3} &{} O_{3 \times 3} &{} O_{3 \times 3} \\ O_{3 \times 3}&{} O_{3 \times 3}&{} F_{33} &{} O_{3 \times 3} &{} O_{3 \times 3} \\ \vdots &{} \vdots &{} \vdots &{}\ddots &{} \vdots \\ O_{3 \times 3} &{} O_{3 \times 3} &{} O_{3 \times 3} &{} \dots &{} F_{88} \end{array} \right) , ~~~ F_{ii} = \left( \begin{array}{ccc} 0 &{} \beta _{AS} \frac{S_i}{N_i} &{} \beta _{IS} \frac{S_i}{N_i} \\ 0 &{} 0 &{}0 \\ 0 &{} 0 &{}0 \end{array} \right) ,\\&O_{3 \times 3} = \left( \begin{array}{ccc} 0 &{} 0 &{}0 \\ 0 &{} 0 &{}0 \\ 0 &{} 0 &{}0 \end{array} \right) \\&V= \left( \begin{array}{cccc} V_{11} &{} V_{12} &{} \dots &{} V_{18} \\ V_{21}&{} V_{22} &{} \dots &{} V_{28} \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ V_{81} &{} V_{82} &{} \dots &{} V_{88} \end{array} \right) ,\\&V_{ii} =\left( \begin{array}{ccc} \kappa _A +\kappa _I + \theta \sum _j \frac{M_{ji}}{Ni} &{} 0 &{} 0 \\ -\kappa _A &{} \gamma _A + \theta \sum _j \frac{M_{ji}}{N_i} &{} 0 \\ -\kappa _I &{} 0 &{} \kappa _R+\kappa _D + \theta \sum _j \frac{M_{ji}}{N_i} \end{array} \right) \\&V_{ij} = \left( \begin{array}{ccc} -\theta \frac{M_{ij}}{N_j} &{} 0 &{} 0 \\ 0 &{} -\theta \frac{M_{ij}}{N_j} &{} 0 \\ 0 &{} 0 &{} -\theta \frac{M_{ij}}{N_j} \end{array} \right) , \end{aligned}$$

We note that for the calculation at $t=0$, we set $\frac{S_i({0})}{N_i({0})}$ in the $F_{ii}$ matrices and $\frac{M_{ji}(0)}{N_i(0)}$, $\frac{M_{ij}(0)}{N_j(0)}$ in $V_{ii}$, $V_{ij}$, respectively.

The reproduction number is the spectral radius of $F V^{-1}$ which in our case has the value

$$\begin{aligned}R_t = 1.3349~ (1.2806-1.4581).\end{aligned}$$

This is exactly the same value one obtains when using Eq. (23) if one completely disregards the mobility terms in matrix V, i.e., with the parameter values of the third column in Table 2. Hence, the change in $R_t$ is due to the different values in third column of Table 2, and not due to the terms containing $M_{ij}$ in matrix V. In other words, the effect of mobility is to change the estimated parameters; while they do not alter the $R_t$ (which, as mentioned earlier is effectively evaluated at the first day of our simulations), they have a large effect on the dynamics later. When mobility is included in the model, the interquartile intervals of each parameter value are significantly wider, which is also reflected in the corresponding interval for $R_t$.

4 Discussion and Conclusion

In the present work, we revisited the formulation of metapopulation models, motivated by the interest toward describing a “relatively small” region (the autonomous community of Andalusia within Spain) with well-defined and available in a time-resolved manner data regarding the mobility across provinces. It is also a region without an extensive influx (or outflux) of populations, e.g., through major international airport hubs. This appears to render this case a fertile ground for the application of metapopulation models.

In that vein, in addition to a prototypical model for each node, involving susceptibles, exposed, asymptomatic and symptomatically infected, as well as recovered from each of these categories and fatalities, we considered different possibilities on how to incorporate human mobility across the nodes. We explored the model for the entire autonomous community of Andalusia (without sub-nodes), the model where the nodes do not feature mobility between them (independent nodes) and the canonical case proposed where mobility is incorporated. One of the main findings of the present work is that in the absence of mobility among nodes the model is unable to predict the wave of infections that took place in the fall of 2020. It has long been known that human mobility is crucial at the beginning stages of an epidemic, when the infection is seeded in various locations (Chinazzi et al. 2020; Kraemer et al. 2020; Wesolowski et al. 2016). It has also been noted that mobility may also affect contact rates which in turn affect disease transmission (Wesolowski et al. 2016). The present study suggests that population flows are critically important in periods during an epidemic when there are no restrictions on mobility. Moreover, while there are numerous ways of incorporating mobility, for example via static origin–destination matrices as calculated via gravity models, we believe that at present the optimal inclusion should be time-resolved. Dynamical information stemming from mobile-phone data seamlessly incorporates aspects such as the weekly or seasonal variations of human mobility; hence it more accurately captures the resulting increases or decreases in the probability of formation of an epidemic wave of infection. However, when this is not possible, we also offer details on how origin–destination matrices obtained by the gravity-law can be calculated to be used in a metapopulation model.

Nevertheless, we certainly refrain from assigning full responsibility to human mobility for the wave of infections in the fall of 2020, or indeed more generally during the second wave of the pandemic. It is clear that there exist numerous factors that may have contributed to the relevant features, including, e.g., seasonality (Danon et al. 2021) and humidity (Drossinos et al. 2022). It would be interesting to further explore these factors and their interplay with mobility both in the context of the second wave (as here) in other regions, but also as concerns subsequent waves of the pandemic, where other key factors, such as the existence and the role of vaccinations (Usherwood et al. 2021) need to be taken into consideration. Such studies will be deferred to future publications.

Appendix A: Origin–Destination matrices

We describe the methodology used to compute origin–destination (O–D) matrices for light-duty vehicle highway travels compatible with empirical data of coarse grained flows in highway transportation networks. We obtained the O–D matrices either via the gravity model or from the mobile-phone data reported by the Ministry of Transportation, Mobility and Urban Agency (Ministerio de Transportes, Movilidad y Agenda Urbana-MITMA https://www.mitma.gob.es/ministerio/covid-19/evolucion-movilidad-big-data) (see, also the discussion in Sect. 2.3 in the main text). Specifically, we constructed the O–D matrix as follows: given population data from the Instituto Nacional de Estadística (https://www.ine.es/en/) and distances of city pairs we applied the gravity law to calculate the vehicle number of trips per day between any two nodes. The gravity-model methodology is presented in Section A.1. Section A.2 describes briefly how we translated the mobile-phone data into population flows, people traveling per day between provinces. Figure 3 in the main text compares the static, pre-pandemic, gravity-model calculated O–D matrix with time-dependent O–D matrices obtained from mobile-phone data for two characteristic working days: Friday, July 10, 2020, and Tuesday, October 27, 2020.

1.1 1. Methodology: Gravity law and traffic counts

Given the population of provinces and distances between the capital city of province pairs, the gravity model as described by Eq. (18) in the main text can be leveraged with the parameters presented in Table 5. When the distance between an O–D pair (ij) is larger than 300 km, $\beta _G$ is set to be N/A, which denotes that the denominator will be approaching 0, as well as $w_{ij}$ would be approaching 0.

Table 5 Parameters of gravity law Balcan et al. (2009); Stefanouli and Polyzos (2017)

The origin–destination matrix for the eight Andalusian provinces calculated from the gravity law with the parameters reported in Table 5 is presented in Table 6, which summarizes the daily number of vehicle trips between O–D pairs (ij). As mentioned in the main text this O–D matrix is static, and the data we used referred to 2019–2020, i.e., before the pandemic started.

Table 6 O–D matrix (daily number of vehicle trips) based on the gravity law

1.2 2. Methodology: Mobile-phone data

All mobility data used in this work are available in the website referenced in MITMA (https://www.mitma.gob.es/ministerio/covid-19/evolucion-movilidad-big-data). The database aggregates more than 13 million anonymized mobile lines to provide data for the number of persons traveling per day, i.e., population flows. The procedure we followed to determine $M_{ij}$, the daily rate of people traveling from province i to province j, was to download the spreadsheet, and then to select the origin and destination of a trip according to following codes: 04 for Almería, 11 for Cádiz, 14 for Córdoba, 18 for Granada, 21 for Huelva, 23 for Jaén, 29 for Málaga, and 41 for Sevilla. The trip date is under the column “fecha” and the trips, one per individual, under the column “viajes”. This information is extracted and assembled into the $M_{ij} (t)$ matrices for day t that provide the desired population flows as persons traveling per day.