Evaluating Strategies For Tuberculosis to Achieve the Goals of WHO in China: A Seasonal Age-Structured Model Study

Abstract

Although great progress has been made in the prevention and mitigation of TB in the past 20 years, China is still the third largest contributor to the global burden of new TB cases, accounting for 833,000 new cases in 2019. Improved mitigation strategies, such as vaccines, diagnostics, and treatment, are needed to meet goals of WHO. Given the huge variability in the prevalence of TB across age-groups in China, the vaccination, diagnostic techniques, and treatment for different age-groups may have different effects. Moreover, the statistics data of TB cases show significant seasonal fluctuations in China. In view of the above facts, we propose a non-autonomous differential equation model with age structure and seasonal transmission rate. We derive the basic reproduction number, ${\mathcal {R}}_{0}$, and prove that the unique disease-free periodic solution, ${\mathcal {P}}_{0}$ is globally asymptotically stable when ${\mathcal {R}}_{0}<1$, while the disease is uniformly persistent and at least one positive periodic solution exists when ${\mathcal {R}}_{0}>1$. We estimate that the basic reproduction number ${\mathcal {R}}_{0}=1.3935$ ($95\%\text{ CI }:(1.3729, 1.4087)$), which means that TB is uniformly persistent. Our results demonstrate that vaccinating susceptible individuals whose ages are over 65 and between 20 and 24 is much more effective in reducing the prevalence of TB, and each of the improved vaccination strategy, diagnostic strategy, and treatment strategy leads to substantial reductions in the prevalence of TB per 100,000 individuals compared with current approaches, and the combination of the three strategies is more effective. Scenario A (i.e., coverage rate $85\%$, diagnosis rate $5\theta _{k}$, relapse rate $0.1\chi _{k}$) is the best and can reduce the prevalence of TB per 100,000 individuals by $98.91\%$ and $99.07\%$ in 2035 and 2050, respectively. Although the improved strategies will significantly reduce the incidence rate of TB, it is challenging to achieve the goal of WHO in 2050. Our findings can provide guidance for public health authorities in projecting effective mitigation strategies of TB.

Appendices

Appendix A The Expressions of $f_{ij}$, $v_{ij}$ and the Existence of Periodic Solutions

$$\begin{aligned} f_{12}= & {} \left[ \begin{array}{cccc} (1-q_{1})\beta _{1}(t)c_{11}(s^{0}_{1}+\eta _{1}v^{0}_{1})&{} (1-q_{1})\beta _{1}(t)c_{12}(s^{0}_{1}+\eta _{1}v^{0}_{1})&{} \cdots &{}(1-q_{1})\beta _{1}(t)c_{1n}(s^{0}_{1}+\eta _{1}v^{0}_{1})\\ (1-q_{2})\beta _{2}(t)c_{21}(s^{0}_{2}+\eta _{2}v^{0}_{2})&{} (1-q_{2})\beta _{2}(t)c_{22}(s^{0}_{2}+\eta _{2}v^{0}_{2})&{} \cdots &{}(1-q_{2})\beta _{2}(t)c_{2n}(s^{0}_{2}+\eta _{2}v^{0}_{2})\\ \vdots &{}\vdots &{}\ddots &{}\vdots \\ (1-q_{n})\beta _{n}(t)c_{n1}(s^{0}_{n}+\eta _{n}v^{0}_{n})&{} (1-q_{n})\beta _{n}(t)c_{n2}(s^{0}_{n}+\eta _{n}v^{0}_{n})&{} \cdots &{}(1-q_{n})\beta _{n}(t)c_{nn}(s^{0}_{n}+\eta _{n}v^{0}_{n})\\ \end{array} \right] , \\ f_{13}= & {} \left[ \begin{array}{cccc} (1-q_{1})\beta _{1}(t)c_{11}\omega _{1}(s^{0}_{1}+\eta _{1}v^{0}_{1})&{} (1-q_{1})\beta _{1}(t)c_{12}\omega _{2}(s^{0}_{1}+\eta _{1}v^{0}_{1})&{} \cdots &{}(1-q_{1})\beta _{1}(t)c_{1n}\omega _{n}(s^{0}_{1}+\eta _{1}v^{0}_{1})\\ (1-q_{2})\beta _{2}(t)c_{21}\omega _{1}(s^{0}_{2}+\eta _{2}v^{0}_{2})&{} (1-q_{2})\beta _{2}(t)c_{22}\omega _{2}(s^{0}_{2}+\eta _{2}v^{0}_{2})&{} \cdots &{}(1-q_{2})\beta _{2}(t)c_{2n}\omega _{n}(s^{0}_{2}+\eta _{2}v^{0}_{2})\\ \vdots &{}\vdots &{}\ddots &{}\vdots \\ (1-q_{n})\beta _{n}(t)c_{n1}\omega _{1}(s^{0}_{n}+\eta _{n}v^{0}_{n})&{} (1-q_{n})\beta _{n}(t)c_{n2}\omega _{2}(s^{0}_{n}+\eta _{n}v^{0}_{n})&{} \cdots &{}(1-q_{n})\beta _{n}(t)c_{nn}\omega _{n}(s^{0}_{n}+\eta _{n}v^{0}_{n})\\ \end{array} \right] , \\ f_{22}= & {} \left[ \begin{array}{cccc} q_{1}\beta _{1}(t)c_{11}(s^{0}_{1}+\eta _{1}v^{0}_{1})&{} q_{1}\beta _{1}(t)c_{12}(s^{0}_{1}+\eta _{1}v^{0}_{1})&{} \cdots &{}q_{1}\beta _{1}(t)c_{1n}(s^{0}_{1}+\eta _{1}v^{0}_{1})\\ q_{2}\beta _{2}(t)c_{21}(s^{0}_{2}+\eta _{2}v^{0}_{2})&{} q_{2}\beta _{2}(t)c_{22}(s^{0}_{2}+\eta _{2}v^{0}_{2})&{} \cdots &{}q_{2}\beta _{2}(t)c_{2n}(s^{0}_{2}+\eta _{2}v^{0}_{2})\\ \vdots &{}\vdots &{}\ddots &{}\vdots \\ q_{n}\beta _{n}(t)c_{n1}(s^{0}_{n}+\eta _{n}v^{0}_{n})&{} q_{n}\beta _{n}(t)c_{n2}(s^{0}_{n}+\eta _{n}v^{0}_{n})&{} \cdots &{}q_{n}\beta _{n}(t)c_{nn}(s^{0}_{n}+\eta _{n}v^{0}_{n})\\ \end{array} \right] , \\ f_{23}= & {} \left[ \begin{array}{cccc} q_{1}\beta _{1}(t)c_{11}\omega _{1}(s^{0}_{1}+\eta _{1}v^{0}_{1})&{} q_{1}\beta _{1}(t)c_{12}\omega _{2}(s^{0}_{1}+\eta _{1}v^{0}_{1})&{} \cdots &{}q_{1}\beta _{1}(t)c_{1n}\omega _{n}(s^{0}_{1}+\eta _{1}v^{0}_{1})\\ q_{2}\beta _{2}(t)c_{21}\omega _{1}(s^{0}_{2}+\eta _{2}v^{0}_{2})&{} q_{2}\beta _{2}(t)c_{22}\omega _{2}(s^{0}_{2}+\eta _{2}v^{0}_{2})&{} \cdots &{}q_{2}\beta _{2}(t)c_{2n}\omega _{n}(s^{0}_{2}+\eta _{2}v^{0}_{2})\\ \vdots &{}\vdots &{}\ddots &{}\vdots \\ q_{n}\beta _{n}(t)c_{n1}\omega _{1}(s^{0}_{n}+\eta _{n}v^{0}_{n})&{} q_{n}\beta _{n}(t)c_{n2}\omega _{2}(s^{0}_{n}+\eta _{n}v^{0}_{n})&{} \cdots &{}q_{n}\beta _{n}(t)c_{nn}\omega _{n}(s^{0}_{n}+\eta _{n}v^{0}_{n})\\ \end{array} \right] , \\ v_{11}= & {} \left[ \begin{array}{ccccc} \sigma _{1}+u+d_{1}+\alpha _{1}&{}0&{}\cdots &{}0&{}0\\ -a_{(k-1)k}\alpha _{1}&{} \sigma _{2}+u+d_{2}+\alpha _{2}&{}\cdots &{}0&{}0\\ \vdots &{}\vdots &{}\ddots &{}\vdots &{}\vdots \\ 0&{}0&{}\cdots &{}-a_{(k-1)k}\alpha _{n-1}&{}\sigma _{n}+u+d_{n}+\alpha _{n}\\ \end{array} \right] , \\ v_{21}= & {} \left[ \begin{array}{ccccc} -\mu _{1}\sigma _{1}&{}0&{}\cdots &{}0\\ 0&{} -\mu _{2}\sigma _{2}&{}\cdots &{}0\\ \vdots &{}\vdots &{}\ddots &{}\vdots \\ 0&{}0&{}\cdots &{} -\mu _{n}\sigma _{n}\\ \end{array} \right] , \\ v_{22}= & {} \left[ \begin{array}{ccccc} \theta _{1}+u+d_{1}+\alpha _{1}&{}0&{}\cdots &{}0&{}0\\ -a_{(k-1)k}\alpha _{1}&{} \theta _{2}+u+d_{2}+\alpha _{2}&{}\cdots &{}0&{}0\\ \vdots &{}\vdots &{}\ddots &{}\vdots &{}\vdots \\ 0&{}0&{}\cdots &{}-a_{(k-1)k}\alpha _{n-1}&{} \theta _{n}+u+d_{n}+\alpha _{n}\\ \end{array} \right] , \\ v_{24}= & {} \left[ \begin{array}{ccccc} -\chi _{1}&{}0&{}\cdots &{}0\\ 0&{} -\chi _{2}&{}\cdots &{}0\\ \vdots &{}\vdots &{}\ddots &{}\vdots \\ 0&{}0&{}\cdots &{} -\chi _{n}\\ \end{array} \right] ,\;\; v_{32}=\left[ \begin{array}{ccccc} -\xi _{1}\theta _{1}&{}0&{}\cdots &{}0\\ 0&{} -\xi _{2}\theta _{2}&{}\cdots &{}0\\ \vdots &{}\vdots &{}\ddots &{}\vdots \\ 0&{}0&{}\cdots &{} -\xi _{n}\theta _{n}\\ \end{array} \right] , \\ v_{33}= & {} \left[ \begin{array}{ccccc} \gamma _{1}+u+d_{1}+\alpha _{1}&{}0&{}\cdots &{}0&{}0\\ -a_{(k-1)k}\alpha _{1}&{} \gamma _{2}+u+d_{2}+\alpha _{2}&{}\cdots &{}0&{}0\\ \vdots &{}\vdots &{}\ddots &{}\vdots &{}\vdots \\ 0&{}0&{}\cdots &{}-a_{(k-1)k}\alpha _{n-1}&{} \gamma _{n}+u+d_{n}+\alpha _{n}\\ \end{array} \right] , \\ v_{41}= & {} \left[ \begin{array}{ccccc} -(1-\mu _{1})\sigma _{1}&{}0&{}\cdots &{}0\\ 0&{} -(1-\mu _{2})\sigma _{2}&{}\cdots &{}0\\ \vdots &{}\vdots &{}\ddots &{}\vdots \\ 0&{}0&{}\cdots &{} -(1-\mu _{n})\sigma _{n}\\ \end{array} \right] , \\ v_{42}= & {} \left[ \begin{array}{ccccc} -(1-\xi _{1})\theta _{1}&{}0&{}\cdots &{}0\\ 0&{} -(1-\xi _{2})\theta _{2}&{}\cdots &{}0\\ \vdots &{}\vdots &{}\ddots &{}\vdots \\ 0&{}0&{}\cdots &{} -(1-\xi _{n})\theta _{n}\\ \end{array} \right] , \;\; v_{43}=\left[ \begin{array}{ccccc} -\rho _{1}\gamma _{1}&{}0&{}\cdots &{}0\\ 0&{}-\rho _{2}\gamma _{2}&{}\cdots &{}0\\ \vdots &{}\vdots &{}\ddots &{}\vdots \\ 0&{}0&{}\cdots &{} -\rho _{n}\gamma _{n}\\ \end{array} \right] , \\ v_{44}= & {} \left[ \begin{array}{ccccc} \chi _{1}+u+d_{1}+\alpha _{1}&{}0&{}\cdots &{}0&{}0\\ -a_{(k-1)k}\alpha _{1}&{} \chi _{2}+u+d_{2}+\alpha _{2}&{}\cdots &{}0&{}0\\ \vdots &{}\vdots &{}\ddots &{}\vdots &{}\vdots \\ 0&{}0&{}\cdots &{}-a_{(k-1)k}\alpha _{n-1}&{} \chi _{n}+u+d_{n}+\alpha _{n}\\ \end{array} \right] . \end{aligned}$$

We divide the population into two age-groups and provide some numerical simulations to support Remark 1. The parameters of System (2) are fixed as $\beta _{1}(t)={\hat{\beta }}_{1}(1+0.99\sin (\frac{\pi }{6}t))$, ${\hat{\beta }}_{1}\in [0.03,0.08]$, $\beta _{2}(t)={\hat{\beta }}_{2}(1+0.99\sin (\frac{\pi }{6}t))$, ${\hat{\beta }}_{2}\in [0.03,0.08]$, $c_{11}=42$, $c_{12}=18$, $c_{21}=19$, $c_{22}=186$, $d_1=1/(100\times 12)$, $d_2=1/(50\times 12)$, $\alpha _1=1/(50\times 12)$, $\alpha _2=0$, $p_1=0.99$, $\nu _2=0.4$, $q_1=0.05$, $q_2=0.05$, $\sigma _1=1.5\times 10^{-4}$, $\sigma _2=2.3\times 10^{-4}$, $\theta _1=30/25$, $\theta _2=30/25$, $\gamma _1=1/6$, $\gamma _2=1/6$, $\rho _1=0.95$, $\rho _2=0.95$, $\mu _1=0.1545$, $\mu _2=0.1545$, $\xi _1=0.89$, $\xi _2=0.89$, $\omega _1=0.4387$, $\omega _2=0.4387$, $\eta _1=0.15$, $\eta _2=0.15$, $\tau _1=1/(10\times 12)$, $\tau _2=1/(5\times 12)$, $\delta _1=0.8$, $\delta _2=0.8$, $\varrho _1=0.8$, $\varrho _2=0.8$, $\chi _1=0.0075/12$, $\chi _2=0.006/12$, $a_{12}=1$, $u=0$. The initial values of System (2) are $(s_{1}(0),s_{2}(0),v_{1}(0),v_{2}(0),e_{1}(0),e_{2}(0),i_{1}(0),i_{2}(0),f_{1}(0),f_{2}(0),r_{1}(0),r_{2}(0)) = (0.5,0.5,0.1,0.1,0.1,0.1,0.1,0.1,0.1,0.1,0.1,0.1)$. According to numerical simulation results, when ${\mathcal {R}}_{0}<1$, System (2) has at least one stable positive periodic solution and one stable disease-free periodic solution. When ${\mathcal {R}}_{0}>1$, System (2) has at least one stable positive periodic solution and one unstable disease-free periodic solution, as shown in Fig. 8.

Fig. 8

The existence of periodic solutions (Color figure online)

Appendix B Contact Matrix

Let ${\overline{A}}$ represent the known contact matrix, as shown in Table 4, and ${\bar{a}}_{ig},i,g=1,2,\cdots ,m$ represents the elements in the contact matrix, where i, g refers to rows and columns, respectively, and m is the number of age-groups in the contact matrix. We use $C=(c_{kj}),k,j=1,2,\cdots ,n$ to denote the modified contact matrix, then we let age-group ${\bar{u}}$ contain narrower age-groups $i=l(k)$ to g(k), where n is the number of age-groups in the modified contact matrix.

Table 4 Contact matrix (Prem et al. 2017)

Table 5 Number of individuals in each age-group (Population Census Office of the State Council of the People’s Republic of China 2021)

The contact rate between an individual in age-group i and another individual in age-group g can be expressed as

$$\begin{aligned} {\bar{d}}_{ij}=\sum ^{{\bar{u}}(j)}_{g=l(j)}{\bar{a}}_{ig}. \end{aligned}$$

Let $N_{i}$ denote the population in age-group i, as shown in Table 5, we can calculate the population weighted average of each element, ${\bar{d}}$, and derive the contact rate between age-group k and age-group j. For elements off-diagonal, we need to calculate the number of contacts between different age-groups. Therefore, the total number of contacts from k to j and j to k can be expressed as

$$\begin{aligned} {\bar{Y}}_{kj}=\sum ^{{\bar{u}}(k)}_{i=l(k)}N_{i}{\bar{d}}_{ij},\;{\bar{Y}}_{jk}=\sum ^{{\bar{u}}(j)}_{i=l(j)}N_{i}{\bar{d}}_{ik}. \end{aligned}$$

In order to ensure that ${\bar{Y}}_{kj}$ and ${\bar{Y}}_{jk}$ are equal, we averaged ${\bar{Y}}_{kj}$ and ${\bar{Y}}_{jk}$, namely

$$\begin{aligned} Z_{kj}=Z_{jk}=\frac{{\bar{Y}}_{kj}+{\bar{Y}}_{jk}}{2}. \end{aligned}$$

In summary, the modified contact matrix element can be expressed as

$$\begin{aligned} c_{kj}=\frac{Z_{kj}}{\sum ^{{\bar{u}}(k)}_{i=l(k)}N_{i}},\;c_{jk}=\frac{Z_{jk}}{\sum ^{{\bar{u}}(j)}_{i=l(j)}N_{i}}, \end{aligned}$$

where $c_{kj}$ is the rate at which an individual in age-group k makes contacts with anyone in age-group j per day. The total contact rate on the diagonal is

$$\begin{aligned} c_{kk}=\frac{\sum ^{{\bar{u}}(k)}_{i=l(k)}N_{i}{\bar{d}}_{ik}}{\sum ^{{\bar{u}}(k)}_{i=l(k)}N_{i}}. \end{aligned}$$

Appendix C Data Collection and Wavelet Analysis

Table 6 Population data from 2005 to 2019 (National Bureau of Statistics 2021a)

Fig. 9

Temporal periodicity analysis of monthly new TB cases for 14 age-groups from January 2005 to December 2017 in mainland China using the wavelet method. (A) The wavelet spectrum analysis corresponding to time series of monthly new TB cases. High power values are colored in red; orange and yellow denote intermediate power; cyan and blue denote low one. Note the black line is the 95% confidence level. (B) The average wavelet spectrum (blue line) and the corresponding 95% confidence contour (red line) (Color figure online)

Fig. 10

3D graph of the fitting results of monthly TB prevalence per 100,000 individuals from January 2005 to December 2017. The 14 age-groups represent 0–4 years old 5–9 years old, 10–14 years old, 15–19 years old, 20–24 years old, 25–29 years old, 30–34 years old, 35–39 years old, 40–44 years old, 45–49 years old, 50–54 years old, 55–59 years old, 60–64 years old, and 65+ years old, respectively. The black circles represent the actual data (Color figure online)

Appendix D Parameter Estimation

Fig. 11

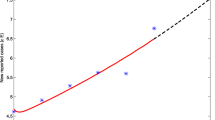
The fitting results of TB prevalence per 100,000 individuals vary with age-groups. The solid red line represents the simulated curve of System (1). The black circles represent training data, and the green circles represent testing data. The $95\%$ confidence and prediction intervals are shown as light red and light blue, respectively. The 14 age-groups represent 0–4 years old, 5–9 years old, 10–14 years old, 15–19 years old, 20–24 years old, 25–29 years old, 30–34 years old, 35–39 years old, 40–44 years old, 45–49 years old, 50–54 years old, 55–59 years old, 60–64 years old, and 65+ years old, respectively (Color figure online)

Fig. 12

Trace plots of unknown parameters and initial values for System (1), estimated by Markov chain Monte Carlo (MCMC) methods. The blue lines represent the $95\%$ confidence interval. The red line represents the mean value (Color figure online)

Table 7 The unknown parameters of System (1)

Table 8 The initial values of System (1)