Global analysis of an age-structured tuberculosis model with an application to Jiangsu, China

Abstract

Diagnostic delay for TB infected individuals and the lack of TB vaccines for adults are the main challenges to achieve the goals of WHO by 2050. In order to evaluate the impacts of diagnostic delay and vaccination for adults on prevalence of TB, we propose an age-structured model with latent age and infection age, and we incorporate Mycobacterium TB in the environment and vaccination into the model. Diagnostic delay is indicated by the age of infection before receiving treatment. The threshold dynamics are established in terms of the basic reproduction number ${\mathcal {R}}_0$. When ${\mathcal {R}}_0<1$, the disease-free equilibrium is globally asymptotically stable, which means that TB epidemic will die out; When ${\mathcal {R}}_0=1$, the disease-free equilibrium is globally attractive; there exists a unique endemic equilibrium and the endemic equilibrium is globally attractive when ${\mathcal {R}}_0>1$. We estimate that the basic reproduction number ${\mathcal {R}}_{0}=0.5320$ (95% CI (0.3060, 0.7556)) in Jiangsu Province, which means that TB epidemic will die out. However, we find that the annual number of new TB cases by 2050 is 1,151 (95%CI: (138, 8,014)), which means that it is challenging to achieve the goal of WHO by 2050. To this end, we evaluate the possibility of achieving the goals of WHO if we start vaccinating adults and reduce diagnostic delay in 2025. Our results demonstrate that when the diagnostic delay is reduced from longer than four months to four months, or 20% adults are vaccinated, the goal of WHO in 2050 can be achieved, and 73,137 (95%CI: (23,906, 234,086)) and 54,828 (95%CI: (15,811, 206,468)) individuals will be prevented from being infected from 2025 to 2050, respectively. The modeling approaches and simulation results used in this work can help policymakers design control measures to reduce the prevalence of TB.

Appendices

Appendix A: Proof of Theorem 1

Note that the total population size N(t) satisfies

$$\begin{aligned} \left. \begin{aligned} \frac{\text{ d }N(t)}{\text{ d }t}&=\frac{\text{ d }S(t)}{\text{ d }t} +\frac{\text{ d }V(t)}{\text{ d }t}+\frac{\text{ d }T(t)}{\text{ d }t}+ \frac{\text{ d }R(t)}{\text{ d }t}+\frac{\text{ d }}{\text{ d }t} \int ^{+\infty }_{0}e(t,b)\text{ d }b\\&\quad +\frac{\text{ d }}{\text{ d }t} \int ^{+\infty }_{0}i(t,a)\text{ d }a. \end{aligned} \right. \end{aligned}$$

(28)

According to Eq. (5), we have

$$\begin{aligned} \int ^{+\infty }_{0}e(t,b)\text{ d }b= & {} \int ^{t}_{0}e(t-b,0)k_{1}(b)\text{ d }b +\int ^{+\infty }_{t}e_{0}(b-t)\frac{k_{1}(b)}{k_{1}(b-t)}\text{ d }b\\= & {} \int ^{t}_{0}e(\tau _{1},0)k_{1}(t-\tau _{1})\text{ d }\tau _{1} +\int ^{+\infty }_{0}e_{0}(\tau _{2})\frac{k_{1}(t+\tau _{2})}{k_{1}(\tau _{2})}\text{ d }\tau _{2}. \end{aligned}$$

Then

$$\begin{aligned} \frac{\text{ d }}{\text{ d }t}\int ^{+\infty }_{0}e(t,b)\text{ d }b= & {} \frac{\text{ d }}{\text{ d }t}\int ^{t}_{0}e(\tau _{1},0)k_{1}(t-\tau _{1})\text{ d }\tau _{1}+ \frac{\text{ d }}{\text{ d }t}\int ^{+\infty }_{0}e_{0}(\tau _{2}) \frac{k_{1}(t+\tau _{2})}{k_{1}(\tau _{2})}\text{ d }\tau _{2}\\= & {} e(t,0)k_{1}(0)+\int ^{t}_{0}e(\tau _{1},0)\frac{\text{ d }}{\text{ d }t} k_{1}(t-\tau _{1})\text{ d }\tau _{1}\\{} & {} +\int ^{+\infty }_{0}\frac{e_{0} (\tau _{2})}{k_{1}(\tau _{2})}\frac{\text{ d }}{\text{ d }t}k_{1}(t+\tau _{2})\text{ d }\tau _{2}.\\ \end{aligned}$$

Note that $k_{1}(0)=1$ and $\frac{\text{ d }}{\text{ d }b}k_{1}(b)=-(\rho \sigma (b)+d)k_{1}(b)$ for almost all $b\ge 0$. Thus, we have

$$\begin{aligned} \frac{\text{ d }}{\text{ d }t}\int ^{+\infty }_{0}e(t,b)\text{ d }b= & {} e(t,0)-\int ^{t}_{0}e(\tau _{1},0)(\rho \sigma (t-\tau _{1}) +d)k_{1}(t-\tau _{1})\text{ d }\tau _{1}\\{} & {} -\int ^{+\infty }_{0}\frac{e_{0}(\tau _{2})}{k_{1}(\tau _{2})} (\rho \sigma (t+\tau _{2})+d)k_{1}(t+\tau _{2})\text{ d }\tau _{2}\\= & {} e(t,0)-\int ^{+\infty }_{0}(\rho \sigma (b)+d)e(t,b)\text{ d }b. \end{aligned}$$

Similarly, we obtain

$$\begin{aligned} \begin{aligned} \frac{\text{ d }}{\text{ d }t}\int ^{+\infty }_{0}i(t,a)\text{ d }a=i(t,0) -\int ^{+\infty }_{0}(\theta (a)+d)i(t,a)\text{ d }a. \end{aligned} \end{aligned}$$

We deduce that N(t) satisfies the following equation

$$\begin{aligned} \begin{aligned} \frac{\text{ d }N(t)}{\text{ d }t}=\varLambda -dN(t). \end{aligned} \end{aligned}$$

Solving the above equation, we have $N(t)=\frac{\varLambda }{d}-\text{ e}^{-dt}(\frac{\varLambda }{d}-N_{0})$ and $\underset{t\rightarrow \infty }{\lim \sup }\;N(t)\le \frac{\varLambda }{d}$ for $t\in {\mathbb {R}}_{+}$, where $N_{0}$ represents the total population at time $t = 0$.

Through the fifth equation of System (2), we obtain

$$\begin{aligned} \frac{\text{ d }W(t)}{\text{ d }t}=\int ^{+\infty }_{0}\xi _{1}(a)i(t,a) \text{ d }a+\xi _{2}T(t)-cW(t)\le \frac{\varLambda ({\bar{\xi }}_{1}+\xi _{2})}{d}-cW(t). \end{aligned}$$

Solving the above equation, we have that $W(t)=\frac{\varLambda ({\bar{\xi }}_{1}+\xi _{2})}{dc}-\text{ e}^{-ct} \Big (\frac{\varLambda ({\bar{\xi }}_{1}+\xi _{2})}{dc}-W_{0}\Big )$ and $\underset{t\rightarrow \infty }{\lim \sup }\;W(t)\le \frac{\varLambda ({\bar{\xi }}_{1}+\xi _{2})}{dc}$ for $t\in {\mathbb {R}}_{+}$, where $W_{0}$ indicates the density of Mycobacterium TB at time $t=0$. This completes the proof. $\square$

Appendix B: Proof of Theorem 2

The characteristic equation corresponding to ${\mathcal {P}}^{0}$ is

$$\begin{aligned} \begin{aligned} G(\iota )&=\big (S^{0}+\eta V^{0}\big )\bigg \{{\mathcal {H}}_{2}(\iota ) +\frac{\beta _{2}{\mathcal {H}}_{3}(\iota )}{\iota +\gamma +d}+ \frac{\beta _{3}[(\iota +\gamma +d){\mathcal {H}}_{4}(\iota ) +\xi _{2}{\mathcal {H}}_{3}(\iota )]}{(\iota +c)(\iota +\gamma +d)}\bigg \}\\&\quad \big [q+\rho (1-q){\mathcal {H}}_{1}(\iota )\big ]-1. \end{aligned} \end{aligned}$$

When $\iota$ is real, we can acquire some basic properties of $G(\iota )$ as follows

$$\begin{aligned} \begin{aligned} G(0)={\mathcal {R}}_{0}-1,\;G'(\iota )<0,\;\underset{\iota \rightarrow - \infty }{\lim }G(\iota )=+\infty ,\;\underset{\iota \rightarrow +\infty }{\lim }G(\iota )=-1. \end{aligned} \end{aligned}$$

Hence, when ${\mathcal {R}}_{0}>1$, the characteristic equation $G(\iota )=0$ has a real positive root. Then, the disease-free equilibrium is unstable. When ${\mathcal {R}}_{0}<1$, the characteristic equation $G(\iota )=0$ does not have a solution with non-negative real part. Otherwise, $G(\iota )=0$ has at least one root $\iota _{0}=\alpha _{0}+i\beta _{0}$ satisfying $\alpha _{0}\ge 0$. Then, we have

$$\begin{aligned} 0=|G(\iota _{0})|\le {\mathcal {R}}_{0}-1, \end{aligned}$$

which contradicts with ${\mathcal {R}}_{0}<1$. Hence, when ${\mathcal {R}}_{0}<1$, the disease-free equilibrium is locally asymptotically stable. This completes the proof. $\square$

Appendix C: Proof of Theorem 3

For $t\ge 0$, let

$$\begin{aligned} \varPsi (t,x)=(S(t),V(t),T(t),R(t),W(t),{\tilde{e}}(t,\cdot ),{\tilde{i}}(t,\cdot )), \end{aligned}$$

and

$$\begin{aligned} \Theta (t,x)=(0,0,0,0,0,\varphi _{e}(t,\cdot ),\varphi _{i}(t,\cdot )), \end{aligned}$$

where

$$\begin{aligned} {\tilde{e}}(t,b)= & {} \left\{ \begin{array}{ll} e(t-b,0)k_{1}(b),&{}\quad 0\le b\le t,\\ 0,&{}\quad 0\le t\le b,\\ \end{array}\right. \quad {\tilde{i}}(t,a)=\left\{ \begin{array}{ll} i(t-a,0)k_{2}(a),&{}\quad 0\le a\le t,\\ 0,&{}\quad 0\le t\le a,\\ \end{array} \right. \\ \varphi _{e}(t,b)= & {} \left\{ \begin{array}{ll} 0,&{}\quad 0\le b\le t,\\ e_{0}(b-t)\frac{k_{1}(b)}{k_{1}(b-t)}, &{}\quad 0\le t\le b,\\ \end{array}\right. \quad \varphi _{i}(t,a)=\left\{ \begin{array}{ll} 0,&{}\quad 0\le a\le t,\\ i_{0}(a-t)\frac{k_{2}(a)}{k_{2}(a-t)},&{}\quad 0\le t\le a,\\ \end{array} \right. \end{aligned}$$

for $x=(S(0),V(0),T(0),R(0),W(0),e_{0}(b),i_{0}(a))$. Clearly, we have $\varPhi (t,x) =\Theta (t,x) + \varPsi (t,x)$. Let ${\mathcal {B}}$ be a bounded subset of ${\mathcal {Y}}$, ${\mathcal {M}}$ is constants greater than $\max \Big \{N_{0},\frac{\varLambda }{d},W_{0},\frac{\varLambda ({\bar{\xi }}_{1}+\xi _{2})}{dc}\Big \}$, for each $x\in {\mathcal {B}}$. Hence, we can derive

$$\begin{aligned} \Vert \Theta (t,x)\Vert _{{\mathcal {Y}}}= & {} \int ^{+\infty }_{t}e_{0}(b-t) \frac{k_{1}(b)}{k_{1}(b-t)}\text{ d }b+ \int ^{+\infty }_{t}i_{0}(a-t)\frac{k_{2}(a)}{k_{2}(a-t)}\text{ d }a\\= & {} \int ^{+\infty }_{0}e_{0}(\tau _{1})\frac{k_{1}(\tau _{1}+t)}{k_{1} (\tau _{1})}\text{ d }\tau _{1}+ \int ^{+\infty }_{0}i_{0}(\tau _{1})\frac{k_{2}(\tau _{1}+t)}{k_{2} (\tau _{1})}\text{ d }\tau _{1}\\= & {} \int ^{+\infty }_{0}e_{0}(\tau _{1})\text{ e}^{-\int ^{\tau _{1} +t}_{\tau _{1}}(\rho \sigma (s)+d)\text{ d }s}\text{ d }\tau _{1}+ \int ^{+\infty }_{0}i_{0}(\tau _{1})\text{ e}^{-\int ^{\tau _{1} +t}_{\tau _{1}}(\theta (s)+d)\text{ d }s}\text{ d }\tau _{1}\\\le & {} \text{ e}^{-dt}\bigg (\int ^{+\infty }_{0}e_{0}(\tau _{1}) \text{ d }\tau _{1}+\int ^{+\infty }_{0}i_{0}(\tau _{1})\text{ d } \tau _{1}\bigg )\le {\mathcal {M}}\text{ e}^{-dt}. \end{aligned}$$

This implies $\underset{t\rightarrow \infty }{\lim }\;{\textrm{diam}}\;\Theta (t, {\mathcal {B}})= 0$. In the following, we will show that $\varPsi (t,x)$ has a compact closure for each $t\ge 0$. We know that S(t), V(t), T(t), R(t), and W(t) remain in the compact set $[0,{\mathcal {M}}]$ for all $t\ge 0$. Thus, we only need to prove that ${\tilde{e}}(t,b)$ and ${\tilde{i}}(t,a)$ remain in a pre-compact subset of $L^{1}_{+}(0,+\infty )$, which is independent of $x\in {\mathcal {B}}$. According to

$$\begin{aligned} 0\le {\tilde{e}}(t,b)=\left\{ \begin{array}{ll} e(t-b,0)k_{1}(b),&{}\quad 0\le b\le t,\\ 0,&{}\quad 0\le t\le b,\\ \end{array} \right. \end{aligned}$$

and assumption (A2), it is easy to show that

$$\begin{aligned} 0\le {\tilde{e}}(t,b)\le (1-q)(1+\eta )({\bar{\beta }}_{1}+\beta _{2} +\beta _{3}){\mathcal {M}}^{2}\text{ e}^{-db}. \end{aligned}$$

Therefore, the conditions (i), (ii) and (iv) of Lemma 2 are satisfied. Next, we verify that condition (iii) of Lemma 2 is satisfied.

$$\begin{aligned} \begin{aligned} \int ^{+\infty }_{0}|{\tilde{e}}(t,b+h)-{\tilde{e}}(t,b)|\text{ d }b&=\int ^{t-h}_{0}|{\tilde{e}}(t,b+h)-{\tilde{e}}(t,b)|\text{ d }b +\int ^{t}_{t-h}|{\tilde{e}}(t,b)|\text{ d }b\\&\le \int ^{t-h}_{0}|e(t-b-h,0)||k_{1}(b+h)-k_{1}(b)|\text{ d }b\\&\quad +\int ^{t-h}_{0}|e(t-b-h,0)-e(t-b,0)||k_{1}(b)|\text{ d }b\\&\quad +(1-q)(1+\eta )({\bar{\beta }}_{1}+\beta _{2}+\beta _{3}){\mathcal {M}}^{2}h, \end{aligned} \end{aligned}$$

where

$$\begin{aligned}{} & {} \int ^{t-h}_{0}|e(t-b-h,0)||k_{1}(b+h)-k_{1}(b)|\text{ d }b\\{} & {} \quad \le (1-q)(1+\eta )({\bar{\beta }}_{1}+\beta _{2}+\beta _{3}){\mathcal {M}}^{2} \bigg (\int ^{t-h}_{0}k_{1}(b)\text{ d }b-\int ^{t-h}_{0}k_{1}(b+h)\text{ d }b\bigg )\\{} & {} \quad =(1-q)(1+\eta )({\bar{\beta }}_{1}+\beta _{2}+\beta _{3}){\mathcal {M}}^{2} \bigg (\int ^{h}_{0}k_{1}(b)\text{ d }b-\int ^{h}_{t-h}k_{1}(b)\text{ d }b -\int ^{t}_{h}k_{1}(s)\text{ d }s\bigg )\\{} & {} \quad =(1-q)(1+\eta )({\bar{\beta }}_{1}+\beta _{2}+\beta _{3}){\mathcal {M}}^{2} \bigg (\int ^{h}_{0}k_{1}(b)\text{ d }b-\int ^{t}_{t-h}k_{1}(s)\text{ d }s\bigg )\\{} & {} \quad \le (1-q)(1+\eta )({\bar{\beta }}_{1}+\beta _{2}+\beta _{3}){\mathcal {M}}^{2}h. \end{aligned}$$

According to System (2), the following inequalities,

$$\begin{aligned}{} & {} \Big |\frac{\text{ d }S(t)}{\text{ d }t}\Big |\le \varLambda +\big [\tau +\delta +\alpha +d+({\bar{\beta }}_{1}+\beta _{2} +\beta _{3}){\mathcal {M}}\big ]{\mathcal {M}},\\{} & {} \Big |\frac{\text{ d }V(t)}{\text{ d }t}\Big |\le \big [\alpha +\eta ({\bar{\beta }}_{1}+\beta _{2}+\beta _{3}){\mathcal {M}}+\tau +d\big ]{\mathcal {M}},\\{} & {} \Big |\frac{\text{ d }T(t)}{\text{ d }t}\Big |\le ({\bar{\theta }} +\gamma +d){\mathcal {M}},\\{} & {} \Big |\frac{\text{ d }R(t)}{\text{ d }t}\Big |\le (\gamma +\delta +d){\mathcal {M}},\\{} & {} \Big |\frac{\text{ d }W(t)}{\text{ d }t}\Big |\le ({\bar{\xi }}_{1}+\xi _{2}+c){\mathcal {M}}, \end{aligned}$$

can be obtained. Next, we prove that $\int ^{+\infty }_{0}\beta _{1}(a)i(t,a)\text{ d }a$ is Lipschitz continuous.

$$\begin{aligned}{} & {} \bigg |\int ^{+\infty }_{0}\beta _{1}(a)i(t+h,a)\text{ d }a-\int ^{+\infty }_{0} \beta _{1}(a)i(t,a)\text{ d }a\bigg |\\{} & {} \quad =\bigg |\int ^{h}_{0}\beta _{1}(a)i(t+h,a)\text{ d }a +\int ^{+\infty }_{h}\beta _{1}(a)i(t+h,a)\text{ d }a-\int ^{+\infty }_{0} \beta _{1}(a)i(t,a)\text{ d }a\bigg |\\{} & {} \quad =\bigg |\int ^{h}_{0}\beta _{1}(a)i(t+h-a,0)k_{2}(a)\text{ d }a +\int ^{+\infty }_{h}\beta _{1}(a)i(t+h,a)\text{ d }a-\int ^{+\infty }_{0} \beta _{1}(a)i(t,a)\text{ d }a\bigg |\\{} & {} \quad \le \Big [q(1+\eta )({\bar{\beta }}_{1}+\beta _{2}+\beta _{3}) {\mathcal {M}}+\rho {\bar{\sigma }}\Big ]{\bar{\beta }}_{1}{\mathcal {M}}h\\{} & {} \qquad +\bigg |\int ^{+\infty }_{0}\beta _{1}(\tau _{1}+h)i(t+h, \tau _{1}+h)\text{ d }\tau _{1}-\int ^{+\infty }_{0}\beta _{1}(a)i(t,a)\text{ d }a\bigg |\\{} & {} \quad =\Big [q(1+\eta )({\bar{\beta }}_{1}+\beta _{2}+\beta _{3}) {\mathcal {M}}+\rho {\bar{\sigma }}\Big ]{\bar{\beta }}_{1}{\mathcal {M}}h\\{} & {} \qquad +\bigg |\int ^{+\infty }_{0}\beta _{1}(\tau _{1}+h)i(t, \tau _{1})\frac{k_{2}(\tau _{1}+h)}{k_{2}(\tau _{1})}\text{ d } \tau _{1}-\int ^{+\infty }_{0}\beta _{1}(a)i(t,a)\text{ d }a\bigg |. \end{aligned}$$

According to assumption (A3), we note that

$$\begin{aligned}{} & {} \bigg |\int ^{+\infty }_{0}\beta _{1}(a+h)i(t,a)\frac{k_{2}(a+h)}{k_{2}(a)} \text{ d }a-\int ^{+\infty }_{0}\beta _{1}(a)i(t,a)\text{ d }a\bigg |\\{} & {} \quad =\bigg |\int ^{+\infty }_{0}\Big (\beta _{1}(a+h)\frac{k_{2}(a+h)}{k_{2}(a)} -\beta _{1}(a)\Big )i(t,a)\text{ d }a\bigg |\\{} & {} \quad =\bigg |\int ^{+\infty }_{0}\beta _{1}(a+h)i(t,a)\Big (\frac{k_{2}(a +h)}{k_{2}(a)}-1\Big )\text{ d }a\\{} & {} \qquad +\int ^{+\infty }_{0}(\beta _{1}(a+h) -\beta _{1}(a))i(t,a)\text{ d }a\bigg |\\{} & {} \quad =\bigg |\int ^{+\infty }_{0}\beta _{1}(a+h)i(t,a)\Big (\text{ e}^{-\int ^{a +h}_{a}(\theta (s)+d)\text{ d }s}-1\Big )\text{ d }a\\{} & {} \qquad +\int ^{+\infty }_{0} (\beta _{1}(a+h)-\beta _{1}(a))i(t,a)\text{ d }a\bigg |\\{} & {} \quad \le {\bar{\beta }}_{1}({\bar{\theta }}+d){\mathcal {M}}h+\bigg |\int ^{ +\infty }_{0}(\beta _{1}(a+h)-\beta _{1}(a))i(t,a)\text{ d }a\bigg |\\{} & {} \quad \le {\bar{\beta }}_{1}({\bar{\theta }}+d){\mathcal {M}}h+\int ^{ +\infty }_{0}\big |\beta _{1}(a+h)-\beta _{1}(a)\big |\big |i(t,a)\big |\text{ d }a\\{} & {} \quad \le \big [{\bar{\beta }}_{1}({\bar{\theta }}+d)+M_{\beta _{1}}\big ]{\mathcal {M}}h. \end{aligned}$$

Hence, we obtain

$$\begin{aligned}{} & {} \bigg |\int ^{+\infty }_{0}\beta _{1}(a)i(t+h,a)\text{ d }a -\int ^{+\infty }_{0}\beta _{1}(a)i(t,a)\text{ d }a\bigg |\\{} & {} \quad \le \Big \{\Big [q(1+\eta )({\bar{\beta }}_{1}+\beta _{2}+\beta _{3}) {\mathcal {M}}+\rho {\bar{\sigma }}\Big ]{\bar{\beta }}_{1}+{\bar{\beta }}_{1} ({\bar{\theta }}+d)+M_{\beta _{1}}\Big \}{\mathcal {M}}h. \end{aligned}$$

According to the above inequality, we have

$$\begin{aligned}{} & {} \big |e(t-b-h,0)-e(t-b,0)\big |\\{} & {} \quad =(1-q)\big |\lambda (t-b-h)\big (S(t-b-h)+\eta V(t-b-h)\big )\\{} & {} \qquad -\lambda (t-b)\big (S(t-b)+\eta V(t-b)\big )\big |\\{} & {} \quad \le (1-q)\bigg (\Big |S(t-b-h)\int ^{+\infty }_{0}\beta _{1}(a)i (t-b-h,a)\text{ d }a\\{} & {} \qquad -S(t-b)\int ^{+\infty }_{0}\beta _{1}(a)i(t-b,a)\text{ d }a\Big |\\{} & {} \qquad +\beta _{2}\big |S(t-b-h)T(t-b-h)-S(t-b)T(t-b)\big |\\{} & {} \qquad +\beta _{3}\Big |S(t-b-h)W(t-b-h)-S(t-b)W(t-b)\Big |\\{} & {} \qquad +\eta \Big |V(t-b-h)\int ^{+\infty }_{0}\beta _{1}(a)i(t-b-h,a) \text{ d }a-V(t-b)\int ^{+\infty }_{0}\beta _{1}(a)i(t-b,a)\text{ d }a\Big |\\{} & {} \qquad +\eta \beta _{2}\big |V(t-b-h)T(t-b-h)-V(t-b)T(t-b)\big |\\{} & {} \qquad +\eta \beta _{3}\Big |V(t-b-h)W(t-b-h)-V(t-b)W(t-b)\Big |\bigg )\le \varUpsilon h, \end{aligned}$$

where

$$\begin{aligned} \varUpsilon= & {} (1-q){\mathcal {M}}^{2}\Big \{\Big [q(1+\eta )({\bar{\beta }}_{1} +\beta _{2}+\beta _{3}){\mathcal {M}}+\rho {\bar{\sigma }}\Big ]{\bar{\beta }}_{1} +{\bar{\beta }}_{1}({\bar{\theta }}+d)+M_{\beta _{1}}\Big \}\\{} & {} +(1-q){\bar{\beta }}_{1}{\mathcal {M}}\Big \{\varLambda +\big [\tau +\delta +\alpha +d+({\bar{\beta }}_{1}+\beta _{2}+\beta _{3}){\mathcal {M}}\big ]{\mathcal {M}}\Big \}\\{} & {} +(1-q)\beta _{2}{\mathcal {M}}\Big \{\varLambda +\big [{\bar{\theta }}+\gamma +d+\tau +\delta +\alpha +d+({\bar{\beta }}_{1}+\beta _{2}+\beta _{3}) {\mathcal {M}}\big ]{\mathcal {M}}\Big \}\\{} & {} +(1-q)\beta _{3}{\mathcal {M}}\bigg \{\varLambda +\big [{\bar{\xi }}_{1} +\xi _{2}+c+\tau +\delta +\alpha +d+({\bar{\beta }}_{1}+\beta _{2} +\beta _{3}){\mathcal {M}}\big ]{\mathcal {M}}\bigg \}\\{} & {} +(1-q)\eta {\mathcal {M}}^{2}\Big \{\Big [q(1+\eta )({\bar{\beta }}_{1} +\beta _{2}+\beta _{3}){\mathcal {M}}+\rho {\bar{\sigma }}\Big ]{\bar{\beta }}_{1} +{\bar{\beta }}_{1}({\bar{\theta }}+d)+M_{\beta _{1}}\Big \}\\{} & {} +(1-q)\eta {\bar{\beta }}_{1}{\mathcal {M}}^{2}\Big \{\alpha +\eta ({\bar{\beta }}_{1}+\beta _{2}+\beta _{3}){\mathcal {M}}+\tau +d\Big \}\\{} & {} +(1-q)\eta \beta _{2}{\mathcal {M}}^{2}\big \{{\bar{\theta }} +\gamma +d+\alpha +\eta ({\bar{\beta }}_{1}+\beta _{2}+\beta _{3}){\mathcal {M}}+\tau +d\big \}\\{} & {} +(1-q)\eta \beta _{3}{\mathcal {M}}^{2}\Big \{{\bar{\xi }}_{1} +\xi _{2}+c+\alpha +\eta ({\bar{\beta }}_{1}+\beta _{2}+\beta _{3}){\mathcal {M}}+\tau +d\Big \}. \end{aligned}$$

Then, we obtain

$$\begin{aligned} \begin{aligned} \int ^{t-h}_{0}|e(t-b-h,0)-e(t-b,0)||k_{1}(b)|\text{ d }b\le \varUpsilon h\int ^{t-h}_{0}e^{-db}\text{ d }b\le \frac{\varUpsilon h}{d}. \end{aligned} \end{aligned}$$

Hence,

$$\begin{aligned} \left. \begin{aligned} \int ^{+\infty }_{0}|{\tilde{e}}(t,b+h)-{\tilde{e}}(t,b)|\text{ d }b \le \Big [2(1-q)(1+\eta )({\bar{\beta }}_{1}+\beta _{2}+\beta _{3}) {\mathcal {M}}^{2}+\frac{\varUpsilon }{d}\Big ]h. \end{aligned} \right. \end{aligned}$$

We have verified that ${\tilde{e}}(t,b)$ satisfies the conditions of Lemma 2. In a similar way, ${\tilde{i}}(t,a)$ also satisfies the conditions of Lemma 2. As a result, ${\tilde{e}}(t,b)$ and ${\tilde{i}}(t,a)$ remain in pre-compact subsets ${\mathcal {A}}^{e}_{{\mathcal {M}}}$ and ${\mathcal {A}}^{i}_{{\mathcal {M}}}$ of $L^{1}_{+}(0,+\infty )$, respectively. Therefore, $\varPsi (t,{\mathcal {B}})\subseteq [0,{\mathcal {M}}]\times [0,{\mathcal {M}}]\times [0,{\mathcal {M}}]\times [0,{\mathcal {M}}]\times [0,{\mathcal {M}}]\times {\mathcal {A}}^{e}_{{\mathcal {M}}}\times {\mathcal {A}}^{i}_{{\mathcal {M}}}$, which has a compact closure in ${\mathcal {Y}}$. This implies that $\varPsi (t,{\mathcal {B}})$ has a compact closure, satisfying the second condition of Lemma 1. Therefore, we conclude that $\{\varPhi (t,\cdot )\}_{t\ge 0}$ is asymptotically smooth. This completes the proof. $\square$

Appendix D: Proof of Theorem 4

Let

$$\begin{aligned} J(t)=T(t)+W(t)+\int ^{+\infty }_{0}e(t,b)\text{ d }b +\int ^{+\infty }_{0}i(t,a)\text{ d }a. \end{aligned}$$

(29)

For any $\varPhi (0,x_{0})\in {\mathcal {D}}_{0}$, we have

$$\begin{aligned} \frac{\text{ d }J(t)}{\text{ d }t}= & {} -(\gamma +d)T(t)+\int ^{+\infty }_{0} \xi _{1}(a)i(t,a)\text{ d }a+\xi _{2}T(t)-cW(t)\\{} & {} -d\int ^{+\infty }_{0}e(t,b)\text{ d }b+\lambda (t)\big (S(t)+\eta V(t) \big )-d\int ^{+\infty }_{0}i(t,a)\text{ d }a\\\ge & {} -(\gamma +d)T(t)-cW(t)-d\int ^{+\infty }_{0}e(t,b)\text{ d }b -d\int ^{+\infty }_{0}i(t,a)\text{ d }a\\\ge & {} -{\bar{a}}J(t), \end{aligned}$$

where ${\bar{a}}=\max \{\gamma +d,c\}$. Then, we obtain $J(t)\ge J(0)\text{ e}^{-{\bar{a}}t}>0$. This implies that $\varPhi (t,{\mathcal {D}}_{0})\in {\mathcal {D}}_{0}$, i.e., ${\mathcal {D}}_{0}$ is positively invariant under the semiflow $\{\varPhi (t,\cdot )\}_{t\ge 0}$.

In addition, for any $\varPhi (0,x_{0})\in \partial {\mathcal {D}}_{0}$, we consider the following system

$$\begin{aligned}{} & {} \frac{\text{ d }T(t)}{\text{ d }t}=\int ^{+\infty }_{0}\theta (a)i(t,a) \text{ d }a-(\gamma +d)T(t),\nonumber \\{} & {} \frac{\text{ d }W(t)}{\text{ d }t}=\int ^{+\infty }_{0}\xi _{1}(a)i(t,a) \text{ d }a+\xi _{2}T(t)-cW(t),\nonumber \\{} & {} \frac{\partial e(t,b)}{\partial t}+\frac{\partial e(t,b)}{\partial b} =-(\rho \sigma (b)+d)e(t,b),\nonumber \\{} & {} \frac{\partial i(t,a)}{\partial t}+\frac{\partial i(t,a)}{\partial a} =-(\theta (a)+d)i(t,a),\\{} & {} e(t,0)=(1-q)\lambda (t)\big (S(t)+\eta V(t)\big ),\nonumber \\{} & {} i(t,0)=q\lambda (t)\big (S(t)+\eta V(t)\big )+\rho \int ^{+\infty }_{0} \sigma (b)e(t,b)\text{ d }b,\nonumber \\{} & {} T(0)=0,W(0)=0,e(0,b)=e_{0}(b),i(0,a)=i_{0}(a),\nonumber \end{aligned}$$

(30)

where $\lambda (t)$ is given by Eq. (1). Since $S(t)+\eta V(t)\le \max \Big \{N_{0},\frac{\varLambda }{d}\Big \}:=\aleph$, then we set up the following comparison system

$$\begin{aligned}{} & {} \frac{\text{ d }{\overline{T}}(t)}{\text{ d }t}=\int ^{+\infty }_{0} \theta (a){\overline{i}}(t,a)\text{ d }a-(\gamma +d){\overline{T}}(t),\nonumber \\{} & {} \frac{\text{ d }{\overline{W}}(t)}{\text{ d }t}=\int ^{+\infty }_{0} \xi _{1}(a){\overline{i}}(t,a)\text{ d }a+\xi _{2}{\overline{T}}(t) -c{\overline{W}}(t),\nonumber \\{} & {} \frac{\partial {\overline{e}}(t,b)}{\partial t}+\frac{\partial {\overline{e}}(t,b)}{\partial b}=-(\rho \sigma (b)+d){\overline{e}}(t,b),\nonumber \\{} & {} \frac{\partial {\overline{i}}(t,a)}{\partial t}+\frac{\partial {\overline{i}}(t,a)}{\partial a}=-(\theta (a)+d){\overline{i}}(t,a),\\{} & {} {\overline{e}}(t,0)=(1-q){\overline{\lambda }}(t)\aleph ,\nonumber \\{} & {} {\overline{i}}(t,0)=q{\overline{\lambda }}(t)\aleph +\rho \int ^{+\infty }_{0} \sigma (b){\overline{e}}(t,b)\text{ d }b,\nonumber \\{} & {} {\overline{T}}(0)=0,{\overline{W}}(0)=0,{\overline{e}}(0,b) =e_{0}(b),{\overline{i}}(0,a)=i_{0}(a),\nonumber \end{aligned}$$

(31)

where ${\overline{\lambda }}(t)=\int ^{+\infty }_{0}\beta _{1}(a){\overline{i}}(t,a)\text{ d }a+\beta _{2}{\overline{T}}(t)+\beta _{3}{{\overline{W}}(t)}$.

Integrating the equations for ${\overline{e}}(t,b)$ and ${\overline{i}}(t,a)$ in System (31) along the characteristic lines, $t-b=\text{ const }$ and $t-a=\text{ const }$, respectively, we obtain

$$\begin{aligned} {\overline{e}}(t,b)=\left\{ \begin{array}{ll} {\overline{e}}(t-b,0)k_{1}(b),&{}\quad 0\le b\le t,\\ e_{0}(b-t)\frac{k_{1}(b)}{k_{1}(b-t)},&{}\quad 0\le t\le b,\\ \end{array}\right. \quad {\overline{i}}(t,a)=\left\{ \begin{array}{ll} {\overline{i}}(t-a,0)k_{2}(a),&{}\quad 0\le a\le t,\\ i_{0}(a-t)\frac{k_{2}(a)}{k_{2}(a-t)},&{}\quad 0\le t\le a.\\ \end{array} \right. \nonumber \\ \end{aligned}$$

(32)

Substituting Eq. (32) into System (31), we obtain

$$\begin{aligned}{} & {} \frac{\text{ d }{\overline{T}}(t)}{\text{ d }t} =\int ^{t}_{0}\theta (a){\overline{i}}(t-a,0)k_{2}(a)\text{ d }a +\int ^{+\infty }_{t}\theta (a)i_{0}(a-t)\frac{k_{2}(a)}{k_{2}(a -t)}\text{ d }a-(\gamma +d){\overline{T}}(t),\nonumber \\{} & {} \frac{\text{ d }{\overline{W}}(t)}{\text{ d }t} =\int ^{t}_{0}\xi _{1}(a){\overline{i}}(t-a,0)k_{2}(a)\text{ d }a +\int ^{+\infty }_{t}\xi _{1}(a)i_{0}(a-t)\frac{k_{2}(a)}{k_{2}(a -t)}\text{ d }a+\xi _{2}{\overline{T}}(t)-c{\overline{W}}(t),\nonumber \\{} & {} {\overline{T}}(0)=0,{\overline{W}}(0)=0. \end{aligned}$$

(33)

According to assumption (A2), one can obtain

$$\begin{aligned}{} & {} \int ^{+\infty }_{t}\theta (a)i_{0}(a-t)\frac{k_{2}(a)}{k_{2}(a-t)} \text{ d }a\le {\bar{\theta }}\int ^{+\infty }_{0}i_{0}(a)\text{ d }a,\\{} & {} \int ^{+\infty }_{t}\xi _{1}(a)i_{0}(a-t)\frac{k_{2}(a)}{k_{2}(a-t)} \text{ d }a\le {\bar{\xi }}_{1}\int ^{+\infty }_{0}i_{0}(a)\text{ d }a,\\{} & {} \int ^{+\infty }_{t}\sigma (b)e_{0}(b-t)\frac{k_{1}(b)}{k_{1}(b-t)} \text{ d }b\le {\bar{\sigma }}\int ^{+\infty }_{0}e_{0}(b)\text{ d }b,\\{} & {} \int ^{+\infty }_{t}\beta _{1}(a)i_{0}(a-t)\frac{k_{2}(a)}{k_{2}(a-t)} \text{ d }a\le {\bar{\beta }}_{1}\int ^{+\infty }_{0}i_{0}(a)\text{ d }a. \end{aligned}$$

For any $\varPhi (0,x_{0})\in \partial {\mathcal {D}}_{0}$, we have

$$\begin{aligned}{} & {} \int ^{+\infty }_{t}\theta (a)i_{0}(a-t)\frac{k_{2}(a)}{k_{2}(a-t)}\text{ d }a=0, \quad \int ^{+\infty }_{t}\xi _{1}(a)i_{0}(a-t)\frac{k_{2}(a)}{k_{2}(a-t)}\text{ d }a=0,\\{} & {} \int ^{+\infty }_{t}\sigma (b)e_{0}(b-t)\frac{k_{1}(b)}{k_{1}(b-t)}\text{ d }b=0, \quad \int ^{+\infty }_{t}\beta _{1}(a)i_{0}(a-t)\frac{k_{2}(a)}{k_{2}(a-t)}\text{ d }a=0. \end{aligned}$$

Let

$$\begin{aligned}{} & {} \overline{L_{e}}(t)={\overline{e}}(t,0)=(1-q){\overline{\lambda }}(t)\aleph ,\\{} & {} \overline{L_{i}}(t)={\overline{i}}(t,0)=q{\overline{\lambda }}(t)\aleph +\rho \int ^{+\infty }_{0}\sigma (b){\overline{e}}(t,b)\text{ d }b, \end{aligned}$$

we have

$$\begin{aligned} \overline{L_{e}}(t)= & {} (1-q)\bigg [\int ^{t}_{0}\beta _{1}(a)\overline{L_{i}}(t-a) k_{2}(a)\text{ d }a+\beta _{2}{\overline{T}}(t)+\beta _{3}{{\overline{W}}(t)}\bigg ]\aleph ,\\ \overline{L_{i}}(t)= & {} q\bigg [\int ^{t}_{0}\beta _{1}(a)\overline{L_{i}}(t-a)k_{2} (a)\text{ d }a+\beta _{2}{\overline{T}}(t)+\beta _{3}{{\overline{W}}(t)}\bigg ] \aleph \\{} & {} +\rho \int ^{t}_{0}\sigma (b)\overline{L_{e}}(t-b)k_{1}(b)\text{ d }b. \end{aligned}$$

Then, System (33) can be rewritten as

$$\begin{aligned} \overline{L_{e}}(t)= & {} (1-q)\bigg [\int ^{t}_{0}\beta _{1}(a)\overline{L_{i}} (t-a)k_{2}(a)\text{ d }a+\beta _{2}{\overline{T}}(t)+\beta _{3}{{\overline{W}}(t)} \bigg ]\aleph ,\nonumber \\ \overline{L_{i}}(t)= & {} q\bigg [\int ^{t}_{0}\beta _{1}(a)\overline{L_{i}} (t-a)k_{2}(a)\text{ d }a+\beta _{2}{\overline{T}}(t)+\beta _{3}{{\overline{W}}(t)} \bigg ]\aleph \nonumber \\{} & {} +\rho \int ^{t}_{0}\sigma (b)\overline{L_{e}}(t-b)k_{1}(b)\text{ d }b,\nonumber \\ \frac{\text{ d }{\overline{T}}(t)}{\text{ d }t}= & {} \int ^{t}_{0}\theta (a) \overline{L_{i}}(t-a)k_{2}(a)\text{ d }a-(\gamma +d){\overline{T}}(t),\\ \frac{\text{ d }{\overline{W}}(t)}{\text{ d }t}= & {} \int ^{t}_{0}\xi _{1}(a) \overline{L_{i}}(t-a)k_{2}(a)\text{ d }a+\xi _{2}{\overline{T}}(t) -c{\overline{W}}(t),\nonumber \\ \overline{L_{e}}(0)= & {} 0,\overline{L_{i}}(0)=0,{\overline{T}}(0)=0, {\overline{W}}(0)=0.\nonumber \end{aligned}$$

(34)

It is easy to show that System (34) has a unique solution $\overline{L_{e}}(t)=0$, $\overline{L_{i}}(t)=0$, ${\overline{T}}(t)=0$, and ${\overline{W}}(t)=0$.

From System (31) and Eq. (32), we obtain that ${\overline{e}}(t,{\overline{t}})=0$ and ${\overline{i}}(t,{\overline{t}})=0$ for $0\le {\overline{t}}\le t$. Hence,

$$\begin{aligned} \Vert {\overline{e}}(t,b)\Vert _{L^{1}_{+}}=\int ^{+\infty }_{t}e_{0}(b-t) \frac{k_{1}(b)}{k_{1}(b-t)}\text{ d }b\le \Vert e_{0}({\bar{t}})\Vert _{L^{1}_{+}}=0. \end{aligned}$$

Similarly, we can also obtain $\Vert {\overline{i}}(t,a)\Vert _{L^{1}_{+}}=0$. Since $T(t)\le {\overline{T}}(t)$, $W(t)\le {\overline{W}}(t)$, $e(t,b)\le {\overline{e}}(t,b)$, and $i(t,a)\le {\overline{i}}(t,a)$, we have

$$\begin{aligned} T(t)=0,\; W(t)=0,\; \Vert e(t,b)\Vert _{L^{1}_{+}}=0,\; \Vert i(t,a)\Vert _{L^{1}_{+}}=0. \end{aligned}$$

This implies that $\partial {\mathcal {D}}_{0}$ is positively invariant under the semiflow $\{\varPhi (t,\cdot )\}_{t\ge 0}$.

Next, we prove that the disease-free equilibrium ${\mathcal {P}}^{0}$ of System (2) is globally asymptotically stable for the semiflow $\{\varPhi (t,\cdot )\}_{t\ge 0}$ restricted to $\partial {\mathcal {D}}_{0}$. Obviously, System (2) can be represented as

$$\begin{aligned}{} & {} \frac{\text{ d }S(t)}{\text{ d }t}=\varLambda +\tau V(t)+\delta R(t)-(\alpha +d)S(t),\nonumber \\{} & {} \frac{\text{ d }V(t)}{\text{ d }t}=\alpha S(t)-(\tau +d)V(t),\\{} & {} \frac{\text{ d }R(t)}{\text{ d }t}=-(\delta +d)R(t).\nonumber \end{aligned}$$

(35)

Obviously, the unique equilibrium $(S^{0},V^{0},0)$ of System (35) is locally asymptotically stable. By solving System (35), we obtain

$$\begin{aligned} S(t)= & {} -\frac{C_{3}\tau }{\alpha +\tau }\text{ e}^{-(d+\delta )t} +\frac{\varLambda (\tau +d)}{d(\alpha +\tau +d)}+\frac{\alpha \delta C_{3}}{(\alpha +\tau )(\alpha -\delta +\tau )}\text{ e}^{-(d+\delta )t}\\{} & {} -C_{1}\text{ e}^{-(\alpha +\tau +d)t}-\frac{\tau C_{1}}{\alpha }\text{ e}^{-dt},\\ V(t)= & {} C_{2}\text{ e}^{-dt}+C_{1}\text{ e}^{-(\alpha +\tau +d)t} -\frac{\alpha \delta }{(\alpha +\tau )(\alpha -\delta +\tau )}\text{ e}^{-(d+\delta )t}\\{} & {} -\frac{\alpha C_{3}}{\alpha +\tau }\text{ e}^{-(d+\delta )t} +\frac{\varLambda \alpha }{d(\alpha +\tau +d)},\\ R(t)= & {} C_{3}\text{ e}^{-(d+\delta )t}, \end{aligned}$$

where $C_{1}, C_{2}, C_{3}$ are constants. Thus, $\lim _{t\rightarrow \infty } S(t)=\frac{\varLambda (\tau +d)}{d(\alpha +\tau +d)}=S^{0}$, $\lim _{t\rightarrow \infty } V(t)=\frac{\varLambda \alpha }{d(\alpha +\tau +d)}=V^{0}$, and $\lim _{t\rightarrow \infty } R(t)=0$. Then, the disease-free equilibrium ${\mathcal {P}}^{0}$ is globally asymptotically stable restricted to $\partial {\mathcal {D}}_{0}$. This completes the proof. $\square$

Appendix E: Proof of Theorem 5

We assume by contradiction that there exists $x_{0}\in W^{s}({\mathcal {P}}^{0})\cap {\mathcal {D}}_{0}$. In this case, one can find a sequence $\{x_{n}\}\in {\mathcal {D}}_{0}$ such that

$$\begin{aligned} \big \Vert \varPhi (t,x_{n})-{\mathcal {P}}^{0}\big \Vert _{{\mathcal {Y}}}<\frac{1}{n},\;t\ge 0. \end{aligned}$$

Here, $\varPhi (t,x_{n}):=(S_{n}(t),V_{n}(t),T_{n}(t),R_{n}(t),W_{n}(t),e_{n}(t,\cdot ),i_{n}(t,\cdot ))$.

Now, we choose $n>0$ large enough to ensure $S^{0}-\frac{1}{n}>0$ and $V^{0}-\frac{1}{n}>0$. For the above given $n>0$, there exists a $t_{1}>0$ such that for $t>t_{1}$,

$$\begin{aligned} S^{0}-\frac{1}{n}<S_{n}(t)<S^{0}+\frac{1}{n},\;V^{0} -\frac{1}{n}<V_{n}(t)<V^{0}+\frac{1}{n}. \end{aligned}$$

Then, System (2) can be written as

$$\begin{aligned}{} & {} \frac{\text{ d }T(t)}{\text{ d }t}\ge \int ^{+\infty }_{0} \theta (a)i(t,a)\text{ d }a-(\gamma +d)T(t),\\{} & {} \frac{\text{ d }W(t)}{\text{ d }t}\ge \int ^{+\infty }_{0} \xi _{1}(a)i(t,a)\text{ d }a+\xi _{2}T(t)-cW(t),\\{} & {} \frac{\partial e(t,b)}{\partial t}+\frac{\partial e(t,b)}{\partial b}\ge -(\rho \sigma (b)+d)e(t,b),\\{} & {} \frac{\partial i(t,a)}{\partial t}+\frac{\partial i(t,a)}{\partial a}\ge -(\theta (a)+d)i(t,a),\\{} & {} e(t,0)\ge (1-q)\lambda (t)\bigg (S^{0}-\frac{1}{n}+\eta (V^{0} -\frac{1}{n})\bigg ),\\{} & {} i(t,0)\ge q\lambda (t)\bigg (S^{0}-\frac{1}{n}+\eta (V^{0}-\frac{1}{n})\bigg )+\rho \int ^{+\infty }_{0}\sigma (b)e(t,b)\text{ d }b,\\{} & {} T(0)=T_{0},W(0)=W_{0},e(0,b)=e_{0}(b),i(0,a)=i_{0}(a), \end{aligned}$$

where $\lambda (t)$ is given by Eq. (1). We consider the following auxiliary system

$$\begin{aligned}{} & {} \frac{\text{ d }{\underline{T}}(t)}{\text{ d }t}=\int ^{+\infty }_{0} \theta (a){\underline{i}}(t,a)\text{ d }a-(\gamma +d){\underline{T}}(t),\nonumber \\{} & {} \frac{\text{ d }{\underline{W}}(t)}{\text{ d }t}=\int ^{+\infty }_{0} \xi _{1}(a){\underline{i}}(t,a)\text{ d }a+\xi _{2}{\underline{T}}(t) -c{\underline{W}}(t),\nonumber \\{} & {} \frac{\partial {\underline{e}}(t,b)}{\partial t}+\frac{\partial {\underline{e}}(t,b)}{\partial b}=-(\rho \sigma (b)+d){\underline{e}}(t,b),\nonumber \\{} & {} \frac{\partial {\underline{i}}(t,a)}{\partial t}+\frac{\partial {\underline{i}}(t,a)}{\partial a}=-(\theta (a)+d){\underline{i}}(t,a),\\{} & {} {\underline{e}}(t,0)=(1-q){\underline{\lambda }}(t)\bigg (S^{0} -\frac{1}{n}+\eta (V^{0}-\frac{1}{n})\bigg ),\nonumber \\{} & {} {\underline{i}}(t,0)= q{\underline{\lambda }}(t)\bigg (S^{0} -\frac{1}{n}+\eta (V^{0}-\frac{1}{n})\bigg )+\rho \int ^{+\infty }_{0} \sigma (b){\underline{e}}(t,b)\text{ d }b,\nonumber \\{} & {} {\underline{T}}(0)=T_{0},{\underline{W}}(0)=W_{0}, {\underline{e}}(0,b)=e_{0}(b),{\underline{i}}(0,a)=i_{0}(a),\nonumber \end{aligned}$$

(36)

where ${\underline{\lambda }}(t)=\int ^{+\infty }_{0}\beta _{1}(a){\underline{i}}(t,a)\text{ d }a+\beta _{2}{\underline{T}}(t)+\beta _{3}{{\underline{W}}(t)}$. By Volterra formulation (5), we have

$$\begin{aligned} {\underline{e}}(t,b)=\left\{ \begin{aligned} {\underline{e}}(t-b,0)k_{1}(b),&\quad 0\le b\le t,\\ e_{0}(b-t)\frac{k_{1}(b)}{k_{1}(b-t)},&\quad 0\le t\le b,\\ \end{aligned}\right. \quad {\underline{i}}(t,a)=\left\{ \begin{aligned} {\underline{i}}(t-a,0)k_{2}(a),&\quad 0\le a\le t,\\ i_{0}(a-t)\frac{k_{2}(a)}{k_{2}(a-t)},&\quad 0\le t\le a.\\ \end{aligned} \right. \nonumber \\ \end{aligned}$$

(37)

By direct calculation, the characteristic equation of System (36) at ${\mathcal {P}}^{0}$ is

$$\begin{aligned} \begin{aligned}&\bigg (S^{0}-\frac{1}{n}+\eta (V^{0}-\frac{1}{n})\bigg )\\&\quad \bigg \{{\mathcal {H}}_{2}(\iota )+\frac{\beta _{2}{\mathcal {H}}_{3}(\iota )}{\iota +\gamma +d}+ \frac{\beta _{3}[(\iota +\gamma +d){\mathcal {H}}_{4}(\iota ) +\xi _{2}{\mathcal {H}}_{3}(\iota )]}{(\iota +c)(\iota +\gamma +d)}\bigg \}\big [q+\rho (1-q){\mathcal {H}}_{1}(\iota )\big ]=1, \end{aligned} \end{aligned}$$

where ${\mathcal {H}}_{1}(\iota )$, ${\mathcal {H}}_{2}(\iota )$, ${\mathcal {H}}_{3}(\iota )$, and ${\mathcal {H}}_{4}(\iota )$ are given by Eq. (23). Let

$$\begin{aligned} \begin{aligned} {\underline{f}}(\iota )&=\bigg (S^{0}-\frac{1}{n}+\eta (V^{0} -\frac{1}{n})\bigg )\bigg \{{\mathcal {H}}_{2}(\iota ) +\frac{\beta _{2}{\mathcal {H}}_{3}(\iota )}{\iota +\gamma +d}+ \frac{\beta _{3}[(\iota +\gamma +d){\mathcal {H}}_{4}(\iota ) +\xi _{2}{\mathcal {H}}_{3}(\iota )]}{(\iota +c)(\iota +\gamma +d)}\bigg \}\\&\qquad \big [q+\rho (1-q){\mathcal {H}}_{1}(\iota )\big ]. \end{aligned} \end{aligned}$$

Clearly, we have ${\underline{f}}'(\iota )<0$ and $\underset{\iota \rightarrow +\infty }{\lim }{\underline{f}}(\iota )=0$. Furthermore, we also have ${\underline{f}}(0)>1$ for sufficiently large n. Hence, when ${\mathcal {R}}_{0}>1$, the characteristic equation of System (36) has a real positive root. This implies that the solution $({\underline{T}}(t),{\underline{W}}(t),{\underline{e}}(t,\cdot ),{\underline{i}}(t,\cdot ))$ of System (36) is unbounded. Since $T(t)\ge {\underline{T}}(t)$, $W(t)\ge {\underline{W}}(t)$, $e(t,\cdot )\ge {\underline{e}}(t,\cdot )$, and $i(t,\cdot )\ge {\underline{i}}(t,\cdot )$, by comparison principle, we obtain that $(T(t),W(t),e(t,\cdot ),i(t,\cdot ))$ is unbounded, which contradicts with Proposition 1. Therefore, $W^{s}({\mathcal {P}}^{0})\cap {\mathcal {D}}_{0}=\emptyset$. By Theorem 4.2 in Hale and Waltman (1989), we conclude that semiflow $\{\varPhi (t,\cdot )\}_{t\ge 0}$ generated by System (2) is uniformly persistent. This completes the proof. $\square$

Appendix F: Proof of Theorem 6

Define a Lyapunov function

$$\begin{aligned} \begin{aligned} {\mathcal {L}}(t)={\mathcal {L}}_{s}(t)+{\mathcal {L}}_{v}(t) +{\mathcal {L}}_{e}(t)+{\mathcal {L}}_{i}(t)+{\mathcal {L}}_{t}(t)+{\mathcal {L}}_{w}(t) \end{aligned} \end{aligned}$$

(38)

where

$$\begin{aligned} {\mathcal {L}}_{s}(t)= & {} \frac{1}{2S^{0}}(S(t)-S^{0})^{2},\;\;{\mathcal {L}}_{v}(t) =\frac{1}{2V^{0}}(V(t)-V^{0})^{2},\\ {\mathcal {L}}_{e}(t)= & {} {\mathcal {F}}_{b}\int ^{+\infty }_{0}{\mathcal {F}}_{e}(b) e(t,b)\text{ d }b,\;\;{\mathcal {L}}_{i}(t)=\big (S^{0}+\eta V^{0}\big ) \int ^{+\infty }_{0}{\mathcal {F}}_{i}(a)i(t,a)\text{ d }a,\\ {\mathcal {L}}_{t}(t)= & {} \big (S^{0}+\eta V^{0}\big )\Bigg (\frac{\beta _{2}}{\gamma +d}+\frac{\beta _{3}\xi _{2}}{c(\gamma +d)}\Bigg )T(t),\;\;{\mathcal {L}}_{w}(t)=\big (S^{0}+\eta V^{0}\big )\frac{\beta _{3}}{c}W(t). \end{aligned}$$

The nonnegative function ${\mathcal {L}}(t)$ is defined with respect to the disease-free equilibrium ${\mathcal {P}}^{0}$, which is a global minimum. We choose

$$\begin{aligned} {\mathcal {F}}_{b}= & {} \big (S^{0}+\eta V^{0}\big )\Bigg ({\mathcal {K}}_{2} +\frac{\beta _{2}{\mathcal {K}}_{3}}{\gamma +d} +\frac{\beta _{3}{\mathcal {K}}_{4}}{c}+\frac{\beta _{3}\xi _{2} {\mathcal {K}}_{3}}{c(\gamma +d)}\Bigg ),\\ {\mathcal {F}}_{e}(b)= & {} \int ^{+\infty }_{b}\rho \sigma (\upsilon ) \text{ e}^{-\int ^{\upsilon }_{b}(\rho \sigma (\varrho )+d)\text{ d }\varrho }\text{ d }\upsilon ,\\ {\mathcal {F}}_{i}(a)= & {} \int ^{+\infty }_{a}\Bigg (\beta _{1}(\upsilon ) +\frac{\beta _{2}\theta (\upsilon )}{\gamma +d}+ \frac{\beta _{3}\xi _{1}(\upsilon )}{c}+\frac{\beta _{3}\xi _{2} \theta (\upsilon )}{c(\gamma +d)}\Bigg )\text{ e}^{-\int ^{\upsilon }_{a} (\theta (\varrho )+d)\text{ d }\varrho }\text{ d }\upsilon . \end{aligned}$$

By direct calculations, one obtains that

$$\begin{aligned} {\mathcal {F}}_{e}(0)= & {} \int ^{+\infty }_{0}\rho \sigma (\upsilon ) \text{ e}^{-\int ^{\upsilon }_{0}(\rho \sigma (\varrho )+d)\text{ d }\varrho } \text{ d }\upsilon =\rho {\mathcal {K}}_{1},\\ {\mathcal {F}}_{i}(0)= & {} \int ^{+\infty }_{0}\Bigg (\beta _{1}(\upsilon ) +\frac{\beta _{2}\theta (\upsilon )}{\gamma +d}+ \frac{\beta _{3}\xi _{1}(\upsilon )}{c}+\frac{\beta _{3}\xi _{2} \theta (\upsilon )}{c(\gamma +d)}\Bigg )\text{ e}^{-\int ^{\upsilon }_{0} (\theta (\varrho )+d)\text{ d }\varrho }\text{ d }\upsilon \\= & {} {\mathcal {K}}_{2}+\frac{\beta _{2}{\mathcal {K}}_{3}}{\gamma +d} +\frac{\beta _{3}{\mathcal {K}}_{4}}{c}+\frac{\beta _{3}\xi _{2} {\mathcal {K}}_{3}}{c(\gamma +d)},\\ \frac{\text{ d }{\mathcal {F}}_{e}(b)}{\text{ d }b}= & {} -\rho \sigma (b) +(\rho \sigma (b)+d){\mathcal {F}}_{e}(b),\\ \frac{\text{ d }{\mathcal {F}}_{i}(a)}{\text{ d }a}= & {} -\Bigg (\beta _{1}(a) +\frac{\beta _{2}\theta (a)}{\gamma +d}+ \frac{\beta _{3}\xi _{1}(a)}{c}+\frac{\beta _{3}\xi _{2}\theta (a)}{c(\gamma +d)}\Bigg )+(\theta (a)+d){\mathcal {F}}_{i}(a). \end{aligned}$$

Calculating the derivative of ${\mathcal {L}}_{s}(t)$, ${\mathcal {L}}_{v}(t)$, ${\mathcal {L}}_{e}(t)$, ${\mathcal {L}}_{i}(t)$, ${\mathcal {L}}_{t}(t)$, and ${\mathcal {L}}_{w}(t)$ along solutions of System (2), respectively. We can obtain

$$\begin{aligned} \frac{\text{ d }{\mathcal {L}}_{s}(t)}{\text{ d }t}= & {} \frac{1}{S^{0}}(S(t) -S^{0})\frac{\text{ d }S(t)}{\text{ d }t}=\frac{1}{S^{0}}(S(t)-S^{0}) \Big (\varLambda +\tau V(t)-\lambda (t)S(t)-(\alpha +d)S(t)\Big )\\= & {} \frac{1}{S^{0}}(S(t)-S^{0})\Big [-(\alpha +d)(S(t)-S^{0})+\tau (V(t) -V^{0})-\lambda (t)(S(t)-S^{0})-\lambda (t)S^{0}\Big ]\\= & {} -\frac{\alpha +d}{S^{0}}(S(t)-S^{0})^{2}+\frac{\tau }{S^{0}}(S(t) -S^{0})(V(t)-V^{0})\\{} & {} -\frac{1}{S^{0}}\lambda (t)(S(t)-S^{0})^{2}-\lambda (t)S(t)+\lambda (t)S^{0}, \end{aligned}$$

where $\lambda (t)$ is given by Eq. (1).

$$\begin{aligned} \frac{\text{ d }{\mathcal {L}}_{v}(t)}{\text{ d }t}= & {} \frac{1}{V^{0}}(V(t) -V^{0})\frac{\text{ d }V(t)}{\text{ d }t} =\frac{1}{V^{0}}(V(t)-V^{0})\big (\alpha S(t)-\eta \lambda (t)V(t)-(\tau +d)V(t)\big )\\= & {} \frac{1}{V^{0}}(V(t)-V^{0})\Big [\alpha (S(t)-S^{0}) -(\tau +d)(V(t)-V^{0})\\{} & {} -\eta \lambda (t)(V(t)-V^{0})-\eta \lambda (t)V^{0}\Big ]\\= & {} \frac{\alpha }{V^{0}}(S(t)-S^{0})(V(t)-V^{0})-\frac{\tau +d}{V^{0}}(V(t) -V^{0})^{2}-\frac{\eta }{V^{0}}\lambda (t)(V(t)-V^{0})^{2}\\{} & {} -\eta \lambda (t)V(t)+\eta \lambda (t)V^{0},\\ \frac{\text{ d }{\mathcal {L}}_{e}(t)}{\text{ d }t}= & {} {\mathcal {F}}_{b} \int ^{+\infty }_{0}{\mathcal {F}}_{e}(b)\frac{\text{ d }e(t,b)}{\text{ d }t}\text{ d }b=-{\mathcal {F}}_{b}\int ^{+\infty }_{0} {\mathcal {F}}_{e}(b)\bigg [(\rho \sigma (b)+d)e(t,b)+\frac{\partial e(t,b)}{\partial b}\bigg ]\text{ d }b\\= & {} {\mathcal {F}}_{b}\bigg (-\int ^{+\infty }_{0}{\mathcal {F}}_{e}(b) (\rho \sigma (b)+d)e(t,b)\text{ d }b-\int ^{+\infty }_{0}{\mathcal {F}}_{e}(b)\text{ d }e(t,b)\bigg )\\= & {} {\mathcal {F}}_{b}\bigg (-\int ^{+\infty }_{0}{\mathcal {F}}_{e}(b) (\rho \sigma (b)+d)e(t,b)\text{ d }b-{\mathcal {F}}_{e}(b)e(t,b) \Big |^{+\infty }_{0}+\int ^{+\infty }_{0}e(t,b)\text{ d }{\mathcal {F}}_{e}(b)\bigg )\\= & {} {\mathcal {F}}_{b}\bigg (-\int ^{+\infty }_{0}{\mathcal {F}}_{e}(b) (\rho \sigma (b)+d)e(t,b)\text{ d }b+{\mathcal {F}}_{e}(0)e(t,0)\\{} & {} +\int ^{+\infty }_{0}e(t,b)\big [-\rho \sigma (b)+(\rho \sigma (b) +d){\mathcal {F}}_{e}(b)\big ]\text{ d }b\bigg )\\= & {} {\mathcal {F}}_{b}\bigg ({\mathcal {F}}_{e}(0)e(t,0)-\int ^{ +\infty }_{0}\rho \sigma (b)e(t,b)\text{ d }b\bigg )\\= & {} {\mathcal {F}}_{b}\bigg (\rho {\mathcal {K}}_{1}e(t,0)-\rho \int ^{+\infty }_{0}\sigma (b)e(t,b)\text{ d }b\bigg )\\= & {} {\mathcal {F}}_{b}\bigg (\rho {\mathcal {K}}_{1}(1-q)(S(t) +\eta V(t))\lambda (t)-\rho \int ^{+\infty }_{0}\sigma (b)e(t,b)\text{ d }b\bigg ),\\ \end{aligned}$$

$$\begin{aligned}= & {} \big (S^{0}+\eta V^{0}\big )\Bigg ({\mathcal {K}}_{2} +\frac{\beta _{2}{\mathcal {K}}_{3}}{\gamma +d} +\frac{\beta _{3}{\mathcal {K}}_{4}}{c}+\frac{\beta _{3}\xi _{2} {\mathcal {K}}_{3}}{c(\gamma +d)}\Bigg )\rho {\mathcal {K}}_{1}(1-q)(S(t)+\eta V(t))\lambda (t)\\{} & {} -\big (S^{0}+\eta V^{0}\big )\Bigg ({\mathcal {K}}_{2} +\frac{\beta _{2}{\mathcal {K}}_{3}}{\gamma +d} +\frac{\beta _{3}{\mathcal {K}}_{4}}{c}+\frac{\beta _{3}\xi _{2}{\mathcal {K}}_{3}}{c(\gamma +d)}\Bigg ) \rho \int ^{+\infty }_{0}\sigma (b)e(t,b)\text{ d }b,\\ \frac{\text{ d }{\mathcal {L}}_{i}(t)}{\text{ d }t}= & {} \big (S^{0} +\eta V^{0}\big )\int ^{+\infty }_{0}{\mathcal {F}}_{i}(a) \frac{\text{ d }i(t,a)}{\text{ d }t}\text{ d }a\\= & {} -\big (S^{0}+\eta V^{0}\big )\int ^{+\infty }_{0}{\mathcal {F}}_{i}(a) \bigg [(\theta (a)+d)i(t,a)+\frac{\partial i(t,a)}{\partial a}\bigg ]\text{ d }a\\= & {} \big (S^{0}+\eta V^{0}\big )\bigg (-\int ^{+\infty }_{0} {\mathcal {F}}_{i}(a)(\theta (a)+d)i(t,a)\text{ d }a-\int ^{+\infty }_{0} {\mathcal {F}}_{i}(a)\text{ d }i(t,a)\bigg )\\= & {} \big (S^{0}+\eta V^{0}\big )\bigg (-\int ^{+\infty }_{0} {\mathcal {F}}_{i}(a)(\theta (a)+d)i(t,a)\text{ d }b-{\mathcal {F}}_{i} (a)i(t,a)\Big |^{+\infty }_{0}\\{} & {} +\int ^{+\infty }_{0}i(t,a)\text{ d }{\mathcal {F}}_{i}(a)\bigg )\\= & {} \big (S^{0}+\eta V^{0}\big )\Bigg \{-\int ^{+\infty }_{0} {\mathcal {F}}_{i}(a)(\theta (a)+d)i(t,a)\text{ d }b+{\mathcal {F}}_{i}(0)i(t,0)\\{} & {} +\int ^{+\infty }_{0}i(t,a)\Bigg [-\Bigg (\beta _{1}(a) +\frac{\beta _{2}\theta (a)}{\gamma +d}+ \frac{\beta _{3}\xi _{1}(a)}{c}+\frac{\beta _{3}\xi _{2} \theta (a)}{c(\gamma +d)}\Bigg )\\{} & {} +(\theta (a)+d){\mathcal {F}}_{i}(a)\Bigg ]\text{ d }a\Bigg \}\\= & {} \big (S^{0}+\eta V^{0}\big )\bigg ({\mathcal {F}}_{i}(0)i(t,0) -\int ^{+\infty }_{0}\beta _{1}(a)i(t,a)\text{ d }a- \frac{\beta _{2}}{\gamma +d}\int ^{+\infty }_{0}\theta (a)i(t,a)\text{ d }a\\{} & {} -\frac{\beta _{3}}{c}\int ^{+\infty }_{0}\xi _{1}(a)i(t,a) \text{ d }a-\frac{\beta _{3}\xi _{2}}{c(\gamma +d)}\int ^{+\infty }_{0}\theta (a)i(t,a)\text{ d }a\bigg )\\ \end{aligned}$$

$$\begin{aligned}= & {} \big (S^{0}+\eta V^{0}\big )\Bigg ({\mathcal {K}}_{2} +\frac{\beta _{2}{\mathcal {K}}_{3}}{\gamma +d} +\frac{\beta _{3}{\mathcal {K}}_{4}}{c}+\frac{\beta _{3}\xi _{2} {\mathcal {K}}_{3}}{c(\gamma +d)}\Bigg )q(S(t)+\eta V(t))\lambda (t)\\{} & {} +\big (S^{0}+\eta V^{0}\big )\Bigg ({\mathcal {K}}_{2} +\frac{\beta _{2}{\mathcal {K}}_{3}}{\gamma +d} +\frac{\beta _{3}{\mathcal {K}}_{4}}{c}+\frac{\beta _{3}\xi _{2} {\mathcal {K}}_{3}}{c(\gamma +d)}\Bigg )\rho \int ^{+\infty }_{0}\sigma (b)e(t,b)\text{ d }b\\{} & {} -\big (S^{0}+\eta V^{0}\big )\bigg (\int ^{+\infty }_{0} \beta _{1}(a)i(t,a)\text{ d }a+ \frac{\beta _{2}}{\gamma +d}\int ^{+\infty }_{0}\theta (a)i(t,a)\text{ d }a\\{} & {} +\frac{\beta _{3}}{c}\int ^{+\infty }_{0}\xi _{1}(a)i(t,a) \text{ d }a+\frac{\beta _{3}\xi _{2}}{c(\gamma +d)}\int ^{+\infty }_{0} \theta (a)i(t,a)\text{ d }a\bigg ),\\ \frac{\text{ d }{\mathcal {L}}_{t}(t)}{\text{ d }t}= & {} \big (S^{0}+\eta V^{0}\big )\Bigg (\frac{\beta _{2}}{\gamma +d}+\frac{\beta _{3} \xi _{2}}{c(\gamma +d)}\Bigg )\frac{\text{ d }T(t)}{\text{ d }t}\\= & {} \big (S^{0}+\eta V^{0}\big )\Bigg (\frac{\beta _{2}}{\gamma +d} +\frac{\beta _{3}\xi _{2}}{c(\gamma +d)}\Bigg )\bigg (\int ^{+\infty }_{0} \theta (a)i(t,a)\text{ d }a-(\gamma +d)T(t)\bigg )\\= & {} \big (S^{0}+\eta V^{0}\big )\Bigg (\frac{\beta _{2}}{\gamma +d} +\frac{\beta _{3}\xi _{2}}{c(\gamma +d)}\Bigg )\int ^{+\infty }_{0} \theta (a)i(t,a)\text{ d }a\\{} & {} -\big (S^{0}+\eta V^{0}\big )\Bigg (\beta _{2} T(t)+\frac{\beta _{3}\xi _{2}}{c}T(t)\Bigg ),\\ \frac{\text{ d }{\mathcal {L}}_{w}(t)}{\text{ d }t}= & {} \big (S^{0}+\eta V^{0} \big )\frac{\beta _{3}}{c}\frac{\text{ d }W(t)}{\text{ d }t}\\= & {} \big (S^{0}+\eta V^{0}\big )\frac{\beta _{3}}{c} \bigg (\int ^{+\infty }_{0}\xi _{1}(a)i(t,a)\text{ d }a+\xi _{2}T(t)-cW(t)\bigg )\\= & {} \big (S^{0}+\eta V^{0}\big )\frac{\beta _{3}}{c} \int ^{+\infty }_{0}\xi _{1}(a)i(t,a)\text{ d }a+\big (S^{0} +\eta V^{0}\big )\frac{\beta _{3}\xi _{2}}{c}T(t)-\big (S^{0}+\eta V^{0}\big ){\beta _{3}}W(t). \end{aligned}$$

Therefore,

$$\begin{aligned} \frac{\text{ d }{\mathcal {L}}(t)}{\text{ d }t}= & {} -\frac{\alpha +d}{S^{0}}(S(t)-S^{0})^{2}+\bigg (\frac{\tau }{S^{0}} +\frac{\alpha }{V^{0}}\bigg )(S(t)-S^{0})(V(t)-V^{0})\\{} & {} -\frac{\tau +d}{V^{0}}(V(t)-V^{0})^{2}-\frac{1}{S^{0}}\lambda (t) (S(t)-S^{0})^{2}-\frac{\eta }{V^{0}}\lambda (t)(V(t)-V^{0})^{2}\\{} & {} -\lambda (t)(S(t)+\eta V(t))+\lambda (t)(S^{0}+\eta V^{0} )+{\mathcal {R}}_{0}\lambda (t)(S(t)+\eta V(t))-\lambda (t)(S^{0}+\eta V^{0}), \end{aligned}$$

where $\lambda (t)$ is given by Eq. (1). To confirm that $\frac{\text{ d }{\mathcal {L}}(t)}{\text{ d }t}$ is a negative semidefinite function, we obtain

$$\begin{aligned}{} & {} -\frac{\alpha +d}{S^{0}}(S(t)-S^{0})^{2}+\bigg (\frac{\tau }{S^{0}} +\frac{\alpha }{V^{0}}\bigg )(S(t)-S^{0})(V(t)-V^{0})-\frac{\tau +d}{V^{0}}(V(t)-V^{0})^{2}\nonumber \\{} & {} \quad =-\frac{\alpha +d}{S^{0}}\bigg [(S(t)-S^{0})^{2}-\frac{\tau V^{0} +\alpha S^{0}}{(\alpha +d)V^{0}}(S(t)-S^{0})(V(t)-V^{0})\nonumber \\{} & {} \qquad +\frac{(\tau +d)S^{0}}{(\alpha +d)V^{0}}(V(t)-V^{0})^{2}\bigg ]\nonumber \\{} & {} \quad =-\frac{\alpha +d}{S^{0}}\Bigg \{(S(t)-S^{0})^{2}-\frac{\tau V^{0} +\alpha S^{0}}{(\alpha +d)V^{0}}(S(t)-S^{0})(V(t)-V^{0})\nonumber \\{} & {} \qquad +\frac{(\tau V^{0}+\alpha S^{0})^{2}}{4(\alpha +d)^{2}(V^{0} )^{2}}(V(t)-V^{0})^{2}-\frac{(\tau V^{0}+\alpha S^{0})^{2}}{4 (\alpha +d)^{2}(V^{0})^{2}}(V(t)-V^{0})^{2}\nonumber \\{} & {} \qquad +\frac{(\tau +d)S^{0}}{(\alpha +d)V^{0}}(V(t)-V^{0})^{2}\Bigg \}\nonumber \\{} & {} \quad =-\frac{\alpha +d}{S^{0}}\Bigg \{\bigg [(S(t)-S^{0})^{2} -\frac{\tau V^{0}+\alpha S^{0}}{2(\alpha +d)V^{0}}(V(t)-V^{0})\bigg ]^{2}\nonumber \\{} & {} \qquad +\frac{4(\tau +d)(\alpha +d)S^{0}V^{0}-(\tau V^{0} +\alpha S^{0})^{2}}{4(\alpha +d)^{2}(V^{0})^{2}}(V(t)-V^{0})^{2}\Bigg \}. \end{aligned}$$

(39)

Substituting $S^{0}=\frac{\tau +d}{\alpha }V^{0}$ into Eq. (39), we have

$$\begin{aligned}{} & {} -\frac{\alpha +d}{S^{0}}\bigg \{\bigg [(S(t)-S^{0})^{2}-\frac{\tau V^{0} +\alpha S^{0}}{2(\alpha +d)V^{0}}(V(t)-V^{0})\bigg ]^{2}\\{} & {} \quad +\frac{4(\tau +d)(\alpha +d)S^{0}V^{0}-(\tau V^{0} +\alpha S^{0})^{2}}{4(\alpha +d)^{2}(V^{0})^{2}}(V(t)-V^{0})^{2}\bigg \}\\{} & {} \quad =-\frac{\alpha +d}{S^{0}}\bigg \{\bigg [(S(t)-S^{0})^{2} -\frac{\tau V^{0}+\alpha S^{0}}{2(\alpha +d)V^{0}}(V(t)-V^{0})\bigg ]^{2}\\{} & {} \qquad +\frac{\alpha d(4\tau +3d)+4d(\tau +d)^{2}}{4 \alpha (\alpha +d)^{2}}(V(t)-V^{0})^{2}\bigg \}\le 0. \end{aligned}$$

Hence, we obtain

$$\begin{aligned} \frac{\text{ d }{\mathcal {L}}(t)}{\text{ d }t}= & {} -\frac{\alpha +d}{S^{0}} \bigg \{\bigg [(S(t)-S^{0})^{2}-\frac{\tau V^{0}+\alpha S^{0}}{2( \alpha +d)V^{0}}(V(t)-V^{0})\bigg ]^{2}\\{} & {} +\frac{\alpha d(4\tau +3d) +4d(\tau +d)^{2}}{4\alpha (\alpha +d)^{2}}(V(t)-V^{0})^{2}\bigg \}\\{} & {} -\frac{1}{S^{0}}\lambda (t)(S(t)-S^{0})^{2}-\frac{\eta }{V^{0}} \lambda (t)(V(t)-V^{0})^{2}+({\mathcal {R}}_{0}-1)(S(t)+\eta V(t))\lambda (t), \end{aligned}$$

where $\lambda (t)$ is given by Eq. (1). Notice that if ${\mathcal {R}}_{0} \le 1$, then $\frac{\text{ d }{\mathcal {L}}(t)}{\text{ d }t}\le 0$, and the equality holds only for $S(t)=S^0$, $V(t)=V^0$, $e(t,b)=0$, $i(t,a)=0$, $T(t)=0$, $R(t)=0$, and $W(t)=0$. LaSalle’s Invariance Principle (LaSalle 1960) implies that the bounded solutions of System (2) converges to the largest compact invariant set of $\big \{(S(t),V(t),T(t),R(t),W(t),e(t,b),i(t,a))\in {\mathcal {D}}:\;{\text{ d }{\mathcal {L}}(t)}/{\text{ d }t}=0\big \}$. Since the disease-free equilibrium ${\mathcal {P}}^{0}$ is the only invariant set of System (2) contained entirely in $\big \{(S(t),V(t),T(t),R(t),W(t),e(t,b),i(t,a))\in {\mathcal {D}}:\;{\text{ d }{\mathcal {L}}(t)}/{\text{ d }t}=0\big \}$. Hence, the disease-free equilibrium ${\mathcal {P}}^{0}$ is globally attractive. By Theorem 2, we obtain that the disease-free equilibrium ${\mathcal {P}}^{0}$ is globally asymptotically stable when ${\mathcal {R}}_{0}<1$, and the disease-free equilibrium ${\mathcal {P}}^{0}$ is globally attractive when ${\mathcal {R}}_{0}=1$. This completes the proof. $\square$

Appendix G: Proof of Theorem 7

Let ${\textbf{p}}(x)=x-1-\ln x$, note that ${\textbf{p}}(x)$ is non-negative and continuous in $(0,+\infty )$ with a unique root at $x = 1$. Define a Lyapunov function

$$\begin{aligned} \begin{aligned} {\mathcal {G}}(t)={\mathcal {G}}_{s}(t)+{\mathcal {G}}_{v}(t)+ {\mathcal {G}}_{e}(t)+{\mathcal {G}}_{i}(t)+{\mathcal {G}}_{t}(t) +{\mathcal {G}}_{w}(t), \end{aligned} \end{aligned}$$

(40)

where

$$\begin{aligned} {\mathcal {G}}_{s}(t)= & {} S^{*}{\textbf{p}}\bigg (\frac{S(t)}{S^{*}}\bigg ), \;\;{\mathcal {G}}_{v}(t)=V^{*}{\textbf{p}}\bigg (\frac{V(t)}{V^{*}}\bigg ),\\ {\mathcal {G}}_{e}(t)= & {} \big (S^{*}+\eta V^{*}\big ){\mathcal {F}}_{a} \int ^{+\infty }_{0}{\mathcal {F}}_{e}(b)e^{*}(b){\textbf{p}} \bigg (\frac{e(t,b)}{e^{*}(b)}\bigg )\text{ d }b,\\ {\mathcal {G}}_{i}(t)= & {} \big (S^{*}+\eta V^{*}\big )\int ^{+\infty }_{0} {\mathcal {F}}_{i}(a)i^{*}(a){\textbf{p}}\bigg (\frac{i(t,a)}{i^{*}(a)} \bigg )\text{ d }a,\\ {\mathcal {G}}_{t}(t)= & {} \big (S^{*}+\eta V^{*}\big ) \Bigg (\frac{\beta _{2}}{\gamma +d}+\frac{\beta _{3}\xi _{2}}{c(\gamma +d)}\Bigg )T^{*}{\textbf{p}}\bigg (\frac{T(t)}{T^{*}}\bigg ),\\ {\mathcal {G}}_{w}(t)= & {} \big (S^{*}+\eta V^{*}\big ) \frac{\beta _{3}}{c}W^{*}{\textbf{p}}\bigg (\frac{W(t)}{W^{*}}\bigg ). \end{aligned}$$

The nonnegative function ${\mathcal {G}}(t)$ is defined with respect to the endemic equilibrium ${\mathcal {P}}^{*}$, which is a global minimum. We choose

$$\begin{aligned} {\mathcal {F}}_{a}= & {} {\mathcal {K}}_{2}+\frac{\beta _{2}{\mathcal {K}}_{3}}{\gamma +d} +\frac{\beta _{3}{\mathcal {K}}_{4}}{c}+\frac{\beta _{3}\xi _{2}{\mathcal {K}}_{3}}{c(\gamma +d)},\\ {\mathcal {F}}_{e}(b)= & {} \int ^{+\infty }_{b}\rho \sigma (\upsilon )\text{ e}^{-\int ^{\upsilon }_{b}(\rho \sigma (\varrho )+d)\text{ d }\varrho }\text{ d }\upsilon ,\\ {\mathcal {F}}_{i}(a)= & {} \int ^{+\infty }_{a}\Bigg (\beta _{1}(\upsilon )+\frac{\beta _{2}\theta (\upsilon )}{\gamma +d}+ \frac{\beta _{3}\xi _{1}(\upsilon )}{c}+\frac{\beta _{3}\xi _{2}\theta (\upsilon )}{c(\gamma +d)}\Bigg )\text{ e}^{-\int ^{\upsilon }_{a}(\theta (\varrho )+d)\text{ d }\varrho }\text{ d }\upsilon . \end{aligned}$$

Calculating the derivative of ${\mathcal {G}}_{s}(t)$, ${\mathcal {G}}_{v}(t)$, ${\mathcal {G}}_{e}(t)$, ${\mathcal {G}}_{i}(t)$, ${\mathcal {G}}_{t}(t)$, and ${\mathcal {G}}_{w}(t)$ along solutions of System (2), respectively, we can obtain

$$\begin{aligned} \frac{\text{ d }{\mathcal {G}}_{s}(t)}{\text{ d }t}= & {} \bigg (1-\frac{S^{*}}{S(t)}\bigg )\frac{\text{ d }S(t)}{\text{ d }t}\nonumber \\= & {} \varLambda \bigg (2-\frac{S(t)}{S^{*}}-\frac{S^{*}}{S(t)}\bigg )+\tau \bigg (V(t)-\frac{V(t)S^{*}}{S(t)}-\frac{V^{*}S(t)}{S^{*}}+V^{*}\bigg )\nonumber \\{} & {} -\int ^{+\infty }_{0}\beta _{1}(a)\Big (S(t)i(t,a)-S^{*}i(t,a)-S(t)i^{*}(a)+S^{*}i^{*}(a)\Big )\text{ d }a\nonumber \\{} & {} -\beta _{2}\big (T(t)S(t)-T(t)S^{*}-T^{*}S(t)+T^{*}S^{*}\big )\nonumber \\{} & {} -\beta _{3}\big (W(t)S(t)-W(t)S^{*}-W^{*}S(t)+W^{*}S^{*}\big ).\end{aligned}$$

(41)

$$\begin{aligned} \frac{\text{ d }{\mathcal {G}}_{v}(t)}{\text{ d }t}= & {} \bigg (1-\frac{V^{*}}{V(t)}\bigg )\frac{\text{ d }V(t)}{\text{ d }t}\nonumber =\alpha \bigg (S(t)-\frac{S(t)V^{*}}{V(t)}-\frac{S^{*}V(t)}{V^{*}}+S^{*}\bigg )\nonumber \\{} & {} -\eta \int ^{+\infty }_{0}\beta _{1}(a)\Big (V(t)i(t,a)-V^{*}i(t,a)-V(t)i^{*}(a)+V^{*}i^{*}(a)\Big )\text{ d }a\nonumber \\{} & {} -\eta \beta _{2}\big (T(t)V(t)-T(t)V^{*}-T^{*}V(t)+T^{*}V^{*}\big )\nonumber \\{} & {} -\eta \beta _{3}\big (W(t)V(t)-W(t)V^{*}-W^{*}V(t)+W^{*}V^{*}\big ). \end{aligned}$$

(42)

We note that

$$\begin{aligned}{} & {} \frac{\partial }{\partial b}{\textbf{p}}\bigg (\frac{e(t,b)}{e^{*}(b)}\bigg ) =\frac{1}{e^{*}(b)}\bigg (1-\frac{e^{*}(b)}{e(t,b)}\bigg )\bigg (\frac{\partial e(t,b)}{\partial b}+(\rho \sigma (b)+d)e(t,b)\bigg ),\\{} & {} \frac{\partial }{\partial a}{\textbf{p}}\bigg (\frac{i(t,a)}{i^{*}(a)}\bigg ) =\frac{1}{i^{*}(a)}\bigg (1-\frac{i^{*}(a)}{i(t,a)}\bigg )\bigg (\frac{\partial i(t,a)}{\partial a}+(\theta (a)+d)i(t,a)\bigg ). \end{aligned}$$

Thus, we obtain

$$\begin{aligned} \frac{\text{ d }{\mathcal {G}}_{e}(t)}{\text{ d }t}= & {} \big (S^{*}+\eta V^{*}\big ) {\mathcal {F}}_{a}\int ^{+\infty }_{0}{\mathcal {F}}_{e}(b)\bigg (1 -\frac{e^{*}(b)}{e(t,b)}\bigg )\frac{\partial e(t,b)}{\partial t}\text{ d }b\\= & {} -\big (S^{*}+\eta V^{*}\big ){\mathcal {F}}_{a}\int ^{+\infty }_{0} {\mathcal {F}}_{e}(b)\bigg (1-\frac{e^{*}(b)}{e(t,b)}\bigg ) \bigg (\frac{\partial e(t,b)}{\partial b}+(\rho \sigma (b)+d)e(t,b)\bigg )\text{ d }b\\= & {} -\big (S^{*}+\eta V^{*}\big ){\mathcal {F}}_{a}\int ^{+\infty }_{0} {\mathcal {F}}_{e}(b)e^{*}(b)\frac{\partial }{\partial b}{\textbf{p}} \bigg (\frac{e(t,b)}{e^{*}(b)}\bigg )\text{ d }b\\= & {} \big (S^{*}+\eta V^{*}\big ){\mathcal {F}}_{a}\bigg [{\mathcal {F}}_{e} (0)e^{*}(0){\textbf{p}}\bigg (\frac{e(t,0)}{e^{*}(0)}\bigg ) -\rho \int ^{+\infty }_{0}\sigma (b)e^{*}(b){\textbf{p}}\bigg (\frac{e(t, b)}{e^{*}(b)}\bigg )\text{ d }b\bigg ]\\= & {} \big (S^{*}+\eta V^{*}\big ){\mathcal {F}}_{a}\rho {\mathcal {K}}_{1} \bigg [(1-q)(S(t)+\eta V(t))\bigg (\int ^{+\infty }_{0}\beta _{1}(a)i(t,a) \text{ d }a+\beta _{2}T(t)\\{} & {} +\beta _{3}W(t)\bigg )-(1-q)(S^{*}+\eta V^{*})\bigg (\int ^{+\infty }_{0} \beta _{1}(a)i^{*}(a)\text{ d }a+\beta _{2}T^{*}+\beta _{3}W^{*}\bigg )\\{} & {} -(1-q)(S^{*}+\eta V^{*})\bigg (\int ^{+\infty }_{0}\beta _{1}(a)i^{*}(a) \text{ d }a+\beta _{2}T^{*}+\beta _{3}W^{*}\bigg )\ln \bigg (\frac{e(t,0)}{e^{*}(0)}\bigg )\bigg ]\\{} & {} -\big (S^{*}+\eta V^{*}\big ){\mathcal {F}}_{a}\rho \int ^{+\infty }_{0} \sigma (b)e^{*}(b){\textbf{p}}\bigg (\frac{e(t,b)}{e^{*}(b)}\bigg )\text{ d }b.\\ \frac{\text{ d }{\mathcal {G}}_{i}(t)}{\text{ d }t}= & {} \big (S^{*}+\eta V^{*}\big ) \int ^{+\infty }_{0}{\mathcal {F}}_{i}(a)\bigg (1-\frac{i^{*}(a)}{i(t,a)} \bigg )\frac{\partial i(t,a)}{\partial t}\text{ d }a\\= & {} -\big (S^{*}+\eta V^{*}\big )\int ^{+\infty }_{0}{\mathcal {F}}_{i}(a) \bigg (1-\frac{i^{*}(a)}{i(t,a)}\bigg )\bigg (\frac{\partial i(t,a)}{\partial a}+(\theta (a)+d)i(t,a)\bigg )\text{ d }a\\ \end{aligned}$$

$$\begin{aligned}= & {} -\big (S^{*}+\eta V^{*}\big )\int ^{+\infty }_{0}{\mathcal {F}}_{i} (a)i^{*}(a)\frac{\partial }{\partial a}{\textbf{p}}\bigg (\frac{i(t, a)}{i^{*}(a)}\bigg )\text{ d }a\\= & {} \big (S^{*}+\eta V^{*}\big )\bigg [{\mathcal {F}}_{i}(0)i^{*}(0) {\textbf{p}}\bigg (\frac{i(t,0)}{i^{*}(0)}\bigg ) -\int ^{+\infty }_{0}\beta _{1}(a)i^{*}(a){\textbf{p}}\bigg (\frac{i(t, a)}{i^{*}(a)}\bigg )\text{ d }a\\{} & {} -\bigg (\frac{\beta _{2}}{\gamma +d}+\frac{\beta _{3}\xi _{2}}{c(\gamma +d)}\bigg )\int ^{+\infty }_{0}\theta (a)i^{*}(a){\textbf{p}}\bigg (\frac{i(t,a)}{i^{*}(a)}\bigg )\text{ d }a\\{} & {} -\frac{\beta _{3}}{c}\int ^{+\infty }_{0} \xi _{1}(a)i^{*}(a){\textbf{p}}\bigg (\frac{i(t,a)}{i^{*}(a)}\bigg )\text{ d }a\bigg ]\\= & {} \big (S^{*}+\eta V^{*}\big ){\mathcal {F}}_{a}\bigg \{q(S(t)+\eta V(t))\bigg (\int ^{+\infty }_{0}\beta _{1}(a)i(t,a)\text{ d }a+\beta _{2}T(t) +\beta _{3}W(t)\bigg )\\{} & {} +\rho \int ^{+\infty }_{0}\sigma (b)e(t,b)\text{ d }b-\bigg [q(S^{*} +\eta V^{*})\bigg (\int ^{+\infty }_{0}\beta _{1}(a)i^{*}(a)\text{ d }a+\beta _{2}T^{*}+\beta _{3}W^{*}\bigg )\\{} & {} +\rho \int ^{+\infty }_{0}\sigma (b)e^{*}(b)\text{ d }b\bigg ]-\bigg [q(S^{*}+\eta V^{*})\bigg (\int ^{+\infty }_{0}\beta _{1}(a)i^{*}(a)\text{ d }a+\beta _{2}T^{*}+\beta _{3}W^{*}\bigg )\\{} & {} +\rho \int ^{+\infty }_{0}\sigma (b)e^{*}(b)\text{ d }b\bigg ]\ln \bigg (\frac{i(t,0)}{i^{*}(0)}\bigg )\bigg \}\\{} & {} -\big (S^{*}+\eta V^{*}\big )\bigg [\int ^{+\infty }_{0}\beta _{1}(a)i^{*}(a){\textbf{p}}\bigg (\frac{i(t,a)}{i^{*}(a)}\bigg )\text{ d }a\\{} & {} +\bigg (\frac{\beta _{2}}{\gamma +d}+\frac{\beta _{3}\xi _{2}}{c(\gamma +d)}\bigg )\int ^{+\infty }_{0}\theta (a)i^{*}(a){\textbf{p}}\bigg (\frac{i(t,a)}{i^{*}(a)}\bigg )\text{ d }a\\{} & {} +\frac{\beta _{3}}{c}\int ^{+\infty }_{0}\xi _{1}(a)i^{*}(a){\textbf{p}}\bigg (\frac{i(t,a)}{i^{*}(a)}\bigg )\text{ d }a\bigg ],\\ \frac{\text{ d }{\mathcal {G}}_{t}(t)}{\text{ d }t}= & {} \big (S^{*}+\eta V^{*}\big )\Bigg (\frac{\beta _{2}}{\gamma +d}+\frac{\beta _{3}\xi _{2}}{c(\gamma +d)}\Bigg )\bigg (1-\frac{T^{*}}{T(t)}\bigg )\frac{\text{ d }T(t)}{\text{ d }t}\\= & {} \big (S^{*}+\eta V^{*}\big )\Bigg (\frac{\beta _{2}}{\gamma +d}+\frac{\beta _{3}\xi _{2}}{c(\gamma +d)}\Bigg )\int ^{+\infty }_{0}\theta (a)i^{*}(a)\\{} & {} \bigg [\frac{i(t,a)}{i^{*}(a)}-\frac{T(t)}{T^{*}}-\frac{T^{*}i(t,a)}{T(t)i^{*}(a)}+1\bigg ]\text{ d }a\\= & {} \big (S^{*}+\eta V^{*}\big )\Bigg (\frac{\beta _{2}}{\gamma +d}+\frac{\beta _{3}\xi _{2}}{c(\gamma +d)}\Bigg )\int ^{+\infty }_{0}\theta (a)i^{*}(a)\\{} & {} \bigg [{\textbf{p}}\bigg (\frac{i(t,a)}{i^{*}(a)}\bigg )-{\textbf{p}}\bigg (\frac{T^{*}i(t,a)}{T(t)i^{*}(a)}\bigg )\bigg ]\text{ d }a\\ \end{aligned}$$

$$\begin{aligned}{} & {} -\big (S^{*}+\eta V^{*}\big )\beta _{2}T^{*}{\textbf{p}}\bigg (\frac{T(t)}{T^{*}}\bigg )-\big (S^{*}+\eta V^{*}\big )\frac{\beta _{3}\xi _{2}}{c}T^{*}{\textbf{p}}\bigg (\frac{T(t)}{T^{*}}\bigg ),\\ \frac{\text{ d }{\mathcal {G}}_{w}(t)}{\text{ d }t}= & {} \big (S^{*}+\eta V^{*}\big )\frac{\beta _{3}}{c}\bigg (1-\frac{W^{*}}{W(t)}\bigg )\frac{\text{ d }W(t)}{\text{ d }t}\\= & {} \big (S^{*}+\eta V^{*}\big )\frac{\beta _{3}}{c}\int ^{+\infty }_{0}\xi _{1}(a)i^{*}(a) \bigg [\frac{i(t,a)}{i^{*}(a)}-\frac{W(t)}{W^{*}}-\frac{W^{*}i(t,a)}{W(t)i^{*}(a)}+1\bigg ]\text{ d }a\\{} & {} +\big (S^{*}+\eta V^{*}\big )\frac{\beta _{3}\xi _{2}}{c}\bigg [\frac{T(t)}{T^{*}}-\frac{W(t)}{W^{*}}-\frac{W^{*}T(t)}{W(t)T^{*}}+1\bigg ]\\= & {} \big (S^{*}+\eta V^{*}\big )\frac{\beta _{3}}{c}\int ^{+\infty }_{0}\xi _{1}(a)i^{*}(a) \bigg [{\textbf{p}}\bigg (\frac{i(t,a)}{i^{*}(a)}\bigg )-{\textbf{p}}\bigg (\frac{W^{*}i(t,a)}{W(t)i^{*}(a)}\bigg )\bigg ]\text{ d }a\\{} & {} +\big (S^{*}+\eta V^{*}\big )\frac{\beta _{3}\xi _{2}}{c}T^{*}\bigg [{\textbf{p}}\bigg (\frac{T(t)}{T^{*}}\bigg )-{\textbf{p}}\bigg (\frac{W^{*}T(t)}{W(t)T^{*}}\bigg )\bigg ]-\big (S^{*}+\eta V^{*}\big )\beta _{3}W^{*}{\textbf{p}}\bigg (\frac{W(t)}{W^{*}}\bigg ). \end{aligned}$$

From the first two equations of System (2) and Eq. (16), we obtain

$$\begin{aligned}{} & {} \big (S^{*}+\eta V^{*}\big ){\mathcal {F}}_{a}[q+\rho (1-q){\mathcal {K}}_{1}]=1,\\{} & {} \varLambda =(S^{*}+\eta V^{*})\bigg (\int ^{+\infty }_{0}\beta _{1}(a)i^{*}(a)\text{ d }a+\beta _{2}T^{*}+\beta _{3}W^{*}\bigg )+dS^{*}+dV^{*},\\{} & {} \alpha =\frac{\eta V^{*}\Big (\int ^{+\infty }_{0}\beta _{1}(a)i^{*}(a)\text{ d }a+\beta _{2}T^{*}+\beta _{3}W^{*}\Big )+(\tau +d)V^{*}}{S^{*}}. \end{aligned}$$

Substituting the expressions of $\varLambda$ and $\alpha$ into Eqs. (41) and (42), respectively, we have

$$\begin{aligned} \frac{\text{ d }{\mathcal {G}}(t)}{\text{ d }t}= & {} \frac{\text{ d }{\mathcal {G}}_{s}(t)}{\text{ d }t}+\frac{\text{ d }{\mathcal {G}}_{v}(t)}{\text{ d }t} +\frac{\text{ d }{\mathcal {G}}_{e}(t)}{\text{ d }t}+\frac{\text{ d } {\mathcal {G}}_{i}(t)}{\text{ d }t} +\frac{\text{ d }{\mathcal {G}}_{t}(t)}{\text{ d }t}+\frac{\text{ d } {\mathcal {G}}_{w}(t)}{\text{ d }t}\\= & {} \tau V^{*}\bigg (2-\frac{S^{*}V(t)}{S(t)V^{*}}-\frac{S(t)V^{*}}{S^{*}V(t)}\bigg )+d V^{*}\bigg (3-\frac{S^{*}}{S(t)}-\frac{V(t)}{V^{*}} -\frac{S(t)V^{*}}{S^{*}V(t)}\bigg )\\{} & {} +dS^{*}\bigg (2-\frac{S(t)}{S^{*}}-\frac{S^{*}}{S(t)}\bigg )+(S^{*} +\eta V^{*})\bigg (\int ^{+\infty }_{0}\beta _{1}(a)i(t,a)\text{ d }a +\beta _{2}T(t)+\beta _{3}W(t)\bigg )\\{} & {} -\bigg (\frac{S^{*}S^{*}}{S(t)}+\eta \frac{S^{*}V^{*}}{S(t)}\bigg ) \bigg (\int ^{+\infty }_{0}\beta _{1}(a)i^{*}(a)\text{ d }a+\beta _{2}T^{*}+\beta _{3}W^{*}\bigg )\\{} & {} +\eta \bigg (V^{*}-\frac{S(t)V^{*}V^{*}}{S^{*}V(t)}\bigg ) \bigg (\int ^{+\infty }_{0}\beta _{1}(a)i^{*}(a)\text{ d }a+\beta _{2}T^{*}+\beta _{3}W^{*}\bigg )\\{} & {} -(S^{*}+\eta V^{*})\bigg [{\mathcal {F}}_{a}\rho {\mathcal {K}}_{1}(1 -q)\ln \bigg (\frac{e(t,0)}{e^{*}(0)}\bigg )+{\mathcal {F}}_{a}q\ln \bigg (\frac{i(t,0)}{i^{*}(0)}\bigg )\bigg ]\\{} & {} \times (S^{*}+\eta V^{*})\bigg (\int ^{+\infty }_{0}\beta _{1}(a)i^{*}(a) \text{ d }a+\beta _{2}T^{*}+\beta _{3}W^{*}\bigg )\\{} & {} -\big (S^{*}+\eta V^{*}\big ){\mathcal {F}}_{a}\rho \int ^{+\infty }_{0} \sigma (b)e^{*}(b){\textbf{p}}\bigg (\frac{e(t,b)}{e^{*}(b)}\bigg )\text{ d }b +\big (S^{*}+\eta V^{*}\big ){\mathcal {F}}_{a}\rho \\{} & {} \times \bigg [\int ^{+\infty }_{0}\sigma (b)e(t,b)\text{ d }b -\int ^{+\infty }_{0}\sigma (b)e^{*}(b)\text{ d }b -\int ^{+\infty }_{0}\sigma (b)e^{*}(b)\text{ d }b\ln \bigg (\frac{i(t,0)}{i^{*}(0)}\bigg )\bigg ]\\{} & {} -\big (S^{*}+\eta V^{*}\big )\bigg [\int ^{+\infty }_{0} \beta _{1}(a)i^{*}(a){\textbf{p}}\bigg (\frac{i(t,a)}{i^{*}(a)}\bigg )\text{ d }a +\frac{\beta _{3}}{c}\int ^{+\infty }_{0}\xi _{1}(a)i^{*}(a) {\textbf{p}}\bigg (\frac{i(t,a)}{i^{*}(a)}\bigg )\text{ d }a\\{} & {} +\bigg (\frac{\beta _{2}}{\gamma +d}+\frac{\beta _{3}\xi _{2}}{c(\gamma +d)}\bigg )\int ^{+\infty }_{0}\theta (a)i^{*}(a){\textbf{p}} \bigg (\frac{i(t,a)}{i^{*}(a)}\bigg )\text{ d }a\bigg ]\\{} & {} +\big (S^{*}+\eta V^{*}\big )\Bigg (\frac{\beta _{2}}{\gamma +d} +\frac{\beta _{3}\xi _{2}}{c(\gamma +d)}\Bigg )\int ^{+\infty }_{0}\theta (a)i^{*}(a)\\{} & {} \bigg [{\textbf{p}}\bigg (\frac{i(t,a)}{i^{*}(a)}\bigg ) -{\textbf{p}}\bigg (\frac{T^{*}i(t,a)}{T(t)i^{*}(a)}\bigg )\bigg ]\text{ d }a\\{} & {} -\big (S^{*}+\eta V^{*}\big )\beta _{2}T^{*}{\textbf{p}} \bigg (\frac{T(t)}{T^{*}}\bigg )-\big (S^{*}+\eta V^{*}\big ) \frac{\beta _{3}\xi _{2}}{c}T^{*}{\textbf{p}}\bigg (\frac{T(t)}{T^{*}}\bigg )\\{} & {} +\big (S^{*}+\eta V^{*}\big )\frac{\beta _{3}}{c}\int ^{+\infty }_{0}\xi _{1}(a)i^{*}(a) \bigg [{\textbf{p}}\bigg (\frac{i(t,a)}{i^{*}(a)}\bigg )-{\textbf{p}} \bigg (\frac{W^{*}i(t,a)}{W(t)i^{*}(a)}\bigg )\bigg ]\text{ d }a\\{} & {} +\big (S^{*}+\eta V^{*}\big )\frac{\beta _{3}\xi _{2}}{c}T^{*} \bigg [{\textbf{p}}\bigg (\frac{T(t)}{T^{*}}\bigg )-{\textbf{p}} \bigg (\frac{W^{*}T(t)}{W(t)T^{*}}\bigg )\bigg ]-\big (S^{*}+\eta V^{*}\big ) \beta _{3}W^{*}{\textbf{p}}\bigg (\frac{W(t)}{W^{*}}\bigg ). \end{aligned}$$

For simplicity, we let

$$\begin{aligned} \frac{\text{ d }{\mathcal {G}}(t)}{\text{ d }t}= & {} \frac{\text{ d }{\mathcal {G}}_{s}(t )}{\text{ d }t}+\frac{\text{ d }{\mathcal {G}}_{v}(t)}{\text{ d }t}+ \frac{\text{ d }{\mathcal {G}}_{e}(t)}{\text{ d }t}+\frac{\text{ d }{\mathcal {G} }_{i}(t)}{\text{ d }t}+\frac{\text{ d }{\mathcal {G}}_{t}(t)}{\text{ d }t} +\frac{\text{ d }{\mathcal {G}}_{w}(t)}{\text{ d }t}\\= & {} {\mathcal {G}}_{1}+{\mathcal {G}}_{2}+{\mathcal {G}}_{3}+{\mathcal {G}}_{4} +{\mathcal {G}}_{5}+{\mathcal {G}}_{6}, \end{aligned}$$

where

$$\begin{aligned} {\mathcal {G}}_{1}= & {} \tau V^{*}\bigg (2-\frac{S^{*}V(t)}{S(t)V^{*}} -\frac{S(t)V^{*}}{S^{*}V(t)}\bigg )+dV^{*}\bigg (3-\frac{S^{*}}{S(t)} -\frac{V(t)}{V^{*}}-\frac{S(t)V^{*}}{S^{*}V(t)}\bigg )\\{} & {} +dS^{*}\bigg (2-\frac{S(t)}{S^{*}}-\frac{S^{*}}{S(t)}\bigg )\le 0,\\ {\mathcal {G}}_{2}= & {} (S^{*}+\eta V^{*}){\mathcal {F}}_{a}q \Bigg \{\int ^{+\infty }_{0}\beta _{1}(a)S^{*}i^{*}(a)\bigg [\frac{i(t,a)}{i^{*}(a)} -\frac{S^{*}}{S(t)}-\ln \bigg (\frac{i(t,0)}{i^{*}(0)}\bigg )\bigg ]\text{ d }a\\{} & {} +\beta _{2}S^{*}T^{*}\bigg [\frac{T(t)}{T^{*}} -\frac{S^{*}}{S(t)}-\ln \bigg (\frac{i(t,0)}{i^{*}(0)}\bigg )\bigg ] +\beta _{3}S^{*}W^{*}\bigg [\frac{W(t)}{W^{*}} -\frac{S^{*}}{S(t)}-\ln \bigg (\frac{i(t,0)}{i^{*}(0)}\bigg )\bigg ]\\{} & {} +\eta \int ^{+\infty }_{0}\beta _{1}(a)V^{*}i^{*}(a)\bigg [\frac{i(t,a)}{i^{*}(a)} -\frac{V^{*}}{V(t)}-\ln \bigg (\frac{i(t,0)}{i^{*}(0)}\bigg )\bigg ]\text{ d }a\\{} & {} +\eta \beta _{2}V^{*}T^{*}\bigg [\frac{T(t)}{T^{*}} -\frac{V^{*}}{V(t)}-\ln \bigg (\frac{i(t,0)}{i^{*}(0)}\bigg )\bigg ] +\eta \beta _{3}V^{*}W^{*}\bigg [\frac{W(t)}{W^{*}} -\frac{V^{*}}{V(t)}-\ln \bigg (\frac{i(t,0)}{i^{*}(0)}\bigg )\bigg ]\Bigg \}\\= & {} (S^{*}+\eta V^{*}){\mathcal {F}}_{a}q\Bigg \{\int ^{+\infty }_{0} \beta _{1}(a)S^{*}i^{*}(a)\bigg [{\textbf{p}}\bigg (\frac{i(t,a)}{i^{*}(a)}\bigg ) -{\textbf{p}}\bigg (\frac{S^{*}}{S(t)}\bigg )\\{} & {} -{\textbf{p}}\bigg (\frac{S(t)i(t,a)i^{*}(0)}{S^{*}i^{*}(a)i(t,0)}\bigg )\bigg ]\text{ d }a\\{} & {} +\beta _{2}S^{*}T^{*}\bigg [{\textbf{p}}\bigg (\frac{T(t)}{T^{*}}\bigg ) -{\textbf{p}}\bigg (\frac{S^{*}}{S(t)}\bigg )-{\textbf{p}} \bigg (\frac{S(t)T(t)i^{*}(0)}{S^{*}T^{*}i(t,0)}\bigg )\bigg ]\\ \end{aligned}$$

$$\begin{aligned}{} & {} +\beta _{3}S^{*}W^{*}\bigg [{\textbf{p}}\bigg (\frac{W(t)}{W^{*}}\bigg ) -{\textbf{p}}\bigg (\frac{S^{*}}{S(t)}\bigg )-{\textbf{p}} \bigg (\frac{S(t)W(t)i^{*}(0)}{S^{*}W^{*}i(t,0)}\bigg )\bigg ]\\{} & {} +\eta \int ^{+\infty }_{0}\beta _{1}(a)V^{*}i^{*}(a) \bigg [{\textbf{p}}\bigg (\frac{i(t,a)}{i^{*}(a)}\bigg ) -{\textbf{p}}\bigg (\frac{V^{*}}{V(t)}\bigg )-{\textbf{p}} \bigg (\frac{V(t)i(t,a)i^{*}(0)}{V^{*}i^{*}(a)i(t,0)}\bigg )\bigg ]\text{ d }a\\{} & {} +\eta \beta _{2}V^{*}T^{*}\bigg [{\textbf{p}}\bigg (\frac{T(t)}{T^{*}}\bigg ) -{\textbf{p}}\bigg (\frac{V^{*}}{V(t)}\bigg )-{\textbf{p}} \bigg (\frac{V(t)T(t)i^{*}(0)}{V^{*}T^{*}i(t,0)}\bigg )\bigg ]\\{} & {} +\eta \beta _{3}V^{*}W^{*}\bigg [{\textbf{p}}\bigg (\frac{W(t)}{W^{*}}\bigg ) -{\textbf{p}}\bigg (\frac{V^{*}}{V(t)}\bigg )-{\textbf{p}} \bigg (\frac{V(t)W(t)i^{*}(0)}{V^{*}W^{*}i(t,0)}\bigg )\bigg ]\Bigg \}\\{} & {} +(S^{*}+\eta V^{*}){\mathcal {F}}_{a}\rho \int ^{+\infty }_{0} \sigma (b)e^{*}(b)\text{ d }b-(S^{*}+\eta V^{*}){\mathcal {F}}_{a} \rho \frac{i^{*}(0)}{i(t,0)}\int ^{+\infty }_{0}\sigma (b)e(t,b)\text{ d }b,\\ {\mathcal {G}}_{3}= & {} (S^{*}+\eta V^{*}){\mathcal {F}}_{a}\rho (1-q){\mathcal {K}}_{1}\Bigg \{\int ^{+\infty }_{0}\beta _{1}(a)S^{*}i^{*}(a)\bigg [\frac{i(t,a)}{i^{*}(a)} -\frac{S^{*}}{S(t)}-\ln \bigg (\frac{e(t,0)}{e^{*}(0)}\bigg )\bigg ]\text{ d }a\\{} & {} +\beta _{2}S^{*}T^{*}\bigg [\frac{T(t)}{T^{*}} -\frac{S^{*}}{S(t)}-\ln \bigg (\frac{e(t,0)}{e^{*}(0)}\bigg )\bigg ] +\beta _{3}S^{*}W^{*}\bigg [\frac{W(t)}{W^{*}} -\frac{S^{*}}{S(t)}-\ln \bigg (\frac{e(t,0)}{e^{*}(0)}\bigg )\bigg ]\\{} & {} +\eta \int ^{+\infty }_{0}\beta _{1}(a)V^{*}i^{*}(a)\bigg [\frac{i(t,a)}{i^{*}(a)} -\frac{V^{*}}{V(t)}-\ln \bigg (\frac{e(t,0)}{e^{*}(0)}\bigg )\bigg ]\text{ d }a\\{} & {} +\eta \beta _{2}V^{*}T^{*}\bigg [\frac{T(t)}{T^{*}} -\frac{V^{*}}{V(t)}-\ln \bigg (\frac{e(t,0)}{e^{*}(0)}\bigg )\bigg ]\\{} & {} +\eta \beta _{3}V^{*}W^{*}\bigg [\frac{W(t)}{W^{*}} -\frac{V^{*}}{V(t)}-\ln \bigg (\frac{e(t,0)}{e^{*}(0)}\bigg )\bigg ]\Bigg \}\\= & {} (S^{*}+\eta V^{*}){\mathcal {F}}_{a}\rho (1-q){\mathcal {K}}_{1} \Bigg \{\int ^{+\infty }_{0}\beta _{1}(a)S^{*}i^{*}(a)\bigg [{\textbf{p}} \bigg (\frac{i(t,a)}{i^{*}(a)}\bigg ) -{\textbf{p}}\bigg (\frac{S^{*}}{S(t)}\bigg )\\{} & {} -{\textbf{p}}\bigg (\frac{S(t)i(t,a)e^{*}(0)}{S^{*}i^{*}(a)e(t,0)} \bigg )\bigg ]\text{ d }a+\beta _{2}S^{*}T^{*}\bigg [{\textbf{p}}\bigg (\frac{T(t)}{T^{*}}\bigg ) -{\textbf{p}}\bigg (\frac{S^{*}}{S(t)}\bigg )-{\textbf{p}} \bigg (\frac{S(t)T(t)e^{*}(0)}{S^{*}T^{*}e(t,0)}\bigg )\bigg ]\\{} & {} +\beta _{3}S^{*}W^{*}\bigg [{\textbf{p}}\bigg (\frac{W(t)}{W^{*}}\bigg ) -{\textbf{p}}\bigg (\frac{S^{*}}{S(t)}\bigg )-{\textbf{p}} \bigg (\frac{S(t)W(t)e^{*}(0)}{S^{*}W^{*}e(t,0)}\bigg )\bigg ]\\{} & {} +\eta \int ^{+\infty }_{0}\beta _{1}(a)V^{*}i^{*}(a)\bigg [{\textbf{p}} \bigg (\frac{i(t,a)}{i^{*}(a)}\bigg ) -{\textbf{p}}\bigg (\frac{V^{*}}{V(t)}\bigg )-{\textbf{p}} \bigg (\frac{V(t)i(t,a)e^{*}(0)}{V^{*}i^{*}(a)e(t,0)}\bigg )\bigg ]\text{ d }a\\ \end{aligned}$$

$$\begin{aligned}{} & {} +\eta \beta _{2}V^{*}T^{*}\bigg [{\textbf{p}}\bigg (\frac{T(t)}{T^{*}}\bigg ) -{\textbf{p}}\bigg (\frac{V^{*}}{V(t)}\bigg )-{\textbf{p}} \bigg (\frac{V(t)T(t)e^{*}(0)}{V^{*}T^{*}e(t,0)}\bigg )\bigg ]\\{} & {} +\eta \beta _{3}V^{*}W^{*}\bigg [{\textbf{p}}\bigg (\frac{W(t)}{W^{*}}\bigg ) -{\textbf{p}}\bigg (\frac{V^{*}}{V(t)}\bigg )-{\textbf{p}} \bigg (\frac{V(t)W(t)e^{*}(0)}{V^{*}W^{*}e(t,0)}\bigg )\bigg ]\Bigg \},\\ {\mathcal {G}}_{4}= & {} \eta \bigg (1+\frac{V^{*}}{V(t)}-\frac{S^{*}}{S(t)} -\frac{S(t)V^{*}}{S^{*}V(t)}\bigg ) \bigg (\int ^{+\infty }_{0}\beta _{1}(a)V^{*}i^{*}(a)\text{ d }a +\beta _{2}V^{*}T^{*}+\beta _{3}V^{*}W^{*}\bigg )\\= & {} \eta \bigg [{\textbf{p}}\bigg (\frac{V^{*}}{V(t)}\bigg ) -{\textbf{p}}\bigg (\frac{S^{*}}{S(t)}\bigg ) -{\textbf{p}}\bigg (\frac{S(t)V^{*}}{S^{*}V(t)}\bigg )\bigg ]\\{} & {} \bigg (\int ^{+\infty }_{0}\beta _{1}(a)V^{*}i^{*}(a)\text{ d }a +\beta _{2}V^{*}T^{*}+\beta _{3}V^{*}W^{*}\bigg ),\\ {\mathcal {G}}_{5}= & {} \big (S^{*}+\eta V^{*}\big ){\mathcal {F}}_{a}\rho \bigg [\int ^{+\infty }_{0}\sigma (b)e(t,b)\text{ d }b-\int ^{+\infty }_{0} \sigma (b)e^{*}(b){\textbf{p}}\bigg (\frac{e(t,b)}{e^{*}(b)}\bigg )\text{ d }b\\{} & {} -\int ^{+\infty }_{0}\sigma (b)e^{*}(b)\text{ d }b-\int ^{+\infty }_{0} \sigma (b)e^{*}(b)\text{ d }b\ln \bigg (\frac{i(t,0)}{i^{*}(0)}\bigg )\bigg ]\\{} & {} -\big (S^{*}+\eta V^{*}\big )\bigg [\int ^{+\infty }_{0}\beta _{1}(a)i^{*} (a){\textbf{p}}\bigg (\frac{i(t,a)}{i^{*}(a)}\bigg )\text{ d }a +\frac{\beta _{3}}{c}\int ^{+\infty }_{0}\xi _{1}(a)i^{*}(a){\textbf{p}} \bigg (\frac{i(t,a)}{i^{*}(a)}\bigg )\text{ d }a\\{} & {} +\bigg (\frac{\beta _{2}}{\gamma +d}+\frac{\beta _{3}\xi _{2}}{c(\gamma +d)}\bigg )\int ^{+\infty }_{0}\theta (a)i^{*}(a){\textbf{p}} \bigg (\frac{i(t,a)}{i^{*}(a)}\bigg )\text{ d }a\bigg ],\\ {\mathcal {G}}_{6}= & {} \big (S^{*}+\eta V^{*}\big )\Bigg (\frac{\beta _{2}}{\gamma +d}+\frac{\beta _{3}\xi _{2}}{c(\gamma +d)}\Bigg )\int ^{+\infty }_{0}\theta (a)i^{*}(a) \bigg [{\textbf{p}}\bigg (\frac{i(t,a)}{i^{*}(a)}\bigg )-{\textbf{p}} \bigg (\frac{T^{*}i(t,a)}{T(t)i^{*}(a)}\bigg )\bigg ]\text{ d }a\\{} & {} -\big (S^{*}+\eta V^{*}\big )\beta _{2}T^{*}{\textbf{p}}\bigg (\frac{T(t)}{T^{*}}\bigg )-\big (S^{*}+\eta V^{*}\big )\frac{\beta _{3}\xi _{2}}{c} T^{*}{\textbf{p}}\bigg (\frac{T(t)}{T^{*}}\bigg )\\{} & {} +\big (S^{*}+\eta V^{*}\big )\frac{\beta _{3}}{c}\int ^{+\infty }_{0} \xi _{1}(a)i^{*}(a) \bigg [{\textbf{p}}\bigg (\frac{i(t,a)}{i^{*}(a)}\bigg )-{\textbf{p} }\bigg (\frac{W^{*}i(t,a)}{W(t)i^{*}(a)}\bigg )\bigg ]\text{ d }a\\{} & {} +\big (S^{*}+\eta V^{*}\big )\frac{\beta _{3}\xi _{2}}{c}T^{*} \bigg [{\textbf{p}}\bigg (\frac{T(t)}{T^{*}}\bigg )-{\textbf{p}} \bigg (\frac{W^{*}T(t)}{W(t)T^{*}}\bigg )\bigg ]-\big (S^{*}+\eta V^{*}\big )\beta _{3}W^{*}{\textbf{p}}\bigg (\frac{W(t)}{W^{*}}\bigg ). \end{aligned}$$

Note that

$$\begin{aligned}{} & {} \big (S^{*}+\eta V^{*}\big ){\mathcal {F}}_{a}\rho \bigg [\int ^{+\infty }_{0}\sigma (b)e(t,b)\text{ d }b-\int ^{+\infty }_{0}\sigma (b)e^{*}(b){\textbf{p}}\bigg (\frac{e(t,b)}{e^{*}(b)}\bigg )\text{ d }b\\{} & {} \quad -\int ^{+\infty }_{0}\sigma (b)e^{*}(b)\text{ d }b-\int ^{+\infty }_{0}\sigma (b)e^{*}(b)\text{ d }b\ln \bigg (\frac{i(t,0)}{i^{*}(0)}\bigg )\\{} & {} \quad +\int ^{+\infty }_{0}\sigma (b)e^{*}(b)\text{ d }b-\frac{i^{*}(0)}{i(t,0)}\int ^{+\infty }_{0}\sigma (b)e(t,b)\text{ d }b\bigg ]\\{} & {} \quad =\big (S^{*}+\eta V^{*}\big ){\mathcal {F}}_{a}\rho \int ^{+\infty }_{0}\sigma (b)e^{*}(b)\bigg [-\frac{i^{*}(0)e(t,b)}{i(t,0)e^{*}(b)}+1+\ln \bigg (\frac{i^{*}(0)e(t,b)}{i(t,0)e^{*}(b)}\bigg )\bigg ]\text{ d }b\\{} & {} \quad =-\big (S^{*}+\eta V^{*}\big ){\mathcal {F}}_{a}\rho \int ^{+\infty }_{0}\sigma (b)e^{*}(b){\textbf{p}}\bigg (\frac{i^{*}(0)e(t,b)}{i(t,0)e^{*}(b)}\bigg )\text{ d }b. \end{aligned}$$

Hence, we have

$$\begin{aligned} \sum ^{6}_{i=2}{\mathcal {G}}_{i}= & {} -(S^{*}+\eta V^{*}){\mathcal {F}}_{a}q\Bigg [\int ^{+\infty }_{0}\beta _{1}(a)S^{*}i^{*}(a) {\textbf{p}}\bigg (\frac{S(t)i(t,a)i^{*}(0)}{S^{*}i^{*}(a)i(t,0)}\bigg )\text{ d }a\nonumber \\{} & {} +\beta _{2}S^{*}T^{*}{\textbf{p}}\bigg (\frac{S(t)T(t)i^{*}(0)}{S^{*}T^{*}i(t,0)}\bigg ) +\beta _{3}S^{*}W^{*}{\textbf{p}}\bigg (\frac{S(t)W(t)i^{*}(0)}{S^{*}W^{*}i(t,0)}\bigg )\nonumber \\{} & {} +\eta \int ^{+\infty }_{0}\beta _{1}(a)V^{*}i^{*}(a){\textbf{p}}\bigg (\frac{V(t)i(t,a)i^{*}(0)}{V^{*}i^{*}(a)i(t,0)}\bigg )\text{ d }a +\eta \beta _{2}V^{*}T^{*}{\textbf{p}}\bigg (\frac{V(t)T(t)i^{*}(0)}{V^{*}T^{*}i(t,0)}\bigg )\nonumber \\{} & {} +\eta \beta _{3}V^{*}W^{*}{\textbf{p}}\bigg (\frac{V(t)W(t)i^{*}(0)}{V^{*}W^{*}i(t,0)}\bigg )\Bigg ]-(S^{*}+\eta V^{*}){\mathcal {F}}_{a}\rho (1-q){\mathcal {K}}_{1}\nonumber \\{} & {} \times \Bigg [\int ^{+\infty }_{0}\beta _{1}(a)S^{*}i^{*}(a){\textbf{p}}\bigg (\frac{S(t)i(t,a)e^{*}(0)}{S^{*}i^{*}(a)e(t,0)}\bigg )\text{ d }a+\beta _{2}S^{*}T^{*}{\textbf{p}}\bigg (\frac{S(t)T(t)e^{*}(0)}{S^{*}T^{*}e(t,0)}\bigg )\nonumber \\{} & {} +\beta _{3}S^{*}W^{*}{\textbf{p}}\bigg (\frac{S(t)W(t)e^{*}(0)}{S^{*}W^{*}e(t,0)}\bigg ) +\eta \int ^{+\infty }_{0}\beta _{1}(a)V^{*}i^{*}(a){\textbf{p}}\bigg (\frac{V(t)i(t,a)e^{*}(0)}{V^{*}i^{*}(a)e(t,0)}\bigg )\text{ d }a\nonumber \\{} & {} +\eta \beta _{2}V^{*}T^{*}{\textbf{p}}\bigg (\frac{V(t)T(t)e^{*}(0)}{V^{*}T^{*}e(t,0)}\bigg ) +\eta \beta _{3}V^{*}W^{*}{\textbf{p}}\bigg (\frac{V(t)W(t)e^{*}(0)}{V^{*}W^{*}e(t,0)}\bigg )\Bigg ]\\{} & {} -S^{*}{\textbf{p}}\bigg (\frac{S^{*}}{S(t)}\bigg )\bigg (\int ^{+\infty }_{0}\beta _{1}(a)i^{*}(a)\text{ d }a +\beta _{2}T^{*}+\beta _{3}W^{*}\bigg )\nonumber \\{} & {} -\eta V^{*}\bigg [{\textbf{p}}\bigg (\frac{S^{*}}{S(t)}\bigg ) +{\textbf{p}}\bigg (\frac{S(t)V^{*}}{S^{*}V(t)}\bigg )\bigg ] \bigg (\int ^{+\infty }_{0}\beta _{1}(a)i^{*}(a)\text{ d }a +\beta _{2}T^{*}+\beta _{3}W^{*}\bigg )\nonumber \\{} & {} -\big (S^{*}+\eta V^{*}\big )\Bigg [{\mathcal {F}}_{a}\rho \int ^{+\infty }_{0}\sigma (b)e^{*}(b){\textbf{p}}\bigg (\frac{i^{*}(0)e(t,b)}{i(t,0)e^{*}(b)}\bigg )\text{ d }b\nonumber \\{} & {} +\Bigg (\frac{\beta _{2}}{\gamma +d}+\frac{\beta _{3}\xi _{2}}{c(\gamma +d)}\Bigg )\int ^{+\infty }_{0}\theta (a)i^{*}(a) {\textbf{p}}\bigg (\frac{T^{*}i(t,a)}{T(t)i^{*}(a)}\bigg )\text{ d }a\nonumber \\{} & {} +\frac{\beta _{3}}{c}\int ^{+\infty }_{0}\xi _{1}(a)i^{*}(a) {\textbf{p}}\bigg (\frac{W^{*}i(t,a)}{W(t)i^{*}(a)}\bigg )\text{ d }a +\frac{\beta _{3}\xi _{2}}{c}T^{*}{\textbf{p}}\bigg (\frac{W^{*}T(t)}{W(t)T^{*}}\bigg )\Bigg ].\nonumber \end{aligned}$$

(43)

We find that all terms in Eq. (43) have the property of the function ${\textbf{p}}(x)=x-1-\ln x$. This means that positive-definite function ${\mathcal {G}}(t)$ has negative derivative $\text{ d }{\mathcal {G}}(t)/\text{d }t$. Furthermore, the equality $\text{ d }{\mathcal {G}}(t)/\text{d }t=0$ holds if and only if $S(t)=S^{*}$, $V(t)=V^{*}$, $e(t,b)=e^{*}(b)$, $i(t,a)=i^{*}(a)$, $T(t)=T^{*}$, $R(t)=R^{*}$, and $W(t)=W^{*}$. LaSalle’s Invariance Principle (LaSalle 1960) implies that the bounded solutions of System (2) converge to the largest compact invariant set of $\big \{(S(t),V(t),T(t),R(t),W(t),e(t,b),i(t,a))\in {\mathcal {D}}:\;{\text{ d }{\mathcal {G}}(t)}/{\text{ d }t}=0\big \}$. Since the endemic equilibrium ${\mathcal {P}}^{*}$ is the only invariant set of System (2) contained entirely in $\big \{(S(t),V(t),T(t),R(t),W(t),e(t,b),i(t,a))\in {\mathcal {D}}:\;{\text{ d }{\mathcal {G}}(t)}/{\text{ d }t}=0\big \}$. Hence, every solution of System (2) in set ${\mathcal {D}}\backslash \{{\mathcal {P}}^{0}\}$ tends to the endemic equilibrium ${\mathcal {P}}^{*}$, which is globally attractive when it exists. This completes the proof. $\square$

Appendix H: Numerical method for System (2)

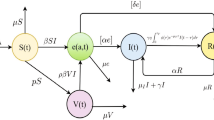
To compute the numerical solution, we use the forward/backward finite difference method for time and age to discretize System (2) (Kenne et al. 2021; Martcheva 2015). We define the finite domain with respect to time and age as follows

$$\begin{aligned} \overline{{\textbf{D}}}=\Big \{(t,a,b):0\le t\le {\mathbb {T}},\;0\le a\le {\mathbb {K}}_{a},\;0\le b\le {\mathbb {K}}_{b}\Big \}. \end{aligned}$$

To discretize the model, we divide the time interval $(0,{\mathbb {T}})$ into ${\mathcal {T}}$ subintervals $(t_{n}, t_{n+1})$ with a time step $\varDelta t=t_{n+1}-t_{n}$, for $n = 0, 1, 2,\cdots , {\mathcal {T}}-1$. Similarly, we also divide the latent age interval $(0,{\mathbb {K}}_{b})$ and the infected age interval $(0,{\mathbb {K}}_{a})$ into $K_{b}$ subintervals $(b_{k},b_{k+1})$ with a time step $\varDelta b=b_{k+1}-b_{k}$ and $K_{a}$ subintervals $(a_{j},a_{j+1})$ with a time step $\varDelta a=a_{j+1}-a_{j}$, respectively, for $k=0, 1, 2, \cdots , K_{b}-1$, $j=0, 1, 2, \cdots , K_{a}-1$. We define the symbol substitution rules as follows

$$\begin{aligned}{} & {} S_{n}=S(t_{n}),\;V_{n}=V(t_{n}),\;T_{n}=T(t_{n}),\;R_{n}=R(t_{n}), \;W_{n}=W(t_{n}),\;i^{j}_{n}=i(t_{n},a_{j}),\\{} & {} e^{k}_{n}=e(t_{n},b_{k}),\;\beta ^{j}_{1}=\beta _{1}(a_{j}), \;\theta ^{j}=\theta (a_{j}),\;\xi ^{j}_{1}=\xi _{1}(a_{j}),\; \sigma ^{k}=\sigma (b_{k}). \end{aligned}$$

Next, we use the trapezoidal rule to approximate several integral expressions in System (2), that is,

$$\begin{aligned}{} & {} \int ^{+\infty }_{0}\beta _{1}(a)i(t,a)\text{ d }a\approx \varDelta a\bigg (\frac{\beta ^{0}_{1}i(t,a_{0})+\beta ^{K_{a}-1}_{1}i(t,a_{K_{a}-1})}{2}\bigg )+\varDelta a\sum ^{K_{a}-2}_{j=1}\beta ^{j}_{1}i(t,a_{j}),\\{} & {} \int ^{+\infty }_{0}\theta (a)i(t,a)\text{ d }a\approx \varDelta a\bigg (\frac{\theta ^{0}i(t,a_{0})+\theta ^{K_{a}-1}i(t,a_{K_{a}-1})}{2}\bigg )+\varDelta a\sum ^{K_{a}-2}_{j=1}\theta ^{j}i(t,a_{j}),\\{} & {} \int ^{+\infty }_{0}\xi _{1}(a)i(t,a)\text{ d }a\approx \varDelta a\bigg (\frac{{\xi ^{0}_{1}}i(t,a_{0})+{\xi ^{K_{a}-1}_{1}}i(t,a_{K_{a}-1})}{2}\bigg )+\varDelta a\sum ^{K_{a}-2}_{j=1}{\xi ^{j}_{1}}i(t,a_{j}),\\{} & {} \int ^{+\infty }_{0}\sigma (b)e(t,b)\text{ d }b\approx \varDelta b\bigg (\frac{{\sigma }^{0}e(t,b_{0})+{\sigma }^{K_{b}-1}e(t,b_{K_{b}-1})}{2}\bigg )+\varDelta b\sum ^{K_{b}-2}_{k=1}{\sigma }^{k}e(t,b_{k}). \end{aligned}$$

Hence, the discrete form of System (2) can be expressed as

$$\begin{aligned}{} & {} \frac{S_{n+1}-S_{n}}{\varDelta t}=\varLambda +\tau V_{n}+\delta R_{n}-\lambda _{n}S_{n}-(\alpha +d)S_{n},\nonumber \\{} & {} \frac{V_{n+1}-V_{n}}{\varDelta t}=\alpha S_{n}-\eta \lambda _{n}V_{n}-(\tau +d)V_{n},\nonumber \\{} & {} \frac{T_{n+1}-T_{n}}{\varDelta t}=\varDelta a\bigg (\frac{\theta ^{0}i^{0}_{n}+\theta ^{K_{a}-1}i^{K_{a}-1}_{n}}{2}\bigg )+\varDelta a\sum ^{K_{a}-2}_{j=1}\theta ^{j}i^{j}_{n}-(\gamma +d)T_{n},\nonumber \\{} & {} \frac{R_{n+1}-R_{n}}{\varDelta t}=\gamma T_{n}-(\delta +d)R_{n},\nonumber \\{} & {} \frac{W_{n+1}-W_{n}}{\varDelta t}=\varDelta a\bigg (\frac{{\xi ^{0}_{1}}i^{0}_{n}+{\xi ^{K_{a}-1}_{1}}i^{K_{a}-1}_{n}}{2}\bigg )+\varDelta a\sum ^{K_{a}-2}_{j=1}{\xi ^{j}_{1}}i^{j}_{n}+\xi _{2}T_{n}-cW_{n},\nonumber \\{} & {} \frac{e^{k}_{n+1}-e^{k}_{n}}{\varDelta t}+\frac{e^{k}_{n}-e^{k-1}_{n}}{\varDelta b}=-(\rho \sigma ^{k}+d)e^{k}_{n},\nonumber \\{} & {} \frac{i^{j}_{n+1}-i^{j}_{n}}{\varDelta t}+\frac{i^{j}_{n}-i^{j-1}_{n}}{\varDelta a}=-(\theta ^{j}+d)i^{j}_{n},\nonumber \\{} & {} e^{0}_{n}=(1-q)\lambda _{n}\big (S_{n}+\eta V_{n}\big ),\nonumber \\{} & {} i^{0}_{n}=q\lambda _{n}\big (S_{n}+\eta V_{n}\big )+\rho \varDelta b\bigg (\frac{{\sigma }^{0}e^{0}_{n}+{\sigma }^{K_{b}-1}e^{K_{b}-1}_{n}}{2}\bigg )+\rho \varDelta b\sum ^{K_{b}-2}_{k=1}{\sigma }^{k}e^{k}_{n},\nonumber \\{} & {} e^{k}_{0}=e_{0}(b_{k}),i^{j}_{0}=i_{0}(a_{j}), \end{aligned}$$

(44)

where $\lambda _{n}=\varDelta a\Big (\frac{\beta ^{0}_{1}i^{0}_{n}+\beta ^{K_{a}-1}_{1}i^{K_{a}-1}_{n}}{2}\Big )+\varDelta a\sum ^{K_{a}-2}_{j=1}\beta ^{j}_{1}i^{j}_{n}+\beta _{2}T_{n}+\beta _{3}W_{n}$. After some algebraic manipulation, the first seven equations of System (44) can be rewritten as

$$\begin{aligned}{} & {} S_{n+1}=S_{n}+\varDelta t\big [\varLambda +\tau V_{n}+\delta R_{n}-\lambda _{n}S_{n}-(\alpha +d)S_{n}\big ],\\{} & {} V_{n+1}=V_{n}+\varDelta t\big [\alpha S_{n}-\eta \lambda _{n}V_{n}-(\tau +d)V_{n}\big ],\\{} & {} T_{n+1}=T_{n}+\varDelta t\bigg [\varDelta a\bigg (\frac{\theta ^{0}i^{0}_{n}+\theta ^{K_{a}-1}i^{K_{a}-1}_{n}}{2}\bigg )+\varDelta a\sum ^{K_{a}-2}_{j=1}\theta ^{j}i^{j}_{n}-(\gamma +d)T_{n}\bigg ],\\{} & {} R_{n+1}=R_{n}+\varDelta t\big [\gamma T_{n}-(\delta +d)R_{n}\big ],\\{} & {} W_{n+1}=W_{n}+\varDelta t\bigg [\varDelta a\bigg (\frac{{\xi ^{0}_{1}}i^{0}_{n}+{\xi ^{K_{a}-1}_{1}}i^{K_{a}-1}_{n}}{2}\bigg )+\varDelta a\sum ^{K_{a}-2}_{j=1}{\xi ^{j}_{1}}i^{j}_{n}+\xi _{2}T_{n}-cW_{n}\bigg ],\\{} & {} e^{k}_{n+1}=\bigg [1-\frac{\varDelta t}{\varDelta b}-\varDelta t(\rho \sigma ^{k}+d)\bigg ]e^{k}_{n}+\frac{\varDelta t}{\varDelta b}e^{k-1}_{n},\\{} & {} i^{j}_{n+1}=\bigg [1-\frac{\varDelta t}{\varDelta a}-\varDelta t(\theta ^{j}+d)\bigg ]i^{j}_{n}+\frac{\varDelta t}{\varDelta a}i^{j-1}_{n},\\{} & {} i^{0}_{n}=q\lambda _{n}\big (S_{n}+\eta V_{n}\big )+\rho \varDelta b\bigg (\frac{{\sigma }^{0}e^{0}_{n}+{\sigma }^{K_{b}-1}e^{K_{b}-1}_{n}}{2}\bigg )+\rho \varDelta b\sum ^{K_{b}-2}_{k=1}{\sigma }^{k}e^{k}_{n},\\{} & {} e^{0}_{n}=(1-q)\lambda _{n}\big (S_{n}+\eta V_{n}\big ). \end{aligned}$$

The explicit expressions for $i^{0}_{n}$ and $e^{0}_{n}$ are as follows

$$\begin{aligned} i^{0}_{n}=\frac{\left( \begin{aligned}&\Bigg [\frac{\rho \varDelta b\sigma ^{0}(1-q)(S_{n}+\eta V_{n})}{2}+q(S_{n}+\eta V_{n})\Bigg ]\Bigg (\varDelta a\frac{\beta ^{K_{a}-1}_{1}i^{K_{a}-1}_{n}}{2}+\varDelta a\sum ^{K_{a}-2}_{j=1}\beta ^{j}_{1}i^{j}_{n}+\beta _{2}T_{n}+\beta _{3}W_{n}\Bigg )\\&+\rho \varDelta b\Bigg (\frac{{\sigma }^{K_{b}-1}e^{K_{b}-1}_{n}}{2}+\sum ^{K_{b}-2}_{k=1}{\sigma }^{k}e^{k}_{n}\Bigg ) \end{aligned}\right) }{1-\frac{q(S_{n}+\eta V_{n})\varDelta a\beta ^{0}_{1}}{2}-\frac{\rho \sigma ^{0}(1-q)(S_{n}+\eta V_{n})\varDelta a\varDelta b\beta ^{0}_{1}}{4}}, \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} e^{0}_{n}=(1-q)(S_{n}+\eta V_{n})\Bigg (\varDelta a\frac{\beta ^{0}_{1}i^{0}_{n} +\beta ^{K_{a}-1}_{1}i^{K_{a}-1}_{n}}{2}+\varDelta a\sum ^{K_{a}-2}_{j=1}\beta ^{j}_{1} i^{j}_{n}+\beta _{2}T_{n}+\beta _{3}W_{n}\Bigg ). \end{aligned} \end{aligned}$$

Appendix I: MCMC method for parameter estimation

Let $\varepsilon$ be the fitting error, and $\varepsilon$ follows the additive independent Gaussian distribution with mean zero and unknown variance $\xi ^{2}$, which is based on the result of the Central Limit Theorem. Then, the observations y can be expressed as follows

$$\begin{aligned} y=f(x,{\widehat{\chi }})+\varepsilon ,\;\;\varepsilon \sim N(0,I\xi ^{2}), \end{aligned}$$

(45)

where $f(x,{\widehat{\chi }})$ is the nonlinear model ($\theta (a)$, ${\mathcal {Z}}_{1}(0,a)$, or ${\mathcal {Z}}_{2}(j,a)$); x are the independent variables; ${\widehat{\chi }}$ are the unknown parameters and initial values.

For ${\hat{\varPsi }}$ independent identically distributed observations, the likelihood function $p(y|{\hat{\chi }}, \xi ^{2})$ from Eq. (45) with a Gaussian error model is

$$\begin{aligned} p(y|{\hat{\chi }}, \xi ^{2})=\Bigg (\frac{1}{\sqrt{2\pi \xi ^2}}\Bigg )^{{\hat{\varPsi }}}\exp \Bigg [\frac{-\textrm{SS}({\hat{\chi }})}{2\xi ^{2}}\Bigg ], \end{aligned}$$

where $\textrm{SS}({\hat{\chi }})$ represents the sum of squares function

$$\begin{aligned} \textrm{SS}({\hat{\chi }})=\overset{{\hat{\varPsi }}}{\underset{i=1}{\sum }} \Big [(y_{i}-f({\hat{\chi }})_{i})^{2}\Big ]. \end{aligned}$$

For simplicity, we assume that the unknown parameters ${\hat{\chi }}$ are an independent Gaussian prior specification, that is,

$$\begin{aligned} {\hat{\chi }}_{j}\sim N(\nu _{j}, \varphi ^{2}_{j}),\;\;j = 1,\ldots , {\hat{M}}. \end{aligned}$$

where ${\hat{M}}$ is the number of unknown parameters. For $\xi ^{-2}$, a Gamma distribution is used as a prior, that is,

$$\begin{aligned} p(\xi ^{-2})\sim \Gamma \Bigg (\frac{n_{0}}{2}, \frac{n_{0}}{2}S^{2}_{0}\Bigg ), \end{aligned}$$

where $S^2_0$ and $n_0$ are the prior mean and prior accuracy of variance $\xi ^{2}$, respectively.

The conditional distribution $p(\xi ^{-2}|y, {\hat{\chi }})$ can be expressed as follows

$$\begin{aligned} \begin{aligned} p(\xi ^{-2}|y, {\hat{\chi }})\propto \big (\xi ^{-2}\big )^{-\frac{{\hat{\varPsi }} +n_{0}}{2}-1}\exp \bigg [-\frac{\textrm{SS}({\hat{\chi }})+n_{0}S^{2}_{0}}{2\xi ^{-2}}\bigg ]. \end{aligned} \end{aligned}$$

Using the conditional conjugacy property of the Gamma distribution, the conditional distribution $p(\xi ^{-2}|y, {\hat{\chi }})$ is also a Gamma distribution with

$$\begin{aligned} p(\xi ^{-2}|y, {\hat{\chi }})=\Gamma \Bigg (\frac{{\hat{\varPsi }}+n_{0}}{2}, \frac{\textrm{SS}({\hat{\chi }})+n_{0}S^{2}_{0}}{2}\Bigg ), \end{aligned}$$

according to which we sample and update $\xi ^{-2}$ for other parameters within each run of Metropolis Hastings simulations. Since we assume independent Gaussian prior specification for parameters ${\hat{\chi }}$, the prior sum of squares for the given parameters ${\hat{\chi }}$ can be calculated as follows

$$\begin{aligned} \textrm{SS}_{\textrm{pri}}({\hat{\chi }})=\overset{{\hat{M}}}{\underset{i=1}{\sum }} \Bigg [\frac{{\hat{\chi }}_{i}-\nu _{i}}{\varphi _{i}}\Bigg ]^{2}. \end{aligned}$$

Then the posterior for the unknown parameters ${\hat{\chi }}$ can be estimated as

$$\begin{aligned} \begin{aligned} p({\hat{\chi }}|y, \xi ^{2})\propto \exp \Bigg [-\frac{1}{2} \bigg (\frac{\textrm{SS}({\hat{\chi }})}{\xi ^2}+\textrm{SS}_{\textrm{pri}}({\hat{\chi }})\bigg )\Bigg ]. \end{aligned} \end{aligned}$$

In the simulation, we use Delayed Rejection Adaptive Metropolis (DRAM) algorithm to generate efficient chains of estimated parameters (Haario et al. 2006). The variance of measured components $\theta (a)$, ${\mathcal {Z}}_{1}(0,a)$, and ${\mathcal {Z}}_{2}(j,a)$ are given by inverse gamma distribution with hyper-parameters (0.01, 0.04), where 0.01 is the initial error variance, which is updated by inverse gamma distribution (Tang et al. 2018). Prior information of unknown parameters is given by $\theta _{1}\in (0, 1000)$, $\theta _{2}\in (0, 1000)$, $\varpi _{1}\in (0, 10000)$, $\varpi _{2}\in (0, 1000)$, $\sigma _{1}\in (0, 10)$, $\sigma _{2}\in (0, 1000)$, $\beta _{1}\in (0, 1\times 10^{-7})$, $\beta _{3}\in (0, 1\times 10^{-7})$, $\xi _{2}\in (0.6, 1)$, $\zeta _{1}\in (0, 1000)$, $T(0)\in (10000, 50000)$, $R(0)\in (2\times 10^{6}, 1\times 10^{7})$, $W(0)\in (1\times 10^{4}, 1\times 10^{5})$, and the proposal density follows a multivariate normal distribution.