Modeling and Research on an Immuno-Epidemiological Coupled System with Coinfection

Abstract

In this paper, a two-strain model with coinfection that links immunological and epidemiological dynamics across scales is formulated. On the with-in host scale, the two strains eliminate each other with the strain having the larger immunological reproduction number persisting. However, on the population scale coinfection is a common occurrence. Individuals infected with strain one can become coinfected with strain two and similarly for individuals originally infected with strain two. The immunological reproduction numbers $R_{j}$, the epidemiological reproduction numbers ${\mathcal {R}}_{j}$ and invasion reproduction numbers ${\mathcal {R}}_{j}^{i}$ are computed. Besides the disease-free equilibrium, there are strain one and strain two dominance equilibria. The disease-free equilibrium is locally asymptotically stable when the epidemiological reproduction numbers ${\mathcal {R}}_{j}$ are smaller than one. In addition, each strain dominance equilibrium is locally asymptotically stable if the corresponding epidemiological reproduction number is larger than one and the invasion reproduction number of the other strain is smaller than one. The coexistence equilibrium exists when all the reproduction numbers are greater than one. Simulations suggest that when both invasion reproduction numbers are smaller than one, bistability occurs with one of the strains persisting or the other, depending on initial conditions.

1 Introduction

Infectious diseases are caused by parasites (viruses, bacteria, etc.) and can spread from person to person. Infectious diseases have always been a great enemy of human health. Historically, infectious disease epidemics have brought great disasters to human survival, national economies and people’s livelihood. For example, during 1519–1530, the prevalence of measles and other infectious diseases reduced the number of Indians in Mexico from 30 million to 3 million. The black death (bubonic plague) had four large-scale epidemics in Europe (AD 600, 1346–1350, 1665–1666, 1720–1722), and each time caused a significant decline in the European population. And the outbreak of novel coronavirus at the end of 2019 in early 2020 has brought great impact to the global economy and people’s lives. For a long time, mankind has waged an indomitable struggle against various infectious diseases and made brilliant achievements. For example, smallpox, which has been rampant for nearly a thousand years, has finally been eliminated. Further, leprosy, poliomyelitis, diphtheria, measles, pertussis and other diseases have been curbed.

However, completely conquering epidemics is still a task for the future. The world health report issued by the World Health Organization shows that infectious diseases are still the primary killer of humans. A variety of infectious diseases, such as cholera, dysentery, malaria, sexually transmitted diseases, tuberculosis, influenza and so on, are still prevalent all over the world. In addition, with the rapid development of livestock and poultry breeding industries and the prosperity of international and domestic trade, a variety of infectious diseases (such as avian influenza, mouth kick disease, etc.) which transmit between animals and affect humans are widely prevalent in the world, which has aroused the extensive attention of governments, medical experts and mathematicians.

In recent years, the research progress in infectious disease dynamics modeling, virus dynamics modeling and immune system dynamics modeling has been very rapid throughout the world. A large number of mathematical models are used to analyze the spread of various infectious diseases, virus infection, immune response and other issues. Most of these models are suitable for studying the general laws of various infectious diseases, viruses and immunity. Infectious disease dynamics mainly takes the total population of a country or a region as the research object. The population of the country or region is divided into several disjoint subclasses, such as susceptible class, infected class, moving out class and so on. Using a flow chart, the corresponding disease transmission model is established and studied. Immune system dynamics mainly takes an individual as the research object. Considering the infection of a virus of certain cells in this individual, this kind of cells in this individual is divided into healthy cells and infected cells, and the corresponding immune system dynamics is established and studied.

In reference (Levin and Pimentel 1981), Levin and Pimental introduced the possibility of superinfection: when an individual infected by virus 1 enters into a contact with an individual who has been infected by virus 2, it is likely that, say, the first individual becomes infected also with virus 2; furthermore, it is assumed that in this case, the individual super-infected with virus 2 will lose the original virus; in other words, no individuals are infected with more than one virus at the same time. Intuitively, when virus 1 has the smaller reproduction number, superinfection can occur. A multi-scale immuno-epidemiological model of super-infection has been studied in Martcheva and Li (2013). However, a more realistic situation is that individuals can be infected with more than one virus at the same time, that is, coinfection may occur. When an individual with virus 1 contacts an individual infected by virus 2, this individual will become coinfected by virus 1 and virus 2. Such infected individuals may continue to carry two viruses or become only one virus due to the competition between the two viruses. Coinfection and super-infection models both within-host and between-host have been studied before (Alizon 2013; Martcheva 2015; Candela et al. 2009).

Immuno-epidemiology has been drawing a significant interest lately (Hellriegel 2001), and the first immuno-epidemiological model of nested type has been developed by Gilchrist and Sasaki (2002). Since then, a number of different multi-scale immuno-epidemiological models have been developed and investigated (Shen et al. 2015; Ratchford and Wang 2019; Hu and Lou 2016; Mideo et al. 2008; Feng et al. 2012; Coombs et al. 2007; Xue and Xiao 2020; Shen et al. 2019, 2019; Martcheva and Pilyugin 2006; Martcheva 2011; Cai et al. 2017). Typical questions addressed with immuno-epidemiological models are the impact of the within-host dynamics on the between-host dynamics (Martcheva 2011; Cai et al. 2017) and the questions related to the evolution of the pathogens (Alizon 2013; Mideo et al. 2008; Coombs et al. 2007). Evolutionary questions often lead to multi-strain frameworks where the competitive exclusion (Dang et al. 2016) and coexistence (Martcheva and Li 2013) of strains is investigated. Super-infection (Martcheva and Li 2013), coinfection (Candela et al. 2009) and mutation (Ball et al. 2007) are all mechanisms that can lead to coexistence of pathogen variants.

In this paper, we strive to extend our results in Martcheva and Li (2013). We formulate a two-strain immuno-epidemiological model coupling the immune process in human body, which was introduced by Webb et al. (2005), and consider the transmission process of infectious diseases in the population with coinfection between strains. Immuno-epidemiological modeling of infectious diseases is a technique that links a with-in host mathematical model with a between-host mathematical model. In the next section, we formulate the with-in host model with coinfection and discuss the basic reproduction numbers, the invasion reproduction numbers and the existence of the coexistence equilibrium within the host. In Sect. 3, we propose a two-strain epidemiological model with coinfection. We discuss the disease-free equilibrium and single-strain equilibrium and their stability. In Sect. 4, we establish the existence of the interior equilibrium under the condition that the reproduction numbers are larger than one. Simulations are conducted in Sect. 5. Finally, we discuss the dynamic relationship between immunology and epidemiology in Sect. 6.

Fig. 1

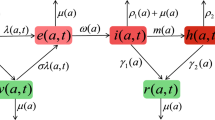
Flow diagram of the model (2.1) and (3.1). The upper panel (blue) is the between-host model. The population is divided into four classes: susceptible, infected by strain 1, infected by strain 2 and co-infected, denoted by S, $I_1$, $I_2$ and J, respectively. The lower panel (green and orange) is the within-host model. The cell population (green) is divided into four classes: healthy, infected by strain 1, infected by strain 2 and co-infected, denoted by x, $y_1$, $y_2$ and y, respectively. $V_1$ and $V_2$ represent virions with strains 1 and 2, respectively (orange). They are produced by infected cells. The viral load of infected people can affect the between-host transmission of the disease (purple line) (Color figure online)

2 The With-In Host Model with Coinfection

In this section, we formulate a two-strain with-in host model with coinfection. Within a host, the time variable is denoted by $\tau$ and signifies time-since-infection. We denote healthy cells by x and cells infected by the ith strain of the virus by $y_i$. The coinfected cells are denoted by y. The number of free virions of strain i is denoted by $V_i$.

In this model, uninfected cells are created at a constant rate r and are infected by interaction with free virions of strain i according to a mass action law with constant rate $\beta _i$. Productively infected cells $y_i$ produce $\gamma _i>1$ new virions of strain i. The parameter $\alpha _i$ denotes new virions of strain i produced by cells coinfected with two strains. The death rates for healthy cells, cells infected with strain i and cells coinfected by two strains are $\mu$, $d_i$ and d, respectively. Here we assume $d_i$ and d are greater than $\mu$. The parameters $\delta _i$ and $s_i$ denote the clearance rate and shedding rate for virions with strain i, respectively. Shedding rate is given by the amount of virus that leaves an infected individual and may serve to infect another individual. The parameter $\eta _1$ denotes the rate at which cells infected by strain 2 are simultaneously infected by the free virus of strain 1, and $\eta _2$ has a similar meaning. This with-in host model with coinfection is given by the following system of ordinary differential equations. A schematic diagram of the model is shown in Fig. 1 (lower panel).

$$\begin{aligned}&\frac{\mathrm {d} x}{\mathrm {d} \tau }=r-\beta _{1} V_{1} x-\beta _{2} V_{2} x-\mu x \nonumber \\&\frac{\mathrm {d} y_{1}}{\mathrm {d} \tau }=\beta _{1} V_{1} x-\eta _{2} \beta _{2} V_{2} y_{1}-d_{1} y_{1}\nonumber \\&\frac{\mathrm {d} y_{2}}{\mathrm {d} \tau }=\beta _{2} V_{2} x-\eta _{1} \beta _{1} V_{1} y_{2}-d_{2} y_{2}\nonumber \\&\frac{\mathrm {d} y}{\mathrm {d} \tau }=\eta _{2} \beta _{2} V_{2} y_{1}+\eta _{1} \beta _{1} V_{1} y_{2}-d y\nonumber \\&\frac{\mathrm {d} V_{1}}{\mathrm {d} \tau }=\gamma _{1} d_{1} y_{1}+\alpha _{1} d y-\left( \delta _{1}+s_{1}\right) V_{1}-\beta _{1} V_{1} x-\eta _{1} \beta _{1} V_{1} y_{2}\nonumber \\&\frac{\mathrm {d} V_{2}}{\mathrm {d} \tau }=\gamma _{2} d_{2} y_{2}+\alpha _{2} d y-\left( \delta _{2}+s_{2}\right) V_{2}-\beta _{2} V_{2} x-\eta _{2} \beta _{2} V_{2} y_{1} \end{aligned}$$

(2.1)

All parameters and dependent variables of this within-host model with coinfection and their definitions are found in Table 1.

Table 1 Description of variables and parameters in model (2.1)

In this within-host model with coinfection, we can determine the infection-free equilibrium $E_{0}=(r/ \mu ,0,0,0,0,0)$. Computing the Jacobian of the model (2.1) at the infection-free equilibrium, we have

$$\begin{aligned} J(E_{0})=\left( \begin{array}{cccccc} -\mu &{} 0 &{} -\beta _{1} x^{*} &{} 0 &{} -\beta _{2} x^{*} &{} 0 \\ 0 &{} -d_{1} &{} \beta _{1} x^{*} &{} 0 &{} 0 &{} 0 \\ 0 &{} \gamma _{1} d_{1} &{} -(\delta _{1}+s_{1})-\beta _{1} x^{*} &{} 0 &{} 0 &{} \alpha _{1} d \\ 0 &{} 0 &{} 0 &{} -d_{2} &{} \beta _{2} x^{*} &{} 0 \\ 0 &{} 0 &{} 0 &{} \gamma _{2} d_{2} &{} -(\delta _{2}+s_{2})-\beta _{2} x^{*} &{} \alpha _{2} d \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} -d \end{array}\right) , \end{aligned}$$

where $x^{*}=r/ \mu$. Considering $\begin{vmatrix}J-\lambda I \end{vmatrix}=0$, we can expand the matrix in terms of the first column. This will give us an eigenvalue $\lambda _{1}=-\mu$. Then, we can expand the remaining matrix around the last row and obtain another eigenvalue $\lambda _{2}=-d$. The remaining eigenvalues are the eigenvalues of the following matrices:

$$\begin{aligned} J_{1}= & {} \left( \begin{array}{cc} -d_{1} &{} \beta _{1} x^{*} \\ \gamma _{1} d_{1} &{} -(\delta _{1}+s_{1})-\beta _{1} x^{*} \\ \end{array}\right) ,\\ J_{2}= & {} \left( \begin{array}{cc} -d_{2} &{} \beta _{2} x^{*} \\ \gamma _{2} d_{2} &{} -(\delta _{2}+s_{2})-\beta _{2} x^{*} \\ \end{array}\right) . \end{aligned}$$

We can see that the above two matrices are the same except that the subscripts of the parameters are different. Therefore, we only consider $J_{1}$. Now we can apply the usual conditions that guarantee that the eigenvalues of $J_{1}$ have negative real parts. We want $\mathrm {Tr} J_{1}<0$ and $\mathrm {Det} J_{1}>0$. $\mathrm {Tr} J_{1}<0$ is obvious, and $\mathrm {Det} J_{1}>0$ leads to the following condition:

$$\begin{aligned} d_{1} \left( \delta _{1}+s_{1}\right) +d_{1} \beta _{1} x^{*}-\beta _{1} \gamma _{1} d_{1} x^{*}>0. \end{aligned}$$

(2.2)

For $J_{1}$ and $J_{2}$, the above inequality (2.2) can be written as

$$\begin{aligned} d_{i} \left( \delta _{i}+s_{i}\right) +d_{i} \beta _{i} x^{*}-\beta _{i} \gamma _{i} d_{i} x^{*}>0 \quad (i=1,2). \end{aligned}$$

Therefore, the within-host reproduction number of strain i in model (2.1) is given by

$$\begin{aligned} R_{i}=\frac{\left( \gamma _{i}-1\right) \beta _{i}}{\delta _{i}+s_{i}} \cdot \frac{r}{\mu }. \end{aligned}$$

(2.3)

We notice that if $R_{i}<1$, then $\mathrm {Det} J_{i}>0$. If $R_{i}>1$, $\mathrm {Det} J_{i}<0$, which implies there exists a positive eigenvalue. Consequently, if both $R_{1}<1$ and $R_{2}<1$ hold, the infection-free equilibrium is locally asymptotically stable. If $R_{i}>1$ for at least one i, then the infection-free equilibrium is unstable. Next we discuss the strain dominance equilibria.

Taking strain 1 as an example. Let the strain 1 dominance equilibrium $E_{1}=(x_{1}^{*},y_{1}^{*},V_{1}^{*},0,0,0)$. It satisfies the following equations:

$$\begin{aligned}&r-\beta _{1} V_{1}^{*} x_{1}^{*}-\mu x_{1}^{*}=0 \\&\beta _{1} V_{1}^{*} x_{1}^{*}-d_{1} y_{1}^{*}=0 \\&\gamma _{1} d_{1} y_{1}^{*}-\left( \delta _{1}+s_{1}\right) V_{1}^{*}-\beta _{1} V_{1}^{*} x_{1}^{*}=0 \\ \end{aligned}$$

The solution is

$$\begin{aligned} x_{1}^{*}=\frac{\delta _{1}+s_{1}}{\beta _{1} \left( \gamma _{1}-1\right) }, \quad y_{1}^{*}=\frac{\beta _{1}}{d_{1}} V_{1}^{*} x_{1}^{*}, \quad V_{1}^{*}=\frac{\mu }{\beta _{1}} \left( R_{1}-1\right) . \end{aligned}$$

It can be seen that when $R_1>1$, $E_1$ exists.

We compute the invasion reproduction number $R_{2}^{1}$, which gives the number of secondary infections that one infected individual with the second strain will produce in a population in which the first strain is at equilibrium. From finding the eigenvalues of the Jacobian matrix at $E_{1}$, we can obtain the following equation

$$\begin{aligned}&-\left( \lambda +d_{2}+\eta _{1} \beta _{1} V_{1}^{*}\right) \left( \lambda +\delta _{2}+s_{2}+\beta _{2} x_{1}^{*}+\eta _2\beta _2y_1^*\right) \left( \lambda +d\right) +\beta _{2} x_{1}^{*} \cdot \alpha _{2} d \cdot \eta _{1} \beta _{1} V_{1}^{*}\\&\quad +\left( \lambda +d_{2}+\eta _{1} \beta _{1} V_{1}^{*}\right) \cdot \alpha _{2} d \cdot \eta _{2} \beta _{2} y_{1}^{*}+\left( \lambda +d\right) \cdot \beta _{2} x_{1}^{*} \cdot \gamma _{2} d_{2}=0. \end{aligned}$$

That is

$$\begin{aligned}&\left( \lambda +d_{2}+\eta _{1} \beta _{1} V_{1}^{*}\right) \cdot \alpha _{2} d \cdot \eta _{2} \beta _{2} y_{1}^{*}+\left( \lambda +d\right) \cdot \beta _{2} x_{1}^{*} \cdot \gamma _{2} d_{2}+\beta _{2} x_{1}^{*} \cdot \alpha _{2} d \cdot \eta _{1} \beta _{1} V_{1}^{*}\\&\quad =\left( \lambda +d\right) \left( \lambda +d_{2}+\eta _{1} \beta _{1} V_{1}^{*}\right) \left( \lambda +\delta _{2}+s_{2}+\beta _{2} x_{1}^{*}\right) . \end{aligned}$$

Dividing both sides of the equation by $\left( \lambda +d\right) \left( \lambda +d_{2}+\eta _{1} \beta _{1} V_{1}^{*}\right)$, we have

$$\begin{aligned}&\frac{\alpha _{2} d \cdot \eta _{2} \beta _{2} y_{1}^{*}}{\lambda +d}+\frac{\beta _{2} x_{1}^{*} \cdot \gamma _{2} d_{2}}{\lambda +d_{2}+\eta _{1} \beta _{1} V_{1}^{*}}+\frac{\beta _{2} x_{1}^{*} \cdot \alpha _{2} d \cdot \eta _{1} \beta _{1} V_{1}^{*}}{\left( \lambda +d\right) \left( \lambda +d_{2}+\eta _{1} \beta _{1} V_{1}^{*}\right) }\\&\quad =\lambda +\delta _{2}+s_{2}+\beta _{2} x_{1}^{*}. \end{aligned}$$

Let

$$\begin{aligned} f(\lambda )&=\frac{\alpha _{2} d \cdot \eta _{2} \beta _{2} y_{1}^{*}}{\lambda +d}+\frac{\beta _{2} x_{1}^{*} \cdot \gamma _{2} d_{2}}{\lambda +d_{2}+\eta _{1} \beta _{1} V_{1}^{*}}+\frac{\beta _{2} x_{1}^{*} \cdot \alpha _{2} d \cdot \eta _{1} \beta _{1} V_{1}^{*}}{\left( \lambda +d\right) \left( \lambda +d_{2}+\eta _{1} \beta _{1} V_{1}^{*}\right) }, \\ g(\lambda )&=\lambda +\delta _{2}+s_{2}+\beta _{2} x_{1}^{*}. \end{aligned}$$

Then, we observe that if $\lambda$ increases, $f(\lambda )$ is decreasing and $g(\lambda )$ is increasing. Therefore, if

$$\begin{aligned} f(0)<g(0), \end{aligned}$$

then the equation $f(\lambda )=g(\lambda )$ does not have roots with non-negative real parts. We can prove this by contradiction. Suppose $\lambda =\xi +i\eta$ with $\xi \ge 0$, then

$$\begin{aligned} |f(\lambda )|\le f(\xi )\le f(0) \end{aligned}$$

and

$$\begin{aligned} |g(\lambda )|\ge g(\xi )\ge g(0). \end{aligned}$$

Thus, $|f(\lambda )|\le f(0)<g(0)\le |g(\lambda )|$ for all $\lambda$ with non-negative real part. In this case, the equilibrium $E_1$ is locally asymptotically stable. On the other hand, if $f(0)>g(0)$, then the equation $f(\lambda )=g(\lambda )$ has a real positive root. Therefore, the equilibrium $E_1$ is unstable.

We rewrite the inequality $f(0)<g(0)$ as follows:

$$\begin{aligned} \alpha _{2} \cdot \eta _{2} \beta _{2} y_{1}^{*}+\frac{\beta _{2} x_{1}^{*} \cdot \gamma _{2} d_{2}}{d_{2}+\eta _{1} \beta _{1} V_{1}^{*}}+\frac{\beta _{2} x_{1}^{*} \cdot \alpha _{2} \cdot \eta _{1} \beta _{1} V_{1}^{*}}{d_{2}+\eta _{1} \beta _{1} V_{1}^{*}}<\left( \delta _{2}+s_{2}+\beta _{2} x_{1}^{*}\right) . \end{aligned}$$

Multiplying both sides of the inequality by $d_{2}+\eta _{1} \beta _{1} V_{1}^{*}$, we have

$$\begin{aligned}&\alpha _{2} \eta _{2} \beta _{2} y_{1}^{*} \cdot d_{2}+\alpha _{2} \eta _{2} \beta _{2} y_{1}^{*} \cdot \eta _{1} \beta _{1} V_{1}^{*}+\beta _{2} x_{1}^{*} \cdot \gamma _{2} d_{2}+\beta _{2} x_{1}^{*} \alpha _{2} \eta _{1} \beta _{1} V_{1}^{*}\\&\quad <\left( \delta _{2}+s_{2}\right) \cdot d_{2}+\left( \delta _{2}+s_{2}\right) \cdot \eta _{1} \beta _{1} V_{1}^{*}+\beta _{2} x_{1}^{*} \cdot d_{2}+\beta _{2} x_{1}^{*} \cdot \eta _{1} \beta _{1} V_{1}^{*}. \end{aligned}$$

Transposing and simplifying, we get

$$\begin{aligned}&\alpha _{2} \eta _{2} \beta _{2} y_{1}^{*} \left( d_{2}+\eta _{1} \beta _{1} V_{1}^{*}\right) +\beta _{2} x_{1}^{*} d_{2} \left( \gamma _{2}-1\right) +\beta _{2} x_{1}^{*} \eta _{1} \beta _{1} V_{1}^{*} \left( \alpha _{2}-1\right) \\&\quad <\left( \delta _{2}+s_{2}\right) \left( d_{2}+\eta _{1} \beta _{1} V_{1}^{*}\right) . \end{aligned}$$

Therefore, the invasion reproduction number is given by

$$\begin{aligned} R_{2}^{1}=\frac{\alpha _{2} \eta _{2} \beta _{2} y_{1}^{*} \left( d_{2}+\eta _{1} \beta _{1} V_{1}^{*}\right) +\beta _{2} x_{1}^{*} d_{2} \left( \gamma _{2}-1\right) +\beta _{2} x_{1}^{*} \eta _{1} \beta _{1} V_{1}^{*} \left( \alpha _{2}-1\right) }{\left( \delta _{2}+s_{2}\right) \left( d_{2}+\eta _{1} \beta _{1} V_{1}^{*}\right) }.\nonumber \\ \end{aligned}$$

(2.4)

We can see that $R_{2}^{1}<1$ is equivalent to $f(0)<g(0)$ and $R_{2}^{1}>1$ is equivalent to $f(0)>g(0)$. Similar results can be obtained for the strain 2 dominance equilibrium $E_2=(x^*_2,0,0,y^*_2,V^*_2,0)$. Its stability depends on the relation between the following invasion reproduction number and one (Martcheva 2015):

$$\begin{aligned} R_{1}^{2}=\frac{\alpha _{1} \eta _{1} \beta _{1} y_{2}^{*} \left( d_{1}+\eta _{2} \beta _{2} V_{2}^{*}\right) +\beta _{1} x_{2}^{*} d_{1} \left( \gamma _{1}-1\right) +\beta _{1} x_{2}^{*} \eta _{2} \beta _{2} V_{2}^{*} \left( \alpha _{1}-1\right) }{\left( \delta _{1}+s_{1}\right) \left( d_{1}+\eta _{2} \beta _{2} V_{2}^{*}\right) }.\nonumber \\ \end{aligned}$$

(2.5)

We summarize the above results in the following proposition:

Proposition 2.1

If $R_i>1$, then the boundary equilibrium $E_i$ exists. If $R_j^i<1$, equilibrium $E_i$ is locally asymptotically stable. If $R_j^i>1$, the equilibrium $E_i$ is unstable.

If we do not remove healthy cells infections with $V_{i}$ and infected cells infections by another strain infected simultaneously with $V_{i}$ from the class of free virions, that is to say, we ignore the last two terms in the $V_{1}$ and $V_{2}$ equation, then the model (2.1) becomes

$$\begin{aligned}&\frac{\mathrm {d} x}{\mathrm {d} \tau }=r-\beta _{1} V_{1} x-\beta _{2} V_{2} x-\mu x \nonumber \\&\frac{\mathrm {d} y_{1}}{\mathrm {d} \tau }=\beta _{1} V_{1} x-\eta _{2} \beta _{2} V_{2} y_{1}-d_{1} y_{1} \nonumber \\&\frac{\mathrm {d} y_{2}}{\mathrm {d} \tau }=\beta _{2} V_{2} x-\eta _{1} \beta _{1} V_{1} y_{2}-d_{2} y_{2} \nonumber \\&\frac{\mathrm {d} y}{\mathrm {d} \tau }=\eta _{2} \beta _{2} V_{2} y_{1}+\eta _{1} \beta _{1} V_{1} y_{2}-d y \nonumber \\&\frac{\mathrm {d} V_{1}}{\mathrm {d} \tau }=\gamma _{1} d_{1} y_{1}+\alpha _{1} d y-\left( \delta _{1}+s_{1}\right) V_{1} \nonumber \\&\frac{\mathrm {d} V_{2}}{\mathrm {d} \tau }=\gamma _{2} d_{2} y_{2}+\alpha _{2} d y-\left( \delta _{2}+s_{2}\right) V_{2} \end{aligned}$$

(2.6)

The within-host reproduction number of this system is

$$\begin{aligned} {\mathbb {R}}_{i}=\frac{\gamma _{i} \beta _{i}}{\delta _{i}+s_{i}} \cdot \frac{r}{\mu }. \end{aligned}$$

(2.7)

And the strain i dominance equilibrium has components

$$\begin{aligned} x_{i}^{*}=\frac{\delta _{i}+s_{i}}{\gamma _{i} \beta _{i}}, \quad y_{i}^{*}=\frac{\beta _{i}}{d_{i}} V_{i}^{*} x_{i}^{*}, \quad V_{i}^{*}=\frac{\mu }{\beta _{i}} \left( {\mathbb {R}}_{i}-1\right) , \quad i=1,2. \end{aligned}$$

We can also calculate the invasion reproduction number of strain i in model (2.6). They are

$$\begin{aligned} {\mathbb {R}}_{2}^{1}=\frac{\alpha _{2} \eta _{2} \beta _{2} y_{1}^{*} \left( d_{2}+\eta _{1} \beta _{1} V_{1}^{*}\right) +\gamma _{2} d_{2} \cdot \beta _{2} x_{1}^{*} +\eta _{1} \beta _{1} V_{1}^{*} \cdot \alpha _{2} \cdot \beta _{2} x_{1}^{*}}{\left( \delta _{2}+s_{2}\right) \left( d_{2}+\eta _{1} \beta _{1} V_{1}^{*}\right) } \end{aligned}$$

(2.8)

and

$$\begin{aligned} {\mathbb {R}}_{1}^{2}=\frac{\alpha _{1} \eta _{1} \beta _{1} y_{2}^{*} \left( d_{1}+\eta _{2} \beta _{2} V_{2}^{*}\right) +\gamma _{1} d_{1} \cdot \beta _{1} x_{2}^{*}+\eta _{2} \beta _{2} V_{2}^{*} \cdot \alpha _{1} \cdot \beta _{1} x_{2}^{*}}{\left( \delta _{1}+s_{1}\right) \left( d_{1}+\eta _{2} \beta _{2} V_{2}^{*}\right) }. \end{aligned}$$

(2.9)

Next we discuss the existence of coexistence equilibrium in model (2.6). When the within-host reproduction numbers and the invasion reproduction numbers are greater than one, there may be a coexistence equilibrium. The coexistence equilibrium $E=(x,y_{1},V_{1},y_{2},V_{2},y)$ of model (2.6) satisfies the following equations:

$$\begin{aligned}&r-\beta _{1} V_{1} x-\beta _{2} V_{2} x-\mu x=0 \nonumber \\&\beta _{1} V_{1} x-\eta _{2} \beta _{2} V_{2} y_{1}-d_{1} y_{1}=0 \nonumber \\&\beta _{2} V_{2} x-\eta _{1} \beta _{1} V_{1} y_{2}-d_{2} y_{2}=0 \nonumber \\&\eta _{2} \beta _{2} V_{2} y_{1}+\eta _{1} \beta _{1} V_{1} y_{2}-d y=0 \nonumber \\&\gamma _{1} d_{1} y_{1}+\alpha _{1} d y-\left( \delta _{1}+s_{1}\right) V_{1}=0\nonumber \\&\gamma _{2} d_{2} y_{2}+\alpha _{2} d y-\left( \delta _{2}+s_{2}\right) V_{2}=0 \end{aligned}$$

(2.10)

The first three equations of the system (2.10) can be solved as follows:

$$\begin{aligned} x=\frac{r}{\beta _{1} V_{1}+\beta _{2} V_{2}+\mu },\quad y_{1}=\frac{\beta _{1} V_{1} x}{\eta _{2} \beta _{2} V_{2}+d_{1}},\quad y_{2}=\frac{\beta _{2} V_{2} x}{\eta _{1} \beta _{1} V_{1}+d_{2}}. \end{aligned}$$

From the fourth equation of the system (2.10), we have

$$\begin{aligned} y=\frac{1}{d} \left[ \eta _{2} \beta _{2} V_{2} \cdot \frac{\beta _{1} V_{1} x}{\eta _{2} \beta _{2} V_{2}+d_{1}}+\eta _{1} \beta _{1} V_{1} \cdot \frac{\beta _{2} V_{2} x}{\eta _{1} \beta _{1} V_{1}+d_{2}}\right] . \end{aligned}$$

Substituting $y_{1},y_{2},y$ into the last two equation of the system (2.10), we get

$$\begin{aligned} \left\{ \begin{aligned}&\gamma _{1} d_{1} \frac{\beta _{1} V_{1} x}{\eta _{2} \beta _{2} V_{2}+d_{1}}+\alpha _{1} \left[ \eta _{2} \beta _{2} V_{2} \cdot \frac{\beta _{1} V_{1} x}{\eta _{2} \beta _{2} V_{2}+d_{1}}+\eta _{1} \beta _{1} V_{1} \cdot \frac{\beta _{2} V_{2} x}{\eta _{1} \beta _{1} V_{1}+d_{2}}\right] =\left( \delta _{1}+s_{1}\right) V_{1},\\&\gamma _{2} d_{2} \frac{\beta _{2} V_{2} x}{\eta _{1} \beta _{1} V_{1}+d_{2}}+\alpha _{2} \left[ \eta _{2} \beta _{2} V_{2} \cdot \frac{\beta _{1} V_{1} x}{\eta _{2} \beta _{2} V_{2}+d_{1}}+\eta _{1} \beta _{1} V_{1} \cdot \frac{\beta _{2} V_{2} x}{\eta _{1} \beta _{1} V_{1}+d_{2}}\right] =\left( \delta _{2}+s_{2}\right) V_{2}.\\ \end{aligned}\right. \end{aligned}$$

Simplifying and substituting into x, we have

$$\begin{aligned} \left\{ \begin{aligned}&\frac{\gamma _{1} d_{1}}{\eta _{2} \beta _{2} V_{2}+d_{1}}+\alpha _{1} \beta _{2} V_{2} \left[ \frac{\eta _{2}}{\eta _{2} \beta _{2} V_{2}+d_{1}}+\frac{\eta _{1}}{\eta _{1} \beta _{1} V_{1}+d_{2}}\right] =\frac{\delta _{1}+s_{1}}{\beta _{1}} \cdot \frac{\beta _{1} V_{1}+\beta _{2} V_{2}+\mu }{r},\\&\frac{\gamma _{2} d_{2}}{\eta _{1} \beta _{1} V_{1}+d_{2}}+\alpha _{2} \beta _{1} V_{1} \left[ \frac{\eta _{2}}{\eta _{2} \beta _{2} V_{2}+d_{1}}+\frac{\eta _{1}}{\eta _{1} \beta _{1} V_{1}+d_{2}}\right] =\frac{\delta _{2}+s_{2}}{\beta _{2}} \cdot \frac{\beta _{1} V_{1}+\beta _{2} V_{2}+\mu }{r}. \end{aligned} \right. \nonumber \\ \end{aligned}$$

(2.11)

We need to judge whether the system (2.11) has a solution. If there is a solution, it means that coexistence equilibrium of the model (2.6) exists. Otherwise, there is no coexistence equilibrium.

Let the left-hand sides of Eq. (2.11) divided by the right-hand side are $f_{1}(V_{1},V_{2})$ and $f_{2}(V_{1},V_{2})$, respectively. Then, we can rewrite the system (2.11) as follows:

$$\begin{aligned} f_{1}(V_{1},V_{2})= & {} \frac{\gamma _{1} d_{1}}{\eta _{2} \beta _{2} V_{2}+d_{1}} \cdot \frac{r}{\mu +\beta _{1} V_{1}+\beta _{2} V_{2}} \cdot \frac{\beta _{1}}{\delta _{1}+s_{1}}\\&+\frac{\alpha _{1} \beta _{2} V_{2} r}{\mu +\beta _{1} V_{1}+\beta _{2} V_{2}} \cdot \frac{\beta _1}{\delta _{1}+s_{1}} \cdot \left[ \frac{\eta _{2}}{\eta _{2} \beta _{2} V_{2}+d_{1}}+\frac{\eta _{1}}{\eta _{1} \beta _{1} V_{1}+d_{2}}\right] \equiv 1. \end{aligned}$$

and

$$\begin{aligned} f_{2}(V_{1},V_{2})= & {} \frac{\gamma _{2} d_{2}}{\eta _{1} \beta _{1} V_{1}+d_{2}} \cdot \frac{r}{\mu +\beta _{1} V_{1}+\beta _{2} V_{2}} \cdot \frac{\beta _{2}}{\delta _{2}+s_{2}}\\&+\frac{\alpha _{2} \beta _{1} V_{1} r}{\mu +\beta _{1} V_{1}+\beta _{2} V_{2}} \cdot \frac{\beta _{2}}{\delta _{2}+s_{2}} \cdot \left[ \frac{\eta _{2}}{\eta _{2} \beta _{2} V_{2}+d_{1}}+\frac{\eta _{1}}{\eta _{1} \beta _{1} V_{1}+d_{2}}\right] \equiv 1 \end{aligned}$$

We want to use $f_{2}(V_{1},V_{2})=1$ to express $V_{2}=h(V_{1})$. Since $f_{2}(V_{1},V_{2})=1$ is a decreasing function of $V_{2}$, if there is a solution, that solution is unique. There will be a solution if $f_{2}(V_{1},0)>1$ for arbitrary $V_{1}$. We have

$$\begin{aligned} f_{2}(V_{1},0)= & {} \frac{\gamma _{2} d_{2}}{\eta _{1} \beta _{1} V_{1}+d_{2}} \cdot \frac{r}{\mu +\beta _{1} V_{1}} \cdot \frac{\beta _{2}}{\delta _{2}+s_{2}}\\&+\frac{\alpha _{2} \beta _{1} V_{1} r}{\mu +\beta _{1} V_{1}} \cdot \frac{\beta _{2}}{\delta _{2}+s_{2}} \cdot \left[ \frac{\eta _{2}}{d_{1}}+\frac{\eta _{1}}{\eta _{1} \beta _{1} V_{1}+d_{2}}\right] . \end{aligned}$$

Then,

$$\begin{aligned} f_{2}(0,0)=\gamma _{2} \frac{r}{\mu } \cdot \frac{\beta _{2}}{\delta _{2}+s_{2}}=\frac{\gamma _{2} \beta _{2}}{\delta _{2}+s_{2}} \cdot \frac{r}{\mu }={\mathbb {R}}_{2}>1, \end{aligned}$$

and

$$\begin{aligned} f_{2}(V_{1}^{*},0)&=\frac{\gamma _{2} d_{2}}{\eta _{1} \beta _{1} V_{1}^{*}+d_{2}} \cdot \frac{r}{\mu +\beta _{1} V_{1}^{*}} \cdot \frac{\beta _{2}}{\delta _{2}+s_{2}}\\&\quad +\frac{\alpha _{2} \beta _{1} V_{1}^{*} r}{\mu +\beta _{1} V_{1}^{*}} \cdot \frac{\beta _{2}}{\delta _{2}+s_{2}} \cdot \left[ \frac{\eta _{2}}{d_{1}}+\frac{\eta _{1}}{\eta _{1} \beta _{1} V_{1}^{*}+d_{2}}\right] \\&=\frac{\gamma _{2} d_{2} \beta _{2} x_{1}^{*}}{\left( \delta _{2}+s_{2}\right) \left( d_{2}+\eta _{1} \beta _{1} V_{1}^{*}\right) }+\frac{\alpha _{2} \beta _{2} \eta _{2}}{\left( \delta _{2}+s_{2}\right) } \cdot y_{1}^{*}\\&\quad +\frac{\eta _{1} \beta _{1} V_{1}^{*} \cdot \alpha _{2} \beta _{2} x_{1}^{*}}{\left( \delta _{2}+s_{2}\right) \left( d_{2}+\eta _{1} \beta _{1} V_{1}^{*}\right) }\\&={\mathbb {R}}_{2}^{1}>1. \end{aligned}$$

Therefore, we only need to prove $f_{2}(V_{1},0)>1$. From $f_{2}(V_{1},0)>1$, we can get

$$\begin{aligned}&\frac{\beta _{2}}{\delta _{2}+s_{2}}\left[ \gamma _{2} d_{2} \cdot r d_{1}+\alpha _{2} \beta _{1} V_{1} r \left( \eta _{2} d_{2}+\eta _{1} \eta _{2} \beta _{1} V_{1}+\eta _{1} d_{1}\right) \right] \nonumber \\&\quad >d_{1}\left[ d_{2} \mu +\left( d_{2} \beta _{1}+\mu \eta _{1} \beta _{1}\right) V_{1}+\eta _{1} \beta _{1}^{2} V_{1}^{2}\right] . \end{aligned}$$

(2.12)

If we want to get (2.12), we need to consider the following two cases.

Case 1: If

$$\begin{aligned} \frac{\beta _{2}}{\delta _{2}+s_{2}} \cdot \alpha _{2} \beta _{1} r \cdot \eta _{1} \eta _{2} \beta _{1}>d_{1} \eta _{1} \beta _{1}^{2}, \end{aligned}$$

that is,

$$\begin{aligned} \frac{\alpha _{2} \beta _{2} r \eta _{2}}{d_{1}\left( \delta _{2}+s_{2}\right) }>1, \end{aligned}$$

then we have

$$\begin{aligned} \frac{\beta _{2}}{\delta _{2}+s_{2}} \cdot \frac{\alpha _{2} r \eta _{2}}{d_{1}} \left[ d_{2}+\frac{\eta _{1}}{\eta _{2}} d_{1}\right] >d_{2}+\mu \eta _{1} \end{aligned}$$

since $d_{1} / \eta _{2} > \mu$ is always true for real solutions. Here we use the truth that the death rate for infected cells $d_1$ is bigger than the natural death rate for healthy cells $\mu$ and the probability $\eta _2\le 1$. Therefore,

$$\begin{aligned} \frac{\beta _{2}}{\delta _{2}+s_{2}} \cdot \alpha _{2} \beta _{1} r \cdot \eta _{2} d_{2}+\frac{\beta _{2}}{\delta _{2}+s_{2}} \cdot \alpha _{2} \beta _{1} r \cdot \eta _{1} d_{1}>d_{1}\left( d_{2} \beta _{1}+\mu \eta _{1} \beta _{1}\right) . \end{aligned}$$

This indicates that $f_{2}(V_{1},0)>1$ for $\forall V_{1}$. So there is a unique solution for all $V_{1}$.

Case 2: If

$$\begin{aligned} \frac{\alpha _{2} r \eta _{2} \beta _{2}}{d_{1} \left( \delta _{2}+s_{2}\right) }<1, \end{aligned}$$

we have

$$\begin{aligned} \lim _{V_{1} \rightarrow \infty }f_{2}(V_{1},0)=\frac{\alpha _{2} r \eta _{2} \beta _{2}}{d_{1} \left( \delta _{2}+s_{2}\right) }<1. \end{aligned}$$

Then, there exists a ${\widetilde{V}}_{1}^{*}$ such that $f_{2}(V_{1},0)>1$ for $\forall V_{1}<{\widetilde{V}}_{1}^{*}$ and $f_{2}({\widetilde{V}}_{1}^{*},0)=1$. Then, there is a unique $V_{2}$ for any $V_{1} \in (0,{\widetilde{V}}_{1}^{*})$ such that $V_{2}=h(V_{1})$.

We define

$$\begin{aligned} F(V_{1})=f_{1}(V_{1},h(V_{1})). \end{aligned}$$

When $V_{1}=0$, $h(0)=V_{2}^{*}$ is the single strain 2 equilibrium. In fact,

$$\begin{aligned} f_{2}(0,V_{2})=\frac{\gamma _{2} \beta _{2}}{\delta _{2}+s_{2}} \cdot \frac{r}{\mu +\beta _{2}V_{2}}=1, \end{aligned}$$

so

$$\begin{aligned} V_{2}=\frac{\mu }{\beta _{2}} \left[ \frac{\gamma _{2} \beta _{2}}{\delta _{2}+s_{2}} \cdot \frac{r}{\mu }-1\right] =\frac{\mu }{\beta _{2}}\left[ {\mathbb {R}}_{2}-1\right] =V_{2}^{*}. \end{aligned}$$

We have

$$\begin{aligned} F(0)&=f_{1}(0,V_{2}^{*}) \\&=\frac{\gamma _{1} d_{1}}{\eta _{2} \beta _{2} V_{2}^{*}+d_{1}} \cdot \frac{r}{\mu +\beta _{2} V_{2}^{*}} \cdot \frac{\beta _{1}}{\delta _{1}+s_{1}}\\&\quad +\frac{\alpha _{1} \beta _{2} V_{2}^{*} r}{\mu +\beta _{2} V_{2}^{*}} \cdot \frac{\beta _{1}}{\delta _{1}+s_{1}}\left[ \frac{\eta _{2}}{\eta _{2} \beta _{2} V_{2}^{*}+d_{1}}+\frac{\eta _{1}}{d_{2}}\right] \\&=\frac{\gamma _{1} d_{1} \beta _{1} x_{2}^{*}}{\left( \delta _{1}+s_{1}\right) \left( \eta _{2} \beta _{2} V_{2}^{*}+d_{1}\right) }+\frac{\alpha _{1} \beta _{2} V_{2}^{*} \cdot \beta _{1} x_{2}^{*}\eta _2}{\left( \delta _{1}+s_{1}\right) \left( \eta _{2} \beta _{2} V_{2}^{*}+d_{1}\right) }+\frac{\alpha _{1} \eta _{1} \beta _{1}}{\delta _{1}+s_{1}} \cdot y_{2}^{*} \\&={\mathbb {R}}_{1}^{2}>1. \end{aligned}$$

Let $V_{2}=0=h({\widetilde{V}}_{1}^{*})$, then

$$\begin{aligned} F({\widetilde{V}}_{1}^{*})&=f_{1}({\widetilde{V}}_{1}^{*},0)=\frac{\gamma _{1} \beta _{1} r}{\left( \delta _{1}+s_{1}\right) \left( \mu +\beta _{1} V_{1}^{*}\right) } \\&<\frac{\gamma _{1} r}{\mu +\beta _{1} V_{1}^{*}} \cdot \frac{\beta _{1}}{\delta _{1}+s_{1}}=\frac{\gamma _{1} r}{\mu {\mathbb {R}}_{1}} \cdot \frac{\beta _{1}}{\delta _{1}+s_{1}} \\&=\frac{\gamma _{1} r}{\gamma _{1} \beta _{1} r} \cdot \frac{\delta _{1}+s_{1}}{\delta _{1}+s_{1}} \cdot \beta _{1}=1. \end{aligned}$$

To show ${\widetilde{V}}_{1}^{*}>V_{1}^{*}$, we assume that ${\widetilde{V}}_{1}^{*}<V_{1}^{*}$; then, there are two values ${\widetilde{V}}_{1}^{*}, \overset{\approx }{V_{1}^{*}}$ which satisfy $f_{2}(V_{1},0)=1$.

$$\begin{aligned} f_{2}(V_{1},0)=\frac{\beta _{2}}{\delta _{2}+s_{2}}\left[ \frac{\gamma _{2} d_{2} r d_{1}+\alpha _{2} \beta _{1} V_{1} r\left[ \eta _{2}\left( d_{2}+\eta _{1} \beta _{1} V_{1}\right) +\eta _{1} d_{1}\right] }{d_{1}\left( d_{2}+\eta _{1} \beta _{1} V_{1}\right) \left( \mu +\beta _{1} V_{1}\right) }\right] =1, \end{aligned}$$

that is,

$$\begin{aligned}&\frac{\beta _{2}}{\delta _{2}+s_{2}}\Big [\gamma _{2} d_{2} r d_{1}+\alpha _{2} \beta _{1} V_{1} r\left[ \eta _{2}\left( d_{2}+\eta _{1} \beta _{1} V_{1}\right) +\eta _{1} d_{1}\right] \Big ] \\&\quad =d_{1}\left( d_{2}+\eta _{1} \beta _{1} V_{1}\right) \left( \mu +\beta _{1} V_{1}\right) \end{aligned}$$

has two positive real solutions in the interval $(0,V_{1}^{*})$.

We can rewrite the above equation about $V_{1}$ as a quadratic equation of one unknown:

$$\begin{aligned} A V_{1}^{2}+B V_{1}+C=0, \end{aligned}$$

where

$$\begin{aligned} A&=\frac{\beta _{2}}{\delta _{2}+s_{2}} \alpha _{2} \beta _{1} r \eta _{1} \eta _{2} \beta _{1}-d_{1} \eta _{1} \beta _{1}^{2}<0, \\ C&=\frac{\beta _{2}}{\delta _{2}+s_{2}} \gamma _{2} d_{2} r d_{1}-d_{1} d_{2} \mu =d_{1} d_{2} \mu \left[ {\mathbb {R}}_{2}-1\right] >0. \end{aligned}$$

Therefore, $C/A<0$, this means that there is only one positive solution for the quadratic equation of one unknown. This conclusion contradicts the hypothesis. Thus, we have ${\widetilde{V}}_{1}^{*}>V_{1}^{*}$ and $f_{2}(V_{1},0)>1$ for $\forall V_{1}<{\widetilde{V}}_{1}^{*}$. For any $V_{1} \in (0,{\widetilde{V}}_{1}^{*})$, there exists a unique $V_{2}$ such that $f_{1}(V_{1},V_{2})=1, f_{2}(V_{1},V_{2})=1$.

Proposition 2.2

Assume ${\mathbb {R}}_{j}>1,j=1,2$ and ${\mathbb {R}}_{1}^{2}>1, {\mathbb {R}}_{2}^{1}>1$. Then, (2.6) has a co-existence equilibrium.

3 The Immuno-epidemiological Model with Coinfection

In this section, we introduce a two-strain epidemiological model with coinfection. S(t) denotes the number of susceptible human individuals, where t is the chronological time. We stratify the infectious individuals by age-since-infection $\tau$. Let $i_{k}(\tau ,t)$ be the density of individuals infected by strain k. Individuals in the class $i_{k}(\tau ,t)$ experience the same within-host dynamics given by model (2.1) with the initial condition of the other strain and the coinfected class set to zero. We use $j(\tau ,t)$ to denote the density of individuals coinfected by the two stains. These individual experience within-host dynamics given by (2.1). The two-strain immuno-epidemiological model with coinfection is given by the following system. The flowchart is shown in Fig. 1.

$$\begin{aligned}&\frac{\mathrm {d} S}{\mathrm {d} t} =\Lambda -\frac{S}{N} \int _{0}^{\infty } \beta _{1}\left( \tau \right) \left( i_{1}+q_{1} j\right) \mathrm {d} \tau -\frac{S}{N} \int _{0}^{\infty } \beta _{2}\left( \tau \right) \left( i_{2}+q_{2} j\right) \mathrm {d} \tau -m_{0} S \nonumber \\&\frac{\partial i_{1}}{\partial \tau }+\frac{\partial i_{1}}{\partial t} =-m_{1}\left( V_{1}(\tau )\right) i_{1}(\tau , t)-\rho _{12} \int _{0}^{\infty } \beta _{2}\left( \tau \right) \left( i_{2}+q_{2} j\right) \mathrm {d} \tau \cdot \frac{i_{1}}{N}+\theta _{2} P_{2} j \nonumber \\&\quad i_{1}(0,t) =\frac{S}{N} \int _{0}^{\infty } \beta _{1}(\tau ) \left( i_{1}+q_{1} j\right) \mathrm {d} \tau \nonumber \\&\frac{\partial i_{2}}{\partial \tau }+\frac{\partial i_{2}}{\partial t} =-m_{2}\left( V_{2}(\tau )\right) i_{2}(\tau , t)-\rho _{21} \int _{0}^{\infty } \beta _{1}\left( \tau \right) \left( i_{1}+q_{1} j\right) \mathrm {d} \tau \cdot \frac{i_{2}}{N}+\theta _{1} P_{1} j \nonumber \\&\quad i_{2}(0,t) =\frac{S}{N} \int _{0}^{\infty } \beta _{2}(\tau ) \left( i_{2}+q_{2} j\right) \mathrm {d} \tau \nonumber \\&\frac{\partial j}{\partial \tau }+\frac{\partial j}{\partial t} =-m_{j}\left( V_{1},V_{2}\right) j-\theta _{1} P_{1} j-\theta _{2} P_{2} j \nonumber \\&\quad j(0,t) =\frac{\rho _{12}}{N} \int _{0}^{\infty } \beta _{2}(\tau ) \left( i_{2}+q_{2} j\right) \mathrm {d} \tau \cdot \int _{0}^{\infty } i_{1}(\tau ,t) \mathrm {d} \tau \nonumber \\&\qquad \qquad \qquad +\frac{\rho _{21}}{N}\int _{0}^{\infty } \beta _{1}(\tau ) \left( i_{1}+q_{1} j\right) \mathrm {d} \tau \cdot \int _{0}^{\infty } i_{2}(\tau ,t) \mathrm {d} \tau \end{aligned}$$

(3.1)

Descriptions of the variables and parameters of the above model are found in Table 2.

Table 2 Description of variables and parameters in model (3.1)

In model (3.1), $\Lambda$ is the recruitment rate, and $m_{0}=m_{k}(0)$ is the natural death rate of susceptible hosts at zero viral load. The infected hosts die at a variable rate dependent on their viral load $m_{k}\left( V_{k}(\tau )\right)$, where $V_{k}(\tau )$ is the viral load of the strain k. Hence, we will assume that the mortality of the infected hosts is

$$\begin{aligned} m_{k}\left( V_{k}(\tau )\right) =m_{0}+m_{k} V_{k}(\tau ), \end{aligned}$$

where $k=1,2$ denotes strain k and $m_{k} V_{k}(\tau )$ is the additional host mortality due to the virus. The mortality rate of hosts coinfected by the two strains is $m_{j}(V_{1},V_{2})=m_{0}+{\widetilde{m}}_{1} V_{1}+{\widetilde{m}}_{2} V_{2}$. The transmission coefficient of the disease $\beta _{k}(\tau )$ is also dependent on the within-host viral load. We suppose that $\beta _{k}(\tau )$ is proportional to the viral load at a given age-since-infection $\tau$, that is,

$$\begin{aligned} \beta _{k}(\tau )=\beta _{k}\left( V_{k}(\tau )\right) =c_{k} V_{k}(\tau ). \end{aligned}$$

The parameters $q_{k}$ denote the probability of successful transmission. The total population size is given by the sum of all classes:

$$\begin{aligned} N(t)=S(t)+\int _{0}^{\infty } i_{1}(\tau ,t) \mathrm {d} \tau +\int _{0}^{\infty } i_{2}(\tau ,t) \mathrm {d} \tau +\int _{0}^{\infty } j(\tau ,t) \mathrm {d} \tau . \end{aligned}$$

The parameters $P_{k}$ take on values zero and one and control the direction of the co-infection. They are the modeling tools for scaling up the outcome of within-host competition to the between-host interactions. The values of $P_{k}$ rely on the size of the invasion reproduction numbers $R_{1}^{2}$ and $R_{2}^{1}$. They can be expressed as follows:

$$\begin{aligned} P_{1}=\left\{ \begin{array}{ll} 0 &{} \text{ if } R_{2}^{1}<1, \\ 1 &{} \text{ if } R_{2}^{1}>1,R_{1}^{2}<1. \end{array}\right. \quad P_{2}=\left\{ \begin{array}{ll} 0 &{} \text{ if } R_{1}^{2}<1, \\ 1 &{} \text{ if } R_{1}^{2}>1,R_{2}^{1}<1. \end{array}\right. \end{aligned}$$

If $R_{1}^{2}>1$ and $R_{2}^{1}>1$, $P_{1}=P_{2}=0$. The parameters $P_{1}$ and $P_{2}$ are not probabilities, but a binary tool to capture two symmetric models in one. Flowchart of the model is given in Fig. 1.

The epidemiological reproduction number of strain k in system (3.1) is given by the following expression:

$$\begin{aligned} {\mathcal {R}}_{k}=\int _{0}^{\infty } \beta _{k}(\tau ) e^{-\int _{0}^{\tau } m_{k}(V_{k}(\sigma )) \mathrm {d} \sigma } \mathrm {d} \tau . \end{aligned}$$

(3.2)

The system (3.1) has one disease-free equilibrium and two strain dominance equilibria. The disease-free equilibrium always exists and is given by

$$\begin{aligned} {\mathcal {E}}_{0}=(S_{0}^{*},0,0,0), \end{aligned}$$

where

$$\begin{aligned} S_{0}^{*}=\frac{\Lambda }{m_{0}}. \end{aligned}$$

We assume that the stain 1 dominance equilibrium is ${\mathcal {E}}_{1}=(S_{1}^{*},i_{1}^{*},0,0)$. Then ${\mathcal {E}}_{1}$ satisfies the following equations:

$$\begin{aligned}&0 =\Lambda -\frac{S_{1}^{*}}{N_{1}^{*}} \int _{0}^{\infty } \beta _{1}(\tau ) i_{1}^{*}(\tau ) \mathrm {d} \tau -m_{0} S_{1}^{*}\nonumber \\&\frac{\mathrm {d} i_{1}^{*}(\tau )}{\mathrm {d} \tau } =-m_{1}(V_{1}(\tau )) i_{1}^{*} \nonumber \\&i_{1}^{*}(0) =\frac{S_{1}^{*}}{N_{1}^{*}} \int _{0}^{\infty } \beta _{1}(\tau ) i_{1}^{*}(\tau ) \mathrm {d} \tau \end{aligned}$$

(3.3)

From the second and third equations in Eq. (3.3), we obtain

$$\begin{aligned} i_{1}^{*}(\tau )=i_{1}^{*}(0)e^{-\int _{0}^{\tau } m_{1}(V_{1}(\sigma )) \mathrm {d} \sigma }. \end{aligned}$$

Replacing $i_{1}^{*}(\tau )$ in the equation for $i_{1}^{*}(0)$, we have

$$\begin{aligned} i_{1}^{*}(0)&=\frac{S_{1}^{*}}{N_{1}^{*}} \int _{0}^{\infty } \beta _{1}(\tau ) i_{1}^{*}(0)e^{-\int _{0}^{\tau } m_{1}(V_{1}(\sigma )) \mathrm {d} \sigma } \mathrm {d} \tau \\&=i_{1}^{*}(0)\frac{S_{1}^{*}}{N_{1}^{*}} \int _{0}^{\infty } \beta _{1}(\tau ) e^{-\int _{0}^{\tau } m_{1}(V_{1}(\sigma )) \mathrm {d} \sigma } \mathrm {d} \tau . \end{aligned}$$

Eliminating $i_{1}^{*}(0)$, we then have

$$\begin{aligned} \frac{S_{1}^{*}}{N_{1}^{*}}=\frac{1}{\int _{0}^{\infty } \beta _{1}(\tau ) e^{-\int _{0}^{\tau } m_{1}(V_{1}(\sigma )) \mathrm {d} \sigma } \mathrm {d} \tau }. \end{aligned}$$

Because

$$\begin{aligned} \frac{S_{1}^{*}}{N_{1}^{*}}+\frac{\int _{0}^{\infty } i_{1}^{*}(\tau ) \mathrm {d} \tau }{N_{1}^{*}}=1, \end{aligned}$$

we have

$$\begin{aligned} \frac{\int _{0}^{\infty } i_{1}^{*}(\tau ) \mathrm {d} \tau }{N_{1}^{*}}=\frac{\int _{0}^{\infty } i_{1}^{*}(0) e^{-\int _{0}^{\tau } m_{1}(V_{1}(\sigma )) \mathrm {d} \sigma } \mathrm {d} \tau }{N_{1}^{*}}=1-\frac{S_{1}^{*}}{N_{1}^{*}}=1-\frac{1}{{\mathcal {R}}_{1}}. \end{aligned}$$

From the first and third equations in (3.3), we obtain

$$\begin{aligned} \Lambda -i_{1}^{*}(0)-m_{0} S_{1}^{*}=0. \end{aligned}$$

Dividing both sides of the equation by $N_{1}^{*}$ and substituting $\frac{S_{1}^{*}}{N_{1}^{*}}$ and $\frac{i_{1}^{*}(0)}{N_{1}^{*}}$, we can get

$$\begin{aligned} \frac{\Lambda }{N_{1}^{*}}=\frac{1}{\int _{0}^{\infty }e^{-\int _{0}^{\tau } m_{1}(V_{1}(\sigma )) \mathrm {d} \sigma } \mathrm {d} \tau } \left( 1-\frac{1}{{\mathcal {R}}_{1}}\right) +m_{0} \frac{1}{{\mathcal {R}}_{1}}. \end{aligned}$$

The solution is

$$\begin{aligned} N_{1}^{*}=\frac{\Lambda \rho _{1} {\mathcal {R}}_{1}}{m_{0} \rho _{1}+{\mathcal {R}}_{1}-1}, \end{aligned}$$

where $\rho _{1}=\int _{0}^{\infty }e^{-\int _{0}^{\tau } m_{1}(V_{1}(\sigma )) \mathrm {d} \sigma } \mathrm {d} \tau$. Therefore, the components of the strain 1 dominance equilibrium are

$$\begin{aligned} S_{1}^{*}=\frac{\Lambda \rho _{1}}{m_{0} \rho _{1}+{\mathcal {R}}_{1}-1}, \quad i_{1}^{*}(\tau )=\frac{\Lambda \left( {\mathcal {R}}_{1}-1\right) }{m_{0} \rho _{1}+{\mathcal {R}}_{1}-1}e^{-\int _{0}^{\tau } m_{1}(V_{1}(\sigma )) \mathrm {d} \sigma } \end{aligned}$$

where

$$\begin{aligned} i_{1}^{*}(0)=\frac{\Lambda \left( {\mathcal {R}}_{1}-1\right) }{m_{0} \rho _{1}+{\mathcal {R}}_{1}-1}. \end{aligned}$$

Similarly, the strain 2 dominance equilibrium is

$$\begin{aligned} S_{2}^{*}=\frac{\Lambda \rho _{2}}{m_{0} \rho _{2}+{\mathcal {R}}_{2}-1}, \quad i_{2}^{*}(\tau )=\frac{\Lambda \left( {\mathcal {R}}_{2}-1\right) }{m_{0} \rho _{2}+{\mathcal {R}}_{2}-1}e^{-\int _{0}^{\tau } m_{2}(V_{2}(\sigma )) \mathrm {d} \sigma } \end{aligned}$$

where

$$\begin{aligned} i_{2}^{*}(0)=\frac{\Lambda \left( {\mathcal {R}}_{2}-1\right) }{m_{0} \rho _{2}+{\mathcal {R}}_{2}-1}, \quad \rho _{2}=\int _{0}^{\infty }e^{-\int _{0}^{\tau } m_{2}(V_{2}(\sigma )) \mathrm {d} \sigma } \mathrm {d} \tau , \end{aligned}$$

and

$$\begin{aligned} N_{2}^{*}=\frac{\Lambda \rho _{2} {\mathcal {R}}_{2}}{m_{0} \rho _{2}+{\mathcal {R}}_{2}-1}. \end{aligned}$$

We consider the equilibrium $(S^{*},0,0,j^{*})$. But through our analysis of the model, we can see that this is impossible.

Next, we study the linearized equations of the disease-free equilibrium. To introduce the linearization at the disease-free equilibrium ${\mathcal {E}}_{0}$, let $S(t)=S_{0}^{*}+x(t), i_{1}(\tau ,t)=z_{1}(\tau ,t),i_{2}(\tau ,t)=z_{2}(\tau ,t),j(\tau ,t)=w(\tau ,t)$. The linearized system is

$$\begin{aligned}&\frac{\mathrm {d} x}{\mathrm {d} t} =-\frac{S_{0}^{*}}{N_{0}^{*}} \int _{0}^{\infty } \beta _{1}(\tau ) \left( z_{1}(\tau ,t)+q_{1} w(\tau ,t)\right) \mathrm {d} \tau \nonumber \\&\qquad \qquad -\frac{S_{0}^{*}}{N_{0}^{*}} \int _{0}^{\infty } \beta _{2}(\tau ) \left( z_{2}(\tau ,t)+q_{2} w(\tau ,t)\right) \mathrm {d} \tau -m_{0} x \nonumber \\&\frac{\partial z_{1}}{\partial \tau }+\frac{\partial z_{1}}{\partial t} =-m(V_{1}(\tau )) z_{1}(\tau ,t) \nonumber \\&\quad z_{1}(0,t) =\frac{S_{0}^{*}}{N_{0}^{*}} \int _{0}^{\infty } \beta _{1}(\tau ) \left( z_{1}(\tau ,t)+q_{1} w(\tau ,t)\right) \mathrm {d} \tau \nonumber \\&\frac{\partial z_{2}}{\partial \tau }+\frac{\partial z_{2}}{\partial t} =-m(V_{2}(\tau )) z_{2}(\tau ,t) \nonumber \\&\quad z_{2}(0,t) =-\frac{S_{0}^{*}}{N_{0}^{*}} \int _{0}^{\infty } \beta _{2}(\tau ) \left( z_{2}(\tau ,t)+q_{2} w(\tau ,t)\right) \mathrm {d} \tau \nonumber \\&\frac{\partial w}{\partial \tau }+\frac{\partial w}{\partial t} =-m_{j}(V_{1},V_{2}) w(\tau ,t) \nonumber \\&\quad w(0,t) =0 \end{aligned}$$

(3.4)

We look for solutions of the form $x(t)={\bar{x}} e^{\lambda t}, z_{1}(\tau ,t)={\bar{z}}_{1}(\tau ) e^{\lambda t}, z_{2}(\tau ,t)={\bar{z}}_{2}(\tau ) e^{\lambda t}, w(\tau ,t)={\bar{w}}(\tau ) e^{\lambda t}$. Then, from the last two equations of the system (3.4), we have ${\bar{w}}(\tau )=0$. In addition, we obtain

$$\begin{aligned} \frac{\mathrm {d} {\bar{z}}_{k}(\tau )}{\mathrm {d} t}&=-\lambda {\bar{z}}_{k}(\tau )-m_{k}(V_{k}(\tau )) {\bar{z}}_{k}(\tau ) \\ {\bar{z}}_{k}(0)&=\frac{S_{0}^{*}}{N_{0}^{*}} \int _{0}^{\infty } \beta _{k}(\tau ) {\bar{z}}_{k}(\tau ) \mathrm {d} \tau \end{aligned}$$

where $S_{0}^{*}/N_{0}^{*}=1$. The solution of the differential equation is

$$\begin{aligned} {\bar{z}}_{k}(\tau )={\bar{z}}_{k}(0) e^{-\lambda \tau -\int _{0}^{\tau }m_{k}(V_{k}(\sigma )) \mathrm {d} \sigma }. \end{aligned}$$

Replacing ${\bar{z}}_{k}(\tau )$ in the equation for ${\bar{z}}_{k}(0)$, we obtain the following characteristic equation for strain k: ${\mathcal {H}}_{k}(\lambda )=1$, where

$$\begin{aligned} {\mathcal {H}}_{k}(\lambda )=\int _{0}^{\infty } \beta _{k}(\tau ) e^{-\lambda \tau -\int _{0}^{\tau }m_{k}(V_{k}(\sigma )) \mathrm {d} \sigma } \mathrm {d} \tau \end{aligned}$$

(3.5)

Therefore, we have the following result.

Proposition 3.1

If $\max \left\{ {\mathcal {R}}_{1},{\mathcal {R}}_{2}\right\} <1$, then the disease-free equilibrium is locally asymptotically stable. If $\max \left\{ {\mathcal {R}}_{1},{\mathcal {R}}_{2}\right\} >1$, it is unstable.

Proof

Assume

$$\begin{aligned} \max \left\{ {\mathcal {R}}_{1},{\mathcal {R}}_{2}\right\} <1. \end{aligned}$$

Consider $\lambda$ with $\mathfrak {R}\lambda \ge 0$ and for such $\lambda$ and each k, we have

$$\begin{aligned} \left| {\mathcal {H}}_{k}(\lambda )\right| \le {\mathcal {H}}_{k}(\mathfrak {R}\lambda ) \le {\mathcal {H}}_{k}(0)={\mathcal {R}}_{k}<1. \end{aligned}$$

Hence, $\mathfrak {R}\lambda <0$, in other words, the solutions of the equations ${\mathcal {H}}_{k}(\lambda )=1$ have negative real part. Thus, the disease-free equilibrium is locally asymptotically stable.

Now we assume

$$\begin{aligned} \max \left\{ {\mathcal {R}}_{1},{\mathcal {R}}_{2}\right\} ={\mathcal {R}}_{k}>1. \end{aligned}$$

If $\lambda =0$, and k is fixed, then we have ${\mathcal {H}}_{k}(0)={\mathcal {R}}_{k}>1$. In addition,

$$\begin{aligned} \lim _{\lambda \rightarrow \infty }{\mathcal {H}}_{k}(\lambda )=0. \end{aligned}$$

Therefore, the equation ${\mathcal {H}}_{k}(\lambda )=1$ has a real positive root. That is, the disease-free equilibrium is unstable. $\square$

To study the local stability of the strain k dominance equilibrium ${\mathcal {E}}_{k}$ for a fixed k, we recall that the equilibrium ${\mathcal {E}}_{k}$ exists if and only if the basic reproduction number corresponding to this strain ${\mathcal {R}}_{k}$ is greater than 1. So we assume that ${\mathcal {R}}_{k}>1$ for a fixed k. What is more, the local stability of the strain k dominance equilibrium depends on the invasion reproduction numbers ${\mathcal {R}}_{1}^{2}$ and ${\mathcal {R}}_{2}^{1}$ for each of the strains. We can give the expression of the invasion reproduction numbers of the first and the second strains:

$$\begin{aligned}&{\mathcal {R}}_{1}^{2} =\frac{S_{2}^{*}}{N_{2}^{*}} \int _{0}^{\infty } \beta _{1}(\tau ) e^{-\rho _{12} B_{2} \tau -\int _{0}^{\tau } m_{1}(V_{1}(\sigma )) \mathrm {d} \sigma } \mathrm {d} \tau \nonumber \\&\quad +q_{1}\left( \frac{\rho _{21}}{N_{2}^{*}}\int _{0}^{\infty } i_{2}^{*}(\tau ) \mathrm {d} \tau +\rho _{12} B_{2} \frac{S_{2}^{*}}{N_{2}^{*}} \cdot {\widetilde{B}}_{2}\right) \int _{0}^{\infty } \beta _{1}(\tau ) e^{-\int _{0}^{\tau } m_{j}(V_{1},V_{2}) \mathrm {d} \sigma } e^{-\theta _1P_1\tau }\mathrm {d} \tau \nonumber \\&{\mathcal {R}}_{2}^{1} =\frac{S_{1}^{*}}{N_{1}^{*}} \int _{0}^{\infty } \beta _{2}(\tau ) e^{-\rho _{21} B_{1} \tau -\int _{0}^{\tau } m_{2}(V_{2}(\sigma )) \mathrm {d} \sigma } \mathrm {d} \tau \nonumber \\&\quad +q_{2}\left( \frac{\rho _{12}}{N_{1}^{*}}\int _{0}^{\infty } i_{1}^{*}(\tau ) \mathrm {d} \tau +\rho _{21} B_{1} \frac{S_{1}^{*}}{N_{1}^{*}} \cdot {\widetilde{B}}_{1}\right) \int _{0}^{\infty } \beta _{2}(\tau ) e^{-\int _{0}^{\tau } m_{j}(V_{1},V_{2}) \mathrm {d} \sigma } e^{-\theta _2P_2\tau }\mathrm {d} \tau \nonumber \\ \end{aligned}$$

(3.6)

where

$$\begin{aligned} {\widetilde{B}}_{1}&=\int _{0}^{\infty } e^{-\int _{0}^{\tau } \left( m_{2}(V_{2}(\sigma ))+\rho _{21} B_{1}\right) \mathrm {d} \sigma } \mathrm {d} \tau , \quad B_{1}=\frac{1}{N_{1}^{*}} \int _{0}^{\infty } \beta _{1}(\tau ) i_{1}^{*}(\tau ) \mathrm {d} \tau , \\ {\widetilde{B}}_{2}&=\int _{0}^{\infty } e^{-\int _{0}^{\tau } \left( m_{1}(V_{1}(\sigma ))+\rho _{12} B_{2}\right) \mathrm {d} \sigma } \mathrm {d} \tau , \quad B_{2}=\frac{1}{N_{2}^{*}} \int _{0}^{\infty } \beta _{2}(\tau ) i_{2}^{*}(\tau ) \mathrm {d} \tau . \end{aligned}$$

The invasion number of the strain two at the equilibrium of strain one ${\mathcal {R}}_{2}^{1}$ gives the number of secondary infections one individual infected with strain two will produce in a population in which strain one is at equilibrium during her/his lifetime as infectious.

The results on the local stability of the strain k dominance equilibrium ${\mathcal {E}}_{k}$ are summarized as follows

Proposition 3.2

Assume for a fixed k, ${\mathcal {R}}_{k}>1$. If ${\mathcal {R}}_{i}^{k}<1$, for $i,k=1,2$, and $i \ne k$, then the strain k dominance equilibrium ${\mathcal {E}}_{k}$ is locally asymptotically stable. If ${\mathcal {R}}_{i}^{k}>1$, the strain k dominance equilibrium ${\mathcal {E}}_{k}$ is unstable.

Proof

In order to simplify the proof process, we will assume without loss of generality that $k=1$, that is, ${\mathcal {R}}_{1}>1$. We study the linearized equations around the strain one dominance equilibrium ${\mathcal {E}}_{1}$. We introduce the following notation for the perturbations $S(t)=S_{1}^{*}+x(t), i_{1}(\tau ,t)=i_{1}^{*}(\tau )+z_{1}(\tau ,t), i_{2}(\tau ,t)=z_{2}(\tau ,t), j(\tau ,t)=w(\tau ,t), N=N_{1}^{*}+n$. The linearized system around the strain one dominance equilibrium ${\mathcal {E}}_{1}$ becomes

$$\begin{aligned} \frac{\mathrm {d} x}{\mathrm {d} t}= & {} -\frac{x}{N_{1}^{*}} \int _{0}^{\infty } \beta _{1}(\tau ) i_{1}^{*}(\tau ) \mathrm {d} \tau -\frac{S_{1}^{*}}{N_{1}^{*}} \int _{0}^{\infty } \beta _{1}(\tau ) z_{1}(\tau ,t) \mathrm {d} \tau \nonumber \\&+\frac{S_{1}^{*}}{N_{1}^{*}} \cdot \frac{n}{N_{1}^{*}} \int _{0}^{\infty } \beta _{1}(\tau ) i_{1}^{*}(\tau ) \mathrm {d} \tau -\frac{S_{1}^{*}}{N_{1}^{*}} q_{1} \int _{0}^{\infty } \beta _{1}(\tau ) w(\tau ,t) \mathrm {d} \tau \nonumber \\&-\frac{S_{1}^{*}}{N_{1}^{*}} \int _{0}^{\infty } \beta _{2}(\tau ) \left( z_{2}(\tau ,t)+q_{2} w(\tau ,t)\right) -m_{0} x \nonumber \\ \frac{\partial z_{1}}{\partial \tau }+\frac{\partial z_{1}}{\partial t}= & {} -m_{1}(V_{1}(\tau )) z_{1}(\tau ,t) -\frac{\rho _{12}}{N_{1}^{*}} \int _{0}^{\infty } \beta _{2}(\tau ) \left( z_{2}(\tau ,t)+q_{2} w(\tau ,t)\right) \mathrm {d} \tau \cdot i_{1}^{*}(\tau )\nonumber \\&+\theta _{2} P_{2} w(\tau ,t) \nonumber \\ z_{1}(0,t)= & {} \frac{x}{N_{1}^{*}} \int _{0}^{\infty } \beta _{1}(\tau ) i_{1}^{*}(\tau ) \mathrm {d} \tau +\frac{S_{1}^{*}}{N_{1}^{*}} \int _{0}^{\infty } \beta _{1}(\tau ) z_{1}(\tau ,t) \mathrm {d} \tau \nonumber \\&-\frac{S_{1}^{*}}{N_{1}^{*}} \cdot \frac{n}{N_{1}^{*}} \int _{0}^{\infty } \beta _{1}(\tau ) i_{1}^{*}(\tau ) \mathrm {d} \tau +\frac{S_{1}^{*}}{N_{1}^{*}} q_{1} \int _{0}^{\infty } \beta _{1}(\tau ) w(\tau ,t) \mathrm {d} \tau \nonumber \\ \frac{\partial z_{2}}{\partial \tau }+\frac{\partial z_{2}}{\partial t}= & {} -m_{2}(V_{2}(\tau )) z_{2}(\tau ,t) -\frac{\rho _{21}}{N_{1}^{*}} \int _{0}^{*} \beta _{1}(\tau ) i_{1}^{*}(\tau ) \mathrm {d} \tau \cdot z_{2}(\tau ,t) +\theta _{1} P_{1} w(\tau ,t) \nonumber \\ z_{2}(0,t)= & {} \frac{S_{1}^{*}}{N_{1}^{*}} \int _{0}^{\infty } \beta _{2}(\tau ) \left( z_{2}(\tau ,t)+q_{2} w(\tau ,t) \right) \mathrm {d} \tau \nonumber \\ \frac{\partial w}{\partial \tau }+\frac{\partial w}{\partial t}= & {} -m_{j}(V_{1},V_{2}) w(\tau ,t) -\theta _{1} P_{1} w(\tau ,t) -\theta _{2} P_{2} w(\tau ,t) \nonumber \\ w(0,t)= & {} \frac{\rho _{12}}{N_{1}^{*}} \int _{0}^{\infty } \beta _{2}(\tau ) \left( z_{2}(\tau ,t)+q_{2} w(\tau ,t) \right) \mathrm {d} \tau \cdot \int _{0}^{\infty } i_{1}^{*}(\tau ) \mathrm {d} \tau \nonumber \\&+\frac{\rho _{21}}{N_{1}^{*}} \int _{0}^{\infty } \beta _{1}(\tau ) i_{1}^{*}(\tau ) \mathrm {d} \tau \cdot \int _{0}^{\infty } z_{2}(\tau ,t) \mathrm {d} \tau \end{aligned}$$

(3.7)

We look for exponential solutions of the form $x(t)=x e^{\lambda t}, z_{k}(\tau ,t)=z_{k}(\tau ) e^{\lambda t}, w(\tau ,t)=w(\tau ) e^{\lambda t}$. We are considering the case when the immune system is converging to strain 1 equilibrium, that is, $P_{1}=0$ and $P_{2}\ne 0$. Substituting $z_{2}(\tau ,t)=z_{2}(\tau ) e^{\lambda t}, w(\tau ,t)=w(\tau ) e^{\lambda t}$ into the differential equations of $z_{2}$ and w, we can obtain the following linear ordinary differential system

$$\begin{aligned} \left\{ \begin{aligned} \frac{\mathrm {d} z_{2}(\tau )}{\mathrm {d} \tau }&=-\lambda z_{2}(\tau ) -m_{2}(V_{2}(\tau )) z_{2}(\tau ) -\rho _{21} \cdot \frac{1}{N_{1}^{*}} \int _{0}^{\infty } \beta _{1}(\tau ) i_{1}^{*}(\tau ) \mathrm {d} \tau \cdot z_{2}(\tau ) \\ z_{2}(0)&=\frac{S_{1}^{*}}{N_{1}^{*}} \int _{0}^{\infty } \beta _{2}(\tau ) \left( z_{2}(\tau )+q_{2} w(\tau ) \right) \mathrm {d} \tau \\ \frac{\mathrm {d} w(\tau )}{\mathrm {d} \tau }&=-\lambda w(\tau ) -m_{j}(V_{1},V_{2}) w(\tau )-\theta _2 P_2 w(\tau ) \\ w(0)&=\frac{\rho _{12}}{N_{1}^{*}} \int _{0}^{\infty } \beta _{2}(\tau ) \left( z_{2}(\tau )+q_{2} w(\tau ) \right) \mathrm {d} \tau \cdot \int _{0}^{\infty } i_{1}^{*}(\tau ) \mathrm {d} \tau \\&\quad +\frac{\rho _{21}}{N_{1}^{*}} \int _{0}^{\infty } \beta _{1}(\tau ) i_{1}^{*}(\tau ) \mathrm {d} \tau \cdot \int _{0}^{\infty } z_{2}(\tau ) \mathrm {d} \tau \end{aligned}\right. \nonumber \\ \end{aligned}$$

(3.8)

Let

$$\begin{aligned} Z=\frac{1}{N_{1}^{*}} \int _{0}^{\infty } \beta _{2}(\tau ) \left( z_{2}(\tau )+q_{2} w(\tau ) \right) \mathrm {d} \tau . \end{aligned}$$

By solving Eq. (3.8), we can get

$$\begin{aligned} z_{2}(\tau )&=S_{1}^{*} Z \cdot e^{-\int _{0}^{\tau } \left( \lambda +m_{2}(V_{2}(\sigma ))+\rho _{21} B_{1}\right) \mathrm {d} \sigma } \\ w(\tau )&=\left[ \rho _{12} Z \cdot \int _{0}^{\infty } i_{1}^{*}(\tau ) \mathrm {d} \tau +\rho _{21} B_{1} S_{1}^{*} Z \int _{0}^{\infty } e^{-\lambda \tau } e^{-\int _{0}^{\tau } \left( m_{2}(V_{2}(\sigma ))+\rho _{21} B_{1}\right) \mathrm {d} \sigma } \mathrm {d} \tau \right] \\&\quad \cdot e^{-\lambda \tau - \theta _{2} P_{2} \tau -\int _{0}^{\tau } m_{j}(V_{1},V_{2}) \mathrm {d} \sigma } \end{aligned}$$

Note

$$\begin{aligned} \int _{0}^{\infty } e^{-\lambda \tau } e^{-\int _{0}^{\tau } \left( m_{2}(V_{2}(\sigma ))+\rho _{21} B_{1}\right) \mathrm {d} \sigma } \mathrm {d} \tau ={\widetilde{B}}_{1}(\lambda ). \end{aligned}$$

Substituting $z_{2}(\tau ),w(\tau )$ into Z and simplifying, we get

$$\begin{aligned} Z&=\frac{S_{1}^{*}}{N_{1}^{*}} Z \cdot \int _{0}^{\infty } \beta _{2}(\tau ) e^{-\lambda \tau } e^{-\int _{0}^{\tau } \left( m_{2}(V_{2}(\sigma ))+\rho _{21} B_{1}\right) \mathrm {d} \sigma } \mathrm {d} \tau \\&\quad +q_{2} \left( \frac{\rho _{12}}{N_{1}^{*}} Z \int _{0}^{\infty } i_{1}^{*}(\tau ) \mathrm {d} \tau +\rho _{21} B_{1} \frac{S_{1}^{*}}{N_{1}^{*}} Z {\widetilde{B}}_{1}(\lambda ) \right) \\&\qquad \int _{0}^{\infty } \beta _{2}(\tau ) e^{-\lambda \tau -\theta _2 P_2 \tau } e^{-\int _{0}^{\tau } m_{j}(V_{1},V_{2}) \mathrm {d} \sigma } \mathrm {d} \tau \end{aligned}$$

We can get rid of Z on both sides of this equation and obtain the following characteristic equation

$$\begin{aligned} 1&=\frac{S_{1}^{*}}{N_{1}^{*}} \cdot \int _{0}^{\infty } \beta _{2}(\tau ) e^{-\lambda \tau } e^{-\int _{0}^{\tau } \left( m_{2}(V_{2}(\sigma ))+\rho _{21} B_{1}\right) \mathrm {d} \sigma } \mathrm {d} \tau \nonumber \\&\quad +q_{2} \left( \frac{\rho _{12}}{N_{1}^{*}} \int _{0}^{\infty } i_{1}^{*}(\tau ) \mathrm {d} \tau +\rho _{21} B_{1} \frac{S_{1}^{*}}{N_{1}^{*}} {\widetilde{B}}_{1}(\lambda ) \right) \nonumber \\&\quad \int _{0}^{\infty } \beta _{2}(\tau ) e^{-\lambda \tau -\theta _2 P_2\tau } e^{-\int _{0}^{\tau } m_{j}(V_{1},V_{2}) \mathrm {d} \sigma } \mathrm {d} \tau \end{aligned}$$

(3.9)

We denote the right-hand side of the equation with ${\mathcal {L}}_{1}(\lambda )$, that is,

$$\begin{aligned} {\mathcal {L}}_{1}(\lambda )&=\frac{S_{1}^{*}}{N_{1}^{*}} \cdot \int _{0}^{\infty } \beta _{2}(\tau ) e^{-\lambda \tau } e^{-\int _{0}^{\tau } \left( m_{2}(V_{2}(\sigma ))+\rho _{21} B_{1}\right) \mathrm {d} \sigma } \mathrm {d} \tau \\&\quad +q_{2} \left( \frac{\rho _{12}}{N_{1}^{*}} \int _{0}^{\infty } i_{1}^{*}(\tau ) \mathrm {d} \tau +\rho _{21} B_{1} \frac{S_{1}^{*}}{N_{1}^{*}} {\widetilde{B}}_{1}(\lambda ) \right) \\&\qquad \int _{0}^{\infty } \beta _{2}(\tau ) e^{-\lambda \tau -\theta _2 P_2\tau } e^{-\int _{0}^{\tau } m_{j}(V_{1},V_{2}) \mathrm {d} \sigma } \mathrm {d} \tau \end{aligned}$$

We can find that ${\mathcal {L}}_{1}(\lambda )$ is a decreasing function of $\lambda$ for $\lambda$ is real. Moreover,

$$\begin{aligned} \lim _{\lambda \rightarrow \infty } {\mathcal {L}}_{1}(\lambda ) =0, \end{aligned}$$

and ${\mathcal {L}}_{1}(0)={\mathcal {R}}_{2}^{1}$. If ${\mathcal {R}}_{2}^{1}>1$, then Eq. (3.9) has at least one positive real root. Hence, the strain one dominance equilibrium ${\mathcal {E}}_{1}$ is unstable. If ${\mathcal {R}}_{2}^{1}<1$, for $\lambda$ with $\mathfrak {R}\lambda \ge 0$, then we have

$$\begin{aligned} \left| {\mathcal {L}}_{1}(\lambda )\right| \le {\mathcal {L}}_{1}(\mathfrak {R}\lambda ) \le {\mathcal {L}}_{1}(0)<1. \end{aligned}$$

Therefore, all the eigenvalues of the equation ${\mathcal {L}}_{1}(\lambda )=1$ have negative real part. In addition, the stability of ${\mathcal {E}}_{1}$ also depends on the eigenvalues of the following system

$$\begin{aligned} \lambda x= & {} -\frac{x}{N_{1}^{*}} \int _{0}^{\infty } \beta _{1}(\tau ) i_{1}^{*}(\tau ) \mathrm {d} \tau - \frac{S_{1}^{*}}{N_{1}^{*}} \int _{0}^{\infty } \beta _{1}(\tau ) z_{1}(\tau ) \mathrm {d} \tau \nonumber \\&+ \frac{S_{1}^{*}}{N_{1}^{*}} \cdot \frac{n}{N_{1}^{*}} \int _{0}^{\infty } \beta _{1}(\tau ) i_{1}^{*}(\tau ) \mathrm {d} \tau -m_{0} x \nonumber \\ \frac{\mathrm {d} z_{1}(\tau )}{\mathrm {d} \tau }= & {} -\lambda z_{1}(\tau ) -m_{1}(V_{1}(\tau )) z_{1}(\tau ) \nonumber \\ z_{1}(0)= & {} \frac{x}{N_{1}^{*}} \int _{0}^{\infty } \beta _{1}(\tau ) i_{1}^{*}(\tau ) \mathrm {d} \tau + \frac{S_{1}^{*}}{N_{1}^{*}} \int _{0}^{\infty } \beta _{1}(\tau ) z_{1}(\tau ) \mathrm {d} \tau \nonumber \\&- \frac{S_{1}^{*}}{N_{1}^{*}} \cdot \frac{n}{N_{1}^{*}} \int _{0}^{\infty } \beta _{1}(\tau ) i_{1}^{*}(\tau ) \mathrm {d} \tau \end{aligned}$$

(3.10)

Solving the differential equation, we obtain

$$\begin{aligned} z_{1}(\tau )=z_{1}(0) e^{-\lambda \tau - \int _{0}^{\tau } m_{1}(V_{1}(\sigma )) \mathrm {d} \sigma }. \end{aligned}$$

To facilitate the calculation, we apply the notation

$$\begin{aligned} \rho _{1}(\lambda )&=\int _{0}^{\infty } e^{-\lambda \tau - \int _{0}^{\tau } m_{1}(V_{1}(\sigma )) \mathrm {d} \sigma } \mathrm {d} \tau \\ {\mathcal {R}}_{1}(\lambda )&=\int _{0}^{\infty } \beta _{1}(\tau ) e^{-\lambda \tau - \int _{0}^{\tau } m_{1}(V_{1}(\sigma )) \mathrm {d} \sigma } \mathrm {d} \tau . \end{aligned}$$

From the first and third equations in Eq. (3.10), we obtain

$$\begin{aligned} \lambda x =-z_{1}(0)-m_{0} x. \end{aligned}$$

The solution is

$$\begin{aligned} x=-\frac{z_{1}(0)}{\lambda +m_{0}}. \end{aligned}$$

(3.11)

Moreover, linearizing the equation for the total population size

$$\begin{aligned} N=S+\int _{0}^{\infty } i_{1}(\tau ,t) \mathrm {d} \tau +\int _{0}^{\infty } i_{2}(\tau ,t) \mathrm {d} \tau + \int _{0}^{\infty } j(\tau ,t) \mathrm {d} \tau , \end{aligned}$$

we have

$$\begin{aligned} n=x+\int _{0}^{\infty } z_{1}(\tau ) \mathrm {d} \tau , \end{aligned}$$

that is,

$$\begin{aligned} n=-\frac{z_{1}(0)}{\lambda +m_{0}}+z_{1}(0) \rho _{1}(\lambda ). \end{aligned}$$

(3.12)

Substituting (3.11) and (3.12) in the equation for $z_{1}(0)$ and canceling $z_{1}(0)$ from both sides of the resulting equation, we can obtain the characteristic equation for $\lambda$: ${\mathcal {F}}_{1}(\lambda )=1$, where

$$\begin{aligned} {\mathcal {F}}_{1}(\lambda )=\frac{1}{\lambda +m_{0}} \cdot \frac{i_{1}^{*}(0)}{N_{1}^{*}} \left[ 1-\frac{N_{1}^{*}}{S_{1}^{*}}\right] -\frac{i_{1}^{*}(0)}{N_{1}^{*}} \rho _{1}(\lambda ) +\frac{S_{1}^{*}}{N_{1}^{*}} {\mathcal {R}}_{1}(\lambda ). \end{aligned}$$

From $\beta _{1}(\tau )=c_{1}V_{1}(\tau )$ and $m_{1}(V_{1}(\tau ))=m_{0}+m_{1}V_{1}(\tau )$ and integration by parts, we have

$$\begin{aligned} {\mathcal {R}}_{1}(\lambda )&=\int _{0}^{\infty } \beta _{1}(\tau ) e^{-\lambda \tau - \int _{0}^{\tau } m_{1}(V_{1}(\sigma )) \mathrm {d} \sigma } \mathrm {d} \tau \\&=c_{1} \int _{0}^{\infty } V_{1}(\tau ) e^{-\left( \lambda +m_{0}\right) \tau } e^{-m_{1} \int _{0}^{\tau } V_{1}(\sigma ) \mathrm {d} \sigma } \mathrm {d} \tau \\&=\frac{c_{1}}{m_{1}} \left[ 1-\left( \lambda +m_{0} \right) \rho _{1}(\lambda ) \right] . \end{aligned}$$

Then we can obtain

$$\begin{aligned} \rho _{1}(\lambda )=\frac{1}{\lambda +m_{0}} \left[ 1-\frac{m_{1}}{c_{1}} {\mathcal {R}}_{1}(\lambda ) \right] . \end{aligned}$$

For $\lambda =0$, we have

$$\begin{aligned} {\mathcal {R}}_{1}=\frac{c_{1}}{m_{1}} \left[ 1-m_{0} \rho _{1} \right] . \end{aligned}$$

Besides, from the previous calculation, we know that

$$\begin{aligned} \frac{S_{1}^{*}}{N_{1}^{*}}=\frac{1}{{\mathcal {R}}_{1}}, \quad \frac{i_{1}^{*}(0)}{N_{1}^{*}}=\frac{{\mathcal {R}}_{1}-1}{{\mathcal {R}}_{1} \rho _{1}}. \end{aligned}$$

Substituting above result in Equation ${\mathcal {F}}_{1}(\lambda )=1$, we get

$$\begin{aligned} \frac{\lambda +m_{0}+\left( {\mathcal {R}}_{1}-1\right) /\rho _{1}}{\lambda +m_{0}+(m_{1}/c_{1})\left( {\mathcal {R}}_{1}-1\right) /\rho _{1}} =\frac{1}{{\mathcal {R}}_{1}} {\mathcal {R}}_{1}(\lambda ). \end{aligned}$$

Because ${\mathcal {R}}_{1}>1$ implies $m_{1}/c_{1}<1$, we have

$$\begin{aligned} \left| \frac{\lambda +m_{0}+\left( {\mathcal {R}}_{1}-1\right) /\rho _{1}}{\lambda +m_{0} +(m_{1}/c_{1}) \left( {\mathcal {R}}_{1}-1\right) /\rho _{1}} \right| >1. \end{aligned}$$

On the other hand, for $\lambda$ with $\mathfrak {R}\lambda \ge 0$,

$$\begin{aligned} \left| \frac{1}{{\mathcal {R}}_{1}} {\mathcal {R}}_{1}(\lambda ) \right| \le \frac{1}{{\mathcal {R}}_{1}} {\mathcal {R}}_{1}(\mathfrak {R}\lambda ) < \frac{1}{{\mathcal {R}}_{1}} {\mathcal {R}}_{1}(0)=1. \end{aligned}$$

Therefore, the characteristic equation ${\mathcal {F}}_{1}(\lambda )=1$ only has solutions with negative real parts. That is, the strain one dominance equilibrium ${\mathcal {E}}_{1}$ is locally asymptotically stable. This completes the proof. $\square$

From the above discussion, we saw that if for exactly one strain the corresponding basic reproduction number and invasion reproduction number are greater than one, the disease becomes endemic and the single-strain equilibrium will be locally asymptotically stable. If all reproduction numbers are less than one, all strains are eliminated and the disease dies out. Moreover, this conclusion can also extended to the case of multiple strains.

4 Existence of Coexistence Equilibrium

In this section, we discuss the existence of an coexistence equilibrium for which both strains are present with coinfection. We consider the coexistence equilibrium when the two basic reproduction numbers ${\mathcal {R}}_{k}$ and the two invasion reproduction numbers ${\mathcal {R}}_{j}^{k}$ corresponding to each strain are all greater than one. In this case, $P_{1}=P_{2}=0$. We assume ${\mathcal {E}}^{*}=(S^{*},i_{1}^{*}(\tau ),i_{2}^{*}(\tau ),j^{*}(\tau ))$ is the coexistence equilibrium of the system (3.1). The coexistence equilibrium satisfies the following equations

$$\begin{aligned} 0= & {} \Lambda -\frac{S^{*}}{N^{*}} \int _{0}^{\infty } \beta _{1}(\tau ) \left( i_{1}^{*}(\tau ) + q_{1} j^{*}(\tau ) \right) \mathrm {d} \tau \nonumber \\&-\frac{S^{*}}{N^{*}} \int _{0}^{\infty } \beta _{2}(\tau ) \left( i_{2}^{*}(\tau ) + q_{2} j^{*}(\tau ) \right) \mathrm {d} \tau -m_{0} S^{*} \nonumber \\ \frac{\mathrm {d} i_{1}^{*}(\tau )}{\mathrm {d} \tau }= & {} -m_{1}(V_{1}(\tau )) i_{1}^{*}(\tau ) -\rho _{12} \int _{0}^{\infty } \beta _{2}(\tau ) \left( i_{2}^{*}(\tau ) + q_{2} j^{*}(\tau ) \right) \mathrm {d} \tau \cdot \frac{i_{1}^{*}(\tau )}{N^{*}} \nonumber \\ i_{1}^{*}(0)= & {} \frac{S^{*}}{N^{*}} \int _{0}^{\infty } \beta _{1}(\tau ) \left( i_{1}^{*}(\tau ) + q_{1} j^{*}(\tau ) \right) \mathrm {d} \tau \nonumber \\ \frac{\mathrm {d} i_{2}^{*}(\tau )}{\mathrm {d} \tau }= & {} -m_{2}(V_{2}(\tau )) i_{2}^{*}(\tau ) -\rho _{21} \int _{0}^{\infty } \beta _{1}(\tau ) \left( i_{1}^{*}(\tau ) + q_{1} j^{*}(\tau ) \right) \mathrm {d} \tau \cdot \frac{i_{2}^{*}(\tau )}{N^{*}} \nonumber \\ i_{2}^{*}(0)= & {} \frac{S^{*}}{N^{*}} \int _{0}^{\infty } \beta _{2}(\tau ) \left( i_{2}^{*}(\tau ) + q_{2} j^{*}(\tau ) \right) \mathrm {d} \tau \nonumber \\ \frac{\mathrm {d} j^{*}(\tau )}{\mathrm {d} \tau }= & {} -m_{j}(V_{1},V_{2}) j^{*}(\tau ) \nonumber \\ j^{*}(0)= & {} \frac{\rho _{12}}{N^{*}} \int _{0}^{\infty } \beta _{2}(\tau ) \left( i_{2}^{*}(\tau ) + q_{2} j^{*}(\tau ) \right) \mathrm {d} \tau \cdot \int _{0}^{\infty } i_{1}^{*}(\tau ) \mathrm {d} \tau \nonumber \\&+\frac{\rho _{21}}{N^{*}} \int _{0}^{\infty } \beta _{1}(\tau ) \left( i_{1}^{*}(\tau ) + q_{1} j^{*}(\tau ) \right) \mathrm {d} \tau \cdot \int _{0}^{\infty } i_{2}^{*}(\tau ) \mathrm {d} \tau \end{aligned}$$

(4.1)

where $m_{j}(V_{1},V_{2})=m_{0}+{\widetilde{m}}_{1}V_{1}+{\widetilde{m}}_{2}V_{2}$.

Define

$$\begin{aligned} Q_{1}&= \frac{1}{N^{*}} \int _{0}^{\infty } \beta _{1}(\tau ) \left( i_{1}^{*}(\tau ) + q_{1} j^{*}(\tau ) \right) \mathrm {d} \tau , \\ Q_{2}&= \frac{1}{N^{*}} \int _{0}^{\infty } \beta _{2}(\tau ) \left( i_{2}^{*}(\tau ) + q_{2} j^{*}(\tau ) \right) \mathrm {d} \tau , \end{aligned}$$

then the system (4.1) becomes

$$\begin{aligned}&0 = \Lambda - S^{*} Q_{1} -S^{*} Q_{2} - m_{0} S^{*} \nonumber \\&\frac{\mathrm {d} i_{1}^{*}(\tau )}{\mathrm {d} \tau } =-m_{1}(V_{1}(\tau )) i_{1}^{*}(\tau ) -\rho _{12} Q_{2} i_{1}^{*}(\tau ) \nonumber \\&i_{1}^{*}(0) = S^{*} Q_{1} \nonumber \\&\frac{\mathrm {d} i_{2}^{*}(\tau )}{\mathrm {d} \tau } =-m_{2}(V_{2}(\tau )) i_{2}^{*}(\tau ) -\rho _{21} Q_{1} i_{2}^{*}(\tau ) \nonumber \\&i_{2}^{*}(0) = S^{*} Q_{2} \nonumber \\&\frac{\mathrm {d} j^{*}(\tau )}{\mathrm {d} \tau } =-m_{j}(V_{1},V_{2}) j^{*}(\tau ) \nonumber \\&j^{*}(0) =\rho _{12} Q_{2} \cdot \int _{0}^{\infty } i_{1}^{*}(\tau ) \mathrm {d} \tau +\rho _{21} Q_{1} \cdot \int _{0}^{\infty } i_{2}^{*}(\tau ) \mathrm {d} \tau \end{aligned}$$

(4.2)

We solve Eq. (4.2) and obtain

$$\begin{aligned} S^{*}&=\frac{\Lambda }{Q_{1}+Q_{2}+m_{0}} \\ i_{1}^{*}(\tau )&=S^{*} Q_{1} e^{-\int _{0}^{\tau } \left( m_{1}(V_{1}(\sigma ))+\rho _{12} Q_{2}\right) \mathrm {d} \sigma }=S^{*} Q_{1} e^{-\rho _{12} Q_{2} \tau } e^{-\int _{0}^{\tau } m_{1}(V_{1}(\sigma )) \mathrm {d} \sigma } \\ i_{2}^{*}(\tau )&=S^{*} Q_{2} e^{-\int _{0}^{\tau } \left( m_{2}(V_{2}(\sigma ))+\rho _{21} Q_{1}\right) \mathrm {d} \sigma }=S^{*} Q_{2} e^{-\rho _{21} Q_{1} \tau } e^{-\int _{0}^{\tau } m_{2}(V_{2}(\sigma )) \mathrm {d} \sigma } \\ j^{*}(\tau )&=\left( \rho _{12} Q_{2} \cdot \int _{0}^{\infty } i_{1}^{*}(\tau ) \mathrm {d} \tau +\rho _{21} Q_{1} \cdot \int _{0}^{\infty } i_{2}^{*}(\tau ) \mathrm {d} \tau \right) e^{-\int _{0}^{\tau } m_{j}(V_{1},V_{2}) \mathrm {d} \sigma } \end{aligned}$$

First, substituting $i_{1}^{*}(\tau ),i_{2}^{*}(\tau )$ in the expression of $j^{*}(\tau )$, we have

$$\begin{aligned} j^{*}(\tau )&= \Big (\rho _{12} Q_{2} \cdot S^{*} Q_{1} \int _{0}^{\infty } e^{-\rho _{12} Q_{2} \tau -\int _{0}^{\tau } m_{1}(V_{1}(\sigma )) \mathrm {d} \sigma } \mathrm {d} \tau \\&\quad +\rho _{21} Q_{1} \cdot S^{*} Q_{2} \int _{0}^{\infty } e^{-\rho _{21} Q_{1} \tau -\int _{0}^{\tau } m_{2}(V_{2}(\sigma )) \mathrm {d} \sigma } \mathrm {d} \tau \Big ) e^{-\int _{0}^{\tau } m_{j}(V_{1},V_{2}) \mathrm {d} \sigma } \end{aligned}$$

Next, we substitute $i_{1}^{*}(\tau ),j^{*}(\tau )$ in the expression of $Q_{1}$ and obtain

$$\begin{aligned} Q_{1}&=\frac{1}{N^{*}} \bigg [ S^{*} Q_{1} \int _{0}^{\infty } \beta _{1}(\tau ) e^{-\rho _{12} Q_{2} \tau -\int _{0}^{\tau } m_{1}(V_{1}(\sigma )) \mathrm {d} \sigma } \mathrm {d} \tau \\&\quad +q_{1} Q_{1} Q_{2} S^{*} \Big ( \rho _{12} \int _{0}^{\infty } e^{-\rho _{12} Q_{2} \tau -\int _{0}^{\tau } m_{1}(V_{1}(\sigma )) \mathrm {d} \sigma } \mathrm {d} \tau \\&\quad + \rho _{21} \int _{0}^{\infty } e^{-\rho _{21} Q_{1} \tau -\int _{0}^{\tau } m_{2}(V_{2}(\sigma )) \mathrm {d} \sigma } \mathrm {d} \tau \Big ) \cdot \int _{0}^{\infty } \beta _{1}(\tau ) e^{-\int _{0}^{\tau } m_{j}(V_{1},V_{2}) \mathrm {d} \sigma } \mathrm {d} \tau \bigg ]. \end{aligned}$$

Let

$$\begin{aligned} f_{1}(Q_{2})&=\int _{0}^{\infty } \beta _{1}(\tau ) e^{-\rho _{12} Q_{2} \tau -\int _{0}^{\tau } m_{1}(V_{1}(\sigma )) \mathrm {d} \sigma } \mathrm {d} \tau , \\ g_{1}(Q_{1},Q_{2})&=q_{1} Q_{2} \bigg ( \rho _{12} \int _{0}^{\infty } e^{-\rho _{12} Q_{2} \tau -\int _{0}^{\tau } m_{1}(V_{1}(\sigma )) \mathrm {d} \sigma } \mathrm {d} \tau + \rho _{21}\\&\quad \int _{0}^{\infty } e^{-\rho _{21} Q_{1} \tau -\int _{0}^{\tau } m_{2}(V_{2}(\sigma )) \mathrm {d} \sigma } \mathrm {d} \tau \bigg ), \end{aligned}$$

then

$$\begin{aligned} Q_{1}=\frac{S^{*}}{N^{*}} Q_{1} \left[ f_{1}(Q_{2})+g_{1}(Q_{1},Q_{2}) \int _{0}^{\infty } \beta _{1}(\tau ) e^{-\int _{0}^{\tau } m_{j}(V_{1},V_{2}) \mathrm {d} \sigma } \mathrm {d} \tau \right] . \end{aligned}$$

Canceling $Q_{1}$, we can get

$$\begin{aligned} 1=\frac{S^{*}}{N^{*}} \left[ f_{1}(Q_{2})+g_{1}(Q_{1},Q_{2}) \int _{0}^{\infty } \beta _{1}(\tau ) e^{-\int _{0}^{\tau } m_{j}(V_{1},V_{2}) \mathrm {d} \sigma } \mathrm {d} \tau \right] . \end{aligned}$$

Similarly, we can also obtain

$$\begin{aligned} 1=\frac{S^{*}}{N^{*}} \left[ f_{2}(Q_{1})+g_{2}(Q_{1},Q_{2}) \int _{0}^{\infty } \beta _{2}(\tau ) e^{-\int _{0}^{\tau } m_{j}(V_{1},V_{2}) \mathrm {d} \sigma } \mathrm {d} \tau \right] . \end{aligned}$$

To determine the expression of $N^{*}$, we note ${\widetilde{m}}_{1}=q_{1} m_{1},{\widetilde{m}}_{2}=q_{2} m_{2}$, then

$$\begin{aligned} \frac{\mathrm {d} N}{\mathrm {d} t}&= \Lambda -m_{0} S -m_{0} \int _{0}^{\infty } i_{1}(\tau ,t) \mathrm {d} \tau -\frac{m_{1}}{c_{1}} \int _{0}^{\infty } c_{1} V_{1}(\tau ) i_{1}(\tau ,t) \mathrm {d} \tau \\&\quad -m_{0} \int _{0}^{\infty } i_{2}(\tau ,t) \mathrm {d} \tau - \frac{m_{2}}{c_{2}} \int _{0}^{\infty } c_{2} V_{2}(\tau ) i_{2}(\tau ,t) \mathrm {d} \tau -m_{0} \int _{0}^{\infty } j(\tau ,t) \mathrm {d} \tau \\&\quad -\frac{q_{1} m_{1}}{c_{1} q_{1}} \int _{0}^{\infty } q_{1} c_{1} V_{1}(\tau ) j(\tau ,t) \mathrm {d} \tau - \frac{q_{2} m_{2}}{c_{2} q_{2}} \int _{0}^{\infty } q_{2} c_{2} V_{2}(\tau ) j(\tau ,t) \mathrm {d} \tau . \end{aligned}$$

Simplifying the above equation, we get

$$\begin{aligned} \frac{\mathrm {d} N}{\mathrm {d} t}&= \Lambda -m_{0} \left( S + \int _{0}^{\infty } i_{1}(\tau ,t) \mathrm {d} \tau + \int _{0}^{\infty } i_{2}(\tau ,t) \mathrm {d} \tau + \int _{0}^{\infty } j(\tau ,t) \mathrm {d} \tau \right) \\&\quad -\frac{m_{1}}{c_{1}} \int _{0}^{\infty } c_{1} V_{1}(\tau ) \left( i_{1}(\tau ,t)+q_{1} j(\tau ,t) \right) \mathrm {d} \tau \\&\quad - \frac{m_{2}}{c_{2}} \int _{0}^{\infty } c_{2} V_{2}(\tau ) \left( i_{2}(\tau ,t)+q_{2} j(\tau ,t) \right) \mathrm {d} \tau . \end{aligned}$$

It follows that

$$\begin{aligned} 0=\Lambda -m_{0} N^{*}-\frac{m_{1}}{c_{1}} Q_{1} N^{*}-\frac{m_{2}}{c_{2}} Q_{2} N^{*}. \end{aligned}$$

The solution is

$$\begin{aligned} N^{*}=\frac{\Lambda }{m_{0}+\alpha _{1} Q_{1}+\alpha _{2} Q_{2}},\quad \text {where} \quad \alpha _{1}=\frac{m_{1}}{c_{1}}, \quad \alpha _{2}=\frac{m_{2}}{c_{2}}. \end{aligned}$$

Therefore, the coexistence equilibrium satisfies the following equations

$$\begin{aligned} \begin{aligned} 1&=\frac{S^{*}}{N^{*}} \left[ f_{1}(Q_{2})+g_{1}(Q_{1},Q_{2}) \int _{0}^{\infty } \beta _{1}(\tau ) e^{-\int _{0}^{\tau } m_{j}(V_{1},V_{2}) \mathrm {d} \sigma } \mathrm {d} \tau \right] , \\ 1&=\frac{S^{*}}{N^{*}} \left[ f_{2}(Q_{1})+g_{2}(Q_{1},Q_{2}) \int _{0}^{\infty } \beta _{2}(\tau ) e^{-\int _{0}^{\tau } m_{j}(V_{1},V_{2}) \mathrm {d} \sigma } \mathrm {d} \tau \right] , \end{aligned} \end{aligned}$$

(4.3)

where

$$\begin{aligned} f_{2}(Q_{1})&=\int _{0}^{\infty } \beta _{2}(\tau ) e^{-\rho _{21} Q_{1} \tau -\int _{0}^{\tau } m_{2}(V_{2}(\sigma )) \mathrm {d} \sigma },\\ g_{2}(Q_{1},Q_{2})&=q_{2} Q_{1} \bigg ( \rho _{21} \int _{0}^{\infty } e^{-\rho _{21} Q_{1} \tau -\int _{0}^{\tau } m_{2}(V_{2}(\sigma )) \mathrm {d} \sigma } \mathrm {d} \tau + \rho _{12}\\&\quad \int _{0}^{\infty } e^{-\rho _{12} Q_{2} \tau -\int _{0}^{\tau } m_{1}(V_{1}(\sigma )) \mathrm {d} \sigma } \mathrm {d} \tau \bigg ). \end{aligned}$$

Setting

$$\begin{aligned} F_{1}(Q_{1},Q_{2})&=\frac{S^{*}}{N^{*}} \left[ f_{1}(Q_{2})+g_{1}(Q_{1},Q_{2}) \int _{0}^{\infty } \beta _{1}(\tau ) e^{-\int _{0}^{\tau } m_{j}(V_{1},V_{2}) \mathrm {d} \sigma } \mathrm {d} \tau \right] , \\ F_{2}(Q_{1},Q_{2})&=\frac{S^{*}}{N^{*}} \left[ f_{2}(Q_{1})+g_{2}(Q_{1},Q_{2}) \int _{0}^{\infty } \beta _{2}(\tau ) e^{-\int _{0}^{\tau } m_{j}(V_{1},V_{2}) \mathrm {d} \sigma } \mathrm {d} \tau \right] . \end{aligned}$$

Then, we need to show that the equation $F_{1}(Q_{1},Q_{2})=1$ and $F_{2}(Q_{1},Q_{2})=1$ have real solutions. From the above equations, we can observe that $F_{1}(Q_{1},Q_{2})$ decreases with respect to $Q_{1}$ and $F_{2}(Q_{1},Q_{2})$ decreases with respect to $Q_{2}$. From the expression of $S^{*}$ and $N^{*}$, we have

$$\begin{aligned} \frac{S^{*}}{N^{*}}= \frac{m_{0}+\alpha _{1} Q_{1}+\alpha _{2} Q_{2}}{m_{0}+Q_{1}+Q_{2}}. \end{aligned}$$

Let $C_{1}=\int _{0}^{\infty } \beta _{1}(\tau ) e^{-\int _{0}^{\tau } m_{j}(V_{1},V_{2}) \mathrm {d} \sigma } \mathrm {d} \tau$, $C_{2}=\int _{0}^{\infty } \beta _{2}(\tau ) e^{-\int _{0}^{\tau } m_{j}(V_{1},V_{2}) \mathrm {d} \sigma } \mathrm {d} \tau$. Hence,

$$\begin{aligned} F_{1}(0,0)&=\int _{0}^{\infty } \beta _{1}(\tau ) e^{-\int _{0}^{\tau } m_{1}(V_{1}(\sigma )) \mathrm {d} \sigma } \mathrm {d} \tau = {\mathcal {R}}_{1}>1,\\ F_{1}(0,Q_{2})&=\frac{m_{0}+\alpha _{2} Q_{2}}{m_{0}+Q_{2}} \left[ f_{1}(Q_{2})+g_{1}(0,Q_{2}) C_{1} \right] . \end{aligned}$$

Since $Q_{2}^{*}=({\mathcal {R}}_{2}-1)/\rho _{2}=B_{2}$, then

$$\begin{aligned} F_{1}(0,Q_{2}^{*})&=\frac{S_{2}^{*}}{N_{2}^{*}} \bigg [ \int _{0}^{\infty } \beta _{1}(\tau ) e^{-\rho _{12} B_{2} \tau -\int _{0}^{\tau } m_{1}(V_{1}(\sigma )) \mathrm {d} \sigma } \mathrm {d} \tau \\&\quad +q_{1} \frac{\int _{0}^{\infty } \beta _{2}(\tau ) i_{2}^{*}(\tau ) \mathrm {d} \tau }{N_{2}^{*}} \bigg ( \rho _{12} \int _{0}^{\infty } e^{-\rho _{12} Q_{2} \tau -\int _{0}^{\tau } m_{1}(V_{1}(\sigma )) \mathrm {d} \sigma } \mathrm {d} \tau \\&\quad + \rho _{21} \int _{0}^{\infty } e^{-\int _{0}^{\tau } m_{2}(V_{2}(\sigma )) \mathrm {d} \sigma } \mathrm {d} \tau \bigg ) C_{1} \bigg ] \\&=\frac{S_{2}^{*}}{N_{2}^{*}} \int _{0}^{\infty } \beta _{1}(\tau ) e^{-\rho _{12} B_{2} \tau -\int _{0}^{\tau } m_{1}(V_{1}(\sigma )) \mathrm {d} \sigma } \mathrm {d} \tau \\&\quad +\bigg [ q_{1} \frac{S_{2}^{*}}{N_{2}^{*}} \cdot \frac{{\mathcal {R}}_{2}-1}{\rho _{2} {\mathcal {R}}_{2}} {\mathcal {R}}_{2} \cdot \rho _{12} \int _{0}^{\infty } e^{-\rho _{12} Q_{2} \tau -\int _{0}^{\tau } m_{1}(V_{1}(\sigma )) \mathrm {d} \sigma } \mathrm {d} \tau \\&\quad + q_{1} \frac{1}{{\mathcal {R}}_{2}} \cdot \frac{i_{2}^{*}(0)}{N_{2}^{*}} {\mathcal {R}}_{2} \cdot \rho _{21} \int _{0}^{\infty } e^{-\int _{0}^{\tau } m_{2}(V_{2}(\sigma )) \mathrm {d} \sigma } \mathrm {d} \tau \bigg ] C_{1} \\&=\frac{S_{2}^{*}}{N_{2}^{*}} \int _{0}^{\infty } \beta _{1}(\tau ) e^{-\rho _{12} B_{2} \tau -\int _{0}^{\tau } m_{1}(V_{1}(\sigma )) \mathrm {d} \sigma } \mathrm {d} \tau \\&\quad +\left( q_{1}\frac{\rho _{21}}{N_{2}^{*}}\int _{0}^{\infty } i_{2}^{*}(\tau ) \mathrm {d} \tau +q_{1} \rho _{12} B_{2} \frac{S_{2}^{*}}{N_{2}^{*}} \cdot {\widetilde{B}}_{2}\right) C_{1}={\mathcal {R}}_{1}^{2}>1 \end{aligned}$$

We know that $F_{1}(Q_{1},Q_{2})$ is a decreasing function of $Q_{1}$. If $Q_{1}=0$, we have $F_{1}(0,Q_{2}) > 1$ when $Q_{2}=0$ and $Q_{2}=Q_{2}^{*}$. Suppose $F_{1}(0,Q_{2}) < 1$ for $Q_{2} \in ({\widetilde{Q}}_{21}^{*},{\widetilde{Q}}_{22}^{*})$. In this interval, $F_{1}(Q_{1},Q_{2})<1$ for $\forall Q_{1}$, that is, the equation $F_{1}(Q_{1},Q_{2})=1$ have no solution. Let $Q_{1}=h(Q_{2})$, then we have $h({\widetilde{Q}}_{21}^{*})=0,h({\widetilde{Q}}_{22}^{*})=0$. Define

$$\begin{aligned} Q_{1}=\left\{ \begin{array}{ll} h(Q_{2}) &{} \text{ when } Q_{2} \notin ({\widetilde{Q}}_{21}^{*},{\widetilde{Q}}_{22}^{*}), \\ 0 &{} \text{ when } Q_{2} \in ({\widetilde{Q}}_{21}^{*},{\widetilde{Q}}_{22}^{*}). \end{array}\right. \end{aligned}$$

This function is continuous.

To show that $F_{1}(Q_{1},Q_{2})<1$ for any $Q_{2}$ and for $Q_{1}$ large enough, letting $Q_{1} \rightarrow \infty$, we obtain

$$\begin{aligned} F_{1}(\infty ,Q_{2})&=\alpha _{1} \left[ f_{1}(Q_{2})+g_{1}(\infty ,Q_{2}) C_{1} \right] \\&=\alpha _{1} \left[ f_{1}(Q_{2})+q_{1} Q_{2} \rho _{12} \int _{0}^{\infty } e^{-\rho _{12} Q_{2} \tau } e^{-\int _{0}^{\tau } m_{1}(V_{1}(\sigma )) \mathrm {d} \sigma } \mathrm {d} \tau \cdot C_{1} \right] \\&=\alpha _{1} \bigg [f_{1}(Q_{2})+q_{1} C_{1} \Big ( -e^{-\int _{0}^{\tau } m_{1}(V_{1}(\sigma )) \mathrm {d} \sigma } e^{-\rho _{12} Q_{2} \tau } \Big |_{0}^{\infty } \\&\quad -\int _{0}^{\infty } \left( m_{0}+m_{1}V_{1}(\tau ) \right) e^{-\int _{0}^{\tau } m_{1}(V_{1}(\sigma )) \mathrm {d} \sigma } e^{-\rho _{12} Q_{2} \tau } \mathrm {d} \tau \Big ) \bigg ] \\&=\alpha _{1} \bigg [f_{1}(Q_{2})+q_{1} C_{1} \left( 1-m_{0} \int _{0}^{\infty } e^{-\int _{0}^{\tau } m_{1}(V_{1}(\sigma )) \mathrm {d} \sigma } e^{-\rho _{12} Q_{2} \tau } \mathrm {d} \tau \right) \\&\quad -q_{1} C_{1} \frac{m_{1}}{c_{1}} \int _{0}^{\infty } \beta _{1}(\tau ) e^{-\int _{0}^{\tau } m_{1}(V_{1}(\sigma )) \mathrm {d} \sigma } e^{-\rho _{12} Q_{2} \tau } \mathrm {d} \tau \bigg ] \\&=\alpha _{1}\left( 1-q_{1} C_{1} \alpha _{1} \right) f_{1}(Q_{2}) \\&\quad +\alpha _{1} q_{1} C_{1} \left( 1-m_{0} \int _{0}^{\infty } e^{-\int _{0}^{\tau } m_{1}(V_{1}(\sigma )) \mathrm {d} \sigma } e^{-\rho _{12} Q_{2} \tau } \mathrm {d} \tau \right) \\&\le \alpha _{1} {\mathcal {R}}_{1} \left( 1-q_{1} C_{1} \alpha _{1} \right) + \alpha _{1} q_{1} C_{1} \\&= \alpha _{1} \cdot \frac{1-m_{0} \rho _{1}}{\alpha _{1}} \left( 1-q_{1} C_{1} \alpha _{1} \right) + \alpha _{1} q_{1} C_{1} \\&= 1-m_{0} \rho _{1} +m_{0} \rho _{1} \cdot q_{1} C_{1} \alpha _{1}. \end{aligned}$$

We can find that $1-m_{0} \rho _{1} +m_{0} \rho _{1} \cdot q_{1} C_{1} \alpha _{1} <1$ if $q_{1} C_{1} \alpha _{1}<1$. In fact,

$$\begin{aligned} \begin{aligned} \alpha _{1} q_{1} C_{1}&=q_{1} \frac{m_{1}}{c_{1}} \int _{0}^{\infty } \beta _{1}(\tau ) e^{-\int _{0}^{\tau } m_{j}(V_{1},V_{2}) \mathrm {d} \sigma } \mathrm {d} \tau \\&=q_{1} \frac{m_{1}}{c_{1}} \int _{0}^{\infty } c_{1} V_{1}(\tau ) e^{-\int _{0}^{\tau } \left( m_{0} +{\widetilde{m}}_{1} V_{1} +{\widetilde{m}}_{2} V_{2}\right) \mathrm {d} \sigma } \mathrm {d} \tau \\&\le q_{1} \left( -\int _{0}^{\infty } e^{-m_{0} \tau } \mathrm {d} e^{-\int _{0}^{\tau } m_{1}(V_{1}) \mathrm {d} \sigma }\right) \\&= q_{1} \left( 1-m_{0} \int _{0}^{\infty } e^{-\int _{0}^{\tau } m_{1}(V_{1}) \mathrm {d} \sigma } \cdot e^{-m_{0}\tau } \mathrm {d} \tau \right) \\&<q_{1} <1. \end{aligned} \end{aligned}$$

That is, we have $F_{1}(\infty , Q_{2})<1$. We can obtain that $F_{1}(Q_{1},Q_{2})=1$ has a positive solution.

Define $G_{2}(Q_{2})=F_{2}(h(Q_{2}),Q_{2})$. We can have $F_{1}(0,Q_{2})>1$. In this case, $h(Q_{2})$ is always defined and not equal to 0. Thus,

$$\begin{aligned} G_{2}(0)=F_{2}(h(0),0)=F_{2}(Q_{1}^{*},0)={\mathcal {R}}_{2}^{1}>1. \end{aligned}$$

$$\begin{aligned} G_{2}(Q_{2})=F_{2}(h(Q_{2}),Q_{2})=\frac{S^{*}}{N^{*}} \left[ f_{2}(h(Q_{2})) +g_{2}(h(Q_{2}),Q_{2}) C_{2} \right] . \end{aligned}$$

When the limit of $Q_{2}$ tends to infinity, the limit of $Q_{1}$ also tends to infinity. In this case, we can easily conclude that

$$\begin{aligned} \lim _{Q_{2} \rightarrow \infty } G_{2}(Q_{2})<1. \end{aligned}$$

That is, we can conclude that the equation $G_{2}(Q_{2})=1$ has a positive solution. It is easy to get $Q_{2}$ corresponding to the value of $Q_{1}$.

To summarize, this establishes the existence of positive solution of the system (4.3). This conclusion can be stated as follows

Proposition 4.1

Assume ${\mathcal {R}}_{1}>1, {\mathcal {R}}_{2}>1$, and ${\mathcal {R}}_{1}^{2}>1, {\mathcal {R}}_{2}^{1}>1$. Then, the system (3.1) has at least one coexistence equilibrium.

5 Simulation

In this section, we provide numerical simulations to confirm and extend our analytical results. Most of the parameter values are chosen from our previous study (Martcheva and Li 2013) (see Tables 1 and 2). Between-host disease transmission is our major concern. It is influenced by the viral load of the infected individuals, which is determined by the parameters of the within-host model. Therefore, we are interested in the impact of within-host parameters on the immuno-epidemiological reproduction numbers as well as the dynamics of the between host model. We studied analytically two within-host models, namely the original model (2.1) and its simplified form (2.6). Figure 2 shows that there is almost no difference of the virion populations for two models. Hence, we will only consider the simplified model (2.6) in the following simulations. In all simulations, we use the same within-host initial condition ($x^0, y_1^0, y_2^0, y^0, V_1^0, V_2^0$)=(100000, 6, 6, 6, 200, 100).

Fig. 2

Prevalences of virions in within-host model (2.1) and its simplified form (2.6). All the parameters are obtained from Table 1. The initial condition is $(x^0, y_1^0, y_2^0, y^0, V_1^0, V_2^0)=(100{,}000, 6, 6, 6, 200, 100)$. (a) shows that the dynamics for $V_1$ are almost the same for model (2.1) and (2.6). (b) shows the same result for $V_2$

First, we choose the clearance rate for virions with strain one $\delta _1$ as an example. We start from looking at the influence of $\delta _1$ on within-host model. Figure 3 shows that strain 1 dominant equilibrium is locally asymptotically stable for $\delta _1=2,3,4,5$ and strain 2 dominant equilibrium is locally asymptotically stable for $\delta _1=6$. This agrees with the analysis results since $\delta _1=2,3,4,5$ correspond to the invasion reproduction numbers $R_2^1<1$, $R_1^2>1$, but $\delta _1=6$ leads to $R_2^1>1$, $R_1^2<1$. From Fig. 3a, d, we can see that as $\delta _1$ increases from 2 to 5, the peak of infected cells with strain 1 $y_1$ and the peak of virus with strain 1 $V_1$ are delayed. Figure 3d also shows that the peak of $V_1$ decreases as $\delta _1$ increases from 2 to 5.

Fig. 3

Prevalences of infected cells and virions in within-host model (2.6) for different values of clearance rate for virions with strain 1 $\delta _1$. All the other parameters are obtained from Table 1. The initial condition is the same as Fig. 2. For $\delta _1=2,3,4,5$, the within-host basic reproduction numbers $R_1>1$, $R_2>1$, the invasion reproduction numbers $R_2^1<1$, $R_1^2>1$, strain 1 dominant equilibrium is locally asymptotically stable. For $\delta _1=6$, $R_1>1$, $R_2>1$, $R_2^1>1$, $R_1^2<1$, strain 2 dominant equilibrium is locally asymptotically stable (Color figure online)

Then, we look at the impact of $\delta _1$ on between-host level. From Fig. 4a, we can see that in general as $\delta _1$ increases, the between host basic reproduction number ${\mathcal {R}}_1$ and the invasion reproduction number ${\mathcal {R}}_1^2$ decrease, while ${\mathcal {R}}_2$ and ${\mathcal {R}}_2^1$ increase. Since ${\mathcal {R}}_1$, ${\mathcal {R}}_2$, ${\mathcal {R}}_2^1$ and ${\mathcal {R}}_1^2$ are important indicators of disease transmission, this implies increasing $\delta _1$ will depress the transmission of strain 1, but is helpful for the transmission of strain 2.

Fig. 4

a Epidemiological basic reproduction numbers ${\mathcal {R}}_1$, ${\mathcal {R}}_2$ and invasion reproduction numbers ${\mathcal {R}}_2^1$, ${\mathcal {R}}_1^2$ for the model (3.1) with respect to $\delta _1$. b–e The prevalences of individuals infected with strain 1, strain 2, co-infected individuals and all infected individuals for different values of $\delta _1$. All the other parameters are obtained from Tables 1 and 2. The within-host initial condition is the same as Fig. 2. The between-host initial condition is $(S^0, i_1^0(\tau ), i_2^0(\tau ), j^0(\tau ))=(1{,}000{,}000, 5, 5, 5)$. (a) shows that in general as $\delta _1$ increases, ${\mathcal {R}}_1$, ${\mathcal {R}}_1^2$ decrease, and ${\mathcal {R}}_2$, ${\mathcal {R}}_2^1$ increase. (b)–(e) show that as $\delta _1$ increases from 2 to 5, only tiny difference in all prevalences. These five cases result in strain 1 dominant equilibria. Another case $\delta _1=6$ leads to strain 2 dominant equilibrium. As $\delta _1$ increases, the prevalence of individuals infected with strain 1 decreases, the prevalence of individuals infected with strain 2 increases and the prevalence of all infected individuals decreases (Color figure online)

Figure 4b–e shows that as $\delta _1$ increases from 2 to 5, that increase causes only tiny difference in all prevalences. These four cases result in strain 1 persisting. Another case $\delta _1=6$ leads to strain 2 persisting. This is in accord with our analytical results. To be more specific, $\delta _1=2,3$ correspond to ${\mathcal {R}}_1>1$ and ${\mathcal {R}}_2<1$, $\delta _1=4,5$ correspond to ${\mathcal {R}}_1>1$, ${\mathcal {R}}_2>1$, ${\mathcal {R}}_1^2>1$, ${\mathcal {R}}_2^1<1$ (see Fig. 4a). In both scenarios, strain 1 dominant equilibrium is locally asymptotically stable. However, $\delta _1=6$ corresponds to ${\mathcal {R}}_1>1$, ${\mathcal {R}}_2>1$, ${\mathcal {R}}_1^2<1$, ${\mathcal {R}}_2^1>1$ (see Fig. 4a), which means strain 2 dominant equilibrium is locally asymptotically stable. From Fig. 4e, we can see that strain replacement happens as $\delta _1$ increases. It shows that the strain 2 dominant state has a lower prevalence of total infected individuals than strain 1 dominant states. However, the influence of $\delta _1$ is small. Similar results are observed for $\delta _2$, $\beta _1$ and $\beta _2$ (see Figs. 6e, 7b, d).

Zooming in Fig. 4b, c, e, we can see that as $\delta _1$ increases, the prevalence of individuals infected with strain 1 decreases (see Fig. 4b), the prevalence of individuals infected with strain 2 increases (see Fig. 4c) and the prevalence of all infected individuals decreases (see Fig. 4e). From Fig. 4d, we can see that $\delta _1=5$ leads to a high peak for the prevalence of co-infected individuals. One possible explanation is that $\delta _1=5$ results in a high peak for co-infected cells in within-host level (see Fig. 3c) and $\delta _1=5$ is close to the intersection of ${\mathcal {R}}_1^2$ and ${\mathcal {R}}_2^1$ (see Fig. 4a). Hence, the transient dynamic is relatively slow.

Zooming in Fig. 4a, we can see there exist some values for $\delta _1$ satisfying both invasion reproduction numbers ${\mathcal {R}}_1^2$ and ${\mathcal {R}}_2^1$ are less than one (see Fig. 5a). Interestingly, even though both $\delta _1=5.3$ and 5.4 lead to strain 1 dominant equilibria in the within-host level (see Fig. 5b), in between-host level they result in strain 1 persistence and strain 2 persistence, respectively (see Fig. 5c, d). From Fig. 5b, we can see that even though $V_2$ goes to zero eventually in both cases, there are several high peaks in the beginning. Besides, ${\mathcal {R}}_1^2$ and ${\mathcal {R}}_2^1$ are less than one, and the order of ${\mathcal {R}}_1^2$ and ${\mathcal {R}}_1^2$ changes at some value between $\delta _1=5.3$ and 5.4. Hence, the dominant strain in within-host level and between-host level might be different.

Fig. 5

a Zoom in part of Fig. 4a. b Within-host virus load for $\delta _1=5.3$ and 5.4. c, d Between-host prevalences for $\delta _1=5.3$ and 5.4. e, f Between-host prevalences for $\delta _1=5.364$ for different between-host initial conditions. All the other parameters are obtained from Tables 1 and 2. For all panels, the within-host initial condition is the same as Fig. 2. The between-host initial condition for (c)–(e) is the same as Fig. 4. The between-host initial condition 2 for (f) is $(S^0, i_1^0(\tau ), i_2^0(\tau ), j^0(\tau ))=(1{,}000{,}000, 0.01, 50, 0.01)$. (a) shows that there exist some values of $\delta _1$ satisfying both invasion reproduction numbers are less then 1. b shows that for both $\delta _1=5.3$ and 5.4, strain 1 dominant in within-host level. c, d show that in between-host level, strain 1 dominant equilibrium is stable when $\delta _1=5.3$ and strain 2 dominant equilibrium is stable when $\delta _1=5.4$. e, f show that when $\delta _1=5.364$, which stain will dominant depends on the initial condition (Color figure online)

In general, when both ${\mathcal {R}}_1^2$ and ${\mathcal {R}}_2^1$ are less than 1, bi-stability may happen. In other words, which strain will dominate depends on the initial conditions. For example, in Fig. 5e, f, we choose the same value for $\delta _1=5.364$, but different initial conditions for between-host model, the system could result in strain 1 dominant or strain 2 dominant. This bi-stability is further verified in Fig. 6.

Fig. 6

a, b Epidemiological basic reproduction numbers and invasion reproduction numbers for the model (3.1) with respect to $\delta _2$. c, d Prevalences for $\delta _2=13.685$ with different between-host initial conditions. e Prevalences of all infected individuals for different values of $\delta _2$. All the other parameters are obtained from Table 1 and 2. For all panels, the within-host initial condition is the same as Fig. 2. The between-host initial condition for (c, d) is the same as Fig. 5e, f. (a) shows that in general as $\delta _2$ increases, ${\mathcal {R}}_1$, ${\mathcal {R}}_1^2$ increase and ${\mathcal {R}}_2$, ${\mathcal {R}}_2^1$ decrease. (b) shows that there exists some value of $\delta _2$ satisfying both invasion reproduction numbers are less than 1. (c, d) shows that when $\delta _2=13.685$, which strain will dominant depends on the initial condition. (e) shows that as $\delta _2$ increases, strain replacement happens. The influence of $\delta _2$ on the prevalence of all infected individuals is small (Color figure online)

From Fig. 6a, we can see that, in general as $\delta _2$ increases, ${\mathcal {R}}_1$, ${\mathcal {R}}_1^2$ increase, and ${\mathcal {R}}_2$, ${\mathcal {R}}_2^1$ decrease. This indicates that increasing $\delta _2$ will depress the transmission of strain 2, but is helpful for the transmission of strain 1. Similarly, increasing $\beta _1$ will depress the transmission of strain 2, but is helpful for the transmission of strain 1 (see Fig. 7a). However, increasing $\beta _2$ will depress the transmission of strain 1, but is helpful for the transmission of strain 2 (see Fig. 7c).

Fig. 7

a, c Epidemiological basic reproduction numbers and invasion reproduction numbers for the model (3.1) with respect to $\beta _1$ and $\beta _2$, respectively. b, d Prevalences of all infected individuals for different values of $\beta _1$ and $\beta _2$. All the other parameters are obtained from Tables 1 and 2. For all panels, the within-host initial condition is the same as Fig. 2. The between-host initial condition for (b) and (d) is the same as Fig. 4. (a) shows that in general as $\beta _1$ increases, ${\mathcal {R}}_1$, ${\mathcal {R}}_1^2$ increase, and ${\mathcal {R}}_2$, ${\mathcal {R}}_2^1$ decrease. (c) shows that in general as $\beta _2$ increases, ${\mathcal {R}}_1$, ${\mathcal {R}}_1^2$ decrease, and ${\mathcal {R}}_2$, ${\mathcal {R}}_2^1$ increase. (b) and (d) show that as $\beta _1$ increases or $\beta _2$ increases, strain replacement happens. The influence of $\beta _1$ and $\beta _2$ on the prevalence of all infected individuals is small (Color figure online)

6 Discussion

In this paper, we have formulated a two-strain model with coinfection. The model links the dynamics of an immune system of two strains and an epidemic model of two strains. Through proper analysis, we know that in the with-in host model, there is only one infection-free equilibrium in the case of $R_{i}<1$, $i=1,2$. When the basic reproduction number $R_{i}>1$, in addition to the infection-free equilibrium, there are single-strain equilibria—one single strain equilibrium corresponding to each strain. When both the basic reproduction numbers and the invasion reproduction numbers are greater than 1, there is a coexistence equilibrium in the model. We define the invasion numbers and we establish that strain i dominance equilibrium is locally asymptotically stable if the invasion reproduction number of strain j is smaller than one. If the invasion reproduction number of strain j is greater than one, then the strain i dominance equilibrium is unstable.

We further define a multi-scale immuno-epidemiological model with two strains and coinfection. We structure each strain and the coinfected class with time-since-infection. Individuals in each of the infectious classes exhibit the same with-in host dynamics; however, if strain i is the only strain present, we start the strain j variables in the within-host model from zero. We study the disease-free and endemic equilibria of the immuno-epidemiological model. We further investigate the local asymptotic behavior of the immuno-epidemiological coupled system. We find that the disease-free equilibrium of the coupled system is locally asymptotically stable if and only if ${\mathcal {R}}_{i}<1$ for $i=1,2$. When ${\mathcal {R}}_{i}>1$ and the corresponding invasion reproduction number ${\mathcal {R}}_{i}^{j}<1$, the strain i dominance equilibrium is locally asymptotically stable; when the invasion reproduction number ${\mathcal {R}}_{i}^{j}$ is greater than 1, the strain i dominance equilibrium is unstable. When all the reproduction numbers and invasion reproduction numbers are greater than 1, we also find that the coupled system has an interior equilibrium, that is, a coexistence equilibrium.

In simulation, we focus on the impact of within-host parameters on the between-host basic reproduction numbers, invasion reproduction numbers as well as the dynamics of the system. As $\delta _1$ or $\beta _2$ increases, ${\mathcal {R}}_{1}$ and ${\mathcal {R}}_{1}^{2}$ decrease, and ${\mathcal {R}}_{21}$ and ${\mathcal {R}}_{2}^{1}$ increase. This indicates that increasing $\delta _1$ or $\beta _2$ will depress the transmission of strain one, but is helpful for the transmission of strain two. This is reasonable since $\delta _1$ is the clearance rate for the virions of strain one and $\beta _2$ represents infection rate of healthy cells infected by strain two. Similarly, we observe that increasing $\delta _2$ or $\beta _1$ will depress the transmission of strain two, but is helpful for the transmission of strain one. As these parameters vary, strain replacement can happen, namely from stain one dominance to strain two dominance or vice versa. In addition, when both invasion reproduction numbers are smaller than one, bistability occurs with one of the strains persisting or the other, depending on initial conditions. However, the influence of within-host parameters on the prevalence of total infected individuals is very small.