A discriminative information-theoretical analysis of the regularity gradient in inflectional morphology

Abstract

Over the last decades, several independent lines of research in morphology have questioned the hypothesis of a direct correspondence between sublexical units and their mental correlates. Word and paradigm models of morphology shifted the fundamental part-whole relation in an inflection system onto the relation between individual inflected word forms and inflectional paradigms. In turn, the use of artificial neural networks of densely interconnected parallel processing nodes for morphology learning marked a radical departure from a morpheme-based view of the mental lexicon. Lately, in computational models of Discriminative Learning, a network architecture has been combined with an uncertainty reducing mechanism that dispenses with the need for a one-to-one association between formal contrasts and meanings, leading to the dissolution of a discrete notion of the morpheme.

The paper capitalises on these converging lines of development to offer a unifying information-theoretical, simulation-based analysis of the costs incurred in processing (ir)regularly inflected forms belonging to the verb systems of English, German, French, Spanish and Italian. Using Temporal Self-Organising Maps as a computational model of lexical storage and access, we show that a discriminative, recurrent neural network, based on Rescorla-Wagner’s equations, can replicate speakers’ exquisite sensitivity to widespread effects of word frequency, paradigm entropy and morphological (ir)regularity in lexical processing. The evidence suggests an explanatory hypothesis linking Word and paradigm morphology with principles of information theory and human perception of morphological structure. According to this hypothesis, the ways more or less regularly inflected words are structured in the mental lexicon are more related to a reduction in processing uncertainty and maximisation of predictive efficiency than to economy of storage.

1 Introduction

In the wake of the so-called “cognitive revolution” (Miller, 2003), many influential language models have been assuming a direct correspondence between linguistic constructs and mental correlates (Clahsen, 2006). In morphology, the assumption was popularised by Pinker and colleagues’ Words and Rules theory (Marcus et al., 1995; Pinker, 1999; Pinker & Ullman, 2002; Prasada & Pinker, 1993), where the traditional distinction between regular and irregular inflection is accounted for by a dual mechanism for lexical access. Regulars are recognised (and produced) through the rule-based assembly/disassembly of morphemes, while irregulars are simply stored and accessed as full forms – in line with a categorical view of the grammar vs. lexicon dichotomy.

Pinker’s theory resonated well with the American post-Bloomfieldian conception of the mental lexicon as an enumerative, redundancy free repository of atomic (sub)lexical units (see Blevins, 2016; Goldsmith & Laks, 2019; Matthews, 1993, for extensive historical overviews). According to this view, lexical knowledge interacts with processing rules in a one-way, top-down fashion, providing declarative, context-free information that is fundamentally independent of rule-driven processing. Lexical building blocks must be available as stored units before the processing of complex words can set in. Likewise, rules exist independently of stored entries, in so far as their working principles do not reflect the way lexical information is stored in the mind. Matters of lexical representation (i.e. what information a lexical entry is expected to contain) are assumed to be independent of matters of processing (i.e. what mechanisms are needed to store and access lexical information).

Over the last few decades, a growing body of evidence on the mechanisms governing lexical learning, access and processing has challenged models of word processing based on such a dichotomized view of memory (the lexicon) and computation (lexical rules). A few relatively independent lines of research have called into question the psychological and linguistic reality of morphemes (see Anderson, 1992; Aronoff, 1994; Baayen et al., 2011; Blevins, 2003, 2006, 2016; Hay, 2001; Hay & Baayen, 2005; Matthews, 1972, 1991; Stump, 2001, among others), suggesting a radical reconceptualisation of the regular-irregular dichotomy in morphology (Albright, 2002, 2009; Beard, 1977; Bybee, 1995; Corbett, 2011; Corbett et al., 2001; Herce, 2019). Accordingly, strictly compartmentalised lexical architectures have given way to more integrative word learning systems (e.g. Baayen et al., 2011, 2019; Bybee & McClelland, 2005; Daelemans & Van den Bosch, 2005; Elman, 2009; Marzi & Pirrelli, 2015), whereby morphological knowledge is bootstrapped from full forms.

Underlying the development of such an integrative view of inflection is the assumption that morphological knowledge develops from stored families of lexically and inflectionally-related full forms, akin to paradigms in classical grammatical descriptions (Blevins, 2016; Finkel & Stump, 2007; Matthews, 1972). In paradigms, full forms are not listed enumeratively, but are partially committed to memory through the underlying implicational structure of paradigm cells (Ackerman & Malouf, 2013; Bonami & Beniamine, 2016; Malouf, 2017). It is this structure that allows a speaker to fill in an empty paradigm cell by extrapolating the evidence provided by other known forms of the same paradigm (Ackerman et al., 2009).

Information-theoretical formalisations of the implicational structure of inflection paradigms have received considerable support from psycholinguistic evidence (Bertram et al., 2000; Kuperman et al., 2010; Kostic et al., 2003; Milin et al., 2009a,b; Moscoso del Prado Martín et al., 2004, to mention but a few). However, comparatively little effort has been put into modelling the relation between the paradigmatic organisation of inflected forms into inflectionally-related families and the way speakers process the same forms online. Models of word recognition have been analysed in information-theoretical terms of uncertainty reduction (Baayen et al., 2007; Balling & Baayen, 2008, 2012), and principles of Bayesian learning (Norris, 2006), but they have been investigated independently of aspects of paradigmatic self-organisation. Even recent computational models of lexical processing (Baayen et al., 2019) have sidestepped the interdependence between online processing and offline representations, using n-gram-based graphs as the surface building blocks of the lexicon.

In our view, such a persisting neglect in the linguistic, psycholinguistic and computational literature has prevented a full appraisal of the theoretical implications of interactive lexical models for morphology, replicating (pace Hockett, 1954) the post-Bloomfieldian dichotomy between lexical processes and (sub)lexical representations. The present contribution tries to address and, hopefully, start filling in this gap. Here, we spell out the probabilistic and algorithmic foundations of a temporal, self-organising neural network (a Temporal Self-organising Map, or TSOM) that learns to store inflected forms through context-sensitive patterns of processing connenctions (Kohonen, 2002; Koutnik, 2007; Pirrelli et al., 2011). In learning full forms, a TSOM develops a strong sensitivity to gradient effects of word frequency, paradigmatic regularity, and probabilistic levels of morphological structure arising from the lexicon, thereby providing a unifying account of a wide range of word processing effects that have traditionally been analysed and accounted for independently in the literature. Such a sweeping array of processing effects will be demonstrated through an information-theoretical analysis of the costs incurred by five, independently trained TSOMs that learn to process regularly and irregularly inflected forms sampled from English, German, French, Italian and Spanish conjugations.

In what follows, we first provide typological evidence supporting a graded view of regularity in inflection (Sect. 2), to then move on to considering the ways speakers are known to process inflected verb forms (Sect. 3). Sections 4 and 5 offer an information-theoretical formalisation of the processing costs of inflectional paradigms and a description of the neural architecture used for our experiments. Simulation data are reported and modelled in Sect. 6, which paves the way to the general discussion of Sect. 7 and our concluding remarks in Sect. 8.

2 Inflectional regularity in a (cross)linguistic perspective

The observation that English walked is a more regular past tense form than – say – thought may strike the reader as so trivial as to require no empirical or terminological justification. In fact, the terms regularity and irregularity, however abundantly used in the linguistic and psycholinguistic literature on inflection, have rarely been formally defined. Herce (2019) has recently argued that the two notions are so ontologically ambiguous that any scientific endeavour should better avoid them. In addition, it is somewhat ironic that a great deal of discussion on morphological regularity was chiefly based on an inflectionally impoverished language such as English, whose inflectional regularity happens to correlate with default productivity (the -ed rule does not select a specific subclass of verbs), combinatoriality (regular inflectional processes are concanenative), predictability (walked can easily be inferred from its base form walk) and phonotactic complexity (ran sounds simpler than *runned). Inflectionally richer languages, such as Romance languages among others, do not exhibit the same range of correlations as English does (see Sect. 2.2), to the extent that any universal claim about inflectional regularity based on English evidence is simply unwarranted.

We agree that the term regularity should be used with care. Like its close terminological companion complexity, regularity has been shown to index a multidimensional cluster of linguistic properties. Some of them (e.g. concatenativity) are contingent on the specific typological properties of a language’s morphology, while some others (e.g. productivity) are inherently graded. Nonetheless, this by no means imply that the term is useless or unworthy of scientific inquiry. In our view, most of the confusion surrounding the notion of morphological (ir)regularity arises from the etymological (and categorical) characterisation of being regular as being generated by a grammatical rule (Latin rēgula), defined as a “mental operation” (Marcus et al., 1995). In fact, in a non-probabilistic rule-based account, a rule either applies (when invoked) or not. We surmise that the elusive nature of regularity does not lie in the vagueness of its definition as an object of scientific inquiry, but rather in the formal inadequacy of the symbolic rule-based framework that has been used in the past to investigate it.

2.1 Following a procedural rule

Drawing on Ullman’s neurocognitive Declarative/Procedural model (Ullman, 2001, 2004), Pinker’s Words and Rules theory claims that speakers’ knowledge of word inflection is subserved by two distinct, functionally segregated brain systems (Pinker & Ullman, 2002). Regularly inflected forms are covered by the procedural system of the human brain, neuro-anatomically located in the basal ganglia and the frontal cortex areas to which the basal ganglia project. Irregulars, in contrast, are stored and accessed by the declarative memory system, which includes more posterior temporal and temporo-parietal regions, together with medial-temporal lobe structures such as the hippocampus.

Accordingly, the procedural system is based on combinatorial rule-driven processes, requiring concatenation of morphological material to a base verb form (a free stem or a bound stem). Rules are assumed to apply in a context-free way, i.e. independently of semantic or phonological properties of the base; hence, they are fully productive. Thirdly, they cover a large set of verb types. Finally, they are insensitive to token frequency effects. Conversely, the declarative system is covered by superpositional memory patterns that obtain only for a restricted number of verbs. The patterns are sensitive to the phonological features of verb bases, they are not combinatorial and they take significantly less time to be produced if they occur frequently.

In spite of their neuroanatomical segregation, the procedural and declarative systems are assumed to interact competitively through lexical blocking. Accordingly, a productive inflection rule is inhibited when the input of the rule is found to fully match an existing entry in the declarative lexicon (e.g. went bleeds the rule-based production of *goed). Nonetheless, since regularly and irregularly inflected forms are assumed to be covered by distinct brain regions, Pinker’s theory makes the prediction that it should not be possible to find “hybrid” inflection systems, whose processes mix the diagnostic properties of regular inflection with those of irregular inflection (Pinker & Prince, 1991).

2.2 Beyond English

From a typological perspective, the conjugation systems of many language families provide abundant evidence that such “hybrid” inflection systems indeed exist. If being morphologically productive implies and is implied by being combinatorial, it is not clear how the Words and Rules theory can deal with introflexive (i.e. root and pattern) inflectional processes, or apophony-based and tonal morphologies (Palancar & Léonard, 2016). Even if we limit ourselves to less exotic verb systems, many irregular inflection processes are, in fact, combinatorial. An irregular French verb like boire ‘drink’ presents the allomorphic stem buv- in the imperfective je buv-ais ‘I drank’, but this form enters into the normal concatenative imperfective subparadigm as the regular j’am-ais ‘I loved’ (Meunier & Marslen-Wilson, 2004). Likewise, Modern Greek provides evidence of a gradient range of aorist formation processes, going from a fully transparent class (mil-o ‘I speak’, mili-s-a ‘I speak’), to a non-systematic stem-allomorphy class (pern-o ‘I take’, pir-a ‘I took’), through an intermediate systematic stem-allomorphy class (lin-o ‘I untie’, e-li-s-a ‘I untied’) (Bompolas et al., 2017; Ralli, 2005, 2006; Tsapkini et al., 2002). Even more complex gradients are found in Russian verb and noun inflection (Brown, 1998; Corbett, 2011; Jakobson, 1948).

Secondly, sensitivity to the formal properties of a verb base is not a hallmark of irregular inflection. In Hebrew, the closed Paal verb class is both unproductive and insensitive to phonological patterns, whereas the open-ended and more productive Piel verb class is porous to effects of phonological similarity (Farhy, 2020). Likewise, Italian speakers are found to analogize target verb forms to clusters of stems that are phonologically similar to the target stem and undergo the same stem transformation. These clusters, called ‘reliability islands’ (Albright, 2002), are operative irrespective of whether the analogized form is regular or irregular, accounting for:

• i) the productivity of irregular inflection patterns, including human acceptability judgements of nonce verb forms (Albright, 2002, 2009; Laudanna et al., 2004), elicited production of irregularly inflected forms from nonce verb bases (e.g. Albright & Hayes, 2003; Bybee & Moder, 1983; Orsolini & Marslen-Wilson, 1997), (see also Say & Clahsen, 2002; Veríssimo & Clahsen, 2014, for somewhat diverging evidence);

• ii) the phonological sensitivity of speakers to regular inflection patterns (Albright, 2002, 2009);

• iii) generalization strategies of both native (L1) (Farhy, 2020; Orsolini et al., 1998; Nicoladis & Paradis, 2012) and non-native (L2) learners (Agathopoulou & Papadopoulou, 2009; Cuskley et al., 2015; Farhy, 2020).

In the light of this evidence, the sharp functional separation between the declarative and the procedural system can hardly be maintained. In addition, it is unclear how the productivity of irregular inflectional patterns can coexist with lexical blocking. If the partial matching of a nonce verb like frink with an existing irregular verb such as drink is sufficient to block a rule-based process and trigger irregularization (frink > frank: Ramscar (2002)), the way the two systems interact ought to be considerably more graded and probabilistic than the simple mechanism of lexical blocking is ready to acknowledge.

3 Psycholinguistic models of lexical access

The early psycholinguistic interest in morphemes as the minimal building blocks for lexical organisation was motivated by the need to address issues of efficient processing and retrieval of words stored in the mental lexicon. However, the question immediately arose as to whether morpheme segmentation can really facilitate lexical access. Early full listing models of the mental lexicon (Butterworth, 1983; Manelis & Tharp, 1977) and later variants thereof (Giraudo & Grainger, 2000; Grainger et al., 1991) answered negatively to this question. They assume that inflected forms are accessed directly, irrespective of how regular and internally structured they are, because, all too often, morphologically complex words are semantically and formally unpredictable (e.g., locality is not the property of being local, and *falled is not the past tense of fall). Nonetheless, some full listing models do not dispense with a level of morphemic units entirely. Rather, they place it above the level of central lexical representations (Fig. 1a). Accordingly, morphemes represent the meaningful atomic units which all members of an inflectional (paradigm) or derivational family project to and activate, thus capturing the systematic correspondence of form and meaning in sets of semantically transparent, morphologically related words. This dynamic suggests a postlexical (or supralexical) view of morphological relatedness, whereby words are recognized first, to then be related morphologically in lexical memory.

Fig. 1

(a) a connectionist version of the full listing model of lexical access. (b) a connectionist version of Pinker’s Words and Rules theory (adapted from Taft, 1994). In both graphs, double circled nodes indicate nodes activated by the input string walked. Only connections between activated nodes are shown

In contrast, the idea that morphemes can function as proper lexical access units enforces a sublexical view of morphological structure, which reverses the processing relation between morphemic and lexical units. As access units, morphemes mediate lexical recognition and co-activation (Fig. 1b). Although sublexical models differ from one another in matters of detail, they understand the role of morphemes in lexical memory in either of the following ways:

• i) as permanent access units to whole words in either full parsing models (Taft & Forster, 1975; Taft, 1994, 2004), or dual mechanism models (Pinker & Prince, 1991);

• ii) as pre-lexical processing routes, running in parallel with full-word access routes and competing with the latter, in variants of the so-called race model (Caramazza et al., 1988; Chialant & Caramazza, 1995; Frauenfelder & Schreuder, 1992; Laudanna & Burani, 1985; Schreuder & Baayen, 1995).

Sublexical and supralexical models of morphological access make some testable predictions about the ways humans process inflectionally regular and irregular forms, as summarized below.

3.1 Lexical recognition and access

That lexical frequency speeds up word recognition is classically interpreted as a memory effect (Howes & Solomon, 1951). The more frequently a word is encountered in the input, the more deeply entrenched its storage representation in the mental lexicon is, and the quicker its access. Frequency effects have largely been used to investigate the nature and organisation of lexical representations (Taft, 1994, 2004; Forster et al., 1987). If reaction times to target forms in a lexical decision task are found to (inversely) correlate with the frequency of the full forms, this has been generally understood as evidence of holistic representation and memory-driven retrieval. Conversely, inverse correlation of response time with the frequency of roots/stems has traditionally been interpreted as a hallmark of parsing-mediated recognition, with the input form being obligatorily split into its constituent parts.

Full listing models accommodate full-form frequency effects on word processing assuming that repeated access of a full-form unit in the lexicon raises the activation level of the unit. As to stem frequency effects, it is assumed that the cumulative frequency of all inflected forms of a lemma (i.e. the lemma’s paradigm frequency) raises the activation level of the lemma unit at the semantic level of Fig. 1. Finally, interactive activation between the lemma unit and all its afferent access units is used to account for priming effects between inflectionally related words (Giraudo & Grainger, 2001): all access units of the same abstract lemma can benefit from the downward flow of activation coming from the lemma when the latter is activated by one of its inflected forms.

In the same vein, sublexical frequency effects (see Bertram et al., 2000; Bradley, 1979; Burani & Caramazza, 1987; Taft, 1979, among others) are straightforwardly accounted for by full parsing models, with obligatory morpheme-based parsing of an input form activating sublexical access units. However, word frequency effects are more difficult to accommodate in this framework. For example, the slow processing speed of a low-frequency form like seeming is not predicted by the high-frequency of its constituent parts. Taft (1979, 2004) suggests to account for word frequency effects as the result of a post-lexical process of morpheme re-integration for semantic interpretation. Accordingly, low word frequency effects arise not because full form units are stored in the lexicon (Taft claims that they are not), but because low-frequency inflected forms contain morphemes that are more difficult to recombine and interpret at the morphosemantic level.

In principle, race models of lexical access are in a better position to account for the factors influencing the interaction between the frequency of a morphologically complex word and the frequency of its parts. One factor affecting this interaction is the ratio of the frequency of the whole word and the frequency of its base: the more frequent the complex form relative to its base, the more salient it is (Hay, 2001; Hay & Baayen, 2005). In addition, the more the parts stand out in the whole word, the stronger the paradigmatic relations the word entertains (Bybee, 1995). Note, however, that also race models run into problems with effects of low frequency words such as seeming. Since seem and ing are both high-frequency units, they are predicted to beat their embedding low-frequency form in the race for lexical access. We are thus left with the problem of why the processing of seeming does not take advantage of its high-frequency parts (at least not as much as the race model would predict).

Priming effects are another important source of evidence for testing models of lexical access. Full listing models can account for priming effects between regularly/irregularly inflected forms and their bases through interactive activation between the activated lemma unit and its inflected forms. However, this mechanism fails to accommodate priming effects between morphologically unrelated words, as with the case of corner priming corn (e.g. Crepaldi et al., 2010; Rastle et al., 2004). Dual mechanism models readily account for priming between regularly inflected forms and their bases, but fail to explain clear-cut evidence that irregularly inflected forms facilitate visual identification of their bases (Crepaldi et al., 2010; Forster et al., 1987; Kielar et al., 2008; Marslen-Wilson & Tyler, 1997; Meunier & Marslen-Wilson, 2004; Pastizzo & Feldman, 2002). Besides, if one assumes that only irregular complex forms are related morphologically after lexical access, degrees of semantic transparency should not affect the priming of regulars, contrary to fact (Jared et al., 2017; Lõo et al., 2022). Finally, any model of lexical access that account for priming effects in terms of co-activation of lexical access units must implement an activation mechanism that explains why (i) levels of priming are continuously affected by degrees of formal transparency of the prime, as with gave priming give better than brought primes bring (Estivalet & Meunier, 2016; Orfanidou et al., 2011; Tsapkini et al., 2002; Voga & Grainger, 2004), and (ii) priming facilitation takes place even when the prime is not fully decomposable into constituent parts (Beyersmann et al., 2016; Hasenäcker et al., 2016; Feldman, 1994; Heathcote et al., 2018; Morris et al., 2007).

3.2 Prediction-driven word processing

So far, we have analysed lexical processing as the outcome of partial matches of the input word with stored lexical and sublexical units that are concurrently activated and compete with one another for recognition. An interesting interpretation of this competition can be gained by looking at the probabilistic dynamics governing efficient selection of the appropriate candidate during online word processing, grounded in the human ability to anticipate upcoming linguistic units in the input (Kuperberg & Jaeger, 2016; Pickering & Clark, 2014; Lowder et al., 2018; McGowan, 2015). This interpretation requires a dynamic, information-theoretical view of how language processing proceeds. Processing unfolds through time in a sequential, incremental fashion, by either attempting one specific prediction at each processing step, or entertaining multiple hypotheses in parallel, each with some degree of probabilistic support. Accordingly, the cost of processing a time-series of symbols is a function of how predictable the series is, given the context in which it appears (Levy, 2008). For example, predictability has been defined in the reading literature as the probability of knowing a word before reading it, and it has been used to understand the variation of gaze duration over words in eye tracking experiments (Bianchi et al., 2020; Kliegl et al., 2006; Rayner, 1998).

It has been suggested (Baayen et al., 2007; Hay & Baayen, 2005) that speakers can accomplish efficient selection of multiple, competing candidates by resorting to two types of information available in lexical memory: the syntagmatic information about the ways symbols are arranged in praesentia, along the linear dimension of time; and the paradigmatic information about the ways words are mutually related in complementary distribution or in absentia (De Saussure, 1959). The syntagmatic dimension informs speakers’ knowledge that -ing is an improbable inflectional ending when preceded by seem, and a probable constituent when preceded by walk. The paradigmatic dimension captures the knowledge that seem is found as a verb stem in words such as seems, seemed and seeming, or that walking and seeming share the same inflectional ending. According to this interpretation, a frequency effect for a full form like seeming provides information about the entrenchment of the connection linking the stem seem with the inflectional ending -ing. In other words, it offers an estimate of the joint probability p(seem,ing), reflecting the combinatorial properties of the two morphological units. In turn, a stem frequency effect provides information about the neat contribution of a verb stem to the processing of all inflected forms that share the same stem. In addition, combined with information for full-form frequency, stem frequency information provides an estimate of the conditional probability of each inflected form given its paradigm: p(ing|seem)=p(seem,ing)/p(seem).¹ Baayen et al. (2007) show that the probabilistic interpretation of frequency effects accords well with the marginal influence of stem frequency on the processing of low frequency words, and the robust facilitatory influence of full form frequency on the processing of low frequency forms. The authors report that the influence of stem frequency is inhibitory for high frequency words and facilitatory for low frequency words.

The number of lexical relations within an inflection paradigm (or paradigm size) is also found to have a direct facilitatory influence on the processing speed of a word’s inflectional variants. Paradigm entropy, an information-theoretical measure of the size of an inflection paradigm, speeds up processing response time (Baayen et al., 2007; Moscoso del Prado Martín et al., 2004; Tabak et al., 2005). Paradigm entropy grows with the number of paradigmatically-related forms, and is a direct function of how uniformly distributed their frequencies are: the more equally frequent the paradigmatically-related forms, the higher their paradigm entropy.

The view that lexical processing is based on competition and selection among paradigmatically related candidates is supported by another effect of paradigmatic distributions on lexical processing: the interaction between paradigm entropy and inflectional entropy, an information-theoretical measure of the distribution of inflectional endings in their own conjugation class. Milin et al. (2009a,b) show that paradigm entropy and inflectional entropy facilitate visual word recognition. However, if the two diverge, a conflict arises resulting in slower word recognition. Ferro et al. (2018) showed that this divergence quantifies the degree of mutual dependence between a stem and its affix, defined as the statistical distance of their joint distribution from the hypothesis of their stochastic independence (Kullback & Leibler, 1951).² This suggests a straightforward linguistic interpretation of the Kullback-Leibler distance in terms of morphological co-selection. When a stem $s_{k}$ strongly selects a specific affixal variant, this variant is likely to have a low probability of following other stems, and a much higher conditional probability of following $s_{k}$. A syntagmatically highly expected affix which is not highly expected paradigmatically appears to inhibit processing.

Summing up, none of the lexical architectures reviewed in this section provides a full account of the vast array of effects on inflection processing reported in the psycholinguistic literature. It is highly unlikely that the variety and gradedness of these effects can be accounted for by multiplying units and levels of representation in the lexicon. In what follows, we propose a different take on the issue. Over the last two decades, principles of information-theory have offered an elegant mathematical framework for quantifying and formalising dynamic aspects of word processing, storage and retrieval, leading to a number of predictions about the role of expectation in word comprehension. From this perspective, word processing and word learning are naturally interpreted as processes of uncertainty reduction (Levy, 2008; Ramscar & Port, 2016). The approach dovetails well with a discriminative view of Word and Paradigm morphology (Baayen et al., 2011; Blevins, 2016) whereby words are assumed to be concurrently stored in our declarative lexical memory, where they are organised and accessed as subsets of morphologically related lexical candidates (paradigms and conjugation classes), combined with dedicated distributional measures that take into account their use and circulation in a language community. In what follows, we first provide a probabilistic, information-theoretical model of some dynamic aspects of the interaction between the syntagmatic and paradigmatic dimensions of word families in lexical memory. We will then take a step away from issues of lexical representation, to focus on issues of word processing from a machine learning perspective. Self-organising discriminative neural networks provide such a perspective.

4 The discriminative dimension of inflectional morphology

Following Blevins (2016), the discriminative dimension of an inflection system defines the amount of full formal contrast realised within the system, and how elements of formal contrast are used to convey the set of morphosyntactic features associated with the paradigm. In an ideal discriminative inflection system, each paradigm cell is filled by a distinct inflected form. To illustrate, the Latin form amo ‘I love’ in Table 1 uniquely conveys a full set of tense, mood, person and number features of Latin verb inflection, making the form unambiguously interpretable out of context.

Table 1 The present indicative (sub)paradigms of Latin amo ‘love’, sum ‘be’ and volo ‘want’ (dashes mark traditional morph boundaries)

Not all inflected forms of a paradigm are equally different from one another in their surface realisation. Some forms differ in one letter/sound only (amas vs. amat), some in two letters/sounds (amo vs. amat), some others in more than two (amo vs. amamus). Irregular paradigms like sum ‘be’ present radically suppletive forms (sum vs. estis), but a minimum of redundancy is nonetheless found in some cells (sum vs. sumus). If all (distinct) inflected forms in the same paradigm were treated as equally different, one could not quantify the varying discriminative potential of regularly vs. irregularly inflected forms.

Limiting ourselves to inflectional processes that involve segmental affixation,³ we can express any inflected form $w_{i}^{s}$ in a paradigm $P^{s}$ as the result of a combination of two morphs: a stem $s_{k}^{s}$ and its affix $a_{h}^{s}$.⁴ Accordingly, we can rewrite the inflected form $w_{i}^{s}$ as the ordered pair $\langle s_{k}^{s},a_{h}^{s}\rangle$, and the probability $p(w_{i}^{s})$ of hearing $w_{i}^{s}$ as $p(s_{k}^{s},a_{h}^{s})$. By indexing both stems and affixes with the $P^{s}$ paradigm they belong to, we are bringing allomorphy into the calculation. In fact, in some paradigms, a stem and an affix can be realised by specific alternating forms, sometimes independently, sometimes jointly.

To illustrate, a present indicative form of Latin volo ‘want’ (Table 1) can start with any of three stem allomorphs (vol-, vi- and vul-), each selecting only a subset of the present indicative paradigm cells. Drawing on information-theoretical metrics for predictive processing (Hale, 2003, 2016; Levy, 2008; Piantadosi et al., 2011), the amount of paradigmatic uncertainty in processing an inflected form $\langle s_{k}^{s} , a_{h}^{s}\rangle$ (e.g. vult ‘(s)he/it wants’) can be quantified as the expected communicative cost incurred by a Latin speaker when the contextually appropriate inflection $a_{h}^{s}$ (e.g., -t) is heard in combination with a specific $s_{k}^{s}$ (e.g. vul-) of the paradigm $P^{s}$ (e.g. volo):

$$ c(\langle s_{k}^{s} , a_{h}^{s}\rangle )=-log_{2}(p(s_{k}^{s} , a_{h}^{s})). $$

(1)

Equation (1) defines the processing cost of an inflected form as the negative logarithmic function of its probability, also known as pointwise entropy (pH) of the form. The cost goes down to 0 if the probability of the form is 1, and takes increasingly larger value as its probability gets smaller. This reflects the intuition that the rarer an event is, the more information it conveys, and the more costly it is to process (i.e., the more processing effort it takes). In other words, more probable events are processed in a more routinised way. But how does knowledge of a form’s paradigm affect its processing cost?

Let us assume that a spoken inflected form is being processed, and that the stem’s form has just been accessed. This information will help recognise the whole form according to Equation (2).

$$ c(\langle s_{k}^{s} , a_{h}^{s}\rangle | s_{k}^{s})=-log_{2}(p(a_{h}^{s}|s_{k}^{s})). $$

(2)

In the equation, the negative logarithmic function takes as argument the conditional probability $p(a_{h}^{s}|s_{k}^{s})$ of hearing $a_{h}^{s}$ after $s_{k}^{s}$ was heard, namely:

$$ p(a_{h}^{s}|s_{k}^{s})= \frac{|\langle s_{k}^{s} , a_{h}^{s}\rangle |}{\displaystyle \sum _{j=1}^{J}|\langle s_{k}^{s} , a_{j}^{s}\rangle |} $$

(3)

where J ranges across the entire set of affixes selected by the stem’s paradigm, and $|\langle s_{k}^{s} , a_{h}^{s}\rangle |$ counts the number of times $\langle s_{k}^{s} , a_{h}^{s}\rangle$ is found in the input.⁵$p(a_{h}^{s}|s_{k}^{s})$ equals 1 when the stem $s_{k}^{s}$ selects one affix only, and it decreases as soon as $s_{k}^{s}$ is found in combination with other affixes. Thus, the logarithmic cost of processing $\langle s_{k}^{s} , a_{h}^{s}\rangle$ after $s_{k}^{s}$ is heard is larger when $s_{k}^{s}$ belongs to a regular paradigm. In fact, an invariant, regular stem removes less processing uncertainty about an upcoming affix than an allomorphic stem does.

The other side of the coin is that stem allomorphy increases the cost of processing a stem given its own paradigm:

$$ H(s^{s}|P^{s})=\displaystyle \sum _{i = 1}^{I}p(s_{i}^{s}|P^{s})c(s_{i}^{s} | P^{s}). $$

(4)

In equation (4), $p(s_{k}^{s}|P^{s})$ is the probability of having $s_{k}^{s}$ selected within its own paradigm:

$$ p(s_{k}^{s}|P^{s})= \frac{\displaystyle \sum _{j=1}^{J}|\langle s_{k}^{s} , a_{j}^{s}\rangle |}{\displaystyle \sum _{i=1}^{I}\displaystyle \sum _{j=1}^{J}|\langle s_{i}^{s} , a_{j}^{s}\rangle |} $$

(5)

where I and J are, respectively, the number of stem allomorphs and the number of affixes in $P^{s}$, and $c(s_{k}^{s}|P^{s})$ is the negative logarithmic function of $p(s_{k}^{s}|P^{s})$.

Equation (4) defines the entropy of the stem distribution within a paradigm. $H(s^{s}|P^{s})$ equals 0 when the paradigm $P^{s}$ has one stem form only (I = 1), and increases as the uncertainty of selecting one particular stem allomorph increases. Note that uncertainty is a function of the number of stem allomorphs and their distribution in the paradigm. The more equiprobable (i.e. uniform) the distribution is, the higher its entropy. Entropy thus measures the pointwise processing cost of a paradigm’s verb stems, averaged by $p(s_{k}^{s}|P^{s})$. A more linguistic implication of equation (4) is that it defines a stem’s processing cost in terms of (un)certainty in stem selection, thereby providing a measure of paradigm regularity by probabilistic levels of stem allomorphy.

As to the distribution of affixes, and their role in apportioning processing costs in word recognition, Milin et al. (2009a) reported that response latencies in a visual decision task are positively correlated with the degree of divergence between the probability distribution of an inflected form in a paradigm, and the distribution of the affix selected by the inflected form. Their evidence shows that speakers are sensitive to both intra-paradigmatic and inter-paradigmatic distributional effects of inflected forms. However strongly an affixal allomorph is selected by a stem, and however high its conditional probability given the stem, speakers find it harder to process the allomorph if it has a comparatively low probability of being selected in its own conjugation class. This effect cannot be predicted by forward conditional probabilities (i.e. probabilities of an upcoming symbol given its preceding context), but requires computation of backward probabilities (i.e. the probability for a stem to be selected, given its suffix). We provisionally conclude that the discriminative dimension of inflectional morphology is governed by both forward and backward distributional factors, and that any plausible model of inflection processing must be able to take all these factors into account. Against this background, we turn now to show that simple principles of discriminative learning, implemented by a recurrent neural network, go a long way in modelling non-linear effects of lexical and sublexical frequency on word processing.

5 Self-organising discriminative lexical memories

All models of lexical access reviewed in Sect. 3 assume the existence of some layers of representational units, and an independent access procedure mapping an input signal (e.g. a time series of sounds) to layered units through cascaded levels of activation. However, these models tell us comparatively little about how units come into existence in the first place. What makes a child memorise a form as an unsegmented access unit, or decompose it into multiple smaller units? Even those approaches where more segmentation hypotheses can be entertained concurrently (as in race models of lexical access), ignore the fundamental question of why a speaker should split an input signal into smaller parts.

The advent of Artificial Neural Networks in the 80’s (Rumelhart & McClelland, 1987) put word learning at the core of the lexical research agenda. Classical multi-layered perceptrons were designed to learn to associate activation patterns across three layers of processing units (an input layer, an output layer and an intermediate hidden layer), via gradual adjustments of internal connection weights. Early connectionist models, however, failed to deal with many aspects of human word processing satisfactorily. First, they represented an input word like ‘$cat$’ (the symbol ‘$’ standing for a word boundary) as the set of trigrams {‘$Ca’, ‘cAt’, ‘aT$’}, where each trigram conjunctively encodes a single character with its embedding context. Sets of conjunctive trigrams could simply not model the intrinsic temporal dynamic of the language input and how human processing expectations change with time. Secondly, word inflection was modelled as the mapping of an input base form onto its inflected output form (e.g. go → went), subscribing to fundamentally derivational and constructive models of lexical production (Baayen, 2007; Blevins, 2006, 2016). Thirdly, gradient descent protocols for training neural networks (Rumelhart & McClelland, 1987) required signal back propagation and supervision, an idea which is difficult to implement in the brain, where biological synapses are known to change their connection weights only on the basis of local signals, i.e. the levels of activation of the neurons they connect. Thus weights cannot depend on the computations of all downstream neurons. In addition, it was not clear what the source of error signalling could possibly be, considering that children’s productions are rarely sensible to external explicit correction (Ramscar & Yarlett, 2007).⁶

To address some of these pitfalls, Baayen et al. (2011) propose a Naïve Discriminative approach to word learning (hereafter NDL), based on a simple two-layer network, where input units representing cues are connected to output units representing outcomes. Weights between cues and outcomes are estimated using an adapted variant of Rescorla-Wagner equations of error-driven learning (Rescorla & Wagner, 1972), that simulate the predictive response of a learner to a conditioned stimulus, i.e. an originally neutral stimulus that became strongly associated with (i.e. conditioned by) an outcome. For cues that are present in the input, the weights to a given outcome are updated, depending on whether the outcome was correctly predicted. The prediction strength or activation for an outcome is defined as the sum of the weights on the connections from the cues in the input to the outcome. If the outcome is present in a learning event, together with the cues, then the weights are increased by a fixed proportion (the network learning rate) of the difference between the maximum prediction strength and the current activation. When the outcome is not present, the weights are decreased by a factor that is inversely proportional to the current activation.

In the NDL literature, cues are represented by ordered pairs (bigrams) or triplets (trigrams) of the units (letters or sounds) making up an input word. Outcomes are localist, one-hot representations of lexico-semantic units.⁷ Unlike interactive activation models, where lexical competition is resolved dynamically through activation and inhibition at processing time, here competition shapes the network connections between the two layers at learning time. In particular, semantic vectors with stronger connection weights enter into a stronger correlation with word frequency. NDL networks are considerably simpler than even the earliest, and simplest connectionist models, thereby addressing some of the biologically most questionable aspects of classical neural networks, such as lack of local error representation and multi-layer back-propagation. Nonetheless, both NDL networks and their more recent, linear variants (Baayen et al., 2019; Heitmeier et al., 2021) represent the linguistic input using set of trigrams. This makes it difficult for them to model the inherent temporal dynamic of lexical representations, and quantitatively analyse their impact on speakers’ serial word processing. In what follows, we introduce a family of recurrent topological neural networks (Temporal Self-Organising Maps or TSOMs: Kohonen, 2002; Koutnik, 2007; Pirrelli et al., 2011) that use principles of discriminative learning to represent and store surface forms dynamically, i.e. as time series of input stimuli.

5.1 TSOMs

A TSOM is a recurrent topological network of processing nodes activated by temporal input signals. An input word, encoded as a time series of symbols, creates an activation pattern that is internally propagated across nodes, and is stored in inter-node connections. By being repeatedly exposed to more and more input words, a TSOM learns to develop increasingly specialised activation patterns, i.e. patterns that are selectively associated with specific words or classes of words.⁸

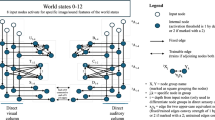
Figure 2 shows three activation patterns for the German input forms kommen (‘come’ inf/1p-3p pres ind), gekommen (‘come’ past part) and kamen (‘came’ 1p-3p past ind). Each pattern consists in a chain of winning nodes (also known as best matching units), i.e. nodes that have responded most strongly to a temporal input signal. As input letters are presented one at a time, nodes are activated accordingly. In the Figure, pointed arrows depict the forward temporal connections linking each winning node to its successor, and represent the direction of the activation flow from one node to another. Each node is labelled with the letter to which the node responds most strongly. Nodes responding to the same letter type are clustered together on the map. In addition, each node in a topological cluster is trained to respond to a context-specific instance of the letter associated with the node’s cluster. For example, the first m in kommen activates a node that was trained to respond to m preceded by o in the string ko. The second m will activate a topologically close node specialised for m preceded by m in the string kom, and so forth. Unlike classical conjunctive representations such as Wickelphones or Open Bigrams, where the length of the embedding context is set a priori once and for all, in a TSOM the length of a conjunctive context varies adaptively, depending on how often the context is found in the input at learning time. The more frequently a TSOM sees a word during training, the more likely it will respond to the word with a pool of specialised nodes, i.e. nodes that are most sensitive to the specific sequence of letters making up that word. Conversely, letters that are found in low-frequency contexts are responded to by less specialised (i.e. less context-sensitive) default nodes. Finally, since temporal connections are trained at learning time, they end up embodying stable conditional expectations for future events based on the current input, thus shaping the strong predictive bias of a TSOM. This highly adaptive, learning-driven behaviour makes TSOMs especially instrumental in investigating dynamic aspects of word processing.

Fig. 2

Activation chains for the German verb forms kommen (‘come’ inf/1p-3p pres ind), gekommen (‘come’ past part) and kamen (‘came’ 1p-3p past ind) in a TSOM trained on German conjugation. Winning nodes for the three input strings are circled. Pointed arrows represent temporal connections linking consecutively activated nodes. All chains start with a ‘#’ node (the form onset symbol) and end to a ‘$’ node (the form offset symbol). Different nodes respond to the substrings kom- and gekom-, and identical nodes respond to the substring -men$. Only connections between winning nodes are shown

5.1.1 The learning algorithm

Self-Organising Maps (SOMs, Kohonen, 2002) were originally designed to simulate the dynamic somatotopic organisation of the human somatosensory cortex, where specialised cortical areas develop to fire to specific classes of input stimuli (Almassy et al., 1998; Tononi et al., 1998). TSOMs are a recurrent variant of SOMs whose nodes are equipped with two layers of connectivity (Fig. 3): i) an input layer (as in classical SOMs) and ii) a recurrent temporal layer. One-way connections on the input layer project the input vector to each map node, which thereby gets attuned to the external stimuli the map is trained on. In addition, one-time delay re-entrant connections on the temporal layer project each node to all map nodes (including itself).

Fig. 3

Architecture of a TSOM “unfolded” over two successive time steps. Solid arrows denote connections between the input vector (rectangle box) and the map proper (square box). The dashed arrow represents recurrent temporal connections, whereby the map activation at time t-1 re-enters the map activation at time t. Nodes are depicted as circles, whose shades of grey denote activation levels

During training, a TSOM is exposed to a pool of input stimuli sampled according to a certain probability distribution. At each learning step, a TSOM adjusts its input connections to learn what stimulus is currently input. A TSOM that has been repeatedly exposed to a specific class of stimuli (e.g. a type of sound or a letter) develops a topologically connected area of nodes specialised in responding to that class (as shown in Fig. 4). In addition, while learning a stimulus, a TSOM adjusts its temporal connections (Fig. 3) to learn when the stimulus appears in the input. Figure 5 pictures the two adaptive steps implementing this mechanism with the input bigram ab:

• (1) (a) the temporal connection from a to b is strengthened, and (b) the connections from a to a few neighbouring nodes within a radial distance r (or neighbourhood radius) from b at time t are strengthened too (connections are depicted as solid arrows in Fig. 5, top panel);

• (2) all other temporal connections to b are concurrently weakened (connections are depicted dashed arrows in Fig. 5, bottom panel).

Fig. 4

Topological self-organisation of nodes in two lexical maps trained on English verb forms with uniform (left) and corpus-based (right) distributions. Nodes are labelled with the letter they respond to most strongly. Different nodes in the same letter cluster are activated by context-specific realisations of the labelling letter

Fig. 5

The two-step learning algorithm of a TSOM temporal layer over successive time ticks. Top: activation spreads from the winning node a at time tick t-1 to the winning node b at time tick t and its neighbouring nodes (light grey circles)). Bottom: selective inhibition goes from all losing nodes at time tick t-1 to the current winning node b

Step (1.a) enforces a delta rule that is common to an entire family of recurrent neural networks (Marzi et al., 2020). In contrast, the strengthening of a’s forward connections to topological neighbours of b (step 1.b), and the weakening of all other connections to b are a special feature of TSOMs. The combination of steps (1) and (2) approximates Rescorla-Wagner equations (Pirrelli et al., 2020; Rescorla & Wagner, 1972). The simultaneous presence of a cue (stimulus a) and an outcome (stimulus b) strengthens the connection between their responding nodes, whereas the absence of a cue when the outcome is present weakens the predictive potential of the cue relative to the outcome. If more cues compete to predict the same response, they will tend to weaken each other.⁹

As in most artificial neural networks, the plasticity of a TSOM, i.e. its ability to change its connectivity to adapt it to changes in the input, diminishes with the amount of training. This is a function of the learning rate with which connection weights are made closer to the current input, and the TSOM’s neighbourhood radius (learning step (1)). Both parameters tend to zero with the number of training epochs.

5.1.2 The learning bias

Figure 6 illustrates the learning bias of a toy TSOM over three training epochs: before training ($e_{0}$), at an intermediate epoch ($e_{j}$), and at the final epoch ($e_{n}$). At $e_{0}$ (leftmost panel), the map is a tabula rasa, with no structural or temporal bias. All nodes respond equally strongly to all stimuli, and their temporal connection weights are distributed uniformly. This corresponds to a level of maximum entropy in the map’s temporal connectivity (see Sect. 6.2.4 for more detail), yielding even levels of activation across all map nodes, represented as light grey circles in the figure.

Fig. 6

Connectivity patterns in a TSOM before training (left), after j training epochs (centre), after n training epochs (right).

Through learning, nodes become increasingly more responsive to some specific input stimuli (letters or sounds) only. At epoch $e_{j}$, the map is trained on two input strings: #abca and #bbcc (with # marking the start of the word). Here, winning nodes (white circles) are labelled with the letter they respond most strongly to. Nodes and their temporal connections (depicted as arrows in the figure) give rise to possibly overlapping data structures known as word graphs. In a word graph, each node can be arrived at through more incoming edges, so that it can be used to represent the same symbol (a letter) that appears in different positions and contexts. For example, the $c_{1}$-node can be arrived at from either a $b_{2}$-node or a $b_{3}$-node, meaning that the node is activated by both #abca and #bbcc. The resulting network is compact and parsimonious, with one processing node firing in multiple contexts, and some connections (solid arrows) that are more heavily weighted than others (dashed arrows). As a result, the entropy of connections at epoch $e_{j}$ is lower than at epoch $e_{0}$. We will refer to context-free nodes such as $c_{1}$ (i.e. nodes that respond to the same letter type in different contexts) as blended nodes.

At the end of training (rightmost panel of Fig. 6), the pattern of node connections in the map resembles a word tree, a data structure where letter nodes are arranged hierarchically starting from the common vertex ‘#’, known as the “root” of the tree. In a word tree, every node has only one parent node, and no, one or many child nodes. Accordingly, onset-sharing strings activate identical processing nodes, but no common nodes are activated by strings where different stems are followed by the same suffix. In the right panel of Fig. 6, the blended node $c_{1}$ is replaced by two specialised nodes (namely $c_{2}$ and $c_{3}$) that are activated by context-specific stimuli. Weights of repeatedly used connections go up to 1 (solid arrows), and weights of unused connections go down to 0. Hence, the entropy of the map’s connectivity is minimised: no branching connections emanate from a string’s uniqueness point, i.e. from the point at which the string diverges from any other string in the input (Marslen-Wilson, 1984). We conclude that the general learning bias of a TSOM is towards an increasing specialisation of its processing resources, enforced by (i) multiplying the number of dedicated nodes, (ii) reducing the number of blended nodes, and (iii) minimising the overall entropy of their temporal connections.

Moving away from a toy-example to a real training scenario, whether a word map ends up developing a more tree-like or a more graph-like data structure is contingent upon the dynamic trade-off between the spreading-activation bias, implemented by step (1) of the learning algorithm, and the specialisation bias enforced by step (2). This dynamic is modulated by the frequency distribution of training items, both in isolation and within their word families. If some high-frequency forms are input to a map, their node connections will tend to specialise more often and inhibit connections of less frequent forms, because items that activate the same pool of processing nodes come into competition with one another for discriminative specialisation (Fig. 5, bottom diagram). Strengthening a connection between two nodes a and b weakens the connections between other nodes and b. From a lexical perspective, the processing competition between forms reflects the topological self-organisation of these forms in the mental lexicon, and the role of word frequency in specialising processing nodes to maximise a map’s processing predictivity (see Sect. 5.1.3). Finally, it sheds light on the role of a word’s relative frequency within its own family of morphologically-related forms, arguably the lexicon’s most salient domain of competitive word co-activation.

5.1.3 Processing and generalisation

A word tree is a maximally discriminative data structure for lexical access. Starting from an input word’s onset, upon reaching the word’s uniqueness point, an optimally discriminative map should have a strong predictive bias for the word’s remaining letters/sounds prior to input offset. Ideally, only one forward connection is available to complete recognition of the input form, and the map’s activation flow propagates to one downstream node. This is a processing advantage, as it reduces uncertainty while strengthening the map’s predictive bias. From a lexical perspective, the bias dynamically describes the state of a long-term memory where the input word is stored holistically.

A map whose processing nodes are structured in a word tree behaves poorly in generalising to novel forms, i.e. forms the map was never trained on. To illustrate, consider the map in Fig. 6 at epoch $e_{n}$. When prompted with the novel string #abcc, the map would find it hard to process it, although it was trained on independent evidence of ab and cc. There is no connection that predicts an upcoming letter c after the string #abc is recognised. In the machine learning literature, this situation is described as a case of overfitting to input data, which arises when a trained map fits too closely to the training data to be able to use already acquired patterns in different contexts. Conversely, the more entropic map at learning epoch $e_{j}$ in Fig. 6 would have no problems in processing the novel string #abcc. In fact, the map’s memory structure contains a blended node ($c_{1}$) that can respond to an input letter (c) shared by more forms.¹⁰ As the node lies at the intersection of two word graphs, it has two alternative post-synaptic connections making different predictions about an upcoming stimulus. This makes room for generalisation, which is possible only when a map is open to more events than those it was originally exposed to, i.e. when it is less certain and more entropic. This condition, however, makes the map less predictive in processing familiar strings, i.e. less able to entertain strong expectations about upcoming events.

Summing up, TSOMs model lexical storage/access implementing a mechanism of functional specialisation of probabilistic node chains that dynamically respond to a continuously changing input signal. The mechanism has a great potential to unravel the intricate cluster of gradient effects on inflection processing reported in the psycholinguistic literature. In the following sections, we focus on such effects by analysing the processing behaviour and the structural self-organisation of TSOMs trained on different verb inflection systems.

6 Experimental evidence

6.1 Materials and method

6.1.1 Training data

Ten TSOMs were independently trained on five sets of inflected verb forms from English, French, German, Italian and Spanish conjugations, sampled with two different training regimes.¹¹ To ensure maximally balanced samples of regular and irregular paradigms in all languages, and minimise the number of paradigm gaps (i.e. the number of forms per paradigm that were not attested in our corpora), verb paradigms were first ranked on the basis of corpus-based cumulative frequencies of their verb forms. The top-50 most frequent paradigms in each language were then used for training.¹²

For each verb paradigm, we used the same set of 15 paradigm cells across all languages: the infinitive and past participle, the present participle for English, German, French and the gerund for Spanish and Italian, the 6 present tense and 6 past tense cells of the indicative. The selection was intended to include a representative (albeit by no means exhaustive) sample of paradigm cells that are known to offer evidence of stem alternation in both Germanic and Romance languages (Fertig, 2020; Hinzelin, 2022). Our sampling decision to select only comparatively few verb forms for training was motivated by the following reasons: (i) the TSOM incremental learning algorithm scales up poorly to a realistically sized lexicon;¹³ (ii) due to the high correlation between word frequency and age of acquisition (Baayen et al., 2006), we could nonetheless hope to focus on basic effects of frequency distributions on early stages of inflection learning; (iii) results from five repetitions of a full training session of 750 items for each language turned out to provide enough statistical power for fundamental frequency effects to be observed (including marginal stem-frequency effects, in line with Baayen et al., 2007); (iv) in a realistic processing scenario, we can expect contextual factors to narrow down the set of potential lexical competitors to a manageable subset of the most likely candidates (see Sect. 7 for a discussion of issues of scalability of the present architecture to a more realistic scenario).

We trained a TSOM on each language sample. All training forms were administered in their standard orthography. Letters in each input form were presented one at a time, in their left-to-right order, encoded as mutually orthogonal one-hot input vectors.¹⁴ No information about morphological segmentation, morpho-syntactic and morpho-lexical features was associated with orthographic codes during training. In the end, each TSOM was trained as an autoencoder, i.e. it had to learn how to store and reproduce, in the correct order, the sequences of letters it was exposed to at learning time.

Two training regimes were used. Input forms were shown to a TSOM in random order, using either (a) a uniform distribution, or (b) a real distribution based on corpus frequency counts. To ensure comparability across corpora of different size, corpus frequencies were scaled to a normalised frequency range in the 1-1001 interval. Thus, the most highly attested word form in each language sample was shown to the map 1001 times per epoch, and all unattested forms (paradigm gaps) were input once per epoch. In the uniform training regime, each form was input to the map 5 times per epoch. This means that syncretic forms, i.e. identical forms functionally associated with more paradigm cells, were input 5 times multiplied by the number of paradigm cells they fill in.

A full training session for each language consisted of 100 learning epochs. At each epoch, all forms in a language sample were randomly presented to the map according to their specific frequency distribution. The map’s learning rate and neighbourhood radius were made decay exponentially over epochs, with a general time constant τ equal to 25 epochs. This means that, after the first 25 training epochs, the initial value of the temporal learning rate, $\gamma _{T}=1$, is reduced to 1/e = 0.368. A training session was repeated 5 times for each language. At the end of a language-specific session, the accuracy of a trained map on two specific lexical tasks (see section on Training evaluation) was measured on the entire sample of input forms. Accuracy scores were then averaged across the five training sessions for that language (see Table 2 for details about the composition of training data for all languages, and accuracy scores in the serial recall task).

Table 2 Composition of training data for TSOM simulations by language: number of regular and irregular paradigms (R/I); number of distinct word types and size of the training set (due to inflectional syncretism, each language-specific training set presents a different number of form types); number of map nodes; mean percentage of serial recall (recall) and standard deviation (sd) for word types in the uniform training regime; mean token frequency (mean f) and mean percentage of serial recall (recall) and standard deviation (sd) in the corpus-based regime. Serial recall defines the process of producing the correct sequence of letters making up an inflected form, from the full set of the form’s winning nodes

To balance the amount of a map’s processing resources allocated for each language and avoid overfitting to training samples containing fewer inflected types, the number of memory nodes in a TSOM varied from one language to another as a function of the enumerative complexity of the inflection paradigms used for training. Due to the learning bias of a TSOM (see Sect. 5.1.2), we thus kept approximately constant the ratio between the number of processing nodes in the map and the number of nodes in the word tree representing all inflected forms in each language sample. As the ratio is insensitive to the frequency distribution of forms in a sample, the number of nodes in a language-specific map was the same in both uniform and corpus-based training regimes.

6.1.2 Training evaluation

Upon the end of a training session, each trained map was evaluated on two tasks: serial word recall and word prediction.

In a serial word recall task, the map is prompted to produce the correct sequence of letters of an inflected form from the full activation pattern of the form’s winning nodes (i.e. the nodes responding most highly to the form during training: Marzi et al., 2012). A map can carry out the task successfully only if the winning nodes “contain” sufficiently accurate information about each symbol and its position in the word. A recalled input form is correct if all letters making up the form are recalled in the correct order. Details of training samples, map size and the map’s performance in the serial recall task for each language are reported in Table 2. That all maps in the 5 languages show near ceiling performance in serial recall indicates that their processing resources are equally suited for the complexity of the input space they were trained on, and no serious language-specific bias was introduced in the experiment set-up.

In a word prediction task, each input word form is presented to a trained map one letter at a time, from the word’s onset (‘#’) to its offset (‘$’). At each time step t, we compute the most likely winning node at time t + 1, given the input context at time t.¹⁵ The label associated with the most highly pre-activated node is the map’s best guess (i.e. the most expected letter $l^{E}_{t+1}$), which is matched against the actually upcoming letter in the input form, or target letter $l^{T}_{t+1}$. The map’s prediction rate (p_rate) is incremented by one for each hit, and reset to 0 for each miss:

$$ p\_rate(t+1) = \textstyle\begin{cases} p\_rate(t)+ 1 , & \text{if } l^{E}_{t+1} = l^{T}_{t+1} \\ 0, & \text{if } l^{E}_{t+1} \neq l^{T}_{t+1}\end{cases} $$

(6)

Every TSOM was tested on the entire training set in the two training regimes of uniform vs. corpus-based distributions. Section 6.2 presents a detailed quantitative analysis of the maps’ performance in the prediction task.

6.1.3 Data annotation

TSOMs were trained on a discretized flow of inflected forms, which are input one character at each time step. Input data include word-boundaries (‘#’ and ‘$’), but provide no structural or featural information about morphological constituent parts. Nonetheless, we deemed it useful to see how time series of a map’s processing responses to an inflected form are aligned with information of the form’s morphological structure, or how they reflect standard criteria of morphological classification. For this purpose, input forms were manually segmented into stem + affix patterns, according to the Aronovian hypothesis that stems are strictly morphomic (Aronoff, 1994), and Spencer’s principle of Maximisation of the stem (Spencer, 2012). In addition, we split our training data into two clusters, namely R-form vs. I-form, depending on whether an inflected form belongs to an inflectionally regular (R) or irregular (I) paradigm. Paradigms whose forms contain no stem alternants (i.e. paradigms selecting a unique surface stem) were classified as regular, and paradigms presenting patterns of stem alternation (whether phonologically or morphologically conditioned) were classified as irregular. The distribution of regular and irregular paradigms in our training set is given in Table 2.

This classification reflects an implicational view of Word and Paradigm morphology, whereby patterns of morphological variation are taken to be interdependent in ways that allow speakers to predict novel forms on the basis of their known paradigm companions (Ackerman & Malouf, 2013; Blevins et al., 2017; Bonami & Beniamine, 2016; Marzi et al., 2020; Marzi, 2020). Accordingly, inflectional regularity is not word-based, since it does not pertain to the intrinsic form of a specific morphological process, but rather paradigm-based: it is a property of the network of morphological relations that each form entertains with other forms within its own inflection paradigm, and qualifies the amount of competition/redundancy that a family network conveys.

Two issues warrant a brief comment. First, cases of purely orthographic, phonologically invariant adjustment (e.g. Italian cerc-are/cerch-i ‘to find/you find present tense 2^nd person singular’, or English change/ chang-ing) were glossed as regular. Phonological stem identity was thus treated differently from orthographic stem identity, a choice that, however morphologically sensible, is not supported by data on visual word recognition, which are known to be possibly affected by specific orthographic effects (e.g., Tsapkini et al., 2002). Secondly, the choice of treating both morphologically and phonologically conditioned allomorphy as determinants of paradigm irregularity is theoretically debatable, particularly in connection with the analysis of prima facie phonological alternation patterns such as diphthongization in Romance languages (see, for diverging theoretical accounts, Albright, 2009; Bermúdez-Otero, 2013; Burzio, 2004; Miret, 1998; O’Neill, 2014; Pirrelli & Battista, 2000). However, for our present concerns, the choice is supported by psycholinguistic evidence attesting human sensitivity to graded patterns of formal transparency within inflectional paradigms, irrespective of whether the patterns are phonologically or morphologically motivated (see Sect. 3 above). Since TSOMs are used here as explanatory models of human lexical storage and access, it made sense to assess their behaviour against a psycholinguistically motivated benchmark.

6.2 Data analysis

6.2.1 Processing

How difficult is it for a trained map to process an inflected form? And what factors affect processing costs? To thoroughly address these questions, we measured how easily a trained TSOM can predict an input form, by showing the entire form to the map one letter at a time from ‘#’ to ‘$’. The idea, borrowed from the literature on word/sentence reading (Bianchi et al., 2020; Kliegl et al., 2006; Rayner, 1998), is that the predictability of an input form correlates inversely with the serial processing cost of the form. Put simply, highly predictable words are easier to process than hardly predictable words. In what follows, we analyse how a map’s prediction rates vary with time, as a function of letter position across each input form. Statistical analyses were modelled with R (R Core Team, 2022) as generalised additive models (gam function), and visualised using non-linear regression plots and contour plots (ggplot and fvisgam functions).¹⁶

6.2.2 (Ir)regularity

Figure 7 shows non-linear regression plots fitting prediction rates of the German map by letter position in the input word, for the two training regimes: a uniform distribution (left plot) and a skewed, corpus-based distribution (right plot). For all forms, the position of each input letter is computed as its distance to the stem-suffix boundary in the input form, based on the manual segmentation of our data. Thus, x = 0 marks the first letter in the suffix of an inflected form, and negative x-values denote the position of each letter in the stem.¹⁷ On the vertical axis, y values represent fitted levels of a map’s prediction rate, as defined by equation 6 above. Rates are plotted for forms in both regular (R) and irregular (I) inflection paradigms (hereafter referred to respectively as R-forms and I-forms), where paradigm regularity is assessed categorically as reported in Sect. 6.1.

Fig. 7

Non-linear regression plots (ggplot function, loess method) fitting a TSOM’s prediction rates with interaction effects between German inflected forms in regular (R) and irregular (I) paradigms and distance to morph boundary (MB); verb forms are administered to the TSOM with uniform (left panel) and corpus-based frequency (right panel) distributions. Shaded areas indicate 95% confidence intervals

In both panels, starting from a word’s onset (leftmost tail of each plot), prediction rates get higher as one moves rightwards to the stem-suffix boundary (x = 0).¹⁸ As more of a word is processed, uncertainty in processing an upcoming letter is expectedly reduced, with the rate of prediction rising accordingly. However, such an ascending trend is far from linear, and variation in prediction rates appears to correlate with morphological structure. In a uniform training regime (left panel of Fig. 7), stems in regular paradigms (or R-stems, blue dashed line) are significantly easier to predict than stems in irregular paradigms (or I-stems, magenta solid line), where partially overlapping stem allomorphs compete for lexical access. Accordingly, y values are significantly lower for I-stems (x<0). In Table 3 we report coefficients from GAMs fitted to prediction rates for German stems in both training regimes.

Table 3 GAMs fitted to prediction rates for stems and suffixes, as a function of letter distance to morph boundary for R-forms and I-forms. Paradigms and words are added as random effects. $R^{2}$ indicates the explained variance of each fitted model

Things change when we focus on the stem-ending transition (x = 0). Here, a deep drop in prediction is observed for R-forms only. In Sect. 4, we argued that this is an expected outcome of the ways conditional probabilities of inflectional endings (given the stem) are shaped by the combinatorial properties of regular inflection. Conversely, I-stems are less combinatorial, as they typically select a smaller range of inflectional endings. This reduces the probabilistic independence between a stem allomorph and a suffix, and increases the conditional expectation for the upcoming letters making up the suffix given the stem, facilitating processing at morph boundaries. Thus, prediction rates for suffixes in irregular paradigms are significantly higher than for suffixes in regular paradigms (see Table 3).

Negative slopes for suffix prediction with uniform distributions are a unique feature of German conjugation, reflecting the structure of its inflection markers. In many cells, longer endings are in fact a one-letter extension of shorter endings (e.g. glaub-e, glaub-e-n, glaub-e-n-d), often making paradigmatically related forms compete with one another until their offset. Finally, corpus-based distributions make suffixes more predictable on average, due to their skewed distribution in paradigms and inflection classes.

Stem prediction rates in the two training regimes for English, French, Spanish and Italian conjugations show the same pattern described for German R-forms vs. I-forms. We observe significantly higher values for prediction rates in R-stems than in I-stems, and lower prediction rates for suffixes in regular paradigms than for suffixes in irregular paradigms (see Table 3).

Prediction trends in Fig. 7 show that TSOMs are sensitive to non trivial structural aspects of R-forms vs. I-forms, where the two classes have been defined a priori. Can a TSOM develop a more endogenous, graded notion of inflectional (ir)regularity? For both training conditions, in Fig. 8, we plotted the predictive bias of a TSOM processing German (top) and Italian (bottom) paradigms, based on the amount of intra-paradigmatic co-activation/competition between stem allomorphs in the mental lexicon. In particular, each non-linear plot is associated with a specific range in the likelihood for a stem allomorph to be selected within its own paradigm: namely, its conditional probability $p(s_{k}^{s}|P^{s})$. Ranges are defined by cutting probability values at the 1^st and 3^rd quartiles of their distribution, with low representing the 1^st quartile, medium the 2^nd-3^rd quartiles, and high the 4^th quartile. In the plots, stems in higher ranges of $p(s_{k}^{s}|P^{s})$ are (i) easier to process, (ii) perceptually more salient, and (iii) more segmentable as sublexical constituents. We interpret this evidence as lending support to a graded view of stem regularity, based on the probabilistic support that each stem allomorph receives from the set of paradigmatically-related surface forms sharing the stem (or stem family). The fewer stem allomorphs compete with one another, the easier their processing. Regression models fitting prediction rates for stems in the 5 languages show that the effect of the stem’s conditional probability is highly significant and accounts for a substantial amount of data variance in both training conditions.¹⁹ For each language, we observed a positive significant effect of stem conditional probability (p-value <0.001), and the following $R\textsuperscript{2}$ values for the uniform and corpus-based training condition respectively: 57.6% and 49.6% (English); 52.4% and 34.8% (German); 63.6% and 52.5% (French); 48.0% and 49.7% (Spanish); 54.5% and 27.9% (Italian).

Fig. 8

Regression plots of interaction effects between stem probability ranges and distance to the morph boundary (distance to MB) fitting prediction scores for German (top panels) and Italian (bottom panels) in both uniform (left, language) and corpus-based (right, language F) training distributions

6.2.3 Frequency

Structural effects significantly interact with word frequency distributions. In Fig. 7 (right panel), prediction rates in the corpus-based training condition for R-forms are comparatively lower than those observed for the uniform distributions, suggesting that R-stems tend to be associated with less entrenched (and less predictive) node chains in a map trained with corpus-based distributions. We interpret this effect as the outcome of a tougher competition between regular and irregular paradigms. In fact, in a corpus-based training regime the frequency of R-forms is significantly lower than that of I-forms (see Table 4), and this accounts for the lower rate of prediction of R-forms in the right panel of Fig. 7. Training a TSOM on corpus-based frequencies makes high-frequency I-forms powerful attractors of processing resources, leaving fewer nodes for the map to recruit for processing R-forms. As a result, average levels of prediction rates in the processing of both classes get considerably closer.

Table 4 Frequency mean values, and statistical distribution differences (Welch two sample t-test), for inflected forms in regular (R) and irregular (I) paradigms in our sample of the 50 most frequent verb paradigms in English, German, French, Spanish and Italian conjugation systems

Figure 9 provides a broadly consistent cross-linguistic picture of the role of corpus-based frequency distributions in this dynamic. Prediction rates are plotted for English, German, French, Spanish and Italian forms, grouped in three frequency bins: low (left panel), medium (mid panel) and high frequency (right panel), corresponding to the 1^st, 2^nd-3^rd and 4^th distribution quartile. All plots give substantial evidence of the inherently gradient effect of morphological discontinuity on predictive processing, even in an inflectionally impoverished system such as English conjugation. In all languages, word frequency raises prediction rates by reducing the average processing surprisal at the stem-suffix boundary (Levy, 2008), i.e. the negative log-probability of processing a suffix at x = 0, upon being shown the input form’s stem at x = −1. This general trend notwithstanding, a few interesting inter-linguistic differences are observed. In English and German, high-frequency R-forms and I-forms show no sign of morphological discontinuity at the stem-suffix boundary. In contrast, in Romance languages the impact of morphological structure on prediction scores is consistent across inflection classes and frequency bins. This is in line with what we know of “hybrid” inflection systems like Romance conjugation, where both regular and irregular paradigms are based on combinatorial patterns (Marzi & Pirrelli, 2022).

Fig. 9

Non-linear regression plots fitting TSOMs’ prediction rates for low, medium and high frequency (F) bins of English, German, French, Spanish and Italian verb inflected forms, with interaction effects between R-forms (dotted lines) and I-forms (solid lines) and letter distance to the morph boundary (distance to MB). For all languages, TSOMs were trained on corpus-based distributions (language F)

Combinatorial patterns are nonetheless affected by a significant interaction with token frequency. In all plots of Fig. 9, word-internal structure is perceived through the gradient support that morphological boundaries receive from the mutual probabilistic dependence (or mutual information) between stems and suffixes, i.e. the extent to which the presence of a stem makes an ensuing suffix more or less likely to occur. On top of this effect, the strong predictive bias prompted by a high-frequency form “smooths” the form’s internal structure, making the processor remarkably less sensitive to morphological discontinuity. A Gestalt-like perception of individual forms appears to override local constituency effects, confirming the role that corpus-based distributions of surface forms play in affecting a TSOM’s predictive bias.

6.2.4 Network connectivity

Input frequency distributions shape a TSOM’s connections between map nodes and the input vector (input connections), as well as the connections linking each map node to any other node at one time delay (temporal connections: see Fig. 3). In particular, lexical frequency effects have a direct impact on the strength of temporal connections, which in turn determine the map’s processing bias. At each processing step, activation flowing from a winner node propagates through its weighted forward temporal connections. If weights are evenly distributed, i.e. if the node’s forward connections are equally strong, many downstream nodes will receive a comparable amount of activation from the winner node and are equally likely to fire at the subsequent time step. This increases processing uncertainty. Conversely, when one forward connection of a node is much stronger than other connections leaving the same node, the downstream node to which the strongest connection projects will have a much greater chance of firing at the ensuing time step. As connection weights are competitively shaped by input frequencies according to Rescorla-Wagner equations, the topological distribution of connection weights across the map provides the explanatory link between input data frequency and the map’s processing bias.

This is shown in Fig. 10, where we plot non-linear regressions of the pointwise entropy (pH) of forward connections from nodes that respond to R-forms and I-forms in the five languages. Once more, full forms are centred on the morph boundary, and grouped in three frequency bins: low (1^st quartile), medium (2^nd-3^rd quartiles) and high (4^th quartile). pH is computed as the negative log-ratio between the weight $c_{\langle W_{t}, W_{t+1}\rangle}^{k}$ on the connection between winner nodes $W_{t}$ and $W_{t+1}$ (respectively at time t and t + 1), and the sum of the weights of all forward connections from $W_{t}$:

$$ pH(t)=-log_{2}( \frac{c_{\langle W_{t}, W_{t+1}\rangle}^{k}}{\displaystyle \sum _{c^{i}\in f\_C(W_{t})}c^{i}}) $$

(7)

where $f\_C(W_{t})$ denotes the set of all forward connections from the winner node $W_{t}$. Equation (7) measures the amount of local, functional uncertainty of a TSOM processing each single letter of an input verb form. pH goes down as more of the input form is processed and the form’s uniqueness point is approached. The tendency mirrors a general structural property of word trees, the number of whose bifurcation points gets smaller as we move away from the root of the tree (i.e from the word’s onset). However steep, the descent is nonetheless non-linear, with the morph boundary sitting in between two inflection points of the curve: a entropy local minimum (left of MB) and an entropy local maximum (right of MB). In most plots, the effect is more pronounced for R-forms, showing that (i) the morph boundary marks a point in the map’s connectivity where the number of forward connections increases, and (ii) the increase is higher for R-forms than I-forms. Finally, pH levels are modulated by token frequency. Accordingly, high-frequency forms appear to prune out forward connections, reducing the number of downstream nodes to which activation may flow.

Fig. 10

Non-linear regression plots fitting pointwise entropy (entropy) of forward connections by letter distance to morph boundary (distance to MB) for R-forms (dotted lines) and I-forms (solid lines) in TSOM maps trained on English, German, French, Spanish and Italian conjugations with corpus-based distributions (F)

The evidence points to a structural effect of training data on the processing bias of the map. Paradigm (ir)regularity has two consequences on the organisation of processing nodes in a lexical map. Firstly, the distribution of connections between nodes that process invariant stems in regular paradigms (R-stems) is less entropic. Since no stem allomorphs compete for activation of a cluster of identical nodes, node chains are more entrenched (i.e. they contain stronger connections with fewer bifurcations) and this facilitates stem processing. However, the statistical independence between R-stems and inflectional endings requires multiple forward connections at the stem-suffix boundary, increasing processing uncertainty. Secondly, in irregular paradigms stem allomorphs compete with one another for lexical access, and are typically followed by a restricted range of inflectional endings. The distribution of connections between stem-processing nodes is thus more entropic, making stem processing more effortful. Conversely, the number of forward connections linking each stem allomorph with its suffixes goes down, and the entropy of the distribution of connection weights goes down accordingly, making suffix processing easier.

It should be emphasised that pH levels are computed from the distribution of weights on forward connections of a map’s winner nodes. These effects cannot just be dismissed as merely epiphenomenal. Pointwise entropy actually measures a structural bias in the way a lexical map organises stored verb forms while learning them. The evidence is in line with the processing costs computed in Sect. 4.

6.2.5 Paradigmatic effects

Here, we intend to assess whether a TSOM’s processing bias is also affected by distribution effects that arise within inflectional paradigms and inflectional classes, and in particular by those interactive frequency effects of stems, suffixes and full forms the human word processor has been shown to be sensitive to (see Sect. 3.1).

Five independent GAMs were fitted to TSOM’s full-form prediction rates in our language sample, using the interaction of surface form frequency, stem frequency and distance to morph boundary as predicting variables, with surface forms and paradigms as random effects. Models show a robust facilitatory effect of surface form frequency, and no significant effects of stem frequency (with the only exception of a marginally significant effect for Italian) on the prediction rates of inflected forms.²⁰

Of central importance for the current study, all languages showed a significant negative interaction between surface form frequency and stem frequency. This is shown by the contour plots of Fig. 11, where prediction rates appear to increase for increasing values of surface frequencies (i.e. moving rightwards from the bottom left corner of a plot). In addition, a null (or slightly inhibitory) effect of stem frequency on low frequency forms gets inhibitory in high-frequency forms (top right corner of the plot). To illustrate, when a TSOM processes a low-frequency form (e.g. seeming), the high frequency of the stem seem appears to compensate for the drop in prediction at the stem-ending boundary, yielding a null effect. However, processing the stem-ending boundary of a medium-high frequency form like looked is not equally facilitated.

Fig. 11

Contour plots of the non-linear interaction of word (full form) frequency (x-axis) and stem frequency (y-axis), in five GAMs fitted to full form prediction for all our languages, as a function of distance to morph boundary in interaction with form frequency and stem frequency. Yellow indicates higher, and green lower prediction rates. The fvisgam function excludes points at 0.2 unit square distance from prediction rates

The evidence is in line with human data reported for English (Baayen et al., 2007) and Dutch (Baayen et al., 2002) verb inflection. Baayen and colleagues (2007) additionally report a small facilitation effect of stem frequency in English low-frequency verb forms of regular paradigms. In fact, when we separately fitted two GAMs to the prediction rates for English R-forms and I-forms, we found a positive effect of stem frequency on the processing of R-forms, and a small negative effect on the processing of I-forms (both statistically significant),²¹ as shown in the contour plots of Fig. 12 (top panel).

Fig. 12

Contour plots of the interaction of word (full form) frequency (x-axis) and stem frequency (y-axis) for R-forms (left plots) and I-forms (right plots) in English (top panel) and Spanish (bottom panel) in GAMs fitted to full form prediction as a function of distance to the morph boundary in interaction with surface word frequency and stem frequency. Yellow indicates higher, and green lower prediction rates. The fvisgam function excludes points at 0.2 unit square distance from prediction rates

Interestingly, other verb systems show a similar pattern, albeit with some subtle, language-specific differences. The bottom panels of Fig. 12 illustrate the situation in Spanish, where regular and irregular paradigms show a similar trend in uncertainty reduction for increasing surface form frequencies (despite a substantial difference in frequency ranges).²²

We can understand more of the prediction patterns found in English (and Spanish) R-forms, by looking at the panels of Fig. 13, plotting four independent contour plots of prediction rates for English stems and suffixes in R-forms and I-forms respectively.²³ In R-forms, an increase in stem frequency makes the stem more predictable irrespective of the frequency of its embedding form (Fig. 13, top left panel). When stem frequency grows, however, the increase in suffix prediction for increasing values of word frequency gets slower, because a stem that occurs in more forms is less likely to predict its ensuing suffix (Fig. 13, top right panel). To a first approximation, the prediction rate of a full form can be computed as a summation of the prediction rates scored on its stem and suffix (see Baayen et al. (2007), for a similar proposal). The slight facilitation of stem frequency for low-frequency English R-forms thus shows that stem prediction increases more quickly than suffix prediction decreases, but only in the low word-frequency range. English I-forms, conversely, present a different dynamic. First, stem prediction increases with word frequency (Fig. 13, bottom left panel), because a high-frequency I-form makes its own stem a stronger competitor of other stem allomorphs. In contrast, the frequency of stems in I-forms appears to be inhibitory, as it negatively correlates with stem length (Pearson’s r = −0.46, p-value <2.2e − 16), and shorter stems can only make a small contribution to an incremental prediction score. As to suffix prediction (Fig. 13, bottom right panel), processing is inhibited by increasing values of stem frequency, for the same reason stem frequency is inhibitory of suffix processing in R-forms. By adding up the two prediction rates of stem and suffix, the end balance for the processing of a full I-form is eventually negative for growing stem frequencies, yielding a net inhibitory effect.

Fig. 13

Contour plots of the interaction of word (x-axis) and stem (y-axis) frequency in GAMs fitted to stem (left plots) and suffix (right plots) prediction for English forms in regular (R, top plots) and irregular (I, bottom plots) paradigms, in interaction with distance to morph boundary, surface word frequency and stem frequency. The fvisgam function excludes points at 0.2 unit square distance from prediction rates

A more dynamic view of the effects on word processing of the interaction between stem and form frequencies for the 5 languages is shown in Fig. 14. Here, we plotted prediction rates for all sampled forms, binned²⁴ by low, medium and high values of the |form|/|stem| ratio, computed dividing the frequency of an inflected form by the frequency of its stem. The ratio measures the conditional probability $p(e_{i}|s_{k})$ of an inflectional ending $e_{i}$ given its stem $s_{k}$ (see Equation (3) above) or, equivalently, the probabilistic weight of an inflected form $< s_{k}, e_{i}>$ within its own stem family. Its values range between 0 and 1 (0 < |form|/|stem| ≤ 1), yielding 1 when the frequency of a form equals the frequency of its stem (i.e. when a stem occurs in one inflected form only), and getting lower for low frequency forms with high stem frequencies. For all languages, low-frequency forms containing high-frequency stems (low |form|/|stem| ratio) get a processing headstart on forms with higher values of |form|/|stem|. Such an early facilitation is followed by a later drop in suffix prediction due to the competition with other forms of the same paradigm. The early headstart in English and Spanish is in line with the facilitation effect of stem frequency in the low word-frequency range observed in Fig. 12 (left panels). Nonetheless, the trend is common to all languages, as shown in Fig. 15, where we plotted prediction rates for low |form|/|stem| ratio forms with low, medium and high frequency: facilitation turns out to be overwhelmingly stronger in the low word-frequency range (red lines).

Fig. 14

Non-linear regression plots fitting prediction rates by letter distance to morph boundary (MB =0) for full forms in the 5 languages, binned by levels of |form|/|stem| ratio: low ratio (magenta), medium ratio (blue), high ratio (black)

Fig. 15

Non-linear regression plots fitting prediction rates by letter distance to morph boundary (MB =0) for full forms with low |form|/|stem| ratios, in three word frequency (F) bins: low F (red), medium F (purple), high F (grey)

Finally, we assessed the role of the frequency distributions of inflectional endings on the processing of inflected forms (see Fig. 16). In this connection, the ratio between the frequency of a form and that of its inflectional ending (|form|/|ending|) proves to be a useful tool. The ratio measures the conditional probability $p(s_{k}|e_{j})$ of a stem given its inflectional ending or, in other words, the amount of probabilistic (in)dependence between a stem and its ending. Its value is 1 when the frequency of a form equals the frequency of its ending (i.e. when an inflectional ending is selected by one form only), and goes down for forms with endings that are selected by many other stems. Five independent GAMs, fitted to prediction rates by levels of |form|/|ending| ratios for all our languages, show that high-frequency endings in low-frequency words (low |form|/|ending| ratio) are processed more easily than endings selected by one or few stems only. This is in line with evidence that inflectional endings selected by a large family of stems are processed more easily by speakers (Baayen et al., 2007). Note in addition that an inflected form $< s_{k}, e_{j}>$ with a strongly selected low-frequency ending has a high relative entropy, since their probability $p(s_{k},e_{j})$ is much larger than the product $p(s_{k})\cdot p(e_{j})$ of the probabilities of their constituents (see Sect. 3.2). This evidence provides a simple explanatory framework for the relative entropy effect observed by Milin et al. (2009a).

Fig. 16

Non-linear regression plots fitting prediction rates by letter distance to morph boundary (MB =0) for full forms in three |form|/|ending| ratio bins: low ratio (orange), medium ratio (cyan), high ratio (slate-grey)

7 General discussion

In essence, a TSOM models lexical access as consisting in discriminating between time-bound cues (e.g. a time-series of letters in dynamic competition for their predictive value) for a target lexical unit to be accessed. During lexical learning, competition proceeds through a continuous, incremental update of a cue’s predictive bias, based on the number of times the cue is seen (or is not seen) be associated with the outcome. Ultimately, a TSOM shows an inherent bias for developing maximally discriminative node chains, i.e. patterns of node activation that maximise predictive processing, and, ultimately, ensure fast and accurate lexical access. During online lexical processing of an input signal, node chains are activated incrementally, with node activation propagating through temporal connections. This allowed us to provide a dynamic analysis of how processing (un)certainty changes while the input unfolds in time, in ways that would be difficult to replicate with human subjects.

In a TSOM, co-activation and competition between candidates for lexical access is modelled as resulting from an interaction between the syntagmatic dimension and the paradigmatic dimension of lexical knowledge (see Sect. 3.2). The effects on lexical access of this dynamic are far reaching. Being a member of a large paradigm family gives an inflected form a processing advantage, since the cumulative frequency of the family strengthens the connections between nodes that are activated by more family members. The effect accounts for uncertainty reduction in the processing of verb stems within (sub)regular paradigms, and dovetails well with well-known effects of facilitation in processing words that belong to large word families.

Co-activation triggers processing competition, since only one member of an activated family will typically be consistent with the input target. TSOMs use competition at learning time to shape inter-node connections. This mechanism provides the explanatory link between the amount of competition in the input and the structural entropy of the forward connections emanating from a TSOM’s chains of activated nodes after training. Evenly distributed connections create a balanced competition that maximises processing uncertainty. Conversely, when one forward connection is much stronger than other connections from the same node, one member of the family will be pre-activated more strongly than other members. We showed that this fundamentally predictive bias can account for a variety of effects in the speakers’ word processing behaviour, including their sensitivity to paradigm entropy and the inflectional (ir)regularity gradient.

7.1 Frequency effects

All our models show a significant facilitatory effect of word token frequency on lexical processing, modulated by morphological structure and length of sublexical constituents. Although token frequency effects have traditionally been interpreted as a hallmark of holistic storage and retrieval, our evidence lends support to Baayen and colleagues’ (2007) information-theoretical interpretation of token frequency as an estimate of the joint probability of the constituent parts of morphologically complex forms.

Our evidence confirms the comparatively marginal role of stem frequency in the processing of an inflected verb form when the form’s surface frequency is taken into account (Baayen et al., 2007). The facilitatory effect of a regular stem on the recognition of a surface form (from the stem’s onset up to its end) is compensated by a drop in prediction at the stem-suffix boundary, caused by the larger entropy in the stem’s continuation cohort (Wurm et al., 2006). This counterbalancing effect is thrown into sharper relief when we look at both ends of lexical frequency distributions. A high-frequency form whose paradigm contains many frequent forms is bound to be processed more slowly than a high-frequency form with fewer paradigm companions, as the former’s stem has a wider range of possible continuations. The effect reverses in low-frequency forms, where the processing boost provided by the shared stem is comparatively stronger.

Our evidence also accounts for the role that the frequency distribution of inflectional endings plays in word processing. High-frequency endings help the recognition of low-frequency target forms because they provide an independent processing boost to an otherwise weakly connected chain of processing nodes. Conversely, when a low-frequency allomorphic ending is strongly selected by an irregular stem, the former slows down recognition of the target word. It looks like the inhibitory effect of a low-frequency ending is not compensated by a lower entropy in the stem’s continuation cohort, due to the overall low-frequency of its surface form. This interaction provides a simple explanation of the relative entropy effect (Milin et al., 2009a). If an inflectional ending is strongly selected by a stem (high relative entropy), the ending’s frequency will closely approximate the frequency of its embedding surface form (their |form|/|ending| ratio being close to 1). Accordingly, low-frequency forms with high relative entropy will be harder to process, since they do not benefit from high-frequency, deeply entrenched endings.

7.2 Structural effects

All present observations are based on non-linear regression models that allow us to focus on the time course of a TSOM’s processing response. This way, we could control for processing variations over time, measured while a TSOM is processing an input form. In addition, by aligning the time window with the structural properties of each input form, we could investigate non-linear changes along multiple dimensions of linguistic information. Such a dynamic analysis of time course data goes well beyond traditional measurements obtained by summarising behavioural data in a certain time window, to arrive at a mean value, or estimate a general trend. In fact, mean values can mask subtle changes in the processing dynamic, while assigning identical linear estimates to substantially different non-linear trends.

Effects of morphological structure on processing are easier to detect in regular verb paradigms than in irregular ones. First, stems in regular paradigms are formally consistent across their inflected forms and have no direct competitors in their own paradigm. They thus benefit from cumulative frequencies and are easier to predict. In addition, they are often longer than stems in irregular paradigms, and this increases their average prediction rates. Finally, they select a larger number of suffix types, with a resulting drop in processing prediction at the stem-suffix transition. All these factors explain a stable processing advantage of R-forms over I-forms in a time window spanning from the verb stem’s onset to its end. However, at least part of this advantage reverses in the processing of the final part of an inflected form, due to a higher probabilistic dependence between stems and inflectional endings in irregular paradigms.

Other factors, such as token frequency distributions and word length, can have an impact on this non-linear dynamic. In particular, when a TSOM is trained on surface forms that are sampled by their token frequency, the processing advantage of R-stems over I-stems diminishes overall. Since we did not change the size of paradigms (each consisting of 15 cells), but only the distribution of the cell forms across the two regimes, lower levels of average prediction for less entropic samples attest a non linear effect of competition between realistically distributed forms: few high-frequency words are better predicted at the expenses of a (Zipfian) tail of low-frequency words. Nonetheless, real frequency effects do not cancel out non-linear structural effects in enumeratively more complex inflection systems, i.e. systems that mark morphological contrast with a larger number of morphological exponents (see Fig. 9).

7.3 Implications for a lexical architecture

All simulations reported in the previous pages were based on self-organisation processes involving surface lexical forms. They were blind to whether two surface forms actually belong to the same paradigm (e.g. fall and fell), or are only accidental lexical neighbours (e.g. tall and tell). We can ask ourselves whether these results extend to a more realistic learning scenario, where lexical semantics is taken into account.

In Fig. 17, we use a TSOM as a layer of topologically self-organised units for lexical access. In the figure, nodes at the bottom layer define the input vector of a TSOM. Double circled nodes are incrementally activated by the input form fell, and propagate their activation to a lexico-semantic layer. Inter-layer propagation is assumed to flow interactively (this is graphically represented by two-pointed arrows), i.e. with activation from lower levels being continuously affected by activation coming back from higher levels. We further assume that propagation takes place in a cascaded way (Peterson & Savoy, 1998), so that access units can (pre-)activate upper lexical nodes before any single candidate has been explicitly selected. Access units are structured as partially overlapping word graphs, whose activation simulates co-activation of multiple candidates that compete for lexical access. The process accounts for the gradient activation of neighbour candidates (e.g. fall and fell), which share a few processing nodes. Since temporal connections are trained on surface forms sampled according to their frequency distributions, high-frequency candidates are activated more strongly than low-frequency candidates.

Fig. 17

A recurrent topological self-organising version of a three-levelled model of lexical access. Double circled nodes indicate nodes activated by the input string fell. Inter-level connections are shown as solid two-pointed arrows between activated nodes. Intra-level dashed lines represent temporal connections between nodes/letters that are serially activated with one-time delay. For convenience, sequences of nodes responding to letter substrings are graphically represented as single multi-letter nodes (e.g. walk- or -ing)

Distributed graph-based representations are not to be confused with morpheme splitting. Although some node graphs can share blended nodes (i.e. winning nodes activated by different surface forms), each word graph is learned to optimally respond to a full surface form, not to sublexical parts, and morphological structure is reflected by the ways probabilistic weights are distributed over temporal connections. In addition, both blended and dedicated processing chains insist on a single level of connectivity, and do not require to be functionally segregated. Such a distributed allocation of probabilistic weights over a single layer of synaptic connectivity accounts for (i) continuously graded levels of morphological structure, and (ii) graded patterns of lexical priming as a function of the formal similarity between surface forms.

How does this framework account for semantically sensitive priming effects (e.g. fell primes fall, but tell fails to prime tall), vs. semantically blind priming effects (e.g. corner primes corn) (Crepaldi et al., 2010)? It is commonly assumed that members of an inflectional paradigm are related semantically in the mental lexicon more strongly than members of a derivational family (e.g. Marslen-Wilson et al., 1994; Levelt et al., 1999). It is thus reasonable to expect reverberation of semantic information from the top layer down to the access layer to affect the topological organisation of inflected forms more consistently than the topological organisation of derivatives. In the end, word graphs of inflected forms will implicitly encode lemma information, whereas word graphs for derivatives will not, thus making access units for derivatives less sensitive to meaning than paradigmatically-related forms.

Other lexical models are certainly compatible with the evidence reported here, Bybee’s Network Morphology being probably the best known and closest example (Bybee, 1995; Bybee & McClelland, 2005). In Bybee’s model, stored words that present overlapping substrings and overlapping meanings are mutually related through paradigmatic connections. The larger the network of paradigmatic connections, the more salient the morphological structure of its members. Conversely, the strength of paradigmatic connections correlates negatively with word token frequency. Hence, high frequency forms are weakly connected with other forms, and tend to be perceived holistically. TSOMs provide a more parsimonious account of the inverse correlation between token frequency and perception of morphological structure via paradigmatic relations. Due to learning step 1, a frequent form develops highly specialised syntagmatic connections, and it weakens its paradigmatic connections with other forms in the same paradigm (learning step 2). Conversely, more evenly distributed paradigmatically related forms develop weaker syntagmatic connections, and a more prominent morphological structure.

Our approach presents several points of contact with Baayen and colleagues’ dynamic modelling of word recognition as a staged process of lexical selection described by information-theoretical equations (Baayen et al., 2007). In particular, we fully agree with the authors’ emphasis on a probabilistic interpretation of word frequency effects as part of a predictive conditional probability $p(e_{j}|s_{k})$. We showed that this interpretation follows naturally from the dynamic operation of Rescorla-Wagner equations in the process of TSOMs’ lexical self-organisation at learning time. In fact, unlike interactive activation models where lexical competition is resolved dynamically at processing time, TSOMs use lexical competition to shape the network of temporal connections between processing nodes at learning time. Thereby, they can develop a long-term, predictive sensitivity to morphological structure that arises in the context of stored full form representations to maximise processing efficiency. From this perspective, the integrative view of processing and learning that underpins a TSOM architecture is in good accord with Apfelbaum and McMurray’s (2017) view that lexical representations are learned while they are processed, and not after processing competition has been resolved.

8 Concluding remarks

The debate on the role played by morphological regularity in the ways speakers process and access inflected words has taken centre stage in the psycholinguistic literature on lexical modelling. Classical two-staged models see sublexical constituents as the peripheral stepping stones from which central lexical representations of morphologically complex items are accessed. Accordingly, regular, high-frequency morphemic constituents are expected to provide a faster route to lexical representations than either low-frequency or subregular morphemic constituents. In assuming a direct correspondence between linguistic units and their mental correlates, two-staged models expect regular forms to be easier to process than irregular forms just because the former (unlike the latter) contain parts that are themselves more frequent and easier to process than their full forms.

Two-staged models have been extremely influential in the psycholinguistic and linguistic literature on lexical competence, as they appeared to offer a firm neuropsychological foundation to a fully compositional, rule-based view of morphological competence. Albeit linguistically appealing, the assumption fails to account for (i) non-categorical, gradient effects of morphological regularity and productivity, (ii) human pervasive sensitivity to both local and global probabilistic distributions in lexical data, (iii) non-compositional and non-linear interactions between surface form frequency and the frequency of sublexical parts. All in all, two-staged approaches appear to comparatively neglect a functional perspective on language, according to which lexical processing and word storage/retrieval are highly time-bound, non-linear processes, modulated by a variety of structural, distributional and semantic factors.

The present contribution offers several reasons to believe that TSOMs provide and interesting experimental and explanatory framework for investigating word processing/storage issues from a functional perspective. First, with its emphasis on the time-bound nature of lexical data, a TSOM approach is in line with the Word and Paradigm view that inflected forms are the basic building blocks of human morphological competence. It thus flies in the face of the reductionist assumption that the properties of a morphologically complex word boil down to the properties of its sublexical parts. We showed that it is simply not possible to model the way humans process an inflected form by replacing information about the form’s frequency with information about the frequency of its parts. This does not mean that sublexical frequencies are irrelevant. In fact, they interact significantly with full form frequencies during processing. However, the interaction does not make full forms dispensable in the least.

Secondly, TSOMs offer a computationally tractable way to simulate aspects of the interaction between word processing, storage and learning that are amenable to a sensible psycholinguistic intepretation. Their architectural simplicity and neurobiological plausibility make them instrumental for investigating adaptive lexical self-organisation in the face of a rich morphological input. Since TSOMs’ mathematical framework is rooted in Rescorla-Wagner equations, our evidence shows that discriminative learning principles can go a long way in approximating Bayesian networks of probabilistic expectations over time-series of lexical data. This also provides an explanatory framework for information-theoretical models of word processing, and justifies our present, exclusive focus on surface forms and lexical and sublexical frequencies, as a way to complement much established work in discriminative word learning, primarily concerned with the mapping of lexical forms onto meanings.

A TSOM approach is also in good accord with psycholinguistic literature that emphasises the role of lexical processing, rather than lexical representation in a strict sense, for our understanding of human word competence (Apfelbaum & McMurray, 2017; Ji et al., 2011; Kuperman et al., 2010; Libben, 2006, 2010). Accordingly, the human processor appears to be able to use all information that is available to it, accessing and integrating data on different time scales (from symbolic units and morphological chunks to full forms and beyond). We showed that, in TSOMs, lexical data are memorised as more or less automatised processing routines (depending on the degree of probabilistic support they receive from the input), since lexical representations consist of the very same nodes that are activated at processing time (Marzi & Pirrelli, 2015). This runs against the functional distinction between dynamic, algorithmic processes (rules) and static memory representations (lexical data) in which two-staged morphological approaches are apparently grounded.

Last but not least, a detailed quantitative analysis of our data showed that the global self-organisation of stored processing patterns reflect the frequency distributions of different levels of word-internal structure, from full words to stems and inflectional endings. Although a TSOM is trained to store and process surface forms, it does not always converge on optimal, one-sized activation patterns. In fact, the level of granularity of the patterns reflects the degree of structural overlapping and frequency-based competition in the input data. TSOMs are thus ultimately supportive of the psychological reality of gradient word structure, according to which sublexical constituents are not just the epiphenomenal by-product of speakers’ word processing habits, but play a significant role in the ways processing expectations are informed by the acquisition and structural organisation of these habits.

For sure, we are not suggesting here that word frequency and structure (ir)regularity are the only factors affecting the processing bias of a speaker. Many other determinants of word processing and learning, such as length, age of acquisition, semantic basicness, perceptual salience, communicative intent, valence and relevance (to name but a few) are found to play a significant role (Baayen et al., 2016). In Sect. 7.3, we discussed how to augment a TSOM with a self-organising layer of lexico-semantic information accounting for semantically-driven effects of word family size. Testing the algorithmic behaviour of such an augmented architecture is an important direction for future research, paving the way to a quantitatively and qualitatively thorough assessment of TSOMs as computational models of speakers’ word processing behaviour. Having said that, it would nonetheless be surprising if the ubiquitous role that frequency and structure play in the processing of inflection were simply the accidental result of a coalition of other independent predictors. We are inclined to favour more functional, explanatory analyses grounded in our current knowledge of the general properties of human memory (Wixted, 2004). Discriminative, information-theoretical models of word processing can help researchers get a principled understanding of the exceedingly tight relationship between word frequency, paradigm entropy and gradient morphological structure in processing inflection, and discover new correlations in verb systems of increasing inferential or enumerative complexity.

Finally, in the present work we have exclusively been concerned with the processing bias of fully-trained TSOMs, by looking into the structural and behavioural end results of their self-organisation. One would nonetheless expect that, due to the neuro-computational interconnection between learning and processing, future analyses of the incremental ways processing (un)certainty and perception of word-internal structure change developmentally with learning epochs will offer fresh insights into the process of language maturation and the acquisition of word knowledge by both children and adults.