Abstract
Frank’s Windkessel model described the hemodynamics of the arterial system in terms of resistance and compliance. It explained aortic pressure decay in diastole, but fell short in systole. Therefore characteristic impedance was introduced as a third element of the Windkessel model. Characteristic impedance links the lumped Windkessel to transmission phenomena (e.g., wave travel). Windkessels are used as hydraulic load for isolated hearts and in studies of the entire circulation. Furthermore, they are used to estimate total arterial compliance from pressure and flow; several of these methods are reviewed. Windkessels describe the general features of the input impedance, with physiologically interpretable parameters. Since it is a lumped model it is not suitable for the assessment of spatially distributed phenomena and aspects of wave travel, but it is a simple and fairly accurate approximation of ventricular afterload.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Models are a simplification of reality which help to understand function. The arterial system has been modeled in many ways: lumped models [18, 73], tube models [8, 41, 80] and anatomically based distributed models [42, 64, 71]. In this paper we will discuss the lumped or Windkessel models. Lumped models of the venous system [67] will not be discussed.
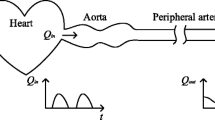
Hales (1735) was the first to measure blood pressure and noticed that pressure in the arterial system is not constant, but varies over the heart beat. He already suggested that the variations in pressure are related to the elasticity of the large arteries. Weber (Weber EH (1827) as cited by Wetterer and Kenner [80]), was probably the first who proposed comparison of the volume elasticity of the large arteries with the Windkessel present in fire engines (Fig. 1).
It was Frank [18] who quantitatively formulated and popularized the so-called two-element Windkessel model consisting of a resistance and a compliance element. Poiseuille’s law states that resistance is inversely proportional to blood vessel radius to the fourth power. The resistance to flow in the arterial system is therefore mainly found in the resistance vessels: the smallest arteries and the arterioles. When all individual resistances in the microcirculation are properly added, the resistance of the entire systemic vascular bed is obtained and we call this (total) peripheral resistance. The peripheral resistance, R, can simply be calculated as:
with P ao,mean and P ven,mean mean aortic and venous pressure and CO cardiac output. The compliant element is mainly determined by the elasticity of the large, or conduit, arteries. It can be obtained by addition of the compliances of all vessels and is therefore called total arterial compliance. The value of total arterial compliance, C, is the ratio of a volume change, ΔV, and the resulting pressure change ΔP:
However, it is very difficult to perform an experiment were a volume is injected into the arterial system without any volume losses through the periphery. Therefore several methods to derive total arterial compliance were developed, and those based on the Windkessel are discussed in detail below. Actually the compliance of the large arteries acts as the Windkessel, but over time it became customary to call these lumped arterial models, made up of resistance and compliance, Windkessel models. The strict separation of conduit (compliant) arteries and small arteries and arterioles (resistance vessels) is not possible, because large, compliant, arteries have small resistive properties as well and resistive vessels have, some, compliance. When accounting for R and C only, we deal with the Frank or two-element Windkessel model.
The two-element Windkessel predicts that in diastole, when the aortic valve is closed, pressure will decay exponentially with a characteristic decay time RC (see below). Frank’s goal was to derive cardiac output. With the characteristic decay time RC, derived from the aortic pressure in diastole and an independent estimate of total arterial compliance the peripheral resistance could be calculated. Mean flow (i.e. cardiac output) is then simply mean aortic pressure divided by peripheral resistance. Frank estimated total arterial compliance from pulse wave velocity in the aorta. This example shows that Windkessel models and wave transmission of pressure in the aorta give complementary information.
The Windkessel is a so-called lumped model. In other words this lumped model describes the whole arterial system, in terms of a pressure-flow relation at its entrance, by two parameters that have a physiological meaning. One cannot study phenomena that take place inside the arterial tree such as wave travel and reflections of waves, etc.
It is interesting to note that in the past hypertension research focused mainly on peripheral resistance, while the contribution of total arterial compliance to blood pressure was often neglected. (The groups of Safar [58] and Westerhof [46] were exceptions in this respect, Fig. 2). In 1997, however, it was shown that pulse pressure is a major predictor of cardiovascular morbidity and mortality [3, 36]. This observation made researchers realize that arterial compliance is also of great importance, especially in old age (systolic) hypertension.
A sudden decrease in arterial compliance, but constant peripheral resistance results in an increase systolic aortic pressure and decrease in diastolic pressure. (Adapted from Randall et al. [46])
The two-element Windkessel model tells us that the load on the heart consists of peripheral resistance and total arterial compliance and that both are important.
2 Improvement of Frank’s Windkessel: the three-element Windkessel
Frank had only (aortic) pressure to base the two-element Windkessel on. The diastolic pressure, P dia(t), in the proximal aorta with closed valves can be described by an exponential decay and the two-element Windkessel indeed predicts such a decay (Fig. 3):
with P es = end-systolic aortic pressure.
In the 1930s and 1940s a number of researchers tried to improve the two-element Windkessel by adding resistance and/or inertance terms and by adding effects of reflected waves. However, a good physiological basis of these models was lacking [34, 80].
With the development of the electromagnetic flow meter and thus measurement of aortic flow, it became clear that in systole the relation between pressure and flow was poorly predicted by the two-element Windkessel [77]. Wetterer [77–80] had already noticed, but not quantified, the shortcomings of the two-element Windkessel. In 1956, Wetterer [78] even showed the quantitative difference between measured and predicted pressure in systole, but he did not suggest what the determinant of this pressure difference is.
Measurement of aortic flow together with the developments in computing capabilities that allowed for Fourier analysis of the pressure and flow signals, the calculation of input impedance became possible [34, 40, 75, 76]. From the input impedance the shortcomings of the two-element Windkessel also became clear, because for high frequencies its modulus reduces to negligible values and its phase angle reaches −90°, while the aortic input impedance derived in mammals showed that the impedance modulus decreases to a plateau value and the phase angle hovers around zero for high frequencies (Fig. 4). The rather constant level of the input impedance modulus at higher frequencies was found to be equal to the characteristic impedance of the proximal aorta. This information led to the addition of aortic characteristic impedance to the two-element Windkessel (Fig. 5). The characteristic impedance in the three-element Windkessel [71, 73], can be seen as a link between the lumped Windkessel model and wave travel aspects of the arterial system since characteristic impedance equals wave speed times blood density divided by (aortic) cross-sectional area.
An example of measured aortic input impedance plotted together with impedances predicted by the two-element Windkessel, the three-element Windkessel, and the four-element Windkessel (Adapted from Westerhof et al. [76])
The two-element Windkessel, the three-element Windkessel, and the four-element Windkessel presented in hydraulic and electrical form Z c is aortic characteristic impedance and equals PWV·ρ/A, it connects Frank’s Windkessel with wave transmission models. PWV Pulse wave velocity in the proximal aorta, ρ is blood density, A is area of the proximal aorta
The oscillations seen on the impedance modulus and phase are not represented by the three-element Windkessel model (see Figs. 4, 6), and therefore this aspect of the arterial system is not modeled [33, 39, 73]. This implies that high frequency details such as the inflection point and the augmentation in aortic pressure cannot be described by the three-element Windkessel model (see Fig. 6). Yet the overall predicted waveforms are close to the measured pressures and the global aspects of pressure and the input impedance are well described by the three-element Windkessel (Fig. 6). The phase difference in the impedance may, in part, result from a time delay between pressure and flow, either as a result of equipment properties of as a result of measurement location [70]. For instance, a time delay between pressure and flow of 8 ms translates into phase of the impedance to 360 × 8 × 10−3 f≈2.9 f, i.e. about 30° at 10 Hz. In other words, this phase effect does not affect the relation between the wave shapes, but only their time delay.
Top Examples of measured pressure and the pressure derived from measured flow and the three-element Windkessel, in the human aorta of a type A beat and a type C beat. Bottom The (averaged) human aortic input impedance of type A beats and type C beats together with the input impedance of the three-element Windkessel, thick line. (Adapted from Murgo et al. [39])
The characteristic impedance has the same dimension as a resistor and is therefore often represented as a resistor. However, the characteristic impedance is not a resistance, and can only be interpreted in terms of oscillatory phenomena. This means that the ratio of mean pressure over mean flow (i.e. 0 Hz) which equals R, is in the three-element Windkessel R + Z c. The use of a resistor for characteristic impedance also causes errors in the low frequency range of the input impedance [59]. However, since characteristic impedance is, in the systemic circulation of all mammals, about 5–7% of peripheral resistance [72] the errors are small.
Wang et al. [68] recently analyzed aortic pressure and flow in the following way. In diastole, when the two-element and three-element Windkessels behave similarly, (with closed valves characteristic impedance does not play a role) these authors fitted the Windkessel and determined total peripheral resistance and total arterial compliance. When this two-element Windkessel was then applied to the entire heart beat a difference was found in systole between the measured pressure and the pressure derived from the two-element Windkessel. This pressure difference, called excess pressure, and according to the definition of Lighthill [30] a pressure proportional to velocity (or flow), is indeed similar in shape to the measured velocity. The value of this resistance is close to the characteristic impedance of the aorta. This result is thus proof, in the time domain, that addition of the characteristic impedance to the two-element Windkessel, thereby resulting in the three-element Windkessel, is necessary to describe pressure and flow throughout the entire cardiac cycle. We interpret this result as support for the three-element Windkessel with characteristic impedance of the aorta (see Fig. 4) as the third element. However, Wang et al., interpret this resistor as the resistance of the conduit arteries. By doing so this would mean that all large conduit arteries would be described by the proximal resistance. This proximal resistance and arterial compliance would reside within the same (conduit) vessels and cannot be separated.
Fogliardi et al. [17] compared the three-element Windkessel with constant compliance and with pressure-dependent compliance. They concluded that “the nonlinear three-element windkessel cannot be preferred over the traditional linear version of this model”. Thus the three-element Windkessel suffices in most studies [50].
3 The four-element Windkessel
In an attempt to reduce the errors in the low frequency range, introduced by the characteristic impedance, a fourth element of the Windkessel has been proposed [63], an element originally suggested by Burattini and Gnudi [7]. This fourth element (Figs. 4, 5) is an inertance equal to the addition of all inertances in the arterial segments, i.e. total arterial inertance [63]. While aortic characteristic impedance takes into account the compliance and inertance of the very proximal ascending aorta, total arterial compliance and total arterial inertance are the summation of all compliances and inertances in the entire arterial system. The total arterial inertance only affects the mean term and very low frequency behavior of the input impedance, i.e. the frequency range where the three-element Windkessel is inaccurate.
Other investigators have introduced an inertance in series with the characteristic impedance [4, 5, 7, 25, 32, 57]. This series inertance does not affect the arterial input impedance at low frequencies but at high frequencies. In theory this inertance implies an increase in the impedance modulus with frequency in the high frequency range, but in practice the inertance is chosen such that this effect is small.
The four-element Windkessel has been used by Segers [51, 53–55] and Burattini [5]. In practice it turns out that the inertance is very difficult to estimate which is an argument to prefer the three-element Windkessel.
Burattini [6, 9] tested several other lumped models for the peripheral arterial system: One lumped model consists of a peripheral resistance with, in parallel, a series resistor and compliance. This arrangement leads to the same form of input impedance, as the three-element Windkessel, namely (a + jωb)/(1 + jωc), with a, b, and c constants. The advantage of this particular model is that at 0 Hz, the peripheral resistance is correctly modeled. The resistance in series with compliance is based on viscoelastic arterial properties. Thus the elements have a different meaning than those of the three-element Windkessel model and this model is therefore not an improvement of Frank’s two-element Windkessel model.
The different aspects of the Windkessel models have been summarized in Table 1.
We conclude that the three-element Windkessel is a necessary improvement of the two-element Windkessel and can model the global aspects of the arterial system with physiologically based parameters.
4 Use and clinical relevance of the Windkessel
The Windkessel teaches us that the main parameters describing the arterial system are peripheral resistance, total arterial compliance and aortic characteristic impedance. In 1997 [3, 36], the importance of pulse pressure in the prediction of cardiovascular mortality and morbidity was shown and the important role of compliance was recognized. It is therefore implicit that, for instance in hypertension, these three Windkessel parameters play a role. Total arterial compliance [35] and, to a lesser extent characteristic impedance, are now important parameters under investigation.
Ambulatory arterial stiffness index. The Windkessel can be used to clarify the meaning of parameters used in epidemiological studies. An example is the ambulatory arterial stiffness index [13]. Assuming the Windkessel predicted decay time of aortic pressure in diastole, as RC, Westerhof et al. [74] derived this stiffness index [13] from first principles and showed that, despite its name, it should be regarded as a ventriculo-arterial coupling factor rather than a compliance estimate.
Windkessel used as load on the heart. The Windkessel models can be used as load for the isolated ejecting heart. Figure 7 shows an example of an isolated ejecting heart loaded with a three-element Windkessel. It may be seen that the generated pressure and flow waves resemble the in vivo pressure and flow waves. The Windkessel parameters may be changed to study cardiac pump function [15, 25, 32, 65]. An example of the effects of peripheral resistance changes and total arterial compliance changes, while cardiac contractility, heart rate and cardiac filling are maintained constant is given in Fig. 8 [15].
Example of the use of an ejecting isolated (cat) heart with a three-element Windkessel as load. The effects of changes in peripheral resistance and total arterial compliance on aortic pressure and flow are shown. (Adapted from Elzinga and Westerhof [15])
The Windkessel used to derive cardiac output. Wesseling et al. [69] developed a method to derive cardiac output from pressure using the three-element Windkessel. The characteristic impedance and total arterial compliance are given as non-linear functions of pressure based on the data of Langewouters [26, 27], using gender, age, body length and weight. An initial value for peripheral resistance in assumed. Stroke volume, SV, is then calculated from pressure. Cardiac output is set to SV·HR and peripheral resistance is calculated as mean pressure over this cardiac output estimate. This resistance value is inserted again in the three-element Windkessel and SV for the next beat is calculated. It turns out that after a few beats convergence is obtained and the true resistance is found: mean pressure over this resistance gives cardiac output. The non-linear behavior of the compliance and characteristic impedance combined with the adaptive peripheral resistance assure excellent tracking of cardiac output [81].
The Windkessel used as load in artificial heart and valve studies. The (nonlinear) Windkessel, has also been used in studies on ventricular assist devices and setups to test artificial valves [1, 12, 14, 19–21, 38, 48, 49]. However, in this field many other models of the arterial system are used as well.
Windkessel used in theoretical analyses. The Windkessel has also been used in theoretical analyses where a heart model and arterial system (Windkessel model) are coupled and the contribution of changes in parameters to blood pressure are calculated [10, 61]. An example of such an analysis is shown in Table 2 [61]. It may be seen that for similar percentage changes in total arterial compliance and peripheral resistance, the resistance contributes a factor 4 more to pressure. This result does not imply that changes in compliance are of little importance since with age resistance may increase 10–20% while compliance may decrease with a factor 2–4. These predictions are supported by experimental data of (see Fig. 8). Several studies have been reported on ventriculo-arterial coupling. In these studies Windkessel models of the arterial system have been used [10, 52, 54, 55]. The Windkessel as load is preferred in this type of analysis since more extensive models are awkward to work with.
The Windkessel used as peripheral bed model. The three-element Windkessel has been used as a simplified representation of peripheral beds in distributed models [64]. However, it should be kept in mind that the characteristic impedance is only a real quantity for large vessels, making the three-element Windkessel a very rough representation of a peripheral bed. Windkessel models with an inertance term have also been used a terminal impedance of the aorta [6, 9].
The Windkessel used in end-ejection identification. Using aortic pressure as input, an uncalibrated flow curve can be calculated from which the time of end-ejection can be identified unambiguously. Since only an uncalibrated flow is required, the parameter estimation reduces to the determination of two time constants which can be conducted in real time [22].
The windkessel used in solving the outflow problem in impedance cardiography. In impedance cardiography, Stroke volume is estimated from the changes in electrical impedance of the thorax [24, 44]. Since blood both enters and leaves the thorax simultaneously, impedance changes cannot be solely attributed to inflow. To solve this so-called outflow problem [16], a Windkessel model was used [23].
The Windkessel used in assessing right ventricular afterload. Windkessel models have also been used extensively to describe the pulmonary vascular bed [33]. Although most of this research on the pulmonary circulation is preclinical, Lankhaar et al. [28] have shown that the Windkessel model can be used to clinically assess differences between groups of patients with different forms of pulmonary hypertension. However, the windkessel turned out to be too simple a model to be able to classify individual patients.
5 Estimation of total arterial compliance
Several methods, based on the Windkessel have been proposed to estimate total arterial compliance [76]. These methods are:
The decay time method [18]. When flow is zero, as in diastole, the decrease of aortic pressure is characterized by the decay time, which equals RC for the two-element Windkessel and three-element Windkessel models, provided the analysis is started with some delay after valve closure (about 10% of the heart period, see Fig. 6), at pressure P 0. The decay time is usually determined by an exponential fit that will decrease to zero pressure. Thus the fit is:
However, pressure may, in reality, not decay to negligible values so that it would be better to fit diastolic pressure with:
The intercept pressure, P i, depends on vasoactive state, and is not easy to obtain, making estimates of RC inaccurate. As an alternative, the intercept pressure and RC could be estimated simultaneously using a nonlinear least-squares method [68].
The Stroke volume over pulse pressure method. This method is rather old [45, 47] but has been reintroduced recently [11]. If the vascular periphery could be completely blocked, i.e. resistance infinite, Stroke volume, ΔV, would increase pressure by ΔP and the ratio would give total arterial compliance: C = ΔV/ΔP. Since part of the Stroke volume leaves the arterial system through the periphery, this ratio overestimates compliance. The overestimation may be as large as 60% [50, 56].
The area method [31]. The decay time in diastole is estimated as the area under the diastolic aortic pressure divided by the pressure difference between start and endpoint.
The area method has been compared with the pulse pressure method [56]. The integration reduces errors due to noise on the pressure signal.
Estimating pressure dependence of total arterial compliance [29, 31]. Use is made of the three-element Windkessel model and the pressure dependence of compliance is accounted for by assuming a specific value for the exponential coefficient, b, of the nonlinear pressure–volume relationship: V = a ebP + c [31, 82]. The expression for the compliance (C) at any pressure is [82]:
where P s and P d are the pressures at end-systole and end-diastole, respectively; A s and A d are the areas under the systolic and diastolic portions of the pressure waveform, respectively; SV is Stroke volume; and b is the nonlinear coefficient (a value of −0.01 is often assumed for this coefficient). Z c is characteristic impedance.
The two-area method is based on the following equation [56]
This equation is applied to two periods of the cardiac cycle; the period of onset of systole to peak systole and the period from peak systole to the end of diastole. Thus using these two equations with two unknowns, R and C, are obtained.
The pulse pressure method [59, 62] is based on fitting the systolic and diastolic pressures, as predicted by the two-element Windkessel with measured aortic flow as input, to the measured values of systolic and diastolic pressure. Although the two-element Windkessel does not produce correct wave shapes, its low frequency impedance is close to the actual impedance, while in three-element Windkessel (by assuming the characteristic impedance as a resistor) introduces errors at the low frequencies. The systolic and diastolic pressure are mainly determined by low frequencies and thus predicted accurately by the two-element Windkessel. The pulse pressure method has been compared with the area method and the SV/PP method and found to be the superior one [56].
The parameter estimation method fits the three-element or four-element Windkessel to measured pressure and flow as a function of time. When aortic flow is fed into the Windkessel model the pressure is predicted. This pressure can be compared to the measured pressure. By minimization of the difference between predicted and measured pressure (i.e. the sum of squared errors), the best Windkessel parameters are obtained. In this way, all the Windkessel parameters can be derived including a good estimate of characteristic impedance. Using the three-element Windkessel the value of compliance is overestimated [50] but this is not the case using the four-element Windkessel [63], however, the inertance estimate is usually poor. Also the inverse procedure may be followed, pressure can be fed into the Windkessel model and optimization of flow is then performed [60].
The input impedance method is similar to the previous method, but is carried out in the frequency domain. The input impedance of the three-element or four-element Windkessel model is fitted to the measured input impedance.
The transient method [66] can be applied when pressure and flow are not in the steady state. In a non steady state peripheral resistance cannot be calculated from mean pressure and mean flow, because aortic flow is not equal to peripheral flow. Using the three-element Windkessel with flow as input, pressure may be calculated while storage of blood in the large conduit arteries is accounted for. By curve fitting of the Windkessel parameters to obtain minimal difference between measured and predicted pressure the Windkessel parameters can be estimated accurately.
General remarks. In the methods where the RC-time is derived, the resistance should be calculated from mean pressure and flow, and compliance is then RC-time divided by R.
It should be emphasized that all Windkessel-based methods rely on accurate pressure measurement in the proximal aorta. The first three methods require accurate pressure measurement and mean flow (cardiac output), while the other methods require ascending aortic pressure and flow wave shape.
Quick et al. have circumvented the use of a lumped model as assumed in all methods described above by incorporating transmission of the pressure wave, as in the real arterial tree, to estimate arterial compliance [43]. Recently, they also showed that for wavelengths longer than the arterial tree, distributed models will be reduced to the lumped Windkessel [37]. Such long wavelengths or high wave speed implies that all pressures and flows behave similarly.
6 Windkessel as full description of the arterial system
Arterial input impedance gives a comprehensive description of the arterial system as load on the heart. However, impedance with its modulus and phase, and its frequency dependence is difficult to interpret. Using the three-element Windkessel a comprehensive description of the arterial load is obtained as well. The three elements are derived and have a physiological meaning and one can see which part of the arterial tree is changed. For instance, a decrease in arterial compliance is not easily seen in the impedance and not easily expressed quantitatively either. Derivation of the Windkessel immediately gives quantitative information on total arterial compliance.
The integrated description of the entire arterial system by means of a lumped system like the Windkessel, can adequately describe pressure-flow relations at the entrance of the system, but pressures within these models have little meaning. e.g., the measurement of pressure distal of the characteristic impedance for instance, does not represent the pressure in the more distal vascular system.
The Windkessel is being used in the so-called Physiome, which attempts to develop mechanistic biophysical models within a unifying framework obedient to fundamental mechanical and physicochemical principles [2]. See, for example, the National Institutes of Health “Roadmap for Medical Research in the 21st Century” (http://nihroadmap.nih.gov) mechanistic systems approach to biological sciences [2].
The windkessel helps to interpret impedance. We interpret the input impedance of the arterial system as follows. For mean pressure and flow and very low frequencies, frequencies <0.2 HR, the distal periphery, i.e. peripheral resistance determines the input impedance. For intermediate frequencies, 0.2 HR < frequencies <3 HR, the more proximal part of the arterial system begins to determine impedance, i.e. total arterial compliance is the main determinant. For very high frequencies, frequencies >3 HR, only the very proximal part of the arterial system, i.e. the aorta contributes, in terms of its characteristic impedance. The characteristic impedance of the aorta is the impedance of the aorta when no reflections exist, apparently at high frequencies the reflections from the many reflection sites return at random times and cancel. Thus the higher the frequency the closer you ‹look’ into the arterial system. The three-element Windkessel indeed contains these three elements.
7 Limitation of the Windkessels
The Windkessel is a lumped model of the arterial system or part thereof. Wave transmission and wave travel cannot be studied. Blood flow distribution and changes in the distribution cannot be represented. Effects of local vascular changes, e.g., change in aortic compliance while other vessels are not affected, cannot be studied. The measurement of pressure distal of the characteristic impedance does not represent the pressure in the more distal vascular system.
8 Conclusion
We have discussed the main aspects and use of the Windkessel. The three-element Windkessel can adequately describe the pressure-flow relations at the entrance of the arterial system. It is a lumped model and has a limited number of physiologically meaningful parameters. These parameters offer better insight into arterial function than input impedance. In contrast to distributed models [42, 64, 71] Windkessel models are easier to construct as hydraulic load on isolated hearts or assist devices. The Windkessel is also easier to use than distributed models when ventriculo-arterial coupling is studied. The Windkessel can be used for the systemic arterial system and the pulmonary arterial bed of all mammals.
References
Aarnoudse W, van den Berg BP, van de Vosse F et al (2004) Myocardial resistance assessed by guidewire-based pressure–temperature measurement: in vitro validation. Catheter Cardiovasc Interv 62:56–63. doi:10.1002/ccd.10793
Beard DA, Bassingthwaighte JB, Greene AS (2005) Computational modeling of physiological systems. Physiol Genomics 23:1–3. doi:10.1152/physiolgenomics.00117.2005
Benetos A, Safar M, Rudnichi A et al (1997) Pulse pressure: a predictor of long-term cardiovascular mortality in a French male population. Hypertension 30:1410–1415
Broemser P (1932) Beitrag zum Winkessel Theory des Kreislaufs. Z Biol 93:149–163
Burattini R, Di Salvia PO (2007) Development of systemic arterial mechanical properties from infancy to adulthood interpreted by four-element Windkessel models. J Appl Physiol 103:66–79. doi:10.1152/japplphysiol.00664.2006
Burattini R, Fogliardi R, Campbell KB (1994) Lumped model of terminal aortic impedance in the dog. Ann Biomed Eng 22:381–391. doi:10.1007/BF02368244
Burattini R, Gnudi G (1982) Computer identification of models for the arterial tree input impedance: comparison between two new simple models and first experimental results. Med Biol Eng Comput 20:134–144. doi:10.1007/BF02441348
Burattini R, Knowlen GG, Campbell KB (1991) Two arterial effective reflecting sites may appear as one to the heart. Circ Res 68:85–99
Burattini R, Natalucci S, Campbell KB (1999) Viscoelasticity modulates resonance in the terminal aortic circulation. Med Eng Phys 21:175–185. doi:10.1016/S1350-4533(99)00041-7
Burkhoff D, Sagawa K (1986) Ventricular efficiency predicted by an analytical model. Am J Physiol 250:R1021–R1027
Chemla D, Hebert JL, Coirault C et al (1998) Total arterial compliance estimated by Stroke volume-to-aortic pulse pressure ratio in humans. Am J Physiol 274:H500–H505
Cochrane T (1991) Simple model of circulatory system dynamics including heart valve mechanics. J Biomed Eng 13:335–340. doi:10.1016/0141-5425(91)90116-O
Dolan E, Thijs L, Li Y et al (2006) Ambulatory arterial stiffness index as a predictor of cardiovascular mortality in the Dublin outcome study. Hypertension 47:365–370. doi:10.1161/01.HYP.0000200699.74641.c5
Dumont K, Yperman J, Verbeken E et al (2002) Design of a new pulsatile bioreactor for tissue engineered aortic heart valve formation. Artif Organs 26:710–714. doi:10.1046/j.1525-1594.2002.06931_3.x
Elzinga G, Westerhof N (1973) Pressure and flow generated by the left ventricle against different impedances. Circ Res 32:178–186
Faes TJ, Raaijmakers E, Meijer JH et al (1999) Towards a theoretical understanding of Stroke volume estimation with impedance cardiography. Ann N Y Acad Sci 873:128–134. doi:10.1111/j.1749-6632.1999.tb09459.x
Fogliardi R, Di DM, Burattini R (1996) Comparison of linear and nonlinear formulations of the three-element Windkessel model. Am J Physiol 271:H2661–H2668
Frank O (1899) Die Grundform des arteriellen Pulses. Z Biol 37:483–526
Geven MC, Bohte VN, Aarnoudse WH et al (2004) A physiologically representative in vitro model of the coronary circulation. Physiol Meas 25:891–904. doi:10.1088/0967-3334/25/4/009
Glower JS, Cheng RC, Giridharan GA et al (2004) In vitro evaluation of control strategies for an artificial vasculature device. Conf Proc IEEE Eng Med Biol Soc 5:3773–3776
Hildebrand DK, Wu ZJ, Mayer JE Jr et al (2004) Design and hydrodynamic evaluation of a novel pulsatile bioreactor for biologically active heart valves. Ann Biomed Eng 32:1039–1049. doi:10.1114/B:ABME.0000036640.11387.4b
Hoeksel SA, Jansen JR, Blom JA et al (1997) Detection of dicrotic notch in arterial pressure signals. J Clin Monit 13:309–316. doi:10.1023/A:1007414906294
Hoetink A (2005) On the origin of the electrical impedance cardiogram. VU University, Amsterdam
Keren H, Burkhoff D, Squara P (2007) Evaluation of a noninvasive continuous cardiac output monitoring system based on thoracic bioreactance. Am J Physiol Heart Circ Physiol 293:H583–H589. doi:10.1152/ajpheart.00195.2007
Kolh P, D’Orio V, Lambermont B et al (2000) Increased aortic compliance maintains left ventricular performance at lower energetic cost. Eur J Cardiothorac Surg 17:272–278. doi:10.1016/S1010-7940(00)00341-9
Langewouters GJ, Wesseling KH, Goedhard WJ (1984) The static elastic properties of 45 human thoracic and 20 abdominal aortas in vitro and the parameters of a new model. J Biomech 17:425–435. doi:10.1016/0021-9290(84)90034-4
Langewouters GJ, Wesseling KH, Goedhard WJA (1985) The pressure dependent dynamic elasticity of 35 thoracic and 16 abdominal human aortas in vitro described by a five component model. J Biomech 18:613–620. doi:10.1016/0021-9290(85)90015-6
Lankhaar JW, Westerhof N, Faes TJ et al (2006) Quantification of right ventricular afterload in patients with and without pulmonary hypertension. Am J Physiol Heart Circ Physiol 291:H1731–H1737. doi:10.1152/ajpheart.00336.2006
Li JK, Cui T, Drzewiecki GM (1990) A nonlinear model of the arterial system incorporating a pressure-dependent compliance. IEEE Trans Biomed Eng 37:673–678. doi:10.1109/10.55678
Lighthill MJ (1978) Waves in fluids. Cambridge [Eng.]. Cambridge University Press, New York
Liu Z, Brin KP, Yin FC (1986) Estimation of total arterial compliance: an improved method and evaluation of current methods. Am J Physiol 251:H588–H600
Livnat A, Yamashiro SM (1981) Optimal control evaluation of left ventricular systolic dynamics. Am J Physiol 240:R370–R383
Lucas CL (1984) Fluid mechanics of the pulmonary circulation. Crit Rev Biomed Eng 10:317–393
Milnor WR (1989) Hemodynamics. Williams & Wilkins, Baltimore
Mitchell GF (1999) Pulse pressure, arterial compliance and cardiovascular morbidity and mortality. Curr Opin Nephrol Hypertens 8:335–342. doi:10.1097/00041552-199905000-00010
Mitchell GF, Moye LA, Braunwald E et al (1997) Sphygmomanometrically determined pulse pressure is a powerful independent predictor of recurrent events after myocardial infarction in patients with impaired left ventricular function SAVE investigators. Survival and ventricular enlargement. Circulation 96:4254–4260
Mohiuddin MW, Laine GA, Quick CM (2007) Increase in pulse wavelength causes the systemic arterial tree to degenerate into a classical windkessel. Am J Physiol Heart Circ Physiol 293:H1164–H1171. doi:10.1152/ajpheart.00133.2007
Mol A, Rutten MC, Driessen NJ et al (2006) Autologous human tissue-engineered heart valves: prospects for systemic application. Circulation 114:I152–I158. doi:10.1161/CIRCULATIONAHA.105.001123
Murgo JP, Westerhof N, Giolma JP et al (1980) Aortic input impedance in normal man: relationship to pressure wave forms. Circulation 62:105–116
Nichols WW, O’Rourke MF (2005) McDonald’s blood flow in arteries theoretic, experimental, and clinical principles. Hodder Arnold, London, p 148 ( Distributed in the U.S.A. by Oxford University Press)
O’Rourke MF (1967) Pressure and flow waves in systemic arteries and the anatomical design of the arterial system. J Appl Physiol 23:139–149
O’Rourke MF, Avolio AP (1980) Pulsatile flow and pressure in human systemic arteries. Studies in man and in a multibranched model of the human systemic arterial tree. Circ Res 46:363–372
Quick CM, Berger DS, Noordergraaf A (1998) Apparent arterial compliance. Am J Physiol 274:H1393–H1403
Raaijmakers E, Faes TJ, Scholten RJ et al (1999) A meta-analysis of three decades of validating thoracic impedance cardiography. Crit Care Med 27:1203–1213. doi:10.1097/00003246-199906000-00053
Randall OS, Esler MD, Calfee RV et al (1976) Arterial compliance in hypertension. Aust N Z J Med 6(suppl 2):49–59
Randall OS, van den Bos GC, Westerhof N (1984) Systemic compliance: does it play a role in the genesis of essential hypertension? Cardiovasc Res 18:455–462. doi:10.1093/cvr/18.8.455
Rosen IT, White HL (1926) The relation of pulse pressure to Stroke volume. Am J Physiol 78:168–184
Rutten MCM, Wijlaars MW, Strijkers GJ et al. (2002) The valve exerciser: a mechanics-based bioreactor for physiological loading of tissue-engineered aortic valves. In: Abstracts of the 13th conference of the European society of biomechanics, Wroclaw, Poland, 2002
Scharfschwerdt M, Misfeld M, Sievers HH (2004) The influence of a nonlinear resistance element upon in vitro aortic pressure tracings and aortic valve motions. ASAIO J 50:498–502. doi:10.1097/01.MAT.0000137038.03251.35
Segers P, Brimioulle S, Stergiopulos N et al (1999) Pulmonary arterial compliance in dogs and pigs: the three-element windkessel model revisited. Am J Physiol 277:H725–H731
Segers P, Georgakopoulos D, Afanasyeva M et al (2005) Conductance catheter-based assessment of arterial input impedance, arterial function, and ventricular-vascular interaction in mice. Am J Physiol Heart Circ Physiol 288:H1157–H1164. doi:10.1152/ajpheart.00414.2004
Segers P, Morimont P, Kolh P et al (2002) Arterial elastance and heart-arterial coupling in aortic regurgitation are determined by aortic leak severity. Am Heart J 144:568–576
Segers P, Steendijk P, Stergiopulos N et al (2001) Predicting systolic and diastolic aortic blood pressure and Stroke volume in the intact sheep. J Biomech 34:41–50. doi:10.1016/S0021-9290(00)00165-2
Segers P, Stergiopulos N, Westerhof N (2000) Quantification of the contribution of cardiac and arterial remodeling to hypertension. Hypertension 36:760765
Segers P, Stergiopulos N, Westerhof N (2002) Relation of effective arterial elastance to arterial system properties. Am J Physiol Heart Circ Physiol 282:H1041–H1046
Segers P, Verdonck P, Deryck Y et al (1999) Pulse pressure method and the area method for the estimation of total arterial compliance in dogs: sensitivity to wave reflection intensity. Ann Biomed Eng 27:480–485. doi:10.1114/1.192
Sharp MK, Pantalos GM, Minich L et al (2000) Aortic input impedance in infants and children. J Appl Physiol 88:2227–2239
Simon AC, Safar ME, Levenson JA et al (1979) An evaluation of large arteries compliance in man. Am J Physiol 237:H550–H554
Stergiopulos N, Meister JJ, Westerhof N (1994) Simple and accurate way for estimating total and segmental arterial compliance: the pulse pressure method. Ann Biomed Eng 22:392–397. doi:10.1007/BF02368245
Stergiopulos N, Meister JJ, Westerhof N (1995) Evaluation of methods for estimation of total arterial compliance. Am J Physiol 268:H1540–H1548
Stergiopulos N, Meister JJ, Westerhof N (1996) Determinants of Stroke volume and systolic and diastolic aortic pressure. Am J Physiol 270:H2050–H2059
Stergiopulos N, Segers P, Westerhof N (1999) Use of pulse pressure method for estimating total arterial compliance in vivo. Am J Physiol 276:H424–H428
Stergiopulos N, Westerhof BE, Westerhof N (1999) Total arterial inertance as the fourth element of the windkessel model. Am J Physiol 276:H81–H88
Stergiopulos N, Young DF, Rogge TR (1992) Computer simulation of arterial flow with applications to arterial and aortic stenoses. J Biomech 25:1477–1488. doi:10.1016/0021-9290(92)90060-E
Suga H, Sagawa K, Shoukas AA (1973) Load independence of the instantaneous pressure–volume ratio of the canine left ventricle and effects of epinephrine and heart rate on the ratio. Circ Res 32:314–322
Toorop GP, Westerhof N, Elzinga G (1987) Beat-to-beat estimation of peripheral resistance and arterial compliance during pressure transients. Am J Physiol 252:H1275–H1283
Wang JJ, Flewitt JA, Shrive NG et al (2006) Systemic venous circulation Waves propagating on a windkessel: relation of arterial and venous windkessels to systemic vascular resistance. Am J Physiol Heart Circ Physiol 290:H154–H162. doi:10.1152/ajpheart.00494.2005
Wang JJ, O’Brien AB, Shrive NG et al (2003) Time-domain representation of ventricular-arterial coupling as a windkessel and wave system. Am J Physiol Heart Circ Physiol 284:H1358–H1368
Wesseling KH, Jansen JR, Settels JJ et al (1993) Computation of aortic flow from pressure in humans using a nonlinear, three-element model. J Appl Physiol 74:2566–2573
Westerhof N, Noordergraaf A (1969) Errors in the measurement of hydraulic input impedance. J Biomech 3:351–356. doi:10.1016/0021-9290(70)90035-7
Westerhof N, Bosman F, De Vries CJ et al (1969) Analog studies of the human systemic arterial tree. J Biomech 2:121–143. doi:10.1016/0021-9290(69)90024-4
Westerhof N, Elzinga G (1991) Normalized input impedance and arterial decay time over heart period are independent of animal size. Am J Physiol 261:R126–R133
Westerhof N, Elzinga G, Sipkema P (1971) An artificial arterial system for pumping hearts. J Appl Physiol 31:776–781
Westerhof N, Lankhaar JW, Westerhof BE (2007) Ambulatory arterial stiffness index is not a stiffness parameter but a ventriculo-arterial coupling factor. Hypertension 49:e7–e9. doi:10.1161/01.HYP.0000254947.07458.90
Westerhof N, Murgo JP, Sipkema P et al (1979) Quantitative cardiovascular studies. In: Hwang NHC, Gross DR, Patel DJ (eds) Quantitative cardiovascular studies. University Park Press, Baltimore
Westerhof N, Stergiopulos N, Noble MIM (2005) Snapshots of hemodynamics an aid for clinical research and graduate education. Springer, New York
Wetterer E (1940) Quantitative Beziehungen zwischen stromstärke und Druck im natürlichen Kreislauf bei zeitlich variabler Elasticität des Artriellen Windkessels. Z Biol 100:260–317
Wetterer E (1954) Flow and pressure in the arterial system, their hemodynamic relationship, and the principles of their measurement. Minn Med 37:77–86
Wetterer E (1956) Die Wirkung der Herztätigkeit auf die Dynamik des Arteriensystems. Verh Dtsch Ges Kreislaufforsch 22:26–60
Wetterer E, Kenner T (1968) Grundlagen der Dynamik des Arterienpulses. Springer, Berlin
de Wilde RB, Schreuder JJ, van den Berg PC et al (2007) An evaluation of cardiac output by five arterial pulse contour techniques during cardiac surgery. Anaesthesia 62:760–768. doi:10.1111/j.1365-2044.2007.05135.x
Yin FC, Ting CT (1992) Compliance changes in physiological and pathological states. J Hypertens Suppl 10:S31–S33. doi:10.1097/00004872-199208001-00009
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
Author information
Authors and Affiliations
Corresponding author
Additional information
J.-W. Lankhaar is supported by a grant from the Netherlands Heart Foundation, the Hague, the Netherlands (NHS2003B274).
Rights and permissions
Open Access This is an open access article distributed under the terms of the Creative Commons Attribution Noncommercial License (https://creativecommons.org/licenses/by-nc/2.0), which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
About this article
Cite this article
Westerhof, N., Lankhaar, JW. & Westerhof, B.E. The arterial Windkessel. Med Biol Eng Comput 47, 131–141 (2009). https://doi.org/10.1007/s11517-008-0359-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11517-008-0359-2