Introduction

Combining metallic nanoparticles (MNPs) and semiconductor quantum dots (SQDs) has been a topic of interest in nanoscience and nanoplasmonic technology. This field has become very attractive to scientists and researchers in recent years, particularly those focused on hybrid nanostructure systems [1,2,3,4,5,6,7,8,9]. A quantum theory of the field-tunable nonlinear Fano effect in the hybrid metal–semiconductor and the Kerr nonlinearity in a four-level quantum system near a plasmonic nanostructure has been developed [10, 11]. Hybrid systems are advantageous due to their optical and nonlinear properties, which can be more easily tuned through the exciton-plasmon interaction [12,13,14,15,16]. A photon Green’s function method based on the exact quantization of electromagnetic field in a dissipative medium, the dependence of the anti-bunching time on the geometrical parameters, has been studied [17]. We found the effect of the core on the absorption in a hybrid nanoshell system, and the absorption can be amplified by using tungsten silicide (WSi) and metallic nano-antenna based on surface plasmons in [18, 19]. The pump-probe response and the nonlinear four-wave mixing (FWM) effect on a molecule in asymmetric tunneling-controlled double quantum dot molecule-metal nanoparticle hybrids have been studied [20,21,22]. Also, Fano resonance in the plasmonic structure, localized surface plasmon resonance, splitting of the effective rabi frequencies for the coherent plasmonic fields, and optical susceptibility have been examined in the hybrid Semiconductor quantum dot-metallic nanoparticles [23,24,25,26]. Numerous theoretical and experimental studies have recently been conducted on energy absorption rate and energy transfer in hybrid nanostructures based on coupled MNPs and SQDs [27,28,29,30,31,32]. The nonlinear energy transfer in a quantum dot (QD) and metallic nanorod (MNR) nanocomposite has been investigated, where an intense probe laser field is applied to monitor two-photon energy transfer from the QD to the MNR and a control laser field is applied to control the energy transfer rate [33]. The light-matter interaction in a quantum emitter and metallic graphene flake (MGF) hybrid system deposited on a polar material and energy transfer from an individual silica nanoparticle to graphene quantum dots and resulting enhancement of photodetector responsivity, as well as ultrafast energy transfer in the metal nanoparticles-graphene nanodisks-quantum dots hybrid systems, have been studied [34,35,36]. A theory for photoluminescence quenching and plasmonic properties in hybrid nanosystems made from three nanosystems such as quantum emitters (QE), metallic nanoparticles (MNP), and graphene (GR) has been developed, where the coupling of resonance energy of surface plasmon polaritons (SPPs) in MNP and GR and exciton energy in the QE plays a very importance role. The exciton in the QE interacts with the SPPs via the dipole-dipole interaction, which has been evaluated in the rotating wave approximation [37]. The double quantum dot (DQD)-MNP structure is introduced for a higher energy absorption rate depending on the high linear and nonlinear optical properties in the DQD structure [38]. Also, the energy absorption rate spectrum of an asymmetric double SQD molecule and energy absorption of an exciton-biexciton system in a hybrid structure have been investigated [39, 40].

We theoretically study the energy absorption rate in a three-dimensional hybrid system while the semiconductor quantum dot (SQD) interacts with three metal nano-ellipsoids (MNEs). The SQD is an inverted Y-type four-level system, while the MNEs are located in three dimensions. The hybrid system interacts with three external fields. We will be examining two cases. In the first case, the direction of the three external fields and the dipole moment of MNEs are along the X, Y, and Z directions. In the second case, the direction of the fields and dipole moment of MNEs are along the X direction. This paper is organized as in "Theoretical Model and Solution" section; we describe the theoretical model and solution of the equations for the SQD-MNE hybrid system. In "Result and Discussion" section, we present the results and discussion. Finally, in "Conclusion" section, we provide our conclusion.

Theoretical Model and Solution

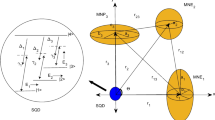
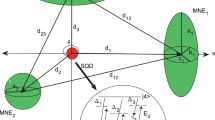
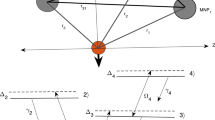
We are discussing a system that combines three metal nano-ellipsoids (MNEs) and a small semiconductor quantum dot (SQD). The MNEs are positioned in three dimensions, with \(MNE_{1}\), \(MNE_{2}\), and \(MNE_{3}\) lying on the X-axis, Y-axis, and Z-axis, respectively. The SQD is located in the center of the axes. Each \(MNE_{j}\) has three semi-axis \(a_{j}\),\(b_{j}\) and \(c_{j}\) where \(\left( j=1,2\mathrm {\;and\;}3\right)\). The dimensions of the semi-axes are such that \(a_{j}\succ b_{j}\succ c_{j}\). The distance between SQD and \(MNE_{j}\) from the center-to-center is denoted as \(r_{j}\), respectively. The distances between \(MNE_{1}\) and \(MNE_{2}\), \(MNE_{1}\) and \(MNE_{3}\) and \(MNE_{2}\) and \(MNE_{3}\) from the center-to-center are denoted as \(r_{21}\), \(r_{31}\), and \(r_{32}\), respectively, as in Fig. 1a. The three MNEs are treated as classical dielectric particles with the dielectric function \(\epsilon _{j}\left( \omega \right)\) for \(MNE_{j}\) where the dielectric function \(\epsilon _{j}\left( \omega \right)\) is obtained by [41]: \(\epsilon _{j}\left( \omega \right) =1-\omega _{pj}^{2}/\left( \omega ^{2}+i\gamma _{pj}\omega \right)\), where \(\omega _{pj}\) and \(\gamma _{pj}\) are the plasma frequency and the damping constant for \(MNE_{j}\), respectively.

Fig. 1
figure 1

a Three different MNEs in the three-dimensional hybrid system. b A schematic diagram of the SQD has four levels with an inverted Y shape

Full size image

The SQD is a four-level system with an inverted Y shape. The four states in this system are labeled \(\left| 1\right\rangle\), \(|2\rangle\), \(| 3\rangle\), and \(| 4\rangle\) with corresponding energies of \(\hbar \omega _{1}\), \(\hbar \omega _{2}\), \(\hbar \omega _{3}\) and \(\hbar \omega _{4}\), respectively, as in Fig. 1. The interband transitions occur at resonance frequencies of \(\omega _{31}=\omega _{3}-\omega _{1}\), \(\omega _{32}=\omega _{3}-\omega _{2}\), and \(\omega _{43}=\omega _{4}-\omega _{3}\). In the hybrid system, there are three external fields denoted as \(E_{1}\), \(E_{2}\), and \(E_{3}\) which derive the excitonic transitions \(| 1\rangle \longleftrightarrow | 3\rangle\), \(| 2\rangle \longleftrightarrow | 3\rangle\), and \(| 3\rangle \longleftrightarrow | 4\rangle\), respectively. The fields can be represented by the equation \(E_{\tau }(t)=E_{\tau }e^{-\grave{\imath }\nu _{\tau }t}\), (\(\tau =1\),2 and 3) where \(E_{\tau }\) and \(\upsilon _{\tau }\) are the amplitude and frequency of the field, respectively.

The Total Hamiltonian and the Polarization of MNEs of the Hybrid System

The total Hamiltonian of the hybrid system is described by the following:

$$\begin{aligned} \begin{aligned}H_{SQD}=&\;\hbar \sum _{n=1}^{4}\omega _{n}\mid n\rangle \langle n\mid - \left[ \mu _{31}E_{SQD}^{1}\mid 3\rangle \langle 1\mid +\mu _{32}E_{SQD}^{2} \mid 3\rangle \langle 2\mid \right. \\&+\left. \mu _{43}E_{SQD}^{3}\mid 4\rangle \langle 3\mid +H.C. \right] \end{aligned} \end{aligned}$$
(1)

where the first term describes the Hamiltonian of the SQD with dipole transition operator: \(|{n}\rangle \langle {n}|\). The second term is the Hamiltonian that describes the interaction between the exciton and plasmon, where \(\mu _{31},\mu _{32}\), and \(\mu _{43}\) are the electric dipole moment of the exciton between the transition levels \(| 1\rangle \longleftrightarrow |3\rangle\), \(| 2\rangle \longleftrightarrow | 3\rangle\), and \(| 3\rangle \longleftrightarrow | 4\rangle\), respectively. \(E_{SQD}^{\tau }\) (\(\tau = 1,2\) and 3) is the total electric fields inside the SQD which consists of the external fields \(E_{\tau }\) and the induced fields are resulted by the polarization of MNEs, which is given by the following:

$$\begin{aligned} \begin{aligned}E_{SQD}^{\tau }&=\;\left[ E_{\tau }+E_{SQD}^{\tau 1}+E_{SQD}^{\tau 2}+E_{SQD}^{\tau 3}\right] / \epsilon _{effQ} \\ \vec {E}_{SQD}^{\tau j}&=\left\{ 3\left( \vec {p}_{\tau j}.\hat{r}_{j}\right) \hat{r}_{j}-\vec {p}_{\tau j}\right\} / 4\pi \epsilon _{0}\epsilon _{b}r_{j}^{3}\end{aligned} \end{aligned}$$
(2)

where \(\epsilon _{effQ}=2\epsilon _{b}+\epsilon _{Q}/ 3\epsilon _{b}\) is the screening factor of SQD and \(\epsilon _{Q}\) and \(\epsilon _{b}\) are the dielectric constant of the SQD and the surrounded material, respectively. \(\vec {E}_{SQD}^{{\tau }{j}}\) is the electric field obtained from the interaction between the SQD and MNEs [42]. \(\hat{r}_{j}\) and \(\vec {p}_{{\tau }{j}}\) are the unite vector along the vector \(\textbf{r}_{j}\) and the vector dipole moments that induce on the surface of the three different \(MNE_{j}\), respectively (\(\tau\) stands for the number of the field, and j stands for the number of \(MNE_{j}\)). We have \(\vec {p}_{\tau j}=\alpha _{\tau j}\vec {E}_{\tau j}\), where \(\alpha _{\tau j}\) is the polarzability for the \(MNE_{j}\) under the effect of field \(E_{\tau }\). \(E_{\tau j}\) is the electric field acting on the three \(MNE_{j}\), which is given by the following:

$$\begin{aligned} \begin{aligned}\vec {E}_{\tau {j}}&=\left\{ \vec {E}_{\tau }+\vec {E}_{\tau {j}}^{\tau {SQD}}+\vec {E}_{\tau {j}}^{\tau {m}}\right\} /\epsilon _{effj}\\ \vec {E}_{\tau {j}}^{\tau {SQD}}&=\left\{ 3(\vec {p}_{\tau {SQD}}.\hat{r}_j)\hat{r}j-\vec {p}_{\tau {SQD}}\right\} /4\pi \epsilon _{0}\epsilon _{b}r^3_j\\ \vec {E}^{\tau {m}}_\tau {j}&=\left\{ 3(\vec {p}_{\tau {m}}.\vec {r}_{jm})\vec {r}_{jm}-\vec {p}_{\tau {m}}\right\} /4\pi \epsilon _{0}\epsilon _{b}r^{3}_{jm}\end{aligned} \end{aligned}$$
(3)

where \(\epsilon _{effj}=(2\epsilon _{b}+\epsilon _{j}\left( \omega \right) )/3\epsilon _{b}\) is the screening factor of \(MNE_{j}\). \(\vec {E}_{\tau j}^{\tau SQD}\) is the field from the SQD on the three \(MNE_{j}\), where \(p_{1SQD}=\mu _{31}\left( \rho _{31}+\rho _{13}\right)\), \(p_{2SQD}=\mu _{32}\left( \rho _{32}+\rho _{23}\right)\), and \(p_{3SQD}=\mu _{43}\left( \rho _{43}+\rho _{34}\right)\). \(\vec {E}_{\tau j}^{\tau \kappa }\) and \(\vec {E}_{\tau j}^{\tau m}\) (\(j\ne \kappa \ne m=1,2,3\)) resulted from the interaction between the dipole of every two of \(MNE_{j}\), where the expression for \(\textbf{E}_{\tau j}^{\tau \kappa }\) is obtained from above equation by replacing m with \(\kappa\). \(r_{jm}\left( r_{j\kappa }\right)\) is the distance between the \(MNE_{j}\) and \(MNE_{m}\) (or \(MNE_{j}\) and \(MNE_{\kappa }\)). We define the effective Rabi frequencies as follows: \(\Omega _{eff1}=\mu _{31}E_{SQD}^{1}/\hbar\), \(\Omega _{eff2}=\mu _{32}E_{SQD}^{2}/\hbar\) and \(\Omega _{eff3}=\mu _{43}E_{SQD}^{3}/\hbar\) and rewrite the total Hamiltonian of the system:

$$\begin{aligned} \begin{aligned} H_{SQD} =&\;\hbar \sum _{n=1}^{4}\omega _{n}\mid n\rangle \langle n\mid -\;\hbar \left[ \Omega _{eff1}\mid 3\rangle \langle 1\mid +\Omega _{eff2}\mid 3\rangle \langle 2\mid \right. \\&+\left. \Omega _{eff3}\mid 4\rangle \langle 3\mid +\;H.C.\right] \end{aligned} \end{aligned}$$
(4)

The Density Matrix Elements

The equations \(\Omega_{eff1} \rho _{13}-\Omega _{eff1}^{*}\) suffix eff1 in \(\left(\Omega_{eff1}\right)\) is Not at the level of suffix eff1 in \(\left(\Omega _{eff1}^{*}\right)\) and so in all equations of motion of density matrix elements for the hybrid system after the rotating wave approximation and the electric dipole approximation can be written as follows [43]:

$$\begin{aligned} \begin{aligned} \dot{\rho }_{11}&=i[ \Omega_{eff1} \rho _{13}-\Omega _{eff1}^{*} \rho _{31}]+2\gamma _{1} \rho _{33}-2\gamma _{0}\left( \rho _{11}- \rho _{22}\right) \\ \dot{\rho }_{22}&=i[\Omega _{eff2} \rho _{23}-\Omega _{eff2}^{*} \rho _{32}]+2\gamma _{2} \rho _{33}+2\gamma _{0}( \rho _{11}- \rho _{22}) \\ \dot{\rho }_{44}&=-i[\Omega _{eff3} \rho _{34}-\Omega _{eff3}^{*} \rho _{43}]-2\gamma _{3} \rho _{44} \\ \dot{\rho }_{13}&=-i\left[ \Omega _{eff1}^{*} \left( \rho _{33}-\rho _{11}\right) -\Omega _{eff2}^{*} \rho _{12}-\Omega _{eff3} \rho _{14} \right] -d_{13} \rho _{13} \\ \dot{\rho }_{23}&=i\left[ \Omega _{eff1}^{*} \rho _{21}-\Omega _{eff2}^{*} \left( \rho _{33}-\rho _{22}\right) +\Omega _{eff3} \rho _{24} \right] -d_{23}\rho _{23} \\ \dot{\rho }_{34}&=-i\left[ \Omega _{eff1} \rho _{14}+\Omega _{eff2} \rho _{24}+\Omega _{eff3}^{*} \left( \rho _{44}-\rho _{33}\right) \right] -d_{34} \rho _{34}\\ \dot{\rho }_{12}&=-i\left[ \Omega _{eff1}^{*} \rho _{32}-\Omega _{eff2} \rho _{13}\right] -d_{12} \rho _{12}\\ \dot{\rho }_{14}&=-i\left[ \Omega _{eff1}^{*} \rho _{34}-\Omega _{eff3}^{*} \rho _{13}\right] -d_{14} \rho _{14}\\ \dot{\rho }_{24}&=-i\left[ \Omega _{eff2}^{*} \rho _{34}-\Omega _{eff3}^{*} \rho _{23}\right] -d_{24} \rho _{24}\end{aligned} \end{aligned}$$
(5)
$$\begin{aligned} \begin{aligned} d_{13}&=\gamma _{1}+\gamma _{2}+\gamma _{0}-i\Delta _{1}, d_{12}=2\gamma _{0}-i\Delta _{1}+i\Delta _{2} \\ d_{23}&=\gamma _{1}+\gamma _{2}+\gamma _{0}-i\Delta _{2}, d_{14}=\gamma _{3}+\gamma _{0}-i\left( \Delta _{1}+\Delta _{3}\right) \\ d_{34}&=\gamma _{1}+\gamma _{2}+\gamma _{3}-i\Delta _{3}, d_{24}=\gamma _{3}+\gamma _{0}-i\left( \Delta _{3}+\Delta _{2}\right) \end{aligned} \end{aligned}$$
(6)

All of these previous equations are under condition \(\sum _{nn}^{4}\rho _{nn}=1\), and \(\rho _{n\iota }=\rho _{\iota n}^{*}\), \(\left( n,\iota =1,2,3,4\right)\). Where \(\gamma _{3},\gamma _{2}\) and \(\gamma _{1}\) are radiative decay rates from the excited state \(\mid 4\rangle\) to \(\mid 3\rangle\) and from \(\mid 3\rangle\) to \(\mid 2\rangle\) and \(\mid 1\rangle\) due to spontaneous emission, respectively. \(\gamma _{0}\) is the non-radiative decay from \(\mid 2\rangle\) to \(\mid 1\rangle\). The detunings of the corresponding fields (\(E_{1}\), \(E_{2}\), \(E_{3}\)) are as follows: \(\Delta _{1}=\left( \omega _{31}-\nu _{1}\right)\), \(\Delta _{2}=\left( \omega _{32}-\nu _{2}\right)\), and \(\Delta _{3}=\left( \omega _{43}-\nu _{3}\right)\), respectively. We study two cases for the direction of the three external fields and dipole moment of MNEs.

The Direction of the Three External Fields and Dipole Moment of MNE are Along (X Y Z) Direction

We take the direction of the external fields \(E_{\tau }\) and dipole moment of \(MNE_{j}\) (\(\tau ,j=1,2\) , 3) are along (X Y Z) directions, respectively. The polarizability for the \(MNP_{j}\) under the effect of the field \(E_{\tau }\) is given by the following [44]:

$$\begin{aligned}\begin{aligned} \alpha _{\tau j}&=\left\{ \frac{4\pi \epsilon _{0}\epsilon _{b}a_{j}b_{j}c_{j}(\epsilon _{j}\left( \omega \right) -\epsilon _{b})}{ 3(\epsilon _{b}+k_{\tau j}\left( \epsilon _{j}\left( \omega \right) -\epsilon _{b}\right) )}\right\} \\ k_{1j}&=\int _{0}^{\infty }\frac{a_{j}b_{j}c_{j}dx}{2\left( x+a_{j}^{2}\right) ^{\frac{3}{2}}\sqrt{\left( x+b_{j}^{2}\right) \left( x+c_{j}^{2}\right) }} \\ k_{2j}&=\int _{0}^{\infty }\frac{a_{j}b_{j}c_{j}dy}{2\left( y+b_{j}^{2}\right) ^{\frac{3}{2}}\sqrt{\left( y+a_{j}^{2}\right) \left( y+c_{j}^{2}\right) }} \\ k_{3j}&=\int _{0}^{\infty }\frac{a_{j}b_{j}c_{j}dz}{2\left( z+c_{j}^{2}\right) ^{\frac{3}{2}}\sqrt{\left( z+a_{j}^{2}\right) \left( z+b_{j}^{2}\right) }}\end{aligned} \end{aligned}$$

where \(k_{1j}\), \(k_{2j}\) and \(k_{3j}\) is the depolarization factor when the three external fields are parallel to the X-axis, Y-axis, and Z-axis, respectively; we define this with the first case (XYZ). The induced fields result from the polarization of MNEs which take the form (\(\tau =1,2,3\)) and ( \(l=3,3,4\)), respectively,

$$\begin{aligned} E^{\tau }_{SQD}=[(f_{\tau {1}}+A_{\tau }L_{\tau {1}})E_{\tau }+(A_{\tau }L_{\tau {2}}){\mu }_{l\tau }\rho _{l\tau }]/\epsilon _{effQ}f_{\tau {1}} \end{aligned}$$
(7)
$$\begin{aligned} \begin{aligned}L_{11}&=(\epsilon _{eff2}\epsilon _{eff3}+\epsilon _{eff3}\alpha _{12}B_{21}+\epsilon _{eff2}\alpha _{13}B_{31})/ \epsilon _{eff2}\epsilon _{eff3}\\ L_{21}&=(\epsilon _{eff1}\epsilon _{eff3}+\epsilon _{eff3}\alpha _{21}B_{21}+\epsilon _{eff1}\alpha _{23}B_{32})/ \epsilon _{eff1}\epsilon _{eff3}\\ L_{31}&=(\epsilon _{eff1}\epsilon _{eff2}+\epsilon _{eff2}\alpha _{31}B_{31}+\epsilon _{eff1}\alpha _{32}B_{32})/ \epsilon _{eff1}\epsilon _{eff2}\\ L_{12}&=(\epsilon _{eff2}\epsilon _{eff3}A_{1}+\epsilon _{eff3}\alpha _{12}B_{21}h_{2}+\epsilon _{eff2}\alpha _{13}B_{31}h_{3})/ \epsilon _{eff2}\epsilon _{eff3}\\ L_{22}&=(\epsilon _{eff1}\epsilon _{eff3}A_{2}+\epsilon _{eff3}\alpha _{21}B_{21}h_{1}+\epsilon _{eff1}\alpha _{23}B_{32}h_{3})/ \epsilon _{eff1}\epsilon _{eff3}\\ L_{32}&=(\epsilon _{eff1}\epsilon _{eff2}A_{3}+\epsilon _{eff2}\alpha _{31}B_{31}h_{1}+\epsilon _{eff1}\alpha _{32}B_{32}h_{2})/ \epsilon _{eff1}\epsilon _{eff2}\end{aligned} \end{aligned}$$
(8)
$$\begin{aligned} \begin{aligned} f_{11}&=\left( \frac{\epsilon _{eff1}}{\alpha _{11}}-\frac{\alpha _{12}}{ \epsilon _{eff2}}B_{21}Z_{21}-\frac{\alpha _{13}}{\epsilon _{eff3}} B_{31}Z_{31}\right) \\ f_{21}&=\left( \frac{\epsilon _{eff2}}{\alpha _{22}}-\frac{\alpha _{21}}{ \epsilon _{eff1}}B_{21}D_{21}-\frac{\alpha _{23}}{\epsilon _{eff3}} B_{32}Z_{32}\right) \\ f_{31}&=\left( \frac{\epsilon _{eff3}}{\alpha _{33}}-\frac{\alpha _{31}}{ \epsilon _{eff1}}B_{31}D_{31}-\frac{\alpha _{32}}{\epsilon _{eff2}} B_{32}D_{32}\right) \end{aligned} \end{aligned}$$
(9)
$$\begin{aligned} \begin{aligned} Z_{21}&=(3r_{1}^{2}-r_{21}^{2})/ 4\pi \epsilon _{0}\epsilon _{b}r_{21}^{5},B_{21}=-3r_{2}r_{1}/ 4\pi \epsilon _{0}\epsilon _{b}r_{21}^{5}\\ Z_{31}&=(3r_{1}^{2}-r_{31}^{2})/ 4\pi \epsilon _{0}\epsilon _{b}r_{31}^{5},B_{31}=-3r_{3}r_{1}/ 4\pi \epsilon _{0}\epsilon _{b}r_{31}^{5}\\ Z_{32}&=(3r_{2}^{2}-r_{32}^{2})/ 4\pi \epsilon _{0}\epsilon _{b}r_{32}^{5},B_{32}=-3r_{3}r_{2}/ 4\pi \epsilon _{0}\epsilon _{b}r_{32}^{5}\\ D_{21}&=(3r_{2}^{2}-r_{21}^{2})/ 4\pi \epsilon _{0}\epsilon _{b}r_{21}^{5},A_{j}=2/ 4\pi \epsilon _{0}\epsilon _{b}r_{j}^{3}\\ D_{31}&=(3r_{3}^{2}-r_{31}^{2})/ 4\pi \epsilon _{0}\epsilon _{b}r_{31}^{5},h_{j}=-1/ 4\pi \epsilon _{0}\epsilon _{b}r_{j}^{3}\\ D_{32}&=(3r_{3}^{2}-r_{32}^{2})/ 4\pi \epsilon _{0}\epsilon _{b}r_{32}^{5}\end{aligned} \end{aligned}$$
(10)

The Energy Absorption Rate (\(EAR_{\tau j}\)) for the First Case (XYZ)

We calculate the energy absorption rate (\(EAR_{\tau j}\)) by the MNEs, for the term which contains the indirect contribution of the SQD via the interaction with the three metal nano-ellipsoids (MNEs) (the term containing \(\mu _{l\tau }\rho _{l\tau }\)). Then, we can write the energy absorption rate (\(EAR_{\tau j}\)), \(\left( j=1,2,3\right)\) [45, 46] as follows:

$$\begin{aligned} EAR_{\tau j}=\frac{1}{2}(\omega _{\tau }\textrm{Im}(\alpha _{\tau j})\left| EI_{\tau j}\right| ^{2}) \end{aligned}$$
(11)

where \(\omega _{\tau }=\omega _{31},\omega _{32}\) and \(\omega _{43}\) for \(\left( \tau =1,2,3\right)\), respectively. \(EI_{\tau j}\) are the three electric fields, which contain the term \(\mu _{l\tau }\rho _{l\tau }\) only, from \(E_{\tau j}\) (Eq. 3). The three electric fields acting on the \(MNE_{j}\) are as follows:

$$\begin{aligned} \begin{aligned} EI_{11}&=[L_{12}\mu _{31}\rho _{31}]/ \alpha _{11}f_{11}\\ EI_{21}&=[ \left( h_{1}f_{21}+D_{21}L_{22}\right) \mu _{32}\rho _{32}]/ \epsilon _{eff1}f_{21} \\ EI_{31}&=[ \left( h_{1}f_{31}+D_{31}L_{32}\right) \mu _{43}\rho _{43}]/ \epsilon _{eff1}f_{31} \\ EI_{12}&=[ \left( h_{2}f_{11}+Z_{21}L_{12}\right) \mu _{31}\rho _{31}]/ \epsilon _{eff2}f_{11}\\ EI_{22}&=[ L_{22}\mu _{32}\rho _{32}]/ \alpha _{22}f_{21}\\ EI_{32}&=[ \left( h_{2}f_{31}+D_{32}L_{32}\right) \mu _{43}\rho _{43}] / \epsilon _{eff2}f_{31}\\ EI_{13}&=[ \left( h_{3}f_{11}+Z_{31}L_{12}\right) \mu _{31}\rho _{31})] / \epsilon _{eff3}f_{11}\\ EI_{23}&=[ \left( h_{3}f_{21}+Z_{32}L_{22}\right) \mu _{32}\rho _{32})] / \epsilon _{eff3}f_{21}\\ EI_{33}&=[ L_{32}\mu _{43}\rho _{43}]/ \alpha _{33}f_{31}\end{aligned} \end{aligned}$$
(12)
$$\begin{aligned} \begin{aligned} EAR_{j}&= AR_{1j}+EAR_{2j}+EAR_{3j} \\ EAR_{T}&=EAR_{1}+EAR_{2}+EAR_{3}\end{aligned} \end{aligned}$$
(13)

where (\(EAR_{j}\)) and (\(EAR_{T}\)) are the energy absorption rate for \(MNE_{j}\) and the total energy absorption rate for MNEs, respectively.

The Direction of the Three External Fields and Dipole Moment of MNE are Along the X Direction

We take the direction of the three external fields and dipole moment of \(MNE_{j}\) along the X direction in the second case (XXX). The polarizability for the \(MNE_{j}\) under the effect of external field \(E_{\tau }\) is given by the following:

$$\begin{aligned} \begin{aligned} \alpha _{j}&=\left\{ \frac{4\pi \epsilon _{0}\epsilon _{b}a_{j}b_{j}c_{j}(\epsilon _{j}\left( \omega \right) -\epsilon _{b})}{ 3[\epsilon _{b}+k_{j}\left( \epsilon _{j}\left( \omega \right) -\epsilon _{b}\right) ]}\right\} \\ k_{j}&=\int _{0}^{\infty }\frac{a_{j}b_{j}c_{j}dx}{2\left( x+a_{j}^{2}\right) ^{\frac{3}{2}}\sqrt{\left( x+b_{j}^{2}\right) \left( x+c_{j}^{2}\right) }}\end{aligned} \end{aligned}$$
(14)

where \(k_{j}\) is the depolarization factor for the \(_{j}\). The total field experienced by the SQD \(E_{SQD}^{\tau }\;(\tau =1,2,3)\) and (\(l=3,3,4\) ), respectively:

$$\begin{aligned} \begin{aligned} E_{SQD}^{\tau }=&\;\left\{ E_{\tau }\left[ 1+\overline{\alpha _{3}}h_{3}+L_{1}(A_{1}+\overline{\alpha _{3}}h_{3}Z_{31})/ f_{1}+M_{1}(h_{2}+\overline{\alpha _{3}}h_{3}h_{32})/ f_{2}\right] \right. \\&\left. +\mu _{l\tau }\rho _{l\tau }\left[ \overline{\alpha _{3}}h_{3}^{2}+L_{2}\left( A_{1}+\overline{\alpha _{3}}h_{3}Z_{31}\right) /f_{1} +M_{2}\left( h_{2}+\overline{\alpha _{3}}h_{3}h_{32}\right) / f_{2} \right] \right\} / \epsilon _{effQ} \end{aligned}\end{aligned}$$
(15)
$$\begin{aligned} \begin{aligned} L_{1}&=\left[ f_{2}\left( \epsilon _{eff3}+Z_{31}\alpha _{3}\right) +\left( \epsilon _{eff3}+\alpha _{3}h_{32}\right) \left( \epsilon _{eff3}Z_{21}+\alpha _{3}Z_{31}h_{32}\right) \right] \\ L_{2}&=\left[ f_{2}\left( \epsilon _{eff3}A_{1}+\alpha _{3}Z_{31}h_{3}\right) +\left( \epsilon _{eff3}Z_{21}+\alpha _{3}Z_{31}h_{32}\right) \left( h_{2}\epsilon _{eff3}+\alpha _{3}h_{32}h_{3}\right) \right] \\ M_{1}&=\left( \epsilon _{eff3}+\alpha _{3}h_{32}\right) +L_{1}\left( Z_{21}\epsilon _{eff3}+\alpha _{3}h_{32}Z_{31}\right) / f_{1}\\ M_{2}&=\left( h_{2}\epsilon _{eff3}+\alpha _{3}h_{32}h_{3}\right) +L_{2}\left( Z_{21}\epsilon _{eff3}+\alpha _{3}h_{32}Z_{31}\right) / f_{1}\\ f_{1}&=\left[ f_{2}\left( \epsilon _{eff3}\epsilon _{eff1}-Z_{31}^{2}\alpha _{3}\alpha _{1}\right) / \alpha _{1}-\left( Z_{21}\epsilon _{eff3}+\alpha _{3}h_{32}Z_{31}\right) ^{2}\right] \\ f_{2}&=\left( \epsilon _{eff2}\epsilon _{eff3}-\alpha _{3}\alpha _{2}h_{32}^{2}\right) / \alpha _{2},\overline{\alpha _{3}} =\alpha _{3}/ \epsilon _{eff3},h_{32}=-1/4\pi \epsilon _{0}\epsilon _{b}r_{32}^{3} \end{aligned} \end{aligned}$$
(16)

The Energy Absorption Rate (\(EARX_{\tau j}\)) for the Second Case (XXX)

We can write the energy absorption rate (\(EARX_{\tau j}\)) in this case for the MNEs, as follows:

$$\begin{aligned} \begin{aligned} EARX_{\tau j}&=\frac{1}{2}(\omega _{\tau }\textrm{Im}(\alpha _{j})|EIX_{\tau j}|^{2}) \\ EIX_{\tau 1}&=\left( L_{2}\mu _{l\tau }\rho _{l\tau }\right) / \alpha _{1}f_{1}\\ EIX_{\tau 2}&=\left( M_{2}\mu _{l\tau }\rho _{l\tau }\right) / \alpha _{2}f_{2},EIX_{\tau 3}=N_{2}\mu _{l\tau }\rho _{l\tau } \\ EARX_{j}&=EARX_{1j}+EARX_{2j}+EARX_{3j} \\ EARX_{T}&=EARX_{1}+EARX_{2}+EARX_{3} \\ N_{2}&=\left( f_{1}f_{2}h_{3}+f_{2}Z_{31}L_{2}+f_{1}h_{32}M_{2}\right) /f_{1}f_{2}\epsilon _{eff3} \end{aligned} \end{aligned}$$
(17)

where \(\omega _{\tau }=\omega _{31},\omega _{32}\), and \(\omega _{43}\) for \(\left( \tau =1,2,3\right)\), respectively. \(EIX_{\tau j}\) \(\left( \tau ,j=1,2,3\right)\) are the three electric fields acting on the \(MNE_{j}\), which contain the term \(\mu _{l\tau }\rho _{l\tau }\) only from \(E_{\tau j}\) (Eq. 3), \(\left( \tau =1,2,3\right)\) and \(\left( l=3,3,4\right)\), respectively. \((EARX_{j})\) and \((EARX_{T})\) are the energy absorption rate for \(MNE_{j}\) and the total energy absorption rate for MNEs, respectively.

Results and Discussion

In the following, we examine the characteristics of the energy absorption rate spectra for \(MNE_{j}\) for the term which contain the indirect contribution of the SQD via the interaction with the three metal nano-ellipsoids (MNEs) (the term containing \(\mu _{l\tau }\rho _{l\tau }\)). We take two cases: (i) in the first case (XYZ), when the direction of external fields (E1, E2 and E\(_{3}\)) and dipole moment of MNE\(_{j}\) \((j=1,2,3)\) are along the X, Y, and Z directions, respectively, we define \((EAR_{j})\) for the energy absorption rate spectra in this case, and (ii) the second case (XXX), when the direction of external fields \((E_{\tau })\) \((\tau =1,2,3)\) and the dipole moment of MNE\(_{j}\) are in the same direction of the X direction, we define \((EARX_{j})\) for the energy absorption rate spectra for the X direction. We take the parameters of SQD-MNEs as follows: the three MNEs are gold with \(\omega _{p_{j}}=9.02ev\), and \(\gamma _{p_{j}}=0.026ev\) [47], \(\Delta _{2}=\Delta _{3}=0\), \(\gamma _{0}=0.001ns^{-1}\), \(\gamma _{1}=1ns^{-1}\), \(\gamma _{2}=\gamma _{3}=0.7ns^{-1}\), \(\mu _{31}=\mu _{32}=\mu _{43}=0.3\) enm, (\(a_{j}\), \(b_{j}\), \(c_{j}\)) = (20, 12, 6) nm, (\(r_{1}\), \(r_{2}\), \(r_{3}\)) = (30, 25, 35) nm, \(\varepsilon _{s}=6\) and \(\varepsilon _{b}=2\). We take the angular frequency of plasmon surface \(\omega =2.4ns^{-1}\) and (\(\omega _{31}\), \(\omega _{32}\), \(\omega _{43}\))=(0.8, 0.01, 0.01) \(ns^{-1}\). The coherence terms \(\rho _{nt}\) and \(\rho _{tn}\) are calculated by solving the density matrix equations at a steady state. The three electromagnetic fields possess the Rabi frequencies: \(\Omega _{1}=(\mu _{31}E_{1})/\hbar\), \(\Omega _{2}=(\mu _{32}E_{2})/\hbar\), and \(\Omega _{3}=(\mu _{43}E_{3})/\hbar\), where (\(\Omega _{1}\),\(\Omega _{2}\), \(\Omega _{3}\)) = ( 0.001, 3, 1) \(ns^{-1}\), respectively. Other parameters are indicated in figure captions and further described in what follows.

Figure 2 displays the energy absorption rate spectra for MNE\(_{j}\) as a function of the probe detuning \(\Delta _{1}\), where we compare two cases (XYZ) and (XXX) direction in Fig. 2a, b, c and d, e, f, respectively, to explain the energy absorption rate spectra. Calculations have been performed when the axis \(b_{j}\) \(=9nm\) of MNE\(_{j}\), (\(j=1,2,3\)) for two cases. We take Fig. 2a and d, b and e, and c and f for \(b_{j}\) (\(j=1,2,3\)), respectively. Blue curve for \(EAR_{1}\) and \(EARX_{1}\), red curve for \(EAR_{2}\) and \(EARX_{2}\), pink curve for \(EAR_{3}\) and \(EARX_{3}\), and black curve for \(EAR_{T}\) and \(EARX_{T}\). We explored the energy absorption rate spectra for the \(EAR_{T}\) and \(EARX_{T}\) have a higher value than any single MNE\(_{j}\). The spectrum of \(EAR_{2}\) has a value close to the value of \(EAR_{T}\) in Fig. 2  and c, i.e., for \(b_{1}\) and \(b_{3}\) in the case (XYZ). In Fig. 2a and d, the spectra of \(EAR_{1}\) and \(EARX_{1}\) have a smaller value than others for (XYZ) and (XXX), respectively. We notice every plot of Fig. 2 has a different phenomenon, which depends on the \(b_{j}\) for MNE\(_{j}\) in each plot and the direction of the fields in (XYZ) or (XXX). Figure 2a and e displays the electromagnetically induced transparency (EIT) phenomenon with different behavior, where for case (XYZ), the EIT phenomenon shows in a small range of \(\Delta _{1}\) (\(-40\) to 40), but for case (XXX), the EIT phenomenon shows in a wide range of \(\Delta _{1}\) (\(-100\) to 100); also, the height of EIT is high value for case (XYZ). Figure 2b shows a large peak with narrow Fano resonance at \(\Delta _{1}=0\), and Fig. 2c displays a high and small narrow peak in a small range of \(\Delta _{1}\) (\(-2\) to 3). Figure 2d presents the spectra for the Autler-Town doublet splitting phenomenon, where the spectra of \(EARX_{1}\), \(EARX_{2}\), and \(EARX_{3}\) have close values. In Fig. 2f, the \(EARX_{T}\), \(EARX_{1}\), \(EARX_{2}\), and \(EARX_{3}\) spectra shift sequentially to higher values and have a trapping phenomenon at \(\Delta _{1}=0\). We conclude from this figure that the axis \(b_{j}\) (\(b_{1},b_{2},b_{3})=9nm\) of MNE\(_{j}\) (MNE\(_{1}\), MNE\(_{2}\), MNE\(_{3}\)), respectively, has an important role in obtaining various characteristics of the spectrum of the energy absorption rate for two cases (XYZ) and (XXX).

Fig. 2
figure 2

The energy absorption rate spectra for MNEs as a function of the probe detuning \(\Delta _{1}\). a, b, c and d, e, f for (XYZ) and (XXX) direction, respectively. \(b_{j}\) \(=9nm\) (\(j=1,2,3\)). a, d, b, e and c, f for \(b_{j}\) \((j=1,2,3)\), respectively. Blue curve for \(EAR_{1}\) and \(EARX_{1}\), red curve for \(EAR_{2}\) and \(EARX_{2}\), pink curve for \(EAR_{3}\) and \(EARX_{3}\), and black curve for \(EAR_{T}\) and \(EARX_{T}\). (\(EAR_{1}\times 20\)) in (c), (\(EAR_{3}\times 10\)) in (c)

Full size image

Figure 3 displays the energy absorption rate spectra for two cases (XYZ) and (XXX) direction in Fig. 3a, b, c and d, e, f, respectively, when the axis \(c_{j}\) \(=8nm\) of MNE\(_{j}\), (\(j=1,2,3\)) for two cases. We show Fig. 3a and d, b and e, and c and f for \(c_{j}\) \((j=1,2,3)\), respectively. Blue curve is taken for \(EAR_{1}\) and \(EARX_{1}\), red curve for \(EAR_{2}\) and \(EARX_{2}\), pink curve for \(EAR_{3}\) and \(EARX_{3}\), and black curve for \(EAR_{T}\) and \(EARX_{T}\). We notice \(EAR_{1}\) and \(EARX_{1}\) have small values in Fig. 3a and d at \(c_{1}=8nm\), also \(EAR_{2}\), \(EARX_{2}\) and \(EAR_{3}\), \(EARX_{3}\) for \(c_{2}\) and \(c_{3}\) in Fig. 3b, e and c, f, respectively. The electromagnetically induced transparency (EIT) phenomenon is displayed in Fig. 3a. Figure 2b and Fig. 3b have the Fano resonance phenomenon, but the energy absorption rate spectra are higher for \(b_{2}\) than for \(c_{2}\), and the range of \(\Delta _{1}\) for \(b_{2}\) is longer than the range of \(\Delta _{1}\) for \(c_{2}\). We observe the Autler-Town doublet splitting phenomenon in Fig. 3c, where \(EAR_{2}\) and \(EAR_{T}\) have high values. Figure 3d shows a wide and long Fano resonance at \(\Delta _{1}=0\). The trapping phenomenon appears in Fig. 3e and f as in Fig. 2f for \(b_{3}\), which have various behaviors according to the different axis \(b_{3}\), \(c_{2}\) and \(c_{3}\). We conclude that the effect of axis \(c_{j}\) on the energy absorption rate spectra for MNE\(_{j}\) is different from the axis \(b_{j}\).

Fig. 3
figure 3

The energy absorption rate spectra for MNEs as a function of the probe detuning \(\Delta _{1}\). a, b, c and d, e, f for (X Y Z) and (X)) direction, respectively. \(c_{j}\) \(=8nm\) \((j=1,2,3)\). a, d, b, e and c, f for \(c_{j}\) \((j=1,2,3)\), respectively. Blue curve for \(EAR_{1}\) and \(EARX_{1}\), red curve for \(EAR_{2}\) and \(EARX_{2}\), pink curve for \(EAR_{3}\) and \(EARX_{3}\), and black curve for \(EAR_{T}\) and \(EARX_{T}\). \((EAR_{1}\times 10)\) in (a), \((EAR_{1}\times 5)\) in (c), \((EARX_{1}\times 5)\) in (d), \((EARX_{2}\times 5)\) in (e), (\(EARX_{3}\times 5\)) in (f)

Full size image

In Fig. 4, we display the effect of the axis \(a_{j}\) of MNE\(_{j}\) \((j=1,2,3)\) with different values on the energy absorption rate spectra \(EAR_{T}\) and \(EARX_{T}\) in Fig. 4a, b, c and d, e, f, respectively. We take Fig. 4a and d, b and e, and c and f for \(a_{j}\) \((j=1,2,3)\), (\(a_{j}=18,21,23)nm\), respectively. Figure 4a exhibits zero absorption EIT phenomenon at \((a_{1}=18nm)\) and shows a peak and a trapping phenomenon on the left and right side, respectively, at \((a_{1}=21nm)\). But at \((a_{1}=23nm))\), the spectrum of \(EAR_{T}\) displays a peak and a trapping phenomenon on the right and left side, respectively. Figure 4b shows a narrow Fano resonance when \((a_{2}=18nm)\) toward the left side. A right peak with an up-and-down trapping phenomenon appears for \((a_{2}=21nm)\). At \((a_{2}=23nm)\), the spectrum shows a left peak with a small up-and-down trapping phenomenon at \(\Delta _{1}=0\). Figure 4c describes three different shapes for the spectrum \(EAR_{T}\) when \((a_{3}=18,21,23)nm\). We show the Autler-Town doublet splitting phenomenon at \((a_{3}=18nm)\) and two peaks where one has a long narrow peak and the other a small peak in a narrow range of \(\Delta _{1}\) at \((a_{3}=23nm)\). At \((a_{3}=21nm)\), the height of the trapping phenomenon is near the right peak. The \(EARX_{T}\) spectra show in the long range of \(\Delta _{1}\) (\(-200\) to 200), in Fig. 4d, we have a broad peak on the right side with a Fano resonance at \(\Delta _{1}=0\) for \((a_{1}=18nm)\), but when \((a_{1}=21nm)\) a broad peak lies on the left side, the Autler-Town doublet splitting phenomenon appears at \((a_{1}=23nm)\). Figure 4e exhibits the spectrum of \(EARX_{T}\) has a long trapping phenomenon towards the left side for \((a_{2}=18nm)\), a long Fano resonance towards the right side for \((a_{2}=21nm)\), and EIT phenomenon for \((a_{2}=23nm)\). Figure 4e presents the spectrum has a down-and-up trapping phenomenon for \((a_{3}=18nm)\), and the Fano resonance lies on the right and left side for (\(a_{3}=21\) and 23)nm, respectively. We conclude that the energy absorption rate spectra, \(EAR_{T}\) and \(EARX_{T}\), have different phenomena at the different values of the axis \(a_{j}\) of MNE\(_{j}\).

Fig. 4
figure 4

The energy absorption rate spectra for MNEs as a function of the probe detuning \(\Delta _{1}\). a, b, c and d, e, f for \(EAR_{T}\) and \(EARX_{T}\), respectively. a, d, b, e, and c, f for \(a_{j}\)(\(=18,21,23\))nm (\(j=1,2,3\)), respectively. Black curve for (\(a_{j}=18nm\)), blue curve for \((a_{j}=21nm)\), and red curve for \((a_{j}=23nm)\) \((j=1,2,3)\). \((EAR_{T}\times 5)\) for \(a_{1}=18\) in a and for \(a_{3}=18\) in c. (\(EAR_{T}\times 500\)) for \(a_{3}=21\) in c. (\(EAR_{T}\times 2\)) for \(a_{3}=18\) and 23 in f

Full size image

In Fig. 5, we illustrate the influence of the axis \(c_{j}\) of MNE\(_{j}\) (\(j=1,2,3\)) with various values on the energy absorption rate spectra \(EAR_{T}\) and \(EARX_{T}\) in Fig. 5a, b, c and d, e, f, respectively. We take Fig. 5a and d, b and e, and c and f for \(c_{j}\) (\(j=1,2,3\) ), respectively, and blue, red, and black curves for (\(c_{j}=6.5,6.75,7\))nm, respectively. Figure 5a displays a zero absorption EIT phenomenon when (\(c_{1}=6.5nm\)), where the two peaks of EIT decrease when increasing \(c_{1}\). The peak with Fano resonance decreases when increasing \(c_{2}\) in Fig. 5b. We have a long and short peak in Fig. 5c, which increases with decreasing (\(c_{3}=6.5nm\)). For \(EARX_{T}\), the long Fano resonance decreases when decreasing \(c_{1}\) in Fig. 5d. Figure 5e and f shows the peak with trapping phenomenon at \(\Delta _{1}=0\), which decreases when increasing (\(c_{2}=c_{3}=7nm\)), respectively. We notice that a zero absorption EIT phenomenon displays when (\(c_{1}=6.5nm\)) for MNE\(_{1}\), like that in Fig. 4, a zero absorption EIT phenomenon displays when (\(a_{1}=18nm\)) for MNE\(_{1}\). Also, the Fano resonance phenomenon appears for \(EARX_{T}\) at \(c_{1}\) and \(a_{1}\) for MNE\(_{1}\).

Fig. 5
figure 5

The energy absorption rate spectra for MNEs as a function of the probe detuning \(\Delta _{1}\). a, b, c and d, e, f for \(EAR_{T}\) and \(EARX_{T}\), respectively. a, d, b, e and c, f for \(c_{j}\)(\(=6.5,6.75,7\))nm (\(j=1,2,3\)), respectively. Blue curve for (\(c_{j}=6.5nm\)), red curve for (\(c_{j}=6.75nm\)), and black curve for (\(c_{j}=7nm\))(\(j=1,2,3\))

Full size image

In Fig. 6, the spectra of the \(EAR_{T}\) and \(EARX_{T}\) represent the energy absorption rate in Fig. 6a, b, c and d, e, f, respectively, when changing the distance \(r_{2}\). The axis \(a_{j}\) (\(=23nm\)) of MNE\(_{j}\), (\(j=1,2,3\)) for two cases. We take Fig. 6a and d, b and e, and c and f for \(a_{j}\) (\(a_{1},a_{2},a_{3}\)), respectively, and blue, red, and black curves for (\(r_{2}=25,30,35\)) nm, respectively. In Fig. 6a, for \(a_{1}=23nm\), the spectrum of \(EAR_{T}\) displays a peak with a deep hole and has a high value at \(r_{2}=25nm\), where the hole towards the left side when \(r_{2}=25nm\) and towards the right side when \(r_{2}=30,35nm\). In Fig. 6b, for \(a_{2}=23nm\), the Fano resonance appears and the peak shifts towards the right side when decreasing the distance \(r_{2}\). In Fig. 6c, for \(a_{3}=23nm\), at small \(r_{2}=25nm\), we notice a short and long peak around \(\Delta _{1}=0\), but we notice the large peak with the Fano resonance shifts towards the right side when increasing the distance \(r_{2}=30,35nm\). Figure 6d shows the Autler-Town doublet splitting phenomenon, and the height of two peaks decreases when the distance \(r_{2}\) increases. Figure 6e displays a peak with a Fano resonance at \(r_{2}=30,35nm\), where the peak shifts towards the right side when increasing the distance \(r_{2}\), while at \(r_{2}=25nm\), the spectrum has (EIT) and a high value. Figure 6f exhibits a peak with a long Fano resonance, while the peak decreases and shifts towards the right side when decreasing the distance \(r_{2}\). We conclude from this figure that the distance \(r_{2}\) and the axis \(a_{j}\) play a significant role in the characteristics of the energy absorption rate spectra for two cases.

Fig. 6
figure 6

The energy absorption rate spectra for MNEs as a function of the probe detuning \(\Delta _{1}\). a, b, c for \(EAR_{T}\), d, e, and f for \(EARX_{T}\). \(a_{j}=23nm\) (\(j=1,2,3\)), a, d, b, e and c, f for \(a_{j}\) nm, (\(j=1,2,3\)), respectively. Blue curve for (\(r_{2}=25nm\)), red curve for (\(r_{2}=30\) nm), and black curve for (\(r_{2}=35nm\))

Full size image

Figure 7 describes the energy absorption rate spectra \(EAR_{T}\) and \(EARX_{T}\) in Fig. 7a, b, c and d, e, f, respectively, under the influence of different values of the Rabi frequency (\(\Omega _{1}\)) when the axis \(b_{j}\) \(=9\) nm and \(r_{j}=r=35\) nm, (\(j=1,2,3\)). We take Fig. 7a and d, b and e, and c and f for \(b_{j}\) (\(b_{1},b_{2},b_{3}\)), and blue, red, and black curves for (\(\Omega _{1}=0.3,0.5,0.7\))\(ns^{-1}\), respectively. Figure 7a shows the EIT, where the width of the upper part of (EIT) increases when increasing \(\Omega _{1}\). In Fig. 7b and c, the peak with long Fano resonance is manifested, which increases when increasing \(\Omega _{1}\). The spectra of \(EARX_{T}\) are different from the spectra of \(EAR_{T}\) as in Fig. 7d; we notice (EIT), which has a large window and two holes on the two sides of the window. The width of the window increases by decreasing \(\Omega _{1}\), but the deep of the holes increases when increasing \(\Omega _{1}\). Figure 7f exhibits a narrow EIT where the height of (EIT) increases when increasing \(\Omega _{1}\). Another phenomenon observed in Fig. 7e is where the spectrum has a peak with a narrow hole burning at \(\Delta _{1}=0\). The deep of the hole burning increases when increasing the \(\Omega _{1}\). We notice EIT phenomenon has different characteristics for the energy absorption rate spectra for two cases at \(b_{1}\) for MNE\(_{1}\) (Fig. 7a and d). The results in this paper are close to the research results [40], where we have three metal nanoparticles in a three-dimensional hybrid system and three external fields that have not been studied where the interaction between the exciton and plasmon becomes more complicated.

Fig. 7
figure 7

The energy absorption rate spectra for MNEs as a function of the probe detuning \(\Delta _{1}\). a, b, c for \(EAR_{T}\), d, e, and f for \(EARX_{T}\). \(b_{j}=9nm\), \(r_{j}=r=35nm\), (\(j=1,2,3\)), a, d, b, e and c, f for \(b_{j}\) (\(j=1,2,3\)), respectively. Blue curve for (\(\Omega _{1}=0.3ns^{-1}\)), red curve for (\(\Omega _{1}=0.5ns^{-1}\)), and black curve for (\(\Omega _{1}=0.7ns^{-1}\))

Full size image

Conclusion

We have studied theoretically the energy absorption rate in the three-dimensional hybrid system for the indirect contribution of the semiconductor quantum dot (SQD) via the interaction with the three metal nano-ellipsoids (MNEs). We have taken two cases for the direction of the external fields in the three-dimensional hybrid system and examined the effect of the direction of the three external fields and the dipole moment of MNEs on the energy absorption rate. We have examined the energy absorption rate spectra for each of the three metal nano-ellipsoids (MNEs) and their total. The high value for the energy absorption rate is obtained for the total three metal nano-ellipsoids (MNEs). The energy absorption rate spectra are affected by the axes of MNEs and therefore the polarizability of the three metal nano-ellipsoids, and also the distance between SQD and MNEs. The influence of the rabi frequency \(\Omega _{1}\) on the energy absorption rate spectra exhibits in several phenomena interesting. There are some phenomena observed in the energy absorption rate spectra, like the electromagnetically induced transparency, Fano resonance, the Autler-Town doublet splitting, trapping phenomena, and the hole burning. Our work can be generalized when it is more complicated for interactions, where the description of plasmon exciton interactions is a powerful tool for plasmonic transistors, modulators, and quantum information devices. Moreover, our results could prove useful in the development of controllable nanosensors, energy absorption, and energy storage devices in the nanoscale and all-optical nanoscience.