The Intensity of the Plasmon–exciton of Three Spherical Metal Nanoparticles On the Semiconductor Quantum Dot Having Three External Fields

Abstract

The influence of the plasmon of three spherical metal nanoparticles (MNPs) on the semiconductor quantum dot (SQD) having three external fields is analyzed. The density matrix equations are modified for the description of the optical properties of the SQD-MNPs nanosystem. We study theoretically the role of the plasmon–exciton dipole coupling in the SQD-MNPs nanosystem. We investigate the dependence of the plasmon–exciton dipole coupling of the SQD-MNPs nanosystem on the position of three spherical MNPs with respect to SQD as well as on the material parameters of the hybrid nanosystem. The direction and detunings of the three external fields play an important role in the characterization of the SQD-MNPs nanosystem.

Introduction

The optical properties of complex nanosystems, that when a semiconductor quantum dot (SQD) is in the vicinity of a metallic nanoparticle (MNP), are the area of considerable current interest. So, the optics of the SQD become strongly sensitive to the structural parameters of the nanosystem, the intensity of the plasmon–exciton dipole coupling and the dielectric constant of the environment when combining semiconductor quantum dot (SQD) and plasmonic nanostructures, and hence, it is carried out in the interdisciplinary applications of nanoscience. The phenomena that have been studied in these research areas are the phase control of absorption and dispersion as well complete optical transparency [1,2,3,4], Fano effects in energy absorption [5,6,7,8], plasmonic electromagnetically induced transparency (EIT) [9,10,11,12], the enhancement of nonlinear Kerr and susceptibilities in several quantum systems [13,14,15,16]. The terahertz generation enhancement from intraband transition in self-assembled SQD molecules near a (MNP) is discussed in [17]. Investigating the spatial properties of coherent plasmonic (CP) field and demonstrating how it depends on the collective molecular states of the SQD-MNP system (bright and dark states) are shown in [18, 19] that when the coherent SQD-MNP molecule is in the dark state, i.e., the SQD does not emit light, the CP field is spatially confined around the MNP. It is studied that there were the states of polarization of coherent plasmonic fields of a SQD-MNP system in the environment surrounding the MNP and investigated how the dynamics of these states were evolved with time when this system was interacting with a time-dependent laser field [20,21,22]. Plasmon-assisted two-photon Rabi oscillations in a semiconductor quantum dot—metal nanoparticle heterodimer are investigated in [23]. The demonstration of multipole effect and the intensity of the plasmon–exciton dipole coupling in the SQD-MNP nanosystem are shown in [24,25,26,27].

In this paper, we consider a single SQD in close vicinity to three spherical MNPs. The present scheme is based on a coupled SQD-MNPs nanosystem in the presence of the pump, control and probe fields. The SQD is taken as a four-level V-type system in which the distinct excitonic transitions occur. Theoretically, we will study the effect of the plasmon–exciton dipole coupling in the SQD-MNP nanosystem and investigate the dependence of the plasmon–exciton dipole coupling of the SQD-MNP nanosystem on the position of MNPs with a SQD as well as on the material parameters of the hybrid nanosystem. The paper is organized as follows: in Section 2, we describe the SQD-MNP nanosystem, derive the density matrix equations describing the dynamics of the system and obtain the form of the plasmon–exciton dipole coupling for the SQD-MNP nanosystem. In Section 3, we discuss our numerical results. Finally, we present our conclusions in Section 4.

Theoretical Model and Description

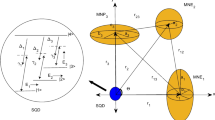
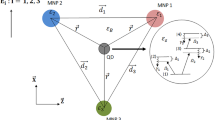
In this paper, we theoretically investigate coherent light–matter interaction in a nanohybrid between a small size of SQD and three spherical MNPs of different radii $R_{1}$, $R_{2}$ and $R_{3}$. The schematic diagram of the nanosystem is considered as a V-type four-level SQD structure. It is composed of four states $\left| 1\right\rangle$, $\left| 2\right\rangle$, $\left| 3\right\rangle$ and $\left| 4\right\rangle$ with energies $\hslash \omega _{1}$, $\hslash \omega _{2}$, $\hslash \omega _{3}$ and $\hslash \omega _{4}$, respectively, as illustrated in Fig. 1. The nanohybrid structure is subjected to the pump, probe and control fields with amplitudes $E_{2},E_{3}$ and $E_{4}$ and frequencies $\nu _{2}$, $\nu _{3}$ and $\nu _{4}$, respectively. The weak probe field derives the excitonic transition $\left| 1\right\rangle \leftrightarrow \left| 3\right\rangle$ with resonance frequency $\omega _{13}$, where $\omega _{nm}=\omega _{n}-\omega _{m}$ and ($n,m=1,2,3,4)$. The pump and control fields derive the excitonic transitions $\left| 1\right\rangle \leftrightarrow \left| 2\right\rangle$ and $\left| 3\right\rangle \leftrightarrow \left| 4\right\rangle$ with resonance frequencies $\omega _{12}$ and $\omega _{34}$ , respectively. The SQD is situated at center-to-center distance $r_{1},$ $r_{2}$ and $r_{3}$ from the first, second and third spherical MNP, respectively. The distance $r_{j}$ has an angle $\theta _{j}$ ($j=1,2,3$) with respect to the $Z-$ axis for the first, second and third spherical MNPs as illustrated in Fig. 1, respectively. We consider a first spherical MNP is positioned at center-to-center distance $r_{12}$ and $r_{13}$ from the second and third spherical MNP, respectively, while the second spherical MNP is at center-to-center distance $r_{23}$ from the third spherical MNP. The excitonic transitions for the SQD $\left| 1\right\rangle \leftrightarrow \left| 2\right\rangle$, $\left| 1\right\rangle \leftrightarrow \left| 3\right\rangle$ and $\left| 3\right\rangle \leftrightarrow \left| 4\right\rangle$ are characterized by the transition dipole moments $\mu _{12}$ , $\mu _{13}$ and $\mu _{34}$, respectively, where the optical excitations in the SQD are excitons and the oscillating external fields give rise to oscillations of conducting electrons in the MNP’s, conventionally called localized surface plasmon (LSP). So, excitons and plasmons are excited in the nanohybrid and interact with each other via the dipole–dipole interaction, which give rise to a renormalization of the field experienced by both the SQD and MNPs. The dielectric constant of the SQD is represented by $\epsilon _{s}$ , and it is surrounded by a material with dielectric constant $\epsilon _{B}$, while the three MNPs are treating as classical dielectric particles with dielectric function $\epsilon _{mj}(\omega )$ and mj stands for MNP$_{j}$ where $(j=1,2,3)$. The dielectric function $\epsilon _{m_{j}}(\omega )$ is obtained for the spherical MNP as [28]:

$$\begin{aligned} \epsilon _{mj}(\omega )=1-\frac{\omega _{pj}^{2}}{\omega ^{2}+i\gamma _{bj}\omega }\qquad(j=1,2,3) \end{aligned}$$

(1)

where $\omega _{pj}$ is the plasma frequency for spherical MNP and $\gamma _{bj}$ is the damping constant. The Hamiltonian of the nanohybrid system can be expressed as:

Fig. 1

A schematic diagram of the SQD and three MNPs (hybrid system). SQD have four-level V-type configuration coupling with three fields

$$\begin{aligned} H_{SQD}\text { }=\text { }\hslash \sum _{j=1}^{4}\omega _{j}\sigma _{jj}-\left[ \mathbf {\mu }_{12}\mathbf {.E}_{SQD}^{2}\sigma _{12}+\mathbf {\mu }_{13}\mathbf {.E}_{SQD}^{3}\mathbf {\sigma }_{13}+\mathbf {\mu }_{34}\mathbf {.E}_{SQD}^{4}\sigma _{34}+H.C.\right] \end{aligned}$$

(2)

where $\sigma _{ij}$ $=\mid i\rangle \langle$ $j\mid$ is the dipole transition operator between$\mid i\rangle$ and $\langle$ $j\mid$ of the SQD. $\mathbf {E}_{SQD}^{i}$ $(i=2,3,4)$ are the fields felt by the SQD polarized along the $\mid 1\rangle \iff$ $\mid 2\rangle$, $\mid 1\rangle \iff$ $\mid 3\rangle$ and $\mid 3\rangle \iff$ $\mid 4\rangle$ transitions, respectively. So, we have :

$$\begin{aligned} \mathbf {E}_{SQD}^{i}=\frac{1}{\varepsilon _{effs}}\left[ \mathbf {E} _{i}+\sum _{j=1}^{3}\mathbf {E}_{SQD}^{ij}\right],\qquad(i=2,3,4) \end{aligned}$$

(3)

where, $\varepsilon _{effs}=[\frac{\epsilon _{s}+2\epsilon _{B}}{3\epsilon _{B}}]$ is the screening of the dielectric material of SQD.

Supposing that we have two cases for the direction of the fields ($\mathbf {E}_{i}$), the first case (ZZY) that means the direction of the fields ($\mathbf {E}_{2},\mathbf {E}_{3}$) is along the Z-axis and the field ($\mathbf {E}_{4}$) is along the $Y-axis$and the second case (ZYZ): the direction of the fields ($\mathbf {E}_{2}\mathbf {,E}_{4}$) is along the $Z-axis$ and the field ($\mathbf {E}_{3}$) is along the Y-axis. $\mathbf {E}_{QD}^{ij}$ are the fields on SQD from the three MNPs and given by:

$$\begin{aligned} \mathbf {E}_{SQD}^{ij}=\frac{1}{4\pi \epsilon _{0}\epsilon _{B}r_{j}^{3}} \left[ 3(\mathbf {p}_{ij}\mathbf {\cdot}\widehat{\mathbf {r}}_{j})\widehat{\mathbf {r}}_{j}-\mathbf {p}_{ij}\right] \end{aligned}$$

(4)

where the unite vector $\widehat{\mathbf {r}}_{j}$ along the vector $\mathbf {r}_{j}$ is given by:

$$\begin{aligned} \widehat{\mathbf {r}}_{j}=\cos \theta _{j}\widehat{Z}+\sin \theta _{j} \widehat{Y}\quad(j=1,2,3). \end{aligned}$$

(5)

The vector dipoles $\mathbf {p}_{ij}$ originate from the charge induced on the surface of the MNPs and direct in the Z-axis, which is given by:

$$\begin{aligned} \mathbf {p}_{ij}=\alpha _{j}\mathbf {E}_{ij}\text {, }\alpha _{j}=\frac{4\pi \epsilon _{0}\epsilon _{B}R_{j}^{3}\gamma _{j}}{\varepsilon _{effm_{j}}} \text {, }\gamma _{j}=\frac{\epsilon _{m_{j}}(\omega )-\epsilon _{B}}{ \epsilon _{mj}(\omega )+2\epsilon _{B}} \end{aligned}$$

(6)

where $\mathbf {E}_{ij}$ (for $i=2,3,4$ & $j=1,2,3$) are the fields acting on the three MNPs and given by:

$$\begin{aligned} \mathbf {E}_{ij}=\frac{1}{\varepsilon _{effm_{j}}}\left[ \mathbf {E}_{i}+ \mathbf {E}_{ij}^{SQD}+\mathbf {E}_{ij}^{ik}+\mathbf {E}_{ij}^{il}\right] \end{aligned}$$

(7)

where $\varepsilon _{effm_{j}}=\frac{\epsilon _{m_{j}}(\omega )+2\epsilon _{B}}{3\epsilon _{B}}$ is the screening of the dielectric material of the three spherical MNPs. $\mathbf {E}_{ij}^{SQD}$ (for $i=2,3,4$ & $j=1,2,3$) are the fields from the SQD on the three MNPs and given by:

$$\begin{aligned} \mathbf {E}_{ij}^{SQD}=\frac{1}{4\pi \epsilon _{0}\epsilon _{B}r_{j}^{3}} \left[ 3(\mathbf {p}_{SQD}^{i}.\widehat{\mathbf {r}}_{j})\widehat{\mathbf {r}} _{j}-\mathbf {p}_{SQD}^{i}\right] ,i=q,4 \end{aligned}$$

(8)

$$\begin{aligned} p_{SQD}^{q}=\mu _{1q}(\rho _{1q}+\rho _{q1}),\quad q=2,3 \end{aligned}$$

(9)

$$\begin{aligned} p_{SQD}^{4}=\mu _{34}(\rho _{34}+\rho _{34}),\qquad i=4. \end{aligned}$$

(10)

Also, the fields $\mathbf {E}_{ij}^{ik}$ and $\mathbf {E}_{ij}^{il}$ result in the interaction between two polarized MNPs for ( j, k, l $=1,2,3$ and $j\ne k\ne l,i=2,3,4)$ and are given by:

$$\begin{aligned} \mathbf {E}_{ij}^{ik}= & {} \frac{1}{4\pi \epsilon _{0}\epsilon _{B}r_{jk}^{3}} \left[ 3(\mathbf {p}_{ik}\mathbf {.}\widehat{\mathbf {r}}_{jk}\mathbf {)} \widehat{\mathbf {r}}_{jk}-\mathbf {p}_{ik}\right] ,\text { }, \end{aligned}$$

(11)

$$\begin{aligned} \mathbf {E}_{ij}^{il}= & {} \frac{1}{4\pi \epsilon _{0}\epsilon _{B}r_{jl}^{3}} \left[ 3(\mathbf {p}_{il}\mathbf {.}\widehat{\mathbf {r}}_{jl})\widehat{\mathbf { r}}_{jl}-\mathbf {p}_{il}\right] \end{aligned}$$

(12)

where $\widehat{\mathbf {r}}_{jk}=\widehat{\mathbf {r}}_{k}-\widehat{\mathbf {r}}_{j}$ and $\widehat{\mathbf {r}}_{jl}=\widehat{\mathbf {r}}_{l}-\widehat{\mathbf {r}}_{j}$. By introducing $\mathbf {E}_{SQD}^{i}$ for $(i=2,3,4)$ into Eq. (2), then the total Hamiltonian of the SQD is expressed as:

$$\begin{aligned} H_{SQD}\text { }=\text { }\hslash \sum _{j=1}^{4}\omega _{j}\sigma _{jj}-\hslash \text { }\Omega _{2}^{eff}\text { }\sigma _{12}-\hslash \text { }\Omega _{3}^{eff}\text { }\sigma _{13}-\hslash \text { }\Omega _{4}^{eff}\text { }\sigma _{34}+H.C. \end{aligned}$$

(13)

where:

$$\begin{aligned} \Omega _{2}^{eff}=\left[ \Omega _{2}(\Psi _{2}+\Gamma _{2})+\Lambda _{2}\rho _{12}\right] , \end{aligned}$$

(14)

$$\begin{aligned} \Omega _{3}^{eff}=\left[ \Omega _{3}(\Psi _{3}+\Gamma _{3})+\Lambda _{3}\rho _{13}\right] , \end{aligned}$$

(15)

$$\begin{aligned} \Omega _{4}^{eff}=\left[ \Omega _{4}(\Psi _{4}+\Gamma _{4})+\Lambda _{4}\rho _{34}\right]. \end{aligned}$$

(16)

For the case (ZZY), we have:

$$\begin{aligned} \Omega _{2}=\frac{\mu _{12}E_{2}}{\hslash \varepsilon _{effs}}\text {, } \Omega _{3}=\frac{\mu _{13}E_{3}}{\hslash \varepsilon _{effs}}\text {, } \Omega _{4}=\frac{\mu _{34}E_{4}}{\hslash \varepsilon _{effs}}\text {,} \end{aligned}$$

(17)

$$\begin{aligned} \Psi _{q}=(1+\sum _{j=1}^{3}\alpha _{j}A_{j}),\quad(q=2,3) \end{aligned}$$

(18)

$$\begin{aligned} \Psi _{4}=(1+\sum _{j=1}^{3}\alpha _{j}C_{j})\text {,} \end{aligned}$$

(19)

$$\begin{aligned} \Gamma _{q}=S_{1}\alpha _{1}\alpha _{2}(A_{1}+A_{2})+S_{2}\alpha _{2}\alpha _{3}(A_{2}+A_{3})+S_{3}\alpha _{3}\alpha _{1}(A_{3}+A_{1})\text {, \ }(q=2,3) \end{aligned}$$

(20)

$$\begin{aligned} \Gamma _{4}=T_{1}\alpha _{1}\alpha _{2}(C_{1}+C_{2})+T_{2}\alpha _{2}\alpha _{3}(C_{2}+C_{3})+T_{3}\alpha _{3}\alpha _{1}(C_{3}+C_{1}) \end{aligned}$$

(21)

$$\begin{aligned} \Lambda _{q}=\left( \frac{\mu _{1q}^{2}}{\text { }\hslash \varepsilon _{effs}}\right) \left[ \sum _{j=1}^{3}\alpha _{j}A_{j}^{2}+2(S_{1}\alpha _{1}\alpha _{2}A_{1}A_{2}+S_{2}\alpha _{2}\alpha _{3}A_{2}A_{3}+S_{3}\alpha _{3}\alpha _{1}A_{3}A_{1})\right] \text {,}\ \ (q=2,3) \end{aligned}$$

(22)

$$\begin{aligned} \Lambda _{4}=\left( \frac{\mu _{34}^{2}}{\text { }\hslash \varepsilon _{effs}} \right) \left[ \sum _{j=1}^{3}\alpha _{j}B_{j}C_{j}+T_{1}\alpha _{1}\alpha _{2}(C_{1}B_{2}+C_{2}B_{1})+T_{2}\alpha _{2}\alpha _{3}(C_{2}B_{3}+C_{3}B_{2})+T_{3}\alpha _{3}\alpha _{1}(C_{3}B_{1}+C_{1}B_{3})\right] \end{aligned}$$

(23)

where

$$\begin{aligned} A_{j}=(3\cos ^{2}\theta _{j}-1)/4\pi \epsilon _{o}\epsilon _{B}r_{j}^{3} \nonumber \\ B_{j}=(3\sin {}^{2}\theta _{j}-1)/4\pi \epsilon _{o}\epsilon _{B}r_{j}^{3} \nonumber \\ C_{j}=(3\sin \theta _{j}\cos \theta _{j})/4\pi \epsilon _{o}\epsilon _{B}r_{j}^{3} \end{aligned}$$

(24)

$$\begin{aligned} S_{1}=\left\{ 3[(r_{2}\cos \theta _{2}-r_{1}\cos \theta _{1})/r_{21}]^{2}-1\right\} /4\pi \epsilon _{o}\epsilon _{B}r_{21}^{3} \nonumber \\ S_{2} =\left\{ 3[(r_{3}\cos \theta _{3}-r_{2}\cos \theta _{2})/r_{32}]^{2}-1\right\} /4\pi \epsilon _{o}\epsilon _{B}r_{32}^{3} \nonumber \\ S_{3} =\left\{ 3[(r_{3}\cos \theta _{3}-r_{1}\cos \theta _{1})/r_{31}]^{2}-1\right\} /4\pi \epsilon _{o}\epsilon _{B}r_{31}^{3} \end{aligned}$$

(25)

$$\begin{aligned} T_{1}=3[r_{2}\cos \theta _{2}-r_{1}\cos \theta _{1}][r_{2}\sin \theta _{2}-r_{1}\sin \theta _{1}]/4\pi \epsilon _{o}\epsilon _{B}r_{21}^{5} \nonumber \\ T_{2} =3[r_{3}\cos \theta _{3}-r_{2}\cos \theta _{2}][r_{3}\sin \theta _{3}-r_{2}\sin \theta _{2}]/4\pi \epsilon _{o}\epsilon _{B}r_{32}^{5} \nonumber \\ T_{3}=3[r_{3}\cos \theta _{3}-r_{1}\cos \theta _{1}][r_{3}\sin \theta _{3}-r_{1}\sin \theta _{1}]/4\pi \epsilon _{o}\epsilon _{B}r_{31}^{5}. \end{aligned}$$

(26)

For the case (ZYZ), we have the same above equations [14,15,16,17,18,19,20,21,22,23,24,25,26,27], but the subscript $(q=2,3)$ in $\Psi _{q},\Gamma _{q}$ and $\Lambda _{q}$ can be exchanged to the subscript $(q=2,4)$ and the subscript 4 in $\Psi _{4},\Gamma _{4}$ and $\Lambda _{4}$ can be exchanged to the subscript 3 (i.e., the value of $\Omega _{3}^{eff}$ and $\Omega _{4}^{eff}$ exchange). For another special case (ZZY) under the condition $\alpha _{1}=\alpha _{2}=\alpha _{3}=\alpha$ and $\theta _{1}=0,$ $\theta _{2}=\pi /2,$ $\theta _{3}=\pi ,$ we can get the property $\Omega _{4}^{eff}=\Omega _{4}$, and this means that the main factor for obtain this result is the direction of the fields.

Under the electric-dipole approximation and the rotating-wave approximation, we define the equation of motion of density matrix elements (the master equation) of the SQD coupled to the three MNPs, as follows:

$$\begin{aligned} \overset{\cdot }{\rho _{22}}=i\ \Omega _{2}^{eff}\rho _{12}-i\ \Omega _{2}^{^{eff^{*}}}\rho _{21}-2\gamma _{2}\rho _{22} \end{aligned}$$

(27)

$$\begin{aligned} \overset{\cdot }{\rho _{33}}=i\ \Omega _{3}^{eff}\rho _{13}-i\ \Omega _{3}^{eff^{*}}\rho _{31}-i\ \Omega _{4}^{eff}\rho _{34}+i\ \Omega _{4}^{eff^{*}}\rho _{43}-2\gamma _{3\text { }}\rho _{33}+2\gamma _{4\text { }}\rho _{44} \end{aligned}$$

(28)

$$\begin{aligned} \overset{\cdot }{\rho _{44}}=i\ \Omega _{4}^{eff}\rho _{34}-i\ \Omega _{4}^{eff^{*}}\rho _{43}-2\gamma _{4\text { }}\rho _{44} \end{aligned}$$

(29)

$$\begin{aligned} \overset{\cdot }{\rho _{21}}=-\beta _{2}\rho _{21}-i\ \Omega _{2}^{eff}(\ \rho _{11}-\rho _{22})-i\ \Omega _{3}^{eff}\rho _{23} \end{aligned}$$

(30)

$$\begin{aligned} \overset{\cdot }{\rho _{31}}=-\beta _{3}\rho _{31}-i\ \Omega _{2}^{eff}\rho _{32}+i\ \Omega _{3}^{eff}(\ \rho _{11}-\rho _{33})+i\ \Omega _{4}^{eff^{*}}\rho _{41} \end{aligned}$$

(31)

$$\begin{aligned} \overset{\cdot }{\rho _{41}}=-\beta _{4}\rho _{41}-i\ \Omega _{2}^{eff}\rho _{42}-i\ \Omega _{3}^{eff}\rho _{43}+i\ \Omega _{4}^{eff}\rho _{31} \end{aligned}$$

(32)

$$\begin{aligned} \overset{\cdot }{\rho _{32}}=-\beta _{5}\rho _{32}-i\ \Omega _{2}^{eff^{*}}\rho _{31}+i\ \Omega _{3}^{eff}\rho _{12}+i\ \Omega _{4}^{eff^{*}}\rho _{42} \end{aligned}$$

(33)

$$\begin{aligned} \overset{\cdot }{\rho _{42}}=-\beta _{6}\rho _{42}-i\ \Omega _{2}^{eff^{*}}\rho _{41}+i\ \Omega _{4}^{eff}\rho _{32} \end{aligned}$$

(34)

$$\begin{aligned} \overset{\cdot }{\rho _{43}}=-\beta _{7}\rho _{43}-i\ \Omega _{3}^{eff^{*}}\rho _{41}-i\ \Omega _{4}^{eff}(\ \rho _{44}-\rho _{33}) \end{aligned}$$

(35)

with the identity $\sum \limits _{n=1}^{4}$ $\rho _{nn}=1$ and

$$\begin{aligned} \beta _{2} =\gamma _{2}+i\Delta _{2} \end{aligned}$$

(36)

$$\begin{aligned} \beta _{3}=\gamma _{3}+i\Delta _{3} \end{aligned}$$

(37)

$$\begin{aligned} \beta _{4}=\gamma _{4}+i(\Delta _{3}+\Delta _{4}) \end{aligned}$$

(38)

$$\begin{aligned} \beta _{5}=(\gamma _{2}+\gamma _{3})-i(\Delta _{2}-\Delta _{3}) \end{aligned}$$

(39)

$$\begin{aligned} \beta _{6}=(\gamma _{2}+\gamma _{4})-i(\Delta _{2}-\Delta _{3}-\Delta _{4}) \end{aligned}$$

(40)

$$\begin{aligned} \beta _{7}=(\gamma _{3}+\gamma _{4})+i\Delta _{4} \end{aligned}$$

(41)

where $\gamma _{2},\gamma _{3}$ and $\gamma _{4}$ represent the radiative decay rates of the excitation states $\left| 2\right\rangle$, $\left| 3\right\rangle$ and $\left| 4\right\rangle$ due to spontaneous emission, respectively. $\Delta _{3}=\nu _{3}-\omega _{31}$ is the frequency detuning for the weak probe field, and $\Delta _{2}=\nu _{2}-\omega _{21}$ and $\Delta _{4}=\nu _{4}-\omega _{43}$ are the frequency detunings for the pump and control fields.

In the following section, we present the results of numerical calculations of the plasmonic effects and dipole–dipole interaction of the hybrid MNPs-SQD nanosystem, where the SQD has a V-type four-level structure

Numerical Results and Discussion

The numerical calculations for the set of density matrix equations (27-35) at the steady state are done to obtain the coherence $\rho _{13}$ and $\rho _{34}$. We study the influence of the strength of the plasmon–exciton dipole interaction as a function of probe field $\mathrm {{Im}}\;\Lambda _{3}\rho _{13}=\mathrm {{Im}}\;\eta _{3}$ and control field $\mathrm {Im}\Lambda _{4}\rho _{34}=\mathrm {Im}\eta _{4}$ for different parameters of the hybrid MNPs-SQD nanosystem. We consider three spherical gold MNPs with radius $a_{j}$. The parameters of the MNPs-SQD are taken as $\hslash \omega _{pj}$ $=9.02$ eV,  $\gamma _{bj}$ $=0.026$ eV, and the dipole $\mu _{12}=\mu _{13}=\mu _{34}=0.65$ e $nm,\gamma _{2}=0.02$ $ns^{-1},$ $\gamma _{3}=1$ $ns^{-1},\gamma _{4}=0.01$ $ns^{-1},\Omega _{3}=0.01$ $ns^{-1},\Omega _{2}=\Omega _{4}=6$ $ns^{-1}$ and ($r_{1},r_{2},r_{3})=10$, 26, 42 nm, respectively. We have $R_{j}=R=7$ nm,  $\epsilon _{s}=2,$ $\epsilon _{B}=12,$ $\theta _{2}=2\pi /3,$ $\theta _{3}=3\pi /2,$ and $\Delta _{2}=\Delta _{4}=\Delta =2$ eV. Other parameters are indicated in the figure captions and described in what follows.

Figure 2 shows the spectrum of the plasmon–exciton dipole interaction $(\mathrm {Im}\eta _{3})$ of the hybrid MNPs-SQD nanosystem for different values of $\theta _{1}$($\pi /9$, $\pi /6$, $5\pi /6$) versus probe field detuning ($\Delta _{3}$). Figure 2 $(a_{1},a_{2})$ is taken for case (ZZY), and Fig. 2 $(b_{1},b_{2})$ is taken for case (ZYZ), while Fig. 2 $(a_{1},b_{1})$ has the data: $\hslash \omega =20$ eV and Fig. 2 $(a_{2},b_{2})$ has the data: $\hslash \omega =2.7$ eV. Figure 2 $(a_{1})$ shows different impacts and distinctive for the absorption spectra when $\hslash \omega =20$ eV and has negative values for all $\theta _{1}$, at small $\theta _{1}=$ $\pi /9$ (dashed curve); the absorption has an optical EIT window at zero detuning ($\Delta _{3}$) besides one peak on each side. With increasing $\theta _{1}=$ $\pi /6$ (solid curve), we have three peaks and notice the optical EIT window disappearing, but at $\theta _{1}=$ $5\pi /6$ (dashed-dotted curve), the peaks are increasing to four peaks. In Fig. 2 $(a_{2})$, the peaks are displacing under the effect of angle $\theta _{1}$ where they have four different peaks with positive values (because of the decrease in $\hslash \omega =2.7$ eV). For case (ZYZ), we notice three peaks only; the peaks for large $\theta _{1}=$ $5\pi /6$ have negative values in Fig. 2 $(b_{1})$. All the peaks for all values of $\theta _{1}$ have negative values for ($\hslash \omega =2.7$ eV) as in Fig. 2 $(b_{2})$ , and also the peaks are displacing under the effect of angle $\theta _{1}$ like Fig. 2 $(a_{2})$. We conclude in this figure the absorption spectrum is asymmetric about the vertical axis at ($\Delta _{3}=0$), we notice also the resonance frequency ($\hslash \omega$) as well the angles, and direction of the fields plays an important role in the plasmon–exciton dipole coupling.

Fig. 2

The spectrum of the plasmon–exciton dipole interaction $(\mathrm {Im}\eta _{3})$ of the hybrid MNPs-SQD nanosystem versus probe field detuning ($\Delta _{3}$). $\epsilon _{s}=2,\epsilon _{B}=12,\theta _{2}=2\pi /3,$ $\theta _{3}=3\pi /2,$ $\Omega _{2}=\Omega _{4}=6$ $ns^{-1}$and $\Delta _{2}=\Delta _{4}=\Delta =2$ eV. Figure 2$(a_{1},a_{2})$ for (ZZY) and Fig. 2$(b_{1},b_{2})$ for (ZYZ). Figure 2$(a_{1},b_{1})$ has: $\hslash \omega =20$ eV and Fig. 2$(a_{2},b_{2})$ has: $\hslash \omega =2.7$ eV. $\theta _{1}=$ $\pi /9$ (dashed curve), $\theta _{1}=$ $\pi /6$ (solid curve) and $\theta _{1}=$ $5\pi /6$ (dashed-dotted curve)

Figure 3 shows the spectrum of the plasmon–exciton dipole interaction $(\mathrm {Im}\eta _{4})$ of the hybrid MNPs-SQD nanosystem for different values of $\theta _{1}$($\pi /9$, $\pi /6$, $5\pi /6$) (as in Fig. 2) versus probe field detuning ($\Delta _{3}$). The data are as in Fig. 2, in addition $\hslash \omega =20$ eV. We have Fig. 3 $(a_{1},a_{2})$ for case (ZZY) and Fig. 3 $(b_{1},b_{2})$ for case (ZYZ), while Fig. 3 $(a_{1},b_{1})$ has the data: $\gamma _{bj}$ $=0.026$ eV and Fig. 3 $(a_{2},b_{2})$ has the data: $\gamma _{bj}$ $=1.6$ eV. At small damping constant ($\gamma _{bj}$ $=0.026$ eV), for case (ZZY) as in Fig. 3 $(a_{1})$ we have an the optical EIT for small $\theta _{1}=$ $\pi /9$ (dashed curve). When increasing $\theta _{1}=$ $\pi /6$ (solid curve), the absorption has three peaks and the optical EIT disappears, but at $\theta _{1}=$ $5\pi /6$ (dashed-dotted curve). It is observed four peaks with negative values. But for case (ZYZ) for all values of $\theta _{1}$, we show three peaks only in the negative values with different heights as in Fig. 3 $(b_{1})$. Figure 3 $(a_{2})$ displays the effect of damping constant when it is large ($\gamma _{bj}$ $=1.6$ eV). For case (ZZY), at $\theta _{1}=$ $\pi /9$, it is observed a hole in the left side which is converted into small peak at $\theta _{1}=$ $\pi /6$. But at $\theta _{1}=$ $\theta_{1}=5\pi/6$, we find different two peaks with positive values in the left side and another different two peaks with negative values in the right side. We have in this figure zero absorption for all values of $\theta _{1}$($\pi /9$, $\pi /6$, $5\pi /6$) at ($\Delta _{3}=-3.2$) approximately. In Fig. 3 $(b_{2}),$ , we observe the middle peak has top value and another two peaks have small values for each value of $\theta _{1}$with different values for peaks. Then, in Fig. 3, the influence of the damping constant on the plasmon–exciton dipole coupling is more obviously for the case (ZZY), and also, the shape of the spectra is asymmetric at ($\Delta_{3}=0$). As well, the optical PEIT in the spectrum appears at small damping constant and the hole in the spectrum appears at large damping constant .

Fig. 3

The spectrum of the plasmon–exciton dipole interaction $(\mathrm {Im}\eta _{4})$ of the hybrid MNPs-SQD nanosystem versus probe field detuning ($\Delta _{3}$). The data as in Fig. 2, in addition $\hslash \omega =20$ eV. Figure 3 ($a_{1},a_{2}$) for (ZZY) and Fig. 3$(b_{1},b_{2})$ for (ZYZ). Figure 3 $(a_{1},b_{1})$ has: $\gamma _{bj}$ $=0.026$ eV and Fig. 3$(a_{2},b_{2})$ has: $\gamma _{bj}$ $=1.6$ eV

Figure 4 shows the spectrum of the plasmon–exciton dipole interaction $(\mathrm {Im}\eta _{4})$ of the hybrid MNPs-SQD nanosystem for different values of $\hslash \omega$ (16, 6,  2.7) versus probe field detuning ($\Delta _{3}$) at $\theta _{1}=$ 0. The another data are as in Fig. 2. Figure 4 $(a_{1},a_{2},a_{3})$ is taken for case (ZZY), and Fig. 4 $(b_{1},b_{2},b_{3})$ is taken for case (ZYZ). Figure 4 $(a_{1},b_{1})$ has the data: $\hslash \omega =16$ eV, Fig. 4 $(a_{2},b_{2})$ has: $\hslash \omega =6$ eV and Fig. 4 $(a_{3},b_{3})$ has: $\hslash \omega =2.7$ eV. We have different impacts and distinctive for the resonance frequency ($\hslash \omega$) on the spectrum $(\mathrm {Im}\eta _{4})$ in this figure, when $\hslash \omega =16$ eV.  Figure 4 $(a_{1},b_{1})$ displays four peaks in the positive values for case (ZZY) and three peaks in the negative values for case (ZYZ), respectively, with different heights. But at $\hslash \omega =6$ eV for case (ZZY), the spectrum exhibits a positive high peak with a Fano-like lineshape in the positive ($\Delta _{3}$) and a negative small peak with a Fano-like lineshape in the negative ($\Delta _{3}$) as in Fig. 4 $(a_{2})$. But in Fig. 4 $(b_{2})$, the spectrum exhibits a negative high peak in the negative ($\Delta _{3}$) and small peak with a Fano-like lineshape in the positive ($\Delta _{3}$). At $\hslash \omega =2.7$ eV for case (ZZY), Fig. 4 $(a_{3})$ displays a positive peak and a negative peak in the negative ($\Delta _{3}$) and also in the positive ($\Delta _{3}$). For case (ZYZ) in Fig. 4 $(b_{3})$ , the spectrum exhibits a trapping at ($\Delta _{3}=0$), and we notice also a negative peak at a certain value ($\Delta _{3}=-30$) and also a positive peak at ($\Delta _{3}=30$) approximately. We conclude in this figure the obvious role of the resonance frequency ($\hslash \omega$) or the dielectric function $\epsilon _{m_{j}}(\omega )$ for MNPs on the spectrum of the plasmon–exciton dipole interaction $(\mathrm {Im}\eta _{4})$. So, it is clear the influence of the metal nanoparticles is to enhance different phenomena in the regime of exciton–plasmon resonance.

Fig. 4

The spectrum of the plasmon–exciton dipole interaction $(\mathrm {Im}\eta _{4})$ of the hybrid MNPs-SQD nanosystem versus probe field detuning ($\Delta _{3}$) at $\theta _{1}=$ 0. Figure 4$(a_{1},a_{2},a_{3})$ for (ZZY) and Fig. 4$(b_{1},b_{2},b_{3})$ for (ZYZ). Figure 4$(a_{1},b_{1})$has : $\hslash \omega =16$ eV, Fig. 4$(a_{2},b_{2})$ has: $\hslash \omega =6$ eV and Fig. 4$(a_{3},b_{3})$ has: $\hslash \omega =2.7$ eV. The another data as in Fig. 2

Figure 5 demonstrates the spectrum of the plasmon–exciton dipole interaction $(\mathrm {Im}\eta _{3})$ and $(\mathrm {Im}\eta _{4})$ of the hybrid MNPs-SQD nanosystem for case (ZZY) when the dielectric constant $\epsilon _{B}$ is small and equal $\epsilon _{s}$ ($\epsilon _{B}=\epsilon _{s}=2$) at $\hslash \omega =20$ eV. The dashed curve is for $\Omega _{2}=\Omega _{4}=6ns^{-1}$ and the solid curve is for $\Omega _{2}=4ns^{-1},\Omega _{4}=8ns^{-1}$. The another data are as in Fig. 4. Figure 5 $(a_{1},a_{2},a_{3})$ is taken for $(\mathrm {Im}\eta _{3})$, where the spectra have negative values, and Fig. 5 $(b_{1},b_{2},b_{3})$ is taken for ($(\mathrm {Im}\eta _{4})$, where the spectra have positive values. Figure 5 $(a_{1},b_{1})$ has ($\Delta =0$), Fig. 5 $(a_{2},b_{2})$ has ($\Delta =2$) and Fig. 5 $(a_{3},b_{3})$ has ($\Delta =5$). The optical EIT, when ($\Omega _{2}=\Omega _{4}=6ns^{-1}$) (in Fig. 5 $(a_{1},b_{1})$), is deep and disappears when increasing the ($\Delta$) (as in Fig. 5 $(a_{3},b_{3})$) . As well, four peaks appeared for ($\Omega _{2}=4ns,\Omega _{4}=8ns^{-1}$) in Fig. 5 $(a_{1},b_{1})$ and decreased to only two peaks when increasing the ($\Delta$) (in Fig. 5 $(a_{3},b_{3})$). Then, the optical EIT is related by the change of ($\Delta$), and the value of the ($\Delta$) plays an important role in the characterization of the spectrum of the plasmon–exciton dipole interaction $(\mathrm {Im}\eta _{3})$ and $(\mathrm {Im}\eta _{4})$.

Fig. 5

The spectrum of the plasmon–exciton dipole interaction $(\mathrm {Im}\eta _{3})$ and $(\mathrm {Im}\eta _{4})$ of the hybrid MNPs-SQD nanosystem for (ZZY) at ($\epsilon _{B}=\epsilon _{s}=2$), $\hslash \omega =20$ eV. Figure 5$(a_{1},a_{2},a_{3})$ is for $(\mathrm {Im}\eta _{3})$ and Fig. 5$(b_{1},b_{2},b_{3})$ for ($(\mathrm {Im}\eta _{4})$. Figure 5$(a_{1},b_{1})$ has ($\Delta =0$), Fig. 5$(a_{2},b_{2})$ has ($\Delta =2$) and Fig. 5$(a_{3},b_{3})$ has ($\Delta =5$). The dashed curve for $\Omega _{2}=\Omega _{4}=6ns^{-1}$ and the solid curve for $\Omega _{2}=4ns^{-1},\Omega _{4}=8ns^{-1}$. The another data as in Fig. 4

Figure 6 exhibits the spectrum of the plasmon–exciton dipole interaction $(\mathrm {Im}\eta _{3})$ and $(\mathrm {Im}\eta _{4})$ of the hybrid MNPs-SQD nanosystem when the dielectric constant $\epsilon _{s}$ is large ($\epsilon _{s}=12$), unlike the above figures, at ($\Delta =0$ and $\theta _{1}=\pi /9$). Figure 6 $(a_{1},a_{2})$ is taken for $(\mathrm {Im}\eta _{3})$ and Fig. 6 $(b_{1},b_{2})$ is taken for ($(\mathrm {Im}\eta _{4})$. Figure 6 $(a_{1},b_{1})$ is for case (ZZY) and Fig. 6 $(a_{2},b_{2})$ is for case (ZYZ). The dashed-dotted curve is for ($\epsilon _{B}=2$), the solid curve for ($\epsilon _{B}=6$) and the dashed curve for ($\epsilon _{B}=12$). The another data are as in Fig. 2. We see that when the dielectric constant $\epsilon _{s}$ is large, the increase in the dielectric constant $\epsilon _{B}$ can be contributed to the enhancement of the optical EIT for case (ZZY) in the spectrums of the plasmon–exciton dipole interaction ($\mathrm {Im}\eta _{3}$ and $\mathrm {Im}\eta _{4}$); when $\epsilon _{s}=$ $\epsilon _{B}=12$, the optical EIT becomes more deep. The optical EIT for case (ZYZ) in the spectrums ($\mathrm {Im}\eta _{3}$ and $\mathrm {Im}\eta _{4}$) is not available, and the three peaks more extend range at increasing the dielectric constant $\epsilon _{B}$ in Fig. 6 $(a_{2},b_{2})$. So, happening of the optical EIT is related by the value of the dielectric constants $\epsilon _{B}$, $\epsilon _{s}$ and the direction of the fields.

Fig. 6

The spectrum of the plasmon–exciton dipole interaction $(\mathrm {Im}\eta _{3})$ and $(\mathrm {Im}\eta _{4})$ of the hybrid MNPs-SQD nanosystem at $\epsilon _{s}=12$, $\Delta =0$ and $\theta _{1}=\pi /9$. Figure 6 $(a_{1},a_{2})$ for $(\mathrm {Im}\eta _{3})$ and Fig. 6 $(b_{1},b_{2})$ for ($(\mathrm {Im}\eta _{4})$. Figure 6 $(a_{1},b_{1})$ for (ZZY) and Fig. 6 $(a_{2},b_{2})$ for (ZYZ). The dashed-dotted curve for ($\epsilon _{B}=2$), the solid curve for ($\epsilon _{B}=6$) and the (dashed curve) for ($\epsilon _{B}=12$) .The another data as in Fig. 2

Figure 7 demonstrates the influence of the size of the three spherical MNPs on the spectrum of the plasmon–exciton dipole interaction $(\mathrm {Im}\eta _{3})$ and $(\mathrm {Im}\eta _{4})$ of the hybrid MNPs-SQD nanosystem for the case (ZZY), and we take the radii with two different values ($R=4,6$ nm) and ($\theta _{1}=0$), taking into consideration that the center-to-center distances are constant. Figure 7 ($a_{1},a_{2}$) is taken for $(\mathrm {Im}\eta _{3})$ and Fig. 7 $(b_{1},b_{2})$ is taken for ($(\mathrm {Im}\eta _{4})$. Figure 7 $(a_{1},b_{1})$ is plotted versus probe field detuning ($\Delta _{3}$) and Fig. 7 $(a_{2},b_{2})$ is plotted versus probe field detuning ($\Delta _{4}$). The dashed curve is for ($R=4$) and the solid curve is for ($R=6$). The another data are as in Fig. 2. In Fig. 7 ($a_{2},b_{2}$), which is plotted versus probe field detuning ($\Delta _{4}$), it does not show peaks on the two sides of the spectrum as in Fig. 7 $(a_{1},b_{1})$. We notice at ($R=4$), the spectrum has small optical EIT; when increasing the radii ($R=6$), the optical EIT becomes obvious as in Fig. 7 $(a_{1},b_{1},a_{2},b_{2})$, where we have from Eq. (22, 23) that the plasmon–exciton dipole interaction ($\Lambda _{3},\Lambda _{4}$) depends on $\alpha _{j}$ which contains $R_{j}$ (i.e., the size of spherical MNPs); when we take the another values in these equations’ constant, the dipole interaction for MNP of ($R=6$) is more powerful than the dipole interaction for MNP of ($R=4$) because the MNP of ($R=6$) is the nearest to SQD unlike the MNP of ($R=4$) when the center-to-center distances are the same for the two cases ($R=6,4$) [also, see [8, 17, 19, 24, 27]. We notice the ratio of the radius of MNP ($R_{j}$) to the center-to-center distance ($r_{j}$), which plays an important role in the plasmon–exciton dipole interaction [24]. Then, the spectrum of the plasmon–exciton dipole interaction $(\mathrm {Im}\eta _{3})$ and $(\mathrm {Im}\eta _{4})$ of the hybrid MNPs-SQD nanosystem is affected by the size of the three spherical MNPs.

Fig. 7

The spectrum of the plasmon–exciton dipole interaction $(\mathrm {Im}\eta _{3})$ and $(\mathrm {Im}\eta _{4})$ of the hybrid MNPs-SQD nanosystem for (ZZY), at ($R_{j}=4,6$ nm) and ($\theta _{1}=0$). Figure 7 $(a_{1},a_{2})$ for $(\mathrm {Im}\eta _{3})$ and Fig. 7 $(b_{1},b_{2})$ for ($(\mathrm {Im}\eta _{4})$. Figure 7 $(a_{1},b_{1})$ is plotted versus probe field detuning ($\Delta _{3}$) and Fig. 7 $(a_{2},b_{2})$ is plotted versus probe field detuning ($\Delta _{4}$). The dashed curve for ($R_{j}=4$) and the solid curve for ($R_{j}=6$). The another data as in Fig. 2

Conclusion

We have derived a compound expression of the effective Rabi frequencies based on the effect of the plasmon–exciton dipole coupling in the SQD-MNPs nanosystem which is composed of three sphere metallic nanoparticles (MNPs) and semiconductor quantum dot (SQD) which have three external fields. The strong exciton–plasmon interaction and multipole effects are considered the main focus of this work. The direction and detunings of the three external fields play an important role in the characterization of the SQD-MNPs nanosystem. We investigated the dependence of the plasmon–exciton dipole coupling of the SQD-MNP nanosystem on the distance between the three MNPs and also the distance between SQD and MNPs. The material parameters of the hybrid nanosystem such as resonance frequency, damping constant and dielectric constant, are demonstrated for many distinct characteristics and phenomena for the spectra of the plasmon–exciton dipole interaction $(\mathrm {Im}\Lambda _{3}\rho _{13})$ and $(\mathrm {Im}\Lambda _{4}\rho _{34})$ of the hybrid MNPs-SQD nanosystem. The optical experiments on the hybrid SQD-MNPs nanosystem may be analyzed by using the results obtained in this work.