Introduction

In the last few years, plasmonics has become one of the most important topics in the field of light-matter interaction [1]. With a view to technical applications, resonant optical antennas are very promising structures [2] because their main purpose is to convert free propagating optical radiation to localized energy efficiently and vice versa. Gold, silver, and other metals are widely used in this area because of their optical and near-IR properties and processability. The tunability of these devices into the visible and the NIR spectral range can be influenced by their specific geometry, material properties, and surrounding material [3]. Optical antennas have a similar role as their radio frequency and microwave counterparts, i.e., to convert the energy of free propagating radiation to localized energy and vice versa [4]. The optical and NIR response function can be tuned according to the application’s needs [5,6,7]. It can be influenced by the length scale over which the free-electron oscillation occurs [8]. However, equations from classical antenna theory cannot be used for optical frequency antennas. Therefore, researchers try to find proper scaling laws for this purpose [9]. In this context, several designs have already been proposed, e.g., L-shaped [12, 14, 15], V-shaped [13], and bowtie-shaped [11] ROAs.

This study investigates the tunability and polarization sensitivity of different cross-shaped nanoantenna designs. All simulations are performed in COMSOL Multiphysics [10], a commercially available software package based on the finite element method (FEM) [16]. Our results indicate design rules for multimodal plasmonic antennas with ultra-high field enhancement. Furthermore, the reported design offers a relatively high field enhancement (\(\left|{E}_{\mathrm{TOT}}\right|/\left|{E}_{\mathrm{IN}}\right|\)) of 45.9 and 149.4 for the high-energy resonance (700- to 800-nm wavelength region) and the low-energy resonance (900- to 1000-nm wavelength region), respectively. Table 1 summarizes the current study compared to the previous work.

Table 1 Comparison of the suggested design with similar structures
Full size table

As is well-known, several scattering models are used in plasmonic theory. However, our wavelength region and nanoparticle size are relevant to Mie’s scattering theory, which defines the total extinction coefficient of small metallic particles as a sum of all-electric and magnetic multipole oscillations contributing to the absorption and scattering of the electromagnetic field [22]. This will be extensively used in the paper.

The paper is organized as follows. After the “Introduction” (Sec. 1), the “Design and Simulation Strategy” (Sec. 2) section shows the design of nanoantennas and the simulation strategy to identify the plasmon length for several types of cross-shaped ROAs. The “Analysis of Single Cross-Shaped Antennas with Different Symmetry Levels,” (Sec. 3) “Analysis of Coupled Cross-Shaped Antennas with Equal Arms,” (Sec. 4) “Polarization of Symmetric Single Cross-Shaped Antennas,” (Sec. 5) and “Triple-Modal Cross-Shaped Antennas” (Sec. 6) sections investigated single and coupled cross-shaped ROAs, polarization sensitivity, and triple-modal single cross-shaped ROAs. The “Possible Fabrication Method” (Sec. 7) section describes the possible fabrication methods of coupled antennas with very small gaps. Discussion and conclusion are in the “Discussion” (Sec. 8) and the “Conclusion” (Sec. 9) sections.

Design and Simulation Strategy

The numerical simulation for the proposed design was carried out using the finite element method (FEM) via COMSOL Multiphysics software [10]. Our cross-shaped antennas are made from gold as the constituting material and the permittivity of gold is taken from the literature [23]. Furthermore, the geometric parameters such as length, width, and height are chosen based on the fabricated structures already reported [24].

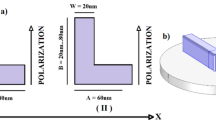
Figure 1 illustrates a cross-shaped antenna under consideration with different arm lengths (\(A\ne B\)). The reported designs consist of an asymmetric cross-shaped gold nanoantenna on a silicon dioxide substrate covered by ITO. For a more detailed investigation of cross-shaped antennas, we will first introduce some notations which are directly related to the level of symmetry. In our investigation, we have three levels of symmetry, as depicted in Fig. 1.

  1. (I)

    A symmetric cross-shaped antenna is a cross-shaped antenna that has symmetry with respect to both vertical and horizontal axes.

  2. (II)

    A partially symmetric cross-shaped antenna is a cross-shaped antenna that has symmetry with respect to the vertical or horizontal axis, but not to both axes at the same time.

  3. (III)

    An asymmetric cross-shaped antenna is a cross-shaped antenna that has symmetry with respect to neither the horizontal nor the vertical axis.

Fig. 1
figure 1

Top view of cross-shaped ROAs (x–y plane) with three types of symmetry level. The antenna arms A and B and arm width W

Full size image

It is worth mentioning that the symmetry is not correlated with the overall arm lengths A and B. Cross-shaped nanostructures can exhibit an axis symmetry even if the arm lengths are different (\(A\ne B\)), but also can be asymmetric even if arm lengths are equal (\(A=B\)).

Analysis of Single Cross-Shaped Antennas with Different Symmetry Levels

Symmetric and Partially Symmetric Single Cross-Shaped Antennas

The investigation starts with single symmetric (type I from Fig. 1) cross-shaped antennas with the same arm lengths (\(A=B=80 \mathrm{nm}\)) as in Fig. 2a. The reported designs are excited with a linearly polarized plane wave normally impinging from the substrate side with an electric field strength of 1 V/m, as shown in Fig. 2. If we accept the coordinate system from Fig. 2, the \(\overrightarrow{k}\) vector of the plane wave is parallel to the z-axis, and the \(\overrightarrow{E}\) vector lays in the x–y plane. As indicated in Figs. 2a, 3a and 4a, in all simulation steps in this work, width W is kept constant at 20 nm. The reported nanoantennas have a fixed height of 30 nm, as indicated in the same figures. In all simulations, the boundary conditions are set to perfect matched layer (PML) with a thickness of 500 nm in x-, y-, and z-directions and the simulation sphere has a radius of 600 nm. In this study, flexible tetrahedron-shaped mesh is used. We employ a fine mesh with a minimum and maximum element size of 1 nm and 6 nm for ROAs, respectively. Additionally, in all simulations of coupled structures where a gap width of 2 nm is investigated, a very small airbox is used for meshing in the small gap. The maximum mesh size applied for that box is 2 nm. Moreover, the edges of the structure are rounded with a radius of 3 nm. The electric field enhancement and optical cross-sections are numerically studied at wavelengths ranging from 500 to 1000/1200 nm.

Fig. 2
figure 2

a Top view of a single partially symmetric cross-shaped ROA (x–y plane) with the antenna arms termed A and B; b 3D model of the single cross-shaped ROA; c absorption cross-sections; d scattering cross-section; e current density of a partially symmetric ROA at wavelength = 707 nm and \({\delta }_{\mathrm{x}}=25\mathrm{ nm}\); f the dependency between \({\delta }_{\mathrm{x}}\) and resonant wavelength for the partially symmetric cross-shaped antenna

Full size image
Fig. 3
figure 3

a Top view of a single partially symmetric cross-shaped ROA (x–y plane) with the antenna arms termed A and B; b 3D model of the single cross-shaped ROA; c absorption cross-section; d scattering cross-section; e the current density of a partially symmetric ROA at the existing three resonances of 630 nm, 698 nm, and 768 nm, respectively. In this study, \({\delta }_{\mathrm{x}}={\delta }_{\mathrm{y}}=10\mathrm{ nm}\)

Full size image
Fig. 4
figure 4

a Top view of a coupled cross-shaped ROA (x–y plane) with equal antenna arms termed A and B where arm B is moved in δx steps in x-direction; b 3D model of the coupled cross-shaped ROA; c field enhancement \(\left|{E}_{\mathrm{TOT}}\right|/\left|{E}_{\mathrm{IN}}\right|\) in the gap center for different values of \({\delta }_{x}\) and gap width of 2 nm; d current density of the bimodal ROA for resonant wavelengths for \({\delta }_{\mathrm{x}}=15 \mathrm{nm}\). The ROA resonant wavelengths are 768 nm and 952 nm. e Field enhancements \(\left|{E}_{\mathrm{TOT}}\right|/\left|{E}_{\mathrm{IN}}\right|\) in the gap center for several values of gap and constant shifting value of \({\delta }_{\mathrm{x}}=15 \mathrm{nm}\)

Full size image

There are several ways to break this structure’s symmetry and set polarization conditions. However, the approach here will be to displace only the arm with length B in horizontal or x-direction as depicted in Fig. 2a. In this way, the partial symmetry of the structure stays because ROA will keep the symmetry with respect to the vertical or y-axis. This corresponds to a transition from type I to type II regarding symmetry definitions. To analyze far-field properties, we will use the structure as in Fig. 2. Figure 2b shows the 3D model in COMSOL Multiphysics. The displacements \({\delta }_{\mathrm{x}}\) and \({\delta }_{\mathrm{y}}\) in this work will be used to control the movement of the rectangular element from its original central position, lowering the symmetry. In this first step of investigation, only relevant displacement value is \({\delta }_{\mathrm{x}}\). The polarization direction is also indicated in the same Fig. 2a. This cross-shaped single ROA is analyzed in terms of its scattering and absorption properties by “morphing” the antenna from a symmetric-shaped antenna (type I) with arm lengths \(A=80 \mathrm{nm}\) and \(B=80 \mathrm{nm}\) to a partially symmetric cross-shaped antenna (type II) by shifting the arm with length B by 5 nm in the horizontal direction for each simulation step. In the last simulation step, this antenna becomes a T-shaped ROA. During this study, the volume and antenna arm lengths are kept constant. Figure 2 c and d show the numerical calculation for the optical cross-sections of the nanoantenna under investigation. It may be noted from this figure that the behavior is still monomodal for the smaller values of the \({\delta }_{\mathrm{x}}\). These results allow for a general statement. If the polarization direction is set along the symmetric arm of the partially symmetric cross-shaped antenna, the antenna exhibits just one resonance which is almost independent on the horizontal rod. It can be seen in Fig. 2c and d that for lower values of \({\delta }_{\mathrm{x}}\), the resonant wavelength is almost constant, but for \({\delta }_{\mathrm{x}}=30\mathrm{ nm}\), a small red-shifting of the resonant wavelength occurs since in this case the cross-shaped antenna becomes T-shaped and this causes a redistribution of the mode energy. Figure 2e shows the current density with current density lines of the partially symmetric ROA at a wavelength of 707 nm for the case \({\delta }_{\mathrm{x}}=20\mathrm{ nm}\). It can be seen from this figure that the nanoantenna shows monomodal behavior and mainly depends on the current distribution in the y-direction. Figure 2f presents the dependency of the resonant wavelength on the displacement \({\delta }_{\mathrm{x}}\). It can be seen from this figure that, for the small values of \({\delta }_{\mathrm{x}}\), the resonant wavelengths remain the same at 707 nm, while at \({\delta }_{\mathrm{x}}\) = 30 nm, the cross-shaped antenna is T-shaped, as seen in Fig. 2a, and the resonant wavelength is slightly shifted to 715 nm.

Asymmetric Single Cross-Shaped Antennas

As shown in Fig. 1, several ways exist to break cross-shaped nanoantennas’ symmetry.

Here, the vertical arm B will be displaced in both horizontal (x) and vertical (y) directions, as depicted in Fig. 3a. In this way, the structure’s symmetry is no longer present because the ROA will not have symmetry to the horizontal or vertical axis.

This corresponds to a transition from type I to type III regarding the symmetry definitions. Again, the investigation begins with single symmetric (type I) cross-shaped antennas with the same arm lengths (\(A=B=80 \mathrm{nm}\)) as shown in Fig. 3a. Figure 3b shows the 3D model in COMSOL Multiphysics software. In this second step of investigation, both displacements \({\delta }_{\mathrm{x}}\) and \({\delta }_{\mathrm{y}}\) are relevant. The polarization direction is also indicated in the same Fig. 3a. In the last simulation step, this antenna becomes an L-shaped ROA. During this study, the volume and antenna arm lengths are kept constant. Figure 3 c and d show numerical results of the optical cross-section at different values of \({\delta }_{\mathrm{x}}\) and \({\delta }_{\mathrm{y}}\). It can be seen from this figure that, at \({\delta }_{\mathrm{x}}={\delta }_{\mathrm{y}}=0\mathrm{ nm}\), the cross-shaped antenna is symmetric to both axes and it shows monomodal behavior. For smaller values of \({\delta }_{\mathrm{x}}=5\mathrm{ nm}\) and \({\delta }_{\mathrm{y}}=5\mathrm{ nm}\), the multimodal behavior is still not obvious, so this case will not be presented. The main part of our investigation starts from \({\delta }_{\mathrm{x}}=10\mathrm{ nm}\) and \({\delta }_{\mathrm{y}}=10\mathrm{ nm}\). For these values, the structure shows already a slight triple-resonance behavior. Similar behavior but less obvious can be seen for \({\delta }_{\mathrm{x}}=15\mathrm{ nm}\) and \({\delta }_{\mathrm{y}}=15\mathrm{ nm}\). If we further increase the values of \({\delta }_{\mathrm{x}}={\delta }_{\mathrm{y}}= 20\mathrm{ nm}\) or \({{\delta }_{\mathrm{x}}={\delta }_{\mathrm{y}}=25\mathrm{ nm}}\), the ROAs show clearly a bimodal behavior. For \({\delta }_{\mathrm{x}}={\delta }_{\mathrm{y}}= 30\mathrm{ nm}\), the cross-shaped ROA becomes an L-shaped ROA. For a better analysis of the trimodal behavior, we will choose the case of \({\delta }_{\mathrm{x}}={\delta }_{\mathrm{y}}= 10\mathrm{ nm}\) which is depicted by the blue color in Fig. 3c. The trimodal nature is especially obvious for the absorption cross-section. From the spectrally dependent cross-sections and the analysis of the current density lines for the three different resonances, as depicted in Fig. 3c, d, and e, it is possible to analyze all three modes. The lowest-frequency ROA eigenmode can be assigned to a smoothly-bent-longitudinal current mode of the longest L-shaped metallic part of the cross-shaped antenna (Fig. 3e for wavelength 768 nm). The highest-frequency ROA eigenmode can be assigned to a smoothly-bent-longitudinal current mode of the shortest L-shaped metallic part of the cross-shaped antenna (Fig. 3e for wavelength 630 nm).

Finally, between the lowest- and the highest-frequency ROA eigenmode, there is an eigenmode which has the current mode signature of an out-of-phase longitudinal resonance oscillating along two individual middle-long L-shaped parts of the cross-shaped antenna (Fig. 3e at the wavelength of 698 nm). For \({\delta }_{\mathrm{x}}={\delta }_{\mathrm{y}}=20\mathrm{ nm}\) and \({\delta }_{\mathrm{x}}={\delta }_{\mathrm{y}}=25\mathrm{ nm}\), the highest energy mode disappears, which is logical because in these cases, the physical dimensions of “longest L” and “middle-long L” are very close to each other.

Analysis of Coupled Cross-Shaped Antennas with Equal Arms

The analysis begins with the two coupled type I cross-shaped antennas with the same arm lengths (\(\mathrm{A}=\mathrm{B}=80\mathrm{ nm}\)) and with a gap width of 2 nm. Also, to analyze near-field properties in this small gap, our first step will be investigating the coupled version of those antennas, as shown in Fig. 4a. Figure 4b shows the 3D model in COMSOL Multiphysics. As in the previous investigation, there are several ways to break the coupled structure’s symmetry, but here will be to displace only the arm with length B in horizontal or x-direction as depicted in Fig. 4a. This corresponds to a transition from type I to type II regarding the symmetry. No matter which way is chosen, geometrical parameters of the antenna, like the lengths of the arms (\(\mathrm{A}=\mathrm{B}\)), gap width, and width of arms, are kept constant. The polarization direction is also indicated in the same Fig. 4a. It can be seen from Fig. 4c that the antenna’s spectral response shows a bimodal behavior even for small δx. The high-energy resonance shifts to higher wavelengths and becomes more pronounced for higher δx. This figure shows that for every shifting of arm B for 5 nm, there is a smaller red-shifting of high-energy resonance (ca. 10 nm) and a bigger red-shifting of the low-energy resonance (ca. 20 nm). This causes an increasing wavelength separation between the two resonant peaks for every shifting step of arm B. A cross-shaped coupled antenna with \({\delta }_{\mathrm{x}}=25 \mathrm{nm}\) (a black line in Fig. 4c) is chosen for the field and mode analysis. The resonant wavelengths for this case are 768 nm and 952 nm. From Fig. 2d, for 952 nm, it can be seen that the “L-part” of the antenna has the strongest influence on low-energy resonance. By increasing \({\delta }_{\mathrm{x}}\), there is an increase of the effective length of the “L-part” and therefore an increase of the resonant wavelength of the longitudinal mode which appears on that part of the structure. This will be even more obvious when we analyze triple-modal single cross-shaped antennas. On the other hand, Fig. 4d for 768 nm shows that the high-energy resonance is influenced by the vertical arm but also by “L-part” of the antenna. This agrees with the results shown in Fig. 4b where the shifting of the first resonance by increasing \({\delta }_{\mathrm{x}}\) is much smaller than the shifting of the low-energy resonance. Finally, it is performed an investigation of the gap influence on field enhancement. For this purpose, antenna with \({\delta }_{\mathrm{x}}=15 \mathrm{nm}\) is chosen. Results are shown in Fig. 4e. It can be noticed that the decreasing of the gap width affects a significant increment of the field enhancement in the gap center, but also the resonance which shifts to the low-energy region. If we decrease the gap width, at the same time, by applying the general formula, we increase the capacitance of the gap. Therefore, we decrease the resonant frequency, which is the red-shifting of the resonance.

Polarization of Symmetric Single Cross-Shaped Antennas

In all previous investigation steps, the polarization direction was set to only vertical (y) direction and we used cross-shaped ROAs with same arm lengths. Here, we will study ROA cross-shaped antenna with different arm lengths since investigation aims to examine the bimodal structure. As shown in Fig. 5, the cross-shaped ROA has arm lengths of 60 nm and 80 nm. It can be seen from this figure that a monomodal behavior for x- or y-polarization (or for polarization angles 0° and 90°, respectively) is observed. However, a bimodal behavior develops for tilted polarization, which is most pronounced at 45°. Figure 5d presents the current density distribution for the two modes, which are excited with a polarization angle of 45°. As mentioned, the cross-shaped antenna can be observed as a combination of two rods with lengths 60 nm and 80 nm. Every one of those rods has its own resonant behavior. At the same time, it is well-known that the rod-shaped antenna is very polarization-sensitive and that the strongest spectral response appears when the polarization direction is along the longitudinal axis of the rod. Therefore, for some polarization angles, the shorter rod is dominant. For some other angles, a longer rod is dominant.

Fig. 5
figure 5

a ROA cross-shaped geometry with polarization direction angles colored by different colors; b absolute absorption section; c scattering cross-sections; d polar diagram of the two longitudinal resonances for 641 nm and 706 nm; e current density distribution for resonant wavelengths of 641 nm and 706 nm. The polarization angle is 45°

Full size image

Triple-Modal Cross-Shaped Antennas

The previous chapters discussed the optical and near-IR properties of resonant cross-shaped bimodal and triple-modal antennas. From Fig. 2d and Fig. 3d, it can be concluded that some “parts” of the cross-shaped antenna have a stronger influence on specific resonance peaks than other “parts.” Fig. 3d shows that in the case of a partially symmetric antenna, the most decisive influence on the resonance stems from the vertical rod when the polarization direction is vertical. Figure 4d shows how some “L-parts” of the asymmetric cross-shaped antenna have an influence on certain resonances of three existing resonances. We now turn to the question of how to design an antenna that exhibits trimodal behavior under some geometric and polarization conditions. From the geometrical point of view, a cross-shaped antenna could be interpreted as a combination of L-shaped and rod-like antennas (Fig. 6). A shorter “L-part” of the cross-shaped antenna can be assigned to the first resonance (blue color in Fig. 6). The “rod-part” of the cross-shaped antenna can be assigned to the second resonance (green color in Fig. 6). Furthermore, finally, the longer “L-part” of the cross-shaped antenna can be assigned to the third resonance (red color in Fig. 6). Thus, it is possible to design a cross-shaped antenna that can exhibit even three resonances in the optical and near-IR spectrum.

Fig. 6
figure 6

A partially symmetric cross-shaped antenna is composed of two L-shaped antennas (shown in blue and red) and one rod-like antenna (shown in green)

Full size image

If we chose a cross-shaped antenna that has a different effective length of the blue, green, and red parts of the antenna from Fig. 6, a triple-resonant structure could be built. It is also essential to study the polarization dependence of the antennas. In all following simulations, the optical properties of partially symmetric antennas which have an axis symmetry in y-direction but not in x-direction are investigated. The influence of different arm lengths on the resulting properties will be studied separately. Analysis will be performed not only by shifting of one of the arms like in the previous investigations but also by changing the dimensions of the structure. Therefore, new notations like \({A}_{\mathrm{LEFT}}\), \({A}_{\mathrm{RIGHT}}\), \({B}_{\mathrm{BELOW}}\), and \({B}_{\mathrm{ABOVE}}\) in Fig. 7a need to be introduced.

Fig. 7
figure 7

a Top view of a single cross-shaped ROA (x–y plane) with the antenna arms \({B}_{\mathrm{BELOW}}\) = \({B}_{\mathrm{ABOVE}}\)  = 65 nm, \({A}_{\mathrm{RIGHT}}\) = 90 nm. \({A}_{\mathrm{LEFT}}\) varies from 30 to 60 nm in steps of 5 nm; b absorption cross-section of ROA; c scattering cross-section of ROA; d current densities of the resonances for resonant wavelengths 670 nm, 814 nm, and 910 nm for \({A}_{\mathrm{LEFT}}=40 \mathrm{nm}\); e current density of the resonance for resonant wavelength 922 nm for \({A}_{\mathrm{LEFT}}=60 \mathrm{nm}\). The color bar represents j (current density) with the vector representation of the current modes for the partially symmetric cross-shaped configuration

Full size image

As was noted in Fig. 7a, in the first simulation set, only the length \({A}_{\mathrm{LEFT}}\) is modified. All the other variables remain constant. The polarization angle is 30° in all simulations, as indicated in Fig. 7a. The simulation results in Fig. 7b show that the second resonant wavelength at about 814 nm remains almost constant. It is attributed to the rod-like antenna mode given by the vertical arm of the antenna (green part in Fig. 6). The field distribution shown in Fig. 7c for 814 nm agrees with this statement. It can be seen from Fig. 7b that there is a slightly red-shifting of the third resonance when \({A}_{\mathrm{LEFT}}\) increases and this could be attributed to the fact that this resonance takes place mainly on the right-hand side “L-part” of the antenna (red “L-part” from Fig. 6). However, on the other hand, due to perturbation, it is a little bit affected by a modification of \({A}_{\mathrm{LEFT}}\). To explain this phenomenon, Table 2 is presented and it shows resonant wavelengths for the third resonance.

Table 2 Resonant wavelengths of low-energy resonances for different values \({A}_{\mathrm{LEFT}}\)
Full size table

For smaller values of \({A}_{\mathrm{LEFT}}\), resonant wavelengths are constant at 908 nm. From \({A}_{\mathrm{LEFT}}=45 \mathrm{nm}\), resonant wavelength starts to rise. It is important to mention that in all simulations, \({B}_{\mathrm{BELOW}}\) and \({B}_{\mathrm{ABOVE}}\) are kept at constant (65 nm). Therefore, we can presume that increasing \({A}_{\mathrm{LEFT}}\) has some influence on low-energy resonance since \({A}_{\mathrm{LEFT}}\) is getting closer to the \({B}_{\mathrm{BELOW}}\) and \({B}_{\mathrm{ABOVE}}\) from geometric point of view. This statement is supported by Fig. 7d where the current density is presented with field lines on resonant wavelength at 922 nm for \({A}_{\mathrm{LEFT}}=60 \mathrm{nm}\). Figure 7d and field lines clearly show significant impact of \({B}_{\mathrm{BELOW}}\) and \({B}_{\mathrm{ABOVE}}\), but also of \({A}_{\mathrm{LEFT}}\) on low-energy resonant wavelength. In the next simulation set, geometry from Fig. 7a is used but only \({A}_{\mathrm{RIGHT}}\) is modified in 5-nm simulation steps while other values are kept at constant (\({B}_{\mathrm{BELOW}}=65 \mathrm{nm}\), \({B}_{\mathrm{ABOVE}}=65 \mathrm{nm}\), and \({A}_{\mathrm{LEFT}}=40 \mathrm{nm})\). Polarization direction angle is again set to 30° which is in the previous case from Fig. 7a. Results in Fig. 8a and b show that the first and second resonant wavelengths are almost constant. The explanation for this is that changing the dimension of \({A}_{\mathrm{RIGHT}}\) causes a changing length of the red “L-part” of the cross-shaped antenna as depicted in Fig. 6. As already mentioned, this red “L-part” of the cross-shaped antenna has the dominant influence on the third resonance. Thus, the other two resonances remain almost constant.

Fig. 8
figure 8

a Absorption cross-section; and b scattering cross-section as a function of the \({A}_{\mathrm{RIGHT}}\) for a partially symmetric cross-shaped ROA while other values are \({B}_{\mathrm{BELOW}}=65 \mathrm{nm}\), \({B}_{\mathrm{ABOVE}}=65\mathrm{ nm}\), and \({A}_{\mathrm{LEFT}}=40 \mathrm{nm}\)

Full size image

In the third simulation set, the effect of shifting the vertical arm in steps of 5 nm is studied again for the geometry from Fig. 7a. From a geometric point of view, this is similar to the investigation from Fig. 2, where a partially symmetric cross-shaped antenna is analyzed. However, here, the polarization angle is set to 30°, as indicated in Fig. 7a. Shifting the vertical arm to the left side, in these terms, means decreasing of \({A}_{\mathrm{RIGHT}}\) and increasing of \({A}_{\mathrm{LEFT}}\) while other values are kept at constant (\({B}_{\mathrm{BELOW}}=65 \mathrm{nm}\) and \({B}_{\mathrm{ABOVE}}=65 \mathrm{nm}\)). As shown in Fig. 9b and c, as the arm B has a constant length, the resonant wavelength of the second resonance remains the same during all simulation steps. The first resonance in Fig. 9 shifts red because increasing \({A}_{\mathrm{LEFT}}\) leads to an increased length of the short “L-part” of the cross-shaped antenna (blue color from Fig. 6), which strongly impacts the first resonance. On the other hand, the third resonance in Fig. 9 shifts blue because the decreasing \({A}_{\mathrm{RIGHT}}\) will decrease the length of the long “L-part” of the cross-shaped antenna (red color from Fig. 6), strongly influencing the third resonance.

Fig. 9
figure 9

a Absorption cross-section; and b scattering cross-section as a function of the \({A}_{\mathrm{LEFT}}\) and \({A}_{\mathrm{RIGHT}}\) for a partially symmetric cross-shaped ROA while other values are \({B}_{\mathrm{BELOW}}=65 \mathrm{nm}\) and \({B}_{\mathrm{ABOVE}}=65 \mathrm{nm}\)

Full size image

The reported single cross-shaped triple-modal antennas are also polarization sensitive, as shown in Fig. 10. Optical properties are shown for a partially symmetric ROA with \({B}_{\mathrm{BELOW}}={B}_{\mathrm{ABOVE}}=65 \mathrm{nm}\), \({A}_{\mathrm{LEFT}}=40 \mathrm{nm}\), and \({A}_{\mathrm{RIGHT}}=90 \mathrm{nm}\). In this case, the arm lengths are both 110 nm. As expected, the spectrum can be tuned for all three resonances. Each spectral response can be tuned because the “L-parts” and “rod-parts” of the cross-shaped antenna are also polarization sensitive. As seen in the case of bimodal cross-shaped antennas, if the light is polarized with proper polarization angle direction, it is possible to tune the spectral response intensity by changing the polarization angle. In the case of trimodal cross-shaped antennas, it is a similar situation.

Fig. 10
figure 10

a Absorption cross-section; and b scattering cross-section as a function of the polarization for a partially symmetric cross-shaped ROA with constant arm lengths

Full size image

Finally, the polarization sensitivity of coupled cross-shaped structure from Fig. 4 is also investigated for several polarization angles and the constant shifting value of \({\delta }_{\mathrm{x}}=15\mathrm{ nm}\). Results are shown in Fig. 11 and they demonstrate that the polarization angle of 90° gives the highest enhancement, which is logical for this kind of configuration. Like in the single cross-shaped polarization investigation, there is no resonant shifting.

Fig. 11
figure 11

Field enhancement \(\left|{E}_{\mathrm{TOT}}\right|/\left|{E}_{\mathrm{IN}}\right|\) in the gap center for different values of polarization angle

Full size image

Possible Fabrication Method

For many years in plasmonic engineering, these types of nanostructures have been fabricated by top-down methods such as electron beam lithography (EBL) and focused ion beam method (FIB) [25]. The EBL has already exploited the technique [26], but there is a certain fabrication limit for smaller gaps due to the limited resolution. Also, FIB technique is used to fabricate nanoantennas with the resolution of sub-5-nm nanopores in solid-state membranes [27]. A new method is proposed to fabricate nanodevices with ultra-small gaps [28]. Applying this technique makes it possible to fabricate sub-3-nm ultra-small gaps on solid-state nanopores. The reported nanoantennas could be fabricated using the abovementioned approach to integrate a sub-3-nm gap plasmonic antenna with a solid-state nanopore. The authors used the abovementioned approach to integrate sub-3-nm gap plasmonic antenna with a solid-state nanopore. The goal here is to fabricate an array of coupled gold nanoantennas. The process starts with the substrate with SiN free-standing membrane where for the first patterning step, a resist layer (poly(methyl methacrylate) or PMMA) is spin-coated on the substrate in Fig. 12. By electron beam lithography, the first array is patterned. Afterward, the gold layer of 30 nm is evaporated onto the substrate. The first cross-shaped antenna, necessary for the coupling, is produced by the usual lift-off technique. A similar procedure is used for the second array of single bowtie-shaped antennas, like in STEP 2 in Fig. 12. By STEP 2, the second cross antenna is coupled to the antenna from the first array.

Fig. 12
figure 12

Description of the two-step fabrication process of sub-3-nm gaps integrated with solid-state nanopores modified after [28]

Full size image

Discussion

We have started from the question, could we use plasmon length definition to make bimodal or trimodal cross-shaped nanoantennas? To make the investigation simpler from the number of parameters’ point of view, we chose nanoantennas with constant width and height. Therefore, particle volume as a variable is only influenced by physical length. By keeping particle width constant, we also keep the transversal particle resonance frequency constant (shown in Figs. 2c, 3c, 5b, 7b, 8b, 9b, 10a) where absorption cross-sections were presented). Therefore, we investigate only longitudinal ROA length. Also, for trimodal antenna structures, cross-shaped antennas can be regarded as a combination of rods and L-shaped parts as shown in Fig. 6. We also used vector representations of the current flows in Figs. 2d, 3d, 4d, 5d, and 6d for further analysis. This concept allowed us to use plasmon length basis functions for building multimodal blocks. In the case of the bimodal cross-shaped nanoantennas, we can reconstruct the eigenmodes of the cross-shaped nanoantenna by using plasmon length basis functions of the rod-like nanoantennas. For analyzing single cross-shaped ROAs, we chose two gold nano-bars with lengths of 60 nm and 80 nm. Resonant wavelengths for the 60-nm and 80-nm gold single nanorod ROAs are 656 nm and 725 nm, respectively. For the cross-shaped antenna, it is clear from Fig. 5 that the plasmon length of the cross-shaped ROA defining the low-energy eigenmode is 706 nm, being significantly shorter than the low-energy mode for the 80-nm individual gold nanorod (725 nm). On the other hand, the plasmon length of the cross-shaped ROA defining the high-energy eigenmode is also shorter compared to the 60-nm individual gold nanorod (641 nm < 656 nm). These energy ROA resonances 641 nm and 706 nm correlate to a plasmon length of rods with lengths 57 nm and 75 nm which we numerically confirmed. The obvious blue-shifting of the resonance can be interpreted due to the perturbation of current flows, thus shortening the effective plasmon length of the cross-shaped antenna arms compared to the original rod-shaped ROAs. Furthermore, it is clear that if we keep the length of one arm constant, the resonance along that arm is almost independent of the exact positioning of the second arm (Figs. 7 and 8). Moreover, we have studied trimodal ROAs. As mentioned, we can regard cross-shaped antennas as a combination of rod-like and L-like antennas like in Fig. 6.

Conclusion

This paper introduced two novel bimodal and triple-modal cross-shaped optical nanoantenna designs with wide spectral tunability and high optical cross-sections. The finite element method via the COMSOL software package has been employed to analyze the proposed nanoantenna’s optical cross-sections and field enhancements. The reported coupled cross-shaped design exhibits bimodal resonance behavior with a high field enhancement of 45.9 for the high-energy and 149.4 for the low-energy resonance. These resonances can be controlled by changing the position of the vertical arm. Furthermore, it is shown that a single cross-shaped structure under certain polarization conditions can exhibit trimodal behavior. The reported designs with multiple plasmon resonances and high optical cross-sections pave the road for multiple plasmon resonance devices that can be easily integrated with future nano-optical circuits with multiple operational wavelengths.