Splitting of the Effective Rabi Frequencies for the Coherent Plasmonic Fields in the Semiconductor Quantum Dot–Metal Nanospheres Hybrids

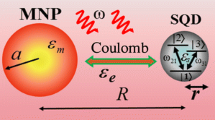
Abstract

Splitting of the effective Rabi frequencies for plasmonic fields when the interaction occurs between semiconductor quantum dot and three metallic nanospheres in the presence of three electromagnetic fields is examined. We study theoretically the role of the dipole–dipole interactions in creating many Multipoles. Then, we split the effective Rabi frequencies into three parts according to the quantitative Multipoles of the plasmonic fields. The density matrix equations are derived for the description of the optical properties of the SQD-MNPs nanosystem. We investigate the influence of each part of the effective Rabi frequencies and compare them with each other individually. The three parts of the effective Rabi frequency for the probe field are affected by changing the angles, the strong probe field and other parameters for the hybrid system.

Introduction

There are a lot of efforts have been made to discuss the semiconductor quantum dot (SQD), metallic nanoparticles (MNP), and the effects of their interaction with optical fields, where it is useful to many contemporary scientific disciplines. It can form a hybrid quantum system which is to exhibit a variety of novel optical properties that are required in the field of optoelectronics [1, 2]. It is shown that the quantum coherence effects in a QD–MNP system can form a barrier (quantum cage) that spatially confines the spatial extent of the coherently normalized plasmonic field of the MNP [3]. Artuso et al. [4] studied how MNP geometry can be used to tailor local fields, coupling, and dynamics of the hybrid structures and found that the response of the system could be tailored by engineering a metal nanoparticle shape and the placement of SQDs on the MNP to control the individual local near fields that couple the MNPs and SQDs. The population dynamics and the absorption properties of a hybrid nanosystem are investigated, to demonstrate how it depends on the collective molecular states of the QD–MNP system [5]. Anomalous Dipole–Dipole Interaction in an Ensemble of Quantum Emitters and Metallic Nanoparticle Hybrids is discovered by [6]. The coherent transfer of excitonic populations in a semiconductor quantum dot (SQD) is modulated by the surface plasmon of a metallic nanoparticle (MNP) which is investigated in [7]. The potential for controlled population inversion in a coupled system comprised of a semiconductor quantum dot and a metal nanoparticle are analyzed [8]. A theoretical study of the two-photon Rabi oscillations of a heterodimer comprising a semiconductor quantum dot and a metal nanosphere is discovered by [9]. A theory for the photoluminescence of dimer nanohybrids and trimer nanohybrids using the density matrix method is developed [10]. A theory for photoluminescence quenching and plasmonic properties in hybrid nanosystems made from three nanosystems such as quantum emitters, metallic nanoparticles, and graphene is developed [11,12,13]. Effect of dipole–dipole interactions on the one-photon and two-photon photoluminescence in an ensemble of quantum dots doped in a polymer matrix is discussed in [14]. The study of the exciton-plasmons system offers many parameters that can be used to control the optical response of the system [15]. It is found that the multipole treatment of the interaction is crucial for the understanding of strongly interacting exciton-plasmon nanosystems [16]. The preparation of quantum states with a defined spin in a hybrid system consisting of a p-doped semiconductor quantum dot (QD) coupled to a metallic nanoparticle is analyzed by [17]. The transport properties of a single plasmon interacting with a hybrid system composed of a semiconductor quantum dot (SQD) and a metal nanoparticle (MNP) coupled to a one-dimensional surface plasmonic waveguide are investigated [18]. Anomalous Photoluminescence Quenching is produced [19]. Jiang et al. [20] demonstrated theoretically a novel double-hole structure to improve the single-emitter emission rate, and the numerical investigations show that the structure possesses a large local electric field. The nonlinear refractive index of a sample including hybrid molecules composed of AuNPs and SiQDs was investigated theoretically and experimentally [21]. Dipole–Dipole Interaction in Two-Photon Spectroscopy of Metallic Nanohybrids are discussed in [22]. A theory of the quantum yield for plasmonic nanowaveguide where the cladding layer is made of an ensemble of quantum dots and the core layer consists of an ensemble of metallic nanoparticles is developed [23]. Thin bilayer films containing Au and CuS nanoparticles, with surface plasmon resonances, exhibited enhanced third harmonic generation over the individual films as a result of dipole–dipole incoherent interactions between the nanoparticles [24]. The optical properties of a hybrid structure consisting of a metal nanoparticle (MNP) and an asymmetric double semiconductor quantum dot (SQD) molecule, which are coupled together, via long-range Coulomb interaction are studied theoretically [25]. In [26] the influence of the strength of the plasmon-exciton dipole interaction for probe field and control field for different parameters of the hybrid SQD-MNPs nanosystem is studied.

In this paper, the present scheme is based on a coupled semiconductor quantum dot (SQD) and metal nanospheres (MNSs) nanosystem in the presence of the three electromagnetic fields. The SQD is taken as a four-level V-type system in which distinct excitonic transitions occur. We derive the polarization of the three electromagnetic fields which induce dipole moments in the three metal nanospheres and semiconductor quantum dot, where these structures interact with each other via the Multipoles interaction. The main focus and motivation of this paper is splitting the effective Rabi frequencies for coherent plasmonic fields into three parts, studying the influence of each part individually, which has a significant effect and comparing the parts with each other. This work is organized as follows: in the “Theoretical Model and Formalism” section, we describe the SQD-MNSs nanosystem, derive the density matrix equations describing the dynamics of the system and obtain the form of the three parts of the effective Rabi frequencies for the hybrid nanosystem. In the “Numerical Results and Discussion” section, we discuss our numerical results. Finally, we present our conclusions in the “Conclusion” section.

Theoretical Model and Formalism

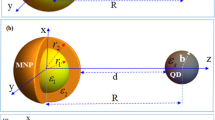
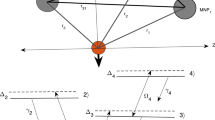
We consider a hybrid nanosystem that consists of a single semiconductor quantum dot (SQD) and three metallic nanospheres (denoted by $MNS_{m}$) of the same radii R. The semiconductor quantum dot (SQD) and the environment surrounding the system have a dielectric constant $\varepsilon _{s}$ and $\varepsilon _{b}$ respectively. We suppose that the SQD is characterized by a four-level $V-type$ atomic system designated by $\left| 1\right\rangle$,  $\left| 2\right\rangle$, $\left| 3\right\rangle$, and $\left| 4\right\rangle$, where the state $\left| 1\right\rangle$ is the ground state. The center-to-center distance between the SQD and the three metallic nanospheres have the same distance (denoted by $r_{m}$), while the center-to-center distance between the three $MNS_{m}$ is $d_{nm}$ ($n, \, m=1,2,3$, $n\ne m$), respectively. All these centers are being in two dimensions (2D), plane (ZOX), where the center of the SQD is situated at the origin O. $\theta _{m}$ ($m=1,2,3$) is the angle confined between the Z-axis and $r_{m}$ for the three $MNS_{m}$ respectively, as illustrated in Fig. 1. The excitonic transitions for the SQD $\mid 1\rangle \iff$ $\mid 2\rangle$, $\mid 1\rangle \iff$ $\mid 3\rangle$ and $\mid 3\rangle \iff$ $\mid 4\rangle$ are characterized by the transition frequencies $\omega _{21}$, $\omega _{31}$, and $\omega _{43}$, where $\omega _{ij}=\omega _{i}-\omega _{j}$, $i\ne j=1,2,3,4$. The system interacts with three electromagnetic fields $\mathbf{E}_{n}(t)=\mathbf{E}_{n}e^{i\nu _{n}t}$ with frequency $\nu _{n}$ ($n=1,2,3$), respectively. These fields create excitons in the semiconductor quantum dot and surface plasmon polaritons (SPP) in the three metallic nanospheres. The excitons and SPP produce dipole electric fields which interact with each other via dipole–dipole interaction (DDI). In this problem, we suppose the three metallic nanospheres are identical. Each $MNS_{m}$ is treated as a classical particle with a dielectric function denoted by $\varepsilon _{m}(\omega )$, according to the generalized Drude theory, it can be written as follows [27]: $\epsilon _{m}(\omega )=(1-\frac{\omega _{p}^{2}}{\omega ^{2}\mathop{+}i\gamma _{b}\omega })$, where $\omega _{p}$ is the plasma frequency for $MNS_{m}$ and $\gamma _{b}$ is the damping constant. The Hamiltonian ($H_{SQD}$) is the Hamiltonian of the interaction of the SQD with $MNS_{m}$ of the hybrid nanosystem which can be expressed as:

$$\begin{aligned} H_{SQD}=-\varvec{\mu }_{21}\cdot \mathbf{E}_{SQD}^{1}\ \sigma _{21}-\varvec{\mu }_{31}\cdot \mathbf{E}_{SQD}^{2}\ \sigma _{31}-\varvec{\mu }_{43}\cdot \mathbf{E}_{SQD}^{3}\ \sigma _{43}+H.C. \end{aligned}$$

(1)

where the operator $\sigma _{ij}=\left| i\right\rangle \left\langle j\right|$, ($i,j=1,2,3,4$) and $\mathbf {\mu }_{ij}$ is the dipole moment of the SQD associated with atomic transition $\left\langle i\right| \longleftrightarrow \left\langle j\right|$. $\mathbf{E}_{SQD}^{n}$ (for $n=1,2,3$) represent the fields that are falling on the SQD due to the contributions of the system components induced by the electromagnetic fields $\mathbf{E}_{n}$. So $\mathbf{E}_{SQD}^{n}$ can be written as: $\mathbf{E}_{SQD}^{n}=\frac{1}{\varepsilon _{e\,f\,f_{s}}}\left[ \mathbf{E}_{n}\mathbf {+}\sum _{m\mathop{=}1}^{3}\mathbf{E}_{SQD}^{n,m}\right]$, Where $\varepsilon _{e\,f\,fs\text { }}=(\varepsilon _{s}+2\varepsilon _{b})/3\varepsilon _{b}$. The fields $\mathbf{E}_{SQD}^{n,m}$ are produced by three $MNS_{m}$ on SQD under the effect of applied field $\mathbf{E}_{n}$ and it can be calculated as follows [28]: $\mathbf{E}_{SQD}^{n,m}=\frac{1}{4\pi \varepsilon _{b}\varepsilon _{0}r_{m}^{3}}[3(\mathbf{P}_{n,m}\varvec{\cdot} \hat{\varvec{r}}_{m})\hat{\varvec{r}}_{m}-\mathbf{P}_{n,m}]$. The vector dipoles $\mathbf{P}_{n,m}$ originate from the charge induced on the surface of the three $MNS_{m}$ and direct in the Z-axis where is given by: $\mathbf{P}_{n,m}=\alpha \mathbf{E}_{n,m}$, $\alpha =4\pi \varepsilon _{b}\varepsilon _{0}R^{3}\gamma$, $\gamma =\frac{\varepsilon _{m}(\omega )\mathop{-}\varepsilon _{b}}{\varepsilon _{m}(\omega )\mathop{+}2\varepsilon _{b}}$, and the unit vector along the vector $\mathbf{r}_{m}$ is given by: $\hat{\varvec{r}}_{m}=\cos \theta _{m}$ $\hat{\varvec{z}+}\sin \theta _{m\text { }}\hat{\varvec{x}}$. $\mathbf{E}_{n,m}$ is the resultant of the fields falls on the $MNS_{m}$ and is given by: $\mathbf{E}_{n,m}=\frac{1}{\varepsilon _{e\,f\,f_{m}}}\left( \mathbf{E}_{n}+\mathbf{E}_{n,m}^{SQD}+\mathbf{E}_{n,m}^{n,l}+\mathbf{E}_{n,m}^{n,k}\right)$, Where $\varepsilon _{e\,f\,f_{m}}=\left( \frac{\varepsilon _{m}(\omega )+2\varepsilon _{b}}{3\varepsilon _{b}}\right)$ is the effective screening of the three ($MNS_{m}$). The electric dipole field $\mathbf{E}_{n,m}^{SQD}$ is due to dipole-dipole interaction from SQD on each one of the $MNS_{m}$, which is given by: $\mathbf{E}_{n,m}^{SQD}=\frac{1}{4\pi \varepsilon _{b}\varepsilon _{0}r_{m}^{3}}[3(\mathbf{P}_{n,SQD}\cdot \hat{\varvec{r}}_{m})\hat{\varvec{r}}_{m}-\mathbf{P}_{n,SQD}]$, $\mathbf{P}_{n,SQD}$ is the dipole moment of SQD for the field $\mathbf{E}_{n}$ and given by: $\mathbf{P}_{1,SQD}=(\mu _{12}\rho _{12}+H.C.)\hat{\varvec{x}}$, $\mathbf{P}_{2,SQD}=(\mu _{13}\rho _{13}+H.C.)\hat{\varvec{x}}$,$\mathbf{P}_{3,SQD}=(\mu _{34}\rho _{34}+H.C.)\hat{\varvec{x}}$. The dipole field $\mathbf{E}_{n,m}^{n,l}$ ($\mathbf{E}_{n,m}^{n,k}$) is due to the dipole-dipole interaction between the metallic nanospheres $MNS_{l}$ ($MNS_{k}$) and $MNS_{m}$ under the electromagnetic field $\mathbf{E}_{n}$. It is given by: $\mathbf{E}_{n,m}^{n,l}=\frac{1}{4\pi \varepsilon _{0}\varepsilon _{b}\left| \mathbf{d}_{lm}\right| ^{3}\text { }}[3(\mathbf{P}_{n,l}\varvec{\cdot } \hat{\varvec{d}}_{lm}) \hat{\varvec{d}}_{lm}-\mathbf{P}_{n,l}]$, where, $\hat{\varvec{d}}_{lm}$ is the unit vector along the vector directed from center of $MNS_{l}$ to center of $MNS_{m}$ as illustrated in Fig. 1. I.e., we can get: $\mathbf{d}_{lm}=d_{lm}^{x}$ $\hat{\varvec{x}}+d_{lm}^{z}$  $\hat{\varvec{z}}$, $d_{lm}^{x}=(r_{m}\sin \theta _{m}-r_{l}\sin \theta _{l})$, $d_{lm}^{z}=(r_{m}\cos \theta _{m}-r_{l}\cos \theta _{l})$. The unit vectors $\hat{\varvec{d}}_{12}$, $\hat{\varvec{d}}_{23}$ and $\hat{\varvec{d}}_{31}$ are directed from $MNS_{1}$to $MNS_{2}$, $MNS_{2}$ to $MNS_{3}$ and $MNS_{3}$ to $MNS_{1}$, respectively. For simplicity, we denoted them by $\hat{\varvec{d}}_{1}$, $\hat{\varvec{d}}_{2}$, and $\hat{\varvec{d}}_{3}$, respectively. To obtain the equations for $\mathbf{E}_{n,m}^{n,k},\mathbf{d}_{km},d_{km}^{x}$ and $d_{km}^{z}$, replace l with k in the above equations. We can obtain an expression for $\mathbf{E}_{SQD}^{n}$ with doing recurrence of the above steps to taking many Multipoles, up to minus of tenth order $(d_{m})^{-10}$. Then the total Hamiltonian of the SQD is expressed as:

$$\begin{aligned} H_{TSQD}\text { }= \hslash \sum _{j\mathop{=}1}^{4}\omega _{j}\sigma _{jj}-\hslash \text { }\Omega _{1}^{e\,f\,f}\sigma _{12}-\hslash \text { }\Omega _{2}^{e\,f\,f}\sigma _{13}-\hslash \text { }\Omega _{3}^{e\,f\,f}\sigma _{34}+H.C. \end{aligned}$$

(2)

where the direction of the electromagnetic fields ($E_{n}$) is along the X-axis. We notice that the effect of the term, which has very small amount of the effective Rabi frequencies, does not appear, when we take the all terms of the effective Rabi frequencies. So, we can put the effective Rabi frequency ($\Omega _{n}^{e\,f\,f}$) for the coherent plasmonic fields in the form of the three parts depending on the rank of distance for Multipoles between the three $MNS_{m}$ (i.e., $d_{1},d_{2},d_{3}$), then we take: $\Omega _{n}^{e\,f\,f}=(\Omega _{n1}^{e\,f\,f}+\Omega _{n2}^{e\,f\,f}+\Omega _{n3}^{e\,f\,f})$, and $\Omega _{1}=\frac{\mu _{12}E_{1}}{\hslash }$, $\Omega _{2}=\frac{\mu _{13}E_{2}}{\hslash }$, $\Omega _{3}=\frac{\mu _{34}E_{3}}{\hslash }$, $B_{m}=\frac{(3\sin {}^{2}\theta _{m}\mathop{-}1)}{4\pi \varepsilon _{b}\varepsilon _{0}}$, $C_{m}=\frac{\left( 3\sin \theta _{m}\cos \theta _{m}\right) }{4\pi \varepsilon _{b}\varepsilon _{0}}$, $L_{lm}=\frac{3d_{lm}^{z}d_{lm}^{x}}{4\pi \varepsilon _{o}\varepsilon _{b}\text { }}$, so we have:

$$\begin{aligned} \Omega _{n1}^{e\,f\,f}=\frac{\Omega _{n}}{\varepsilon _{e\,f\,f\,s}}+\left( \frac{\alpha }{\varepsilon _{e\,f\,f_{m}}}\right) \left[ \frac{\Omega _{n}}{\varepsilon _{e\,f\,f\,s}r^{3}}\sum _{m\mathop{=}1}^{3}C_{m}+\frac{\mu _{jk}^{2}\rho _{jk}}{\text { }\hslash \varepsilon _{e\,f\,f\,s}r^{6}}\sum _{m\mathop{=}1}^{3}B_{m}C_{m}\right] \end{aligned}$$

(3)

$$\begin{aligned} \Omega _{n2}^{e\,f\,f}= & \ \left( \frac{\alpha }{\varepsilon _{e\,f\,f_{m}}}\right) ^{2}\left\{ \frac{\Omega _{n}}{\varepsilon _{e\,f\,f\,s}r^{3}}\left[ \frac{L_{1}}{d_{1}^{5}}(C_{1}+C_{2})\right.\right.\\ &+ \left.\frac{L_{2}}{d_{2}^{5}}(C_{2}+C_{3})+\frac{L_{3}}{d_{3}^{5}}(C_{3}+C_{1})\right] \\ & +\frac{\mu _{jk}^{2}\rho _{jk}}{\hslash \varepsilon _{e\,f\,f\,s}r^{6}}\left[ \frac{L_{1}}{d_{1}^{5}}(C_{1}B_{2}+C_{2}B_{1})\right.\\&+\left.\frac{L_{2}}{d_{2}^{5}}(C_{2}B_{3}+C_{3}B_{2})\right. \left. \left. +\frac{L_{3}}{d_{3}^{5}}(C_{3}B_{1}+C_{1}B_{3}\right] \right\} \end{aligned}$$

(4)

and $\Omega _{n3}^{e\,f\,f}=(\Omega _{n31}^{e\,f\,f}+\Omega _{n32}^{e\,f\,f})$, where

$$\begin{aligned} \Omega _{n31}^{e\,f\,f}= & \left( \frac{\alpha }{\varepsilon _{e\,f\,f_{m}}}\right) ^{3}\frac{\Omega _{n}}{\varepsilon _{e\,f\,f\,s}r^{3}}\left\{ C_{1}\left[ \left( \frac{L_{1}}{d_{1}^{5}}\right) ^{2}\right.\right. \\&+ \left.\left.\left( \frac{L_{3}}{d_{3}^{5}}\right) ^{2}+\left( \frac{L_{1}L_{2}}{d_{1}^{5}d_{2}^{5}}\right) +\left( \frac{L_{2}L_{3}}{d_{2}^{5}d_{3}^{5}}\right) \right] \right. \\{} & {} +C_{2}\text { }\left[ \left( \frac{L_{1}}{d_{1}^{5}}\right) ^{2}+\left( \frac{L_{2}}{d_{2}^{5}}\right) ^{2}+\left( \frac{L_{1}L_{3}}{d_{1}^{5}d_{3}^{5}}\right)\right. \\&+\left.\left.\left( \frac{L_{2}L_{3}}{d_{2}^{5}d_{3}^{5}}\right) \right] + C_{3}\text { }\left[ \left( \frac{L_{2}}{d_{2}^{5}}\right) ^{2}+\left( \frac{L_{3}}{d_{3}^{5}}\right) ^{2}\right.\right.\\&+\left.\left.\left( \frac{L_{1}L_{3}}{d_{1}^{5}d_{3}^{5}}\right) +\left( \frac{L_{1}L_{2}}{d_{1}^{5}d_{2}^{5}}\right) \right] \right\} \end{aligned}$$

(5)

$$\begin{aligned} \Omega _{n32}^{e\,f\,f}= & {} \left( \frac{\alpha }{\varepsilon _{e\,f\,f_{m}}}\right) ^{3}\frac{\mu _{jk}^{2}\rho _{jk}}{\text { }\hslash \varepsilon _{e\,f\,f\,s}r^{6}}\left\{ C_{1}\left[ \left( \frac{L_{1}}{d_{1}^{5}}\right) ^{2}B_{1}\right.\right.\\&+\left.\left.\left( \frac{L_{3}}{d_{3}^{5}}\right) ^{2}B_{1}+\left( \frac{L_{2}L_{3}}{d_{2}^{5}d_{3}^{5}}\right) B_{2}+\left( \frac{L_{1}L_{2}}{d_{1}^{5}d_{2}^{5}}\right) B_{3}\right] \right. \\{} & {} +C_{2}\left[ \left( \frac{L_{1}}{d_{1}^{5}}\right) ^{2}B_{2}+\left( \frac{L_{2}}{d_{2}^{5}}\right) ^{2}B_{2}+\left( \frac{L_{1}L_{3}}{d_{1}^{5}d_{3}^{5}}\right) B_{3}\right.\\&+\left.\left( \frac{L_{2}L_{3}}{d_{2}^{5}d_{3}^{5}}\right) B_{1}\right] +\left. C_{3}\text { }\left[ \left( \frac{L_{2}}{d_{2}^{5}}\right) ^{2}+\left( \frac{L_{3}}{d_{3}^{5}}\right) ^{2}\right.\right.\\&+\left.\left.\left( \frac{L_{1}L_{3}}{d_{1}^{5}d_{3}^{5}}\right) +\left( \frac{L_{1}L_{2}}{d_{1}^{5}d_{2}^{5}}\right) \right] \right\} \end{aligned}$$

(6)

where, $j,k=1,2$ & 1,3 & 3,4 for $n=1$ & 2& 3, respectively and $m=1,2,3$. Putting $L_{12}=L_{1}$, $L_{23}=L_{2}$, $L_{13}=L_{3}$, and $r_{1}=r_{2}=r_{3}=r$ in the above equations. We notice from the equation of the effective Rabi frequency, the rank of distance $d_{m}$ increases. The first part of the effective Rabi frequency (FPERF) $\ \Omega _{n1}^{e\,f\,f}$ have the terms which contain ($d_{m}^{0}$). The second part of the effective Rabi frequency (SPERF) $\Omega _{n2}^{e\,f\,f}$ have the terms which contain ($d_{m}^{-5}$). The third part of the effective Rabi frequency (TPERF) $\Omega _{n3}^{e\,f\,f}$ have the terms which contain $(d_{m}^{-5})^{2}$ and [$d_{l}^{-5}d_{m}^{-5}$], so we can put it in the form $(d_{m}^{-5})^{n}$ and [$d_{l}^{-5}d_{m}^{-5}$]$^{n}$ ($n=0,1,2$) for the three parts. If we have more Multipoles so the effective Rabi frequencies can be divided into many more than three parts and the rank of distance becomes n $\succ 2$. We can study the influence of each part of the effective Rabi frequencies in the hybrid nanosystem, and compare it with other parts. The behavior of the $\mathrm{Im}\ \Omega _{2}^{e\,f\,f}$ become similar to $\mathrm{Im}\ \Omega _{21}^{e\,f\,f}$ only (i.e., the terms which contain $d_{m}^{0}$). It is observed that FPERF is proportional to $(\frac{\alpha }{\varepsilon _{e\,f\,f_{m}}})$, SPERF proportional to $(\frac{\alpha }{\varepsilon _{e\,f\,f_{m}}})^{2}$ and TPERF proportional to $(\frac{\alpha }{\varepsilon _{e\,f\,f_{m}}})^{3}$, it’s mean when increasing the rank of distance, it is increased rank of $(\frac{\alpha }{\varepsilon _{e\,f\,f_{m}}})$ ($(\frac{\alpha }{\varepsilon _{e\,f\,f_{m}}})^{n}$, $n=1,2,3$).

Fig. 1

A schematic diagram of the SQD and three $MNS_{m}$ (hybrid nanosystem). The SQD has four-level V-type configuration coupling with three electromagnetic fields

Under the electric dipole approximation and the rotating-wave approximation [29], we define the equation of motion of density matrix elements (the master equation) of the SQD coupled to the three $MNS_{m}$, as follows:

$$\begin{aligned} \frac{d}{dt}\rho _{11}=&\ 2\gamma _{1}\rho _{22}+2\gamma _{2}\rho _{33}+i\text { }\Omega _{1}^{e\,f\,f*}\rho _{21}\\&-i\text { }\Omega _{1}^{e\,f\,f}\rho _{12}+i\text { }\Omega _{2}^{e\,f\,f*}\rho _{31}-i\text { }\Omega _{2}^{e\,f\,f}\rho _{13}\text {,} \end{aligned}$$

(7)

$$\begin{aligned} \frac{d}{dt}\rho _{22}=-2\gamma _{1}\rho _{22}+i\text { }\Omega _{1}^{e\,f\,f}\rho _{12}-i\text { }\Omega _{1}^{e\,f\,f*}\rho _{21}\text {,} \end{aligned}$$

(8)

$$\begin{aligned} \frac{d}{dt}\rho _{44}=-2\gamma _{3}\rho _{44}+i\text { }\Omega _{3}^{e\,f\,f}\rho _{34}-i\text { }\Omega _{3}^{e\,f\,f*}\rho _{43}\text {,} \end{aligned}$$

(9)

$$\begin{aligned} \frac{d}{dt}\rho _{21}=-\beta _{1}\rho _{21}-i\text { }\Omega _{1}^{e\,f\,f}(\rho _{22}-\rho _{11})-i\text { }\Omega _{2}^{e\,f\,f}\rho _{23}\text {,} \end{aligned}$$

(10)

$$\begin{aligned} \frac{d}{dt}\rho _{31}=-\beta _{2}\rho _{31}-i\text { }\Omega _{1}^{e\,f\,f}\rho _{32}-i\text { }\Omega _{2}^{e\,f\,f}(\rho _{33}-\rho _{11})+i\text { }\Omega _{3}^{e\,f\,f*}\rho _{41}\text {,} \end{aligned}$$

(11)

$$\begin{aligned} \frac{d}{dt}\rho _{41}=-\beta _{3}\rho _{41}-i\text { }\Omega _{1}^{e\,f\,f}\rho _{42}-i\text { }\Omega _{2}^{e\,f\,f}\rho _{43}+i\text { }\Omega _{3}^{e\,f\,f}\rho _{31}\text {,} \end{aligned}$$

(12)

$$\begin{aligned} \frac{d}{dt}\rho _{32}=-\beta _{4}\rho _{32}-i\text { }\Omega _{1}^{e\,f\,f*}\rho _{31}+i\text { }\Omega _{2}^{e\,f\,f}\rho _{12}+i\text { }\Omega _{3}^{e\,f\,f*}\rho _{42}\text {,} \end{aligned}$$

(13)

$$\begin{aligned} \frac{d}{dt}\rho _{42}=-\beta _{5}\rho _{42}-i\text { }\Omega _{1}^{e\,f\,f*}\rho _{41}+i\text { }\Omega _{3}^{e\,f\,f}\rho _{32}\text {,} \end{aligned}$$

(14)

$$\begin{aligned} \frac{d}{dt}\rho _{43}=-\beta _{6}\rho _{43}-i\text { }\Omega _{2}^{e\,f\,f*}\rho _{41}-i\text { }\Omega _{3}^{e\,f\,f}(\rho _{44}-\rho _{33})\text {.} \end{aligned}$$

(15)

Where the density matrix elements have the identity property $\sum _{i\mathop{=}1}^{i\mathop{=}4}\rho _{ii}=1$, while $\beta _{1}=\gamma _{1}+i\Delta _{1}$, $\beta _{2}=\gamma _{2}+i\Delta _{2}$, $\beta _{3}=\gamma _{3}+i(\Delta _{2}+\Delta _{3})$, $\beta _{4}=(\gamma _{1}+\gamma _{2})+i(\Delta _{2}-\Delta _{1})$, $\beta _{5}=(\gamma _{1}+\gamma _{3})+i(\Delta _{2}+\Delta _{3}-\Delta _{1})$, $\beta _{6}=(\gamma _{2}+\gamma _{3})+i\Delta _{3}$. Where $\gamma _{1},\gamma _{2}$ and $\gamma _{3}$ represent the radiative decay rates of the excitation states $\left| 2\right\rangle$, $\left| 3\right\rangle$ and $\left| 4\right\rangle$ due to spontaneous emission respectively. $\Delta _{1}=\omega _{21}-\nu _{1},$ $\Delta _{2}=\omega _{31}-\nu _{2}$ and $\Delta _{3}=\omega _{43}-\nu _{3}$ are the frequency detuning for the three fields.

Numerical Results and Discussion

In this section, we discuss the role of the three parts of the effective Rabi frequency $(\Omega _{2}^{e\,f\,f}$) and its influence in the hybrid nanosystem. The three $MNS_{m}$ are silver (Ag) with plasma frequency and relaxation damping 9.02eV and 0.026eV, respectively [30,31,32]. The probe field $E_{2}$ is taken as the strong field to find out its effect on the hybrid nanosystem. The parameters of hybrid nanosystem are taken as $R=6$ nm, $\mu _{12}=\mu _{13}=\mu _{34}=1.2$ e nm, $\gamma _{1}=0.02$ $ns^{-1}$, $\gamma _{2}=1$ $ns^{-1}$, $\gamma _{3}=0.01$ $ns^{-1}$, $\varepsilon _{s}=2$, $\varepsilon _{b}=2$, $\theta _{2}=5\pi /6$, $\theta _{3}=3\pi /2$ and $r=12$ nm. We have $\Omega _{1}=4$ $ns^{-1}$, $\Omega _{2}=1ns^{-1}$ and $\Omega _{3}=8$ $ns^{-1}$ and $\Delta _{1}=\Delta _{3}=\Delta =0$. Other changes of parameters are indicated in the figure captions and described in what follows.

Figure 2 demonstrates the spectra of the parts of $\mathrm{Im}\ \Omega _{2}^{e\,f\,f}$ for different values of r (10, 12)nm at $\Delta =1$. Figure 2$\text{a}_{1}$, $\text{a}_{2}$ and $\text{a}_{3}$ are taken for $\mathrm{Im}\ \Omega _{21}^{e\,f\,f}$, $\mathrm{Im}\ \Omega _{22}^{e\,f\,f}$ and $\mathrm{Im}\ \Omega _{23}^{e\,f\,f}$ respectively at $\theta _{1}=\pi /3$ and Fig. 2$\text{b}_{1}$, $\text{b}_{2}$, and $\text{b}_{3}$ are taken for $\mathrm{Im}\ \Omega _{21}^{e\,f\,f}$, $\mathrm{Im}\ \Omega _{22}^{e\,f\,f}$, and $\mathrm{Im}\ \Omega _{23}^{e\,f\,f}$ respectively at $\theta _{1}=\pi /6$. The asymmetric shape is shown in this figure due to the strong interaction between the Multipoles of fields at $\Delta =1$. We notice when the distance r increase, the absolute value of the spectra of $\mathrm{Im}\ \Omega _{2}^{e\,f\,f}$ decreases resulting a weak interaction. Figure 2$\text{a}_{1}$ shows three holes in negative values of the spectrum $\mathrm{Im}\ \Omega _{21}^{e\,f\,f}$. Figure 2$\text{a}_{2}$ and $\text{a}_{3}$ illustrate positive values of the spectrum $\mathrm{Im}\ \Omega _{22}^{e\,f\,f}$ and $\mathrm{Im}\ \Omega _{23}^{e\,f\,f}$ respectively. We notice, when $\theta _{1}=\pi /3$, the distances between the three nanospheres $\text{d}_{1}$, $\text{d}_{2}$, and $\text{d}_{3}$ are different. But at $\theta _{1}=\pi /6$, the distances between the three nanospheres $\text{d}_{1}$, $\text{d}_{2}$, and $\text{d}_{3}$ are equal. Then when r increases, $\text{d}_{1}$, $\text{d}_{2}$, and $\text{d}_{3}$ increase (showing from numerical results by using Matlab). We conclude that when the angle between $r_{i}$ and $r_{j}$ ($i\ne j,$ i, $j=1,2,3$ ) equal $2\pi /3$, the distances $\text{d}_{1}$, $\text{d}_{2}$, and $\text{d}_{3}$ are equal. Then the interaction between the Multipoles is strongly effective when equal the distance between the three $MNS_{m}$ and SQD, also the distance between each of the three $MNS_{m}$. So, the splitting of the $\Omega _{n}^{e\,f\,f}$ has an important role in the clarification of the strong interaction between the Multipoles of $SQD-MNS_{m}$.

Fig. 2

The spectra of the parts of $\mathrm{Im}\ \Omega _{2}^{e\,f\,f}$ as a function of $\Delta _{2}$, at $\Delta =1$. $\mathbf{a}_{\mathbf{1}},\ \mathbf{a}_{\mathbf{2}}$ and $\mathbf{a}_{\mathbf{3}}$ for $\mathrm{Im}\ \Omega _{21}^{e\,f\,f}$, $\mathrm{Im}\ \Omega _{22}^{e\,f\,f}$ and $\mathrm{Im}\ \Omega _{23}^{e\,f\,f}$ respectively at $\theta _{1}=\pi /3$. $\mathbf{b}_{\mathbf{1}},\mathbf{b}_{\mathbf{2}}$ and $\mathbf{b}_{\mathbf{3}}$ for $\mathrm{Im}\ \Omega _{21}^{e\,f\,f}$, $\mathrm{Im}\ \Omega _{22}^{e\,f\,f}$ and $\mathrm{Im}\ \Omega _{23}^{e\,f\,f}$ respectively at $\theta _{1}=\pi /6$. (red curve) for $r=12\ nm$ and (blue curve) for $r =10\ nm$

Figure 3 illustrates the spectra of the parts of $\mathrm{Im}\ \Omega _{2}^{e\,f\,f}$ as a function of $\Delta _{2}$ when the strong probe field have different values ($\Omega _{2}=(1$, $4)ns^{-1}$) at $\theta _{1}=\pi /3$. Figure 3$\text{a}_{1}$, $\text{a}_{2}$, and $\text{a}_{3}$ are taken, for $\mathrm{Im}\ \Omega _{21}^{e\,f\,f}$, $\mathrm{Im}\ \Omega _{22}^{e\,f\,f}$, and $\mathrm{Im}\ \Omega _{23}^{e\,f\,f}$ respectively when $\Omega _{1}=$ $\Omega _{3}=4$ $ns^{-1}$. Figure 3$\text{b}_{1}$, $\text{b}_{2}$, and $\text{b}_{3}$ are taken for $\mathrm{Im}\ \Omega _{21}^{e\,f\,f}$, $\mathrm{Im}\ \Omega _{22}^{e\,f\,f}$ and $\mathrm{Im}\ \Omega _{23}^{e\,f\,f}$ respectively when $\Omega _{1}=4$ $ns^{-1}$, $\Omega _{3}=20$ $ns^{-1}$. The three parts of $\mathrm{Im}\ \Omega _{2}^{e\,f\,f}$ are affected by changing the strong probe field. Figure 3$\text{a}_{1}$, $\text{a}_{2}$ and $\text{a}_{3}$ show two small peaks on the two sides and a sharp peak in the middle of $\Delta _{2}$ when $\Omega _{2}=1$, while at $\Omega _{2}=4$, the sharp peak decrease rapidly. Figure 3$\text{b}_{1}$, $\text{b}_{2}$, and $\text{b}_{3}$ appear broad window having two holes at $\Omega _{2}=1$, when increasing $\Omega _{2}$ ($=4$) the two holes disappear from the window and the spectrum shows two peaks on the two sides of $\Delta _{2}$.

Fig. 3

The spectra of the parts of $\mathrm{Im}\ \Omega _{2}^{e\,f\,f}$ as a function of $\Delta _{2}$ at $\theta _{1}=\pi /3$. $\mathbf{a}_{\mathbf{1}},\mathbf{a}_{\mathbf{2}}$ and $\mathbf{a}_{\mathbf{3}}$ for $\mathrm{Im}\ \Omega _{21}^{e\,f\,f}$, $\mathrm{Im}\ \Omega _{22}^{e\,f\,f}$ and $\mathrm{Im}\ \Omega _{23}^{e\,f\,f}$ respectively at $\Omega _{1}=$ $\Omega _{3}=4$ $ns^{-1}$. $\mathbf{b}_{\mathbf{1}},\mathbf{b}_{\mathbf{2}}$ and $\mathbf{b}_{\mathbf{3}}$ for $\mathrm{Im}\ \Omega _{21}^{e\,f\,f\,c}$, $\mathrm{Im}\ \Omega _{22}^{e\,f\,f\,c}$ and $\mathrm{Im}\ \Omega _{23}^{e\,f\,f\,c}$ respectively at $\Omega _{1}=4$ $ns^{-1}$, $\Omega _{3}=20$ $ns^{-1}$. (blue curve) for $\Omega _{2}=1$ $ns^{-1}$, (red curve) for $\Omega _{2}=4$ $ns^{-1}$

Figure 4 illustrates the spectra of the parts of $\mathrm{Im}\ \Omega _{2}^{e\,f\,f}$ for different values of $\theta _{1}(\pi /9$, $\pi /5$, $\pi /4)$. Figure 4$\text{a}_{{1}}$, $\text{a}_{{2}}$, and $\text{a}_{{3}}$ are taken for $\mathrm{Im}\ \Omega _{21}^{e\,f\,f}$, $\mathrm{Im}\ \Omega _{22}^{e\,f\,f}$ and $\mathrm{Im}\ \Omega _{23}^{e\,f\,f}$ respectively at $\theta _{2}=5\pi /6$ and Fig. 4$\text{b}_{1}$, $\text{b}_{2}$ and $\text{b}_{3}$ are taken for $\mathrm{Im}\ \Omega _{21}^{e\,f\,f}$, $\mathrm{Im}\ \Omega _{22}^{e\,f\,f}$, and $\mathrm{Im}\ \Omega _{23}^{e\,f\,f}$ respectively at $\theta _{2}=2\pi /3$. We notice the parts of $\mathrm{Im}\ \Omega _{2}^{e\,f\,f}$ have three holes in the window of the spectrum, for every value of $\theta _{1}$ the behavior of the spectrum in each part of the $\mathrm{Im}\ \Omega _{2}^{e\,f\,f}$ is different according to the different Multipole interaction. We conclude that the behavior of the three parts of $\mathrm{Im}\ \Omega _{2}^{e\,f\,f}$ differ from one to other according to the value of $\theta _{1}$and $\theta _{2}$, so angles play an important role in modifying the three parts of $\mathrm{Im}\ \Omega _{2}^{e\,f\,f}$ which leading to the strong interaction between $SQD-MNS_{m}$.

Fig. 4

The spectra of the parts of $\mathrm{Im}\ \Omega _{2}^{e\,f\,f}$ as a function of $\Delta _{2}$. $\mathbf{a}_{\mathbf{1}},\mathbf{a}_{\mathbf{2}}$ and $\mathbf{a}_{\mathbf{3}}$ for $\mathrm{Im}\ \Omega _{21}^{e\,f\,f}$, $\textrm{Im} \Omega _{22}^{e\,f\,f}$ and $\mathrm{Im}\ \Omega _{23}^{e\,f\,f}$ respectively at $\theta _{2}=5\pi /6$; $\mathbf{b}_{\mathbf{1}},\mathbf{b}_{\mathbf{2}}$ and $\mathbf{b}_{\mathbf{3}}$ for $\textrm{Im} \Omega _{21}^{e\,f\,f\,c}$, $\mathrm{Im}\ \Omega _{22}^{e\,f\,f\,c}$ and $\mathrm{Im}\ \Omega _{23}^{e\,f\,f\,c}$ respectively at $\theta _{2}=2\pi /3$. (blue curve) for $\theta _{1}=\pi /9$, (black curve) for $\theta _{1}=\pi /5$ and (red curve) for $\theta _{1}=\pi /4$

In Fig. 5, we present three-dimensional plots of the $\mathrm{Im}\ \Omega _{21}^{e\,f\,f}$, $\mathrm{Im}\ \Omega _{22}^{e\,f\,f}$, $\mathrm{Im}\ \Omega _{23}^{e\,f\,f}$ and $\mathrm{Im}\ \Omega _{2}^{e\,f\,f}$ as a function of the detuning $\Delta _{2}$ and the dielectric constant $\varepsilon _{b}$ at $\theta _{1}=\pi /3$. Figure 5$\text{a}_{1}$, $\text{a}_{2}$, $\text{a}_{3}$ and $\text{a}_{4}$ are shown for $\mathrm{Im}\ \Omega _{21}^{e\,f\,f}$, $\mathrm{Im}\ \Omega _{22}^{e\,f\,f}$, $\mathrm{Im}\ \Omega _{23}^{e\,f\,f}$, and $\mathrm{Im}\ \Omega _{2}^{e\,f\,f}$ respectively. We notice Fig. 5$\text{a}_{1}$ and $\text{a}_{4}$ ($\mathrm{Im}\ \Omega _{21}^{e\,f\,f}$ and $\mathrm{Im}\ \Omega _{2}^{e\,f\,f}$) are identical, so when the effective Rabi frequency is taken completely, without splitting (as in Fig. 5$\text{a}_{4}$), it exhibits like Fig. 5$\text{a}_{1}$ (i.e., $\mathrm{Im}\ \Omega _{21}^{e\,f\,f}$) this means that ($\mathrm{Im}\ \Omega _{2}^{e\,f\,f}$) exhibits the effect of $\mathrm{Im}\ \Omega _{21}^{e\,f\,f}$ only. Then it is necessary to split the effective Rabi frequencies to show the effect of $\mathrm{Im}\ \Omega _{22}^{e\,f\,f}$ and $\mathrm{Im}\ \Omega _{23}^{e\,f\,f}$.

Fig. 5

The three-dimensional spectra of the $\mathrm{Im}\ \Omega _{21}^{e\,f\,f}$, $\mathrm{Im}\ \Omega _{22}^{e\,f\,f}$, $\mathrm{Im}\ \Omega _{23}^{e\,f\,f}$ and $\mathrm{Im}\ \Omega _{2}^{e\,f\,f}$ as a function of detuning $\Delta _{2}$ and dielectric constant $\varepsilon _{b}$ at $\theta _{1}=\pi /3$. $\mathbf{a}_{\mathbf{1}},\mathbf{a}_{\mathbf{2}},\mathbf{a}_{\mathbf{3}}$ and $\mathbf{a}_{\mathbf{4}}$ are shown for $\mathrm{Im}\ \Omega _{21}^{e\,f\,f}$, $\mathrm{Im}\ \Omega _{22}^{e\,f\,f}$, $\mathrm{Im}\ \Omega _{23}^{e\,f\,f}$ and $\mathrm{Im}\ \Omega _{2}^{e\,f\,f}$ respectively

In Fig. 6, we present three-dimensional plots of the three parts of the $\Omega _{2}^{e\,f\,f}$ as a function of the detuning $\Delta _{2}$ and the dielectric constant $\varepsilon _{s}$ at $\theta _{1}=\pi /3$. Figure 6$\text{a}_{1}$, $\text{a}_{2}$ and $\text{a}_{3}$ are shown for $\textrm{Re}\Omega _{21}^{e\,f\,f}$, $\textrm{Re}\Omega _{22}^{e\,f\,f}$, and $\textrm{Re}\Omega _{23}^{e\,f\,f}$ respectively and Fig. 6$\text{b}_{1}$, $\text{b}_{2}$ and $\text{b}_{3}$ are shown for $\mathrm{Im}\ \Omega _{21}^{e\,f\,f}$, $\mathrm{Im}\ \Omega _{22}^{e\,f\,f}$ and $\mathrm{Im}\ \Omega _{23}^{e\,f\,f}$ respectively. We notice the height of the three spectra $\textrm{Re}\Omega _{21}^{e\,f\,f}$, $\textrm{Re}\Omega _{22}^{e\,f\,f}$ and $\textrm{Re}\Omega _{23}^{e\,f\,f}$ decrease rapidly when increasing the dielectric constant $\varepsilon _{s}$. Figure 6$\text{b}_{2}$ ($\mathrm{Im}\ \Omega _{22}^{e\,f\,f}$) and Fig. 6$\text{b}_{3}$ ($\mathrm{Im}\ \Omega _{23}^{e\,f\,f}$) display three holes in the large window at small values of the dielectric constant $\varepsilon _{s}$ when increasing the dielectric constant $\varepsilon _{s}$ the spectra have one hole in the window. The strength of Multipole interaction depends on the dielectric constant $\varepsilon _{s}$, when increasing the dielectric constant $\varepsilon _{s}$ the strength of Multipole interaction decreases.

Fig. 6

The three-dimensional spectra of the parts of $\Omega _{2}^{e\,f\,f}$as a function of detuning $\Delta _{2}$ and dielectric constant $\varepsilon _{s}$ at $\theta _{1}=\pi /3$. $\mathbf{a}_{\mathbf{1}},\mathbf{a}_{\mathbf{2}}$ and $\mathbf{a}_{\mathbf{3}}$ for $\textrm{Re}\Omega _{21}^{e\,f\,f}$, $\textrm{Re}\Omega _{22}^{e\,f\,f}$ and $\textrm{Re}\Omega _{23}^{e\,f\,f}$ respectively; $\mathbf{b}_{\mathbf{1}},\mathbf{b}_{\mathbf{2}}$ and $\mathbf{b}_{\mathbf{3}}$ for $\mathrm{Im}\ \Omega _{21}^{e\,f\,f}$, $\mathrm{Im}\ \Omega _{22}^{e\,f\,f}$ and $\mathrm{Im}\ \Omega _{23}^{e\,f\,f}$ respectively

Figure 7 displays three-dimensional plots of the three parts of the $\Omega _{2}^{e\,f\,f}$ as a function of the detuning $\Delta _{2}$ and the Rabi frequency $\Omega _{3}$ at $\theta _{1}=\pi /6$ and $\varepsilon _{s}=20$. Figure 6$\text{a}_{1}$, $\text{a}_{2}$ and $\text{a}_{3}$ are shown for $\textrm{Re}\Omega _{21}^{e\,f\,f}$, $\textrm{Re}\Omega _{22}^{e\,f\,f}$, and $\textrm{Re}\Omega _{23}^{e\,f\,f}$ respectively and Fig. 6$\text{b}_{1}$, $\text{b}_{2}$ and $\text{b}_{3}$ are shown for $\mathrm{Im}\ \Omega _{21}^{e\,f\,f}$, $\mathrm{Im}\ \Omega _{22}^{e\,f\,f}$ and $\mathrm{Im}\ \Omega _{23}^{e\,f\,f}$ respectively. It is observed that $\textrm{Re}\Omega _{21}^{e\,f\,f}$, $\textrm{Re}\Omega _{22}^{e\,f\,f}$, and $\textrm{Re}\Omega _{23}^{e\,f\,f}$ show distinct shapes completely, $\textrm{Re}\Omega _{21}^{e\,f\,f}$ have a positive constant value for all values of $\Omega _{3}$ and $\Delta _{2}$. $\textrm{Re}\Omega _{22}^{e\,f\,f}$ and $\textrm{Re}\Omega _{23}^{e\,f\,f}$ show the spectra have sharp dispersion in a small range of the probe detuning and Rabi frequency $\Omega _{3}$. Figure 6$\text{b}_{2}$ exhibits one sharp peak in the center of $\Delta _{2}$ at a small Rabi frequency $\Omega _{3}$, with increasing the Rabi frequency $\Omega _{3}$ the spectra appear high peaks with holes on the two sides of center $\Delta _{2}$. Figure 6$\text{b}_{1}$ and $\text{b}_{3}$ show one deep hole at small values of the Rabi frequency $\Omega _{3}$ in the region $\Delta _{2}=0$, at increasing $\Omega _{3}$, they exhibit two small holes in the nonresonant probe detuning region. Then when changing the Rabi frequency $\Omega _{3}$ at constant $\varepsilon _{s}=20$ and $\theta _{1}=\pi /6$, the three parts of $\mathrm{Im}\ \Omega _{2}^{e\,f\,f}$ and $\textrm{Re}\Omega _{2}^{e\,f\,f}$ become have different strengths in the interaction.

Fig. 7

The three-dimensional spectra of the parts of $\Omega _{2}^{e\,f\,f}$ as a function of detuning $\Delta _{2}$ and Rabi frequency $\Omega _{3}$ at $\theta _{1}=\pi /6$, $\varepsilon _{s}=20$. $\mathbf{a}_{\mathbf{1}},\mathbf{a}_{\mathbf{2}}$ and $\mathbf{a}_{\mathbf{3}}$ for $\textrm{Re}\Omega _{21}^{e\,f\,f}$, $\textrm{Re}\Omega _{22}^{e\,f\,f}$ and $\textrm{Re}\Omega _{23}^{e\,f\,f}$ respectively; $\mathbf{b}_{\mathbf{1}},\mathbf{b}_{\mathbf{2}}$ and $\mathbf{b}_{\mathbf{3}}$ for $\mathrm{Im}\ \Omega _{21}^{e\,f\,f}$, $\mathrm{Im}\ \Omega _{22}^{e\,f\,f}$ and $\mathrm{Im}\ \Omega _{23}^{e\,f\,f}$ respectively

Conclusion

We have investigated the exciton-plasmon interaction of the hybrid nanostructure composed of semiconductor quantum dot and three metallic nanospheres via three electromagnetic fields which led to many Multipoles. We noticed when the effective Rabi frequency is taken completely (all terms), the effect of the term which has very small amount of the effective Rabi frequencies does not appear, so the effective Rabi frequencies for coherent plasmonic fields have been split into three parts according to the quantitative of Multipoles of the plasmonic fields and we studied each part separately to show its importance. It is observed that (FPERF) proportional to $(\frac{\alpha }{\varepsilon _{e\,f\,f_{m}}})$, (SPERF) proportional to $(\frac{\alpha }{\varepsilon _{e\,f\,f_{m}}})^{2}$ and (TPERF) proportional to $(\frac{\alpha }{\varepsilon _{e\,f\,f_{m}}})^{3}$, it’s mean when increased the rank of distance for Multipoles, it is increased rank of $(\frac{\alpha }{\varepsilon _{e\,f\,f_{m}}})$. The three parts of the $\Omega _{2}^{e\,f\,f}$ are affected by changing the angles and the strong probe field, other parameters like the Rabi frequency $\Omega _{3}$ and dielectric constants ($\varepsilon _{b},\varepsilon _{s}$) have also strong effect on these spectra. Lastly, we wish the results of splitting of the effective Rabi frequencies for coherent plasmonic fields can be benefitted and used in analyzing optical experiments of hybrid nanosystems.