1 Introduction

In soft soil layers, piles are frequently loaded laterally by horizontal soil movements caused by eccentric loading or unloading of the ground surface around the piles (Fig. 1). According to [14] piles subjected to such a lateral pressure are termed “passive piles”, while piles subjected to horizontal loads at the pile head caused by the superstructure are termed “active piles”.

Fig. 1
figure 1

Lateral pressure on piles due to horizontal soil movement (after [13])

Full size image

In many cases, the lateral pressure acting on piles due to horizontal soil movements is calculated with empirical approaches or analytically based on plasticity or earth pressure theory, respectively. [35] classify design methods for piles subjected to lateral loads as

  • empirical methods,

  • pressure-based methods,

  • displacement-based methods,

  • finite element analyses.

Previous studies (e.g. [3, 18, 21, 23, 30]) indicate that the lateral pressure on piles depends on various parameters such as

  • the roughness of the pile–soil interface,

  • the size of the pile cross section,

  • the pile shape,

  • pile group effects.

Neglecting these parameters, in design practice, frequently the following simplified expression is applied to define the ultimate lateral pressure Pult for the ultimate limit state:

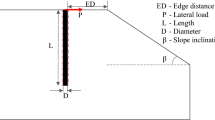
$$P_{{{\text{ult}}}} = \chi \cdot s_{{\text{u}}}\cdot d_{{\text{p}}} \,{\text{or}}\,P_{{{\text{ult}}}} = \chi \cdot s_{{\text{u}}} \cdot a_{{\text{p}}}$$
(1)

where χ is an empirically or theoretically derived coefficient, su is the undrained shear strength, dp is the pile diameter and ap is the edge length of the pile. Table 1 gives an overview on the range of values for the coefficient χ defined in the literature.

Table 1 Coefficient χ for the estimation of the lateral pressure Pult
Full size table

However, it can be assumed that in many practically relevant cases the ultimate lateral pressure will not be reached since the bearing capacity of the strip foundation is significantly higher than the surface load causing the horizontal soil movements and the loading rate is relatively small. Therefore, for the estimation of the resulting lateral pressure for pile design pre-failure conditions appear to be decisive with the influences of the parameters mentioned above on the relative displacement between pile and soil being largely unknown.

The European standard on geotechnical design EC 1997-1 (EC7-1) [17] requires proof against the effects caused by lateral pressure, but does not specify an analysis method to quantify these effects. In the German supplementary rules to the EC7-1, DIN EN 1997-1 (DIN 1054) [16], for the calculation of the lateral pressure reference is made to the Recommendations on Piling (DGGT 2014 [15]) listed in Table 1.

As part of a research project to overcome some of the limitations mentioned above this paper presents the results of 1 × g model tests and of a numerical parametric study on piles subjected to lateral pressure which led to the development of an improved analysis approach.

2 1 × g Model tests

2.1 Test set-up

The 1 × g model tests in Kaolin clay comprised 25 tests on single piles and 11 tests on pile rows with up to 3 piles. In all tests, the soil was flowing around fixed single piles or pile rows, respectively, while the following parameters were varied:

  • shear strength su of the Kaolin clay (su = 0.6 kPa to su = 5.2 kPa),

  • pile shape (circular and square cross section, respectively),

  • pile diameter dp or edge length ap (20 mm, 30 mm and 40 mm),

  • roughness of the pile–soil interface (“smooth” piles and “rough” piles, respectively),

  • displacement rate v of the soil flowing around the pile (v = 0.01 mm/min to v = 1.00 mm/min)

  • pile spacing s in the pile group tests (s = 2⋅dp to s = 10⋅dp)

Figure 2 shows the test set-up. The soil is located in a box on a cart which is pulled displacement controlled by means of a hydraulic press which is connected to the cart by means of a steel cable with ball bearings at both ends. During the tests, each model pile was fixed by means of two guyings aligned with the direction of the soil movement. The guyings, a steel cable connected to a load cell which allowed for the measurement of forces, were connected with the back of the pile near the pile head and the pile base, respectively. The 200 mm long model piles were fabricated from aluminium profiles with circular or square cross sections, respectively. The plain surfaces of the aluminium profiles are considered as “smooth” in the scope of this work. For the investigation of “rough” piles, sandpaper was glued on the aluminium profiles.

Fig. 2
figure 2

Test set-up of the model tests

Full size image

For the model tests kaolin clay was used to ensure a high reproducibility of the tests [7]. The kaolin clay with a very soft consistency and water content close to the liquid limit or even higher yielding a liquidity index IL ≥ 1 was placed in ~ 3 cm thick layers in the box. Every layer was smoothened before the next layer was placed to minimise inclusions of air in the clay. Under the assumption that the structure of kaolin clay does not change significantly during consolidation [34] and to proceed with the testing programme in a reasonable time frame, the tests started immediately after the soil placement—that is, no time was given for consolidation under self-weight. The undrained shear strength was determined in the test box in preliminary tests and after each test with a small vane penetrometer at 30 to 40 locations in the test box. Immediately after each test at six locations in the test box, soil samples were taken to determine the water content and the uniformity of the soil installation was controlled by means of a small-scale cone penetration test [7]. Based on extensive preliminary tests, the relationship between the water content and the undrained shear strength of the kaolin clay was well established and was confirmed during the tests. With the water contents of the kaolin clay varying between w = 34% and w = 50% during the tests, undrained shear strength between su = 0.6 kPa and su = 5.2 kPa were achieved. The properties of the Kaolin clay are summarised in [7].

The tests were analysed with the PIV-Method (e.g. [41]) using dispersed fine sand as a tracer on top of the Kaolin clay surface. Based on the PIV observations, the zone of deforming soil around the piles did not extend to the container boundaries. [7] provide a detailed documentation of test set-up, soil properties and sample preparation.

2.2 Test results

In the scope of this paper, the lateral pressure acting on the pile p and the relative displacement between the pile and the soil body δ were normalised by the undrained shear strength su and the pile diameter dp or pile edge length ap, respectively. The relative displacement between pile and soil body δ was assumed to be equivalent to the displacement of the box. The lateral pressure of the pile p was derived from the measured forces on the pile P divided by the pile length hw and the pile diameter dp or pile edge length ap, respectively:

$$p = {\raise0.7ex\hbox{$P$} \!\mathord{\left/ {\vphantom {P {h_{{\text{w}}} a_{{\text{p}}} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${(h_{{\text{w}}} \cdot d_{{\text{p}}}) }$}}{\text{ or}}\, p = {\raise0.7ex\hbox{$P$} \!\mathord{\left/ {\vphantom {P {h_{{\text{w}}} a_{{\text{p}}} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${(h_{{\text{w}}} \cdot a_{{\text{p}}}) }$}}$$
(2)

Similar to the work published by [23, 27, 28], the model tests were carried out up to a maximum relative displacement of δ/dp ≈ δ/ap ≈ 1 which is also assumed to be a value that in engineering practice usually will not be exceeded. Therefore, the model tests focus on pre-failure conditions since the ultimate lateral pressure acting on the pile was not reached in the current model tests.

All results presented in the scope of this paper were derived from tests with a displacement rate of the soil flowing around the pile of v = 0.1 mm/min. [7] discuss the influence of the displacement rate on the lateral pressure.

Figure 3 shows the results of the PIV analysis of two tests with an undrained shear strength su ≈ 2.2 kPa (dp = 40 mm) and su ≈ 5.2 kPa (dp = 30 mm), respectively, for a relative displacement between pile and soil, i.e. the displacement of the box, of δ ≈ 0.1⋅dp. The PIV analyses were carried out up to a relative displacement of δ ≈ 1.0⋅dp. For su ≤ 1 kPa generally a flow around the soil could be observed in the model tests [4]. For su ≈ 2 kPa, a gap developed behind the piles with relative displacements increasing δ ≥ 0.2⋅dp. For su ≈ 5 kPa, the gap developed immediately with the start of the test. This gap extended over the complete length of the pile which is in agreement with earth pressure theory [4]. However, due to the significantly higher stresses in the soil, gaps of this size will not occur at large-scale piles. The magnitude of the undrained shear strength also influenced the pattern of soil movement adjacent to the pile.

Fig. 3
figure 3

Model tests—contour lines of the displacement of the soil surface derived from the PIV-analysis for single piles

Full size image

Figure 4 shows the variation of normalised soil displacement δ/dp with the normalised pressure acting on the piles p/su for smooth circular piles. On the one hand, the tests exhibited increased values for p/su for lower values of su. This can be explained with the different patterns of soil movement adjacent to the piles (Fig. 3) where soil flow around the piles yields higher lateral pressures than an accumulation of soil in front of the piles. On the other hand, the tests show no significant influence of the pile size on the pressure p which might be explained by the very small size of the piles in the model tests [7].

Fig. 4
figure 4

Models tests—variation of the normalised pressure acting on piles p/su with normalised relative displacement δ/dp: Influence of the pile diameter dp and shear strength of the soil su

Full size image

Figure 5 shows a comparison of test results for smooth piles and rough piles for an undrained shear strength of su = 0.8 kPa and su = 2.4 kPa, respectively. The rough piles exhibit lateral pressures 19–32% higher than the smooth piles. Moreover, it appears that the difference between smooth and rough piles is more pronounced for higher values of su. This test result corresponds with the analytical solution by [30] predicting an ultimate pressure p for a perfectly rough pile approximately 30% higher than for a perfectly smooth pile.

Fig. 5
figure 5

Model tests—variation of the normalised pressure acting on piles p/su with normalised relative displacement δ/dp: Influence of the pile roughness

Full size image

Figure 6 compares pile rows with two piles perpendicular to the soil movement with varying pile spacing where the lateral pressure was measured for each pile separately and then averaged. For a spacing of s ≤ 8⋅dp, the lateral pressure acting on the piles in the row is smaller than the lateral pressure on a comparable single pile. In general, the investigations show the lateral pressure decreasing with decreasing pile spacing. Similar results as in the current model tests were presented by [23, 28].

Fig. 6
figure 6

Model tests—variation of the normalised pressure acting on piles p/su with normalised relative displacement δ/dp: Pile rows with two piles and varied pile spacing

Full size image

Apart from the main research project [4], additional tests results are documented in [6, 7].

3 Numerical parametric study

3.1 Preliminary remarks

The aim of the numerical parametric study based on the finite element method was to systematically quantify the influencing parameters on the lateral pressure and to develop a simplified analysis approach applicable for engineering practice which considers these parameters. Since the shear strength and stiffness of the soil in the aforementioned 1 × g model tests are not comparable with in situ soil conditions, the back analysis of the 1 × g model tests was used to show the general suitability of the numerical model to simulate lateral pressure on piles [8], i.e. the 1 × g model tests were not applied for the determination of design parameters for the prototype scale. The further verification of the numerical model then comprised the back analysis of in situ measurements [4, 31]. The suitability of the finite element method simulating the lateral pressure on piles was also confirmed by e.g. [20, 26, 37].

The results presented by [8] showed a good agreement between the model tests and numerical back analyses, which was carried out by means of total stress finite element analysis with undrained shear parameters on one hand and effective stress analysis with effective shear parameters on the other. The numerical parametric studies on single piles confirmed the significant influence of the undrained shear strength, the pile shape, the pile diameter and the roughness of the pile–soil interface on the normalised lateral pressure. The numerical back analysis of pile groups with piles lined up perpendicular or longitudinal, respectively, to the direction of the soil movement showed diminishing group effects with increasing pile spacing. It is interesting to note that [2, 3] also achieved good agreement with the model tests by [6, 7] as well as with the results of the finite element analysis by [8] carrying out numerical simulations with the Convected Particle Domain Interpolation (CPDI1). The CPDI1 is a further development of the material point method (MPM) and can be used to simulate very large deformations in the soil (e.g. [1, 19]).

Reul et al. [31] present the back analysis of a large-scale test on a pile group in cohesive soil subjected to lateral pressure documented by [25] by means of 3D finite element coupled pore pressure–displacement analyses. A reasonable agreement between the measured bearing behaviour of the pile foundation, and the finite element analysis was achieved. Especially the consolidation process and the creep deformations, which were modelled by means of a visco-hypoplastic soil model were reproduced well in the finite element analysis. Additionally, [4] presents the back analyses of a large-scale test documented by [38] and centrifuge tests documented by [10].

3.2 Finite element model

The numerical parametric study presented in this research work was carried out with the system and boundary conditions shown in Fig. 7, and the 3D finite element models shown in Figs. 8 and 9. The soil and the piles are represented by 15-order solid finite elements of wedge shape. The circular piles were replaced by dodecagonal cross sections with approximately the same shaft circumference. Contact between soil and piles was modelled using interface elements (Fig. 8b).

Fig. 7
figure 7

System and boundary conditions for the investigations on single piles

Full size image
Fig. 8
figure 8

Finite element model for the investigations on single piles

Full size image
Fig. 9
figure 9

Finite element model for the investigations on pile groups

Full size image

The soil stratigraphy comprises an upper sand layer with a thickness of 1.0 m underlain by a cohesive soil layer with the thickness hw varying in the parametric study. The cohesive soil layer is followed by a lower sand layer which extends down to the bottom surface of the model. The groundwater level is located at the top of the cohesive soil layer.

The lateral pressure acting on the piles is caused by a fully flexible vertical load located at ground level. A pile cap with a thickness of 1.0 m was placed above the piles which extends to the horizontal model boundaries. Preliminary studies showed no significant influence of the size of the pile cap on the lateral pressure acting on a pile group [4].

Pile length were held constant at Lp = 17.0 m. For the investigations with the finite element model shown in Fig. 8a, the following parameters were varied:

  • shear strength su of the cohesive soil (4–36 kPa),

  • stiffness ES of the cohesive soil (0.1–11 MPa),

  • thickness of the cohesive soil layer hw (1.0–12.0 m),

  • pile shape (circular and square cross section, respectively),

  • pile diameter dp or edge length ap (0.3–3.0 m),

  • roughness of the pile–soil interface (“smooth” piles and “rough” piles, respectively).

Based on the configuration shown in Fig. 8a, the effect of a significantly stiffer layer embedded in the cohesive soil layer was further investigated (Fig. 7c). For this purpose, the shear strength su and the stiffness ES of the cohesive soil layer as well as the depth of the significantly stiffer layer zSE were varied in the bandwidth mentioned above with the thickness of the significantly stiffer layer ranging between 0.5 and 2.0 m [4].

In the investigations for single, rough piles the distance between the pile and the surface load was varied between 1.0 and 36.0 m (Fig. 8c).

The parametric study for pile groups was carried out for groups of 2 × 2, 2 × 3, 3 × 3, 4 × 3, 4 × 4 and 5 × 5 piles (Fig. 9b) with the piles spacing varying between s = 3⋅dp to s = 9⋅dp.

The material behaviour of the sand layers (incl. a significantly stiffer layer with the material parameters of the upper sand embedded in the cohesive soil layer) was modelled with a linear elastic-perfect plastic soil model applying the Mohr–Coulomb failure criteria and a nonassociated flow rule for the plastic deformations. Preliminary studies varying the material parameters of the sand layers showed no significant influence on the lateral pressure. For the results presented in the scope of this paper, the material behaviour of the cohesive soil layer was modelled with the Hardening Soil-Model [11]. The influence of creep deformations on the lateral pressure was investigated by [4] and is not in the focus of this paper.

Interface elements with a linear elastic-perfect plastic material behaviour were applied for the simulation of the pile–soil interaction. For the applied Mohr-Coulomb failure criteria, the shear parameters of the surrounding soil were used. For the remainder of this paper, piles with an interface shear strength ratio of Rinter = 0.33 are termed “smooth” and for an interface shear strength of Rinter ≥ 0.67 are termed “rough”. If not indicated otherwise all results presented in the scope of this paper were derived for an interface shear strength ratio Rinter = 0.67, i.e. for rough piles.

The piles and the pile cap are considered to behave linear elastically. The material parameters applied in the finite element analyses are summarised in Tables 2, 3 and 4.

Table 2 Material properties of the sand (Mohr–Coulomb model)
Full size table
Table 3 Material properties of the cohesive soil as basis for the parametric study (hardening soil model)
Full size table
Table 4 Material properties of piles and the pile cap (linear elastic)
Full size table

Preliminary studies carried out for undrained conditions and drained conditions under consideration of consolidation processes showed that undrained conditions yield the maximum lateral pressure decisive for pile design [4]. In the scope of the parametric study presented in this paper, undrained conditions were considered.

The finite element analysis included the following steps:

  1. 1.

    Generation of the in situ stress state.

  2. 2.

    Installation of the piles using the “wished-in-place” technique, i.e. no changes in the soil surrounding the piles caused by the installation process were modelled.

  3. 3.

    Application of the load.

The first two analysis steps were carried out under drained conditions while during the application of the load in step 3 undrained conditions were considered resulting in the buildup of excess pore pressure.

The results of the parametric study are evaluated by means of the constrained stiffness modulus ES and the undrained shear strength su both acting in the in situ stress state. The mean value of the constrained stiffness modulus for the cohesive soil layer (Fig. 10a) was derived from the material parameters of the Hardening Soil-Model (Table 3) applying the approach suggested by [11]:

$$E_{{\text{S}}} \approx E_{{50}}^{{{\text{ref}}}} {\text{ }}\left( {\frac{{c^{\prime } \cdot \cos \varphi ^{\prime } - \sigma ^{\prime } _{y} \cdot \sin \varphi ^{\prime } }}{{c^{\prime } \cdot \cos \varphi ^{\prime } + p^{{{\text{ref}}}} \cdot \sin \varphi ^{\prime } }}} \right)^{m}$$
(3)

where \({E}_{50}^{ref}\) is the reference stiffness modulus corresponding to the reference confining pressure \({p}^{{\text{ref}}}\) = 0.1 MPa and m is the power for the stress level dependency of stiffness.

Fig. 10
figure 10

Estimation of mean values of the constrained modulus ES and the undrained shear strength su for the cohesive soil layer

Full size image

The mean value of the undrained shear strength for the cohesive soil layer was derived from numerical simulations of undrained triaxial tests as indicated in Fig. 10b applying the drained shear parameters φ' and c' of the Hardening Soil-Model (Table 3).

Due to the boundary conditions and the pile cap considered in the finite element models (Figs. 8, 9), the load q can be significantly higher than the ultimate capacity of a comparable strip foundation qult (Fig. 11b). The soil then reaches its ultimate capacity in the vicinity of the piles with the ultimate lateral pressure pult acting on the piles (Fig. 11a). Therefore, the numerical model applying loads q > qult yield higher lateral pressures, i.e. a conservative design approach, than what can be expected under boundary conditions typical for engineering practice. For the evaluation of the parametric study again, the mean value of the lateral pressure is considered (Fig. 12).

Fig. 11
figure 11

Surface load q causing the lateral pressure

Full size image
Fig. 12
figure 12

Mean value of the lateral pressure

Full size image

The ultimate capacity for the strip foundation was established by means of a φ−c-reduction for a system without piles and the pile cap replaced by the upper sand layer. If not mentioned otherwise, all results presented in the scope of this paper were derived for q = qult.

3.3 Results of the numerical study for single piles

Figure 13 shows the variation of the normalised pressure acting on the piles, pmean/su, with the normalised surface load q/qult for the basic model (Fig. 8a, b, Table 3: Cohesive soil A) where the influence of the stiffness and strength of the cohesive soil, \({E}_{50}^{{\text{ref}}}\) and c' (Fig. 13a), of the pile–soil interface roughness, Rinter (Fig. 13b), and of the pile cross section, dp and ap (Fig. 13c), were investigated.

Fig. 13
figure 13

Numerical study on single piles—variation of the normalised mean pressure acting on piles p/su with the normalised surface load q/qult

Full size image

For q/qult ≤ 1, Fig. 13 shows the normalised pressure, pmean/su, varying approximately linearly with q/qult for all parameters investigated which corresponds to in situ measurements documented by [42], who studied a 2 × 2 pile group supporting a bridge abutment in a 10.5-m-thick cohesive soil layer which was subjected to a load of q ≈ 100 kPa caused by the backfilling of the abutment. Similar to the model tests the numerical analyses show the normalised pressure, pmean/su,

  • decreasing with increasing shear strength (see Figs. 4 and 13a),

  • increasing with increasing roughness of the pile–soil interface (see Figs. 5 and 13b).

Moreover, in the numerical analyses the normalised pressure, pmean/su,

  • decreased for increasing pile diameter (Fig. 13c),

  • was larger for rectangular piles than for circular piles (Fig. 13c),

  • increased for increasing cohesive soil stiffness, \({E}_{50}^{{\text{ref}}}\), (Fig. 13a).

Investigations carried out with the FE-model indicate that besides the stiffness and shear strength of the cohesive soil, the thickness of the cohesive soil layer, hw, the pile diameter, dp, or edge length, ap, and the magnitude of the load, q, significantly affect the range of influence of the lateral pressure while the shape of the pile cross section, i.e. circular or rectangular, and the roughness of the pile–soil interface are of minor importance [4]. In the investigations of a significantly stiffer layer embedded in the cohesive soil layer, the stiffness ratio and the location of the stiffer layer in particular increase the lateral pressure. Some of the results are discussed below.

Figure 14 shows the variation of the coefficient χdq with the distance dq between the pile and the surface load for cohesive soil B, cohesive soil C and cohesive soil D representing clayey soils of varying stiffness and strength (Table 3), for different thickness of the cohesive layer, hw and for the surface load q = 0.1⋅qult and q = 0.9⋅qult, respectively. The factor χdq is defined as

$$\chi_{dq} = \frac{{\left( {p_{{{\text{mean}}}} /s_{{\text{u}}} } \right)_{{\text{d}}} }}{{\left( {p_{{{\text{mean}}}} /s_{{\text{u}}} } \right)_{{\text{a}}} }}$$
(4)

where (pmean/su)d is the normalised lateral pressure in a distance dq from the surface load, and (pmean/su)a is the normalised lateral pressure adjacent to the surface load, i.e. in a distance of dq = 1.0 m.

Fig. 14
figure 14

Numerical study on single piles—variation the factor χdq (Eq. 4) with the distance dq between the pile and the surface load q and the thickness of the cohesive soil layer hw

Full size image

As an example for the investigations on cohesive soil B and piles with a diameter of dp = 0.5 m and dp = 1.5 m, Fig. 14 leads to the conclusion that higher surface loads generally yield a larger range of influence, i.e. higher values for χdq. Only for thin cohesive soil layers, e. g. hw = 2.0 m, a surface load of q = 0.1⋅qult yields higher values for χdq than q = 0.9⋅qult, at least at distances larger than 10 m. This is possibly caused by the fact that the area of influence is limited to the geometry of the already developing failure mechanism in the cohesive soil, which has only a small range due to the comparatively small layer thickness.

Furthermore, the following conclusions can be drawn from the results presented in Fig. 14:

  • χdq increases for increasing thickness of the cohesive soil layer, hw.

  • χdq increases for stiffer soils, i.e. with higher stiffness and shear strength, although this effect is less pronounced for increasing thickness of the cohesive soil layer.

  • For a thickness of the cohesive soil layer of hw ≥ 6 m, a pile diameter of dp = 1.5 m yields higher values for χdq, while for hw = 2 m, the piles with dp = 0.5 m show higher values for χdq.

3.4 Results of the numerical study for pile groups

The group factor χGP relates the normalised lateral pressure of a pile within a pile group, (pmean/su)G, to the normalised lateral pressure of a single pile, (pmean/su)S:

$$\chi_{{{\text{GP}}}} = \frac{{\left( {p_{{{\text{mean}}}} /s_{{\text{u}}} } \right)_{{\text{G}}} }}{{\left( {p_{{{\text{mean}}}} /s_{{\text{u}}} } \right)_{{\text{S}}} }}$$
(5)

Preliminary investigations carried out with the FE-model shown in Fig. 9 indicated that the factor χGP in particular depends on the stiffness and the shear strength of the soil, the pile diameter or edge length and the roughness of the pile–soil interface [4]. Piles with a rectangular cross section always yield smaller group factors than piles with a circular cross section provided ap = dp. The thickness of the cohesive soil layer, hw, has a negligible influence on the group factor. Since group effects proved to be more significant for higher surface loads the results presented subsequently were derived for q = qult. The material parameters applied for the cohesive soil are summarised in Table 3.

Generally, the further back the piles are located within the group the smaller the lateral pressure and the group factor χGP will become. This can be attributed to the shielding effect of the piles standing in front of them on the one hand and to the greater distance to the surface load on the other hand. For pile rows perpendicular to the soil movement (Fig. 9b, R1 to R5), the piles located at the edge of the group (Fig. 9b, pile type A) show a higher group factor χGP than the piles located inside the group (Fig. 9b, pile type I). Selected results are presented in Fig. 15 with the group factor χGP plotted versus the number of the pile rows perpendicular to the soil movement for the pile spacing s = 3⋅dp.

Fig. 15
figure 15

Numerical study on pile groups—variation the factor χGP (Eq. 5) with the pile position relative to the surface load (Fig. 9b) for piles arranged one behind the other in rows

Full size image

For the cohesive soil B, Fig. 15a shows the influence of the size of the pile group on the group factor χGP for pile type A with a diameter of dp = 0.5 m and an interface roughness of Rinter = 1.00. For each row, the pile group with the smallest number of piles yields the highest group factor χGP. An upper limit curve (Fig. 15a, curve “Max.”) can be derived from this maximum group factor. All remaining results presented in Fig. 15b, c and d are based on such an upper limit curve, determined in each case from pile groups comprising 2 × 2, 3 × 3, 4 × 4 and 5 × 5 piles.

For pile row R1 in ultimate vicinity to the surcharge load the piles with dp = 1.5 m show higher group factors than the piles with dp = 0.5 m, while for all other pile rows, the opposite holds true (Fig. 15b). Figure 15c compares the group factor χGP of pile types A and I and for soil types cohesive soil B, cohesive soil C and cohesive soil D (Table 3) with pile type A generally showing higher group factors than pile type I. For higher stiffness and shear strength, the group factor becomes gradually higher. However, this effect is not as significant as the variation of the group factor resulting from different pile positions.

The roughness of the pile–soil interface only has a small influence on the group factors as indicated in Fig. 15d. For pile rows close to the surface load (R1, R2) the piles with a smoother surface (Rinter = 0.33) show higher group factors while for pile rows further away (R4, R5) rough surfaces (Rinter = 1.00) give marginally higher values. This is in agreement with the results achieved by [33] for square pile groups in undrained soil who observed a negligible influence of pile–soil roughness on the group lateral limiting pressure if piles in large groups are spaced closely together.

Figure 16 extends the investigations on the group effects on the lateral pressure with the group factor χGP plotted versus the number of the pile rows perpendicular to the soil movement for pile groups comprising 2 × 2, 2 × 3, 3 × 3, 4 × 3, 4 × 4 and 5 × 5 piles and pile spacings between s = 3⋅dp and s = 9⋅dp. Parameters varied in the study were the soil type (Cohesive soil B, Cohesive soil C and Cohesive soil D according to Table 3), the pile diameter (dp = 0.5 m; dp = 1.5 m) and the roughness of the pile–soil interface (Rinter = 0.33; Rinter = 1.00), while the thickness of the cohesive soil layer was held constant at hw = 6.0 m. The values for the group factor χGP given in Fig. 16 represent the maximum values derived from the parametric study.

Fig. 16
figure 16

Numerical study on pile groups—variation of factor χGP (Eq. 5) with the pile position relative to the surface load (Fig. 9): Influence of the pile spacing for piles arranged one behind the other in rows as well as in staggered rows

Full size image

From the results presented in Fig. 16, it is possible to draw the following conclusions:

  • For pile spacings s ≥ 9⋅dp, the piles in row R1 adjacent to the surface load behave as a comparable single pile, i.e. χGP = 1.0.

  • For pile spacings s < 9⋅dp, the lateral pressure acting on a group pile is smaller than the lateral pressure on a comparable single pile, χGP < 1.0.

  • As could be expected, for larger piles spacings group effects diminish. However, when looking at pile rows orientated parallel to the soil movement (or for example comparing the same pile type in row R1 and row R5) the increasing distance between the piles in the back rows and the surface load yields a decrease in the group factor which could be interpreted as an increase in group effects.

  • Model tests by [7] not presented in the scope of this paper show that with decreasing pile spacing the lateral pressure on the piles is decreasing for front row piles as well as for back row piles. In the numerical study, this effect is reflected when comparing the results for row R1 (front row pile) for s = 3⋅dp (χGP ≈ 0.93) and s = 9⋅dp (χGP = 1.0). The piles in the back rows R2 to R5 are shielded by the front row piles, while at the same time, the movement of the soil around the front row piles is obstructed by the back row piles.

4 Approach for the analysis of piles subjected to lateral pressure

Based on the results of the numerical parametric study [4] developed an improved approach for the analysis of piles subjected to lateral pressure to overcome the limitations in Recommendations on Piling (DGGT 2014 [15]) discussed by [5]. The approach modifies Eq. (1) as follows:

$$P_{{{\text{ult}}}} = \left( {6 \cdot \chi \cdot s_{{\text{u}}} \cdot \mu + \Delta p_{{\text{t}}} } \right) \cdot d_{{\text{p}}} \quad {\text{or}}\quad P_{{{\text{ult}}}} = \left( {6 \cdot \chi \cdot s_{{\text{u}}} \cdot \mu + \Delta p_{{\text{t}}} } \right) \cdot a_{{\text{p}}}$$
(6)

where: 6 is the ratio of the normalised pressure, pmean/su, in the basic element model shown in Fig. 7a (circular single pile) with the parameters in Tables 2, 3 and 4, su is the undrained shear strength of the cohesive soil layer, μ is the degree of utilisation of the strip foundation (Fig. 11b), Δpt is the lateral pressure acting on the pile due to creep deformations, dp is the pile diameter, ap is the edge length of the pile and, χ is the combination of several coefficients:

$$\chi = \chi_{{{\text{su}}}} \cdot \chi _{{{\text{hw}}}} \cdot \chi { }_{{{\text{Es}}}} \cdot \chi_{{\text{d}}} \cdot \chi_{{{\text{SE}}}} \cdot \chi_{{{\text{dq}}}} \cdot \chi_{{{\text{GP}}}}$$
(7)

where: χsu is the coefficient for the undrained shear strength su (see Table 5), χhw is the coefficient for the thickness of the cohesive soil layer hw (see Table 6), χEs is the coefficient for the confined stiffness modulus of the cohesive soil layer ES (see Table 7), χd is the coefficient for the shape and the cross-section area of the pile (see Table 8), χSE is the coefficient for the effect of a significantly stiffer layer embedded in the cohesive soil layer (see Table 9), χdq is the coefficient for the distance between the pile and the surface load dq (see Table 10), χGP is the coefficient for pile group effects (see Table 11 and Fig. 16).

Table 5 Coefficient χsu
Full size table
Table 6 Coefficient χhw
Full size table
Table 7 Coefficient χE
Full size table
Table 8 Coefficient χd
Full size table
Table 9 Coefficient χSE in dependency of λ (Eq. 8)
Full size table
Table 10 Coefficient χdq
Full size table
Table 11 Coefficient χGP
Full size table

The coefficients represent the upper limits derived from the parametric studies. In the following Table 5 to Table 11, intermediate values can be interpolated linearly. The system configuration with the definition of the relevant parameters is shown in Figs. 7 and 9b.

The parameter \(\lambda\) in Table 9 is calculated as follows:

$$\lambda = \frac{{E_{S,s} }}{{E_{S,c} }}$$
(8)

where: \({E}_{S,s}\) is the confined stiffness modulus of the significantly stiffer layer embedded in the cohesive soil layer, \({E}_{S,c}\) is the confined stiffness modulus of the cohesive soil layer.

The lateral pressure \({\Delta p}_{t}\) acting on the pile due to creep deformations can be approximated for a time period of 50 years as follows:

$$p_{t} = 700 \cdot I_{v}$$
(9)

where: \({I}_{v}\) is the viscosity index according to [18, 22]

To further investigate the parameter \({\Delta p}_{t}\), future research may incorporate more sophisticated visco-hypoplastic models such as, e.g. the AVISA model [36].

To establish the degree of utilisation, available analytical approaches to establish the stability, e.g. of a strip foundation (e.g. [29]) or a slope (e.g. [9]) can be applied.

As documented by [24], this new approach has since replaced the approach documented in the Recommendations on Piling (DGGT 2014 [15]). For a detailed documentation, it is referred to [4] and the upcoming 3rd edition of the Recommendations on Piling of the DGGT.

5 Summary and conclusions

This paper documents selected results of a research project investigating the influencing variables on the lateral pressure on piles by means of 1 × g model tests and numerical studies. As a first step, a total of 40 model tests were carried out to experimentally determine main parameters influencing the lateral pressure. On the basis of these model tests and large-scale and centrifuge tests documented in the literature, a finite element model was developed in [4]. The finite element model was then used for a parametric numerical study to systematically investigate the influence of a surcharge load on the lateral pressure acting on an adjacent pile group.

Key results derived from the model tests and the parametric numerical study can be summarised as follows:

  • The lateral pressure increases with

    • -increasing shear strength of the cohesive soil,

    • -increasing stiffness of the cohesive soil and

    • -increasing roughness of the pile–soil interface.

  • The lateral pressure decreases with

    • -increasing pile diameter and

    • -increasing distance between the pile and the surface load.

  • The lateral pressure acting on group piles is smaller than the lateral pressure on a comparable single pile. In general, the lateral pressure decreases with decreasing pile spacing.

  • For piles at the back of a pile group, the lateral pressure is smaller than for piles in the front row closer to the pressure inducing surface load, i.e. “leeward” to the loading.

Based on the results of the numerical parametric study with in total more than 1400 configurations for single piles and pile groups investigated, coefficients to quantify the influence of the above mentioned parameters were established. Using these coefficients, an improved method was developed for the analysis of piles subjected to lateral pressure which as documented by [24] has since replaced the approach documented in the Recommendations on Piling (DGGT 2014 [15]).