1 Introduction

The mining sector's economic impact has exceeded $1,800 billion in recent years, emphasizing the need for measures to ensure operational efficiency, financial sustainability, worker health, and safety. With the growing global demand for mineral resources, the prevention of rockburst and spalling failures remains an ongoing challenge facing the industry, particularly in deep mines situated in hard and brittle rock formations and weak rocks at shallow depth. Despite ongoing research, these challenges persist and continue to be unresolved. This detrimental failure in highly stressed deep mining and tunnels is one of the biggest challenges and unsolved dilemmas in deep underground excavation [24]. In highly-stressed tunnels, the predominant failure mechanism of underground rock is controlled by stress-induced fractures parallel to the excavation boundaries in terms of spalling failures or, in some severe cases, a violent slab ejection that forms a V-shaped notch around the excavation walls. Spalling failures have shown to be mainly associated with the crack initiation (CI) stress level, i.e. the onset of dilation. Under compression, several stress thresholds can readily identify from the stress–strain response of underground rock, namely: crack initiation (CI), crack damage (CD), peak strength (PS), and residual strength (RS) [68]. The accurate determination of CI is deemed necessary in understanding the progressive failure of rock and establishing the rock strength criterion while the determination of CD is of great value in the long-term stability analysis of large-scale projects [12]. The CI has been suggested by many researchers as an estimate of the operational spalling strength around tunnel sidewall [3, 37, 38]. The methods that are used to determine the CI can be grouped into three categories: (i) stress–strain based methods (i.e. volumetric strain method, lateral strain method, extensional strain method, TLSR, crack volumetric strain method, etc.), (ii) stress-based method (i.e. modified Griffith and Hoek–Brown criterion under triaxial loading condition), and (iii) instrumentation-based methods (i.e. electrical resistivity, optical diffraction patterns, laser speckle interferometry, ultrasonic probing, digital image processing methods, and AE) [47]. The stress–strain methods provide an effective tool to determine the CI, given the ease of measuring the stress and strain response of underground rock in environmentally controlled experiments. Knowing that the stress-induced cracks initiate at approximately 30% to 60% of the unconfined compressive strength regardless of the loading or environmental conditions, a crack initiation ratio (CIR) concept is defined as a ratio of crack initiation stress (\({\sigma }_{ci}\)) threshold to the peak strength was proposed as a dimensionless predictor of spalling failure [38]. Moving up the stress–strain curve towards the plastic deformation zone, the cracks tend to coalesce and grow unstably in a so-called crack damage (CD) stage where the crack damage stress (\({\sigma }_{cd}\)) is the reversal point of the volumetric strain (\({\varepsilon }_{v}\)) curve. Like the CIR concept, a crack damage ratio (CDR) concept was also proposed as the ratio of the crack damage stress (\({\sigma }_{cd}\)) to the peak stress. The CDR is a dimensionless predictor of the damage stress threshold and is usually in the range of 70%–90% of the peak stress. Both the crack initiation and crack damage can be better characterized in a dimensionless domain.

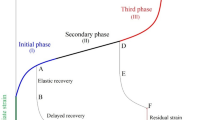
Previous research shows that in addition to the material elasticity, porosity, and tensile strength, confining pressure could also impact the crack initiation, coalescence, and propagation [47, 49, 67]. The confining pressure not only affects the crack initiation threshold (\({\sigma }_{ci}\)) but also can shape the cracking mode at a crack initiation level from splitting mode at low confinement to sliding mode at high confinement [67]. Previous research also shows that the intermediate principal stress has a significant influence on crack propagation, and hence spalling failure around the periphery of the tunnel [20]. This study aimed to investigate the effect of minor principal stress on the crack initiation threshold (\({\sigma }_{ci}\)) and CIR, which have received limited attention in existing literature. The investigation led to the introduction of a novel concept, termed the crack mode-changing stress (CMCS), which represents the minimum principal stress required to change the crack initiation mode from splitting under low confinement to sliding under high confinement. This newly proposed concept has important implications for understanding the behavior of materials subjected to complex stress conditions [46]. Figure 1 shows the graphical representation of the CMCS as the point where the \({\sigma }_{ci}\) deviates from its linearity. Therefore, highlights the critical point at which the minimum principal stress required to change the crack initiation mode from splitting to sliding can be determined. However, the newly proposed concept of CMCS still requires further validation, including testing (i) across a wide range of intermediate principal stresses, (ii) using the dimensionless CIR, and (iii) in laboratory-scale circular tunnels. These additional investigations will help to confirm the applicability of the CMCS concept for understanding crack initiation and propagation.

Fig. 1
figure 1

Crack mode-changing stress (CMCS) for sandstone cubes at \({\sigma }_{2}\)= 40 and 60 MPa [46]

Full size image

Moreover, the stress-induced tensile fractures of spalling failure in highly-stressed tunnels subjected to true triaxial loading (where \({\sigma }_{1}>{\sigma }_{2}>{\sigma }_{3}\)) are typically formed and propagate parallel to the excavation boundaries along the tunnel side walls. However, the propagation of these fractures under generalized triaxial tensile stress state, where (\({\sigma }_{1}={\sigma }_{2}>{\sigma }_{3}\)), has not been thoroughly investigated. In addition to the above, the post-spalling failure mode of circular tunnels may undergo a change from a circular to an oval shape at high stresses, as reported in the literature [35]. However, there is a knowledge gap in the literature regarding the determination of the principal stresses required to induce such a change.

Based on the above knowledge gap, this study aims to investigate the CMCS concept under a wide range of intermediate principal stresses and further validate the concept using laboratory-scale circular tunnels of porous sandstone subjected to polyaxial stress conditions, including uniaxial (\({\sigma }_{1}={\sigma }_{c}\)), biaxial (\({\sigma }_{1}>{\sigma }_{2} , {\sigma }_{3}=0\)), generalized triaxial compression stress state (\({\sigma }_{1}>{\sigma }_{2}={\sigma }_{3})\), true triaxial (\({\sigma }_{1}>{\sigma }_{2}>{\sigma }_{3})\), and generalized triaxial tensile stress state (\({\sigma }_{1}={\sigma }_{2}>{\sigma }_{3}\)). The study will also investigate the role of polyaxial stresses in controlling the post-spalling failure.

2 Background and overview

As a consequence of the Industrial Revolution, the living standards have increased profoundly, along with the demand for more minerals. To meet such an ever-increasing demand for mineral supplies, underground mining has progressed to record depths associated with tremendous improvements in drilling techniques and instrumentation methods. As a result, the global mining production of different ores, minerals, and commodities has ascended 27 times in the last century, providing over $1,800 billion to the global economy [9, 43, 45]. The year 2020 was a challenging year due to the outbreak of the COVID-19 pandemic, which affected many sectors, including the mining industry. However, mining is one of the few industries that emerged from the COVID-19 pandemic, achieving a historic revenue exceeding $800 billion in 2021, as shown in Fig. 2 [53]. To meet the ever-increasing demand for renewable energy technologies, the exploitation of some critical minerals essential for such technology has increased steadily. All these factors prioritize the need to solve the challenges facing the mining industry at a governmental level. Ahead of these challenges is the well-known rockburst and spalling failure, which is associated with the initiation of internal cracks in high-stress tunnels.

Fig. 2
figure 2

Mining industry revenue from 2007 to 2021 [53]

Full size image

Following the rock bursting in the British Tin mine in Stafford in 1738 as the first-ever reported incident, this phenomenon came to sight and brought more attention [6, 22]. Over 22 rockburst incidents with fatalities were reported in five different mines of the Coeur d’Alene district in northern America in the past 60 years [69]. From 1984 to 1993, the mining damage of rockburst in South African gold mines caused fatalities to around 3,275 workers [8]. In a global-wise record, more than 54,722 rockburst incidents were reported in the period from 2002 to 2016. In 2016, the death toll from coal mines alone due to rock bursting in China exceeds 538 [64]. In addition to the above, rockburst and its related incidents were reported in many countries around the globe including Australia as shown in Fig. 3.

Fig. 3
figure 3

A historical rockburst map between 1995–2019 [5, 65]

Full size image

Rockburst can occur violently in the form of strain burst, fault-slip, pillar burst, or less severe ejection as a spalling or slabbing failure. However, spalling can trigger rockburst by forming thin rock slabs which facilitate the sudden release of energy and therefore cause violent rock ejection [14]. Spalling is defined as the formation of stress-induced slabs on the boundary of underground excavation and is closely related to the propagation and coalescence of internal tension cracks surrounding the rock [38]. As rockburst, spalling failure has been reported in many locations around the globe including Australia; the Hongtoushan copper mine in China, Nickel mines in the Sudbury Basin of Canada, Metal mines in North America, Champion reef mines of Kolar gold fields in India, Garpenberg zinc mine in Sweden, Onkalo tunnel in Finland, the Steg Lateral Adit of the Lo¨tschberg Base Tunnel in Switzerland, Neyriz marble mine in Iran, NorthConnex project in New South Wales in Australia, Northside Storage tunnels and Elgas Cavern in Sydney in Australia, Bringelly Shale tunnels and Newport Formation in Sydney in Australia, the Kalgoorlie mines in Western Australia, the Mount Isa Mines in Queensland state in Australia [6, 10, 13, 15, 16, 29, 37, 39,40,41, 46, 54, 63, 71].

Unlike rockburst, spalling failure can occur in shallow depths of weaker or lightly cemented rock (i.e. sandstone) associated with pure tensile cracks near the excavation boundaries like the reported incidents in Kundana, Bounty, Mt Charlotte, Big Bell, and Kanowna Belle operations at depths of 300 to 600 m in Western Australia [28, 50]. At depth, the spalling failure induces a more complex combination of both tensile and shear failure in the form of V-shaped notches along the tunnel axis or excavation boundaries. Knowing that the crack initiates within the elasticity zone of stressed rock, numerous crack initiation models were developed based on the stress–strain behavior of underground rock; volumetric strain method, lateral strain method, extensional strain method, and true triaxial lateral strain response (TLSR) method as summarized in Table 1.

Table 1 Determination of crack initiation stress through some stress–strain models
Full size table

The excavation of the tunnel changes the stress state of the rock mass near the excavation boundary where the tangential stress (\({\sigma }_{\uptheta }\)) increases gradually, the radial stress (\({\sigma }_{\mathrm{r}}\)) decreases rapidly, and the axis stress (\({\sigma }_{\mathrm{a}}\)) varies slightly as shown in Fig. 4 [61]. According to Kirsch’s solution, the maximum tangential stresses (\({\sigma }_{\theta max}\)) at the circular tunnel excavation boundary are a function of maximum and intermediate principal stresses as per Eq. (\(1\)). At the excavation boundary, the radial stress is relieved completely while it increases by going far from the face of the excavation [61]. Furthermore, the excavation triggers shear stresses (\(\tau\)) on the surfaces due to the constraint of surrounding rock.

Fig. 4
figure 4

Stress state of representative rock mass before and after tunnel excavation [61]

Full size image
$${\sigma }_{\theta max}=3{\sigma }_{1}-{\sigma }_{2}$$
(1)

A review of published case histories where the shape of the slabbing region has been measured and documented shows that the V-shaped notch is likely to develop regardless of the geometrical shape of the tunnels [62]. As shown in Fig. 5, the location, extent, and depth of the V-shaped notch can vary with the tunnel’s geometrical shape, but in general, perpendicular to the maximum far-field stress direction (\({\sigma }_{max}= {\sigma }_{1}\)). In practical engineering, the tunnel axis could be along the direction of the minor or intermediate principal stress or the oblique crossing direction of the intermediate principal stress [20].

Fig. 5
figure 5

V-shaped notch development in different geometrical shaped tunnels along with the orientation of the maximum and minimum in situ stresses [62]

Full size image

The development of true triaxial testing facilities in the past 50 years was obvious which paved the way for more promising research including the realistic mimic of the in-situ condition where the underground rock is exposed to three-dimensional stresses: major (\({\sigma }_{1}\)), intermediate (\({\sigma }_{2}\)), and minor (\({\sigma }_{3}\)) principal stresses. The conventional way to induce spalling using experimental models through true triaxial testing apparatus was through sudden unloading of one face of a block-shaped specimen to simulate the in-situ sudden release of energy during the excavation [1].

Afterwards, and for the sake of a more realistic simulation of the spalling failure in tunnels, many scholars have adopted the method of using opening holes in rock blocks. For example, Fakhimi et al. [17] simulated the rockburst on an underground roadway of sandstone through a scaled circular model under biaxial loading conditions. He et al. [23] simulated the impact rockburst of deep roadway sandstone under disturbed load polyaxially through a laboratory-scaled circular tunnel model. Fengqiang et al. [18] simulated roadway spalling of sandstone samples containing circular holes caused by stress concentration under triaxial loading conditions. Gong et al. [20] experimented the spalling phenomena of scaled circular tunnel models under four different initial stress states. Hu et al. [25] tested granite samples containing circular holes under biaxial loading and captured the rockburst characteristics using acoustic emission (AE). The effect of the curvature radius of tunnels on the spalling failure has been investigated experimentally by Hui et al. [26] where the radius of curvature of circular tunnels affects fracture morphology and the mechanism of slabbing. However, the shape of the underground tunnels is not always circular and could take other shapes, such as elliptical, square, or inverted U-shaped. Therefore, the influence of an opening’s geometrical shapes on spalling failure and associated V-shaped formation has been investigated in the literature as shown in Fig. 6. Experimental results indicated that the failure process of the sidewall can be divided into four stages: quiet period, small particle ejection, spalling, and rockburst.

Fig. 6
figure 6

Formation of V-shaped notches in laboratory-scaled samples with different geometrical shapes a circular sandstone tunnel [66], b elliptical sandstone tunnel [66], c, rectangular granite tunnel [21], and d inverted U-shaped synthetic marble tunnel [72]

Full size image

3 Experimental setup

A multifunctional true triaxial testing system available at the Geotechnical Engineering Centre (GEC) of the University of Queensland was utilized in this study with the ability to perform the following: true triaxial loading, rock permeability of up to 10 MPa, hydraulic fracking of up to 52 MPa in three directions, thermo-mechanical modelling with an elevated temperature of up to 100 degrees with relative humidity control and configured to accommodate acoustic emissions and ultrasonic testing to detect the progressive damage to underground rock (see Fig. 7).

Fig. 7
figure 7

The true triaxial load testing facility at the University of Queensland [48]

Full size image

Bulk sandstones extracted from a quarry in Queensland state were used in this study and grouped into: 50 mm cubic sandstones used to investigate the CMCS concept under wide ranges of intermediate principal stresses (i.e. 40, 60, 80, and 100 MPa) and 50 mm laboratory-scale sandstones samples with 20 mm circular tunnels. To prepare the cubic and laboratory-scale tunnels, the cutting, grinding, and rotary coring machine available at the GEC was utilized. The microprocessor-controlled cutting machine has a cutting capacity of up to 90/115 mm of solid stock with 250/300 mm diameter cut-off wheels. The grinding machine has two hydraulic pumps connected to two 250 mm diameter metal wheels used for the vertical grinding of concrete, rock, and rock-like materials on two parallel faces. The rotary coring machine is equipped with an auger drilling pit setup with different diameters and lengths used to create holes into plain concrete, and porous rock or rock-like materials. Then, the bulk sandstone was cut into 50 mm cubic sizes, ground in all six faces to ensure smoothness and perpendicularity, and some of which were vertically augured to create 20 mm circular tunnels (see Fig. 8). Afterwards, all samples were oven-dried for 24 h at 50° C and then positioned inside the true triaxial cell for testing. Finally, both the cubic and scaled tunnels were tested under uniaxial (\({\sigma }_{1}={\sigma }_{c}\)), biaxial (\({\sigma }_{1}>{\sigma }_{2} , {\sigma }_{3}=0\)), generalized triaxial compression stress state (\({\sigma }_{1}>{\sigma }_{2}={\sigma }_{3})\), true triaxial (\({\sigma }_{1}>{\sigma }_{2}>{\sigma }_{3})\), and generalized triaxial tensile stress state (\({\sigma }_{1}={\sigma }_{2}>{\sigma }_{3}\)) tests as per the designated loading path of Table 2. An initial seating load of 5 kN was maintained to avoid the eccentricity of the sample before loading. Then, a loading rate of 15 kN/min was applied to satisfy the ISRM recommendations in the direction of the major (\({\sigma }_{1}\)), intermediate (\({\sigma }_{2}\)), and minor (\({\sigma }_{3}\)) principal stresses [19, 70] For triaxial and true triaxial tests, all principal stresses were increased simultaneously from the initial seating load to the designated minor principal stress load of \({\sigma }_{3}\) = 5, 10, 20, and 40 MPa. Then both \({\sigma }_{1}\) and \({\sigma }_{2}\) were increased simultaneously to the designated \({\sigma }_{2}\) value, whereupon \({\sigma }_{1}\) further increased to the spalling failure load of the tunnel. The loading path specified in Table 2 is based on reported spalling incidents that have occurred in weak rock formations such as sandstone at shallow depths ranging from 300–600 m [28]. According to Stephansson et al. [60], the minor in-situ stress at this depth typically is higher than 5 MPa assuming an average rock bulk density of 22 kN/m3. Thus, the loading path has been designed to encompass a wide range of confinements, representing field conditions.

Fig. 8
figure 8

Test setups: a Sandstone cubes for the true triaxial testing, and b A typical 20 mm laboratory-scale tunnel used in this study

Full size image
Table 2 Designated loading path of the tested sandstone
Full size table

4 Characterization and strength parameters

4.1 Chemical and mineralogical characterization

The chemical composition and crystalline structures of rocks should be considered in underground rock applications due to their possible reaction with cement (i.e. shotcrete used to prevent/remedy rockburst and spalling). As a future thought, the metals or metal oxides that exist in underground rock could be a potential source of electricity in deep structures. The literature is replete with various methods to detect the chemical composition of rocks, among them is the X-ray fluorescence (XRF) technique which has been used widely to analyze the chemistry of rocks and soils [30]. To determine the chemical composition of the tested sandstone, an XRF analysis was carried out on the sandstone core as summarized in Table 3. The light elements consist of two major groups of LiBeB (lithium, beryllium, and boron) and CNO (carbon, nitrogen, and oxygen) [52]. However, the most abundant light elements are carbon, nitrogen, and oxygen (CNO) [4]. The percentage of light elements in the tested core is 63% which are mainly in the form of silica (SiO2) given that the silicon percentage is over 26% (see Table 3). Typically, silica which comes in the form of quartz is the most common mineral component of sand. Other abundant elements in the tested sandstone are Aluminum (Al) and Iron (Fe) with 6% and 3%; respectively.

Table 3 Chemical analysis of sandstone performed using XRF
Full size table

In addition to the chemical composition, the presence of water in soft or porous rocks can degrade the strength [57]. From this point of view, measuring sandstone porosity is important. The sandstone porosity was measured as per the ISRM suggested methods and found to be in the range of 10–13%. To further investigate the orientation and distribution of the voids or pores along the sandstone at a microscopic level, a 2.0–3.0 mm thin section was prepared, glued on a rough glass-slide by an epoxy resin, and tested through a 10 × magnification polarizing microscope at the Institute for Molecular Bioscience (IMB) of The University of Queensland. As shown in Fig. 9, the voids (black spots) are distributed in a random fashion with some places being conglomerated by continuous voids. This indicates the high porosity of the sandstone.

Fig. 9
figure 9

The thin-section imaging of the sandstone under 10× magnification with a polarizing microscope

Full size image

4.2 Elastic and strength parameters

The proper estimation of rock or rock-like material strength, deformation, and elastic parameters characteristics is deemed necessary for a safe and sustainable design of underground structures. The Brazilian tensile strength (BTS) is widely accepted to determine rock indirect tensile strength (\({\sigma }_{\mathrm{t}}\)) where the ISRM suggests using an arc to apply a distributed load that has an angle range between 10–15° [55, 56]. The BTS test was carried out on disc samples (54 mm diameter and 27 mm thickness) by using an Instron 4505 load frame with a maximum capacity of 100 kN, loading rates of 100 N/sec, and a 25% stress sensitivity. A high-speed camera with a capability of recording up to 1,000,000 frames per second (fps) at a reduced resolution or 22.5 kHz at a full resolution of 1280 × 800 pixels was used to capture the initiation of tensile-induced cracks, as shown in Fig. 10. Phantom Camera Control (PCC) image processing software was used to identify the frame position where the first macro crack became visible and the last frame in which the sample became completely disintegrated. The BTS test results are in the range of 3.50–3.70 MPa with an average value of 3.6 MPa (see Table 4). The UCS is the most common, conventional, and simple test to determine the strength of rock samples. The cylindrical samples (40 mm diameter and 100 mm height) were prepared and tested as per the guidelines of the ISRM suggested methods for determining the uniaxial compressive strength and deformability of rock materials (1979) using the same loading frame, loading rate, and loading sensitivity of the BTS test. The average UCS of sandstone is 40 MPa as presented in Table 4. All measurements were made at atmospheric pressure and room temperature.

Fig. 10
figure 10

High-speed camera recording of the BTS test with a tensile crack speed of 164.60 m/s

Full size image
Table 4 Average elastic, uniaxial, and tensile strength parameters of the sandstone samples
Full size table

In common practice, the elastic parameters (i.e. Elastic modulus (\(E\)) and Poisson’s ratio (\(\nu\))) of rocks are measured using uniaxial compressive strength (UCS). To measure the elastic parameters (i.e. \(E\) and \(\nu\)) of the tested sandstone, strain gauges of a rosette type which contain vertical and horizontal elements were arranged so that the UCS sample had four in total equally spaced in the middle of the cylinder (Fig. 11). The elastic modulus is simply that applied vertical stress (\({\sigma }_{v})\) which causes a vertical strain captured by the vertical element of the rosette type strain gauge (\({\varepsilon }_{V SGs}\)), whereas Poisson’s ratio is simply the ratio between the horizontal to vertical strain measured by both elements of the strain gauges. The elastic parameters of sandstone (i.e., \(E\) and \(\nu\)) in addition to the uniaxial compressive strength (\({\sigma }_{c}\)) and the tensile strength (\({\sigma }_{t}\)) are summarized in Table 4.

Fig. 11
figure 11

Elastic parameter measurements through strain gauges at UCS test

Full size image

5 CMCS of cubic sandstone

Sandstone cubes were tested under uniaxial, biaxial, generalized triaxial compression stress state, true triaxial, and generalized triaxial tensile stress state loading conditions following the designated loading path of Table 2. Figure 12 summarizes the polyaxial failure results of the sandstone cubes where the peak strength of the sandstone first increased and then decreased with the increase of \({\sigma }_{2}\) at constant \({\sigma }_{3}\) values but in general is higher than the peak strength at the generalized triaxial compression stress state which agrees with the reported observations in the literature.

Fig. 12
figure 12

Polyaxial testing of the sandstone cubes

Full size image

Early attempts to apply three independent loads on underground rock specimens through a true triaxial load testing apparatus were not very successful until Mogi established a failure envelope in terms of the previously ignored combination of both \({\sigma }_{2}\) and \({\sigma }_{3}\) [11, 44]. This criterion asserted that failure will occur when the distortional strain energy reaches a critical value that increases monotonically with (\({\sigma }_{m,2})\) and, therefore, the fracture plane is resisted by the mean normal stress (\({\sigma }_{m,2})\) rather than the octahedral mean stress (\({\sigma }_{oct})\) [2]. Which is expressed as:

$${\tau }_{\mathrm{oct}}=\frac{1}{3}\sqrt{{\left({\sigma }_{1}-{\sigma }_{2}\right)}^{2}+{\left({\sigma }_{2}-{\sigma }_{3}\right)}^{2}+{\left({\sigma }_{1}-{\sigma }_{3}\right)}^{2}}$$
(2)
$${\tau }_{\mathrm{oct}}=a+b{\sigma }_{m,2}$$
(3)
$${\sigma }_{m,2}=\frac{{\sigma }_{1}+{\sigma }_{3}}{2}$$
(4)

The curve fitting parameters \(a\) and \(b\) represent the intersection and the inclination of \({\tau }_{oct}\)-axis, respectively. In triaxial data, the linear Mogi criterion coincides with the Coulomb criterion [2]. Therefore, the curve fitting parameters \(a\) and \(b\) can be related directly to material cohesion (\(c\)) and the angle of internal friction (\(\varphi\)) under triaxial stress states through the Mogi-Coulomb model as follows:

$$a=\frac{2\sqrt{2}}{3}C\,\,\mathrm{ cos}\varphi , b=\frac{2\sqrt{2}}{3}\mathrm{ sin}\varphi$$
(5)

To fit the Mogi-Coulomb criterion into the experimental data, the octahedral shear stress \({(\tau }_{oct})\) is plotted versus the effective mean normal stress (\({\sigma }_{m,2}\)) based on the applied principal stresses as presented in Fig. 13, where the curve fitting parameters are \(a=\) 13.814 and \(b=\) 0.4422. Then, the corresponding cohesion and angle of internal friction is calculated implicitly by minimizing the root mean square error (RMSE) (defined as the difference between the square root of the actual applied stress to the calculated stress). The relevant \(c\) and \(\varphi\) values for a minimum RMSE were 16.6 MPa and 27.9°, respectively. Figure 14 presents the best-fit curve of the tested sandstone via the Mogi-Coulomb failure criterion with the minimum RMSE of 2.6.

Fig. 13
figure 13

Mogi-Coulomb fitting parameters (\(a\),\(b\)) under true triaxial loading for sandstone samples

Full size image
Fig. 14
figure 14

Best fitting of Mogi-Coulomb failure criterion with minimum RMSE for the tested sandstone samples

Full size image

In addition to the Mogi-Coulomb failure criterion, other widely adopted three-dimensional failure criteria in the literature include Murrell, Stassi d’Alia, and Christensen. However, Mogi-Coulomb failure criterion produced lower errors and higher accuracy in fitting wider ranges of rock and rock-like materials [34, 42]. However, despite the simplicity of Christensen's criterion in fitting the intact rock failure using uniaxial compressive and uniaxial tensile strength, it has been shown that the model has some inherent mathematical characteristics which limit its potential for predicting the strength of rocks in compression [51].

The crack initiation stress (\({\sigma }_{\mathrm{ci}}\)) and crack initiation ratio (CIR) were determined using the volumetric strain, lateral strain, extensional strain, and TLSR methods as summarized in Table 5 (see also Fig. 15). To investigate the CMCS concept under wide ranges of intermediate principal stresses, the CI and CIR determination under \({\sigma }_{2}\)= 40, 60, 80, and 100 MPa for different values of \({\sigma }_{3}\)= 0, 5, 10, 20, and 40 MPa (represented by red rectangular in Fig. 12) were plotted in Figs. 16 and 17; respectively. From these figures, it is observed that for the same \({\sigma }_{3}\) value, the crack initiation stress threshold and the crack initiation ratio are almost the same for different values of \({\sigma }_{2}\)= 40, 60, 80, and 100 MPa. Therefore, it can be deduced that the variation in both \({\sigma }_{ci}\) and CIR is highly dependent on the minor principal stress. It can also be observed from Fig. 16 that the crack initiation stress first increases steadily in a linear trend at low values of \({\sigma }_{3}\) and, as it increases, the trend becomes increasingly non-linear for higher \({\sigma }_{3}\) values. That is, there is a certain value at which the CI stress threshold tends to deviate from its linearity and that could be attributed to the change of cracking mode from splitting (at low confinement) to sliding (at higher confinement) and that is in line with the newly proposed crack mode-changing stress (CMCS) concept. It is inferred from Fig. 17 that the crack initiation ratio first increases and then decreases. From this, two observations can be drawn. Firstly, the crack initiation ratio first increases steadily in a linear trend at low values of \({\sigma }_{3}\) and, as it increases, the trend of increase then decrease becomes non-linear at higher \({\sigma }_{3}\) values which means that there is a certain value where the CIR deviates from its linearity. Secondly, there is a reversal point after which the CIR decreases. The first observation supports the CMCS concept in a dimensionless domain through the most indicative predictor of crack initiation. It is deduced from the second observation that there is a certain value of the minor principal stress, where the crack initiation ratio decreases, which is equivalent to approximately 70% of the unconfined compressive strength. These findings of Figs. 16 and 17 support the CMCS concept proposed by Mutaz et al. [46] in (i) wide ranges of intermediate principal stresses and (ii) in a dimensionless domain of CIR which is the most indicative predictor of the in-situ spalling strength. Both figures show that the CMCS value is around 20 MPa.

Table 5 Crack initiation stress and crack initiation ratio of the sandstone cubes
Full size table
Fig. 15
figure 15

Determination of CI via a volumetric strain method, b lateral strain method in the direction of \({\varepsilon }_{2}\), c lateral strain method in the direction of \({\varepsilon }_{3}\), d extensional strain method in the direction of \({\varepsilon }_{2}\), e extensional strain method in the direction of \({\varepsilon }_{3}\), and f TLSR method (\({\sigma }_{1}=\) 100 MPa, \({\sigma }_{2}=\) 100 MPa, \({\sigma }_{3}=\) 10 MPa)

Full size image
Fig. 16
figure 16

Variation in crack initiation stress by \({\sigma }_{3}\) for \({\sigma }_{2}\)= 40, 60, 80 and 100 MPa

Full size image
Fig. 17
figure 17

Variation in crack initiation ratio by \({\sigma }_{3}\) for \({\sigma }_{2}\)= 40, 60, 80 and 100 MPa

Full size image

Unlike the intermediate principal stress, the minor principal stress has a more profound effect on both the crack initiation stress threshold and the crack initiation ratio, and it plays a vital role in controlling the crack mode at the crack initiation level. While the intermediate principal stress controls the crack damage stage, the minor principal stress has a greater role at the crack initiation level. This finding is practically very important since it suggests that designing structures in rock formations prone to spalling would be very sensitive to the accurate determination of the major and minor principal stresses at the site. The role of minor principal stress is not small or trivial in inducing spalling failure and should be carefully considered.

6 Validation of CMCS in laboratory-scale circular tunnels

6.1 Stress-induced spalling of the laboratory-scale circular tunnels

To study the formation and propagation of the stress-induced spalling fractures around the sidewall of high-stressed laboratory-scale tunnels under polyaxial loading conditions, 22 sandstone cubes (50 × 50 × 50 mm) with 20 mm central circular tunnels were tested following the designated loading path of Table 2 (see Fig. 18). The principal stresses that induce spalling failure of the tested scaled tunnels are summarized in Table 6 and graphically presented in Fig. 19. Limited three-dimensional models for spalling failure of circular tunnels are encountered in the literature. Hence, Fig. 19 presents a three-dimensional model for circular tunnels of porous sandstone.

Fig. 18
figure 18

Laboratory-scale circular tunnel positioned inside the true triaxial cell

Full size image
Table 6 Principal stresses of the 20 mm circular tunnels
Full size table
Fig. 19
figure 19

Uniaxial, biaxial, triaxial and true triaxial testing of laboratory-scale tunnels

Full size image

It is obvious from Fig. 19 that the peak strength (i.e.,\({\sigma }_{1}\)) of the circular tunnels increases in a non-linear fashion from the generalized triaxial compression stress (\({\sigma }_{1}>{\sigma }_{2}={\sigma }_{3})\) to the generalized triaxial tensile stress (\({\sigma }_{1}={\sigma }_{2}>{\sigma }_{3}\)) at different \({\sigma }_{2}\) values under constant values of\({\sigma }_{3}\). Therefore, the peak strength of the tunnels first increased and then decreased with the increase of \({\sigma }_{2}\) at constant \({\sigma }_{3}\) values but in general is higher than the peak strength at the generalized triaxial compression stress state similar to what was observed with the cubic sandstone (see Fig. 12).

For a better characterization of the stress-induced spalling failure of the circular tunnel in a dimensionless domain, one can derive a peak stress ratio (PSR) defined as the ratio of the peak stress of the cubic sandstone (i.e., intact rock) to the peak stress of the laboratory-scale tunnel as following:

$$\mathrm{PSR}=\frac{{\sigma }_{1\left(p-\mathrm{intact}\right)}}{{\sigma }_{1\left(p-circular \,tunnel\right)}}$$
(6)

In fact, the PSR can be treated as the CIR of the circular tunnels where the measured peak strength induces spalling failure around the tunnel sidewall (\({\sigma }_{1(p-circular tunnel)}\)) is compared to the correspondence peak strength at intact conditions (\({\sigma }_{1(p-\mathrm{intact})}\)). From this perspective, the PSR is measured by comparing \({\sigma }_{1(p-\mathrm{circular tunnel})}\) from Table 6 with the corresponding value of the intact cubic sandstone (\({\sigma }_{1(p-\mathrm{intact})}\)) from Table 5 and summarized in Table 7 below. It can be deduced from Table 7 that the PSR is ranging from 0.33 to 0.71. The lowest PSR value is under the uniaxial loading condition. That is, the PSR can be considered as the CIR of circular tunnels with typical ranges and concepts.

Table 7 Principal stresses of both cubic samples and laboratory-scale circular tunnels
Full size table

Kirsch’s equation provides a planner solution to the in-situ stresses developing around a horizontal tunnel of a circular cross-section in which the rock mass is assumed to be a continuous, homogenous, and isotropic medium obeying Hook’s law [27]. Since the past century, Kirsch’s equation presented a famous equation concerning the stresses in an infinite plane with a circular hole and has been used widely in different rock mechanic aspects [27]. According to Kirsch’s equation, the induced tangential stress components at the boundaries of deep tunnels (i.e. circular openings in an infinite medium) are independent of the tunnel diameter. In the literature, Kirsch’s solution has been used also to determine the maximum tangential stresses (\({\sigma }_{\theta max}\)) in laboratory-scale tunnels by assuming that the rock mass can be regarded as an elastic body [20, 21, 35, 58]. However, experimental results revealed that tangential stresses around the boundary of an opening in laboratory-scale models are mainly independent of the hole diameter when the ratio of specimen size to hole diameter is over 10 [34]. Previous studies shows that the tunnel diameter (\(d\)) has a great influence on the development of the maximum tangential stress and hence the spalling failure around the sidewall (refer to Fig. 20) [33, 34, 37]. The ratio of the maximum tangential stress to the unconfined compressive strength is always greater than 1 when \(d\) < 75 mm due to the strength size effect which is related to the formation of microcracking in the region of a high-stress gradient that affects the failure mode and fracture mechanism of spalling failure and is more pronounced in smaller diameter holes and approaching or exceeding twice the unconfined compressive strength when \(d\le\) 20 mm [20, 26, 31, 34]. That is, the smaller the diameter is, the more obvious the strength size effect is [35]. This implies that the geometrical shape of scaled tunnels requires careful consideration in crack initiation studies [33, 34]. As the hole diameter in this study is 20 mm with a ratio of specimen size to hole diameter of 2.5, the results as presented in Table 8 (where \({\sigma }_{\theta max}\)/\({\sigma }_{1}\) > 1 in the sidewall of the circular tunnels) show an obvious strength size effect and are consistent with the reported work in the literature [20, 36]. In addition to the above, a 20 mm diameter hole was preferred in order to provide sufficient space for identifying the severity of spalling based on the intensity of small fragments ejection, and also to enable better visual observation of the formation of V-shaped notches under different stress conditions.

Fig. 20
figure 20

Effect of hole diameter on the tangential stresses of circular tunnels [20, 37]

Full size image
Table 8 Maximum tangential stresses (\({\sigma }_{\theta max}\)) of the laboratory-scale circular tunnels
Full size table

6.2 True triaxial testing

To better understand the effect of both the intermediate and the minor principal stresses on the induced spalling failure around the sidewall of the scaled tunnels, the variation of both the peak applied stress (\({\sigma }_{1}\)) and the peak stress ratio (PSR) with \({\sigma }_{2}\) and \({\sigma }_{3}\) were investigated. In Fig. 21 the variation of \({\sigma }_{1}\) with \({\sigma }_{2}\) at different values of \({\sigma }_{3}\)= 5, 10, 20 and 40 MPa was plotted. A significant increase of \({\sigma }_{1}\) from 34 to 71 MPa was observed followed by a slight decrease with the increase of \({\sigma }_{2}\). In other words, the major principal stress (i.e., peak stress) first increases steadily at low values of \({\sigma }_{2}\) and, as \({\sigma }_{2}\) increases beyond 50% of \({\sigma }_{1}\), the trend becomes slightly decreasing. Higher dispersion of \({\sigma }_{1}\) was observed especially at lower and higher \({\sigma }_{2}\) values.

Fig. 21
figure 21

Variation in \({\sigma }_{1}\) by \({\sigma }_{2}\) for \({\sigma }_{3}\)= 5, 10, 20 and 40 MPa for circular tunnels

Full size image

The PSR can better characterize the spalling failure of circular tunnels in a dimensionless domain. From this perspective, the variation of the PSR with both \({\sigma }_{2}\) and \({\sigma }_{3}\) has been investigated, as shown in Figs. 22 and 23, respectively. At the same \({\sigma }_{3}\), the PSR increased and then decreased by the increase of \({\sigma }_{2}\) as shown in Fig. 22. On the other hand, at the same \({\sigma }_{2}\), the dispersion of PSR is high, and no obvious trend of variation is observed.

Fig. 22
figure 22

Variation in PSR by \({\sigma }_{2}\) for \({\sigma }_{3}\)= 5, 10, 20 and 40 MPa for circular tunnels

Full size image
Fig. 23
figure 23

Variation in PSR by \({\sigma }_{3}\) for \({\sigma }_{2}\)= 40 and 60 MPa for circular tunnels

Full size image

Sets of \({\sigma }_{1}>{\sigma }_{2}\ge {\sigma }_{3}\) at \({\sigma }_{2}\)= 40 and 60 MPa at different values of \({\sigma }_{3}\)= 5, 10, 20 and 40 MPa were deliberately selected from Fig. 19 to study the variation of the peak stress ratio. Figure 23 represents the variation in the peak stress ratio with \({\sigma }_{3}\) at constant values of \({\sigma }_{2}\)= 40 and 60 MPa. It is inferred that the peak stress ratio first decreased with the increase of \({\sigma }_{3}\) at constant values of \({\sigma }_{2}\)= 40 and 60 MPa. The highest value of PSR was reported at \({\sigma }_{3}\) = 5 MPa and \({\sigma }_{2}\)= 40 MPa. By the increase of \({\sigma }_{3}\) from 5 to 40 MPa, the PSR decreased significantly by over 40%. On the other hand, at the same \({\sigma }_{3}\) value, the PSR decreased with the increase of \({\sigma }_{2}\). Despite that the dispersion of the PSR is relatively high, there is a certain value where the dispersion becomes the minimum and independent of \({\sigma }_{2}\) as highlighted by the red rectangle in Fig. 23. Interestingly, the dispersion-less point of PSR is at \({\sigma }_{3}\)= 20 MPa which is the CMCS as discussed before. That is, this dispersion-less point of \({\sigma }_{3}\) coincides with the mean of the proposed crack mode-changing stress (CMCS) concept.

As an outcome of this study carried out on laboratory-scale circular tunnels, the CMCS concept can be expanded to include the point at which the dispersion of the peak stress ratio (defined as the ratio of the peak stress of the cubic rock to the peak stress of the circular tunnel) becomes the minimum and independent of \({\sigma }_{2}\) at the same \({\sigma }_{3}\) value.

6.3 Post-spalling failure shape

The failure process of the laboratory-scale tunnels before the induced spalling occurs is basically similar for all samples. At the early stage of failure, the sidewall begins to undergo failure at the location of the maximum tangential stress around the sidewall in terms of rapid ejection of small fragments which fly from the sidewall to the floor with an initial velocity. As the applied vertical stress (i.e., major principal stress \({\sigma }_{1}\)) increases, the cracks around the hole propagate continuously and coalesce to form rock slabs of spalling failure parallel to the sidewall along the direction of out-of-plane stress (i.e., \({\sigma }_{3}\)). Then, rock slabs flake, causing rock fragment ejection, and as a result, an obvious failure zone forms along the sidewall due to the buckling deformation, forming a V-shaped notch. However, it has been observed that post-spalling failure is not similar for all scale tunnels and is highly dependent on the applied 3D stresses.

Under biaxial conditions, obvious shear cracks were formed associated with rock fragments ejection that propagates from the sidewall to the far-field stress direction especially under low intermediate principal stresses as depicted in Fig. 24. To investigate the effect of the applied principal stresses on post-spalling failure, the tested tunnels were grouped based on the applied \({\sigma }_{2}\) at the same \({\sigma }_{3}\), as detailed in Fig. 25.

Fig. 24
figure 24

Stress-induced fractures of tested sandstone under biaxial condition: a \({\sigma }_{1}=28\mathrm{ MPa}, { \sigma }_{2}=5\mathrm{ MPa}\), b \({\sigma }_{1}=30\mathrm{ MPa}, { \sigma }_{2}=10\mathrm{ MPa}\), and c \({\sigma }_{1}=43\mathrm{ MPa}, { \sigma }_{2}=20\mathrm{ MPa}\)

Full size image
Fig. 25
figure 25

Post-spalling failure of the circular tunnels at [1]\({\sigma }_{3}=5\mathrm{ MPa}\): a \({\sigma }_{1}=34\mathrm{ MPa}, {\sigma }_{2}=5\mathrm{ MPa}\) b \({\sigma }_{1}=35\mathrm{ MPa}, {\sigma }_{2}=10\mathrm{ MPa}\) c \({\sigma }_{1}=54\mathrm{ MPa}, {\sigma }_{2}=20\mathrm{ MPa},\) [2]\({\sigma }_{3}=10\mathrm{ MPa}\): d \({\sigma }_{1}=46\mathrm{ MPa}, {\sigma }_{2}=10\mathrm{ MPa}\) e \({\sigma }_{1}=54\mathrm{ MPa}, {\sigma }_{2}=20\mathrm{ MPa}\) f \({\sigma }_{1}=63\mathrm{ MPa}, {\sigma }_{2}=40\mathrm{ MPa}\), [3]\({\sigma }_{3}=20\mathrm{ MPa}\): g \({\sigma }_{1}=54\mathrm{ MPa}, {\sigma }_{2}=20\mathrm{ MPa}\) h \({\sigma }_{1}=68\mathrm{ MPa}, {\sigma }_{2}=40\mathrm{ MPa}\) i \({\sigma }_{1}=71\mathrm{ MPa}, {\sigma }_{2}=60\mathrm{ MPa}\), [4]\({\sigma }_{3}=40\mathrm{ MPa}\): j \({\sigma }_{1}=71\mathrm{ MPa}, {\sigma }_{2}=40\mathrm{ MPa}\) k \({\sigma }_{1}=72\mathrm{ MPa}, {\sigma }_{2}=60\mathrm{ MPa}\) l \({\sigma }_{1}=71\mathrm{ MPa}, {\sigma }_{2}=71\mathrm{ MPa}\)

Full size image

The stress-induced spalling fractures for the generalized triaxial tensile stress conditions under low values of \({\sigma }_{3}\) propagated diagonally along the sidewall at an angle of 45° to the direction of \({\sigma }_{2}\). However, at higher values of \({\sigma }_{3}\) of 20 and 40 MPa, the spalling fractures around the tunnel axis propagated in two diagonal directions at angles of 45° and 135° to the direction of \({\sigma }_{2}\) (see Fig. 25). This change in crack pattern is dependent on the applied out-of-plane minor principal stress. In other words, there is a critical value of the minimum principal stress at which the stress-induced fractures of the spalling failure around circular tunnels undergo a change in the propagation pattern under a generalized triaxial tensile stress state. Given that the CMCS is 20 MPa, moving from \({\sigma }_{3}\) of 5 and 10 MPa (i.e., \({\sigma }_{3}\)< CMCS) to \({\sigma }_{3}\) of 20 and 40 MPa (i.e., \({\sigma }_{3}\ge\) CMCS) under the generalized triaxial tensile stress conditions changes the cracking pattern from single diagonal cracks at 45° to the direction of \({\sigma }_{2}\) to double diagonal cracks at 45° and 135° to the direction of \({\sigma }_{2}\) (see the schematic drawings of Fig. 26). That is, under a generalized triaxial tensile stress state, the CMCS has a significant effect on changing the crack propagation pattern along the sidewall of the tunnels.

Fig. 26
figure 26

Schematic drawing of the fracture propagation angles at generalized triaxial tensile stress state

Full size image

Referring to Fig. 25, the post-spalling failure shape of the circular tunnels changed to an oval shape at \({\sigma }_{3}\ge 20\mathrm{ MPa}\). Giving that the CMCS = 20 MPa, it can be deduced that the post-spalling failure shape of the circular tunnels tends to change to an oval shape when the applied out-of-plane stress exceeds the CMCS. An explanation of this change in shape at spalling failure could be attributed to the fact that at the CMCS point, the crack initiation threshold, as an indicative predictor of spalling failure, experiences a change in the fracturing pattern from splitting to sliding. This change in pattern can affect the overall failure shape around the tunnel, and hence the tunnel shape changes from circular to an oval shape. From the fracture angle perspective, at the CMCS, the fracture angle variation of the cubic samples becomes non-linear [45], while from the failure shape of tunnels' point of view, at the CMCS, the failure shape changes from circular to oval. A similar observation has been reported in the literature by Luo et al. [35] on sandstone cubes by increasing the out-of-plane stress (i.e., \({\sigma }_{3}\)) from 51 to 73 MPa as shown in Fig. 27.

Fig. 27
figure 27

Post-spalling failure mode of red sandstone tunnels: a circular shape at \({\sigma }_{3}=51\mathrm{ MPa}\), b oval shape at \({\sigma }_{3}=73\mathrm{ MPa}\) [35]

Full size image

It can be concluded that the CMCS has a profound effect on shaping spalling failure. From a practical point of view, determining the minor principal stress or the out-of-plane stress is deemed necessary in understanding the spalling phenomenon and should be considered in the design of underground tunnels.

7 Summary and conclusion

Simulating the spalling failure using laboratory-scale tunnels can mimic the in-situ condition in more realistic way. Based on experimental testing carried on 50 mm cubic sandstones with 20 mm circular central tunnels tested under uniaxial, biaxial, generalized triaxial compression stress state, generalized triaxial tensile stress state, and true triaxial loading, the following outcomes were drawn from this study:

  • The applied peak stress of the circular tunnels (\({\sigma }_{1}\)) first increased and then decreased with the increase of \({\sigma }_{2}\) at constant \({\sigma }_{3}\) values but in general is higher than the peak strength at the generalized triaxial compression stress state. This behavior is like what was observed with the cubic samples under polyaxial stress loading.

  • While the induced tensile crack of spalling failure propagates along the sidewall parallel to the excavation boundary in the direction of the out-of-plane principal stress, the propagation of the spalling failure becomes in the diagonal direction to the tunnel axis under generalized triaxial tensile stress state with an angle of 45 degrees with the direction of the intermediate principal stress.

  • Approaching the CMCS and beyond, the propagation pattern of the tensile-induced cracks under generalized triaxial tensile stress state becomes in two diagonal patterns along the tunnel sidewall at angles of 45 and 135 degrees to the direction of the intermediate principal stress. In conclusion, the CMCS not only changed the crack initiation mode but can also change the crack propagation pattern along the sidewall of circular tunnels under a generalized triaxial tensile stress state.

  • For a better characterization of the stress-induced spalling failure of the circular tunnel in a dimensionless domain, a peak stress ratio (PSR) defined as the ratio of the peak stress of the cubic samples (i.e., intact rock) to the peak stress of the laboratory-scale circular tunnels is introduced as a predictor of the crack initiation ratio (CIR) of circular tunnels. The measured PSR of the laboratory-scale tunnels is having the typical range of the CIR for the cubic samples.

  • At the same \({\sigma }_{3}\), the PSR increased and then decreased with the increase of \({\sigma }_{2.}\) On the other hand, the PSR decreases with the increase of \({\sigma }_{3}\) at same \({\sigma }_{2}\) value.

  • At the CMCS, the dispersion of the PSR becomes the minimum and independent \({\sigma }_{2.}\).

  • At the post-spalling failure, the shape of the circular tunnels tends to change to an oval shape when the applied out-of-plane stress exceeds the CMCS.

As a result of this study, the CMCS concept can be broadened to interpret the spalling failure of the laboratory-scale circular tunnels as follows: the CMCS is the point where the spalling failure around the circular tunnels has a change in the propagation pattern at the generalized triaxial tensile stress state from a single diagonal crack with 45° from the direction of the intermediate principal stress to double diagonal cracks with 45° and 135° from the direction of the intermediate principal stress, or the point where the dispersion of the PSR becomes the minimum and independent of the intermediate principal stress, or the point where the post-spalling failure shape of circular tunnels changes from circular to an oval shape.