1 Introduction

The time-dependent characteristics of rock mass significantly affect the long-term stability of underground constructions. Rock creep behavior as a challenging and significant topic has a considerable application in geotechnical and mining engineering (Tarifard et al. 2022). Underground energy storage facilities, oil and gas well drilling, and long-term stability of deep underground spaces and mining operations are some applications of creep analysis in rock engineering projects (Sharifzadeh et al. 2013; Firme et al. 2018; Dehghan and Khodaei 2021; Liu et al. 2023). Many factors also affect the creep behavior of rocks, such as temperature, stress level, rock anisotropy, water content, etc., which highlight the intricate nature of rocks’ creep behavior (Li et al. 2020b; Shan et al. 2021; Kou et al. 2023).

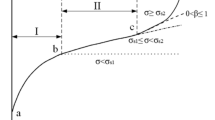
Generally, the creep deformation of rocks is separated into three phases, primary (first or transient), steady-state (secondary), and third (tertiary or accelerated) creep stages. According to Fig. 1, the initial stress leads to immediate strain, while the creep strain occurs over time under constant stress. Previous experimental investigations have shown that the strain rate decreases with time in the transient creep stage. Releasing the stress at point A rapidly decreases strain to point B, followed by a gradual decline to zero at point C. Thus, the first region (I) can be classified as viscoelastic properties. For the secondary creep stage, the strain rate remains constant over time and the creep will be stable. The viscoplastic behavior refers to permanent deformation that occurs upon stress removal. The third phase of creep behavior is characterized by increased microcracking within the material, reducing strength and stiffness. Eventually, the material fails and loses its ability to withstand further loads (Wang et al. 2019; Frenelus et al. 2022).

Fig. 1
figure 1

Common rock creep deformation caused by constant stress

Full size image

Creep behavior also can be characterized based on the acting stress, volumetric and deviatoric creep. The volumetric creep behavior includes the first phase of creep, and then it generally stabilizes; the constant volumetric stress creates it. According to the shear mobilization, deviatoric creep may encompass either all three phases or not. The constant deviatoric stress is the primary factor leading to deviatoric creep. Only the initial creep phase takes place when the deviatoric stress remains low. However, once a specific threshold of shear mobilization is surpassed, the secondary stage succeeds the primary phase, which can potentially progress into the accelerated phase and ultimately result in creep rupture.

In previous research, many vital studies were performed on the rock’s creep behavior and its application in underground construction. Creep constitutive models represent a crucial aspect in the study of rock creep; typically, they can be categorized into empirical, component-based, and mechanism-based (Zhou et al. 2013). The empirical models rely on the creep experimental results and contain fewer parameters. Standard elements like the Hooke spring, Newton dashpot, frictional elements, etc., are combined to create the component models. Although they can flexibly describe various creep deformations, their constitutive equations are mathematically challenging (Zhou et al. 2011). The primary focus of the mechanism-based creep models is on the mechanical response, including micro-scale cracking and the growth of damage (Li et al. 2020b).

The time-dependent stability analysis of underground constructions excavated in soft and weak rocks has been researched broadly. For instance, Tarifard et al. (2022) analyzed the long-term stability of the Shibli tunnel excavated in the highly fractured weak rock mass by considering the creep characteristics of rocks and groundwater effect. Many researchers also focus on the creep behavior of rock salt because of its application in the industry (Wu et al. 2022; Zhao et al. 2022); it has been determined that salt rock mass with low porosity and permeability is ideal for storing crude oil and natural gas (Zhou et al. 2011). The effect of rock creep behavior on oil wells’ stability is another significant challenge in the oil industry (Dehghan and Khodaei 2021). The next special issue in rock creep studies is the creep model’s parameters identification. Ground movement monitoring and creep test results were utilized to determine the parameters of the creep model. For instance, Sharifzadeh et al. (2013) employed a displacement-based direct back analysis to adopt creep model parameters for weak rock mass.

The primary objective of this study is to analyze various creep constitutive models by discussing their key characteristics and applicability in geomechanics. To achieve this, we initially reviewed the creep models, with a specific focus on their ability to replicate the accelerated phase of rock creep and their corresponding damage variables. Subsequently, we discussed the accuracy of the existing models in simulating tertiary creep phases in rocks by comparing their performance with various creep test data. Lastly, we explained the practical application of creep analysis in geotechnical engineering projects, highlighting the employed creep models and the methods utilized for determining creep parameters in rock masses.

2 Creep constitutive models

As previously mentioned, creep models are generally classified into empirical, component, and mechanism-based models. This section introduces previously proposed models for each category and discusses their key features.

2.1 Empirical creep models

Empirical models, which are typically fitted using creep test results, have been employed to predict the creep behavior of rocks. These models can explain rheological behaviors under various stress paths but need many creep experiments to establish (Jia et al. 2018). An important consideration when suggesting empirical models is choosing the proper fitting function. The Power, Exponential, and Morgan Mercer Flodin growth functions are the most common fitting functions in the empirical models (Table 1) (Chen and Kulatilake 2015; Sun et al. 2016). The Norton Power Law is also used frequently for modeling rock creep behavior, but this model cannot simulate the accelerated stage of rock creep (Liu et al. 2021c). The Bailey-Norton Law, or Time Hardening Law, is another empirical model utilized to model the first and steady-state phases of creep, and it is essential to adopt a positive initial time (May et al. 2013). The Exponential function has been used to simulate the first and second phases of creep (Chen and Kulatilake 2015). As shown in Table 1, the Morgan Mercer Flodin growth is an asymmetrical sigmoidal function with four parameters (Sun et al. 2016).

Table 1 The common fitting function for empirical creep models
Full size table

Empirical creep studies were conducted using the different fitting functions and creep test results. For instance, Sun et al. (2016) proposed a novel empirical model derived from triaxial drained creep experiments conducted on grave clay within the slip zone. They used the Morgan Mercer Flodin growth function for this purpose. Chen and Kulatilake (2015) used the Power and Exponential functions to propose an empirical model that describes the creep characteristics of marble. The study found that the Exponential function, which utilizes two parameters, aligns well with the experimental findings. Eslami et al. (2018) analyzed the creep test results of salt to create an experimental creep model using linear and nonlinear regression. The suggested empirical model and the updated Lubby 2 model were compared to the creep test results to validate the obtained results. At an approximate determination factor of 93%, both models exhibited relatively favorable conformity with the data obtained from the creep tests. Lai et al. (2010) proposed the unsaturated Singh-Mitchell creep model based on unsaturated triaxial creep test results. They recommended a novel stress intensity that accounted for matric suction and developed the Singh and Mitchell creep model.

2.2 Component-combined creep models

Component-combined models have been widely used and play a significant role in rock rheological behavior. These types of models, typically, are composed of elastic, dashpot, and plastic elements, connected in series and parallel combinations. Table 2 represents the common elements used in the elements-combined models.

Table 2 The common elements used in the elements-combined models
Full size table

Hooke’s element was employed to represent elastic behavior, while Newton’s dashpots were utilized to represent viscous behavior. The St. Vincent component serves as a plastic element characterized by yield stress (or long-term strength), and through a suitable combination with other elements, viscoplastic deformation and the tertiary phase of rock creep could be effectively simulated. This combination remains inactive when stress is below the long-term strength threshold but becomes active when stress surpasses this threshold.

Previously, certain components were developed based on the framework of fractional calculus theory. The fractional calculus theory, as a fascinating approach to address complex problems in mathematical physics modeling, can provide a more accurate representation of the nonlinear creep properties exhibited by materials. (Zhou et al. 2011). Presently, three widely acknowledged definitions of the fractional derivative exist, the Riemann–Liouville fractional derivative, the Caputo fractional derivative, and the Grünwald Letnikov fractional derivative (Feng et al. 2021). A typical example of a fractional calculus application is the Abel dashpot (Table 2). For this dashpot, the connection between stress and strain is deduced using the principles of the Riemann–Liouville operator (Lyu et al. 2021). When the fractional order falls between 0 and 1, the Abel dashpot can effectively replicate the viscoelastic behavior. In addition, the Abel dashpot was used to simulate the tertiary stage of rock creep, where the fractional order exceeds 1 (Liu et al. 2020). Figure 2 shows that by adjusting the fractional order, various creep curve patterns can be achieved.

Fig. 2
figure 2

Creep curves of Abel dashpot: a fractional order is between 0 and 1; b fractional order is higher than 1

Full size image

Feng et al. (2021) proposed the VFT–Caputo–Mainardi dashpot by utilizing the combination of the Caputo-Mainardi dashpot and the temperature-dependent viscosity. This innovative dashpot was employed to model viscoelastic behavior by considering temperature effects.

By combining the elements, different phases of rock creep can be simulated. Table 3 represents the classical creep models and Fig. 3 shows creep curves for most known component-combined models. As shown in Table 3, the Maxwell model includes the elastic body and viscous dashpot combined in series. The Maxwell model can successfully model the instantaneous and incremental strain but cannot simulate the visco-plastic behavior. For the Kelvin model, the spring is connected in parallel with Newton’s dashpot. The Kelvin model can replicate the initial stage of creep in rocks. The generalized Kelvin model, also called the three-element model, incorporates the Kelvin model and an elastic component in a sequential arrangement. This model can simulate the instantaneous strain and first stage of creep.

Table 3 The classic elements-combined models
Full size table
Fig. 3
figure 3

Creep curves for different classic models

Full size image

On the other hand, the Burger creep model is constructed by connecting the Kelvin and Maxwell models in series, which can successfully model the instantaneous strain, the first and secondary stages of creeps. The Burger and the Lubby 2 models contain the same framework. In the Lubby 2 model, the Kelvin and Maxwell bodies variables have a non-linear relationship with stress. Like the Burger model, it simulates the first and secondary creep phases well but cannot explain the tertiary stage’s behavior. When simulating the injection and withdrawal cycles, the Lubby 2 constitutive model may anticipate a negative strain rate (reverse creep) proportionate to the unloading rate, which will direct how caverns operate (Eslami et al. 2018).

The Bingham model is composed of an elastic unit connected in series with a viscoplastic body, which includes the dashpot with the coefficient of viscosity \(\eta\) and the slider with threshold stres \({\sigma }_{s}\). In this model when \(\sigma <{\sigma }_{s}\), the slider and the viscoplastic element are inactive. The j-body model is constructed from a series of elastic and Maxwell bodies; this model cannot simulate the third creep stage.

Table 3 shows the Burger-creep visco-plastic (CVISC) model. The model behaves as a visco-elastoplastic material if the applied stress is greater than the yielding stress of the slider. On the contrary, when the model is subjected to stress below the point of yielding, it behaves similarly to the Burger body. In addition, the Nishihara model is formed through the arrangement of elastic, viscoelastic, and viscoplastic bodies in a series configuration. In the case of \(\sigma < {\sigma }_{s}\) the viscoplastic element is not active, so the model behaves like the generalized Kelvin model, when \(\sigma \ge {\sigma }_{s}\) all three parts of the model become active.

Other researchers have also proposed various models by combining and improving different elements. Niu et al. (2021) enhanced the Nishihara model by supposing a time-dependent viscosity coefficient for the viscoplastic body determined using Eq. (1). The creep strain corresponding to the tertiary phase under uniaxial stress state was then proposed as Eq. (2).

$${\acute{\eta}}_{2}(t)=\frac{{\eta }_{2}}{A{t}^{2}-Bt+C}$$
(1)
$${\varepsilon }_{3}=\frac{\sigma -{\sigma }_{s}}{{\eta }_{2}}\left(\frac{A}{3}{t}^{3}-\frac{B}{2}{t}^{2}+Ct\right)$$
(2)

where A, B, and C are constant. The three-dimensional creep equations for this model (refer to Table 4) were proposed under the assumption of zero volume strain during creep. To validate the model, triaxial creep test results of damaged sandstone were employed, demonstrating a high degree of fitting. Yu et al. (2020) also enhanced the Nishihara model by introducing a nonlinear viscous dashpot with a strain trigger to simulate the third stage of rock creep. The constitutive equation of this dashpot was calculated as:

Table 4 Component-combined creep models
Full size table
$${\varepsilon }_{3}=\frac{\sigma }{{\eta }_{{\text{nl}}}}{\left(\frac{t-{t}_{F}}{{t}_{{\text{un}}}}\right)}^{n}$$
(3)

here, \({t}_{F}\) represents the time at which rocks enter the tertiary creep phase and is determined based on creep test results. The rheological index, denoted by n, signifies the rate at which the accelerated creep rate rises by increasing n. \({t}_{{\text{un}}}\) was utilized to remove the constant time dimension and was supposed to be 1. The model was validated using triaxial creep test results conducted on strongly weathered sandstone and sandy mudstone sourced from the dam foundation, and rocks surrounding the tunnel, demonstrating its applicability.

Yang and Li (2018) substituted the viscous elements in the Nishihara model with fractional derivative soft-matter components, enhancing the simulation of primary and steady-state creep phases. Subsequently, they introduced a novel viscoplastic body, as outlined in Table 4, to effectively capture the tertiary phase of rock creep. Furthermore, they assumed that the viscosity coefficient of the soft-matter components varies as a function of stress and time. Validation of the model was achieved through creep test results on frozen soft rock. Equation (4) illustrates the creep strain of rock during the tertiary phase.

$${\varepsilon }_{3}=\frac{\sigma }{\eta }\left\{{e}^{{\left[\frac{t-{t}_{2}}{t-{t}_{c}}\right]}^{r}}-1\right\}$$
(4)

here \({t}_{2}\) corresponds to the start time of the accelerated stage and \({t}_{c}\) is the failure time. Meanwhile, Yang et al. (2014) suggested a visco-elastoplastic creep model that simulates diabase’s first, second, and tertiary creep stages by combining Hooke, a visco-elastoplastic Schiffman, and viscoplastic bodies. The suggested model was integrated into the FLAC3D software, and its creep analysis was compared with the CVISC model for validation. The comparative results indicated that at low stress levels, the creep curves of both models are the same. They concluded that at high stress levels, the CVISC model fails to accurately capture the steady-state creep and tertiary creep induced by viscoplastic properties.

2.3 Mechanism-based creep constitutive models

The mechanism-based creep models’ central objective is to study the mechanical reactions occurring at the microscopic level, such as cracking and the expansion of damage. Damage mechanics primarily examines the phase preceding the emergence of macroscopic visible cracks or deficiencies (the stage of initiation, growth, convergence, and spread of microcracks) (Yan et al. 2020). Many kinds of research showed that rock damage exhibits time-dependent properties (Hou et al. 2019). Damage variables play an essential role in determining the structural and mechanical properties of geotechnical materials. Developing damage creep models necessitates defining the appropriate damage variable. Li et al. (2023b) stated that the established theoretical foundations for defining damage variables can be categorized into three groups: the effective bearing area, geometric damage theory, and statistical damage theory.

The Nishihara model, one of the popular models, has been enhanced by researchers to represent the rock’s creep behavior more accurately. Feng et al. (2021) modified the Nishihara model and replaced viscosity dashpots with the Caputo-Mainardi and the VFT–Caputo–Mainardi dashpots, introducing the fractional temperature-dependent Nishihara-type model (TDNM), as shown in Table 5. In this model, the thermal damage effective stress ( \({\sigma }_{{\text{eff}}}\)) was defined to characterize the tertiary phase of rock creep by considering the continuum damage mechanics, and the Weibull distribution statistics as Eq. (6).

Table 5 Examples of modified Nishihara constitutive models
Full size table
$$D=1-{\text{exp}}\left\{-{\left(\frac{{\sigma }_{1}-2\mu {\sigma }_{3}}{E}\right)}^{aT+b}\right\}$$
(5)
$${\sigma }_{{\text{eff}}}=\frac{\sigma }{1-D}={\sigma }_{1}{\text{exp}}\left\{{\left(\frac{{\sigma }_{1}-2\mu {\sigma }_{3}}{E}\right)}^{aT+b}\right\}$$
(6)

here, D is the damage variable, \(\mu\) is the Poisson ratio, and a, and b are constants. Similarly, Wang et al. (2018) made alterations to the Nishihara model and considered the effects of thermal damage and stress (Table 5). In this paper, a novel viscous dashpot and a damage variable were incorporated into the Nishihara model to simulate the accelerated stage of creep. These components become active when the stress surpasses the long-term strength, and the strain exceeds the value associated with the initiation of the tertiary phase (\({\varepsilon }_{a}\)). The damage variable influenced by both temperature and stress, was proposed as Eq. (7), while the creep strain associated with the accelerated phase was calculated using Eq. (8):

$$D= 1-{\text{exp}}\left[-{\left(\frac{{\varepsilon }_{z}E-(1-2\mu {)\sigma }_{3}}{\lambda E}\right)}^{A{T}^{2}+BT+C}\right]$$
(7)
$${\varepsilon }_{3}=\frac{(\sigma -{\sigma }_{s})(1-D)}{{\eta }_{2}}t+\frac{\sigma }{{\eta }_{3}}(t-{t}_{a})$$
(8)

In this context, A, B, and C denote parameters obtained from the triaxial compression test, \({\varepsilon }_{z}\) represents the maximum axial strain, μ is Poisson’s ratio, and λ is the mean microstrain of all micro units. It’s important to note that the model’s validation relies on creep test results of sandstone conducted at a temperature of 600 °C. However, to establish a comprehensive understanding, it is essential to compare the model with creep test results under varied temperature conditions and diverse lithological characteristics.

Furthermore, Li et al. (2021) suggested a creep model that considers the coupling of temperature, damage, and stress. They replaced the viscosity dashpots of the Nishihara model with the Abel dashpots. The creep strain related to the tertiary phase in on-dimensional stress condition was calculated as:

$${\varepsilon }_{3}=\frac{(\sigma -{\sigma }_{s})}{{\eta }_{2}^{\gamma }(1-{D}_{c})}\frac{{t}^{\gamma }}{\Gamma (1+\gamma )}$$
(9)

The validity of this model was confirmed through the examination of the creep behavior of frozen sandstone. During the creep tests, the temperature was maintained at −10 ℃, aligning with the average temperature of the freezing wall anticipated during vertical shaft construction. The outcomes from the uniaxial creep tests revealed an approximately linear relationship between the creep damage of frozen sandstone (\({D}_{c}\)) and the applied stress. Deng et al. (2022a) also modified the Nishihara model and introduced an innovative fractional creep model for coal rock by incorporating temperature-stress and temperature-stress-time coupled damage variables. They established the temperature-stress-time coupled damage variable by considering that the strength of rock follows the Weibull distribution law and is aligned with the Drucker–Prager (D–P) yield failure criterion as:

$$D\left(\sigma ,T,t\right)=1-{\text{exp}}\left[-{\left(\frac{\frac{{\text{sin}}\varphi }{\sqrt{3(3+{{\text{sin}}}^{2}\varphi )}}{I}_{1}+\sqrt{{J}_{2}}-\frac{3c.{\text{cos}}\varphi }{\sqrt{3(3+{{\text{sin}}}^{2}\varphi )}}}{{F}_{0}}\right)}^{m}-\omega t\right]$$
(10)

In the equation provided, \(\varphi\) is the internal friction angle, \({F}_{0}\) represents the average value of the strength parameter, c is the cohesion, m is the shape parameter, and \(\omega\) is the coefficient of the time-dependent damage variable. The damage variable influences the viscosity coefficient linked to the tertiary phase, and the creep strain related to the accelerated phase was computed as:

$${\varepsilon }_{3}=\frac{\sigma +{\xi }_{1}.\Delta T-{\sigma }_{s}}{{\eta }_{2}\left(\sigma ,T,t\right)}{t}^{\gamma }{E}_{1,\gamma +1}\left(\omega t\right)$$
(11)

Zhou et al. (2022) also proposed a damage-hardening creep model designed explicitly for soft rocks (refer to Table 5). In this study, the authors proposed that the hardening characteristic of rock influences the viscosity coefficient of the Kelvin body, as expressed in Eq. (12). Additionally, they introduced the damage variable to the Hook body, detailed in Eq. (13). To simulate the third phase of rock creep, they introduced a dashpot with adhesive properties, incorporating a nonlinear viscosity coefficient characterized by the Power function. The validity of this model was confirmed through the examination of creep test results conducted on deep soft rock.

$${\eta }_{1}={C{\sigma }^{r}{t}^{1-\alpha }\eta }_{0}$$
(12)
$$D=1-{\left(1-\frac{t}{{t}_{f}}\right)}^{\frac{1}{1+n}}$$
(13)
$${\varepsilon }_{3}=\frac{{t}^{k+1}}{\left(k+1\right){\eta }_{1}}\left({\sigma }_{0}-{\sigma }_{s}\right)$$
(14)

In the provided equations, C, r, and α represent material parameters, n fitting coefficients, and \({t}_{f}\) denotes the creep failure time. The condition k > 1 is specified.

Fractional derivative creep models have captured considerable attention from researchers due to their notable advantages, such as a small number of parameters, simplicity, and broad applicability. For long-term stability analysis of salt cavern storage, Lyu et al. (2021) proposed the fractional derivative creep-damage (FDCD) model, which connects the elastic element, Abel dashpot, and viscoplastic damage elements using a modified Mohr–Coulomb criterion (Table 6). In this study, the viscosity coefficient of the viscoplastic body was influenced by the damage variable, and the creep equation for the third phase is expressed as Eq. (16):

Table 6 Examples of fractional derivative creep models
Full size table
$$D=1-{e}^{-\alpha {t}^{\beta }}$$
(15)
$${\varepsilon }_{3}=\frac{\sigma -{\sigma }_{s}}{{\eta }_{\beta }\alpha }\left({e}^{\alpha {\left(t-{t}_{a}\right)}^{\beta }}-1\right)$$
(16)

here \({t}_{a}\) denotes the initial time of the tertiary creep phase, α and β are parameters associated with damage evolution. Through validation with the salt rock’s creep test outcomes, they demonstrated that the FDCD model is effective. The model was subsequently implemented in the FLAC3D software for analyzing the long-term behavior of gas storage. Numerical results obtained with the FDCD model exhibited strong agreement with sonar monitoring data. However, it is important to note that in this analysis, considerations such as temperature changes, the impact of cyclic loading, and gas seepage were not considered in the numerical modeling.

Xu et al. (2022) suggested a new fractional damage model where the damage variable was defined by following the Weibull distribution law as Eq. (17). For simulating the accelerated creep phase, the damage variable affects the viscosity coefficient of the Abel dashpot, the creep strain associated with the tertiary phase in a one-dimensional stress condition was proposed as Eq. (18).

$$D=1-{e}^{-{(t/\alpha )}^{\zeta }}$$
(17)
$${\varepsilon }_{3}=\frac{\sigma -{\sigma }_{s}}{{\eta }_{p}\Gamma (\beta )}{\int }_{0}^{t}{(t-x)}^{\beta -1}{e}^{(x/\alpha {)}^{\zeta }}{\text{d}}x$$
(18)

where α and ζ are material parameters. The suggested model was validated using the uniaxial compressive creep test results of salt rock. Additionally, they suggested a closed-form analytical solution derived from this model to analyze the creep behavior of rock surrounding a circular tunnel. The obtained results were then compared with actual tunnel convergence measurements in the Jinping II hydropower station. They concluded that the analytical solution based on the proposed model effectively simulates the creep deformation of underground spaces. Liu et al. (2021a) proposed an unsteady viscoplastic element which is a function of water content and time. As shown in Table 6, this element is coupled in series with the Maxwell body, wherein the Newton dashpot is switched to the Abel dashpot to construct a novel FVP model. The validity of this model was confirmed through verification with indoor direct shear test results, conducted on soft rock samples with varying water contents. Moreover, a closed-form analytical solution was formulated for displacement in the viscoplastic region around the circular tunnel wall. A comparison between numerical modeling and monitoring data for the Nabetachiyama tunnel demonstrated that the solution effectively simulates the time-dependent convergence of the tunnel.

He et al. (2022) suggested a nonlinear creep model that combines the Poyting–Thomson (P–T) model, the Abel dashpot, and the nonlinear damage dashpot element to describe the creep-damage behavior of salt rock. The results obtained from the long-term graded loading creep test on salt rock from the Pingdingshan salt mine were employed to validate the proposed model. The findings indicated that the proposed model offered the most effective fit when compared to other classic models. The damage variable and creep strain for the nonlinear damage dashpot are expressed as:

$$D=1-{\left(\frac{t-{t}_{f}}{{t}_{0}-{t}_{f}}\right)}^{\frac{1}{1+\nu }}$$
(19)
$${\varepsilon }_{3}=\frac{{\sigma }_{1}-{\sigma }_{s}}{{\eta }_{3}}\frac{\upsilon +1}{\upsilon }\left({t}_{f}-{t}_{0}\right)\left[{\left(\frac{-{t}_{f}}{{t}_{0}-{t}_{f}}\right)}^{\frac{\upsilon }{\upsilon +1}}-{\left(\frac{{t}_{f}-t}{{t}_{f}-{t}_{0}}\right)}^{\frac{\upsilon }{\upsilon +1}}\right]$$
(20)

where υ is the material parameters, \({t}_{f}\) corresponds to the damage-failure state (D = 1), and \({t}_{0}\) is related to the non-destructive state (D = 0). Furthermore, Xuan et al. (2022) developed a nonlinear fractional damage creep model to analyze the frozen soil’s creep behavior. The damage variable was calculated as Eq. (21) where μ represents the damage factor influenced by both the temperature difference during freeze-thaw and the number of freeze-thaw cycles.

$$D=1-\frac{\sigma }{{\sigma }_{1}}{e}^{-\mu \left(\Delta T,N\right)t}$$
(21)
$${\varepsilon }_{3}=\frac{\sigma -{\sigma }_{s}}{\eta }(t-{t}_{F}{)}^{n}$$
(22)

Liu et al. (2021b) suggested a novel creep model by combining Hooke’s element, a variable-order fractional component (for viscoelastic behavior), and the parallel coupling of the slide element and variable-order fractional element (for viscoplastic behavior) as presented in Table 6. In this study, the assumption was made that the fractional order is a function of time \((\gamma =\alpha \left(t\right), \alpha \left(t\right)\ge 0)\), so they considered three fractional orders for different phases of creep. The damage variable and creep strain for the accelerated phase were expressed as:

$$D=1-{e}^{-\omega t}$$
(23)
$${\varepsilon }_{3}=\frac{{\sigma }_{1}-{\sigma }_{3}-{\sigma }_{s}}{3{\eta }_{3}}(t-{t}_{2}{)}^{{\alpha }_{3}}{E}_{\mathrm{1,1}+{\alpha }_{3}}(\omega t)$$
(24)

here \(\omega\) is a damage parameter. In addition, Liu et al. (2020) introduced a fractional creep model for weakly cemented soft rock. In this model, the Abel dashpot is parallel with the plastic element, simulating the third phase of rock creep when the deviator stress is above the long-term strength. This model was validated using triaxial creep test results conducted on weakly cemented soft rock with varying water content and deviator stress. The parameters of the model were acquired initially using the trust-region method, and further optimization was performed through the ant colony optimization method. This approach appears to be effective and represents a novel method for determining creep parameters.

Many researchers also improved and modified the Burger model by considering damage variables, water effects, etc. Li et al. (2022a) evaluated the influence of water-induced weakening damage on shale and introduced a nonlinear visco-elastoplastic unloading creep constitutive model (UCCM) by connecting the Burger model to the viscoplastic-damaged body (refer to Table 7). In this model, it was considered that the damage law influences all components of the model, and the creep strain related to the tertiary phase was suggested as Eq. (26).

$$D=1-{e}^{-\alpha ({w}_{s})t}$$
(25)
$${\varepsilon }_{3}=\frac{\sigma -{\sigma }_{s}}{{\eta }_{3}{\text{exp}}(-\alpha \left({w}_{s}\right)t)}{t}^{n}$$
(26)

where \(\alpha \left({w}_{s}\right)\) was obtained through \(\alpha \left({w}_{s}\right)={\alpha }_{0}(1+{w}_{s})\), \({w}_{s}\) represents the saturation coefficient, and \({\alpha }_{0}\) is the value of the dried specimen. The suggested model was verified using the unloading creep test results of shale with varying water saturation coefficients.

Table 7 Examples of modified Burger constitutive models
Full size table

Lin et al. (2020) connected the Burger model with the viscoplastic body and developed a new model that employs the Kachanov creep damage law to explain time-dependent shear strength. The damage variable and shear strain during the accelerated creep stage were proposed as:

$$D=1-{\left(\frac{{t}_{R}-t}{{t}_{R}-{t}_{s}}\right)}^{\frac{1}{\delta +1}}$$
(27)
$$\gamma =\frac{\tau -\sigma {\text{tan}}\alpha }{{\eta }_{{\text{VP}}}}\left[\left(t-{t}_{s}\right)+\left({t}_{R}-{t}_{s}\right)\frac{\delta +1}{\delta +2}\left[{\left[\phi \left(t\right)\right]}^{\frac{\delta +2}{\delta +1}}-1\right]\right]$$
(28)

In the provided equations, \({t}_{R}\) represents the final moment of rock creep (when \({t=t}_{R}, D=1\)), and \({t}_{s}\) is the moment at which the rock starts the tertiary phase (when \({t=t}_{s}, D=0\)). The parameter δ serves as an indicator of the deformation and damage characteristics of the rock, illustrating the progression of internal cracks within the rock during accelerated creep. The proposed model was validated by rock samples taken from the discontinuity of Wulong County, China. Furthermore, Li et al. (2023b) suggested a new creep model incorporating residual strength by introducing a damaged viscoelasto body and a correction factor for residual strength. In this research, two damage variables were introduced, \({D}_{1}\) corresponds to the generation and expansion of microcracks, and \({D}_{2}\) is related to the damage properties inside the rock.

$$\left\{\begin{array}{l}{D}_{1}=1-{\left(1-\frac{t}{{t}_{f}}\left(1-{\left(1-\delta \right)}^{1+n}\right)\right)}^{\frac{1}{1+n} }\\ {D}_{2}=1-{e}^{-at}\end{array}\right.$$
(29)

In the equations, \(\delta =\sqrt{\frac{{\sigma }_{r}}{{\sigma }_{c}}}\) is the residual strength correction factor, \({\sigma }_{r}\) is the residual strength, \({\sigma }_{c}\) is the long-term strength, n is the material parameter, \({t}_{f}\) is the time when creep failure occurs, and a represents the material’s internal property. Additionally, the creep strain for the damaged viscoelasto body was expressed as:

$${\varepsilon }_{{\text{ve}}}=\frac{\sigma -{\sigma }_{s}}{{E}_{4}\left(1-{D}_{1}\right)\left(1-{D}_{2}\right)}+\frac{\sigma -{\sigma }_{s}}{{\eta }_{4}\left(1-{D}_{2}\right)}\frac{\left(1+n\right)}{n}\frac{{t}_{f}}{{\left(1-\delta \right)}^{1+n}-1}[{\left(1-{D}_{1}\right)}^{n}-1]$$
(30)

The validity of the model was confirmed through uniaxial and triaxial creep test results conducted on four different rock types (tuff, sandstone, salt, and sandy shale). The findings stated that the model provides a better reflection of the creep behavior of rocks compared to the Burger model.

Yang and Jiang (2022) considered bedding and freeze-thaw damages and suggested a nonlinear creep damage model for slates. In this study, three damage variables were introduced to consider the effects of bedding angle, freeze-thaw cycle, and stress as shown in Eq. (31).

$$\left\{\begin{array}{l}{D}_{\beta }=1-\frac{{E}_{\beta }}{{E}_{0}}\\ {D}_{n}=1-\frac{{E}_{n}}{E}\\ {D}_{s}=1-{e}^{-\alpha t}\end{array}\right.$$
(31)

The damage variable related to the bedding angle (\({D}_{\beta }\)) was formulated based on the elastic modulus of slate rock (\({E}_{\beta }\)) with bedding angle \(\beta\), and the elastic modulus of the slate rock with zero bedding angle (\({E}_{0}\)). \({D}_{n}\) is the freeze-thaw damage variable, \({E}_{n}\) represents the elastic modulus after n freeze-thaw cycles, \({D}_{s}\) is the load damage caused by stress in the tertiary phase, and α is the material constant. The creep strain associated with the accelerated phase was formulated as:

$${\varepsilon }_{3}=\frac{\sigma^{\prime}{-\sigma }_{s}(1-{D}_{\beta ns})}{{\eta }_{B}(1-{D}_{\beta ns})}\frac{{t}^{{m}_{2}}}{\Gamma (1+{m}_{2})}$$
(32)

where \({D}_{\beta ns}\) is the total coupled damage variable. Furthermore, they conducted a comparison between the triaxial creep test results of slate rock with various bedding angles after 80 freeze-thaw cycles with the results obtained from the proposed model. Additionally, Li et al. (2023a) enhanced the Burger model to incorporate the effect of an acidic environment and introduced a stress-acidity-strain–time model. In this study, it was assumed that the elastic module in the Kelvin body is a function of acidity and time according to Eq. (33).

$${E}_{2}=\left(aln\left(t\right)+b\right)pH+c{t}^{d}$$
(33)

where, a, b, c, and d are the fitting parameters, and pH represents acidity. The model was validated using shear-creep test results on red-bed soft-rock with weak interlayers under different pH conditions. The authors noted that as acidity increases, the concentration of hydrogen ions rises, resulting in an escalation of associated physical and chemical reactions.

Another novel constitutive model for granite was introduced by Zhou et al. (2023). In this study, a new damaged dashpot was introduced to simulate the third phase of creep by incorporating the damage variable into the fractional order of the Abel dashpot (Eq. 34). The damage variable was proposed based on the Weibull probability distribution and following the Drucker–Prager (D–P) criterion, as expressed in Eq. (35). The creep strain of the new damaged dashpot can be formulated after employing the Riemann–Liouville (R–L) fractional integral operator, as depicted in Eq. (36).

$$\sigma \left(t\right)={\eta }_{2}\frac{{d}^{1+D}\varepsilon (t)}{d{t}^{1+D}}$$
(34)
$$D=1-{\text{exp}}\left\{-{\left[\frac{\left[E{\varepsilon }_{1}+{\sigma }_{3}(2\mu -1)\right]\sqrt{3+{{\text{sin}}}^{2}\varphi }-3c {\text{cos}}\varphi }{3K{\varepsilon }_{0}{\text{sin}}\varphi }\right]}^{m}\right\}$$
(35)
$${\varepsilon }_{3}=\frac{{\sigma }_{0}}{{\eta }_{2}}\frac{{t}_{1}^{2-{\text{exp}}\left\{-{\left[\frac{{(\sigma }_{1}-{\sigma }_{3})\sqrt{3+{{\text{sin}}}^{2}\varphi }-3c{\text{cos}}\varphi }{3K{\varepsilon }_{0}{\text{sin}}\varphi }\right]}^{m}\right\}}}{\Gamma \left(3-{\text{exp}}\left\{-{\left[\frac{{(\sigma }_{1}-{\sigma }_{3})\sqrt{3+{{\text{sin}}}^{2}\varphi }-3c{\text{cos}}\varphi }{3K{\varepsilon }_{0}{\text{sin}}\varphi }\right]}^{m}\right\}\right)}$$
(36)

In the equations, m is the shape parameter, representing the degree of material homogeneity and defined as a homogeneity index. Triaxial creep test results of granite were employed to verify the model, and the proposed model exhibited superior fitting performance with fewer model parameters in comparison to other fractional creep damage models. Additionally, Li et al. (2022c) modified the Burger model and developed a damage creep model by replacing the viscous element with a fractional viscous element and considering the temperature-damage-stress interaction. The suggested model was validated using creep test results of frozen sandstone. They utilized the fractional viscoplastic body by combining the Abel dashpot and plastic slider (Table 7). The constitutive equation for simulating the third phase is expressed as follows:

$${\varepsilon }_{3}=\frac{\sigma -{\sigma }_{s}}{abc.{{\eta }_{3}}^{\lambda }}\frac{{t}^{\lambda }}{\Gamma \left[1+\lambda \right]}$$
(37)
$$\left\{\begin{array}{l}a=1-{D}_{T}\\ b=1-{D}_{W}\\ c=1-{D}_{C}\end{array}\right.$$
(38)

In the given context, \({D}_{T}\) represents the rock’s initial damage, \({D}_{W}\) is the damage occurring during instantaneous loading in the attenuation creep stage, and \({D}_{C}\) is the damage induced during long-term loading in the tertiary creep stage.

Lv et al. (2019) presented a creep damage model by incorporating the Kachanov damage evolution rule and damage theory into the J-body model. In this model, the elastic component in the J-body model was replaced by the damaged body (Table 8). In their approach, the damage variable resulting from a nonpersistent joint under uniaxial compression loads (\({D}_{j}\)) and the damage variable related to mesoscopic flaws (\(D\left(t\right)\)) were coupled to propose the creep equation for the rock mass with one nonpersistent joint, formulated as Eq. (41).

Table 8 Examples of mechanic-based creep constitutive models
Full size table
$$D\left(t\right)=1-{\left(1-\frac{t}{{t}_{F}}\right)}^{1/n+1}$$
(39)
$${D}_{j}=1-\frac{1}{1+\left(2/V\right)(1/{\sigma }^{2}){\int }_{0}^{A}\left({K}_{I}^{2}+{K}_{II}^{2}\right){\text{d}}A}$$
(40)
$${D}_{c}=1-\frac{(1-{D}_{j})(1-D\left(t\right))}{1-{D}_{j}D\left(t\right)}$$
(41)

In the provided equations, \({t}_{F}\) represents the critical time of failure, n is the material constant, V is the volume of the rock mass, \({K}_{I}\) and \({K}_{II}\) are the first and second stress intensity factors (SIFs) at the joint tip, respectively, and A is the joint area.

Zhao et al. (2017) introduced the visco-elastoplastic rheological model (EVPR) for hard rocks. They used the spring element for instantaneous elastic deformation, the Hooke and plastic slide combination for an immediate plastic response, the Kelvin element for viscoelastic behavior, and the generalized Bingham body for viscoplastic behavior (Table 8). In this study, triaxial creep tests involving loading and unloading processes were conducted on iherzolite samples. The loading duration was 90 h for each deviatoric stress, and the unloading period ranged from 20 to 30 h. The proposed model demonstrated a detailed description of all creep phases, particularly focusing on the tertiary creep stage. Furthermore, Jun and Jia (2017) proposed the creep-damage model for mudstone to analyze the tertiary phase of rock creep, incorporating a fractional order damage element. In this study, the verification was carried out using creep test results of mudstone. The damage variable and the creep strain for the tertiary phase were formulated as:

$$D=1-{\text{exp}}\left[-\frac{(\sigma -{\sigma }_{s})t}{b}\right]$$
(42)
$${\varepsilon }_{3}=\frac{{\sigma }_{0}{\text{exp}}\left[(\sigma -{\sigma }_{s})t/b\right]-{\sigma }_{s}}{{\eta }_{2}}\frac{{t}^{\beta }}{\Gamma (1+\beta )}$$
(43)

where b is the rock material constant.

Wang et al. (2020) also suggested a nonlinear creep model consisting of an improved Hooke’s body, Scott Blair fractional element, and a nonlinear viscoplastic body. Based on the creep test results of silty mudstone, they assumed that the elastic modulus is a function of stress, and the creep strain for the tertiary phase was proposed as:

$${E}_{0}=m{\sigma }_{0}+n$$
(44)
$$\varepsilon =\frac{{\sigma }_{0}-{\sigma }_{s}}{\alpha {\eta }_{2}}{e}^{\alpha (t-{t}_{0})}$$
(45)

where m and n are all dimensionless coefficients, \({t}_{0}\) is the start time of the accelerated creep stage, and \(\alpha\) is the nonlinearity constant. Li et al. (2022b) developed a creep model capable of capturing the time-dependent behavior of rocks under varying moisture contents, where the shear modulus and viscosity coefficients of viscoelastic and improved Maxwell elements were dependent on moisture. The improved Maxwell body becomes active when the moisture content (\(w\)) is higher than zero (Table 8).

Other researchers have also proposed various models to study creep behavior in different geological materials. The grain-scale creep models were developed recently and become popular because of some advantages such as the evolution of microcracking in granular rocks, Li et al. (2020b) introduced the 3D grain-based creep model (3D-GBCM) using the Particle Flow Code (PFC). In this research, the time-dependent mechanism between the parallel bond contacts inside the grains was assumed to be a function of temperature and stress level, as given in Eq. (46). The Mohr-Coulomb criterion was employed to evaluate the state of failure in bonded contacts under complex stress conditions.

$$\frac{{\text{d}}{\overline{D} }_{i}}{{\text{d}}t}=\left\{{\beta }_{1}{\text{exp}}\left(-\left(\frac{Q}{RT}\right){\left(\frac{{\bar{\sigma }}_{i}}{{\bar{\sigma }}_{c}}\right)}^{{\beta }_{2}}\right), \begin{array}{ll}0,& {\bar{\sigma }}_{i}<{\bar{\sigma }}_{a} \\ &{\bar{\sigma }}_{a}\le {\bar{\sigma }}_{i}<{\bar{\sigma }}_{c}\\ \infty,& {\bar{\sigma }}_{i}\ge {\bar{\sigma }}_{c}\end{array}\right.$$
(46)

In the provided equation, \({\bar{\sigma }}_{i}\) represents the parallel bond normal stress at the i-th contact, \({\bar{\sigma }}_{a}\) is the micro-activation stress, \({\bar{\sigma }}_{c}\) is the tensile strength of the parallel bond contact, Q represents the apparent activation energy, T denotes the absolute Kelvin temperature, R is the universal gas constant, \({\beta }_{1}\), and \({\beta }_{2}\) are constants in the Power function model. To create a three-dimensional geometric grain structure, a Voronoi polyhedral technique was employed. To evaluate the microcracking behavior of salt rock and understand failure modes, numerical modeling using the 3D-GBCM model was compared with experimental data. The results indicated that the macro-failure surfaces are primarily composed of intra-grain microcracks, particularly induced by tensile failure.

Considering rock heterogeneity and micro-fractures, Wang and Cai (2020) introduced a grain-based Time-to-Failure (TtoF) creep model. This model enabled the deformation analysis during the initial two creep phases and the initiation and propagation of cracks in the third stage of creep. In this model, it was supposed that the creep behavior of a grain cell follows the Burgers creep model to simulate the first and second creep phases. A damage index (\({D}_{z}\)) is defined based on the strength parameters and the center-driving-stress ratio at time t as given in Eq. (47).

$${D}_{z}=1-\underset{0}{\overset{t}{\int }}{\left[{\acute{t}}_{0}{\text{exp}}\left(\frac{1}{\acute{k}}\left(1-{\left({r}_{{\text{sc}}}\left(t\right)\right)}^{a}\right)\right)\right]}^{-1}{\text{d}}t$$
(47)

where \({r}_{{\text{sc}}}\) is the center-driving-stress ratio which can be determined from Mohr’s diagram, \({\acute{t}}_{0}, {\acute{k}}\) are micro-parameters of the element. To verify the time-to-failure (TtoF) model, a set of uniaxial and triaxial compression tests were carried out on granite.

Li et al. (2017) also presented a thermal-mechanical creep model for salt rock. In this study, salt rock was treated as a collection of individual particles, and a hybrid model was created by employing Burger’s Contact Model and Linear Parallel Contact Model. In this hybrid model, it was assumed that the spring elements in Kelvin and Maxwell bodies are temperature-dependent. Assuming that the only mechanism of thermal transfer in the numerical models is heat conduction between particles, the proposed model can represent both the microscopic creep behavior and the thermal effect in a normal direction at contacts between particles. The results of numerical simulations in this study closely match the data from laboratory creep tests, indicating that salt rock exhibits creep characteristics dependent on temperature and stress. Microscale observations showed that the cracks caused by mechanical loads and high temperatures lead to an increase in axial strain at the macroscopic level. In addition, Xu et al. (2020) proposed a new grain-based numerical model to simulate the time-dependent behavior of transversely isotropic rocks. For modeling the tertiary creep phase, they modified the Burger Contact model by introducing the damage variable as expressed in Eq. (48). In addition, they used the bonded parallel contact (BPC) and the smooth joint contact (SJC) to describe the transversely isotropic rocks. They supposed that the damage-evolutional rule applies to all parameters of the Burger Contact model when the contact force surpasses the contact strength.

$$D=1-{e}^{-\alpha t}$$
(48)

where α is the damage parameter.

The creep and seepage behavior in clayey rock, including the effects of fracture damage and self-healing on permeability change, was assessed by Jia et al. (2018) using a coupled hydro-mechanical model. Permeability equations for clayey rock were developed, with a specific focus on integrating the damage and self-healing mechanisms. The creep damage criterion for clay rock was proposed as given in Eq. (49), and a modified empirical Power function was adopted to describe the creep deformation, as expressed in Eq. (50).

$${f}^{{\text{dc}}}\left({\varepsilon }_{c}, {D}_{c}\right)={\text{exp}}\left(\frac{{\varepsilon }_{c}}{{\varepsilon }_{{\text{cmax}}}. \omega }\right)-1-\frac{{D}_{c}}{{A}_{0}}\le 0$$
(49)
$${\dot{\varepsilon }}_{c}={A}_{1}{{(\bar{\sigma }}_{{\text{cr}}})}^{n}{t}^{m}H({\bar{\sigma }}_{{\text{cr}}}-{{\bar{\sigma }}_{{\text{cr}}}}^{*})/(1-{D}_{c})$$
(50)

where \({A}_{0}={\text{exp}}(-1/\omega )\), \(m={{B}_{1}\varepsilon }_{c}+{C}_{1}\), \(\omega , {A}_{1}, {B}_{1}, {C}_{1},n\) are the model parameters, \({\varepsilon }_{{\text{cmax}}}\) is the maximum creep strain, \({D}_{c}\) is the creep damage, \({{\bar{\sigma }}_{{\text{cr}}}}^{*}\) is the threshold value of the equivalent creep stress, and \({\bar{\sigma }}_{{\text{cr}}}\) is the equivalent creep stress. A coupled creep and seepage model was developed using ABAQUS software to assess the hydro-mechanical behavior of underground constructions. The results demonstrated that the suggested model effectively captures the initial increase in permeability due to excavation and creep damage, as well as the subsequent decrease in permeability attributed to the self-healing effect of clayey rock.

In another study, Zhang et al. (2019) suggested a creep damage model by adjusting the Nishihara model and incorporating a damage variable that was derived from the minimum energy consumption theory and the stress–strain state. This model successfully explained the evolution law of creep damage in sandstone. In this study, by solving the energy dissipation equation, the damage variable was calculated as Eq. (51).

$$D=\frac{1}{2}\left[\sqrt{{(1-{\eta }_{2}\alpha )}^{2}-4(t-{\eta }_{2}\alpha +C)}-1\right]$$
(51)

where \(\alpha =3{U}_{d}/({\sigma }_{1}*({\sigma }_{1}-{\sigma }_{3}-{\sigma }_{s}))\), C represents a creep test parameter, and \({U}_{d}\) is the energy dissipation. Their study showed that at low-stress levels, a significant portion of the energy during compaction is absorbed by numerous pores in the rocks. The damage to the rocks during the primary creep phase is minimal, resulting in low dissipation energy. However, the energy dissipation increases significantly with increasing stress levels.

In the context of claystone, Jung et al. (2022) introduced a novel constitutive model that considered anisotropy. Their approach incorporated transverse isotropic elasticity, anisotropic Mohr-Coulomb criterion, and anisotropic Lemaitre creep law to formulate an anisotropic constitutive model. For the transverse isotropic elasticity, two Young’s moduli (perpendicular and parallel to the plane of isotropy), two Poisson’s ratios, and one shear modulus should be determined. Based on the anisotropic Lemaitre creep law, the axial creep strain was calculated as:

$${\varepsilon }_{\overline{\theta }}\left(t\right)=a{\beta }^{v}(\overline{\theta }){\langle {\beta }^{p}\left(\overline{\theta }\right){\sigma }_{\overline{\theta }}-{\sigma }_{c}\rangle }^{n}{t}^{\alpha }$$
(52)

where α, a, and n are the fitting parameters. The anisotropy in viscosity and plasticity are carried by the functions \({\beta }^{v}\left(\overline{\theta }\right)\), and \({\beta }^{p}\left(\overline{\theta }\right)\), respectively. \({\sigma }_{c}\) is the stress threshold.

Pramthawee et al. (2017) extended the modified hardening soil model into the creep analysis and proposed the Hardening Soil Creep (HSC) model specifically for rockfill materials. This model was implemented in the ABAQUS software to assess the time-dependent behavior of the Nam Ngum 2 dam. The efficacy of the HSC model in accurately predicting movement in the dam body is demonstrated through comparisons between monitored data and simulated results, encompassing both without creep and with creep scenarios. The integrated model effectively captured both the immediate and delayed strains exhibited by the rockfill material under multistage loading tests.

Additionally, Wang et al. (2014) presented a creep-damage model that accounted for the first, second, and tertiary creep-damage phases. They also investigated the long-term dilatancy of rock salt using the dilatancy boundary theory. The model’s accuracy was validated by comparing it with triaxial creep test results for salt rock, demonstrating its ability to explain creep-damage-rupture characteristics adequately. The damage evolution equation was formulated as Eq. (53).

$$\dot{D}={\left[\frac{{\sigma }^{*}}{B(1-D)(1-\langle D-{D}_{a}\rangle )}\right]}^{r}$$
(53)
$${\sigma }^{*}=\sigma {\left[\frac{2}{3}\left(1+{\nu }_{0}\right)+3\left(1-2{\nu }_{0}\right){\left(\frac{{\sigma }_{1}+{\sigma }_{2}+{\sigma }_{3}}{3\sigma }\right)}^{2}\right]}^{0.5}$$
(54)

In the provided equation, B and r are material coefficients and \({D}_{a}\) is the damage accelerating limit. The research demonstrated that the creep-damage model can capture the creep-damage-rupture properties of rock salt throughout the entire process.

2.4 Comparison of models’ ability to simulate the accelerated creep phase

In this section, we compared different creep models’ ability to simulate the tertiary phase of rock creep. It is essential to note that certain models exhibit specific capabilities, such as considering temperature effects, moisture content, etc., which make them suitable for particular conditions. However, for this comparison, we selected uniaxial creep test results of salt, sandstone, and shale (Zhang et al. 2019; Zhao et al. 2021; Wu et al. 2020), and assessed the models’ effectiveness through fitting analysis, emphasizing the tertiary phase, and corresponding damage variables. The results of the comparison analysis are presented in Table 9 and Fig. 4. Table 9 also summarizes the different creep equations utilized for simulating the tertiary phase of rocks under one-dimensional stress conditions. We used the coefficient of determination (\({R}^{2}\)) and the root mean square error (RMSE) as two metrics to evaluate how well the models fit the experimental data.

Table 9 Fitting analysis results
Full size table
Fig. 4
figure 4

Fitting analysis results of creep tests a shale; b salt; c sandstone

Full size image
$$\text{RMSE}=\sqrt{\frac{1}{n}\sum_{t=1}^{n}{\left({y}_{t, {\text{test}}}-{y}_{t,{\text{theor}}}\right)}^{2}}$$
(55)
$${R}^{2}=1-\frac{\sum_{t=1}^{m}{\left({y}_{t,{\text{theor}}}-{y}_{t,\mathrm{ test}}\right)}^{2}}{\sum_{t=1}^{m}{\left({y}_{t,{\text{theor}}}-{\overline{y} }_{t, {\text{test}}}\right)}^{2}}$$
(56)

where, \({y}_{t, {\text{test}}}\), and \({y}_{t,{\text{theor}}}\) are the test and theoretical results at time t, respectively, n is the total amount of data, and the average value of \({y}_{t, {\text{test}}}\) is \({\overline{y} }_{t,\mathrm{ test}}\).

As presented in Table 9, most of the models exhibit high values of \({R}^{2}\) and low values of RMSE, indicating they successfully simulate the third phase of rock creep. However, the methods proposed by Wang et al. (2020), Yang and Li (2018), Zhou et al. (2023), and Zhou et al. (2022) stand out with the highest coefficient of determination and Fig. 4 further illustrates that the creep curves proposed by these methods have a superior fitting effect. Overall, the comparison results indicate that the damaged Abel dashpot, the exponential relationship between strain and time power function, and the power function, have the best fitting effect with the accelerating phase of rock creep, while the polynomial function of degree 2 was found to be less effective in simulating the beginning of the accelerating phase.

3 Application of creep analysis in geomechanics

Several studies have explored the application of creep analysis in different geomechanics scenarios. In the context of tunneling, Tarifard et al. (2022) analyzed the long-term stability of the Shibli tunnel by considering both the creep behavior of the rock and the groundwater effect. The CVISC model was employed, and a direct back analysis technique was utilized to adopt the model’s parameters for the rock mass. The results of our previous research, depicted in Fig. 5a, indicated that the tunnel’s spring-line is more susceptible to induced stresses caused by subsurface water and the creep behavior of the rock. In this specific case study, the stability time of the tunnel lining in the fault zone was observed to decrease by approximately 10 years for every 20 m increase in the water table. Li et al. (2020a) employed a new fractional damage model based on the internal variable thermodynamics theory to analyze the creep behavior of rocks in the DXL tunnel by implementing it into the FLAC3D software. The tunnel was constructed by the double-shield TBM machine and the model parameters were obtained by the inversion analysis of deformation data. The tunnel convergence measurements showed good agreement with the outcomes obtained using their suggested model. Sun et al. (2022) developed a coupled strain softening and creep damage model into the FLAC3D software for assessing the long-term stability of the tunnel excavated in the hard rock. The results indicated that after 3000 h, local plate cracking failure at the two arch waists became evident, and a shear failure zone emerged in the roadway vault. The numerical findings aligned well with the observations from actual engineering work. In analyzing the behavior of the Dapingshan tunnel, Deng et al. (2022b) utilized the CVISC model in the context of crushed argillaceous sandstone and high stress. In this case study, they determined the creep parameters by utilizing triaxial creep test results and employed displacement back analysis to calculate the geo-stress.

Fig. 5
figure 5

Some applications of creep analysis in geomechanics

Full size image

Dehghan and Khodaei (2021) investigated casing collapse and wellbore tightening during drilling, considering the creep behavior of salt rock. They employed the CVISC model and derived the creep parameters through experimental data. Their conclusion highlighted that optimizing mud weight can decrease wall deformation for the wellbore without casing by considering salt’s creep behavior (Fig. 5b). Additionally, they analyzed the impact of salt’s creep behavior on casing deformation. The findings revealed that the creep behavior of rock concentrates stress and increases the wall’s deformation rate when the cement behind the casing is absent. Considering the stability of side-exposed backfill, Wang and Li (2022) examined the long-term stability by incorporating the creep behavior of rock mass using the CVISC model. They found that in deep mines, significant creep in rocks can lead to instability in side-exposed backfill, often resulting in crushing failure. The results from numerical modeling suggested that the minimum required cohesion of side-exposed backfill, influenced by the creep behavior of rock mass, is significantly higher compared to the rock mass without creep behavior (Fig. 5c).

Wang and Cai (2021) studied the long-term stability of granite pillar walls using the grain-based time-to-failure model (GBM-TtoF). As depicted in Fig. 5d, they highlighted that the long-term strength of the pillar was influenced by shear damage occurring in the pillar core and spalling damage on the pillar wall. This failure mechanism was successfully modeled by the GBM-TtoF model. Their analysis also showed that for the stress higher than the long-term strength, the squat pillars could withstand longer than slender pillars.

Huang et al. (2021) assessed the creep behavior of rock mass in large cross-section tunnels using the Burger model. They evaluated various tunnel support systems and found that confined concrete can be an effective support system compared to other alternatives because of its stable bearing capacity and good ductility. Furthermore, Xu and Gutierrez (2021) analyzed the stability of tunnel lining, considering the degradation of the initial support system, elastoplastic damage of the final lining, and the creep behavior of rock mass. The study emphasized the remarkable influence of in-situ pressures on the response and damage of the tunnel’s final lining. In the case of tunnel lining in phyllite, Xu et al. (2020) investigated the failure mechanism of the secondary lining in the layered stratum. To analyze the creep behavior of transversely isotropic rocks, they employed Burger’s damage contact model. Results showed that both the geo-stress field and the foliation inclination angle had an impact on the development of cracks in the lining.

Wang et al. (2022) focused on the stability of an air energy storage power plant, considering the combined effects of creep and fatigue. Their numerical modeling results revealed that when creep and fatigue interact, rock deformation and tunnel volume shrinkage are considerably higher than creep behavior alone. The numerical modeling findings suggested that, when considering the fatigue effect, the maximum subsidence at the top of the cavern after 20 years is approximately six times that of the condition where fatigue is not considered (Fig. 5e). Taheri et al. (2020) assessed the long-term behavior of halite salt rock, both experimentally and numerically, with a specific focus on the creep effect in casing collapses of the Gachsaran oil formation. The numerical results demonstrated that the creep behavior of the rock decreased the safety factor by three times over 24 years, indicating that creep behavior is the major factor contributing to casting collapse (Fig. 5f). Analyzing salt cavern gas storage, Lyu et al. (2021) employed the FDCD model to assess long-term stability. They compared the numerical modeling results with sonar monitoring data and demonstrated the FDCD model’s ability to predict time-dependent deformation and estimate the time-dependent stability of salt caverns. Following the verification of numerical modeling with monitoring data, they analyzed cavern deformation and volume shrinkage under cyclic gas pressure for 30 years. Table 10 and Fig. 5 summarize the application of rock creep analysis in engineering projects.

Table 10 Examples of the application of rock’s creep analysis in engineering projects
Full size table

4 Discussion

The creep behavior of rocks and the long-term stability of underground spaces have been studied in detail by many academics. Regarding the creep constitutive models, many vital types of research have been conducted that try to consider the full creep behavior of rocks and factors affecting creep characteristics of rocks; however, because of the complexity of rocks’ time-dependent behavior, there is still a need for improvement in this issue. The previously proposed creep models for rocks can be examined from various perspectives, but it is crucial to evaluate their specific capabilities that render them suitable for certain applications. In simulating the third phase, several noteworthy models have been proposed in recent years. Our analysis presented in Table 9 and Fig. 4 indicates that the methods proposed by Zhou et al. (2023), Yang and Li (2018), Wang et al. (2020), and Zhou et al. (2022) exhibit the most effective fitting for modeling the accelerated phase of rock creep. In contrast, the second-degree polynomial function was observed to be less effective in simulating the beginning of the tertiary phase. The grain-based creep models have also demonstrated advantages in describing the micro-mechanical responses of materials, such as a detailed description of cracking and damage growth at the micro-scale.

Currently, the understanding of rock mass creep behavior can be an ongoing and evolving field of research in geotechnical engineering and rock mechanics. Further research needs to focus on several aspects to enhance our understanding and predictive capabilities related to rock mass creep behavior. As the rock mass contains weak planes like bedding, jointing, layering, and other discontinuities, unfortunately, there is limited research conducted to issue this important topic. Although Lv et al. 2019 introduced the damage variable which is caused by one nonpersistent joint under uniaxial compression loads to simulate the effect of joint on the creep deformation of rock, there is a strong need to research the creep models that consider the joints’ properties and shear stress. In the case of rock anisotropy, the anisotropic constitutive model proposed by Jung et al. (2022), which considered the transverse isotropic elasticity, anisotropic Mohr–Coulomb criterion, and anisotropic Lemaitre creep law, provides a more detailed representation of material behavior. The incorporation of the bedding angle effect by introducing damage variables based on elastic modulus, as done by Yang and Jiang (2022), is another valuable approach. The approach proposed by Xu et al. (2020) for simulating the transverse isotropy of the rocks could indeed serve as a leading idea for modeling anisotropy in micro-scale and grain-based numerical simulations. Overall, the investigation of joints’ effect and rock anisotropy in creep behavior models is a promising avenue for future research in the field.

It’s evident that various models have been developed to address the effect of water on the creep behavior of rocks, each offering unique advantages and considerations. The model developed by Liu et al. (2021a), with its close-form solution for circular tunnels, offers practicality and ease of use. However, the model proposed by Li et al. (2023a), which accounts for acidity effects on long-term rock behavior, introduces an important consideration for environmental conditions. Additionally, the model proposed by Jia et al. (2018), which incorporates fracture damage and self-healing effects on permeability changes, offers a robust approach to modeling the complex interactions within rock masses. Each of these models contributes to a more comprehensive understanding of how water influences rock creep behavior, highlighting the importance of considering environmental factors in rock mechanics studies. The consideration of temperature effects in constitutive models for the creep behavior of rock is crucial, given its significant impact on material properties and their broad applications like deep mining, frozen walls, and freeze-thaw cyclic. The grain-based model proposed by Li et al. (2017), particularly for microscopic creep behavior, is seen as a promising idea. Overall, the ongoing exploration of models that consider temperature and water effects on rock’s creep behavior demonstrates the commitment to capturing the multifaceted nature of rock mechanics in varying environmental conditions.

Since the fractional calculus approach provides a powerful mathematical framework for describing the complex and nonlinear creep properties of materials. Notably, researchers have employed fractional-based components not only for simulating the viscoelastic behavior but also for capturing the accelerated phase of rock creep. The model proposed by Zhou et al. (2023) stands out due to its advantages, including a decreased set of model parameters and a fractional order that reflects the material’s damaged states, adding to the physical significance of the fractional order. Moreover, the fitting analysis in Table 9 underscores the high effectiveness of this model in simulating the accelerating phase of rock creep. Another fractional creep model, the FDCD model has demonstrated its effectiveness in simulating the long-term behavior of gas storage using FLAC3D software. Nevertheless, there is potential for improvement by incorporating considerations for temperature, gas seepage, and cyclic loading effects. Addressing these factors could enhance the model’s applicability and accuracy in representing the complex conditions encountered in gas storage scenarios.

The application of creep models in real engineering projects and the determination of model parameters for rock masses are crucial aspects that need further attention. By addressing considerations like developing more closed-form solutions, implementing creep models into widely used commercial rock mechanics software, conducting more field validation studies where the presented creep models are applied to rock masses, developing methodologies or optimization techniques for robust and accurate determination of model parameters for rock mass, investigating how geological conditions, such as rock type, structure, and heterogeneity, influence the applicability and performance of different creep models, researchers can contribute to bridging the gap between theoretical developments in creep modeling and their practical application in engineering projects.

5 Conclusion

The different types of rock creep constitutive models were discussed, and their key characteristics were assessed. The models’ ability to simulate the accelerated phase of rock creep was also analyzed through the comparison of their performance with creep test results from various rock types. In this study, the applications of creep analysis in geomechanics and some case studies were mentioned. The following are the study’s main findings:

  • Empirical models typically rely on experimental tests with shorter durations than real engineering case studies. This disparity may cause an error between the predicted and measured creep deformations. The empirical models have limitations when it comes to accurately simulate the accelerated creep phase in rocks.

  • The mechanism-based models have proven successful in effectively simulating complete creep phases. These models often integrate various phenomena and factors, such as temperature effects, rock damage evolution, rock anisotropy, etc., to provide a more comprehensive representation of the time-dependent behavior of rocks. The grain-based creep models have also demonstrated advantages in the elaborate depiction of the development of cracking and damage progression at the micro-scale.

  • While many of the proposed models have been validated using experimental creep data, only a limited number have been developed to simulate the long-term behavior of underground constructions. To enhance their applicability and credibility, further investigation is essential to bridge the gap between theoretical advancements in creep modeling and their practical implementation in engineering projects.

  • Fractional derivative creep models have captured considerable attention from researchers due to their notable advantages, such as a small number of parameters, simplicity, and broad applicability. The Abel dashpot is utilized as a representation of the fractional derivative of the Newton dashpot and has been employed to simulate various phases of rock creep by adjusting the fractional order.

  • The findings from the comparative analysis in this research suggest that the damaged Abel dashpot, the exponential relationship between strain and time power function, and the power function exhibit the most accurate fitting with the accelerating phase of rock creep, whereas the polynomial function of degree 2 was observed to be less effective in simulating the beginning of the accelerating phase.

  • Presently, only a limited number of creep models have been proposed for rock masses. Rock mass behavior is influenced by various factors, including joint properties, the presence of underground water, and other geological and environmental conditions. To address the challenges and enhance the understanding of rock mass creep behavior, future research is essential.

  • Long-term stability of underground spaces such as tunnels, rock pillars, and gas storage constructed in high-stress conditions or weak and soft rock mass is one of the significant applications of creep analysis in geomechanics. The CVISC model is one of the popular models in analyzing long-term stability; in this model, the simulation of primary and secondary creep phases corresponds to the Burger model, while the plastic constitutive law is associated with the Mohr–Coulomb model. To study the long-term failure of rocks, it is advisable to utilize recently proposed constitutive models specifically designed to capture rock rupture.

  • Adopting appropriate creep parameters for rock mass has a significant influence on assessing the time-dependent behavior of rock mass. The back analysis techniques using long-time measured monitoring data were successfully used for finding rock mass creep parameters. Nevertheless, there is a pressing need for extensive research in this domain.